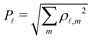Phase diagram of SALR fluids on spherical surfaces†
Stefano
Franzini
 *,
Luciano
Reatto
and
Davide
Pini
*,
Luciano
Reatto
and
Davide
Pini

Dipartimento di Fisica “A. Pontremoli”, Università di Milano, Via Celoria 16, 20133 Milano, Italy. E-mail: stefano.franzini93@gmail.com
First published on 18th November 2021
Abstract
We investigate the phase diagram of a fluid of hard-core disks confined to the surface of a sphere and whose interaction potential contains a short-range attraction followed by a long-range repulsive tail (SALR). Based on previous work in the bulk we derive a stability criterion for the homogeneous phase of the fluid, and locate a region of instability linked to the presence of a negative minimum in the spherical harmonics expansion of the interaction potential. The inhomogeneous phases contained within this region are characterized using a mean-field density functional theory. We find several inhomogeneous patterns that can be separated into three broad classes: cluster crystals, stripes, and bubble crystals, each containing topological defects. Interestingly, while the periodicity of inhomogeneous phases at large densities is mainly determined by the position of the negative minimum of the potential expansion, the finite size of the system induces a richer behavior at smaller densities.
1 Introduction
Colloids interacting through a combination of a short-range attraction and a long-range repulsive tail (SALR potential) can be obtained by combining electrostatic interactions described by the DLVO theory, which provide the long-range repulsive part, and depletion effects due to non-adsorbing crowders, such as polymers interspersed in the solution, which create a tunable short-range attraction.1,2 The interest in fluids with competing interactions stems from the theoretical prediction that their phase diagram would contain a plethora of inhomogeneous mesophases, such as cluster or bubble crystals, but also cylinders, lamellae, and even bicontinuous structures such as gyroids,3–7 although sampling some of these phases experimentally is still an open challenge.8The richness of this phase diagram is possible thanks to the unique competition between the attractive part of the potential, which induces the aggregation of the colloids, and its repulsive tail, which prevents global phase separation and promotes the formation of aggregates of limited size instead.
This phenomenon can also be observed in two-dimensional fluids of colloids adsorbed on a surface, for example on a liquid–liquid or air–liquid interface, in which case the phase diagram contains clusters, stripes and bubbles.9 Here attractive interactions can be mediated by the substrate through a variety of mechanisms such as capillary interactions, lateral depletion forces or Casimir attractions,10–13 while the repulsive part of the potential can still be explained by electrostatic forces.
Of particular interest to the present study are models in which particles of the SALR fluid are constrained to move on a curved surface, such as that of a sphere. These models can be used to represent protein inclusions on the surface of biological vesicles or micelles, or pickering emulsions, where solid colloids adsorb at the interface between two liquid phases (water and oil for example).14,15 Previous studies have shown that SALR fluids on a spherical surface still form patterns similar to the ones found in the planar case, providing a mechanism to obtain vesicles or colloidosomes covered with anisotropic patches with a controllable geometry.16,17
The possibility of exploiting the self-assembling properties of these fluids on a spherical substrate as a path to bottom-up production of patchy particles motivates us to study their phase diagram. Patchy particles are colloids that display anisotropic interactions either due to their shape or because of the presence on their surface of functionalized patches, from which they take their name.18 They find applications in multiple fields, such as in medicine, where they get used for targeted drug delivery,19 in material science, as building blocks for hierarchically self-assembled structures,20,21 and in industry, where they are used in a variety of emerging technologies.22 One of the major challenges in the field is the scalability of production techniques. Top-down manufacturing strategies, such as photolithography, tend to incur into size and processing limitations18 that new bottom-up techniques seek to overcome by self-assembling the target anisotropic particle.23
Previous studies on SALR fluids on a sphere16,17 focused on describing the patterns forming at different temperatures and densities using Monte Carlo simulations, however no phase diagrams have been proposed. Hence we use a mean-field density functional theory (DFT) to obtain the phase diagram of the SALR fluids. We show that at large enough densities the patterns can be predicted from the harmonic order of the absolute negative minimum found in the spherical harmonics series of the non-singular part of the potential.
The outline of this paper is as follows: in Section 2 we will present details of the SALR model, as well as the DFT functional and Monte Carlo simulations we have used to study it; in Section 3 we will first review results about the homogeneous phase and its instability region, we will then present a thorough investigation of the phase diagram according to DFT, and finally we will show some of the metastable phases and discuss the difference with respect to soft-core fluids forming microphases (such as the generalized Gaussian model of exponent 4, or GEM424); in Section 4 we will summarize our findings and discuss future perspectives.
2 Methods
2.1 The SALR model
In our model we describe particles constrained to a spherical surface and interacting via a two-body, isotropic potential v(r) given by a hard core followed by a short-range attractive and long-range repulsive (SALR) tail w(r), with r being the euclidean distance, which we model as the sum of two Yukawa functions of opposite signs: | (1) |
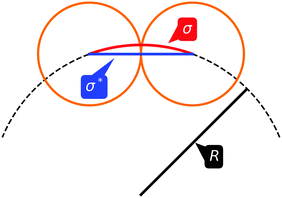
This definition introduces four different lengthscales: R is the radius of the sphere; the diameter  is defined in terms of the curvilinear diameter σ, i.e. the minimum geodesic distance two particles can achieve without overlapping (see Fig. 1); γ1/σ* and γ2/σ* are the inverse of the attractive and repulsive ranges respectively. We will measure lengths in units of R and set
is defined in terms of the curvilinear diameter σ, i.e. the minimum geodesic distance two particles can achieve without overlapping (see Fig. 1); γ1/σ* and γ2/σ* are the inverse of the attractive and repulsive ranges respectively. We will measure lengths in units of R and set 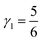 and
and  , so that we only need to specify one lengthscale, namely σ. Fixing the ratio γ1/γ2 = 2 is a well-established choice in the literature.3,9,25–27
, so that we only need to specify one lengthscale, namely σ. Fixing the ratio γ1/γ2 = 2 is a well-established choice in the literature.3,9,25–27
The other quantities which define the potential are the attractive amplitude ε, which we set to 1, and the repulsive amplitude A. Here we follow a previous work:3 we chose A so that  , where
, where ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) represents the coordinates of a point on the surface of a unitary sphere. In order to do so, we adopt the standard prescription of fixing the tail inside the hard-core region to its minimum, w(σ*). This gives us the following expression for the amplitude:
represents the coordinates of a point on the surface of a unitary sphere. In order to do so, we adopt the standard prescription of fixing the tail inside the hard-core region to its minimum, w(σ*). This gives us the following expression for the amplitude:
 | (2) |
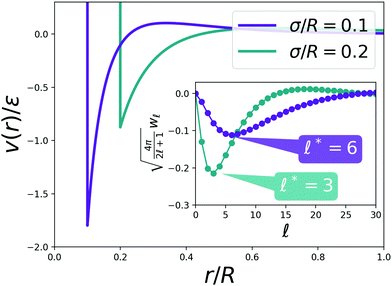
Examples of the potential can be seen in Fig. 2, where we also plot the spherical harmonics coefficients of the SALR tail, defined by:
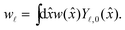 | (3) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ,0(
,0(![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) ), thanks to the rotational symmetry of the potential. Moreover we consider real spherical harmonics, since all the functions we consider are real. These coefficients display negative minima at
), thanks to the rotational symmetry of the potential. Moreover we consider real spherical harmonics, since all the functions we consider are real. These coefficients display negative minima at ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) * = 6 and
* = 6 and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) * = 3 respectively for σ/R = 0.1 and σ/R = 0.2: we will show in the next section that this property leads to the formation of microphases.
* = 3 respectively for σ/R = 0.1 and σ/R = 0.2: we will show in the next section that this property leads to the formation of microphases.
Of course, such a behavior is not peculiar to the values of γ1 and γ2 adopted here. An analysis of w![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) as a function of γ1 and γ2 has been provided in Fig. S1 and S2 of the ESI.† In short, for γ1 > γ2, the coefficients w
as a function of γ1 and γ2 has been provided in Fig. S1 and S2 of the ESI.† In short, for γ1 > γ2, the coefficients w![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) always feature a minimum at some
always feature a minimum at some ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) *, which is an increasing function of both γ1 and γ2. Interestingly, the depth of the minimum |w
*, which is an increasing function of both γ1 and γ2. Interestingly, the depth of the minimum |w![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) *| increases on decreasing γ2 at fixed γ1, whereas it displays a nonmonotonic dependence on γ1 at fixed γ2 so that, at given γ2, there is an optimal γ1 for microphase formation.
*| increases on decreasing γ2 at fixed γ1, whereas it displays a nonmonotonic dependence on γ1 at fixed γ2 so that, at given γ2, there is an optimal γ1 for microphase formation.
We also introduce here the other quantities which we are going to use throughout the paper. The density of N particles on the sphere is given by ρ = N/(4πR2). For simplicity we shall use the adimensional quantity ρR2. Since the particles have a finite size σ we also introduce the packing fraction η which is the ratio between the area occupied by the particles and the total surface area of the sphere. Using the equation for the area of a spherical cap of curvilinear diameter σ we obtain 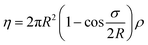 . Notice that while in principle η can vary between 0 and 1, the actual upper limit is given by the close packing fraction of the disks, which on a plane would be achieved by the hexagonal lattice packing
. Notice that while in principle η can vary between 0 and 1, the actual upper limit is given by the close packing fraction of the disks, which on a plane would be achieved by the hexagonal lattice packing  . The problem of finding the optimal packing of N disks on a spherical surface is still open, but since we will consider small σ/R ratios we can consider the planar close packing as an appropriate approximate upper boundary for the packing fraction η. We measure the temperature of the system in reduced units T* = kBT/ε, where kB is the Boltzmann constant. Notice that some of the attractive effective interactions that may lead to the SALR potential can be described by athermal phenomena (such as depletion), so the inverse temperature β = ε/kBT can also be interpreted as a concentration of depletants. Finally, since we will work in the grand canonical ensemble, we also introduce the chemical potential μ.
. The problem of finding the optimal packing of N disks on a spherical surface is still open, but since we will consider small σ/R ratios we can consider the planar close packing as an appropriate approximate upper boundary for the packing fraction η. We measure the temperature of the system in reduced units T* = kBT/ε, where kB is the Boltzmann constant. Notice that some of the attractive effective interactions that may lead to the SALR potential can be described by athermal phenomena (such as depletion), so the inverse temperature β = ε/kBT can also be interpreted as a concentration of depletants. Finally, since we will work in the grand canonical ensemble, we also introduce the chemical potential μ.
2.2 Density functional theory
The SALR potential is well known to form clusters and other inhomogeneous phases.3,9 The attractive part of the potential helps particles aggregate when the density of the fluid is large enough, however the repulsive tail keeps the size of the agglomerates finite, leading to a complex behavior in which particles arrange in a variety of different patterns depending on the thermodynamic state of the system.In the next section we will build the tools needed to make this qualitative argument for the emergence of inhomogeneous phases in SALR fluids more quantitative and obtain a phase diagram of the system, similarly to what was done for soft-core fluids on a sphere.28
To describe this system we use DFT, which expresses the grand potential βΩ of the fluid as a functional of its density profile ρ(![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) ). For interacting systems the exact functional is generally unknown, so we resort to an approximation where a simple mean-field perturbation is applied to a reference functional which contains the ideal-gas and the hard-core contributions. The former is known exactly, but the latter must again be obtained from some sort of approximation. A local density approximation (LDA) for the free energy of a fluid of hard disks can be obtained from equation of states known in the literature, which in turn have been derived by a variety of tools such as virial expansion and integral equations. Here we follow Archer9 in using the scaled-particle approximation. This gives us the following grand potential functional defined on the unit sphere S2
). For interacting systems the exact functional is generally unknown, so we resort to an approximation where a simple mean-field perturbation is applied to a reference functional which contains the ideal-gas and the hard-core contributions. The former is known exactly, but the latter must again be obtained from some sort of approximation. A local density approximation (LDA) for the free energy of a fluid of hard disks can be obtained from equation of states known in the literature, which in turn have been derived by a variety of tools such as virial expansion and integral equations. Here we follow Archer9 in using the scaled-particle approximation. This gives us the following grand potential functional defined on the unit sphere S2
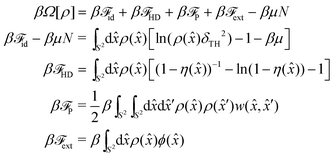 | (4) |
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) id is the ideal-gas free energy,
id is the ideal-gas free energy, ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) HD is the hard-disk contribution,
HD is the hard-disk contribution, ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) ext is the contribution due to the action of an external field ϕ and
ext is the contribution due to the action of an external field ϕ and ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) P is the excess free energy due to the contribution of the interaction potential. We have also introduced the thermal length
P is the excess free energy due to the contribution of the interaction potential. We have also introduced the thermal length 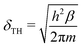 , h being the Planck constant and m being the mass of a particle.
, h being the Planck constant and m being the mass of a particle.
It should be noted that the functional we employ is quite crude with respect to more accurate functionals available in the literature, both for the hard-disk contribution and for the excess free energy term. For example, fundamental measure theory provides reference functionals for the hard-disk contribution that can accurately probe the fluctuations of the density profile even on the lengthscale of the disk diameter,29 while the LDA functional used here will only provide useful information about the profile on the much larger lengthscale of the meso-structures found in the system.9 Moreover we derive the reference functional from an equation of state which is valid for a planar system, and one may be concerned that a spherical system would require corrections to this equation of state and hence to the functional: however numerical solutions of the Percus–Yevick equation for hard disks on a sphere surface30 show that the correction is of second order in σ/R and does not have a large impact for the relatively small values of this parameter considered here.
On the other hand, the excess free energy due to the non-singular part of the potential which we use is known to be inaccurate when describing the critical point of the phase diagram, because it is the result of a mean-field approximation. This inaccuracy was brought forth in a simulation study of a three-dimensional SALR fluid in the bulk,31 which showed that the phase portrait is qualitatively different from the mean-field picture, especially as the high-temperature limit of the inhomogeneous phases is reached, and thermal fluctuations become important. In fact, both approaches predict the same kind of periodic structures, namely, cluster, tubular and lamellar phases in order of increasing density. However, according to the mean-field DFT all of the above phases survive up to the highest temperature at which the system is inhomogeneous, whereas in the simulation, as the temperature increases, the cluster phase melts first, to be followed by the tubular phase, and finally by the lamellae. Moreover, the whole inhomogeneous domain is shifted to higher densities compared to the mean-field DFT predictions.
The fact that these discrepancies should be traced back to the mean-field approximation was made clear in a subsequent theoretical investigation,32 in which fluctuations are taken into account on top of the mean-field result, and the phase diagram thus obtained displays the same qualitative features obtained in the simulations.
All the above concerns are well funded, but here we opt for simplicity, even though this may affect the accuracy of our findings. We will not be able to describe the internal structure of clusters and other meso-structures, and we will not obtain an accurate description of the critical point in the phase diagram using this functional. Nevertheless, we will be able to compute a qualitative phase diagram of the system. We will also be able to compare our results for the homogeneous fluid to simulations we performed.
Once we have a functional, we can obtain the equilibrium density profile by solving the Euler–Lagrange equations in search of a global minimum of the thermodynamic potential:
 | (5) |
In general these equations do not have a single solution for a given thermodynamic state, meaning that the system has different metastable states, so one needs to obtain the profiles of different minima and compare their grand potentials. Moreover, these equations are usually not analytically solvable, so the results are obtained through numerical methods.3,28,33
The homogeneous fluid is a special case in which one can obtain an analytical solution by plugging into the equations a flat density profile. Using a homogeneous density does not always lead to a stable solution, that is, the homogeneous fluid may not be a local minimum of the grand potential. However, one can always recast the functional in terms of the density of the homogeneous solution ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) and its packing fraction
and its packing fraction ![[small eta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c8.gif) , instead of the chemical potential μ. From the homogeneous solution of the Euler–Lagrange equations we obtain
, instead of the chemical potential μ. From the homogeneous solution of the Euler–Lagrange equations we obtain
 | (6) |
 | (7) |
Since we will study the phase diagram in terms of the density ρ of the fluid, rather than its chemical potential μ, this parametrization of μex will simplify the task of exploring the thermodynamic states of the system, by allowing us to obtain an approximate location of each sampled thermodynamic state in the phase diagram.
In order to solve the Euler–Lagrange equations we adapt the minimization algorithm previously developed for spherical systems28 of soft particles, which uses the SHTOOLS python module to compute spherical harmonics.34,35 This algorithm discretizes the density profile over a K × 2K grid of equispaced points in θ and ϕ, and proceeds to minimize the grand potential of the discretized density profile using an optimized version of the gradient descent algorithm. In this way we allow the algorithm to freely explore virtually any density profile, instead of limiting ourselves to a set of profiles obtained a priori. This is especially useful because the sphere topology prevents the formation of perfect lattices and the positions of the disclinations defects can be difficult to guess a priori. Moreover, it lets us explore unexpected metastable patterns, such as spiral phases, which would be discarded otherwise. The trade-off is that the algorithm still needs a set of initial density profiles from which to start the gradient descent, which must be chosen so as to explore as much of the free energy landscape as possible. We employ different starting conditions using (i) random patterns, (ii) striped patterns, (iii) high-density spots at the vertices of regular polyhedra, (iv) low-density spots at the vertices of regular polyhedra, and (v) profiles obtained from previous runs of the minimization algorithm. Even with this setup, it must be noted that there is no absolute guarantee that the final density profile is truly the global minimum. However, by comparing our results with previous ones we can achieve a good degree of confidence in their overall correctness. We set the parameter K determining the number of grid points at K = 256. For this choice of K, the algorithm is still rapidly convergent, as shown in Fig. S3 of the ESI,† while at the same time its results are basically unaffected by the discretization. In fact, halving or doubling K does not lead to appreciable changes in the grand potential at convergence, as displayed in Fig. S4 of the ESI.† Moreover, we show in Fig. S5–S7 of the ESI† that the equilibrium distribution at three different densities is also unaffected by halving or doubling K.
We still need to show that the system allows the formation of equilibrium inhomogeneous patterns. To do so, consider the functional we have described: the trivial homogeneous solution to the Euler–Lagrange equations is not necessarily a minimum of the grand potential. For this to be the case, it must satisfy the additional condition that the density profile ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) is stable with respect to arbitrary small fluctuations δρ(
is stable with respect to arbitrary small fluctuations δρ(![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) )
)
 | (8) |
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) ,
, ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) ′) given by
′) given by | (9) |
We remark that the above definition also contains the ideal gas contribution to c(![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) ,
, ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) ′). For a homogeneous fluid, the direct correlation function is isotropic, so c(
′). For a homogeneous fluid, the direct correlation function is isotropic, so c(![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) ,
, ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) ′) ≡ c(cos
′) ≡ c(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ), where θ = arccos(
θ), where θ = arccos(![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) ·
·![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) ′), and we can write it as a spherical harmonics series
′), and we can write it as a spherical harmonics series
 | (10) |
We can then use the spherical convolution theorem to rewrite the condition (8) as
 | (11) |
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) ) can be chosen arbitrarily, becomes
) can be chosen arbitrarily, becomes 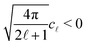 for any
for any ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . Finally, we can compute these coefficients explicitly to obtain
. Finally, we can compute these coefficients explicitly to obtain | (12) |
If the non-singular part of the interaction potential has any negative harmonic coefficients w![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , one can find some thermodynamic state for which the condition is not satisfied at least for some harmonic degree
, one can find some thermodynamic state for which the condition is not satisfied at least for some harmonic degree ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) .28,36 Then there will be a negative minimum of the coefficients w
.28,36 Then there will be a negative minimum of the coefficients w![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) at some harmonic order
at some harmonic order ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) * which defines the largest region in the phase diagram in which the homogeneous solution is unstable. This region will then necessarily be populated by some inhomogeneous phases which are stable solutions of eqn (5), so that the existence of a negative minimum w
* which defines the largest region in the phase diagram in which the homogeneous solution is unstable. This region will then necessarily be populated by some inhomogeneous phases which are stable solutions of eqn (5), so that the existence of a negative minimum w![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) * in the harmonic coefficients of the potential becomes the criterion for microphase separation to be possible. The boundary of this instability region is defined by
* in the harmonic coefficients of the potential becomes the criterion for microphase separation to be possible. The boundary of this instability region is defined by
 | (13) |
![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) at hand, it is not necessarily the equilibrium solution.
at hand, it is not necessarily the equilibrium solution.
As shown in the inset of Fig. 2, w![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) does indeed display a negative minimum at
does indeed display a negative minimum at ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) * = 6 for σ/R = 0.1 and at
* = 6 for σ/R = 0.1 and at ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) * = 3 for σ/R = 0.2, which means the phase diagram of the SALR system contains inhomogeneous phases.
* = 3 for σ/R = 0.2, which means the phase diagram of the SALR system contains inhomogeneous phases.
2.3 Monte Carlo simulations
In order to test the reliability of our mean-field approximation, we will use Monte Carlo (MC) simulations of the SALR model in the canonical ensemble, that is at a fixed number of particles N, surface area A, and temperature T, following the same framework we used for the GEM4 fluid.28The moves of the MC are rotations of a particle around a random axis orthogonal to its position vector. More specifically, we consider a particle of coordinates ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) = [cos
= [cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ
ϕ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, sin
θ, sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ
ϕ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, cos
θ, cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ] and use its position as the north pole of a new coordinate system, so that its new coordinates are
θ] and use its position as the north pole of a new coordinate system, so that its new coordinates are ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 0 = [0, 0, 1]. Then, we randomly choose a new value cos
0 = [0, 0, 1]. Then, we randomly choose a new value cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ′ for its third component z in the interval [1, 1 − δ] (setting the maximum stride of the particle to δ = 0.4R), and choose a direction for the move ϕ′ ∈ [0, 2π]. The new position in the new coordinate system is given by
θ′ for its third component z in the interval [1, 1 − δ] (setting the maximum stride of the particle to δ = 0.4R), and choose a direction for the move ϕ′ ∈ [0, 2π]. The new position in the new coordinate system is given by  . Finally we return to the original coordinate system by applying the rotation that satisfies
. Finally we return to the original coordinate system by applying the rotation that satisfies ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif)
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 0 =
0 = ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) , so that we obtain the new coordinates as
, so that we obtain the new coordinates as  .
.
Contrary to the GEM4 model and other soft-core fluids, the presence of a hard core in the SALR model presents the additional challenge of avoiding metastable configurations in which particles can easily get stuck: obtaining a faithful representation of the inhomogeneous phases through simulations at high density can be difficult and goes beyond the scope of this paper. Hence, our simulations will only focus on the homogeneous fluid in the low-density regime. This requires using a low number of particles, so we only sample the interval N ∈ [2, 150].
Each sampled trajectory contains 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps, but the first 150
000 steps, but the first 150![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps are discarded when computing the correlation functions, in order to allow the system to thermalize.
000 steps are discarded when computing the correlation functions, in order to allow the system to thermalize.
3 Results
3.1 Correlation functions and the λ-line
Before we consider the full phase diagram, we can characterize the homogeneous fluid. As discussed in the previous section, in this regime correlation functions are isotropic and can be computed directly from the functional. Once one has computed the direct correlation function c(![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) ,
, ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) ′), the total correlation function h(
′), the total correlation function h(![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) ,
, ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) ′) can be obtained by solving the Ornstein–Zernike equation38,39 for the spherical harmonics coefficients
′) can be obtained by solving the Ornstein–Zernike equation38,39 for the spherical harmonics coefficients | (14) |
 | (15) |
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) ,
, ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) ′), so that in (12) the hard-disk contribution has no dependence on the harmonic order
′), so that in (12) the hard-disk contribution has no dependence on the harmonic order ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . An alternative route to correlations is using the Percus test-particle method:40 using the functional defined in (4), we consider the action of a single particle fixed at the north pole of the sphere on the rest of the fluid, that is, we set ϕ(
. An alternative route to correlations is using the Percus test-particle method:40 using the functional defined in (4), we consider the action of a single particle fixed at the north pole of the sphere on the rest of the fluid, that is, we set ϕ(![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) ) = v(
) = v(![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) ). Then the equilibrium distribution for states above the λ-line is proportional to the radial distribution function g(r) = ρ(
). Then the equilibrium distribution for states above the λ-line is proportional to the radial distribution function g(r) = ρ(![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) )/ρ, and from this definition one can easily obtain the structure factor S
)/ρ, and from this definition one can easily obtain the structure factor S![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) using the previous relations.
using the previous relations.
In Fig. 3 we show an example of the radial distribution function obtained at T* = 1, σ/R = 0.1 and N = 75, comparing theory and simulation. Clearly, the chemical potential of the functional was adjusted so as to give the same density ρR2 = 5.96 of the canonical simulation. Theory is able to describe the first shell of neighboring particles (the peak at r/σ* = 1) and the long-range behavior of the correlation function well enough, however it is not able to completely capture the complexity of its short-range behavior; in particular, it underestimates the contact value and does not account for the shoulder at r/σ ≃ 2.5. This shoulder is related to the short-range structure due to the hard-core interaction. In fact, it disappears at lower densities such that N ≲ 50, whereas for N ≳ 100 it develops into a minimum between 1.5σ and 2σ and a maximum between 2σ and 2.5σ, corresponding to the second-neighbor shell of the g(r) of a hard-disk fluid, see Fig. S8 of the ESI,† which displays g(r) at several densities.
A similar structure has been obtained many times in bulk 3D systems with hard-core SALR potentials in the homogeneous region.25,40–43 At the same time, it is not surprising that it is not reproduced by the present DFT approach, in light of the fact that, as discussed in Section 2.2, the LDA adopted here for the hard-disk contribution to the grand potential is unable to describe the structure at lengthscales ∼σ. Clearly, the test-particle route in not sufficient to fix this shortcoming. To this purpose, a more accurate treatment based on fundamental measure theory would be needed.40
We quantify the agreement of theory and simulations by computing the mean square difference between the correlation functions computed with the two methods  , where K = 256 is the number of the sampled points. We plot Δ in the inset of Fig. 3: it shows that on average the error is small with respect to the absolute value of the sampled point, with differences between theory and simulations increasing near the λ-line.
, where K = 256 is the number of the sampled points. We plot Δ in the inset of Fig. 3: it shows that on average the error is small with respect to the absolute value of the sampled point, with differences between theory and simulations increasing near the λ-line.
In Fig. 4 we compare the structure factors28,44,45 obtained from theory and simulations for the same set of parameters. We find good agreement between the two at small harmonic orders ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , which account for the large-scale behavior of the system, and we stress especially that both theory and simulation predict the same value for the position
, which account for the large-scale behavior of the system, and we stress especially that both theory and simulation predict the same value for the position ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) * of the maximum (
* of the maximum (![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) * = 6 in the figure, in agreement with the prediction of eqn (12), (14) and (15)). This is important because the eventual divergence of this peak at larger densities signals the instability of the homogeneous fluid with respect to fluctuations of that harmonic order, giving a clue about the characteristics of the inhomogeneous phases found under the λ-line (in terms of temperatures). One expects the prediction of the theory to become unreliable9 at short length scales, corresponding to
* = 6 in the figure, in agreement with the prediction of eqn (12), (14) and (15)). This is important because the eventual divergence of this peak at larger densities signals the instability of the homogeneous fluid with respect to fluctuations of that harmonic order, giving a clue about the characteristics of the inhomogeneous phases found under the λ-line (in terms of temperatures). One expects the prediction of the theory to become unreliable9 at short length scales, corresponding to 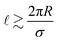 , but we find good agreement between theory and simulation even beyond this threshold.
, but we find good agreement between theory and simulation even beyond this threshold.
 | ||
Fig. 4 Comparison of the structure factors S![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) computed using the test particle approximation and Monte Carlo simulations at T* = 1, σ/R = 0.1 and N = 75 (ρR2 = 5.96). computed using the test particle approximation and Monte Carlo simulations at T* = 1, σ/R = 0.1 and N = 75 (ρR2 = 5.96). | ||
The λ-line itself can be obtained by using eqn (13). In Fig. 5 we plot the maximum temperature T* reached by the λ-line as a function of the ratio σ/R, both for the spherical and the planar case. The latter depends trivially on σ/R because of the factor R in the two-Yukawa tail of potential (1), so we isolate this factor in order to better show the differences between the two cases.
Similarly to what happens for the GEM4 fluids,28 the λ-line for the spherical system displays kinks corresponding to values of σ/R where the position of ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) * shifts (with
* shifts (with ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) * being the position of the negative minimum of the potential, or of the maximum of the structure factor). This also has consequences on the structure of the inhomogeneous phases found in each region, although the details of the phase diagram are not uniquely determined by the position of
* being the position of the negative minimum of the potential, or of the maximum of the structure factor). This also has consequences on the structure of the inhomogeneous phases found in each region, although the details of the phase diagram are not uniquely determined by the position of ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) *.
*.
3.2 The phase diagram
Using the functional developed in the previous sections we can now obtain theoretical predictions for the phase diagram of the SALR fluid. We search for the equilibrium density profile for different values of the mean density ρ, of the temperature T*, and of the ratio between the size of the particles and the radius of the sphere σ/R.The boundaries between two phases A and B are obtained by a Maxwell construction, i.e. by imposing the conditions μA = μB, βΩA = βΩB. The first condition can be rewritten in terms of the trial densities as ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) A =
A = ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) B. However, since the actual density of the system ρ is obtained a posteriori, we stress that ρA is not equal to ρB at the transition, leading to the appearance of a coexistence region that separates the two phases.
B. However, since the actual density of the system ρ is obtained a posteriori, we stress that ρA is not equal to ρB at the transition, leading to the appearance of a coexistence region that separates the two phases.
We also remark that, as detailed in our previous work,28,46 one cannot truly have a phase transition on a sphere, as it is a finite system, and even metastable phases can contribute to its thermodynamics. Instead of a discontinuity in the density ρ at the transition chemical potential, one expects a smooth crossover of ρ, which roughly corresponds to the coexistence regions defined by the Maxwell construction.
We start by considering the phase diagram in the ρ − T* plane, at σ/R = 0.1 corresponding to ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) * = 6, which we show in Fig. 6. Fixing a temperature below the critical one and moving from lower to higher densities, the fluid is initially homogeneous. However as density increases, it undergoes a series of transitions to different cluster crystal phases, in which the particles aggregate into clusters arranged on an ordered lattice. Contrary to the bulk cases,3,9 where only one kind of cluster crystal is found, the finite size of the sphere leads to the appearance of multiple geometries, characterized by having a different number of clusters (2, 6, 8, 9, 10, or 12).
* = 6, which we show in Fig. 6. Fixing a temperature below the critical one and moving from lower to higher densities, the fluid is initially homogeneous. However as density increases, it undergoes a series of transitions to different cluster crystal phases, in which the particles aggregate into clusters arranged on an ordered lattice. Contrary to the bulk cases,3,9 where only one kind of cluster crystal is found, the finite size of the sphere leads to the appearance of multiple geometries, characterized by having a different number of clusters (2, 6, 8, 9, 10, or 12).
As one approaches the center of the diagram, one encounters stripe patterns, in which particles arrange in alternating high density (replete) and low density (depleted) stripes around an axis. At σ/R = 0.1 we observe two such patterns: one with 4 replete and 3 depleted stripes, and another, its reciprocal, having 4 depleted and 3 replete stripes. We refer to them as the replete and depleted stripe patterns, respectively. Interestingly, contrary to what happens in the bulk in two9 and three dimensions,3 the stripe phases do not reach the top of the diagram, which is instead occupied by the 12-cluster crystal phase.
At even higher densities, one finds a bubble phase: particles form a percolating matrix in which depleted spots, dubbed bubbles, are arranged in an ordered manner. The 12-bubble configuration encountered for σ/R = 0.1 corresponds to an inverted 12-cluster configuration, with bubbles arranged in the same geometry as the clusters.
One can notice a symmetry through the center of the diagram, as phases on either side of the transition between the two stripe phases are the negative of each other: one stripe pattern is depleted where the other is replete, and vice-versa; and the same is true for the 12-cluster phase and the 12-bubble phase. This, however, is broken by the presence of the low-density cluster phases, which do not have corresponding bubble patterns. An explanation for this behavior will be proposed further on.
Notwithstanding the differences described above, the overall sequence of the cluster, stripe, and bubble phases is similar to that found in the two-dimensional bulk,9 and in both cases is driven by the presence of the hard-core part of the potential. While in soft-core fluids such as the GEM428 the density inside the clusters can grow indefinitely, and clusters actually become more localized as particles are added to the system, in the SALR fluid the hard core prevents particles from overlapping, forcing clusters to grow larger and larger. As the density increases, each phase is superseded by another one with higher packing efficiency. However, for the case at hand of a system confined on a spherical surface, also finite-size effects play a role, and entail a wider geometrical variability of such phases, and the presence of topological defects.
In the case of cluster and bubble phases, topological disclination defects can be understood as lattice points having a defective number of nearest neighbors,47 whereas stripe patterns also contain two disclination defects located at the poles of the sphere.48 While the variety of geometries encountered in the phase diagram manifests these topological defects in different ways, all obey the same conservation law which states that49
 | (16) |
 , while stripe patterns always contain two pole disclinations with charge 1.
, while stripe patterns always contain two pole disclinations with charge 1.
Another aspect in which the SALR model on a sphere differs from its bulk counterpart is the aforementioned presence of different cluster crystals for the same value of σ/R. This also marks a difference with respect to the GEM4 fluid on the sphere considered in a former study:28 in that case, only one kind of cluster crystal was observed at each fixed value of σ/R, independently of density or temperature. More specifically, our choice of  was made to obtain
was made to obtain ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) * = 6 at σ/R = 0.1: for this value of
* = 6 at σ/R = 0.1: for this value of ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) * the phase diagram of the GEM4 fluid only contains configurations with 12 clusters, whereas in the SALR fluid we also observe configurations with fewer clusters, albeit the expected 12-cluster configuration still occupies the largest portion of the region of the phase diagram inhabited by cluster crystals.
* the phase diagram of the GEM4 fluid only contains configurations with 12 clusters, whereas in the SALR fluid we also observe configurations with fewer clusters, albeit the expected 12-cluster configuration still occupies the largest portion of the region of the phase diagram inhabited by cluster crystals.
The explanation of this more complex behavior could lie in the presence of the short-range attraction, which allows particles to aggregate into clusters even at low densities, whereas clustering in purely repulsive systems emerges only as a collective behavior at high densities. In fact, we even managed to find a metastable phase having a single cluster: this configuration never becomes the equilibrium distribution, as it is superseded by either the 2-cluster configuration or the homogeneous phase at all densities; however, its existence still proves that, contrary to systems with purely repulsive interactions, the attractive part of the SALR potential can indeed stabilize isolated structures.
To further illustrate the differences between the low-density and high-density behavior of the system, we introduce the local grand potential βωD, which is the grand potential of a single cell in our grid
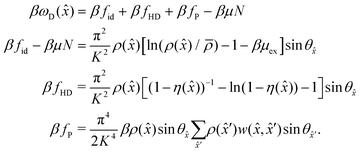 | (17) |
In Fig. 7 we plot the density profiles and the local grand potential around the centers of clusters in different configurations (1 cluster, 2 clusters, and 12 clusters), and at different densities ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) . We recall that
. We recall that ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) does not generally coincide with the actual average density observed in the system, but is an intuitive way of parametrizing the chemical potential.
does not generally coincide with the actual average density observed in the system, but is an intuitive way of parametrizing the chemical potential.
Isolated clusters at low densities are all surrounded by an unstable ring, denoted by a positive local grand potential at the interface between the cluster itself and the depleted exterior: this is due to a smaller number of neighbors for particles at the interface, as well as to the repulsive tail of the potential of particles at the center of the cluster. However, the presence of a local frustration actually helps the overall structural integrity of the cluster: the number of frustrated particles is proportional to the diameter γ of the cluster, while the surface of the cluster itself is proportional to γ2. Because of this, splitting a cluster into two smaller ones covering the same area leads to an increase of the number of frustrated particles proportional to  .
.
Interestingly, the 12-cluster crystal does not display this characteristic at higher densities: the stability of the configuration is ensured by the presence of neighboring clusters pushing against each other, which also leads to deeper local grand potential wells. Being able to exploit a different clustering mechanism, the SALR fluid displays unexpected cluster phases at low densities, but it recovers the same configurational behavior of the GEM4 fluid at higher densities, where collective effects become dominant. This also offers an explanation for the asymmetry of the phase diagram, i.e. the absence of 2, 6, 8, 9, and 10-bubble phases: bubble configurations only rely on collective effects for stability, exploiting the long-range repulsions between particles. This only allows the formation of patterns with the symmetry dictated by ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) *.
*.
This can be seen in Fig. 8, where we analyze some of the quantitative features of the inhomogeneous phases, measured at T* = 0.5 and σ/R = 0.1. We also compare the properties of the stable phases to those of two metastable ones, shown at the bottom of the figure: a single cluster phase and a helix phase, which we were able to obtain thanks to the unconstrained minimization algorithm we employed. Helix phases have been previously observed in SALR fluids, not only on spherical surfaces,16,50 but also in 3D systems confined inside pores of various shapes.51,52 However, contrary to what is reported for the cases considered there,16,51 the helix phase which we observe is never the equilibrium distribution on the sphere.
In the top panel we compare the total power at harmonic degree ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) * = 6,
* = 6,  of different phases. This quantifies the degree to which the geometry of the observed patterns overlaps with spherical harmonics of degree
of different phases. This quantifies the degree to which the geometry of the observed patterns overlaps with spherical harmonics of degree ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) *, all characterized by the same overall periodicity.
*, all characterized by the same overall periodicity.
We observe that, at high density, the range over which a phase is stable roughly corresponds to the range of densities at which its P![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) * is the largest among those of the other phases. However this is not quite true at lower densities, further emphasizing the presence of two different stability mechanisms between the two regimes. The helix phase, which is only present at higher densities, has a much lower P
* is the largest among those of the other phases. However this is not quite true at lower densities, further emphasizing the presence of two different stability mechanisms between the two regimes. The helix phase, which is only present at higher densities, has a much lower P![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) * with respect to the other phases and never becomes the equilibrium one. This suggests that phases with a large P
* with respect to the other phases and never becomes the equilibrium one. This suggests that phases with a large P![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) * are better able to exploit the characteristic lengthscale introduced by the potential and thus be more stable.
* are better able to exploit the characteristic lengthscale introduced by the potential and thus be more stable.
In the middle panel we show the maximum packing fraction for the various phases. For all configurations η is much smaller than the close-packing fraction on the plane: this physical behavior is recovered despite the fact that ηCP ≃ 0.9069 is not a parameter of our density functional theory, in fact according to the scaled-particle approximation used here, all values of η up to η = 1 would be allowed. Notice that here we refer to the planar value for the close-packing fraction of hard disks, because its spherical counterpart depends on the number of particles and is not known for large ensembles.53,54 One can also notice that the densities achieved by the system inside the mesoscopic structures are compatible with crystal states,55 although we are not able to probe their internal structure due to the local density approximation.
Finally, in the bottom panel we show the typical size γ of the mesoscopic structures, measured as the half width at half maximum of the high-density patches for the cluster, replete stripe and helix phases, and of the low-density patches for the depleted stripe and bubble phases. Interestingly, none of the lower density cluster phases (i.e. all except the 12-cluster crystal) are stable beyond γ/σ = 3, which roughly corresponds to the position of the maximum of the tail potential, as shown in Fig. 2. For higher density phases we observe that symmetric patterns (i.e. 12 clusters and 12 bubbles, or replete stripes and depleted stripes) display a roughly symmetrical behavior of γ, simply because depleted patches become smaller and smaller as particles are added to the system.
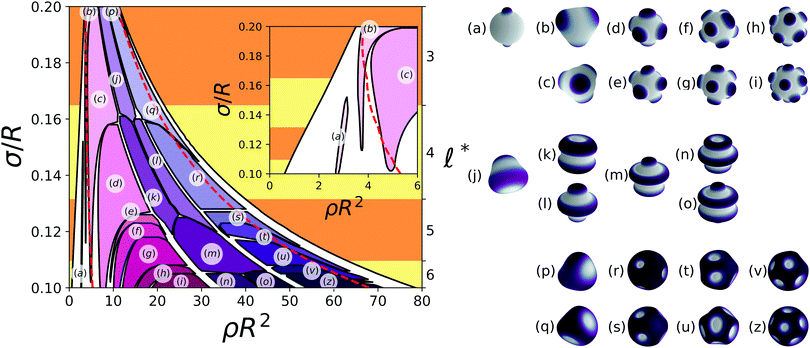
Next we consider the phase diagram in the ρ − σ/R plane, at fixed temperature T* = 0.5, shown in Fig. 9. The homogeneous fluid occupies the low- and high-density regions, but the middle section of the diagram is occupied by a plethora of inhomogeneous patterns. We can partition this region into three domains: at lower densities we encounter cluster crystals, the middle portion is occupied by stripe patterns, and at high densities we find bubble phases. As observed for the phase diagram in the ρ − T* plane, one can trace an approximate symmetry axis passing through the middle of the stripe region, so that phases on opposite sides, excluding the cluster crystals at low densities, are the negative of each other. In particular one notices that some of the stripe phases are their own negative, so that they extend over a larger region on the two sides of the symmetry axis.
We also notice that, as for the previously studied GEM4 fluid,28 the equilibrium phases are roughly determined by the value of ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) *. For example, the region of stability of each stripe pattern roughly corresponds to a single
*. For example, the region of stability of each stripe pattern roughly corresponds to a single ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) * domain of Fig. 9. Cluster crystal phases, instead, display a peculiar behavior, whereby at low densities they extend a tail into regions of lower σ/R. This means that cluster phases characterized by a smaller
* domain of Fig. 9. Cluster crystal phases, instead, display a peculiar behavior, whereby at low densities they extend a tail into regions of lower σ/R. This means that cluster phases characterized by a smaller ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and a larger inter-cluster distance than the optimal ones for the value of σ/R at hand do not disappear abruptly, but still survive at low density, in line with the discussion of the case σ/R = 0.1 carried out above.
and a larger inter-cluster distance than the optimal ones for the value of σ/R at hand do not disappear abruptly, but still survive at low density, in line with the discussion of the case σ/R = 0.1 carried out above.
We conclude our assay of the phase diagram by remarking that the phases we find are qualitatively consistent with previous studies of the SALR model through MC simulations,16 albeit some differences in the implementations of the SALR potential prevent us from comparing the phase diagram to the phases found in that study on a one-to-one basis. While we are able to find some interesting metastable patterns (such as the single cluster phase, or the helix phase), we did not observe labyrinth patterns or stable helix phases.16,51 At least in the case of labyrinth patterns, our inability to obtain them may be due to the fact that we consider values of σ/R much larger than those at which these phases are predicted to occur (i.e. σ/R = 0.0116).
4 Conclusions
In this work we have studied the phase diagram of a model fluid of hard particles constrained to the surface of a sphere interacting via a short-range attractive potential with a long-range repulsive tail, which is known to undergo microphase separation in both the 3D and the 2D bulk. We computed the equilibrium configurations of a wide set of thermodynamic states, changing the density ρ, the temperature T, and the ratio between the particle diameter and the radius of the sphere σ/R. To do so we performed a fully unconstrained numerical minimization of a simple mean-field functional. The sequence of the equilibrium inhomogeneous phases in the phase diagram from lower to higher densities is consistent with previous studies in the bulk,9 showing a sequence of clusters, stripes, and bubbles. However, in this case one also needs to consider the additional lengthscale of the sphere radius, as well as its topology: these two factors introduce a more complex behavior in the phase diagram. One consequence is that even regular patterns include ineliminable topological defects (disclinations),49 which manifest as structures with a number of neighbors smaller than that expected in the plane for cluster and bubble crystals, and with pole defects in stripe patterns. The second consequence is that by changing the ratio σ/R one finds patterns with different numbers of clusters, stripes, or bubbles. Nevertheless, similarly to the bulk case, we find that the periodicity of the patterns can still be roughly determined from the properties of the non-singular part of the interaction potential. Namely, in this case the periodicity is related to the harmonic degree![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) * of the negative minimum of the spherical harmonic expansion of the potential. Interestingly, however, we find that this is not the case for the cluster phases at low density, which display density modulations of lengthscale larger than expected, due to the fact that in these phases clustering is achieved via the short-range attraction, rather than through a collective phenomenon mediated by long-range repulsions.
* of the negative minimum of the spherical harmonic expansion of the potential. Interestingly, however, we find that this is not the case for the cluster phases at low density, which display density modulations of lengthscale larger than expected, due to the fact that in these phases clustering is achieved via the short-range attraction, rather than through a collective phenomenon mediated by long-range repulsions.
Here we fixed the values of γ1 and γ2 with respect to the σ/R parameter, in order to simplify the phase diagram. However, it is not necessary to do so: one could as well explore the configurations obtained by varying these two parameters independently. If this is done by preserving the overall qualitative structure of the potential (i.e. by still requiring short-range attractions and long-range repulsions), we expect that this operation would only change the value of ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) *, giving birth to structures (clusters, bubbles, and stripes) with different periodicity. It may also be possible to tune the parameters in order to make some metastable phases (such as the helix one) the equilibrium ones, at least in some regions of the phase diagram. If one relaxes the requirements about the specific shape of the potential, one can also obtain hard-core particles interacting via purely repulsive potentials, which can still induce the formation of inhomogeneous patterns.56–60
*, giving birth to structures (clusters, bubbles, and stripes) with different periodicity. It may also be possible to tune the parameters in order to make some metastable phases (such as the helix one) the equilibrium ones, at least in some regions of the phase diagram. If one relaxes the requirements about the specific shape of the potential, one can also obtain hard-core particles interacting via purely repulsive potentials, which can still induce the formation of inhomogeneous patterns.56–60
It is important to note that our theory, while being useful to obtain a qualitative picture of the phase diagram, is still quite crude with respect to more advanced ones (such as fundamental measure theory), so the results should not be expected to be quantitatively accurate.
Nevertheless, we remark that our work gives a clear blueprint for devising interaction potentials between particles to induce microphase formation: the phase diagrams we derived show the importance of tuning the value of ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) * to control the symmetry of the inhomogeneous patterns. Our results also highlight the fact that clusters, stripes, and bubbles of the selected symmetry are stable over a wide range of densities and temperatures, and are not susceptible to small changes in the ratio σ/R. We believe all of these observations will be helpful to scientists who aim at building self-assembling patchy particles by design.
* to control the symmetry of the inhomogeneous patterns. Our results also highlight the fact that clusters, stripes, and bubbles of the selected symmetry are stable over a wide range of densities and temperatures, and are not susceptible to small changes in the ratio σ/R. We believe all of these observations will be helpful to scientists who aim at building self-assembling patchy particles by design.
A complementary study to the one presented here could investigate the dynamical aspects of microphase separation in the same model fluid, using classical dynamic density functional theory61,62 to analyze the way in which the system reaches equilibrium and the transitions between different phases. This could lead to interesting results, as the ordered equilibrium configurations we found in the phase diagram were in close competition with a multitude of metastable phases, such as the helix phase shown in Fig. 8, where the system could easily become stuck indefinitely for kinetic reasons, as simulations seem to suggest. Another interesting dynamical aspect that may be studied is particle diffusion between different clusters.
Other future venues of investigation could explicitly include the interaction between the substrate and the particles embedded in it, as done for a similar model in a former study.63 In this picture the short-range attraction could arise as an effective interaction mediated by the curvature induced in the substrate by the presence of an embedded particle: one could then study not only microphase separation, but also the resulting shape of the substrate at equilibrium.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
One of the authors (S. F.) wishes to thank Laboratorio di Calcolo e Multimedia (LCM) for providing machine time on their cluster. One of the authors (D. P.) acknowledges the financial support by Università degli Studi di Milano, project No. PSR2019_DIP_008-Linea 2.References
- H. Sedgwick, S. U. Egelhaaf and W. C. K. Poon, J. Phys.: Condens. Matter, 2004, 16, S4913 CrossRef CAS.
- E. Mani, W. Lechner, W. K. Kegel and P. G. Bolhuis, Soft Matter, 2014, 10, 4479 RSC.
- D. Pini and A. Parola, Soft Matter, 2017, 13, 9259 RSC.
- A. Ciach, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 061505 CrossRef CAS PubMed.
- A. Ciach and W. T. Góźdź, Condens. Matter Phys., 2010, 13, 23603 CrossRef CAS.
- A. Ciach, J. Pekalski and W. T. Góźdź, Soft Matter, 2013, 9, 6301 RSC.
- M. Edelmann and R. Roth, Phys. Rev. E, 2016, 93, 062146 CrossRef PubMed.
- C. P. Royall, Soft Matter, 2018, 14, 4020 RSC.
- A. J. Archer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 031402 CrossRef.
- N. Dan, P. Pincus and S. A. Safran, Langmuir, 1993, 9, 2768 CrossRef CAS.
- R. R. Netz, J. Phys. I, 1997, 7, 833 CrossRef CAS.
- C. van der Wel, A. Vahid, A. Šarić, T. Idema, D. Heinrich and D. J. Kraft, Sci. Rep., 2016, 6, 32825 CrossRef CAS.
- N. Destainville, M. Manghi and J. Cornet, Biomolecules, 2018, 8, 104 CrossRef PubMed.
- Z. Rozynek, A. Mikkelsen, P. Dommersnes and J. O. Fossum, Nat. Commun., 2014, 5, 3945 CrossRef CAS PubMed.
- K. L. Thompson, M. Williams and S. P. Armes, J. Colloid Interface Sci., 2015, 447, 217 CrossRef CAS.
- G. J. Zarragoicoechea, A. G. Meyra and V. A. Kuz, Mol. Phys., 2009, 107, 549 CrossRef CAS.
- A. G. Meyra, G. J. Zarragoicoechea and V. A. Kuz, Mol. Phys., 2010, 108, 1329 CrossRef CAS.
- A. B. Pawar and I. Kretzschmar, Macromol. Rapid Commun., 2010, 31, 150 CrossRef CAS PubMed.
- Z. Poon, S. Chen, A. C. Engler, H. Il Lee, E. Atas, G. vonMaltzahn, S. N. Bhatia and P. T. Hammond, Angew. Chem., Int. Ed., 2010, 49, 7266 CrossRef CAS PubMed.
- B. Fang, A. Walther, A. Wolf, Y. Xu, J. Yuan and A. Müller, Angew. Chem., Int. Ed., 2009, 48, 2877 CrossRef CAS PubMed.
- I. C. Gârlea, E. Bianchi, B. Capone, L. Rovigatti and C. N. Likos, Curr. Opin. Colloid Interface Sci., 2017, 30, 1 CrossRef.
- C. Liddell, C. Summers and A. Gokhale, Mater. Charact., 2003, 50, 69 CrossRef CAS.
- S. C. Glotzer, Science, 2004, 306, 419 CrossRef CAS PubMed.
- B. M. Mladek, D. Gottwald, G. Kahl, M. Neumann and C. N. Likos, Phys. Rev. Lett., 2006, 96, 045701 CrossRef PubMed.
- D. Pini, G. Jialin, A. Parola and L. Reatto, Chem. Phys. Lett., 2000, 327, 209 CrossRef CAS.
- A. Imperio and L. Reatto, J. Phys.: Condens. Matter, 2004, 16, S3769 CrossRef CAS.
- D. F. Schwanzer and G. Kahl, J. Phys.: Condens. Matter, 2010, 22, 415103 CrossRef PubMed.
- S. Franzini, L. Reatto and D. Pini, Soft Matter, 2018, 14, 8724 RSC.
- R. Roth, K. Mecke and M. Oettel, J. Chem. Phys., 2012, 136, 081101 CrossRef PubMed.
- S. Lishchuk, Phys. A, 2006, 369, 266 CrossRef.
- Y. Zhuang, K. Zhang and P. Charbonneau, Phys. Rev. Lett., 2016, 116, 098301 CrossRef PubMed.
- A. Ciach, Soft Matter, 2018, 14, 5497 RSC.
- D. Pini, A. Parola and L. Reatto, J. Chem. Phys., 2015, 143, 034902 CrossRef PubMed.
- M. Wieczorek, M. Mesch, E. S. D. Andrade, I. Oshchepkov, B. Xu and A. Walker, Shtools/Shtools: Version 4.1, 2017 Search PubMed.
- M. Frigo and S. Johnson, Proc. IEEE, 2005, 93, 216 Search PubMed.
- C. N. Likos, A. Lang, M. Watzlawek and H. Löwen, Phys. Rev. E, 2001, 63, 031206 CrossRef CAS.
- A. J. Archer, C. N. Likos and R. Evans, J. Phys.: Condens. Matter, 2004, 16, L297 CrossRef CAS.
- J. P. Hansen and I. R. McDonald, Theory of Simple Liquids, 3rd edn, Academic, New York, 2006 Search PubMed.
- G. Tarjus, F. Sausset and P. Viot, Statistical Mechanics of Liquids and Fluids in Curved Space, Wiley-Blackwell, 2011, pp. 251–310 Search PubMed.
- A. J. Archer, D. Pini, R. Evans and L. Reatto, J. Chem. Phys., 2007, 126, 014104 CrossRef CAS PubMed.
- J.-M. Bomont, J.-L. Bretonnet and D. Costa, J. Chem. Phys., 2010, 132, 184508 CrossRef.
- J.-M. Bomont and D. Costa, J. Chem. Phys., 2012, 137, 164901 CrossRef PubMed.
- J.-M. Bomont, D. Costa and J.-L. Bretonnet, Phys. Chem. Chem. Phys., 2017, 19, 15247 RSC.
- A. L. Božič and S. Čopar, Phys. Rev. E, 2019, 99, 032601 Search PubMed.
- A. Božič, S. Franzini and S. Čopar, Phys. Fluids, 2021, 33, 047109 Search PubMed.
- T. L. Hill, Thermodynamics of Small Systems, Dover Publications, 2013 Search PubMed.
- T. Needham, Visual Complex Analysis, Oxford University Press, Oxford, 2000 Search PubMed.
- M. Monastyrsky, Riemann, Topology, and Physics, Birkhäuser, Boston, 1999 Search PubMed.
- V. Koning and V. Vitelli, Crystals and Liquid Crystals Confined to Curved Geometries, Wiley-Blackwell, 2016, ch. 19, pp. 369–385 Search PubMed.
- J. Pekalski and A. Ciach, Soft Matter, 2018, 148, 174902 Search PubMed.
- J. Pekalski, E. Bildanau and A. Ciach, Soft Matter, 2019, 15, 7715 RSC.
- H. Serna, E. G. Noya and W. T. Góźdź, Soft Matter, 2020, 16, 718 RSC.
- K. Zhang, IEEE Trans. Inf. Theory, 2017, 63, 4572 Search PubMed.
- J. Károli Böröczky and G. Wintsche, Discrete and Computational Geometry, Springer, 2003, pp. 235–251 Search PubMed.
- A. Mulero, C. Galán, M. I. Parra and F. Cuadros, Theory and simulation of hard-sphere fluids and related systems, Springer, 2008, pp. 37–109 Search PubMed.
- M. A. Glaser, G. M. Grason, R. D. Kamien, A. Košmrlj, C. D. Santangelo and P. Zhierl, EPL, 2007, 78, 46004 CrossRef.
- G. Pauschenwein and G. Kahl, Soft Matter, 2008, 4, 1396 RSC.
- G. Pauschenwein and G. Kahl, J. Chem. Phys., 2008, 129, 174107 CrossRef PubMed.
- J. Fornleitner and G. Kahl, EPL, 2008, 82, 18001 CrossRef.
- J. Fornleitner and G. Kahl, J. Phys.: Condens. Matter, 2010, 22, 104118 CrossRef PubMed.
- U. M. B. Marconi and P. Tarazona, J. Chem. Phys., 1999, 110, 8032 CrossRef CAS.
- A. J. Archer and R. Evans, J. Chem. Phys., 2004, 121, 4246 CrossRef CAS PubMed.
- M. O. Lavrentovich, E. M. Horsley, A. Radja, A. M. Sweeney and R. D. Kamien, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 5189 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sm01257f |
| This journal is © The Royal Society of Chemistry 2022 |