Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Advances in predictive chemistry enable a multi-scale rational design approach for biofuels with advantaged properties†
Katherine S.
Lockwood
a,
Sheikh F.
Ahmed
b,
Nabila A.
Huq
b,
Sadie C.
Stutzman
 a,
Thomas D.
Foust
a,
Thomas D.
Foust
 *bc and
Nicole J.
Labbe
*ad
*bc and
Nicole J.
Labbe
*ad
aDepartment of Mechanical Engineering, University of Colorado Boulder, Boulder, CO, USA
bNational Bioenergy Center, National Renewable Energy Laboratory, Golden, CO, USA
cDr Thomas D. Foust, Address: Center 5100, Catalytic Carbon Transformation and Scale-up Center, National Renewable Energy Laboratory, 15013 Denver West Parkway Golden, CO 80401-3305, USA. E-mail: Thomas.Foust@nrel.gov; Tel: +1(303) 384-7755
dDr Nicole J. Labbe, UCB 427–Mechanical Engineering, 1111, Engineering Drive, Boulder, CO 80309-0427, USA. E-mail: Nicole.Labbe@colorado.edu; Tel: +1(303) 735-4821
First published on 14th October 2022
Abstract
Recent advances in computational resources and algorithm development have spurred progress toward rational chemical design. However, progress towards automated rational chemical design in fuel development and gas phase chemical systems in general have fallen behind other fields such as pharmaceuticals and material discovery. In this manuscript, recent advancements in automated fuel ignition/gas phase reaction kinetics tool development are leveraged to create a systematic process to develop reaction mechanisms for biofuel ignition properties and apply these mechanisms to practical applications to understand the link between chemical structure and observable chemical phenomena. The proof-of-concept application of this work uses our modeling methodology to extract the chemical rational for disparate ignition behavior between two linear alcohols: n-butanol and n-pentanol. Our methodology can accurately predict the ignition behavior of both fuels across wide temperature ranges without any influence of experimental data or adjustment, and for the first time, can successfully pinpoint the differences in ignition behavior to the δ-pentanol carbon site. This work is demonstrated in the context of low carbon biofuels and accurate prediction of ignition delay times to show the versatility and utility of this method that can also be applied to many other sustainable gas phase reaction applications, including CO2 reduction and utilization approaches.
Introduction
With advances in both computational resources and more sophisticated algorithm development in recent years, approaches toward chemical modeling have also changed1 to include an increasing emphasis on rational chemical design and predictive chemical modeling. While notable examples of this have been applied to materials design,2 pharmaceutical discovery,3 organic synthesis,4,5 and catalytic selectivity,6 predictive model development for biofuel development and other sustainable gas phase chemical processes has had comparatively less success with predictive computational chemistry. Circular economy approaches that utilize gas phase reaction systems such as CO2 reduction and utilization processes is a sustainable gas phase chemical field that could benefit from advances in predictive gas phase reaction modeling techniques developed here.One of the largest impediments for progress in predictive modeling is the automation of gas phase reaction mechanisms given the vastness of the reaction schemes. The gas-phase nature of these systems provides more opportunity for unique combinatorial reactions, in addition to being in an environment where particularly reactive free-radicals can exist in large numbers. Combustion and fuel design provides an ideal example of the complications associated with gas phase reacting systems. Practical transportation fuels such as gasoline or diesel are mixtures of hundreds of unique chemical species, and while in a flame, undergo hundreds of thousands of unique chemical reactions whilst creating tens of thousands of additional intermediate species. The challenge of creating models for combustion is compounded when considering novel biofuel development where vast experimental data sets are not readily available for model validation testing.
Despite the reaction complexity, fuel design is a field that is ideally suited for predictive gas phase reaction modeling. Traditional approaches to new chemical and fuel development such as high throughput screening for parameters of interest followed by extensive testing and certification can be very time and resource intensive, which serves as an impediment to new chemical and fuel development. This is especially true for fuels and chemicals produced from biomass. The introduction of oxygen functionality greatly increases the variety and number of potential chemicals and fuels that require screening, making new chemical or fuel introduction from biomass a daunting endeavor using traditional screening-based approaches. However, rapid accurate kinetic model development could allow fuel scientists to explore and explain gas phase reaction phenomena over a wide variety of conditions, and thus identify key fuel candidates without the time or expense of traditional testing and certification.
Given the benefits of chemical modeling for rational fuel design, in addition to the complexity of gas-phase chemistry for combustion, this manuscript will focus on combustion chemistry as the demonstration application. Efforts to predict the chemistry of combustion have a rich history. While experiments have been devised to directly measure reaction rate constants in the gas phase7–10 the majority of mechanism development has been based in modeling and theory.11,12 These efforts generally fall into two different categories of work: estimation methods and electronic structure theory methods.
The quickest method of reaction mechanism development is through estimation methods, where either the reaction class13–15 or molecular functional groups16 are used to estimate reaction rate constants. These estimation methods have performed well for certain reaction classes,13–16 allowing for the rapid generation of kinetic mechanisms capable of accurately predicting properties such as flame speeds, ignition timing, and speciation data for a wide variety of molecules. One downside of rate coefficient estimation methods is they are not broadly applicable for reaction classes that are highly pressure-sensitive including pyrolysis and low-temperature ignition chemistry. In other cases, estimation methods may produce reaction rates with large errors if the basis for estimation is not ideally suited for the reaction at hand.17,18 As a result, these estimation-based mechanisms are often a good starting point but require rate tuning to reproduce experimental data targets for accuracy. This limits the suitability of estimation-based approaches for rational biofuel design.
Alternatively, electronic structure theory combined with reaction rate theory may be used to directly calculate rate constants. High-fidelity methods have reported uncertainties in reaction barriers and molecular energetics as low as ±0.3 kcal mol−119 increasing reliability of theoretically calculated rates over estimations. However, higher accuracy electronic structure theory methods, such as coupled-cluster methods scale as N7 (where N is a measure of the system size) which highlights the tradeoff between accuracy and computational cost.20 Thus, utilizing computational chemistry methods can become computationally prohibitive for large mechanisms and hence not directly well suited for rational biofuel design either.
Recent advances in automation of combustion chemistry have produced several tools for rapid mechanism generation. Automatic mechanism generators, such as Reaction Mechanism Generator (RMG) 21–23 and EXGAS,24 use group additivity methods in conjunction with rate-based algorithms to identify all reactions of importance for a given fuel and set of reaction conditions, and export estimates reaction rates for all the newly identified reactions. This automates the otherwise tedious human-based efforts for estimation-based mechanism development. Other works have focused on speeding up electronic structure theory methods, including automatic identification of reactive potential energy surfaces (PESs)25 and reaction rate calculations.26 Perhaps the closest effort to theory-based mechanism full automation is AutoMech,27 which calculates rate constants for the unimolecular reactions of a given molecule using a high-level theoretical approach. These tools have made rate generation significantly more accessible, but currently lack a direct link for use in practical design applications, where molecules with large numbers of heavy atoms prevail as is the case for many practical biofuels. Hence the novel approaches outlined in this manuscript allow us to extend quantum methods to advantaged biofuels developent.
Machine learning methods have tried to bridge the gap between chemical structure and direct application. One of several examples of this is the YSI Estimator28–30 and ALFABET31,32 tools out of the National Renewable Energy Laboratory. Both tools use machine learning techniques and curated yield sooting index (YSI) and bond dissociation energies (BDE) respectively to predict these properties based on molecular structure. While often successful, these tools are empirically derived and do not give fundamental understanding of why structure influences these properties. Additionally, these methods do have points of failure, as highlighted in a study by Kim et al.33 on methyl cyclohexenes. The YSI Estimator was found to fail at accurately predicting YSI trends for methyl cyclohexenes, and it was determined that this was due to the ability of methyl cyclohexenes to undergo retro Diels Alder reactions. Errors such as these would be avoided by direct connection to fundamental kinetics rather than empirical data fitting.
In this manuscript, we leverage recent advances in predictive gas phase chemistry tool development to provide a systematic methodology which calculates reaction mechanisms for gas phase reactive systems and apply these mechanisms to understand the link between chemical structure and application. This methodology is:
1. Universal: this technique should work for any gas phase reaction system regardless of chemical formula. However the selection of reaction systems to study will be limited by the availability of kinetic knowledge of the system of interest. Hopefully as the kinetic knowledge field progresses, kinetic descriptions of important reaction systems will increase and this will extend the applicability of this methodology.
2. Comprehensive: through semi-automated tools, we hit 99% of all possible reactions in the scope of our search within reasonable energy thresholds, making it less prone to human error. We explain in the Results and Discussion Approach section to what degree the steps are automated.
3. Multi-scale: by having our end “product” be detailed elementary kinetic models, we can explore atomistic trends for global property behavior.
4. Flexible: our sub-mechanisms can be used with the user's preferred base mechanism if it has the final products of our sub-mechanism included.
5. Accurate for less time: our method hits the middle ground of using detailed approaches that let us approximate full computational accuracy while reducing overall time for development, making our method faster than many detailed computational chemistry methods while also more accurate than many estimation methods.
6. Detailed: the completeness of the mechanism generation allows the user to link observable chemical behaviors to chemical structural features through reaction networks.
For this manuscript, we present the development of sub-mechanisms for the low-temperature ignition of two alcohols that may be derived from bio-renewable resources: n-butanol and n-pentanol, which are a natural choice for our proof-of-concept application for several reasons. First, despite the lack of comprehensive understanding in the low-temperature ignition mechanism for these fuels, many experimental ignition studies exist to which we can benchmark our models. Second, the data available for ignition over a wide range of temperatures and pressures allows us to highlight the benefits of having calculated pressure dependencies in our models which estimation methods cannot incorporate accurately at this time. Third, the resultant models would be the first published theory based sub-mechanisms for low-temperature ignition chemistry of these two fuels. Finally, this unique set of alcohol fuels highlights that through the addition of a single CH2 group to extend the alkane chain, the chemistry can change dramatically, causing negative temperature coefficient (NTC) behavior to arise at low and intermediate pressures for the longer-chain alcohol, n-pentanol, which can be probed directly through our modeling efforts. Through this study, we show how our methodology can be applied to this complex chemical problem, to not only accurately predict the ignition behavior of these two alcohol fuels, but to also correlate ignition behavior to chemical structure, directly providing insight for rational fuel design that other techniques would not have the ability to provide.
Background–low-temperature ignition reaction mechanism
Ignition chemistry can be a particularly challenging chemical problem for combustion scientists. While it is relatively simple to measure the length of time for ignition to occur,34 experimentally detecting the chemical steps from initial fuel and oxidizer mixture to full flame is far more challenging.35–38 The distinct reaction steps assumed to occur for ignition39 may be categorized into initiation and propagation.| F + X ⇒ R + HX | (R1) |
| R + O2 ⇒ ROO | (R2) |
The resultant ROO radical is highly reactive and can quickly undergo various isomerization or HO2 elimination reactions. More specifically, a hydroperoxyl radical and an unsaturated molecule can be formed via a concerted reaction of the ROO. The predominate isomerizations involve an internal hydrogen abstraction to form a new radical species denoted QOOH, as the parent R radical has now donated an H-atom to the peroxyl site.
| ROO ⇒ HO2 + unsaturated molecule | (R3) |
| ROO ⇒ QOOH | (R4) |
Should QOOH form, that too can undergo further reactions. Like the ROO, the QOOH can eliminate a hydroperoxyl radical to form an unsaturated molecule, or it can undergo a concerted reaction to eliminate a hydroxyl radical and form a cyclic molecule. The QOOH can also undergo a 2nd O2 addition to form OOQOOH which can further decompose to a keto-hydroperoxide molecule (KHP) and hydroxyl radical.
| QOOH ⇒ HO2 + unsaturated molecule | (R5) |
| QOOH ⇒ OH + cyclic molecule | (R6) |
| QOOH + O2 ⇒ OOQOOH | (R7) |
| OOQOOH ⇒ KHP + OH | (R8) |
The competition between reactions forming HO2, a somewhat reactive flame radical, and those forming OH, a highly reactive flame radical, can directly drive the ignition behavior of a fuel. Fuels that favor R3 and R5 over R4 and subsequent reactions R6–R8, tend to react slower than those that favor the OH-forming pathways. The correlation between ignition speed and predominant radical formation may be seen in fuels exhibiting negative temperature coefficient (NTC) behavior, in which a fuel's ignition tendency deviates from a linear behavior with temperature. Typically, a fuel's IDT decreases (ignition becomes faster) as temperature rises, as reactions generally become faster with elevated temperature. However, for some fuels as temperature increases, the competition between R3 and R4 can swing more in the favor of R3, resulting in non-linear ignition delay time versus temperature behavior.40. Normal alcohols can display this type of behavior. N-butanol does not exhibit NTC-behavior,41,42 whereas n-pentanol is the smallest linear chain alcohol that shows NTC-behavior at low and intermediate pressures.43–45
Given the high interest in renewable low carbon alcohols produced from biomass, many alcohol combustion models have been developed as reviewed by Sarathy et al.46 Many of these mechanisms do perform well for certain combustion conditions but very notably, Sarathy et al.46 highlights the lack of data available for the important low-temperature chemistry reactions, specifically R2–R8 for many alcohol fuels. Furthermore, these initial low-temperature oxidation reactions are highly pressure dependent and can directly influence ignition behavior.
For n-butanol ignition kinetics, although studies have presented experimental ignition delay time (IDT) data,42,47–53 an even smaller subset include temperatures for which low-temperature chemistry is dominant (T < 1000 K).42,51,53,54 In their review, Sarathy et al.46 point out the difficulty of building comprehensive models that can capture low-temperature oxidation, NTC behavior, and high-temperature combustion. Only a handful of mechanisms exist containing the highly pressure and temperature sensitive peroxy chemistry which governs auto-ignition in the low-temperature regime for n-butanol.42,54–56 To the authors' knowledge, only one study has directly investigated the oxidation of the hydroxybutyl radicals. Welz et al.57 used multiplex tunable synchrotron photoionization mass spectrometry in conjunction with potential energy surfaces for the decomposition of each ROO and the subsequent QOOH radicals to uncover the dominate pathways. No theoretically based reaction rates for the low-temperature oxidation of n-butanol have been published up to this point. Thus, in the models that include this chemistry,42,55–57 rates for the peroxy decomposition reactions were assigned using estimation methods based on theoretical work for alkane58,59 or ethanol oxidation.60 The most recent model by Saggese et al.55 also incorporates updated thermochemistry and reaction rates for n-butanol H-abstraction chemistry based on theoretical work.
N-pentanol has received less attention in the literature than n-butanol, especially regarding its low-temperature oxidation chemistry. In 2011, Togbé et al.61 proposed a kinetic model, for n-pentanol validated by experiments in a jet stirred reactor and combustion bomb, at intermediate temperatures (800 K–1200 K). Their mechanism is based on adapting models for smaller carbon alcohols to include n-pentanol chemistry by employing group additivity methods. Modifications to rate constants in this mechanism were done in 2013 by C. Tang et al.62 and were estimated by an n-butanol mechanism.63 In a 2013 experimental study44 and 2017 theoretical study,64 attempts were made to correlate structural features to ignition phenomena. Work done in 2013 by Heufer, Bugler, and Curran,44 studied the reactivity between n-alcohols and n-alkanes and also considered carbon chain length. In 2012, Heufer et al.43 developed a mechanism covering the low and high temperature oxidation of n-pentanol using modeling rules previously published for n-butanol.65,66 More recently, Pelucchi et al.56 published a lumped kinetic model containing oxidation and pyrolysis chemistry for the n-C3–C6 alcohols including n-pentanol. A follow up paper67 included new experimental data for this subset of alcohols including new low-temperature rapid compression machine ignition delay times. Two theorical studies focusing on the 1–hydroxy–1-pentyl radical + O2 pathway to form the 1–hydroxy–1-peroxypentyl radical have been published.65,66 Bu et al.,65 focusing on a wider range of oxygenated C5 molecules, used theoretical methods to calculate bond dissociate energies and energetics for the decomposition of the 1–hydroxy–1-peroxypentyl radical presented in the form of a potential energy surface. Duan et al.45 used high level ab initio calculations resulting in rate constants for the decomposition of one ROO formed during the low-temperature oxidation of n-pentanol.
Results and discussion
Approach
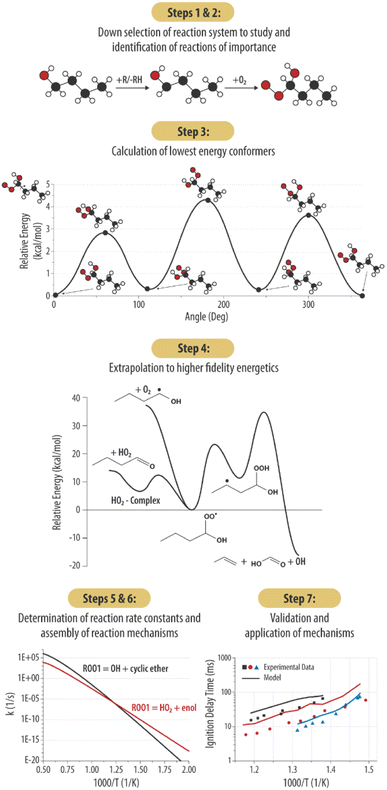
In this section we will outline and elaborate on our process of applying computational chemistry calculations and kinetics tools to gas phase organic chemistry problems for chemistry informed design applications. This goal is achieved through building predictive gas-phase chemical mechanisms faster and less computationally intensive using state of the art semi-automated chemical tools and linking the predicted chemical reactivity to underlying chemical structure information. Our process may be described in 7 steps as outlined in Fig. 1.To illustrate the process, we will describe each step and then provide a specific example from our current work on either n-butanol or n-pentanol when relevant. Of note, Steps 2–6 are completed without the influence of target experimental data sets (e.g., ignition delay times). As such, the results of Step 7 are presented without modification, highlighting the predictive value of our methodology. This contrasts with the common practice in combustion modeling to adjust reaction rates to achieve better fits to experimental data.
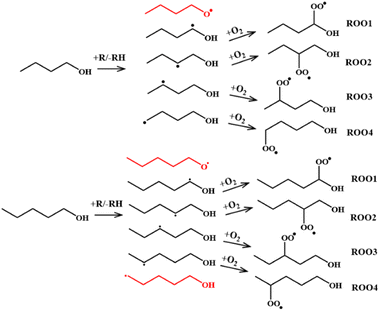
Initiation steps. As stated earlier, two primary reaction classes are responsible for ignition initiation: unimolecular decomposition reactions and H-abstraction reactions. These initial reactions are highly important because they determine which radicals are likely generated, which determines the composition of the initial radical pool from which the ROO radicals form. For n-butanol and n-pentanol there are 5 and 6 possible fuel radicals respectively that can form via abstraction (Fig. 2), each of which can form a unique ROO species and undergo subsequent series of reactions. Not all radicals will be favored to form, so determining the most favorable abstraction sites up front will help reduce the computational work scope.
Thermal decomposition is unlikely to play a significant role in ignition initiation for alcohols under low-temperature ignition conditions since the reaction energy thresholds for thermal decomposition reactions are high. This means abstraction reactions are most likely the only class of initiation reactions of importance. A literature search revealed several studies in which rates for abstraction reactions for n-butanol and n-pentanol were determined. Galano et al.68 studied abstraction reactions of n-butanol via hydroxyl radical. In their study, high fidelity rates calculated at the CCSD(T)//BHandHLYP/6-311G(d,p) level of theory were calculated over the 298–500 K temperature range. The calculations were later updated by Seal et al.69 using the M08-HX/MG3S level of theory over a wider temperature range of 200–2400 K and were compared directly against experiment. Focusing on the updated theory, abstraction from the α-site (carbon next to the hydroxyl group) is favored, with up to 70% of all abstraction occurring from that one location. Abstraction from the β- and γ-carbons are next most favored, followed by the terminal δ-carbon. In another study, Welz et al.58 combined quantum chemistry calculations and multiplexed tunable synchrotron photoionization mass spectrometry (MPIMS) experiments to find active pathways in 4 of the 5 possible ROO radicals denoted ROO1 through ROO4 in Fig. 2. This combined with the knowledge that O2 is unlikely to add to an O-atom under the temperature conditions relevant to ignition, leads to the conclusion that only 4 of the 5 fuel radicals may play an active role for ignition.
More limited information is available on n-pentanol abstraction reactions. Bond dissociation energy calculations performed by Heufer et al.43 at the CBS-QB3 level of theory shows the O–H bond is the higher than all other C–H bonds by 3.4 kcal mol−1. Following similar logic as with n-butanol, abstraction from the hydroxyl site is unlikely to play a role in the low-temperature oxidation chemistry, thus the resultant fuel radical does not need to be explored computationally. The kinetics of eight linear chain alcohols + OH including n-pentanol were examined theoretically70 and found the H on the α-carbon to be the most easily abstracted for all eight alcohols. This suggests the α radical will play a dominate role and should be included in our study. Sarathy et al.46 used these studies to select rates for n-pentanol + OH and suggested that the α, γ, and δ fuel radicals form most often. However, in a theoretical study by Aazaaad & Lakshmipathi,71 the abstraction reaction energy barriers for three pentanol isomers were calculated using M06-2X/6-311+G(d,p). Their work suggests the barrier to form the β-radical is the lowest followed by the α, γ, and δ but did not calculate rate constants. Taking all this into account, the α, β, γ, and δ fuel radicals for n-pentanol were deemed of importance. All eight studied radicals for our two parent fuels and their associated ROO species are highlighted in Fig. 2.
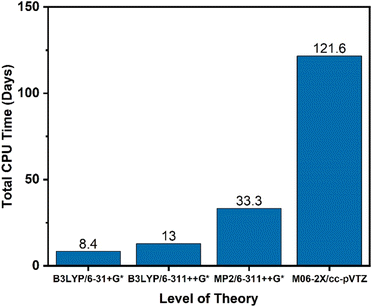
In addition to identification of the starting molecule of interest, two key parameters must be identified for the simulations: the level of theory at which the scan should be performed, and the cutoff threshold for which reactions to include. For this work, KinBot scans were run at the B3LYP/6-311++G* level of theory. This method was chosen for its computational speed and accuracy compared to other density functional methods. To test whether our method selection was important, KinBot was run at three other levels of theory for a job with seven heavy atoms (i.e., atoms other than H-atom), the results of which are shown in Fig. 3. In addition to the B3LYP/6-311++G* level of theory, we chose the same level of theory with a smaller basis set (B3LYP/6-31+G*), a more sophisticated method with the same basis set (MP2/6-311++G*), and the level of theory we typically perform our geometry and frequency calculations at (M06-2X/cc-pVTZ). The M06-2X method has been demonstrated to perform better than B3LYP and other DFT methods for a wide variety of molecule classes and calculation types.72,73 All other parameters within the KinBot input files such as reaction threshold (60 kcal mol−1 in this work) were kept identical. The computational time study demonstrated the significant time savings achieved using a lower level of theory like B3LYP/6-311++G* which took only 16 days of CPU time compared to the ideal level of theory M06-2X/cc-pVTZ which took over 120 days of CPU time to complete the same job. The MP2/6-311++G* took about 35 days of CPU time but missed many important reactions altogether. For this reason, it was eliminated. Based on this time study, we found it more efficient to run KinBot at a lower level of theory and refine the important pathways manually. Additional details of the settings and features used in our KinBot jobs can be found in the ESI.†
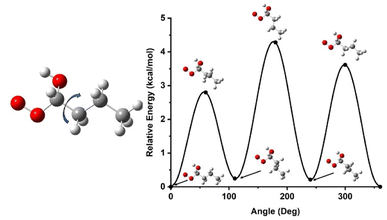
Once the initial geometries were found with the M06-2X/cc-pVTZ level of theory, relaxed 1-D hindered rotor scans were performed at the same level of theory, scanning every 10 degrees for 360 degrees on all rotatable bonds (Fig. 4). We have developed codes in house that identifies rotors and runs relaxed scans, though these sometime require user intervention if the automated method fails to return to the initial geometry point. Additional codes check for minima below the initial rotor energy in rotor scans and rerun rotor scans to confirm lowest energy confirmers. Another code takes the minimum energy structure and runs high fidelity energetics calculations from that, and a final code can take the various inputs and put together a skeleton Master Equation System Solver (MESS) file for reaction calculations. The scans provide energy potentials for bond rotations relative to the minimum energy geometry which is used to help describe the internal rotational motion of the molecule in the rate constant calculations. The hindered rotor scans also help confirm the lowest energy conformer has been identified. If a lower conformer is identified, the new geometry becomes the starting point, and the hindered rotor analysis is repeated.
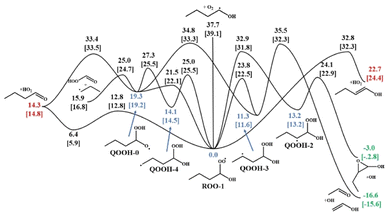 | ||
| Fig. 5 An example potential energy surface showing the results from KinBot for the ROO-1 radical of n-butanol. Energies of the ROO and QOOH wells are shown in blue, OH producing routes shown in green, and HO2 producing routes shown in red. Energetics from Welz et al.58 are given in [brackets] for comparison. | ||
The extent of the multi-reference characteristic was checked for each stationary point using the T1 diagnostic which is a measure of multireference effects. Typically, structures governed by strong electron correlation effects can have high T1 diagnostic values.77 If the T1 diagnostic was below 0.2 for stable species or 0.3 for radical species, single reference methods were suitable for those molecules. For the best accuracy, stationary points with higher T1 diagnostic values should be treated with multi-reference methods, but because this hybrid method is replacing rates developed with estimation methods, we expect the errors associated with not using multi-reference methods to be on the par with the errors associated with the estimation methods themselves.
Zero-point energy correction factors from the density functional theory (DFT) calculations were included in our final energies calculated at the CCSD(T)/cc-pV∞Z//M06-2X/cc-pVTZ level of theory. These energies were then used to produce more accurate PESs for each ROO radical in this study. The described process was repeated for QOOH radicals including reactions with formation barriers below the R + O2 energy barrier. Upon completion of the PES, the reactions were re-examined to determine if more reactions could be eliminated from the rate constant calculations, hence requiring user input. Using a combination of energetics and preliminary rate constant calculations, specific QOOH decomposition pathways 5 kcal mol−1 higher than the R + O2 energy barrier were eliminated from the final rate constant calculations. These pathways were unlikely to be active at the low temperatures where this chemistry is dominate. Removing these pathways from the rate constant calculations help stabilize the rates and further reduce unnecessary computational work. A detailed comparison of the calculated energies and those found in the literature45,58 can be found in the PESs in the ESI.†
Rates were calculated between pressures of 0.01 and 100 atm and temperatures between 300–1500 K (in 100 K intervals). All rates generated in this work are presented as a function of pressure using a standard PLOG format accepted by Chemkin81 which uses logarithmic interpolation to calculate the rate between specified pressure values. A full list of rate constants calculated in this work along with a species glossary can be found in the ESI.†
The product of this method is truly a sub-mechanism. In this case, we used Chemkin's81 mechanism merge tool but several tools exist to merge mechanisms on the condition your chemical naming scheme is consistent with whatever base mechanism you wish to merge it into. We did not attempt automatic merging as most literature mechanisms have variable species naming schemes which are often not explicitly explained in universal chemical naming methods (e.g., InChI or SMILES). In this way it can be highly flexible, as the limitation of where the sub-mechanism ends is the user's choice.
Results
Of note, the ignition behavior from a ST is fundamentally different than that observed in an RCM. For an RCM, low-to-intermediate temperature auto-ignition response is observed. In Fig. 6, experimental RCM data for n-butanol include the compressed air driven single piston University of Leeds RCM79 measurement data at P = 20 bar, and the heated dual piston RCM data at 30 bar.51 For n-pentanol, the RCM ignition delay times at 19 bar43 measured in the twin-opposed piston RCM configuration from NUI Galway80 were used for model validation. Also, for n-pentanol, ST data was selected for comparison from Heufer et al.44. However, ST experiments are most relevant for high-temperature auto-ignition measurements. The two sets of experiments combined probe ignition across most engine-relevant temperatures.
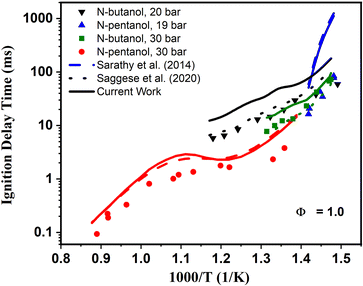 | ||
| Fig. 6 Measured (symbols) and simulated ignition delay times of n-butanol and n-pentanol at ϕ = 1.0. N-butanol: RCM data from Agbro et al.80 at 20 bar (black) and RCM data from Weber et al.51 at P = 30 bar (green). N-pentanol: ST data from Heufer et al.43,44 at 30 bar (red) and RCM data at P = 19 bar (blue). The original alcohol n-butanol base mechanism from Saggese et al.55 is represented by the dotted lines, and the reduced n-pentanol base mechanism from Sarathy et al.46 by the dashed lines. The current models produced in Step 6 are represented by the solid lines. | ||
The next step involved direct application of the newly generated n-butanol and n-pentanol models to these experimental data sets. The constant and variable volume closed homogeneous ignition delay module of Chemkin-Pro81 was used as the numerical simulation tool in this study. The pressure histories from oxygen-driven non-reactive tests were used to generate the volume histories necessary for all the RCM variable-volume ignition delay simulations to account for facility effects regarding heat loss in the experiments. The simulated ignition delay time for RCM measurements was defined as the time between the end of compression and the maximum slope of the pressure rise at ignition. On the other hand, the simulated shock tube ignition delay time is simply defined as the time to reach the maximum rate of change in pressure, (dP/dt)max. For performance comparison, two sets of simulations were conducted. The original base mechanisms46,55 were used to demonstrated baseline performance of the models and compared directly in Fig. 6 to the new kinetic mechanisms generated in Step 6.
Model performance for ignition delay time predictions
Upon inspection of the simulation results in Fig. 6, we begin to see deviations between predicted IDTs between our newly generated models from Step 6 (solid lines) and the base models46,55 predictions (dashed lines). For n-butanol we see the updated model predicts longer IDTs than the Saggese et al.55 base mechanism across all pressures and temperatures. Interestingly, for n-pentanol there is much less deviation between the base and updated model predictions. Upon first glance, the differences noted between the model predictions may seem like an indication that our updated mechanisms are not capturing ignition behavior correctly. The reason for these discrepancies is two-fold. First, the original mechanisms were developed specifically to model these data sets. Generally, for mechanisms such as these, kinetic rate constants are adjusted within uncertainty parameters to match the experimental data sets as best as possible. This may be done either by purposely choosing the rate constants when multiple rates are available in the literature for ideal data fitting, selecting molecules to which rate constants may be estimated by analogy that have rates beneficial for data modeling, or through manual adjustment of A-factors within the rate constant's perceived uncertainty bounds until an acceptable fit is reached. While these are all valid approach to kinetic modeling, manual “tuning” of models to experiments may have impacts on accuracy for temperature and pressure regions outside of the validation data range. Hence, it is a significant advantage that our new kinetic models are created completely agnostic of adjustment to data sets. The overall good agreement highlights the power of the theoretical approach outlined in this work to achieve similar accuracy without any adjustment.The second reason for the discrepancies centers around the newly calculated reaction rate constants and those within original n-butanol55 and n-pentanol46 mechanisms themselves. A first order sensitivity analysis can be used to indicate in a mechanism which reactions have the largest parameter effect in ignition predictions. In the first order sensitivity analysis, the A-factor in a rate constant Arrhenius expression is multiplied by a factor of 2, and the model results are compared to the unperturbed model. This process is sequentially performed for each reaction rate. Then the change in the model parameter of choice (in this case IDT) are normalized, giving the sensitivity coefficient. Thus, the largest (most positive) sensitivity coefficients indicate which reactions most speed up the overall ignition delay time, and in effect promote ignition, while the smallest (most negative) sensitivity coefficients indicate which reactions slow the IDTs most, and in effect inhibit ignition.
Fig. 7 shows an example sensitivity analysis performed at a temperature of 740 K for the 30 bar stoichiometric n-pentanol data set. The blue reactions in Fig. 7 indicate reactions which were directly calculated as part of this work. Two reactions in particular have an influence on the model results for n-pentanol. O2 addition to a fuel radical (C5H10OH + O2 = PC4H9CHO + HO2) for example was the second most responsible reaction for retarding IDT in the Sarathy et al.46 mechanism but was found to be inconsequential with our more accurate theoretical mechanism development. Another example is the decomposition reaction of a QOOH radical back to a fuel radical + O2 (C5H9OH–4OOH = C5H10OH + O2), which was not included in the original model, but was found to be sensitive for retarding IDT in the new mechanism. These directly show how mechanistic differences exist in between the original and new models. The reactions in black text in Fig. 7 are those that are unchanged between the two models, however, still show significant deviations in relative magnitude of sensitivity. Indirectly, this is a measure of the differences in the reactivity of the resultant R + O2 cascade. The sensitivity analysis indicated that in our model, the β-pentanol radical has less of an influence on IDT predictions due to the subsequent decomposition chemistry being altered. Thus, the relative sensitivity of the rate limiting reactions to form the β-pentanol radical are relatively less sensitive than in the original Sarathy et al.46n-pentanol mechanism.
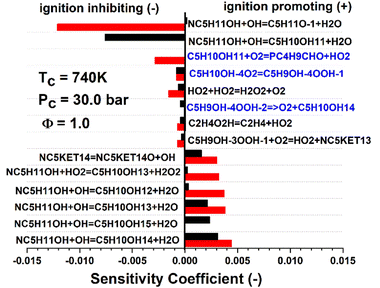 | ||
| Fig. 7 Sensitivity analysis of the ignition of n-pentanol with conditions of Tc = 740 K, Pc = 30 bar at Phi = 1.0. The top 5 most positively and negatively sensitive reactions of the reduced Sarathy et al.46 mechanism (red) and current mechanism (black) are included. Since this was a temperature A-factor sensitivity, a positive coefficient corresponds to an increase in temperature, thus a faster IDT. The reactions in red text are those that were calculated in the current work. | ||
Linking observable NTC ignition behavior to chemical structural features through model framework
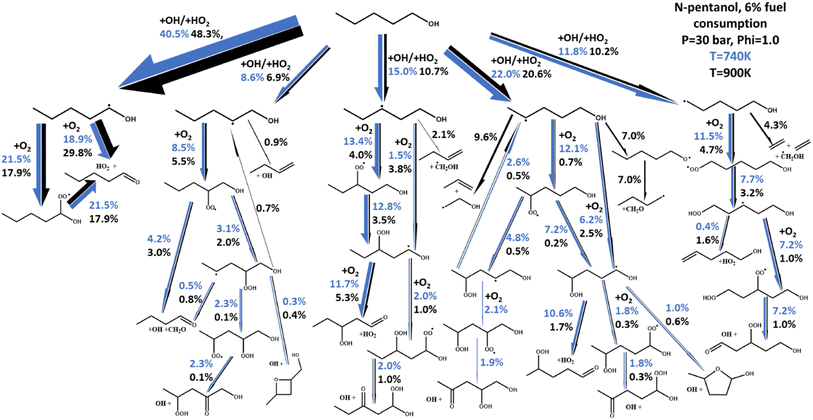
Of particular interest is the ability of both models to capture negative temperature coefficient (NTC) behavior, or lack thereof, observed experimentally. In n-butanol, almost no NTC behavior is experimentally observed, with the two data sets showing near linear ignition versus temperature behavior. This is true for other ignition data outside of those presented in Fig. 6.48,50,52,53 For n-pentanol however, significant NTC behavior is observed, best highlighted by the ST data from Heufer et al.44 and is exceptionally well captured by our newly developed kinetic model.The fundamental chemical foundation of our newly developed models allows us to link the observation of NTC behavior with the extension of the alkyl chain in n-butanol to n-pentanol using a reaction flux analysis of n-pentanol as shown in Fig. 8. In this figure, the net reaction flux for all reactions linking the two sets of molecular species between each arrow is calculated and normalized relative to the reaction flux from n-pentanol to the largest yield product, the α-pentanol radical. The thickness of each arrow in Fig. 8 correlates to the total flux, which is also reported in cumulative percentages on the figure. Finally, the two colors indicated two different experimental simulation points for the 30 bar, p = 1.0 n-pentanol in air simulations; blue is 740 K, at the onset of NTC behavior, black is 900 K, as NTC behavior is about to end. The differences in the magnitude for each set of arrows highlight how temperature affects the chemistry of n-pentanol, changing the radical cascade. The chemistry of the α-pentanol radical, for example, has some differences between the percentage of R + O2 resulting in formation of a-ROO versus direct HO2 elimination. However, the temperature effects on whether R + O2 forms α-ROO or HO2 directly, has almost no difference in the chemistry since all of the α-ROO radical forms the same products as the direct HO2 formation.
A stark difference is noted in the reactions originating from the δ-pentanol radical. As stated earlier, HO2 and OH are both readily formed by O2 addition to a fuel radical and its subsequent reactions. While both radicals contribute to propagating chemistry leading to ignition, HO2 is notably less reactive than OH, so an increase in OH production would decrease IDT, and vice versa. The addition of the δ-pentanol CH2 group is the unique structural difference between n-butanol and n-pentanol. Closer inspection of the reactions resulting from the δ-pentanol radical reveals why NTC behavior is observed in n-pentanol and not in n-butanol. At temperatures just below the onset of NTC behavior, nearly all the δ-pentanol radical is consumed via O2 addition reactions, resulting in the typical ROO chemical cascade which ultimately forms reactive HO2 and OH radicals. However, at temperatures where NTC behavior is active, one notable difference is that the β-scission to propene + vinyl alcohol radical or isomerization and β-scission to formaldehyde and C4H9 radical have become the dominant two sets of products, reducing the number of reactive radicals produced. The result is an 84% reduction in HO2 production pathways and 81% reduction in OH production pathways from the δ-pentanol radical. Hence, we can tie the origination of NTC behavior in n-pentanol specifically to the δ-CH2 group.
Conclusions
The rapid development of accurate kinetic models for sustainable, low carbon energy gas phase reactions is a growing need in the chemicals and fuels community as we continue to search for renewable fuels and chemicals that have advantaged properties for specific market applications. This work outlines a flexible semi-automated theoretical method that can predict gas phase chemical behavior agnostic of experimental data which can be used to extrapolate insights between chemical structure and observable behaviors. This study highlights how recent developments in automated chemical kinetics tools can be leveraged for a complicated gas phase system: renewable fuel combustion. In this manuscript we highlighted which steps and approaches are automated and which require user input. Specifically, the updated models generated with our outlined methodology allowed for linear alcohol ignition delay time predictions capturing both the non-NTC behavior of n-butanol and the NTC-behavior of n-pentanol without adjusting to fit experimental data. This technique also allowed for insights into the chemical reasoning as to why the extension of the alkyl chain in n-butanol to n-pentanol significantly changed ignition chemical behavior, highlighting the importance of the δ-pentanol fuel radical in the NTC region.While this work was demonstrated in the context of advantaged low carbon biofuels and accurate prediction of ignition delay times, we want to highlight the versatility and utility of this method to gas phase reaction systems. Our outlined approach can be applied in a wide range of gas phase chemical systems to develop predictive kinetic models. Perhaps more importantly, the rigorous fundamental techniques used in developing the kinetic models provide the information needed to extract molecular insight on why chemical behaviors are observed in real world applications, truly linking molecular properties to global observables. This feature is a powerful link that can be leveraged for rational chemical design in any number of gas-phase reaction applications towards addressing decarbonization such as CO2 reduction and utilization approaches.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to acknowledge William Pitz and Chiara Saggese from Lawrence Livermore National Laboratory for their help with the n-pentanol mechanism reduction as well as their valuable insights and discussions on the relevant pathways in the low-temperature oxidation of n-pentanol. A portion of this research was conducted as part of the Co- Optimization of Fuels & Engines (Co-Optima) project sponsored by the U.S. Department of Energy–Office of Energy Efficiency and Renewable Energy, Bioenergy Technologies and Vehicle Technologies Offices. Work at the National Renewable Energy Laboratory was performed under Contract No. DE347AC36-99GO10337. Parts of this work were also supported by Co-Optima through Program Award Number DE-EE0007983 and an Alliance Partner University Program contract UGA-0-41026-110 under prime Contract No. DE-AC36-08GO28308. K. S. Lockwood was supported by the Department of Defense (DoD) through the National Defense Science & Engineering Graduate Fellowship (NDSEG) Program. This work utilized the RMACC Summit supercomputer, which is supported by the National Science Foundation (awards ACI-1532235 and ACI-1532236), the University of Colorado Boulder, and Colorado State University. The Summit supercomputer is a joint effort of the University of Colorado Boulder and Colorado State University. We gratefully acknowledge the assistance of G. Barney Ellison in this work.The views expressed in the article do not necessarily represent the views of the U.S. Department of Energy or the U.S. Government. The U.S. Government retains and the publisher, by accepting the article for publication, acknowledges that the U.S. Government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this work, or allow others to do so, for U.S. Government purposes.
References
- T. F. G. G. Cova and A. A. C. C. Pais, Front. Chem., 2019, 7, 809 CrossRef CAS PubMed.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- G. Schneider, Nat. Rev. Drug Discovery, 2018, 17, 97–113 CrossRef CAS PubMed.
- D. T. Ahneman, J. G. Estrada, S. Lin, S. D. Dreher and A. G. Doyle, Science, 2018, 360, 186–190 CrossRef CAS PubMed.
- J. N. Wei, D. Duvenaud and A. Aspuru-Guzik, ACS Cent. Sci., 2016, 2, 725–732 CrossRef CAS PubMed.
- A. F. Zahrt, J. J. Henle, B. T. Rose, Y. Wang, W. T. Darrow and S. E. Denmark, Science, 2019, 363, 6424 CrossRef PubMed.
- J. V. Michael and K. P. Lim, Annu. Rev. Phys. Chem., 1993, 44, 429–458 CrossRef CAS.
- R. K. Hanson and D. F. Davidson, Prog. Energy Combust. Sci., 2014, 44, 103–114 CrossRef.
- K. Kohse-Höinghaus, P. Oßwald, T. A. Cool, T. Kasper, N. Hansen, F. Qi, C. K. Westbrook and P. R. Westmoreland, Angew. Chem., Int. Ed., 2010, 49, 3572–3597 CrossRef PubMed.
- K. A. Bhaskaran and P. Roth, Prog. Energy Combust. Sci., 2002, 28, 151–192 CrossRef CAS.
- H. J. Curran, Proc. Combust. Inst., 2019, 37, 57–81 CrossRef CAS.
- J. A. Miller, R. Sivaramakrishnan, Y. Tao, C. F. Goldsmith, M. P. Burke, A. W. Jasper, N. Hansen, N. J. Labbe, P. Glarborg and J. Zádor, Prog. Energy Combust. Sci., 2021, 83, 100886 CrossRef.
- K. Zhang, C. Banyon, U. Burke, G. Kukkadapu, S. W. Wagnon, M. Mehl, H. J. Curran, C. K. Westbrook and W. J. Pitz, Combust. Flame, 2019, 206, 123–137 CrossRef CAS.
- C. K. Westbrook, W. J. Pitz, O. Herbinet, H. J. Curran and E. J. Silke, Combust. Flame, 2009, 156, 181–199 CrossRef CAS.
- H. J. Curran, Int. J. Chem. Kinet., 2006, 38, 250–275 CrossRef CAS.
- S. W. Benson, “Thermochemical kinetics. Methods for the Estimation of Thermochemical Data and Rate Parameters.” 2d ed., John Wiley & Sons, Inc., New York 1976 Search PubMed.
- J. Bugler, K. P. Somers, E. J. Silke and H. J. Curran, J. Phys. Chem. A, 2015, 119, 7510–7527 CrossRef CAS PubMed.
- J. Prager, H. N. Najm, K. Sargsyan, C. Safta and W. J. Pitz, Combust. Flame, 2013, 160, 1583–1593 CrossRef CAS.
- D. Feller and K. A. Peterson, J. Chem. Phys., 2007, 26, 114105 CrossRef PubMed.
- L. Gyevi-Nagy, M. Kállay and P. R. Nagy, J. Chem. Theory Comput., 2021, 17, 860–878 CrossRef CAS PubMed.
- C. W. Gao, J. W. Allen, W. H. Green and R. H. West, Comput. Phys. Commun., 2016, 203, 212–225 CrossRef CAS.
- G. R. Magoon and W. H. Green, Comput. Chem. Eng., 2013, 52, 35–45 CrossRef CAS.
- J. W. Allen, C. F. Goldsmith and W. H. Green, Phys. Chem. Chem. Phys., 2011, 14, 1131–1155 RSC.
- V. Warth, F. Battin-Leclerc, R. Fournet, P. A. Glaude, G. M. Côme and G. Scacchi, Comput. Chem., 2000, 24, 541–560 CrossRef CAS PubMed.
- R. Van de Vijver and J. Zádor, Comput. Phys. Commun., 2020, 248, 106947 CrossRef CAS.
- C. Cavallotti, M. Pelucchi, Y. Georgievskii and S. J. Klippenstein, J. Chem. Theory Comput., 2019, 15, 1122–1145 CrossRef CAS PubMed.
- S. N. Elliott, K. B. Moore, A. V. Copan, M. Keçeli, C. Cavallotti, Y. Georgievskii, H. F. Schaefer and S. J. Klippenstein, Proc. Combust. Inst., 2021, 38, 375–384 CrossRef CAS.
- D. D. Das, P. C. St. John, C. S. McEnally, S. Kim and L. D. Pfefferle, Combust. Flame, 2018, 190, 349–364 CrossRef CAS.
- “YSI Estimator.” https://ysi.ml.nrel.gov/.
- P. C. St. John, P. Kairys, D. D. Das, C. S. McEnally, L. D. Pfefferle, D. J. Robichaud, M. R. Nimlos, B. T. Zigler, R. L. McCormick, T. D. Foust, Y. J. Bomble and S. Kim, Energy Fuels, 2017, 31, 9983–9990 CrossRef.
- P. C. S. John, Y. Guan, Y. Kim, S. Kim and R. S. Paton, Nat. Commun., 2020, 11, 2328 CrossRef PubMed.
- “BDE Estimator.” https://bde.ml.nrel.gov/.
- S. Kim, G. M. Fioronia, P. Ji-Woong, D. J. Robichaud, D. D. Das, P. C. St.John, L. Tianfeng, C. S. McEnally, L. D. Pfefferle, R. S. Paton, T. D. Foust and R. L. McCormick, Proc. Combust. Inst., 2019, 37, 1083–1090 CrossRef CAS.
- D. F. Davidson, S. C. Ranganath, K.-Y. Lam, M. Liaw, Z. Hong and R. K. Hanson, J. Propul. Power, 2010, 26, 280–287 CrossRef CAS.
- N. Hansen, K. Moshammer and A. W. Jasper, J. Phys. Chem. A, 2019, 123, 8274–8284 CrossRef CAS PubMed.
- I. O. Antonov, J. Zádor, B. Rotavera, E. Papajak, D. L. Osborn, C. A. Taatjes and L. Sheps, J. Phys. Chem. A, 2016, 120, 6582–6595 CrossRef CAS PubMed.
- B. Rotavera, J. D. Savee, I. O. Antonov, R. L. Caravan, L. Sheps, D. L. Osborn, J. Zádor and C. A. Taatjes, Proc. Combust. Inst., 2017, 36, 597–606 CrossRef CAS.
- J. D. Savee, E. Papajak, B. Rotavera, H. Huang, A. J. Eskola, O. Welz, L. Sheps, C. A. Taatjes, J. Zádor and D. L. Osborn, Science, 2015, 347, 643–646 CrossRef CAS PubMed.
- J. Zádor, C. A. Taatjes and R. X. Fernandes, Prog. Energy Combust. Sci., 2011, 37, 371–421 CrossRef.
- W. Liang and C. K. Law, Combust. Flame, 2018, 188, 162–169 CrossRef CAS.
- C. Treviño, M. Díaz and J. C. Prince, Combust. Theor. Model., 2018, 22, 1176–1193 CrossRef.
- S. Vranckx, K. A. Heufer, C. Lee, H. Olivier, L. Schill, W. A. Kopp, K. Leonhard, C. A. Taatjes and R. X. Fernandes, Combust. Flame, 2011, 158, 1444–1455 CrossRef CAS.
- K. A. Heufer, S. M. Sarathy, H. J. Curran, A. C. Davis, C. K. Westbrook and W. J. Pitz, Energy Fuels, 2012, 26, 6678–6685 CrossRef CAS.
- K. A. Heufer, J. Bugler and H. J. Curran, Proc. Combust. Inst., 2013, 34, 511–518 CrossRef CAS.
- Y. Duan, M. Monge-Palacios, E. Grajales-Gonzalez, D. Han, K. H. Møller, H. G. Kjaergaard and M. Sarathy, Combust. Flame, 2020, 219, 20–32 CrossRef CAS.
- S. M. Sarathy, P. Oßwald, N. Hansen and K. Kohse-Höinghaus, Prog. Energy Combust. Sci., 2014, 44, 40–102 CrossRef.
- J. T. Moss, A. M. Berkowitz, M. A. Oehlschlaeger, J. Biet, V. Warth, P.-A. Glaude and F. Battin-Leclerc, J. Phys. Chem. A, 2008, 112, 10843–10855 CrossRef CAS PubMed.
- K. E. Noorani, B. Akih-Kumgeh and J. M. Bergthorson, Energy Fuels, 2010, 24, 5834–5843 CrossRef CAS.
- G. Black, H. J. Curran, S. Pichon, J. M. Simmie and V. Zhukov, Combust. Flame, 2010, 157, 363–373 CrossRef CAS.
- B. W. Weber, K. Kumar, Y. Zhang and C.-J. Sung, Combust. Flame, 2011, 158, 809–819 CrossRef CAS.
- I. Stranic, D. P. Chase, J. T. Harmon, S. Yang, D. F. Davidson and R. K. Hanson, Combust. Flame, 2012, 159, 516–527 CAS.
- D. M. A. Karwat, S. W. Wagnon, P. D. Teini and M. S. Wooldridge, J. Phys. Chem. A, 2011, 115, 4909–4921 CrossRef CAS PubMed.
- K. A. Heufer, R. X. Fernandes, H. Olivier, J. Beeckmann, O. Röhl and N. Peters, Proc. Combust. Inst., 2011, 33, 359–366 CrossRef CAS.
- C. Saggese, C. M. Thomas, S. W. Wagnon, G. Kukkadapu, S. Cheng, D. Kang, S. S. Glodsborough and W. J. Pitz, Proc. Combust. Inst., 2021, 38, 415–423 CrossRef CAS.
- M. Pelucchi, S. Namysl, E. Ranzi, A. Rodriguez, C. Rizzo, K. P. Somers, Y. Zhang, O. Herbinet, H. J. Curran, F. Battin-Leclerc and T. Faravelli, Energy Fuels, 2020, 34, 14688–14707 CrossRef CAS PubMed.
- S. M. Sarathy, M. J. Thomson, C. Togbé, P. Dagaut, F. Halter and C. Mounaim-Rousselle, Combust. Flame, 2009, 156, 852–864 CrossRef CAS.
- O. Welz, J. Zádor, J. D. Savee, L. Sheps, D. L. Osborn and C. A. Taatjes, J. Phys. Chem. A, 2013, 117, 11983–12001 CrossRef CAS PubMed.
- M. Mehl, W. J. Pitz, C. K. Westbrook and H. J. Curran, Proc. Combust. Inst., 2011, 33, 193–200 CrossRef CAS.
- S. M. Sarathy, C. K. Westbrook, M. Mehl, W. J. Pitz, C. Togbe, P. Dagaut, H. Wang, M. A. Oehlschlaeger, U. Niemann, K. Seshadri, P. S. Veloo, C. Ji, F. N. Egolfopoulos and T. Lu, Combust. Flame, 2011, 158, 2338–2357 CrossRef CAS.
- J. Zádor, C. A. Taatjes and R. X. Fernandes, Prog. Energy Combust. Sci., 2011, 37, 371–421 CrossRef.
- C. Togbé, F. Halter, F. Foucher, C. Mounaim-Rousselle and P. Dagaut, Proc. Combust. Inst., 2011, 33, 367–374 CrossRef.
- C. Tang, L. Wei, X. Man, J. Zhang, Z. Huang and C. K. Law, Combust. Flame, 2013, 160, 520–529 CrossRef CAS.
- J. Zhang, L. Wei, X. Man, X. Jiang, Y. Zhang, E. Hu and Z. Huang, Energy Fuels, 2012, 26, 3368–3380 CrossRef CAS.
- L. Bu, P. N. Ciesielski, D. J. Robichaud, S. Kim, R. L. McCormick, T. D. Foust and M. R. Nimlos, J. Phys. Chem. A, 2017, 121, 5475–5486 CrossRef CAS PubMed.
- K. Yasunaga, T. Mikajiri, S. M. Sarathy, T. Koike, F. Gillespie, T. Nagy, J. M. Simmie and H. J. Curran, Combust. Flame, 2012, 159, 2009–2027 CrossRef CAS.
- S. M. Sarathy, S. Vranckx, K. Yasunaga, M. Mehl, P. Oßwald, W. K. Metcalfe, C. K. Westbrook, W. J. Pitz, K. Kose-Höinghaus, R. X. Fernandes and H. J. Curran, Combust. Flame, 2012, 159, 2028–2055 CrossRef CAS.
- M. Pelucchi, S. Namysl, E. Ranzi, A. Rodriguez, C. Rizzo, K. P. Somers, Y. Zhang, O. Herbinet, H. J. Curran, F. Battin-Leclerc and T. Faravelli, Energy Fuels, 2020, 34, 14708–14725 CrossRef CAS PubMed.
- A. Galano, J. R. Alvarez-Idaboy, G. Bravo-Pérez and M. E. Ruiz-Santoyo, Phys. Chem. Chem. Phys., 2002, 4, 4648–4662 RSC.
- P. Seal, G. Oyedepo and D. G. Truhlar, J. Phys. Chem. A, 2013, 117, 275–282 CrossRef CAS PubMed.
- A. Hatipoğlu and Z. Çinar, J. Mol. Struct., 2003, 631, 189–207 CrossRef.
- B. Aazaad and S. Lakshmipathi, Mol. Phys., 2018, 116, 1153–1165 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- D. Jacquemin, E. A. Perpète, I. Ciofini, C. Adamo, R. Valero, Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2010, 6, 2071–2085 CAS.
- Gaussian 16, Revision C. 01, M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, and D. J. Fox, Gaussian, Inc., Wallingford CT, 2016.
- J. M. L. Martin, Chem. Phys. Lett., 1996, 259, 669–678 CrossRef CAS.
- J. A. Miller and S. J. Klippenstein, J. Phys. Chem. A, 2003, 107, 2680–2692 CAS.
- L. Freitag, S. Knecht, C. Angeli and M. Reiher, J. Chem. Theory Comput., 2017, 13, 451–459 CrossRef CAS PubMed.
- Y. Georgievskii, J. A. Miller, M. P. Burke and S. J. Klippenstein, J. Phys. Chem. A, 2013, 117, 12146–12154 CrossRef CAS PubMed.
- E. Agbro, A. S. Tomlin, M. Lawes, S. Park and S. M. Sarathy, Fuel, 2017, 187, 211–219 CrossRef CAS.
- S. M. Gallagher, H. J. Curran, W. K. Metcalfe, D. Healy, J. M. Simmie and G. Bourque, Combust. Flame, 2008, 153, 316–333 CrossRef CAS.
- ANSYS CHEMKIN 17.0 (15151), ANSYS Reaction Design: San Diego, 2016.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2se00773h |
| This journal is © The Royal Society of Chemistry 2022 |