Exploration of the photocatalytic cycle for sacrificial hydrogen evolution by conjugated polymers containing heteroatoms

Abstract

We analyze the photocatalytic activity of heteroatom containing linear conjugated polymers for sacrificial hydrogen evolution using a recently proposed photocatalytic cycle. We find that the thermodynamic barrier to electron transfer, relevant both in the presence and absence of noble metal co-catalysts, changes with polymer composition, reducing upon going from electron-rich to electron-poor polymers, and disappearing completely for the most electron-poor polymers in a water rich environment. We discuss how the latter is probably the reason why electron-poor polymers are generally more active for sacrificial hydrogen evolution than their electron-rich counterparts. We also study the barrier to hydrogen–hydrogen bond formation on the polymers rather than the co-catalyst and find that it too changes with composition but is always, at least for the polymers studied here, much larger than that experimentally reported for platinum. Therefore, it is expected that in the presence of any noble metal particles these will act as the site of hydrogen evolution.

---

1 Introduction

Carbon-free fuels may be of great importance in helping reduce the impact of global warming. Molecular hydrogen is widely considered to be the most promising of these as only water is produced upon combustion in a boiler, combustion engine or fuel cell. As a result of this a great deal of work is being undertaken to find cheap, sustainable, and environmentally friendly ways of producing hydrogen, not to mention ways of storing it efficiently.

One possible synthetic route for molecular hydrogen is through photocatalytic water splitting. Here one takes advantage of the natural abundance of solar energy, 885 million terawatt-hours of energy in the form of sunlight reaches the earth's surface per year according to the International Energy Agency,¹ and in the simplest terms only needs water, light and the photocatalyst to sustainably produce molecular hydrogen and oxygen. Commonly, crystalline inorganic solids are employed as the photocatalyst.^2–4 However, in recent years dispersions and films of organic materials and specifically conjugated oligomers/polymers, such as conjugated linear oligomers and polymers,^5–15 covalent organic frameworks^16–20 and carbon nitride^21–23 to name but a few, have also been shown to act as a photocatalyst for hydrogen and/or oxygen evolution. Often this activity is reported in the presence of sacrificial agents, which get oxidized (hydrogen evolution) or reduced (oxygen evolution) instead of water, but there are now also a number of studies reporting polymeric materials that are active for the overall splitting of water.^23–28 The interest in polymeric photocatalysts has been mainly driven by the relative ease by which the specific properties of the material can be tuned, though co-polymerization and functionalization, the fact that in the presence of solubilizing side-chains the polymers are solution processable, as well as the fact that the constituent elements are typically earth-abundant. Often noble/transition metal co-catalyst particles, such as Pd or Pt, are also present in or on the polymer. These co-catalyst particles may be intentionally added or may remain from the catalyst used to synthesize the polymer, which can be difficult to remove post-synthesis. It has been reported^29,30 that the evolution of hydrogen dramatically increases as a function of Pd content with essentially no hydrogen being evolved for Pd concentrations less than 1 ppm. Despite this, there are also reports in the literature of hydrogen evolution from organic materials that contain negligible noble metals or have been synthesized using metal-free pathways.^31,32

The evolution of molecular hydrogen using particulate polymeric photocatalysts is believed to occur with the exciton, formed through photoexcitation, driving one of the solution half-reactions and the remaining electron/hole the other. As a result of the typically large exciton binding energy in organic materials,³³ excitons, or at least excitons generated with light absorbed near the absorption onset of a material and hence with little excess energy, do not spontaneously dissociate to free electrons and holes in particles/films of conjugated polymers. Transient absorption spectroscopy has been used to confirm the presence of electrons/electron polarons in polymeric photocatalysts under sacrificial operating conditions,^7,11,34 suggesting that the exciton drives the transfer of an electron between the sacrificial electron donor (SED) and the polymer, oxidizing the SED in the process, and that the electron transferred to the polymer subsequently drives the reduction of protons. Previously, we used computational chemistry to explore a potential photocatalytic cycle for hydrogen evolution using poly(p-phenylene) as a prototypical linear conjugated photocatalyst and triethylamine (TEA) as the SED.³⁵ There a thermodynamic barrier was observed for the one-electron transfer step from TEA to the photoexcited P1 species when the calculations were performed in a low-dielectric environment akin to the likely experimental conditions for P1. As P1 is considerably hydrophobic the experimentally used mixture of TEA, methanol and water phase segregates at the microscale, enriching the local environment of the polymer particles in TEA and depleting it in water.⁷ This thermodynamic barrier would persist even in the presence of a noble metal co-catalyst, the likely site of hydrogen formation in the presence of any noble metal,³⁵ which could help explain, besides the fact that P1 absorbs little of the visible spectrum, why P1 is a relatively poor hydrogen evolution photocatalyst.

Here we extend our study of the photocatalytic cycle to electron-rich and electron-poor polymers in an attempt to shed light on the varying hydrogen evolution rates of these materials observed experimentally.^5,6,8 We investigate this cycle not only in thermodynamic terms but also pay considerable attention to the hydrogen formation barriers in the absence of a noble metal co-catalyst.

2 Computational details

2.1 Computational models

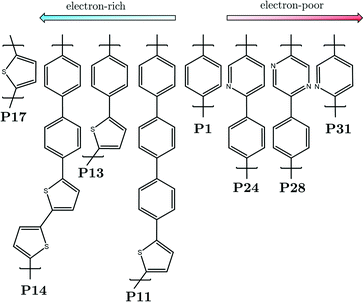
Each polymeric material of interest is modeled as a single oligomer containing 8 individual sub-units, the smallest repeat unit of each polymer of interest is shown in Fig. 1. The naming of the polymers, e.g. P1 for poly(p-phenylene), is that used in the experimental literature.^5,6,8 The oligomers were generated systematically from the relaxed scan around the dihedral coordinate of the dimer, ensuring a low-energy conformation was found for each. The oligomers are then embedded in either water or TEA, to approximate the environment of the polymer near the interface between the polymer particles/film and water or TEA. The effect of the solvent on the oligomers is simulated by an implicit polarizable continuum model (PCM), which recovers the main dielectric effect of solvation on the properties of the oligomers, whilst only slightly increasing the computational cost of the calculation. This simplistic model of a polymeric material has been used in previous studies to predict potentials of charge carriers and exciton species in organic conjugated polymers, and found to agree well when compared to available experimental photoelectron spectroscopy on polymeric solids,^11,36 and in the aforementioned P1 study.³⁵

Fig. 1 Smallest repeat unit of the various polymers of interest, where the number of repeat units used within each oligomeric model is varied such that the total number of thiophene, phenyl, pyridine and pyrazine building-blocks present in an oligomer equaled eight, polymers labeled P1 to P31.

2.2 Density functional theory

All density functional theory (DFT) calculations are performed with Gaussian 16 (Revision A.03).^37–39 As described above each oligomeric model of a polymer is embedded in a polarizable continuum model,^40–42 specifically the integral equation formalism (IEF)-PCM,⁴³ matching the relative dielectric permittivity (ε_r) of either water (ε_r = 78.36) or TEA (ε_r = 2.38). For the prediction of excited state properties, we utilize the linear response, time-dependent (TD), extension to DFT (TD-DFT).⁴⁴ All relevant structures were confirmed as minimum energy arrangements on the multi-dimensional potential energy surface via computation of the Hessian matrix, subsequently ensuring positive curvature of each vibrational mode, with the exception of the predicted transition state structures which had negative curvature along one mode pertaining to the reaction coordinate. All energy differences considered herein, unless otherwise stated, are adiabatic meaning that the geometry of the polymer is optimized for the specific electronic state of interest, and in equilibrium with the external reaction field. This is not the case for the predicted absorption spectra as this is considered a vertical process, due to the differing timescale of electron and nuclear motion, for which a non-equilibrium approach, which only considers the rapid solvent polarization from the shift in electron density, is used. All transition states were validated through intrinsic reaction coordinate (IRC) calculations, following both the forward and reverse direction of the transition vector and subsequently performing a geometry optimization.⁴⁵ In some instances IRC calculations were not possible, in which case the reaction profile was validated by manual displacement of the imaginary mode, once again optimizing these displaced structures. The B3LYP^46–48 and CAM-B3LYP⁴⁹ exchange-correlations functionals were used with Dunning's triple-ζ basis set, cc-pVTZ.^50,51 In all calculations dispersion interactions were included through Grimme's D3 dispersion correction.⁵² With the exception of vertical excitation energies and subsequent comparison to these, which are in terms of electronic energies, all values provided are in terms of free energies obtained from standard ideal gas, rigid rotor and harmonic oscillator statistical models to the translational, rotational and vibrational energy levels of the species at 298 K. No free energy standard state corrections were included as these corrections would be small and only be relevant for TEA, when in the TEA extremum, and water, when in the water extremum, or when the number of reactant and product molecules differ. Unless explicitly stated otherwise, all values discussed herein are predicted using B3LYP/cc-pVTZ. Values predicted using CAM-B3LYP are provided in the accompanying ESI†.

3 Results and discussion

3.1 Cycle overview

As mentioned previously, in an earlier publication³⁵ we investigated a possible photocatalytic cycle involving the overall oxidation of TEA to diethylamine (DEA) and acetaldehyde (MeCHO) in the presence of water, culminating with the formation of molecular hydrogen. In this previous work we focused on the conjugated linear polymer poly(p-phenylene), P1, as the catalytic light-harvesting material and proposed cycles in the absence and presence of a noble metal co-catalyst. Here we build on this previous work and investigate the proposed photocatalytic cycles when the electronic character of the polymer changes to electron rich, after substitution of phenyl monomers for thiophene, or electron poor, after insertion of pyridine or diazine monomers. See Fig. 1 for all the polymers of interest (x) and the nomenclature used.

The overall metal-free cycle can be decomposed into two connected sub-cycles, sub-cycle I which involves the initial sacrificial electron donor, TEA, and sub-cycle II which involves the dehydrogenated TEA radical, TEAR˙ (N(CHCH₃)(CH₂CH₃)₂), a product of sub-cycle I. These sub-cycles have been illustrated in Fig. 2. In both sub-cycles the first step, step A, is photoexcitation of the polymer, resulting in the formation of a localized S_n exciton, where n represents an electronically excited state with a non-zero oscillator strength, on the organic material which, due to Kasha's rule, would rapidly internally convert to the S₁ state, subsequently relaxing to a lower-energy S₁ minimum energy geometry (x*). As the exciton binding energy (EBE) in these materials, as discussed above, typically far exceeds the thermal energy available at room temperature (EBE > k_BT)³³ the photogenerated exciton normally remains bound and does not spontaneously fall apart to free-charge carriers. Instead, the exciton can accept an electron (electron transfer, ET) from either TEA, step B1, or TEAR˙, step B2, resulting in the formation of an electron/electron-polaron polymeric species (x˙⁻). Subsequently, proton transfer (PT) from either the one-electron oxidized TEA, TEA˙⁺ in step C1, or one-electron oxidized TEAR˙, TEAR⁺ in step C2, to x˙⁻ can take place, ultimately resulting in the formation of a polymer with a hydrogen atom adsorbed (x–H˙). The cycle culminates with the formation of one molecule of molecular hydrogen for every two polymers with a hydrogen atom adsorbed. These hydrogen-adsorbed polymers may originate from sub-cycle I and/or sub-cycle II, even if stoichiometry dictates that on average a molecule of hydrogen should form from one species with a hydrogen atom adsorbed from each sub-cycle. Therefore, in the thermodynamic analysis we assume that half a molecule of molecular hydrogen is produced upon completion of each sub-cycle, step D. The sequential electron and proton transfer steps in each of the sub-cycles can also in principle occur synchronously, step E (see also Fig. S1†), resulting in the transfer of a hydrogen atom in one step to the photoexcited polymer, i.e., proton-coupled-electron transfer or hydrogen atom transfer, as explored in the case of water oxidation by Domcke and co-workers.⁵³

Fig. 2 The proposed hydrogen evolution photocatalytic cycles in the absence (a) and presence (b) of a noble metal co-catalyst, when using triethylamine as the initial sacrificial electron donor. Step A, B, C and D are the same for both sub-cycle I (red) and II (blue). Step E corresponds to the case of synchronous instead of sequential electron and proton transfer. A specific cycle for the synchronous transfer can be found in the ESI (Fig. S1†).

The proposed catalytic cycle in the presence of a noble metal co-catalyst is similar to its counterpart in the absence of metal, with ET following photoexcitation and relaxation of the polymer, which can once again happen from either TEA or TEAR˙. The major difference between the two cycles is that instead of proton transfer, the x˙⁻ species instead transfers an electron to a noble metal particle, such as Pt, which would then act as the catalytic site for molecular hydrogen formation.

3.2 Free energy profiles

We begin with an exploration of the predicted free energy profiles of sub-cycles I and II. The free energy profiles for oligomers of electron-rich polymers immersed in water and TEA are shown in Fig. 3a and b, respectively. The equivalent free energy profiles for electron-poor materials are shown in Fig. 3c and d. In all spectra the P1 profile is shown for reference.

Fig. 3 The predicted free energy profiles for sub-cycle I and II, left and right of the dashed line respectively, for oligomers of electron-rich materials immersed in water (a) and triethylamine (b), and for oligomers of electron-poor materials immersed in water (c) and triethylamine (d). In all panels P1 has been added for reference (green diamonds). All values are predicted using D3-B3LYP/cc-pVTZ and are relative to the neutral polymer and triethylamine. For each oligomer the lowest-energy hydrogen adsorption site was used. The x-axis labels omit any reference to triethylamine or the degradation products. See Fig. S11† for values predicted using D3-CAM-B3LYP/cc-pVTZ.

All free energy profiles follow a somewhat similar trend with the initial ET process after photoexcitation and photoexcitation itself, step B1 and A respectively, uphill in energy with the rest of the steps downhill, except for electron-poor polymers immersed in water, where the initial ET step is also thermodynamically favorable. To make this clearer the predicted free energy change for step B1 (ΔB1) and its B2 counterpart (ΔB2) in both environments are shown in Fig. 4a and b, respectively. For electron-rich materials, step B1 is predicted to be endergonic in water (ΔB1 > 0), with the degree of endergonicity increasing with the relative thiophene content in the polymer and its adiabatic electron affinity (see Fig. S7 and Table S5†). In TEA, the initial ET step becomes even more unfavorable for electron-rich polymers when compared to the high-dielectric water environment, with predicted ΔB1 values in excess of 1.5 eV (see Table S6†). For electron-poor polymers, we instead predict that step B1 is exergonic in water (ΔB1 < 0). However, just as for electron-rich polymers this step is once again predicted to be endergonic in TEA. For all polymers ET from TEAR˙ is exergonic (ΔB2 < 0), more so for electron-poor polymers and in the high-dielectric environment.

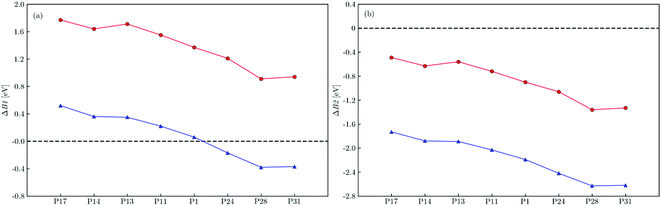Fig. 4 The predicted free energy difference for electron transfer to the photoexcited polymer from triethylamine, ΔB1, (a) and dehydrogenated triethylamine, ΔB2, (b) within a dielectric continuum representing water (blue triangles) and triethylamine (red circles). All values predicted using D3-B3LYP/cc-pVTZ. See Fig. S12† for values predicted using D3-CAM-B3LYP/cc-pVTZ.

After ET the next step of the catalytic cycle, in the absence of any co-catalyst, involves PT. For each polymer we modeled various hydrogen adsorption sites, see Fig. S10† for an illustration of these sites and Tables S1 and S2† for the corresponding free energies. We only studied hydrogen adsorption at the terminal units of each oligomer as in our previous work on P1 we found these to be the lowest free energy adsorption sites. Hydrogen adsorption on the units in the middle of the P1 oligomer was predicted to be slightly less favorable yet similar enough that the values determined for the terminal units are representative for hydrogen adsorption on similar sites across the oligomer. For P1 the lowest free energy site was site C₃ in both environments. For electron-rich polymers the lowest free energy site was once again predicted to be a carbon atom, site C₁, with adsorption on the sulfur atom predicted to upwards of 1.8 eV less favorable in free energy in both dielectric environments. Instead, for electron-poor materials adsorption at the heteroatom, nitrogen, is the most favorable. For example, in P31 hydrogen adsorption on the nitrogen atom is predicted to be 0.33 eV lower in free energy than adsorption on the most favorable carbon atom, site C₁, in both dielectric environments. The PT free energies in the following discussion are calculated for the most favorable hydrogen adsorption site of each oligomer, denoted by a green circle in Fig. S10†.

For all polymers the PT step C1 is predicted to be exergonic, more so for electron-rich polymers. Switching from the high-dielectric to low-dielectric environment results in a drastic increase in the exergonicity of step C1, for P17 the free energy difference of step C1 was predicted to be −0.41 eV and −1.78 eV in water and TEA, respectively. As previously reported, this is due to the similar stabilization of the non-charged species in both environments, therefore essentially gaining back the additional energy cost of the previous ET reaction, B1, in TEA. An analogous situation is predicted for step C2, however, the exergonicity is increased by approximately 0.1 eV when compared to step C1.

Up to this point, we have thought of ET and PT occurring sequentially. However, as discussed in the introduction, ET and PT may occur synchronously, via the transfer of a hydrogen atom to x*. The predicted free energy difference of steps E1 (ΔE1) and E2 (ΔE2) are shown in Fig. S12 and S13 and in Tables S5 and S6.† Step E1 is predicted to be exergonic for all polymers and dielectric environments except for P17-water, with an ΔE1 of 0.11 eV. However, when using the CAM-B3LYP functional step E1 is also predicted to be exergonic in this case, a rare qualitative difference in values predicted by B3LYP and CAM-B3LYP. For step E2 the exergonicity is drastically increased when compared to step E1 as a result of the increased reductant character of TEAR˙.

Finally, the formation of molecular hydrogen, step D, was found to be exergonic for all polymers and dielectric environments.

3.3 Onset of light absorption

Compared to P1, both the electron-poor and electron-rich polymers studied show, in line with what we observed in previous work,^6,8 a clear redshift of the onset of light absorption. This redshift is most pronounced in the case of the electron-rich polymers with the S₁ vertical excitation energy (VEE) of P17 and P28 immersed in water predicted to be 2.07 eV and 3.02 eV, respectively, compared with 3.51 eV for P1. The differences between the VEE in water and TEA are minimal with the largest deviation of 0.06 eV for P31. See Tables S5 and S6† for the predicted S₁ VEE of all the polymers.

3.4 Hydrogen formation barriers

In addition to the thermodynamic pathway and onset of light absorption by the polymers, we also investigate the kinetic barrier to molecular hydrogen formation for the case where the polymer rather than a noble-metal co-catalyst catalyzes the hydrogen bond formation step. For this scenario we find for all polymers, using dimer oligomers as models, a transition state (structure 2) linking the reactant and product species, the former being a stack of two polymers with each one hydrogen atom adsorbed (structure 1) and the latter the stack of two polymers and molecular hydrogen (structure 3), see Fig. 5. The hydrogen formation barriers can be predicted with respect to various hydrogen adsorption sites on the polymers, see Fig. S10† for the labels of the different sites where the outer units form the complete oligomer in this reduced dimer model. Here, unless states otherwise, we present hydrogen formation barriers relative to the lowest free-energy adsorption site for an oligomer, as discussed in Section 3.2.

Fig. 5 The predicted free energy reaction profile of hydrogen formation (structures 1–3) for P17 (cyan double line), P1 (green dashed line), P24 (yellow solid line), P28 (purple dashed double dotted line) and P31 (red dotted line) oligomers immersed in water, starting in all cases from the most stable hydrogen adsorption site. The competing crosslinking reaction pathway (structures 1–3’’) has also been provided for P1 and P31 immersed in water. All values predicted using D3-B3LYP/cc-pVTZ, given in terms of eV and relative to two polymers with a hydrogen atom adsorbed, structure 1. An illustration of the hydrogen formation pathway and the crosslinking pathway are shown using P1 as an example.

For P1 in water a barrier height of 0.19 eV was predicted. This value is significantly lower than that predicted in our previous work,³⁵ which employed a rigid scan starting from a tail-to-tail rather than a stacked arrangement. For electron-poor polymers the barrier heights were predicted to be far larger, upwards of 0.92 eV when modeled within water. In addition to the nitrogen heteroatom site in P31, we also considered barriers starting from hydrogen adsorbed on carbon sites (see Fig. S15†). This change in adsorption site results in a vast reduction in predicted barrier heights for P31 in water. For example, the barrier for P31 in water starting from hydrogen adsorbed on the C₁ site is 0.33 eV, which is comparable to that of P1. However, as adsorption on the carbon sites rather than the nitrogen sites in P31 and other electron-poor polymers is, as discussed above in Section 3.2, much less thermodynamically favorable, there is an extra energetic penalty to pay. If one considers the free energy difference between a stack of two polymers with hydrogen atoms adsorbed on the nitrogen and C₁ site, 0.73 eV in the case of the dimer used here and approximately twice the value discussed above in Section 3.2, then the effective barrier height when going via the C₁ site is 1.06 eV (0.73 eV + 0.33 eV), not that dissimilar from the barrier height directly calculated for the nitrogen site (0.98 eV).

For P17 in water a barrier of 0.93 eV was predicted, despite once again involving a carbon atom as the site of hydrogen adsorption. We also predicted the barrier height for P17 in TEA and found it to be 0.91 eV. The minimal difference for the calculations in water and TEA is expected as all species involved in the reaction profile are electronically neutral and supports our choice to perform these calculations in only one of the two environments.

Hydrogen formation barriers for other polymers have also been predicted by other authors in previous work using a similar computational setup.^54,55 Xiang et al. predicted hydrogen formation barriers upwards of 1.54 eV for a series of electron-withdrawing, F, and electron-donating, methoxy, substituted benzothiadiazole units in various co-polymers.⁵⁵ In these calculations the hydrogen adsorption site was taken to be one of the nitrogen atoms in the benzothiadiazole sub-unit. Araujo et al. predicted a barrier of 1.32 eV, once again involving a benzothiadiazole based co-polymer and hydrogen adsorption on a nitrogen atom.⁵⁴ Part of the difference between the barrier heights for the similar substitution sites results from the use of different functionals, Xiang et al. used ωB97XD and Araujo et al. B3LYP. All barriers predicted here, irrespective of the hydrogen adsorption site, were found to be lower than those predicted for the donor–acceptor materials in these previous papers.

During the exploration of the hydrogen formation mechanism, a competing pathway was observed starting from a stack of two polymers with a hydrogen atom adsorbed where, instead of molecular hydrogen and two polymers, a structure with a covalent bond between the two polymer strands (structure 3’’) was formed, see Fig. 5 and 6, effectively crosslinking two polymer strands. This competing reaction with a transition state (structure 2’’) which resembles structure 1, is predicted to have in the case of P1 immersed in water a barrier height of 0.03 eV and is thus kinetically the most favorable pathway. Despite being kinetically favorable, the hydrogen formation pathway (1→3) is still the most thermodynamically favorable reaction, with hydrogen formation, free energy change −2.54 eV, predicted to be three times more exergonic than crosslinking, free energy change −0.8 eV. The product of the kinetically favorable crosslinking 1→3” pathway may act as a hydrogen trap due to the predicted barrier of 0.83 eV to revert to the non-crosslinked stacked structure 1, thereby inhibiting the formation of molecular hydrogen. We also explored the crosslinking pathway for P31 in water for which a barrier of 0.28 eV is predicted between the non-crosslinked, structure 1, and crosslinked structure, structure 3”, almost an order of magnitude larger than that for P1 in water but still much lower compared to that of the hydrogen formation pathway. Just as for P1 the crosslinking pathway for P31 in water starting from structure 1 is predicted to be less favorable, predicted free-energy change −0.32 eV, than the hydrogen evolution pathway, predicted free energy change −1.59 eV. However, the crosslinked structure 3” again can act as hydrogen trap with a predicted reverse barrier of 0.60 eV between the crosslinked, structure 3”, and non-crosslinked structure, structure 1. A similar crosslinked structure as for P1 and P31 is also observed for the other pyridine-based polymer, P24. The 1→3” barrier for P24 was not calculated explicitly, however, we expect them to be similar to those predicted for P31. No sign of a crosslinked structure was observed for P17.

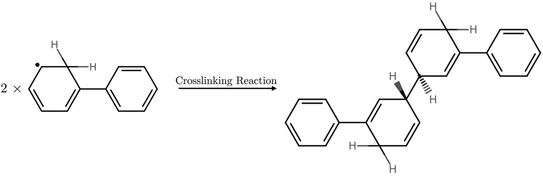Fig. 6 Chemical Structures of the reactants and product species involved in the P1 crosslinked reactions.

Considering the free-energy profile shown in Fig. 5 and the discussion of the two competing pathways above, any 1 formed by proton transfer to two nearby polymer sites in the case of all polymers studied, with the exception of P17, will rapidly interconvert to 3”. Hydrogen evolution can then be described as 3”→1→3. Because the barrier for the back reaction from 1 to 3” is always 3–4 times lower than the barrier for the forward reaction from 1 to 3, as well as lower than the barrier from 3” to 1, the conversion of 1 to 3 with transition state 2 is likely the rate-determining step, just like it would be in the absence of the crosslinked structure 3. However, the effective barrier for P1 and P31 will not simply be the 1→2 barrier height but the sum of it and the free energy difference between 3” and 1, i.e. 0.99 eV in the case of P1 and 1.30 eV for P31. Similarly, we estimate the effective barrier for P24 to be 1.37 eV (0.92 eV + 0.45 eV). Taking this into account the nitrogen containing electron-poor polymers are predicted to have considerably higher effective barriers to hydrogen evolution than P1 and P17. However, even the predicted effective barriers for P1 and P17 are considerably larger than that measured experimentally for platinum (0.1–0.2 eV depending on the surface⁵⁶).

4 Discussion

In the above we calculated free energy profiles, onset of light absorption and barriers to hydrogen evolution for oligomers of the different polymers in a dielectric continuum as models for particles of these polymers immersed in the mixture of TEA, water and methanol used experimentally in sacrificial hydrogen evolution experiments. We specifically modeled two extremes, oligomers in pure water and in pure TEA. Previous molecular dynamics calculations⁷ demonstrated that in the presence of the polymer the reaction mixture phase-separates on the nanoscale with the environment of the polymer being enriched with TEA for hydrophobic polymers such as P1 and enriched in water for more hydrophilic polymers. The behaviour of polymers immersed in the TEA, water and methanol reaction mixture will thus likely lie in between that predicted for the two studied extremes, with hydrophobic polymers behaving more akin to the TEA extreme and the more hydrophilic polymers more similar to the water extreme. Moreover, because the shift of EA*, and other potentials, with the dielectric permittivity of the environment is non-linear⁵⁷ and proportional to 1/ε_r, the polymer environment is always more water-like than naively expected based on the local water concentration.

For P1 and the electron-rich polymers electron transfer between the polymers and the sacrificial electron donor, TEA, when immersed in water is predicted to be endergonic thus indicating the presence of a thermodynamic barrier for this step. In contrast, for electron-poor polymers under the same conditions this electron transfer step is exergonic and as such no thermodynamic barrier to electron transfer is observed. When immersed in TEA, finally, a thermodynamic barrier to electron transfer is predicted to exist for all polymers, more so for electron-rich polymers. The second electron transfer from dehydrogenated TEA is predicted to be exergonic for all polymers, independent if immersed in water or TEA, as a result of the increased reductant strength of dehydrogenated TEA. For P1 we previously argued that because of its hydrophobicity the local environment near the polymer particles will likely be enriched with TEA, making the polymer behave more like in TEA than in water, and that hence the height of the thermodynamic barrier to electron transfer from TEA in this local low-dielectric permittivity environment was one of the reasons why P1 is not a particular active hydrogen evolution photocatalyst. The heteroatom containing polymers studied here are all likely to be more hydrophilic than P1, but it is unclear by how much. However, even if in the case of the most favorable scenario, the pure water extreme, our calculations predict that for electron-rich polymers there will be a substantial thermodynamic barrier to electron transfer from TEA which should limit their activity for hydrogen evolution. Similarly, the calculations predict that the thermodynamic barrier to electron transfer from TEA is in both dielectric extremes lower for electron-poor polymers than for electron-rich polymers, suggesting that electron-poor polymers are always a better choice in terms of the thermodynamics of hydrogen evolution. The latter conclusion is in line with what a simpler analysis in terms of the potentials of charge carriers and excitons in the polymers and those of the solution reactions predicts.^6,8 Finally, as transient spectroscopy suggests that even in the presence of a noble metal co-catalyst the exciton dissociates on the polymer by accepting an electron from TEA^7,11 the presence of a thermodynamic barrier for electron transfer will also be a potential limiting factor when the noble metal particle catalyzes the hydrogen formation. Thus, even with a noble metal co-catalyst electron-poor polymers are preferred over electron-rich polymers in terms of thermodynamics.

The proton transfer step following electron transfer, or the transfer of the electron to the co-catalyst in the presence of metal nanoparticles, is in direct competition with the ground state back reaction, where the extra electron is transferred back from the reduced polymer to TEA˙⁺/TEAR⁺ forming the polymer and TEA/TEAR˙ in their ground electronic states, see Tables S3 and S4† for the reaction energetics in both water and TEA (x˙⁻ + TEA˙⁺/TEAR⁺ → x + TEA/TEAR˙). The back reaction in the case of TEA˙⁺ as the electron acceptor is extremely exergonic, more so in TEA. Whilst still extremely exergonic, the exergonicity of this reaction is lower for electron-rich and electron poor polymers when compared to P1 and lowers as the thiophene/nitrogen content increases. In terms of the back reaction involving TEAR⁺ as the electron acceptor the exergonicity of this unwanted reaction is much reduced when compared to TEA˙⁺. In water the back reaction with TEAR⁺ even becomes endergonic for the most electron-rich polymers (P28 and P31) and very close to for P17, thereby significantly reducing how competitive the back electron transfer step will be with proton transfer or electron transfer to the co-catalyst. In TEA, the back reaction with TEAR⁺ is still considerably exergonic for all polymers. The back reaction is thus likely a significant loss channel, in the presence and absence of a co-catalyst, and irrespective of the environment of the polymer.

There is potentially also a back reaction starting from the polymer with the adsorbed hydrogen (i.e. x–H˙ + TEAR˙ → x + TEA and x–H˙ + DEA + MeCHO → x + TEAR⁺ + H₂O). However, that back reaction in both water and TEA is less exergonic than its counterpart starting from x˙⁻ when TEAR˙ accepts the electron and proton, and generally endergonic when DEA and MeCHO should accept the electron and proton. While the back reaction starting from x˙⁻ is barrierless, this back reaction also has a barrier of −ΔC1/−ΔC2 (see Tables S5 and S6†) to overcome. This barrier is typically moderate in size in the water extreme but rather large for the TEA extreme. As a result, the back reaction starting from the polymer with the adsorbed hydrogen will probably be less of a loss channel than its x˙⁻ counterpart, especially for the more hydrophobic polymers.

If electron and proton transfer would take place in a concerted fashion rather than sequentially, as discussed above, the free energy profile is all downhill after excitation for all polymers, except possibly P17, in both the pure water and TEA extremes. As a result, there would be no thermodynamic barrier under any condition, one again with the exception of possibly P17. There will be a back reaction starting from x–H˙, along the lines discussed above, though in this case it might be barrierless, depending on if the back electron and proton transfer would also take place in a concerted fashion. It is difficult to rule out concerted electron and proton transfer computationally, at least using the type of calculations performed here, but a concerted mechanism appears at odds with the experimental observation of electron polarons in polymer photocatalysts under sacrificial operating conditions by transient absorption spectroscopy. While the latter experiments were performed in the presence of a noble metal co-catalyst, it would at least suggest that sequential electron transfer to the polymer and proton transfer, in this case, to the co-catalyst is not only possible but clearly the dominant mechanism under these conditions. The same may hold true in the absence of co-catalysts.

The optical gap is another property of the polymers which impacts the formation of molecular hydrogen. The greater the overlap between a polymer's absorption spectrum and the solar spectrum the more excitons that can be formed. Compared to P1, which only starts absorbing light on the edge of the visible and the ultraviolet (predicted absorption onset of 3.5 eV), the predicted absorption onset of all the electron-rich and electron-poor polymers studied here are redshifted, with P17 having the lowest absorption onset on the red-side of the visible spectrum (predicted absorption onset 2.1 eV). The absorption onset of P28, which was the lowest of all electron-rich polymers, is predicted to be 3.1 eV, which is lower than P1 but around 1 eV higher than that of P17. Therefore, in contrast to the analysis in terms of the thermodynamics, in terms of light absorption and the number of excitons generated from solar light, within the set of polymers studied here at least, the electron-rich polymers have the edge over the electron-poor polymers.

Independent of the heteroatom present, our calculations predict that polymers should be able to catalyze the formation and evolution of hydrogen in the absence of any co-catalyst. However, even the best polymer studied here would do this much less efficiently than noble metal particles due to the higher hydrogen–hydrogen bond formation barriers predicted for the polymers. Diffusion of adsorbed hydrogen atoms on the polymers also likely will be slower than on noble metal surfaces. Therefore, we would argue, as we already did in our original work on P1, that in the presence of a noble metal co-catalyst, most if not all, hydrogen will be evolved on the noble metal co-catalyst. In the absence of any noble metal, electron-rich P17 and P1 are predicted to be the best choice in terms of the barrier for hydrogen evolution. However, with barrier heights of the order of 40k_BT at room temperature the reaction rates might be in practice very low and possibly vanishingly small.

As an aside, the fact that the barrier height for the hydrogen–hydrogen bond formation step differs with the type of sites present in the polymer and that the sites that give rise to the lowest barrier, e.g. aromatic carbons when present, are not necessarily active as other sites adsorb hydrogen atoms more strongly, e.g. pyridinic nitrogens, means that one should be careful with extrapolating the observation for a few polymers that the catalytic activity completely disappears when removing all noble metal to all polymers. That said, as the rates over the polymers, as discussed above, could be very low, they might be difficult to observe experimentally.

The energy required to overcome barriers, be them the thermodynamic barriers discussed above or the kinetic barrier of the hydrogen–hydrogen bond formation, should come from the heating up of the material through the absorption of light. The latter takes the form of the absorption of infrared light through vibrational transitions, where not absorbed by water, and energy dissipated in the material after light absorption in the form of vertical internal conversion from higher excited-states to the lowest singlet excited-state and subsequent geometrical relaxation on its potential energy surface. The difference between the vertical and adiabatic excitation energies, suggests that geometrical relaxation already typically results in the dissipation of 0.2–0.5 eV per photon absorbed.

Summarizing the above, our analysis of the proposed photocatalytic cycle suggests that in terms of thermodynamics electron-poor polymers should be the optimal choice both in the absence and presence of a noble metal co-catalyst. In contrast, in terms of the optical gap and overlap with the solar spectrum electron-rich polymers appear the best choice. Finally, in the case of the hydrogen–hydrogen bond formation step in the absence of a noble metal co-catalyst there is less of a link to the electronic properties of the polymers and more to specific adsorption sites on the polymers. That said the pyridinic nitrogen atoms which make the electron-poor polymers electron-poor, give rise to the highest barrier for hydrogen evolution of all sites considered. We can compare these conclusions to the experimental hydrogen evolution rates for the polymers discussed here,^6,8 all measured in the presence of Pt, as well as in most cases residual Pd remaining from the catalyst used in polymer synthesis. The electron poor P28, P31 and P24 polymers are experimentally the most active with P17 the least, which appears to follow the trend expected from the thermodynamic barrier height to electron transfer predicted here. Conversely, the fact that P11, P13 and P14 are experimentally more active than P1, while in terms of the electron transfer barrier height the opposite would be expected. However, that could be explained, as we concluded in our previous work when modelling the system using the potentials of charge carriers and excitons in the polymers and those of the solution reactions,⁸ by a trade-off between the thermodynamic driving force, i.e. the electron transfer barrier height, and a reduced optical gap and thus an increase in light absorbed and excitons created.

Finally, the crosslinked structures observed for P1 and P31, when studying the barriers for hydrogen–hydrogen bond formation, could potentially store the energy of absorbed light when no co-catalyst is present to consume the excited electrons and the barrier for hydrogen–hydrogen bond formation by the polymer itself is too high. Such a dark energy storage process has been previously demonstrated in the case of carbon nitride.⁵⁸ There, if a soluble co-catalyst, e.g. colloidal platinum, is added to carbon nitride material containing particular structural defects which was previously illuminated in the presence of a sacrificial electron donor but in the absence of co-catalyst, hydrogen evolution in the dark takes place driven by electrons stored during illumination. In the case of carbon nitride these electrons are stored as electrons or possibly adsorbed hydrogen atoms based on electron paramagnetic resonance (EPR) spectroscopy. Our prediction would be that in P1 and P31 and probably other (co-)polymers the charge could and would be stored in the form of the crosslinked structures as it is the lowest energy intermediate in the cycle before hydrogen–hydrogen bond formation. Upon addition of a soluble co-catalyst the hydrogen atoms trapped in the metastable crosslinked structure are likely able to untrap and form hydrogen because the co-catalyst unlocks a new low(er) barrier hydrogen evolution pathway and by its mobility in solution can hoover up adsorbed hydrogen atoms from crosslinked structures. Studying dark energy storage in polymers mediated by the crosslinked structures will, however, be challenging. Firstly, the crosslinked structures are singlets and thus EPR silent. When optimized as a triplet the crosslinked structures revert to the non-crosslinked structure. Secondly, crosslinked structures are also associated with less dramatic changes in the UV-vis spectra and thus colour (see Fig. S4†) than for open-shell defects (though are associated with specific infrared modes, see Section S9 of the ESI,† which might allow for identification that way). Additionally, it might be difficult to remove any residual palladium left over from synthesis which might act as a co-catalyst and hence prevent dark energy storage from occurring.

5 Conclusions

We explored a photocatalytic cycle for sacrificial hydrogen evolution by heteroatom substituted linear polymers both in the absence and presence of a noble metal co-catalyst. We predict that all steps in the catalytic cycle are thermodynamically downhill after the initial excitation by light other than, for most polymers, the first electron transfer between the sacrificial electron donor, TEA, and the polymer. As a result, this electron transfer step is predicted to give rise to a thermodynamic barrier, which changes both with polymer composition and the local dielectric properties of the water sacrificial electron donor mixture close to the polymer particle solution interface. This thermodynamic barrier is largest for electron-rich polymers when the local environment is enriched in TEA and is absent for electron-poor polymers in a water rich environment. We analyzed the ability of the different polymers to catalyze the hydrogen–hydrogen bond formation and thus hydrogen evolution. We found that while polymers indeed appear able to act as hydrogen–hydrogen bond formation catalysts that the predicted barriers of 0.9–1.3 eV are much larger than those reported experimentally for noble-metals. Based on this we believe that in the presence of any noble metal this will act as a co-catalyst and instead of the polymer will be the site of hydrogen evolution. Finally, in the process of studying the hydrogen–hydrogen bond formation on polymers we discovered that for some polymers, polymer chains with an adsorbed hydrogen atom can spontaneously crosslink, forming a carbon–carbon bond between the polymer chains. As the creation of these crosslinked structures is less energetically favorable than molecular hydrogen formation, they will likely only exist fleetingly. However, their ability to act as hydrogen traps is predicted to influence the hydrogen–hydrogen bond formation kinetics. Also, in the absence of any co-catalyst and for sufficiently sluggish inherent hydrogen–hydrogen bond formation activity of the polymer, these crosslinked structures might give rise to dark energy storage, similar to what was previously demonstrated for carbon nitride.

Associated content

The TD-DFT predicted absorption spectra, DFT predicted infrared spectra, DFT predicted spin densities and all energetic properties of interest (PDF).

D3-B3LYP/cc-pVTZ optimized geometries of all relevant structures (ZIP).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We kindly acknowledge Dr Niklaas J. Buurma, Prof. Michael J. Porter, Dr David M. Rowley and an anonymous referee for discussion and the Leverhulme Trust (RPG-2019-209) and the UK Engineering and Physical Sciences Research Council (EP/N004884/1) for funding.

References

1. C. Philibert, Solar Energy Perspectives. IEA Publications: Paris, 2011.
2. S. Chen, T. Takata and K. Domen, Particulate photocatalysts for overall water splitting, Nat. Rev. Mater., 2017, 2(10), 17050.
3. Z. Wang, C. Li and K. Domen, Recent developments in heterogeneous photocatalysts for solar-driven overall water splitting, Chem. Soc. Rev., 2019, 48(7), 2109–2125.
4. Q. Wang and K. Domen, Particulate Photocatalysts for Light-Driven Water Splitting: Mechanisms, Challenges, and Design Strategies, Chem. Rev., 2020, 120(2), 919–985.
5. R. S. Sprick, B. Bonillo, R. Clowes, P. Guiglion, N. J. Brownbill, B. J. Slater, F. Blanc, M. A. Zwijnenburg, D. J. Adams and A. I. Cooper, Visible-Light-Driven Hydrogen Evolution Using Planarized Conjugated Polymer Photocatalysts, Angew. Chem., Int. Ed., 2016, 55(5), 1792–1796.
6. R. S. Sprick, L. Wilbraham, Y. Bai, P. Guiglion, A. Monti, R. Clowes, A. I. Cooper and M. A. Zwijnenburg, Nitrogen Containing Linear Poly(phenylene) Derivatives for Photo-catalytic Hydrogen Evolution from Water, Chem. Mater., 2018, 30(16), 5733–5742.
7. M. Sachs, R. S. Sprick, D. Pearce, S. A. J. Hillman, A. Monti, A. A. Y. Guilbert, N. J. Brownbill, S. Dimitrov, X. Shi, F. Blanc, M. A. Zwijnenburg, J. Nelson, J. R. Durrant and A. I. Cooper, Understanding structure-activity relationships in linear polymer photocatalysts for hydrogen evolution, Nat. Commun., 2018, 9(1), 4968.
8. R. S. Sprick, C. M. Aitchison, E. Berardo, L. Turcani, L. Wilbraham, B. M. Alston, K. E. Jelfs, M. A. Zwijnenburg and A. I. Cooper, Maximising the hydrogen evolution activity in organic photocatalysts by co-polymerisation, J. Mater. Chem. A, 2018, 6(25), 11994–12003.
9. Y. Bai, L. Wilbraham, B. J. Slater, M. A. Zwijnenburg, R. S. Sprick and A. I. Cooper, Accelerated Discovery of Organic Polymer Photocatalysts for Hydrogen Evolution from Water through the Integration of Experiment and Theory, J. Am. Chem. Soc., 2019, 141(22), 9063–9071.
10. A. Liu, C.-W. Tai, K. Holá and H. Tian, Hollow polymer dots: nature-mimicking architecture for efficient photocatalytic hydrogen evolution reaction, J. Mater. Chem. A, 2019, 7(9), 4797–4803.
11. D. J. Woods, S. A. J. Hillman, D. Pearce, L. Wilbraham, L. Q. Flagg, W. Duffy, I. McCulloch, J. R. Durrant, A. A. Y. Guilbert, M. A. Zwijnenburg, R. S. Sprick, J. Nelson and A. I. Cooper, Side-chain tuning in conjugated polymer photocatalysts for improved hydrogen production from water, Energy Environ. Sci., 2020, 13(6), 1843–1855.
12. C. M. Aitchison, M. Sachs, M. A. Little, L. Wilbraham, N. J. Brownbill, C. M. Kane, F. Blanc, M. A. Zwijnenburg, J. R. Durrant, R. S. Sprick and A. I. Cooper, Structure–activity relationships in well-defined conjugated oligomer photocatalysts for hydrogen production from water, Chem. Sci., 2020, 11(33), 8744–8756.
13. R. S. Sprick, Z. Chen, A. J. Cowan, Y. Bai, C. M. Aitchison, Y. Fang, M. A. Zwijnenburg, A. I. Cooper and X. Wang, Water Oxidation with Cobalt-Loaded Linear Conjugated Polymer Photocatalysts, Angew. Chem., Int. Ed., 2020, 59(42), 18695–18700.
14. J. Kosco, M. Bidwell, H. Cha, T. Martin, C. T. Howells, M. Sachs, D. H. Anjum, S. Gonzalez Lopez, L. Zou, A. Wadsworth, W. Zhang, L. Zhang, J. Tellam, R. Sougrat, F. Laquai, D. M. DeLongchamp, J. R. Durrant and I. McCulloch, Enhanced photocatalytic hydrogen evolution from organic semiconductor heterojunction nanoparticles, Nat. Mater., 2020, 19(5), 559–565.
15. S. Han, T. Huang, Y. Pan, J. Zhao, H. Lin, H. Lin, Z. Ding, H. Xi and J. Long, Tunable linear donor–π–acceptor conjugated polymers with a vinylene linkage for visible-light driven hydrogen evolution, Catal. Sci. Technol., 2021, 11(12), 4021–4025.
16. L. Stegbauer, K. Schwinghammer and B. V. Lotsch, A hydrazone-based covalent organic framework for photocatalytic hydrogen production, Chem. Sci., 2014, 5(7), 2789–2793.
17. V. S. Vyas, F. Haase, L. Stegbauer, G. Savasci, F. Podjaski, C. Ochsenfeld and B. V. Lotsch, A tunable azine covalent organic framework platform for visible light-induced hydrogen generation, Nat. Commun., 2015, 6(1), 8508.
18. X. Wang, L. Chen, S. Y. Chong, M. A. Little, Y. Wu, W.-H. Zhu, R. Clowes, Y. Yan, M. A. Zwijnenburg, R. S. Sprick and A. I. Cooper, Sulfone-containing covalent organic frameworks for photocatalytic hydrogen evolution from water, Nat. Chem., 2018, 10(12), 1180–1189.
19. P. Pachfule, A. Acharjya, J. Roeser, T. Langenhahn, M. Schwarze, R. Schomäcker, A. Thomas and J. Schmidt, Diacetylene Functionalized Covalent Organic Framework (COF) for Photocatalytic Hydrogen Generation, J. Am. Chem. Soc., 2018, 140(4), 1423–1427.
20. K. Gottschling, G. Savasci, H. Vignolo-González, S. Schmidt, P. Mauker, T. Banerjee, P. Rovó, C. Ochsenfeld and B. V. Lotsch, Rational Design of Covalent Cobaloxime–Covalent Organic Framework Hybrids for Enhanced Photocatalytic Hydrogen Evolution, J. Am. Chem. Soc., 2020, 142(28), 12146–12156.
21. X. Wang, K. Maeda, A. Thomas, K. Takanabe, G. Xin, J. M. Carlsson, K. Domen and M. Antonietti, A metal-free polymeric photocatalyst for hydrogen production from water under visible light, Nat. Mater., 2009, 8(1), 76–80.
22. K. Maeda, X. Wang, Y. Nishihara, D. Lu, M. Antonietti and K. Domen, Photocatalytic Activities of Graphitic Carbon Nitride Powder for Water Reduction and Oxidation under Visible Light, J. Phys. Chem. C, 2009, 113(12), 4940–4947.
23. G. Zhang, Z.-A. Lan, L. Lin, S. Lin and X. Wang, Overall water splitting by Pt/g-C₃N₄ photocatalysts without using sacrificial agents, Chem. Sci., 2016, 7(5), 3062–3066.
24. J. Liu, Y. Liu, N. Liu, Y. Han, X. Zhang, H. Huang, Y. Lifshitz, S.-T. Lee, J. Zhong and Z. Kang, Metal-free efficient photocatalyst for stable visible water splitting via a two-electron pathway, Science, 2015, 347(6225), 970–974.
25. Y. Wang, A. Vogel, M. Sachs, R. S. Sprick, L. Wilbraham, S. J. A. Moniz, R. Godin, M. A. Zwijnenburg, J. R. Durrant, A. I. Cooper and J. Tang, Current understanding and challenges of solar-driven hydrogen generation using polymeric photocatalysts, Nat. Energy, 2019, 4(9), 746–760.
26. D. Kong, X. Han, J. Xie, Q. Ruan, C. D. Windle, S. Gadipelli, K. Shen, Z. Bai, Z. Guo and J. Tang, Tunable Covalent Triazine-Based Frameworks (CTF-0) for Visible-Light-Driven Hydrogen and Oxygen Generation from Water Splitting, ACS Catal., 2019, 9(9), 7697–7707.
27. S. Zhang, G. Cheng, L. Guo, N. Wang, B. Tan and S. Jin, Strong-Base-Assisted Synthesis of a Crystalline Covalent Triazine Framework with High Hydrophilicity via Benzylamine Monomer for Photocatalytic Water Splitting, Angew. Chem., Int. Ed., 2020, 59(15), 6007–6014.
28. Z. Pan, M. Liu, G. Zhang, H. Zhuzhang and X. Wang, Molecular Triazine–Heptazine Junctions Promoting Exciton Dissociation for Overall Water Splitting with Visible Light, J. Phys. Chem. C, 2021, 125(18), 9818–9826.
29. J. Kosco, M. Sachs, R. Godin, M. Kirkus, L. Francas, M. Bidwell, M. Qureshi, D. Anjum, J. R. Durrant and I. McCulloch, The Effect of Residual Palladium Catalyst Contamination on the Photocatalytic Hydrogen Evolution Activity of Conjugated Polymers, Adv. Energy Mater., 2018, 8(34), 1802181.
30. J. Kosco and I. McCulloch, Residual Pd Enables Photocatalytic H₂ Evolution from Conjugated Polymers, ACS Energy Lett., 2018, 3(11), 2846–2850.
31. Z. Zhang, J. Long, L. Yang, W. Chen, W. Dai, X. Fu and X. Wang, Organic semiconductor for artificial photosynthesis: water splitting into hydrogen by a bioinspired C₃N₃S₃ polymer under visible light irradiation, Chem. Sci., 2011, 2(9), 1826–1830.
32. C. Han, P. Dong, H. Tang, P. Zheng, C. Zhang, F. Wang, F. Huang and J.-X. Jiang, Realizing high hydrogen evolution activity under visible light using narrow band gap organic photocatalysts, Chem. Sci., 2021, 12(5), 1796–1802.
33. P. Guiglion, C. Butchosa and M. A. Zwijnenburg, Polymer Photocatalysts for Water Splitting: Insights from Computational Modeling, Macromol. Chem. Phys., 2016, 217(3), 344–353.
34. V. L. Piercy, K. H. Saeed, A. W. Prentice, G. Neri, C. Li, A. M. Gardner, Y. Bai, R. S. Sprick, I. V. Sazanovich, A. I. Cooper, M. J. Rosseinsky, M. A. Zwijnenburg and A. J. Cowan, Time-Resolved Raman Spectroscopy of Polaron Formation in a Polymer Photocatalyst, J. Phys. Chem. Lett., 2021, 12(44), 10899–10905.
35. A. W. Prentice and M. A. Zwijnenburg, Hydrogen evolution by polymer photocatalysts; a possible photocatalytic cycle, Sustainable Energy Fuels, 2021, 5(10), 2622–2632.
36. P. Guiglion, A. Monti and M. A. Zwijnenburg, Validating a Density Functional Theory Approach for Predicting the Redox Potentials Associated with Charge Carriers and Excitons in Polymeric Photocatalysts, J. Phys. Chem. C, 2017, 121(3), 1498–1506.
37. P. Hohenberg and W. Kohn, Inhomogeneous Electron Gas, Phys. Rev., 1964, 136(3B), B864–B871.
38. W. Kohn and L. J. Sham, Self-Consistent Equations Including Exchange and Correlation Effects, Phys. Rev., 1965, 140(4A), A1133–A1138.
39. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. A.01, Wallingford, CT, 2016.
40. S. Miertuš, E. Scrocco and J. Tomasi, Electrostatic interaction of a solute with a continuum. A direct utilizaion of AB initio molecular potentials for the prevision of solvent effects, Chem. Phys., 1981, 55(1), 117–129.
41. R. Cammi and J. Tomasi, Remarks on the use of the apparent surface charges (ASC) methods in solvation problems: Iterative versus matrix-inversion procedures and the renormalization of the apparent charges, J. Comput. Chem., 1995, 16(12), 1449–1458.
42. G. Scalmani and M. J. Frisch, Continuous surface charge polarizable continuum models of solvation. I. General formalism, J. Chem. Phys., 2010, 132(11), 114110.
43. J. Tomasi, B. Mennucci and R. Cammi, Quantum Mechanical Continuum Solvation Models, Chem. Rev., 2005, 105(8), 2999–3094.
44. E. Runge and E. K. U. Gross, Density-Functional Theory for Time-Dependent Systems, Phys. Rev. Lett., 1984, 52(12), 997–1000.
45. K. Fukui, The path of chemical reactions - the IRC approach, Acc. Chem. Res., 1981, 14(12), 363–368.
46. C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B, 1988, 37(2), 785–789.
47. A. D. Becke, A new mixing of Hartree–Fock and local density-functional theories, J. Chem. Phys., 1993, 98(2), 1372–1377.
48. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields, J. Phys. Chem., 1994, 98(45), 11623–11627.
49. T. Yanai, D. P. Tew and N. C. Handy, A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP), Chem. Phys. Lett., 2004, 393(1), 51–57.
50. T. H. Dunning, Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 1989, 90(2), 1007–1023.
51. D. E. Woon and T. H. Dunning, Gaussian basis sets for use in correlated molecular calculations. III. The atoms aluminum through argon, J. Chem. Phys., 1993, 98(2), 1358–1371.
52. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate AB initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132(15), 154104.
53. W. Domcke, A. L. Sobolewski and C. W. Schlenker, Photooxidation of water with heptazine-based molecular photocatalysts: Insights from spectroscopy and computational chemistry, J. Chem. Phys., 2020, 153(10), 100902.
54. P. B. Pati, G. Damas, L. Tian, D. L. A. Fernandes, L. Zhang, I. B. Pehlivan, T. Edvinsson, C. M. Araujo and H. Tian, An experimental and theoretical study of an efficient polymer nano-photocatalyst for hydrogen evolution, Energy Environ. Sci., 2017, 10(6), 1372–1376.
55. Y. Xiang, X. Wang, L. Rao, P. Wang, D. Huang, X. Ding, X. Zhang, S. Wang, H. Chen and Y. Zhu, Conjugated Polymers with Sequential Fluorination for Enhanced Photocatalytic H2 Evolution via Proton-Coupled Electron Transfer, ACS Energy Lett., 2018, 3(10), 2544–2549.
56. N. M. Marković, B. N. Grgur and P. N. Ross, Temperature-Dependent Hydrogen Electrochemistry on Platinum Low-Index Single-Crystal Surfaces in Acid Solutions, J. Phys. Chem. B, 1997, 101(27), 5405–5413.
57. P. Guiglion, C. Butchosa and M. A. Zwijnenburg, Polymeric watersplitting photocatalysts; a computational perspective on the water oxidation conundrum, J. Mater. Chem. A, 2014, 2(30), 11996–12004.
58. V. W.-h. Lau, D. Klose, H. Kasap, F. Podjaski, M.-C. Pignié, E. Reisner, G. Jeschke and B. V. Lotsch, Dark Photocatalysis: Storage of Solar Energy in Carbon Nitride for Time-Delayed Hydrogen Generation, Angew. Chem., Int. Ed., 2017, 56(2), 510–514.

---

Footnote

† Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d1se02032c

---