A theoretical roadmap for the best oxygen reduction activity in two-dimensional transition metal tellurides

Abstract

Developing highly active and cost-effective electrocatalysts to replace Pt-based catalysts for the sluggish oxygen reduction reaction (ORR) is a major challenge in the commercialization of fuel cells. Although two-dimensional (2D) transition-metal tellurides have recently been proposed as alternative low-cost ORR catalysts, a fundamental study on the origin of the activity is required to further optimize their composition and performance. Herein, we investigated the electronic properties and ORR catalytic performances of a series of exfoliable 2D transition-metal tellurides to uncover the underlying mechanisms by means of density functional theory simulations. Our in-depth analysis shows that the activation of the ORR mainly depends on the partially filled p_z state of active Te atoms, which can simultaneously accept and donate electrons behaving similarly to both the occupied and unoccupied d orbitals of Pt atoms. This results in a linear relationship between the p_z-band center and the adsorption free energies of O₂ and intermediates, indicating that the p_z-band center might be used as an effective descriptor to probe the performance of telluride catalysts. On this basis, we predicted several 2D transition-metal tellurides with promising catalytic performance and reduced precious-metal contents, where NbRhTe₄ reaches the top of the activity volcano with a limiting potential of 0.96 V. This study provides theoretical guidance to design high-performing 2D telluride ORR catalysts, and its principle might be applicable to other electrochemical reactions in 2D chalcogenides.

---

Introduction

Proton exchange membrane fuel cells (PEMFCs) are recognized as one of the most effective technologies for growing clean and sustainable energy demands, as they can directly convert chemical energy into electricity.^1–3 Generally, the overall performance of PEMFCs depends largely on the kinetics of the cathodic oxygen reduction reaction (ORR), as it is much slower than the anodic hydrogen oxidation reaction (HOR), and other reactions including the hydrogen evolution reaction (HER) and oxygen evolution reaction (OER).⁴ The key to overcoming this bottleneck is finding highly efficient catalysts to boost the sluggish ORR kinetics, which are currently dominated by Pt-based catalysts (e.g., Pt nano-frameworks and Pt alloys) owing to their high activity and good stability.^5–7 However, the high cost of Pt-based catalysts significantly hampers large-scale applications of PEMFCs.^8,9 Thus, there is an urgent need to design highly efficient ORR catalysts with a reduced Pt (precious metal) content for the sustainable development of fuel cells.

Emerging two-dimensional (2D) materials have shown great potential as efficient catalysts owing to their high specific surface area and minimum migration distance for carriers.^10–14 Among them, doped transition metal dichalcogenides (TMDs) and metal(M)–N–C single-atom catalysts (SACs), produced by embedding atomically dispersed metal species into graphene, were found to exhibit good ORR catalytic activity.^15–19 Unfortunately, the advantages of 2D morphology for most of these materials are not well utilized, because their pristine basal planes are catalytically inactive. To fully leverage the potential of 2D materials for the catalytic ORR, it is essential to seek 2D catalysts with high basal plane activity, where there has recently been increasing attention focused on metallic transition metal telluride monolayers.^20–28 For instance, layered PtTe₂ was demonstrated to show ORR activity on par with the commercial Pt/C catalyst.²¹ Monolayer PtTe was predicted to have a limiting potential of 0.86 V,²² which outperforms Pt (111) electrodes (0.78 V). The precious metal free NiTe and TaTe₂ monolayers were soon after demonstrated with similar catalytic performance compared to Pt electrodes.²³ The activity of 2D Ni₂SbTe₂ was also recently examined,²⁷ where the endothermic O₂ adsorption might prohibit the ORR process on the basal plane. Although 2D transition metal tellurides indeed exhibit excellent catalytic activity towards the ORR, PtTe, with currently the best overall performance, still contains a large amount of the precious metal (50% formula weight) hindering its practical applications. Rational design of transition metal tellurides is desired to achieve better performance in both cost and catalytic activity. This remains untouched, primarily due to the lack of knowledge of the ORR activity origin of tellurides. In particular, unlike Pt-based catalysts, the electronic characteristics of Te atoms vary in different tellurides, as the electronegativity difference between Te and the transition metal is different. Thus, elucidating the catalytic activity origin of the Te atom is fundamental in the design of high-performing 2D telluride ORR catalysts that may extend to other chalcogenides.

In this study, we theoretically explore the ORR catalytic performance of a series of 2D stable nanosheets, NbTe₂, WTe₂, MoTe₂, and M_xX_yTe_z nanosheets (M = Nb and Ta and X = transition metals), which can readily be exfoliated from their bulk phases.^29–37 By combining the electronic density of states and molecular orbital analysis, we found that the partially filled p_z state of Te atoms can simultaneously accept electrons from the orbital and donate electrons to the π* orbital of the O₂ molecule, endowing telluride nanosheets with activities for O₂ fixation and protonation. The adsorption energies of O₂, O, and OH are thus linearly related to the p_z-band center of Te atoms, where the closer the band center to the Fermi level, the stronger the binding of the adsorbates. The constructed ORR activity volcano plot allows the p_z-band center derivation between −2.5 and −1.8 eV for telluride monolayers with potentially high activity. Following this guidance, several telluride monolayers, such as MXTe₄ and Ta₄Pd₃Te₁₆, were identified with limiting potentials of 0.73–0.96 V in the four-electron (4e⁻) pathway and precious-metal contents of less than 24%, implying that they are potentially highly performing ORR catalysts.

Results and discussion

Geometric and electronic properties

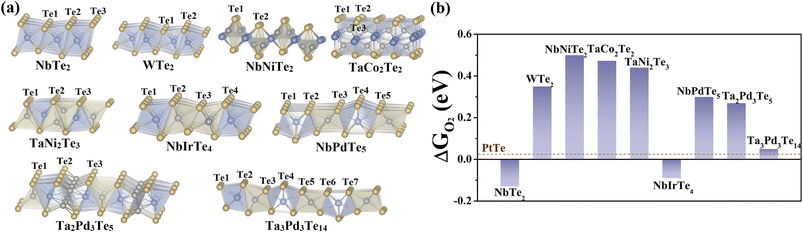
We first selected nine telluride monolayers with various stoichiometries and compositions in conjunction with previously studied 2D telluride catalysts to probe the nature and origin of the electrocatalytic ORR activity of telluride nanosheets. The selected nine tellurides are NbTe₂, WTe₂, NbNiTe₂, TaCo₂Te₂, TaNi₂Te₃, NbIrTe₄, NbPdTe₅, Ta₂Pd₃Te₅, and Ta₃Pd₃Te₁₄ (Fig. 1). Because all of these 2D tellurides have experimentally synthesized bulk counterparts,^29–37 the cleavage energies (E_cl) were evaluated to assess the experimental exfoliation feasibility by using a five-layer slab. As presented in Fig. S1,† the E_cl of NbTe₂, WTe₂, TaNi₂Te₃, NbIrTe₄, and NbPdTe₅ are comparable to that of exfoliated 2D MoS₂ (0.42 J m⁻²),³⁸ which can be classified as easily exfoliated according to the report of Mounet and coworkers.³⁹ Other telluride nanosheets have slightly higher E_cl and can be regarded as potentially exfoliated. Therefore, isolation of these 2D tellurides from their parent phases via exfoliation is experimentally feasible. Structurally, each nanosheet comprises transition metal atomic layers sandwiched between two Te atomic layers, where NbTe₂, WTe₂, NbIrTe₄, NbPdTe₅, and Ta₃Pd₃Te₁₄ comprise one metal layer, while others comprise two or three metal layers. Specifically, NbTe₂, WTe₂, and NbIrTe₄ are composed of MTe₆ (XTe₆) octahedra. Similarly, TaNi₂Te₃ consists of XTe₄ tetrahedra and MTe₆ octahedra, which are also contained in Ta₂Pd₃Te₅, where one of the octahedral apexes is X (MTe₅X octahedra). NbPdTe₅ and Ta₃Pd₃Te₁₄ are formed of MTe₈ decahedra and MTe₆ (XTe₆) octahedra. The rest of the two tellurides, NbNiTe₂ and TaCo₂Te₂, do not possess the above polyhedra. The dynamic stability of the monolayers was confirmed from their computed phonon frequencies, as reported in Materials Cloud two-dimensional crystals databases³⁹ and database C2DB⁴⁰ of 2D materials. The calculated band structures and density of states (DOS) of the above nanosheets reveal that NbIrTe₄ is semi-metallic with a zero bandgap that exhibits metallic behaviors,⁴¹ and the other nanosheets are well-defined metals (Fig. S2†). Moreover, we also examined the charge distribution of these tellurides through the Bader charge analysis. As shown in Table S1,† most Te atoms are negatively charged due to the charge transfer from inner transition metal atoms to outer Te atoms. Only Te₃ atoms in NbIrTe₄ are positively charged with around 0.25 e transferred from Te to Ir.

Fig. 1 (a) Side views of optimized structures of monolayer NbTe₂, WTe₂, NbNiTe₂, TaCo₂Te₂, TaNi₂Te₃, NbIrTe₄, NbPdTe₅, Ta₂Pd₃Te₅, and Ta₃Pd₃Te₁₄. The blue, grey and yellow balls represent M, X, and Te atoms, respectively. (b) The O₂ adsorption energy of monolayer tellurides.

Origin of O₂ activation

After determining the stability and electronic properties of these nanosheets, we proceeded to explore the adsorption of the O₂ molecule, which is the prerequisite for an efficient ORR process. The most favorable O₂ adsorption configurations and calculated adsorption energies (ΔG_O2) are shown and summarized in Fig. 1b and S3, and Table S2–3.† The ΔG_O2 of NbTe₂ and NbIrTe₄ monolayers is −0.13 and −0.09 eV, respectively, suggesting that O₂ can be chemisorbed. The moderate ΔG_O2 of 0.05 eV indicates that O₂ might be physisorbed on the Ta₃Pd₃Te₁₄ monolayer that is similar to the PtTe monolayer. Other telluride monolayers possess ΔG_O2 larger than 0.20 eV, where the endothermic nature suggests that O₂ molecules are hardly adsorbed on these telluride monolayers to trigger the ORR process. Moreover, the O–O bond length is significantly stretched from 1.23 Å in the gas phase to 1.38 and 1.39 Å when O₂ is adsorbed on NbTe₂ and NbIrTe₄, respectively. The weakening of O–O bonds is expected to facilitate the subsequent ORR steps. From the nudged-elastic-band (NEB) calculations, the energy barriers of O₂ dissociation into two adsorbed O* are around 0.42 and 0.54 eV for NbTe₂ and NbIrTe₄, respectively (Fig. S4†), which are comparable to the O₂ dissociation barrier on Pt (111) (0.38–0.50 eV),^42,43 indicating that O₂ has been effectively activated.

Since O₂ activation plays a crucial role in the ORR process, uncovering the origin of O₂ adsorption is beneficial for designing efficient ORR catalysts. Previously, an electron activation mechanism was proposed for the positively charged Te in the PtTe monolayer.²² According to this mechanism, the Te–O bond strength depends on the number of electrons the Te atom gains/loses (N_e), where the smaller N_e leads to stronger binding of O₂. Thus, we examined the correlation between N_e and ΔG_O2 of the studied telluride monolayers (Fig. S5†). Unlike the observed linear relationship between N_e and the binding energy of adsorbates in other systems, we found that ΔG_O2 does not depend on N_e. Either the positively or negatively charged Te atom can activate the O₂ molecule. Moreover, for most telluride monolayers, a larger N_e causes a stronger adsorption of O₂ that is opposite to the proposed mechanism. Therefore, O₂ adsorption cannot be simply described by the electron activation mechanism.

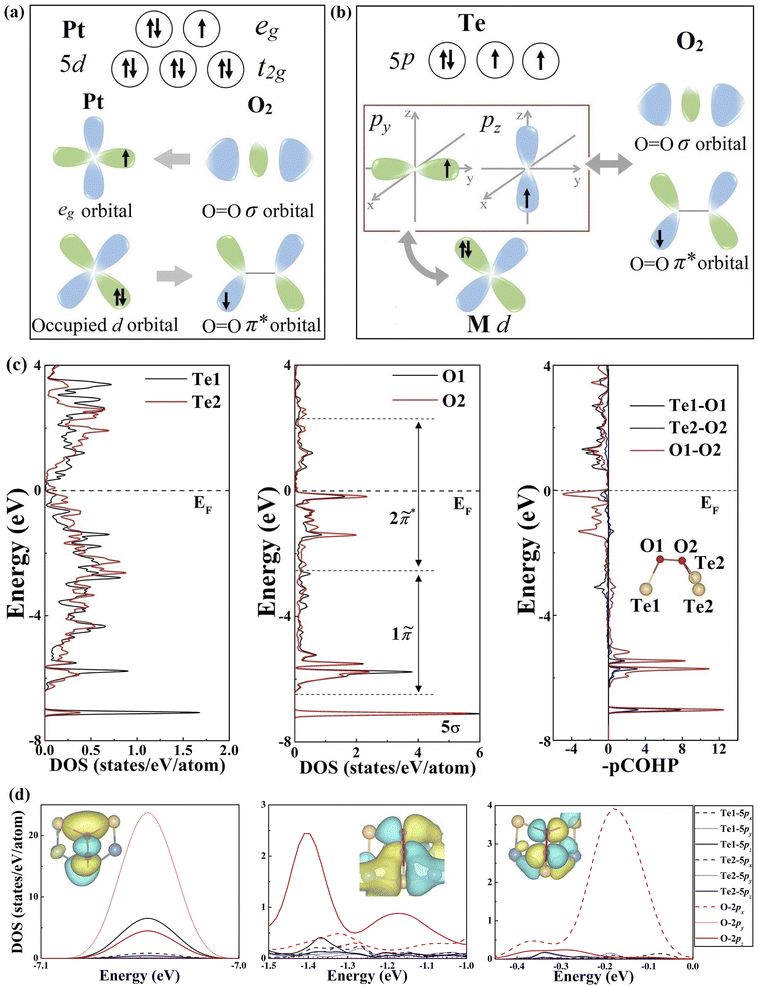
To gain a better understanding of the underlying O₂ adsorption mechanism, we further analyzed the orbital configuration of Te atoms in comparison with Pt-based catalysts. For the Pt atom (Fig. 2a), the coexistence of unoccupied and occupied d orbitals can facilitate O₂ adsorption and activation through a two-way charge transfer, where the unoccupied e_g orbital accepts lone-pair electrons from O₂, and the occupied t_2g orbital donates electrons back to O₂ antibonding orbitals.^44,45 This donation and back-donation concept is standard in molecular chemistry (Blyholder model) and has been successfully employed to describe the interaction between small molecules (e.g., N₂, C₂H₄, and CO) and transition metal and boron-based catalysts.^46–53 Interestingly, the Te atom possesses an orbital configuration analogous to that of Pt and B atoms in transition metal stuffed boron nitride nanotubes. As illustrated in Fig. 2b, the valence electronic configuration of the Te atom is 5s²5p⁴ regardless of the charge transfer between Te and transition metal atoms, resulting in one fully occupied p orbital and two partially filled p orbitals. Therefore, the Te atom is eligible to drive a similar “donation and back-donation” process to adsorb the O₂ molecule, as shown in Fig. 2b.

Fig. 2 (a) Simplified schematic of O₂ bonding to Pt. (b) Mechanism of activation of monolayer NbIrTe₄ for O₂ adsorption (c) DOS and pCOHP curves of O₂-adsorbed tellurides. The orbitals of O₂ in O₂-adsorbed tellurides are marked here. (d) pDOS and the corresponding molecular orbital of the O₂-adsorbed NbIrTe₄ monolayer.

To verify our inference, the charge density difference between O₂* and telluride monolayers was calculated to reveal the underlying charge transfer. As shown in Fig. S6–9,† O₂* exhibits a clear picture of the two-way charge transfer exhibiting charge accumulation (yellow) and depletion (blue). Interestingly, Te atoms seem to deviate from this mechanism as electrons barely accumulate around them.

To decipher this phenomenon, we then evaluated the O–O and O₂–Te interactions by a combined electronic structure and projected crystal orbital Hamilton populations (pCOHP) analysis, taking the NbIrTe₄ monolayer as an example. The quantity of −(pCOHP) was used to directly correspond the positive and negative values with bonding and antibonding states, respectively. The molecular orbital (MO) diagram, projected density of states (pDOS), and pCOHP of the free O₂ molecule were examined first, as presented in Fig. S10.† By analyzing the pDOS and pCOHP, it is clear that the fully occupied 5σ and 1π orbitals contribute to the bonding of the O₂ molecule, while the partially filled 2π* orbital is antibonding.

After O₂ adsorption on the NbIrTe₄ monolayer, the sharp localized MOs of O₂ in a vacuum hybridize with surface Te p states that broaden into rather delocalized states and shift down to lower energy (Fig. 2c). The new hybrid states are marked as “tildes” of the original orbitals to indicate the difference (Fig. S11†). The 5[small sigma, Greek, tilde] band showed up in a narrow energy range at around −7.05 eV relative to the Fermi level, and the electron density of the 5[small sigma, Greek, tilde] band is reduced compared to the 5σ orbital of free O₂. This agrees with the Blyholder picture of σ forward donation, as reflected by the flow of 0.23 electrons from O₂ to Te atoms, resulting in the formation of a novel Te DOS peak, mainly composed of the p_z state of the Te1 atom in the same energy range and σ-type Te–O bonds (Fig. S6–9).† The degenerated 1π MO split into two narrow 1π bands at around −6.4 and −5.5 eV, respectively, and broad bands P̃_1π and P̃_2π* between −5.3 and −1.1 eV upon hybridization with Te states and 2π* MO. Importantly, the unoccupied 2π* MO of free O₂ became partially populated and transformed into 2[small pi, Greek, tilde]* bands in the energy range between −1.0 and 2.3 eV, where 0.5 electrons were back-donated from the Te atom to the 2π* orbital of O₂ (Fig. S6†). The net charge transfer from Te to O₂ agrees with the Bader charge analysis, as O has a higher electronegativity, implying that the back-donation is a more dominant Te–O interaction. Interestingly, p_z of the Te₁ atom was also the main contribution for the back-donation. Therefore, Te atoms could accept and donate electrons from and to O₂ molecules simultaneously, while the p_z orbital of the Te₁ atom contributes the most. The electron depletion of Te can thus be understood, as the two-way charge transfer mainly takes place in the same orbital, and the net charge transfer between Te and O₂ is negative. Other studied telluride monolayers, such as PtTe, NbTe₂, and Ta₃Pd₃Te₁₄, also present the same phenomenon (Fig. S7–9).† Therefore, the origin of O₂ activation on 2D tellurides is a unique “donation and back-donation” mechanism that stretches and weakens the O–O bond.

ORR catalytic performance

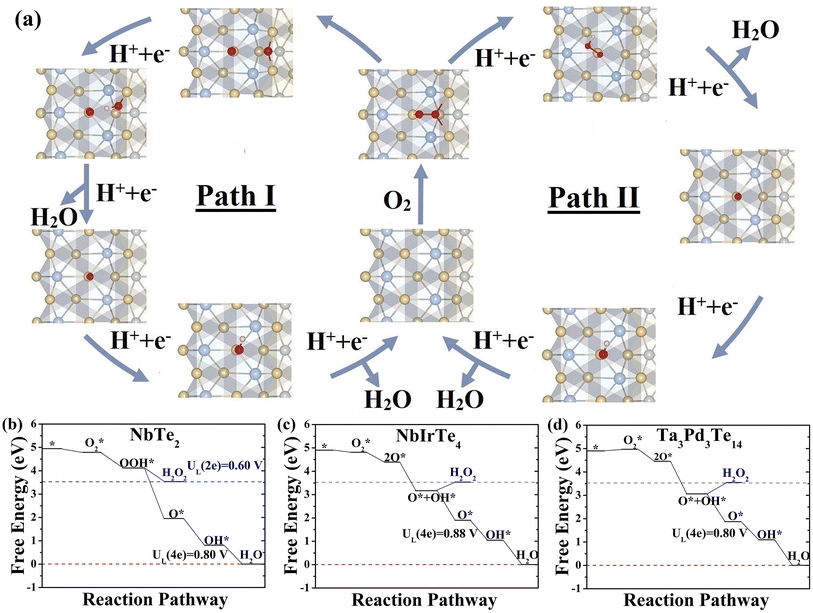
We assessed the catalytic performance of telluride monolayers for the reduction of O₂ to H₂O. The typical association and dissociation mechanisms (Fig. 3), including all possible intermediate reactants (Fig. S12 and 13)† were widely investigated for NbTe₂, NbIrTe₄, and Ta₃Pd₃Te₁₄ monolayers. For other telluride monolayers, we only calculated the adsorption energies of O and OH for comparison. As illustrated in Fig. 3, the NbTe₂ monolayer shows similar catalytic behaviors to the TaTe₂ monolayer,²³ where the association pathway has a higher limiting potential (U_L) of 0.80 V (OH* reduction to H₂O) than the dissociation pathway of 0.63 V (Fig. S12†), suggesting that the association mechanism exhibits higher efficiency. Alternatively, the dissociation mechanism is more efficient in NbIrTe₄ and Ta₃Pd₃Te₁₄ monolayers, as their U_L of 0.88 and 0.80 V (O* reduction to OH*) are higher than the association ones of 0.65 and 0.45 V (O₂ to OOH*), respectively (Fig. 3 and S13†). In addition to the 4e electrochemical processes, we also examined the 2e reduction pathways for the dominant reduction mechanism. The free energy diagrams show that the U_L of the 2e association pathway is 0.6 V for the NbTe₂ monolayer, which is lower than that of the 4e association pathway. The H₂O₂ formation is endothermic for the dissociation pathway of NbIrTe₄ and Ta₃Pd₃Te₁₄ monolayers, indicating that it is difficult to occur during the ORR process. These results suggest that NbTe₂, NbIrTe₄, and Ta₃Pd₃Te₁₄ monolayers are rather good ORR catalysts with high 4e pathway selectivity. Considering that monolayers are generally more difficult to obtain than multilayers, we also explored the electrocatalytic performance of bilayer and trilayer NbIrTe₄ (Fig. S14–16†). The electrocatalytic performance of bilayer and trilayer NbIrTe₄ is similar to that of the monolayer with limiting potentials of 0.89 and 0.81 V.

Fig. 3 (a) Scheme of the possible two ORR reaction pathways of monolayer NbIrTe₄. Calculated free energy diagrams for the ORR pathway on monolayer (b) NbTe₂ in an association pathway and (c) NbIrTe₄ and (d)Ta₃Pd₃Te₁₄ in a dissociation pathway.

A previously established theory for transition metal-based catalysts suggested that the adsorption energies of O-containing intermediates, governing the catalytic performance, are linearly correlated.^54–60 Thus, the catalytic activity can be described by the adsorption energies of a single intermediate reactant. Similar to transition metal-based catalysts, linear scaling relationships between ΔG_OH* and other reactants were also identified in telluride monolayers (Fig. 4a and S17†). For example, ΔG_OH* and ΔG_OOH* are related to each other by a constant of approximately 3.3 eV that is close to 3.2 eV, observed in transition metal-based catalysts (Fig. S17b†). Given the excellent linear relationship, we plotted U_L as a function of ΔG_OH* for telluride monolayers, where the transition metal-based catalysts were also included for comparison (Fig. 4b).^{22,23,27,61,62} This leads to the observation of a universal volcano relationship that follows the century-old Sabatier principle, where an ideal catalyst must bind the intermediate reactants with an intermediate strength: not too weak to activate the reactants, and not too strong to desorb the products. The estimated highest limiting potential is approximately 0.94 V, which demonstrates that the dissociation pathway can elevate the limiting potential close to 0.1 V compared with the previously suggested U_L of 0.86 V for an ideal ORR catalyst. For an efficient catalyst with a limiting potential higher than that of Pt (111), one should search for tellurides with a ΔG_OH* between 0.8 and 1.2 eV.

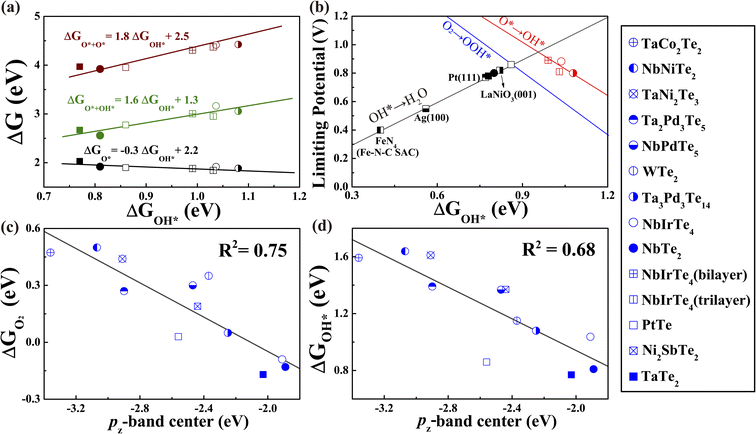Fig. 4 (a) The variation of adsorption energy of intermediate adsorbates in the ORR dissociation pathway as a function of ΔG_OH* (b) Volcano plot of the ORR limiting potentials for studied tellurides and other known catalysts.^{15,22,23,63,64} The blue line (O₂ to OOH*) was taken from previous work.⁶⁴ Other details are shown in Fig. S17.† (c) The O₂ adsorption energy and (d) OH adsorption energy versus the p_z-band center of active Te sites for initially studied monolayer tellurides.

Activity descriptor

Since the simulated limiting potential of 2D tellurides relates well to the binding energy of intermediate adsorbates, similarly to that of transition metal-based catalysts, we proceed to seek a simple descriptor that can correlate the adsorption energy with the intrinsic properties of tellurides like the d-band center model for transition metals.^50,65–70 As we already know that the partially filled p_z orbital is responsible for the Te–O interactions upon O₂ adsorption, we introduced a descriptor ε_pz defined as the centroid of the projected density of states of the p_z orbital relative to the Fermi level analogous to the d-band center.^71–75 As presented in Fig. 4c and d, ε_pz of the active Te atoms shows a reasonable linear relationship to the adsorption energies of O₂ and intermediate oxygen-containing adsorbates. The linear relationships between ΔG_O2 and other possible descriptors, such as the p-band center ε_p, are also calculated as shown in Fig. S18,† all of which are inferior to that of ε_pz. Similar to the d-band center model, the closer the ε_pz to the Fermi level, the stronger the binding strength of the adsorbates on telluride monolayers.⁶³ This can be understood through the bond order, which is half of the difference between the electron number of the bonding orbital and the antibonding orbital according to molecular orbital theory. A high bond order corresponds to strong binding and vice versa. When O-containing groups are adsorbed on telluride monolayers, the O 2p orbitals hybridize with the Te 5p_z orbital forming a fully filled bonding state and partially filled antibonding state. A high ε_pz results in a low filling of the antibonding state and hence a large bond order that could lead to enhanced Te–O binding strength. On the contrary, a low bond order corresponding to low ε_pz and high filling of the antibonding state weakens the telluride-adsorbate interaction, destabilizing the Te–O bond. In this sense, the p_z-band center, ε_pz, can serve as a simple catalytic activity descriptor for telluride monolayers. An efficient 2D telluride catalyst with a ΔG_OH* between 0.8 and 1.2 eV and the ability for O₂ chemisorption are predicted to possess a ε_pz between −2.5 and −1.8 eV. Thus, we obtained the screening criterion.

Rational screening of efficient ORR catalysts

With the established activity descriptor, we moved on to search for potential 2D telluride catalysts that may possess a better catalytic performance. We further evaluated the electronic properties of T_d-MoTe₂, TaNiTe₂, NbRhTe₄, TaRhTe₄, TaIrTe₄, Ta₂Ni₃Te₅, and Ta₄Pd₃Te₁₆ monolayers. Except for NbRhTe₄, the bulk phases of these monolayers have also been experimentally synthesized.^29,76–78 The thermodynamic stability of bulk NbRhTe₄ was confirmed by constructing the Nb–Rh–Te ternary phase diagram as shown in Fig. S19(a),† which is in line with previous theoretical studies.^79,80 As shown in Fig. S19(b),† the isolation of these 2D tellurides from their bulk phases via exfoliation is experimentally feasible. Among them, NbRhTe₄, TaRhTe₄, TaIrTe₄, and Ta₄Pd₃Te₁₆ have ε_pz values between −2.5 and −1.8 eV that meet the criteria for efficient ORR catalysts. Thus, as previously, we focused on the catalytic activity of these four tellurides for both dissociation and association pathways and calculated the adsorption free energies of the rest of the tellurides for comparison and construction of the correlation. The calculated ΔG_O2 shows that O₂ molecules can be chemisorbed on NbRhTe₄, TaRhTe₄, TaIrTe₄, and Ta₄Pd₃Te₁₆ to trigger the ORR process as expected. The free energy diagrams (Fig. S20–22)† show that the dissociative pathway generally exhibits higher limiting potential than the associative pathway. The rate limiting step is OH* to H₂O, O* to OH*, O* to OH*, and O + OH* to O* for NbRhTe₄, TaRhTe₄, TaIrTe₄, and Ta₄Pd₃Te₁₆, respectively. The corresponding limiting potentials are all above 0.78 eV, which are comparable to that of Pt (111) and the PtTe monolayer. Encouragingly, these MXTe₄ and Ta₄Pd₃Te₁₆ tellurides contain small amounts of precious metals of 17% and 13% formula weight. In particular, the NbRhTe₄ monolayer has a limiting potential as high as 0.96 V, that is close to the predicted U_L of 0.94 V for an ideal catalyst, indicating that the NbRhTe₄ monolayer could reach the top of the 4e ORR activity volcano (Fig. 5b). Herein, we also explored the electrocatalytic performance of bilayer and trilayer NbRhTe₄ (Fig. S23†). The limiting potential of bilayer and trilayer NbRhTe₄ is similar to that of the monolayer with 0.95 and 0.85 V.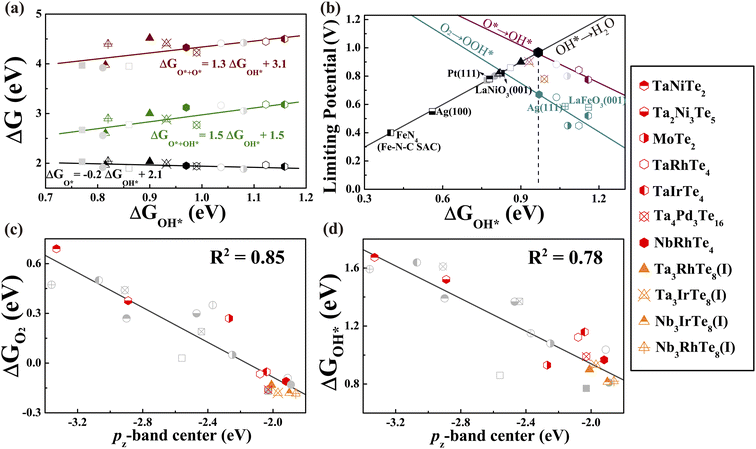

Fig. 5 (a) The variation of adsorption energy of intermediate adsorbates in the ORR dissociation pathway as a function of ΔG_OH*. (b) Volcano plot of the ORR limiting potentials for all studied monolayer tellurides and other known catalysts. (c) The O₂ adsorption energy and (d) OH adsorption energy versus the p_z-band center of active Te sites for all studied monolayer tellurides. The grey circle and square points represent initially studied tellurides and known catalysts in other studies^{15,22,23,63,64} shown in Fig. 4. The star and triangle points represent newly studied tellurides and M-doped variants, respectively.

Notably, the newly identified promising MXTe₄ type telluride catalysts can be viewed as X substituted MTe₂ (50% substitution). Thus, by varying the substitution ratio, we may obtain potential telluride catalysts with an even lower precious-metal content, while maintaining high activity, as they should possess ε_pz close to that of MXTe₄ or MTe₂ monolayers. Hence, we designed two hypothetical M₃XTe₈ (25% substitution) structures, phase I and II that possess similar energies, as a tentative attempt (Fig. S24a and b†). The calculated formation energy of the bulk phases of these hypothetical monolayers was between 20 and 25 meV/atom, suggesting that the hypothetical M₃XTe₈ phases are metastable and might be realized in the experiments (Fig. S24†). Similarly, we considered both dissociation and association pathways. Fig. S25 and 26† presented the detailed ORR process and the calculated free energy diagrams of phase I Nb₃RhTe₈, Ta₃RhTe₈, Ta₃IrTe₈, and phase II Nb₃IrTe₈, which showed better ORR performance in these two phases (the details of another phase are summarized in Table S4 and S5†). As shown in the free energy diagrams, the limiting-potential of phase I of Nb₃RhTe₈ and Ta₃RhTe₈, and phase II of Nb₃IrTe₈ is predicted to be 0.82, 0.90, and 0.81 V, respectively, with the limiting step of OH* → H₂O. Differently, the limiting step of phase I of Ta₃IrTe₈ is predicted to be O + OH* → O*, with a ΔG of −0.90 eV. These hypothetical substituted monolayers show superior ORR activity with a decreased precious-metal content (8%).

Finally, we re-examined the correlation between the adsorption energies of oxygen-containing groups and ε_pz by including all studied telluride monolayers. A better linear relationship between ΔG_adsorbates and ε_pz was also observed (Fig. 5c, d and S27†), indicating that all these 2D telluride catalysts should have a similar underlying mechanism, and the p_z orbital is primarily responsible, so that ε_pz could be used to describe the interaction between reactants and substrates. Therefore, once the optimal ε_pz is established, one can rationally design highly active 2D telluride-based ORR catalysts through this simple activity descriptor. Notably, as we only considered transition metal tellurides in the current study, a large discrepancy may occur for the catalytic activity prediction of tellurides containing main-group elements or with different activation mechanisms, where the descriptor should be corrected accordingly.

Conclusions

In summary, systematical density functional theory calculations were employed to investigate the nature and origin of ORR activities of a series of experimentally synthesizable 2D transition-metal telluride catalysts. Our results suggested that the partially occupied p_z state of Te atoms can effectively drive the “donation-back-donation” process through a two-way charge transfer, playing an important role in the activation of O₂. The subsequent O₂ reduction processes proceed through the four-electron pathway, where most of the tellurides take the dissociative pathway. The binding strength of O₂ and intermediates is linearly dependent on the p_z-band center, implying that the latter can serve as an indicator to probe the catalytic activity of tellurides. By adopting this concept to justify the volcano plot between the limiting potential and OH adsorption free energy, we predicted that MXTe₄, Ta₃Pd₃Te₁₄, and Ta₄Pd₃Te₁₆ are potential ORR catalysts, where NbRhTe₄ shows the highest limiting potential of 0.96 V among studied transition metal telluride catalysts, reaching the top of the activity volcano with a precious-metal content of only 17%. The hypothetical substitution of MXTe₄ leads to Ta₃IrTe₈ with a limiting potential of 0.90 V and a precious-metal content of 8%. Our study demonstrates that transition metal telluride nanosheets are highly compelling ORR electrocatalysts and proves the generality of the physically derived descriptor for screening active tellurides. We further expect the presented strategy to be extended to other electrocatalysis processes to identify descriptors to rationally and efficiently design highly active catalysts among 2D chalcogenides.

Methods

Density functional theory computations were performed by using the Vienna Ab initio simulation package (VASP) within the projected augmented wave method.^81,82 The Perdew−Burke−Ernzerhof (PBE) functional in the generalized gradient approximation (GGA) was used to describe the exchange-correlation potential.⁸³ A plane-wave energy cut-off of 500 eV was used, and all atoms were fully relaxed using the conjugate gradient algorithm with a criterion of convergence of 10⁻⁵ eV and 0.03 eV per atom.⁸⁴ For multilayer systems, the DFT-D3 empirical correction was used to describe van der Waals (vdW) interactions, which has been proven reliable for describing long-range vdW interactions.⁸⁵ The phonon spectra of 2D tellurides were computed using the finite displacement method, as implemented in the Phonopy code.⁸⁶ Bader's quantum theory of atoms in molecules (QTAIM) analysis was employed for the charge transfer calculations.⁸⁷ The bonding was further analyzed by calculating the projected crystal orbital Hamilton populations (pCOHPs) using the LOBSTER package.^88–90 The energy barriers were calculated using the climbing image nudged-elastic-band (CI-NEB) methods implemented in the VASP.⁹¹ The ORR processes were calculated on the basis of the computational hydrogen electrode (CHE) model.⁹²

Data availability

The data supporting the findings of this study are available in the manuscript and ESI† and from the corresponding author upon reasonable request.

Author contributions

Yu Xie conceived the presented idea. Xin Yang, Zexing Qu, and Yu Xie performed the first-principles calculations. Xin Yang, Hanyu Liu, Yu Xie and Yanming Ma wrote the manuscript. All authors discussed the results and assisted during manuscript preparation.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant no. 12022408), the Interdisciplinary Integration and Innovation Project of JLU, Fundamental Research Funds for the Central Universities and the Program for JLU Science and Technology Innovative Research Team (JLUSTIRT). This paper is dedicated to the 70th anniversary of College of Physics of Jilin University. Part of the calculations were performed at the High Performance Computing Center of Jilin University.

Notes and references

1. B. C. H. Steele and A. Heinzel, Nature, 2001, 414(6861), 345–352.
2. M. K. Debe, Nature, 2012, 486(7401), 43–51.
3. A. Rabis, P. Rodriguez and T. J. Schmidt, ACS Catal., 2012, 2(5), 864–890.
4. M. Shao, Q. Chang, J. P. Dodelet and R. Chenitz, Chem. Rev., 2016, 116(6), 3594–3657.
5. L. Huang, S. Zaman, X. Tian, Z. Wang, W. Fang and B. Y. Xia, Acc. Chem. Res., 2021, 54(2), 311–322.
6. C. Cui, X. Hu and L. Wen, J. Semicond., 2020, 41(9), 091705.
7. H. A. Gasteiger, S. S. Kocha, B. Sompalli and F. T. Wagner, Appl. Catal., B, 2005, 56(1–2), 9–35.
8. X. Huang, Z. Zhao, L. Cao, Y. Chen, E. Zhu, Z. Lin, M. Li, A. Yan, A. Zettl and Y. M. Wang, Science, 2015, 348(6240), 1230–1234.
9. Y. Kang, X. Ye, J. Chen, Y. Cai, R. E. Diaz, R. R. Adzic, E. A. Stach and C. B. Murray, J. Am. Chem. Soc., 2013, 135(1), 42–45.
10. D. Deng, K. S. Novoselov, Q. Fu, N. Zheng, Z. Tian and X. Bao, Nat. Nanotechnol., 2016, 11(3), 218–230.
11. X. Chia and M. Pumera, Nat. Catal., 2018, 1(12), 909–921.
12. K. Lasek, J. Li, S. Kolekar, P. M. Coelho, L. Guo, M. Zhang, Z. Wang and M. Batzill, Surf. Sci. Rep., 2021, 76(2), 100523.
13. Z. Pei, J. Gu, Y. Wang, Z. Tang, Z. Liu, Y. Huang, Y. Huang, J. Zhao, Z. Chen and C. Zhi, ACS Nano, 2017, 11(6), 6004–6014.
14. H. Zhang, Y. Tian, J. Zhao, Q. Cai and Z. Chen, Electrochim. Acta, 2017, 225, 543–550.
15. Y. Wang, Y. J. Tang and K. Zhou, J. Am. Chem. Soc., 2019, 141(36), 14115–14119.
16. G. Wu, K. L. More, C. M. Johnston and P. Zelenay, Science, 2011, 332(6028), 443–447.
17. S. Lin, H. Xu, Y. Wang, X. C. Zeng and Z. Chen, J. Mater. Chem. A, 2020, 8(11), 5663–5670.
18. C. Deng, Y. Su, F. Li, W. Shen, Z. Chen and Q. Tang, J. Mater. Chem. A, 2020, 8(46), 24563–24571.
19. H. Jiang, J. Gu, X. Zheng, M. Liu, X. Qiu, L. Wang, W. Li, Z. Chen, X. Ji and J. Li, Energy Environ. Sci., 2019, 12(1), 322–333.
20. N. Karmodak, L. Bursi and O. Andreussi, J. Phys. Chem. Lett., 2022, 13(1), 58–65.
21. N. F. Rosli, C. C. Mayorga-Martinez, N. M. Latiff, N. Rohaizad, Z. Sofer, A. C. Fisher and M. Pumera, ACS Sustainable Chem. Eng., 2018, 6(6), 7432–7441.
22. Y. Wang, Y. Li and T. Heine, J. Am. Chem. Soc., 2018, 140(40), 12732–12735.
23. Y. Wang and K. Zhou, Green Energy Environ., 2022, 7(3), 525–532.
24. S. Zhao, K. Wang, X. Zou, L. Gan, H. Du, C. Xu, F. Kang, W. Duan and J. Li, Nano Res., 2019, 12(4), 925–930.
25. N. Zhang, F. Zheng, B. Huang, Y. Ji, Q. Shao, Y. Li, X. Xiao and X. Huang, Adv. Mater., 2020, 32(22), e1906477.
26. L. H. Li, J. H. Yuan, K. H. Xue, M. Xu, M. Xu, J. F. Wang and X. S. Miao, J. Phys. Chem. C, 2020, 124(6), 3671–3680.
27. L. Zhao, G. Yu, X. Huang and W. Chen, Inorg. Chem., 2022, 61(4), 2284–2291.
28. T. Liu, Y. Wang and Y. Li, J. Phys. Chem. C, 2021, 125(35), 19164–19170.
29. A. Mar, S. Jobic and J. A. Ibers, J. Am. Chem. Soc., 1992, 114(23), 8963–8971.
30. A. Mar and J. A. Ibers, J. Solid State Chem., 1992, 97(2), 366–376.
31. B. E. Brown, Acta Crystallogr., 1996, 20(2), 264–267.
32. E. W. Liimatta and J. A. Ibers, J. Solid State Chem., 1988, 77(1), 141–147.
33. E. W. Liimatta and J. A. Ibers, J. Solid State Chem., 1989, 78(1), 7–16.
34. W. Tremel, Angew. Chem., Int. Ed., 1992, 31(2), 217–220.
35. J. Neuhausen, V. K. Evstaf'iev, T. Block, E. W. Finckh, W. Tremel, L. Augustin, H. Fuchs, D. Voss and P. Krüger, Chem. Mater., 1998, 10(12), 3870–3878.
36. J. Neu, K. Wei, X. He, O. Delaire, R. Baumbach, Z. Feng, Y. Fu, Y. Zhang, D. J. Singh and T. Siegrist, Phys. Rev. B, 2019, 100(14), 144102.
37. Y. Liu, C. Q. Xu, W. H. Jiao, P. G. Cai, B. Li, W. Zhou, B. Qian, X. F. Jiang, R. Sankar and X. L. Ke, Tungsten, 2021, 1–7.
38. T. Bjorkman, A. Gulans, A. V. Krasheninnikov and R. M. Nieminen, Phys. Rev. Lett., 2012, 108(23), 235502.
39. N. Mounet, M. Gibertini, P. Schwaller, D. Campi, A. Merkys, A. Marrazzo, T. Sohier, I. E. Castelli, A. Cepellotti, G. Pizzi and N. Marzari, Nat. Nanotechnol., 2018, 13(3), 246–252.
40. S. Haastrup, M. Strange, M. Pandey, T. Deilmann, P. S. Schmidt, N. F. Hinsche, M. N. Gjerding, D. Torelli, P. M. Larsen and A. C. Riis-Jensen, 2D Materials, 2018, 5(4), 042002.
41. M. Jin, P. Yu, C. Fan, Q. Li, P. Kong, Z. Shen, X. Qin, Z. Chi, C. Jin, G. Liu, G. Zhong, G. Xu, Z. Liu and J. Zhu, Adv. Sci., 2021, 8(24), e2103250.
42. V. Tripković, E. Skúlason, S. Siahrostami, J. K. Nørskov and J. Rossmeisl, Electrochim. Acta, 2010, 55(27), 7975–7981.
43. H. A. Hansen, V. Viswanathan and J. K. Nørskov, J. Phys. Chem. C, 2014, 118(13), 6706–6718.
44. F. Lu, W. Xie, D. Yi, Y. Wang, F. Zhang, Y. Xu, B. Zhou, S. Liu, X. Wang and J. Yao, CCS Chem., 2021, 3(11), 180–188.
45. Y. Zhou, Q. Gu, K. Yin, Y. Li, L. Tao, H. Tan, Y. Yang and S. Guo, Angew. Chem., Int. Ed., 2022, e202201416.
46. A. Föhlisch, M. Nyberg, P. Bennich, L. Triguero, J. Hasselström, O. Karis, L. G. M. Pettersson and A. Nilsson, J. Chem. Phys., 2000, 112(4), 1946–1958.
47. A. Föhlisch, M. Nyberg, J. Hasselström, O. Karis, L. G. M. Pettersson and A. Nilsson, Phys. Rev. Lett., 2000, 85(15), 3309.
48. J. Suntivich, H. A. Gasteiger, N. Yabuuchi, H. Nakanishi, J. B. Goodenough and Y. Shao-Horn, Nat. Chem., 2011, 3(7), 546–550.
49. J. K. Norskov, T. Bligaard, J. Rossmeisl and C. H. Christensen, Nat. Chem., 2009, 1(1), 37–46.
50. C. Ling, X. Niu, Q. Li, A. Du and J. Wang, J. Am. Chem. Soc., 2018, 140(43), 14161–14168.
51. H. B. Tao, L. Fang, J. Chen, H. B. Yang, J. Gao, J. Miao, S. Chen and B. Liu, J. Am. Chem. Soc., 2016, 138(31), 9978–9985.
52. S. Zhou, X. Yang, X. Xu, S. X. Dou, Y. Du and J. Zhao, J. Am. Chem. Soc., 2020, 142(1), 308–317.
53. Y. Jiao, Y. Zheng, M. Jaroniec and S. Z. Qiao, J. Am. Chem. Soc., 2014, 136(11), 4394–4403.
54. J. K. Nørskov, T. Bligaard, J. Rossmeisl and C. H. Christensen, Nat. Chem., 2009, 1(1), 37–46.
55. I. C. Man, H. Y. Su, F. Calle-Vallejo, H. A. Hansen, J. I. Martínez, N. G. Inoglu, J. Kitchin, T. F. Jaramillo, J. K. Nørskov and J. Rossmeisl, ChemCatChem, 2011, 3(7), 1159–1165.
56. M. M. Montemore and J. W. Medlin, Catal. Sci. Technol., 2014, 4(11), 3748–3761.
57. M. Andersen, S. V. Levchenko, M. Scheffler and K. Reuter, ACS Catal., 2019, 9(4), 2752–2759.
58. E. M. Fernandez, P. G. Moses, A. Toftelund, H. A. Hansen, J. I. Martinez, F. Abild-Pedersen, J. Kleis, B. Hinnemann, J. Rossmeisl, T. Bligaard and J. K. Norskov, Angew. Chem., Int. Ed., 2008, 47(25), 4683–4686.
59. A. Vojvodic, A. Hellman, C. Ruberto and B. I. Lundqvist, Phys. Rev. Lett., 2009, 103(14), 146103.
60. F. Abild-Pedersen, J. Greeley, F. Studt, J. Rossmeisl, T. R. Munter, P. G. Moses, E. Skulason, T. Bligaard and J. K. Norskov, Phys. Rev. Lett., 2007, 99(1), 016105.
61. A. Kulkarni, S. Siahrostami, A. Patel and J. K. Norskov, Chem. Rev., 2018, 118(5), 2302–2312.
62. A. Mahata, A. S. Nair and B. Pathak, Cataly. Sci. Technol., 2019, 9(18), 4835–4863.
63. Y. L. Lee, M. J. Gadre, Y. Shao-Horn and D. Morgan, Phys. Chem. Chem. Phys., 2015, 17(33), 21643–21663.
64. V. Viswanathan, H. A. Hansen, J. Rossmeisl and J. K. Norskov, J. Phys. Chem. Lett., 2012, 3(20), 2948–2951.
65. J. R. Kitchin, J. K. Norskov, M. A. Barteau and J. G. Chen, J. Chem. Phys., 2004, 120(21), 10240–10246.
66. V. Pallassana, M. Neurock, L. B. Hansen, B. Hammer and J. K. Nørskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60(8), 6146.
67. F. H. B. Lima, J. Zhang, M. H. Shao, K. Sasaki, M. B. Vukmirovic, a. E. A. Ticianelli and R. R. Adzic, J. Phys. Chem. C, 2007, 111(1), 404–410.
68. N. Liu, S. Zhou and J. Zhao, Mater. Today Phys., 2021, 16, 100312.
69. Y.-L. Lee, J. Kleis, J. Rossmeisl, Y. Shao-Horn and D. Morgan, Energy Environ. Sci., 2011, 4(10), 3966–3970.
70. B. Wang and F. Zhang, Angew. Chem., Int. Ed., 2022, 61(4), e202111026.
71. X. Zhu, X. Tan, K. H. Wu, S. C. Haw, C. W. Pao, B. J. Su, J. Jiang, S. C. Smith, J. M. Chen, R. Amal and X. Lu, Angew. Chem., Int. Ed., 2021, 60(40), 21911–21917.
72. Y. Chang, Y. Cheng, Y. Feng, K. Li, H. Jian and H. Zhang, ACS Appl. Mater. Interfaces, 2019, 11(13), 12224–12231.
73. S. Zhou, W. Pei, Y. Zhao, X. Yang, N. Liu and J. Zhao, npj Comput. Mater., 2021, 7(1), 1–34.
74. C. F. Dickens, J. H. Montoya, A. R. Kulkarni, M. Bajdich and J. K. Nørskov, Surf. Sci., 2019, 681, 122–129.
75. S. Zhou, X. Yang, W. Pei, N. Liu and J. Zhao, Nanoscale, 2018, 10(23), 10876–10883.
76. A. Tamai, Q. S. Wu, I. Cucchi, F. Y. Bruno, S. Riccò, T. K. Kim, M. Hoesch, C. Barreteau, E. Giannini, C. Besnard, A. A. Soluyanov and F. Baumberger, Phys. Rev. X, 2016, 6(3), 031021.
77. W. Tremel, Angew. Chem., 1991, 103(7), 900–903.
78. A. Mar and J. A. Ibers, J. Chem. Soc. Dalton Trans., 1991, 4, 639.
79. J. Liu, H. Wang, C. Fang, L. Fu and X. Qian, Nano Lett., 2017, 17(1), 467–475.
80. A. Sufyan, G. Macam, C. Hsu, Z. Huang, S. Huang, H. Lin and F. Chuang, Chinese J. Phys., 2021, 73, 95.
81. Y. Wang and J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43(11), 8911–8916.
82. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169.
83. J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45(23), 13244–13249.
84. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13(12), 5188–5192.
85. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32(7), 1456–1465.
86. A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78(13), 134106.
87. W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21(8), 084204.
88. R. Dronskowski and P. E. Bloechl, J. Phys. Chem., 1993, 97(33), 8617–8624.
89. V. L. Deringer, A. L. Tchougreeff and R. Dronskowski, J. Phys. Chem. A, 2011, 115(21), 5461–5466.
90. S. Maintz, V. L. Deringer, A. L. Tchougreeff and R. Dronskowski, J. Comput. Chem., 2016, 37(11), 1030–1035.
91. G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113(22), 9901–9904.
92. J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2004, 108(46), 17886–17892.

---

Footnote

† Electronic supplementary information (ESI) available: Details of computational methods, structures, electronic properties, adsorption energies, energy barriers of O₂ dissociation, free energy diagrams and linear relationships. See https://doi.org/10.1039/d2sc03686j

---