Open Access Article
Open Access ArticleDimerization of sub-nanoscale molecular clusters affords broadly tuneable viscoelasticity above the glass transition temperature†
Xin
Zhou
,
Junsheng
Yang
 *,
Jia-Fu
Yin
,
Wei
Liu-Fu
,
Jiayi
Huang
,
Mu
Li
,
Yuan
Liu
,
Linkun
Cai
,
Tao Lin
Sun
and
Panchao
Yin
*,
Jia-Fu
Yin
,
Wei
Liu-Fu
,
Jiayi
Huang
,
Mu
Li
,
Yuan
Liu
,
Linkun
Cai
,
Tao Lin
Sun
and
Panchao
Yin
 *
*
State Key Laboratory of Luminescent Materials and Devices & South China Advanced Institute for Soft Matter Science and Technology, South China University of Technology, Guangzhou 510640, China. E-mail: yinpc@scut.edu.cn; jsyang20@scut.edu.cn
First published on 20th September 2022
Abstract
Materials with promising mechanical performance generally demonstrate requirements for the critical sizes of their key building units, e.g. entanglements and crystal grains. Herein, only with van der Waals interaction, viscoelasticity with broad tunability has been facilely achieved below the critical size limits: the dimers of ∼1 nm polyhedral oligomeric silsesquioxane (POSS) with Mw < 4 kD and size < 5 nm, which demonstrate distinct material physics compared to that of polymer nanocomposites of POSS. The dimeric POSSs are confirmed by scattering and calorimetrical measurements to be intrinsic glassy materials with glass transition temperatures (Tgs) lower than room temperature. From rheological studies, their viscoelasticity can be broadly tuned through the simple tailoring of the dimer linker structures above their Tg. In dimer bulks, each POSS cluster is spatially confined by the POSSs from other dimers and therefore, the correlation of the dynamics of the two linked POSS clusters, which, as indicated by dynamics analysis, is regulated by the length and flexibilities of linkers, contributes to the caging dynamics of POSS confined by their neighbours and the resulting unique viscoelasticity. Our discoveries update the understanding of the structural origin of viscoelasticity and open avenues to fabricate structural materials from the design of sub-nanoscale building blocks.
Introduction
The realization of promising mechanical performance generally sets high requirements for the size limit of materials' key building units, e.g. polymers and metals, with the critical lengths of polymers passing the entanglement limit and the metal grain sizes over several nm.1,2 As model systems for the studies of general material physics, granular materials, composed of densely packed nano- or macro-scale particles, demonstrate unique impact- and shock-resistant properties that are highly dependent on the sizes, morphologies and surface structures of the building units.3–5 When their sizes approach the tens of nanometer scale, the dynamics of particles can be manipulated by the complex interactions among the particles in their assemblies, giving rise to unexpected and often exceptional mechanical performances.6,7 Their sizes are further narrowed down to ca. 5–7 nm known as the critical size for granular materials, and exciting transitions of viscoelastic properties are discovered: the particles with sizes smaller than 5 nm behave like small molecules with high mobilities and their bulk materials thus possess fast dynamics and appear as viscous liquids above glass transition temperatures (Tgs) while the counterparts with sizes larger than 7 nm demonstrate robust elasticity even at temperatures 100 K higher than their Tgs.8,9 Meanwhile, by tailoring the surface functional groups of colloids, inter-particle attractions around their close-packed neighbors can be achieved, leading to tunable elasticity, robustness and resilience under extreme conditions.10–13 It can be conjectured that novel mechanical properties can be achieved via the correlation of particle dynamics from the import of inter-particle attractions. However, the capability for colloid surface functionalization only allows the construction of non-selective and symmetric interactions with their closest neighboring units, providing few options for the further design of granular materials. Therefore, it would be of great interest to develop an effective protocol to correlate the dynamics of selected particles in a designed manner with targeted interaction potentials and explore their connections to the materials' typical mechanical performances. More importantly, it is a fundamental issue in materials science to test whether the critical size effect for general materials can be challenged via the introduction of correlated dynamics among the building units.Originating from their multiple dynamic relaxations associated with the polymer chain structures at different length scales, polymeric materials show unique and remarkable viscoelasticity and extraordinary mechanical strengths.14,15 Generally, the construction of hierarchical structures across multiple length scales, e.g. chain segments to overall dimensions of polymers, is required for the design of viscoelastic materials while the topologies of polymers can be deviated from linear features for enriched viscoelastic performances.16–19 Complex architectures combined with different topologies of polymers can deliver unique viscoelasticity for tissue engineering and impact resistance.20–22 Basically, high molecular weight and complex architectures are the key to the broadly tunable viscoelasticity, which, however, require considerable amount of synthetic efforts. It still remains a challenge to design viscoelastic materials from low Mw and small-size material systems without supramolecular or covalent bonding interactions among the building units. Molecular clusters (MCs) are a group of giant molecules with sizes ranging from sub-nm to 10 nm, which is applied popularly as model systems for soft matter, nanomaterials and catalysis research for their well-defined structures with enriched morphologies.23–25 More importantly, MCs by themselves can exhibit a broad range of functionalities individually and independently similar to nanoparticles (NPs) while they can be precisely tailored like small molecules via typical organic synthetic methods.23–25 MCs have been incorporated with the star polymer and polymer brush topology, respectively, and unexpected elasticity has been reported that originated from the physical interpenetration and inter-locking of MC structures.26,27 Herein, a 1 nm MC, isooctyl-functionalized polyhedral oligomeric silsesquioxane (OPOSS),28 is covalently dimerized to dumbbell/bola topologies. The correlation of the dynamics of the two linked OPOSS clusters can be regulated via the flexibility of the linkers while their viscoelastic behavior can be tuned. Neither long range ordering nor assemblies can be observed in the bulks of OPOSS dimers in their scattering data, confirming the absence of dominant supramolecular interactions. The low Mw and sub-nm particle system with the introduction of inter-molecular/particle correlations provides a new concept to design the structural materials with the required viscoelasticity, which should be different from the concept of the polymer nanocomposites of POSS.29 Our discoveries can be generally extended to a broad range of chemical and material systems ranging from small molecules to macromolecules and colloidal NPs.
Results and discussion
Molecular design of OPOSS dimeric structures
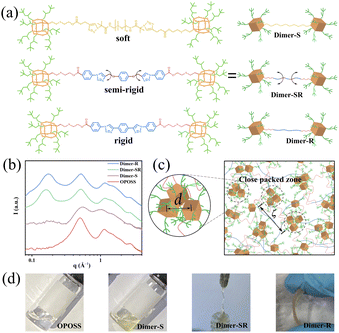
Linkers with varied flexibilities are applied to covalently bond with two OPOSS clusters to correlate their dynamics in a controlled manner. With the surface fully covered by isooctyl groups, the physical and chemical properties of OPOSS are dominated by the short and highly branched alkyl chains: their fast dynamics endows OPOSS with high mobilities and low glass transition temperature (Tg ∼ −40 °C)30 while their branches rule out possible supramolecular interactions and hinder long range ordering. Mono-functionalized OPOSSs are coupled via different linkers (Fig. 1a), and the material systems are named Dimer-S, Dimer-SR and Dimer-R, respectively, according to the flexibilities of the linkers. A correlation between the dynamics of the two linked OPOSS can be expected: for highly rigid linkers, the dimers behave like dumbbell molecules and the dynamics of the linked clusters are fully correlated while the OPOSS clusters would behave independently and similar to monomeric OPOSS when highly flexible linkers are applied.Structural analysis of OPOSS dimers
All the designed OPOSS dimers behave as intrinsic glassy materials with neither long-range ordering nor supramolecular assemblies. The chemical structures and purities of all dimers have been confirmed by nuclear magnetic resonance (NMR) measurements, mass spectrum and gel permeation chromatography (GPC) studies (ESI; Fig. S1†). Small angle X-ray scattering (SAXS) measurements rule out the domination of supramolecular interaction due to the absence of form factors of supramolecular assemblies (Fig. 1b). Meanwhile, there is no obvious peak signal around 1.84 Å−1 (0.34 nm) corresponding to π–π stacking from the SAXS results, confirming the absence of strong supramolecular interaction.31–34 The structure factor peak at 0.509 Å−1 characterizes the close packing of OPOSS (d) units from different dimer molecules, which is further confirmed by its consistency with that of the melt of pure OPOSS. The second peak in the low q range (0.161 to 0.173 Å−1), corresponds to the correlation length (ζ) of close packed zones of OPOSSs (Fig. 1c). Interestingly, the absence of ζ in Dimer-S originates from the lack of correlation between the OPOSSs in the dimer molecule. The SAXS data of aged dimers (3 months after their synthesis) show no obvious change, confirming the robustness of the dimers as well as the absence of strong supramolecular interactions (Fig. S2a†). Moreover, the SAXS data with increasing temperature show no obvious change, further confirming the robustness of the dimers (Fig. S2b†). The structural features of Dimer-S are coincident with its physical appearance as a viscous liquid under ambient conditions similar to pure monomeric OPOSS, while the appearance of dimers changes to the solid state as the flexibility of the linker varies from semi-rigid to rigid (Fig. 1d). Dimer-SR and Dimer-R possess characteristic Tgs (−18.8 and −11.7 °C, respectively) that are higher than that of single OPOSS (−37.6 °C) but still far below room temperature (Fig. S3a†). Moreover, when the test temperature of DSC increased to 200 °C, only one glass transition was observed and this result also proved that the sample was stable enough (Fig. S3b†). The dimers show higher Tgs with less flexible linkers, suggesting their stronger molecular correlation and slower segment dynamics. The single OPOSS conjugated with linkers demonstrates a distinct physical appearance in comparison to the dimers, confirming the key role of topological interaction in their mechanical performance (Fig S4 and S5†).Tunable viscoelasticity of OPOSS dimers
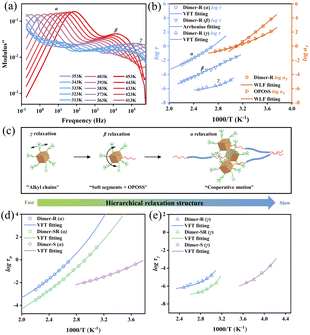
The OPOSS dimers can be tuned from a viscous to a viscoelastic appearance through the tailoring of the dimer linker structures although they have low Mw and small sizes. The typical rheological studies via the small amplitude oscillatory shear (SAOS) technique suggest that Dimer-S (4.45 × 103 Pa s) behaves as a shear thinning liquid with viscosity similar to that of pure OPOSS (7.36 × 103 Pa s) (Fig. S6 and 7†). For Dimer-SR and Dimer-R, their rheological master curves are similar to those of linear polymers with multiple relaxation stages: characteristic terminal relaxation (τt) with G′ ∼ ω−2 and G′′ ∼ ω−1 below 10 rad s−1 corresponding to the diffusive motion of the entire dimer molecule. The modulus of Dimer-R is higher than that of Dimer-SR at the measured time scale and the relaxation time τt of Dimer-SR is 15 times faster than that of Dimer-R due to the extra functional groups (C–O–C) with high rotational freedom in the linker of Dimer-SR (Fig. 2a and b). The van der Waals force dominates the interaction among all the dimers in their bulks30 and it can be conjectured that the appropriate rigidity of the linkers can facilitate the correlation between OPOSS dynamics in the same dimers and further manipulate the spatial jamming among dimers for their unique, tunable viscoelasticity, which is proved in the following dynamics analysis and molecular dynamics (MD) studies.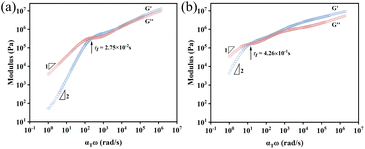 | ||
| Fig. 2 Master curves constructed from SAOS data from 273 K to 323 K. (a) Dimer-SR and (b) Dimer-R at a reference temperature of 323 K. The horizontal shifting factor aT of dimer molecules and OPOSS collected from time–temperature superposition of the small-amplitude oscillatory shear (SAOS) data (Fig. S6†). The relationship between αT and 1/T is well established by fitting to the WLF formula as is shown in Fig. S9.† | ||
Hierarchical dynamics of OPOSS dimers
The tunable viscoelasticity could originate from the hierarchical relaxation dynamics of the dimers, which are characterized by broadband dielectric spectroscopy (BDS) studies.35,36 Three dynamic relaxation processes can be observed, which represent the dynamics of the surface alkyl groups of OPOSS (γ), single OPOSS with soft fragments of linkers (β) and the cooperative dynamics of neighboring OPOSSs from different dimers (α),26 respectively (Fig. 3a and S10†). Temperature dependences of the characteristic relaxation time (τ) from BDS analysis and the time–temperature superposition shift factor (αT) of SAOS measurements are used to unify the dynamic behaviors from different measurements and all the dimer samples (Fig. 3b, c and S10†). The γ relaxation of both Dimer-SR and Dimer-R exhibits similar temperature-dependence to the rheological behavior of pure OPOSS, revealing the microscopic nature of γ relaxation of dimers as the dynamics of OPOSS surface alkyl groups. Originating from the structural relaxation of OPOSS with linkers, the β relaxation of all the dimers shows Arrhenius type temperature dependence with similar apparent activation energy (Ea) (Table S1 and Fig. S11†). The β relaxation is attributed to local dynamics and shows limited correlation with the overall packing or physical interaction among dimer molecules. As the slowest observable dynamics mode of dimers, the α relaxation shows similar Vogel–Fulcher–Tammann (VFT) temperature dependence to their rheological dynamics, suggesting its association with the cooperative relaxation of the aggregates of multiple OPOSSs (Fig. 3b and S10†). Therefore, the α relaxation characterizes the correlation of inter-molecular dynamics among dimers. The α relaxation time (τα) increases with the enhancement of rigidities of the linkers, suggesting stronger inter-molecular correlation. The α relaxation characterizes the correlation of inter-molecular dynamics among dimers while the temperature dependences of α relaxation time can be used to quantify the degree of correlation. As the fractions of the rigid segment in dimer linkers increase, the inter-molecular correlation turns out to be stronger and the elasticity becomes more dominant in the viscoelastic performances, suggesting the connection between inter-molecular cooperative dynamics and dimers' viscoelasticity (Fig. 3d). A similar trend can be observed for γ relaxation, suggesting a strong ‘caging effect’ among OPOSS in their aggregated zones (Fig. 3e). The above dynamics analysis suggests that the correlation of the dynamics of the two linked OPOSSs can be strengthened through the rigidness of the linkers and it can further promote the caging dynamics among neighboring dimer molecules for enhanced elasticity.27,37Microscopic mechanism for tunable viscoelasticity
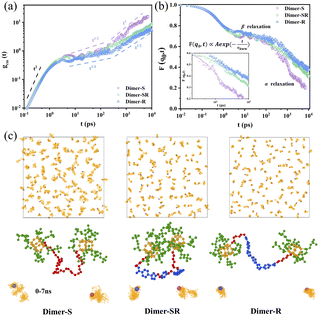
More microscopic understanding of the relationship among linker rigidness, structural dynamics and viscoelasticity is provided through the all-atom molecular dynamics (MD) studies (Fig. 4). The slice of the structure packing for the three typical systems (Fig. S13†) shows that the length distribution of two OPOSSs in the dimer molecules with soft linkers is random; conversely, for dimers with rigid linkers, the length distribution is not only almost consistent but also nearest neighbor OPOSSs are spatially restricted, which is consistent with our structural predictions from SAXS data. The mean square displacement (MSD) of the center-of-mass motions of OPOSSs (gcm(t)) in Dimer-S (Fig. 4a) follows a power-law distribution gcm(t) ∝ t1/2 at intermediate times, which is similar to that of an unentangled polymer system. For Dimer-SR and Dimer-R systems, the evolution of gcm(t) appears in a wide regime in the form of gcm(t) ∝ t1/4, which is due to spatial confinements imposed by neighboring OPOSS and the power-law is similar to that of a highly entangled polymer system.38 The self-part of the intermediate scattering function F(q0, t) (Fig. 4b) decays less rapidly and the wide plateau for Dimer-R at intermediate times further confirmed that OPOSS motion is constrained by neighboring OPOSSs. According to the Kohlrausch–Williams–Watts (KWW) relaxation function (inset of Fig. 4b),39,40 the characteristic relaxation time τkww is about 1.3 ns, 2.3 ns and 2.8 ns, respectively, for Dimer-S, Dimer-SR and Dimer-R systems. Center-of-mass motions of OPOSSs were applied to elucidate that the rigidity of linkers can regulate the cooperative dynamics of dimers induced by closed packed zones of OPOSSs (Fig. 4c and S14†). The center-of-mass motions of OPOSSs in Dimer-S undergo free diffusive motion (gcm(t) ∝ 6Dt) for a long time, similar to the typical Brownian thermal motion of pure OPOSS, explaining the origin of the similar physical appearance to monomeric OPOSS. Meanwhile, for dimers with semi-rigid and rigid linkers, the OPOSS shows characteristics of Rouse-like motion, mainly originating from the spatial confinement by their neighbors and contributes to the visco-elasticity of bulk materials. The correlation between the two linked OPOSSs imposes great difficulty for the diffusion of dimer molecules with rigid linkers, which allow the cooperative diffusion of OPOSSs' inter- and intra-dimer structures.The caging dynamics of crowded OPOSSs is governed by the linkers and a tiny structural variation of the linkers can lead to distinct mechanical performance of the melts of dimers. For Dimer-SR and -R, the structural difference is two symmetrically added C–O–C bonds in the linker while they behave distinctly as a visco-elastic solid and elastomer, respectively. Note that the C–O–C fragment was introduced to increase the flexibility of the linker and had no significant effect on the molecular size. The C–O–C fragment possesses high rotating freedom and endow high flexibility and fast segmental dynamics to the linker units, which can be confirmed from the lower Tg the Dimer-SR possesses when compared to Dimer-R (Fig. S3†). Another pair of dimers, Dimer-R′ and Dimer-SR′, with longer linkers than the above two dimers, are further used to confirm the role of C–O–C fragments (Scheme S4†). Dimer-SR′ possesses two extra C–O–C fragments when compared to Dimer-S′. Dimer-R′ shows higher Tg and modulus than Dimer-SR′, which further proves that a tiny structural variation of the linkers can lead to distinct mechanical performance of the melts of dimers (Fig. S16 and 17†). To quantify the linker effect, the rotational stiffness and flexural resistance of the linker are defined by the angle between the two vectors from the center to the end of the linker, as seen in Fig. S18,†θ1 and θ2 represent that of the rigid segment and all linkers, and are statistical averages from 64 dimer molecules in the bulk, respectively. The size sorting of the shear viscosity (η), given by the Green–Kubo method,41 is consistent with our experimental measurements (Fig. S8 and 17†). The dimer molecular size is defined as the end to end distance, Ree, and mean square radius of gyration (Rg) (Table S2†). Actually, there is no obvious change of the dimer molecular size with the introduction of the C–O–C fragment. Thus, the variation of viscoelasticity of the dimer system mainly comes from the regulation of rotational stiffness and flexural resistance of linkers. To further verify this conclusion, the van der Waals (VdW) (EVdW), bond stretching (Ebond), bond bending (Eangle) and torsional (Edihed) interactions of different dimer molecular systems are calculated based on the COMPASS force field (Table S3†). It is clear that the differences of EvdW are very tiny, which also excluded supramolecular interaction. For the intra-chain interactions, the values of torsional (Edihed) interactions of Dimer-SR reduced by about 4–7 times compared to that of Dimer-R, which is consistent with the viscoelasticity change of the dimer system.
To further confirm the strength of correlation with the rotational stiffness of the dimer linker and size of the dimer molecule, the correlation is predicted by the SISSO (a machine learning method for Symbolic Regression based on Compressed Sensing Algorithm)42 based on the dataset of Table S2.† Interestingly, the results show that the shear viscosity (η) is only associated with the rotational stiffness (−cos(θ1) and −cos(θ2)) of dimer linkers, and satisfies the following equation:
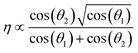 | (1) |
The cooperative dynamics of close-packed OPOSS units from neighboring dimer molecules is highly regulated by the flexibility of linkages, which further directs the diffusive motion of dimers in their bulks and the thus-resulting materials' visco-elasticity. A single OPOSS cluster possesses high mobility and shows fast diffusive dynamics in its bulk originating from its small size and the intrinsically fast dynamics of surface branched alkyl chains. For the dimer molecules, the dynamics of individual OPOSS can be correlated with the linkers and the degree of correlation is defined by the flexibilities of the linkers. The viscous flow of dimers, characterized microscopically as the diffusive dynamics of the complete dimer structures, requires both (1) the collective motion of the OPOSS unit in the same dimer for the effective translational diffusion of the dimer molecule and (2) the cooperative dynamics of the close-packed OPOSS units among neighboring dimers for the diffusion out of the caging zone. However, the collective and cooperative dynamics of OPOSS units could be disrupted by the linker-imposed correlation of the OPOSS units, leading to the typical caging dynamics of single OPOSS and the resulting visco-elasticity of materials. It can be conjectured that the degree of correlation for OPOSS is controlled by the rigidness of dimer linkers. Basically, the more rigid the linker is, the more strongly correlated the OPOSSs are and higher elasticities the materials possess. The attenuation of nanoparticle dynamics by linkers can be applied generally for nanomaterials. Adjusting the length and stiffness of linkers can well control the intra- and intermolecular interactions and contribute extensively to the regulation of caging dynamics and topological interaction. This finally endows the capability for the modulation of the nanomaterials' mechanical performance.
Compared with previously reported polymer nanocomposites of POSS, the dimer system demonstrates distinct material physics.29 For POSS dimers, the basic structural unit is dimer nanoparticles and their visco-elasticity is regulated by the topological interaction among the dimers. For polymer nanocomposites of POSS, the structural units are polymer chains and POSS, and their viscoelasticity is dominated by polymer chain relaxation while POSS is only applied to strengthen the mechanical properties of polymers. In our dimer systems, their Mw and size are far below that of polymeric materials and the dimers represent the only supramolecular interaction-free small molecule system that can demonstrate tunable visco-elasticity.
Conclusions
In summary, viscoelasticity with tunability can be achieved in the OPOSS dimer systems with low Mw and small sizes. In the supramolecular interaction-free system, OPOSS dimers stay as glassy materials with no long-range ordering and assemblies. The OPOSSs' ultra-small size and surface enriched short, branched alkyl chains and the linker-directed correlation between OPOSSs leads to the hierarchical dynamics. Different from the fast dynamics of monomeric OPOSS, the diffusion dynamics of OPOSS in the dimer are co-determined by its cooperative dynamics with neighboring close-packed OPOSSs from different dimers and the dynamics correlation with the other OPOSSs with the same dimer. Therefore, the OPOSS diffusion is severely hindered and demonstrated caging dynamics when rigid linker structures are applied in the dimers. The linker imposed correlation of particle dynamics and the caging dynamics of their assemblies can be extended to various particles, macromolecules, and molecular systems as long as the dynamics of the applied system can be attenuated by temperature variation, which, we believe, should be general properties of most of the chemical systems. General particles can be tuned to exhibit fast diffusive dynamics at certain temperatures and their monomers should behave as fluids. The covalent linkage between the single particles enables the correlated dynamics, further resulting in caging dynamics. For general chemical systems, as long as the synthetic route is available, they can be processed to show enriched dynamics and mechanical properties via the linker-imposed dynamics correlation. We believe our discoveries will update the understanding on the structural origin of viscoelasticity and open avenues to fabricate molecular cluster-based functional granular materials and nanocomposites.Data availability
All experimental and computational data associated with this article have been included in the main text and the ESI.†Author contributions
P. Y. and J. Y. conceived the project and designed the experiments. X. Z. carried out most of the experiments and analysed the data. J. Y. contributed to theoretical simulation. W. L. F. contributed to sample synthesis. T. L. S. contributed to rheological studies of the materials. J. H. carried out the SISSO machine learning. J. F. Y., M. L. and Y. L. performed dielectric and scatting characterizations and data analysis. All the authors discussed the results and commented on the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the financial support from the National Natural Science Foundation of China (No. 51873067 and 21961142018), Natural Science Foundation of Guangdong Province (No. 2021A1515012024 and 2016ZT06C322), China Postdoctoral Science Foundation (No. 2021M701236, 2022M711189, and BX20220114) and the Guangdong-Hong Kong-Macao Joint Laboratory for Neutron Scattering Science and Technology.Notes and references
- M. Pütz, K. Kremer and G. S. Grest, Europhys. Lett., 2000, 49, 735–741 CrossRef.
- X. Li and K. Lu, Acc. Mater. Res., 2021, 2, 108–113 CrossRef CAS.
- S. J. Antony, W. Hoyle and Y. Ding, Granular materials: fundamentals and applications, Royal Society of Chemistry, 2004, pp. 1–2 Search PubMed.
- H. M. Jaeger, S. R. Nagel and R. P. Behringer, Rev. Mod. Phys., 1996, 68, 1259–1273 CrossRef.
- D.-H. Nguyen, E. Azéma, P. Sornay and F. Radjai, Phys. Rev. E, 2015, 91, 032203 CrossRef.
- M. Cui, T. Emrick and T. P. Russell, Science, 2013, 342, 460–463 CrossRef CAS PubMed.
- R. Klajn, K. J. Bishop, M. Fialkowski, M. Paszewski, C. J. Campbell, T. P. Gray and B. A. Grzybowski, Science, 2007, 316, 261–264 CrossRef CAS.
- G. Liu, X. Feng, K. Lang, R. Zhang, D. Guo, S. Yang and S. Z. D. Cheng, Macromolecules, 2017, 50, 6637–6646 CrossRef CAS.
- M. Antonietti, T. Pakula and W. Bremser, Macromolecules, 1995, 28, 4227–4233 CrossRef CAS.
- D. Lee, S. Jia, S. Banerjee, J. Bevk, I. P. Herman and J. W. Kysar, Phys. Rev. Lett., 2007, 98, 026103 CrossRef PubMed.
- L. C. Hsiao, R. S. Newman, S. C. Glotzer and M. J. Solomon, Proc. Natl. Acad. Sci. U.S.A., 2012, 109, 16029–16034 CrossRef CAS PubMed.
- K. E. Mueggenburg, X.-M. Lin, R. H. Goldsmith and H. M. Jaeger, Nat. Mater., 2007, 6, 656–660 CrossRef CAS PubMed.
- N. M. James, C.-P. Hsu, N. D. Spencer, H. M. Jaeger and L. Isa, J. Phys. Chem. Lett., 2019, 10, 1663–1668 CrossRef CAS PubMed.
- M. T. Shaw and W. J. MacKnight, Introduction to polymer viscoelasticity, John Wiley & Sons, 2018, pp. 1–6 Search PubMed.
- M. Rubinstein and R. H. Colby, Polymer physics, Oxford university press, New York, 2003 Search PubMed.
- E. Vereroudakis, K.-T. Bang, M. Karouzou, A. Ananiadou, J. Noh, T.-L. Choi, B. Loppinet, G. Floudas and D. Vlassopoulos, Macromolecules, 2020, 54, 235–248 CrossRef.
- G. Liu, S. Cheng, H. Lee, H. Ma, H. Xu, T. Chang, R. P. Quirk and S.-Q. Wang, Phy. Rev. Lett., 2013, 111, 068302 CrossRef.
- Q. Huang, J. Ahn, D. Parisi, T. Chang, O. Hassager, S. Panyukov, M. Rubinstein and D. Vlassopoulos, Phy. Rev. Lett., 2019, 122, 208001 CrossRef CAS PubMed.
- K. Shimokawa, K. Ishihara and Y. Tezuka, Topology of polymers, Springer, 2019, pp. 1–5 Search PubMed.
- W. F. M. Daniel, J. Burdyńska, M. Vatankhah-Varnoosfaderani, K. Matyjaszewski, J. Paturej, M. Rubinstein, A. V. Dobrynin and S. S. Sheiko, Nat. Mater., 2016, 15, 183–189 CrossRef CAS.
- C. Liu, N. Morimoto, L. Jiang, S. Kawahara, T. Noritomi, H. Yokoyama, K. Mayumi and K. Ito, Science, 2021, 372, 1078–1081 CrossRef CAS PubMed.
- G. Bishko, T. C. B. McLeish, O. G. Harlen and R. G. Larson, Phy. Rev. Lett., 1997, 79, 2352–2355 CrossRef CAS.
- A. Pinkard, A. M. Champsaur and X. Roy, Acc. Chem. Res., 2018, 51, 919–929 CrossRef CAS PubMed.
- P. Jena and Q. Sun, Chem. Rev., 2018, 118, 5755–5870 CrossRef CAS PubMed.
- R. Jin, C. Zeng, M. Zhou and Y. Chen, Chem. Rev., 2016, 116, 10346–10413 CrossRef CAS PubMed.
- J.-F. Yin, Z. Zheng, J. Yang, Y. Liu, L. Cai, Q.-Y. Guo, M. Li, X. Li, T. L. Sun, G. X. Liu, C. Huang, S. Z. D. Cheng, T. P. Russell and P. Yin, Angew. Chem., Int. Ed., 2021, 60, 4894–4900 CrossRef CAS PubMed.
- J.-F. Yin, H. Xiao, P. Xu, J. Yang, Z. Fan, Y. Ke, X. Ouyang, G. Liu, T. L. Sun, L. Tang, S. Z. D. Cheng and P. Yin, Angew. Chem., Int. Ed., 2021, 60, 22212–22218 CrossRef CAS PubMed.
- M. Soldatov and H. Liu, Prog. Polym. Sci., 2021, 119, 101419 CrossRef CAS.
- S.-W. Kuo and F.-C. Chang, Prog. Polym. Sci., 2011, 36, 1649–1696 CrossRef CAS.
- Y. Liu, G. Liu, W. Zhang, C. Du, C. Wesdemiotis and S. Z. D. Cheng, Macromolecules, 2019, 52, 4341–4348 CrossRef CAS.
- J. Wang, L. Li, W. Yang, Z. Yan, Y. Zhou, B. Wang, B. Zhang and W. Bu, ACS Macro Lett., 2019, 8, 1012–1016 CrossRef CAS.
- X. Feng, L. Sosa-Vargas, S. Umadevi, T. Mori, Y. Shimizu and T. Hegmann, Adv. Funct. Mater., 2015, 25, 1180–1192 CrossRef CAS.
- Z. Shen, Y. Jiang, T. Wang and M. Liu, J. Am. Chem. Soc., 2015, 137, 16109–16115 CrossRef CAS PubMed.
- R. Yang, L. Ding, W. Chen, L. Chen, X. Zhang and J. Li, Macromolecules, 2017, 50, 1610–1617 CrossRef CAS.
- X. Zhang, W. Wei, X. Jin and H. Xiong, Macromolecules, 2020, 53, 5627–5637 CrossRef CAS.
- X. Zhang, W. Liu, D. Yang and X. Qiu, Adv. Funct. Mater., 2019, 29, 1806912 CrossRef.
- X. Zhou, J. Yang, J. Yang and P. Yin, J. Phys. Chem. Lett., 2022, 13, 7009–7015 CrossRef CAS PubMed.
- V. C. Chappa, D. C. Morse, A. Zippelius and M. Muller, Phys. Rev. Lett., 2012, 109, 148302 CrossRef PubMed.
- F. Alvarez, A. Alegra and J. Colmenero, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 7306 CrossRef.
- S. Chung and J. Stevens, Am. J. Phys., 1991, 59, 1024–1030 CrossRef CAS.
- J.-P. Rivet, Complex Syst, 1987, 1, 839–851 Search PubMed.
- R. Ouyang, S. Curtarolo, E. Ahmetcik, M. Scheffler and L. M. Ghiringhelli, Phys. Rev. Mater., 2018, 2, 083802 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Synthesis procedures, characterization methods, structural characterization, rheological raw data and detailed molecular dynamics simulation methods. See https://doi.org/10.1039/d2sc03651g |
| This journal is © The Royal Society of Chemistry 2022 |