Torsionally broken symmetry assists infrared excitation of biomimetic charge-coupled nuclear motions in the electronic ground state

Abstract

The concerted interplay between reactive nuclear and electronic motions in molecules actuates chemistry. Here, we demonstrate that out-of-plane torsional deformation and vibrational excitation of stretching motions in the electronic ground state modulate the charge-density distribution in a donor-bridge-acceptor molecule in solution. The vibrationally-induced change, visualised by transient absorption spectroscopy with a mid-infrared pump and a visible probe, is mechanistically resolved by ab initio molecular dynamics simulations. Mapping the potential energy landscape attributes the observed charge-coupled coherent nuclear motions to the population of the initial segment of a double-bond isomerization channel, also seen in biological molecules. Our results illustrate the pivotal role of pre-twisted molecular geometries in enhancing the transfer of vibrational energy to specific molecular modes, prior to thermal redistribution. This motivates the search for synthetic strategies towards achieving potentially new infrared-mediated chemistry.

---

Introduction

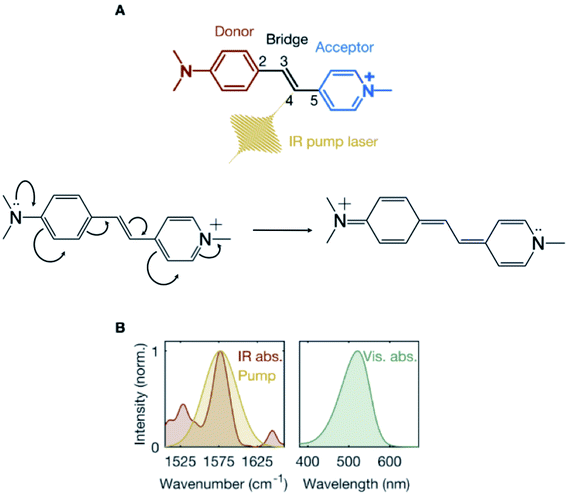
Charge transfer is a ubiquitous phenomenon.^1,2 It has been shown to facilitate isomerization reactions initiating the function of diverse biological photoreceptors.³ The canonical example is the photoisomerization of the retinal chromophore in the visual pigment, rhodopsin.⁴ Upon electronic photoexcitation to the first singlet excited state (S₁), the translocation of a positive charge along the chromophore-conjugated backbone “unlocks” an ethylenic moiety that becomes prone to isomerization. The resulting charge-coupled nuclear motions (CCNM) associated with the isomerization are then driven by the slope of the S₁ potential energy surface (PES).

Here, we explore the possibility of using vibrational excitation in the electronic ground state (S₀) to trigger CCNM initiating a double-bond torsional deformation, without resorting to photoinduced electronic excitation. We consider a model system – a push–pull stilbazolium-based donor-bridge-acceptor molecule,^5–8trans-4-[4-(N,N-dimethylamino)styryl]-1-methylpyridinium iodide (DASPMI, Fig. 1A). It features an ethylenic bridge connecting the amino-based donor and positively-charged pyridinium-ion acceptor units. There is a growing consensus in recent years advocating the vibrational perturbation of the bridge between a donor and an acceptor to successfully manipulate charge transfer, albeit in S₁.^9–14 Here, we investigate the effect of the vibrational excitation of the ethylenic bridge moiety in DASPMI in S₀. In a π-conjugated polyene (such as DASPMI), it may be envisaged to cause bond-length alternation (BLA) – the elongation of the double bonds coupled with a shortening of the single bonds. As illustrated in Fig. 1A, this would, in principle, prompt the translocation of the pyridinium charge and, effectively, electronically unlock the central double-bond ethylenic bridge. Here, we utilise an experimentally amenable infrared-active high-frequency BLA mode to increase the vibrational energy of the ethylenic bridge and follow the energy flow towards coupled key reactive torsional modes. Our results demonstrate the activation of a low-frequency vibrational mode, which remains detectable for several picoseconds. The underlying mechanism is revealed by complementary computational studies, which support the hypothesis that the vibrational perturbation ultimately results in the activation of biomimetic CCNM, corresponding to the bridge torsion. The simulations also reveal that the vibrational activation requires a pre-existing torsional symmetry-breaking of the bridge-localized ethylenic bond. In fact, only with a thermally pre-twisted configuration, the deposited infrared photon energy can efficiently initiate double-bond bridge-centric torsion.^15,16 This offers the intriguing prospect of synthetically modifying the molecule or its environment to populate larger segments of the S₀ isomerization path.

Fig. 1 Ground-state vibrational excitation of the donor-bridge-acceptor molecule. (A) Structure of the donor-bridge-acceptor, trans-4-[4-(N,N-dimethylamino)styryl]-1-methylpyridinium iodide (DASPMI), where the infrared (IR) pump laser induces S₀ vibrations along the ethylenic bridge, C₂–C₃=C₄–C₅. The translocation of the pyridinium charge effectively unlocks the ethylenic bridge. (B) Measured steady-state IR and visible absorption spectra of DASPMI in dichloromethane along with the spectral intensity of the IR pump laser.

Experimental setup and methodology

To prepare a vibrationally-excited S₀ population, a mid-infrared pump laser pulse is tuned to spectrally coincide with the steady-state absorption peak, denoting the S₀ ethylenic-stretch bridge vibration in DASPMI (Fig. 1B). The vibronic overlap between S₀ and S₁ is mapped by a time-delayed broadband supercontinuum probe pulse in the visible. A schematic representation of the experimental setup is shown (ESI Fig. S1†). The mid-infrared pump laser pulse is derived from an optical parametric amplifier (Orpheus-One and Lyra, Light Conversion), which is pumped by 200 mW of a femtosecond laser (Pharos, Light Conversion), operated at a repetition rate of 1 kHz. The output of the laser, at a central wavelength of 1030 nm, is also used to generate a broadband supercontinuum probe pulse by focussing into a 2 mm thick sapphire crystal. The pump pulse, tuned to a central frequency of 1577 cm⁻¹ and with a spectral bandwidth of 50 cm⁻¹ (Fig. 1B), is passed through a germanium filter and time-delayed with respect to the probe pulse, using a computer-controlled motorized delay stage. The maximum energy of the pump pulse used in the experiments is measured to be 760 nJ, corresponding to an incident pump fluence of ∼6 mJ cm⁻². The cross-correlation time between the pump and probe pulses is estimated to be ∼350 fs at the sample position. An optical chopper is used to modulate the repetition rate of the pump pulse. The detector comprises a computer-controlled spectrograph (Sciencetech), coupled to a linear CCD image sensor (Hamamatsu). The transient absorption signal is calculated as ΔA = log(pump_off/pump_on), averaged typically over 5000–7000 spectra at each time-delay. The entire data acquisition is fully synchronised and automated. The home-built sample flow-cell consists of two 1 mm thick BaF₂ windows, separated by a 0.1 mm thick stainless-steel spacer and fitted with a peristaltic pump, which is tested for steady and bubble-free flow. The sample is prepared by dissolving DASPMI (Sigma-Aldrich) in dichloromethane to a concentration of 1 mM. In order to negate any possible effect due to the cumulative heating of the solvent, despite continuously flowing the sample, control experiments are performed with (1) only the solvent, dichloromethane, excited at the target frequency of 1577 cm⁻¹; (2) a DASPMI solution in dichloromethane, excited at frequencies corresponding to the nearest-lying vibrational modes of dichloromethane – namely, 1426 cm⁻¹ and 1264 cm⁻¹. The control experiments produce non-detectable transient absorption signals. Additional experiments are also performed by varying the sample concentration and the pump laser energy (ESI Fig. S3†), tuning the wavelength of the mid-infrared pump laser (ESI Fig. S4†) and in a different solvent, ethanol (ESI Fig. S5†). The steady-state mid-infrared absorption spectrum of DASPMI in dichloromethane (Fig. 1B) is measured using a commercial pre-calibrated Fourier-transform infrared (FTIR) spectrometer (VERTEX 70v, Bruker). The laser spectrum (Fig. 1B) is measured at the position of the sample with a calibrated mid-infrared spectrograph (Infrared Systems), fitted with a liquid-nitrogen-cooled HgCdTe (MCT) detector. We estimate that 24% of the molecules in the focal volume are infrared-excited and that the transient absorption spectrum corresponds to 6% of the excited population fraction.

Results and discussion

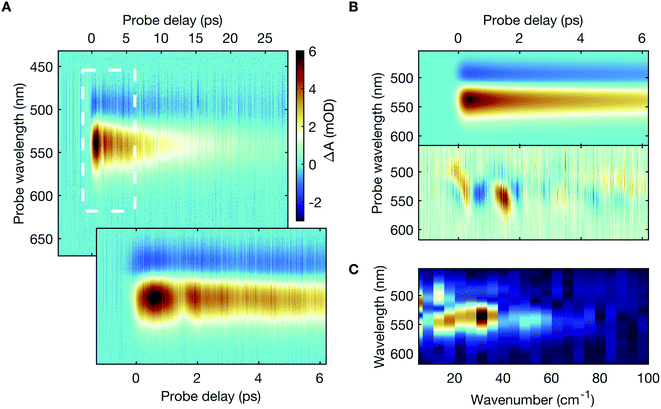
The transient absorption spectra (Fig. 2A) primarily exhibit two prominent spectral features – a weak negative differential absorption feature, peaked at 493 nm, adjacent to and partially obscured by a strong positive feature, centred at 539 nm, with pronounced temporal oscillations (also shown in ESI Fig. S2†). The spectral features scale linearly, both with the incident mid-infrared photon flux and the sample concentration (ESI Fig. S3†), thereby eliminating any potential artifact due to non-linear excitation or aggregate formation. Besides, detuning the spectral overlap between the mid-infrared pump laser pulse and the targeted absorption peak out of resonance leads to a progressive reduction in the spectral intensity of the transient absorption signal (ESI Fig. S4†).

Fig. 2 Mid-infrared-induced transient absorption signal of DASPMI in dichloromethane. (A) Raw experimental transient absorption spectra measured as a function of the time delay between the vibrational pump and the electronic probe. The negative signal (blue), peaked at 493 nm, represents the bleach of the initial thermally-populated low-lying vibrational levels (predominantly v = 0) in S₀. The positive signal (red), peaked at 539 nm, represents the vibrationally-excited population in S₀, projected onto S₁. A magnified view of the highlighted region in the top panel is presented in the bottom panel in order to clearly depict the coherent temporal oscillations. (B) Fitted transient absorption dynamics obtained after a global bi-exponential fit with time-constants of 1.7 ps and 13.6 ps (top panel) and the oscillatory residues (bottom panel), presented on a normalised colour-scale for better visualization. (C) Normalised Fourier power spectrum of the oscillatory residues with frequency components up to 50 cm⁻¹, with a distinct spectral peak at 30 cm⁻¹.

A global fitting analysis of the transient absorption spectra allows examining the population decay following the vibrational excitation, which is consistent with typical vibrational relaxation dynamics (Fig. 2B). Distinct time-domain oscillations, manifested in the global-analysis residuals (Fig. 2B), correspond to Fourier-domain frequencies up to 50 cm⁻¹, with a prominent spectral peak at 30 cm⁻¹ (Fig. 2C).

The negative differential absorption signal can be attributed to the bleach of the initial thermally-populated low-lying vibrational levels (predominantly v = 0) in S₀. It arises due to the population transfer to the higher vibrational levels in S₀. The projection of this vibrationally-excited S₀ population onto S₁ produces the positive differential absorption signal. The anharmonicity of S₀ determines its Franck–Condon overlap with S₁, and therefore the spectral location of the transient absorption signals. The temporal oscillations in the transient absorption signal may be assigned to the vibrational coherence due to the excitation of an anharmonically coupled low-frequency mode.

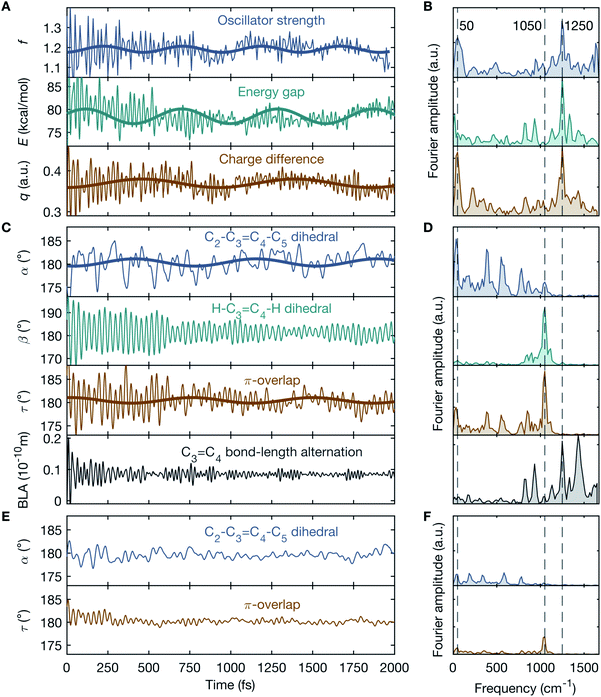
In order to gain insight into the vibrationally-induced dynamics, simulations within the multi-configurational complete active space self-consistent field and second-order perturbation theory (CASPT2//CASSCF) framework¹⁷ are performed. The population dynamics of a realistic fully solvated model of the entire DASPMI chromophore in dichloromethane is simulated over a time-period of 2 ps with 400 trajectories (further details in ESI and Fig. S6–S15†). On creating the vibrationally-excited BLA-activated S₀ population, the oscillator strength, f, for the electronic transition from S₀ to S₁ increases by ∼30% from f = 0.86 to f = 1.11 (ESI Fig. S7†). This is a consequence of the geometric changes induced by the vibrational excitation and accounts for the appearance of the transient absorption signal observed experimentally. Moreover, the temporal evolution of f reflects a pronounced oscillatory behaviour (Fig. 4A) with conspicuous frequency components peaked at 50 cm⁻¹ and in the vicinity of 1250 cm⁻¹ (Fig. 4B). The former low-frequency component matches the experimentally observed time-domain oscillations in the transient absorption signal (Fig. 2C), whereas the latter high-frequency components are beyond the time-resolution limit of our experimental detection scheme. The time-domain oscillations with frequencies of 50 cm⁻¹ and 1250 cm⁻¹ are further echoed in the energy gap, E, and the charge difference, q, between S₀ and S₁ (Fig. 4A and B).

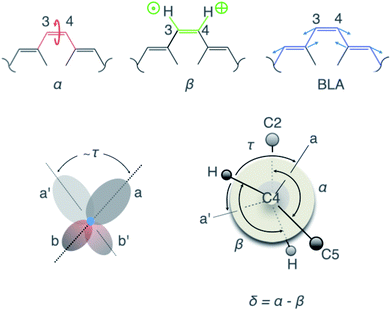Fig. 3 Visualisation of the geometric parameters. The C₂–C₃=C₄–C₅ dihedral angle, α, the H–C₃=C₄–H dihedral angle, β, the BLA along the ethylenic bridge, and the π-overlap, τ.

Fig. 4 Mechanistic interpretation of the vibronic coupling. Simulation results for a fully solvated model of the DASPMI chromophore in dichloromethane over a time-period of 2 ps for the BLA-activated vibrationally-excited S₀ population. In order to distinguish the effect of the initially pre-twisted thermal configuration, 54 trajectories are selected out of the 400 trajectories according to a velocity threshold of >1° fs⁻¹ on the π-overlap angle, τ, for the initial thermal population. (A) Temporal dynamics of the oscillator strength, f, for the S₀ → S₁ transition along with the energy gap, E, and the charge difference, q, between S₀ and S₁. (B) The corresponding Fourier spectra, showing distinct frequency components at 50 cm⁻¹ and 1250 cm⁻¹. The former is in close agreement with the experimentally observed oscillations in the transient absorption signal, reflected by f. (C) Temporal dynamics of the C₂–C₃=C₄–C₅ dihedral angle, α, the H–C₃=C₄–H dihedral angle, β, the π-overlap, τ, and the BLA along the ethylenic bridge. (D) The corresponding Fourier spectra. The low-frequency oscillations at 50 cm⁻¹ in f, E and q may be attributed to the torsional deformation, α, whereas the high-frequency oscillations at 1250 cm⁻¹ may be assigned to the BLA. Consequently, the oscillatory temporal dynamics of the electronic parameters f, E and q may be correlated to the vibrational parameters, α and BLA, accounting for the vibronic coupling between S₀ and S₁. On the contrary, the oscillations in β, which represents the in-phase HOOP motion, at 1050 cm⁻¹ is not reflected in f, E and q and therefore β does not contribute to the vibronic coupling. (E and F) The evolution of the remaining (400–54) trajectories with a primarily planar (or non-twisted) initial thermal configuration, with diminished oscillatory behaviour.

To correlate the observed oscillatory temporal dynamics in f, E and q to mechanistic information in terms of CCNM, we survey the time evolution of bridge-localized modes that are anharmonically coupled. Of particular interest are the C₂–C₃=C₄–C₅ dihedral angle, α, the H–C₃=C₄–H dihedral angle, β, the π-overlap, τ = (α + β)/2, describing the double-bond torsional deformation, and the BLA localized mode of the ethylenic bridge (Fig. 3). It immediately follows (Fig. 4A–D) that the low-frequency oscillations around 50 cm⁻¹ in f, E and q may be attributed to a torsional deformation of the ethylenic bridge, represented by α. This is accompanied by vibrations along the BLA coordinate, which are responsible for inducing the high-frequency oscillations around 1250 cm⁻¹ in f, E and q. On the contrary, β, signifying the in-phase hydrogen-out-of-plane (HOOP) motion, displays oscillations at a frequency of 1050 cm⁻¹, which is not manifested in the observed temporal dynamics of f, E and q. Consequently, these results trace the origin of the vibronic coupling between S₀ and S₁ by attributing the modulations in the electronic parameters, f, E and q, to the vibrational parameters, BLA and α. To summarise, the BLA-activated S₀ vibrations, which initiate the translocation of the pyridinium charge and the electronic unlocking of the C₃=C₄ ethylenic bridge, are primarily responsible for the modulation of the oscillator strength, f, for the S₀ → S₁ transition, when coupled to α (further details in ESI and Table S1†). This accounts for the experimental transient absorption signal and reproduces the observed mode-coupling effect, reflecting the vibronic nature of the key modes, BLA and α. Furthermore, α determines, together with β, the magnitude of τ, and therefore the change in the p-orbital overlap associated with the C₃=C₄ π-bond torsional deformation.

Our simulations use a hybrid quantum mechanics/molecular mechanics (QM/MM) model of the solvated molecule and therefore include all the vibrational degrees of freedom of the system – both solute and solvation shell. The forces, which are computed on-the-fly along the trajectories, are quantum-chemical (that is, not parametrised) for DASPMI and empirical for the solvent molecules, and thus include the description of the anharmonic PES. Therefore, the thermally equilibrated S₀ population contains pre-twisted structures that rapidly couple low-frequency torsional modes and high-frequency stretching modes upon relaxation. Trajectory analysis shows that the oscillatory modulation in the dynamics (Fig. 4A–D) predominantly originates from this pre-twisted initial thermal sub-population (values of α far from planarity), defined by a velocity threshold of >1° fs⁻¹ on the π-overlap angle, τ, along the ethylenic bridge. In other words, it is necessary to have a substantial torsionally broken symmetry for the infrared excitation to efficiently produce the observed CCNM event. This is further illustrated by the demarcation between the pre-twisted (Fig. 4A–D) and the primarily planar initial thermal S₀ sub-populations (Fig. 4E and F). In the initial planar configuration (Fig. 4E and F), BLA and α are uncoupled and do not lead to a detectable oscillatory motion in the simulation. This is markedly different from the initial pre-twisted configuration (Fig. 4A–D), which enhances the torsional deformation along α through the vibrational coupling with BLA.

The observed oscillatory dynamics corresponds to the initial progression along a double-bond isomerization coordinate in S₀ induced by a CCNM event. This is corroborated by mapping the S₀ PES (Fig. 5A) along the BLA and α coordinates (further details in ESI†). Noticeably, the PES map discloses two S₀ isomerization paths separated by the minimum-energy conical intersection, CI, between S₀ and S₁ (Fig. 5A). Both paths involve transition states (TS) with highly non-planar and torsionally distorted (α ∼ 90°) geometries. However, the region characterized by increased BLA is associated with increased charge-transfer character, consistent with a CCNM event, and quantified by the partial charge, ρ, localized on the acceptor moiety. This reiterates the significance of both BLA and α, which are known to be intricately linked to facilitating S₁ charge transfer in conjugated polyenes.¹⁸ The salient feature of the PES map, however, is that the charge-transfer transition state, TS_CT, mediating heterolytic bond-breaking, provides a significantly lower energy barrier (39 kcal mol⁻¹), compared to the diradical (or covalent) transition state, TS_dir (49 kcal mol⁻¹), responsible for homolytic bond-breaking. Essentially, the CCNM event prompted by the vibrational excitation reallocates the charge-density distribution in DASPMI. This causes a decrease in the π-overlap along the ethylenic bridge, which permits a more unrestrained torsional motion that mimics the S₁ unlocking event described above. Of course, while such an S₁ event would lead to isomerization, in S₀, the reported energy barrier results in the population of only the initial segment of the S₀ isomerization coordinate leading to TS_CT, reaching torsional deformations up to ∼40° (Fig. 6).

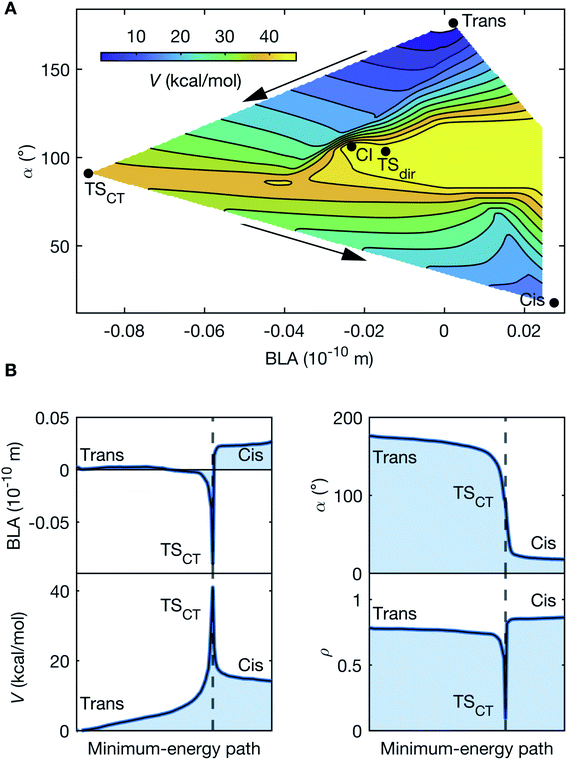Fig. 5 Ground-state reaction pathways. (A) PES of S₀ as a function of the torsional deformation represented by the C₂–C₃=C₄–C₅ dihedral angle, α, and the BLA coordinates. The potential energy, V, is defined relative to the reactant trans-isomer (0 kcal mol⁻¹). Two isomerization pathways may readily be recognised, separated by the conical intersection (CI, 53 kcal mol⁻¹). One isomerization channel proceeds via the transition state, TS_dir, constituting an energy barrier of 49 kcal mol⁻¹, towards the formation of the product cis-isomer (12 kcal mol⁻¹). This pathway does not involve any significant variation in the partial charge, ρ, localized on the acceptor. TS_dir may therefore be assigned a covalent character, driving homolytic bond-breaking, which results into a diradical at the torsionally distorted (α ∼ 90°) structure. A conspicuously lower energy barrier of 39 kcal mol⁻¹ is offered by the alternate isomerization channel (indicated by the arrows) via the transition state, TS_CT, where the charge-transfer character driving heterolytic bond-breaking varies from ρ_trans = 0.76 for the reactant, to ρ_CT = 0.10, and finally ρ_cis = 0.85 for the product. This signifies near-complete charge transfer, since (ρ_trans − ρ_CT)/ρ_trans = 0.87. Similar to TS_dir, TS_CT is associated with a α ∼ 90° distorted geometry, which, however, has a very different (and negative) value for the BLA. Table 1 denotes the parameter space along α and BLA accessed by the vibrationally-excited population in the course of the simulation trajectories and is characterized by a potential energy of ∼8 kcal mol⁻¹ and ρ_sim = 0.27, where (ρ_trans − ρ_sim)/ρ_trans = 0.64, and the S₀–S₁ energy gap always exceeds 41 kcal mol⁻¹. This is representative of the degree to which charge-transfer character is induced in the course of the simulations. The similarity of this PES with Fig. 7 demonstrates the biomimetic nature of DASPMI. (B) Trace of the minimum-energy path for S₀ isomerization, starting from the reactant trans-isomer and resulting in the product cis-isomer via the transition state, TS_CT, as a function of the BLA and the torsion, α. The variation in the potential energy, V, and the charge-transfer character, ρ, is also shown, where ρ = 0 and ρ = 1 represent ψ_CT and ψ_COV, respectively.

Table 1 Maximum amplitude observed in the trajectory simulations

Parameters	Average minimum	Average maximum	Absolute minimum	Absolute maximum
BLA (10^−10 m)	−0.024	0.202	−0.33	0.57
α (°)	171.42	185.02	146.26	215.99
ρ	0.61	0.97	0.27	1.02

---

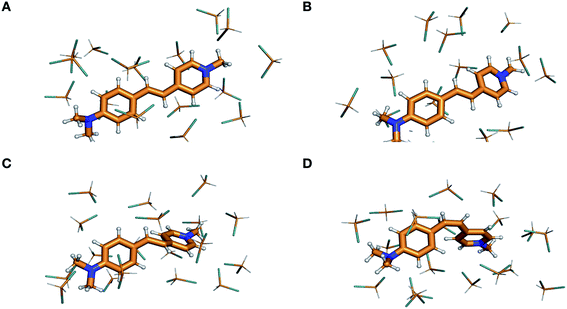Fig. 6 Visualization of the ground-state isomerization pathway in DASPMI. Optimized geometries for (A), the planar reactant trans-isomer, (B), a representative snapshot from one of the 400 trajectories, showing a torsional deformation of ∼40°, (C), the highly distorted charge-transfer transition state, TS_CT, and (D), the product cis-isomer. (ESI Fig. S15† provides the view along the molecular plane to illustrate the torsional deformation induced in the course of the trajectory simulations.)

The charge-transfer parameter, ρ, for the vibrationally-excited S₀ population reaches a maximum value of 0.27 in the simulations, which equates to a fractional change of 0.64 with respect to the trans-isomer reactant state. For comparison, the fractional change in ρ for TS_CT is 0.87. This shows the considerable charge-transfer character (ψ_CT) imparted to the vibrationally-excited S₀ state, which initially has a primarily covalent character (ψ_COV).

Interestingly, the S₀ PES of DASPMI (Fig. 5A) has a striking resemblance to that in bovine rhodopsin (Fig. 7), the retinal protein responsible for mammalian vision. The retinal isomerization in rhodopsin-like photoreceptors^4,19–21,30 represents an archetypal example of complex biological machinery amenable to precise experimental and theoretical inspection. In addition to the widely studied photoisomerization channel in rhodopsin triggered by electronic excitation, quantum chemical modelling of the S₀ PES of rhodopsin (Fig. 7) has unveiled the existence of a thermal isomerization pathway.³ The reaction (Fig. 7) is initially mediated by a high-frequency BLA stretching mode, which is coupled to a reactive double-bond torsional deformation, α, and ultimately forms a fully twisted charge-transfer transition state, TS_CT. This imitates the S₀ dynamics in DASPMI and justifies its biomimetic nature.

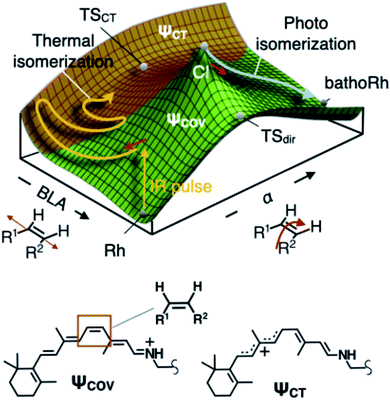Fig. 7 Ground-state thermal isomerization in rhodopsin. Schematic representation of the S₀ PES of the retinal chromophore in bovine rhodopsin, Rh, to demonstrate the biomimetic nature of DASPMI. The PES is mapped as a function of the BLA and the torsion, α, coordinates.³ The different regions are representative of the different predominant electronic configurations, denoted by the covalent and charge-transfer electronic wavefunctions, ψ_COV and ψ_CT, respectively. The photoisomerization pathway following electronic excitation proceeds via the conical intersection (CI) towards the formation of the isomerization product state, bathoRh. The CI is energetically located above the transition state with diradical character, TS_dir. On the contrary, S₀ thermal activation provides an isomerization pathway via a charge-transfer transition state, TS_CT, which offers the lowest energy barrier threshold between the reactant and product states in S₀. The Lewis resonance formulae associated with the covalent and the charge-transfer electronic configurations of the cationic rhodopsin chromophore (the protonated Schiff base of 11-cis retinal) are also shown, highlighting the reactive ethylenic bond, along which the isomerization occurs.

Conclusions and outlook

To conclude, we demonstrate that the S₀ vibrational excitation of the ethylenic bridge in the donor-bridge-acceptor molecule, DASPMI, reveals the vibronic coupling between S₀ and S₁. This is manifested in the vibrationally-induced modulation of the molecular electronic wave-function, fuelling a CCNM event. In essence, our results exemplify a noteworthy scenario, where S₀ vibrational excitation affects the electronic character of a molecule in solution phase. This may evoke comparisons with recent studies investigating the coupling of phonon modes to the optical band-gap in lattice structures, following terahertz excitation.²² Our experimental observations display vibrational coherence in the transient absorption spectra, which, based on our simulations, is attributed to the excitation of a torsional deformation along the ethylenic bridge. Our simulations identify the reaction coordinate as a function of the key reactive modes, namely the infrared-excited BLA and the anharmonically-coupled ethylenic torsion. This is particularly significant since there exists no generic prescription for the a priori identification of an experimentally accessible handle – a strongly infrared-absorbing vibrational mode that also couples strongly to the reaction coordinate – as a precursor to infrared-induced S₀ chemistry. Previous instances^23–29 of vibrationally-mediated S₀ reactivity have typically targeted weak chemical bonds in small molecules, where the key reactive modes could be intuitively predicted.

Furthermore, our simulations provide evidence that the coupling between the BLA and torsional modes is intrinsically enhanced by the thermal pre-twisting of the DASPMI molecular framework about the reactive double bond. In order to experimentally achieve further progress along the isomerization coordinate, this mode-coupling needs to be adequately enhanced. This may be made possible by synthetic modifications, resulting in an enhanced pre-twisted initial population. Alternatively, incorporating the reactant in specific molecular environments (such as molecular cavities) can amplify the mode-coupling to decrease the activation threshold and reach the critical TS_CT state. Our results may be envisaged to encourage the synthesis of DASPMI homologues or suitable molecular hosts, leading to lower isomerization barriers as models for future investigations. The implications of our results can also be appreciated in perspective of the ubiquity of charge-transfer reactions. Contrary to S₁ charge-transfer processes, the capacity to regulate the input vibrational energy posits a means to control the extent of a CCNM event in S₀ (Fig. 5). Here, it provides the premise for driving isomerization – yet another ubiquitous process in chemistry and biology – in S₀.

Data availability

The data are available from the corresponding authors on reasonable request.

Author contributions

A. J. and G. C. conceived the research under the supervision of R. J. D. M. The molecular system was suggested by J. D. G. C., A. J. and V. T. built the experimental setup and performed the experiments with H. G. D. F. T. designed the data acquisition interface. G. C. analysed the data with V. P. G. C. and A. J. interpreted the experimental results. The theoretical framework was developed by M. O. The simulations were performed, analysed and interpreted by M. O., A. B. G. and M. M. N. F. implemented the vibrational frequency analysis at the QM/MM level. The manuscript was written by G. C. with A. J. and M. O. All authors read and commented on the manuscript.

Conflicts of interest

The authors declare no competing interests.

Acknowledgements

The experimental work was funded by the Max-Planck-Gesellschaft. The authors acknowledge Prof. Nils Huse (University of Hamburg) and the Sample Preparation and Characterization (SPC) Facility of EMBL Hamburg for access to their FTIR spectrometers and Dr Stephan Niebling (EMBL Hamburg) for assistance with the FTIR measurements. The authors further thank Djordje Gitaric, Hendrik Schikora and Jan-Philipp Leimkohl (MPSD) for technical support, Dr Shreetama Karmakar (TIFR) for initial discussions and Dr Michal Kochman (MPSD) for preliminary simulations. M.O. is grateful to the National Science Foundation for grant no. CHE-1710191, for a MIUR Department of Excellence Grant 2018–2022 and to the Fondazione Banca d'Italia and the Ohio Supercomputer Center for the provided computational facilities and services.

References

1. D. N. Beratan, C. Liu, A. Milgliore, N. F. Polizzi, S. S. Skourtis, P. Zhang and Y. Zhang, Charge transfer in dynamical biosystems, or the treachery of (static) images, Acc. Chem. Res., 2015, 48, 474–481.
2. V. Coropceanu, X.-K. Chen, T. Wang, Z. Zheng and J.-L. Brédas, Charge-transfer electronic states in organic solar cells, Nat. Rev. Mater., 2019, 4, 689–707.
3. S. Gozem, H. L. Luk, I. Schapiro and M. Olivucci, Theory and simulation of the ultrafast double-bond isomerization of biological chromophores, Chem. Rev., 2017, 117, 13502–13565.
4. S. Gozem, I. Schapiro, N. Ferré and M. Olivucci, The molecular mechanism of thermal noise in rod photoreceptors, Science, 2012, 337, 1225–1228.
5. M. Sczepan, W. Rettig, A. I. Tolmachev and V. V. Kurdyukov, The role of internal twisting in the photophysics of stilbazolium dyes, Phys. Chem. Chem. Phys., 2001, 3, 3555–3561.
6. B. Carlotti, et al., Intramolecular charge transfer of push–pull pyridinium salts in the triplet manifold, J. Phys. Chem. A, 2014, 118, 7782–7787.
7. M. Aschi, et al., Photoexcitation and relaxation kinetics of molecular systems in solution: towards a complete in silico model, Phys. Chem. Chem. Phys., 2016, 18, 28919–28931.
8. S. Karmakar, et al., Transient Raman snapshots of the twisted intramolecular charge transfer state in a stilbazolium dye, J. Phys. Chem. Lett., 2020, 11, 4842–4848.
9. P. Roy, et al., Ultrafast bridge planarization in donor-π-acceptor copolymers drives intramolecular charge transfer, Nat. Commun., 2017, 8, 1716.
10. Z. Lin, et al., Modulating unimolecular charge transfer by exciting bridge vibrations, J. Am. Chem. Soc., 2009, 131, 18060–18062.
11. M. Delor, et al., Toward control of electron transfer in donor-acceptor molecules by bond-specific infrared excitation, Science, 2014, 346, 1492.
12. A. A. Bakulin, et al., Mode-selective vibrational modulation of charge transport in organic electronic devices, Nat. Commun., 2015, 6, 7880.
13. M. Delor, et al., On the mechanism of vibrational control of light-induced charge transfer in donor–bridge–acceptor assemblies, Nat. Chem., 2015, 7, 689.
14. M. Delor, et al., Directing the path of light-induced electron transfer at a molecular fork using vibrational excitation, Nat. Chem., 2017, 9, 1099.
15. C. B. Gorman and S. R. Marder, An investigation of the interrelationships between linear and nonlinear polarizabilities and bond-length alternation in conjugated organic molecules, Proc. Natl. Acad. Sci. U. S. A., 1993, 90, 11297.
16. Z. R. Grabowski, K. Rotkiewicz and W. Rettig, Structural changes accompanying intramolecular electron transfer: focus on twisted intramolecular charge-transfer states and structures, Chem. Rev., 2003, 103, 3899–4032.
17. N. Ferré and M. Olivucci, Probing the rhodopsin cavity with reduced retinal models at the CASPT2//CASSCF/AMBER level of theory, J. Am. Chem. Soc., 2003, 125, 6868–6869.
18. C. B. Gorman and S. R. Marder, An investigation of the interrelationships between linear and nonlinear polarizabilities and bond-length alternation in conjugated organic molecules, Proc. Natl. Acad. Sci. U. S. A., 1993, 90, 11297.
19. P. J. M. Johnson, et al., Local vibrational coherences drive the primary photochemistry of vision, Nat. Chem., 2015, 7, 980.
20. D. Polli, et al., Tracking the primary photoconversion events in rhodopsins by ultrafast optical spectroscopy, Photochem. Photobiol. Sci., 2015, 14, 213–228.
21. C. Schnedermann, et al., Evidence for a vibrational phase-dependent isotope effect on the photochemistry of vision, Nat. Chem., 2018, 10, 449–455.
22. H. Kim, et al., Direct observation of mode-specific phonon-band gap coupling in methylammonium lead halide perovskites, Nat. Commun., 2017, 8, 687.
23. L. Windhorn, et al., Getting ahead of IVR: A demonstration of mid-infrared induced molecular dissociation on a sub-statistical time scale, J. Chem. Phys., 2003, 119, 641–645.
24. T. Witte, et al., Controlling molecular ground-state dissociation by optimizing vibrational ladder climbing, J. Chem. Phys., 2003, 118, 2021–2024.
25. R. Schanz, V. Boţan and P. Hamm, A femtosecond study of the infrared-driven cis-trans isomerization of nitrous acid (HONO), J. Chem. Phys., 2005, 122, 044509.
26. V. Botan, R. Schanz and P. Hamm, The infrared-driven cis-trans isomerization of HONO. II: Vibrational relaxation and slow isomerization channel, J. Chem. Phys., 2006, 124, 234511.
27. J. Y. Shin, M. A. Shaloski, F. F. Crim and A. S. Case, First evidence of vibrationally driven bimolecular reactions in solution: reactions of br atoms with dimethylsulfoxide and methanol, J. Phys. Chem. B, 2017, 121, 2486–2494.
28. T. Stensitzki, et al., Acceleration of a ground-state reaction by selective femtosecond-infrared-laser-pulse excitation, Nat. Chem., 2018, 10, 126.
29. A. Thomas, et al., Tilting a ground-state reactivity landscape by vibrational strong coupling, Science, 2019, 363, 615.
30. X. Yang, Quantum–classical simulations of rhodopsin reveal excited-state population splitting and its effects on quantum efficiency, Nat. Chem., 2022, 14, 441–449.

---

Footnotes

† Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2sc02133a

‡ Present address: Central Laser Facility, Science and Technology Facilities Council, Research Complex at Harwell, Rutherford Appleton Laboratory, Harwell Campus, Didcot OX11 0QX, UK.

§ These authors contributed equally to this work.

¶ Present address: The Rosalind Franklin Institute, Rutherford Appleton Laboratory, Harwell Campus, Didcot OX11 0FA, UK.

---