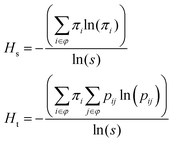View PDF VersionPrevious ArticleNext Article
 
DOI: 10.1039/D2RP00066K (Paper) Chem. Educ. Res. Pract., 2022, 23, 714-724

Adapting gaze-transition entropy analysis to compare participants’ problem solving approaches for chemistry word problems

Philip Nahlik * and Patrick L. Daubenmire
Department of Chemistry and Biochemistry, Loyola University Chicago, Chicago, IL 60660, USA. E-mail: pnahlik@luc.edu

Received 4th March 2022 , Accepted 21st May 2022

First published on 23rd May 2022

Abstract

A method is adapted for calculating two measures of entropy for gaze transitions to summarize and statistically compare eye-tracking data. A review of related eye-tracking studies sets the context for this approach. We argue that entropy analysis captures rich data that allows for robust statistical comparisons and can be used for more subtle distinctions between groups of individuals, expanding the scope and potential for eye-tracking applications and complementing other analysis methods. Results from two chemistry education studies help to illuminate this argument and areas for further research. The first experiment compared the viewing patterns of twenty-five undergraduate students and seven instructors across word problems of general chemistry topics. The second experiment compared viewing patterns for eighteen undergraduate students divided into three intervention groups with a pre- and post-test of five problems involving periodic trends. Entropy analysis of the data from these two experiments revealed significant differences between types of questions and groups of participants that complement both visualization techniques like heat maps and quantitative analysis methods like fixation counts. Finally, we suggest several considerations for other science education researchers to standardize entropy analyses including normalizing entropy terms, choosing between collapsed sequences or transitions within areas of interest, and noting if fixations in blank spaces are included in the analysis. These results and discussion help to make this powerful analysis technique more accessible and valuable for eye-tracking work in the field of science education research.

Introduction

Methods and applications of eye-tracking research

The sophisticated technology and technical vocabulary of eye-tracking research might give the impression that the field is relatively new. In fact, research involving eye-tracking goes back at least to 1879 with studies involving perception and cognition in reading (Rayner, 1998). Since then, studies have branched into wide-ranging applications, such as neuroscience, psychology, industrial engineering, marketing/advertising, and computer science (Duchowski, 2002). The breadth of these studies helps to show the success of eye-tracking research in providing information about human cognition. A basic argument for the value of this research approach is that eye movements during reading or visual searches provide direct information about cognitive processes because they are synchronous with perception and less filtered than tasks like speaking (Just and Carpenter, 1980; Rayner, 2009). The continued activity in this field and development of new methods, including technology, testify to the value of these data for research.

Eye-tracking methods have been developed for and applied to a wide variety of areas, including interpreting mechanical diagrams (Graesser et al., 2005), completing repetitive visual tasks (Manelis and Reder, 2012), grouping flight paths by air traffic controllers (Kang and Landry, 2015), learning Kanji symbols (Roderer and Roebers, 2014), solving arithmetic word problems (Hegarty et al., 1995), physiological responses to viewing garden scenes (Liu, et al., 2020), and using algebraic equations (Susac et al., 2014).

Several key terms from these studies will help make sense of our own research. Early work began to describe eye behavior as a combination of fixations—focused attention on an individual point or area—and saccades—movements between points during which information is not perceived (Rayner, 1998). Scanpaths are one method of describing the sequence of saccades across visual data (Kang and Landry, 2015; Day et al., 2018; Peysakhovich and Hurter, 2018). More recent analyses have considered researcher-defined areas of interest (AOIs) and the transitions or collective saccades between them (Kang and Landry, 2015; Susac et al., 2014). The various ways of describing eye movement data allow for statistical analyses that differ widely between applications. We will take a more focused look at science education research to frame the purpose of our study.

Eye-tracking in science education research

Specifically in science education, eye-tracking has become a powerful tool to describe differences between groups of people and their development of scientific understandings (Havanki and VandenPlas, 2014; VandenPlas et al., 2018). Studies have considered eye movements of high school and college students (Tsai et al., 2012; Ho et al., 2014; O’Keefe et al., 2014), pre-service teachers (Slykhuis et al., 2005; Tai et al., 2006), or in-service teachers and content experts (Dogusoy-Taylan and Cagiltay, 2014).

Several Chemistry Education studies show the breadth of eye-tracking methods within a single discipline. Topczewski et al. (2017) used pattern analysis of AOIs to study how students with varying levels of organic chemistry experience worked through NMR problems. Cullipher and Sevian (2015) similarly presented students with spectral data and compared the sequences of their fixations with their verbal explanations of the problem. Stieff et al. (2011) relied on fixation duration and diagrams of transitions between AOIs to study which type of representations students use to answer questions about bonding and molecular shape. Cook et al. (2008) worked with a large group of high school students to study their eye gaze patterns across micro and macro-representations of molecular diffusion scenarios. Tang and Pienta (2012) investigated the complexity of gas law problems via eye-tracking to show differences between successful and unsuccessful problem-solvers. Tang et al. (2014) showed how eye-tracking can be used to help develop stoichiometry problems of varying difficulty by changing complexity factors like the number format. Chen et al. (2015) studied how teaching with dynamic or static representations of orbital diagrams affected students’ eye fixations patterns based on their spatial abilities. Williamson et al. (2013) studied student fixation data in their use of ball-and-stick or electrostatic potential images to answer questions about molecular features like charge or electron density. Nehring and Busch (2018) studied differences in fixation counts and durations for video demonstrations using different Gestalt principles for instrumentation arrangements.

Limitations and solutions for eye-tracking in chemistry education

Although the topics and audiences of eye-tracking research in science education have been wide, the rigorousness of statistical applications has been limited. Attempts to capture the complexity of eye-movements in chemistry education studies have included numerical counts of fixations or fixation duration (Stieff et al., 2011; Williamson et al., 2013; Tang, et al., 2014; Nehring and Busch, 2018; Hansen et al., 2019), combinations of fixations and pupillometric measures (Karch et al., 2019), visualizations like heat maps that try to show more complex relationships (Stieff et al., 2011; Tang and Pienta, 2012; Chen et al., 2015), or pattern analysis to account for the sequence of transitions between AOIs (Cook et al., 2008; Cullipher and Sevian, 2015; Topczewski et al., 2017). Numerical measures like fixation counts or duration sacrifice subtle details about eye-tracking data like the sequential patterns of transitions between AOIs and treat eye-tracking more as descriptive data. Visualizations like heat maps communicate different types of data, but they take more explanation and interpretation by people who are unfamiliar with eye-tracking. There is a need for statistical measures that capture different complexities of eye-tracking patterns while being simple to understand and work with.

In a recent example, Rodemer et al. (2020) introduced the fixation/transition ratio to distinguish viewing behavior for advanced and beginner chemistry students. In their analysis, a lower ratio indicated more comparative viewing of AOIs, and a higher ratio indicated more focused viewing. This ratio allows for more sophisticated comparisons such as a time-based analysis to distinguish stages of problem solving.

Another potential solution has been developed by Krzyzstof Krejtz and colleagues (Kreitz et al., 2014, 2015, 2016). Their entropy analyses treat eye-tracking data as Markov chains (Ciuperca and Girardin, 2007), which test the extent to which sequences of gaze transitions are ordered or random. Two statistical terms can be assigned based on these analyses to describe the randomness or entropy of these transition sequences. Fig. 1 presents a graphical representation of these two terms for dramatized cases of transitions between four AOIs.


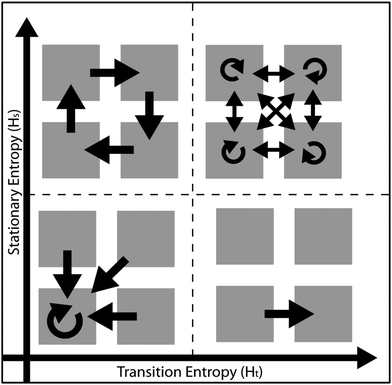image file: d2rp00066k-f1.tif
Fig. 1 Illustration of entropy terms with example AOIs (shown as gray boxes) and the transitions (black arrows) within or between them.

Transition entropy (Ht) correlates with the randomness of the sequence of transitions between visual data. A lower Ht indicates a more predictable, less random, series of transitions between AOIs. For example, the two cases on the left side of Fig. 1 show transitions between AOIs that are highly-structured and predictable, which therefore have low Ht. Stationary entropy (Hs) correlates with the distribution of attention or fixations across the AOIs on a display. A higher Hs indicates more equal distribution of attention across AOIs. For example, the two cases at the top of Fig. 1 show more equally-distributed attention across the four AOIs and, therefore, high Hs as might be expected for visual images with equally interesting or useful AOIs. Considered together, Ht and Hs can quickly summarize complex viewing behaviors and provide another option for statistical comparisons.

A recent set of publications have employed this type of entropy analysis to study strings of AOI transitions. Day et al. (2018) describe their use of scanpath analysis and transition entropy calculations to distinguish significant differences between groups of students. Tang and Pienta (2018) provide a detailed explanation of these types of analyses for chemistry education researchers. A related article from Tang et al. (2018) gives a more technical description of the GrpString package in R that can facilitate the entropy calculations. This type of pattern analysis helps to capture more detail about the way participants view problems, yet it relies on various methods of collapsing the data into isolated patterns of transitions, losing the overall view of fixations and heat maps.

Of course, no single analysis will capture all nuances of eye-tracking data, but we argue that stationary and transition entropy terms can be a powerful option for Science Education researchers to study and describe subtle differences between groups. Next, we consider two example studies to illustrate how entropy analyses might be used.

Methods and procedure

We designed two studies based on previous work with eye-tracking in chemistry education. The intent of the eye-tracking in our studies was to independently measure how each participant approached introductory chemistry problems (Rayner, 1998; Stieff et al., 2011), triangulating data collection with a think-aloud process and written notes (Bowen, 1994). Unlike other research methods, eye-tracking can be less intrusive to participants’ natural thinking processes (Roderer and Roebers, 2014), allowing the capture of more objective data. Locations where participants look on a screen can indicate areas considered either confusing or useful (Stieff et al., 2011) and can suggest information about the problem's perceived complexity (Tang et al., 2014). The eye-tracking data in these studies were used to complement the predominantly qualitative data collected from verbal and written reports (Reed et al., 2018). For the purposes of this article, we focus on the eye-tracking data to illustrate the potential and limitations of entropy analysis.

Research questions

This investigation set out to test how entropy analyses can be applied to eye-tracking data from two different Chemistry Education research studies. Our main research questions are:

1. Will entropy measures help reveal statistically significant differences between participants or groups across types of questions, placement of AOIs, pre- and post-tests, or major?

2. If so, what additional insights does entropy analysis provide compared to visualization techniques like heat maps and quantitative analysis techniques like fixation counts?

We then use the results of this study to comment on the kinds of information that can be described by entropy analysis and some potential future applications of entropy analysis in science education research.

Eye-tracking procedure and participants

The same eye-tracking set-up was used in both experiments. Participants were seated approximately 60 cm away from a computer monitor with a Tobii desk stand X120 eye-tracker just below the monitor at an angle of 30°. Participants were oriented with a nine-point calibration slide before beginning each experiment. Minimum fixation time was set at 80 ms with a fixation filter set to a velocity threshold of 30° s−1 and with eye movements recorded at 120 Hz. The default Tobii Studio software (version 3.0.3.239-beta) was used to collect data for experiment 1 (Tobii Studio Software, 2011), and OGAMA software was used for experiment 2 (Voßkühler et al., 2008), which offered more options for transition analysis at the time of the experiment.

Because these projects involved human subjects, Institutional Review Board approval was obtained through Loyola University Chicago for both projects before any data collection began (application numbers #1483 and #3905 for experiment 1 and 2 respectively). Informed consent was obtained from each participant with a signed form at the beginning of each session. All procedures and data were handled in compliance with the approved protocols.

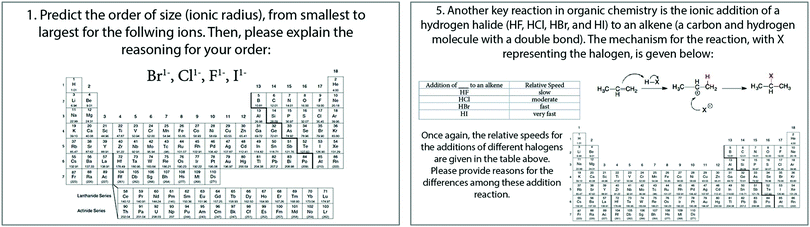
For experiment 1, twenty-five students total volunteered from a second-semester general chemistry course. As compensation, they were entered into a raffle to win a restaurant gift card. Seven instructors who taught general chemistry (n = 5) or Advanced Placement chemistry (n = 2) within the past five years were also recruited to participate. After calibrating the eye-tracker on the computer monitor, each participant was presented with four word-problems involving general chemistry topics such as calculating concentrations and bond enthalpy. They were asked to think-aloud as they solved each problem (Bowen, 1994), and a researcher took notes to record their answers. The data were collected in two separate rounds over two years. The first round, with 3 instructors and 15 students, was designed with four single-answer problems, while the second round, with 4 additional instructors and 10 additional students, included the first two single-answer problems along with two additional open-ended problems.

For experiment 2, eighteen students were recruited from introductory science classes or by reference from other participants. Nine of the students were science majors, and nine were non-science majors. A computer randomizer placed participants into three separate groups with three majors and three non-majors in each group. Each group was provided with a set of video modules about periodic trends and a corresponding set of diagrams to use when solving a set of problems. Group 1 was only provided with a standard periodic table. Group 2 was provided a standard periodic table and a color-coded periodic table with no instruction on it. Group 3 was provided a standard periodic table, color-coded periodic table with instruction about its use, and an electron shell diagram. A 30 minute pre- and post-test of five questions was given to each participant while their eye movements were recorded. The first three questions focused on using periodic trends in general chemistry, and the last two questions focused on using the trends in organic chemistry. Two example slides are shown in Fig. 2. The students were asked to watch their assigned videos before returning for the post-test up to two months later. During the pre- and post-tests, participants were told to keep their eyes on the screen, read the question in their head, and verbally explain their answer to the question. Every answer was written down by a researcher for reference.


image file: d2rp00066k-f2.tif
Fig. 2 Example slides for experiment 2 for questions 1 (left image) and 5 (right image).

Entropy analysis procedures

To test our research questions, we adapted the method of Krejtz et al. (2014) to the data from these experiments to calculate stationary and transition entropy values. We present a summary of our adaptation and lessons learned to inform future studies.

First, AOIs are defined for each slide (Fig. 3 and 4), either equally dividing the slide with a grid overlay or intentionally placing them through semantic designation (Holmqvist et al., 2011; Day et al., 2018). Second, transition matrices are calculated for each participant and each slide using a software like OGAMA (Voßkühler et al., 2008). Sample data are shown in Table 1 for an instructor participant from experiment 1 with transitions n counted across three AOIs (A, B, and C) placed via grid overlay on question 4 (the left side of Fig. 4).


image file: d2rp00066k-f3.tif
Fig. 3 Example slides for experiment 1 showing question 1 with AOIs outlined in purple and placed via grid overlay (left image) or semantic designation (right image).

image file: d2rp00066k-f4.tif
Fig. 4 Example slides from experiment 1 showing question 4 with AOIs outlined in purple and placed via grid overlay (left image) or semantic designation (right image).
Table 1 Example transition matrix for an instructor participant from experiment 1 for question 4 with AOIs placed via grid overlay
AOI To A To B To C
From A 53 43 1
From B 36 132 43
From C 8 35 36

Some analyses exclude transitions within a single AOI or collapse the scanpath sequences to exclude repeated letters (Day et al., 2018), equivalent to omitting the cells found diagonally in the matrix from top left to bottom right.

Additionally, when using semantic designation, an AOI can be defined for the blank space not covered by any other AOI, or transitions can only be counted between more meaningful AOIs. Our analyses follow Kreitz et al. (2014) to include transitions within an AOI to account for the relative interest of each AOI. With semantic designation, we also included transitions to or from the blank space on a slide under the assumption that these transitions also provide meaningful data about viewing behavior. Future work is needed to compare the advantages or disadvantages to each approach.

Third, marginal distributions ni, proportional maximum likelihood estimators (MLEs) of the transition probabilities pij, and MLEs of the stationary distribution πi are calculated using the transition matrices in a program like Excel via the formulas below. The transition matrix P for the sample data gives each MLE of the theoretical probability pij of transitions nij from initial AOI i to final AOI j as a proportion of total transitions ni from each AOI. The vector π gives the stationary probabilities needed to calculate each entropy term.

image file: d2rp00066k-t1.tif
With these values, stationary and transition entropies can be calculated, following Krejtz et al. (2014), where the full set of AOIs is represented as φ = {1,…,s}. To standardize the presentation of these data, we normalized the final values over the natural log of the number of AOIs ln(s) so that the range of potential entropies was between 0 and 1.
image file: d2rp00066k-t2.tif
Our sample data give the following values for each entropy term.
Hs = 0.914, Ht = 0.801
After entropy terms are calculated, different types of statistical analyses might be appropriate depending on the data and the experimental design. For example, Nehring and Busch (2018) use a non-parametric analysis for eye-tracking data with one-tailed Mann–Whitney U tests.

We present an example of our process for two experiments to facilitate other researchers’ reflection on and use of these methods. Tang et al. (2018) developed an R package GrpString for importing and analyzing eye-tracking data as groups of strings including options for transition entropy. Tang and Pienta (2018) applied this approach specifically to a Chemistry Education Research study. Our analyses highlight some of the necessary choices in this entropy approach to illuminate it for other researchers. We will revisit these methods in more depth in the Results and discussion section.

All statistical tests for this article were run using SPSS with data organized in Excel. We highlight some of our results in the discussion to illustrate how these tests might be used in future studies. Future work is needed to define how these values might contribute to eye-tracking research in science education research and to create more stringent criteria for evaluating them.

Results and discussion

Application to experiment 1: comparing disparate groups and AOI placements

For experiment 1, we calculated stationary and transition entropy terms for each student and instructor participant for each question using two methods of AOI placement. Because sample sizes were sharply different, we ran Levene's test for homogeneity of variance for each entropy comparison. All comparisons passed with p > 0.05, except for the stationary entropy for question 4 with semantic AOIs (Levene's test F(1,12) = 5.023, p = 0.045 with Welch statistic F(1,3.352) = 2.972, p = 0.174). Therefore, all other terms can be compared validly using ANOVAs. We ran a one-way ANOVA for each round because the groups of participants differed between rounds, with only a subset included in the second round that included question 4. The goal of the ANOVAs was to answer our first research question and describe how statistically significant differences revealed information about these two groups. We focus here on two illustrative examples of questions from the experiment.

Question 1 was a text-based problem that asked participants to calculate the percent by mass concentration of a perchloric acid solution (Fig. 3). AOIs were placed semantically around types of information in the question, including: any numbers, the phrase “perchloric acid,” the word “water,” any other nouns, as well as an AOI count of any remaining spaces on the slide. Question 4 included a data table of bond enthalpies and asked participants to arrange four compounds in order of increasing heat of vaporization (slide shown with AOI arrangement in Fig. 4). Results of the entropy analyses for these two questions are shown in Table 2.

Table 2 Entropy term statistics for experiment 1. Terms that differed significantly (p < 0.05) on one-way ANOVAs between students and instructors are bold
Student average stationary entropy (±SD) Instructor average stationary entropy (±SD) Student average transition entropy (±SD) Instructor average transition entropy (±SD)
Significance values for these comparisons are (a) 0.008 and (b) 0.047. *Hs for question 4 with semantic AOIs failed Levene's test F(1,12) = 5.023, p = 0.045) with Welch statistic F(1,3.352) = 2.972, p = 0.174, so the ANOVA result cannot be taken as significant.
Question 1 with semantic AOIs 0.8929 ± 0.0446 (n = 25) 0.9132 ± 0.0240 (n = 7) 0.8066 ± 0.0446 (n = 25) 0.8374 ± 0.0435 (n = 7)
Question 1 with grid overlay AOIs 0.9111 ± 0.0490 (n = 25) 0.9066 ± 0.0307 (n = 7) 0.7748 ± 0.0634 (n = 25) 0.8276 ± 0.0399 b (n = 7)
Question 4 with semantic AOIs 0.9189 ± 0.0759* (n = 10) 0.7415 ± 0.2001* (n = 4) 0.5369 ± 0.1026 (n = 10) 0.4913 ± 0.1335 (n = 4)
Question 4 with grid overlay AOIs 0.9520 ± 0.0245 (n = 10) 0.8897 ± 0.0513 a (n = 4) 0.7489 ± 0.0627 (n = 10) 0.7606 ± 0.0494 (n = 4)

For question 1, instructors had a significantly higher transition entropy than students across grid overlay AOIs. This result suggests that instructors generally viewed the slide more randomly or in a less predictable order than students. One explanation might be that students follow a more rote process for solving standard problems such as percent by mass calculations. Their scanning through the slide might appear more ordered because they carefully read line by line through a problem while solving it. On the other hand, instructors are more likely to adapt their problem solving strategy, easily identifying the type of problem and then finding the information needed to solve it. Because the averages differed for grid overlay AOIs but not for semantic AOIs, instructors viewed the slide in a more spatially-random way, rather than viewing the types of information differently.

Interestingly, the stationary entropy did not differ significantly for either placement of AOIs on question 1. Similar to comparing fixation counts, this result suggests that both groups placed the same relative visual weight on each type of information or area of the slide. Fig. 5 shows the composite heat maps which visualize relative fixation counts on a slide. The numbers in the problem seemed to receive the most attention from each group, reflected by the density of warm colors over those values, and the high average values of Hs. Stationary entropy allows for statistical comparisons between groups for those data. In the case of question 1, the visual differences in the heat maps are not accompanied by statistical differences in stationary entropy values between students and instructors.


image file: d2rp00066k-f5.tif
Fig. 5 Composite heat maps for question 1 of experiment 1 for students (left image) and instructors (right image).

For question 4, the stationary entropy terms differed significantly between instructors and students for grid overlay AOIs. Students had significantly higher stationary entropy values, suggesting that their attention was more equally distributed across the slide. Based on the verbal responses to this question, we know that most instructors ignored the bond enthalpy data, which is unnecessary to order compounds by their heats of vaporization, whereas all the students used this information to answer the question. Fig. 6 shows the composite heat maps for this question where students had the highest fixation density in the bond enthalpy table while instructors had very little density in the same location. The stationary entropy term highlights the statistical difference reflected by these strategies and visualized in the heat maps.


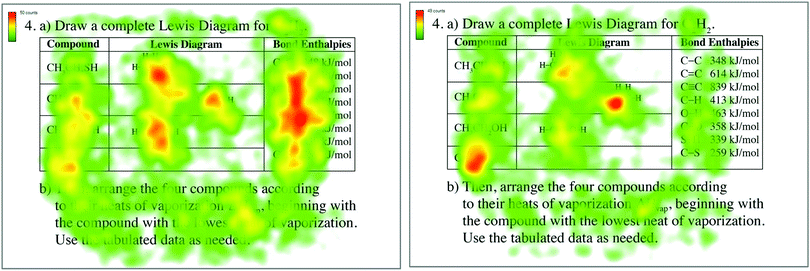image file: d2rp00066k-f6.tif
Fig. 6 Composite heat maps for question 4 of experiment 1 for students (left image) and instructors (right image).

The transition entropy terms were not significantly different for either placement of AOIs on question 4, which implies that the scanpaths of instructors and students were equally structured, even though Hs comparisons revealed differences in the overall focus of visual attention. Additionally, Ht means for semantic AOIs were relatively lower in value (0.5369 and 0.4913) suggesting more structured, less random scanpaths throughout problem 4 as compared to problem 1.

Several insights became clear through our work with these data. First is that intentionally and equally placed AOIs can reveal different types of information. For problems with more visual information, like question 4, semantically placed AOIs can reveal differences in the use of different types of data. Especially for students, including distracting information can clearly distinguish levels of problem-solving ability through eye tracking. For problems that are more text-based or for which clear AOIs are difficult to identify, like question 1, equally placed AOIs are a useful option that still allow for statistical comparisons of entropy terms. Another insight that answers our second research question is that the stationary entropy term can be used to complement visualization methods like heat maps or transition diagrams with statistical comparisons (Stieff et al., 2011). The differences suggested visually by heat maps can be statistically confirmed or nuanced by entropy analysis.

Application to experiment 2: comparing similar groups, intervention effects, and changes over time

To answer our first research question for experiment 2, we ran two separate, repeated-measure MANOVAs to compare Ht and Hs as the dependent variables across the independent variables of: question (numbers 1–5), Time (pre or post-test), Major (Chemistry or non-Chemistry), and Treatment Group (1, 2, or 3). See our Methods section for more information about the experimental design. Main effect results are shown in Table 3. Cases that failed Maulchy's test of sphericity are shown with Greenhouse–Geisser corrected values. These cases included: Ht across question number (Maulchy's test χ2 = 17.925, p = 0.040, Greenhouse–Geisser ε = 0.487) and Hs across question number (Maulchy's test χ2 = 26.425, p = 0.002, Greenhouse–Geisser ε = 0.468).
Table 3 MANOVA results for experiment 2 showing main effects of within and between subject variables. Significant p-values are bolded and starred
Variable Type III sum of squares df Mean square F Sig. Partial eta squared
a Maulchy's test of sphericity was violated, so Greenhouse–Geisser corrected values were used instead.
Question Ht (within subject)a 0.539 1.948, 17.532 0.277 18.943 <0.001* 0.678
Time Ht (within subject) 0.001 1, 9 0.001 0.042 0.843 0.005
Major Ht (between subjects) 0.069 1, 9 0.069 3.106 0.112 0.257
Treatment Group Ht (between subjects) 0.016 2, 9 0.008 0.364 0.705 0.075
Question Hs (within subject)a 0.229 1.874, 16.865 0.122 8.201 0.004* 0.477
Time Hs (within subject) 0.003 1, 9 0.003 0.613 0.454 0.064
Major Hs (between subjects) 0.000 1, 9 0.000 0.084 0.779 0.009
Treatment Group Hs (between subjects) 0.027 2, 9 0.014 2.871 0.109 0.390

Question had a significant main effect for both transition entropy (F(1.948,17.532) = 18.943, p < 0.001) and stationary entropy (F(1.874,16.865) = 8.201, p = 0.004). Both effect sizes were quite large (partial eta squared > 0.14; see Richardson, 2011). To better visualize these data, mean values are displayed for Ht (Fig. 7) and Hs (Fig. 8) across each question with averages for majors and non-majors displayed as dotted lines.


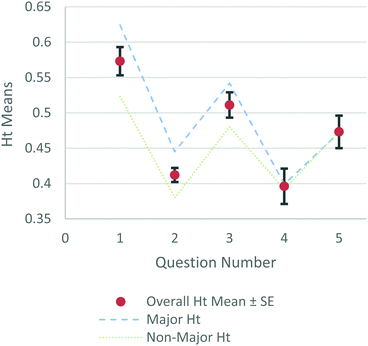image file: d2rp00066k-f7.tif
Fig. 7 Graph of transition entropy means for questions 1–5 of experiment 2 with standard error shown with brackets and averages for majors and non-majors shown with lines.

image file: d2rp00066k-f8.tif
Fig. 8 Graph of stationary entropy means for questions 1–5 of experiment 2 with standard error shown with brackets and averages for majors and non-majors shown with lines.

No other variables had a significant main effect. Additionally, there were no significant interaction effects for transition entropy. The significant interaction effects for stationary entropy were question × major (F(4,36) = 3.603, p = 0.014) and major × group (F(2,9) = 4.691, p = 0.040).

Our experience with data from experiment 2 solidified several lessons about working with entropy terms and statistical comparisons. The first lesson was the question-dependence of transition and stationary entropy. The variety of types of statistical comparisons that can be used helps to emphasize the value of these entropy terms as simple values that capture and help tell the story of complex data. The second lesson was the surprise that sometimes groups that were expected to be more visually efficient problem-solvers, like chemistry majors, could have higher transition entropy values on certain questions although no overall statistical differences were found for major. This counter-intuitive result also occurred in our first experiment, where instructors had higher average transition entropy than students, and emphasized the need to understand more about participants’ problem-solving strategies to avoid simplistic understandings of the entropy terms. The third lesson was that entropy terms can help bridge the gap between small and large groups of participants in eye-tracking studies. Because of the limitation of methodologies for visualizing eye-tracking data, like heat maps or transition diagrams, many studies use very small participant groups. Simpler methods like fixation duration or counts allow for larger group comparisons but sacrifice some complexities of eye-tracking data. Entropy terms offer another approach that captures details about the distribution and randomness of participants gaze patterns that are appropriate to both small and large groups.

Comparison with traditional eye-tracking methods

To answer our second research question more directly, we also compared the fixation counts for each AOI across the five questions of experiment 2. Because the number and placement of AOIs differed across question, separate repeated measure MANOVAs were run on each question with time and AOI as within subject factors and with major and treatment group as between subject factors. Results are shown in Table 4.
Table 4 Main effects of AOI on fixation counts for each question of experiment 2
Question Type III sum of squares df Mean square F Sig. Partial eta squared
a For measures that failed Maulchy's test (questions 1–3), Greenhouse–Geisser corrected values are displayed.
1a 64405.053 1.467, 13.205 43895.642 12.635 0.002* 0.584
2a 854171.655 1.298, 12.979 658098.486 53.080 <0.001* 0.841
3a 229547.155 2.114, 21.141 108576.716 44.197 <0.001* 0.815
4 217683.396 4, 36 54420.849 34.709 <0.001* 0.794
5 51519.516 5, 45 10303.903 5.494 <0.001* 0.379

The MANOVAs for each question revealed a significant and large effect for AOI on fixation count. For questions 1–4, one AOI had significantly more fixations compared with at least one other AOI. The areas with the most fixations included important visual data like tables on which the question was based and were often located in the center of the slide. This result is unsurprising from a visual and problem-solving perspective but helps to confirm the visual and question-dependence of fixations. No other significant main or interaction effects were found.

The entropy terms carry several advantages over more traditional methods of analyzing or visualizing eye-tracking data. First, Ht correlates with the sequence of transitions rather than only the total number of fixations or gaze density. Quantifying the entropy of these sequences can tell us how participants compare AOIs to each other rather than only which AOI receives the most attention, as visualized in heat maps or compared through fixation counts. Second, the entropy measures assign a value to summarize entire sequences of eye-tracking data, rather than needing complicated diagrams or multiple measures to compare. The simplicity of these terms makes studies with larger groups of participants more feasible. Hs conveys similar information as fixation counts because it is based on the cumulative transitions between AOIs. However, summarizing this information in a single, normalized value like Hs can allow for clearer comparisons between different stimuli or experiments.

Comparison of entropy and string analysis methods

A recent set of articles describe methods to analyze scanpaths as strings including a similar approach to transition entropy (Day et al., 2018; Tang and Pienta, 2018; Tang et al., 2018). This approach carries several unique features and provides a basis to consider how entropy terms might be used further in science education research.

String analysis requires identifying windows or phases of analysis for scanpaths, which allows for deep comparisons of shorter time frames or stages of problem-solving. Strings are often represented as series of letters to identify the order of AOI fixations, including repeated letters for transitions with an AOI or only including unique transitions between AOIs. The typical practice is to collapse strings which removes the relative weight of fixations within AOIs. These three articles used semantically-placed AOIs and transition entropy, although grid overlay AOIs and stationary entropy offer another set of data to consider. Using an R package like GrpString helps to automate the analysis especially for researchers who are less familiar with the methods. Our exploration of entropy analysis in this article is provided to facilitate deeper reflection and discussion among researchers about these methods.

We propose several considerations for other researchers. First is to normalize entropy terms as we did to allow for easier comparisons between experiments and stimuli. Second is to consider the value of using collapsed sequences or transitions within AOIs. Third is to clarify if an analysis uses fixations within blank space on a stimulus, especially with semantic AOIs. Future work with problem-solving should include questions designed to separate groups more clearly, such as including visual elements, potentially distracting information, and uncluttered visual arrangements. Statistical analyses would also benefit from comparing similar types of questions and AOIs as a repeated measure of entropy terms.

Limitations

We acknowledge significant limitations in our use of these entropy terms and their potential applications. As with any attempt to summarize the large data sets that eye-tracking provides, the entropy terms omit information and lose some statistical power by focusing on the distribution of attention and the order of transitions between AOIs. However, these terms capture different types of information that have not yet been studied widely and help add more texture to other eye-tracking methods. Future statistical development of these terms can help to strengthen their power and standardize the method for other research. Our example experiments still used relatively-small sample sizes, ranging from 4 participants in a comparison group in experiment 2 to 25 students in experiment 1. These small populations helped to illustrate the potential of entropy terms to compare groups. We expect that comparing larger sample sizes (a quite limited area of eye-tracking work in chemistry education) will be more possible and interesting with these entropy terms.

Conclusions and future research

We argue for the value of transition and stationary entropy terms to help analyze eye-tracking data in chemistry education studies. In answer to our first research question, our experimental results showed that entropy analysis can reveal significant differences between groups of participants across types of questions and levels of expertise. Other experimental designs might find correlations with other significant variables. In answer to our second research question, entropy analysis can help complement visualization techniques like heat maps with statistical comparisons. In comparison to fixation counts which can track the type of information participants view, entropy analysis helps to compare how participants use those data. Both stationary and transition entropy add another set of tools for researchers to consider as they develop future eye-tracking studies.

Our discussion helped to unpack some of the nuance of interpreting entropy terms, such as the surprise of higher transition entropy for more advanced groups. To interpret entropy well, researchers must understand more about how participants are solving the problems, through previous research or other data collection. Finally, the visual cues in these experiments must be designed in a way that significant visual differences are expected. Examples from our studies were the use of visual data like diagrams or data tables. Purely text-based problems were not as appropriate for this analysis.

Overall, transition and stationary entropy simplify large amounts of data while preserving significant differences in the distribution of visual attention. These terms allow for statistical comparisons between similar or disparate groups at a single point or over time. Entropy terms are powerful tools to explain how participants use visual data in complex ways, distributing attention and developing transition sequences to solve problems. There is great potential to develop the use of these tools for different applications like videos, websites, and visualizations where assigning AOIs can be consistent.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

Loyola University Chicago provided funding for a portion of this project through the Loyola Undergraduate Research Opportunities Program (LUROP). We also want to thank Thomas H. Sullivan, Linda C. Brazdil, Mary T. van Opstal, Victoria E. Kaloudis, and the rest of our Chemistry Education Research Group at Loyola University Chicago for ongoing support and the development of an earlier version of this project.

References

  1. Bowen, C. W., (1994), Think-aloud methods in chemistry education: Understanding student thinking, J. Chem. Educ., 71(3), 184–190 DOI:10.1021/ed071p184.
  2. Chen, S.-C., Hsiao, M.-S. and She, H.-C., (2015), The effects of static versus dynamic 3D representations on 10th grade students’ atomic orbital mental model construction: Evidence from eye movement behaviors, Comput. Hum. Behav., 53, 169–180 DOI:10.1016/j.chb.2015.07.003.
  3. Ciuperca, G. and Girardin, V. (2007) Estimation of the entropy rate of a countable Markov chain, Commun. Stat.—Theory Methods, 36: 2543–2557.
  4. Cook, M., Wiebe, E. N. and Carter, G., (2008), The influence of prior knowledge on viewing and interpreting graphics with macroscopic and molecular representations, Sci. Educ., 92(5), 848–867 DOI:10.1002/sce.20262.
  5. Cullipher, S. and Sevian, H., (2015), Atoms versus bonds: How students look at spectra, J. Chem. Educ., 92(12), 1996–2005 DOI:10.1021/acs.jchemed.5b00529.
  6. Day, E. L., Tang, H., Kendhammer, L. K. and Pienta, N. J., (2018), Sequence analysis: Use of scanpath patterns for analysis of students’ problem-solving strategies, in VandenPlas J. R., Hansen S. J. R. and Cullipher S. (ed.) Eye tracking for the chemistry education researcher, ACS Symposium Series 1292, American Chemical Society, pp. 73–97.
  7. Dogusoy-Taylan, B. and Cagiltay, K., (2014), Cognitive analysis of experts’ and novices’ concept mapping processes: An eye tracking study, Comput. Hum. Behav., 36, 82–93 DOI:10.1016/j.chb.2014.03.036.
  8. Duchowski, A. T., (2002), A breadth-first survey of eye-tracking applications, Behav. Res. Methods, Instrum., Comput., 34, 455–470.  DOI:10.3758/BF03195475.
  9. Graesser, A. C., Lu, S., Olde, B. A., Cooper-Pye, E. and Whitten, S., (2005), Question asking and eye tracking during cognitive disequilibrium: Comprehending illustrated texts on devices when the devices break down, Memory and Cognition, 33(7), 1235–1247.  DOI:10.3758/BF03193225.
  10. Hansen, S. J. R., Hu, B., Riedlova, D., Kelly, R. M., Akaygun, S. and Villalta-Cerdas, A., (2019), Critical consumption of chemistry visuals: Eye tracking structured variation and visual feedback of redox and precipitation reactions, Chem. Educ. Res. Pract., 20(4), 837–850.  10.1039/c9rp00015a.
  11. Havanki, K. L. and VandenPlas, J. R., (2014), Eye Tracking Methodology for Chemistry Education Research, In D. M. Bunce and R. S. Cole (ed.), Tools of chemistry education research, ACS Symposium Series 1166, American Chemical Society, pp. 191–218.
  12. Hegarty, M., Mayer, R. E. and Monk, C. A., (1995), Comprehension of arithmetic word problems, J. Educ. Psychol., 87(1), 18–32.  DOI:10.1037/0022-0663.87.1.18.
  13. Ho, H. N. J., Tsai, M.-J., Wang, C.-Y. and Tsai, C.-C., (2014), Prior knowledge and online inquiry-based science reading: Evidence from eye tracking, Int. J. Sci. Math. Educ., 12(3), 525–554.  DOI:10.1007/s10763-013-9489-6.
  14. Holmqvist K., Nyström N., Andersson R., Dewhurst R., Jarodzka H. and Van de Weijer J. (ed.), (2011), Eye tracking: A comprehensive guide to methods and measures. Oxford University Press.
  15. Just, M. A. and Carpenter, P. A., (1980), A theory of reading: From eye fixations to comprehension, Psychol. Rev., 87(4), 329–354.  DOI:10.1037/0033-295X.87.4.329.
  16. Kang, Z. and Landry, S. J., (2015), An eye movement analysis algorithm for a multielement target tracking task: Maximum transition-based agglomerative hierarchical clustering, IEEE Trans. Hum.-Mach. Syst., 45 (1): 13–24.
  17. Karch, J. M., García Valles, J. C. and Sevian, H., (2019), Looking into the black box: Using gaze and pupillometric data to probe how cognitive load changes with mental tasks, J. Chem. Educ., 96(5), 830–840.  DOI:10.1021/acs.jchemed.9b00014.
  18. Krejtz, K., Szmidt, T., Duchowski, A. T. and Krejtz, I., (2014), Entropy-based statistical analysis of eye movement transitions, Eye Tracking Research and Applications Symposium (ETRA), 159–166.
  19. Krejtz, K., Duchowski, A., Szmidt, T., Krejtz, I., González Perilli, F., Pires, A., Vilaro, A. and Villalobos, N., (2015), Gaze transition entropy, ACM Trans. Appl. Perceptions, 13(1), 4.  DOI:10.1145/2834121.
  20. Krejtz, K., Duchowski, A., Krejtz, I., Szarkowska, A. and Kopacz, A., (2016), Discerning ambient/focal attention with coefficient k, ACM Trans. Appl. Perceptions, 13(3), 11.  DOI:10.1145/2896452.
  21. Liu, C., Herrup, K., Goto, S. and Shi, B. E., (2020), Viewing garden scenes: Interaction between gaze behavior and physiological responses, J. Eye Movement Res., 13(1), 6  DOI:10.16910/jemr.13.1.6.
  22. Manelis, A. and Reder, L. M., (2012), Procedural learning and associative memory mechanisms contribute to contextual cueing: Evidence from fMRI and eye-tracking, Learn. Memory, 19(11), 527–534.  DOI:10.1101/lm.025973.112.
  23. Nehring, A. and Busch, S., (2018), Chemistry demonstrations and visual attention: Does the setup matter? Evidence from a double-blinded eye-tracking study, J. Chem. Educ., 95(10), 1724–1735.  DOI:10.1021/acs.jchemed.8b00133.
  24. O’Keefe, P. A., Letourneau, S. M., Homer, B. D., Schwartz, R. N. and Plass, J. L., (2014), Learning from multiple representations: An examination of fixation patterns in a science simulation, Comput. Hum. Behav., 35, 234–242.  DOI:10.1016/j.chb.2014.02.040.
  25. Peysakhovich, V. and Hurter, C., (2018), Scanpath visualization and comparison using visual aggregation techniques, J. Eye Movement Res., 10(5), 9.  DOI:10.16910/jemr.10.5.9.
  26. Rayner, K., (1998), Eye movements in reading and information processing: 20 years of research, Psychol. Bull., 124(3), 372–422.  DOI:10.1037//0033-2909.124.3.372.
  27. Rayner, K., (2009), The 35th Sir Frederick Bartlett Lecture: Eye movements and attention in reading, scene perception, and visual search, Q. J. Exp. Psychol., 62(8), 1457–1506.  DOI:10.1080/17470210902816461.
  28. Reed, J. J., Schreurs, D. G., Raker, J. R. and Murphy, K. L., (2018), Coupling eye tracking with verbal articulation in the evaluation of assessment materials containing visual representations, in VandenPlas J. R., Hansen S. J. R. and Cullipher S. (ed.) Eye tracking for the chemistry education researcher, ACS Symposium Series 1292, American Chemical Society, pp. 165–181.
  29. Richardson, J. T. E., (2011), Eta squared and partial eta squared as measures of effect size in educational research, Educ. Res. Rev., 6(2), 135–147.  DOI:10.1016/j.edurev.2010.12.001.
  30. Rodemer, M., Eckhard, J., Graulich, N. and Bernholt, S., (2020), Decoding case comparisons in organic chemistry: Eye-tracking students’ visual behavior, J. Chem. Educ., 97(10), 3530–3539.  DOI:10.1021/acs.jchemed.0c00418.
  31. Roderer, T. and Roebers, C., (2014), Can you see me thinking (about my answers)? Using eye-tracking to illuminate developmental differences in monitoring and control skills and their relation to performance, Metacognition Learn., 9(1), 1–23.
  32. Slykhuis, D. A., Wiebe, E. N. and Annetta, L. A., (2005), Eye-tracking students' attention to PowerPoint photographs in a science education setting, J. Sci. Educ. Technol., 14(5/6), 509–520.  DOI:10.1007/s10956-005-0225-z.
  33. Stieff, M., Hegarty, M. and Deslongchamps, G., (2011), Identifying representational competence with multi-representational displays, Cognit. Instr., 29(1), 123–145.
  34. Susac, A., Bubic, A., Kaponja, J., Planinic, M. and Palmovic, M., (2014), Eye movements reveal students’ strategies in simple equation solving, Int. J. Sci. Math. Educ., 12(3), 555–577.  DOI:10.1007/s10763-014-9514-4.
  35. Tai, R. B., Loehr, J. F. and Brigham, F. J., (2006), An exploration of the use of eye-gaze tracking to study problem-solving on standardized science assessments, Int. J. Res. Method Educ., 29, 185–208.
  36. Tang, H. and Pienta, N. J., (2012), Eye-tracking study of complexity in gas law problems. J. Chem. Educ., 89(8), 988–994.  DOI:10.1021/ed200644k.
  37. Tang, H. and Pienta, N. J., (2018), Advanced methods for processing and analyzing eye-tracking data using R. in VandenPlas J. R., Hansen S. J. R. and Cullipher S. (ed.) Eye tracking for the chemistry education researcher, ACS Symposium Series 1292, American Chemical Society, pp. 99–117.
  38. Tang, H., Kirk, J. and Pienta, N. J., (2014), Investigating the effect of complexity factors in stoichiometry problems using logistic regression and eye tracking, J. Chem. Educ., 91(7), 969–975.  DOI:10.1021/ed4004113.
  39. Tang, H., Day, E. L., Atkinson, M. B. and Pienta, N. J., (2018), GrpString: An R package for analysis of groups of strings, R J., 10(1), 359–369.
  40. softwareTobii Studio Software, version 3.0.3.239-beta, Tobii Technology AB. 2011–2012.
  41. Topczewski, J. J., Topczewski, A. M., Tang, H., Kendhammer, L. K. and Pienta, N. J., (2017), NMR spectra through the eyes of a student: Eye tracking applied to NMR items, J. Chem. Educ., 94(1), 29–37.  DOI:10.1021/acs.jchemed.6b00528.
  42. Tsai, M.-J., Hou, H.-T., Lai, M.-L., Liu, W.-Y. and Yang, F.-Y., (2012), Visual attention for solving multiple-choice science problem: An eye-tracking analysis, Comput. Educ., 58(1), 375–385.  DOI:10.1016/j.compedu.2011.07.012.
  43. VandenPlas, J. R., Hansen, S. J. R. and Cullipher, S. (ed.), (2018), Eye tracking for the chemistry education researcher. ACS Symposium Series 1292. American Chemical Society DOI:10.1021/bk-2018-1292.
  44. Voßkühler, A., Nordmeier, V., Kuchinke, L. and Jacobs, A. M., (2008), OGAMA (Open Gaze and Mouse Analyzer): open-source software designed to analyze eye and mouse movements in slideshow study designs, Behav. Res. Methods, 40(4), 1150–1162.
  45. Williamson, V. M., Hegarty, M., Deslongchamps, G., Williamson, K. C. and Shultz, M. J., (2013), Identifying student use of ball-and-stick images versus electrostatic potential map images via eye tracking. J. Chem. Educ., 90(2), 159–164.  DOI:10.1021/ed200259j.
This journal is © The Royal Society of Chemistry 2022