Open Access Article
Open Access ArticleQuantum tailoring of electronic properties in covalently functionalized graphene: application to ammonia gas detection
A. Dammaka,
F. Raouafia,
A. Cavanna b,
P. Rudolf
b,
P. Rudolf c,
D. di Caprio
c,
D. di Caprio d,
V. Sallete,
A. Madourib and
J. M. Jancu*f
d,
V. Sallete,
A. Madourib and
J. M. Jancu*f
aUniversity of Carthage, IPEST, LPC2M, Route de Sidi Bou Saïd 2075 La Marsa, Tunisia
bC2N, University of Paris-Saclay, 10 Bd. Thomas Gobert, 91120 Palaiseau, France
cSurfaces and Thin Films Group, Zernike Institute for Advanced Materials, University of Groningen, The Netherlands
dIRCP, Chimie ParisTech, University of PSL, CNRS, 11 rue P. et M. Curie, 75005 Paris, France
eGEMaC, Université Versailles St-Quentin-en-Yvelines, France
fUniv Rennes, INSA Rennes, CNRS, Institut FOTON – UMR 6082, F-35000 Rennes, France. E-mail: jean-marc.jancu@insa-rennes.fr
First published on 15th December 2022
Abstract
Functionalized graphene offers great potential in the field of rapid detection of gases at room temperature. We performed first-principles calculations to study the suitability of 4-sulfobenzenediazonium salts (4SBD) as bandgap modifier in graphene. The signature of unpaired spins is evidenced near the Fermi level owing to the symmetry breaking of graphene sublattices. 4SBD-chemisorbed on graphene is found to be electronically sensitive to the presence of ammonia NH3 with increasing gas concentration.
1 Introduction
Pristine graphene is a single two-dimensional layer of sp2 bonded carbon atoms arranged in a honeycomb lattice.1 In recent decades, it has been the subject of considerable study in most fields of science and engineering due to its unprecedented physical and chemical properties. In particular, graphene exhibits a large surface area, high electrical conductivity, optical transparency, exceptional thermal and mechanical behaviors, and ability to adsorb and desorb organic molecules.2,3 It has been proposed for application in photovoltaics,4 flexible electronics, gas sensors,4,5 biosensors6 and hydrogen storage.7–10 Gas sensors are used in a wide range of applications for environmental monitoring, gas leak detection in industrial production, security, medical diagnostics, aircraft cabin air monitoring and food quality controls.11,12 Solid state gas sensors represent a significant technological advancement in terms of low power consumption and specific active materials used for each type of application that determine their performance.13,14 However, they suffer from long-term stability and some cannot operate at room temperature.14 Chemically modified graphene is becoming one of the most versatile material for gas detection with superior performance in terms of electrical properties and sensitivity.15–17 Both covalent and non-covalent approaches have been investigated for this purpose.2,15–18 Covalent functionalization takes place when a functional group is covalently bonded to the surface. This enhances the aromatic character of graphene and improves long-term performance and structural stability compared to a non-covalent functionalization.19,20 The generation of new covalent bonds in graphene can be easily obtained by free-radical addition using aryldiazonium salt chemistry.19–23 For electron-withdrawing substituents on the aromatic ring, the overall process involves a transfer of a π-electron from graphene to the diazonium cation becoming an aryl radical after nitrogen removal. The resulting radical reacts directly with the graphene network forming an sp3 covalent bond. In recent years, many research efforts have focused on controlling the density and spatial distribution of grafting sites.17,24 Particularly noteworthy for covalent functionalization is the surface binding mechanism that can be customized depending on the substituent nature into the benzene ring.25 Consequently, the lattice undergoes a non-uniform deformation, identical to a stress–strain response, which should be promising for engineering the electronic properties of functionalized graphene.26,27 Covalently modified materials show a semiconductive behavior with finite bandgap and magnetic properties induced by the sp3 hybridization.17,28 On a theoretical level, previous ab initio calculations have been performed at different computational levels exploring a wide range of issues associated to the chemical configuration and binding energies of common organic molecules adsorbed on graphene.29–36 In this context, the covalent functionalization of graphene with aromatic aziridines is found to open the bandgap from 0.3 eV to 0.5 eV.35,36 However, very little is known about the functionalization of graphene with aryldiazonium salts.In this work, we studied the electronic response of functionalized graphene with 4-sulfobenzenediazonium tetrafluoroborate (4SBD). We performed first-principles pseudopotential plane wave calculations based on spin-polarized density functional theory (DFT) and generalized gradient approximation (GGA) to model the electronic structure of 4SBD-modified graphene. The minimum energy path (MEP) governing the 4SBD dissociation within the kinetic process was determined by using the climbing image-nudged elastic band method (CI-NEB). The formation of local magnetic moments was addressed by the self-consistent calculation of the occupation for up and down spin states in the different orbitals of the complex. Graphene sublattices, hereafter referred to as A and B, are triangular lattices that span the honeycomb hexagon. We found that the sublattice imbalance induced by sulfobenzene adsorbates governs the bandgap properties and induces spin-polarized electronic states in the complex. The adsorption properties of ammonia molecules on modified graphene is investigated.
The article is organized as follows. In Section 2, we describe the computational approach. In Section 3, we present the adsorption properties of a single 4SBD molecule absorbed on graphene. In Section 4, we discuss the electronic and magnetic properties of functionalized graphene. In Section 5, we discuss the adsorption properties of NH3 on 4SBD-decorated graphene. Summary in Section 5 concludes the article.
2 Computational details
Self-consistent DFT calculations were performed without spin–orbit coupling using the pseudopotential projector-augmented wave method implemented37,38 in the Vienna ab initio simulation package (VASP 5.4.1) with an energy cutoff of 520 eV. Exchange–correlation (XC) effects were treated using the Perdew–Burke–Ernzerhof functional (PBE) generalized gradient approximation (GGA) functional.38,39 A (9 × 9 × 1) and (12 × 12 × 1) Γ-centered k-points mesh was used to sample the Brillouin zone for geometry optimization and electronic structure respectively. We accounted for van der Waals (vdW) interactions in the dispersion-corrected DFT using the empirical correction approach.13,14 Optimized lattice constants for pristine graphene are: a = 2.46 Å, b = 2.46 Å, α = β = 90° and γ = 120°, in excellent agreement with experimental results. Total energy calculations were performed using 4 × 4 and 6 × 6 supercells on the xy-plane. Since boundary conditions are applied in three dimensions, a 25 Å-thick vacuum region along the z-direction was included preventing any unphysical interaction between the periodic images of the slabs. All atomic sites were relaxed using the Hellman–Feynman theorem until forces are below of 0.01 eV Å−2 with a total energy tolerance of 10−6 eV.3 Adsorption of a single molecule on graphene
Physisorption (eqn (1)) and chemisorption (eqn (2)) correspond to the following reactions:| 4SBD + Gr → 4SBD–Gr | (1) |
| 4SBD + Gr → 4SB–Gr + N2 | (2) |
| Ephysads = E(4SBD–Gr) − E(4SBD) − E(Gr) | (3) |
E(4SBD–Gr) is the total energy of the complex, E(4SBD) the total energy of the free 4SBD molecule and E(Gr) the total energy of pristine graphene.
Similarly, the 4SBD-chemisorption energy is:
| Echemads = E(4SBD–Gr) − E(N2) − E(Gr) − E(4SB) | (4) |
E(4SB) is the total energy of the free 4SB molecule and E(N2) the total energy of nitrogen N2.
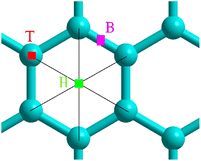
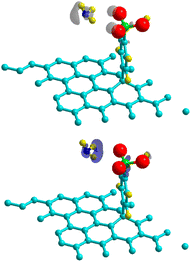
Adsorption was studied using a 6 × 6 graphene supercell by positioning the molecule N2 near the preferential sites shown in Fig. 1. We fixed a carbon atom as reference while the remaining atomic coordinates were relaxed to minimum energy.
3.1 Physisorption
Table 1 lists the nearest nitrogen-surface distances Sep for the physisorption sites. Geometry optimization was performed with an initial separation Sep = 2 Å, resulting in a strong overlap in electron density. The interplay between the short-range repulsive forces and van der Waals interaction leads to a relatively large separation Sep = 3.2 Å owing to the concave adsorption geometry displayed in Fig. 2a for the hollow site. We found a physisorption well depth of about 0.27 eV for all sites, which is similar to the binding energy of −0.38 eV for benzene adsorption on graphene.40 The calculations are clearly site-independent thus demonstrating a non-localized process as expected for physical adsorption.17| B | H | T | |
|---|---|---|---|
| Ephysads (eV) | −0.27 | −0.27 | −0.27 |
| Sep (Å) | 3.22 | 3.16 | 3.19 |
3.2 Chemisorption
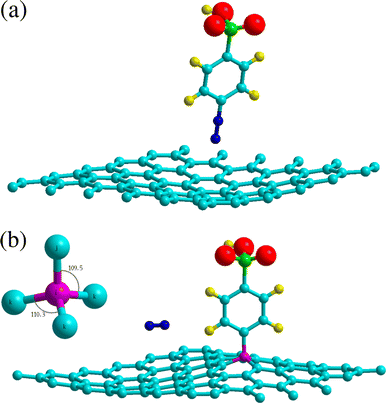
Chemisorption is site specific. Table 2 evidences that the 4SBD-adsorption at the T site is favored due to the equilibrium bond-distance dij = 1.56 Å corresponding to the interatomic bond-length of 1.54 Å in diamond. Indices i and j are referenced in Fig. 2b. The 1.8 eV chemisorption well depth is related to the electron-withdrawing character of the sulfo group (SO3H) into the benzene ring25 allowing an efficient binding of the molecule to the surface. In comparison, a DFT calculation gives Echemads = −0.99 eV for the phenyl radical C6H5 adsorbed on graphene.40 Conversely, chemisorption at sites B and H is unlikely because the corresponding bond length dij is twice of the covalent radius rconv = 0.76 Å for sp3 carbon according to the Pauling's equation. The 4SBD-optimized lattice is presented in Fig. 2b. Interestingly, atom i brings out a tetrahedral geometry with the 109.5° near-ideal bond angles. Its nearest-neighbor atoms k form the triangular basis and are seen to satisfy the threefold rotational symmetry along the i–j axis. Atoms k are therefore equivalent but their interatomic distance dik = 1.51 Å differs sensibly from the 1.42 Å bond-length in graphene. Chemisorption thus causes deformation where the surrounding of the grafting site experiences a tensile strain of 6%. Nevertheless, the bond-length variation turns out to be negligible in the nearest neighboring layer of atoms k, which stems from the ability of graphene to accommodate the adsorbate-induced strain beyond the grafting site.| B | H | T | |
|---|---|---|---|
| Echemads (eV) | −0.564 | −0.558 | −1.815 |
| dij (Å) | 2.893 | 2.847 | 1.565 |
It has been widely reported that diazonium salts spontaneously adsorb onto a wide range of materials including graphene.22,41,42 A DFT simulation can shed light on this process by depositing the 4SB intermediate near the T site and the molecule N2, for example, at 2 Å from the lattice. We observed that the radical steers adiabatically towards the adsorption site while N2 bounces to 3.3 Å in height. In addition, the resulting adsorption parameters, Echemads = −1.34 eV and dij = 1.565 Å, agree well with those of 4-SBD chemisorption.
3.3 Physisorption + dissociative chemisorption
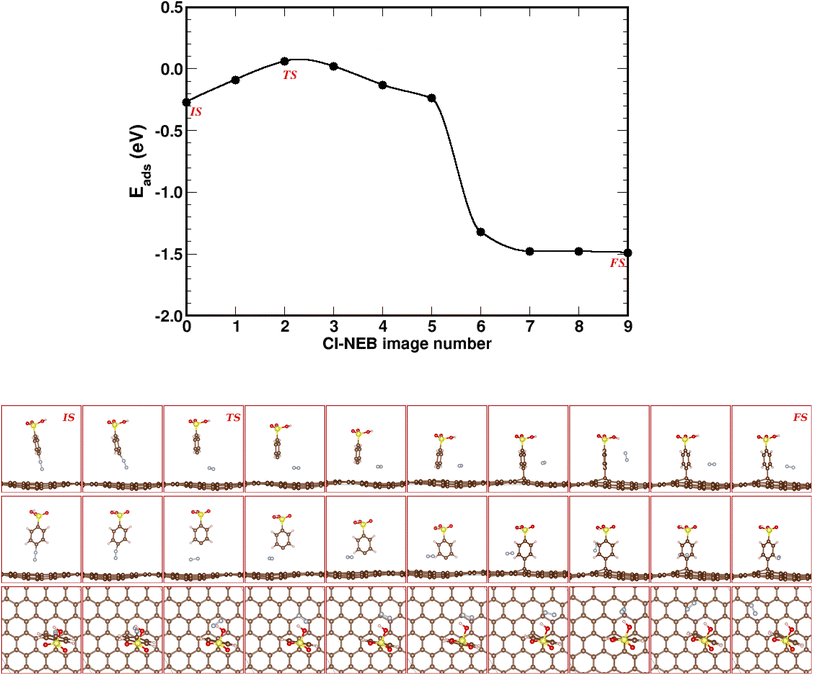
The CI-NEB method allows to determine the minimum energy path (MEP) and transition state (TS) from an initial state (IS) to a final state (FS). Here, the MEP connects the 4SBD-physisorption (IS) to the chemisorbed product (FS). We estimated the MEP with a set of ten images shown in Fig. 3.The dissociative energy barrier is calculated as the energy difference between the initial state IS (image 0) and the transition state TS (image 2) where the carbon–nitrogen bond is broken. We found an energy of 0.33 eV, which suggests an easy dissociation of nitrogen since it requires only a small amount of activation energy. Image 6 shows the covalent bonding of 4SB to the top site T. As seen in image 7, nitrogen diffuses easily on the surface since the adsorption energy decreases by 0.17 eV compared to image 6. The MEP gives a final state FS (image 9) less than the initial state IS (image 0). The chemical reaction therefore requires no activation energy defining a spontaneous grafting.
3.4 Charge density difference of 4SB on graphene
When the 4SB radical reacts with the graphene sheet, the complex experiences two modifications: a charge rearrangement and a distortion of its geometry (deformation effects). We calculated the DFT charge density difference as follows:| Δρ(r) = ρGr–4SB(r) − ρGr(r) − ρ4SB(r) | (5) |
4 Spin-polarized density functional theory calculations
4.1 Electronic structure
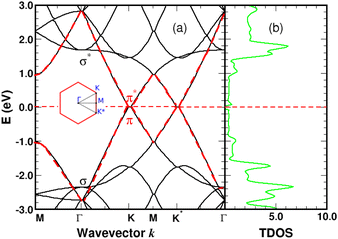
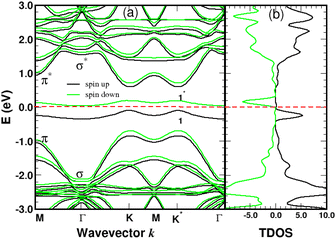
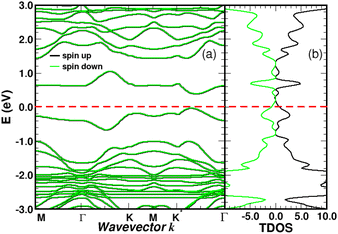
We performed spin-polarized band structure calculations to account for the net magnetic moment of the complex. We used a 4 × 4 graphene supercell with a single 4SB molecule corresponding to a surface coverage rate of 25%. Fig. 5 shows the folded-band structure and total density of states (TDOS) of pristine graphene along the high symmetry directions. Band-folding can be observed at the M-point where the energy states are fourfold degenerate (with spin degeneracy) compared to the second-order degeneracy in the primitive cell (2 atoms). Many papers have been published on graphene properties43 focusing on the bonding (lower-energy valence-band) and anti-bonding (higher-energy conduction-band) states, referred π and π* respectively. As illustrated in Fig. 5, the bandgap between the π and π* bands closes at the Fermi level EF lying at the Dirac energy ED on the K-points. Near the Dirac point ED, the energy-band dispersion increases linearly with the wave vector k and the π-electrons are generally imaged as “massless Dirac fermion”. Therefore, neglecting thermal excitations, the intrinsic charge carrier density is strictly zero in the pristine structure. Identifying a suitable approach to control the Fermi level and thus dissociate EF from ED is of crucial importance to overcome the low carrier density in graphene. Highly p-doped graphene can be obtained by introducing strong electron-withdrawing substituents into the aromatic ring.44 Such a trend is evidenced for 4SBD-chemisorbed on graphene with a Fermi level lowered by 40 meV compared to the Dirac point ED.The spin-polarized bands of the complex and partial density of states (PDOS) of selected atoms are illustrated in Fig. 6 and 7. The calculations were performed without spin–orbit coupling (real and spin spaces are decoupled) leading to two independent sets of majority and minority spin bands. Clearly, the π-like bands, dominated by the pz orbitals of graphene, are very sensitive to the local chemical environment induced by the 4SB adsorbate. At the K-points, band-degeneracy of the π states in the primitive cell is lifted, determining the valence-band-maximum (VBM) and conduction-band-minimum (CBM). Therefore, the bandgap has a direct character allowing an optical excitation of 1.45 eV. Note that the 6-fold symmetry is broken in the complex because of non-uniform strain and the K-points become inequivalent. Interestingly, the energy-band dispersion at the band edges is parabolic and consequently the effective-mass approximation is valid. It should be noted that the σ-like states compare well with their equivalent (sp2 hybridized) in Fig. 5 and the small energy differences are related to the lattice relaxation-induced lifting of the σ-degeneracy evidenced in Fig. 6. Therefore, the s, px and py orbitals of each carbon in graphene are weakly perturbed by the adsorbate-induced potential. Finally, the Bloch states derived from the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) of 4SB are found to be weakly dispersive in the Brillouin zone and lying in energy at −2.04 eV and 1.63 eV respectively.
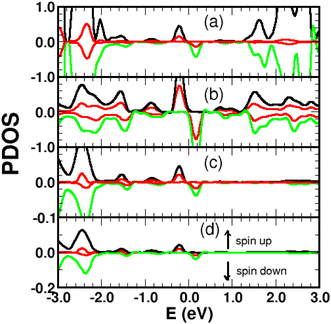 | ||
| Fig. 7 Spin-polarized projected density of states (PDOS) in arbitrary units for a single 4SB molecule chemisorbed on graphene. (a) 4SB molecule; (b) first-shell neighbors k; (c) atom j; (d) atom i. The indices i, j, k are referenced in Fig. 2. The pz-orbital contributions are shown in red. | ||
4.2 π-Magnetism
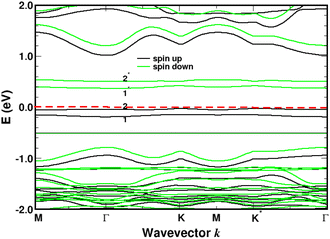
Graphene is non-magnetic with negligible spin–orbit coupling, which should make it suitable for spin-polarized applications. Fig. 6a and b show that the chemical functionalization leads to two midgap impurity states near the Fermi energy defined by an occupied spin-up (marked 1) and an unoccupied spin-down (marked 1*) character. The unpaired electron 1 derives from the pz orbitals with a PDOS mainly localized around the grafting site as seen in Fig. 7b and c. Of note for graphene spintronics is the large spin separation of 420 meV in the TDOS peaks associated to the states 1 and 1* (Fig. 6b). Accordingly, we calculated a total spin magnetic moment μS = 0.98μB that results from the sublattice imbalance in line with the following considerations. μS can be decomposed into the site-projected local spin moments as: −0.01μB for the reference atom i (A-site), 0.51μB for the first-shell neighbors k (three B-sites), −0.28μB for the second-shell neighbors (six A-sites), 0.42μB for the third-shell neighbors (six B-sites) and 0.31μB for the fourth-shell neighbors (six B-sites). The more distant layers and the 4SB molecule contribute to a lesser extent. These values suggest that the long-range magnetic interaction mediated by direct exchange is favored. Therefore, the functionalization of graphene with 4SBD gives an antiferromagnetic character due to opposite signs on the A and B sublattices where their uncompensated local spin moments lead to the finite value of μS. Our findings are in agreement with Elton's DFT calculations34 performed on a wide range of adsorbates on graphene. It is worth noting that the π-magnetism induced by one single-carbon vacancy features a similar electronic band-diagram with magnetic states lying at midgap.45 Further insight can be provided from the band-structure decomposition into a bonding contribution due to adsorbate–surface interactions and a mechanical contribution due to structural relaxation. The second one, displayed in Fig. 8, represents the electronic structure of strained graphene upon chemisorption. The energy-band dispersion is broadly similar to that calculated for pristine graphene.There are no magnetic quantum states and lattice relaxation lifts all degeneracies from the primitive cell, resulting in a 150 meV bandgap at the K-points. In Conclusion, chemical bonding governs the electronic and magnetic properties of 4SBD-chemisorbed on graphene related to bandgap modification.
4.3 Coverage-dependent adsorption
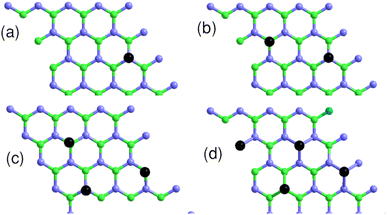
We studied the properties for a coverage of NSB molecules of sulfobenzene chemisorbed on a 4 × 4 graphene supercell. A functionalization ratio of 50% (NSB = 2) to 100% (NSB = 4) is considered by placing one 4SB molecule above a carbon atom on the B-sublattice and the others 4SB above the carbon atoms on the A-sublattice as illustrated in Fig. 9. Additional studies of configuration effects are certainly appropriate but require detailed chemisorption modeling, which is beyond the scope of this article. The DFT adsorption energy per molecule shown in Fig. 10a is defined by:| Eads = E(4SB–Gr) − E(Gr) − NSBE(4SB) | (6) |
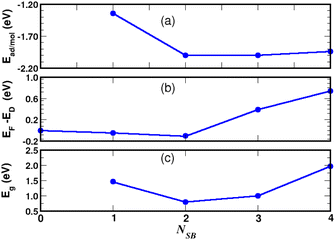 | ||
| Fig. 10 Chemisorption of NSB molecules on graphene. Site occupancy is given in Fig. 9. Adsorption energy (a), Fermi level with respect to the Dirac energy ED of pristine graphene (b), and VBM-to-CBM bandgap (c). | ||
We observed in the calculations that the bond-length dij associated with a given Eads are all equivalent between the grafting sites at approximately 0.005 Å. Fig. 9b addresses NSB = 2 where the two molecules are separated from each other by the fifth-nearest neighboring shell. Therefore, no overlapping orbitals or adsorbate–adsorbate interactions should alter the binding properties of the complex. Moreover, we calculated an interatomic distance dij = 1.58 Å reflecting an efficient chemisorption process with the bonding of the two molecules at the surface. As a result, the Fermi level EF and the binding energy shown in Fig. 10b and c increases in absolute value from NSB = 1 to NSB = 2 due to the enforced surface–adsorbate interactions. Very interestingly, the band-structure evidences in Fig. 11 the long-range ordered properties related to the equipartition of the SB molecules on the A and B sublattices for the layout NSB = 2. Particular emphasis is placed on the suppression of the magnetic spin states leading to μS = 0. This result is in agreement with Lieb's theorem,46 where any imbalance in the number of absorption sites between the two sublattices leads to a magnetic ground state. Hydrogen chemisorption experiments on graphene also confirm finite or zero value of the total spin magnetic moment depending on the relative position of adsorbates on the two sublattices.47 Moreover, the bandgap strongly decreases from NSB = 1 to NSB = 2 (Fig. 10c), which is a typical behavior of ordering as already observed in ordered semiconductor alloys.48 Finally, we will note on the Fig. 11 the position of the Fermi level near the valence-band maximum occurring between the Γ and K*-points. Therefore, the electrical conductivity of the complex is expected to increase compared to NSB = 1 (Fig. 6).
 | ||
| Fig. 11 Band structure (a) and density of states in arbitrary units (b) for two molecules of sulfobenzene adsorbed on graphene. 4SB-site occupancies are given in Fig. 9b. The Fermi level of the complex is the zero-energy reference. | ||
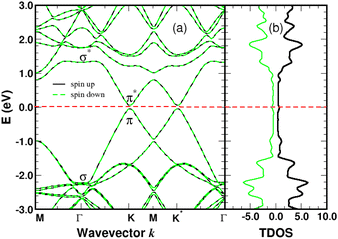
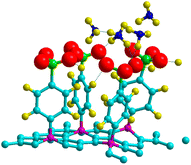
For NSB = 3 and NSB = 4, the lateral or repulsive interactions between the adsorbates49 are evidenced by the simulation of a stable binding energy with increasing surface coverage. A bond-length of dij = 1.59 Å is found in the two coverages and still compares well with the bulk diamond interatomic distance of 1.54 Å. Therefore, a high functionalization coverage with NSB = 4 is a plausible scenario for 4SBD-chemisorbed on graphene and we used as a structure model in the following section. We would like also to point out that an ordered structure at high surface coverage should decrease the lateral interactions since ordering phenomena during atomic relaxation lead to a better accommodation of neighboring adsorbates. Finally, the spin-polarized electronic band-structure for NSB = 4 is illustrated in Fig. 12. The modified material exhibits a strong semiconductor character with a VBM-to-CBM bandgap of 1.96 eV occurring at the Γ-point and the associated energy-band dispersion is parabolic. Moreover, a net spin magnetic moment of μS = 2μB is calculated, deriving from the unpaired electron states labeled 1 and 2 in Fig. 12. This result is in agreement with Lieb's theorem and the imbalance of two 4SB adsorbates between the A and B sublattices. These two singly states lying below the Fermi energy should allow the transfer of two electrons from graphene to them, thus increasing the p-doping of the complex compared to NSB = 1 (Fig. 6).
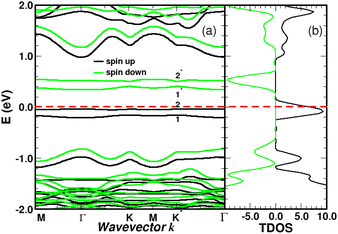 | ||
| Fig. 12 Band structure (a) and density of states in arbitrary units (b) for four molecules of sulfobenzene adsorbed on graphene. 4SB-site occupancies are given in Fig. 9d. The spin impurity states deriving from the sp3 hybridization are labeled 1, 2, 1*, and 2*. The Fermi level is the zero-energy reference. | ||
5 Ammonia adsorption on 4SBD-decorated graphene
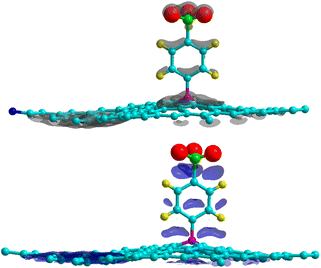
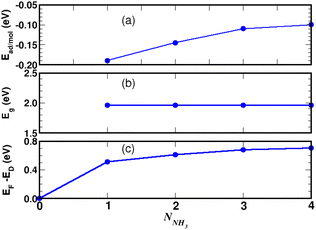
Theoretical and experimental findings showed that the binding energy of NH3 on pristine graphene lies in the physisorption values around 30–60 meV, with the interactions being dominated by the van der Waals forces.50–52 Here, we demonstrated that the process can be enhanced with the use of 4SBD-decorated graphene (NSB = 4) due to the strong orbital mixing between ammonia and the sulfo group, thus demonstrating a chemical contribution to the adsorption bond. Fig. 13 illustrates the charge density changes after adsorption of a single ammonia on the complex. An isovalue of ±0.003 e Å−3 was used to display the accumulation of charge density within the interaction/bonding regions. Adsorption is evidenced by the accumulation of electron density in the vicinity of the oxygen regions and depletion near hydrogen atoms. The adsorption properties was investigated as function of the number NNH3 of ammonia molecules upon the complex. The optimized geometry is given in Fig. 14 for NNH3 = 4 and displays some differences compared to the atomic structure of 4SBD-modified graphene without the gas. There is a formation of a single ammonium NH4+ due to the elimination of the proton from the sulfo group. Calculations showed that the SO3− fragment shortens the S–O single bond-length by 0.02 Å compared to that of sulfonic acid while the S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O double bond-lengths increase slightly by 0.005 Å. Moreover, the hydrogen atoms belonging to the other three NH3 molecules are located approximately at 2.4 Å from the substituent.
O double bond-lengths increase slightly by 0.005 Å. Moreover, the hydrogen atoms belonging to the other three NH3 molecules are located approximately at 2.4 Å from the substituent.
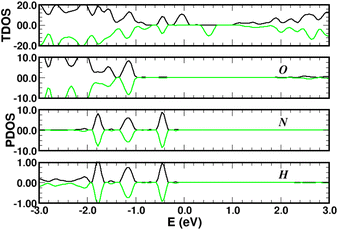
Turning now to the electronic structure for NNH3 = 4 (Fig. 15 and 16) we note that the band energies and TDOS are similar to those displayed in Fig. 12. Therefore, the gas interacts only weakly with the complex, which is suited for applications in sensors. Differences are related to the emergence of well-definite ammonia-derived TDOS peaks (located at −0.44 eV, −1.15 eV and −1.75 eV) with a sharp linewidth (0.14 eV full width at half maximum) that give considerable strength for physisorption. These adsorbate-induced peaks results from hybridization between the molecular orbitals of ammonia and the sulfonic acid and from the tendency of the gas to form hydrogen bonds with oxygen atoms, i.e. the sulfo group is a hydrogen bond acceptor. This analysis is supported by the calculation of the adsorption energies shown in Fig. 17a and defined as:
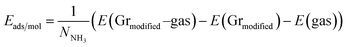 | (7) |
Moreover, the Fermi level (Fig. 17c) increases significantly in the complex as function of the number NNH3 and such a process can be explained by the action of ammonia as charge donors.51 Finally, we would like to point out that the electronic structure upon adsorption processes as a whole, involving the 4SBD diazonium salt and ammonia molecules, induces an opposite type of doping in the graphene surface (p-type with 4SBD and n-type with NH3). Consequently, the electrical conductivity is expected to decrease with increasing gas concentration.
6 Conclusion
In summary, we investigated from DFT the chemisorption properties and electronic structure of graphene functionalized with sulfobenzenediazonium salts. The functional group forms a stable molecular system and interacts strongly with graphene even at high coverage giving an efficient chemisorption process. The electronic properties of 4SBD-modified graphene are governed by the lattice imbalance due to the difference in the number of adsorbed atoms in the individual sublattices. Calculations also revealed spin signature of individual sp3-type defects near the Fermi level making the magnetic properties directly accessible in experiment. The complex is found sensitive to the adsorption of ammonia and demonstrate efficient desorption activity. Further modeling concerns the dependence of the electronic structure on the different adsorbate configurations related to the surface properties of graphene.Author contributions
Conceptualization, V. S., A. C. and A. M.; methodology, F. R. and J. M. J.; software, D. d. C., A. D. and F. R.; formal analysis, F. R. and J. M. J.; investigation, A. D., D. d. C. and F. R.; resources, D. d. C.; writing – original draft preparation, A. D. and F. R.; writing – review and editing, P. R., F. R. and J. M. J.; supervision, F. R. and J. M. J.; All authors have read and agreed to the published version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the financial support of the partenariat Hubert Curien Utique PHC UTIQUE 17G1207 from the French ministry Ministère de l’Europe et des Affaires Etrangères and the Tunisian ministry Ministère de l’Enseignement Supérieur et de la Recherche Scientifique.Notes and references
- G. W. Flynn, J. Chem. Phys., 2011, 135, 050901 CrossRef PubMed.
- J. Park and M. Yan, Acc. Chem. Res., 2013, 46, 181–189 CrossRef CAS PubMed.
- W. Yan, Y. Xu and Y. Chen, J. Nanosci. Nanotechnol., 2015, 15, 2020–2026 CrossRef CAS PubMed.
- D. Akinwande, N. Petrone and J. Hone, Nat. Commun., 2014, 5, 5678 CrossRef CAS PubMed.
- A. C. Ferrari, F. Bonaccorso and V. Fal’ko, R. Soc. Chem., 2015, 7, 4598–4810 CAS.
- C. Chung, Y.-K. Kim, D. Shin, S. Ryoo, B. Hong and D. Min, Acc. Chem. Res., 2013, 46, 2211–2224 CrossRef CAS PubMed.
- C.-S. Liu and Z. Zeng, Appl. Phys. Lett., 2010, 96, 123101 CrossRef.
- K. Ghosh, H. Rahaman and P. Bhattacharyya, IEEE Trans. Electron Devices, 2017, 64, 4738–4745 CAS.
- M. Seydou, Y. J. Dappe, S. Marsaudon, J.-P. Aimé, X. Bouju and A.-M. Bonnot, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 045410 CrossRef.
- X. Huang, Z. Zeng, Z. Fan, J. Liu and H. Zhang, 2D Mater., 2012, 24, 5979–6004 CAS.
- X. Liu, S. Cheng, H. Liu, S. Hu, D. Zhang and H. Ning, Sensors, 2012, 12, 9635–9665 CrossRef PubMed.
- S. Seba, L. Sunil, K. Singh, S. Sundaram and A. Ahmed, Sens. Actuators, B, 2015, 24, 160–183 Search PubMed.
- W. Tao, H. Da, Y. Zhi, X. Shusheng, H. Guilin, X. Li, H. Nantao, H. Dannong and Z. Liying, Nano-Micro Lett., 2016, 8, 95–119 CrossRef PubMed.
- P. T. Moseley, Meas. Sci. Technol., 1997, 8, 223–237 CrossRef CAS.
- A. Maio, I. Pibiri, M. Morreale and a. R. S. Francesco Paolo La Mantia, Nanomaterials, 2021, 11, 1717 CrossRef CAS PubMed.
- A. Kaplan, X. S. Chu, Z. Yuan, J. D. Benck, A. G. Rajan, Q. H. Wang and M. S. Strano, Chem. Soc. Rev., 2017, 46, 4530–4571 RSC.
- V. Georgakilas, M. Otyepka, A. B. Bourlinos, V. Chandra, N. Kim, K. C. Kemp, P. Hobza, R. Zboril and K. S. Kim, Am. Chem. Soc., 2012, 112, 6156–6214 CAS.
- I. A. Vacchi, C. Menard-Moyon and A. Bianco, Phys. Sci. Rev., 2017, 103, 2016 Search PubMed.
- G. L. C. Paulus, Q. H. Wang and M. S. Strano, Acc. Chem. Res., 2013, 46, 160–170 CrossRef CAS PubMed.
- J. Greenwood, T. H. Phan, Y. Fujita, Z. Li, O. Ivasenko, W. Vanderlinden, H. V. Gorp, W. Frederickx, G. Lu, K. Tahara, H. U.-i. Yoshito Tobe, S. F. L. Mertens and S. D. Feyter, Am. Chem. Soc., 2015, 9, 5520–5535 CAS.
- A. A. Mohamed, Z. Salmi, S. A. Dahoumane, A. Mekki, B. Carbonnier and M. M. Chehimi, Adv. Colloid Interface Sci., 2015, 225, 16–36 CrossRef CAS PubMed.
- C. K. Chan, T. E. Beechem, T. Ohta, M. T. Brumbach, D. R. Wheeler and K. J. Stevenson, J. Phys. Chem. C, 2013, 117, 12038–12044 CrossRef CAS.
- G. Ambrosio, G. Drera, G. D. Santo, L. Petaccia, L. Daukiya, A. Brown, B. Hirsch, S. D. Feyter, L. Sangaletti and S. Pagliara, J. Phys. Chem. C, 2020, 10, 4114 CAS.
- P. M. Kirkman, A. G. Güell, A. S. Cuharuc and P. R. Unwin, Am. Chem. Soc., 2014, 136, 36–39 CrossRef CAS PubMed.
- T. Menanteau, M. Dias, E. Levillain, A. J. Downard and T. Breton, J. Phys. Chem. C, 2016, 120, 4423–4429 CrossRef CAS.
- R. Skomski, P. A. Dowben, M. S. Driverb and J. A. Kelber, Mater. Horiz., 2014, 1, 563 RSC.
- G. G. Naumis, S. Barraza-Lopez, M. Oliva-Leyva and H. Terrones, Rep. Prog. Phys., 2017, 80, 096501 CrossRef PubMed.
- N. Salma, Z. Zhongfu, W. Hao and I. Muhammad, RSC Adv., 2017, 7, 51546 RSC.
- D. Henwood and J. D. Carey, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 245413 CrossRef.
- U. Patil and N. M. Caffrey, J. Chem. Phys., 2018, 149, 094702 CrossRef PubMed.
- M. Seydou, K. Lassoued, F. Tielens, F. Maurel, F. Raouafi and B. Diawara, RSC Adv., 2015, 5, 14400 RSC.
- P. Plachinda, D. Evans and R. Solanki, AIMS Mater. Sci., 2017, 4, 340–362 CAS.
- A. Quesne-Turin, J. Touzeau, Y. J. Dappe, B. Diawara, F. Maurel and M. Seydou, Superlattices Microstruct., 2017, 105, 139–151 CrossRef CAS.
- E. J. G. Santos, A. Ayuela and D. Sánchez-Portal, New J. Phys., 2012, 14, 043022 CrossRef.
- S. Baachaoui, S. Aldulaijan, F. Raouafi, R. Besbes, L. Sementa, A. Fortunelli, N. Raouafi and A. Dhouib, RSC Adv., 2021, 11, 7070 RSC.
- S. Baachaoui, S. Aldulaijan, L. Sementa, A. Fortunelli, A. Dhouib and N. Raouafi, J. Phys. Chem. C, 2021, 125, 26418–26428 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- B. Hammer, L. B. Hansen and J. K. Nørskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413–7421 CrossRef.
- A. Markevich, S. Kurasch, O. Lehtinen, O. Reimer, X. Feng, K. Müllen, A. Turchanin, A. N. Khlobystov, U. Kaiserb and E. Besley, R. Soc. Chem., 2016, 8, 2711–2719 CAS.
- Z. Xia, F. Leonardi, M. Gobbi, Y. Liu, V. Bellani, A. Liscio, A. Kovtun, R. Li, X. Feng, E. Orgiu, P. Samorì, E. Treossi and V. Palermo, ACS Nano, 2016, 10, 7125–7134 CrossRef CAS PubMed.
- D. Hetemi, V. Noël and J. Pinson, Biosensors, 2020, 10, 1–32 CrossRef PubMed.
- D. Siegel, PhD thesis, University of California, Berkeley, 2012.
- G. L. C. Paulus, Q. H. Wang and M. S. Strano, Acc. Chem. Res., 2013, 46, 160–170 CrossRef CAS PubMed.
- J.-J. Chen, H.-C. Wu, D.-P. Yuab and Z.-M. Liao, Nanoscale, 2014, 6, 8814–8821 RSC.
- E. H. Lieb, Phys. Rev. Lett., 1989, 62, 1201 CrossRef PubMed.
- H. González-Herrero, J. M. Gómez-Rodríguez, P. Mallet, M. Moaied, J. J. Palacios, C. Salgado, M. M. Ugeda, J. Veuillen, F. Yndurain and I. Brihuega, Science, 2016, 352, 437–441 CrossRef PubMed.
- S. Wei and A. Zunger, Appl. Phys. Lett., 1991, 58, 2684 CrossRef CAS.
- I. Chorkendorff and J. W. Niemantsverdriet, Concepts of Modern Catalysis and Kinetics, Wiley, 2003, pp. 3–527 Search PubMed.
- Z. Zhang, X. Zhang, W. Luo, H. Yang, Y. He, Y. Liu, X. Zhang and G. Peng, Nanoscale Res. Lett., 2015, 10, 359 CrossRef PubMed.
- F. Schedin, A. Geim, S. Morozov, E. Hill, P. Blake and M. Katsnelson, Nat. Mater., 2007, 6, 652 CrossRef CAS PubMed.
- O. Leenaerts, B. Partoens and F. Peeters, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 125416 CrossRef.
| This journal is © The Royal Society of Chemistry 2022 |