Open Access Article
Open Access ArticleMechanical and thermal properties of carbon nanotubes in carbon nanotube fibers under tension–torsion loading†
Mowen Niuae,
Chongxiao Cuiab,
Rui Tiana,
Yushun Zhao*abd,
Linlin Miaoab,
Weizhe Haoab,
Jiaxuan Liab,
Chao Sui*abd,
Xiaodong Hebcd and
Chao Wang *abd
*abd
aSchool of Astronautics, Harbin Institute of Technology, Harbin 150080, China. E-mail: yushunzhao@hit.edu.cn; suichao@hit.edu.cn; chaowang@hit.edu.cn
bCenter for Composite Materials and Structures, Harbin Institute of Technology, Harbin 150080, China
cShenzhen STRONG Advanced Materials Research Institute Co., Ltd, Shenzhen 518000, China
dNational Key Laboratory of Science and Technology on Advanced Composites in Special Environments, Harbin Institute of Technology, Harbin 150080, P. R. China
eBeijing Institute of Astronautical Systems Engineering, Beijing 100076, China
First published on 21st October 2022
Abstract
In carbon nanotube fibers (CNFs) fabricated by spinning methods, it is well-known that the mechanical and thermal performances of CNFs are highly dependent on the mechanical and thermal properties of the inherent CNTs. Furthermore, long CNTs are usually preferred to assemble CNFs because the interaction and entanglement between long CNTs are effectively stronger than between short CNTs. However, in CNFs fabricated using long CNTs, the interior carbon nanotubes (CNTs) inevitably undergo both tension and torsion loading when they are stretched, which would influence the mechanical and thermal performances of CNFs. Here, molecular dynamics (MD) simulations were carried out to study the mechanical and thermal properties of individual CNTs under tension–torsion loading. As for mechanical properties, it was found that both the fracture strength and Young's modulus of CNTs decreased as the twist angle α increased. Besides, step-wise fracture happened due to stress concentration when the twisted CNTs are stretched. On the other hand, it could be seen that the thermal conductivity of CNTs decreased as α increased. This work presents the systematic investigation of the mechanical and thermal properties of CNTs under tension–torsion loading and provides a theoretical guideline for the design and fabrication of CNFs.
1. Introduction
Since discovered in 1991 by Iijima,1 carbon nanotubes (CNTs) are regarded as a promising candidate for fabricating super-strong micro-scale fibers due to their excellent mechanical, thermal, and electrical properties,2–7 and high aspect ratio.8,9 In order to exert such superior properties of individual CNTs, spinning the nanoscale CNTs into macroscale carbon nanotube fibers (CNFs) has been considered a feasible route.10–14 Thus far, there are mainly two methods to fabricate CNFs. One is called the “dry spinning” method, wherein the CNFs are spun from a CNT array or CNT films.15–17 The other one is called the “wet spinning” method, in which the CNFs are formed from various mixed CNT solutions by squeezing or injecting processes.18–20 It has been verified that assembling CNTs into macroscale CNFs by the spinning method is an efficient way to obtain metamaterials.21–23 For instance, as for mechanical properties, Ghemes et al.24 prepared CNT yarns by dry spinning, which yielded a fracture strength of 1068 MPa, Young's modulus of 55 GPa and an effective load capacity of 0.81 N. Wang et al.25 obtained a CNF with high strength (4.34 GPa) and elongation (10%) using CNTs by pressurized rolling. Taylor et al.26 produced a neat CNF with strength of 4.2 GPa. To improve thermal properties, Jakubinek et al.27 obtained CNT yarns spun from multi-walled carbon nanotube (MWCNT) arrays produced, and the room-temperature thermal conductivity of the 10 μm yarn was (60 ± 20) W (m K)−1. However, although the mechanical and thermal properties of these fabricated fibers are much higher than commonly used metal-based materials, they are still much lower than those of individual CNTs.13,28,29 The main reasons for this are that the length of CNTs in the fiber is usually finite, and the van der Waals interaction between CNTs is much weaker than the axial strength of a single CNT.29,30 To improve the mechanical and thermal properties, a highly twisting operation is adopted to increase the density of CNFs, which leads to the twisted morphology of CNTs.31 In such typical CNFs, long CNTs are usually preferred because the interaction and entanglement between long CNTs are much stronger than those between short CNTs, which cause the interior carbon nanotubes (CNTs) to inevitably undergo torsion.32 Besides, when axial tension is applied, every single CNT in these CNFs would undergo both tension and torsion loading, which may influence the mechanical and thermal performance of CNFs. Notably, many works have focused on the mechanical properties of CNTs under tensile, torsion and tension–torsion loadings.33–36 For example, Liew et al. performed molecular dynamics simulations to investigate the mechanical properties of multi-walled CNTs under axial tension, and the results showed that fracture always happened in the outermost layer.33 Chang studied the torsional behavior of chiral single-walled CNTs and found that the torsional behavior is highly dependent on the loading direction.34 Jeong et al. investigated the tensile mechanical behavior of different kinds of single-walled CNTs under tension and combined tension–torsion loading, and the combined tension–torsion was applied simultaneously. They found that tensile strength is dependent on the kind of filling materials and under applied torsion, tensile strength decreases linearly when structures are under combined tension–torsion loading.36 However, in the case of spun CNFs, CNTs are twisted first during the spinning process. When CNFs are stretched, CNTs in CNFs undergo both tension and torsion deformation, which is different from the cases discussed above. To the best of our knowledge, only a few studies37–40 have focused on this topic, which is of great importance to understanding the mechanical and thermal enhancement mechanisms in CNFs.Besides, it is difficult to directly simulate the mechanical and thermal behaviors of CNTs in spun CNFs under tension because the corresponding system is too large, and the computational cost is high. Therefore, in this work, molecular dynamics (MD) simulations have been utilized to investigate the mechanical and thermal properties of three typical types of CNTs under tension–torsion loading. The findings show that the mechanical and thermal properties of MWCNTs are highly dependent on the twist and tensile degree, which indicates that the mechanical and thermal properties of CNFs can be efficiently tuned by changing the related parameters. This work systematically studies the combined influence of tension–torsion loading on the mechanical and thermal properties of MWCNTs and provides an important reference for the fabrication and application of CNT-based materials.
2. Computational methods
2.1. Force field
With the rapid development of computing science and increase in the popularity of machine learning, many potentials, such as Gaussian approximation potential (GAP), LCBOP, PPBE-G, ReaxFF and AIREBO, have been developed.41–43 It has been verified that, in different carbon-based systems, these potentials provide accurate results that are comparable to DFT results. For example, the first-principles-based ReaxFF force field can accurately calculate the chemical and mechanical behavior of carbon-based materials and is capable of treating thousands of atoms with near quantum-chemical accuracy.44 Recently, it has been demonstrated that, when trained using machine learning, GAP could simulate the thermal and mechanical properties of pristine and defective carbon.42,45 Especially, AIREBO has been widely used to study the thermal and mechanical properties of carbon-based materials,46–51 and the obtained results are reasonable and widely acknowledged. Furthermore, it is well-known that, in molecular dynamics simulations, the simulated results obtained using different potentials are slightly different. Therefore, in order conveniently compare the results derived from this work with other works, the commonly used AIREBO potential is adopted in this work. In order to study the mechanical and thermal properties of MWCNTs under tension–torsion loading, a large-scale atomic/molecular massively parallel simulator (LAMMPS) code package has been utilized.52,53 The adaptive intermolecular reactive empirical bond-order (AIREBO) potential has been adopted to describe the C–C interactions.54,55 The AIREBO potential consists of three terms:
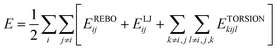 | (1) |
2.2. Relaxation of MWCNTs
To simplify the model, three different kinds of typical MWCNTs, which were built using Virtual Nanotube, were selected. The length of each MWCNT was approximately 240 Å, and α = θ/L was defined to characterize the torsion degree, where θ is the twist angle, and L is the initial length of MWCNTs. The employed chiralities of the single-walled carbon nanotube (SWCNT), double-walled carbon nanotube (DWCNT) and triple-walled carbon nanotube (TWCNT) were (15, 15), (15, 15)–(10, 10) and (15, 15)–(10, 10)–(5, 5), respectively. The total number of atoms for SWCNTs, DWCNTs and TWCNTs were 6000, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 12
000 and 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, respectively. To ensure that the farthest atom in the model was included in the boundary range, the non-periodic boundary condition was utilized, and the size of the simulation box was 40 Å × 40 Å × 250 Å. Prior to the MD simulations of uniaxial loading and thermal conductivity analysis, the MWCNTs were first quasi-statically relaxed to a local minimum configuration through the conjugate gradient method,56 in which the designative energy and force tolerances were set as 1.0 × 10−8 eV and 1.0 × 10−8 eV Å−1, respectively. To ensure that the structure had no internal stress, relaxation was carried out with an adequate simulation time of 10 ps under the NVT (constant number of atoms N, constant volume V, and constant temperature T) ensemble subsequently. Importantly, in the relaxation stage, the two ends of the twisted CNT were only allowed to slide along the axial direction to eliminate axial stress. The timestep was 0.001 ps. It is known that when the temperature is high, atomic vibrations are strong, which could lead us to miss some fracture details of MWCNTs during the tensile process. As shown in Fig. S1,† there was no obvious change in the morphology of CNTs under different temperatures. Therefore, the temperature is set to 1 K in this work.
000, respectively. To ensure that the farthest atom in the model was included in the boundary range, the non-periodic boundary condition was utilized, and the size of the simulation box was 40 Å × 40 Å × 250 Å. Prior to the MD simulations of uniaxial loading and thermal conductivity analysis, the MWCNTs were first quasi-statically relaxed to a local minimum configuration through the conjugate gradient method,56 in which the designative energy and force tolerances were set as 1.0 × 10−8 eV and 1.0 × 10−8 eV Å−1, respectively. To ensure that the structure had no internal stress, relaxation was carried out with an adequate simulation time of 10 ps under the NVT (constant number of atoms N, constant volume V, and constant temperature T) ensemble subsequently. Importantly, in the relaxation stage, the two ends of the twisted CNT were only allowed to slide along the axial direction to eliminate axial stress. The timestep was 0.001 ps. It is known that when the temperature is high, atomic vibrations are strong, which could lead us to miss some fracture details of MWCNTs during the tensile process. As shown in Fig. S1,† there was no obvious change in the morphology of CNTs under different temperatures. Therefore, the temperature is set to 1 K in this work.
2.3. Tensional force of MWCNTs
To perform the simulation of tensile forces in MWCNTs, one end of the MWCNT was fixed and the other end was moved at a constant velocity of 0.01 Å ps−1. The tensile forces were calculated from the virial stress tensor components on each atom. Engineering stress is defined as
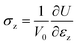 | (2) |
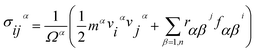 | (3) |
2.4. Thermal properties of MWCNTs
To investigate the thermal properties of MWCNTs under tension–torsion loading, the non-equilibrium molecular dynamics (NEMD) method, in which heat flux is imposed on the system to form a temperature gradient,57–59 and the velocity-Verlet calculation approach were utilized. To analyze the thermal properties, the MWCNT was partitioned into 20 thin slabs. The 1st and 20th slabs were fixed while the 2nd and 19th slabs were regarded as the heat source and sink slab, respectively. Then, the temperature gradient was achieved by injecting/releasing the heat flux Q = 10 eV ps−1, and the NVE (constant number of atoms N, constant volume V, and constant energy E) ensemble was utilized. The temperature profile was obtained after averaging over a 5 ns time interval,46,60 and the thermal conductivity was calculated using the Fourier law as:
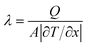 | (4) |
| A = π × d × h | (5) |
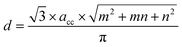 | (6) |
3. Results and discussion
As shown in Fig. 1a, all the CNFs fabricated via the spinning method were well-aligned with each other, and there existed a twist angle θ between the CNTs and axis of the CNFs. From our previous molecular dynamics simulation of a twisted CNT fiber assembled using infinite-long CNTs, it was found that the self-torsion of CNTs would inevitably happen when fibers are twisted.31 Experimentally, the spinning method can also induce self-torsion to some extent though the CNTs are finite, and the CNTs would maintain their morphologies due to strong van der Waals interactions. Furthermore, as for CNFs fabricated using super-long CNTs,32 the CNTs can be regarded as infinite-long CNTs, and it is clear that torsion happens under such a circumstance. Therefore, some CNTs undergo both tension and torsion loadings when the spun CNFs are stretched. To investigate the influence of tension–torsion loadings on the mechanical properties of CNFs under such circumstances and reveal the corresponding enhancement mechanisms, a single CNT was selected considering the extremely big molecular model of CNFs and high computational cost. As shown in Fig. 1b, firstly, the bottom end of the MWCNT was fixed, and the upper end was twisted by a certain angle under the load of torque M. Secondly, the twisted MWCNT was stretched along the axial direction by tensile force P. The snapshots of SWCNT, DWCNT and TWCNT with the same α are shown. It can be seen that the SWCNT and DWCNT collapsed due to high torsion degrees, whereas TWCNT could retain its tubular shape due to high torsional rigidity. Besides, the maximum α values of the SWCNT, DWCNT and TWCNT were 2.25° Å−1 (θ = 540°), 1.75° Å−1 (θ = 420°) and 0.75° Å−1 (θ = 180°), respectively, and fracture would happen when the torsion degree is increased further, which is not considered in this work. Such mechanical behaviors have also been found in other works.34,60,62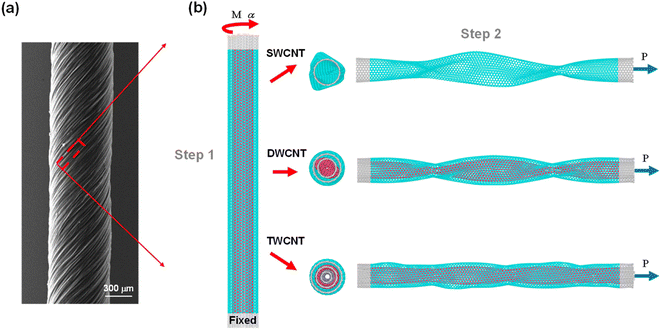 | ||
| Fig. 1 (a) The SEM image of CNF;28 (b) diagram of tension–torsion coupling in SWCNT (15, 15), DWCNT ((10, 10)–(15, 15)) and TWCNT ((15, 15)–(10, 10)–(5, 5)). | ||
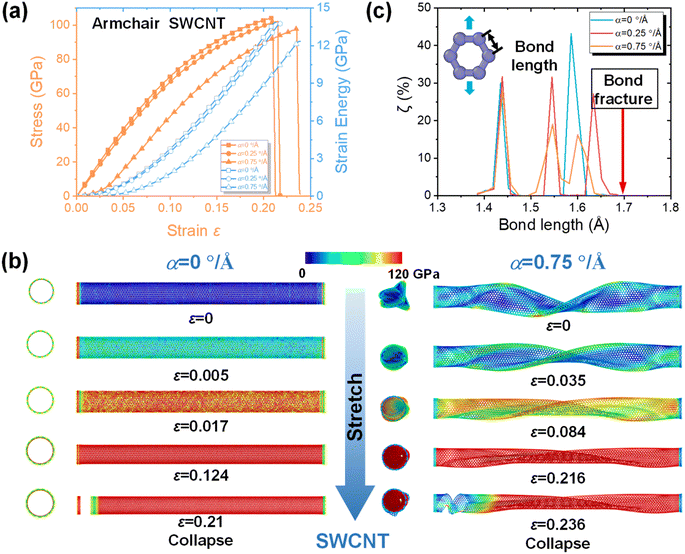
In order to study the influence of α on the mechanical properties of MWCNTs, axial tension was applied on the MWCNTs with different α (0–2.25° Å−1 for SWCNT, 0–1.75° Å−1 for DWCNT, 0–0.75° Å−1 for TWCNT). To further characterize the mechanical behavior of the twisted MWCNTs during the tensile process, the stress–strain curves of representative SWCNTs with α values 0, 0.25 and 0.75° Å−1 are shown in Fig. 2a. It can be seen that SWCNT showed linear elasticity, and strain energy increased as the tensile strain increased. Brittle fracture was also found, which is in agreement with theoretical predictions and experiments in other works.63–65 Besides, the SWCNT with a higher torsion degree possessed higher stretchability. Fig. 2b shows the snapshots of SWCNTs with α = 0 and 0.75° Å−1 during the tensile process, and the atoms are colored based on von Mises stress. Unlike pristine SWCNT, the stresses showed a highly non-uniform distribution along the SWCNT under axial tension when twisted. Moreover, due to the introduction of the twisting operation, higher stress concentration happened at the wrinkled parts, which led to local fractures. Further, bond fracture always happened along the zigzag direction, and single atomic carbon chains were observed at the breakage edges, which has also been proven in other works.66,67 Furthermore, in order to elucidate the potential mechanical mechanisms, the bond length distribution in SWCNTs with different α before fracture was plotted, as presented in Fig. 2c, where ζ is the ratio of the bond lengths. The plot revealed three peaks in SWCNTs with α = 0.25 and 0.75° Å−1, while only two peaks existed in pristine SWCNT, and the maximum bond lengths in the SWCNT with different torsion degrees were in the range of 1.65–1.69 Å. This indicates that the perfect hexagonal lattice of CNT was distorted by the twisting operation. The corresponding tensile process can be found in Videos S1 and S2.†
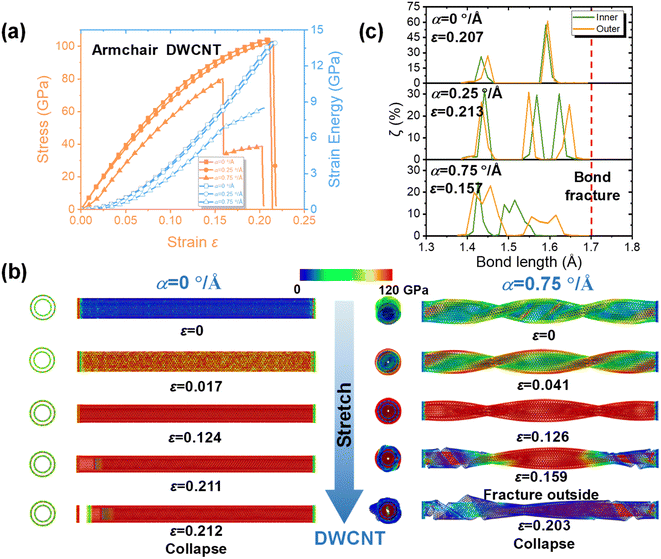
On the other hand, to study the influence of torsion degree on the mechanical properties of MWCNTs, more details about typical DWCNTs and TWCNTs with different α are shown in Fig. 3 and S2,† respectively. It can be seen from Fig. 3a and S2a† that, similar to SWCNT, DWCNT and TWCNT showed linear elasticity before fracture. However, when the torsion degree was high, step-wise fracture could be found during the tensile process. Further, in the strain energy–strain curves, strain energy quadratically increased as the tensile strain was increased, which confirms the linear elasticity of CNTs under tension–torsion loadings, and during the fracture process, the slope of the strain energy–strain curves decreased, indicating that the load-carrying capacity of the CNTs had decreased. For example, two peaks could be found in the DWCNT when the tensile strain was 15.9% and 20.3%, respectively. The corresponding snapshots of DWCNTs with α = 0 and 0.75° Å−1 are shown in Fig. 3b. Similar to SWCNT, the DWCNT was wrinkled due to a high torsion degree, and a super-high stress concentration was found. However, as for the TWCNT in Fig. S2b,† as the tensile strain was increased, the wrinkles caused by the twisting operation disappeared. As the strain was further increased, the stress along the MWCNT was uniformly distributed, and the initial fracture happened in the outer CNT. Then, successive fractures happened from the outer layer to the inner layers. The bond distributions of DWCNT and TWCNT with different torsion degrees were also collected, as shown in Fig. 3c and S2c.† They revealed that the bond length in the outer CNT was longer than the other bonds, which is due to the fact that the outer CNT undergoes a larger twisting effect when the MWCNT is twisted by a certain α. When the MWCNT is further stretched, the bond in the outer CNT reaches the fracture length first, and then the bonds in the other CNTs fracture successively; this is the main reason for the step-wise fracture seen in MWCNT. The corresponding tensile process can be seen in Videos S3–S6.†
Fig. 4 shows the σf and E of MWCNTs with different α, and it is important to note that some data points are missing because the corresponding MWCNTs were unstable due to excessive torsion. It is clear that the values of tensile strength and Young's modulus of MWCNTs were up to 104.85 GPa and 823.28 GPa, respectively, which are comparable to experimental results.68,69 In Fig. 4a, it can be seen that when the α of MWCNT was increased from 0° Å−1 to 2.25° Å−1, the σf of the MWCNT decreased from 104.85 GPa to 23.84 GPa. Furthermore, when α was in the range of 0–0.25° Å−1, the mechanical properties of the three typical CNT models were basically similar and σf exceeded 100 GPa, which is very close to the σf of pristine CNTs.33 When α was higher than 0.25° Å−1, the σf of the MWCNT started to decrease drastically with increasing α. For example, the σf of SWCNT decreased from 104.49 GPa to 69.01 GPa, while α was in the range of 0.25–2.25° Å−1. As for E, it was found that the E of SWCNT and DWCNT decreased as α increased. Furthermore, it was found that when α reached 0.5° Å−1, 0.75° Å−1 and 0.75° Å−1 for SWCNT, DWCNT and TWCNT, respectively, the drop in σf and E was dramatic, which is mainly caused by the generation of wrinkles, as shown in Fig. 4b. Chowdhury et al. have also studied the mechanical properties of SWCNTs with and without defects under compression, tension–torsion and combined torsion-axial loadings, and similar trends were discovered.70 However, the range of torsion angle was limited, and the case of MWCNT was not considered and hence could not provide a comprehensive reference for all possible conditions that happen to CNTs in CNFs. Therefore, it can be concluded that the twisting operation can impair the mechanical properties of MWCNT; however, when the SWCNT was reshaped into the columnar shape, the density and E of SWCNT improved, which has not been found in other works. Interestingly, E increased from 61.36 GPa to 276.98 GPa as α increased from 0.75° Å−1 to 2.25° Å−1 in the highly twisted SWCNT.
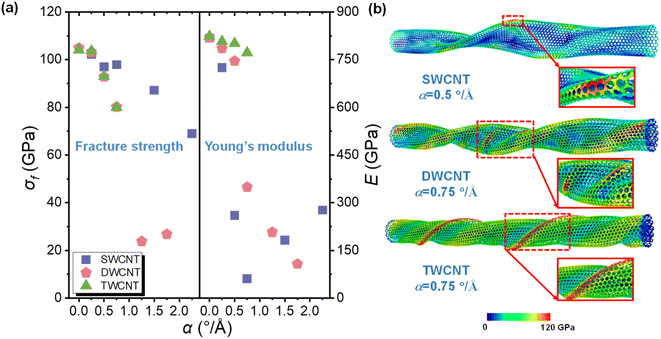 | ||
| Fig. 4 (a) The σf and E of SWCNT, DWCNT and TWCNT under different α. (b) Schematic of the local wrinkle in MWCNTs under tension–torsion strain; the atoms are colored based on von Mises stress. | ||
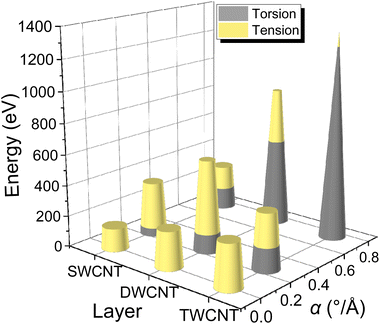
To further investigate the contribution of tension and torsion loadings on the fracture of MWCNT, corresponding tension energy and torsion energy during the tensile process were collected, as displayed in Fig. 5. Tension energy is the energy induced by axial tensile loading in pristine MWCNT, and torsion energy is the energy difference between pristine MWCNT and MWCNT under torsion. It was found that the energies of SWCNT, DWCNT and TWCNT were in the range of 146–348 eV, 244–900 eV and 292–1341 eV, respectively, and the energy increases when α was increased. The maximum percentage of torsion energy was up to 93% for TWCNT with α = 0.75° Å−1. Therefore, this indicates that more energy is needed for MWCNTs with more layers to reach their maximum mechanical limit, and torsion is the main cause of failure in highly twisted MWCNTs with more layers.
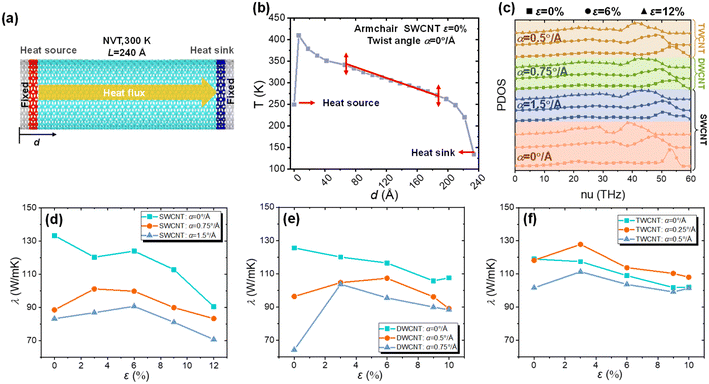
Fig. 6a shows a schematic of the thermal conductivity calculation in a representative MWCNT. The temperature gradient in SWCNT with zero tension and torsion strain is shown in Fig. 6b. Notably, due to the fact that the lattice vibrations of the heat source and heat sink do not match the lattice vibration of the remaining CNT structure, temperature jumps will occur near the heat source and heat sink area, which is commonly observed in NEMD. From Fig. 6b, it can be seen that the temperature in the middle part of the system was approximately linear in the steady state; therefore, the temperature gradient of the CNT was calculated by the linear fitting method for the middle part. According to the method above, the thermal conductivity of the MWCNT with α = 0° Å−1 was around 133.25 W (m K)−1, which is in good agreement with related modeling studies.71,72 However, it is lower than the experiment value because the size of the CNT model established in this paper is much shorter than the phonon mean free path (1 μm) in CNTs.73
To study the effect of tension–torsion loading on the thermal conductivity of MWCNTs, the thermal conductivity of MWCNTs under different tensile strains (0–12%, at 300 K) and α (0° Å−1, 0.75° Å−1, 1.5° Å−1 for SWCNT; 0° Å−1, 0.5° Å−1, 0.75° Å−1 for DWCNT; 0° Å−1, 0.25° Å−1, 0.5° Å−1 for TWCNT) were calculated. To reveal the influence of torsion and tension loadings on the thermal transport properties of MWCNTs, the phonon density of states (PDOS) of MWCNTs under different tension–torsion loadings were collected, as shown in Fig. 6. The PDOS was obtained through the Fourier transform of the velocity autocorrelation function (VACF). It could be seen that when MWCNTs were stretched, the higher frequency peaks in the phonon spectra were dramatically softened. That is, the phonon group velocities are slowed down, which leads to a decrease in thermal conductivity. Similar behavior has also been found in another work.74 Importantly, when the MWCNTs are highly twisted, the tubular MWCNTs are wrinkled, resulting in a non-linear relationship between the thermal conductivity of the MWCNT and the corresponding geometric parameters. In Fig. 6d–f, the thermal conductivity ranges from 64.36 W (m K)−1 to 133.25 W (m K)−1, which indicates that the thermal conductivity of the MWCNT could be efficiently adjusted via tuning α and tensile strain. Moreover, the thermal conductivity basically decreased as the tensile strain increased. For example, the thermal conductivity of SWCNT decreased from 133.25 W (m K)−1 to 70.71 W (m K)−1 when the SWCNT was stretched from 0% to 12%. Similar results have also been observed by Xu et al.60 However, Xu et al. did not consider the coupling influence of tension and torsion loading on the thermal properties of CNTs, and only SWCNTs were studied.
On the other hand, we found that at a certain tensile strain, increasing α leads to a decline in the thermal conductivity of SWCNT and DWCNT. Due to the formation of wrinkles, the cross-sectional area of the CNT collapses into flat nanoribbons as α increases. Therefore, the decline in thermal conductivity is induced by the deviation in the heat flow conduction direction and the increase in interface resistance at the crease, which further increases the scattering centers of the particles and energy dissipation. However, the TWCNT showed abnormal behavior, that is the thermal conductivity at α = 0.25° Å−1 was higher than those with α = 0° Å−1 and α = 0.5° Å−1. This may be because, in TWCNTs, the slightly twist angle improves the thermal flux between CNTs, which leads to higher thermal conductivity. However, when the TWCNT is further twisted, the CNTs tend to wrinkle, and thermal conductivity decreases. Therefore, this indicates that it is possible to improve the thermal conductivity of CNFs by changing the torsion or tension degree in experiment.
4. Conclusions
In summary, we investigated the mechanical and thermal properties of MWCNT under tension–torsion loading. Based on the simulation results, it was found that both σf and E of MWCNT decrease as α increases. However, in SWCNTs, when α is larger than 0.75° Å−1, E increases with increasing α; this is mainly due to the reshaping of tubular SWCNT to columnar shape. As for thermal properties, the thermal conductivity of MWCNT decreases when the MWCNT is stretched, while for SWCNT and DWCNT, torsion loading impairs thermal properties. It is important to note that, in TWCNTs, when α is small, torsion degree plays a positive role; however, when α is increased, the thermal properties of TWCNT decrease. This work reveals the mechanical and thermal behaviors of MWCNTs under tension and torsion loading and provides an important reference for the fabrication and application of super-strong CNT fibers.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge the financial support from the National Natural Science Foundation of China (NSFC, Grant No. 11872164). This work was also supported by Shenzhen Science and Technology Program (Grant No. KQTD2016112814303055), Science Foundation of National Key Laboratory of Science and Technology on Advanced Composites in Special Environments (Grant No. 6142905212703).References
- S. Iijima, Nature, 1991, 354, 56–58 CrossRef CAS.
- R. Saito, G. Dresselhaus and M. S. Dresselhaus, Physical Properties of Carbon Nanotubes, 1998 Search PubMed.
- S. Berber, Y. K. Kwon and D. Tomanek, Phys. Rev. Lett., 2000, 84, 4613–4616 CrossRef CAS PubMed.
- Y. Zare and K. Y. Rhee, Eng. Comput., 2022, 38, 315–324 CrossRef.
- R. Wang, W. Xu, D. Chen, R. Zhou, Q. Wang, W. Gao, J. Kono, L. Xie and Y. Ying, ACS Appl. Mater. Interfaces, 2020, 12, 40629–40634 CrossRef CAS PubMed.
- J. A. Roberts, P.-H. Ho, S.-J. Yu, X. Wu, Y. Luo, W. L. Wilson, A. L. Falk and J. A. Fan, Phys. Rev. Appl., 2020, 14, 044006 CrossRef CAS.
- S. Saadatyar, M. H. Beheshty and R. Sahraeian, Polym. Polym. Compos., 2021, 29, S74–S84 CAS.
- V. Popov, Mater. Sci. Eng., R, 2004, 61–102, DOI:10.1016/j.mser.2003.10.001.
- A. K. Jagadeesan, K. Thangavelu and V. Dhananjeyan, Carbon Nanotubes: Synthesis, Properties and Applications, Surface Science, 2020 Search PubMed.
- G. Hou and M. J. Schulz, in Carbon Nanotube Fibers and Yarns, ed. M. Miao, Woodhead Publishing, 2020, pp. 37–59, DOI:10.1016/B978-0-08-102722-6.00003-1.
- V. Reguero, B. Alemán, B. Mas and J. J. Vilatela, Chem. Mater., 2014, 26, 3550–3557 CrossRef CAS.
- L. Kou, Y. Liu, C. Zhang, L. Shao, Z. Tian, Z. Deng and C. Gao, Nano-Micro Lett., 2017, 9, 51 CrossRef PubMed.
- Y. Y. Shang, Y. Wang, S. H. Li, C. F. Hua, M. C. Zou and A. Y. Cao, Carbon, 2017, 119, 47–55 CrossRef CAS.
- C. Zhang, Y. Song, H. Zhang, B. Lv, J. Qiao, N. Yu, Y. Zhang, J. Di and Q. Li, Nanoscale, 2019, 11, 4585–4590 RSC.
- M. Zhang, K. R. Atkinson and R. H. Baughman, Science, 2004, 306, 1358 CrossRef CAS PubMed.
- Y.-L. Li, I. A. Kinloch and A. H. Windle, Science, 2004, 304, 276 CrossRef CAS PubMed.
- K. Jiang, Q. Li and S. Fan, Nature, 2002, 419, 801 CrossRef CAS PubMed.
- A. B. Dalton, S. Collins, E. Muñoz, J. M. Razal, V. H. Ebron, J. P. Ferraris, J. N. Coleman, B. G. Kim and R. H. Baughman, Nature, 2003, 423, 703 CrossRef CAS PubMed.
- L. M. Ericson, H. Fan, H. Peng, V. A. Davis, W. Zhou, J. Sulpizio, Y. Wang, R. Booker, J. Vavro, C. Guthy, A. N. G. Parra-Vasquez, M. J. Kim, S. Ramesh, R. K. Saini, C. Kittrell, G. Lavin, H. Schmidt, W. W. Adams, W. E. Billups, M. Pasquali, W.-F. Hwang, R. H. Hauge, J. E. Fischer and R. E. Smalley, Science, 2004, 305, 1447 CrossRef CAS PubMed.
- B. Vigolo, A. Pénicaud, C. Coulon, C. Sauder, R. Pailler, C. Journet, P. Bernier and P. Poulin, Science, 2000, 290, 1331 CrossRef CAS PubMed.
- X. F. Zhang, Q. W. Li, T. G. Holesinger, P. N. Arendt, J. Y. Huang, P. D. Kirven, T. G. Clapp, R. F. DePaula, X. Z. Liao, Y. H. Zhao, L. X. Zheng, D. E. Peterson and Y. T. Zhu, Adv. Mater., 2007, 19, 4198–4201 CrossRef CAS.
- A. S. Wu and T.-W. Chou, Mater. Today, 2012, 15, 302–310 CrossRef CAS.
- C. Zhao, Z. Luo, S. Ao, M. Feng, W. Liu and R. Zhang, Carbon, 2017, 125, 269–279 CrossRef CAS.
- A. Ghemes, Y. Minami, J. Muramatsu, M. Okada, H. Mimura and Y. Inoue, Carbon, 2012, 50, 4579–4587 CrossRef CAS.
- J. N. Wang, X. G. Luo, T. Wu and Y. Chen, Nat. Commun., 2014, 5, 3848 CrossRef CAS PubMed.
- L. W. Taylor, O. S. Dewey, R. J. Headrick, N. Komatsu, N. M. Peraca, G. Wehmeyer, J. Kono and M. Pasquali, Carbon, 2021, 171, 689–694 CrossRef CAS.
- M. B. Jakubinek, M. B. Johnson, M. A. White, C. Jayasinghe, G. Li, W. Cho, M. J. Schulz and V. Shanov, Carbon, 2012, 50, 244–248 CrossRef CAS.
- Y. Zhao, F. Xue, L. Miao, C. Wang, C. Sui, Q. Peng and X. He, Carbon, 2021, 172, 41–49 CrossRef CAS.
- Y. Wu, X. Zhao, Y. Shang, S. Chang, L. Dai and A. Cao, ACS Nano, 2021, 15, 7946–7974 CrossRef CAS PubMed.
- M. Sadeghalvaad, E. Dabiri, S. Zahmatkesh and P. Afsharimoghadam, J. Nanostruct., 2019, 9, 453–467 CAS.
- Y. Zhao, C. Wang, L. Miao, J. Li, Z. Xu, C. Sui and X. He, ACS Appl. Nano Mater., 2020, 3, 5521–5529 CrossRef CAS.
- Y. Bai, R. Zhang, X. Ye, Z. Zhu, H. Xie, B. Shen, D. Cai, B. Liu, C. Zhang, Z. Jia, S. Zhang, X. Li and F. Wei, Nat. Nanotechnol., 2018, 13, 589–595 CrossRef CAS PubMed.
- K. M. Liew, X. Q. He and C. H. Wong, Acta Mater., 2004, 52, 2521–2527 CrossRef CAS.
- T. C. Chang, Appl. Phys. Lett., 2007, 90, 201910 CrossRef.
- E. W. Bucholz and S. B. Sinnott, J. Appl. Phys., 2012, 112, 123510 CrossRef.
- B.-W. Jeong, J.-K. Lim and S. B. Sinnott, Appl. Phys. Lett., 2007, 90, 023102 CrossRef.
- X. Liu, W. Lu, O. M. Ayala, L. P. Wang, A. M. Karlsson, Q. Yang and T. W. Chou, Nanoscale, 2013, 5, 2002–2008 RSC.
- Z. Wang, M. Devel and B. Dulmet, Surf. Sci., 2010, 604, 496–499 CrossRef CAS.
- X. Nie, L. Zhao, S. Deng and X. Chen, Int. J. Heat Mass Transfer, 2020, 160, 120234 CrossRef CAS.
- A. S. Wu, X. Nie, M. C. Hudspeth, W. W. Chen, T.-W. Chou, D. S. Lashmore, M. W. Schauer, E. Towle and J. Rioux, Appl. Phys. Lett., 2012, 100, 201908 CrossRef.
- V. L. Deringer and G. Csányi, Phys. Rev. B, 2017, 95, 094203 CrossRef.
- P. Rowe, V. L. Deringer, P. Gasparotto, G. Csanyi and A. Michaelides, J. Chem. Phys., 2020, 153, 034702 CrossRef CAS PubMed.
- I. V. Lebedeva, A. S. Minkin, A. M. Popov and A. A. Knizhnik, Phys. E, 2019, 108, 326–338 CrossRef CAS.
- A. C. T. van Duin, S. Dasgupta, F. Lorant and W. A. Goddard, J. Phys. Chem. A, 2001, 105, 9396–9409 CrossRef CAS.
- C. Davini, A. Favata and R. Paroni, J. Mech. Phys. Solids, 2017, 104, 96–114 CrossRef CAS.
- N. Wei, Y. Chen, K. Cai, J. Zhao, H.-Q. Wang and J.-C. Zheng, Carbon, 2016, 104, 203–213 CrossRef CAS.
- E. F. Hacopian, Y. Yang, B. Ni, Y. Li, X. Li, Q. Chen, H. Guo, J. M. Tour, H. Gao and J. Lou, ACS Nano, 2018, 12, 7901–7910 CrossRef CAS PubMed.
- A. L. Bowman, E. P. Chan, W. B. Lawrimore and J. K. Newman, Nano Lett., 2021, 21, 5991–5997 CrossRef CAS PubMed.
- Y. Hou, Z. Dai, S. Zhang, S. Feng, G. Wang, L. Liu, Z. Xu, Q. Li and Z. Zhang, Nat. Commun., 2021, 12, 5069 CrossRef CAS PubMed.
- B. Goh, K. J. Kim, C.-L. Park, E. S. Kim, S. H. Kim and J. Choi, Carbon, 2021, 184, 452–462 CrossRef CAS.
- Z. Bie, X. Liu, J. Tao, J. Zhu, D. Yang and X. He, Carbon, 2021, 179, 240–255 CrossRef CAS.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- A. J. Kulik, A. Kis, B. Lukic, K. Lee and L. Forró, Mechanical Properties of Carbon Nanotubes, Fundamentals of Friction and Wear, 2007 Search PubMed.
- D. W. Brenner, O. A. Shenderova, J. A. Harrison, S. J. Stuart, B. Ni and S. B. Sinnott, J. Phys.: Condens. Matter, 2002, 14, 783–802 CrossRef CAS.
- O. Shenderova, D. Brenner, A. Omeltchenko, X. Su and L. Yang, Phys. Rev. B, 2000, 61, 3877–3888 CrossRef CAS.
- M. R. Hestenes and E. L. Stiefel, J. Res. Natl. Bur. Stand., 1952, 49, 409–436 CrossRef.
- T. Ikeshoji and B. Hafskjold, Mol. Phys., 1994, 81, 251–261 CrossRef CAS.
- P. Jund and R. Jullien, Phys. Rev. B, 2007, 59, 13707–13711 CrossRef.
- F. Müller-Plathe, J. Chem. Phys., 1997, 106, 6082–6085 CrossRef.
- Z. Xu and M. J. Buehler, Nanotechnology, 2009, 20, 185701 CrossRef PubMed.
- A. Maffucci, G. Miano and F. Villone, IEEE Trans. Nanotechnol., 2009, 8, 345–354 Search PubMed.
- C. L. Zhang and H. S. Shen, J. Phys.: Condens. Matter, 2007, 19, 386212 CrossRef.
- K. I. Tserpes, P. Papanikos and S. A. Tsirkas, Composites, Part B, 2006, 37, 662–669 CrossRef.
- R. Shikata, H. Suzuki, Y. Hayashi, T. Hasegawa, Y. Shigeeda, H. Inoue, W. Yajima, J. Kametaka, M. Maetani, Y. Tanaka, T. Nishikawa, S. Maeda, Y. Hayashi and M. Hada, Nanotechnology, 2022, 33, 235707 CrossRef PubMed.
- K. Shirasu, G. Yamamoto and T. Hashida, Mater. Res. Express, 2019, 055047 CrossRef CAS.
- C. S. Casari, M. Tommasini, R. R. Tykwinski and A. Milani, Nanoscale, 2016, 8, 4414–4435 RSC.
- E. Kano, M. Takeguchi, J.-i. Fujita and A. Hashimoto, Carbon, 2014, 80, 382–386 CrossRef CAS.
- N. Khandoker, S. C. Hawkins, R. Ibrahim, C. P. Huynh and F. Deng, Procedia Eng., 2011, 10, 2572–2578 CrossRef CAS.
- B. Peng, M. Locascio, P. Zapol, S. Li, S. L. Mielke, G. C. Schatz and H. D. Espinosa, Nat. Nanotechnol., 2008, 3, 626–631 CrossRef CAS PubMed.
- S. C. Chowdhury, B. Z. Haque, J. W. Gillespie and D. R. Hartman, Comput. Mater. Sci., 2012, 65, 133–143 CrossRef CAS.
- C. W. Padgett, O. Shenderova and D. W. Brenner, Nano Lett., 2006, 6, 1827–1831 CrossRef CAS PubMed.
- X. Zhang, W. Lu, G. Zhou and Q. Li, Adv. Mater., 2020, 32, 1902028 CrossRef CAS PubMed.
- K. Sääskilahti, J. Oksanen, S. Volz and J. Tulkki, Phys. Rev. B, 2015, 91, 115426 CrossRef.
- N. Wei, L. Xu, H. Q. Wang and J. C. Zheng, Nanotechnology, 2011, 22, 105705 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ra05360h |
| This journal is © The Royal Society of Chemistry 2022 |