Structure, magnetism and magnetocaloric effect in a new triangular lattice compound Gd₃Cu₉(OH)₁₉Br₈

Abstract

A new triangular lattice compound Gd₃Cu₉(OH)₁₉Br₈ has been synthesized by the hydrothermal method. The structure, magnetism and magnetocaloric effect of Gd₃Cu₉(OH)₁₉Br₈ have been studied by X-ray diffraction, magnetic susceptibility, isothermal magnetization and specific heat measurements. In Gd₃Cu₉(OH)₁₉Br₈, the Cu²⁺ ions form a Kagome lattice along the ab plane, and Gd³⁺ ions are located in the center of hexagonal holes of the Kagome layer. The Cu-sublattice and Gd-sublattice overlap and constitute a magnetic triangular lattice. The temperature dependence of susceptibility and specific heat curves indicate no magnetic transition down to 2 K, suggesting a paramagnetic-like behavior at low temperature. The magnetocaloric effect (MCE) at low temperature has been calculated according to Maxwell's equations. The maximum value of magnetic entropy change −ΔS_M is 26.04 J kg⁻¹ K⁻¹ and adiabatic temperature change ΔT_ad is 13.79 K, for a field change of 0–7 T, indicating a potential application of this compound in the field of magnetic refrigeration at low temperature. The influence of 4f–3d interaction on magnetism and MCE is also discussed.

---

Introduction

In recent years, spin frustrated antiferromagnets have attracted intensive attention in theory and experiment due to their exotic magnetic phenomena, such as spin ice, spin glass and quantum spin liquid states.^1–4 Among them, S = 1/2 Heisenberg antiferromagnets with a Kagome lattice have been considered as potential quantum spin liquid (QSL) candidates due to their strong spin frustration.^5,6 The typical QSL candidates include ZnCu₃(OH)₆Cl₂ and ZnCu₃(OH)₆FBr, in which the Cu²⁺ ions constitute a geometrical perfect Kagome lattice.^7–9 However, the existence of anti-site disorder between Cu²⁺ and Zn²⁺ ions induces the bond randomness and plays significant influence on the magnetic ground state in the above compounds.^10,11

To avoid anti-site disorder, the trivalent yttrium ion (Y³⁺) has been tried to substitute the nonmagnetic Zn²⁺ ions. A new compound YCu₃(OH)₆Cl₃ without any Cu²⁺/Y³⁺ mixing has been successfully synthesized and used to investigate the possible QSL state.^12–14 Following the study of YCu₃(OH)₆Cl₃, a series of similar systems, such as YCu₃(OH)₆Br₂[Br_x(OH)_1−x] (x ≈ 0.51),¹⁵ Y₃Cu₉(OH)₁₉C_l8,¹⁶ LnCu₃(OH)₆C_l3 (Ln = Gd, Tb, Dy),¹⁷ and RCu₃(OH)₆C_l3 (R = Nd and Sm),¹⁸ have been synthesized and further used to study the magnetic ground state. By replacing the Y³⁺ ions into magnetic lanthanides Ln³⁺ ions, the magnetic topological structure of these compounds became a triangular lattice constituted by Cu²⁺ and Ln³⁺ ions and a significant influence of lanthanides on Cu-Kagome lattice has been revealed in magnetic studies. Especially for compounds with heavy lanthanides, the existence of heavy lanthanides ions can suppress the strong antiferromagnetic (AFM) spin interaction and lead to the reduction of Weiss temperature.¹⁷

Compared with other lanthanides, heavy lanthanide Gd³⁺ ion owns a large spin quantum number (S = 7/2) and no orbital angular momentum. With applying magnetic field, the Gd-based compounds usually release a considerable magnetic entropy change and exhibit remarkable performance in giant magnetocaloric effect (MCE), which is benefit for the potential application in magnetic refrigeration technology.^19–22 Among them, the 4f–3d interaction plays an important role in magnetism and MCE. For example, the AFM 4f–3d interactions in compound MCE.^23,24 While, the existence of weak 4f–3d interactions in GdCrO₄ promotes the spin polarization and enhances the MCE.²⁵

In this work, we have synthesized high-quality single crystals of Gd₃Cu₉(OH)₁₉Br₈ by a traditional hydrothermal method. The X-ray diffraction (XRD) results of Gd₃Cu₉(OH)₁₉Br₈ reveal that the Cu²⁺ ions form a two-dimensional Kagome lattice and Gd³⁺ ions are located in the center of hexagonal hole in the Kagome layer. The magnetic ground state and magnetocaloric effect have been studied by the magnetic susceptibility, magnetization and specific heat measurements. No magnetic transition is observed as the temperature down to 2 K, accompanying with a small value of Weiss temperature. A paramagnetic-like state is expected at 2 K in this system, different from the magnetic behavior of LnCu₃(OH)₆Cl₃ (Ln = rare earth ions) reported previously.^17,18 This peculiar magnetic phenomenon can be attributed to a significant influence of Gd³⁺ ions on the Cu-Kagome lattice.

Experimental details section

Synthesis

Gd₃Cu₉(OH)₁₉Br₈ was synthesized by a traditional hydrothermal method. After several iterations of experiment, high-quality single crystals of Gd₃Cu₉(OH)₁₉Br₈ were grown from a mixture of 0.4514 g Gd(NO₃)₃·6H₂O (1 mmol), 0.7248 g Cu(NO₃)₂ (3 mmol), 0.7203 g NaBr (7 mmol) and 1 ml deionized water. All the starting chemical reactants were analytical grade purity and used as-received without any further purification. These starting materials were sequentially added into a 25 ml Teflon-lined and stirred thoroughly. The Teflon liner was sealed in a stainless steel vessel and heated at 503 K for 3 days, then cooled to room temperature for 3 days. The green single crystals with hexagonal shape (maximum size ≈ 1.0 mm in diameter and 0.2 mm in thickness) were obtained by washing with deionized water.

Crystal structure and thermal analysis

The crystal structure of Gd₃Cu₉(OH)₁₉Br₈ were checked by powder X-ray diffraction at room temperature. The relative Rietveld powder diffraction profile fitting software FULLPROF was used to refine the crystal structure by compared with Y₃Cu₉(OH)₁₉Cl₈.¹⁶ Thermogravimetric analysis of Gd₃Cu₉(OH)₁₉Br₈ was performed in the TA TGA5500 instruments under a nitrogen atmosphere with a heating rate of 10 K min⁻¹. The samples were placed in an Al₂O₃ crucible and heated from room temperature to 1173 K.

Magnetic and specific heat measurements

The magnetic properties were measured using the superconducting quantum interference device vibrating sample magnetometer (SQUID-VSM; Quantum Design). The single crystals were placed in a quartz sample holder. Before each measurement, the samples were zero-field cooled from 300 K to the desired temperature. Specific heat in the temperature range from 2 to 30 K was measured using the relaxation method on a Physical Property Measurement System (PPMS; Quantum Design).

Results and discussion

Crystal structure

Fig. 1 shows the Rietveld refinement of powder XRD pattern for Gd₃Cu₉(OH)₁₉Br₈ by compared with isostructural Y₃Cu₉(OH)₁₉Cl₈.¹⁶ The XRD analysis exhibits that Gd₃Cu₉(OH)₁₉Br₈ crystallizes in trigonal crystal system with space group R3̄ (no. 148). The unit cell parameters of Gd₃Cu₉(OH)₁₉Br₈ are a = b = 11.6525(2) Å and c = 17.9962(1) Å. The refined atomic coordinates are shown in Table 1. Compared with GdCu₃(OH)₆Cl₃ and YCu₃(OH)₆Br₂[Br_x(OH)_1−x] (x ≈ 0.51), the crystal symmetry of Gd₃Cu₉(OH)₁₉Br₈ reduces and the size of unit cell becomes larger.^15,17 In an asymmetric unit, there are two Gd atoms, two Cu atoms, four O atoms and two Br atoms. Cu atoms have two independent crystallographic sites. Each Cu²⁺ ion was surrounded by four O²⁻ ions and two Br⁻ ions with Cu–O bond lengths ranging from 1.84(3) to 2.23(4) Å and Cu–Br bond lengths ranging from 2.866(7) to 2.902(13) Å, forming a distorted [CuO₄Br₂] octahedron. Gd atoms have two independent crystallographic sites, among them Gd1 is coordinated by seven atoms, forming a [GdO₇] polyhedron with Gd–O bond lengths ranging from 2.301(6) to 2.36(19) Å, while Gd2 is coordinated by six oxygen atoms and two bromine atoms, forming a [GdO₆Br₂] polyhedron with the identical Gd–O bond length of 2.52(4) Å and Gd–Br bond length of 2.887(11) Å.

Fig. 1 Rietveld refinements of XRD pattern for Gd₃Cu₉(OH)₁₉Br₈. The green vertical bars represent the expected Bragg reflection positions. The blue lines indicate the difference between the experimental and calculated data. The inset shows a picture of a 1 × 1 × 0.2 mm³ sized crystal.

Table 1 The refined atomic coordinates of Gd₃Cu₉(OH)₁₉Br₈

Atom	Wyckoff position	x/a	y/b	z/c
Cu(1)	18f	0.6641(10)	0.8244(16)	0.5022(4)
Cu(2)	9d	0.5000	1.0000	0.5000
Gd(1)	6c	0.3333	0.6667	0.5388(3)
Gd(2)	3b	1.0000	1.0000	0.5000
Br(1)	18f	0.6616(12)	0.9953(14)	0.6187(1)
Br(2)	6c	1.0000	1.0000	0.3396(6)
O(1)	3a	0.3333	0.6667	0.6667
O(2)	18f	0.793(4)	0.797(4)	0.5439(8)
O(3)	18f	0.529(15)	0.658(16)	0.559(4)
O(4)	18f	0.490(5)	0.842(5)	0.4671(11)

---

Fig. 2(a) and (b) show the two-dimensional (2D) structure of Gd₃Cu₉(OH)₁₉Br₈ viewed along the ab plane and c axis, respectively. The [CuO₄Br₂] octahedra are connected with each other by edge-sharing, forming a slight distorted 2D Kagome lattice along the ab plane. Within ab plane, the direct spatial distances between the two neighboring Cu²⁺ ions are 3.274(8) Å, 3.392(11) Å and 3.429(8) Å. For each layer, the Gd³⁺ ions are located in the central position of hexagonal hole in the Cu-Kagome lattice. Whereas, the Gd³⁺ ions are not coplanar with the Cu-Kagome layer, when viewed along the ab plane. Fig. 2(c) exhibits the magnetic topological structure composed by Cu²⁺ and Gd³⁺ ions by removing the nonmagnetic ions. The Cu-sublattice and Gd-sublattice overlap and form a 2D magnetic triangular lattice.

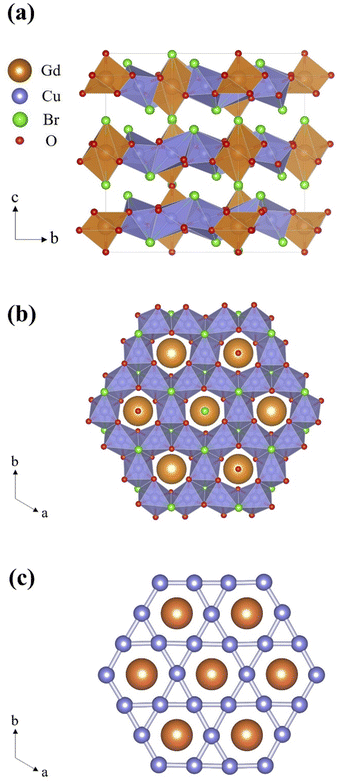Fig. 2 Two-dimensional layered structure of Gd₃Cu₉(OH)₁₉Br₈ viewed along the ab plane (a) and c axis (b). (c) Magnetic topological structure formed by Cu²⁺ and Gd³⁺ ions.

Thermal analysis

The thermogravimetric analysis can be used to investigate the thermal stability of Gd₃Cu₉(OH)₁₉Br₈. Fig. 3 exhibits the thermogravimetric (TG) and the corresponding differential of thermogravimetric (DTG) curves from room temperature to 1173 K. The TG curve can be divided into two main stages, similar to that of YCu₃(OH)₆Br₂[Br_x(OH)_1−x] (x ≈ 0.51).¹⁵ Below 600 K, Gd₃Cu₉(OH)₁₉Br₈ is found to be stable. With increasing temperature to 622 K, the first loss of mass starts, then a plateau can be observed between 700 and 763 K. The first mass loss is 17.44% from 622 K to 700 K, which is close to the calculated value 16.50% for the removal of 9.5 water molecules and two bromine ions per formula. The second step occurred from 763 K to 996 K with a mass loss of 38.56%, which can be attributed to the volatilization of two GdBr₃ molecules per formula with a theoretical value of 39.57% in Gd₃Cu₉(OH)₁₉Br₈. The final residuals of thermal analysis are not further characterized because the residuals were melted with the bucket.

Fig. 3 The TG and DTG curves of Gd₃Cu₉(OH)₁₉Br₈ measured from room temperature to 1173 K.

Magnetic properties

Fig. 4(a) and (d) show the temperature-dependent zero-field-cooled (ZFC) heating and field-cooled (FC) magnetic susceptibility curves measured at 0.1 T for magnetic fields perpendicular (χ_⊥) and parallel (χ_∥) to the crystallographic c axis, respectively. With decreasing temperature to 2 K, the susceptibility increases gradually and no obvious magnetic transition is observed at two field-directions. The inverse of susceptibility above 50 K can be well fitted by Curie–Weiss law. The deduced Weiss temperatures are θ_⊥ = −2.79(2) K and θ_∥ = −3.99(4) K, respectively. Compared with Y₃Cu₉(OH)₁₉Br₈, the much smaller absolute value of Weiss temperature existed in Gd₃Cu₉(OH)₁₉Br₈ indicates a net weak AFM spin coupling in this compound, suggesting that the existence of Gd³⁺ ions play significant influence on magnetism. The slight difference between χ_⊥ and χ_∥ demonstrate a weak magnetic anisotropy of this compound. The calculated effective magnetic moments are μ^⊥_eff = 15.39 μ_B and μ^∥_eff = 15.95 μ_B. The values are close to the theoretical effective moment 14.70 μ_B of Gd₃Cu₉(OH)₁₉Br₈ estimated by . Fig. 4(b) and (e) exhibit the ZFC and FC curves measured at 0.01 T, 0.02 T and 0.05 T below 50 K. No ZFC-FC splitting is observed, which excludes the existence of ferromagnetic moment and indicates a paramagnetic state at 2 K.

Fig. 4 The temperature dependence of magnetic susceptibility curves measured at 0.1 T with field perpendicular (a) and parallel (d) to the c axis, as well as the corresponding inverse susceptibility and Curie–Weiss fit. The ZFC and FC curves below 50 K measured at 0.01 T, 0.02 T and 0.05 T for field perpendicular (b) and parallel (e) to the c axis, respectively. Magnetic hysteresis loops and Brillouin fitting at 2 K and 300 K for field perpendicular (c) and parallel (f) to the c axis, respectively.

Fig. 4(c) and (f) show the magnetic hysteresis loops measured at 2 K and 300 K for applied magnetic fields perpendicular and parallel to c axis, respectively. The magnetization increases smoothly with the increasing magnetic field and no field hysteresis is observed. As the increase of applied magnetic field, these weakly coupled spins can easily rotate towards the direction of magnetic field. The magnetization curves seem to saturate with a magnetic moment of 25 μ_B per f.u. at 7 T and 2 K, which is smaller than the expected saturated magnetic moment 30 μ_B per f.u. (Gd³⁺: S = 7/2, g = 2; Cu²⁺: S = 1/2, g = 2). The dashed lines represent the fitting curves of Brillouin function, 3B_7/2(y) + 9B_1/2(y), for isolated Gd³⁺ and Cu²⁺ ions. At 2 K, the experimental curves do not follow the Brillouin function. The difference between experimental and fitting data should originate from the existence of AFM spin correlation in this system.

Specific heat

Fig. 5(a) shows the temperature dependence of specific heat between 2 K and 30 K measured under different applied magnetic fields perpendicular to the crystallographic c axis. No λ anomaly is observed in zero-field specific heat curve, in agreement with the susceptibility data and further supporting the absence of magnetic order at low temperatures. As the decrease of temperature, the zero-field specific heat data exhibits an upturn below 3 K. With increasing magnetic field, a broad peak occurred and moved to high temperature gradually. Such behavior can be attributed to the formation of short-range spin correlation at low temperature. In order to obtain more information on the nature of magnetic ground state, the contribution of magnetic specific heat C_mag is calculated by subtracting the phonon contribution from the total specific heat data. The phonon contribution is estimated by fitting the zero-field specific heat data above 10 K to the polynomial formula C_bg = aT³ + bT⁵ + cT⁷ with a = 9.56 × 10⁻³ J K⁻⁴ mol⁻¹, b = −9.20 × 10⁻⁶ J K⁻⁶ mol⁻¹, and c = 3.67 × 10⁻⁹ J K⁻⁹ mol⁻¹. The temperature dependence of magnetic entropy S_mag is shown in Fig. 5(b). The calculated values of magnetic entropy are 9.88 J mol⁻¹ K⁻¹ at H = 0 T and 44.69 J mol⁻¹ K⁻¹ at H = 7 T, which are much smaller than the theoretically maximum value of magnetic entropy 103.73 J mol⁻¹·K⁻¹ for the compound, indicating the existence of spin correlation below 2 K.

Fig. 5 (a) Temperature dependence of specific heat at different applied magnetic fields. (b) The magnetic specific heat and magnetic entropy from 2 to 30 K.

Magnetocaloric effect

Materials with giant magnetocaloric effect can be used to achieve magnetic refrigeration technology with the advantage of higher energy efficiency and environment friendly.^19,21,22 The rare-earth Gd³⁺ ions have a large spin quantum number and no orbital angular moment, which benefits for realizing a large magnetocaloric effect in Gd-based compounds.^24–28 In Gd₃Cu₉(OH)₁₉Br₈, no magnetic transition and a paramagnetic-like behavior are observed at low temperature. Under the applied magnetic field, these weakly coupled spins can easily rotate towards the direction of magnetic field, accompanying with a considerable magnetic entropy change in this process. The isothermal magnetic entropy change ΔS_M and adiabatic temperature change ΔT_ad with changing magnetic field are two main parameters to character the magnetocaloric effect.

In order to calculate the magnetic entropy change ΔS_M, a series of isothermal magnetization curves are measured from 2 to 40 K, as shown in Fig. 6(a). With increasing temperature, the magnitude and curvature of the magnetization curves decrease gradually. Integrating the Maxwell's equation , the temperature dependence of −ΔS_M was obtained and shown in Fig. 6(b). With decreasing temperature, the value of −ΔS_M increases monotonously. At 2 T, the maximum value of −ΔS_M reaches 23.78 J kg⁻¹ K⁻¹ and 26.04 J kg⁻¹ K⁻¹ for the field changes of 0–3 T and 0–7 T, respectively. Fig. 7 exhibits the temperature dependence of Adiabatic temperature change ΔT_ad, calculated by the equation 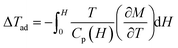. With decreasing temperature, the value of ΔT_ad increases gradually and reaches maximum around 5 K for a field change of 0–1 T. With increasing magnetic field, the maximum values of ΔT_ad reach 7.72 K and 13.79 K under the field changes of 0–3 T and 0–7 T, respectively.

Fig. 6 (a) Magnetization curves measured at different temperatures. (b) Temperature dependence of magnetic entropy change −ΔS_M.

Fig. 7 Temperature dependence of adiabatic temperature change ΔT_ad.

Table 2 shows the maximum values of magnetic entropy change −ΔS_M and adiabatic temperature change ΔT_ad of Gd₃Cu₉(OH)₁₉Br₈, compared with some other Gd-based compounds.^29–32 As shown in Table 2, the obtained values of Gd₃Cu₉(OH)₁₉Br₈ are much larger than the values of other Gd-based compounds, indicating this compound can be considered as a potential magnetic refrigerant material at low temperature. The enhancement of magnetocaloric effect in frustrated systems with pyrochlore and Kagome lattice have been predicated in theory and further confirmed in experiment.^33,34 The frustrated framework can promote the disorder of spin at low temperature and release a considerable magnetic entropy change under the applied magnetic field.

Table 2 A comparison of magnetocaloric effect between Gd₃Cu₉(OH)₁₉Br₈ and some Gd-based oxides

Materials	−ΔS^maxM (J kg^−1 K^−1)			ΔT^maxad (K)		Ref.
	1 T	3 T	7 T	5 T	7 T
GdCrO3	∼2.5	∼18	39.97	∼13	19.12	29
Gd3BWO9	9.22	36.75	54.80	—	9.16	30
GdMnO3	1.60	6.80	15.40	∼3.8	∼5.3	31
GdCo3B2	∼2.8	—	11.6	∼5.2	∼6.4	32
GdAlO3	∼1.5	∼8	∼35	∼4.3	∼5.5	31
Gd3Cu9(OH)19Br8	4.87	18.27	26.04	11.14	13.79	This work

---

Discussion

The analyses of crystal structure reveal that the crystal symmetry of Gd₃Cu₉(OH)₁₉Br₈ is isostructural with Y₃Cu₉(OH)₁₉Cl₈.¹⁶ By replaced the nonmagnetic Y³⁺ ions into Gd³⁺ ions, there are three kinds of magnetic coupling existing in Gd₃Cu₉(OH)₁₉Br₈, including the Cu–Cu (3d–3d) spin coupling, Gd–Cu (4f–3d) spin coupling and Gd–Gd (4f–4f) spin coupling. Among them, the direct spatial distances between two neighboring Gd³⁺ ions are 6.7367(6) Å and 6.8710(16) Å with the exchange path Gd–O–Cu–O–Gd in ab plane. Along the c axis, the direct spatial distances between two neighboring Gd³⁺ ions is 4.602(8) Å with the exchange path Gd–O–Gd along the c axis. Compared with the super-exchange Cu–Cu spin coupling [Cu–O–Cu exchange path] and Gd–Cu spin coupling [Cu–O–Gd exchange path], the spin coupling between two neighboring Gd³⁺ ions should be relatively weaker. Thus, the dominant spin correlation in Gd₃Cu₉(OH)₁₉Br₈ can be attributed to the Cu–Cu (3d–3d) spin coupling and Gd–Cu (4f–3d) spin coupling.

Firstly, we consider the Cu–Cu (3d–3d) spin coupling. Within the Kagome layer, the direct spatial distances between two neighboring Cu²⁺ ions are d₁ = 3.274(8) Å with the corresponding Cu–O–Cu bond angle 107.5(7)°, d₂ = 3.392(11) Å with the corresponding Cu–O–Cu bond angle 120.8(5)° and d₃ = 3.429(8) Å with the corresponding Cu–O–Cu bond angle 112.8(5)°. According to the Goodenough–Kanamori rules, the magnetic coupling between two neighboring Cu²⁺ ions is AFM.^35–37 As reported in Y₃Cu₉(OH)₁₉Cl₈, the strong AFM interaction is observed due to the frustrated Cu-Kagome lattice.¹⁶ However, the magnetic analyses of Gd₃Cu₉(OH)₁₉Br₈ exhibit a small value of Weiss temperature and suggest a weak spin coupling in this system, which is inconsistent with the strong AFM interaction derived from the Cu-Kagome lattice.

Considering the existence of Gd³⁺ ions, the magnetic topological lattice of title compound is a triangular lattice constituted by magnetic Cu²⁺ and Gd³⁺ ions. Thus, a considerable Gd–Cu (4f–3d) spin coupling exists in this system and plays significant influence on the magnetic ground state. The influence of 4f–3d interaction on magnetism and magnetocaloric effect is an open subject.^38–40 For the light lanthanides system LnCu₃(OH)₆Cl₃ (Ln = Nd and Sm), the influence of lanthanide ions on the magnetism of Cu-Kagome lattice is relatively small. These compounds undergo AFM order below 20 K.¹⁸ For the heavy lanthanides systems LnCu₃(OH)₆Cl₃ (Ln = Gd, Tb, Dy), the heavy lanthanides ions may modulate Dzyaloshinskii–Moriya (DM) interaction and further induce a ferromagnetic correlation, which mask the strong AFM interaction originated from the Cu-Kagome lattice, but do not prevent the AFM order at low temperature.¹⁷ In Gd₃Cu₉(OH)₁₉Br₈, no obvious magnetic transition is observed in magnetic susceptibility and specific heat data. The small value of Weiss temperature indicates that the 4f–3d interaction is probably ferromagnetic and compete with the AFM interaction between Cu²⁺ ions. The existence of 4f–3d interactions suppress the occurrence of AFM order and enhance the spin disorder at low temperature in our compound. These weakly coupled spins can easily rotate towards the direction of magnetic field and generate a considerable magnetic entropy under a small magnetic field.

Conclusions

In this work, we reported the structure, magnetism and magnetocaloric effect of Gd₃Cu₉(OH)₁₉Br₈. The basic magnetic lattice of Gd₃Cu₉(OH)₁₉Br₈ is a two-dimensional triangular lattice formed by magnetic Cu²⁺ and Gd³⁺ ions, in which the Cu²⁺ ions constitute a Kagome lattice and Gd³⁺ ions are located in the center of the hexagonal hole. No magnetic transition is observed in magnetic susceptibility curve, which is further confirmed in zero-field specific heat curve. Compared with isostructural Y₃Cu₉(OH)₁₉Cl₈, the strong spin frustration in the Cu-Kagome lattice is obviously suppressed and a paramagnetic-like ground state is observed in Gd₃Cu₉(OH)₁₉Br₈ due to the existence of Gd³⁺ ions. Under the applied magnetic field, these weakly coupled spins rotate towards the direction of applied magnetic field and yield a considerable MCE. Thus, Gd₃Cu₉(OH)₁₉Br₈ can be considered as a potential candidate for magnetic refrigeration at low temperature.

Author contributions

Dong-Er Cheng synthesized samples and data analysis. Yi-Yan Wang helped experiments and interpreted data. Yan Sun, Hui Liang, Dan-Dan Wu and Qiuju Li funded this work. Xuefeng Sun supervised and reviewed this work. Xiao-Yu Yue performed conceptualization and wrote the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant No. 12104010, U1832209, 11874336, 11904003, 52102333 and 12104011) and the Natural Science Foundation of Anhui Province (Grant No. 1908085MA09 and 2108085MA16).

References

1. M. J. P. Gingras and P. A. McClarty, Rep. Prog. Phys., 2014, 77, 056501.
2. J. A. Mydosh, Rep. Prog. Phys., 2015, 78, 052501.
3. P. W. Anderson, Science, 1987, 235, 1196.
4. O. Tanaka, Y. Mizukami, R. Harasawa, K. Hashimoto, K. Hwang, N. Kurita, H. Tanaka, S. Fujimoto, Y. Matsuda, E. G. Moon and T. Shibauchi, Nat. Phys., 2022, 18, 429.
5. L. Balents, Nature, 2010, 464, 199–208.
6. M. Yang, S. Y. Zhang, W. B. Guo, Y. Y. Tang and Z. Z. He, Dalton Trans., 2015, 44, 15396.
7. J. S. Helton, K. Matan, M. P. Shores, E. A. Nytko, B. M. Bartlett, Y. Yoshida, Y. Takano, A. Suslov, Y. Qiu, J. H. Chung, D. G. Nocera and Y. S. Lee, Phys. Rev. Lett., 2007, 98, 107204.
8. T. H. Han, J. S. Helton, S. Y. Chu, D. G. Nocera, J. A. Rodriguez-Rivera, C. Broholm and Y. S. Lee, Nature, 2012, 492, 406–410.
9. Z. Feng, Z. Li, X. Meng, W. Yi, Y. Wei, J. Zhang, Y. C. Wang, W. Jiang, Z. Liu, S. Li, F. Liu, J. Luo, S. Li, G. Q. Zheng, Z. Y. Meng, J. W. Mei and Y. Shi, Chin. Phys. Lett., 2017, 34, 077502.
10. M. Rozenberg and R. Chitra, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 132406.
11. Y. Y. Huang, Y. Xu, L. Wang, C. C. Zhao, C. P. Tu, J. M. Ni, L. S. Wang, B. L. Pan, Y. Fu, Z. Hao, C. Liu, J. W. Mei and S. Y. Li, Phys. Rev. Lett., 2021, 127, 267202.
12. W. Sun, Y. X. Huang, S. Nokhrin, Y. Pan and J. X. Mi, J. Mater. Chem., 2016, 4, 8772.
13. A. Zorko, M. Pregelj, M. Klanjšek, M. Gomilšek, Z. Jagličić, J. S. Lord, J. A. T. Verezhak, T. Shang, W. Sun and J. X. Mi, Phys. Rev. B, 2019, 99, 214441.
14. A. Zorko, M. Pregelj, M. Gomilšek, M. Klanjšek, O. Zaharko, W. Sun and J. X. Mi, Phys. Rev. B, 2019, 100, 144420.
15. X. H. Chen, Y. X. Huang, Y. Pan and J. X. Mia, J. Magn. Magn. Mater., 2020, 512, 167066.
16. P. Puphal, M. Bolte, D. Sheptyakov, A. Pustogow, K. Kliemt, M. Dressel, M. Baenitz and C. Krellner, J. Mater. Chem. C, 2017, 5, 2629.
17. Y. Fu, L. L. Huang, X. F. Zhou, J. Chen, X. Y. Zhang, P. Y. Chen, S. M. Wang, C. Liu, D. P. Yu, H. F. Li, L. Wang and J. W. Mei, Chin. Phys. B, 2021, 30, 100601.
18. W. Sun, Y. X. Huang, Y. Pan and J. X. Mi, Dalton Trans., 2017, 46, 9535.
19. D. Matsunami, A. Fujita, K. Takenaka and M. Kano, Nat. Mater., 2015, 14, 73.
20. L. H. Yin, J. Yang, P. Tong, X. Luo, W. H. Song, J. M. Dai, X. B. Zhu and Y. P. Sun, Appl. Phys. Lett., 2017, 110, 192904.
21. V. Franco, J. S. Bláquez, J. J. Ipus, J. Y. Law, L. M. Moreno-Ramíez and A. Conde, Prog. Mater. Sci., 2018, 93, 112.
22. J. R. Gómez, R. F. Garcia, A. D. M. Catoira and M. R. Gómez, Renewable Sustainable Energy Rev., 2013, 17, 74.
23. J. K. Murthy, K. D. Chandrasekhar, S. Mahana, D. Topwal and A. Venimadhav, J. Phys. D: Appl. Phys., 2015, 48, 355001.
24. D. D. Lei, Z. W. Ouyang, X. Y. Yue, L. Yin, Z. X. Wang, J. F. Wang, Z. C. Xia and G. H. Rao, J. Appl. Phys., 2018, 124, 233904.
25. A. Midya, N. Khan, D. Bhoi and P. Mandal, J. Appl. Phys., 2014, 115, 17E114.
26. Y. Y. Tang, W. B. Guo, S. Y. Zhang, M. Yang, H. P. Xiang and Z. Z. He, Dalton Trans., 2015, 44, 17026.
27. F. S. Guo, Y. C. Chen, J. L. Liu, J. D. Leng, Z. S. Meng, P. Vrábel, M. Orendáč and M. L. Tong, Chem. Commun., 2012, 48, 12219.
28. M. Balli, B. Roberge, P. Fournier and S. Jandl, Crystals, 2017, 7, 44.
29. S. Mahana, U. Manju and D. Topwal, J. Phys. D: Appl. Phys., 2018, 51, 305002.
30. L. L. Li, X. Y. Yue, W. J. Zhang, H. Bao, D. D. Wu, H. Liang, Y. Y. Wang, Y. Sun, Q. J. Li and X. F. Sun, Chin. Phys. B, 2021, 30, 077501.
31. S. Mahana, U. Manju and D. Topwal, J. Phys. D: Appl. Phys., 2017, 50, 035002.
32. L. W. Li, K. Nishimura, H. Igawa and D. X. Huo, J. Alloys Compd., 2011, 509, 4198.
33. M. Semjan and M. Žukovic, Acta Phys. Pol., A, 2020, 137, 622.
34. R. K. Li, G. J. Li and C. Greaves, J. Mater. Chem. A, 2018, 6, 5230.
35. J. B. Goodenough, Phys. Rev., 1955, 100, 564.
36. J. Kanamori, J. Phys. Chem. Solids, 1959, 10, 87–98.
37. W. Geertsma and D. Khomskii, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 3011.
38. E. Palacios, C. Tomasi, R. Sáez-Puche, A. J. Dos santos-García, F. Fernández-Martínez and R. Burriel, Phys. Rev. B, 2016, 93, 064420.
39. A. A. Wagh, K. G. Suresh, P. S. Anil Kumar and S. Elizabeth, J. Phys. D: Appl. Phys., 2015, 48, 135001.
40. M. Das, S. Roy and P. Mandal, Phys. Rev. B, 2017, 96, 174405.

---