Open Access Article
Open Access ArticleMembrane tension controls the phase equilibrium in fusogenic liposomes
Laura Maria Schmitta,
Georg Dreissena,
Rejhana Kolasinaca,
Agnes Csiszára and
Rudolf Merkel *b
*b
aForschungszentrum Julich, Institute of Biological Information Processing 2: Mechanobiology, Julich, Germany
bForschungszentrum Julich, Institute of Biological Information Processing 2: Mechanobiology, Julich, Germany. E-mail: r.merkel@fz-juelich.de; Fax: +49 2461 613907; Tel: +49 2461 613080
First published on 24th August 2022
Abstract
Fusogenic liposomes have been widely used for molecule delivery to cell membranes and cell interior. However, their physicochemical state is still little understood. We tested mechanical material behavior by micropipette aspiration of giant vesicles from fusogenic lipid mixtures and found that the membranes of these vesicles are fluid and under high mechanical tension even before aspiration. Based on this result, we developed a theoretical framework to determine the area expansion modulus and membrane tension of such pre-tensed vesicles from aspiration experiments. Surprisingly high membrane tension of 2.1 mN m−1 and very low area expansion modulus of 63 mN m−1 were found. We interpret these peculiar material properties as the result of a mechanically driven phase transition between the usual lamellar phase and an, as of now, not finally determined three dimensional phase of the lipid mixture. The free enthalpy of transition between these phases is very low, i.e. on the order of the thermal energy.
1 Introduction
Liposomes with extraordinarily high fusion potential were described first by Csiszár et al. ten years ago.1 They are formed by a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of a cationic lipid and a neutral phospholipid and the addition of a few percent of an aromatic compound.1,2 Owing to their unique ability to rapidly fuse with cell membranes they have been widely used for the delivery of molecules to cells.3–5 However, their physicochemical properties remain largely unexplored. In a first attempt to clarify the structure of these unique lipid particles Kolasinac et al. used small angle neutron scattering.6 They report coexistence of a usual lamellar phase (i.e. a bilayer) with ellipsoidal inclusions of a size of about 20 nm and unknown inner structure whereas the membranes of usual phospholipid bilayers are exclusively in the lamellar phase.6 Due to this distinction in structure, unusual physicochemical properties of fusogenic liposomes are expected.
1 mixture of a cationic lipid and a neutral phospholipid and the addition of a few percent of an aromatic compound.1,2 Owing to their unique ability to rapidly fuse with cell membranes they have been widely used for the delivery of molecules to cells.3–5 However, their physicochemical properties remain largely unexplored. In a first attempt to clarify the structure of these unique lipid particles Kolasinac et al. used small angle neutron scattering.6 They report coexistence of a usual lamellar phase (i.e. a bilayer) with ellipsoidal inclusions of a size of about 20 nm and unknown inner structure whereas the membranes of usual phospholipid bilayers are exclusively in the lamellar phase.6 Due to this distinction in structure, unusual physicochemical properties of fusogenic liposomes are expected.
Seminal experiments on basic physicochemical properties and processes of ordinary lipid membranes have been performed on Giant Unilamellar Vesicles (GUVs).7–10 These micron-sized structures are closed shells formed by single lipid bilayers. Their surface area is mostly determined by the number of lipid molecules within the membrane. Such GUVs can be conveniently studied by light microscopy and micromanipulation. An overview of the present state of this dynamic research field can be found in the book by Dimova and Marques.11
Here, we focus on mechanical material parameters. For a graceful and enlightening review by a pioneer of the field see.12 Because the thickness of biomembranes is negligible compared to the overall size of vesicles, their mechanics is best described by membrane theory where mechanical stress (units force per area) is replaced by membrane tension, τ, (units force per length) and the usual linear elastic constants (Young's modulus and Poison's ratio) by bending rigidity, kc, and area expansion modulus, kA. As the bilayers of cell membranes are in the fluid phase, they exhibit no rigidity against in plane shear. We will show evidence that the same holds also for fusogenic liposomes.
Typical phospholipid membranes in the fluid phase exhibit area expansion moduli of about 250 mN m−1 and bending rigidities in the range from 10 kBT to 40 kBT.10,12–14 Because water readily permeates biomembranes while hydrophilic solutes are retained, the volume of GUVs is determined by the osmotic pressure difference between the enclosed medium and the external medium which balances against the Laplace pressure caused by mechanical tension of the curved membrane shell. Thus, volume can be regulated by changing the osmolarity of the external medium. Upon osmotic deflation, membrane tension is reduced to extremely low values of some few μN m−1. As a consequence, vesicle shapes undergo thermally driven fluctuations, often described as flickering.7,10,15,16 Alternatively, flickering is induced by even modestly increased temperature due to the high thermal expansivity of lipid bilayers.17,18 When such flaccid GUVs are aspirated by a micropipette, their fractional area expansion can be reliably determined as a function of the acting membrane tension.8,14,19 In the low tension regime, thermally driven fluctuations are progressively suppressed or flattened out by tension whereas in the high tension regime the membrane area proper, that is the distance between individual lipid molecules, is increased. Therefore the bending rigidity is determined from the low tension regime of the aspiration curve and the area expansion modulus from the high tension regime. This approach was pioneered by the group of Evan Evans.8,12,14 Later work pointed out complications that arose due to the different possibilities to define the seemingly simple quantity “membrane tension”.20 Nevertheless, in-depth theoretical analyses validated the original approach.21,22 With respect to our results, it is noteworthy that initial aspiration of vesicles required extremely low suction pressures in all these experiments.
The present work focuses on the mechanical properties of large, unilamellar vesicles from a fusogenic lipid mixture, also called FL-GUVs. Even though the membrane of FL-GUVs is fluid, there are marked differences to usual GUVs with fluid membranes. On one hand, the nanosized inclusions observed by Kolasinac et al.6 point at the coexistence of two different thermodynamic phases. On the other hand, we will show indications for significant membrane tension even after osmotic or thermal “deflation”. This unusual property necessitated to adapt the well-established frame work for the determination of membrane mechanical properties by micropipette aspiration.
Starting from experimental observations and the hypothesis that the number of osmotically active molecules within a given FL-GUV is constant, we analyze area expansion and volume change of a FL-GUV aspirated by a micropipette and derive equations to determine area expansion modulus as well as tension of the free vesicle. Along the way, we justify the choice of linear elastic area expansion as material law. Analyzing experimental results, we find unusually small area expansion moduli and surprisingly high tension which we interpret as the result of a mechanically driven phase transition.
2 Materials and Methods
2.1 Chemicals
Lipids 1,2-dioleoyl-3-trimethylammonium-propane (chloride salt) (DOTAP), 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine (DOPE), 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine-N-[methoxy(polyethylene glycol)-350] (DOPE-PEG350), 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine-N-[methoxy(polyethylene glycol)-2000] (DOPE-PEG2000), 1,2-dioleoyl-sn-glycero-3-phosphoethanol-amine-N-[(dipyrrometheneboron difluoride)butanoyl] (TF-DOPE), 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC), and 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC) were purchased from Avanti Polar Lipids, Inc. (Alabaster, AL, USA). Avidin (from egg white) and bovine serum albumin (fraction V) for coating were purchased from Merck KGaA (Darmstadt, Germany). Sucrose and glucose were obtained from Carl Roth (Karlsruhe, Germany). N-2-Hydroxyethylpiperazine-N-2 ethane sulfonic acid (HEPES) was bought at VWR (Darmstadt, Germany). All chemicals were used without further purification. Ultra pure water was produced by ion exchange (Milli-Q Gradient A10, Merck Millipore, Darmstadt, Germany).2.2 Vesicle preparation
For the preparation of FL-GUVs DOTAP, DOPE, and TF-DOPE were dissolved in chloroform (Merck Millipore, Darmstadt, Germany) at a concentration of 10 mg mL−1 and mixed at a mass ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1 (m m−1). Lipid solution (15 μL) was deposited on indium tin oxide (ITO) coated glass slides. Electroswelling was performed at 2.5 °C as follows. The dried plates (15 min under vacuum) were mounted in a Teflon chamber containing 2 mL of 150 mM sucrose solution. The distance between the plates was 1 mm. Vesicles were swollen applying an alternating electric voltage of 2.1 V (peak to peak) at 800 Hz for 3 h and kept at 4 °C until the measurement.
0.1 (m m−1). Lipid solution (15 μL) was deposited on indium tin oxide (ITO) coated glass slides. Electroswelling was performed at 2.5 °C as follows. The dried plates (15 min under vacuum) were mounted in a Teflon chamber containing 2 mL of 150 mM sucrose solution. The distance between the plates was 1 mm. Vesicles were swollen applying an alternating electric voltage of 2.1 V (peak to peak) at 800 Hz for 3 h and kept at 4 °C until the measurement.
For some control experiments 1.25% (per mass of total lipid) of DOPE-PEG were added to the lipid mix. GUVs were prepared as described before besides that drying of was performed over night. GUVs from DOPC stained with 1% (m m−1) TF-DOPE were produced by electroswelling at 1.5 V, 10 Hz, and room temperature. All other parameters were kept identical.
Small unilamellar vesicles for differential scanning calorimetry (DSC) were prepared by the hydration method. Lipids dissolved in chloroform were mixed at the desired ratio and disposed in glass vials. Solvent was removed by drying under reduced pressure (30 min). For FL the dry lipid film was hydrated by 300 mM sucrose in water; for DPPC 20 mM HEPES was used instead. After 15 min the solution was vortexed. Final lipid concentration was 10 mg mL−1.
2.3 Differential scanning calorimetry
Samples were filled in dedicated vials from Hastelloy and inserted into a multi-cell differential scanning calorimeter (MC-DSC, TA instruments, New Castle, DE, USA). Thermograms were recorded at a heating rate of 1 °C min−1 and corrected against a baseline measured on an identical, solvent-filled vial. Enthalpy and entropy of transition were determined by the manufacturer's software (NanoAnalyze 3.4.0).2.4 Fluctuation analysis
Giant unilamellar vesicles were prepared as described above and dispensed into a measurement chamber from acrylic glass filled with 150 mM glucose solution. A cover glass, passivated for 10 min with a 1 mg mL−1 solution of either avidin (for FL-GUVs) or bovine serum albumin (for GUVs from DOPC), formed the chamber bottom. Giant unilamellar vesicles were imaged by a confocal fluorescence microscope (LSM 710, Carl Zeiss microimaging, Jena, Germany) equipped with an EC PlanNeofluar 40/1.3 oil Ph3 lens (Zeiss). Excitation was 488 nm, emission was detected in the range from 490 nm to 539 nm. Image sequences were captured with focus on the equatorial plane (50–150 frames, total length 12 s to 44 s, pinhole 1 Airy unit). Measurements were done after heating to 37 °C in the microscope incubator (type XL, Zeiss).Fluctuation amplitudes were characterized by the following routine implemented in Python (version 3.8). Each frame was first smoothed by a Gaussian kernel (width 3 pixel; pixel size 90 nm throughout). In the central step, the watershed algorithm (as implemented in the community-maintained image processing toolbox scikit-image version 0.19.0. dev0) was used on the gray scale image to separate inner and outer area. This algorithm needs one starting point for flooding in each of the final areas. For the outer area the upper left corner of the image was selected. For the inner area the smoothed image was intensity segmented (mean intensity as threshold) and the center of gravity of the resulting mask area was used as starting point. The resulting border line between inner and outer area was used as vesicle contour. For each frame, the distance of each point to the center of gravity of this contour was calculated and divided by the average distance. The variance of these normalized distances was determined for each time step and averaged over the whole image series.
2.5 Fluorescence recovery after photobleaching (FRAP)
Preparation for FRAP measurements was identical as for fluctuation analysis. The only exception was that 100 μL phosphate buffered saline (PBS, diluted with water to an osmolality of 150 mOsm kg−1) was added to the 1.5 mL glucose solution that filled the measurement chamber to promote weak adhesion of FL-GUVs to the avidin-covered glass. The same confocal laser scanning microscope was used equipped with a C-Apochromat 40×/1.2 W lens (Zeiss). Fluorescence was detected from 495 to 599 nm, detection pinhole 1 Airy unit. Excitation (1% laser power) and bleaching (100% laser power) were done with the built in argon ion laser (488 nm). Round regions at the bottom (radius r = 1.2 μm) were bleached and the average intensity in these regions recorded over time (10 points before bleaching, 40 afterwards, time increment 39.3 ms). Intensities were normalized by division with the average pre-bleach intensity. Diffusion constants were determined as proposed by Soumpasis.23 The time point of half-recovery, t1/2, was determined using linear interpolation between the neighboring measurement points and the diffusion constant, D, calculated via| D = 0.224r2/t1/2 | (1) |
2.6 Micropipette aspiration technique
Micropipettes were pulled from borosilicate glass capillaries (outer diameter 1 mm, inner diameter 0.5 mm; Hilgenberg, Malsfeld, Germany) using a pipette puller (model P-97, Sutter Instruments, Novato, CA, USA) and opened on a microforge where they were first inserted into a molten drop of glass solder and after cooling retracted whereupon the originally needle-shaped raw pipettes broke open into a cylindrical shape. For passivation the micropipette was filled with avidin solution (1 mg mL−1 for 10 min) using a hollow quartz capillary (Microfil MF28G, World Precision Instruments, Sarasota, FL, USA). In the next step, the micropipette was mounted in a three-axis micromanipulator (Narishige Scientific Instrument Lab, Tokyo, Japan) connected to a light microscope (Axiovert 200, Carl Zeiss Microimaging, Jena, Germany) equipped with a long distance lens (LD-Achroplan 40/0.6 korr, Carl Zeiss) and a metal-halide light source (X-cite 120, EXFO, Mississauga, Ontario, Canada). The micropipette was hydraulically connected to a height-adjustable water-reservoir for control of the aspiration pressure.24 The measurement chamber was from acrylic glass with cover slips on top and bottom. One side was open for micropipette access. The bottom cover slip was passivated with avidin (1 mg mL−1 for 10 min) and the chamber filled with 150 mM glucose solution. A small amount of vesicle solution was added and allowed to sediment for 10 min. Vesicle aspiration was observed with fluorescence microscopy (filter set 13, Carl Zeiss; CCD-camera sensicam qe, PCO, Kehlheim, Germany). Neutral aspiration pressure was found by observing vesicle motion during height adjustment of the reservoir. All geometric parameters were measured interactively using Fiji.252.7 Further software
Symbolic calculation and numerical evaluation of expressions was done with Maple (version 2020.2, Maplesoft, Waterloo Maple Inc., Waterloo, Ontario, Canada). Curve fitting was done with Maple, Igor Pro (Igor Pro 8, version 8.0.4.2, Wavemetrics, Lake Oswego, Oregon, USA) or Origin (2019 pro, version 9.60; Originlab Corp. Northampton, MA).3 Results and discussion
3.1 Thermal analysis
Fusogenic giant unilamellar vesicles (FL-GUVs) were successfully prepared in the cold and remained stable upon gentle warming up to room temperature. Because FL-GUVs could not be produced at room temperature or above, we expected the existence of a phase transition below room temperature. Therefore we used differential scanning calorimetry to search for transitions accompanied by changes in heat capacity, cf. Fig. 1. However, no clearly discernible transitions were found. For comparison we also measured DPPC in a weak buffer (20 mM HEPES) because the thermodynamics of this system is firmly established. These samples showed a pretransition at 35.5 °C (transition enthalpy 3.9 kJ mol−1, entropy 0.012 kJ mol−1 K−1) and a main transition at 41.5 °C (transition enthalpy 31.8 kJ mol−1, entropy 0.101 kJ mol−1 K−1), that is, a thermal behavior in full agreement with literature.26 | ||
| Fig. 1 Thermogram of fusogenic liposomes measured with differential scanning calorimetry (full line). For comparison to usual lipids DPPC in 20 mM HEPES is shown as well (dashed line). | ||
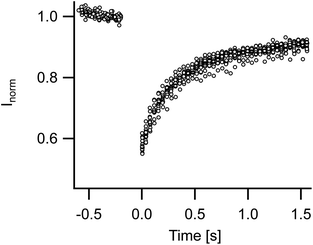
3.2 Membrane fluidity and undulations
Membrane fluidity of FL-GUVs was tested by FRAP. Measurements on 14 different vesicles gave very similar results with fast and almost complete recovery. The diffusion constant amounted to 1.5 μm2 s−1 (standard deviation 0.17 μm2 s−1), cf. Fig. 2. Because of the modest size of FL-GUVs (radius of about 5 μm), only a small spot (radius 1.2 μm) could be bleached. Under these conditions FRAP measurements are influenced by the finite resolution of the light microscope. Thus the true value might differ by some 20%, but the rapid diffusion and the high level of recovery clearly indicate a fluid state of the membrane.In the light microscope FL-GUVs always appeared as perfectly spherical objects. They frequently exhibited patches of higher fluorescence intensity but never showed any non-spherical forms or dynamic shape fluctuations. To quantify this observation we prepared GUVs from FL and from DOPC, respectively, and heated them to 37 °C. Shapes were recorded over 50 to 150 frames and analyzed by the algorithm described in Section 2. The variances of the normalized distances between border and center were significantly larger for DOPC vesicles (average over eight GUVs 29 10−5) as compared to FL-GUVs (average over five GUVs 6.7 10−5), cf. Fig. 3. A closer inspection of FL-GUV results showed that the remaining variance was not primarily caused by dynamic shape fluctuations but mostly by some bright inclusions that frequently occurred in FL-GUVs. Even osmotic deflation, which is a proven way to induce shape transformations and pronounced shape fluctuations for giant unilamellar vesicles from ordinary lipids, did not induce any visible shape fluctuations in FL-GUVs.
3.3 Micropipette aspiration
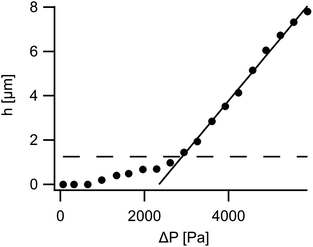
Micropipette aspiration of FL-GUVs turned out to be possible, albeit the pipette had to be changed after each lysis of an aspirated vesicle. A typical measurement is shown in Fig. 4. Compared to the aspiration of normal GUVs, see Fig. 5, remarkably high aspiration pressures were needed to form a visible dome in the pipette, cf. the micrographs in Fig. 4. In all experiments the aspirated length, h, as measured from the apex of the aspirated dome to the mouth of the pipette, first increased little upon increasing aspiration pressure, ΔP, then rose with a pronounced curvature and only entered a linear regime upon the formation of a half-spherical cap connected to a cylindrical membrane piece within the pipette. In contrast to this, GUVs from DOPC displayed a cylindrical portion within the pipette even at smallest aspiration pressures (see Fig. 5). Moreover, the aspirated lengths rose fast at small pressures and much less at higher pressures as is well documented for GUVs from ordinary phospholipids.8,12,14We never observed wrinkles, folds or non-spherical shapes in any aspiration experiment on FL-GUVs. Such structures would be typical for the large scale deformation of vesicles with stiffness against in plane shear or, in other words, with rigid shells. For micrographs of aspirated rigid vesicles see e.g. ref. 27. This again supports our conclusion with regards to the absence of in plane shear stiffness.
Overall, 31 measurements on FL-GUVs could be evaluated. Despite our efforts to improve micropipette passivation, we frequently observed irregularities like the hump between 1 kPa and 2 kPa in the displayed example, Fig. 4B. These irregularities were suppressed by addition of 1.25% PEG-DOPE to the lipid mixture which confirmed insufficient passivation of the glass pipette as source. Unfortunately, pegylated FL-GUVs were much more fragile than normal FL-GUVs. Therefore all measurements displayed here were performed on normal FL-GUVs.
3.4 Mechanical analysis of micropipette aspiration
As described in the previous section, FL-GUVs never showed any indication of excess area like non-spherical shapes, form fluctuations or instabilities. Moreover, the slope at high pressures was much lower than is usual for GUVs from normal lipids and the curvature of the length versus pressure curve was opposite, compare Fig. 4 and 5. For these reasons the standard analysis of GUV aspiration that relies on tension-induced suppression of shape fluctuations and, at high aspiration pressures, extension of the membrane could not be used here and had to be replaced.From the above observations we concluded that the membrane of FL-GUVs is always under significant membrane tension, τ. As will be shown later, membrane extensibility had to be included. Rigidity against in plane shear can be excluded because the membranes of FL-GUVs are in a fluid state, cf. Fig. 2. We also neglected membrane bending rigidity because we never observed any smoothly curved shapes neither at the mouth of the pipette nor in free vesicles upon increasing osmolarity of the outside medium.
In the course of an aspiration experiment a given FL-GUV assumes three distinctly different geometries, cf. Fig. 6. Before the aspiration, the vesicle is perfectly spherical. In the following, we call this state the “reference state”. Upon formation of a seal between membrane and pipette, the vesicle shape consists of two spherical caps that are fused at the pipette mouth. We call the radii of these two spherical caps R0 (outside the pipette) and R1 (inside the pipette), respectively. In this phase of aspiration only spherical shapes are compatible with the above described assumption because membrane tension and internal pressure are the only forces that act. Two different radii form because the hydrostatic pressure difference across the membrane differs between the aspirated part (R1) and the free part (R0). This state of the aspirated vesicle is termed “Geometry 1”.
With increasing suction pressure R1 decreases until a hemispherical cap is formed. This hemisphere has the same radius as the pipette, RP, and stays stable upon further aspiration. Now, a cylindrical membrane piece is formed that connects the hemispherical cap with the free part of the membrane. This shape is called “Geometry 2′′ in the remainder. The shape of the cylindrical membrane piece is stabilized by counterforces of the pipette wall. Please note, in micropipette experiments on GUVs from normal lipids in the fluid phase excess area of the GUV is caused by osmotic deflation and the GUV immediately assumes Geometry 2.
Please note that our classification of the geometry is just a device to facilitate calculations. It is based on the boundary conditions of membrane aspiration by a cylindrical pipette. No sudden changes of membrane parameters or states are involved.
The mechanical analysis of FL-GUV aspiration relies on two very likely assumptions. First, the number of osmotically active particles enclosed remains constant and, second, membrane area is increased by membrane tension. The first assumption is unavoidable because otherwise a given FL-GUV would shrink under the influence of its membrane tension and the internal pressure generated by it. The observation that FL-GUVs are stable for hours or even days proves this assumption. The second assumption corresponds to standard linear elastic area expansion which is the norm for bio- and model membranes. However, as FL-GUVs are composed of a standard lamellar lipid phase in coexistence with a three-dimensional lipid phase, they are in a thermodynamic two phase state. Therefore, deformation at constant membrane tension is conceivable. Nevertheless, we will show later that this is not compatible with observation.
In the end, each geometry contains two unknown variables (R0 and R1 for Geometry 1 and R0 and h for Geometry 2). We can solve for these two variables by an analysis of the forces acting on the membrane. Micropipette suction results in an increased mechanical membrane tension and, because the membrane is curved, also increased internal pressure. The total surface area of the membrane is then calculated assuming a linear relation between membrane tension and area. Because water can easily permeate biomembranes while hydrophilic solutes, here glucose and succrose, are retained, the enclosed volume is set by a balance of osmotic and hydrostatic pressures across the membrane. In view of the high aspiration pressure needed here, cf. Fig. 4, a noticeable increase of the osmolality of the inner medium must be expected whereas this effect can be mostly neglected for the aspiration of normal lipid bilayers, cf. Fig. 5.
Overall, area balance and volume balance yield two independent equations and thus enable calculation of the aspiration curve for known membrane tension in the reference state, τR, and area expansion modulus, kA. However, our task is a bit more complicated because these two material parameters are not known. We decided to base our method to determine kA and τR on the aspiration pressure where Geometry 1 converts to Geometry 2 (ΔPL) and the slope of h versus ΔP in Geometry 2. This choice was made because artifacts were less frequent at higher suction pressures.
The calculation proceeds in several steps. In the beginning we assume that all material parameters are known and first calculate the number of particles enclosed in the vesicle at the reference state. Then we derive equations to connect membrane tension and suction pressure and put up area and volume balance which are mathematically expressed as root of the difference between area (volume) as determined from geometry and from forces and material laws. For volume balance osmotic activity is included.
These calculations are easiest done in dimensionless variables. To this end we relate all lengths to the vesicle radius in the reference state, area is normalized by the surface area of the reference sphere, and volume to its value in the reference state. Analytical approximations are derived for the aspiration pressure where Geometry 1 converts to Geometry 2 and the derivative of dimensionless aspiration length with respect to dimensionless pressure. In the final step physical parameters are reintroduced and the resulting equations solved for the material constants τR and kA.
For the sake of readability the explicit calculations and equations are presented in an appendix after the discussion of results.
3.5 Mechanical properties of FL-GUVs
As mentioned before, membrane tension before aspiration, τR, and area expansibility modulus, kA, were determined in Geometry 2 (h > RP) from a line fit of the aspirated lengths h as function of the suction pressure ΔP. An example is shown in Fig. 7. The slope of this fitted line was taken as and the suction pressure where the fitted line assumed the value RP was taken as cross-over pressure ΔPL. Together with the osmolality of the measurement buffer (150 mM kg−1), the measured pipette (RP) and vesicle radius (RR), these formed the input data for numerical determination of kA and τR for each vesicle. To this end we solved area and volume balance by the “fsolve” utility of Maple stabilized by entering the approximate values of kA and τR, cf. eqn (26), as initial values for the algorithm. Here, the series expansions of pL, eqn (24), and
and the suction pressure where the fitted line assumed the value RP was taken as cross-over pressure ΔPL. Together with the osmolality of the measurement buffer (150 mM kg−1), the measured pipette (RP) and vesicle radius (RR), these formed the input data for numerical determination of kA and τR for each vesicle. To this end we solved area and volume balance by the “fsolve” utility of Maple stabilized by entering the approximate values of kA and τR, cf. eqn (26), as initial values for the algorithm. Here, the series expansions of pL, eqn (24), and  , eqn (25), including fourth order terms in ρ were used. For equations see the Appendix 4.
, eqn (25), including fourth order terms in ρ were used. For equations see the Appendix 4.
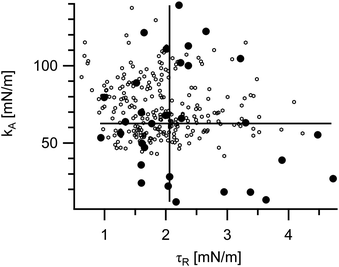
In total 31 measurements were successfully evaluated. For kA we obtained a median value of 63 mN m−1 and for τR 2.1 mN m−1. For average and standard deviation see Table 1. The individual results are presented together with the approximate values (eqn (26)) in Fig. 8.
 | ||
| Fig. 8 Measured material parameters. Each point represents one vesicle. Shown are the results of the numerical evaluation (filled circles) and of the analytical approximation, eqn (26) (open circles). Moreover, for the numerically determined values medians are indicated by full lines (kA 63 mN m−1, τR 2.1 mN m−1) and averages by dashed lines (kA 64 mN m−1, τR 2.3 mN m−1). | ||
3.6 Uncertainty and error analysis
The analyses described in Sections 3.5, 4.1, and 4.1.1 are limited by two different sources of error. On one hand, we made broad use of approximations in the derivation of eqn (24) and (25) and, on the other hand, measurement uncertainties cause a difficult to estimate scatter in the resulting material parameters. We analyzed the former by numerical solution of area and volume balance in both geometries. For the latter, we simulated measurement curves by adding noise to all parameters of the measurements (all measured lengths, RR, RP, and h, as well as lysis pressure) and analyzed these synthetic measurements just as the real ones.We calculated the “ideal” aspiration curve separately for both geometries. As input we selected median material parameters kA and τR and average geometrical parameters RR (5.32 μm) and RP (1.59 μm). Moreover, the osmotic strength of the measurement buffer of 150 mM kg−1 was used. In Geometry 2 we solved for each aspiration pressure the fully non-linear eqn (16) and (19) (see Appendix) for ε and h using Maple's fsolve routine.
In Geometry 1, this straightforward approach turned out to be numerically unstable. Therefore, we expanded the volume balance, eqn (30), to first order in ε (around ε = 0) and solved the resulting linear equation for ε. Then, we increased the parameter that describes the dimensionless radius of curvature of the aspirated membrane piece, δ (see Section 4.1.1), stepwise and calculated to each preselected δ the corresponding ε in the aforementioned first order approximation. For each couple of (ε, δ) aspiration pressure ΔP and aspirated length h were calculated and stored. This algorithm converged rapidly for small and moderate values of δ but became unstable as soon as the radius of curvature of the aspirated membrane section, R1, approached the pipette radius. This is not surprising because here the arguments of the square root terms w1 and w2 in eqn (29) and (30) approach zero, the value where the square root function exhibits infinite slope. Nevertheless, this instability caused only the small gap in the synthetic data that is visible in Fig. 9.
We analyzed these synthetic data with the same algorithms used for measurements. As there, we fitted a straight line to the part of the synthetic data where h > RP, interpolated the pressure ΔPL where h = RP and treated this and the fitted slope just as any other pair of measured values. For τR we obtained a value of 2.13 mN m−1 instead of 2.1 mN m−1 and for kA 60.7 mN m−1 instead of 62.5 mN m−1. That is, τR was by 1% too large and kA by 3% too small which is by far within the uncertainty of the experiment.
A possible source of systematic error in the calculation is the use of van't Hoff's law for the osmotic pressure. This law holds only for dilute, ideal solutions. If this is not the case, e.g. because of very high concentrations, van't Hoff's law must be replaced. However, for the solutions used in our experiments the activity coefficients differ little from the value of an ideal solution (1.0). We find values of 1.05 for 150 mM sucrose and 1.02 for 150 mM glucose.28 Moreover, as can be seen in Fig. 9, volume changes are most pronounced for very low concentrations of the medium where van't Hoff's law is generally a very good approximation. At higher concentrations volume changes are so low that deviations from ideal behavior can be easily accounted for by using the measured osmolality of the solution instead of its molarity.
An obvious and familiar source of scatter in the results are measurement uncertainties of the input data. To estimate the impact of experimental noise on the results we simulated measurements. Here, we first calculated an ideal aspiration curve, h(ΔP), and then added random numbers to each aspiration length, h, and to the geometrical parameters, RR and RP. In detail, for the material parameters, kA and τR, we used the median measurement results and for the geometrical ones, RR and RP, averages. Step width in pressure was selected to be 0.33 kPa, the most frequently used value in the experiments. The exact equations, eqn (16) and (19) (see Section 4.1), were solved for Geometry 2 just as described above. In the next step, we calculated 256 synthetic data sets as follows. First, to model the spread of lysis pressures, a random number was drawn from a uniform probability density in the range from 3 kPa to 5.9 kPa (adapted to experimental observations) and the ideal aspiration curve cut off at this pressure. Second, a random number drawn from a Gaussian distribution with standard deviation 0.2 μm centered around zero was added to each remaining value of h. Third, random numbers (again normal distribution 0.2 μm standard deviation centered around zero) were added to the correct values of RP and RR. These “noisy” values were used in the following. Fourth, the curve was again limited to aspiration pressures where h > RP. In the last step, the remaining noisy curve was analyzed for kA and τR exactly as any measured curve. The results are displayed, together with the measured values, in Fig. 10; numerical values are shown in Table 2.
| τR | kA | |
|---|---|---|
| Median | 1.8 | 69 |
| Average | 1.9 | 73 |
| SD | 0.67 | 18 |
In these simulations, a standard deviation of 0.2 μm was used for all geometrical parameters, because diameters were determined in fluorescence microscopy with a lens of numerical aperture of 0.6. Overall, these synthetic data result in a little bit less scatter in the results than found in the measurements. This is not surprising because the simulations could not model experimental artifacts like vesicle adhesion to the pipette (cf. the “hump” at about 1.5 kPa in Fig. 4B). Intriguingly, the results did not scatter uniformly around the input values but deviated systematically. The median value of kA turned out to be 10% too large whereas the median of τR was 13% too small. Moreover, we noted a weak correlation of the values of τR with RP that was not present for kA. It can be understood from eqn (26) and cautions against the use of large pipettes.
From these simulations we concluded that our measurement results are compatible with all FL-GUVs exhibiting the same material parameters kA and τR. Moreover, we must accept the possibility that our results are systematically shifted with respect to the true material parameters with kA being probably about 10% smaller and τR about 10% larger.
3.7 Mechanically driven phase separation
From our micropipette aspiration experiments on FL-GUVs we must conclude that these vesicles are under high tension of 2.1 mN m−1 even before aspiration and exhibit a surprisingly low area expansion modulus of 63 mN m−1. Vesicles from ordinary lipids, for example phosphatidylcholines, display area expansion moduli that are at least twice as large, typical values are even higher.8,19 Moreover, vesicles from normal lipids can be osmotically deflated. After this procedure, they exhibit only minute membrane tensions in the range of some ten μN m−9. This holds also for GUVs from positively charged lipids, as was demonstrated convincingly by Seth and coworkers29 who used micropipette aspiration to determine the mechanics of membranes from the unsaturated double-tailed cationic surfactant diethylesterdimethyl ammonium chloride (diC18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 DEEDMAC). They found normal osmotic deflation of these cationic giant unilamellar vesicles and report a bending modulus, kc, of 6–10 kBT and an area expansion modulus, kA, of 100 mN m−1.
1 DEEDMAC). They found normal osmotic deflation of these cationic giant unilamellar vesicles and report a bending modulus, kc, of 6–10 kBT and an area expansion modulus, kA, of 100 mN m−1.
In striking contrast, FL-GUVs are taut spherical structures without any visible shape fluctuations even after a substantial increase of the osmolarity of the outside buffer. Their membrane tension before aspiration is at least hundredfold higher than for ordinary lipid vesicles. These differences lead us to the hypothesis that vesicles from fusogenic lipid mixtures react to membrane tension by a different mechanism than ordinary lipid bilayers.
Further support for this hypothesis comes from small angle neutron scattering6 where a coexistence of ellipsoidal inclusions of about 10 nm size with a bilayer phase was observed. Therefore, the visible membrane of FL-GUVs is likely composed of two different phases, one where the lipid forms the usual lamellar phase and one where a 3D phase with high local curvatures is formed. In thermodynamic equilibrium such a system exists in a conformation that minimizes the overall free enthalpy, also called Gibbs' free energy, G. If one molecule crosses the phase boundary from the lamellar phase (henceforth indicated by the index 2D) to the 3D phase (index 3D), the area occupied by each phase will change. If these area changes are different in magnitude, that is, if the total surface area of the GUV changes, this, in turn, will result in mechanical work performed on the system by the micropipette. Therefore, increasing membrane tension will alter the phase equilibrium. In essence, we hypothesize that the exceptional properties of FL-GUVs originate from a mechanically driven phase transition.
Throughout the whole aspiration process, the membrane is in a two-phase region of the thermodynamic phase diagram. Increased membrane tension moves the system a small distance towards the lamellar phase but the border of the two-phase region is never reached. This basic idea is also illustrated in Fig. 11.
A related effect was observed by Kwok and Evans in GUVs from neat dimyristoylphosphatidylcholine (DMPC) for the lipid's main phase transition.30 Upon heating through this transition, membrane area increases by approximately 12% and therefore elevated membrane tension shifts the transition temperature to lower values. Because this transition is connected to a significant heat, the shift is rather small.30
The observation that FL-GUVs can be only prepared at low temperatures hints at a reversal of roles between lamellar and 3D phase at a certain temperature. At very low temperatures the usual lamellar (2D) phase exhibits a lower Gibbs free energy than the three dimensional phase whereas at room temperature this is the case for the three dimensional phase. Once a GUV is formed from a fusogenic lipid mixture at low temperature and heated towards room temperature, the three dimensional phase grows at the expense of the lamellar phase. Because the specific area increase per molecule is much lower in the three dimensional phase than in the lamellar one, the surface area of the GUV shrinks upon heating until this is stopped by the mechanical surface tension of the membrane caused by the osmotic pressure of the enclosed solutes. In this scenario FL-GUVs at room temperature are metastable objects that can only exist as long as their shell is under significant mechanical tension which also explains why FL-GUVs cannot be osmotically deflated.
Moreover, the observations that membrane tension could be increased by aspiration and that FL-GUVs are stable in a whole range of temperatures indicates that this thermodynamic two-phase system exhibits at least two thermodynamic degrees of freedom (tension and temperature). Therefore Gibbs phase rule indicates that at least two different components must be present.
For a more formal treatment we observe that the total molecule number of each molecular species, nti, where i denotes any of the three species (DOPE, DOTAP, and TF-DOPE), is constant within a given vesicle. Nevertheless, each molecule can distribute between both phases (2D and 3D), or
| n2Di + n3Di = nti ∀ i ∈ {1, 2, 3} | (2) |
Here and in the following, molecular species are indicated by subscripts and thermodynamic phases by superscripts. Molar fractions, xPi, are given for each species i in phase P by
 | (3) |
The chemical potential of molecular species i in phase P, μPi, is given by
 | (4) |
In thermal equilibrium the chemical potential of a given molecular species is identical in all phases, μ2Di = μ3Di, from which follows directly the tension dependent partition coefficient αi of molecules between the two phases:
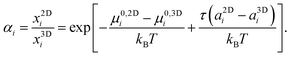 | (5) |
The physical meaning of this equation is simple: increasing membrane tension drives molecules into the phase where their area is larger. This is counteracted by the specific free enthalpy of transfer Δμ0i = μ0,2Di − μ0,3Di and the entropy of mixing.
Eqn (2), (3), and (5) combined yield an equation for the overall molecular number ratio of the 2D phase to the 3D phase, β
 | (6) |
If the free enthalpies of transfer, Δμ0i, and the change in specific membrane area per molecule, a2Di − a3Di, were known for each molecule, eqn (6) could be solved for the number ratio of the phases β. Unfortunately, these six unknown quantities cannot be retrieved from only two measured values kA and τR. One could vary temperature or membrane composition to obtain the necessary additional measurement points but the results would be of dubious value because we assumed an ideal mixture which is most likely an oversimplification. For a rigorous treatment, one would need to determine the full phase diagram. Unfortunately, the experimental effort to do so is prohibitive.
Moreover, we have assumed a defined Gibbs free energy for each molecule in the 3D phase, μ0,3Di. However, the energetics of the three dimensional phase must be size-dependent because Kolasinac et al.6 report structures of a well-defined size. Because our measurement technique cannot resolve sizes on the nanometer scale this effect was ignored here.
What we can learn from eqn (6) despite all limitations is that at least one molecular species, say i, must prefer the lamellar (2D) phase, αi > 1 and at least another one, say j, must prefer the non-lamellar (3D) one, αj < 1. This results by simple arithmetic from the fact that β is a positive number by definition.
From this we can estimate the order of magnitude of the free enthalpies of transfer as follows. Because vesicles from fusogenic lipid mixtures, FL-GUVs, do not exist at small membrane tensions, a tension of τR is necessary to fulfill the above condition. Moreover, a normal lipid with unsaturated chains occupies an area of about 0.7 nm2 in the lamellar phase.31 As the lamellar phase is formed by a molecular bilayer, the membrane area increases by half this value upon insertion of one molecule. In all possible 3D phases, the visible membrane consists of much more than two monolayers, therefore the area increase upon addition of one molecule must be much less. These considerations imply that the mechanical work delivered by the micropipette upon insertion of one molecule in the lamellar phase must approximately compensate the specific free enthalpy of transfer for at least one species. Thus the free enthalphy of transfer, Δμ0, must be on the order of 2.1 mN m−1 × 0.35 nm2 ≈ 0.7 × 10−21 J which corresponds to a mere fifth of the thermal energy, kBT, at room temperature. This very low value is further supported by our calorimetry experiments, cf. Fig. 1, where no transitions could be observed.
Overall, we arrive at a scenario where transfer of molecules between both phases is accompanied by extremely small free energies and can therefore be strongly influenced by mechanical tension of the membrane.
A related mechanism for membrane softening has been observed for lipid bilayers in aqueous solutions of bile acid by Evans et al.,32 in solutions of oleic acid by Mally et al.,33 and for lipid bilayers that contained lysolipid by Zhelev.34 These authors used a similar tension dependent term in the chemical potential of the detergent (bile acid, oleic acid or lysolipid) in the bilayer and calculated the partition coefficient between membrane and solution. However, in those experiments the aqueous solution of detergent served as infinite reservoir of molecules which resulted in a constant chemical potential of the detergent set by its concentration. Thus these systems are at constant chemical potential whereas in our case the overall molecule number was fixed which complicated the analysis substantially. Nevertheless, close to the critical micelle concentration Evans et al. report an elastic area expansion modulus of almost the same small size as we observed here.32 We believe that this is not just a coincidence because the molecular areas of bile acid and the lipids studied by us are similar which results in the end in similar membrane area increase upon tension increase.
4 Conclusions
In this work, we report that the membranes of fusogenic liposomes exhibit highly unusual material behavior. They are under permanent mechanical tension that cannot be removed without destroying the liposomes. Moreover, they are remarkably soft against area expansion. We developed a framework for the analysis of such material behavior with micropipette aspiration that can be applied to all pretensed, large liposomes with fluid membranes. The material behavior is interpreted as the result of a mechanically driven phase transition. Remarkably, the lamellar phase, that is, the planar membrane, is metastable and stabilized only by the presence of significant mechanical surface tension.Author contributions
L. M. S.: investigation, methodology; R. K.: DSC investigation, proposal of structure; G. D.: software; A. C.: conceptualization, supervision, writing – review and editing; R. M.: conceptualization, formal analysis, methodology, supervision, visualization, writing – original draft, writing – review and editing.Conflicts of interest
There are no conflicts to declare.Appendix—explicit calculations
Calculation of the number of particles within the vesicle
For putting up the volume balance we need to calculate the number of osmotically active particles enclosed in the vesicle. Even before aspiration, FL-GUVs are tensed. According to the equation of Laplace, the pressure difference ΔP across the membrane of a sphere of radius RR exhibiting a membrane tension of τR amounts to ΔP = 2τR/RR. This pressure difference must be balanced by an equal difference in osmotic pressures of the solutions ΔPosm. We use van't Hoff's law, Posm = kBTc, where kB is Boltzmann's constant, T the absolute temperature, and c the number density of osmotically active particles, in our experiments, sugar molecules. Van't Hoff's and Laplace's laws together imply that the osmolality of the enclosed medium must be higher than the one of the outer medium. For the sake of simplicity, and in accord with our experiments, we assume that all measurements are done in the same buffer with a number density of osmotically active particles of cR and arrive at the following expression for the number Ni of particles enclosed in the vesicle:
 | (7) |
Calculations for Geometry 2
Because Geometry 2 is composed of simple geometrical shapes, it is straightforward to calculate surface area, A, and enclosed volume, V.| A = 2πRP2 + 2πRP(h − RP) + 2πR0(h0 + R0) | (8) |
 | (9) |
We use the following shorthand notation:
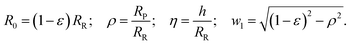 | (10) |
Please note, with the normalization of all lengths to the radius of the vesicle before aspiration, η and ε are variables, while ρ is just a fixed parameter. Moreover, with this definition ε ≪ 1 (cf. Fig. 4). For the normalized area, FA,1 = A/(4πRR2), we obtain
 | (11) |
 | (12) |
In the next step, we have to calculate the forces acting on membrane (tension) and inner medium (pressure). Membrane tension, τ, is set by the Laplace equation and the pressure balance. For the hemispherical cap within the pipette this reads 2τ/RP = Pin − PP and for the spherical cap outside 2τ/R0 = Pin − Pout. With the aspiration pressure, ΔP = Pout − PP, this yields:
 | (13) |
This result has been used extensively in micropipette aspiration.8,21,22
At this point, a material law is needed to set the area balance. The simplest material law for a membrane in which two thermodynamic phases coexist would be constant membrane tension. However, this assumption is contradicted by the experimental observation of an almost constant radius of the free part of the membrane, for an example see Fig. 4C. This can be seen as follows. From eqn (13) we get R0 = [1/RP − ΔP/(2τ)]−1. If τ were fixed, we would have to conclude from the observation of an almost constant R0 that τ ≫ ΔPRP/2. On the other hand, measurements were typically done at ρ ≈ 1/3 and ε ≈ 0. Inserted into eqn (13) this gives τ ≈ ΔPRP3/4 which contradicts the above conclusion τ ≫ ΔPRP/2. Thus membrane tension must vary during aspiration.
We use the usual assumption of linear elasticity with an area expansion modulus kA, sometimes also called area compressibility modulus:
 | (14) |
This material law can be regarded as a linearization of a more general material law around the reference state. Based on this we can now give the area of the tensed vesicle, also normalized by the area of the reference state
 | (15) |
 | (16) |
For putting up the volume balance we need to consider volume changes upon aspiration. To do so we follow the approach of Evans and Waugh35 who considered water flow through the membrane under the combined action of osmotic pressure difference, ΔPosm, and hydrostatic pressure, ΔPhydro, across the membrane. These are local pressures, both defined outside minus inside. Following these authors, we assume water flow to occur only at free parts of the membrane, that is at the hemispherical cap within the pipette, area Ain, and at the spherical cap outside, area Aout. Based on a linear mass flow, ṁ = k(ΔPhydro − ΔPosm) a stationary condition is reached if the water flux that enters the pipette through the hemispherical cap is exactly balanced by the influx of water through the spherical cap outside the pipette.
| Ain(Pin − PP + kBTcR − kBTcin) + Aout(Pin − Pout + kBTcR − kBTcin) = 0. | (17) |
In this equation we have used again van't Hoff's law for the osmotic pressure. Again the hydrostatic pressure differences can be replaced by 2τ/R where R is the radius of curvature of the respective membrane part. The resulting equation can be solved for cin which together with Nin/V = cin and eqn (7) yields the volume of the tensed vesicle, again scaled by the volume of the vesicle before aspiration
 | (18) |
The volume balance, FV,1 = FV,2, can again be written as the root of a function FV
| FV = FV,1 − FV,2 = 0. | (19) |
Eqn (16) and (19) are two independent equations for the two unknown variables ε and η. These equations depend on a number of parameters, namely kA, RR, T, cR, ΔP, and τR that we can combine into three dimensionless parameters p, a, and b.
 | (20) |
With these the area balance is given by
 | (21) |
 | (22) |
 | (23) |
In cases where the osmotic correction to the volume can be neglected Fosm = 1.
From the measured material parameters (see Table 1 in Section 3.5) and the osmolality used throughout (150 mM kg−1 or kBTcR = 366 kPa), the relative area expansion in the reference state, a = τR/kA, takes a value of 0.033, the osmotic correction factor, b = kA/(RRkBTcR), amounts to 0.032, and the dimensionless aspiration pressure, p = RRΔP/kA, was in all experiments in the range between 0 and 0.51.
Because both, area balance, eqn (21), and volume balance, eqn (22), are linear in η, one of these equations can be solved for η, the result inserted into the other, and the resulting highly non-linear equation in only one variable solved numerically. However, this procedure requires numeric values for the dimensionless parameters p, a, and b which we cannot give because the material parameters kA and τR are exactly the quantities to be determined. To obtain those values an explicit expression for η as function of all other parameters is needed. Unfortunately, we could not derive an exact and manageable closed-form solution. Instead, we resorted to an approximation that relies on the smallness of ε, see Fig. 4C. For convenience we also used that the osmotic volume correction is small, i.e. b ≪ 1.
In detail, we expanded area (eqn (21)) and volume balance (eqn (22) and (23)) to first order in ε and b. Terms proportional to b × ε are of second order and were therefore neglected. Both equations are linear in η and were solved for it. The intersection of the resulting functions ηA(ε) and ηV(ε) was calculated. The resulting ε was inserted into the expression for η which was, for simplicity, linearized again in ε. With these operations we achieved an explicit expression for η as function of the parameters p, a, and b. We do not reproduce this function ηfoa(p, a, b) here because the expression is very long. If needed it can be easily produced by a computer algebra system, see Fig. 12.
At this point it was necessary to decide upon a scheme for measurement analysis. Because experimental artifacts were less frequent at higher suction pressures, we chose to base our analysis scheme on the linear part of the measured aspiration curve. As two parameters were unknown, we needed to calculate two quantities that could be easily extracted from the measured data and decided on the slope of the aspiration curve h(ΔP) and the interpolated aspiration pressure at which h = RP. Translated into our scaled variables, we had to calculate the scaled pressure pL at which η(pL) = ρ and the derivative of η with respect to p at this scaled pressure.
The equation η(p) = ρ is quadratic with two real solutions of which only one is positive for realistic parameters. We selected this one for pL and calculated also the derivative of η with respect to p at this scaled pressure. Again, the resulting equations turned out to be too long for reproduction. A Maple code to produce the full equations is shown in Fig. 12. Here, we give the first terms of a series expansion in ρ = RP/RR.
 | (24) |
 | (25) |
Typically ρ was about 1/3 and vesicle lysis occurred at aspiration lengths of two to three times the pipette radius. To test for linearity of the exact curve, we also calculated the slope of η(p) at η = 2ρ. We found that the leading term of a series expansion of the slope at 2ρ minus the one at ρ, eqn (25), was a mere −ρ4/2, i.e. of fourth order in ρ with an added term in ρ3 × b that is for reasonable values of b effectively of fifth or sixth order in ρ. For this reason eqn (24) and (25) are of sufficient accuracy for most purposes.
For analysis of experiments, we inserted the definitions of the scaled parameters, eqn (20), into the series expansions in ρ for pL, eqn (24), and the slope, eqn (25). The resulting equations can be best solved numerically. Neglecting osmosis (b = 0) the following compact, yet rough, closed-form analytical approximation for τR and kA can be given from the first terms of the expansion in ρ
 | (26) |
Calculations for Geometry 1
This case turned out to be more cumbersome. On one hand, the mathematical treatment was much more complicated and, on the other hand, experiments were more prone to artifacts at these much lower aspiration pressures. Therefore, we describe the approach to this geometry in less detail.For aspiration lengths below RP, the aspirated membrane assumes a form of two spherical caps connected at the mouth of the pipette, see Fig. 6. The radius of curvature of the membrane part outside the pipette is called R0, the one inside R1. Because the suction force of the pipette is in the end balanced against its opening, the outer part must bulge beyond the edge of the pipette or, in more mathematical terms, R0 > RP. Moreover, for geometrical reasons R0 > R1 and R1 > RP. As in Geometry 2 we scaled all lengths by the radius of the vesicle before aspiration, RR, and introduce dimensionless variables. We keep the abbreviations eqn (10) and add
 | (27) |
Please note, whereas both dimensionless variables must be positive, only ε ≪ 1 while δ can almost reach 1 − ρ which in typical experiments amounts to about 0.7.
From the law of Laplace applied to this geometry, we derive the membrane tension
 | (28) |
As for Geometry 2, we derive functions for volume balance and area balance from geometry and either the material law for area expansion, eqn (14), or osmotically determined enclosed volume of the tensed vesicle. For the osmotic volume correction (compare eqn (18)) we assume that all membrane area is permeated by water because the membrane is pressed against the glass pipette only along a line at the mouth of the pipette, cf. Fig. 6.
From these considerations we obtain for the area balance:
 | (29) |
 | (30) |
In these equations we use the dimensionless variables a, b, and p as defined in eqn (20). As in the case of Geometry 2, the two variables, here ε and δ, are found by solving the equations
 | (31) |
Unfortunately, both functions are nonlinear in ε and δ. Therefore, we linearize both functions in ε and still receive complicated equations for all cases where δ became sizable. At very small suction pressure we derive the following approximation
 | (32) |
Here, terms of order ρ4 or more were neglected. Unfortunately, eqn (32) is of little practical use because the extremely small aspiration lengths at very low suction pressures were difficult to measure and experimental artifacts were especially frequent at these ultra-low pressures. Please note that for small aspiration pressures δ ∝ΔP and therefore eqn (28) does not diverge but will approach τR, the membrane tension in the reference state before aspiration.
Acknowledgements
We are grateful to Jens Konrad, Forschungszentrum Julich, for expert technical assistance and to Moritz Sokolowski, University of Bonn, for valuable feedback and suggestions regarding the manuscript. This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – 491111487.Notes and references
- A. Csiszar, N. Hersch, S. Dieluweit, R. Biehl, R. Merkel and B. Hoffmann, Bioconjugate Chem., 2010, 21, 537–543 CrossRef CAS PubMed.
- R. Kolasinac, C. Kleusch, T. Braun, R. Merkel and A. Csiszar, Int. J. Mol. Sci., 2018, 19, 346 CrossRef PubMed.
- S. Kube, N. Hersch, E. Naumovska, T. Gensch, J. Hendriks, A. Franzen, L. Landvogt, J.-P. Siebrasse, U. Kubitscheck, B. Hoffmann, R. Merkel and A. Csiszar, Langmuir, 2017, 33, 1051–1059 CrossRef CAS PubMed.
- M. Hubert, E. Larsson, N. V. G. Vegesna, M. Ahnlund, A. I. Johansson, L. W. K. Moodie and R. Lundmark, eLife, 2020, 9, e55038 CrossRef CAS PubMed.
- M. Hoffmann, N. Hersch, S. Gerlach, G. Dreissen, R. Springer, R. Merkel, A. Csiszar and B. Hoffmann, Int. J. Mol. Sci., 2020, 21, 2244 CrossRef CAS PubMed.
- R. Kolasinac, S. Jaksch, G. Dreissen, A. Braeutigam, R. Merkel and A. Csiszar, Nanomaterials, 2019, 9, 1025 CrossRef CAS PubMed.
- M. Mutz and W. Helfrich, J. Phys., 1990, 51, 991–1002 CrossRef CAS.
- E. Evans and W. Rawicz, Phys. Rev. Lett., 1990, 64, 2094–2097 CrossRef CAS PubMed.
- J. O. Radler, T. J. Feder, H. H. Strey and E. Sackmann, Phys. Rev. E, 1995, 51, 4526–4536 CrossRef PubMed.
- P. Girard, J. Prost and P. Bassereau, Phys. Rev. Lett., 2005, 94, 088102 CrossRef CAS PubMed.
- The Giant Vesicle Book, ed. R. Dimova and C. Marques, CRC Press, Taylor and Francis Group, Boca Raton, FL, USA, 2020 Search PubMed.
- E. Evans, W. Rawicz and B. A. Smith, Faraday Discuss., 2013, 161, 591–611 RSC.
- R. Dimova, Adv. Colloid Interface Sci., 2014, 208, 225–234 CrossRef CAS PubMed.
- W. Rawicz, K. C. Olbrich, T. McIntosh, D. Needham and E. Evans, Biophys. J., 2000, 79, 328–339 CrossRef CAS.
- S. T. Milner and S. A. Safran, Phys. Rev. A, 1987, 36, 4371–4379 CrossRef CAS PubMed.
- H. G. Dobereiner, G. Gompper, C. K. Haluska, D. M. Kroll, P. G. Petrov and K. A. Riske, Phys. Rev. Lett., 2003, 91, 4 CrossRef PubMed.
- D. Needham, T. J. McIntosh and E. Evans, Biochemistry, 1988, 27, 4668–4673 CrossRef CAS PubMed.
- J. Pan, S. Tristram-Nagle, N. Kucerka and J. F. Nagle, Biophys. J., 2008, 94, 117–124 CrossRef CAS PubMed.
- E. Parra-Ortiz and D. Needham, The Giant Vesicle Book, CRC-Press, Tayler & Francis Group, Boca Raton, FL, USA, 2020, pp. 283–304 Search PubMed.
- G. Gueguen, N. Destainville and M. Manghi, Soft Matter, 2017, 13, 6100 RSC.
- J.-B. Fournier, A. Ajdari and L. Peliti, Phys. Rev. Lett., 2001, 86, 4970–4973 CrossRef CAS PubMed.
- J. R. Henriksen and J. H. Ipsen, Eur. Phys. J. E, 2004, 14, 149–167 CrossRef CAS PubMed.
- D. M. Soumpasis, Biophys. J., 1983, 41, 95–97 CrossRef CAS PubMed.
- S. Dieluweit, A. Csiszar, W. Rubner, J. Fleischhauer, S. Houben and R. Merkel, Langmuir, 2010, 26, 11041–11049 CrossRef CAS PubMed.
- J. Schindelin, I. Arganda-Carreras, E. Frise, V. Kaynig, M. Longair, T. Pietzsch, S. Preibisch, C. Rueden, S. Saalfeld, B. Schmid, J.-Y. Tinevez, D. J. White, V. Hartenstein, K. Eliceiri, P. Tomancak and A. Cardona, Nat. Methods, 2012, 9, 676–682 CrossRef CAS PubMed.
- Phospholipid Handbook, ed. G. Cevc, Marcel Dekker, New York, 1993 Search PubMed.
- P. Ratanabanangkoon, M. Gropper, R. Merkel, E. Sackmann and A. P. Gast, Langmuir, 2003, 19, 1054–1062 CrossRef CAS.
- CRC Handbook of Chemistry and Physics, ed. J. R. Rumble, CRC Press, Boca Raton, FL, USA, 102nd edn, 2021 Search PubMed.
- M. Seth, A. Ramachandran and L. G. Leal, Langmuir, 2013, 29, 14057–14065 CrossRef CAS PubMed.
- R. Kwok and E. Evans, Biochemistry, 1982, 21, 4874–4879 CrossRef PubMed.
- D. Marsh, Handbook of Lipid Bilayers, CRC Press, Taylor & Francis, Boca Raton, FL, USA, 2013 Search PubMed.
- E. Evans, W. Rawicz and A. F. Hofmann, Bile acids in gastroenterology: basics and clinical advances, Kluwer Academic Publ., Dordrecht, Netherlands, 1995, vol. 80, ch. 5, pp. 59–68 Search PubMed.
- M. Mally, P. Peterlin and S. Svetina, J. Phys. Chem. B, 2013, 117, 12086–12094 CrossRef CAS PubMed.
- D. V. Zhelev, Biophys. J., 1998, 75, 321–330 CrossRef CAS PubMed.
- E. A. Evans and R. Waugh, Biophys. J., 1977, 20, 307–313 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2022 |