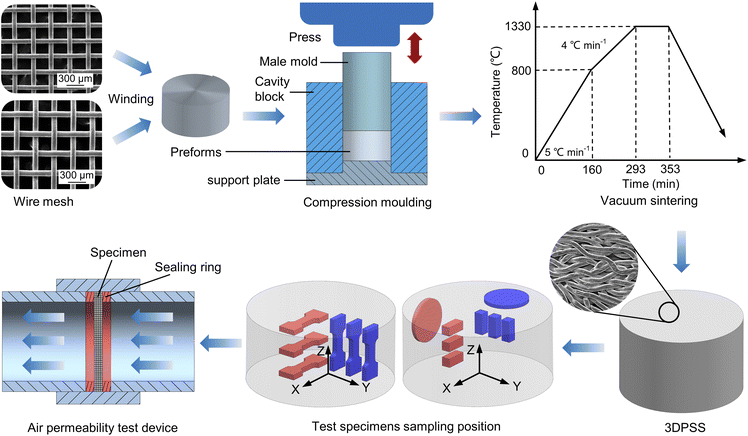
Open Access Article
Open Access ArticlePreparation and characterization of permeability and mechanical properties of three-dimensional porous stainless steel
Chaozhong Li and
Zhaoyao Zhou *
*
Guangdong Key Laboratory for Processing and Forming of Advanced Metallic Materials, National Engineering Research Center of Near-Net-Shape Forming for Metallic Materials, School of Mechanical and Automotive Engineering, South China University of Technology, Guangzhou 510640, People's Republic of China. E-mail: zhyzhou@scut.edu.cn
First published on 3rd October 2022
Abstract
Porous materials are indispensable in biomedical and chemical catalysis fields, but it is still a challenging task to fabricate them with excellent permeability and mechanical properties at the same time. Herein, a new type of three-dimensional porous stainless steel (3DPSS) was fabricated by compression moulding and vacuum sintering. The pore size distribution, air permeability, and mechanical properties of 3DPSS were studied. The results indicated that the radial air permeability reached 3.1 × 10−11 m2, which was approximately 19.7 times greater than the axial air permeability. Interestingly, the axial compressive strength was 91.3% higher than the radial compressive strength and reached 1249 MPa, which was significantly better than that of conventional porous stainless steel and porous titanium as well as porous high entropy alloys. The main characteristics of 3DPSS fracture were metallurgical bonding surface fracture, necking fracture and shear fracture of the wire mesh. This study provides an effective method for the preparation of three-dimensional porous materials, which is convenient for industrial production. It is of great significance to expand the potential application range of porous materials, in particular in fields requiring comprehensive permeability and mechanical properties.
1. Introduction
Porous materials are characterized by a light weight and large specific surface area due to a large number of pore structures inside them1,2 and are widely used in filtration,3,4 energy storage,5,6 heat dissipation7 and other fields. With the further development of their application field, the demands on the properties of porous materials are increasing. For example, in the biomedical field,8,9 porous bodies must have enough connected pores to meet the needs of regeneration of cells and the transmission of nutrients and must have good mechanical properties as implants. In the field of chemical catalysis,10,11 porous materials not only need to have good permeability to ensure high catalytic efficiency, but also need to maintain sufficient strength for making parts with a three-dimensional (3D) porous structure. Therefore, it is of great significance to develop new 3D porous materials with both excellent permeability and mechanical properties.In recent years, many scholars have conducted extensive research on porous materials. The common methods to produce porous materials are laser sintering, freeze casting, sintering, and powder injection moulding. Xie et al.12 fabricated planar porous stainless steel by laser-beam powder-bed fusion technology. Najafi et al.13 prepared porous ceramics by the freezing casting method. Yan et al.14 prepared porous titanium scaffolds with layered structures by bidirectional freeze casting technology. Tang et al.15 used braided copper wire mesh as a raw material to prepare a porous multiple wick structure and applied it to an ultrathin heat pipe through sintering and oxidation treatment. Wei et al.16 used nickel and titanium powders as raw materials and prepared a porous foam material with high porosity by using the sintering method. Qin et al.17 prepared porous scaffolds with excellent antibacterial properties and compressive strength via an in situ synthesis method using graphene and silver nanoparticles as raw materials. Zakaria et al.18 prepared porous titanium-hydroxyapatite composites by using the powder injection moulding process and removing the binder via a two-step degreasing process. Maurath et al.19 printed honeycomb ceramics with highly open porous structure based on ink of capillary suspension. Zhao et al.20 fabricated nano porous stainless steel by liquid metal dealloying processes.
However, the porous materials produced by foaming have high porosity but low mechanical properties. Selective laser sintering easily produces porous materials with complex structures, but it still has the disadvantage of high energy consumption, and the surface bonded powder easily plugs the pores, reducing the permeability. The traditional powder metallurgy method requires the addition of a large number of pore-forming agents, which increases the degreasing process and aggravates environmental pollution. Honeycomb ceramics showed exceptionally high specific strength, but their compressive strength is still low. At present, 3D porous materials still have some defects, such as permeability and mechanical properties that cannot be taken into account at the same time, high energy consumption and serious pollution in the manufacturing process, which seriously restrict their further development. In our previous study,21 we used the method of rolling wire mesh to produce flat porous stainless steel; however, there are no studies on 3D porous materials. Planar porous materials need to be bent when they are made into 3D parts. However, the bending process easily changes the porous structure, and the parts are prone to delamination, cracks and other defects. This severely restricts the development and application of porous 3D parts. Since 3D porous materials can be directly fabricated into 3D parts, the processing step is reduced, the production efficiency is improved and additional defects and damage are avoided. Moreover, as far as we know, there are still few reports on 3D porous materials with both excellent permeability and mechanical properties.
The main purpose of this work was to develop a 3DPSS with excellent air permeability and mechanical properties. A 304 stainless steel braided wire mesh was fabricated into a 3D porous material with a connected pore structure by compression moulding and vacuum sintering. Because the wire mesh has the original mesh structure, it easily forms a connected porous structure in the material, which is conducive to the material obtaining better permeability, and the wire mesh as a continuous dense body has good mechanical properties. The process of compression moulding and vacuum sintering can form an effective metallurgical bonding point of the wire mesh, which is beneficial to further enhance the mechanical properties. The pore size distribution, permeability, and tensile and compression properties of 3DPSS were investigated. The fracture morphology of 3DPSS was observed, and the fracture mechanism was analysed.
2. Materials and methods
2.1 Fabrication process of the 3DPSS
The manufacturing process of the 3DPSS is shown in Fig. 1. First, 304 stainless steel wire mesh with diameters of 80 μm and 100 μm was wound to form the preforms. Then, the preforms were put into the mold for pressing. The preform was surrounded by the cavity block and supported by the support plate; through a pressing force of 315 tons in press extrusion, the male mold pressed the preform, causing the wire mesh to be in close contact. Then, the preform was placed into a vacuum sintering furnace (WHS-20, Kaixuan Vacuum Technology and Engineering Co., Ltd., Zhongshan, China) at approximately 5 × 10−2 Pa for vacuum sintering. The heating method of segment sintering was used. First, the furnace was heated to 800 °C at a rate of 5 °C min−1 and then to 1330 °C at a rate of 4 °C min−1, and the temperature was held for 1 h. Finally, the preform was cooled to room temperature in the furnace. The surface morphology of 3DPSS was observed by scanning electron microscope (Quanta 200, FEI, Netherlands).2.2 Pore size distribution, XRD and air permeability test
First, the 3DPSS was cut according to the area shown in Fig. 1. The x-axis was defined as the radial direction of the sample, and the z-axis was defined as the axial direction of the sample. Samples with wire mesh diameters of 80 μm and 100 μm were cut in the radial (80R and 100R, respectively) and axial (80L and 100L, respectively) directions. Because the 3DPSS samples were all made of 304 stainless steel, it was suitable to use the mass volume method22 to calculate the porosity, as shown in eqn (1).| P = (1 − (m/ρv)) × 100% | (1) |
The bubble-point method utilizes the capillary flow principle of the liquid wetting agent in the channel, and the tested pore diameter is the diameter of the equivalent circle at the narrowest point of the channel.23 The calculation formula of the pore diameter is shown in eqn (2). The pore size distribution characteristics include pore size distribution and the cumulative pore size distribution, where pore size distribution curve represents the percentage of pore diameter calculated by size, and cumulative pore size distribution represents the function of pore size distribution less than or greater than a certain pore size value. In this paper, the pore size distribution characteristics of 3DPSS were tested by an aperture analyser (PSDA-20, GaoQ Functional Materials Co., Ltd., Nanjing, China).
| d = 4γcosθ/p | (2) |
The phase structures were examined by an X-ray diffraction (XRD, Bruker Advance D8) with Cu Ka radiation at a scan rate of 12° min−1 over the range from 20° to 120° with a step width of 0.013°.
Permeability reflects the ability of fluid through porous media under differential pressure. When the flow rate is low, Darcy’s law is obeyed.24 With the increase in fluid velocity, the energy dissipation of friction between the fluid and channel intensifies. Therefore, fluid pressure loss is generally accompanied by inertia loss, resulting in a nonlinear increase in the pressure drop. Forchheimer modified Darcy’s law and presented the empirical relationship of fluid flow resistance through porous media,25,26 as shown in eqn (3).
| (Pi2 − Po2)/(2PoL) = (μ/K1)vf + (ρ/K2)vf2 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 325 Pa); Pi is the absolute inlet air pressure (Pa); L is the thickness of the porous materials (m); μ is the viscosity of air (1.79 × 10−5 Pa s); ρ is the air density (1.205 kg m−3); K1 is the Forchheimer permeability coefficient (m2); K2 is the inertial permeability coefficient (m); and vf is the average velocity of airflow (m s−1).
325 Pa); Pi is the absolute inlet air pressure (Pa); L is the thickness of the porous materials (m); μ is the viscosity of air (1.79 × 10−5 Pa s); ρ is the air density (1.205 kg m−3); K1 is the Forchheimer permeability coefficient (m2); K2 is the inertial permeability coefficient (m); and vf is the average velocity of airflow (m s−1).
The specific process of air permeability testing was as follows: first, 3DPSS was cut into a circular sample with a diameter of 24 mm and a thickness of 2 mm, as shown in Fig. 1. Then, the circular sample was installed in the air permeability test device. Rubber rings were used to seal both ends of the sample. Finally, the least square method was used to fit the flow velocity differential pressure diagram and calculate the values of K1 and K2.27 The least square method was used to fit the flow rate differential pressure value, and the parabolic model was used: y = ax + bx2. According to eqn (3), K1 = μ/a and K2 = ρ/b. The correlation coefficient R2 is the index to evaluate the fitting quality of curves.
2.3 Uniaxial tensile and compressive test
The tensile and compressive properties of the specimens were tested according to Chinese GB/T 228.1-2010 and GB/T 7314-2005, respectively. Specimens were taken at different locations of the 3DPSS (Fig. 1). The tensile specimen width was 5 mm, the thickness was 3 mm, the gauge length was 8 mm, and the transition fillet radius was 10 mm. The compression specimen was a cuboid with a length and width of 5 mm and a height of 12 mm. The test was carried out on an electronic universal testing machine (UTM5105SYXL, Suns, China) at a tensile rate of 0.1 mm min−1 and a compression rate of 1 mm min−1. Three specimens were used in each direction for the test, and the average value was taken as the test result. The fracture morphology of 3DPSS was observed by scanning electron microscope (Quanta 200, FEI, Netherlands), and the fracture mechanism was analysed.3. Results and discussion
3.1 Pore size distribution, XRD and air permeability
Fig. 2 shows the pore size distribution and XRD patterns of 3DPSS. The pore sizes of 80R (Fig. 2a), 80L (Fig. 2b), 100R (Fig. 2c) and 100L (Fig. 2d) were below 32.7 μm, 18.7 μm, 52.6 μm and 44.5 μm, respectively.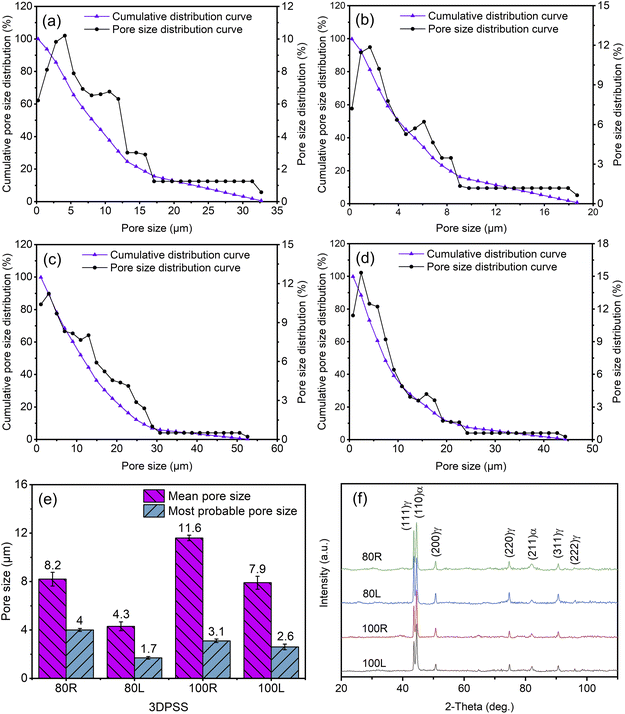 | ||
| Fig. 2 Pore size distribution and XRD patterns of the 3DPSS. (a) 80R; (b) 80L; (c) 100R; (d) 100L; (e) pore size distribution statistics; and (f) XRD patterns. | ||
The main pore size distribution was close to the small size side. This shows that the pore size distribution of 3DPSS was not uniform. Fig. 2e shows that the mean pore size of 3DPSS was always larger than the most probable pore size. The most probable pore size is the largest pore size in the pore size distribution of porous materials. Because 3DPSS contains a high proportion of large pore structures, the mean pore size was increased so that the mean pore size was always greater than the most probable pore size. The larger the wire mesh diameter is, the larger the pore size (Fig. 2e). This result is because the 100 μm wire mesh has a larger original pore structure than the 80 μm wire mesh. Second, the larger diameter of the wire mesh made the material in the process of moulding deformation smaller and the gap formed between the wire mesh layers larger. Another significant characteristic was that the radial pore size was larger than the axial aperture (Fig. 2e). This phenomenon is closely related to the manufacturing process of 3DPSS. On the one hand, the preform of 3DPSS was made by winding the wire mesh, and the opening of the wire mesh faced the radial direction, which was conducive to the formation of a larger pore structure. On the other hand, in the compression moulding process, the axial direction was the main bearing direction, and the pore size decreased to a greater extent.
The XRD patterns (Fig. 2f) of 3DPSSs indicates that the face-centered cubic (FCC (γ)) and body-centered cubic (BCC (α)) phases are present in 3DPSSs. The reason for this is that the austenite structure of 3DPSSs was completely formed after high temperature sintering. In the cooling process, carbon atoms fully diffused to austenite while ferrite formed. This is beneficial to the formation of a mixture of ferrite and austenite in 3DPSSs.
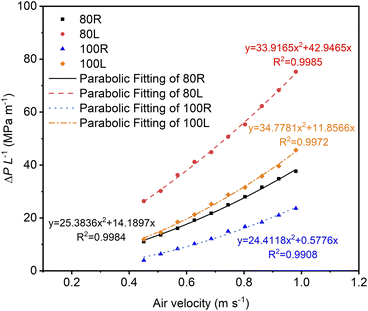
Fig. 3 shows the air permeability curves of 3DPSS. The permeability coefficient of 3DPSS is shown in Table 1. With increasing flow rate, the pressure difference increases monotonically. Among them, the pressure difference of 100R increases the slowest with increasing flow rate, while the pressure difference of 80L increases the fastest, which indicates that the air permeability of 100R is the strongest, while that of 80L is the weakest. The permeability of the radial specimens was significantly higher than that of the axial specimens, and 3DPSS with a larger wire mesh diameter had better permeability (Fig. 3). This interesting phenomenon is due to the larger wire mesh diameter, resulting in a larger aperture inside the material, which facilitates the smooth passage of gas.
| 3DPSS | Porosity (%) | Forchheimer permeability coefficients K1 × 10−11 (m2) | Inertial permeability coefficients K2 × 10−8 (m) |
|---|---|---|---|
| 80R | 39.67 | 0.13 | 4.75 |
| 80L | 32.79 | 0.04 | 3.55 |
| 100R | 36.06 | 3.1 | 4.94 |
| 100L | 32.31 | 0.15 | 3.46 |
3.2 Mechanical properties
Fig. 4 shows the mechanical properties of 3DPSS. Fig. 4a shows the uniaxial tensile engineering stress–strain curves of 3DPSS. In the elastic stage, the engineering stress of 80R was less than 44.5 MPa. In the plastic stage, the engineering stress of 80R was between 44.5 MPa to 131.9 MPa, and after the ultimate tensile strength of 131.9 MPa was the fracture stage. In contrast, in the elastic stage, the engineering stress of 80L was less than 42.6 MPa. In the plastic stage, the engineering stress of 80L was between 42.6 MPa to 96 MPa, and after the ultimate tensile strength of 96 MPa was the fracture stage. This phenomenon indicates that 3DPSS has better tensile properties in the radial direction.28,29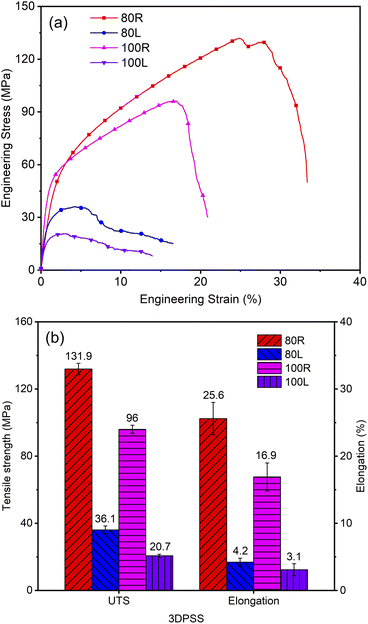 | ||
| Fig. 4 Tensile properties of the 3DPSS. (a) Uniaxial tensile curves; and (b) statistical chart of tensile properties. | ||
Fig. 4b shows that the tensile properties of 3DPSS with a wire mesh diameter of 80 μm were better than those with a wire mesh diameter of 100 μm. The ultimate tensile strength (UTS) of 80R was approximately 37.4% higher than that of 100R, and the UTS of 80L was approximately 74.4% higher than that of 100L. This indicates that a smaller wire mesh diameter was beneficial to improve the tensile properties of 3DPSS.30 This is because a smaller wire mesh diameter facilitates the formation of more metallurgical joints per unit volume. In addition, the tensile strength of 3DPSS in the radial direction was significantly better than that in the axial direction. Specifically, the UTS of 80R was approximately 265.4% higher than that of 80L. The UTS of 100R was 363.8% higher than that of 100L. This result is mainly related to the deformation of the wire mesh during the moulding process. Due to the main axial compression force of 3DPSS, the wire mesh in the vertical state was folded and overlapped by the axial force (Fig. 6a), which increased the stress area during stretching and was conducive to the improvement of tensile properties. The axial compression force makes the contact surface between the wire mesh layers in the preform gradually vertical with the axial state (Fig. 6e), reducing the stress area and tensile properties of 3DPSS.
Fig. 5a shows the uniaxial compression engineering stress–strain curves of 3DPSS. In the elastic stage, the engineering stress of 80L was less than 62 MPa. In the plastic stage, the engineering stress of 80L was between 62 MPa to 1249 MPa, and after the ultimate tensile strength of 1249 MPa was the fracture stage. In contrast, in the elastic stage, the engineering stress of 100L was less than 53 MPa. In the plastic stage, the engineering stress of 100L was between 53 MPa to 435 MPa, and after the ultimate tensile strength of 435 MPa was the fracture stage. This phenomenon is because the surface energy of the larger diameter wire mesh was lower than that of the fine wire mesh,31 there were fewer metallurgical bonding points between the wire mesh layers in the process of vacuum sintering, and the material was more prone to fracture failure under compressive stress. Moreover, a larger diameter of the mesh structure prolongs the process of fracture failure.
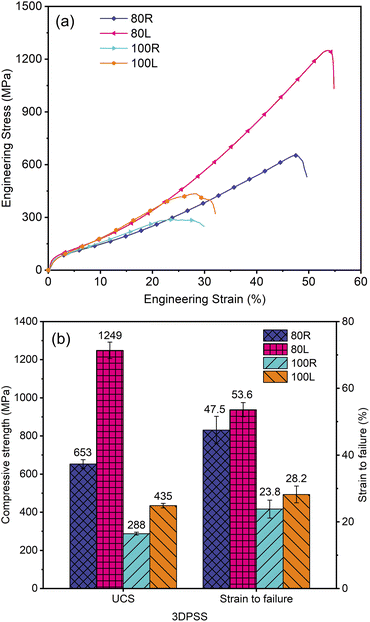 | ||
| Fig. 5 Compression properties of the 3DPSS. (a) Uniaxial compression curves; and (b) statistical chart of compression properties. | ||
Fig. 5b shows that the compression properties of 3DPSS with a wire mesh diameter of 80 μm were significantly better than those of 3DPSS with a wire mesh diameter of 100 μm. Among them, the ultimate compressive strength (UCS) of 80R was 126.7% higher than that of 100R, and the UCS of 80L was 187.1% higher than that of 100L. This result is because a thinner wire mesh diameter tends to form more metallurgical joints, which improves the compression properties. The compressive strength of 3DPSS in the axial direction was significantly better than that in the radial direction. Specifically, the UCS of 80L was 91.3% higher than that of 80R, and the UCS of 100L was 51% higher than that of 100R. This phenomenon is because the axial direction was the main bearing direction, and the wire mesh surface gradually presents a nearly vertical state with the axial direction in the compression moulding process (Fig. 6e), while the wire mesh formed staggered inclined planes in the radial direction (Fig. 6a). The angle between the wire mesh surface in the axial direction and the direction of compressive force was large, and slipping did not easily occur between the wire mesh surfaces. As the compression displacement increases, the densification of 3DPSS intensifies, further improving the compressive strength of the material.32 The wire mesh in the radial direction easily slips along the inclined plane, which reduces the degree of work hardening of the specimen and makes the specimen fracture in advance.
3.3 Fracture morphology
Fig. 6 shows the tensile and compression fracture morphology of 3DPSS. The tensile side fracture morphology of 100R (Fig. 6a) shows that the wire mesh plane was inclined to the tensile direction, with a structure of staggered and overlapping wire mesh layers. This shows that the larger wire mesh surface was involved in the tensile process, which was conducive to the improvement of the tensile strength. The tensile side fracture morphology of 100L (Fig. 6e) shows that most of the wire mesh planes were nearly vertical to the tensile direction, which makes only a few wire mesh planes bear the tensile load. Therefore, the difference between radial and axial internal structures was one of the important reasons for the anisotropy of mechanical properties. Fig. 6a shows that the whole lateral fracture was the primary crack, and several secondary cracks remained below the primary crack. It was indicated that cracks originated from the metallurgical junction points between the wire mesh layers.33 As the stretching process occurs, the weft of the wire mesh bends and deforms along the stretching direction, and the warp of the wire mesh slightly necks until fracture (Fig. 6d and h), forming a typical wedge fracture (Fig. 6b and f). From the front fracture morphology of 100R (Fig. 6c) and 100L (Fig. 6g), it can be seen that in the radial direction, not only the metallurgical bonding surface between the wire mesh layers bears the load but also a large number of wire mesh layers bear the load through the way of necking fracture, while in the axial direction, the metallurgical bonding point between the wire mesh layers mainly bears the load. This results in a great difference between radial and axial tensile properties.The compression side fracture morphology of 80R (Fig. 6i) shows two main cracks, while 80L (Fig. 6k) shows a 45° crack. In the radial direction, there was mostly interlacing of wire mesh layers leading to an overlapping structure (Fig. 6a), and in the axial direction, there was a nearly vertical structure (Fig. 6e). Therefore, 80R was prone to multiple cracks, and its compressive strength was significantly lower than that of 80L. As the overlapping of the wire mesh surfaces inside 80L was close to vertical with the axis direction, 80L can continuously produce work hardening under compressive stress until fracture.34 The lateral fracture morphology of 80R and 80L both contained fish scale cracks. This interesting phenomenon was due to the continuous reduction of pores in the compression process of 3DPSS, and cracks occurred between the wire mesh layers, which makes the wire mesh surrounded by cracks and forms fish scale cracks. The radial fracture process was also quite different from the axial process. Fig. 6j shows the wedge fracture morphology of the wire mesh at the 80R crack centre, while Fig. 6l shows the tear surface of the wire mesh at the 80L crack centre. This is mainly because 80L has a stronger work hardening ability and higher compressive strength. After sufficient work hardening, the wire mesh under the action of shear stress forms a tear surface shape of the fracture.
Fig. 7 shows the air permeability and compression properties of porous materials according to this paper and previous reports. As shown in Fig. 7a, while maintaining moderate porosity, the permeability of 3DPSS was significantly better than that of nuclear graphite,35 porous Al2O3 ceramic36 and porous cementitious37 and was close to that of porous titanium.38 Fig. 7b shows that the compressive strength of 3DPSS was significantly better than that of porous Ti/Mg composites39 and porous Ti-6Al-4V materials.40 To achieve a compressive strength close to that of 3DPSS with a wire mesh diameter of 100 μm, the porosity of porous 316L stainless steel41 needs to be significantly reduced. However, the reduction in the porous structure will greatly reduce its permeability. In the case of similar porosity, the compressive strength of 3DPSS with a mesh diameter of 80 μm was at the same level as that of porous TiB/TiC composites.42 The compressive strength of 3DPSS with a wire mesh diameter of 100 μm was comparable to that of a porous high entropy alloy.43 Therefore, 3DPSS has wide application prospects due to its light weight, microporous structure, and excellent permeability and compressive mechanical properties.
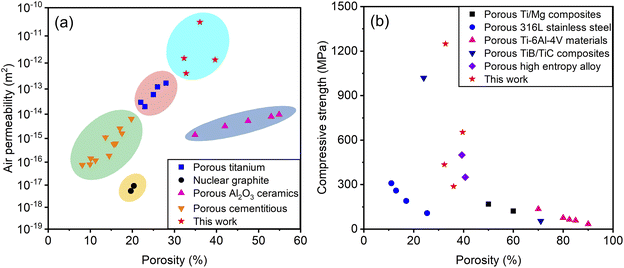 | ||
| Fig. 7 Summary of the air permeability and compression properties of porous materials from the literature and this work. (a) Air permeability; and (b) compression properties. | ||
4. Conclusions
In summary, an effective way to fabricate 3D porous materials with excellent air permeability and compressive strength was proposed. The results revealed that 3DPSS with larger wire mesh diameter has larger mean pore size, better air permeability. The pore size distribution, air permeability and mechanical properties of 3DPSS presented obvious anisotropy. The mean pore size in the radial direction was larger than that in the axial direction. The air permeability of 3DPSS in the radial direction reached 3.1 × 10−11 m2, approximately 19.7 times greater than that in the axial direction, and significantly better than that of porous titanium and porous ceramics with the same porosity. The axial compressive strength was higher than the radial compressive strength. The ultimate compressive strength of 3DPSS reached 1249 MPa, which was significantly superior to that of traditional porous stainless steel, porous titanium, and porous high entropy alloys. The main reason for the anisotropy of 3DPSS was the different structures of wire mesh winding and overlapping in the radial and axial directions. The principal characteristics of 3DPSS fracture were metallurgical bonding surface fracture, necking fracture and shear fracture of the wire mesh. It is worth mentioning that the 3DPSS is lightweight and has a microporous structure and excellent air permeability and compressive strength, all of which make it particularly valuable in the biomedical and chemical catalysis fields.Author contributions
Chaozhong Li: conceptualization, investigation, methodology, data curation, formal analysis, writing – original draft. Zhaoyao Zhou: funding acquisition, project administration, resources, supervision, validation, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The project was financially supported by the Science and Technology Program of Guangzhou, China (No. 201604016015).Notes and references
- B. R. Thompson, T. S. Horozov, S. D. Stoyanov and V. N. Paunov, J. Mater. Chem. A, 2019, 7, 8030–8049 RSC.
- P. S. Liu and X. M. Ma, Mater. Des., 2020, 188, 108413 CrossRef.
- J. Li, J. Zhang, X. Wu, J. Zhao, M. Wu and W. Huan, RSC Adv., 2020, 10, 30304–30313 RSC.
- P. Song and Q. Lu, Sep. Purif. Technol., 2020, 238, 116454 CrossRef CAS.
- F. Mahmood, C. Zhang, Y. Xie, D. Stalla, J. Lin and C. Wan, RSC Adv., 2019, 9, 22713–22720 RSC.
- Y. Zheng, Y. Lian, D. Wang, C. Ban, J. Zhao and H. Zhang, Vacuum, 2020, 181, 109746 CrossRef CAS.
- A. Ghahremannezhad, H. Xu, M. R. Salimpour, P. Wang and K. Vafai, Appl. Therm. Eng., 2020, 179, 115731 CrossRef CAS.
- J. Li, Z. Li, R. Li, Y. Shi, H. Wang, Y. Wang and G. Jin, RSC Adv., 2018, 8, 36512–36520 RSC.
- R. Xiao, X. Feng, R. Fan, S. Chen, J. Song, L. Gao and Y. Lu, Composites, Part B, 2020, 193, 108057 CrossRef CAS.
- C. Goldhahn, J. A. Taut, M. Schubert, I. Burgert and M. Chanana, RSC Adv., 2020, 10, 20608–20619 RSC.
- J. Liu, Y. Gao, Y. Fan and W. Zhou, Int. J. Hydrogen Energy, 2020, 45, 10–22 CrossRef CAS.
- D. Xie and R. Dittmeyer, Addit. Manuf., 2021, 47, 102261 CAS.
- S. Parsa Saeb, A. Najafi, F. Golestanifard and H. R. Rezaie, Mater. Res. Express, 2020, 7, 105005 CrossRef.
- L. Yan, J. Wu, L. Zhang, X. Liu, K. Zhou and B. Su, Mater. Sci. Eng. C, 2017, 75, 335–340 CrossRef CAS PubMed.
- H. Tang, C. Weng, Y. Tang, H. Li, T. Xu and T. Fu, Appl. Therm. Eng., 2021, 183, 116203 CrossRef CAS.
- L. Wei, X. Zhang and L. Geng, Vacuum, 2019, 162, 15–19 CrossRef CAS.
- L. Qin, J. Yi, L. Xuefei, L. Li, X. Kenan and X. Lu, RSC Adv., 2020, 10, 28397–28407 RSC.
- M. Y. Zakaria, M. I. Ramli, A. B. Sulong, N. Muhamad and M. H. Ismail, J. Mater. Res. Technol., 2021, 12, 478–486 CrossRef CAS.
- J. Maurath and N. Willenbacher, J. Eur. Ceram. Soc., 2017, 37, 4833–4842 CrossRef CAS.
- C. Zhao, T. Wada, V. De Andrade, G. J. Williams, J. Gelb, L. Li, J. Thieme, H. Kato and Y. K. Chen-Wiegart, ACS Appl. Mater. Interfaces, 2017, 9, 34172–34184 CrossRef CAS.
- L. Duan, Z. Zhou and B. Yao, Materials, 2018, 11, 156 CrossRef PubMed.
- Y. Tang, W. Zhou, M. Pan, H. Chen, W. Liu and H. Yu, Int. J. Hydrogen Energy, 2008, 33, 2950–2956 CrossRef CAS.
- J. Yu, X. Hu and Y. Huang, Sep. Purif. Technol., 2010, 70, 314–319 CrossRef CAS.
- K. Balasubramanian, F. Hayot and W. F. Saam, Phys. Rev. A: At., Mol., Opt. Phys., 1987, 36, 2248–2253 CrossRef PubMed.
- M. D. M. Innocentini and V. C. Pandolfelli, J. Am. Ceram. Soc., 2001, 84, 941–944 CrossRef CAS.
- L. Biasetto, M. D. M. Innocentini, W. S. Chacon, S. Corradetti, S. Carturan, P. Colombo and A. Andrighetto, J. Nucl. Mater., 2013, 440, 70–80 CrossRef CAS.
- N. Dukhan, Ö. Bağcı and M. Özdemir, Exp. Therm. Fluid Sci., 2014, 57, 425–433 CrossRef.
- P. Liu, G. He and L. Wu, Mater. Sci. Eng., A, 2009, 509, 69–75 CrossRef.
- W. Zhou, Y. Tang, M. Pan, X. Wei and J. Xiang, Mater. Sci. Eng., A, 2009, 525, 133–137 CrossRef.
- G. He, P. Liu and Q. Tan, J. Mech. Behav. Biomed. Mater., 2012, 5, 16–31 CrossRef CAS.
- X. B. Chen, Y. C. Li, P. D. Hodgson and C. Wen, Acta Biomater., 2009, 5, 2290–2302 CrossRef CAS PubMed.
- D. Wang, G. He, Y. Tian, N. Ren, J. Ni, W. Liu and X. Zhang, J. Mater. Sci. Technol., 2020, 44, 160–170 CrossRef.
- J. Zhou, K. Zhong, C. Zhao, H. Meng and L. Qi, Ceram. Int., 2021, 47, 6597–6607 CrossRef CAS.
- A. Falkowska, A. Seweryn and A. Tomczyk, Int. J. Fatig., 2018, 111, 161–176 CrossRef CAS.
- K. L. Jones, G. M. Laudone and G. P. Matthews, Carbon, 2018, 128, 1–11 CrossRef CAS.
- Y. Li, X. Yang, D. Liu, J. Chen, D. Zhang and Z. Wu, Ceram. Int., 2019, 45, 5952–5957 CrossRef CAS.
- T. H. Panzera, J. C. Rubio, C. R. Bowen and P. J. Walker, Cem. Concr. Compos., 2008, 30, 649–660 CrossRef CAS.
- Q. Xu, B. Gabbitas and S. Matthews, Powder Technol., 2014, 266, 396–406 CrossRef CAS.
- Y. Qi, K. G. Contreras, H. D. Jung, H. E. Kim, R. Lapovok and Y. Estrin, Mater. Sci. Eng. C, 2016, 59, 754–765 CrossRef CAS PubMed.
- Y. C. Wu, C. N. Kuo, M. Y. Shie, Y. L. Su, L. J. Wei, S. Y. Chen and J. C. Huang, Mater. Des., 2018, 158, 256–265 CrossRef CAS.
- K. Essa, P. Jamshidi, J. Zou, M. M. Attallah and H. Hassanin, Mater. Des., 2018, 138, 21–29 CrossRef CAS.
- B. Song, C. Kenel and D. C. Dunand, Addit. Manuf., 2020, 35, 101412 CAS.
- Z. Xu, Z. Zhu, P. Wang, G. K. Meenashisundaram, S. M. L. Nai and J. Wei, Addit. Manuf., 2020, 35, 101441 CAS.
| This journal is © The Royal Society of Chemistry 2022 |