Theoretical analysis of sulfuric acid–dimethylamine–oxalic acid–water clusters and implications for atmospheric cluster formation

Abstract

In recent years, organic compounds potentially involved in atmospheric particle formation have received increased attention. However, the contributions of organic acids as precursors in nucleation remain ambiguous. In this study, the low-lying structures and thermodynamics of the sulfuric acid–dimethylamine–oxalic acid–water system are obtained at the M06-2X/6-311+G(2d,p) level, and the single point energy of the clusters has been calculated at the DF-LMP2-F12/VDZ-F12 level. The formations of the multicomponent clusters are predicted based on thermodynamics, involving proton transfer and hydrogen bonding interactions. Oxalic acid can synergistically promote the formation of the sulfuric acid–dimethylamine–oxalic acid–water system while inhibiting this with the addition of more sulfuric acid molecules. The results of hydrate distribution show that un-hydrate clusters play a dominant role during formation. Moreover, dimethylamine and oxalic acid have similar effects on Rayleigh scattering properties, and the clusters involving complex mixtures of compounds can have high optical activities.

---

1. Introduction

Global and regional models show that new particle formation (NPF) is a significant source of atmospheric aerosols and cloud condensation nuclei,^1–3 which can affect the earth's radiation balance and global climate change through cloud physics and precipitation processes.^4,5 Ultrafine particles generated by the new particles also have a significant impact on human health,⁶ contributing to asthma and cancer, by destroying cell membranes and generating free radicals. The direct measurement of the physicochemical properties of newly formed particles and their precursors in the ambient atmosphere is the basis of studying the formation mechanisms of new particles, and it is also one of the most challenging studies in the field of atmospheric chemistry. Several methods, including field observation, laboratory simulation, and model calculations, are important means to investigate the formation mechanisms of new particles. At present, the instrumentation used for new particle formation research is improving, but there are still great limitations in the study of nucleation mechanisms.

Gaseous sulfuric acid (H₂SO₄, SA) has been widely identified as a crucial precursor involved in the nucleation process.^7,8 However, the traditional sulfuric acid–water (H₂O, W) binary homogeneous nucleation theory, as well as activated nucleation and kinetic nucleation theory based on the quantitative relationship between gaseous sulfuric acid and nucleation rate, can explain the low nucleation rate, but cannot fully explain the new particle formation events with high nucleation rates.^9,10 Therefore, substances that can reduce the saturated vapor pressure of gaseous sulfuric acid and promote nucleation have been considered, such as sulfuric acid–water–ammonia ternary nucleation,^11,12 ion-induced nucleation,¹³ and iodine participation in nucleation.^14,15 Due to the high concentration of volatile organic compounds (VOC) in the atmosphere, the low volatility of their oxidation products is also considered to be involved in the formation of new particles.¹⁶ Many organic compounds, including organic acids and amines, have experimentally been shown to play an important role in the formation of new particles.^17–20 Compared with ammonia, organic amine and sulfuric acid molecules can combine to form a more stable cluster, which has a significant impact on the concentration of newly formed particles.^8,12,21–24 Smoke chamber studies have shown that adding amines, aromatic acids, or pinonic acid to the sulfuric acid–water system can significantly increase the nucleation capacity of sulfuric acid, to levels matching the nucleation rate in the atmosphere.^25–27 Field observations also revealed a significant correlation between atmospheric organic acid content and nucleation rates.²⁸ Model calculations performed by Paasonen et al.²⁹ and Wang et al.³⁰ can also reproduce the nucleation process in the atmosphere. Although organic acids play an important role in NPF, their formation mechanisms have not been clarified.

As one of the most abundant organic species in the atmosphere, dicarboxylic acids, which have lower vapor pressures than monocarboxylic acids, may play an important role in particle formation.³¹ Anthropogenic and biological hydrocarbon emissions and photochemical oxidation can produce large quantities of organic acids such as formic acid, acetic acid, oxalic acid, malonic acid, and succinic acid. The concentrations of common organic acids are 10⁸ to 10¹¹ cm⁻³, close to that of ammonia in the atmosphere, and greater than amines by about 10 to 1000 times.^32,33 Low molecular weight dicarboxylic acids have been confirmed to significantly promote the nucleation of SA and subsequent particle growth.^25,34–36 Oxalic acid (C₂H₂O₄, OA) is one of the most common dicarboxylic acids with a gas phase concentration in the range of 9.3 × 10¹⁰ to 5.4 × 10¹² cm⁻³.³⁷ Additionally, OA is a major constituent of aerosol particles.^38,39 Xu et al. stated that OA charges positively and can stabilize sulfuric acid–oxalic acid–water complexes to promote NPF in the atmosphere.³⁵ Meanwhile, several studies also suggested that OA participates in the formation and growth of particles based on predictions for clusters of OA–NH₃–W,^40,41 OA–SA–W/NH₃/methylamine (MA),^42–44 OA–methanesulfonic–MA–W,^45,46 and OA–dimethylamine (CH₃NHCH₃, DMA)–W.⁴⁷ The thermodynamic properties of amines may reveal the potential synergistic effects of SA–OA–MA on the formation of an initial cluster and subsequent growth.⁴⁴ As one of the most common and strongest bases in the atmosphere, DMA has been verified to enhance neutral and ion-induced SA–W nucleation.^26,48,49 Previous studies indicated that molecular complexes containing DMA and OA may play important roles in affecting local atmospheric conditions.^42,47 The combined contributions of OA and DMA to induce SA–W nucleation remains unknown. Therefore, the effect of OA on the nucleation of SA–DMA–W clusters deserves examination.

However, few studies have focused on the molecular mechanisms of organic acids participating in the nucleation system of sulfuric acid–dimethylamine–water, and the effects of organic acids on molecular clusters remain unclarified. Here, the structures and thermodynamics of SA_m.DMA.OA.W_n (m = 1–2, n = 0–4) are investigated. Meanwhile, topological analysis, atmospheric relevance, concentration ratio, and Rayleigh scattering properties are also investigated to better understand the contributions of mixed precursors to NPF.

2. Methods

To sample the cluster structures, we employ our recently developed systematic sampling technique, where the basin-hopping (BH) algorithm coupled with semiempirical PM7 is implemented in MOPAC 2016.^47,50–53 For each cluster size, four independent BH searches are conducted, and a total of 500 sample structures for each search at the Boltzmann temperature are identified. Two steps are performed to obtain the low energy configurations for each cluster size. First, the BH algorithm generates initial isomer geometries by random displacement of the molecules and then obtains the local minimal structures using semi-empirical PM7 methods. Secondly, the initially optimized low-energy structure is used to judge whether the energy of newly generated geometries is lower, and if lower, then the initial structure will be replaced, otherwise, the original is retained. The most stable isomers within 5 kcal mol⁻¹ are optimized using the M06-2X method with 6-311++G(2d,p) basis sets. The optimization of cluster configurations and frequency calculations are performed using Gaussian 09 to ensure that no imaginary frequencies existed.⁵⁴ The single point energies of all the selected stable isomers are calculated at the DF-LMP2-F12/VDZ-F12 level of theory in the Molpro program.⁵⁵

Based on previous benchmark studies,^47,56–58 the M06-2X method should perform reliably in evaluating the electronic energy of organic clusters. Meanwhile, the 6-311++G(2d,p) basis set is applied in the current system consisting of DMA, OA, and W,⁴⁷ and the results demonstrated that decreasing the basis set from 6-311++G(3df,3pd) to 6-311++G(2d,p) can greatly reduce the calculation time and only causes minor errors in the thermal contribution to the free energy and subsequent single point energy calculation. In conclusion, the DF-LMP2-F12/VDZ-F12//M06-2X/6-311++G(2d,p) can achieve reasonable balance between computational efficiency and accuracy. The detailed benchmark information was provided in a previous study.⁴⁷

The amounts of hydrogen bonding and proton transfer, and the specific molecular configurations, offer better metrics to estimate the strength of intermolecular interaction and stability in the cluster. Therefore, the non-covalent interactions of the clusters are investigated, implemented in Multiwfn 3.8,⁵⁹ and visualized using the visual molecular dynamics (VMD) program.⁶⁰

In this study, the optical properties of the complex pre-nucleation clusters consisting of acid, amine, organic acid, and water molecules are elucidated. Light scattering intensities (, a.u.), the isotropic mean polarizabilities ([small alpha, Greek, macron], a.u.), anisotropic polarizabilities (Δα, a.u.), and depolarization ratio (σ_n) are performed at the CAM-B3LYP/aug-cc-pVDZ level of theory. Previous studies^61,62 successfully employed CAM-B3LYP/aug-cc-pVDZ to calculate the optical properties. This method effectively balances accuracy and efficiency, yielding good agreement with experimental, CCSD(T), and MP2 results. The detailed calculation methods are introduced in the ESI,† including relative hydrate distribution, concentration ratio, and Rayleigh light scattering properties.

3. Results and discussion

3.1 Structural analysis

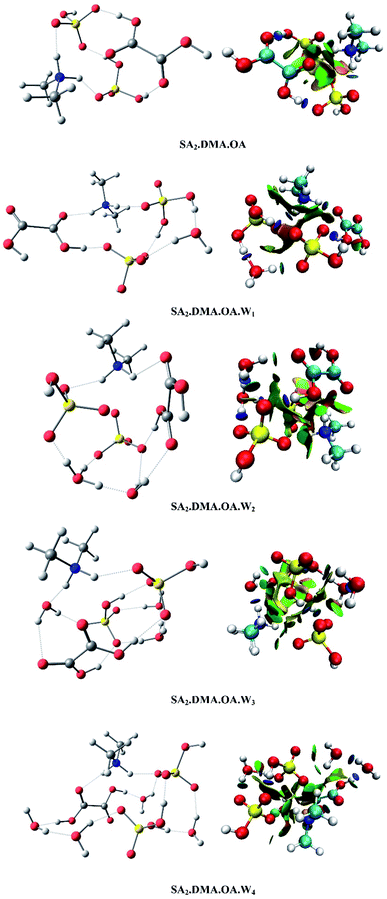
The most stable configurations of SA_m.DMA.OA.W_n (m = 1–2, n = 0–4) clusters are displayed in Fig. 1 and 2. The un-hydrated cluster of SA.DMA.OA occurs due to proton transfer by forming an [HSO₄]⁻[(CH₃)₂NH₂]⁺ ion pair, creating a circular planar structure through hydrogen bonding. When water molecules are added, the structures of clusters gradually shift from ring structures to complicated cage structures. For SA.DMA.OA.W₁ and SA.DMA.OA.W₂ clusters, proton transfer takes place between SA and DMA, and a hydrogen atom of OA is transferred to SA at the same time. When added to the second SA molecule, two protons are transferred to form two ion pairs of [HSO₄]⁻[(CH₃)₂NH₂]⁺ and [HSO₄]⁻[H₃O]⁺, in which two sulfuric acids provide two protons, and DMA or W act as a proton acceptor, respectively. In conclusion, as the number of precursors increases, the complexity of structures, and the number of hydrogen and proton transfer increases. Meanwhile, although OA does not directly participate in proton transfer as a donor, it promotes acid–base proton transfer indirectly through hydrogen atom transfer.

Fig. 1 Global minima of SA.DMA.OA.W_n (n = 0–4) calculated at the M06-2x/6-311+G(2d,p) level and the corresponding isosurfaces (s = 0.5 a.u.) are presented.

Fig. 2 Global minima of SA.DMA.OA.W_n (n = 0–4) calculated at the M06-2x/6-311+G(2d,p) level and the corresponding isosurfaces (s = 0.5 a.u.) are presented.

Visualization of the non-covalent interactions in real space can be helpful to confirm the intermolecular non-covalent and covalent interactions of SA_m.DMA.OA.W_n (m = 1–2, n = 0–4) clusters. In the right half of Fig. 1 and 2, the reduced gradient isosurfaces (s = 0.5 a.u.) are shown, where the blue represents hydrogen bonds, green represents van der Waals forces, and red represents steric hindrance. As shown in Fig. 1 and 2, the number of hydrogen increases, and the geometries become more complex as the number of water molecules increases, and the reduced gradient isosurfaces agree with the previous structural analysis.

Proton transfer from the acid molecules to base molecules is dependent on the strength of the acids and bases.⁶³ The proton transfer parameter (ρ_PT, Å),^64,65 which reflects the degree of proton transfer in the hydrogen bond and includes the hydrogen shorting and covalent hydrogen prolongation, is determined to evaluate the degree of ionization. The formula is given by:

ρ_PT = (r_OH − r⁰_OH) − (r_H⋯N − r⁰_H⋯N)

here, r_OH and r⁰_OH represent the distance of the hydrogen bond in SA or OA in the clusters and the O–H distance in the free monomers, respectively. r_H⋯N and r⁰_H⋯N are the distance of H–N in the SA_m.DMA.OA.W_n (m = 1–2, n = 0–4) and the H–N distance in fully protonated DMA, respectively. Proton transfer occurs in the clusters where the second term (r_H⋯N − r⁰_H⋯N) is zero and ρ_PT has a positive value.

Table 1 presents the proton transfer parameters of SA_m.DMA.OA.W_n (m = 1–2, n = 0–4) clusters. The proton transfer parameters are positive for all cluster sizes, which indicates that proton transfer takes place and forms an [HSO₄]⁻[(CH₃)₂NH₂]⁺ ion pair, where SA is the proton donor and DMA is the acceptor. Meanwhile, in SA₂.DMA.OA.W_n clusters with two or three water molecules, proton transfer occurs between sulfuric acid and water to form an [HSO₄]⁻[H₃O]⁺ ion pair, in which SA is the proton donor and W is the acceptor. In conclusion, the number of proton transfers does not exceed the number of SA molecules in the SA_m.DMA.OA.W_n (m = 1–2, n = 0–4) clusters.

Table 1 Proton transfer parameter (ρ_PT, Å) for SA_m.DMA.OA.W_n (m = 1–2, n = 0–4) clusters. The total number of proton transfers (n) and the proton donor and acceptor are also presented

Cluster	rOH (Å)	rH⋯N (Å)	ρPT (Å)	Proton donor	Proton accept	n
SA.DMA.OA	1.68	1.032	0.724	SA	DMA	1
SA.DMA.OA.W1	1.786	1.04	0.812	SA	DMA	1
SA.DMA.OA.W2	1.803	1.048	0.819	SA	DMA	1
SA.DMA.OA.W3	1.911	1.047	0.924	SA	DMA	1
SA.DMA.OA.W4	1.668	1.025	0.726	SA	DMA	1
SA2.DMA.OA	1.813	1.03	0.848	SA	DMA	1
SA2.DMA.OA.W1	1.773	1.031	0.808	SA	DMA	1
SA2.DMA.OA.W2	1.987	1.027	1.023	SA	DMA	2
	1.607	1.043	0.596	SA	H2O
SA2.DMA.OA.W3	1.95	1.051	0.957	SA	DMA	2
	1.437	0.992	0.527	SA	H2O
SA2.DMA.OA.W4	1.83	1.027	0.87	SA	DMA	1

---

3.2 Thermochemical analysis

Analysis of the thermodynamic properties is necessary to explain the molecular interactions and nucleation mechanisms. Considering multiple collision methods, five typical reaction paths are summarized as follows. Tables 2 and 3 present reaction Gibbs free energies (ΔG, kcal mol⁻¹) of the most stable clusters associated with the six reaction paths, considering an ambient temperature of 298.15 K. The formation of electronic energies (ΔE, kcal mol⁻¹) and enthalpies (ΔH, kcal mol⁻¹) are listed in Tables S1–S6.† The detailed reaction paths are given by:

Path 1: ΔG = G_{SAm.DMA.OA.Wn} − mG_SA − G_DMA − G_OA− nG_W

Path 2: ΔG = G_{SAm.DMA.OA.Wn} − G_{SAm.DMA.OA.Wn−1} − G_W

Path 3: ΔG = G_{SAm.DMA.OA.Wn} − G_SAm.DMA.Wn − G_OA

Path 4: ΔG = G_{SAm.DMA.OA.Wn} − G_SA.DMA − (m − 1)G_SA − G_OA − nG_W

Path 5: ΔG = G_{SAm.DMA.OA.Wn} − G_SA.OA − (m − 1)G_SA − G_DMA − nG_W

Path 6: ΔG = G_{SAm.DMA.OA.Wn} − G_DMA.OA − mG_SA − nG_W

Table 2 Gibbs free energies at 298.15 K (ΔG) for SA_m.DMA.OA.W_n (m = 1–2, n = 0–4) according to reaction paths 1–3. Energies are calculated at DF-LMP2-F12/VDZ-F12//M06-2x/6-311+G(2d,p) level of theory (in kcal mol⁻¹)

Cluster	Path 1	Path 2	Path 3
SA.DMA.OA	−19.83		−6.14
SA.DMA.OA.W1	−21.30	−1.47	−4.66
SA.DMA.OA.W2	−20.75	0.56	−4.53
SA.DMA.OA.W3	−16.19	2.84	−0.63
SA.DMA.OA.W4	−16.82	−0.63	−2.02
SA2.DMA.OA	−29.85		−0.09
SA2.DMA.OA.W1	−29.44	−0.11	−0.31
SA2.DMA.OA.W2	−30.14	−1.26	−0.76
SA2.DMA.OA.W3	−33.27	1.00	3.62
SA2.DMA.OA.W4	−27.45	1.69	6.55

---

Table 3 Gibbs free energies at 298.15 K (ΔG) for SA_m.DMA.OA.W_n (m = 1–2, n = 0–4) according to reaction paths 4–6. Energies are calculated at DF-LMP2-F12/VDZ-F12//M06-2x/6-311+G(2d,p) level of theory (in kcal mol⁻¹)

Cluster	Path 4	Path 5	Path 6
SA.DMA.OA	−6.14	−17.45	−15.68
SA.DMA.OA.W1	−7.61	−18.92	−17.14
SA.DMA.OA.W2	−7.06	−18.37	−16.59
SA.DMA.OA.W3	−2.50	−13.81	−12.03
SA.DMA.OA.W4	−3.12	−14.43	−12.66
SA2.DMA.OA	−16.15	−27.46	−25.69
SA2.DMA.OA.W1	−15.75	−27.06	−25.28
SA2.DMA.OA.W2	−16.44	−27.75	−25.98
SA2.DMA.OA.W3	−15.44	−26.75	−24.97
SA2.DMA.OA.W4	−13.76	−25.07	−23.29

---

Path 1 presents the energy change of SA_m.DMA.OA.W_n clusters formed by four different monomer collisions. As shown in Table 2, the Gibbs free energy changes for each hydration step are invariably negative. For SA.DMA.OA.W_n clusters, SA.DMA.OA.W₁ shows the most negative value, the subsequent addition of water is less favorable for formation. The hydration of SA₂.DMA.OA.W_n is stronger than that of SA.DMA.OA.W_n, and SA₂.DMA.OA.W₃ is the most favorable form. The Gibbs free energy drops sharply when the fourth water molecule is added, suggesting that adding more water molecules may be difficult.

The stepwise hydration free energies of SA_m.DMA.OA.W_n clusters are summarized in Table 2. Half of the reactions of step-by-step addition of water molecules are unfavorable, with small positive values for Gibbs energies. The small change of Gibbs free energy per water molecule is caused by the recombination of the hydrogen bond network during hydration, which is due to the increase of volume and size and the entropy loss driven by more water molecules joining the parent cluster. These results are consistent with the previous study of SA.MA.NH₃.W_n.⁵⁰

Reaction path 3 estimates the impact of OA on the formation of stable clusters consisting of SA, DMA, and W under atmospheric conditions. As seen in Table 2, the OA affinities to nucleating SA_m.DMA.W_n clusters strongly depend on the molar fraction of sulfuric acid and water. For SA.DMA.W_n clusters, the affinity gradually decreases as the water content grows. When the clusters contain two sulfuric acids, the affinity of OA declines sharply, and the Gibbs free energies become disfavored when more than two water molecules added. These findings suggest that OA contributes to a synergistic effect in SA.DMA.OA.W_n clusters, while the synergistic effect is weakened as the second sulfuric acid is added, and then disappears with the addition of water molecules.

Hydration of particle formation has been proposed to depend strongly on the initial cluster nucleus. Here, three initial cluster nuclei, such as SA.DMA, SA.OA, and DMA.OA, are discussed in detail. The formation Gibbs free energies of SA_m.DMA.OA.W_n clusters associated with paths 4–6 are summarized in Table 3. The Gibbs free energy changes are all negative, which indicates that the initial cluster nucleus is capable of forming stable pre-nucleation clusters. The order of ΔG values is SA.OA < DMA.OA < SA.DMA in all cases, which implies that the initial cluster nucleus of SA.OA has a significant effect on stabilizing DMA and initiates acid–base reactions. The initial cluster nucleus of SA.DMA is more stable than that of SA.OA and DMA.OA, because the proton transfer reaction occurs in the SA.DMA nucleus, while for SA.OA and DMA.OA nuclei, adding water molecules or other monomers is necessary to effectively promote proton transfer and form stable clusters.

Comparing the six reaction paths, the monomer collision reaction is more favorable than other paths, while the stepwise hydration of the SA_m.DMA.OA.W_n clusters is slightly favorable. In addition, the initial cluster nucleus plays an important role in SA_m.DMA.OA.W_n cluster formation, exhibiting formation Gibbs free energies that are close to path 1, especially for the SA.OA and DMA.OA nuclei, which indicates that the two paths are competitive with path 1. The synergistic effect, or multiple driving forces, can promote the formation of SA.DMA.OA.W_n clusters, which indicates that the existence of OA can enhance the stability of SA.DMA.W_n clusters.

3.3 Hydrate distribution and influence of humidity

Several studies have shown that hydration plays an important role in the nucleation of organic acid and amine, which can affect proton transfer.^52,66 Hydration is related to relative humidity (RH) in the atmosphere. To better understand the extent of hydration under different circumstances, hydration distributions at different RH (20%, 40%, 60%, 80%, and 100%) are performed. The detailed method and explanation are shown in the ESI.†

As shown in Fig. 3a, for SA.DMA.OA.W_n (n = 0–4), the un-hydrated cluster always plays a dominant role, the monohydrate accounts for a small proportion, while the dihydrate, trihydrate, and tetrahydrate are almost nonexistent. As the RH increase from 20 to 100%, the un-hydrated cluster steadily decreases from 93 to 73%, while the proportion of the monohydrate cluster increases gradually from 7 to 27%. Fig. 3b displays the distribution of hydrated SA₂.DMA.OA clusters. Un-hydrated clusters dominate the cluster distribution at various RH, with the percentage decreasing from 99 to 95%. With increasing RH, the percentage of the monohydrate and dehydrate increase slightly from 2 to 4%, and 0 to 1%, respectively. Larger hydrates clusters are practically nonexistent. Hence, the hydration of SA₂.DMA.OA clusters is so weak that it stays completely un-hydrated, no matter how the RH increases, which indicates that the hydrate distribution of SA₂.DMA.OA clusters is not sensitive to RH.

Fig. 3 Hydrate distribution of (a) SA.DMA.OA.W_n (n = 0–4) and (b) SA₂.DMA.OA.W_n (n = 0–4) clusters at five different RH.

In conclusion, larger hydrate clusters with more than two water molecules are almost non-existent even when the relative humidity reaches 100%. These results are consistent with organic clusters investigated in previous studies, such as methylamine–ammonia–sulfuric acid,⁵⁰ sulfuric acid–amide,⁶⁷ acetic acid–dimethylamine,⁵¹ and glutaric acid–amine hydration clusters.⁶⁸ These results suggest that structural effects are related to hydration. The addition of many water molecules increases both its mass and volume and then affects the rates of collisions between clusters. Thus, hydration plays a dilution role in the structure, making the clusters less stable, which is in accordance with the Gibbs free energy changes in stepwise hydration reactions (Table 2). Oxalic acid contains two hydrophilic hydroxyl groups, but not enough to compensate for its dilution. In addition, from the perspective of the reaction paths, hydration does not effectively promote the formation of clusters. Thus, the water retention capacity of SA_m.DMA.OA clusters is weak, indicating that the un-hydrated cluster is the main form under the most tropospherically reasonable conditions.

3.4 Atmospheric relevance

Previous research on NPF has shown that the formation of a stable SA dimer is a crucial step in the acid–base cluster formation and growth.^29,69,70 It is assumed that the SA dimer composed of two sulfuric acids, two base molecules, and multiple water molecules is large and active enough to grow by colliding with acids other than SA. Nadykto et al.⁷¹ investigated the concentration ratios of ternary dimers, with ammonia or methylamine, to SA₂.W_n dimers. However, the concentration ratios for clusters consisting of organic acids and bases are unexplored, which may have different effects on NPF. In this section, the concentration ratios are calculated to evaluate the maximum new nucleation production and its correlation with the concentration of organic acids and bases, RH, and other relevant parameters. The detailed computational methods are provided in the ESI.†

From Fig. 4, two important conclusions can be found based on the concentration ratio curves. Firstly, the concentration ratio of SA₂.DAM.OA.W_n to SA₂.W_n decreases slightly with the increase of RH, which indicates that low RH is the favorable condition, which can effectively support the formation of stable SA₂.DAM.OA.W_n clusters. This result is consistent with the previous study that investigated quaternary clusters containing two different bases by Chunyu Wang;⁵⁰ however, this result is different from the SA₂.MA.W and SA₂.NH₃.W systems,⁷¹ where the concentration ratio is sensitive to the RH and SA₂.MA.W dominates over SA₂.W_n under dry and low RH conditions only. The RH dependency of the hydrated SA₂.DAM.OA and SA₂.MA.NH₃ clusters are almost negligible, while the fractions of the hydrated SA₂.MA, and SA₂.NH₃ clusters decrease quickly with increasing RH. Secondly, the concentration ratio depends strongly on the atmospheric concentrations of DMA and OA, with significant positive correlation. Comparing Fig. 4a and 4b, the [SA₂.DMA.OA.W_n]/[SA₂.W_n] ratio is much lower with [OA] and [DMA] exceeding 1 ppb. However, SA₂.DMA.W_n clusters dominate over SA₂.W_n, even with DMA at 0.01 ppt, which implies that the stability of SA₂.DAM.W_n clusters is large enough to overcome low concentrations ranging from a fraction of ppt to several ppt.

Fig. 4 Concentration ratios of SA₂.DMA.OA.W_n (a) and SA₂.DMA.W_n (b) clusters to binary SA₂.W_n clusters as a function of RH. Different symbols in part a refer to the 1 ppb background concentration of DMA at different concentration of OA, or 1 ppb background concentration of OA at different concentration of DMA.

Fig. 5 Rayleigh scattering and polarizability properties of clusters: (a) isotropic mean polarizability; (b) Rayleigh light scattering intensity; (c) anisotropic polarizability; (d) depolarization ratio of water molecules for SA_m.DMA.OA.W_n (m = 1–2, n = 0–4) clusters.

3.5 Optical properties

Atmospheric aerosols can indirectly affect the climate through scattering or absorbing the incident solar radiation.⁷² The light scattering off clusters and particles with diameters much smaller than the wavelength of the incoming radiation is determined by the mechanism of Rayleigh scattering.⁷³ The presence of organic acid molecules contributes to aerosol particle formation and influences the climate-relevant particle properties such as light scattering. However, it is still unclear which species of organic acids are involved in NPF processes. Here, the Rayleigh scattering properties of quaternary pre-nucleation clusters involving organic acids are investigated for the first time.

The Rayleigh light scattering and cluster polarizability properties are presented in Fig. 5. The isotropic mean polarizabilities [small alpha, Greek, macron] are dependent on the number of water molecules, increasing linearly. In Fig. 5b, the Rayleigh scattering intensity of has a non-linear dependence on the number of water molecules, following the trend of a second-order polynomial with correlation coefficients of 0.99565 and 0.99001, respectively. This phenomenon can be attributed to the gradually increasing isotropic mean polarizabilities [small alpha, Greek, macron], which play a dominant role in the Rayleigh scattering intensity. When a second SA molecule is added, the [small alpha, Greek, macron] and increase significantly, which suggests that SA has a more significant influence on the Rayleigh scattering properties. These results are consistent with SA.W_n,⁶¹ DMA.W_n,⁶² SA.OA.W_n,⁴³ and glutaric acid–ammonia/amine/amide clusters.⁶⁸

Fig. 5c and d present the anisotropic polarizabilities Δα and depolarization ratio σ_n as functions of the number of water molecules in SA_m.DAM.OA.W_n clusters. The Δα and σ_n are different from [small alpha, Greek, macron] and , which have no clear dependence on the number of water molecules. The addition of sulfuric acid enhances Δα more effectively. The depolarization ratio σ_n fluctuates from 0.058 to 0.077, which is due to an increase of the [small alpha, Greek, macron] in combination with the Δα, playing a leading role in the depolarization ratio. In Fig. 1 and 2, the structure gradually varies from quasi-planar ring structures to a more complex cage structure as the number of water molecules increases. This follows the expectation that clusters transition from a molecular cluster into a spherical isotropic particle.⁶¹

Previous studies have reported that Rayleigh scattering is not only dependent on the size but also related to the composition of the precursors that participated in the pre-nucleation.⁶⁸ To compare the effects of different precursors on Rayleigh scattering properties, the isotropic mean polarizabilities and Rayleigh scattering intensities for SA.W_n, SA.DMA.W_n, and DMA.OA.W_n (n = 1–4) clusters are provided in the ESI,† and the information regarding SA.OA.W_n (n = 1–4) clusters is available in the literature.⁴³ The [small alpha, Greek, macron] (88–116 a.u.) and (360 000–610 000 a.u.) of DMA.OA.W_n are slightly larger than those of the SA.DMA.W_n clusters, with [small alpha, Greek, macron] (85–113 a.u.) and (320 000–580 000 a.u.). This finding indicates that SA can enhance cluster stability more strongly than OA, while OA has more influence on the Rayleigh scattering properties. In addition, the two optical properties ([small alpha, Greek, macron] = 88–113 a.u., = 370 000–580 000 a.u.) are close for SA.OA.W_n and SA.DMA.W_n clusters, which indicates that OA and DMA have similar effects on optical properties. For SA.DMA.OA.W_n, [small alpha, Greek, macron] (123–151 a.u.) and (810 000–1 200 000 a.u.) are larger than other clusters, which may suggest that clusters involving complex mixtures of compounds can have high optical activities.

4. Conclusions

The configurations and thermodynamics of SA_m.DAM.OA.W_n (m = 1–2, n = 0–4) have been calculated at the DF-LMP2-F12/VDZ-F12//M06-2X/6-311++G(2d,p) level. Hydrogen bonding and proton transfer enhance the stability of SA_m.DAM.OA.W_n clusters. The Gibbs free energies of different reaction pathways imply that the initial cluster nucleus plays an important role in SA_m.DMA.OA.W_n cluster formation, which is competitive with the monomer collision reaction, while the stepwise hydration is unfavorable with positive Gibbs free energies. Moreover, our results show that the synergistic effects of OA can promote nucleation while inhibiting when the addition of more sulfuric acid molecules. As humidity increases, the distribution of un-hydrated clusters decreases slightly, and the un-hydrated clusters are always dominant. The concentration ratio of SA₂.DAM.OA.W_n to SA₂.W_n depends on the concentrations of the precursors and RH. Finally, DMA and OA have similar effect on Rayleigh scattering properties, and the clusters involving complex mixtures of compounds could make high optical activity.

This theoretical study demonstrates the formation of aerosol particles from the sulfuric acid–carboxylic acid–amine, which may provide a reference for understanding the role of organic acids in nucleation events. Further quantitative experimental studies and theoretical simulations are required to study the synergistic effects involved in complex mixtures of compounds and their dependence on the actual atmospheric environment.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Innovative Development Project of Anhui Meteorological Bureau (grant no. CXB202101), the Natural Science Foundation of Anhui Province (grant no. 2108085QD183).

References

1. J. Merikanto, D. Spracklen, G. Mann, S. Pickering and K. Carslaw, Atmos. Chem. Phys., 2009, 9, 8601–8616.
2. D. V. Spracklen, K. S. Carslaw, M. Kulmala, V. M. Kerminen, S. L. Sihto, I. Riipinen, J. Merikanto, G. W. Mann, M. P. Chipperfield and A. Wiedensohler, Geophys. Res. Lett., 2008, 35, L06808.
3. J. Pierce, W. Leaitch, J. Liggio, D. Westervelt, C. Wainwright, J. Abbatt, L. Ahlm, W. Al-Basheer, D. Cziczo and K. Hayden, Atmos. Chem. Phys., 2012, 12, 3147–3163.
4. K. Carslaw, L. Lee, C. Reddington, K. Pringle, A. Rap, P. Forster, G. Mann, D. Spracklen, M. Woodhouse and L. Regayre, Nature, 2013, 503, 67–71.
5. V. M. Kerminen, H. Lihavainen, M. Komppula, Y. Viisanen and M. Kulmala, Geophys. Res. Lett., 2005, 32, L14803.
6. C. Sioutas, R. J. Delfino and M. Singh, Environ. Health Perspect., 2005, 113, 947–955.
7. M. Sipilä, T. Berndt, T. Petäjä, D. Brus, J. Vanhanen, F. Stratmann, J. Patokoski, R. L. Mauldin III, A.-P. Hyvärinen and H. Lihavainen, Science, 2010, 327, 1243–1246.
8. T. Kurten, V. Loukonen, H. Vehkamäki and M. Kulmala, Atmos. Chem. Phys., 2008, 8, 4095–4103.
9. M. Kulmala, K. Lehtinen and A. Laaksonen, Atmos. Chem. Phys., 2006, 6, 787–793.
10. Z. Wang, M. Hu, D. Yue, J. Zheng, R. Zhang, A. Wiedensohler, Z. Wu, T. Nieminen and M. Boy, Atmos. Chem. Phys., 2011, 11, 12663–12671.
11. M. Kulmala, L. Pirjola and J. M. Mäkelä, Nature, 2000, 404, 66–69.
12. V.-M. Kerminen, T. Petäjä, H. Manninen, P. Paasonen, T. Nieminen, M. Sipilä, H. Junninen, M. Ehn, S. Gagné and L. Laakso, Atmos. Chem. Phys., 2010, 10, 10829–10848.
13. J. Kirkby, J. Curtius, J. Almeida, E. Dunne, J. Duplissy, S. Ehrhart, A. Franchin, S. Gagné, L. Ickes and A. Kürten, Nature, 2011, 476, 429–433.
14. C. D. Dowd, J. Geophys. Res.: Atmos., 2001, 106, 1545–1549.
15. J. Allan, P. I. Williams, J. Najera, J. Whitehead, M. Flynn, J. Taylor, D. Liu, E. Darbyshire, L. Carpenter and R. Chance, Atmos. Chem. Phys., 2015, 15, 5599–5609.
16. N. Ng, M. Canagaratna, Q. Zhang, J. Jimenez, J. Tian, I. Ulbrich, J. Kroll, K. Docherty, P. Chhabra and R. Bahreini, Atmos. Chem. Phys., 2010, 10, 4625–4641.
17. J. N. Smith, M. Dunn, T. VanReken, K. Iida, M. R. Stolzenburg, P. H. McMurry and L. Huey, Geophys. Res. Lett., 2008, 35, L04808.
18. T. Berndt, F. Stratmann, M. Sipilä, J. Vanhanen, T. Petäjä, J. Mikkilä, A. Grüner, G. Spindler, L. Mauldin III and J. Curtius, Atmos. Chem. Phys., 2010, 10, 7101–7116.
19. I. G. Kavouras, N. Mihalopoulos and E. G. Stephanou, Nature, 1998, 395, 683–686.
20. L. Wang, A. F. Khalizov, J. Zheng, W. Xu, Y. Ma, V. Lal and R. Zhang, Nat. Geosci., 2010, 3, 238–242.
21. R. Zhang, A. Khalizov, L. Wang, M. Hu and W. Xu, Chem. Rev., 2012, 112, 1957–2011.
22. R. Zhang, Science, 2010, 328, 1366–1367.
23. B. Bzdek, D. Ridge and M. Johnston, Atmos. Chem. Phys., 2010, 10, 3495–3503.
24. B. Bzdek, D. Ridge and M. Johnston, Atmos. Chem. Phys., 2011, 11, 8735–8743.
25. R. Zhang, I. Suh, J. Zhao, D. Zhang, E. C. Fortner, X. Tie, L. T. Molina and M. J. Molina, Science, 2004, 304, 1487–1490.
26. J. Almeida, S. Schobesberger, A. Kürten, I. K. Ortega, O. Kupiainen-Määttä, A. P. Praplan, A. Adamov, A. Amorim, F. Bianchi and M. Breitenlechner, Nature, 2013, 502, 359–363.
27. F. Riccobono, S. Schobesberger, C. E. Scott, J. Dommen, I. K. Ortega, L. Rondo, J. Almeida, A. Amorim, F. Bianchi and M. Breitenlechner, Science, 2014, 344, 717–721.
28. M. Kulmala, J. Kontkanen, H. Junninen, K. Lehtipalo, H. E. Manninen, T. Nieminen, T. Petäjä, M. Sipilä, S. Schobesberger and P. Rantala, Science, 2013, 339, 943–946.
29. P. Paasonen, T. Olenius, O. Kupiainen, T. Kurten, T. Petäjä, W. Birmili, A. Hamed, M. Hu, L. G. Huey and C. Plass-Duelmer, Atmos. Chem. Phys., 2012, 12, 9113–9133.
30. Z. Wang, M. Hu, D. Mogensen, D. Yue, J. Zheng, R. Zhang, Y. Liu, B. Yuan, X. Li and M. Shao, Atmos. Chem. Phys., 2013, 13, 11157–11167.
31. B. Noziere, M. Kalberer, M. Claeys, J. Allan, B. D'Anna, S. Decesari, E. Finessi, M. Glasius, I. Grgic and J. F. Hamilton, Chem. Rev., 2015, 115, 3919–3983.
32. Y. I. Tsai, L.-Y. Hsieh, T.-H. Weng, Y.-C. Ma and S.-C. Kuo, Anal. Chim. Acta, 2008, 626, 78–88.
33. C. Pio, P. Silva, M. Cerqueira and T. Nunes, Atmos. Environ., 2005, 39, 1817–1827.
34. A. B. Nadykto and F. Yu, Chem. Phys. Lett., 2007, 435, 14–18.
35. Y. Xu, A. B. Nadykto, F. Yu, L. Jiang and W. Wang, J. Mol. Struct.: THEOCHEM, 2010, 951, 28–33.
36. Y. Xu, A. B. Nadykto, F. Yu, J. Herb and W. Wang, J. Phys. Chem. A, 2010, 114, 387–396.
37. P. K. Martinelango, P. K. Dasgupta and R. S. Al-Horr, Atmos. Environ., 2007, 41, 4258–4269.
38. X.-F. Huang, M. Hu, L.-Y. He and X.-Y. Tang, Atmos. Environ., 2005, 39, 2819–2827.
39. B. Zobrist, C. Marcolli, T. Koop, B. P. Luo, D. M. Murphy, U. Lohmann, A. A. Zardini, U. Krieger, T. Corti and D. J. Cziczo, Atmos. Chem. Phys., 2006, 6, 3115–3129.
40. X.-Q. Peng, T. Huang, S.-K. Miao, J. Chen, H. Wen, Y.-J. Feng, Y. Hong, C.-Y. Wang and W. Huang, RSC Adv., 2016, 6, 46582–46593.
41. X.-Q. Peng, Y.-R. Liu, T. Huang, S. Jiang and W. Huang, Phys. Chem. Chem. Phys., 2015, 17, 9552–9563.
42. W. Xu and R. Zhang, J. Phys. Chem. A, 2012, 116, 4539–4550.
43. S.-K. Miao, S. Jiang, J. Chen, Y. Ma, Y.-P. Zhu, Y. Wen, M.-M. Zhang and W. Huang, RSC Adv., 2015, 5, 48638–48646.
44. Y. Zhao, Y.-R. Liu, S. Jiang, T. Huang, Z.-H. Wang, C.-X. Xu, Y.-J. Feng and W. Huang, Atmos. Environ., 2020, 233, 117609.
45. K. D. Arquero, R. B. Gerber and B. J. Finlayson-Pitts, Environ. Sci. Technol., 2017, 51, 2124–2130.
46. K. D. Arquero, J. Xu, R. B. Gerber and B. J. Finlayson-Pitts, Phys. Chem. Chem. Phys., 2017, 19, 28286–28301.
47. J. Chen, S. Jiang, Y.-R. Liu, T. Huang, C.-Y. Wang, S.-K. Miao, Z.-Q. Wang, Y. Zhang and W. Huang, RSC Adv., 2017, 7, 6374–6388.
48. V. Loukonen, T. Kurtén, I. Ortega, H. Vehkamäki, A. A. Padua, K. Sellegri and M. Kulmala, Atmos. Chem. Phys., 2010, 10, 4961–4974.
49. W. Glasoe, K. Volz, B. Panta, N. Freshour, R. Bachman, D. Hanson, P. McMurry and C. Jen, J. Geophys. Res.: Atmos., 2015, 120, 1933–1950.
50. C.-Y. Wang, S. Jiang, Y.-R. Liu, H. Wen, Z.-Q. Wang, Y.-J. Han, T. Huang and W. Huang, J. Phys. Chem. A, 2018, 122, 3470–3479.
51. J. Li, Y.-J. Feng, S. Jiang, C.-Y. Wang, Y.-J. Han, C.-X. Xu, H. Wen, T. Huang, Y.-R. Liu and W. Huang, Atmos. Environ., 2019, 219, 117005.
52. Y.-J. Han, Y.-J. Feng, S.-K. Miao, S. Jiang, Y.-R. Liu, C.-Y. Wang, J. Chen, Z.-Q. Wang, T. Huang and J. Li, Phys. Chem. Chem. Phys., 2018, 20, 25780–25791.
53. Z.-Q. Wang, Y.-R. Liu, C.-Y. Wang, S. Jiang, Y.-J. Feng, T. Huang and W. Huang, Atmos. Environ., 2021, 263, 118683.
54. M. Frisch, G. Trucks, H. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. Petersson, Gaussian 09, revision D. 01, Gaussian Inc, Wallingford, CT, 2009.
55. H. Werner, P. Knowles, G. Knizia, F. Manby, M. Schütz, P. Celani, T. Korona, R. Lindh, A. Mitrushenkov and G. Rauhut, MOLPRO a package of ab initio programs molpro, version 2010.1, University College Cardiff Consultants Limited, Cardiff, UK, 2010.
56. Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157–167.
57. J. Elm, M. Bilde and K. V. Mikkelsen, J. Chem. Theory Comput., 2012, 8, 2071–2077.
58. J. Elm, M. Bilde and K. V. Mikkelsen, Phys. Chem. Chem. Phys., 2013, 15, 16442–16445.
59. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
60. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
61. J. Elm, P. Norman, M. Bilde and K. V. Mikkelsen, Phys. Chem. Chem. Phys., 2014, 16, 10883–10890.
62. J. Chen, S. Jiang, S.-K. Miao, X.-Q. Peng, Y. Ma, C.-Y. Wang, M.-M. Zhang, Y.-R. Liu and W. Huang, RSC Adv., 2015, 5, 91500–91515.
63. J. Xu, B. J. Finlayson-Pitts and R. B. Gerber, J. Phys. Chem. A, 2017, 121, 2377–2385.
64. I. J. Kurnig and S. Scheiner, Int. J. Quantum Chem., 1987, 32, 47–56.
65. S. W. Hunt, K. J. Higgins, M. B. Craddock, C. S. Brauer and K. R. Leopold, J. Am. Chem. Soc., 2003, 125, 13850–13860.
66. W. Xu and R. Zhang, J. Chem. Phys., 2013, 139, 064312.
67. P. Ge, G. Luo, Y. Luo, W. Huang, H. Xie and J. Chen, Chemosphere, 2018, 213, 453–462.
68. S. Ni, F. Bai and X. Pan, Chemosphere, 2021, 275, 130063.
69. T. Olenius, O. Kupiainen-Määttä, I. Ortega, T. Kurtén and H. Vehkamäki, J. Chem. Phys., 2013, 139, 084312.
70. J. Elm, N. Myllys and T. Kurtén, Mol. Phys., 2017, 115, 2168–2179.
71. A. B. Nadykto, J. Herb, F. Yu, Y. Xu and E. S. Nazarenko, Entropy, 2015, 17, 2764–2780.
72. J. Haywood and O. Boucher, Rev. Geophys., 2000, 38, 513–543.
73. J. W. Strutt, London, Edinburgh Dublin Philos. Mag. J. Sci., 1871, 41, 447–454.

---

Footnote

† Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ra03492a

---