Open Access Article
Open Access ArticleMolecular insights into the ‘defects’ network in the thermosets and the influence on the mechanical performance†
Fugui Zhao,
Haobo Zhang,
Dujuan Zhang,
Xiaomu Wang,
Dingxuan Wang,
Junying Zhang ,
Jue Cheng* and
Feng Gao
,
Jue Cheng* and
Feng Gao *
*
Key Laboratory of Carbon Fiber and Functional Polymers, Ministry of Education, Beijing University of Chemical Technology, Beijing 100029, People's Republic of China. E-mail: gaofeng@mail.buct.edu.cn; chengj@mail.buct.edu.cn
First published on 10th August 2022
Abstract
The introduction of ‘defects’ to the thermoset crosslinking network is one of the most applicable strategies for improving the modulus and toughness simultaneously. However, the reinforcement effect disappears when the ‘defects’ proportion exceeds the threshold. The speculated mechanism was that the aggregation and entanglement of the ‘defects’ chains changed the matrix topology, making the stacking structure more compact. However, the ‘defects’ are hardly directly observed in the experiment. As the result, the relationship between the ‘defects’ proportion and the package state of the matrix, and the effect on the material's mechanical performance was not explored. Herein, the network of bisphenol-A diglycidyl (DGEBA) with diethyltoluenediamine (DETDA) as the hardener was constructed using MD simulation, and n-butylamine was decorated on the matrix by replacing a proportion of DETDA acting as the ‘defects’. The results indicated that the aliphatic chains aggregated and entangled at a low concentration, occupying the voids in the rigid aromatic crosslinking structure, thus lowering the free volume. The strong non-bonding interactions drew the matrix segments close together, thus reinforcing the resin. However, the microphases formed by the aliphatic chains no longer filled the voids but created a new free volume and loosened the network when the content increased, which reduced the mechanical performance of the material. The experimental results were consistent with the findings in the simulations. The moduli of the resin increased with the increase in the n-butylamine content first and then declined. The maximum moduli of the thermosets was 3.4 GPa in S30, which was about 25% higher compared with the control; the corresponding elongation at break was 8.9%, which was about 46% improved compared with the control.
Introduction
Thermosets with outstanding mechanical properties, anticorrosion ability, and processing fluidity are widely used as structural components in a variety of fields, such as aerospace, aircraft, and automotives.1 It is one of the most primary targets of researchers to design and fabricate the thermosets with high strength and high toughness simultaneously; however, it remains a challenge.2 The moduli of cured thermosets were dominated by the 3D network structure, and it was one of the most straightforward strategies to enhance the thermosets' moduli by increasing the crosslinking degree.3 However, the dense crosslinking network limited the segments motion, thus greatly reducing the toughness of the material.4 As the result, there is a trade-off between the strength and toughness in the thermoset design and fabrication. Strategies were employed to reinforce the thermosets with lesser impact to the toughness in the recent decades. The participation of the elastomer particles was able to toughen the epoxy resin; however, the negative effects on the mechanical performance, such as the glass transition temperature (Tg), moduli, and viscosity, were not totally eliminated.5–9 The inducing of graphene10 and carbon nanotubes11 was able to improve the moduli without affecting the toughness and Tg. However, it was difficult to uniformly disperse the fillers with the nanoscale dimension into the thermosets.12Beside the participation of fillers, constructing the ‘defects’ in the thermoset matrix by designing or adjusting the network topology could also vary the physical and chemical properties.13–15 Our previous works introduced the aliphatic dangling chains as the ‘defects’ into the epoxy network, and the tensile strength was enhanced from 52.3 MPa to 98.5 MPa; the elongation at break was increased from 2.7% to 6.1%, and the tensile modulus was improved from 2.9 GPa to 3.1 GPa.15–17 Sharifi et al. added a solvent into the polymer matrix as the ‘defects’, thus increasing the volumetric energy capacity based on the Reactive Encapsulation of Solvent/Drying theory (RESD).13 The results showed that the toughness of the cured matrix was increased without a significantly change in the glassy moduli and Tg. Sharifi et al. then rearranged the polymer network heterogeneously into the nanoscale and created the ‘defects’ via the partially reacted substructure (PRS) processing method without changing the chemical composition.14 The results demonstrated the significantly improved fracture toughness, and the thermal and mechanical performance. Brian et al. constructed the ‘defects’ in the anhydride-cured epoxy matrix by introducing polydicyclopentadiene, which led to an increase in the strength and toughness simultaneously.18 Microphase separation was obtained after the introduction of the ‘defects’, which was supposed to toughen the thermosets; however, the corresponding strengthening mechanism is not clear.
In our previous work, it was speculated that the molecular chains involved in the ‘defects’ aggregated and entangled, thus changing the matrix topology and making the stacking structure more compact.15,16 The relationship between the intermolecular interactions and mechanical performance was studied in the recent decades. Varley et al. suggested that the modulus was mostly dependent on short-range motions rather than long-range microstructural variations, indicating that the crosslinking degree may not dominate the moduli.19 Morel et al. also pointed out that the dominating factor influencing the moduli was not the crosslinking density but the cohesive energy which, was reflected by the change in the free volume.20 Vallo et al. compared the moduli of amine-cured epoxy resins prepared with different stoichiometric ratios; the results showed that the moduli were dominated by the packing density and sub-vitreous relaxations.21 However, the influence of the free volume change caused by the ‘defects’ toward the mechanical performance is yet to be systematically studied as the ‘defects’ were difficult to be directly observed and quantified in the experiment because of the complexity and ambiguous decisive factors of the 3D network.
Molecular dynamics (MD) simulation was employed in this work for exploring the relationship between the ‘defects’ proportion and the package state of the matrix, and the effect on the material's mechanical performances. The MD simulation, as a theoretical calculation method for polymer simulation, has been proved to be effective in predicting the material properties in various fields, such as physics, chemistry, biology, and engineering.22–26 The MD simulation showed the feasibility in the epoxy system. Yarovsky et al. developed the static methodology and constructed the epoxy crosslinking models with the help of MD simulation.27 Varshney et al. established the cured epoxy structure using MD simulation and predicated the mechanical properties successfully.28 As a result, the MD simulation was recognized as a powerful and accurate tool to study the relationship between the structure and the properties of the epoxy systems. Li et al. explored the relationship between the evolution of the network topology and the glass transition temperature, yield stress, and stiffness using the MD simulation.29 Masoumi et al. monitored the epoxy resins' crosslinking structure with the help of MD simulation based on the accurate calculation of the glass transition temperature, coefficient of thermal expansion, and elastic constants.30 In the presented work, a rigid aromatic resin matrix was constructed using DGEBA with DETDA as the hardener. The flexible aliphatic n-butylamine chains were decorated on the DGEBA-EDTDA network, replacing a proportion of DETDA acting as the ‘defects’. The molar ratio between the epoxy group and the –NH2 groups was kept at 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 constantly in all the formulations. Li et al. demonstrated that the MD simulation could predict the mechanical performance of the DGEBA-DETDA system accurately.31 The radial distribution function (RDF) of the system was recorded to evaluate the aggregation. The cohesive bonding energy, X-ray spectra, and free volume of the system were determined for the quantitative evaluation of the ‘defects’. The tensile strength and glass transition temperature were determined, and the relationship between the ‘defects’ and the mechanical performance was constructed and discussed.
1 constantly in all the formulations. Li et al. demonstrated that the MD simulation could predict the mechanical performance of the DGEBA-DETDA system accurately.31 The radial distribution function (RDF) of the system was recorded to evaluate the aggregation. The cohesive bonding energy, X-ray spectra, and free volume of the system were determined for the quantitative evaluation of the ‘defects’. The tensile strength and glass transition temperature were determined, and the relationship between the ‘defects’ and the mechanical performance was constructed and discussed.
Results and discussion
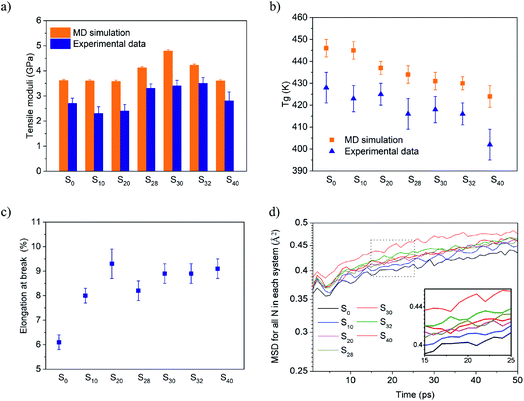
The formulation and abbreviation of each sample is demonstrated in Table 1. The rigid 3D network was constructed via the crosslinking of DGEBA with tetrafunctional DETDA. The flexible bifunctional n-butylamine was then induced into the system, replacing DETDA and creating the ‘defects’ in the matrix. The tensile moduli of all the samples were simulated with 1% deformation, and are plotted in Fig. 1a. Yang et al. reported that the MD simulation was able to predict the tensile moduli accurately with a small deformation rate.26 The tensile moduli of the net DGEBA-DETDA thermosets (S0) calculated by the dynamic simulation was about 3.6 ± 0.12 GPa with a transfer rate more than 90% in this work. Also, the corresponding experimental value was 2.7 ± 0.10 GPa, which was lower than the simulated one as the crosslinking degree was difficult to reach the simulation level under the real experimental condition. The simulated tensile moduli of S0, S10, and S20 showed no significant difference when n-butylamine was induced with low concentration. However, the tensile moduli increased to 4.1 ± 0.07 GPa, 4.7 ± 0.05 GPa, and 4.2 ± 0.02 GPa for S28, S30, and S32, respectively, with the content of n-butylamine. The experimental tensile strength with 1% deformation showed a similar changing trend as that of the simulated values, and the corresponding values for S28, S30, and S32 were 3.3 ± 0.18 GPa, 3.4 ± 0.22 Gpa, and 3.5 ± 0.24 GPa, respectively. However, the simulated and experimental tensile moduli for S40 reverted back to 3.6 ± 0.05 GPa and 2.8 ± 0.36 GPa, respectively, indicating that the ‘defects’ only reinforced the thermosets at a low concentration. The Tg was defined as the intersection of the bilinear fitting of the volume–temperature data points in the MD simulation26 (the fitting curves are presented in the ESI section†), and is demonstrated by Fig. 1b. The Tg decreased gradually from 446 ± 4 K for S0 to 424 ± 5 K for S40 with the increase in the n-butylamine content. The experimental Tg was measured by DSC and plotted, as shown in Fig. 1b, which followed the same changing trend of the simulated values, however, significantly lower. The reason was that the cooling rate of DSC measurement was 10 K min−1, which was about 10 orders lower than that of the MD simulation (10 K/50 ps), and the glass transition lagged in the DSC measurement. The toughness of the thermosets was evaluated by the elongation at break, which was plotted as shown in Fig. 1c. The S0 sample broke with only 6.1 ± 0.3% elongation due to the rigid 3D network structure of DGEBA-DETDA, and the stress–strain curves were presented by the ESI section.† The elongation at break increased with the introduction of n-butylamine, which became 8.1 ± 0.4% and 9.3 ± 0.6% for S10 and S20 respectively, and remained about 9% for S28 to S32. Interestingly, S20 showed a significantly higher elongation at break than that of S28, and the proposed explanation was the compact network of S20 caused by the entanglement of the aliphatic chains, which is discussed in the next section. The MD simulation can hardly predict the elongation at break due to the high deformation rate. However, the toughness could be roughly reflected by the mean square displacement (MSD) of the atoms in the matrix.26,34–36 Fig. 1d presented the MSD of nitrogen in these systems. Fig. 1d inset clearly shows that the flexibility of the N atom increased when a portion of the rigid aromatic network was replaced by the aliphatic chains, showing an increase in the toughness caused by the ‘defects’, which was roughly consistent with the experimental results. The ‘defects’ were generated in the matrix as the rigid aromatic DETDA and flexible aliphatic n-butylamine were at opposite ends. At the same time, the crosslinking degree of the thermosets decreased from 2288 mol m−3 for S0 to 2067 mol m−3 for S40 when the tetrafunctional DETDA was gradually replaced by the bifunctional n-butylamine. As a result, the tensile moduli should decrease. However, both the simulated and experimental results showed that S28, S30, and S40 were reinforced and toughened significantly and simultaneously when n-butylamine was introduced. Also, the reinforcement effect disappeared when the ‘defects’ content increased. All these results were consistent with the finding of our previous work that the low concentration of the ‘defects’ was able to reinforce and toughen the thermosets simultaneously.| System | DGEBA | DETDA | n-Butylamine |
|---|---|---|---|
| S0 | 400 | 200 | 0 |
| S10 | 400 | 195 | 10 |
| S20 | 400 | 190 | 20 |
| S28 | 400 | 186 | 28 |
| S30 | 400 | 185 | 30 |
| S32 | 400 | 184 | 32 |
| S40 | 400 | 180 | 40 |
The behavior of the atoms from n-butylamine was explored via MD simulation in order to discover the reinforcement mechanism of the ‘defects’ in the thermosets. The RDF described the position characteristics of the carbon and nitrogen from n-butylamine in the epoxy resin. The relationship between each parameter was described by eqn (1),30 where χα and χβ represent the mole fraction of α and β atoms, respectively, N is the number of atoms in the system, ρ is the system density, and δ is the number of atoms existing in a specified area.
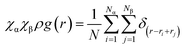 | (1) |
g(r) represents the probability of finding an atom with the same characteristic within the r radius for each atom in the amorphous cell. As presented in Fig. 2b–g, all the g(r) curves remain zero in the beginning due to the volume exclusion effect, and fluctuations were reflected by all the curves because of the rotation of the C–C bonds of n-butylamine.34 The definition of N, C1 to C4 was demonstrated by Fig. 2a, and C1 represented the terminal carbon of n-butylamine. The r value when the g(r) became non-zero is C1, which was abbreviated as rmin(C1) for short. The rmin(C1) in the S10 system was 13.325 Å, which was longer than the cut-off radius of van der Waals' interaction (12.5 Å), indicating that there was no interaction between the single-ended aliphatic amine chains in the S10 formulation. The rmin(C1) became less than 12.5 Å when the n-butylamine content increased and reached about 3.7 Å for S40. Similar trends were reflected by C2, C3, C4, and N in each formulation. The above results indicated that the single-ended aliphatic amine chains were drawn to each other in the defects network when the n-butylamine content was increased. The g(r) values for all the atoms in S10 fluctuated after reaching the rmin and showed a similar trend with that of the net n-butylamine system, which is presented in the ESI section.† The peaks were reflected by g(r) in the S20 system once reaching rmin, and were significantly higher than the fluctuations. This trend became more obvious in S28, S30, and S32 systems, where the g(r) values were almost zero after the peaks. The peaks were also reflected in S40; however, they were no longer significantly higher than the fluctuations. It was reflected that n-butylamine was random decorated on the matrix, and the aliphatic chains rotated freely in S10. However, the aliphatic chains were packed more regularly when the concentration of n-butylamine increased; thus, the g(r) became negligible once the significant peaks appeared after the rmin in S20 to S32. The constraint to the aliphatic chains was weakened and disappeared when the n-butylamine concentration increased. The RDF results indicated that the packing state of the flexible aliphatic chains (the ‘defects’) in the rigid aromatic thermosets matrix was greatly influenced by its concentration. The RDF of S40 at 400 K is presented by Fig. 2h, indicating that the increase in the temperature was able to promote the aggregation of the aliphatic chains. This could be one of the reasons behind the decrease in the Tg caused by the ‘defects’, where the aliphatic chains moved inversely during the increasing in the temperature.
As indicated by Morel et al., the free volume plays an important role in affecting the mechanical performance of the thermosets.20 A probe atom with 0.8 Å radius was employed in our model for the detection of the free volume and the calculation of the distribution.31 The free volume void with irregular shape for each formulation was calculated and described as the volume-equivalent sphere, as shown in Fig. 3. The free volume voids' size distribution in the range from 0 to 7 Å is presented in Fig. 3c. The proportion of the large voids (r > 4 Å) disappeared after the introduction of n-butylamine in S10, and that of the medium voids (2 Å < r < 4 Å) increased significantly. The number of large voids kept decreasing in S20, where the proportion of the small voids (r < 2 Å) increased. The large voids almost disappeared in the S30 system, and the portion of small voids increased significantly. However, the large voids appeared again when the concentration of n-butylamine kept increasing. Also, the distribution shifted to the right side in S40, indicating the increase in the voids' dimension in this case. This trend is reflected clearly in Fig. 3a, which presents the voids' size cumulative distribution. The cumulative portion of the voids for S30 was significantly higher than that of S0 to S20. The number of voids with different size for all the formulations is plotted in Fig. 3b; the distribution shifted from the right side to the left when the formulation changed from S10 to S30; however, it turned to the right side again in S40. The total free volume and the corresponding fraction of the thermosets for all the formulations was calculated and is presented in Fig. 3d and e, respectively. The simulation results indicated that the large voids in the rigid aromatic thermosets matrix were occupied with the introduction of the aliphatic chains leading to the reduction of the free volume. However, large voids appeared again when the defects concentration increased. Hypothesis was raised that the n-butylamine chains showed no significant influence on the free volume of the thermosets at low concentration due to the lack of interactions between the aliphatic chains (as presented by the RDF simulations). These ‘defects’ chains aggregated and entangled when the concentration increased, and occupied the large voids in the matrix. However, the aggregation of the ‘defects’ was too large to fit the voids and generated a new free volume with an increasing concentration of n-butylamine.
The intermolecular cohesive energy was examined and is compiled in Table 2 in order to verify the raised hypothesis. The results indicated that the intermolecular interaction was greatly affected when n-butylamine was induced. The total cohesive energy for the DGEBA-DETDA was 8283 ± 75 kcal mol−1 and 8211 ± 76 kcal mol−1 for S10, thus showing no significant change. This value increased gradually to 8333 ± 72 kcal mol−1 for S20 and 8761 ± 71 kcal mol−1 for S30, respectively; however, it decreased to 7754 ± 75 kcal mol−1 for S40. The electrostatic energy for the system kept decreasing with an increase in the aliphatic chains' proportion as the regular network structure was gradually destroyed by the defects. However, the van der Waals energy of S10, S20, and S30 showed a significant increase compared with that of the control and reverted back to 1376 ± 39 kcal mol−1 for S40. The calculation of the cohesive energy was consistent with the RDF simulation and verified the hypothesis. No significant intermolecular interaction was presented by the aliphatic chains when the concentration was low as the van der Waals energy showed no significant change in S10. However, the aromatic network was destroyed by the introduction of these ‘defects’ as the electrostatic energy kept decreasing with the increase in the n-butylamine proportion. The ‘defects’ chains begun to interact in S20 as the distance between the chains was within the cut-off radius of van der Waals interaction, leading to a significant increase in the van der Waals energy. This trend became more obvious in S30 where the van der Waals energy was 2175 ± 27 kcal mol−1, almost twice that of the control. However, the aggregation of the aliphatic chains was weakened in S40.
| System | Cohesive energy, kcal mol−1 | van der Waals energy, kcal mol−1 | Electrostatic energy, kcal mol−1 |
|---|---|---|---|
| S0 | 8283 ± 75 | 926 ± 34 | 7357 ± 43 |
| S10 | 8211 ± 76 | 980 ± 41 | 7231 ± 37 |
| S20 | 8333 ± 72 | 1339 ± 36 | 6994 ± 41 |
| S30 | 8761 ± 71 | 2175 ± 27 | 6585 ± 44 |
| S40 | 7754 ± 75 | 1376 ± 39 | 6377 ± 34 |
Interestingly, the change in the tensile moduli of the sample sets followed the variation in the ‘defects’ chain aggregation. The packing topology of the epoxy matrix was explored in order to clarify the relationship between the participation of the ‘defects’ and the mechanical performance. Fig. 4a demonstrated the RDF of all the N atoms (including the N from n-butylamine and DETDA), which reflected the change in the crosslinking topology. The r value corresponding to the peak of g(r) reflected the mean distance between the two N atoms in the amorphous cell. The curves of S10, S20, and S40 hold the same position compared with the control. However, the g(r) peak of S30 shifted to the left significantly, which showed the more compact 3D network structure compared with the control. The X-ray scattering spectrum was simulated and is presented in Fig. 4b. The wavelength was set as 1.54178 Å with the 2θ ranging from 5 to 45°. The X-ray spectrum could help to qualitatively identify the average distance between the molecular segments in the system. No diffraction peak was presented in all the formulations, which indicated that the thermosets with ‘defects’ in this simulation remained amorphous. The spectrum shifted to the right with the increase in the n-butylamine proportion. However, the spectrum shifted to the left when the formulation changed from S30 to S40. The X-ray simulation was consistent with the RDF, where the compact degree of the crosslinking network increased with the introduction of the ‘defects’ aggregation; however, it decreased when the ‘defects’ proportion exceeded the threshold value. As a result, the closely packed network structure led to higher tensile moduli. This could explain the reason that the low proportion of the ‘defects’ in the matrix could reinforce and toughen the thermosets simultaneously.
The behaviors of the ‘defects’ in the thermoset matrix could be explained based on the above simulated and experimental results, which are demonstrated in Fig. 5. n-Butylamine (f = 2) replaced DETDA (f = 4), reducing the crosslinking degree. As a result, the resin showed a decreasing Tg and increasing elongation at break. The flexible aliphatic chains acted as the ‘defects’ when decorated in the rigid aromatic crosslinking network and showed no significant intermolecular interactions at a low concentration as the distance between the aliphatic chains was larger than the van der Waals distance. However, the n-butylamine chains begun to aggregate and entangle when the concentration exceeded the threshold value, where the distance between the aliphatic chains was shorter than the van der Waals distance, thus forming the microphase segments that was able to insert and occupy the voids in the aromatic matrix and reduce the free volume of the system. The strong entanglement of the chains drew the network close together and reduced the distance between each segment in the matrix. As a result, the whole crosslinking network of the thermosets became compact and reinforced under this situation. However, the microphase formed by the ‘defects’ chains became too large for the voids in the system when the proportion kept increasing, thus generating a new free volume, which, on the contrary, loosened the network structure and reduced the tensile strength of the material. At the same time, the aggregation of the ‘defects’ chain was promoted when the temperature was increased. The behavior of these aliphatic chains was opposite to that of the resin matrix during heating, which contributed to the reduction of Tg. The snapshots of the amorphous cells for S0 to S40 at the end of the simulation were captured and are presented in the ESI section.†
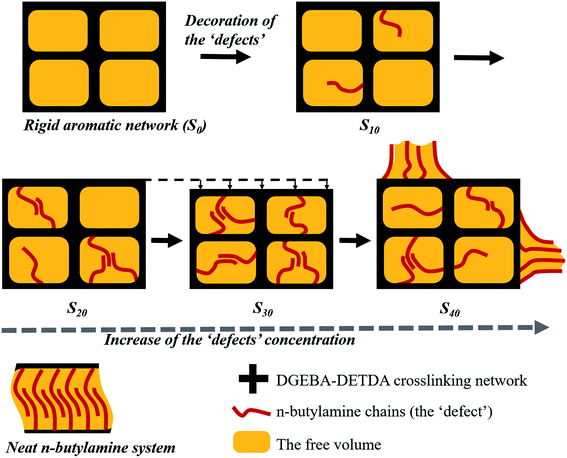 | ||
| Fig. 5 Schematically demonstration of the enhancement mechanism generated by the defects in the thermosets. | ||
Conclusions
Molecular insights into the ‘defects’ network in the thermosets were obtained using the MD simulation, and the influence on the mechanical properties was evaluated. The rigid aromatic DGEBA-DETDA crosslinking network structure was constructed with flexible aliphatic n-butylamine as the ‘defects’. The simulations and experimental data in this work verified that the ‘defects’ in the thermosets were able to reinforce and toughen the material simultaneously. The ‘defects’ chains showed no intermolecular interaction at the low concentration; however, they began to aggregate and entangle when the proportion increased, where the interval between the aliphatic chains was shorter than the van der Waals distance. The microphases were generated by the aggregation and were able to insert into the voids in the matrix. The strong cohesive interaction of the entanglement reduced the distance between each segment in the matrix, making the crosslinking network compact and enhancing the moduli. The microphases kept increasing with the increase in the ‘defects’ concentration; however, they were no longer able to insert into the voids. A new free volume was generated by the microphases, which, on the contrary, loosened the network structure and reduced the tensile strength of the material. The results verified the fact that the low proportion ‘defects’ in the crosslinking network was able to reinforce and toughen the thermosets simultaneously, and clarified the corresponding mechanism. It may provide polymeric material designers a new strategy to reinforce and toughen the thermosets simultaneously without the participation of fillers.Experimental
Amine-cured epoxy simulation systems were established using the software Materials Studio. The atomic interactions in this simulation were defined by the non-reaction force filed PCFF,20,21 which is the typical force field used in the simulation of the epoxy resin volume change26,27,32 with the time step set to 1 fs. A smart algorithm was employed with an energy convergence standard of 0.0001 kcal mol−1 and force convergence of 0.005 kcal mol−1 Å−1 for the geometric optimization. During the MD simulation, the temperature was controlled by the Nose–Hoover thermostat, and the pressure was controlled by Berendsen barostat. The structures of DGEBA, DETDA, and n-butylamine are demonstrated in Fig. 2a. The DGEBA-DETDA backbone polymer was constructed and placed into a cubic cell; the molar ratio between each type of molecules is presented in Table 1. n-Butylamine molecules were manually tethered onto the DGEBA molecules before the amorphous structure modeling as the aliphatic amine had higher reactivity than that of the aromatic amine. The initial density of the amorphous cell was preset to 1.0 g cm−3, which was consistent with the experimental data33 in order to reduce the calculated time cost by the equilibrium process. The 3D periodic boundary conditions were applied to the cubic cell, ensuring a constant atom account maintaining the system density. Subsequently, a geometry optimization based on a smart algorithm and a 50 ps NVT MD simulation at 300 K was performed on the initial models to rationalize the configuration. A multistep crosslinking procedure written in Perl language was performed on these equilibrated models to form the 3-D network structure.During the ring-opening and the new bond formation processes, the secondary carbon in DGEBA and the nitrogen in DETDA were set as the reactive atoms, and the chemical reactions occurred once the reactive atoms were judged as close contact atoms in a prescribed cut-off distance. The curing conversion was increased by gradually raising the cut-off distance from 4 Å to 15 Å with an interval of 1 Å. Meanwhile, 3D equilibration cycles were adapted within every cut-off distance, thus relaxing the systems and ensuring that all the reactive atoms fully reacted under each specified cut-off distance. The crosslinking process did not stop until the final crosslinking conversion was reached or the cut-off distance was greater than the customized maximum value. Models with more than 90% conversion rate were constructed after the crosslinking process. A series of optimization processes including a geometry optimization, a 50 ps (the time step was 0.2 fs in this part specially) NVT MD at 300 K, a 50 ps NVT MD at 300 K, and a 1 ns NPT MD at 300 K were performed on the crosslinked models, thus eliminating the internal stress. The free volume was simulated by the calculation of the unoccupied space in the amorphous cells with the help of an atom probe (r = 0.8 Å).31 The glass transition temperature (Tg) in this work was calculated by a cooling procedure, in which the structure was equilibrated by NPT MD for 100 ps at 550 K under atmospheric pressure, and then cooled at a rate of 10 K/50 ps from 550 K to 300 K. The Tg was determined as the inflection point of the density–temperature curve.
Conflicts of interest
All the authors declare there is no conflict of interest.Acknowledgements
This work was supported by grants from the Science Foundation of Aeronautics of China (No. 201718S9001).Notes and references
- C. Y. Li and A. Strachan, J. Polym. Sci., Part B: Polym. Phys., 2015, 53(2), 103–122 CrossRef CAS.
- T. Vidil, F. Tournilhac, S. Musso, A. Robisson and L. Leibler, Control of reactions and network structures of epoxy thermosets, Prog. Polym. Sci., 2016, 62, 126–179 CrossRef CAS.
- E. M. Petrie, Epoxy Adhesive Formulations, 2006 Search PubMed.
- R. Ramsdale-Capper and J. P. Foreman, Polymer, 2018, 146, 321–330 CrossRef CAS.
- R. A. Pearson and A. F. Yee, J. Mater. Sci., 1991, 26(14), 3828–3844 CrossRef CAS.
- A. F. Yee and R. A. Pearson, J. Mater. Sci., 1986, 21(7), 2462–2474 CrossRef CAS.
- Z. J. Thompson, M. A. Hillmyer, J. Liu, H.-J. Sue, M. Dettloff and F. S. Bates, Macromolecules, 2009, 42(7), 2333–2335 CrossRef CAS.
- F. Meng, S. Zheng, W. Zhang, H. Li and Q. Liang, Macromolecules, 2006, 39(2), 711–719 CrossRef CAS.
- E. E. Hamurcu and B. M. Baysal, Polymer, 1993, 34(24), 5163–5167 CrossRef CAS.
- Y. T. Park, Y. Qian, C. Chan, T. Suh, M. G. Nejhad, C. W. Macosko and A. Stein, Adv. Funct. Mater., 2015, 25(4), 575–585 CrossRef CAS.
- F. H. Gojny, M. H. G. Wichmann, B. Fiedler and K. Schulte, Compos. Sci. Technol., 2005, 65(15), 2300–2313 CrossRef CAS.
- W. Duan, Y. Chen, J. Ma, W. Wang, J. Cheng and J. Zhang, Composites, Part B, 2020, 189, 107878 CrossRef CAS.
- M. Sharifi, C. W. Jang, C. F. Abrams and G. R. Palmese, J. Mater. Chem. A, 2014, 2(38), 16071–16082 RSC.
- M. Sharifi, C. Jang, C. F. Abrams and G. R. Palmese, Macromolecules, 2015, 48(20), 7495–7502 CrossRef CAS.
- L. H. Ba, Q. Zou, X. C. Tan, J. P. Song, J. Cheng and J. Y. Zhang, RSC Adv., 2016, 6(94), 91875–91881 RSC.
- Y. Huang, Y. Tian, Y. Li, X. Tan, Q. Li, J. Cheng and J. Zhang, RSC Adv., 2017, 7(77), 49074–49082 RSC.
- T. Yang, R. Wang, X. Hou, J. Cheng and J. Zhang, Mater. Lett., 2016, 166, 150–153 CrossRef CAS.
- B. J. Rohde, K. M. Le, R. Krishnamoorti and M. L. Robertson, Macromolecules, 2016, 49(23), 8960–8970 CrossRef CAS.
- R. J. Varley, J. H. Hodgkin and G. P. Simon, Polymer, 2001, 42(8), 3847–3858 CrossRef CAS.
- E. Morel, V. Bellenger, M. Bocquet and J. Verdu, J. Mater. Sci., 1989, 24(1), 69–75 CrossRef CAS.
- C. I. Vallo, P. M. Frontini and R. J. J. Williams, Polym. Gels Networks, 1993, 1(4), 257–266 CrossRef CAS.
- H. Du, Z. Yang, Z. Tian, M. Huang, W. Yang, L. Zhang and A. Li, Chem. Eng. J., 2018, 333, 310–319 CrossRef CAS.
- J. Zhao, X. Liu, Z. Zhu, N. Wang, W. Sun, C. Chen and Z. He, Appl. Surf. Sci., 2017, 416, 757–765 CrossRef CAS.
- E. Yildirim, M. Yurtsever, E. Yilgör, I. Yilgör and L. Wilkes Garth, J. Polym. Sci., Polym. Phys., 2017, 56(2), 182–192 CrossRef.
- E. Colangelo, Q. Chen, A. M. Davidson, D. Paramelle, M. B. Sullivan, M. Volk and R. Lévy, Langmuir, 2017, 33(1), 438–449 CrossRef CAS PubMed.
- S. Yang and J. Qu, Polymer, 2012, 53(21), 4806–4817 CrossRef CAS.
- I. Yarovsky and E. Evans, Polymer, 2002, 43(3), 963–969 CrossRef CAS.
- V. Varshney, S. S. Patnaik, A. K. Roy and B. L. Farmer, Macromolecules, 2008, 41(18), 6837–6842 CrossRef CAS.
- C. Li and A. Strachan, Polymer, 2015, 75, 151–160 CrossRef CAS.
- S. Masoumi, B. Arab and H. Valipour, Polymer, 2015, 70, 351–360 CrossRef CAS.
- C. Li and A. Strachan, Polymer, 2016, 97, 456–464 CrossRef CAS.
- H. B. Fan and M. M. F. Yuen, Polymer, 2007, 48(7), 2174–2178 CrossRef CAS.
- D. Ratna, R. Varley, R. K. S. Raman and G. P. Simon, J. Mater. Sci., 2003, 38(1), 147–154 CrossRef CAS.
- K. Li, Y. Li, Q. Lian, J. Cheng and J. Zhang, J. Mater. Sci., 2016, 51(19), 9019–9030 CrossRef CAS.
- Z. Wang, Q. Lv, S. Chen, C. Li, S. Sun and S. Hu, ACS. Appl. Mater. Interfaces, 2016, 8(11), 7499–7508 CrossRef CAS.
- Z. K. Wang, Q. Lv, S. H. Chen, C. L. Li, S. Q. Sun and S. Q. Hu, Mol. Simul., 2015, 41(18), 1515–1527 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ra03099c |
| This journal is © The Royal Society of Chemistry 2022 |