Reversible functionalization and exfoliation of graphite by a Diels–Alder reaction with furfuryl amine

Abstract

Furfuryl amine-functionalized few-layered graphene was prepared via a mechanochemical process by a [4 + 2] cycloaddition under solvent-free conditions. By employing ball milling, active sites are merged mostly at the edge of the graphene sheets which makes them prone to Diels–Alder click reactions (D–A) in the presence of a diene precursor. Consequently, one-pot grafting with furfuryl amine onto the graphene sheets, exfoliates pristine graphite resulting in functionalized few-layered graphene which is soluble in organic solvents. Thereafter, the cleavage of the bonds in the adduct can occur by exposure to an external stimulus like temperature, to initiate a retro-Diels–Alder reaction. The success of the thermoreversible functionalization of the few-layered graphene was confirmed by Raman spectroscopy, TGA, XPS, EDX, contact angle and XRD analysis. The morphology of the samples was investigated by scanning electron microscopy and AFM. The latter was utilized to estimate graphene thickness. The results showed that functionalization proceeded under nitrogen with dry ball milling and mild temperatures efficiently.

---

Introduction

Compared to various carbon materials^1–6 graphite is the most chemically stable allotrope of carbon with sp²-hybridized carbon atoms. Its unique and exceptional characteristics are utilized in a wide range of applications. The related graphene is a two-dimensional allotrope and the base structure of all graphitic forms. The structure of this wonderful material is a one-atom-thick planar sheet of sp²-bonded carbon atoms that are tightly bonded in a honeycomb crystal lattice with carbon–carbon bond lengths of 0.142 nm. Due to the fascinating properties of graphene a broad range of novel studies have been reported.^7–18

The functionalization of graphene and its derivatives plays a crucial role to modulate their properties and fabricate graphene-based conjugates with new characteristics and applications.^18–25 Graphene can be covalently or non-covalently functionalized. In the first case, strong and stable covalent bonds are formed, but in the second one, there is the formation of weak bonds like hydrogen bonds, π–π interactions and van der Waals interactions. Covalent modification of graphene causes rehybridization of sp²-carbon atoms of the aromatic structure to sp³-carbon atoms, while in non-covalent functionalization the sp² structure is maintained. Edge functionalization of the graphene sheets is the upmost possible phenomenon when changing of hybridization occurs in covalent addition reactions.²⁶

The covalent functionalization can be categorized into nucleophilic addition, atomic radical addition, free radical addition, electrophilic substitution, and cycloaddition reactions on the surface, at the edge and at the defect sites. One of the most basic and important reaction in synthetic organic chemistry is the Diels–Alder reaction, the classical [4 + 2] cycloaddition,^27,28 between a diene and a dienophile to produce a stable cyclohexene derivative.^29,30 This reaction shows a thermally reversible character, especially with furan derivatives at relatively low temperatures. In 2011, Haddon and co-workers demonstrated that graphite or graphene have dual functions in the D–A reaction due to the presence of π-conjugation and being a zero-band gap (the conduction and valence bands touch at the Fermi level (Dirac point)), Fig. 1.^27,31 Since then, a wide range of research has been reported regarding the function of graphite or graphene as either diene or dienophile under a variety of reaction conditions.^32–37

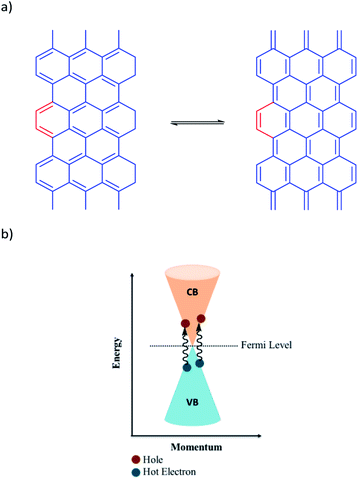Fig. 1 (a) Two possible resonance forms of graphite (b) schematic diagram of energy band of graphene.

Graphite in comparison with graphene is less prone to a D–A reaction, because of its lower specific surface area.^38,39 Hence, a suitable method needs to facilitate the D–A reaction of graphite. Recently, Chen et al.⁴⁰ reported the synthesis of graphene from graphite via wet ball milling and in situ reversible modification with a Diels–Alder reaction starting from graphite and maleic anhydride. Yet, maleic anhydride is moisture sensitive and the retro-Diels–Alder reaction needs with this dienophile reasonable high temperatures. Due to our interest in the application of functionalized graphene derivatives^6,23–25 and considering that furan-derivatives are undergoing retro-Diels–Alder under the mildest conditions,⁴¹ we were interested to combine the functionalization of graphite with ball milling and furan as diene in order to obtain furan-derivative functionalized graphene. For this purpose, we report here a solvent-free mechanochemical method driven by ball milling. In this efficient way, functional groups could be mostly introduced to the broken edges of graphene sheets. Rotating balls in the system can transfer their kinetic energy to the milled materials which included graphite as a dienophile and furfuryl amine as a diene and breaking strong bonding interactions and creating new and chemically active edges and surfaces. The diene reacts well to produce D–A adducts mostly at the edges and to some extent on the surfaces.

At the graphene sheets edges, which can be either zig-zag or arm-chair structures, Fig. 2, the achievement of aromatic sextets is frustrated in most of the rings where zig-zag edges are concerned and are therefore thermodynamically unstable and more reactive than arm-chair edges.^42–44

Fig. 2 Zigzag and Armchair edges of graphene lattice.

Experimental

Materials and reagents

Materials. Natural graphite flake from Alfa Aesar-10 mesh, 99.9% (metal basis), furfuryl amine from Fluka. Ethanol, THF and acetone (technical grade), HCl (37%). XRD measurements were performed with AXS D8 Advance from Bruker, using cupper (K-alpha) radiation with a wavelength of 0.154 nm, 2θ angle from 20 to 80° in 0.02° steps and step time 3 s. TGA was carried out with TGA/SDTA851 from the Mettler Toledo device. The heating rate and Argon stream were 5 K per minute and 55 mL per minute, respectively. SEM images were taken by a “NEON 40” from Zeiss (Carl Zeiss Microscopy Deutschland GmbH). EDX was done in high current mode and the detector was an “UltraDry” from Thermo Fisher Scientific Inc. AFM device was “Dimension Icon PT” from Bruker. We used Peak Force Tapping in Air mode. Contact angles were measured by a Krüss Drop shape Analyzer 25e. All Raman investigations in this work were performed with a Renishaw In-Via-Raman spectroscope (Renishaw plc, United Kingdom) with Leica DM 2500 M microscope at a wavelength of 532 nm (He/Ne laser). The X-ray photoelectron spectroscope Omicron ESCA+, of the company Omicron Nanotechnology system, which is integrated with the PIA-SIS of the University of Paderborn, was used. It works with an aluminum K_α-X-ray source which delivers monochromatic radiation of 1486.7 eV.

Synthesis of G-FA. Pristine graphite (2.5 g) and furfuryl amine (5 g) were added into a thick glass container which included small (0.5 mm) and bigger stainless-steel balls (2 mm) under solvent-free conditions (for the setup see Fig. S1 in the ESI†). The container was sealed and charged/discharged with nitrogen gas and placed in an oil bath of 80 °C. The ball milling step (medium speed) was carried out in a non-continuous process, after milling for 2 hours, the mixer was turned off for 1 h and again milling for 2 hours. This cycle repeated for 3 times resulting in an overall milling time of 6 h and 3 h without milling.

Subsequently, the container was kept under 70 °C in the oil bath for 24 h. Afterward, the product was treated with HCl (37%) in order to remove iron impurities from the milling process and the material was further washed with water until the pH value was close to 7. Thereafter the product was washed with THF to remove unreacted furfuryl amine. In the end, the product was left to dry in the oven at 70 °C. The G-FA was collected as powder and kept in a sealed glass container after freeze-drying to make it ready for further analytical measurements.

Control reactions

G-BM. As a contrast, the control reaction was exposing graphite flakes to the ball mills under the same conditions as G-FA but without furfuryl amine. The powder of G-BM was obtained via the freeze dryer.

G-TFA. This control reaction was the reaction between pristine graphite and furfuryl amine, only in the presence of temperature (70 °C) and without any ball milling process. This reaction was kept for 2 days under 70 °C.

ReG-FA. Retro-Diels–Alder reaction of G-FA: the reverse D–A reaction of G-FA was conducted under 150 °C for 2 h.

The processes were repeated three times and the average yield of the G-FA product per batch was found to be around 3 g. Based on the total mass of the reactant in every batch (7.5 gram). The yield of the G-FA can be calculated as around 40% from the overall applied material or close to 100% functionalized graphene, if considering the starting mass of the graphite as a basis for the yield.

Results and discussion

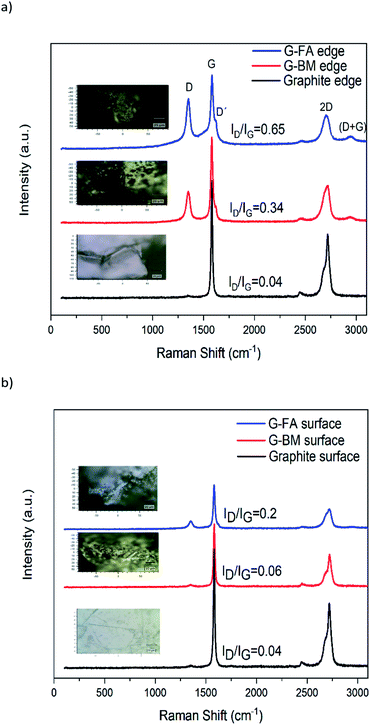
The facile route of dry ball milling is depicted in Scheme 1, and the thermal reversibility is studied via a reverse D–A reaction in this work. Under this mild strategy, graphite acts as a dienophile and furfuryl amine as a diene to produce the desired adduct. By applying two sizes of balls in the ball mill, the efficiency of creating active sites on the graphite was improved and the reaction rate between diene and dienophile effectively increased. First, reactants were exposed to the non-continuously ball milling in a sealed glass container under nitrogen gas and in an oil bath of 70 °C, respectively. The container was kept at 70 °C for 24 hours without milling to provide an efficient condition for the D–A reaction. Finally, the product displayed excellent dispersibility in polar solvents. The retro-Diel–Alder happened simply by heat treatment of the functionalized graphite (150 °C for 2 hours).

Scheme 1 Ball-milling schematic of graphite and furfuryl amine that leads to cycloaddition adduct.

Raman spectra were compared at the edge and also on the surface positions of each sample. As shown in Fig. 3, the Raman spectra of the pristine graphite, G-BM and G-FA displayed two distinguishable peaks at 1340 and 1580 cm⁻¹, which correspond to the D band (the vibrations of the sp³-hybridized carbons) and G band (in-plane vibration of sp² carbon atoms), respectively. Generally, the intensity ratio of the D-band to G-bands (I_D/I_G) is a good indicator of the level of defects, which are mainly sp³ carbons on the graphene. These show the degree of functionalization introduced into the graphene sheets.^45,46 For the pristine graphite, the D band intensity at the edge and also on the basal plane is remarkably small. Comparing the Raman spectra on the surface and at the edges of the product can clearly reveal that functionalization has been occurred in both positions, due to the higher intensity ratio of I_D/I_G compared to the pristine graphite. Although the degree of functionalization in G-FA is significantly higher at the edges in comparison with surfaces. I_D/I_G ratio for pristine graphite, G-BM and G-FA at the edge, are 0.04, 0.30 and 0.65 respectively, while these ratios on the surface are 0.04, 0.06 and 0.20. This comparison clearly confirms that functionalization has occurred mostly at the edge of the graphene sheets. Due to the occurrence of the D–A reaction, G-FA exhibits more sp³ carbons in the adduct product. The results suggest that a small quantity of defects was introduced into the graphite flakes during the ball milling process (G-BM). The damage to the graphite lattice structure in the ball milling process rises the ratio of I_D/I_G in G-FA and the other is contributed to the destruction of the π-conjugated structure of graphene by the D–A cycloaddition reaction that occurred between graphite and furfuryl amine, which lead to the growth in the number of sp³ carbon atoms mostly at the edges.

Fig. 3 Raman spectrum (a) at the edge and (b) on the surface of pristine graphite, G-FA and G-BM.

Another distinguished spectral feature of carbon-based materials is the appearance of a 2D band which is the result of a two-phonon lattice vibrational process. The shape, intensity and location (cm⁻¹) changes of the 2D peak reveal evidence of the number of layers of graphene sheets. The 2D-band peak position is shifted to higher numbers, i.e., from 2702 cm⁻¹ for 3-layer graphene to 2720 cm⁻¹ for 10-layer graphene and 2725 cm⁻¹ for a graphite thickness of 40 nm.⁴⁷ According to the Raman spectra of the samples at the edges, the 2D peak location of pristine graphite and G-FA are 2722 and 2708 cm⁻¹, respectively. These numbers for the surface of the samples are 2722 and 2715 cm⁻¹. It can be obviously confirmed that the ball milling process and the functionalization could decrease the number of layers from around 40 nm thickness of pristine graphite to less than 10 layers at the edge of G-FA (estimation is between 6–8 layers).

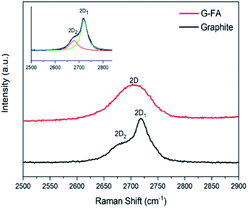
Another difference in the Raman spectrum of pristine graphite and G-FA is the shape of the 2D band which is formed from two Lorentzian peaks. The intense 2D₁ band and a low-energy shoulder called the 2D₂ band are present in Fig. 4. The 2D band originates from a two-phonon double resonance process and it is interrelated to the band structure of graphene layers. According to the approach of A. C. Ferrari et al.⁴⁸ a further decrease in layers leads to a significant increase of the relative intensity of the lower frequency 2D₁ peaks. Also, Cancado et al.⁴⁹ have shown that as the disorder increases, the 2D₂ shoulder shift upwards and finally merges into the 2D₁ band. As a result, the 2D band exhibits a single peak profile and the peak becomes asymmetrical. It can be a good confirmation that the thickness and the numbers of layers in the G-FA at the edge of the graphene sheets are less than in pristine graphite and due to high c-axis disorder, the two-peak profile of graphite is not maintained in the G-FA.

Fig. 4 The expansion of the 2D peak of pristine graphite and G-FA.

In addition, the D′ peak (1620 cm⁻¹) is also observed in the Raman spectra of G-BM and G-FA, which indicates defects of the graphene because the defects will lead to an increase in the D′ intensity.⁵⁰ On the other hand, the appearance of the peak (D + G) strongly supports the higher disorder in the G-FA sample, although this peak is sharper at the edges of the graphene sheets in the G-FA compared with the surface, and it shows another evidence of the higher degree of disorders at the edge of the G-FA, Fig. 3b.

The thermal behavior of pristine graphite, G-BM, G-TFA and G-FA were analyzed by thermogravimetric analysis (TGA). As shown in Fig. 5 the pristine graphite displayed high thermal stability until 700 °C due to the perfect conjugated structure and the weight loss was only about 0.7% at 1000 °C. As it is clear in Fig. 6, G-TFA did not show any weight loss at the temperature less than 500 °C and it was the sign of no D–A functionalization. Thus, further analytical measurements were not carried out for this sample. In another analytical measurement, we compared pristine graphite, G-BM and G-FA. The G-FA pattern displayed in the beginning a weight loss at low temperature in the range of 30 to 300 °C that could be attributed to the detachment of the furfuryl amine on graphene sheets, while as shown in Fig. 7 the ReG-FA had a very small amount of weight loss in the range of 30 to 250 °C which is comparable with the G-BM pattern. At 250 °C, the weight loss for ReG-FA is 0.7% and for G-BM is 0.6%. This indicated that ReG-FA had better thermal stability than G-FA due to the separation of the furfuryl amine from the graphene sheets and the repaired conjugated structure during the reverse D–A reaction. These results show that furfuryl amine had been grafted on graphene sheets successfully. The TGA is also a suitable measurement to calculate the degree of the functionalization (DOF) of the G-FA product.⁵¹ TGA pattern for G-FA shows 2.1% weight loss at 250 centigrade degrees, which can be used to calculate DOF. Hence, furfuryl amine has been attached to the graphene layers with high DOF = 0.26. Also, the solubility test confirms the existence of amine groups on the graphene sheet which facilitates the solubility property of graphene in polar solvents such as ethanol. The photo in Fig. 7 shows a G-FA sample dispersed in ethanol after 10 min of sonication. The suspension was stable for 3 weeks at room temperature. Indeed, it was still stable after 1 year. In addition, a sample of ReG-FA in ethanol under the same condition as G-FA is depicted. No suspension was formed.

Fig. 5 TGA curves of pristine graphite, G-BM and G-FA.

Fig. 6 TGA curves of pristine graphite and G-TFA.

Fig. 7 TGA curves of G-FA vs. ReG-FA confirmed by photographs of the solubility properties of G-FA (right) and ReG-FA (left) in ethanol after 3 weeks standing at rt.

The XRD patterns of pristine graphite, G-BM and G-FA are shown in Fig. S2, ESI.† As it is clear the obtained patterns from all samples exhibit two diffraction peaks at 26.40 and 54.5, which are attributed to (002) and (004) crystalline lamellae of the graphite.^52,53 For all of them the basal reflection peak is at 2θ = 26.4 but different shape and broadness of the peaks, and with high difference in intensity. Fig. S2† shows that the intensity of graphite (002) is greater with a sharp and strong diffraction peak compared with that of graphene and it confirms high quality and perfect crystalline structure of pristine graphite. A dramatic decrease in the peak intensity of G-FA is caused by the decrease in the thickness of the graphite due to the impact of ball milling to break the inner crystalline structure of graphite which has resulted in the exfoliation of the graphene sheets. The latter indicates that the D–A reaction does not change the characteristic crystalline structure of graphite considerably.

The thickness and number of graphene layers can be found by analyzing XRD results.⁵⁴ The shape of the (002) reflection depends on the thickness of the graphite sample. Thinner graphite samples result in a broader peak with a maximum at lower diffraction angles due to the increased contribution of intercalated planes on the top/bottom of the graphitic flakes.^55,56 The application of the Scherrer equation on the (002) diffraction line allows for an estimation of the average crystalline size (D).^56,57

Fig. S2b† indicates a symmetric 002 peak for pristine graphite but an asymmetric one for G-FA. After the Gaussian peak fitting in Fig. S2c,† it is obviously clear that there are two distinguishable peaks in G-FA (002). In one peak, 2θ shifted to the left in comparison with the Gaussian peak fitting of graphite. 2θ for the pristine graphite after the peak fitting is 26.42° while this number for the G-FA sample is detected as 26.36 and 26.51°. According to Bragg's law, the distance between the graphene layers in the G-FA is higher than in the graphite flakes. Therefore, after calculating the thickness of the samples (D), the thickness of the lower 2θ in G-FA, has been turned from 40.57 nm to 7.45 nm. This evidence can be interpreted as a good indicator for the exfoliation of graphite due to the ball milling process integrated with the functionalization of the graphite. Referring also to other analytical measurements like Raman spectroscopy, it can be determined that different locations on the graphene sheets have different functionalization degrees and thicknesses at the edge (7.45 nm) which is much lower compared to the surface (29.5 nm). Table 1 shows the calculated FWHM and the crystalline size of the pristine graphite and functionalized graphene (G-FA). According to the data in Table 1, the first fitted peak in the G-FA with 1.095 degree of FWHM can be interpreted as lower thickness at the edges of the graphene sheets and the second fitted peak with 0.277 degree of FWHM indicated compressed layers mostly on the surfaces, although these data showed lower thicknesses on the surfaces after ball milling compared to the pristine graphite with 0.201 degree of FWHM and 40.57 nm thickness. On the other hand, due to further destruction of the crystal structure of G-FA due to the D–A reaction, the diffraction peak of G-FA was weaker and broader than that of G-BM.

Table 1 XRD parameters and calculation the thickness (D) of pristine graphite and G-FA according to Scherrer equation after the Gaussian peak fitting. K and λ are 0.9 and 0.15406 nm respectively

	Pristine graphite	G-FA
2θ (degree)	26.42	26.36	26.51
FWHM (degree)	0.201	1.095	0.277
D (nm)	40.57	7.45	29.5

---

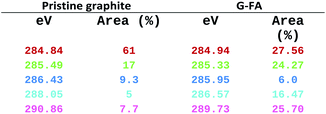
G-FA and pristine graphite were also examined by high-resolution XPS. As it is shown in Fig. S3a, ESI,† the pristine graphite flakes exhibit two prominent peaks for carbon and oxygen, while the G-FA shows a nitrogen peak too. This peak for nitrogen appears at 399.7 eV and displays the grafting of the primary amine to the graphene sheets and confirms a D–A functionalization of graphite. On the other hand, the amount of oxygen increased in the G-FA sample from 1.5% to 6.4% due to attaching furfuryl amine function to the graphite. So, the sharp changes are mainly attributed to higher oxygen content and the appearance of nitrogen peak in the G-FA. Moreover, detailed information of C 1s regions can be detected to confirm the change of the chemical structure.

In Fig. S3b, ESI,† the black lines are raw data curves for the pristine graphite and the G-FA, while the other colored lines are gauss fitted ones, which is finalized in Table 2. As it is clearly seen, the ratio of the sp³/sp² carbon in the G-FA is higher than in the pristine graphite, and a new peak assigned to a C–N bond appeared at 285.95 (eV), which confirms the existence of a carbon–nitrogen bond in the G-FA. Also, peaks at 286.43 (eV) in graphite and 286.57 (eV) in G-FA are attributed to C–O and C–O–C bonds which exhibit an increase from 5% in graphite to 16.47 in G-FA. All these facts, are in good agreement with other analytical data and confirm the successful D–A functionalization of graphene.

Table 2 High resolution C 1s, Gauss fitting. Colors in the Table are attributes to the colors in the spectra (Fig. S3b)

---

Samples were also examined by investigating of the interactions between water and two samples (G-BM and G-FA) surfaces via contact angle measurements.^58–60

As shown in Fig. 8, the contact angle for G-BM is around 105° compared to around 32° for G-FA. Based on these results, it can be determined that due to the attachment of amine functional groups to the graphene sheets, the interaction between water with G-FA is much higher than of graphite and G-FA exhibits a high wettability and higher hydrophilic properties than the pristine graphite.

Fig. 8 Contact angle of G-BM and G-FA with water on silicon wafer.

The morphologies of graphite and G-MA were compared using SEM. As shown in Fig. S4a, ESI† p. S5, the pristine graphite, the left image, has smooth surfaces while G-FA displays a coarse surface (right image). The grain size is smaller in G-FA. SEM images from the edges of the two samples clearly show the layer-like morphology with little aggregation at the edge of the graphene sheets of G-FA, Fig. S4b right, ESI.† On the contrary, the edges of the graphite obviously show firmly stacked layers Fig. S4b† left. On the other hand, as shown in Fig. S4c,† exfoliated edges of G-FA are coarser than the edges located in the pristine graphite. According to these distinguishable differences, effective functionalization onto the surface and mostly at the edges of the graphene sheets occurred in G-FA. SEM images in the ESI,† p. S5, clearly show that the edge of the few-layered graphene is uneven besides the exfoliation of the layers at the edges. The left and right images in Fig. S4c† are from G-FA samples but with different scales to show the edge location better.

Energy Dispersive X-ray Analysis (EDX) was performed to identify the elemental composition of the samples. Spectral data of G-BM and G-FA were measured at a voltage of 5 KV. Table 3, has been ordered by atom percentages for the two mentioned samples. As it is clear, due to the D–A reaction on G-FA, the nitrogen and oxygen content increased compared to G-BM. Also, the EDX measurements were a good indicator to clarify the purity of G-FA. According to the EDX results, there are no impurities in the product.

Table 3 EDX data for G-BM and G-FA based on atom%

Sample	Carbon	Nitrogen	Oxygen
G-FA	86.50	4.79	8.71
G-BM	97.45	0.00	2.55

---

Finally, the samples were evaluated via atomic force microscopy (AFM). Single-layer graphene is ∼0.34 nm thick and this value adds up accordingly for multilayer graphene. However, due to the surface roughness of graphene, changing cohesive forces between graphene and supporting substrates and variation introduced by AFM, graphene thickness and number of layers are difficult to determine the number of layers precisely. Sometimes the graphene surface absorbs water vapors and a very thin layer of water is formed on graphene films. Sometimes different contaminations stay on the surface of the graphene films. Hence, it is difficult to determine the actual thickness of the graphene films. Often, the single-layer graphene thickness is recorded between 0.4 nm and 1.0 nm, instead of 0.34 nm. Yao et al. demonstrated the use of histograms and found that the flake thicknesses of 1, 2, and 4-layer graphene were 1.5, 1.9, and 2.73 nm, respectively, by AFM.⁶¹

As shown in Fig. S5, ESI,† the average thickness of particles in the G-FA sample is around 4 nm, while this number is for graphite flakes around 40 nm. It can be estimated that G-FA has less than 10 layers. These results are comparable with the results from the XRD to some extent. This is another suitable indicator for the low thickness and the low number of layers of G-FA due to the successful ball milling and functionalization process.

Conclusions

In the presented approach, we functionalized directly graphite by a D–A cycloaddition reaction with furfuryl amine to transform it to functionalized few-layered graphene to make it soluble in polar solvents. To achieve this goal the D–A was carried out in the ball milling process and at increased temperatures. The combination of all three parameters has not been reported so far and resulted in very good yields. Various techniques were employed to reveal the confirmation of the functionalization, the location of the functional groups on the graphene sheets and also the thickness and layer numbers of the samples. According to all of this revealed evidence, furfuryl amine attached effectively mostly at the edges of the graphene sheets and caused the edges of the sample to lower the thickness compared to pristine graphite. The preparation of the presented material with this discussed approach will be beneficial for the synthesis of thermoreversible composite in the future by utilizing the presented retro-D–A reaction.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work has been funded by FKLEM (NRW Forschungskolleg “Leicht – Effizient – Mobil”) of Paderborn University. The success of this assignment owed to the guidance and assistance of some people in several research groups. We thank Prof. Dr Guido Grundmeier and Prof. Dr Michael Tiemann and their working group members at Paderborn University for cooperating in conducting some analytical measurements. Also, we appreciate Prof. Dr Ilona Horwath, Dr Horst Hintze-Bruening, and Dr Oliver Seewald for their support and advice to help to complete this assignment. We acknowledge support by Open Access Publishing Fund of Clausthal University of Technology.

Notes and references

1. L. Chai, Z. Hu, X. Wang, L. Zhang, T.-T. Li, Y. Hu, J. Pan, J. Qian and S. Huang, Carbon, 2021, 174, 531–539.
2. X. Wang, A. Dong, Y. Hu, J. Qian and S. Huang, Chem. Commun., 2020, 56, 10809–10823.
3. D. Jain, A. Winkel and R. Wilhelm, Small, 2006, 2, 752–755.
4. D. Jain and R. Wilhelm, Carbon, 2007, 45, 602–606.
5. A. Winkel, D. Jain and R. Wilhelm, Organometallics, 2008, 27, 3430–3434.
6. F. Pippert and R. Wilhelm, Carbon Trends, 2021, 4, 100075.
7. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669.
8. C. Lee, X. Wei, J. W. Kysar and J. Hone, Science, 2008, 321, 385–388.
9. Y. Zhu, S. Murali, W. Cai, X. Li, J. W. Suk, J. R. Potts and R. S. Ruoff, Adv. Mater., 2010, 22, 3906.
10. J. Moser, A. Barreiro and A. Bachtold, Appl. Phys. Lett., 2007, 91, 163513.
11. A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183.
12. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos and A. A. Firsov, Nature, 2005, 438, 197–200.
13. Y. Zhang, Y. W. Tan, H. L. Stormer and P. Kim, Nature, 2005, 438, 201–204.
14. A. A. Balandin, S. Ghosh, W. Bao, I. Calizo, D. Teweldebrhan, F. Miao and C. N. Lau, Nano Lett., 2008, 8, 902–907.
15. H.-X. Wang, Q. Wang, K.-G. Zhou and H.-L. Zhang, Small, 2013, 9, 1266–1283.
16. S. Eigler and A. Hirsch, Angew. Chem., Int. Ed., 2014, 53, 7720–7738.
17. H. B. Lee, A. V. Raghu, K. S. Yoon and H. M. Jeong, J. Macromol. Sci., Part B: Phys., 2010, 49, 802–809.
18. T. Mathew, R. A. Sree, S. Aishwarya, K. Kounaina, A. G. Patil, P. Satapathy, S. P. Hudeda, S. S. More, K. Muthucheliyan, T. N. Kumar, A. V. Raghu, K. R. Reddy and F. Zameer, FlatChem, 2020, 23, 100184.
19. D. P. Suhas, T. M. Aminabhavi, H. M. Jeong and A. V. Raghu, RSC Adv., 2015, 5, 100984–100995.
20. D. P. Suhas, A. V. Raghu, H. M. Jeong and T. M. Aminabhavi, RSC Adv., 2013, 3, 17120–17130.
21. D. A. Nguyen, A. V. Raghu, J. T. Choi and H. M. Jeong, Polym. Polym. Compos., 2010, 18, 351–358.
22. S. Kumar, K. R. Reddy, C. V. Reddy, N. P. Shetti, V. Sadhu, M. V. Shankar, V. G. Reddy, A. V. Raghu and T. M. Aminabhavi, in Nanostructured Materials for Environmental Applications, ed. S. Balakumar, Springer, 2021, pp. 485–519.
23. A. Wolk, M. Rosenthal, S. Neuhaus, K. Huber, K. Brassat, J. K. N. Lindner, R. Grothe, G. Grundmeier, W. Bremser and R. Wilhelm, Sci. Rep., 2018, 8, 5843.
24. A. Wolk, M. Rosenthal, J. Weiß, M. Voigt, J. Wesendahl, M. Hartmann, G. Grundmeier, R. Wilhelm, G. Meschut, M. Tiemann and W. Bremser, Prog. Org. Coat., 2018, 122, 280–289.
25. M. Rosenthal, J. K. N. Lindner, U. Gerstmann, A. Meier, W. G. Schmidt and R. Wilhelm, RSC Adv., 2020, 10, 42930–42937.
26. L. Yan, Y. B. Zheng, F. Zhao, S. Li, X. Gao, B. Xu, P. S. Weiss and Y. Zhao, Chem. Soc. Rev., 2012, 41, 97–114.
27. S. Sarkar, E. Bekyarova, S. Niyogi and R. C. Haddon, J. Am. Chem. Soc., 2011, 133, 3324–3327.
28. S. Sarkar, E. Bekyarova and R. C. Haddon, Acc. Chem. Res., 2012, 45, 673–682.
29. K. C. Nicolau, S. A. Snyder, T. Montagnon and G. Vassilikogiannakis, Angew. Chem., Int. Ed., 2002, 41, 1668–1698.
30. F. Fringuelli and A. Taticchi, The Diels–Alder Reaction: Selected Practical Methods, John Wiley & Sons, Chichester, UK, 2004.
31. S. Santanu, B. Elena and R. C. Haddon, Acc. Chem. Res., 2012, 45, 673.
32. B. Willocq, V. Lemaur, M. E. Garah, A. Ciesielski, P. Samori, J. M. Raquez, P. Dubois and J. Cornil, Chem. Commun., 2016, 52, 7608–7611.
33. J. Yuan, G. Chen, W. Weng and Y. Xu, J. Mater. Chem., 2012, 22, 7929.
34. N. Zydziak, B. Yameen and C. Barner-Kowollik, Polym. Chem., 2013, 4, 4072–4086.
35. J. Li, M. Li, L. L. Zhou, S. Y. Lang, H. Y. Lu, D. Wang, C. F. Chen and L. J. Wan, J. Am. Chem. Soc., 2016, 138, 7448–7451.
36. Z. Ji, J. Chen, L. Huang and G. Shi, Chem. Commun., 2015, 51, 2806–2809.
37. R. Cao, Y. Wang, S. Chen, N. Han, H. Liu and X. Zhang, ACS Appl. Mater. Interfaces, 2019, 11, 8982–8991.
38. P. A. Denis, Chem. Phys. Lett., 2017, 684, 79–85.
39. P. A. Denis, Chem.–Eur. J., 2013, 46, 15719–15725.
40. J. Xu, X. Zhao, F. Liu, L. Jin and G. Chen, New J. Chem., 2020, 44, 1236–1244.
41. C.-R. Oh, S.-H. Lee, J.-H. Park and D.-S. Lee, Nanomaterials, 2019, 9, 434.
42. K. P. Loh, Q. Bao, P. K. Ang and J. Yang, J. Mater. Chem., 2010, 20, 2277–2289.
43. D. E. Jiang, B. G. Sumpter and S. Dai, J. Chem. Phys., 2007, 126, 134701.
44. T. Wassmann, A. P. Seitsonen, A. M. Saitta, M. Lazzeri and C. F. Mauri, J. Am. Chem. Soc., 2010, 132, 3440–3451.
45. M. M. Lucchese, F. Stavale, E. H. M. Ferreira, C. Vilani, M. V. O. Moutinho, R. B. Capaz, C. A. Achete and A. Jorio, Carbon, 2010, 48, 1592–1597.
46. A. C. Ferrari and J. Robertson, Phys. Rev. B, 2000, 61, 14095.
47. T. Cui, S. Mukherjee, C. Cao, P. M. Sudeep, J. Tam, P. M. Ajayan, C. V. Singh, Y. Sun and T. Filleter, Carbon, 2018, 136, 168–175.
48. A. C. Ferrari, J. C. Meyer, V. Scardaci, C. Casiraghi, M. Lazzeri, F. Mauri, S. Piscanec, D. Jiang, K. S. Novoselov, S. Roth and A. K. Geim, Phys. Rev. Lett., 2006, 97, 187401.
49. L. G. Cancado, K. Takai, T. Enoki, M. Endo, Y. A. Kim, H. Mizusaki, N. L. Speziali, A. Jorio and M. A. Pimenta, Carbon, 2008, 46, 272–275.
50. Y. Hernandez, V. Nicolosi, M. Lotya, F. M. Blighe, Z. Sun, S. De, I. T. McGovern, B. Holland, M. Byrne, Y. K. GunKo, J. J. Boland, P. Niraj, G. Duesberg, S. Krishnamurthy, R. Goodhue, J. Hutchison, V. Scardaci, A. C. Ferrari and J. N. Coleman, Nat. Nanotechnol., 2008, 3, 563–568.
51. M. Schirowski, F. Hauke and A. Hirsch, Chem.–Eur. J., 2019, 25, 12761–12768.
52. C. P. Feng, H. Y. Ni, J. Chen and W. Yang, ACS Appl. Mater. Interfaces, 2016, 8, 19732–19738.
53. G. Chen, H. Wang and W. Zhao, Polym. Adv. Technol., 2008, 19, 1113–1117.
54. M. Mauro, V. Cipolletti, M. Galimberti, M. Longo and G. Guerra, J. Phys. Chem. C, 2012, 116, 24809–24813.
55. H. Fujimoto, Carbon, 2003, 41, 1585–1592.
56. C. N. R. Rao, K. Biswas, K. S. Subrahmanyam and A. Govindaraj, J. Mater. Chem., 2009, 19, 2457–2469.
57. B. F. Machado and P. Serp, Catal. Sci. Technol., 2012, 2, 54–75.
58. S. Tian, L. Li, W. Sun, X. Xia, D. Han, J. Li and C. Gu, Sci. Rep., 2012, 2, 511.
59. D. P. Suhas, T. M. Aminabhavi and A. V. Raghu, Appl. Clay Sci., 2014, 101, 419–429.
60. D. P. Suhas, T. M. Aminabhavi and A. V. Raghu, Polym. Eng. Sci., 2014, 54, 1774–1782.
61. Y. Yao, L. Ren, S. Gao and S. Li, J. Mater. Sci. Technol., 2017, 33, 815–820.

---

Footnote

† Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ra02566c

---