Effects of axial pressure on the evolution of core–shell heterogeneous structures and magnetic properties of Fe–Si soft magnetic powder cores during hot-press sintering

Abstract

Silicon dioxide (SiO₂) has attracted much attention as an ideal coating material for iron (Fe)-based soft magnetic powder cores (SMPCs). However, maintaining the integrity and uniformity of Fe-based/SiO₂ core–shell heterostructures is still a challenge. The evolution mechanism of core–shell heterostructures determines the performance of Fe-based SMPCs. Herein, the evolution of the core–shell structures and heterogeneous interfaces of Fe–Si@SiO₂ SMPCs with axial pressure and the influence of the evolution on the SMPCs performance were investigated. The results show that in the axial pressure range of 10–15 kN, the core–shell heterostructures were gradually integrated, whereas the SiO₂ insulation coatings underwent an amorphous-to-crystalline transformation. At axial pressure above 16 kN, the Fe–Si powder melted partially, and the core–shell heterostructure collapsed due to overheating, caused by the gradient temperature field during the hot-press sintering. When the core–shell heterostructure was intact, the Fe–Si@SiO₂ SMPCs showed a permeability of over 38 with a wide and stable frequency range of 100–300 kHz, a saturation magnetisation of 231.7 emu g⁻¹, resistivity of 0.8 mΩ cm and total loss of 704.7 kW m⁻³ at 10 mT and 100 kHz. When the core–shell heterostructure was destroyed, the resistivity dropped dramatically and the loss increased to 765.0 and 897.4 kW m⁻³. These results show the relationship between the core–shell heterostructure of Fe–Si@SiO₂ SMPCs, axial pressure and magnetic properties, which would be vital in achieving high power density, high efficiency and miniaturisation in SMPCs.

---

Introduction

Achieving high efficiency and miniaturisation of electrical devices requires electromagnetic elements with small size, low weight and excellent magnetic performance.¹ Conventional silicon–steel electromagnetic elements do not meet the rapidly increasing demands for high-frequency and power density applications. Soft magnetic powder cores (SMPCs) can enable the miniaturisation and diversification of electromagnetic devices, exhibit low eddy current loss under a wide frequency range and fill the application gap between silicon–steel and ferrite electromagnets.² Thus, SMPCs are promising candidates for efficient and lightweight electromagnetic devices.

SMPCs consist of a highly saturated ferromagnetic powder core and a high-resistivity insulating shell, resulting in a core–shell heterogeneous structure. Thus, they have high permeability, high saturation magnetisation (M_s), high resistance and very low eddy current loss.³ Various insulating materials and coating methods have been investigated extensively to optimise the performance of SMPCs. Oxide ceramic insulating materials have higher heat resistance and lower cost than traditional organic insulating materials,⁴ thus can increase the moulding temperature and improve magnetic conductivity while maintaining good insulation. As a result, various advanced sintering technologies, such as hot-press sintering (HPS),^5,6 hot isostatic pressing (HIP)^7,8 and spark plasma sintering (SPS),^9,10 have been developed to prepare SMPCs with oxide ceramic insulating materials.

Core–shell heterostructures within SMPCs limit the induced current during AC magnetisation inside the insulating and conductive particles, reducing the eddy current radius and minimising energy loss.¹¹ To obtain high-performance SMPCs, the core–shell heterostructure should maintain its integrity and uniformity. However, as-developed oxide ceramic insulating materials, such as SiO₂, MgO, ZrO₂ and Al₂O₃, are brittle and susceptible to fracture under high-pressure and temperature conditions, making the core–shell heterogeneous structure prone to destruction during sintering. As an important parameter in the sintering process, axial pressure is a key determinant of the structure and magnetic properties of SMPCs with oxide ceramic insulating materials. Low moulding pressure results in low material density and imperfect grain morphology, whereas high moulding pressure can destroy the integrity of the core–shell heterostructure, reducing the limiting effect on the induced current. However, current research on sintering conditions (temperature, pressure, etc.) mainly focuses on material density and magnetic properties; only a few studies have investigated the evolution of core–shell heterostructures.

In this study, Fe–Si SMPCs with SiO₂ insulating materials (denoted Fe–Si@SiO₂) were fabricated through fluidised gas-phase in situ deposition combined with the HPS process. By observing the structural and interfacial changes in Fe–Si@SiO₂ in a high-pressure environment, the evolution behaviour of the Fe–Si@SiO₂ heterostructure and its relationship with the magnetic properties were determined, which filling the theoretical gap between microstructure and macroscopic properties. The obtained relationship will help improve the performance of SMPCs and promote the application and development of SMPCs.

Experimental

Materials

Commercial atomised Fe–Si powders (Si content 6.62 wt%, purity exceeding 99.9 wt%) with an average particle size of 50 μm were purchased from Hualiu New Materials Co., Ltd., China Tetraethyl orthosilicate (C₈H₂₀O₄Si, 99.0 wt%) was provided by Zhiyuan Chemical Reagent Co. Ltd., China Argon gas (Ar, 99.99 wt%) was purchased from Tianze Gas Co. Ltd, China.

Synthesis

Fe–Si@SiO₂ core–shell powders, with Fe–Si powders as the core and SiO₂ as the shell, were synthesised via fluidised gas-phase in situ deposition. During the process of the fluidised gas-phase in situ deposition, the of Fe–Si particles was placed on a stainless steel strainer, with 30 μm-diameter pores, within a vertical tube furnace and fluidised using Ar dilution gas. Tetraethyl orthosilicate (outgassed at around 150 °C) was introduced into the furnace by another Ar carrier gas flow (at a rate of 300 mL min⁻¹) for 60 min when the furnace temperature reached 647 °C. The Fe–Si/SiO₂ composite particles were collected after the furnace cooled to room temperature. Then, an appropriate amount of the as-synthesised Fe–Si@SiO₂ core–shell powders were poured into a graphite die and compacted in an HPS furnace (Changjiang Jinggong Material Technology Co. Ltd., China). The sintering temperature was increased to 910 °C over 10 min and then maintained for another 10 min. Afterward, the temperature was reduced to 50 °C at the rate of 50 °C min⁻¹. The axial pressure was maintained at 10–17 kN until the temperature reached 910 °C. After sintering, the SMPCs were annealed at 650 °C for 120 min. The height of SMPCs was 5 mm, and the inner and outer diameters were 20 and 30 mm, respectively.

Characterisation

Differential scanning calorimetry (DSC) was performed using a Netzsch thermal analyser (STA-499C, NETZSCH, Germany, first heating curve with a temperature range from 0 to 1200 °C, while the warming rate was 10 °C min⁻¹) to evaluate the temperature and the corresponding thermal effects of phase changes in the Fe–Si@SiO₂ core–shell powder. X-ray diffraction (XRD, Bruker D8 Advance, Bruker, Germany) with Cu K_α radiation was employed to analyse the phase compositions of the Fe–Si@SiO₂ core–shell powder and SMPCs. The morphologies and local chemical homogeneity of the samples were characterised by scanning electron microscopy (SEM, Tescan MIRA3 XMU, TESCAN, Czech) with energy-dispersive spectroscopy (EDS, JED-2300, TESCAN, Czech). Changes in the electronic structure of SMPCs were characterised by X-ray photoelectron spectroscopy (XPS, PHI-5000 Versaprobe, ULVAC-PHI, Japan). The hysteresis loops were measured at room temperature using a vibrating sample magnetometer (MPMS-3, Quantum Design, America) within the magnetic-field strength of −20 000 to 20 000 Oe with a step size of 50 Oe. The electrical resistivity of the Fe–Si@SiO₂ SMPCs was measured using a resistivity tester (ST2253y, Suzhou Jingge Electronic Co., LTD, China). The core loss values were determined using a B–H analyser (SY-8258, IWATSU, Japan).

Results and discussion

Microstructures of Fe–Si@SiO₂ heterostructure powders

XRD was employed to investigate the chemical components of the powder samples. The XRD patterns of the Fe–Si alloy powders before and after the deposition are shown in Fig. 1(a). Three diffraction peaks were observed at 44.82° (110), 65.24° (200) and 82.64° (211). The peaks are attributed to the body-centred cubic α-Fe(Si) solid-solution (ICDD09-065-9130), whose crystal has an Im3m space group (229). After the deposition, the XRD pattern showed a wide amorphous diffraction peak at 2θ = 23° in addition to the aforementioned α-Fe(Si)-phase diffraction peaks, indicating that SiO₂ formed an amorphous layer on the surface of Fe–Si alloy powders, which is consistent with previous reports.^12,13 To characterise the core–shell structure of the coated powders, SEM images and EDS spectra of the Fe–Si powders were recorded before and after deposition (Fig. 1(b)–(e)). Despite the presence of some wrinkles and pits, the surface of the Fe–Si powders remained relatively smooth. Numerous SiO₂ insulating particles, which were synthesised and deposited on the surface of the Fe–Si powder substrate, were layered and uniform in size. The SEM images reveal that the Fe–Si powders are tightly coated by an integrated, continuous insulating layer. The SEM (planar and cross-sectional) images and EDS spectra of the Fe–Si@SiO₂ composites were mapped to demonstrate the formation of the core–shell structure (Fig. 1(f)–(g)). The elemental distribution maps show that Si is distributed throughout the cross-section of the powders, whereas O and Fe are mostly distributed in the shell and core, respectively.¹⁴ The EDS results reveal that the Fe–Si powders are tightly packed by an integrated continuous uniform insulating layer. The above results show that Fe–Si@SiO₂ powders with fine microstructural core–shell heterostructure characteristics can be obtained using the proposed method.^12,15

Fig. 1 (a) X-ray diffraction (XRD) patterns, (b–e) Scanning electron microscopy (SEM) images and (f, g) energy-dispersive spectroscopy (EDS) results of deposited Fe–Si powders.

Microstructural evolution of Fe–Si@SiO₂ SMPCs

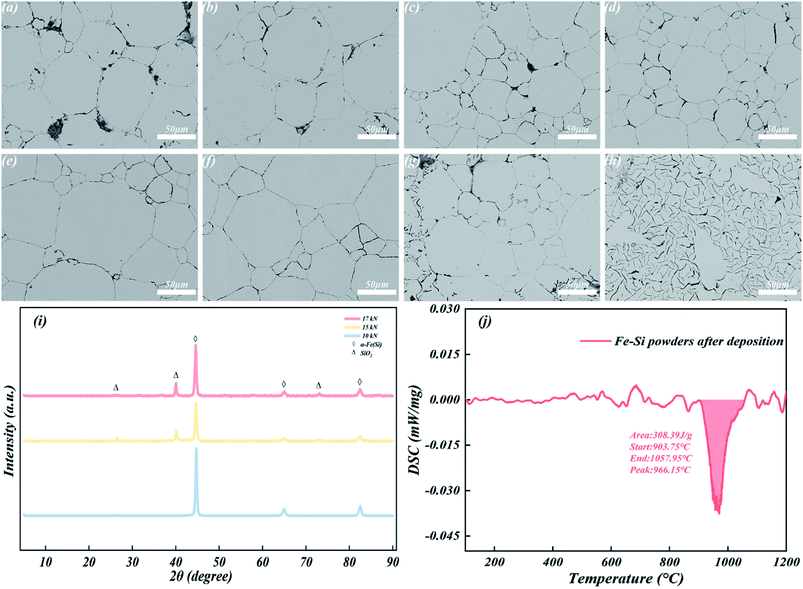
BSE images of the polished surfaces of Fe–Si@SiO₂ SMPCs, sintered at different pressures, are shown in Fig. 2(a)–(h). SMPCs sintered at 10 kN contains few pores due to the poor fluidity of the powders owing to the large frictional force induced by the nano-SiO₂ particles during the moulding process.¹⁶ Moreover, the coated SiO₂ accumulated at the particle-to-particle interface. With an increase in the axial pressure, SMPCs sintered at 11, 12, 13, 14 and 15 kN (Fig. 2(b)–(e)) showed fewer pores in the surface boundaries than those sintered at 10 kN (Fig. 2(a)). The concentration of the coated SiO₂ gradually increases along the edges of the Fe–Si powders, where the layers are evenly wrapped, owing to the increase in density and decrease in porosity with increasing pressure. Further, the core–shell structure is completely preserved in the pressure range of 10–15 kN. Fig. 2(f) shows that as the axial pressure increases up to 16 kN, an uncoated grey region appears and a part of the insulating layer disappears. As the axial pressure continues to increase, a black region begins to disperse in the grey region, which gradually becomes more chaotic and disordered (Fig. 2(h)). The internal Fe–Si also begins to melt; thus, Fe–Si cannot support the SiO₂ coating and heterointerface under the axial pressure. Consequently, the core–shell heterostructure collapses and is destroyed. The partial melting of the Fe–Si powders, as mentioned above, is caused by HPS. During HPS, axial pressure is applied to the SMPCs, which promotes the diffusion of atoms into the material, strengthens the dynamic conditions of sintering, increases the heating rate and shortens the sintering time.¹⁷ The sintering heat required to prepare SMPCs from Fe–Si@SiO₂ core–shell heterostructure composite powders depends on the thermal energy between the Fe–Si alloy powders and that absorbed by the Fe–Si alloy. The superposition of the two thermal effects at the heterogeneous interface generates a local high temperature on the surface of the Fe–Si alloy powders and forms a gradient temperature field in the powders,¹⁸ which decreases from the surface to the interior. Based on this mechanism, simultaneous high densification of the core (an Fe–Si alloy with a low melting point) and shell (a SiO₂ insulating film with a high melting point) at different sintering temperatures can be achieved. Furthermore, the axial pressure applied to SMPCs makes them thermoplastic during sintering, which promotes the contact and diffusion of powders, thereby promoting the sintering of SMPCs. However, when the pressure is too high, the thermoplastic Fe–Si powders are deformed, and the original gradient temperature field is destroyed. Due to the external high temperature, Fe–Si powders melt locally and lose the support of the outer SiO₂ layer, resulting in the collapse and destruction of the core–shell heterostructure.

Fig. 2 BSE images of polished surfaces of Fe–Si@SiO₂ soft magnetic powder cores (SMPCs) sintered at different pressures: (a) 10 kN, (b) 11 kN, (c) 12 kN, (d) 13 kN, (e) 14 kN, (f) 15 kN, (g) 16 kN and (h) 17 kN. (i) X-ray diffraction (XRD) patterns and (j) differential scanning calorimetry (DSC) curves of Fe–Si@SiO₂ SMPCs.

Fig. 2(i) shows the XRD patterns of Fe–Si@SiO₂ SMPCs sintered at different pressures. Three diffraction peaks are observed at 44.59°, 65.00° and 82.45°, corresponding to the (110), (200) and (211) planes of the FCC α-Fe (Si) phase, respectively. The space group of the crystal is Im3m (229). To further investigate the formation mechanism of Fe–Si@SiO₂ composites, DSC was employed and the curves are shown in Fig. 2(j). The Fe–Si@SiO₂ composites show a characteristic peak at 903.75–1057.95 °C, centred at 966.15 °C, which can be attributed to the crystallisation of the amorphous SiO₂ phase obtained from C₈H₂₀O₄Si.¹⁹ A comprehensive analysis of the XRD patterns of the powder and bulk material showed that SiO₂ exists in an amorphous state on the surface of the Fe–Si powder; however, after high-temperature sintering, the broad peak indicating the amorphous SiO₂ disappears. On the other hand, the local overheating phenomenon promotes the transformation of SiO₂ to the crystalline state during the high-temperature forming process, as revealed by the DSC curve. XRD showed that when the axial pressure increases beyond 15 kN, SiO₂ crystallisation is enhanced; the crystalline characteristic peak of SiO₂ (26.44°, 40.05° and 73.12°) becomes highly pronounced, and the peak intensity increases. The crystalline characteristic peaks of SiO₂ (26.44°, 40.05° and 73.12°) became very obvious, and the peak intensity increased. This is because with a further increase in axial pressure, the Fe–Si powder melts and SiO₂ is no longer confined to the edge of the particles but diffuses widely.

To further analyse the reactions, surface chemistry and composition of the Fe–Si@SiO₂ SMPCs, X-ray photoelectron spectroscopy (XPS) was performed, and the spectra are shown in Fig. 3. The peak positions and atomic ratios were obtained by curve fitting, and the electron binding energy of the C 1s peak was set to 284.8 eV to correct the positions of the other peaks. The spectrum of Si 2p (Fig. 3(a)) contains four deconvolution curves with peak electron binding energies of 101.60 eV (19.91 at%), 102.04 eV (15.31 at%), 102.98 eV (49.69 at%) and 103.82 eV(15.08 at%), indicating the presence of four Si radicals constituting an Si–O–Si structure. According to literature,²⁰ the composition of the four Etx groups is given as (Si(OC₂H₅)_x(OH)_4−x, x = 0–3), and their levels are Et0, Et3, Et2 and Et1. Therefore, the binding energy bands correspond to the Et2 (101.60 eV), Et0 (102.04 eV), Et3 (102.98 eV) and Et1 (103.82 eV) groups. Similarly, the corresponding relationship between the binding state of O 1s and the binding energy of electrons is derived from the O atoms of the Et2 (529.80 eV), Et0 (531.06 eV), Et1 (531.60 eV) and Et3 (532.39 eV) groups and the atom connected to Fe, whose binding energy is 533.60 eV, as shown in Fig. 3(b). The total number of O atoms (49.64 at%) from the Et3 group (42.52 at%) and its connection with Fe atoms (7.12 at%) are almost equal to the number of Si atoms in the Et3 group (49.69 at%). This shows that the O atom connected to the Fe atom also originates from the Et3 group, and the connection reduces the electron binding energy of the O atom. These results imply the formation of interfacial covalent bonds between the Fe–Si core and the SiO₂ shell.²¹ As the pressure increases to 17 kN, the Et3-group proportion derived from Si decreases to 32.75 at%, whereas the Et3- and Fe–O-group proportions of O 1s slightly increase (46.44 at%) and decrease (3.62 at%), respectively, which can be attributed to the breakage of the interfacial bonds due to the disruption of the core–shell heterostructure.

Fig. 3 XPS images of Fe–Si@SiO₂ SMPCs sintered at 14 kN (Si 2p (a) and O 1s (b)) and 17 kN (Si 2p (c) and O 1s (d)).

Effects of axial pressure on magnetic properties

Fig. 4 shows the hysteresis loops of SMPCs prepared at different axial pressures. All SMPCs exhibit high saturation magnetisation (M_s) when the coercivity is maintained at 10–30 Oe. However, owing to the limitations of the testing instrument, the hysteresis loop was detected at 50 Oe, which is much higher than the actual value. Therefore, coercivity cannot be used as the basis to compare performance. With increasing pressure, M_s first increases from 204.2 to 233.2 emu g⁻¹. This is because as the axial pressure increases, the density of SMPCs increases, SiO₂ insulation becomes more evenly distributed, and the core–shell heterostructure becomes more complete, thereby reducing the porosity and increasing the total magnetic moment per unit volume. However, as the axial pressure continues to increase to 16–17 kN, the pores generated by the destruction of the core–shell heterostructure led to a decrease in M_s. This trend is observed because M_s depends on the total magnetic moment per unit volume,²² the disruption of the core–shell heterostructure leads to the re-emergence of pores, thereby causing a moderate change in M_s.²³

Fig. 4 Hysteresis curves showing the saturation magnetisation (M_s) of Fe–Si@SiO₂ SMPCs sintered at different axial pressures.

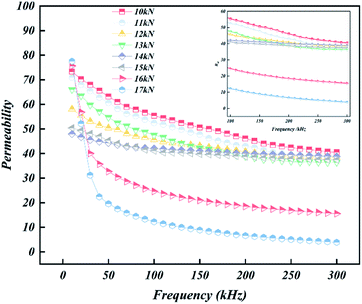
Fig. 5 shows the influence of the core–shell heterostructure of the compound powder on frequency stability and permeability due to changes in axial pressure. As a general trend, the permeability of SMPCs decreases with increasing frequency. The permeability of samples with an intact core–shell heterostructure (14 and 15 kN) is lower than that of samples with an incomplete core–shell heterostructure (10, 11, 12 and 13 kN), which is attributed to the magnetic dilution effect in more complete and dense insulating layers, which prevents the Fe–Si powder from contacting each other and; thus, increases the magnetoresistance. It can also be attributed to the exchange coupling between the SiO₂ particles and Fe–Si powder, resulting in an effective surface spin orientation. However, samples with intact core–shell heterostructures (14 and 15 kN) stabilise at lower frequencies because, as the frequency increases, a complete insulating layer favours an increase in the depth of the skin effect and; therefore, the frequency stability of the permeability. When the axial pressure is further increased (16 and 17 kN), permeability drops again due to the internally chaotic magnetic domain structure caused by the destruction of the core–shell heterostructure. Considering the magnetic dilution and eddy current effects, when the axial pressure is 14 kN, higher and relatively stable magnetic permeability is maintained in a larger frequency range.

Fig. 5 Variation of the permeability of Fe–Si@SiO₂ SMPCs sintered at different axial pressures.

It is difficult to quantify the uniformity of SMPCs coatings. Qualitatively, better uniformity indicates higher inter-particle electrical insulation, which not only hinders the generation of inter-particle eddy currents but also reduces the magnetic weakening caused by additional non-magnetic agglomeration.²⁴ Consequently, resistivity was used to characterise the electrical insulation of the prepared Fe–Si@SiO₂ SMPCs. The variation in resistivity is shown in Fig. 6. As the axial pressure increases, the internal pores disappear and the resistivity decreases gradually.

ρ = 1/neμ, (1)

where n is the carrier concentration of the semiconductor material, e the charge on an electron and μ the semiconductor mobility. Above 15 kN, owing to the excessively, high axial pressure during sintering, the actual temperature between the particles inside the SMPCs is much higher than the set sintering temperature, even higher than the melting point of the Fe–Si powder. Consequently, the arrangement of the crystal structure gradually becomes chaotic, the vacancies originally existing in the amorphous layer are compensated, the carrier concentration increases, and the resistivity decreases.¹² Furthermore, the powder melts, and the insulating layer loses its support and gradually becomes scattered and disordered, thereby reducing the resistivity.

Fig. 6 Variation resistivity of Fe–Si@SiO₂ SMPCs sintered at different axial pressures.

Fig. 7(a) shows the loss distribution diagram of the Fe–Si@SiO₂ powders formed in SMPCs after sintering at different pressures. The total loss of SMPCs sintered at all pressures increases with increasing test frequency, and the total loss first decreases and then increases with increasing axial pressure. Under the conditions of 10 mT and 100 kHz, the total loss of SMPCs sintered at 17 kN is up to 897.4 kW m⁻³, whereas that of the sample sintered at 14 kN is the lowest (699.4 kW m⁻³, 21.1% decrease), followed by that of the samples sintered at 15 kN (704.7 kW m⁻³, 21.5% decrease). This shows that as the axial pressure increases, the pores decrease gradually, the core–shell heterostructure becomes complete and the loss decreases gradually. As the axial pressure continues to increase, the Fe–Si powder melts, which distorts the core–shell heterostructure. Consequently, the magnetic domain structure is destroyed, and the potential barrier to the displacement of the domain wall increases, thereby increasing the total loss. To further analyse the influence of the core–shell structure on the total loss, according to the classic Bertotti's loss separation theory, the total mass lost P_cv (kW m⁻³) can be separated into three different physical parts: hysteresis loss (P_hyst), eddy current loss (P_ec) and excess loss (P_exc).²⁵ The model can be expressed as follows:

P_cv = P_hyst + P_ec + P_exc. (2)

Fig. 7 (a) Total loss of Fe–Si@SiO₂ SMPCs sintered at different axial pressures. (b) Hysteresis loss, (c) eddy current loss and (d) excess loss after the loss distribution of Fe–Si@SiO₂ SMPCs sintered at 14 and 17 kN.

P_hyst is the area of the quasi-static hysteresis loop multiplied by the frequency, which is expressed as follows:

P_hyst = C_hystB_m^αf, (3)

where C_hyst represents the hysteresis coefficient, B_m the maximum induction, f the frequency and α the simulation coefficient (between 1.6 and 2.2 for most ferromagnetic materials and alloys). In soft magnetic composites, P_ec can be expressed as follows:

P_ec = P^inter_ec + P^intar_ec = π²d_eff²B_m²f²/6/[1 − 0.633(w/h)tanh(1.58h/w)]ρ_s + π²d²B_m²f²/β₂ρ_p (4)

where P^inter_ec and P^intar_ec are the inter- and intra-particle eddy current coefficients, respectively, d_eff the effective eddy current dimension (the specimen thickness) and d the particle size. ρ_s and ρ_p are the bulk resistivity of the specimen and particles, respectively. β₁ is the rectangular cross-sectional geometrical factor, and w and h are the width and height of the rectangle, respectively. β₂ is a granular geometrical factor with different values for different geometries (for spheres, β₂ = 20).²⁶ Empirically, P_exc ∝ f1.5 is assumed to be an oversimplification; the excess loss depends on several variables, such as the test frequency, applied magnetic field, cross-sectional area of the material perpendicular to the magnetic flux, and number of active magnetic objects under quasi-static and dynamic magnetisation.²⁷ Accordingly, the expression is be modified as follows:

P_exc = C_excB_m^xf^y, (5)

where C_exc is the excess coefficient, and x and y are coefficients related to the applied magnetic field and frequency, respectively.

The P_cv/f versus f curve was first simulated for different maximum magnetic flux densities using a polynomial-curve simulation method. Then, the intercepts representing hysteresis losses under quasi-static conditions were obtained by extrapolating the simulation curve to zero frequency. By fitting the quasi-static hysteresis loss under different external fields, C_hyst and α were obtained, and the coefficient of eddy current loss was calculated using eqn (4). Finally, the parameters obtained from the curve fitting and calculations were substituted into eqn (5) to fit the parameters C_exc, x and y.²⁸ The final fitting results are listed in Table 1. To better understand the influence of core–shell heterostructures on various losses, SMPCs sintered at 14 and 17 kN with intact and damaged core–shell heterostructures, respectively, were analysed, as shown in Fig. 7(b)–(d).

Table 1 Coefficients of C_hyst, C_ec, C_exc and other fitting parameters of Fe–Si@SiO₂ SMPCs sintered at different axial pressures

Sample axial pressure (kN)	Hysteresis component		Eddy current component	Excess component			R-square
	Chyst	α	Cec	Cexc	x	y
10	31.520	1.971	0.164	0.852	1.938	1.735	0.9991
11	35.004	2.011	0.171	0.688	1.906	1.719	0.9986
12	27.090	1.973	0.176	1.112	2.038	1.621	0.9999
13	27.103	1.972	0.191	0.589	1.859	1.552	0.9987
14	24.674	1.968	0.199	1.192	2.037	1.509	0.9991
15	27.014	1.992	0.240	0.547	1.906	1.757	0.9996
16	30.968	2.003	0.371	0.497	1.892	1.771	0.9997
17	35.622	1.998	0.421	0.533	1.881	1.763	0.9999

---

Fig. 7(a) shows that the total loss of SMPCs first decreases and then increases with increasing axial pressure. Initially, the pores in the SMPCs gradually decrease, the core–shell heterostructure is progressively refined, and the induced anisotropy caused by the impurity diffusion and hindering effect between the magnetic domains is weakened, thereby reducing the total loss. When the axial pressure is 14 to 15 kN, the core–shell heterostructure remains intact, and a minimum total SMPCs loss is achieved. As the axial pressure increases, local overheating during the sintering process causes the core–shell heterostructure to rupture gradually. The internal structure of SMPCs becomes chaotic, increasing the total loss. Fig. 7(b)–(d) compare various losses of SMPCs prepared at 14 and 17 kN before and after the destruction of the core–shell heterostructure. Compared with samples having collapsed core–shell heterostructures, the eddy current loss of those having complete core–shell heterostructures decreased by 53.9%, whereas the hysteresis loss decreased by only 23.1%. Thus, the main effect of axial pressure on SMPCs is the reduction in eddy current loss.

SMPCs sintered at different are compared in Table 2. For samples sintered at 910 °C for 10 min, 14 kN is the optimum axial pressure considering the magnetic properties.

Table 2 Overall comparison of magnetic properties at different axial pressures

Sample axial pressure (kN)	Amplitude permeability (300 kHz)	Saturation magnetisation (emu g^−1)	Resistivity (mΩ cm)	Total loss at 10 mT, 100 kHz (kW m^−3)
10	40.52	204.2	0.88	883.9
11	37.68	208.8	0.85	841.0
12	38.53	212.6	0.83	736.2
13	36.38	233.2	0.82	719.0
14	38.78	231.7	0.8	699.4
15	37.39	218.9	0.77	704.7
16	15.52	206.1	0.41	765.0
17	3.89	206.1	0.35	897.4

---

Although the core loss of the Fe–Si@SiO₂ composite compacts herein is still relatively high, the obtained core–shell structures can increase the electrical resistivity and reduce the core loss of Fe–Si alloys. In our future studies, we shall investigate the insulating shell-coating methods, the control of the uniformity and thickness of insulating shells and process optimisation of HPS.

Conclusions

In this study, the effects of axial pressure on the microscopic characteristics of core–shell heterostructures and the magnetic properties of Fe–Si@SiO₂ SMPCs were investigated. In the pressure range of 10–15 kN, the core–shell heterostructures are well integrated and become more uniform with increasing pressure. M_s increases and the resistivity and total loss decrease with an increase in axial pressure. However, when the pressure exceeds 16 kN, the core–shell heterostructure is destroyed, whereas M_s changes slightly, the resistivity, loss increases, and the resistivity decreases gradually. The Fe–Si@SiO₂ SMPCs exhibit the best magnetic properties at an axial pressure of 14 kN. The sample has a permeability of over 38 with a wide and stable frequency range of 100–300 kHz, M_s of 231.2 emu g⁻¹ and resistivity of 0.8 mΩ cm. Its total loss decreases by 21.47% from the maximum value. The obtained relationship between the core–shell heterostructures and the magnetic properties will help improve the performance of SMPCs and promote the application and development of SMPCs.

Author contributions

Yue Qiu, Writing – Original draft, Formal analysis and Investigation; Rui Wang, Original draft, Investigation and Methodology; Yihai He, Performance Test; Hui Kong, Picture Rendering and Review; Shaogang Li, Review and Editing; Zhaoyang Wu, Project administration.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This project was supported by the the Open Fund of the State Key Laboratory of Refractories and Metallurgy, Wuhan University of Science and Technology (No. G201901), National Natural Science Foundation of China (51904002), Natural Science Foundation of Anhui Province (1908085QE190) and Anhui Provincial Special Support Plan (T000609). The authors would like to thank Chao Wang, Lei He from Shiyanjia Lab (https://www.shiyanjia.com) for the XRD and XPS analysis. Yue Qiu and Rui Wang contributed equally to this work and should be considered co-first authors.

Notes and references

1. B. Zhou, Y. Dong, Q. Chi, Y. Zhang, L. Chang, M. Gong, J. Huang, Y. Pan and X. Wang, Ceram. Int., 2020, 46, 13449–13459.
2. S. Jena, D. K. Mishra, S. Mondal, S. Chakravarty, S. Hussain and P. Mallick, Appl. Phys. A, 2021, 127, 975.
3. Q. Zhai, W. Zhai, B. Gao, Y. Shi and X. Cheng, Colloids Surf., A, 2021, 625, 20.
4. J. Wang, S. Song, H. Sun and Z. Xue, J. Mater. Sci.: Mater. Electron., 2021, 32, 8545–8556.
5. Z.-T. Shu, B. Zheng, G.-F. Ding, S.-C. Liao, J.-H. Di, S. Guo, R.-J. Chen, A. R. Yan and L. Shi, Chin. Phys. B, 2020, 29, 057501.
6. S. P. Bennett, S. Kota, H. ElBidweihy, J. F. Parker, L. A. Hanner, P. Finkel and M. W. Barsoum, Scr. Mater., 2020, 188, 244–248.
7. T. Naito, A. Ogino, H. Fujishiro and S. Awaji, IEEE Trans. Appl. Supercond., 2020, 30, 1–6.
8. D. Gajda, A. J. Zaleski, A. J. Morawski, M. Babij, D. Szymański, G. Gajda, M. A. Rindfleisch, M. Shahbazi and M. S. A. Hossain, J. Alloys Compd., 2021, 871, 5.
9. W. Q. Liu, Z. Z. Cui, X. F. Yi, M. Yue, Y. B. Jiang, D. T. Zhang, J. X. Zhang and X. B. Liu, J. Appl. Phys., 2010, 107, 09A179.
10. R. Gopalan, H. Sepehri-Amin, K. Suresh, T. Ohkubo, K. Hono, T. Nishiuchi, N. Nozawa and S. Hirosawa, Scr. Mater., 2009, 61, 978–981.
11. Y. Pan, J. Peng, L. Qian, Z. Xiang and W. Lu, Mater. Res. Express, 2020, 7, 016115.
12. Z. Gao, J. Jia, Q. Zhao, H. Kong, Z. Wu and J. Li, J. Magn. Magn. Mater., 2022, 549, 168891.
13. A. H. Gemeay, B. E. Keshta, R. G. El-Sharkawy and A. B. Zaki, Environ. Sci. Pollut. Res. Int., 2020, 27, 32341–32358.
14. C. Zhang, P. Tao, K. Zhu, Y. Chen, W. Zhang and Y. Yang, J. Supercond. Novel Magn., 2021, 34, 2389–2396.
15. Z. Wu, Z. Gao, Q. Zhao, H. Kong, M. Li and J. Jia, Crystals, 2021, 11, 963.
16. K. L. Zheng, P. F. Yan, X. S. Wei and B. Yan, Wear, 2022, 494–495, 204268.
17. M. S. El-Eskandarany, N. Ali and M. Saeed, Nanomaterials, 2020, 10, 849.
18. Z.-H. Zhang, Z.-F. Liu, J.-F. Lu, X.-B. Shen, F.-C. Wang and Y.-D. Wang, Scr. Mater., 2014, 81, 56–59.
19. L. Han, J. Song, C. Lin, J. Liu, T. Liu, Q. Zhang, Z. Luo and A. Lu, J. Eur. Ceram. Soc., 2018, 38, 4533–4542.
20. Z. Y. Wu, C. Xian, J. X. Jia, X. W. Liao, H. Kong, X. S. Wang and K. Xu, J. Phys. Chem. Solids, 2020, 146, 109626.
21. B. Bai, Y. Zhu, J. Miao, X. Wang, S. Bi, L. Kong, W. Liu and L. Zhang, Ceram. Int., 2022, 48, 2755–2762.
22. M. Tajabadi, I. Rahmani, S. M. Mirkazemi and H. Goran Orimi, Adv. Powder Technol., 2021, 33, 103366.
23. Q. Chi, L. Chang, Y. Dong, Y. Zhang, B. Zhou, C. Zhang, Y. Pan, Q. Li, J. Li, A. He and X. Wang, Adv. Powder Technol., 2021, 32, 1602–1610.
24. Z. Luo, X. a. Fan, B. Feng, Z. Yang, D. Chen, S. Jiang, J. Wang, Z. Wu, X. Liu, G. Li and Y. Li, Adv. Powder Technol., 2021, 32, 4846–4856.
25. M. M. Nell, B. Schauerte, T. Brimmers and K. Hameyer, COMPEL, 2022, 41, 600–614.
26. W. Li, Y. Pu, Y. Ying, Y. Kang, J. Yu, J. Zheng, L. Qiao, J. Li and S. Che, J. Alloys Compd., 2020, 829, 154533.
27. C. Liu, Y. Liu, Z. Dang, S. Zeng and C. Li, Appl. Surf. Sci., 2021, 544, 148886.
28. Z. Guo, J. Wang, W. Chen, D. Chen, H. Sun, Z. Xue and C. Wang, Mater. Des., 2020, 192, 108769.

---