Open Access Article
Open Access ArticleScreening ionic liquids for dissolving hemicellulose by COSMO-RS based on the selective model†
Jinzheng Zhao,
Guohui Zhou*,
Timing Fang ,
Shengzhe Ying
,
Shengzhe Ying and
Xiaomin Liu
and
Xiaomin Liu *
*
School of Chemistry and Chemical Engineering, Qingdao University, 308 Ningxia Road Shinan District, Qingdao, Shandong 266071, P. R. China. E-mail: liuxiaomin@qdu.edu.cn; zhouguohui@126.com
First published on 6th June 2022
Abstract
The utilization of biomass resources has attracted more and more attention due to the consumption of non-renewable resources. Compared with cellulose and lignin, hemicellulose has been less studied. Some ionic liquids (ILs) have been proved to be excellent solvents for lignocellulosic pretreatment. However, screening of more efficient ILs is difficult due to numerous possible ILs. Computational chemistry has been proved effective in solvent screening, but a precise model is indispensable. In this work, we focused on building several appropriate models and selected the most suitable one. According to the structure of hemicellulose, six hemicellulose models were constructed and the mid-dimer of the xylan chain hemicellulose (MDXC) model was proved to be the best compared with the reported experimental results. Based on the MDXC model, 1368 ILs were screened to evaluate their ability to dissolve hemicellulose by Conductor-like Screening Model for Real Solvents (COSMO-RS). The activity coefficient (γ), excess enthalpy (HE), and σ-profile indicated that the hydrogen-bond (H-bond) played a vital role in the dissolution of hemicellulose. Anions played a more critical role than cations, where small anions with H-bond acceptor groups could enhance the molecular interactions with hemicellulose. This work provided a thermodynamic understanding of hemicellulose and IL solvent systems. It highlights the importance of building appropriate solute models, which may be necessary to predict of the other thermodynamic properties in the future.
1. Introduction
Lignocellulosic biomass is considered one of the most abundant renewable sources in nature. Compared with fossil resources, lignocellulosic biomass has the advantages of being renewable, environmentally friendly, and of large yield.1–3 Hemicellulose is a polymer with xylan as the main chain, and is an essential component of lignocellulose.3 It can be successfully converted into biofuels, materials, chemicals, and functional food ingredients due to its bioactivity, biocompatibility, and biodegradability.4–6 In the cell wall, hemicellulose is bonded to cellulose by hydrogen bonds and to lignin by covalent bonds.7 The hydrogen bonds and covalent interactions with other cell wall constituents restrict the release of hemicelluloses from the plant cell wall.1 It is necessary to extract hemicelluloses thoroughly before converting them into value-added products. The common approaches are the alkaline solvent system method and the hydrothermal method, which usually cause environmental problems and hemicellulose degradation into by-products.8–10 Therefore, it is of great significance to explore new green solvents that can fully and efficiently dissolve hemicelluloses for applying to utilize lignocellulosic biomass.Ionic liquids (ILs) have several remarkable properties such as having low vapor pressure, excellent chemical and thermal stability, and being nonflammable.11–15 As a new type of green solvents, ILs can dissolve carbohydrates, swell the cell walls, and decrease the crystallinity of cellulose.9 It have been reported16 that imidazole-based ILs with anions of Ac−, Cl−, Br−, I− could dissolve hemicellulose efficiently at temperatures ranging from 80 to 150 °C. Peng17 found that two hydroxyl groups of the xylan chain in hemicellulose can form electron donor-electron acceptant (EDA) with [Bmim]Cl, which could accelerate the hemicellulose dissolution process. Morais18 studied the interaction between ILs and hemicellulose through NMR. They concluded that the anion alkalinity was the key for hemicellulose dissolution. Cheng19 showed the advantages of conducting a suitable model compound to explain the dissolution mechanism of the experimental results. Up to now, hundreds of ILs with excellent solubility to cellulose or lignocellulose have been found,20–23 but hemicelluloses were relatively few investigated. Due to the complexity of hemicellulose, its dissolution in ILs and its interaction with ILs were still unclear.2
As the numerous potential ILs with different cations and anions bring difficulty to screen, it is important to use a high-efficiency method to predict hemicellulose solubility in ILs.24 Conductor-like Screening Model for Real Solvents (COSMO-RS) is a model based on the continuum solvation theory for a specific problem in the molecular structures.25 H-bonds, van der Waals, and misfits interactions in the solvent systems are combined to predict the logarithmic activity coefficient (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ) at infinite dilution.15 The ln
γ) at infinite dilution.15 The ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ can reflect the solubility of solute in ILs. Combining statistical thermodynamics and quantum chemistry, COSMO-RS is considered25 to be one of the most high-efficiency methods for prediction and screening of ILs.
γ can reflect the solubility of solute in ILs. Combining statistical thermodynamics and quantum chemistry, COSMO-RS is considered25 to be one of the most high-efficiency methods for prediction and screening of ILs.
In recent years, several studies26–29 have demonstrated that COSMO-RS could predict ILs dissolving capabilities. It has been proved that low activity coefficient and low numerical HE of lignocellulose in ILs were related to high solubility.26 Kahlen et al.30 screened more than 2000 ILs for dissolving cellulose and showed that the anion was the major determinant in the dissolving process based on COSMO-RS calculation. Liu15 emphasized the importance of suitable models in investigating the dissolving process, the mid-monomer part of cellotriose was proved to be the most consistent with the experimental results. Moreover, different conformations of the molecules in the dissolved system led to different termodynamic properties predicted by COSMO-RS.31 He et al. 32 developed an automated computational framework MoDoop based on COMSO-RS to predict the lignin solubility in ILs. In Mohans' studies,33,34 the researchers used cellobiose as a model for cellulose, whereas hemicellulose is represented with an equimolar combination of both glucose and xylose. The ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ of cellulose and hemicellulose in thousands of ILs have been predicted by COSMO at room temperature, and the interaction between solute and solvent has been analyzed using a variety of computational methods combined with experiments, which is a relatively complete and systematic work. However, the solute model has great influence on the calculation results, a suitable solute model determines the accuracy of the prediction, and is essential for future hemicellulose studies. The fact that different solute model can drastically change the thermodynamic estimations using COSMO-RS is of significant concern.
γ of cellulose and hemicellulose in thousands of ILs have been predicted by COSMO at room temperature, and the interaction between solute and solvent has been analyzed using a variety of computational methods combined with experiments, which is a relatively complete and systematic work. However, the solute model has great influence on the calculation results, a suitable solute model determines the accuracy of the prediction, and is essential for future hemicellulose studies. The fact that different solute model can drastically change the thermodynamic estimations using COSMO-RS is of significant concern.
This study focuses on the construction and selection of suitable hemicellulose models, aiming to obtain the most appropriate hemicellulose model and screen a large amount of ILs. Understand the thermodynamic properties of hemicellulose dissolution in ILs. ILs with different cations, anions (bounded with several types of functional groups) were considered due to their accessibility and eco-friendly properties. We developed six different models, and the reported experimental data16,35 were used to verify the predictions of several hemicellulose models' ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ at infinite dilution. The mid-dimer of xylan chain (MDXC, Model 3) was proved to be the best model. This study also summarizes the dissolution rules of ILs for hemicellulose from the perspectives of cation type and alkyl-chain length, and complementarity of the σ-profile between anion-solute molecules was quantified and the rationality of this screening method was confirmed.
γ at infinite dilution. The mid-dimer of xylan chain (MDXC, Model 3) was proved to be the best model. This study also summarizes the dissolution rules of ILs for hemicellulose from the perspectives of cation type and alkyl-chain length, and complementarity of the σ-profile between anion-solute molecules was quantified and the rationality of this screening method was confirmed.
2. Computational details and calculation sets of hemicellulose models and ionic liquids
2.1 COSMO-RS computation details
In this study, the quantum chemistry Turbomole (TmoleX) package was used to optimize the molecular geometries of ions and solutes of the studied compounds at the B3LYP/6-31++G (d,p) level, and COSMO continuum solution models were calculated using the BP-TZVP-FINE level theory. The conformations of all the molecules and ions used in the calculations were provided in ESI Table S1.† The logarithmic activity coefficient, excess enthalpy, σ-potential, and σ-profile were determined by COSMO-RS (implementation: COSMOtherm 2020 version 20.0.0, revision 5273, COSMOlogic, Leverkusen, Germany). In the reported work,33,34 most of calculation studies on hemicellulose are room temperature or below 100 °C. However, experimental studies16,35 have confirmed that most ILs have better dissolution effects on biomass solution at higher temperatures(>100 °C). Therefore, different from Mohan's work,33 the calculation temperature for COSMO-RS was set to 130 °C in this work, and the experimental determination of bamboo solubility was measured at the same temperature.16,35 This is more consistent with the temperature range of biomass dissolution and degradation in production and application.To calculate excess enthalpies in the COSMO-RS program, the molar fraction of hemicellulose, IL cation, and IL anion was set to 0.5, 0.25, 0.25, respectively. The method to calculate ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ at infinite dilution and HE was described in previous studies.31,36
γ at infinite dilution and HE was described in previous studies.31,36
2.2 Hemicellulose models and model validation
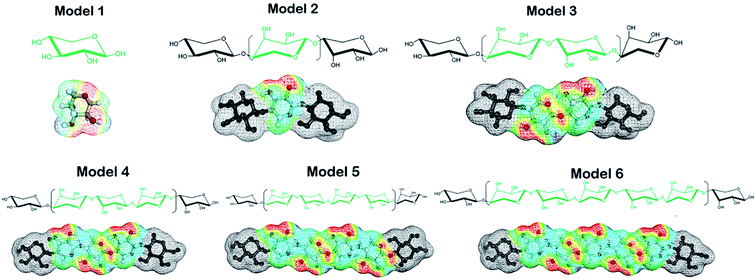
Hemicellulose is an amorphous polymer containing a main chain of xylan (Fig. 1). The composition of branched chains in hemicellulose varies with the type of biomass. A suitable hemicellulose model is crucial for COSMO-RS to find ILs with a good ability to dissolve hemicellulose. In the reported studies, D-xylose (a hexose sugar) and D-glucose (a pentose sugar) were the most popular models.33,34 The authenticity and objectivity of solute theoretical models have been largely ignored. In this study, one of our purposes is to establish a model for the main chain structure of hemicellulose. The experimental solubility data of hemicellulose in this work comes from bamboo hemicellulose, in which xylan accounts for about 70% of the hemicellulose component. Six potential models based on different xylan chains were proposed. Based on the COSMO-RS calculations, the end groups of the polymer for repeating units are deactivated using a “weighted string” function.26
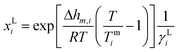 | (1) |
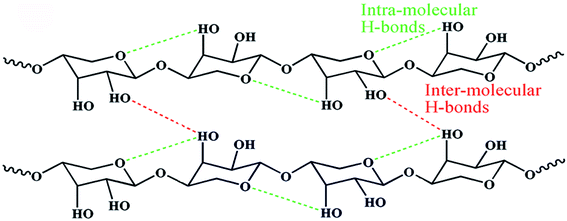 | ||
| Fig. 1 Schematic representation of hemicellulose.37 Inter- and intramolecular hydrogen bonds are also shown. | ||
The ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ at infinite dilution of solute is often considered as a qualitative measurement of solute solubility. According to Formula 1, the reciprocal of the activity coefficient represents the solubility of hemicellulose in their respective ILs.30 In this formula, xLi represents the mole fraction of dissolved i versus undissolved i in a saturated solution. Δhm,i, Tmi represents the enthalpy of melting and the melting temperature of component i, respectively. In this work, the ln
γ at infinite dilution of solute is often considered as a qualitative measurement of solute solubility. According to Formula 1, the reciprocal of the activity coefficient represents the solubility of hemicellulose in their respective ILs.30 In this formula, xLi represents the mole fraction of dissolved i versus undissolved i in a saturated solution. Δhm,i, Tmi represents the enthalpy of melting and the melting temperature of component i, respectively. In this work, the ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ at infinite dilution of each hemicellulose model in ILs were calculated using COSMO-RS. These values served as quantitative measurements of solubility in ILs. Description of the activity coefficient is the key of this work. Linear regression was performed on the experimental solubility of hemicellulose and the values of ln
γ at infinite dilution of each hemicellulose model in ILs were calculated using COSMO-RS. These values served as quantitative measurements of solubility in ILs. Description of the activity coefficient is the key of this work. Linear regression was performed on the experimental solubility of hemicellulose and the values of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ. The performance of each hemicellulose model was measured by R-squared (R2, it measures the goodness fit of the data regression equation) and the residual sum of squares (RSS), which reflected the prediction accuracy. The structures and charge surface files(σ-surface) of the six models are shown in Fig. 2, generated with the procedures in Section 2.1.
γ. The performance of each hemicellulose model was measured by R-squared (R2, it measures the goodness fit of the data regression equation) and the residual sum of squares (RSS), which reflected the prediction accuracy. The structures and charge surface files(σ-surface) of the six models are shown in Fig. 2, generated with the procedures in Section 2.1.
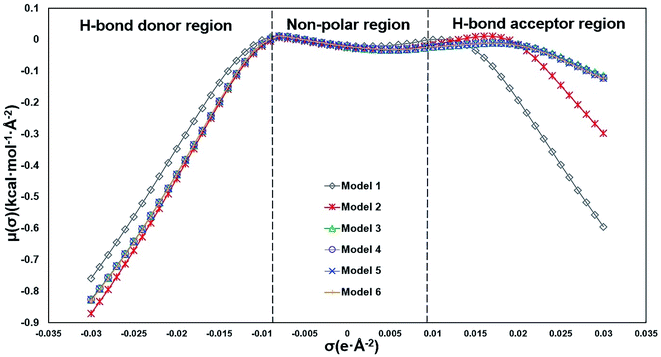
In COSMO-RS, σ-potential25 measures the system's affinity to a surface of polarity σ. Three regions defined based on σ-potential: H-bond donor region (σ <−0.0082 e Å−2), H-bond acceptor region (σ >+0.0082 e Å−2), and non-polar region (−0.0082< σ <+0.0082 e Å−2). The σ-potential lines of Models 3 to 6 almost overlap in the whole region (Fig. 3), which means that their representation of hemicellulose is almost identical in the solution system based on COSMO-RS calculation. The σ-potential of Model 1 is more negative than that of other models in the H-bond acceptor region, which means that Model 1 has more affinity to H-bond acceptor surfaces than other models. Model 3 has the strongest hydrogen-bonding acceptor affinity due to a more negative σ-potential in the H-bond donor region and a more positive σ-potential in the H-bond acceptor region. The performance of Model 2 is somehow in between.
The ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ of the six hemicellulose models by COSMOtherm along with the experimental bamboo solubilitie16,35 is in the ten ILs were listed in Table 1. Linear regression was performed between ln
γ of the six hemicellulose models by COSMOtherm along with the experimental bamboo solubilitie16,35 is in the ten ILs were listed in Table 1. Linear regression was performed between ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ and experimental solubilities. R2, RSS, and optimization time, which characterize the performance of the models were listed in Fig. 4. R2 of the longer xylan chain (R2 = 0.82) models were higher among the six hemicellulose models. R2 of the intermediate trimer, tetramer, and pentamer models were the same as those of the mid-dimer models. However, the RSS values of the mid-dimer of xylan chain model (MDXC, Model 3) in the ten ILs was smaller. With the increase of chain length, the molecular structure's optimizing time of more complex models increased sharply. It showed that Model 3 was a good representation of the long-chain structure of hemicellulose. Combined with the calculation time of different models, Model 3 was the best among the six models.
γ and experimental solubilities. R2, RSS, and optimization time, which characterize the performance of the models were listed in Fig. 4. R2 of the longer xylan chain (R2 = 0.82) models were higher among the six hemicellulose models. R2 of the intermediate trimer, tetramer, and pentamer models were the same as those of the mid-dimer models. However, the RSS values of the mid-dimer of xylan chain model (MDXC, Model 3) in the ten ILs was smaller. With the increase of chain length, the molecular structure's optimizing time of more complex models increased sharply. It showed that Model 3 was a good representation of the long-chain structure of hemicellulose. Combined with the calculation time of different models, Model 3 was the best among the six models.
| ILs | Solubility (g·100 g−1 IL) | ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ prediction results by COSMO-RS γ prediction results by COSMO-RS |
|||||
|---|---|---|---|---|---|---|---|
| Model 1 | Model 2 | Model 3 | Model 4 | Model 5 | Model 6 | ||
| a Data from Hu et al., 2020;35b Data from Xia et al., 2020.16 | |||||||
| EmimAc | 13.51a | −6.03 | −0.86 | −1.63 | −2.77 | −3.96 | −5.18 |
| BmimAc | 12.46b | −5.58 | −0.73 | −1.29 | −2.21 | −3.19 | −4.19 |
| BmimCl | 11.03b | −2.83 | −0.67 | −1.57 | −2.67 | −3.82 | −5.00 |
| BmimAcr | 4.02b | −4.48 | −0.60 | −1.01 | −1.75 | −2.55 | −3.38 |
| BmimBr | 2.61b | −1.12 | −0.34 | −0.95 | −1.71 | −2.51 | −3.35 |
| HoemimAc | 0.78a | −3.98 | −0.39 | −0.63 | −1.24 | −1.90 | −2.60 |
| BmimBut | 0.21b | −5.13 | −0.65 | −0.96 | −1.66 | −2.42 | −3.20 |
| BmimGly | 0.30b | −3.54 | −0.45 | −0.85 | −1.51 | −2.20 | −2.94 |
| BmimBen | 2.10b | −4.07 | −0.51 | −0.64 | −1.15 | −1.70 | −2.29 |
| BmimEtHOCOO | 0.36b | −3.38 | −0.44 | −0.73 | −1.29 | −1.90 | −2.55 |
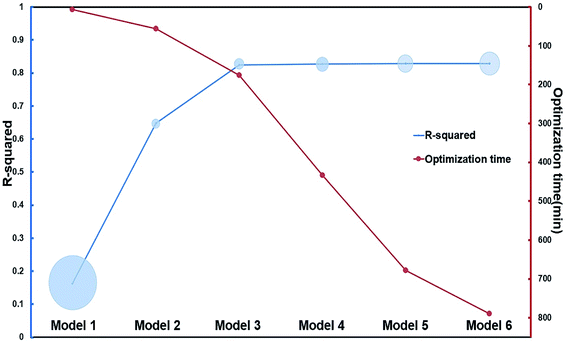 | ||
| Fig. 4 Optimization time and R2 of six hemicellulose models. The area of the blue circle indicates the value of the RSS, a smaller RSS represents a better goodness of fit. The data in this figure are shown in ESI.† | ||
2.3 Structure of cations and anions
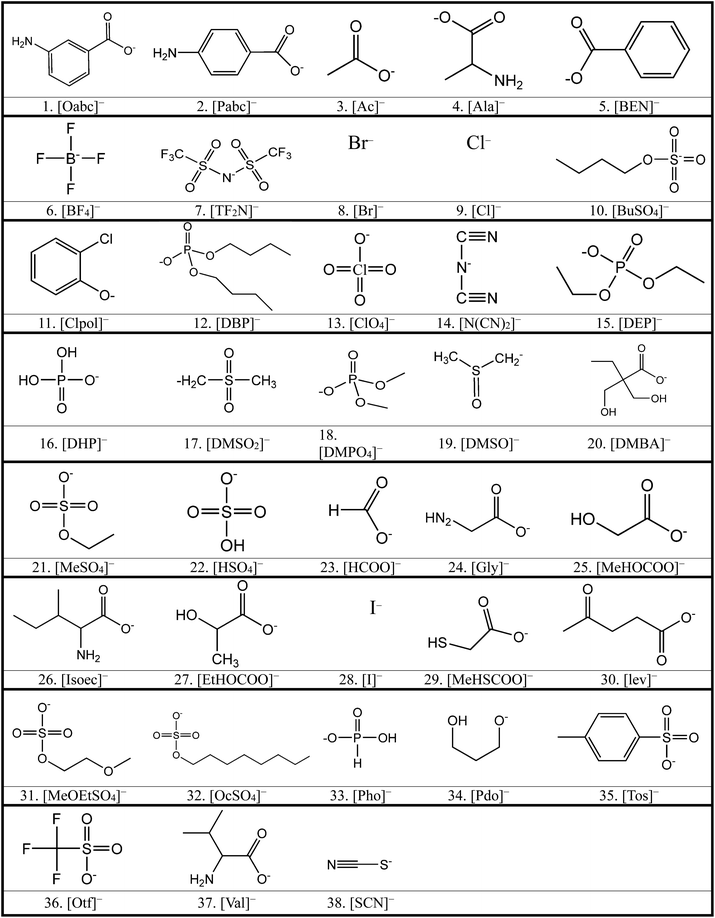
We considered 36 cations (Table 2) including pyrrolidinium-based, morpholinium-based, quaternary ammonium-based with the functional groups of methyl, allyl, hydroxyethyl, methoxyethyl and ester. These cations formed 1368 ILs, combining with the 38 anions (Table 3) studied in this work.3. Results and discussion
3.1 Prediction of the logarithmic activity coefficient at infinite dilution
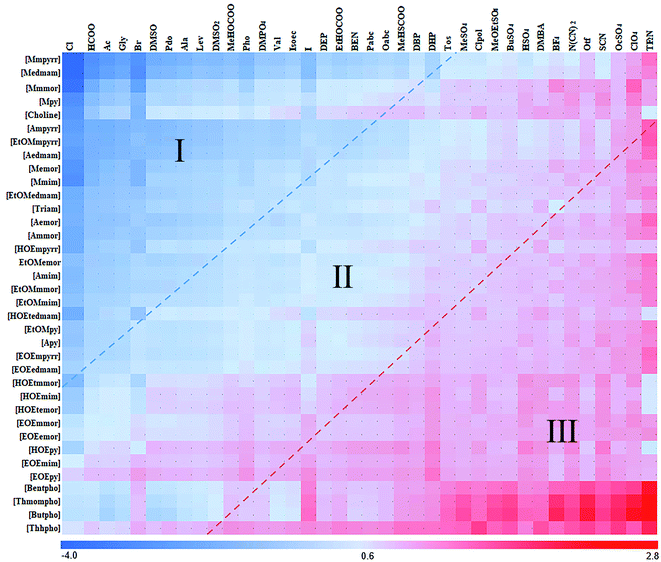
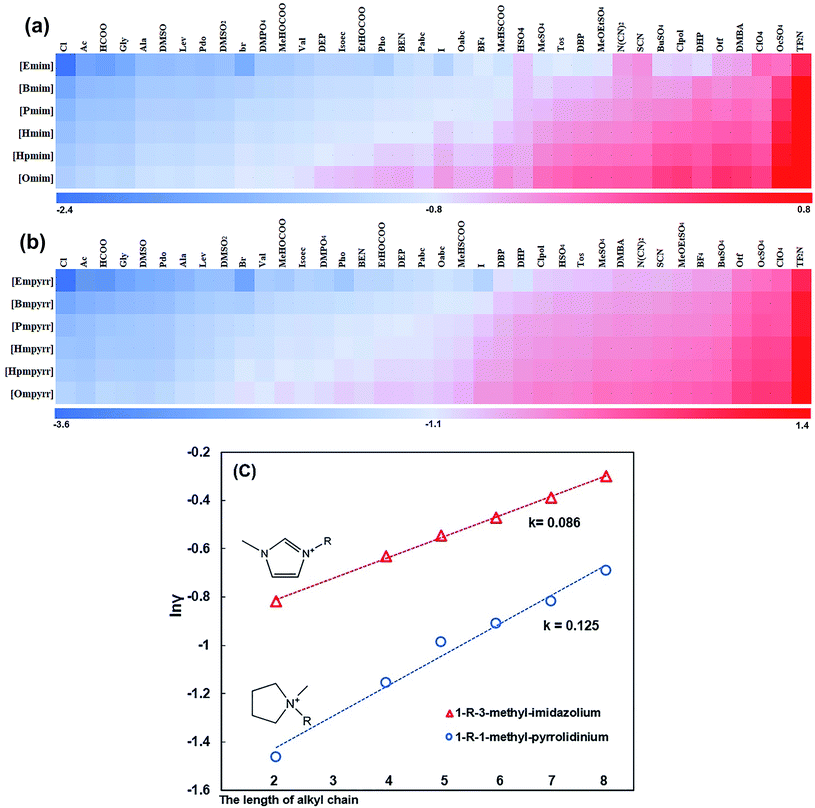
The predicted ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ (methods described in Section 2.2) of Model 3 in 1368 ILs were depicted in Fig. 5. The cations and anions were listed in the order of the calculated logarithmic activity coefficient values. The ILs with high solubility were shown in the upper-left corner of the image, and the ILs with low solubility were shown in the down-right corner. The red and blue dotted lines roughly divided 1368 ILs into three regions according to the ln
γ (methods described in Section 2.2) of Model 3 in 1368 ILs were depicted in Fig. 5. The cations and anions were listed in the order of the calculated logarithmic activity coefficient values. The ILs with high solubility were shown in the upper-left corner of the image, and the ILs with low solubility were shown in the down-right corner. The red and blue dotted lines roughly divided 1368 ILs into three regions according to the ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ. The ln
γ. The ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ varies notably between different kinds of anions (Fig. 5). However, little difference was found between different cations, indicating that the dissolution of hemicellulose in ILs was mainly attributed to the anion. It could be explained that ILs containing the anions including Cl−, Ac−, HCOO−, Gly−, Br− had a strong ability to dissolve hemicellulose. It is consistent with the experimental results of Santo et al.,38 where they indicated the relative interaction strength between smaller anions and cations were stronger,38,39 and could promote the dissolution of xylan chain.
γ varies notably between different kinds of anions (Fig. 5). However, little difference was found between different cations, indicating that the dissolution of hemicellulose in ILs was mainly attributed to the anion. It could be explained that ILs containing the anions including Cl−, Ac−, HCOO−, Gly−, Br− had a strong ability to dissolve hemicellulose. It is consistent with the experimental results of Santo et al.,38 where they indicated the relative interaction strength between smaller anions and cations were stronger,38,39 and could promote the dissolution of xylan chain.
It has been widely recognized that anions played a significant role in the dissolution of lignocellulose. But the cations cannot be ignored in the dissolution of hemicellulose. In Mohan's calculation34 of the ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ at room temperature, the cation species had little influence on the ln
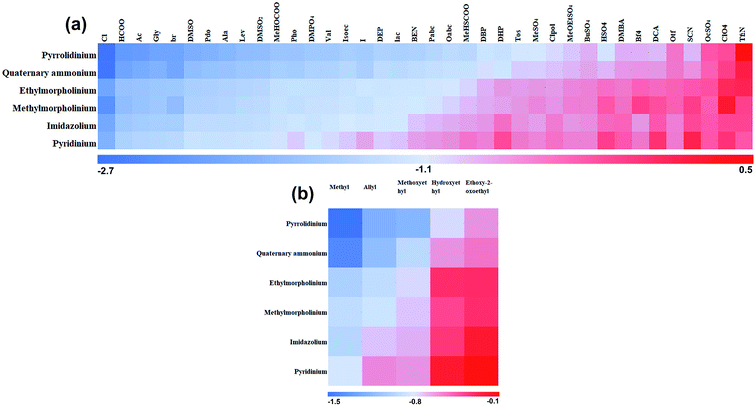
γ at room temperature, the cation species had little influence on the ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ. In this work, it can be seen that cation type and cation branched-chain type has a more significant effect on hemicellulose in ILs at 130 °C (Fig. 5), which may be caused by the temperature effect. High-effective ILs can be obtained by designing ILs cations with different functional groups. The hemicellulose has a relative high solubility in pyrrolidinium-based ILs than other ILs (Fig. 6a). The second highest are the ILs with ethyl-morpholine, and followed by methyl-morpholine, imidazolium, and pyridinium ILs. Fig. 6b showed the average ln
γ. In this work, it can be seen that cation type and cation branched-chain type has a more significant effect on hemicellulose in ILs at 130 °C (Fig. 5), which may be caused by the temperature effect. High-effective ILs can be obtained by designing ILs cations with different functional groups. The hemicellulose has a relative high solubility in pyrrolidinium-based ILs than other ILs (Fig. 6a). The second highest are the ILs with ethyl-morpholine, and followed by methyl-morpholine, imidazolium, and pyridinium ILs. Fig. 6b showed the average ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ of 30 cations with five different R-group, where the order of solubility is methyl > allyl > methoxyethyl > hydroxyethyl > ethoxy-2-oxoethyl. The presence of alkaline oxygen atoms in the side chain could interfere with hydrogen-bond formation between the anions and the hydroxyl groups in the xylan chain, for example, cations with alkoxy or alkoxyalkyl groups.40
γ of 30 cations with five different R-group, where the order of solubility is methyl > allyl > methoxyethyl > hydroxyethyl > ethoxy-2-oxoethyl. The presence of alkaline oxygen atoms in the side chain could interfere with hydrogen-bond formation between the anions and the hydroxyl groups in the xylan chain, for example, cations with alkoxy or alkoxyalkyl groups.40
In this work, we compared the methylmorpholinium-based and ethyl-morpholinium-based ILs. We found that cation with longer alkyl chain had a negative effect on the dissolution of hemicellulose compared with shorter alkyl-chain. To investigate the effect of the cation alkyl chain length on hemicellulose dissolution, methylimidazolyl-based and methylpyrrolidinium-based ILs with alkyl chain of different lengths were selected from the COSMOtherm ILs database. After combining with the 38 anions, the ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ of those ILs were calculated. The results were shown in Fig. 7, which verifies the inhibition long alkyl chain on hemicellulose dissolution, which is consistent with the experimental phenomenon.41 Pyrrolidinium ILs were more affected by the length of alkyl chain than imidazole ILs (Fig. 7c).
γ of those ILs were calculated. The results were shown in Fig. 7, which verifies the inhibition long alkyl chain on hemicellulose dissolution, which is consistent with the experimental phenomenon.41 Pyrrolidinium ILs were more affected by the length of alkyl chain than imidazole ILs (Fig. 7c).
3.2 Prediction of excess enthalpy
As the temperature derivative of Gibbs free energy, excess enthalpy (HE) which is attributed to H-bonds, misfits and van der Waals forces, reflected the behavior of different solute in solution. Casas et al.39 pointed out that the H-bond energy calculated by COSMO-RS reflected the affinity between ILs and lignocellulose, thus a low H-bond energy value represent higher solubility of lignocellulose in ILs. The histogram showed that the H-bond interaction between the hemicellulose model and ILs apparently influences hemicellulose solubility (Fig. 8), followed by misfits and van der Waals force. The ILs with the same cation and different anions had different excess enthalpies, which is not shown in ILs with the same anion and different cations. The result further confirmed that anion plays a more critical role in hemicellulose dissolution than cation.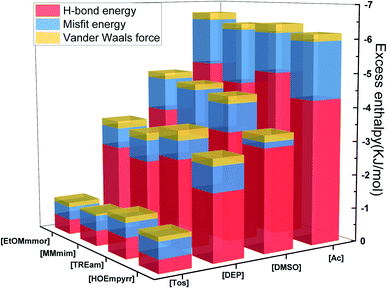 | ||
| Fig. 8 Excess enthalpies of Model 3 and 16 ILs from different regions in Fig. 5. | ||
3.3 Prediction of σ-profile
The calculation results of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ and HE showed that the dissolution of hemicellulose is strongly dependent on the anion. In addition, the σ-profile curve of COSMO-RS theory can reflect the relative number of environmental polar fragments on the molecular surface. The complementarity of the curve peak in the H-bond acceptor region can be used to describe the interaction ability between ions and solute molecules.31 The ILs anions were classified into categories I, II and III according to their ability to dissolve hemicellulose (Fig. 9a). The σ-profile curves of the category I anions had better complementarity with the curve of hemicellulose model in the polar region (+0.015–+0.022). Then, we tried to find the most appropriate way to quantify this feature. After analyzing the anions' σ-profile curves in the polar region, we found that the integral area under the σ-profile curves of the anions can reflect the complementarity between anions and the hemicellulose model better (Fig. 9b). We calculated the integral areas under the σ-profile curve of 38 anions in the polar region (+0.015–+0.023) and correlated them with the average ln
γ and HE showed that the dissolution of hemicellulose is strongly dependent on the anion. In addition, the σ-profile curve of COSMO-RS theory can reflect the relative number of environmental polar fragments on the molecular surface. The complementarity of the curve peak in the H-bond acceptor region can be used to describe the interaction ability between ions and solute molecules.31 The ILs anions were classified into categories I, II and III according to their ability to dissolve hemicellulose (Fig. 9a). The σ-profile curves of the category I anions had better complementarity with the curve of hemicellulose model in the polar region (+0.015–+0.022). Then, we tried to find the most appropriate way to quantify this feature. After analyzing the anions' σ-profile curves in the polar region, we found that the integral area under the σ-profile curves of the anions can reflect the complementarity between anions and the hemicellulose model better (Fig. 9b). We calculated the integral areas under the σ-profile curve of 38 anions in the polar region (+0.015–+0.023) and correlated them with the average ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ of each anion's ILs. In order to determine the most appropriate complementary region, we took multiple regions for calculation and comparison. We found that data points of the 38 anions had the best correlation (R2 = 0.779) in the range of (+0.016–+0.021) (Fig. 9c, other interval data detailed in ESI, Table S3†). The method can quantify the complementarity of the σ-profiles curves between compounds in the vital interval of the polarity region. The anions with the largest integral area within the region were highly consistent with the anions with better solubility. In addition, the curve of σ-profiles in the H-bond acceptor region also showed that the interaction between the anions and the hydroxyl group of the hemicellulose plays an essential role in the dissolution process. The solubility followed the hydrogen bonding acceptor affinity or alkalinity42 of the anion. The σ-profile method for ILs was a new and more intuitive method for the high throughput screening of ILs.
γ of each anion's ILs. In order to determine the most appropriate complementary region, we took multiple regions for calculation and comparison. We found that data points of the 38 anions had the best correlation (R2 = 0.779) in the range of (+0.016–+0.021) (Fig. 9c, other interval data detailed in ESI, Table S3†). The method can quantify the complementarity of the σ-profiles curves between compounds in the vital interval of the polarity region. The anions with the largest integral area within the region were highly consistent with the anions with better solubility. In addition, the curve of σ-profiles in the H-bond acceptor region also showed that the interaction between the anions and the hydroxyl group of the hemicellulose plays an essential role in the dissolution process. The solubility followed the hydrogen bonding acceptor affinity or alkalinity42 of the anion. The σ-profile method for ILs was a new and more intuitive method for the high throughput screening of ILs.
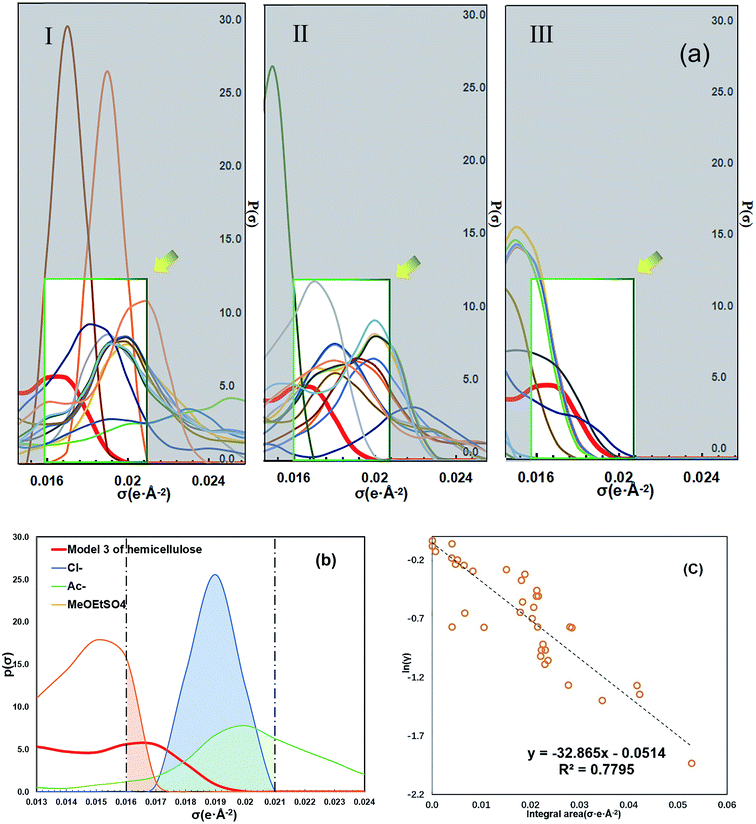 | ||
Fig. 9 A new screen method of ILs. (a) σ-profile curves of hemicellulose and 38 anions. The red curve is the σ-profile of the hemicellulose model. The anions are divided into three groups according to the order of activity coefficients in Fig. 5. (Due to the limitation of the size of the figure, the detail annotated figure of the 38 anions is presented in ESI†). (b) The integral area of three anions in the polar receptor region. The red curve is the σ-profile of the hemicellulose model. (c) The integral area in the polar receptor region (+0.016–+0.021) and corresponding ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ of 38 anions. γ of 38 anions. | ||
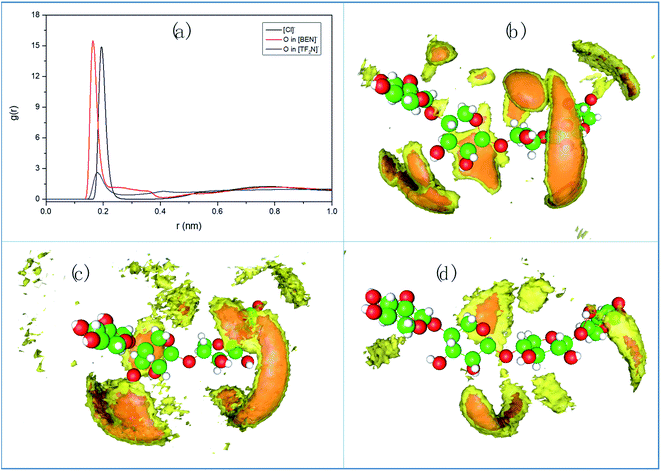
To further verify the reliability of the σ-profile, we used molecular dynamics (MD) simulation for three ILs with different abilities in dissolving hemicellulose. The cation is [Bmim]+, and the three anions are [Cl]−, [BEN]− and [TF2N]−, respectively. The simulations were performed with GROMACS software package.43,44 Each system contains 1000 ILs and 15 molecules (Model 3), and the content of the molecule is 1.48 mol%. The initial configuration was generated by randomly placing Model 3 in the ILs by Packmol package.45 Then energy was minimized, followed by NVT and NPT simulation. The equilibration simulation was extended to 50 ns, and production phase lasted for another 50 ns at 130 °C. The cutoff distance between LJ and Coulomb interaction is 1.2 nm. Temperature control using Nosé–Hoover thermostat46 with a coupling time of 0.2 ps, and pressure (1.0 bar) controlled by Parrinello–Rahman constant47 with a coupling time of 2.0 ps.
Fig. 10a shows the radial distribution functions (RDFs) between the hydroxyl H on the two middle rings of hemicellulose and the anion. By comparison, it is found that the interaction between H atom and oxygen atom in [TF2N]− is much smaller than the interaction for [Cl]− or carbonyl O in [BEN]−. This is consistent with the poor solubility of [Bmim][TF2N]. The spatial distribution function (SDF) reflects the density distribution of components from a three-dimensional perspective intuitively, which represents the interaction strength of all components. We calculated the SDF of anions around hemicellulose, as shown in Fig. 10b–d. The anions are mainly distributed around the hydroxyl of the hemicellulose molecules, because their interaction is mainly the H-bond between the hemicellulose and the negatively charged atoms on the anion. The difference between the three anions is obvious, the H-bond interactions from strong to weak are [Cl]−, [BEN]− to [TF2N]−, which is consistent with the result of the above σ-profile. To sum up, the σ-profile prediction method is effective and reliable.
4. Conclusion
In this study, a variety of hemicellulose models were tested in COSMO-RS calculation. And the result show that the MDXC is the best model to well correlated with the experimental data (R2 = 0.82). The ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ is a reliable character reflecting the solubility in ILs with different cations and anions. Especially, ILs with anions of Ac−, Cl−, HCOO−, Gly− and DMSO− were predicted to have a promising advantage for the hemicellulose dissolution. Compared with the reported work, cations have a greater influence on the dissolution of hemicellulose by increasing the temperature. In terms of cations, pyrrolidinium-based and quaternary ammonium-based ILs have strong H-bond formation ability with hemicellulose, which accelerate the dissolution process. The order of R-groups contribute to solubility is methyl > allyl > methoxyethyl > hydroxyethyl > ethoxy-2-oxoethyl. The solubility of ILs for hemicellulose is decreased with the extend of alkyl chain length in cation. The H-bond interaction is the primary contributor in the dissolution of hemicellulose, with misfits' force and van der Waals force being subsequent ones. Further, the σ-profile method is effective for large-scale ILs screening. In all, this work highlighted the importance of selecting an appropriate solute model, and it provided an understand of the thermodynamic behavior of hemicellulose and ILs solvent systems, which is necessary for predicting the other thermodynamic properties.
γ is a reliable character reflecting the solubility in ILs with different cations and anions. Especially, ILs with anions of Ac−, Cl−, HCOO−, Gly− and DMSO− were predicted to have a promising advantage for the hemicellulose dissolution. Compared with the reported work, cations have a greater influence on the dissolution of hemicellulose by increasing the temperature. In terms of cations, pyrrolidinium-based and quaternary ammonium-based ILs have strong H-bond formation ability with hemicellulose, which accelerate the dissolution process. The order of R-groups contribute to solubility is methyl > allyl > methoxyethyl > hydroxyethyl > ethoxy-2-oxoethyl. The solubility of ILs for hemicellulose is decreased with the extend of alkyl chain length in cation. The H-bond interaction is the primary contributor in the dissolution of hemicellulose, with misfits' force and van der Waals force being subsequent ones. Further, the σ-profile method is effective for large-scale ILs screening. In all, this work highlighted the importance of selecting an appropriate solute model, and it provided an understand of the thermodynamic behavior of hemicellulose and ILs solvent systems, which is necessary for predicting the other thermodynamic properties.
Author contributions
Jinzheng Zhao: conceptualization, experiment, writing reviewing and editing. Guohui Zhou: data curation, software, visualization. Timing Fang: formal analysis. Shengzhe Ying:data curation, software. Xiaomin Liu: methodology, supervision.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (22178187, 22108139), the Taishan Scholars Program of Shandong Province (tsqn201909091), Natural Science Foundation of Shandong Province (ZR202102180830). The authors thank the High-Grade Talents Plan of Qingdao University for financial support and all the other friends in this work for their direct and indirect help to me. The authors would also like to thank the journal editors and the reviewers who raised valuable points that help to improve the quality of the presentation of this article.References
- G. De Bhowmick, A. K. Sarmah and R. Sen, Bioresour. Technol., 2018, 247, 1144–1154 CrossRef CAS PubMed.
- V. Zargar, M. Asghari and A. Dashti, ChemBioEng Rev., 2015, 2, 204–226 CrossRef.
- K. C. Badgujar and B. M. Bhanage, Bioresour. Technol., 2015, 178, 2–18 CrossRef CAS PubMed.
- A. El-Naggar, S. M. Shaheen, S. X. Chang, D. Y. Hou, Y. S. Ok and J. Rinklebe, ACS Sustainable Chem. Eng., 2021, 9, 6864–6874 CrossRef CAS.
- J. C. Jackson, C. H. M. Camargos, V. T. Noronha, A. J. Paula, C. A. Rezende and A. F. Faria, ACS Sustainable Chem. Eng., 2021, 9, 6534–6540 CrossRef CAS.
- L. L. Zhao, X. F. Chen, X. Y. Liu, G. Q. Xu, X. C. Guo and Y. Yang, ACS Sustainable Chem. Eng., 2021, 9, 6697–6706 CrossRef CAS.
- F. Peng, J. L. Ren, F. Xu, J. Bian, P. Peng and R. C. Sun, J. Agric. Food Chem., 2009, 57, 6305–6317 CrossRef CAS PubMed.
- M. J. Cocero, A. Cabeza, N. Abad, T. Adamovic, L. Vaquerizo, C. M. Martinez and M. V. Pazo-Cepeda, J. Supercrit. Fluids, 2018, 133, 550–565 CrossRef CAS.
- A. K. Kumar and S. Sharma, Bioresour. Bioprocess., 2017, 4, 7 CrossRef PubMed.
- R. B. Stoffel, P. V. Neves, F. E. Felissia, L. P. Ramos, L. M. Gassa and M. C. Area, Biomass Bioenergy, 2017, 107, 93–101 CrossRef CAS.
- K. Zhang, G. H. Zhou, T. M. Fang, K. Jiang and X. M. Liu, J. Phys. Chem. Lett., 2021, 12, 2273–2278 CrossRef CAS PubMed.
- G. H. Zhou, K. Jiang, Z. L. Wang and X. M. Liu, Chin. J. Chem. Eng., 2021, 31, 42–55 CrossRef CAS.
- N. Wang and J. K. Lee, J. Org. Chem., 2019, 84, 14593–14601 CrossRef CAS PubMed.
- C. Wei, K. Jiang, T. Fang and X. Liu, J. Mol. Liq., 2021, 338, 116641 CrossRef CAS.
- Y. R. Liu, K. Thomsen, Y. Nie, S. J. Zhang and A. S. Meyer, Green Chem., 2016, 18, 6246–6254 RSC.
- Q. Xia, H. Peng, L. Yuan, L. F. Hu, Y. Zhang and R. Ruan, RSC Adv., 2020, 10, 11643–11651 RSC.
- X. W. Peng, J. L. Ren and R. C. Sun, Biomacromolecules, 2010, 11, 3519–3524 CrossRef CAS PubMed.
- E. S. Morais, A. M. D. Lopes, M. G. Freire, C. S. R. Freire, J. A. P. Coutinho and A. J. D. Silvestre, Molecules, 2020, 25, 3652 CrossRef CAS PubMed.
- F. Cheng, H. Wang, G. Chatel, G. Gurau and R. D. Rogers, Bioresour. Technol., 2014, 164, 394–401 CrossRef CAS PubMed.
- Y. Li, J. J. Wang, X. M. Liu and S. J. Zhang, Chem. Sci., 2018, 9, 4027–4043 RSC.
- W. E. S. Hart, J. B. Harper and L. Aldous, Green Chem., 2015, 17, 214–218 RSC.
- H. Y. Li, X. Chen, Y. J. Li, X. F. Cao, S. N. Sun and R. C. Sun, Sep. Purif. Technol., 2018, 191, 364–369 CrossRef CAS.
- P. Moyer, M. D. Smith, N. Abdoulmoumine, S. C. Chmely, J. C. Smith, L. Petridis and N. Labbe, Phys. Chem. Chem. Phys., 2018, 20, 2508–2516 RSC.
- Z. Guo, B. M. Lue, K. Thomasen, A. S. Meyer and X. B. Xu, Green Chem., 2007, 9, 1362–1373 RSC.
- A. Klamt, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 699–709 CAS.
- C. Loschen and A. Klamt, Ind. Eng. Chem. Res., 2014, 53, 11478–11487 CrossRef CAS.
- M. Gonzalez-Miquel, J. Palomar, S. Omar and F. Rodriguez, Ind. Eng. Chem. Res., 2011, 50, 5739–5748 CrossRef CAS.
- A. Casas, S. Omar, J. Palomar, M. Oliet, M. V. Alonso and F. Rodriguez, RSC Adv., 2013, 3, 3453–3460 RSC.
- J. Palomar, M. Gonzalez-Miquel, A. Polo and F. Rodriguez, Ind. Eng. Chem. Res., 2011, 50, 3452–3463 CrossRef CAS.
- J. Kahlen, K. Masuch and K. Leonhard, Green Chem., 2010, 12, 2172–2181 RSC.
- M. Gonzaez-Miquel, M. Massel, A. DeSilva, J. Palomar, F. Rodriguez and J. F. Brennecke, J. Phys. Chem. B, 2014, 118, 11512–11522 CrossRef PubMed.
- Y. H. Chu and X. Z. He, ACS Omega, 2019, 4, 2337–2343 CrossRef CAS PubMed.
- M. Mohan, C. Balaji, V. V. Goud and T. Banerjee, J. Solution Chem., 2015, 44, 538–557 CrossRef CAS.
- M. Mohan, P. Viswanath, T. Banerjee and V. V. Goud, Mol. Phys., 2018, 116, 2108–2128 CrossRef CAS.
- L. F. Hu, H. Peng, Q. Xia, Y. Zhang, R. Ruan and W. G. Zhou, J. Mol. Struct., 2020, 1210 Search PubMed.
- J. Reinisch, A. Klamt, F. Eckert and M. Diedenhofen, Fluid Phase Equilib., 2011, 310, 7–10 CrossRef CAS.
- R. S. Payal, R. Bharath, G. Periyasamy and S. Balasubramanian, J. Phys. Chem. B, 2012, 116, 833–840 CrossRef CAS PubMed.
- A. M. Fernandes, M. A. A. Rocha, M. G. Freire, I. M. Marrucho, J. A. P. Coutinho and L. M. N. B. F. Santos, J. Phys. Chem. B, 2011, 115, 4033–4041 CrossRef CAS PubMed.
- A. Casas, J. Palomar, M. V. Alonso, M. Oliet, S. Omar and F. Rodriguez, Ind. Crops Prod., 2012, 37, 155–163 CrossRef CAS.
- H. Zhao, G. A. Baker, Z. Y. Song, O. Olubajo, T. Crittle and D. Peters, Green Chem., 2008, 10, 696–705 RSC.
- Y. L. Zhao, X. M. Liu, J. J. Wang and S. J. Zhang, Chemphyschem, 2012, 13, 3126–3133 CrossRef CAS PubMed.
- H. Wang, G. Gurau and R. D. Rogers, Chem. Soc. Rev., 2012, 41, 1519–1537 RSC.
- D. Van der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718 CrossRef CAS PubMed.
- L. Laaksonen, J. Mol. Graphics, 1992, 10, 33–34 CrossRef CAS PubMed.
- L. Martinez, R. Andrade, E. G. Birgin and J. M. Martinez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef CAS PubMed.
- M. D'Alessandro, A. Tenenbaum and A. Amadei, J. Phys. Chem. B, 2002, 106, 5050–5057 CrossRef.
- M. H. Ulz, J. Elasticity, 2013, 113, 93–112 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ra02001g |
| This journal is © The Royal Society of Chemistry 2022 |