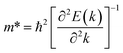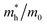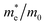Theoretical exploration of mechanical, electronic structure and optical properties of aluminium based double halide perovskite

Abstract

The mechanical, electronic structure and optical properties of aluminium based double halide perovskite were calculated by density functional theory. The formation energy and elastic constant confirm the stability of the cubic perovskite materials. The materials are all ductile and suitable for flexible photovoltaic and optoelectronic devices. The band gap values vary from 0.773 eV to 3.430 eV, exactly corresponding to the range of ideal band gap values for good photoresponse. The band structure analysis shows that all the materials possess small effective mass, which indicates a good transport of carriers. And these materials have a broad energy range of optical absorption for utilization and a detector of photons. Moreover, less expensive K₂AgAlBr₆ were investigated for comparison with materials containing a cesium element, and according to the results, is also a candidate for photoelectronic devices due to the similar properties.

---

1 Introduction

Perovskites are a series of ABX₃-type materials named after a Russian mineralogist Lev Perovski, such as CaTiO₃ and BaTiO₃, and originally used for ferroelectric¹ and piezoelectric materials.^2,3 For the last decade, perovskites have been studied for photovoltaic and optoelectronic purposes due to their appropriate energy band structures and good light absorption. T. Miyasaka et al. made the earliest application of organic–inorganic perovskite materials in dye-sensitized solar cells in 2009.⁴ However, at the first, they did not attract much attention because of the low efficiency and poor stability until N. G. Park et al. reported a perovskite solar cell with power conversion efficiency over 9% and 500 hour stability in air conditions.⁵ From then, perovskite solar cells became a very popular objective and many perovskite lead-free materials have been explored by experiments and theoretical studies. Several preliminary studies were carried out with attractive results and redrew attention to chalcogenide perovskite AZrS₃, which exhibits great potential in photovoltaic applications.^6,7 However, most studies about optoelectronic and photovoltaic application still focus on halide perovskites. Nowadays, the newest world record of halide perovskite solar cells is over 25%⁸ and these can be used for commercial purposes. The application area of perovskites also includes photodetectors,^9–11 light emitting diodes^12–14 and photocatalytics.^15,16 Furthermore, a variety of novel double perovskite materials can be built by replacing two B²⁺ ions by one M⁺ ion and one M³⁺ ion. For example, the band gap and light absorbing properties of Cs₂AgBiX₆ (X = Cl, Br) materials have been studied since 2016 (ref. 17–19) and used as photocatalysts in CO₂ reduction and H₂ evolution.^20,21 Cs₂AgInCl₆ has been synthesized and applied in the field of organic degradation and fast ultraviolet detectors.^22–24 Cs₂AgSbCl₆ shows a superior blue photoluminescence quantum yield of 31.33%, and excellent air stability.²⁵ Therefore, it is assumed that cesium–silver based perovskites are potential in optoelectronics field. Cai et al. have given out a primary high-throughput computational study of Cs₂MM′Cl₆.²⁶ Cs₂InBiCl₆ and Cs₂InSbCl₆ have been considered as candidate for traditional MAPbI₃ because of their proper direct band gap.²⁷ However, they have not been synthesized yet as a result of the extreme instability of In⁺ ions. On the other hand, Cs₂AgSbCl₆ and Cs₂AgInCl₆ have been investigated by both experiment and theoretical calculation.^28–30 Recently, the properties of similar Cs₂CuBiX₆ have been calculated by density functional theory.³¹ The results show that these materials with indirect band gap are not suitable for photoelectronic devices. From the advance studies, it is predicted that Cs₂AgMCl₆ (M = Al, Ga, In, Tl) have direct band structures. Thus, In- and Ga-based materials were reported to exhibit suitable direct bandgaps within the optimal range of 0.9–1.6 eV, preferable to previous Ag/Bi based double perovskites, showing a promising utilization prospect.³² With similar electronic structure, aluminium and thallium element are of great potential to substitute for indium and gallium as well. Tl-based perovskite materials have already experimentally and theoretically characterized and show a relatively outstanding light absorption and carrier mobility.^33,34 However, the application of thallium is under strict control due to the high toxicity of this heavy metal element. Up to now, although few researchers focused on perovskite containing aluminium, the aluminium compound AlCl₃ has been successfully introduced into perovskite material to improve the photoluminescence and photoresponse.³⁵ Consequently, considering the abundant amount and low toxicity, only Al-based double halide perovskite were studied by density functional theory (DFT) calculation in this paper. Furthermore, there is a conflict between small reserves of cesium and its huge demand in other high tech field, such as atomic clocks, drilling fluid and ion propulsion engine, which indicates that reserves of cesium may not meet the large-scale application of photoelectronic devices. Hence, we also discuss the properties of substitutable alkali metal Rb₂AgAlBr₆ and K₂AgAlBr₆ to explore the feasibility of these two materials.

2 Computational methods

All geometry optimizations, electronic structures, mechanical properties and optical properties are carried out by DFT methods within the Perdew–Burke–Ernzerhof generalized gradient approximation (GGA-PBE) as implemented in the Cambridge Sequential Total Energy Package (CASTEP) based on Materials Studio software.^36,37 The OTFG ultrasoft pseudo-potential is adopted to describe the electron–ion interactions. The Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm was adopted to optimize the crystal structures. For geometric optimization, a 8 × 8 × 8 Monkhorst–Pack grid³⁸ is used and a plane wave kinetic energy cut-off of 600 eV is chosen, and all structures are relaxed until the forces on the atoms are less than 0.03 eV Å⁻¹ while the total energy change becomes less than 1.0 × 10⁻⁵ eV, crystal internal stress is less than 0.05 GPa and maximum displacement of atoms is less than 0.001 Å. Due to the discontinuity of exchange–correlation energy, the GGA-PBE function often underestimates the energy band value of compounds,^39,40 a more accurate hybrid HSE06 functional with norm-conserving pseudo-potential is used to correct the electronic structures and optical properties.^41,42 In addition, the energy cutoff and k-point mesh were set to 700 eV and 4 × 4 × 4, respectively.

3 Results and discussion

3.1. Crystal structure and thermodynamics stability

For conventional ABX₃ perovskites, the structure is usually cubic-centered. Therefore, in this paper, the theoretical models of double halide perovskite are built as Fm3̄m space group, and there are two cations at B sites (B′ and B′′) with oxidization states of +1 and +3, which may have different orderings. As shown in Fig. 1, in a unit cell of double perovskite structure, the A site is occupied with Cs⁺, Rb⁺ or K⁺, the +1 B′ sites and +3 B′′ sites are initialized with Ag⁺ and Al³⁺, respectively, and X is halogen anion (Cl⁻, Br⁻ or I⁻). The calculated lattice constants are shown to be 10.11 Å, 10.65 Å, 11.47 Å, 10.57 Å and 10.52 Å for Cs₂AgAlCl₆, Cs₂AgAlBr₆, Cs₂AgAlI₆, Rb₂AgAlBr₆ and K₂AgAlBr₆, respectively. It is obvious that the lattice constants increase with the increased atomic number of halogen anions and alkali cations.

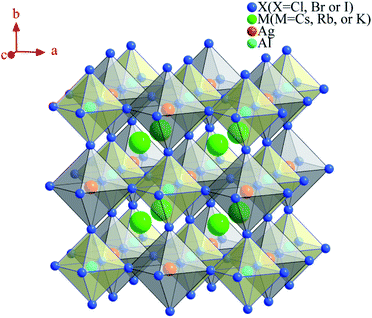Fig. 1 Crystal structure of face-centered-cubic double perovskite M₂AgAlX₆ (M = Cs, Rb or K; X = Cl, Br or I).

In perovskite, the Goldschmidt tolerance factor is widely used as a reliable test for the formation of perovskite structure, which is defined as , where r_A, r_B and r_X represent the radii of the A site cation, B site cation and X site anion, respectively. Generally, perovskite structures tend to form in the range of 0.8 ≤ t ≤ 1.0 while perovskite with t in the range of 0.9–1.0 tends to have a perfect structure.^43–45 In this work, the Shannon ionic radii⁴⁶ are used, and similar to previous work on A site alloying, the average of radii of the two B site cations as r_B, that is, 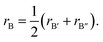The calculated Goldschmidt tolerance factors t are listed in Table 1. All the results of t values are within the best range, confirming the perfect perovskite structure.

Table 1 The calculated crystal lattice constants (a), ion radii, tolerance factor (t), binding energy (E_b) and formation energy (E_f) of double perovskite M₂AgAlX₆ (M = Cs, Rb or K; X= Cl, Br or I)

Materials	a (Å)	Volume (Å^3)	rA	rAg	rAl	rX	t	Eb (eV)	Ef (eV)
Cs2AgAlCl6	10.11	1032.63	1.88	1.15	0.535	1.81	0.982	−3.72	−0.82
Cs2AgAlBr6	10.65	1209.90	1.88			1.96	0.969	−3.32	−0.32
Cs2AgAlI6	11.47	1508.40	1.88			2.20	0.948	−2.91	1.64
Rb2AgAlBr6	10.57	1180.27	1.72			1.96	0.929	−3.29	−0.31
K2AgAlBr6	10.52	1164.86	1.64			1.96	0.908	−3.30	−0.52

---

In addition, to study the thermodynamics stability of these perovskites, the formation energy E_f and the binding energy E_b are calculated using the following formula:⁴⁷

E_b = E_M2AgAlX6 − n_M × μ_M − n_Ag × μ_Ag − n_Al × μ_Al − n_X × μ_X

E_f = E_M2AgAlX6 − n_M × E_M − n_Ag × E_Ag − n_Al × E_Al − n_X × E_X

where E_M2AgAlX6 is the total energy of perovskite crystals, E_M, E_Ag, E_Al are the energy of single alkali metal, Ag, Al and halogen atoms, respectively. The μ represents the chemical potential of individual atom and the n represents the number of atoms. The results are listed in Table 1. Except from the formation energy of Cs₂AgAlI₆, the other values are all negative, which indicates that Cs₂AgAlI₆ may not be thermodynamic stable and is difficult to be synthesized through experiment. However, the E_f change from positive to negative for halogen atom varied from Br to I. Generally, there may be some stable structure of iodine doped Cs₂AgAlBr₆, namely Cs₂AgAlBr_xI_1−x. Moreover, the lower the formation energy means that the structure is more stable,⁴⁸ which reveals that Cs₂AgAlCl₆ is the most stable among the studied materials.

3.2. Elastic properties

Elastic constants are important and interesting parameters linked to the physical properties of solid materials. Due to the symmetry of cubic structures, the independent stiffness constants are reduced to 3, which are C₁₁, C₁₂ and C₄₄ respectively. Other elastic constants are also given in Table 2 in detail, including bulk modulus (B), shear modulus (G), Young modulus and Poisson ratio. Our results are only for reference due to the lack of previous study. These values seem to be low which makes strains occur easily in these perovskites. And Cs₂AgAlCl₆ possesses the largest B and G, which can be explained as Cs₂AgAlCl₆ have maximum response to uniaxial strain with large incompressibility and rigidity. The nature of interaction and chemical bonding between atoms can be preliminarily gained through analyzing the Cauchy's pressures C₁₂–C₄₄.⁴⁹ The positive value corresponds to the ionic nature of crystal bond and the negative value corresponds to the covalent nature of crystal bond.^50,51 The calculated values are all positive, which indicate that all perovskite materials are ionic compounds.

Table 2 The calculated elastic properties of double perovskite M₂AgAlX₆ (M = Cs, Rb or K; X= Cl, Br or I)

Composition	C11 (GPa)	C12 (GPa)	C44 (GPa)	B	G	B/G	A	Young modulus	Poisson ratio
Cs2AgAlCl6	46.78	25.52	14.60	32.61	12.86	2.54	1.37	34.09	0.33
Cs2AgAlBr6	45.38	20.46	11.86	28.77	12.10	2.38	0.95	31.83	0.32
Cs2AgAlI6	39.85	16.09	10.25	24.01	10.87	2.21	0.86	28.34	0.30
Rb2AgAlBr6	49.51	19.54	10.61	29.53	12.19	2.42	0.71	32.14	0.32
K2AgAlBr6	50.17	19.20	9.17	29.52	11.33	2.61	0.59	30.13	0.33

---

Mechanical stability of the cubic materials can be checked by introducing the following Born–Huang stability criterion:⁵²

C₁₁ − C₁₂ > 0, C₁₁ > 0, C₄₄ > 0, C₁₁ + 2C₁₂ > 0

The results all fulfill the stability criterion which proves these perovskite are mechanically stable. Combining the thermodynamic and mechanically stability, these perovskite derivatives are stable except pure Cs₂AgAlI₆.

The Pugh's ratios (B/G) are calculated to differentiate whether the material is ductile (B/G > 1.75) or brittle (B/G < 1.75).⁵³ All B/G values are over the critical value 1.75, which indicate that the materials are ductile. Furthermore, the Poisson' ratio can also testify the above inference. The critical limit of Poisson's ratio for ductile compounds is υ > 0.26,⁵⁴ which is consistent with the calculated values. It shows the potential of these perovskites applied in flexible or wearable optoelectronic devices.

In addition, the anisotropy of materials can be studied by the criteria of the elastic anisotropy coefficient A proposed by Zener:⁵⁵

If the A value is 1, the perovskite materials have isotropic physical properties, otherwise it is anisotropic. Neither the elastic anisotropy coefficient of all materials equals to 1, meaning that they are all anisotropic and have distinct properties in different directions while Cs₂AgAlBr₆ have the most isotropic properties.

3.3. Band structure and density of states

The band structure of perovskites is very important for photoelectric applications. In order to understand the electronic properties of perovskites, the band structure were corrected using HSE06 functional and depicted in Fig. 2. It can be seen that both valence band maximum (VBM) and conduction band minimum (CBM) located at gamma point in Brillouin zone. All the perovskite materials have direct band structure which is beneficial for the carrier transition between VBM and CBM. This is similar to the previous results based on In-containing double perovskites.^56,57 The band gap values vary from 0.773 eV to 3.430 eV, just in the ideal energy gap range of semiconductor. The halogen anions have a great influence on the band gap value while alkali metal does not. In general, the band gap value can be modulated to a certain extent by alloying or doped with other elements.^58,59 Besides, the hydrostatic pressure is another effective tool that can bring about band gap variation.⁷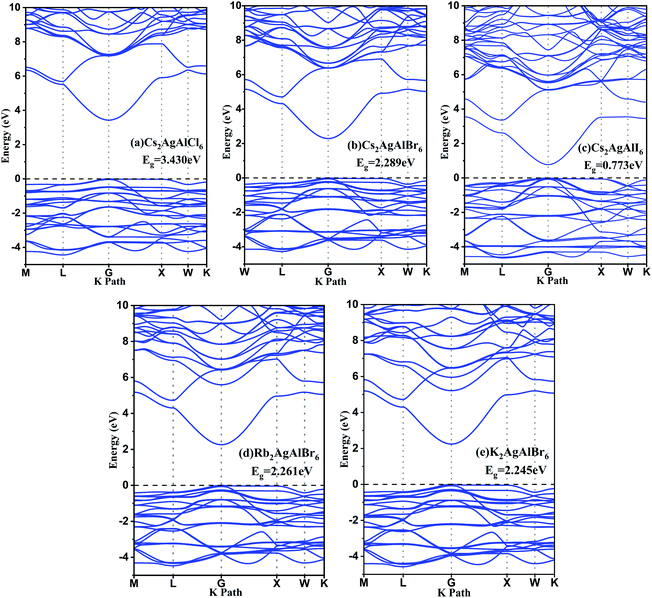

Fig. 2 The energy band structure of (a) Cs₂AgAlCl₆, (b) Cs₂AgAlBr₆, (c) Cs₂AgAlI₆, (d) Rb₂AgAlBr₆, and (e) K₂AgAlBr₆ calculated by hybrid HSE06 functional.

Meanwhile, total densities of states and partial densities of states are also plotted in Fig. 3 and help to understand the variation of electronic structure and optoelectronic properties. The contribution to the hybridization and inter-band transition comes from valence electrons, and their contribution near the Fermi surface is shown in Fig. 3. The Cs cation makes little contribution to the VBM and plays nearly no role in the dispersion of CBM. The valence band maximum is dominated mainly by X-p orbitals and partially by Ag-d orbitals,⁶⁰ whereas conduction bands are in an anti-bonding manner predominated by the Al-s/p orbitals with the Br-p orbital.⁶¹ According to the previous study,²⁷ comparing with Cu and Au, Ag-containing compounds have larger band gaps due to the lowest-energy d states and the VBM derives from hybridization between Cu/Ag/Au-d and Cl-p orbitals. For the M = Ag series, for M′ = Ga, In, Tl, the CBM is derived from anti-bonding M′-s and Cl-p states. Cs₂AgAlCl₆ has the largest band gap because Al-s state is shallow, and the hybridization of Al–Cl is strong, leading to a high-lying Al–Cl anti-bonding level. In this case, the CBM is no longer Al–Cl states but Ag–Cl states.

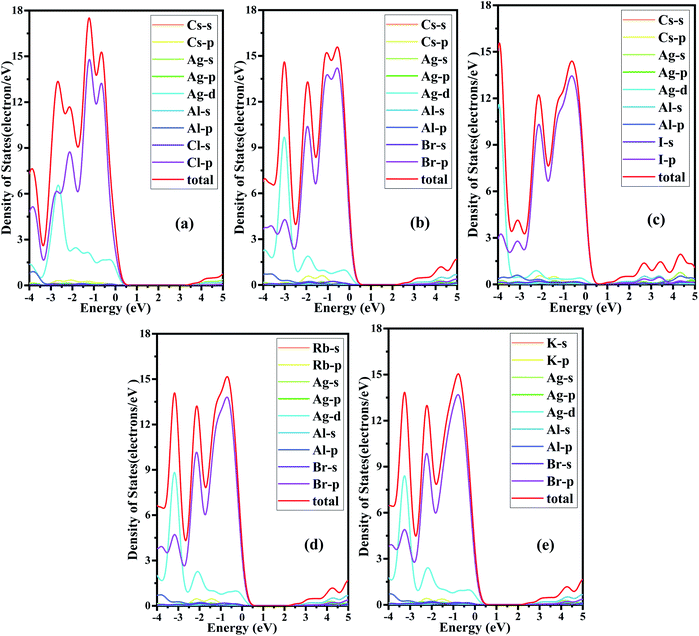Fig. 3 The total densities of states and partial densities of states of (a) Cs₂AgAlCl₆, (b) Cs₂AgAlBr₆, (c) Cs₂AgAlI₆, (d) Rb₂AgAlBr₆, and (e) K₂AgAlBr₆ calculated using hybrid HSE06 functional.

The effective mass of holes and electrons is a critical electronic property which has great effect on the separation efficiency and the mobility of photogenerated carriers.⁶² It can be obtained by the following formula:⁶³

where E(k) and k represent the eigenvalues of energy band and the wave vector along different directions, respectively. And ℏ is reduced Planck constant. The effective masses near VBM and CBM in different direction are most attractive and calculated in this paper, while m₀ represents the inertial mass of an electron. 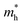As shown in Table 3, the effective masses of electrons and holes of these perovskite materials are very small, and only the of Cs₂AgAlCl₆ along the G → X direction is slightly large than m₀, showing an advantage in carrier transport. Along the G → L and G → X directions, the values of effective mass of carriers gradually decrease in the order of Cs₂AgAlCl₆, Cs₂AgAlBr₆, and Cs₂AgAlI₆, so does the value in the order of Cs₂AgAlBr₆, Rb₂AgAlBr₆ and K₂AgAlBr₆. It is evident both the smaller alkali metal atom and larger halogen atom help to decrease the effective mass and improve the electronic properties.^62,64,65

Table 3 The effective mass of holes and electrons

Materials	Directions
		G → L	G → X	G → L	G → X
Cs2AgAlCl6		0.321	1.091	0.126	0.167
Cs2AgAlBr6		0.211	0.320	0.091	0.091
Cs2AgAlI6		0.200	0.153	0.055	0.054
Rb2AgAlBr6		0.201	0.284	0.094	0.094
K2AgAlBr6		0.194	0.265	0.094	0.094

---

3.4. Optical properties

The optical properties play an essential role for optoelectronic materials and should be analyzed in some detail. Generally, the complex dielectric function is described byε(ω) = ε₁(ω) + iε₂(ω),⁶⁶ where ε₁(ω) represents the real part of dielectric function and ε₂(ω) represents the imaginary part of the dielectric function. The real part ε₁(ω) usually depicts the polarization degree of medium under an external electric field and can be deduced from the Kramers–Kronig relationship.⁶⁷ As for the real part ε₂(ω), it usually depicts the electron transitions from occupied states to unoccupied states while light passing through a medium, and it can be obtained by the momentum matrix of electronic transitions.^68,69 Other important optical parameters such as n(ω), k(ω), R(ω), α(ω), L(ω) and σ(ω) can be deduced through the complex dielectric function.^70,71 The calculated ε₁(ω), ε₂(ω) spectra, refractive index n(ω) and extinction coefficient k(ω) of M₂AgAlX₆ are shown in Fig. 4.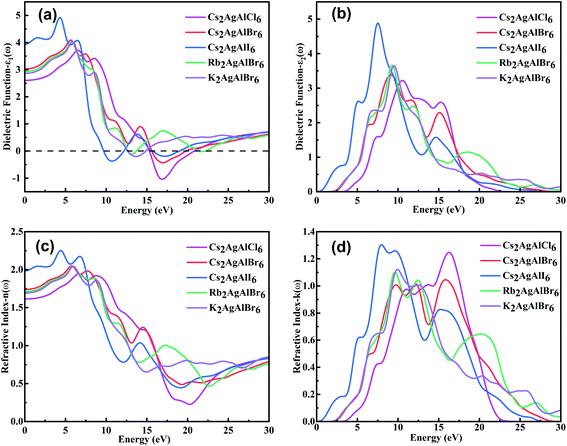

Fig. 4 The calculated (a) ε₁(ω), (b) ε₂(ω) spectra, (c) refractive index n(ω) and (d) extinction coefficient k(ω) of M₂AgAlX₆.

Fig. 4(a) and (b) show the curves of ε₁(ω) and ε₂(ω), respectively. The static dielectric constants ε₁(0) are respectively 2.61, 3.03, 3.95, 2.93 and 2.87 in the order of Cs₂AgAlCl₆, Cs₂AgAlBr₆, Cs₂AgAlI₆, Rb₂AgAlBr₆ and K₂AgAlBr₆. Static values of ε₁(ω) and band gap (E_g) are according to the Penn's model ε₁(0) ≈ 1 + (ℏω_p/E_g),² where ℏ is the Planck constant and ω_p is plasma frequency.⁷² Then as the photon energy increases, the ε₁(ω) of Cs₂AgAlCl₆, Cs₂AgAlBr₆, Cs₂AgAlI₆, Rb₂AgAlBr₆ and K₂AgAlBr₆ reach their maximum values at 6.54 eV, 5.63 eV, 4.32 eV, 5.81 eV and 5.86 eV, respectively. The maximum values of these compounds gradually increase as the anion changes from Cl⁻ to Br⁻ and then to I⁻ and slightly increase cation changes from K⁺ to Rb⁺ and then to Cs⁺. It is noteworthy that there are negative values of ε₁(ω) between 15.33 and 20.76 eV for Cs₂AgAlCl₆, 15.60–19.73 eV for Cs₂AgAlBr₆, 9.73–12.13 eV and 15.73–18.95 eV for Cs₂AgAlI₆, 12.65–13.70 eV and 21.54–22.15 eV for Rb₂AgAlBr₆ and 12.69–14.84 eV for K₂AgAlBr₆, which means that strong reflection and the photons in these energy range can not transport in the materials.

The ε₂(ω) spectra of the M₂AgAlX₆ materials are related to their behavior of light absorption. The thresholds of light absorption shift to lower photon energy with decrease in bandgap values of the studied compounds. The main peaks appear in the energy range lower than ∼10.5 eV with their peak positions respectively locating at 10.51, 9.15, 7.54, 9.28 and 9.50 eV in the order of Cs₂AgAlCl₆, Cs₂AgAlBr₆, Cs₂AgAlI₆, Rb₂AgAlBr₆ and K₂AgAlBr₆. The main peaks locating in the deep-ultraviolet light range are composed of electronic transitions from the top valence bands to the conduction bands far away from the Fermi surface. It may indicate the potential of ultraviolet-light detector and photocatalytic.

The complex refractive indexes of solids can be described by ñ(ω) = n(ω) + ik(ω), where n(ω) is the refractive index and k(ω) is the extinction coefficient. The refractive index n(ω) illustrates the dispersion of light when falling on material surface. As depicted in Fig. 4(c) and (d), we can see that n(ω) and k(ω), respectively, have the similar variation trends as ε₁(ω) and ε₂(ω). From Fig. 4(a), the calculated static refractive indexes n(0) are respectively 1.61, 1.74, 1.98, 1.71 and 1.69 for Cs₂AgAlCl₆, Cs₂AgAlBr₆, Cs₂AgAlI₆, Rb₂AgAlBr₆ and K₂AgAlBr₆. It is obvious that n(ω) values of M₂AgAlX₆ perovskites gradually increase and reach the maximum at the range of 8–10 eV. The range n(ω) less than K(ω) means that no photons in this energy region can be transported in the materials. The result is consistent with the dielectric function ε₁(ω). The calculated reflectivities R(ω), loss function L(ω), conductivity σ(ω) and absorption coefficient α(ω) of M₂AgAlX₆ are shown in Fig. 5.

Fig. 5 The calculated (a) reflectivities R(ω), (b) loss function L(ω) (c) conductivity σ(ω) and (d) absorption coefficient α(ω) of M₂AgAlX₆.

Fig. 5(a) displays the reflectivities of M₂AgAlX₆ double perovskites. The calculated static reflection coefficients R(0) for M₂AgAlX₆ double perovskites are, respectively, 0.055, 0.073, 0.109, 0.069 and 0.066 for Cs₂AgAlCl₆, Cs₂AgAlBr₆, Cs₂AgAlI₆, Rb₂AgAlBr₆ and K₂AgAlBr₆. However, except from the R(ω) of Cs₂AgAlCl₆, their values are very small in the observed energy region, and even the maximum values of M₂AgAlX₆ in the range of energy smaller than 10 eV regions are around 0.25, that is, most photons in this energy region can be absorbed by the materials or pass through the materials instead of being reflected by the materials.

The loss functions L(ω) of M₂AgAlX₆ double perovskites were shown in Fig. 5(b), revealing the energy loss of a fast electron passing through a material. It indicates that loss functions for M₂AgAlX₆ double perovskites are very small with their maximum value of ∼0.3 in the visible and ultraviolet light range (<10 eV).

The calculated real part of optical conductivity of the M₂AgAlX₆ compounds are presented in Fig. 5(c) to investigate their optical response, which is caused by the conduction of electrons in the compounds.⁷³ It can be found that Cs₂AgAlI₆ shows the largest σ(ω) in the lower photon energy range of 0–9.0 eV among the studied compounds, while the σ(ω) of Cs₂AgAlCl₆ is the largest in the photon energy range of 10.20–16.90 eV.

Absorption coefficient α(ω) is an important parameter of optoelectronic materials. As shown in Fig. 5(d), all the α(ω) of studied materials are small in the visible wavelength and sharply increase from 5 eV of the photon energy, meaning that the materials have strong responses to photon in ultraviolet wavelength and can work in this condition. The absorption edges shift with the same regularity with the band gaps. From 3.0–14.0 eV, the variations of M₂AgAlBr₆ are in broad agreement, indicating similar optical responses and the possibility of cheaper K atom substitute for Cs atom.

4 Conclusions

In this paper, aluminium based double halide perovskite M₂AgAlX₆ were optimized and calculated by DFT. The thermodynamic and mechanical stabilities of M₂AgAlX₆ perovskite were checked through Born–Huang stability criterion and confirmed by calculating the tolerance factor, the formation energy and the binding energy except for Cs₂AgAlI₆, indicating the possibility of experimental synthesis and commercial application. Elastic constants analysis shows that the studied materials are all ductile and suitable for flexible optoelectronic devices. All the materials have direct band structures. The energy band gap varies from 0.773 eV to 3.430 eV, and the substitution of alkali metal atoms does not change the band gap. The band gap can be modulated by halogen atom doping. The effective masses of all materials are very small in both G → L and G → X direction, which is conducive to carrier mobility. The optical properties show the materials have strong optical response in ultraviolet wavelength and may be applied for ultraviolet detector and photocatalytic. Cheaper K atoms substitute derivatives have similar properties as Cs-based materials, which show the potential of large-scale utilization.

Conflicts of interest

The authors have no conflicts to disclose.

Acknowledgements

This work is supported by the National Natural Science Foundation of China (No. 11164004, 61835003), the Guizhou Provincial Photonic Science and Technology Innovation Team (Qianke Joint Talents Team [2015] 4017) and the First-class Physics Promotion Programme (2019) of Guizhou University.

References

1. W. Gao, Y. Zhu, Y. Wang, G. Yuan and J. M. Liu, A review of flexible perovskite oxide ferroelectric films and their application, J. Materiomics, 2020, 6(1), 1–16,  DOI:10.1016/j.jmat.2019.11.001.
2. B. Jaffe, R. S. Roth and S. Marzullo, Piezoelectric properties of lead zirconate-lead titanate solid-solution ceramics, J. Appl. Phys., 1954, 25(6), 809–810,  DOI:10.1063/1.1721741.
3. Y. Saito, H. Takao, T. Tani, T. Nonoyama, K. Takatori, T. Homma, T. Nagaya and M. Nakamura, Lead-free piezoceramics, Nature, 2004, 432(7013), 84–87,  DOI:10.1038/nature03028.
4. A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, Organometal halide perovskites as visible-light sensitizers for photovoltaic cells, J. Am. Chem. Soc., 2009, 131(17), 6050–6051,  DOI:10.1021/ja809598r.
5. H. S. Kim, C. R. Lee, J. H. Im, K. B. Lee, T. Moehl, A. Marchioro, S. J. Moon, R. Humphry-Baker, J. H. Yum, J. E. Moser, M. Gratzel and N. G. Park, Lead iodide perovskite sensitized all-solid-state submicron thin film mesoscopic solar cell with efficiency exceeding 9%, Sci. Rep., 2012, 2, 591,  DOI:10.1038/srep00591.
6. C. S. Lee, K. M. Kleinke and H. Kleinke, Synthesis, structure, and electronic and physical properties of the two SrZrS3 modifications, Solid State Sci., 2005, 7(9), 1049–1054,  DOI:10.1016/j.solidstatesciences.2005.02.010.
7. A. Majumdar, A. A. Adeleke, S. Chakraborty and R. Ahuja, Emerging piezochromism in lead free alkaline earth chalcogenide perovskite AZrS₃ (A = Mg, Ca, Sr and Ba) under pressure, J. Mater. Chem. C, 2020, 8, 16392,  10.1039/d0tc04516k.
8. J. J. Yoo, G. Seo, M. R. Chua, T. G. Park, Y. Lu, F. Rotermund, Y. K. Kim, C. S. Moon, N. J. Jeon, J. P. Correa-Baena, V. Bulović, S. S. Shin, M. G. Bawendi and J. Seo, Efficient perovskite solar cells via improved carrier management, Nature, 2021, 590, 587–593,  DOI:10.1038/s41586-021-03285-w.
9. F. Cao, L. Meng, M. Wang, W. Tian and L. Li, Gradient energy band driven high-performance self-powered perovskite/CdS photodetector, Adv. Mater., 2019, 31(12), 1806725,  DOI:10.1002/adma.201806725.
10. J. L. Miao and F. J. Zhang, Recent progress on highly sensitive perovskite photodetectors, J. Mater. Chem. C, 2019, 7(7), 1741–1791,  10.1039/c8tc06089d.
11. C. Chen, L. Gao, W. R. Gao, C. Y. Ge, X. Du, Z. Li, Y. Yang, G. D. Niu and J. Tang, Circularly polarized light detection using chiral hybrid perovskite, Nat. Commun., 2019, 10, 1972,  DOI:10.1038/s41467-019-09942-z.
12. L. C. Chen, Y. H. Tian and J. J. Tian, Influence of surface passivation on perovskite CsPbBr_1.2I_1.8 quantum dots and application of high purity red light-emitting diodes, J. Alloys Compd., 2021, 892, 162140,  DOI:10.1016/j.jallcom.2021.162140.
13. X. Li, Y. Wei, P. Dang, X. Xiao, H. Xiao, G. Zhang, G. Li and J. Lin, Enhancing the stability of perovskite quantum dots CsPbX₃ (X=Cl, Br, I) by encapsulation in porous Y₂O₃ nanoparticles for WLED applications, Mater. Res. Bull., 2022, 146, 111592,  DOI:10.1016/j.materresbull.2021.111592.
14. P. Cheng, D. Zheng, L. Feng, Y. Liu, J. Liu, J. Li, Y. Yang, G. Wang and K. Han, Doped all-inorganic cesium zirconium halide perovskites with high-efficiency and tunable emission, J. Energy Chem., 2022, 65, 600–604,  DOI:10.1016/j.jechem.2021.06.033.
15. Z. W. Zhou, J. Y. Xu, Y. Liu, W. Chen, H. Zhang and Q. Wang, Zn-alloyed MAPbBr(3) crystals with improved thermoelectric and photocatalytic properties, Mater. Chem. Front., 2021, 5(24), 8319–8332,  10.1039/d1qm00993a.
16. A. Kipkorir, J. DuBose, J. Cho and P. V. Kamat, CsPbBr₃-CdS heterostructure: stabilizing perovskite nanocrystals for photocatalysis, Chem. Sci., 2021, 12(44), 14815–14825,  10.1039/d1sc04305f.
17. A. H. Slavney, T. Hu, A. M. Lindenberg and H. I. Karunadasa, A bismuth-halide double perovskite with long carrier recombination lifetime for photovoltaic applications, J. Am. Chem. Soc., 2016, 138(7), 2138–2141,  DOI:10.1021/jacs.5b13294.
18. E. T. Mcclure, M. R. Ball, W. Windl and P. M. Woodward, Cs₂AgBiX₆ (X = Br, Cl): new visible light absorbing, lead-free halide perovskite semiconductors, Chem. Mater., 2016, 28(5), 1348–1354,  DOI:10.1021/acs.chemmater.5b04231.
19. M. R. Filip, S. Hillman, A. A. Haghighirad, H. J. Snaith and F. Giustino, Band gaps of the lead-free halide double perovskites Cs₂BiAgCl₆ and Cs₂BiAgBr₆ from theory and experiment, J. Phys. Chem. Lett., 2016, 7(13), 2579–2585,  DOI:10.1021/acs.jpclett.6b01041.
20. Y. Wang, H. Huang, Z. Zhang, C. Wang, Y. Yang and Q. Li, Lead-free perovskite Cs₂AgBiBr₆@g-C₃N₄ Z-scheme system for improving CH₄ production in photocatalytic CO₂ reduction, Appl. Catal., B, 2021, 282, 119570,  DOI:10.1016/j.apcatb.2020.119570.
21. T. Wang, D. Yue, X. Li and Y. Zhao, Lead-free double perovskite Cs₂AgBiBr₆/RGO composite for efficient visible light photocatalytic H-2 evolution, Appl. Catal., B, 2020, 268, 118399,  DOI:10.1016/j.apcatb.2019.118399.
22. F. Locardi, M. Cirignano, D. Baranov, Z. Dang, M. Prato, F. Drago, M. Ferretti, V. Pinchetti, M. Fanciulli, S. Brovelli, L. De Trizio and L. Manna, Colloidal synthesis of double perovskite Cs₂AgInCl₆ and Mn-doped Cs₂AgInCl₆ nanocrystals, J. Am. Chem. Soc., 2018, 140(40), 12989–12995,  DOI:10.1021/jacs.8b07983.
23. K. Li, S. Li, W. Zhang, Z. Shi, D. Wu, X. Chen, P. Lin, Y. Tian and X. Li, Highly-efficient and stable photocatalytic activity of lead-free Cs₂AgInCl₆ double perovskite for organic pollutant degradation, J. Colloid Interface Sci., 2021, 596, 376–383,  DOI:10.1016/j.jcis.2021.03.144.
24. J. Luo, S. Li, H. Wu, Y. Zhou, Y. Li, J. Liu, J. Li, K. Li, F. Yi, G. Niu and J. Tang, Cs₂AgInCl₆ double perovskite single crystals: parity forbidden transitions and their application for sensitive and fast UV Photodetectors, ACS Photonics, 2018, 5(2), 398–405,  DOI:10.1021/acsphotonics.7b00837.
25. K. X. Lv, S. P. Qi, G. N. Liu, Y. B. Lou, J. X. Chen and Y. X. Zhao, Lead-free silver-antimony halide double perovskite quantum dots with superior blue photoluminescence, Chem. Commun., 2019, 55(98), 14741–14744,  10.1039/c9cc07397c.
26. Y. Cai, W. Xie, Y. T. Teng, P. C. Harikesh, B. Ghosh, P. Huck, K. A. Persson, N. Mathews, S. G. Mhaisalkar, M. Sherburne and M. Asta, High-throughput Computational Study of Halide Double Perovskite Inorganic Compounds, Chem. Mater., 2019, 31(15), 5392–5401,  DOI:10.1021/acs.chemmater.9b00116.
27. X. G. Zhao, J. H. Yang, Y. H. Fu, D. W. Yang, Q. L. Xu, L. P. Yu, S. H. Wei and L. J. Zhang, Design of lead-free inorganic halide perovskites for solar cells via cation-transmutation, J. Am. Chem. Soc., 2017, 139(7), 2630–2638,  DOI:10.1021/jacs.6b09645.
28. J. C. Dahl, W. T. Osowiecki, Y. Cai, J. K. Swabeck, Y. Bekenstein, M. Asta, E. M. Chan and A. P. Alivisatos, Probing the stability and band gaps of Cs₂AgInCl₆ and Cs₂AgSbCl₆ lead-free double perovskite nanocrystals, Chem. Mater., 2019, 31(9), 3134–3143,  DOI:10.1021/acs.chemmater.8b04202.
29. J. Zhou, X. M. Rong, M. S. Molokeev, X. W. Zhang and Z. G. Xia, Exploring the transposition effects on the electronic and optical properties of Cs₂AgSbCl₆ via a combined computational-experimental approach, J. Mater. Chem. A, 2018, 6(5), 2346–2352,  10.1039/C7TA10062K.
30. W. Deng, Z. Y. Deng, J. W. He, M. Z. Wang, Z. X. Chen, S. H. Wei and H. J. Feng, Synthesis of Cs₂AgSbCl₆ and improved optoelectronic properties of Cs₂AgSbCl₆/TiO₂ heterostructure driven by the interface effect for lead-free double perovskites solar cells, Appl. Phys. Lett., 2017, 111(15), 151602,  DOI:10.1063/1.4999192.
31. D. Y. Hu, X. H. Zhao, T. Y. Tang, L. M. Lu, L. Li, L. K. Gao and Y. L. Tang, First-principles study on the structural, elastic, electronic and optical properties of lead-free double perovskites Cs₂CuBiX₆ (X=I, Br, Cl), Mater. Today Commun., 2021, 29, 102842,  DOI:10.1016/j.mtcomm.2021.102842.
32. J. Dai, L. Ma, M. G. Ju, J. S. Huang and X. C. Zeng, In- and Ga-based inorganic double perovskites with direct bandgaps for photovoltaic applications, Phys. Chem. Chem. Phys., 2017, 19(32), 21691–21695,  10.1039/c7cp03448b.
33. G. Murtaza, T. Alshahrani, R. M. A. Khalil, Q. Mahmood, T. H. Flemban, H. Althib and A. Laref, Lead free double perovskites halides X2AgTlCl6 (X = Rb, Cs) for solar cells and renewable energy applications, J. Solid State Chem., 2021, 297, 121988,  DOI:10.1016/j.jssc.2021.121988.
34. M. Delor, A. H. Slavney, N. R. Wolf, M. R. Filip, J. B. Neaton, H. I. Karunadasa and N. S. Ginsberg, Carrier diffusion lengths exceeding 1 μm despite trap-limited transport in halide double perovskites, ACS Energy Lett., 2020, 5(5), 1337–1345,  DOI:10.1021/acsenergylett.0c00414.
35. S. S. Ghosh and A. Sil, Enhancement of photoresponse property of perovskite solar cell by aluminium chloride (AlCl3), Semicond. Sci. Technol., 2018, 33(5), 055002,  DOI:10.1088/1361-6641/aab455.
36. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, First principles methods using CASTEP, Z. Kristallogr. Krist., 2005, 220, 567–570,  DOI:10.1524/zkri.220.5.567.65075.
37. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868,  DOI:10.1103/PhysRevLett.77.3865.
38. H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13(12), 5188–5192,  DOI:10.1103/PhysRevB.13.5188.
39. A. J. Cohen, P. Mori-Sanchez and W. Yang, Fractional charge perspective on the band gap in density-functional theory, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77(11), 115123,  DOI:10.1103/PhysRevB.77.115123.
40. S. N. Maximoff, Current-dependent extension of the Perdew-Burke-Ernzerhof exchange-correlation functional, J. Chem. Phys., 2004, 120(5), 2105–2109,  DOI:10.1063/1.1634553.
41. R. Peverati and D. G. Truhlar, Screened-exchange density functionals with broad accuracy for chemistry and solid-state physics, Phys. Chem. Chem. Phys., 2012, 14(47), 16187–16191,  10.1039/c2cp42576a.
42. A. K. Singh and R. G. Hennig, Computational prediction of two-dimensional group-IV mono-chalcogenides, Appl. Phys. Lett., 2014, 105(4), 042103,  DOI:10.1063/1.4891230.
43. W. Travis, E. N. K. Glover, H. Bronstein, D. O. Scanlonbc and R. G. Palgrave, On the application of the tolerance factor to inorganic and hybrid halide perovskites: a revised system, Chem. Sci., 2016, 7(7), 4548–4556,  10.1039/c5sc04845a.
44. C. Li, X. Lu, W. Ding, L. Feng, Y. Gao and Z. Guo, Formability of ABX₃(X = F, Cl, Br, I) halide perovskites, Acta Crystallogr., Sect. B: Struct. Sci., 2008, 64, 702–707,  DOI:10.1107/S0108768108032734.
45. Y. P. Fu, M. P. Hautzinger, Z. Y. Luo, F. F. Wang, D. X. Pan, M. M. Aristov, I. A. Guzei, A. L. Pan, X. Y. Zhu and S. Jin, Incorporating large a cations into lead iodide perovskite cages: relaxed Goldschmidt tolerance factor and impact on exciton–phonon interaction, ACS Cent. Sci., 2019, 5(8), 1377–1386,  DOI:10.1021/acscentsci.9b00367.
46. R. D. Shannon, Revised effective ionic radii and systematic studies of interatomic distances in halide and chalcogenides, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32(5), 751–767,  DOI:10.1107/S0567739476001551.
47. X. Du, D. F. He, H. Y. Mei, Y. H. Zhong and N. P. Cheng, Insights on electronic structures, elastic features and optical properties of mixed-valence double perovskites Cs₂Au₂X₆ (X=F, Cl, Br, I), Phys. Lett. A, 2020, 384(8), 126169,  DOI:10.1016/j.physleta.2019.126169.
48. L. Lin, F. Wang, L. Yang, L. J. Chen, Z. Liu and Y. M. Wang, Microstructure investigation and first-principle analysis of die-cast AZ91 alloy with calcium addition, Mater. Sci. Eng., A, 2011, 528(15), 5283–5288,  DOI:10.1016/j.msea.2011.03.084.
49. N. F. Mott and H. Jones, The Theory of the Properties of Metals and Alloys, Nature, 1937, 139, 348–349,  DOI:10.1038/139348a0.
50. V. P. Mikhal'chenko, On the born relation for crystals with diamond and sphalerite structure, Phys. Solid State, 2003, 45, 453–458,  DOI:10.1134/1.1562230.
51. H. Ledbetter and A. Migliori, Elastic-constant systematics in f.c.c. metals, including lanthanides-actinides, Phys. Status Solidi B, 2008, 245(1), 44–49,  DOI:10.1002/pssb.200743075.
52. M. Born and K. Huang, Dynamical theory of crystal lattices, Am. J. Phys., 1955, 23, 474,  DOI:10.1119/1.1934059.
53. S. F. Pugh, XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals, Philos. Mag., 2009, 45, 823–843,  DOI:10.1080/14786440808520496.
54. N. Noor, S. Alay-e-Abbas, M. Hassan, I. Mahmood, Z. Alahmed and A. Reshak, The under-pressure behaviour of mechanical, electronic and optical properties of calcium titanate and its ground state thermoelectric response, Philos. Mag., 2017, 97(22), 1884–1901,  DOI:10.1080/14786435.2017.1320440.
55. C. Zener, Elasticity and Anelasticity of Metals, University of Chicago Press, 1948.
56. M. Tariq, M. A. Ali, A. Laref and G. Murtaz, Anion replacement effect on the physical properties of metal halide double perovskites Cs₂AgInX₆ (X=F, Cl, Br, I), Solid State Commun., 2020, 314, 113929,  DOI:10.1016/j.ssc.2020.113929.
57. J. Su, Z. Zhang, J. Hou, M. Y. Liu, Z. H. Lin, Z. S. Hu, J. J. Chang and Y. Hao, Pressure-Dependent Mechanical and Thermal Properties of Lead-Free Halide Double Perovskite Cs₂AgB′′X₆(B′′=In, Bi; X=Cl, Br, I), Adv. Theory Simul., 2019, 2(12), 1900164,  DOI:10.1002/adts.201900164.
58. K. Kim, H. Kim and J. Park, Bandgap modulation of Cs₂AgInX₆ (X = Cl and Br) double perovskite nano- and microcrystals via Cu²⁺ doping, ACS Omega, 2021, 6(41), 26952,  DOI:10.1021/acsomega.1c03290.
59. D. W. Liu, G. S. Yao, S. F. Jin, J. M. Chen, B. Y. Lou, Q. H. Li and R. J. Sa, The effects of cation and halide anion on the electronic and optical properties of Ti-based double perovskite: a first-principles calculations, J. Phys. Chem. Solids, 2021, 150, 109852,  DOI:10.1016/j.jpcs.2020.109852.
60. Z. Zhang, J. Su, J. Hou, Z. H. Lin, Z. S. Hu, J. J. Chang, J. C. Zhang and Y. Hao, Potential applications of halide double perovskite Cs₂AgInX₆(X = Cl, Br) in flexible optoelectronics: Unusual effects of uniaxial strains, J. Phys. Chem. Lett., 2019, 10(5), 1120–1125,  DOI:10.1021/acs.jpclett.9b00134.
61. A. Menedjhi, N. Bouarissa, S. Saib and K. Bouamama, Halide double perovskite Cs2AgInBr6 for photovoltaic's applications: optical properties and stability, Optik, 2021, 243, 167198,  DOI:10.1016/j.ijleo.2021.167198.
62. Y. Tang, J. H. Zhang, X. L. Zhong, Q. J. Wang, H. Zhang, C. L. Ren and J. B. Wang, Revealing the structural, electronic and optical properties of lead-free perovskite derivatives of Rb₂SnX₆ (X = Cl, Br and I): a theory calculation, Sol. Energy, 2019, 190, 272–277,  DOI:10.1016/j.solener.2019.08.030.
63. J. F. Zhang, P. Zhou, J. J. Liu and J. G. Yu, New understanding of the difference of photocatalytic activity among anatase, rutile and brookite TiO₂, Phys. Chem. Chem. Phys., 2014, 16(38), 20382–20386,  10.1039/c4cp02201g.
64. Y. Cai, W. Xie, H. Ding, Y. Chen, K. Thirumal, L. H. Wong, N. Mathews, S. G. Mhaisalkar, M. Sherburne and M. Asta, Computational Study of Halide Perovskite-Derived A₂BX₆ Inorganic Compounds: Chemical Trends in Electronic Structure and Structural Stability, Chem. Mater., 2017, 29, 7740–7749,  DOI:10.1021/acs.chemmater.7b02013.
65. P. R. Varadwaj, A₂AgCrCl₆ (A = Li, Na, K, Rb, Cs) halide double perovskites: a transition metal-based semiconducting material series with appreciable optical characteristics, Phys. Chem. Chem. Phys., 2020, 22, 24337,  10.1039/d0cp01896a.
66. F. Hamioud, G. S. AlGlianali, S. Al-Omari and A. A. Mubarak, Ab initio investigation of the structural, electronic, magnetic and optical properties of the perovskite TlMnX₃ (X = F, Cl) compounds, Int. J. Mod. Phys. B, 2016, 30(7), 1650031,  DOI:10.1142/S0217979216500314.
67. M. Gajdoš, K. Hummer, G. Kresse, J. Furthmüller and F. Bechstedt, Linear optical properties in the projector-augmented wave methodology, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 045112,  DOI:10.1103/PhysRevB.73.045112.
68. M. Dadsetani and A. Pourghazi, Optical properties of strontium monochalcogenides from first principles, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 195102,  DOI:10.1103/PhysRevB.73.195102.
69. H. G. Sun, Z. X. Zhou, C. X. Yuan, W. L. Yang and H. Wang, Structural, eElectronic and optical properties of KTa_0.5Nb_0.5O₃ surface: a first-principles study, Chin. Phys. Lett., 2012, 29(1), 017303,  DOI:10.1063/1.2902433.
70. V. S. Zhandun and V. I. Zinenko, The effect of structural ordering on the magnetic, electronic, and optical properties of the LaPbMnSbO₆ double perovskite, J. Alloys Compd., 2016, 671, 184–191,  DOI:10.1016/j.jallcom.2016.02.085.
71. Z. H. Jin, Y. M. Wu, S. Li, Q. F. Wu, S. J. Chen, Y. Chen, W. B. Zhang and C. Z. Zhang, Electronic structure, elastic, optical and thermodynamic properties of cubic perovskite NaBaF₃ with pressure effects: first-principles calculations, Results Phys., 2021, 22, 103860,  DOI:10.1016/j.rinp.2021.103860.
72. G. K. H. Madsena and D. J. Singh, BoltzTraP. A code for calculating band-structure dependent quantities, Comput. Phys. Commun., 2006, 175(1), 67–71,  DOI:10.1016/j.cpc.2006.03.007.
73. N. A. Noor, M. W. Iqbal, T. Zelai, A. Mahmood, H. M. Shaikh, S. M. Ramay and W. Al-Masry, Analysis of direct band gap A₂ScInI₆ (A = Rb, Cs) double perovskite halides using DFT approach for renewable energy devices, J. Mater. Res. Technol., 2021, 13, 2491–2500,  DOI:10.1016/j.jmrt.2021.05.080.

---