DOI:
10.1039/D2RA00805J
(Paper)
RSC Adv., 2022,
12, 12573-12582
Pressure-driven thermoelectric properties of defect chalcopyrite structured ZnGa2Te4: ab initio study
Received
7th February 2022
, Accepted 17th April 2022
First published on 26th April 2022
Abstract
The pressure induced structural, electronic, transport, and lattice dynamical properties of ZnGa2Te4 were investigated with the combination of density functional theory, Boltzmann transport theory and a modified Debye–Callaway model. The structural transition from I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) to I
to I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2m occurs at 12.09 GPa. From the basic observations, ZnGa2Te4 is found to be mechanically as well as thermodynamically stable and ductile up to 12 GPa. The direct band gap of 1.01 eV is inferred from the electronic band structure. The quantitative analysis of electron transport properties shows that ZnGa2Te4 has moderate Seebeck coefficient and electrical conductivity under high pressure, which resulted in a large power factor of 0.63 mW m−1 K−2 (750 K). The ultralow lattice thermal conductivity (∼1 W m−1 K−1 at 12 GPa) is attributed to the overlapping of acoustic and optical phonon branches. As a result, the optimal figure of merit of 0.77 (750 K) is achieved by applying a pressure of 12 GPa. These findings support that ZnGa2Te4 can be a potential p-type thermoelectric material under high pressure and thus open the door for its experimental exploration.
2m occurs at 12.09 GPa. From the basic observations, ZnGa2Te4 is found to be mechanically as well as thermodynamically stable and ductile up to 12 GPa. The direct band gap of 1.01 eV is inferred from the electronic band structure. The quantitative analysis of electron transport properties shows that ZnGa2Te4 has moderate Seebeck coefficient and electrical conductivity under high pressure, which resulted in a large power factor of 0.63 mW m−1 K−2 (750 K). The ultralow lattice thermal conductivity (∼1 W m−1 K−1 at 12 GPa) is attributed to the overlapping of acoustic and optical phonon branches. As a result, the optimal figure of merit of 0.77 (750 K) is achieved by applying a pressure of 12 GPa. These findings support that ZnGa2Te4 can be a potential p-type thermoelectric material under high pressure and thus open the door for its experimental exploration.
I. Introduction
The advancement of renewable energy sources is vital for future technologies as the world is completely reliant on electricity.1 Fortunately numerous renewable energy conversion techniques exist, including solar, wind power, hydropower, and geothermal power. Nonetheless thermoelectricity, which facilitates direct conversion of heat energy into electricity, plays a crucial role. The efficiency of thermoelectric (TE) materials can be characterized by the dimensionless figure of merit, zT = (S2σ/ke + kL)T. Here, S is the Seebeck coefficient, σ is electrical conductivity, T is the temperature, and ke and kL are the electronic and lattice thermal conductivity. A promising TE material should have zT ≥ 1 at suitable operating temperature.2 Low energy electron filtering,3 strain engineering,4 and band engineering5 are a few advancements that have been made to improve the TE power factor (S2σ) of materials. Most of these approaches were interesting, besides, the coupled behaviour of S and σ resists practical implementations. Hence, researchers focus on tailoring the lattice thermal conductivity by phonon scattering through rattlers,6 nano-structuring,7 defect engineering,8 etc. However, attaining high TE efficiency is challenging. Apart from these experimental strategies, theoretical aspects also provide a way to enhance TE properties by tuning the effective mass of the carriers using the band convergence approach,9 phonon softening,10 increasing the band degeneracy and forming band valleys (Nv) by adjusting the carrier concentrations.11
However, the present study mainly focuses on two strategies: firstly, exploring new earth abundant and less hazardous materials to replace the benchmark candidates (such as Bi2Te3 and PbTe). In this aspect, theoretical predictions such as first-principles calculations combined with Boltzmann transport theory were extremely effective for materials discovery, design, development and understanding the fundamentals. Recently, J.-H. Pohls et al.12 predicted rare earth phosphides, RECuZnP2 (RE = Pr, Nd, Er) as a thermoelectric material through a computational search and validated by performing experiments. Backing to this argument further, F. Garmroudi et al.5 also reported the enhancement of TE performance in Ta/Si doped Fe2VAl by band engineering computationally and supported their findings through experiments.
Secondly, application of high pressure causes changes in electronic band structure, carrier concentration, chemical bonds, etc., in most of the chalcogenide semiconductors. These changes help to tune the power factor of the material. In technical aspect, the experimental constraints and the increase of thermal conductivity upon pressure limits their practical implications.13 Despite these limitations, there are few research studies that justifies the noteworthy enrichment in zT by the effect of pressure.14–16 In this way, Liu-Cheng Chen et al.,17 reported maximum zT ∼ 1.7 under an external pressure of 3 GPa for Cr doped PbSe. Likewise, over 5 times improved zT upon pressure (2.5 GPa) for p-type CuInTe2 is also reported which is due to the increased phonon anharmonicity with pressure.18 Zhang et al.,19 claimed that subjecting the material to external pressure helps to attain high zT at low temperature. However, in order to resolve the experimental constraints in measuring the TE parameters, V. V. Shchennikov et al.,20 designed a reliable high-pressure cell that is capable of generating pressure upto ∼30 GPa. In this context, TE properties of the unexplored narrow band gap semiconductor, ZnGa2Te4 has been extensively studied under hydrostatic pressure.
Herein, the reason for high zT of ZnGa2Te4 have been examined systematically. For this purpose, the structural, elastic, electronic, and transport properties were investigated within the framework of Density Functional Theory (DFT). In order to understand its thermodynamical stability, phonon dispersion spectra have been calculated. To facilitate the importance of phonon contribution to thermal conductivity, kL has been computed by employing modified Debye–Callaway (mDC) method. The summary of the research discussed in Section IV, suggests that the proposed material can be a promising p-type TE material and its performance can be enhanced by pressure.
II. Methods of calculation
The first principles calculations were performed using DFT implemented in Vienna Ab initio Simulation Package (VASP).21–23 The Projector Augmented Wave (PAW)21 method with Perdew–Burke–Ernzerhof (PBE) along with Generalized Gradient Approximation (GGA) was used to compute electronic properties.24 The kinetic energy cut-off was set as 500 eV. In the Monkhorst–Pack scheme, 9 × 9 × 5 k-mesh was used for Brillouin zone integration. The energy and ionic force convergence criterion for structure relaxation were set as 10−8 eV and 10−7 eV Å−1 respectively. The elastic constants were calculated by finite deformation method using ElaStic code.25 By collecting stress tensors of 21 deformed structures, the elastic constants (Cij) were computed. The lattice dynamical properties were studied using Phonopy code.26 A 2 × 2 × 1 supercell was adopted for calculating the interatomic force constants (IFC). The static calculations were performed for the displaced structures with energy and force convergence criterion as 10−8 eV and 10−6 eV Å−1 respectively. Later, force sets were collected from various displaced structures and 11 × 11 × 11 q-mesh was used to calculate the dynamical matrix. Using the finite difference method of the parabolic band fitting model, the effective mass was calculated with the help of effmass code.27
The Boltzmann transport properties were calculated using BoltzTraP2 code working under Constant Relaxation Time Approximation (CRTA) by solving Boltzmann transport equations (eqn (1)–(3)).28 According to CRTA, the relaxation time is treated as a constant. From the calculated electronic band structure, the transport properties were computed by Rigid Band Approximation (RBA) and 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 k-points were adopted to attain reliable results.29 The carrier concentration (n) is given by eqn (4).
000 k-points were adopted to attain reliable results.29 The carrier concentration (n) is given by eqn (4).
| |
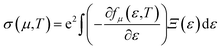 | (1) |
| |
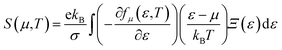 | (2) |
| |
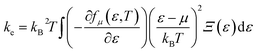 | (3) |
| |
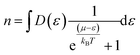 | (4) |
where,
μ is the chemical potential,
kB is the Boltzmann constant,
ε is the energy,
fμ is the Fermi–Dirac distribution function,
Ξ(
ε) is the transport distribution function and
D(
ε) is the density of states.
The lattice thermal conductivity was calculated using modified Debye–Callaway30 method implemented in AICON2 (Ab Initio Conductivities) program.31 Here, the lattice thermal conductivity (kL) is calculated from transverse acoustic branches, longitudinal acoustic branch, and pseudo-optical branches using the following formulation from mDC model,
| |
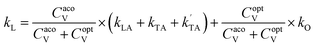 | (5) |
where,
CacoV,
CoptV are the specific heat of acoustical and optical branches.
ki =
ki1 +
ki2, here
i is the acoustic (TA, TA′, LA) and optical modes (O).
ki1and
ki2 is given by,
| |
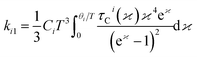 | (6) |
| |
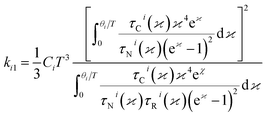 | (7) |
| |
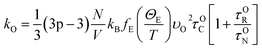 | (8) |
Here,
θi – Debye temperature,
p-number of atoms in primitive cell, 3
p − 3 – number of optical phonon branches,
N-number of primitive cells,
V-volume of the primitive cell,
υO – average velocity of optical phonon,
ΘE – Einstein temperature and
fE – Einstein function. According to this model, the second order IFC were obtained from three different volumes (equilibrium volume, slightly higher and lower volumes) at each pressure using Phonopy. For each unit cell there exist 28 displaced structures. By performing static calculations on all these structures, the IFCs were obtained to calculate
kL.
III. Results and discussions
A. Geometry of the crystal structure and bonding nature
The crystal structure with chemical formula II–III2–VI4 is known as defect chalcopyrite, a subgroup of chalcopyrite family. Removing the alternate central and corner cations from chalcopyrite structure results in vacancy ordered defect chalcopyrite structure.32 ZnGa2Te4 is one among this family. Hahn et al.33 reported that ZnGa2Te4 exist in two tetragonal polymorphs with space groups I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2m, Z = 2 (no.: 121) and I
2m, Z = 2 (no.: 121) and I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) , Z = 2 (no.: 82), its crystal structure is generated using VESTA software34 and is shown in Fig. 1(a and b). The Wyckoff positions for both the structures and a strong discrepancy in its ground state structure were discussed in the previous report.35 In order to understand the case, Birch–Murnaghan equation of states (BM-EOS)36 fit have been done and displayed in Fig. 1(c). The minimum energy of the I
, Z = 2 (no.: 82), its crystal structure is generated using VESTA software34 and is shown in Fig. 1(a and b). The Wyckoff positions for both the structures and a strong discrepancy in its ground state structure were discussed in the previous report.35 In order to understand the case, Birch–Murnaghan equation of states (BM-EOS)36 fit have been done and displayed in Fig. 1(c). The minimum energy of the I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) structure is ∼4 eV lesser than I
structure is ∼4 eV lesser than I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2m in BM-EOS fit, which suggests I
2m in BM-EOS fit, which suggests I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) defect chalcopyrite structure as the ground state. The variation of enthalpy as a function of pressure, shown in Fig. 1(d) reveals that the phase transition from I
defect chalcopyrite structure as the ground state. The variation of enthalpy as a function of pressure, shown in Fig. 1(d) reveals that the phase transition from I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) to I
to I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2m takes place at ∼12 GPa which is consistent with earlier report.35 In other words, I
2m takes place at ∼12 GPa which is consistent with earlier report.35 In other words, I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) structured ZnGa2Te4 is stable up to 12 GPa. With these inferences, the present study has been carried out on ZnGa2Te4 (I
structured ZnGa2Te4 is stable up to 12 GPa. With these inferences, the present study has been carried out on ZnGa2Te4 (I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) ) upto 12 GPa pressure. Whereas, the other I
) upto 12 GPa pressure. Whereas, the other I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2m phase is neglected because of its metallic nature.
2m phase is neglected because of its metallic nature.
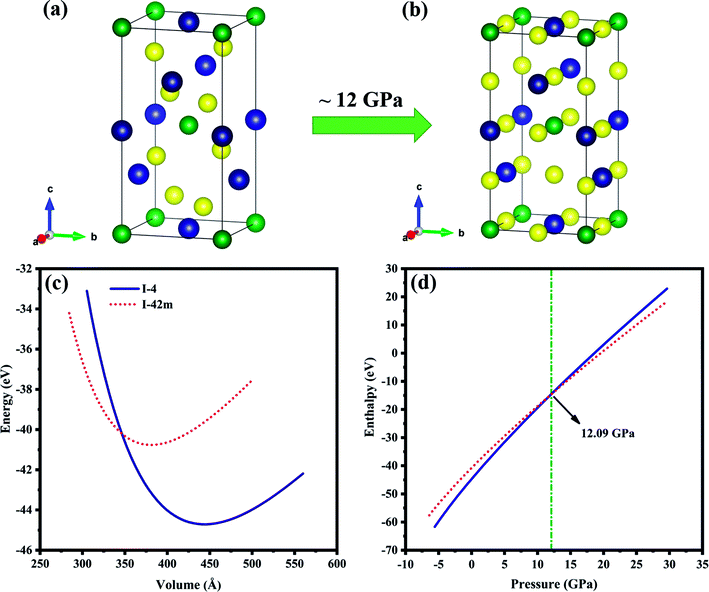 |
| | Fig. 1 Unit cell of ZnGa2Te4 (a) I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) , (b) I , (b) I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2m phases. The green, blue and yellow balls represent Zn, Ga and Te atoms respectively. (c) BM-EOS fit, (d) enthalpy as a function of pressure. 2m phases. The green, blue and yellow balls represent Zn, Ga and Te atoms respectively. (c) BM-EOS fit, (d) enthalpy as a function of pressure. | |
The optimized lattice constants are a = b = 6.07 Å and c = 12.03 Å (α = β = γ = 90°), which are reasonably consistent with earlier reports [refer Table 1]. The bond lengths of Zn–Te as well as Ga–Te are 2.69 Å and 2.67 Å respectively. The bonding nature strongly determines the physical and chemical properties of the materials. Hence, the bond analysis has been carried out through Electron Localization Function (ELF) given in Feng et al.37 ELF can take values from 0 to 1, with ELF = 0, 0.5 and 1 corresponding to delocalization (red), metallic bond (green) and complete localization (blue). The ELF plot along (0 1 0), (0 0 1) and (0 0 ![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) planes capturing the bond between Zn–Te and Ga–Te are displayed in Fig. 2(a–c). The strong localization of electrons between Ga and Te shows that the bond is covalent in nature, whereas the weak bonding between Zn–Te can be ionic. It is observed that more electrons are localized near the Te atoms, which is due to the larger electronegativity of Te than Ga.
) planes capturing the bond between Zn–Te and Ga–Te are displayed in Fig. 2(a–c). The strong localization of electrons between Ga and Te shows that the bond is covalent in nature, whereas the weak bonding between Zn–Te can be ionic. It is observed that more electrons are localized near the Te atoms, which is due to the larger electronegativity of Te than Ga.
Table 1 Comparison of the cell parameters and band gap (Eg) of ZnGa2Te4
| ZnGa2Te4 |
Lattice parameters |
Eg (eV) |
References |
| a (Å) |
c (Å) |
| Present work |
6.07 |
12.03 |
1.01 |
— |
| Experimental works |
5.93 |
11.85 |
— |
Rashmi and U. Dhawan38 |
| 5.92 |
11.80 |
— |
Errandonea et al.35 |
| 5.93 |
11.85 |
1.33 |
S. S. Fouad et al.39 |
| Theoretical works |
6.60 |
12.06 |
1.02 |
Ayeb Yakoub, et al.40 |
| 5.90 |
11.64 |
1.85 |
S. Chandra et al.41 |
| 6.24 |
11.97 |
0.94 |
Sahariya et al.42 |
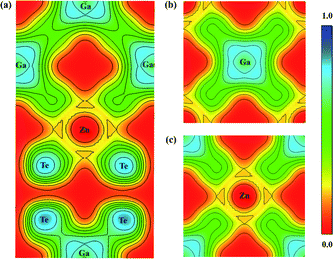 |
| | Fig. 2 Electron localization function of ZnGa2Te4 along (a) (0 1 0), (b) (0 0 1), and (c) (0 0 ![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ). ). | |
B. Elastic properties and mechanical stability
In order to analyze the mechanical properties, the elastic constants were calculated for ZnGa2Te4 under various pressure. For tetragonal systems, there remain six elastic constants, namely, C11, C12, C13, C33, C44, and C66. The satisfactory of Born criteria resembles the mechanical stability of a material.43 The Born criteria for the tetragonal symmetry without applied pressure are given by,| | |
C11 > |C12|; 2C132 < C33(C11 + C12); C44 > 0; C66 > 0
| (9) |
The calculated elastic constants are tabulated (Table 2). It is noted that ZnGa2Te4 fulfills the Born criteria. Further the stability criteria for tetragonal system under pressure given by, (C11 + 2C12) + P > 0; (C11 − C12) − P > 0; (C44 − P) > 0; (C66 − P) > 0; (C33 − P) (C11 + C12) − 2(C13 + P)2 > 0 are also satisfied indicating the stability of the structure upto 12 GPa.44 According to Voigt–Reuss–Hill approximation,45 the bulk modulus (B), shear modulus (G), and Young's modulus (Y) can be calculated by eqn (10) and the values are shown in Table 2.
| |
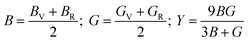 | (10) |
where,
Table 2 Elastic properties of ZnGa2Te4 at various pressures
| Elastic properties |
Pressure (GPa) |
| 0 |
4 |
8 |
12 |
| C11 |
63.83 |
90.72 |
115.13 |
137.49 |
| C12 |
31.43 |
45.19 |
57.83 |
69.28 |
| C13 |
32.38 |
45.83 |
58.17 |
69.32 |
| C33 |
60.46 |
86.20 |
109.20 |
129.55 |
| C44 |
0.04 |
4.06 |
8.09 |
12.05 |
| C66 |
16.20 |
22.76 |
28.65 |
34.10 |
| B |
42.23 |
60.36 |
76.93 |
92.01 |
| G |
3.25 |
5.83 |
8.25 |
10.55 |
| Y |
9.51 |
16.96 |
23.91 |
30.49 |
| G/B |
0.07 |
0.09 |
0.10 |
0.11 |
| υ |
0.46 |
0.45 |
0.44 |
0.44 |
| A100 |
0.00 |
0.19 |
0.29 |
0.37 |
A1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0 0 |
0.00 |
0.25 |
0.39 |
0.49 |
| A001 |
1.00 |
1.00 |
1.00 |
1.00 |
| Cp |
63.79 |
86.66 |
107.04 |
125.44 |
The calculated bulk modulus is comparable with the one obtained from the BM-EOS fit (41.68 GPa). It is also observed that elastic modulus increases consistently upon pressure, indicating the highly resistive nature of the material towards compression. The material with Pugh's ratio (G/B) greater than 0.57 is brittle, whereas lesser than 0.57 is ductile. The G/B ratio is found to increase with pressure. ZnGa2Te4 retained its ductile nature upto 12 GPa which is also evident from the Poisson's ratio (υ > 0.26, ductile) and positive values of Cauchy's pressure, Cp(C11 − C44). The variation of the elastic anisotropic factor along different directions confirmed the anisotropic characteristics of the titled material.
C. Lattice dynamical properties and thermodynamical stability
The phonon dispersion spectra of ZnGa2Te4 along Γ–X–M–Γ–Z–R–A–Z–R–X–A–M direction within the Brillouin zone at various pressures is shown in Fig. 3(a–d). Being a tetragonal system with I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) space group ZnGa2Te4, possess 42 modes of vibrations. According to symmetry analysis, it constitutes of 3 acoustic (B + 1E + 2E) and 39 optical (39A) branches, which is also evident from the phonon spectra.46 The transverse acoustic (TA, TA′), longitudinal acoustic (LA), and optical branches in the spectra were differentiated by red, blue, green, and black color in Fig. 3. The real (positive) frequency over the entire Brillouin zone at 0 K depicts that ZnGa2Te4 is thermodynamically stable even upto 12 GPa. The frequency range of the overall phonon branches falls within 8 THz. The frequency of the longitudinal optical phonon branch is 1.3 THz (at 0 GPa) and these low-lying modes were further decreased with pressure which may lead to soft lattice as well as low group velocity and thus low lattice thermal conductivity.
space group ZnGa2Te4, possess 42 modes of vibrations. According to symmetry analysis, it constitutes of 3 acoustic (B + 1E + 2E) and 39 optical (39A) branches, which is also evident from the phonon spectra.46 The transverse acoustic (TA, TA′), longitudinal acoustic (LA), and optical branches in the spectra were differentiated by red, blue, green, and black color in Fig. 3. The real (positive) frequency over the entire Brillouin zone at 0 K depicts that ZnGa2Te4 is thermodynamically stable even upto 12 GPa. The frequency range of the overall phonon branches falls within 8 THz. The frequency of the longitudinal optical phonon branch is 1.3 THz (at 0 GPa) and these low-lying modes were further decreased with pressure which may lead to soft lattice as well as low group velocity and thus low lattice thermal conductivity.
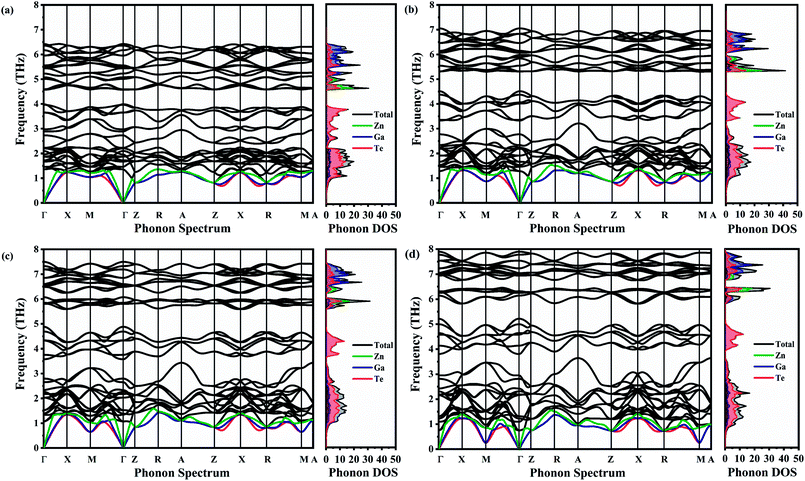 |
| | Fig. 3 Phonon dispersion spectra with corresponding phonon DOS at (a) 0 GPa, (b) 4 GPa, (c) 8 GPa and (d) 12 GPa. | |
It is also observed that there is no acoustical–optical (A–O) band gap at ambient and higher pressures (i.e., strong coupling between the acoustic and optical branches). This strong coupling leading to low mean free path can promote the phonon scattering process, which may result in low lattice thermal conductivity. There is a noticeable decoupling between the acoustic and optical phonon branches upon pressure which may result in enhancement of kL. The impact of this coupling and decoupling on kL upon pressure is discussed later (Section III(G)). The shorter propagation length of the acoustic phonon modes along Γ–Z than Γ–X indicates that the lattice thermal conductivity along Z-direction may be lower than the one along X-direction which stands as a support with the elastic anisotropic factor. This shorter propagation length may be due to the weak interatomic interactions and strong anharmonicity. It follows a similar fashion over the entire pressure range.
The projected phonon density of states of ZnGa2Te4 and its response to the hydrostatic pressure is captured in Fig. 3(a–d). It depicts that the low frequency acoustic branches are mainly contributed by vibrations of Te (higher atomic mass) atoms, whereas the high frequency optical branches by Zn and Ga (lower atomic mass) atoms. The clear picture of the acoustic–optic coupling and the optical–optical band gap is observed in the phonon DOS. Upon increasing the pressure, decoupling of the optical branches results the optical–optical band gap observed around 3 THz to 7 THz frequency ranges.
D. Electronic properties and effective mass
The calculated electronic band structure and density of states (DOS) of ZnGa2Te4 at various pressure were shown in Fig. 4(a–d). The high symmetry k-path in irreducible Brillouin zone of the tetragonal system is Γ–X–M–Γ–Z–R–A–Z–R–X–A–M. The presence of both valence band maximum (VBM) and conduction band minimum (CBM) at the Γ-point (0, 0, 0) depicts that ZnGa2Te4 is a direct band gap semiconductor and it retained the same till 12 GPa. At ambient pressure, the calculated band gap (Eg) is 1.01 eV. It is also observed that there is a slight energy difference of 80 meV (ΓVB − ZXVB) and 61 meV (ΓCB − MCB) between successive VBM and CBM indicating the presence of energetically degenerate bands. The calculated band gap agrees well with the previous results (see Table 1), which suggest that PBE-GGA exchange correlational functional is appropriate for the present system. Under hydrostatic pressure, noticeable changes in both valence and conduction bands can be seen in the band structure. In addition, the band gap is reduced to 0.81 eV, 0.53 eV and 0.31 eV for an applied pressure of 4 GPa, 8 GPa and 12 GPa respectively. Furthermore, the atomic contributions to the band have been investigated by partial and total DOS. It is vivid from partial DOS that the valence band is dominated by Te atoms, whereas the conduction band by the Ga and Te atoms.
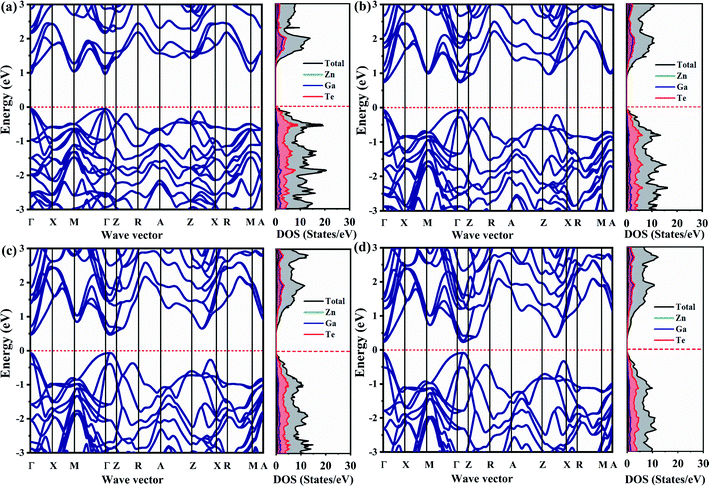 |
| | Fig. 4 Electronic band structure with corresponding DOS at (a) 0 GPa, (b) 4 GPa, (c) 8 GPa, and (d) 12 GPa. | |
The effective mass is related to the Seebeck coefficient (S), carrier mobility (μ) and electron group velocity (vg) by the following relations:2,37,47
| |
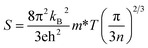 | (11) |
| |
 | (12) |
| |
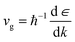 | (13) |
Hence, the effective mass,  is calculated from band structure at the band edges. The effective mass for holes
is calculated from band structure at the band edges. The effective mass for holes 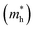 and electrons
and electrons  are 0.09me and 0.4me at 0 GPa which decreases upon pressure as shown in Fig. 5. This decrease in effective mass may end up in decreasing Seebeck coefficient, increasing carrier mobility contributing to high electrical conductivity, increasing group velocity and thus increasing electronic thermal conductivity with pressure.
are 0.09me and 0.4me at 0 GPa which decreases upon pressure as shown in Fig. 5. This decrease in effective mass may end up in decreasing Seebeck coefficient, increasing carrier mobility contributing to high electrical conductivity, increasing group velocity and thus increasing electronic thermal conductivity with pressure.
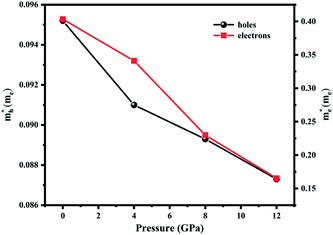 |
| | Fig. 5 Effective mass of the carries as a function of pressure. | |
E. Directional anisotropy in transport properties
The chemical potential (μ) dependent transport properties of ZnGa2Te4 at 300 K along different directions are shown in Fig. 6(a–f). The positive and negative chemical potentials correspond to p-type and n-type doping respectively. The directional dependency of the transport properties clearly depicts that the studied chalcopyrite system is anisotropic and sensitive to pressure. The maximum Seebeck coefficient (S) for both n-type and p-type doping are −1543 μV K−1 and 1547 μV K−1 respectively at 0 GPa along x and y axis, which decreases considerably upon pressure as inferred earlier from the effective mass discussion, whereas along z axis it is of −1535 μV K−1 (n-type) and 1545 μV K−1 (p-type). The modification of electronic transport with different doping concentrations can be analyzed by studying the variation of σ with μ. The directional dependency of the electronic conductivity with relaxation time (σ/τ) follows the same trend as that of the Seebeck coefficient, whereas their magnitude increases with pressure. For n-type doping, the highest σ/τ is found along x and y directions (4.437 × 1020 Ω−1 m−1 s−1 at 12 GPa). This may be due to the larger carrier mobility along the specified directions. On contrary, for p-type doping, highest σ/τ is along z direction (2.932 × 1020 Ω−1 m−1 s−1 at 12 GPa). This anisotropy can also be attributed to the effective mass of the carriers along those directions as expected from the earlier discussions in elastic and lattice dynamical properties. Hence, the optimum TE performance of ZnGa2Te4 can be attained by growing the crystal along specific orientations.
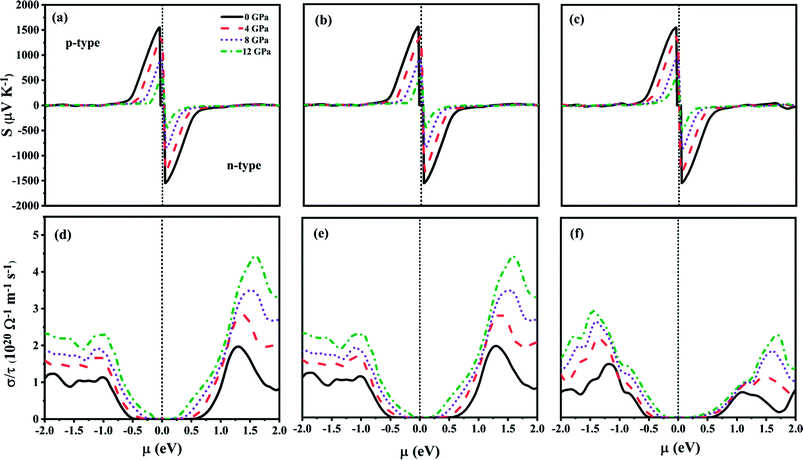 |
| | Fig. 6 Transport properties as a function of chemical potential for various pressure at 300 K along (a and d) x-direction, (b and e) y-direction and (c and f) z-direction. | |
F. Seebeck coefficient and electrical conductivity
The dependency of S and σ of ZnGa2Te4 on temperature along with pressure at a fixed chemical potential is shown in Fig. 7(a and b). The chemical potential is fixed using the following relation:48| |
 | (14) |
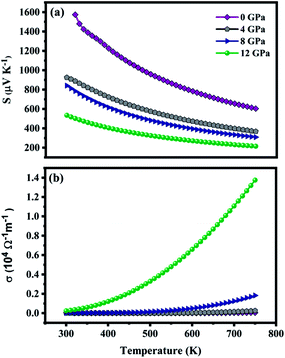 |
| | Fig. 7 (a) Seebeck coefficient and (b) electrical conductivity as a function of temperature at various pressures. | |
According to the relation, the chemical potential lies at the middle of the band gap at T = 0 K. In addition, the relaxation time is taken as 10−14 s. The temperature range has been fixed from 300 K to 750 K as the melting point of the titled material is around 740 K.49 The positive value of S depicts that ZnGa2Te4 is a p-type semiconductor with holes as their majority carriers which can be attributed to its crystal structure. i.e., in general, the defect chalcopyrite structure becomes stable by creating an ordered vacancy at the cation site. It leads to the formation of hole in the valence band contributing for p-type conduction. Subsequently, the decrease of S with temperature is obvious from the relation given by Goldsmid and Sharp,50 Smax = Eg/2eTmax, and Mott's formula. The maximum S observed at 0 GPa is 1573 μV K−1 (300 K). The reduction of S is about 66% for an applied pressure of 12 GPa at 300 K. This decrease can be due to the smaller potential difference across the hot and cold side created by the reduced band gap and is also inferred from the flattening of DOS near Fermi energy upon pressure. The response of σ to temperature is shown in Fig. 7(b). It is evident that σ increases with temperature due to the excited carriers near the VBM and CBM and shows opposite trend compared with S. At lower temperatures, σ is contributed only by the carriers near CBM and VBM, whereas at higher temperatures the carriers at second CBM and VBM will also take part in the conduction. In addition, the increased carrier mobility also significantly contributes to σ. With the application of hydrostatic pressure, σ increases considerably due to the increased carrier transport attributed to the reduced band gap. At 750 K, the magnitude of σ is 0.004 × 104 Ω−1 m−1, which on applying pressure of 12 GPa increased to 1.374 × 104 Ω−1 m−1. Thus, the significant increase of electrical conductivity and moderate suppression of Seebeck co-efficient upon pressure is expected to yield large power factor.
G. Thermal conductivity
The total thermal conductivity (k) is derived from electronic (contribution of electrons) and lattice (contribution of phonon) thermal conductivity. Firstly, the electronic thermal conductivity (ke) from the BoltzTraP2 is under closed circuit condition. Physical meaning of the ke is “the heat current per unit temperature gradient” which is for open circuit conditions.51 Hence, ke obtained from BoltzTraP2 cannot be used directly without any correction. In this regard, the electronic thermal conductivity was calculated using Wiedemann–Franz law, i.e., ke = LσT, where L-Lorentz number (2.4 × 10−8 W Ω K−2) as it is for open circuit conditions. Fig. 8(a) shows the increment of ke with respect to temperature which is due to the thermally agitated carriers at higher temperatures contributing to large thermal transportation at 0 GPa. Pressure induced modification in the band structure plays a significant role in the electronic thermal conductivity. The decrement of band gap and effective mass of the carriers upon pressure led to increment of carriers flow at 12 GPa. However, the attained maximum ke is less than 0.25 W m−1 K−1 even at high temperature and pressure.
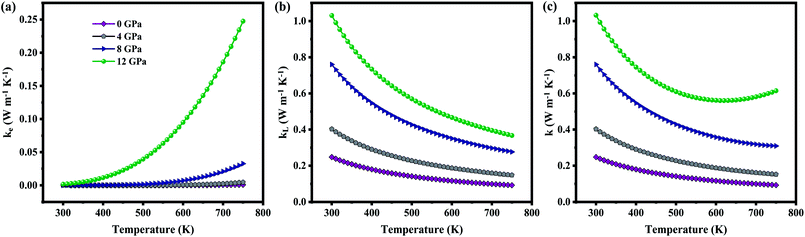 |
| | Fig. 8 (a) Electronic, (b) lattice, (c) total thermal conductivity as a function of temperature at various pressure. | |
On the other hand, lattice thermal conductivity was calculated by implementing modified Debye–Callaway model. Fig. 8(b) shows that kL decreases with temperature which may be due to the scattering of phonons at higher temperatures. The maximum observed kL at 300 K for 0 GPa is 0.24 W m−1 K−1. In general, the acoustic–optical (A–O) and optical–optical (O–O) band gap contributes to higher kL. As discussed in Section III(C), phonon band structures of the present system have strong coupling between acoustic and optical branches around 1.45 THz resulted in ultralow lattice thermal conductivity of ZnGa2Te4 at 0 GPa although there is a O–O gap between 3.98 THz and 4.59 THz. The lattice thermal conductivity is observed to increase consistently with pressure (1.03 W m−1 K−1 at 12 GPa) for two possible reasons: one is due to a slight decoupling between acoustic and optical branches coexisting with two strong O–O band gaps upon the applied hydrostatic pressure. The another one is the increment of overall frequency to 8 THz at 12 GPa. In addition, the dependency of kL upon pressure and temperature is also evident by the following equation from linear model:
| |
 | (15) |
where,
α-thermal expansion coefficient,

-pressure derivative of bulk modulus (4.77), and
ϕ-constant (7 ± 1).
52
The total thermal conductivity (k) calculated from the sum of ke and kL shown in Fig. 8(c) is found to decrease upon temperature. When the titled material is subjected to pressure there is an increase in k. At 750 K, the observed k is 0.09 W m−1 K−1 (0 GPa) and 0.61 W m−1 K−1 (12 GPa), which is lower than Pb–GeTe (1.20 W m−1 K−1 at 673 K)53 and Na–PbTe (0.90 W m−1 K−1 at 773 K).54 It is noted that the contribution of lattice thermal conductivity to total thermal conductivity is almost twice higher than that of electronic thermal conductivity. Hence, the tuning of kL will be a promising approach to enhance the TE performance of the material.
H. Power factor and figure of merit
The transport properties calculated at fixed chemical potential were used to compute temperature dependance of thermoelectric properties such as power factor (PF) and figure of merit (zT) as shown in Fig. 9(a and b). The PF (S2σ) is found to increase with temperature due to the excited carriers. In ZnGa2Te4, the major contribution to the PF is from the electrical conductivity that is why it follows the same path of σ. Further, its pressure dependency is also consistent with σ. At 750 K, power factor attained is 0.017 mW m−1 K−2, which on applied pressure of 12 GPa gets increased by 97%. The strong correlation between S and σ acts as a challenge in attaining high power factor. The moderate mobility, effective mass and band gap promotes PF of the material. Furthermore, techniques such as band engineering and electron filtering can be implemented to tune the thermoelectric power factor.
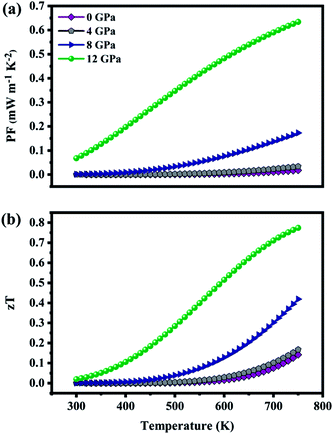 |
| | Fig. 9 (a) Thermoelectric power factor (b) figure of merit as a function of temperature at various pressure. | |
Fig. 9(b) picturizes the variation of zT (including both ke and kL) with temperature. It is obvious that zT increases with temperature and hydrostatic pressure. The maximum zT of 0.14 (n = 0.009 × 1019 holes per cm3) is obtained at 750 K, however with a 12 GPa applied pressure zT of 0.15 is achieved even at 430 K, and is 0.77 (increased by 82%) at 750 K. This optimal zT is attributed to high electrical conductivity and power factor as well as low thermal conductivity. These results imply that ZnGa2Te4 can be competitive with p-type candidate PbTe (zTmax = 0.8 at 600 K, ∼12 GPa).55 These findings also recommend the application of high pressure as a tool to tune their operating temperatures.
IV. Conclusions
In summary, structural, mechanical, thermodynamical stability, and electronic properties of ZnGa2Te4 were theoretically investigated using the first principles. In ZnGa2Te4, the structural transition from I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) to I
to I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2m occurred at 12.09 GPa. The elastic properties showed that the material is ductile and mechanically stable even up to 12 GPa. Furthermore, its thermodynamical stability till 12 GPa is inferred from the real frequencies of the phonon dispersion spectra. The computed electronic band structure indicated that ZnGa2Te4 with a defect chalcopyrite structure is a direct band gap semiconductor with band gap of 1.01 eV at 0 GPa. Upon pressure, band gap as well as effective mass of the carriers were decreased, which were the preliminary signs of increased electrical conductivity. Besides, the electronic transport properties strongly supported the anisotropic nature of the titled material. The investigations on the dependency of Seebeck coefficient and electrical conductivity on temperature at fixed chemical potential suggested the p-type charge transport in ZnGa2Te4. The larger Seebeck coefficient of 1573 μV K−1 at 300 K was attributed to the larger band gap. A significant decrease of S with temperature and corresponding pressure is observed due to the reduction of band gap, whereas the electrical conductivity increases notably. In addition, a strong coupling between the acoustic and optical modes led to ultralow lattice thermal conductivity. Although, the application of hydrostatic pressure resulted in the increment of kL, it is still considerable. Moreover, it is observed that the total thermal conductivity of ZnGa2Te4 is low when compared with the benchmark materials, which is mainly contributed by its lattice part. To a greater extent, the calculated thermoelectric power factor (0.63 mW m−1 K−2) and figure of merit (0.77) at 12 GPa (750 K) with n = 0.371 × 1019 holes per cm3 were remarkably high.
2m occurred at 12.09 GPa. The elastic properties showed that the material is ductile and mechanically stable even up to 12 GPa. Furthermore, its thermodynamical stability till 12 GPa is inferred from the real frequencies of the phonon dispersion spectra. The computed electronic band structure indicated that ZnGa2Te4 with a defect chalcopyrite structure is a direct band gap semiconductor with band gap of 1.01 eV at 0 GPa. Upon pressure, band gap as well as effective mass of the carriers were decreased, which were the preliminary signs of increased electrical conductivity. Besides, the electronic transport properties strongly supported the anisotropic nature of the titled material. The investigations on the dependency of Seebeck coefficient and electrical conductivity on temperature at fixed chemical potential suggested the p-type charge transport in ZnGa2Te4. The larger Seebeck coefficient of 1573 μV K−1 at 300 K was attributed to the larger band gap. A significant decrease of S with temperature and corresponding pressure is observed due to the reduction of band gap, whereas the electrical conductivity increases notably. In addition, a strong coupling between the acoustic and optical modes led to ultralow lattice thermal conductivity. Although, the application of hydrostatic pressure resulted in the increment of kL, it is still considerable. Moreover, it is observed that the total thermal conductivity of ZnGa2Te4 is low when compared with the benchmark materials, which is mainly contributed by its lattice part. To a greater extent, the calculated thermoelectric power factor (0.63 mW m−1 K−2) and figure of merit (0.77) at 12 GPa (750 K) with n = 0.371 × 1019 holes per cm3 were remarkably high.
In light of these systematic evaluations, the authors envisage that subjecting the material to pressure is an effective route to tailor its thermoelectric performance. Ultimately, the findings insights a theoretical approach for discovering novel TE materials. Present work not only suggests pressure as a viable strategy to regulate the operating temperature but also supports the fact of reducing the lattice thermal conductivity to tune zT. This work also calls for further experimental explorations on this defect chalcopyrite.
Author contributions
Prakash Govindaraj: software, formal analysis, investigation, writing-original draft. Mugundhan Sivasamy: visualization. Kowsalya Murugan: data curation. Kathirvel Venugopal: conceptualization, methodology, supervision, resources. Pandiyarasan Veluswamy: validation, writing-editing.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
Authors thank High Performance Computing Center, SRM Institute of Science and Technology for providing the computational facility.
References
- J. Bedi and D. Toshniwal, Renewable Sustainable Energy Rev., 2021, 136, 110413 CrossRef.
- G. J. Snyder and E. S. Toberer, Materials for Sustainable Energy: A Collection of Peer-reviewed Research Review Articles from Nature Publishing Group, 2011, pp. 101–110 Search PubMed.
- D. Kim, Y. Park, D. Ju, G. Lee, W. Kwon and K. Cho, Chem. Mater., 2021, 33, 4853–4862 CrossRef CAS.
- C.-M. Lin, W.-C. Chen and C.-C. Chen, Phys. Chem. Chem. Phys., 2021, 23, 18189–18196 RSC.
- F. Garmroudi, A. Riss, M. Parzer, N. Reumann, H. Müller, E. Bauer, S. Khmelevskyi, R. Podloucky, T. Mori and K. Tobita, Phys. Rev. B, 2021, 103, 085202 CrossRef CAS.
- C. Chen, Z. Zhang and J. Chen, Front. Energy Res., 2018, 6, 34 CrossRef.
- V. Akshay, M. Suneesh and M. Vasundhara, Inorg. Chem., 2017, 56, 6264–6274 CrossRef CAS PubMed.
- Y. Liu, M. Calcabrini, Y. Yu, S. Lee, C. Chang, J. David, T. Ghosh, M. C. Spadaro, C. Xie and O. Cojocaru-Mirédin, ACS Nano, 2021, 16(1), 78–88 CrossRef PubMed.
- E. Nshimyimana, S. Hao, X. Su, C. Zhang, W. Liu, Y. Yan, C. Uher, C. Wolverton, M. G. Kanatzidis and X. Tang, J. Mater. Chem. A, 2020, 8, 1193–1204 RSC.
- G. Xie, Z. Li, T. Luo, H. Bai, J. Sun, Y. Xiao, L.-D. Zhao, J. Wu, G. Tan and X. Tang, Nano Energy, 2020, 69, 104395 CrossRef CAS.
- N. Wang, M. Li, H. Xiao, Z. Gao, Z. Liu, X. Zu, S. Li and L. Qiao, npj Comput. Mater., 2021, 7, 1–13 CrossRef.
- J.-H. Pöhls, S. Chanakian, J. Park, A. M. Ganose, A. Dunn, N. Friesen, A. Bhattacharya, B. Hogan, S. Bux and A. Jain, Mater. Horiz., 2021, 8, 209–215 RSC.
- N. V. Morozova, I. V. Korobeinikov and S. V. Ovsyannikov, J. Appl. Phys., 2019, 125, 220901 CrossRef.
- K. Yuan, Z. Sun, X. Zhang and D. Tang, Sci. Rep., 2019, 9, 1–12 Search PubMed.
- T. Nishimura, H. Sakai, H. Mori, K. Akiba, H. Usui, M. Ochi, K. Kuroki, A. Miyake, M. Tokunaga and Y. Uwatoko, Phys. Rev. Lett., 2019, 122, 226601 CrossRef CAS PubMed.
- N. M. Alsaleh, E. Shoko and U. Schwingenschlögl, Phys. Chem. Chem. Phys., 2019, 21, 662–673 RSC.
- L.-C. Chen, P.-Q. Chen, W.-J. Li, Q. Zhang, V. V. Struzhkin, A. F. Goncharov, Z. Ren and X.-J. Chen, Nat. Mater., 2019, 18, 1321–1326 CrossRef CAS PubMed.
- H. Yu, L.-C. Chen, H.-J. Pang, X.-Y. Qin, P.-F. Qiu, X. Shi, L.-D. Chen and X.-J. Chen, Mater. Today Phys., 2018, 5, 1–6 CrossRef.
- Y. Zhang, S. Hao, L.-D. Zhao, C. Wolverton and Z. Zeng, J. Mater. Chem. A, 2016, 4, 12073–12079 RSC.
- V. V. Shchennikov, S. V. Ovsyannikov and A. V. Bazhenov, J. Phys. Chem. Solids, 2008, 69, 2315–2324 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B, 1996, 54, 11169 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B, 1993, 47, 558 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- R. Golesorkhtabar, P. Pavone, J. Spitaler, P. Puschnig and C. Draxl, Comput. Phys. Commun., 2013, 184, 1861–1873 CrossRef CAS.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- L. D. Whalley, J. Open Source Softw., 2018, 3, 797 CrossRef.
- G. K. Madsen, J. Carrete and M. J. Verstraete, Comput. Phys. Commun., 2018, 231, 140–145 CrossRef CAS.
- M.-S. Lee and S. D. Mahanti, Phys. Rev. B, 2012, 85, 165149 CrossRef.
- J. Callaway, Phys. Rev. B, 1959, 113, 1046 CrossRef CAS.
- T. Fan and A. R. Oganov, Comput. Phys. Commun., 2021, 266, 108027 CrossRef CAS.
- X. Jiang and W. R. Lambrecht, Phys. Rev. B, 2004, 69, 035201 CrossRef.
- H. Hahn, G. Frank, W. Klingler, A. D. Störger and G. Störger, Z. Anorg. Allg. Chem., 1955, 279, 241–270 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2008, 41, 653–658 CrossRef CAS.
- D. Errandonea, R. Kumar, O. Gomis, F. J. Manjón, V. Ursaki and I. Tiginyanu, J. Appl. Phys., 2013, 114, 233507 CrossRef.
- S. Rahman, H. Saqib, J. Zhang, D. Errandonea, C. Menéndez, C. Cazorla, S. Samanta, X. Li, J. Lu and L. Wang, Phys. Rev. B, 2018, 97, 174102 CrossRef CAS.
- Z. Feng, T. Jia, J. Zhang, Y. Wang and Y. Zhang, Phys. Rev. B, 2017, 96, 235205 CrossRef.
- Rashmi and U. Dhawan, Powder Diffr., 2002, 17, 41–43 CrossRef CAS.
- S. S. Fouad, G. Sakr, I. Yahia and D. A. Basset, Mater. Res. Bull., 2011, 46, 2141–2146 CrossRef CAS.
- Y. Ayeb, A. Benghia, M. B. Kanoun, R. Arar, B. Lagoun and S. Goumri-Said, Solid State Sci., 2019, 87, 39–48 CrossRef CAS.
- S. Chandra, A. Sinha and V. Kumar, Int. J. Mod. Phys. B, 2019, 33, 1950340 CrossRef CAS.
- J. Sahariya, A. Soni and P. Kumar, AIP Conf. Proc., 2018, 1942, 140079 CrossRef.
- F. Mouhat and F.-X. Coudert, Phys. Rev. B, 2014, 90, 224104 CrossRef.
- F. Cleri, J. Wang and S. Yip, J. Appl. Phys., 1995, 77, 1449–1458 CrossRef CAS.
- R. Hill, Proc. Phys. Soc. A, 1952, 65, 349 CrossRef.
- E. Kroumova, M. Aroyo, J. Perez-Mato, A. Kirov, C. Capillas, S. Ivantchev and H. Wondratschek, Phase Transitions, 2003, 76, 155–170 CrossRef CAS.
- Y. Li, G. Tang, B. Fu, M. Zhang and X. Zhao, ACS Appl. Energy Mater., 2020, 3, 9234–9245 CrossRef CAS.
- K. Charles and P. McEuen, Kittel's Introduction to Solid State Physics, John Wiley & Sons, 2018 Search PubMed.
- S. Fouad, G. Sakr, I. Yahia, D. Abdel-Basset and F. Yakuphanoglu, Mater. Res. Bull., 2014, 49, 369–383 CrossRef CAS.
- H. Goldsmid and J. Sharp, J. Electron. Mater., 1999, 28, 869–872 CrossRef CAS.
- N. Wang, M. Li, H. Xiao, X. Zu and L. Qiao, Phys. Rev. Appl., 2020, 13, 024038 CrossRef CAS.
- M. Manga and R. Jeanloz, J. Geophys. Res.: Solid Earth, 1997, 102, 2999–3008 CrossRef.
- Y. Gelbstein, J. Davidow, S. N. Girard, D. Y. Chung and M. Kanatzidis, Adv. Energy Mater., 2013, 3, 815–820 CrossRef CAS.
- H. Wang, J. Hwang, M. L. Snedaker, I.-h. Kim, C. Kang, J. Kim, G. D. Stucky, J. Bowers and W. Kim, Chem. Mater., 2015, 27, 944–949 CrossRef CAS.
- L. Xu, Y. Zheng and J.-C. Zheng, Phys. Rev. B, 2010, 82, 195102 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a and
Pandiyarasan Veluswamy
*a and
Pandiyarasan Veluswamy *b
*b
![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) to I
to I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2m occurs at 12.09 GPa. From the basic observations, ZnGa2Te4 is found to be mechanically as well as thermodynamically stable and ductile up to 12 GPa. The direct band gap of 1.01 eV is inferred from the electronic band structure. The quantitative analysis of electron transport properties shows that ZnGa2Te4 has moderate Seebeck coefficient and electrical conductivity under high pressure, which resulted in a large power factor of 0.63 mW m−1 K−2 (750 K). The ultralow lattice thermal conductivity (∼1 W m−1 K−1 at 12 GPa) is attributed to the overlapping of acoustic and optical phonon branches. As a result, the optimal figure of merit of 0.77 (750 K) is achieved by applying a pressure of 12 GPa. These findings support that ZnGa2Te4 can be a potential p-type thermoelectric material under high pressure and thus open the door for its experimental exploration.
2m occurs at 12.09 GPa. From the basic observations, ZnGa2Te4 is found to be mechanically as well as thermodynamically stable and ductile up to 12 GPa. The direct band gap of 1.01 eV is inferred from the electronic band structure. The quantitative analysis of electron transport properties shows that ZnGa2Te4 has moderate Seebeck coefficient and electrical conductivity under high pressure, which resulted in a large power factor of 0.63 mW m−1 K−2 (750 K). The ultralow lattice thermal conductivity (∼1 W m−1 K−1 at 12 GPa) is attributed to the overlapping of acoustic and optical phonon branches. As a result, the optimal figure of merit of 0.77 (750 K) is achieved by applying a pressure of 12 GPa. These findings support that ZnGa2Te4 can be a potential p-type thermoelectric material under high pressure and thus open the door for its experimental exploration.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 k-points were adopted to attain reliable results.29 The carrier concentration (n) is given by eqn (4).
000 k-points were adopted to attain reliable results.29 The carrier concentration (n) is given by eqn (4).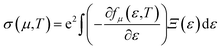
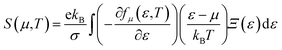
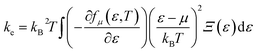
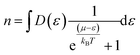
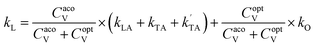
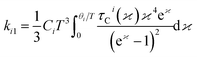
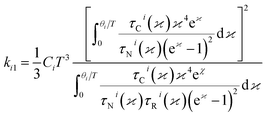
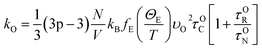
![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2m, Z = 2 (no.: 121) and I
2m, Z = 2 (no.: 121) and I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) , Z = 2 (no.: 82), its crystal structure is generated using VESTA software34 and is shown in Fig. 1(a and b). The Wyckoff positions for both the structures and a strong discrepancy in its ground state structure were discussed in the previous report.35 In order to understand the case, Birch–Murnaghan equation of states (BM-EOS)36 fit have been done and displayed in Fig. 1(c). The minimum energy of the I
, Z = 2 (no.: 82), its crystal structure is generated using VESTA software34 and is shown in Fig. 1(a and b). The Wyckoff positions for both the structures and a strong discrepancy in its ground state structure were discussed in the previous report.35 In order to understand the case, Birch–Murnaghan equation of states (BM-EOS)36 fit have been done and displayed in Fig. 1(c). The minimum energy of the I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) structure is ∼4 eV lesser than I
structure is ∼4 eV lesser than I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2m in BM-EOS fit, which suggests I
2m in BM-EOS fit, which suggests I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) defect chalcopyrite structure as the ground state. The variation of enthalpy as a function of pressure, shown in Fig. 1(d) reveals that the phase transition from I
defect chalcopyrite structure as the ground state. The variation of enthalpy as a function of pressure, shown in Fig. 1(d) reveals that the phase transition from I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) to I
to I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2m takes place at ∼12 GPa which is consistent with earlier report.35 In other words, I
2m takes place at ∼12 GPa which is consistent with earlier report.35 In other words, I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) structured ZnGa2Te4 is stable up to 12 GPa. With these inferences, the present study has been carried out on ZnGa2Te4 (I
structured ZnGa2Te4 is stable up to 12 GPa. With these inferences, the present study has been carried out on ZnGa2Te4 (I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) ) upto 12 GPa pressure. Whereas, the other I
) upto 12 GPa pressure. Whereas, the other I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2m phase is neglected because of its metallic nature.
2m phase is neglected because of its metallic nature.

![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) , (b) I
, (b) I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2m phases. The green, blue and yellow balls represent Zn, Ga and Te atoms respectively. (c) BM-EOS fit, (d) enthalpy as a function of pressure.
2m phases. The green, blue and yellow balls represent Zn, Ga and Te atoms respectively. (c) BM-EOS fit, (d) enthalpy as a function of pressure.![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) planes capturing the bond between Zn–Te and Ga–Te are displayed in Fig. 2(a–c). The strong localization of electrons between Ga and Te shows that the bond is covalent in nature, whereas the weak bonding between Zn–Te can be ionic. It is observed that more electrons are localized near the Te atoms, which is due to the larger electronegativity of Te than Ga.
) planes capturing the bond between Zn–Te and Ga–Te are displayed in Fig. 2(a–c). The strong localization of electrons between Ga and Te shows that the bond is covalent in nature, whereas the weak bonding between Zn–Te can be ionic. It is observed that more electrons are localized near the Te atoms, which is due to the larger electronegativity of Te than Ga.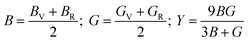
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0
0![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) space group ZnGa2Te4, possess 42 modes of vibrations. According to symmetry analysis, it constitutes of 3 acoustic (B + 1E + 2E) and 39 optical (39A) branches, which is also evident from the phonon spectra.46 The transverse acoustic (TA, TA′), longitudinal acoustic (LA), and optical branches in the spectra were differentiated by red, blue, green, and black color in Fig. 3. The real (positive) frequency over the entire Brillouin zone at 0 K depicts that ZnGa2Te4 is thermodynamically stable even upto 12 GPa. The frequency range of the overall phonon branches falls within 8 THz. The frequency of the longitudinal optical phonon branch is 1.3 THz (at 0 GPa) and these low-lying modes were further decreased with pressure which may lead to soft lattice as well as low group velocity and thus low lattice thermal conductivity.
space group ZnGa2Te4, possess 42 modes of vibrations. According to symmetry analysis, it constitutes of 3 acoustic (B + 1E + 2E) and 39 optical (39A) branches, which is also evident from the phonon spectra.46 The transverse acoustic (TA, TA′), longitudinal acoustic (LA), and optical branches in the spectra were differentiated by red, blue, green, and black color in Fig. 3. The real (positive) frequency over the entire Brillouin zone at 0 K depicts that ZnGa2Te4 is thermodynamically stable even upto 12 GPa. The frequency range of the overall phonon branches falls within 8 THz. The frequency of the longitudinal optical phonon branch is 1.3 THz (at 0 GPa) and these low-lying modes were further decreased with pressure which may lead to soft lattice as well as low group velocity and thus low lattice thermal conductivity.


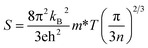

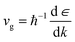
 is calculated from band structure at the band edges. The effective mass for holes
is calculated from band structure at the band edges. The effective mass for holes 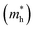 and electrons
and electrons  are 0.09me and 0.4me at 0 GPa which decreases upon pressure as shown in Fig. 5. This decrease in effective mass may end up in decreasing Seebeck coefficient, increasing carrier mobility contributing to high electrical conductivity, increasing group velocity and thus increasing electronic thermal conductivity with pressure.
are 0.09me and 0.4me at 0 GPa which decreases upon pressure as shown in Fig. 5. This decrease in effective mass may end up in decreasing Seebeck coefficient, increasing carrier mobility contributing to high electrical conductivity, increasing group velocity and thus increasing electronic thermal conductivity with pressure.




 -pressure derivative of bulk modulus (4.77), and ϕ-constant (7 ± 1).52
-pressure derivative of bulk modulus (4.77), and ϕ-constant (7 ± 1).52

![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) to I
to I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2m occurred at 12.09 GPa. The elastic properties showed that the material is ductile and mechanically stable even up to 12 GPa. Furthermore, its thermodynamical stability till 12 GPa is inferred from the real frequencies of the phonon dispersion spectra. The computed electronic band structure indicated that ZnGa2Te4 with a defect chalcopyrite structure is a direct band gap semiconductor with band gap of 1.01 eV at 0 GPa. Upon pressure, band gap as well as effective mass of the carriers were decreased, which were the preliminary signs of increased electrical conductivity. Besides, the electronic transport properties strongly supported the anisotropic nature of the titled material. The investigations on the dependency of Seebeck coefficient and electrical conductivity on temperature at fixed chemical potential suggested the p-type charge transport in ZnGa2Te4. The larger Seebeck coefficient of 1573 μV K−1 at 300 K was attributed to the larger band gap. A significant decrease of S with temperature and corresponding pressure is observed due to the reduction of band gap, whereas the electrical conductivity increases notably. In addition, a strong coupling between the acoustic and optical modes led to ultralow lattice thermal conductivity. Although, the application of hydrostatic pressure resulted in the increment of kL, it is still considerable. Moreover, it is observed that the total thermal conductivity of ZnGa2Te4 is low when compared with the benchmark materials, which is mainly contributed by its lattice part. To a greater extent, the calculated thermoelectric power factor (0.63 mW m−1 K−2) and figure of merit (0.77) at 12 GPa (750 K) with n = 0.371 × 1019 holes per cm3 were remarkably high.
2m occurred at 12.09 GPa. The elastic properties showed that the material is ductile and mechanically stable even up to 12 GPa. Furthermore, its thermodynamical stability till 12 GPa is inferred from the real frequencies of the phonon dispersion spectra. The computed electronic band structure indicated that ZnGa2Te4 with a defect chalcopyrite structure is a direct band gap semiconductor with band gap of 1.01 eV at 0 GPa. Upon pressure, band gap as well as effective mass of the carriers were decreased, which were the preliminary signs of increased electrical conductivity. Besides, the electronic transport properties strongly supported the anisotropic nature of the titled material. The investigations on the dependency of Seebeck coefficient and electrical conductivity on temperature at fixed chemical potential suggested the p-type charge transport in ZnGa2Te4. The larger Seebeck coefficient of 1573 μV K−1 at 300 K was attributed to the larger band gap. A significant decrease of S with temperature and corresponding pressure is observed due to the reduction of band gap, whereas the electrical conductivity increases notably. In addition, a strong coupling between the acoustic and optical modes led to ultralow lattice thermal conductivity. Although, the application of hydrostatic pressure resulted in the increment of kL, it is still considerable. Moreover, it is observed that the total thermal conductivity of ZnGa2Te4 is low when compared with the benchmark materials, which is mainly contributed by its lattice part. To a greater extent, the calculated thermoelectric power factor (0.63 mW m−1 K−2) and figure of merit (0.77) at 12 GPa (750 K) with n = 0.371 × 1019 holes per cm3 were remarkably high.




