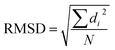Open Access Article
Open Access ArticleIdentifying molecular structural features by pattern recognition methods†
Qing Lu *
*
Beijing National Laboratory for Molecular Sciences, Institute of Chemistry, Chinese Academy of Sciences, Beijing, 100190, China. E-mail: qinglu@iccas.ac.cn
First published on 14th June 2022
Abstract
Identification of molecular structural features is a central part of computational chemistry. It would be beneficial if pattern recognition techniques could be incorporated to facilitate the identification. Currently, the quantification of the structural dissimilarity is mainly carried out by root-mean-square-deviation (RMSD) calculations such as in molecular dynamics simulations. However, the RMSD calculation underperforms for large molecules, showing the so-called “curse of dimensionality” problem. Also, it requires consistent ordering of atoms in two comparing structures, which needs nontrivial effort to fulfill. In this work, we propose to take advantage of the point cloud recognition using convex hulls as the basis to recognize molecular structural features. Two advantages of the method can be highlighted. First, the dimension of the input data structure is largely reduced from the number of atoms of molecules to the number of atoms of convex hulls. Therefore, the dimensionality curse problem is avoided, and the atom ordering process is saved. Second, the construction of convex hulls can be used to define new molecular descriptors, such as the contact area of molecular interactions. These new molecular descriptors have different properties from existing ones, therefore they are expected to exhibit different behaviors for certain machine learning studies. Several illustrative applications have been carried out, which provide promising results for structure–activity studies.
1 Introduction
Feature recognition of molecular structures is essential in many fields of chemistry, such as conformer exploration, molecule assembling, and molecular descriptor definition. In computational chemistry, the most common scenario is probably to differentiate molecular structures, such as comparing atomic coordinates between theoretical and experimental structures. Such a comparison is often the starting point for various sophisticated computational studies.1–7 Besides this fundamental application, there are studies combining existing benchmark sets to generate a more inclusive benchmark set.8 The construction of such a super set therefore needs the attention of recognizing unique molecules. Another important application is to construct molecular descriptors by mapping atomic coordinates into a more suitable representation.9The molecular descriptor is a central part of the quantitative structure–activity relationship (QSAR) analysis. Various molecular descriptors have been defined such as structural formula,10 different dimensional QSAR descriptors,11–13 and quantum chemical descriptors.14 It has been well documented that descriptors regarding the molecular shape are powerful predictors for medicine studies. A notable example relates to the polar surface area, which has been widely used for estimation of molecular transport properties.15
With the help of machine learning techniques, novel molecular descriptors have been defined to facilitate QSAR studies. Most unsupervised learning algorithms need to distinguish the structural similarities.9 To examine structural similarities, the root-mean-square-deviation (RMSD) calculation is the most commonly used method. It calculates the square sum of distances between corresponding atoms (di) in the two structures, and takes the division by the total number of atoms (N), followed by a square root operation.
However, there are several limitations regarding RMSD calculations. First, the RMSD calculation suffers the so-called “curse of dimensionality” problem that it becomes less capable to distinguish pairwise differences between conformations with increasing system size.16 A grave consequence of this problem is that all RMSD-based analysis would be accordingly impacted. In addition, the RMSD calculation needs consistent ordering of atoms between two comparing structures. Yet this alignment step is not easily accomplished, especially for large molecule.17 Moreover, the construction of atom pairwise correspondence gives rise to combinatorial searches, which is usually very time-consuming. In addition, the RMSD measurement also suffers other limitations such as being difficult for interpretation, and lack of normalization.18–20 Some improvements upon RMSD have been proposed to remedy these problems, such as introducing weighting functions into the calculation of RMSD,20 or taking advantage of the graph theory21 or symmetry.22 Other alternatives include configuration fingerprint vector,23 global and local descriptors,24 geometric hashing algorithm,25 blob detection,26 and different score functions.18,27–32
On another aspect, the iterative closest point (ICP) method was brought up in recent years and received significant attention in the area of pattern recognition.33 One of its many successful applications is mobile robotics. In such an application, the features of an object (such as a vehicle) are represented as a point cloud, and the object recognition is reduced to tracing and matching different point clouds.
Following this wisdom, the molecules could be represented as a point cloud as well. The atoms are naturally the first choice as the basis to constitute point clouds. However, this choice cannot avoid the dimensionality curse problem as mentioned above. In addition, the ICP iterations may converge to a local optimal point, which would lead to false positive recognition. Nonetheless, if ICP can be successfully applied to molecular systems, then the ordering of atoms in two comparing structures is no longer necessary. Accordingly, all RMSD-based analysis can be facilitated by using ICP.
In this work, we propose to take advantage of the ICP algorithm to recognize molecular structural features using convex hulls as the basis to constitute the point cloud instead of the whole molecule. The convex hull is the smallest polyhedron enclosing the molecule. Two features can be highlighted. First, the size of the input data structure is largely reduced, especially for large molecules. Therefore, the dimensionality curse problem is circumvented, and the ordering of atoms in two comparing molecules is saved. Second, the construction of convex hulls can be used to define new molecular descriptors. By creating the convex hulls, the molecular volume and surface area are defined. It is therefore potential to combine these new molecular descriptors with other machine learning techniques. A few preliminary applications are bought up to exhibit their potentials, which show promising results.
2 Methods
In this work, chemical bonds are removed from molecular structure images. Accordingly, the problem of recognizing molecules is equivalent to extracting the structural features of a point cloud. Such a treatment implies that all atoms in the molecule are viewed as massless points. An important feature of such treatment is that the ordering of atoms in two structures is no longer necessary. Although different molecules may give similar point clouds, (i.e., CH4 vs. SiH4), the difference in bond lengths would lead to different cloud distributions.As will be discussed later, the iterative closest point algorithm (ICP)33 will be used to match two point clouds. In practice, however, we found that the ICP method often leads the iteration process into a local minimum. Consequently, the matching of two point clouds will be falsely fulfilled. To avoid such local minimum trap, a pre-treatment of orientation is found critical. Specifically, the center-of-mass of the molecule is first translated to the coordinate origin. And then, the principal axes are aligned along XYZ axes. Such a pre-treatment is found capable of providing a good initial guess for the ICP process.
Before conducting ICP iterations, the molecular convex hull is first constructed. The convex hull is the smallest polyhedron that encloses a set of points, where intersections between any points in the polyhedron are still in the polyhedron. For a given molecule or a given point cloud, its convex hull is unique.34 Therefore, one can use the convex hull as the basis for point clouds instead of the whole molecule. As the size of the convex hull is usually much smaller than the whole molecule, the time for matching two structures can be significantly reduced. To construct the 3-dimensional convex hull for a molecule, the quick convex hull method is followed.35,36 The core idea of the method is based on the Beneath–Beyond theorem,37 where the convex hull is constructed by incrementally adding facets to an initial simplex. Let P be a set of n point in the 3-dimensional space, the convex hull 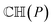 is constructed as follows:
is constructed as follows:
(1) Define the oriented plane ![[S with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0053_20d1.gif) consisted by point (pi, pj, pk), so that
consisted by point (pi, pj, pk), so that
![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) ![[S with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0053_20d1.gif) + d = 0 + d = 0
| (1) |
![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) is the norm to the plane and d is the distance of
is the norm to the plane and d is the distance of ![[S with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0053_20d1.gif) to the origin:
to the origin:
![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) = (pj − pi) × (pk − pi) = (pj − pi) × (pk − pi)
| (2) |
d = −![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) pi pi
| (3) |
(2) Define the signed distance of a point p to the plane ![[S with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0053_20d1.gif) :
:
dist(p)=(![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) ![[S with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0053_20d1.gif) + d)/‖ + d)/‖![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) ‖ ‖
| (4) |
The point p is above, below, or on the plane, if dist(p) > 0, dist(p) < 0 or dist(p) = 0.
(3) Construct an initial simplex with 4 points, p1, p2, p3 and p4. Preferably, theses points are the outmost points with either a maximum or minimum coordinate of either X, Y or Z coordinate.
(4) For each facet (F) of the tetrahedron, loop over each point p that does not consist of the initial simplex. If p is above the plane F, then assign p to the F's outside set. If the point is above multiple planes, then assign p to an arbitrary facet's outside set.
(5) For each facet F which has a non-empty outside set, find the furthest point to F within its outside set, and label the facet as “visible” to p if p is above the plane. Initialize a visible set V to store F. The two facets are defined as neighbors if they share a ridge.
(5.1) Loop over all unvisited neighbors N of facets in V, if p is above N, then add N to V.
(5.2) Construct a set L which stores all outside sets of facets in V.
(5.3) The ridge is defined as boundary if one of the facet is visible to p while the other facet is invisible. Construct the set R to store all boundary ridges. Loop over R, create a few facet from R to p, and update the neighbors for the new facet.
(5.4) For each new facet F′, loop over L. If an unassigned point q in L is above F′, then add it to the outside set of F′.
(5.5) Delete the facets in V.
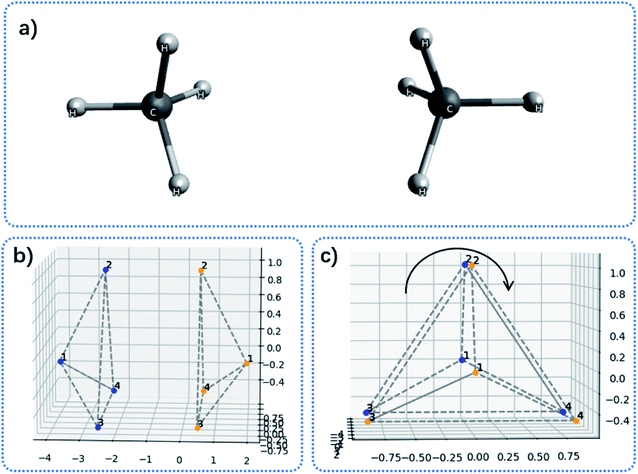
By the increment method, the convex hull can be constructed. Illustrations of convex hulls for some simple molecules can be found in Fig. 1.
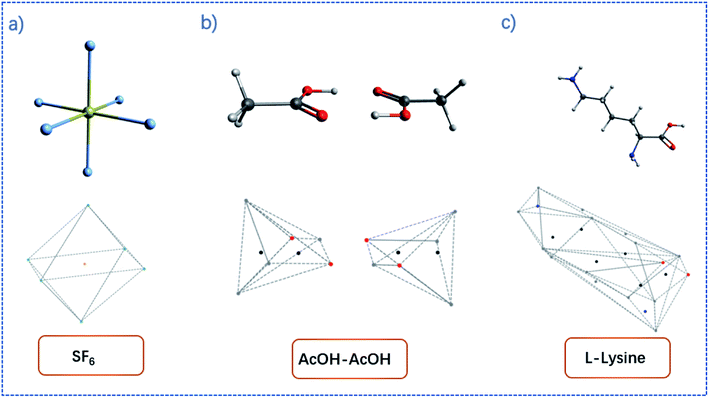 | ||
| Fig. 1 Examples of convex hulls (dashed lines) constructed for (a) SF6 molecule; (b) AcOH dimer system; (c) L-lysine. | ||
For the matching process, the iterative closest point (ICP) method is used.33 The core idea of the method is to minimize the RMSD between two point clouds iteratively by optimizing the rotation matrix. For two sets of points, M = [m1, m2,…mn] and N = [n1, n2,…nn], the ICP method optimizes the rotation matrix ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) and translation matrix T by minimizing the target function f, where
and translation matrix T by minimizing the target function f, where
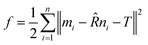 | (5) |
Defining the center of mass for the two sets as μm and μn, the target function f is transformed as:
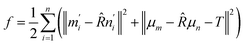 | (6) |
| m′i = ni − μm, n′i = ni − μn | (7) |
The optimization of the translation matrix (T*) is usually trivial. Thus, the difficulty is to obtain the optimized rotation matrix R*.
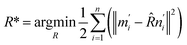 | (8) |
Expanding eqn (8) gives
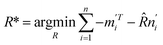 | (9) |
Let 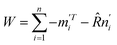 . The singular value decomposition (SVD) of W gives:
. The singular value decomposition (SVD) of W gives:
| W = UΣVT | (10) |
When W is of full rank, the optimized rotation matrix and translation matrix can be obtained as:
| R* = UVT | (11) |
T* = μm − ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) μn μn
| (12) |
In practice, the threshold for iteration convergence is set as 0.001. Since the molecules have been pre-treated for consistent orientation, the local minimum trap can be effectively circumvented.
As mentioned, the point cloud is represented by convex hulls instead of the whole molecule. For large molecules like proteins, the convex hulls usually just consist of dozens of atoms. Therefore, the size of the input data structure is largely reduced. Importantly, the dimensionality problem of RMSD in calculating large molecules can be avoided. When iteration convergence reaches, the corresponding rotation matrix for matching two convex hulls can be established. If desired, this rotation matrix can be operated upon the whole molecule.
To test the proposed method, an arbitrarily chosen protein (Protein Database code 1AKI) is compared to its randomly distorted counterpart. This distorted protein stands for the structure obtained by means other than crystallography, such as protein structure prediction. To generate the distorted protein, the atoms of the original protein is first shuffled, so that the ordering of atoms is completely different. Next, the shuffled protein is arbitrarily translated and rotated by a certain distance and angle. Lastly, each atom in the shuffled protein is added with a uniformly distributed random noise between ±0.5 Å along all XYZ axes. It should be cautious that the convex hulls may not have the same number of atoms after introducing noise. To solve that problem, the common convex hull is constructed by the K-nearest neighbor (KNN) algorithm. A weight of 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 is introduced during the KNN clustering. To exhibit the potentials of the convex hulls in revealing chemical insights, a few illustrative studies were carried out. The molecular density and molecular specific surface area are first defined as new molecular descriptors for different size of fullerenes. The molecular density was calculated as the molecular mole mass over the total volume of the convex hull. The molecular surface area was calculated as the total surface area of all facets of the convex hull. The specific molecular area was calculated as the molecular surface area over the molecular mole mass. Next, the methane dimer and the cubane dimer were calculated with different conformations. The conformations were generated by rotating one of the monomer around the symmetry axis. The contact surface (S) was calculated as:
1 is introduced during the KNN clustering. To exhibit the potentials of the convex hulls in revealing chemical insights, a few illustrative studies were carried out. The molecular density and molecular specific surface area are first defined as new molecular descriptors for different size of fullerenes. The molecular density was calculated as the molecular mole mass over the total volume of the convex hull. The molecular surface area was calculated as the total surface area of all facets of the convex hull. The specific molecular area was calculated as the molecular surface area over the molecular mole mass. Next, the methane dimer and the cubane dimer were calculated with different conformations. The conformations were generated by rotating one of the monomer around the symmetry axis. The contact surface (S) was calculated as:
S = ∑(S1 + S2) × cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/2 θ/2
| (13) |
3 Results and discussion
3.1 ICP matching based on the convex hulls
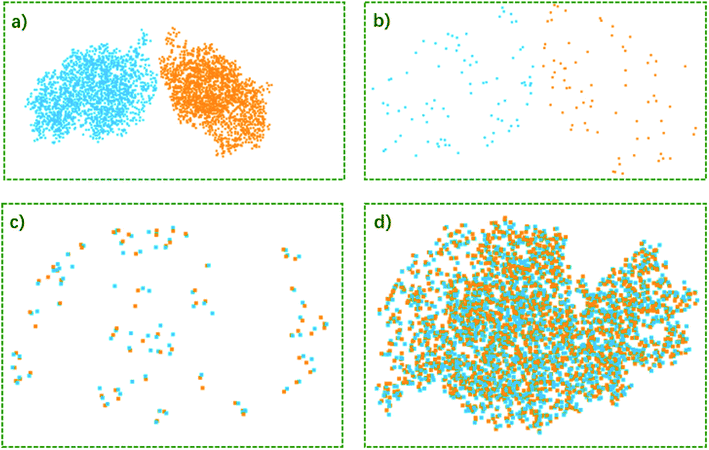
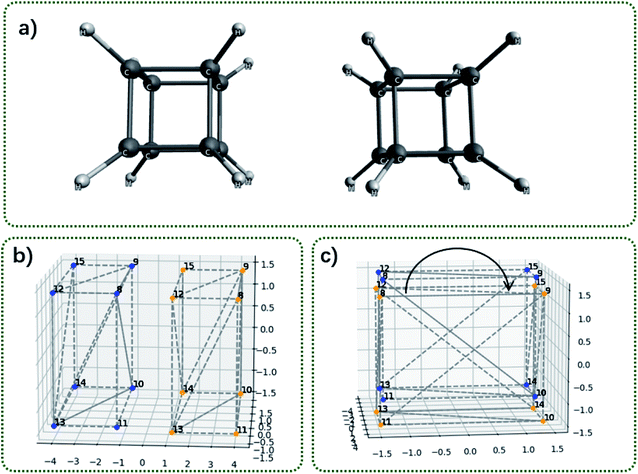
The convex hull is the smallest polyhedron that encloses the molecule. Fig. 1 shows some examples of molecules with their convex hulls. The grey dashed lines represent convex hulls, while the colored dots represent atoms for easier visualization. For high-symmetry molecules, such as SF6 (Oh point group) in Fig. 1a, its convex hull is an octahedron. The 6 fluorine atoms are located on the vertices of the octahedron, while the sulfur atom sits in the center. By definition, all atoms are enclosed in the octahedron. And the convex hull vertices are overlapped with the “periphery” atoms. Fig. 1b and c show two other examples with more complicated geometric features and their convex hulls. It can be seen that the number of points defining convex hulls is no larger than the number of atoms in the molecule. Furthermore, the larger the molecule is, the more savings can be obtained for the size of the input data structure. More examples of convex hulls of different conformers can be found in Fig. S1 in the ESI.†Fig. 2 shows the example of utilizing the proposed method to compare two structures: an arbitrary protein (Protein Database code, 1AKI, in orange) and the distorted, shuffled protein structure (in blue), as shown in Fig. 2a. Fig. 2b shows the atoms constituting convex hulls of the two structures. It is obvious that the number of points is largely reduced from the number of the protein to the number of the convex hull. Fig. 2c shows the superposition of two convex hulls after orientation and the ICP iterations. It can be seen that the method well distinguishes the convex hulls of protein and its distorted counterpart. In addition, the method is not influenced by the shuffle of atoms at all. Fig. 2d shows the corresponding superposition of the proteins instead of convex hulls. They are obtained by multiplying the rotation matrix with the original coordinates. The rotation matrix was obtained during matching the convex hulls. Therefore, the size of input data structure is reduced. The difference between two structures is quantified by calculating the RMSD of convex hulls. In Fig. 2c, the RMSD is 0.700 Å as the random noise was generated between ±0.5 Å. If the random number range is set as ±1.5 Å, the RMSD then changes to 1.498 Å (as shown in Fig. S2† in ESI). Overall, the ICP matching based on the basis of convex hulls can effectively distinguish molecular structural features. To obtain a statistical evaluation, a total of 1690 entries were obtained from the wwPDB database38–40 from the folder of “00” to the folder “99” and from the folder “a1” to the folder “a5”. The comparison is carried out between these database structures and the distorted structures. The distorted structures are generated by adding a random number to the X, Y, Z coordinates of each atom. Four sets of random numbers (Rand2, Rand5, Rand10, Rand20) are utilized, which are generated between ±0.02 Å, ±0.05 Å, ±0.1 Å, and ±0.2 Å, respectively. Table 1 shows the averaged RMSD between database structures and distorted structures using the whole molecule and using the convex hulls respectively at different levels of distortions.
| RMSD (whole molecule, Å) | Wall time (s) | RMSD (convex hull, Å) | Wall time (s) | |
|---|---|---|---|---|
| Rand2 | 0.025 | 234 | 0.024 | 337 |
| Rand5 | 0.055 | 235 | 0.055 | 352 |
| Rand10 | 0.105 | 236 | 0.105 | 349 |
| Rand20 | 0.205 | 231 | 0.204 | 343 |
The RMSD calculated using the proposed method well reproduces the results by the conventional method. The required wall time is longer because of the construction of convex hulls. In addition, the convex hulls for the database structures and the distorted structures are not necessarily of the same size, and the order of the vertices, which constitute the convex hull, are not necessarily the same. Thus the ordering of convex hull indices is also responsible for the longer wall time.
One limitation of the proposed method is that the core structures of molecules are not considered. For large molecules, this is less likely a problem since the core structure of complex molecules should not share the same structures. For simpler molecules, such as CH4, SiH4 and GeH4, one may concern the distinguishability of the proposed method. Fig. S3† shows the tetrahedral convex hulls for these molecules. Since the bond lengths are different, the tetrahedrons have different sizes. After orientation and ICP iterations, the vertices of the tetrahedron can be well distinguished, but the center atoms are overlapped. Another bothering situation is about cage molecules, for instance, the lanthanide elements in fullerenes, Ln@C60. For these systems, the convex hulls are identical, but the center atoms are different. In these cases, if one is interested in the core structures, one can peel off the atoms constituting the convex hull, and repeat the whole procedure with the remaining part of the molecule. One may argue that the inner structures should not be neglected. But that argument depends on the research goals. It is well known that the molecule shape is important in drug designs. Thus at the pre-screen step, one can focus on the molecular convex hulls instead of the whole molecules. It is interesting to mention that one can even make the convex hull evolve to describe the molecular structures, which would be helpful for the docking studies.41
Overall, the ICP algorithm using convex hulls as the basis is efficient in distinguishing geometry features and comparing molecular structures. As the ICP is used for matching two structures, the ordering of atoms for two molecules is no longer necessary. As the pre-orientation is applied before ICP iteration, the local minimum trap can be avoided. As the convex hulls are used as the basis, the size problem of calculating RMSD for large molecules is avoided. In addition, the time required for ICP iteration is reduced.
3.2 Molecular descriptors based on the convex hulls
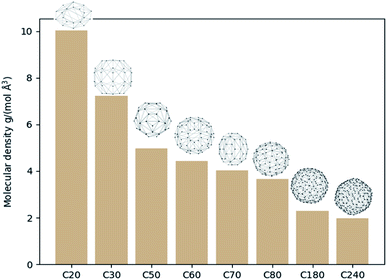
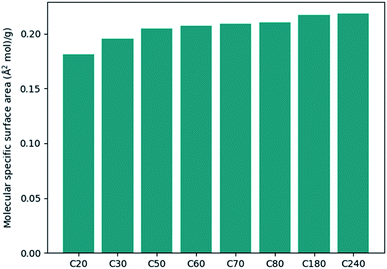
On another aspect, it is appealing to take further advantage of the convex hull, especially its property of being the smallest polyhedron enclosing the molecule. With this thought, the molecular density and the specific surface area can be defined as new molecular descriptors. For molecular density, it is calculated as the molecular mole mass over the volume of the convex hull. Although one can also calculate the density by dividing the mole mass over the volume of a cubic cell, this cubic cell volume cannot reflect the shape of the molecule (cf. the SF6 molecule). And the volume of the cubic cell would always be larger than that of the convex hull. Such a difference may lead to a difference in the data training, and the molecular density obtained based on convex hulls might be a better molecule descriptor. Fig. 3 shows the molecular density and corresponding convex hulls for different sizes of fullerenes. It is evident that the molecular density decreases as the sphere size increases.The calculation of surface area is another possible application regarding convex hulls. The specific surface area is an important parameter in studying adsorption processes. Fig. 4 shows the specific surface area for different types of fullerenes. It can be seen that the specific area variates less than the molecular density. If we approximate that the inner surface is equal to the outer surface of the polyhedron, the method can be further used to study the adsorption processes of zeolites or nanotubes.
Fig. 5 shows two methane molecules and their corresponding convex hulls. For each monomer, the total surface area for the tetrahedron is 5.48 Å2, thus the averaged surface area for each triangular facet is 1.37 Å2. The distance between two hydrogen atoms is measured as 1.78 Å. Applying some geometry algebra, it is easy to confirm that the area for each facet is 1.37 Å2 as well. The two molecules are oriented so that the overall symmetry is in the C3v point group. At this initial conformation, the contact hydrogens form two triangles in an eclipse manner (Fig. 5c). By rotating one monomer along the C3 symmetry axis, the effective contact surface is expected to decrease, which then influence the interaction energy.
The symmetry adapted perturbation theory (SAPT) analysis42 was carried out to monitor the energy changes during the rotation. The SAPT0 calculation43 with jun-cc-pvdz basis sets44 were carried out for each conformer with the C–C distance being 3.717 Å. Table 2 shows the exchange energy, dispersion energy and the contact surface area as a function of the rotation angle. It can be seen that the contact surface area well correlates with decomposed energies. As the conformation mutates from the eclipse conformation to the staggered conformation, the effective contact surface decreases. Meanwhile, the exchange energy is also lowered, which can be understood as the relax of the steric tension. In addition, the dispersion energy is also lowered, which reveals the fact that the distance between hydrogens increases.
| 0° | 15° | 30° | 45° | 60° | |
|---|---|---|---|---|---|
| Contact surface area (Å2) | 1.368 | 1.322 | 1.185 | 0.968 | 0.684 |
| Exchange (a.u.) | 0.582 | 0.578 | 0.567 | 0.555 | 0.551 |
| Dispersion (a.u.) | −0.559 | −0.556 | −0.549 | −0.542 | −0.539 |
Fig. 6 shows two cubane molecules and their corresponding convex hulls. The convex hull consists of the 8 vertical hydrogen atoms; thus, each face of the cube is a square and each face consists of two triangular facets. The distance between two vertical hydrogen atoms is 2.82 Å2. The area of the square is 7.96 Å2. It is worthy to repeat that for each face of the cube there are two triangular facets (Fig. 6b). The blue facets S8–9–10 and S8–10–11 interact with the orange facets S12–13–14 and S12–14–15 (the subscripts indicates the vertex labels). Thus, the contact surface should be larger than the area of the square and slightly smaller than the twice of the square area (S8–9–10 interacts with S12–13–14 and S12–14–15; S8–10–11 interacts with S12–13–14 and S12–14–15).
Table 3 shows the exchange energy, dispersion energy and the contact surface area as a function of the rotation angle around the C4 symmetry axis. The contact surface area correlates with decomposed energies as well. At the eclipse conformation, the contact surface area is calculated as 15.91 Å2, smaller than the twice of the square area.
| 0° | 15° | 30° | 45° | |
|---|---|---|---|---|
| Contact surface area (Å2) | 15.911 | 15.369 | 13.779 | 11.251 |
| Exchange (a.u.) | 2.996 | 2.688 | 2.101 | 1.846 |
| Dispersion (a.u.) | −4.356 | −4.319 | −4.197 | −4.134 |
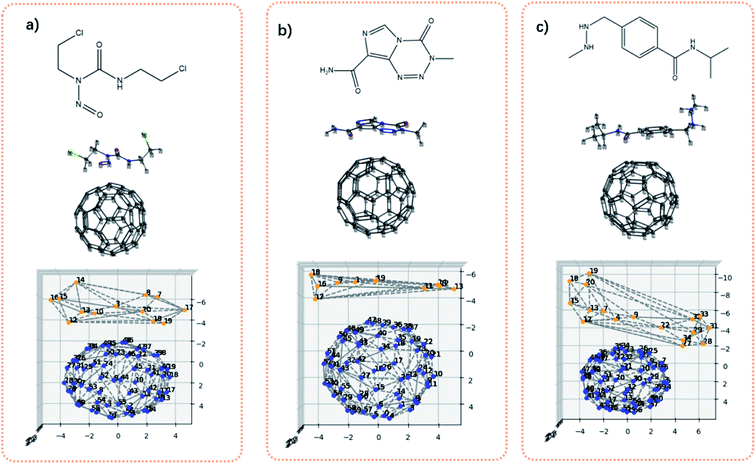
Fig. 7 shows the bis-chloroethylnitrosourea (BCNU)-C60 complex, temozolomide (TMZ)-C60 complex and the procarbazine (PCZ)-C60 complex. Theses C60-loaded drug molecules were theoretically studied as a brain anticancer drug.45 Visually, it can be seen that the interaction surface area between drug molecules and C60 increases from BCNU complex to TMZ complex to PCZ complex. Table 4 shows the computed adsorption energies and the contact surface area. The contact surface area indeed increases from BCNU to TMZ to PCZ. In addition, the interactions between the drug molecule and the C60 should be governed by non-covalent interactions. Therefore in principle, the interaction energy should be dependent on the distance between two interacting fragments, and the contacts between the two fragments. If we approximate that the distances for all systems are more or less similar, then the interaction energy is a function of the contact area. It can be seen from Table 4 that the contact surface area well correlates with the previous calculated adsorption energies, in the sense that as the contact surface area increases, the adsorption energy increases as well.
Lastly, it is worthy to make comparisons with existing similar descriptors. The polar surface area has been widely used in studies of drug transport properties.15 It sums up the molecular (usually van der Waals) surface area of polar atoms. An improvement upon this descriptor is the topological polar surface area (TPSA), which is based on tabulated surface contributions of polar atoms.46 These descriptors have shown tremendous success in medicine studies. Yet in a sharp contrast, the new descriptors defined in this work is irrelevant to polar or nonpolar atoms. Hence the new descriptors might be favored for a different QSAR study, where the nonpolar atoms are mainly studied. Another widely used method47 to calculate the contact surface is the supermolecule approach. As to this method, the area of each monomer is first calculated, and then the complex area is calculated. The contact surface is obtained by the subtraction:
| Scontact = Scomplex − (Smonomer1 + Smonomer2) |
Obviously, this method depends on the way of the docking of two monomers. Thus, the new descriptor based on convex hulls should exhibit different features from existing ones. This provide an alternative basis for machine learning studies, since the nature of descriptors largely influences the prediction power.
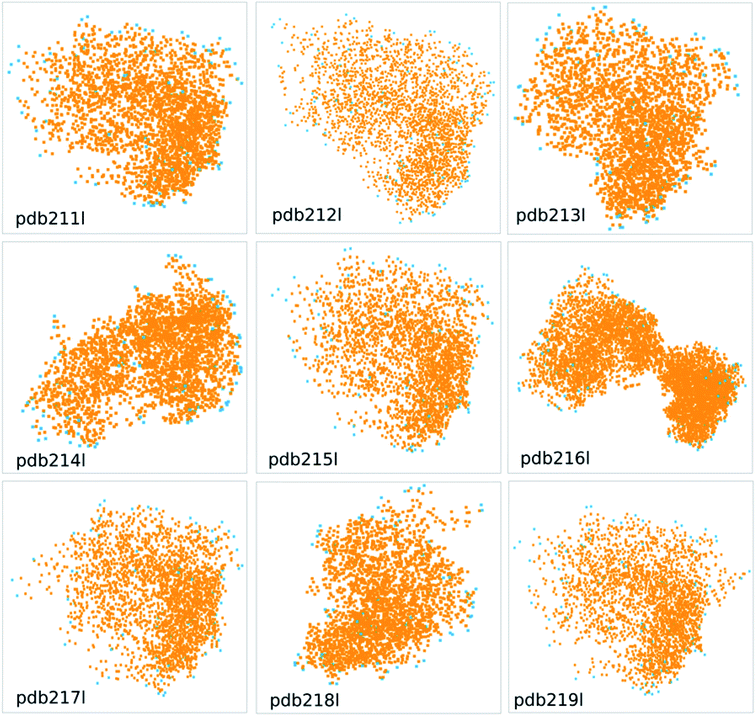
Table 5 shows the comparison of the area and volume of convex hulls with TPSA, solvent accessible surface area (SASA) and van der Waals molecule volume for protein pdb211l to pdb219l from the wwPDB database (Fig. 8). The comparison of a lager molecule set can be found in Fig. S4 and S5,† and there is a good correlation between these descriptors. In Fig. 8, the orange dots represent atoms in the protein, while the blue dots represent the atoms constituting the convex hull. The calculated area and volume of convex hulls are different from existing methods in terms of absolute values and the trend. This is as expected since their definitions are different. The different descriptors can be viewed as different basis which spans the feature space. Thus the advantage or disadvantage of the proposed method over existing ones depends on the specific situation.
| Convex hull area (Å2) | TPSA (Å2) | SASA (Å2) | Convex hull volume (Å3) | vdW volume (Å3) | |
|---|---|---|---|---|---|
| Pdb211l | 5094 | 7837 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 974 974 |
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 046 046 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 418 418 |
| Pdb212l | 5146 | 8025 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 364 364 |
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 511 511 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 766 766 |
| Pdb213l | 5029 | 7797 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 744 744 |
29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 564 564 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 256 256 |
| Pdb214l | 5437 | 7796 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 779 779 |
32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 565 565 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 266 266 |
| Pdb215l | 5067 | 7837 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 926 926 |
29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 828 828 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 390 390 |
| Pdb216l | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 836 836 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 647 647 |
31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 610 610 |
87![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 781 781 |
28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 665 665 |
| Pdb217l | 5192 | 7845 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 056 056 |
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 853 853 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 493 493 |
| Pdb218l | 5457 | 7793 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 708 708 |
32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 219 219 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 244 244 |
| Pdb219l | 5150 | 7909 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 063 063 |
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 449 449 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 504 504 |
4 Conclusions
In this work, pattern recognition techniques are developed for molecular structure recognition. The method provides a new approach to recognize molecular geometrical features, and thus can be used for structural identifications. The new method uses the point clouds to represent the molecule for structural comparisons. Therefore, the process of ordering atoms can be saved. In addition, the recognition of molecules is achieved by using convex hulls as the basis instead of the whole molecule for point clouds. As a result, the size problem met in calculating RMSD for large molecules can be avoided. While applying ICP iterations to match two point clouds, it is found that the ICP process is possible to converge to a local minimum, which leads to fault positive results. To remedy this, the pre-orientation is proposed before the ICP iteration to avoid the local minimum trap. Overall, the proposed method provide a new handy approach to distinguish molecular structure features.On another aspect, new molecular descriptors are defined based on the convex hulls, which provide insights in understanding chemical processes, such as the adsorption process. A unique property of convex hulls is that the convex hulls represent the smallest polyhedron enclosing the molecule. Therefore, the new descriptors defined based on convex hulls have different features from previous ones, and could be more suitable for certain applications. A set of new descriptors are defined, including the molecular density, molecular specific surface area, and the contact surface between two interacting species. A modest set of calculations are carried out to exhibit applications based on these descriptors. These descriptors have distinct definitions from other descriptors. As the machine learning algorithms rely on the definition of feature inputs, the different definitions of descriptors should in principle exhibit different performance, which may facilitate QSAR studies. The showcase studies using fullerenes exhibit promising results. Further study is under development in this lab.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The author gratefully acknowledges the support from the Beijing Municipal Natural Science Foundation (No. 2214065) and the National Natural Science Foundation of China (No. 22003068).References
- M. Zhang, H. Wu, J. Yang and G. Huang, ACS Catal., 2021, 11, 4833–4847 CrossRef CAS.
- Q. Lu, F. Neese and G. Bistoni, Phys. Chem. Chem. Phys., 2019, 21, 11569–11577 RSC.
- Q. Lu, F. Neese and G. Bistoni, Angew. Chem., Int. Ed., 2018, 57, 4760–4764 CrossRef CAS PubMed.
- J. Yang, I. Anishchenko, H. Park, Z. Peng, S. Ovchinnikov and D. Baker, Proc. Natl. Acad. Sci., 2020, 117, 1496–1503 CrossRef CAS PubMed.
- G. J. Kleywegt, J. Mol. Biol., 1999, 285, 1887–1897 CrossRef CAS PubMed.
- J. A. Barker and J. M. Thornton, Bioinformatics, 2003, 19, 1644–1649 CrossRef CAS PubMed.
- N. Sylvetsky, M. K. Kesharwani and J. M. L. Martin, AIP Conf. Proc., 2017, 1906, 030006 CrossRef.
- S. T. Schneebeli, A. D. Bochevarov and R. A. Friesner, J. Chem. Theory Comput., 2011, 7, 658–668 CrossRef CAS PubMed.
- F. Musil, A. Grisafi, A. P. Bartók, C. Ortner, G. Csányi and M. Ceriotti, Chem. Rev., 2021, 121, 9759–9815 CrossRef CAS PubMed.
- Z. Cheng, Q. Chen, S. Cervantes, Q. Tang, X. Gao, Y. Tan, S. Liu, Y. Ma and Z. Shen, J. Hazard. Mater., 2020, 394, 121811 CrossRef CAS PubMed.
- W. Gu, Q. Li and Y. Li, J. Hazard. Mater., 2020, 393, 122339 CrossRef CAS PubMed.
- J. P. Ataide Martins, M. A. Rougeth de Oliveira and M. S. Oliveira de Queiroz, J. Comput. Chem., 2018, 39, 917–924 CrossRef CAS PubMed.
- G. M. Damale, N. S. Harke, A. F. Kalam Khan, B. D. Shinde and N. J. Sangshetti, Mini-Rev. Med. Chem., 2014, 14, 35–55 CrossRef PubMed.
- L. Wang, J. Ding, L. Pan, D. Cao, H. Jiang and X. Ding, Chemom. Intell. Lab. Syst., 2021, 217, 104384 CrossRef CAS.
- S. Prasanna and R. J. Doerksen, Curr. Med. Chem., 2009, 16, 21–41 CrossRef CAS PubMed.
- K. Sargsyan, C. Grauffel and C. Lim, J. Chem. Theory Comput., 2017, 13, 1518–1524 CrossRef CAS PubMed.
- B. Temelso, J. M. Mabey, T. Kubota, N. Appiah-Padi and G. C. Shields, J. Chem. Inf. Model., 2017, 57, 1045–1054 CrossRef CAS PubMed.
- J. C. Baber, D. C. Thompson, J. B. Cross and C. Humblet, J. Chem. Inf. Model., 2009, 49, 1889–1900 CrossRef CAS PubMed.
- P. C. D. Hawkins, J. Chem. Inf. Model., 2017, 57, 1747–1756 CrossRef CAS PubMed.
- A. Wagner and H.-J. Himmel, J. Chem. Inf. Model., 2017, 57, 428–438 CrossRef CAS PubMed.
- B. Helmich and M. Sierka, J. Comput. Chem., 2012, 33, 134–140 CrossRef CAS PubMed.
- W. J. Allen and R. C. Rizzo, J. Chem. Inf. Model., 2014, 54, 518–529 CrossRef CAS PubMed.
- A. Sadeghi, S. A. Ghasemi, B. Schaefer, S. Mohr, M. A. Lill and S. Goedecker, J. Chem. Phys., 2013, 139, 184118 CrossRef PubMed.
- A. Ramirez-Manzanares, J. Peña, J. M. Azpiroz and G. Merino, J. Comput. Chem., 2015, 36, 1456–1466 CrossRef CAS PubMed.
- A. C. Wallace, N. Borkakoti and J. M. Thornton, Protein Sci., 1997, 6, 2308–2323 CrossRef CAS PubMed.
- Q. Lu, RSC Adv., 2021, 11, 35879–35886 RSC.
- Y. Zhang and J. Skolnick, Proteins: Struct., Funct., Bioinf., 2004, 57, 702–710 CrossRef CAS PubMed.
- A. Zemla, Nucleic Acids Res., 2003, 31, 3370–3374 CrossRef CAS PubMed.
- S. Cristobal, A. Zemla, D. Fischer, L. Rychlewski and A. Elofsson, BMC Bioinf., 2001, 2, 5 CrossRef CAS PubMed.
- L. Rychlewski, D. Fischer and A. Elofsson, Proteins: Struct., Funct., Bioinf., 2003, 53, 542–547 CrossRef CAS PubMed.
- A. Zemla, Č. Venclovas, J. Moult and K. Fidelis, Proteins: Struct., Funct., Bioinf., 1999, 37, 22–29 CrossRef.
- N. Siew, A. Elofsson, L. Rychlewski and D. Fischer, Bioinformatics, 2000, 16, 776–785 CrossRef CAS PubMed.
- P. Bergström and O. Edlund, Comput. Optim. Appl., 2014, 58, 543–561 CrossRef.
- K. J. Butler, master, Oregon State University, 1963.
- C. B. Barber, D. P. Dobkin and H. Huhdanpaa, ACM Trans. Math Software, 1996, 22, 469–483 CrossRef.
- M. T. Berg, M. J. Kreveld and M. H. Overmars, Computational Geometry: Algorithms and Applications, 2008 Search PubMed.
- B. Grünbaum, The PyMOL Molecular Graphics System, Version 1.2r3pre, Schrödinger, LLC, 1963 Search PubMed.
- H. M. Berman, K. Henrick and H. Nakamura, Nat. Struct. Mol. Biol., 2003, 10, 980 CrossRef CAS PubMed.
- S. K. Burley, H. M. Berman, G. J. Kleywegt, J. L. Markley, H. Nakamura and S. Velankar, Methods Mol. Biol., 2017, 1607, 627–641 CrossRef CAS PubMed.
- H. Berman, K. Henrick, H. Nakamura and J. L. Markley, Nucleic Acids Res., 2007, 35, D301–D303 CrossRef CAS PubMed.
- R. Zhao, Z. Cang, Y. Tong and G.-W. Wei, Bioinformatics, 2018, 34, i830–i837 CrossRef CAS PubMed.
- T. M. Parker, L. A. Burns, R. M. Parrish, A. G. Ryno and C. D. Sherrill, J. Chem. Phys., 2014, 140, 094106 CrossRef PubMed.
- E. G. Hohenstein, R. M. Parrish, C. D. Sherrill, J. M. Turney and H. F. Schaefer, J. Chem. Phys., 2011, 135, 174107 CrossRef PubMed.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- P. N. Samanta and K. K. Das, J. Mol. Graphics Modell., 2017, 72, 187–200 CrossRef CAS PubMed.
- P. Ertl, B. Rohde and P. Selzer, J. Med. Chem., 2000, 43, 3714–3717 CrossRef CAS PubMed.
- The PyMOL Molecular Graphics System, Version 1.2r3pre, Schrödinger, LLC, http://pymol.sourceforge.net/faq.html#:~:text=So%2C%20if%20your%20journal%20is%20hip%20enough%20to,to%20the%20list%20of%20publications%20which%20used%20PyMOL Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ra00764a |
| This journal is © The Royal Society of Chemistry 2022 |