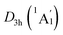The unique sandwich K₆Be₂B₆H₆ cluster with a real borozene B₆H₆ core

Abstract

Theoretical evidence is reported for a boron-based K₆Be₂B₆H₆ sandwich cluster, showing a perfectly D_6h B₆H₆ ring, being capped by two tetrahedral K₃Be ligands. Due to the comfortable charge transfer, the sandwich is viable in [K₃Be]³⁺[B₆H₆]⁶⁻[BeK₃]³⁺ ionic complex in nature. The [B₆H₆]⁶⁻ core with 6π aromaticity vividly imitates the benzene (C₆H₆), occurring as a real borozene. In contrast, the tetrahedral [K₃Be]³⁺ ligand is 2σ three-dimensional aromatic, acting as the simple superatom. Thus, this complex possesses a collectively three-fold 2σ/6π/2σ aromaticity. The interlaminar interaction is governed by the robust electrostatic attraction. The unique chemical bonding gives rise to interesting dynamic fluxionality.

---

1. Introduction

The electron-deficiency of boron leads to unconventional structures in its allotropes and compounds,^1–11 which is quite different from its neighbour carbon. The pure boron clusters favor the (quasi-)planar geometries over a wide range of sizes. Most of the planar boron clusters are controlled by the double (σ + π) aromaticity, especially, their π frameworks are analogous to those in benzene^1,12,13 or polycyclic aromatic hydrocarbons (PAHs).^14–17 The planar B₇³⁻, B₈²⁻, and B₉⁻ clusters^12,18–22 are representative, possessing the identical 6π aromaticity to C₅H₅⁻, C₆H₆, and C₇H₇⁺. Thus, they are endowed a relevant name of “borozene” by L. S. Wang, albeit that they are 6σ aromatic as well.²³ The “borozene” was first proposed for the planar B₁₂H₆ cluster by N. G. Szwacki.²⁴ Moreover, the metal-doped boron molecular wheels^25–30 and various inorganic benzene analogues^31,32 with double aromaticity are also widely investigated.

Strictly speaking, the real “borozene” is corresponding to the planar and aromatic B₆H₆⁶⁻ ring, assuming as a derivative of C₆H₆ by replacing the C atom with B⁻, just like the CH₄ and BH₄⁻ anion. However, the boron hydrides and their dianion species like forming the three-dimensional (3D) geometries, the latter are extremely stable with the 3D aromaticity.³³ Thus, it is more challenging to flatten the boron hydrides in chemistry. Additionally, the repulsion in highly charged B₆H₆⁶⁻ is drastic, need to neutralize with the counter-cations. In 2003, A. I. Boldyrev computationally investigated the Li₆B₆H₆ cluster in the spirit of C₆H₆, providing a theoretical proof for existence of aromatic B₆H₆⁶⁻ motif, albeit with a somewhat low D_2h symmetry.^34,35 The chemists have paid a lot of efforts into designing the transition metal centred M©B₆H₆ molecular wheels. Unfortunately, none of B₆H₆ motifs can be recognized as real “borozene” in view of the strong covalent interaction between the central metal atom and B₆H₆ ring, and abnormal charge distribution.^36–39 Last year, the author computationally reported a “Big Mac” sandwich of Rb₆Be₂B₆ cluster, consisting of a hexagonal B₆ ring and two tetrahedral Rb₃Be ligands, which skilfully mimics the style of ferrocene. The hexagonal B₆ core exists in the B₆⁶⁻ charge state with double 6π/6σ aromaticity, being sufficiently stable in the cationic field provided by two [Rb₃Be]³⁺ ligands.⁴⁰ The bare planar B₆ ring as a structural motif has been found in the crystal structure of a solid state phase (Ti₇Rh₄Ir₂B₈),⁴¹ and be discovered in some inverse sandwich clusters.^28,42,43 One interesting question arises, whether the planar [B₆H₆]⁶⁻ ring can be stabilized in the similar field of counter-cation? If it is feasible, the real “borozene” will be achieved.

The target of present work lies in probing the viability of aromatic [B₆H₆]⁶⁻ in K₆Be₂B₆H₆ cluster, which is consist of a perfectly planar B₆H₆ ring and two tetrahedral K₃Be ligands. The natural charge analyses show that K₆Be₂B₆H₆ cluster is a typical ionic complex, can be described by [K₃Be]³⁺[B₆H₆]⁶⁻[BeK₃]³⁺ formula. The perfectly planar [B₆H₆]⁶⁻ ring possesses the 6π aromaticity merely, occurring as a real “borozene”. In contrast, the tetrahedral [K₃Be]³⁺ ligand with 2σ delocalized electrons has the 3D aromaticity (or spherical aromaticity), serving as the superatom. Thus, this sandwich cluster has a collectively three-fold 2σ/6π/2σ aromaticity, whose three components are hold together via the robust electrostatic attraction. We believe that the stabilization of [B₆H₆]⁶⁻ borozene in K₆Be₂B₆H₆ complex is not an individual case. The planar aromatic [B₅H₅]⁶⁻ and [B₇H₇]⁶⁻ ring might be viable in such sandwich complexes.

2. Methods

We have theoretically designed a quaternary K₆Be₂B₆H₆ sandwich cluster basing on the concept of charge transfer and multi-fold aromaticity. The potential energy surface scan for K₆Be₂B₆H₆ cluster was performed using the Coalescence Kick (CK) algorithm^44,45 at the B3LYP/6-31G level, aiding with the manual constructions. Various possible initial structures were explored and fully reoptimized at the PBE0/6-311+G(d,p) level.⁴⁶ Vibrational frequencies were checked at the same level to guarantee that all presented isomers are true minima. The accurate energies of top five low-lying isomers at the PBE0/6-311+G(d,p) level were further estimated at the single-point CCSD(T)/6-311+G(d,p)//PBE0/6-311+G(d,p) level.⁴⁷ The transition state (TS) structures were searched using the QST2 method, and verified by intrinsic reaction coordinate (IRC) calculations.

For interpreting the stabilization of K₆Be₂B₆H₆ cluster, we have performed the Wiberg bond indices (WBIs) and natural atomic charges calculation using the NBO 6.0 program⁴⁸ at the PBE0/6-311+G(d,p) level. Chemical bonding was elucidated using the canonical molecular orbital (CMO), electron localization functions (ELFs),^49,50 and adaptive natural density partitioning (AdNDP) methods.⁵¹ The AdNDP calculations were performed at the PBE0/6-31G level due to the low sensitivity to the theoretical level. The ELFs and AdNDP data were visualized using Molekel 5.4.0.8.⁵² The nucleus-independent chemical shifts (NICSs)⁵³ were calculated at the PBE0/6-311+G(d,p) level. Born–Oppenheimer molecular dynamics (BOMD) simulations were performed at the PBE0/6-31G* level at the temperature of 300 and 600 K.⁵⁴ All electronic structure calculations and BOMD simulation were done using the Gaussian 09 package.⁵⁵

3. Results and discussion

3.1. Geometric structures

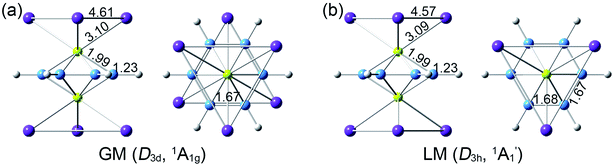
Extensive structural searches and density functional theory calculations at the PBE0/6-311+G(d,p) level suggest that the K₆Be₂B₆H₆ cluster possesses two almost degenerated isomers (Fig. 1), the global minimum (GM) (D_3d, ¹A_1g) and the closest low-lying isomer (LM) . Both isomers adopt the fascinating sandwich architectures, featuring a perfectly D_6h B₆H₆ ring being jammed by two tetrahedral K₃Be ligands. As a whole, two isomers are ingeniously assembled on the basis of the hierarchy of electronegativity. They are discrepant in assembling style of K₃Be ligands, a staggered fashion for GM and eclipsed one for LM. Their cartesian coordinates are given in Table S1 (ESI†). At the PBE0/6-311+G(d,p) level, D_3d (¹A_1g) GM is marginally more stable by 0.04 eV than LM with the zero-point energy (ZPE) corrections. Noted the dispersion corrections are not sensitive for present system according to the results at the PBE0-D3/6-311+G(d,p) level. The relative energies of two degenerated isomers were further refined at the CCSD(T)/6-311+G(d,p)//PBE0/6-311+G(d,p) level, which gives an energy distinction of 0.05 eV merely. The T₁ diagnostic factors of CCSD(T) for the GM and LM are 0.019, indicating the reliable CCSD(T) data. The other low-lying isomers (see Fig. S1, ESI†) are highly unstable, being at least 0.34 eV above the GM at the CCSD(T) level. Frankly, given the extremely complicated potential energy surface, we cannot completely ensure the true global minimum of the quaternary system. We have performed the minima hopping (MH)⁵⁶ search for this system (about 500 stationary points) as well, and did not find more stable isomers than the D_3d (¹A_1g) GM structure.

Fig. 1 Optimized geometries for (a) D_3d (¹A_1g) global-minimum (GM) and (b) low-lying isomer (LM) of K₆Be₂B₆H₆ cluster at the PBE0/6-311+G(d,p) level, along with the bond distances (in Å). Both side- and top-views are presented.

3.2. The bond distances, Wiberg bond indices and natural atomic charges

The bond distances for D_3d (¹A_1g) GM and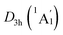 LM at the PBE0 level are shown in Fig. 1. Two structures have almost identical bond distances, all of them are within 0.01 Å, apart from the K–K bonds (0.04 Å). Specifically, the B–B distances are 1.67 Å in the GM and 1.68/1.67 Å in the LM, respectively, being slightly shorter than the standard B–B single bond (1.70 Å).⁵⁷ The B–H bond distances are 1.23 Å. The B–Be/Be–K/K–K bond distances are distinctly longer than their referenced single bonds, suggesting the weak covalent interaction of them.

The WBIs for GM and LM structures are in accordance with the bond distances. The B–B bonds have the WBIs of 1.34 for the D_3d (¹A_1g) GM (Fig. S2(a), ESI†) and 1.35/1.33 for 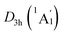LM (Fig. S2(c), ESI†), being intermediate between the single and double bonds. Thus, they are dominated by the delocalized bonds apart from the two-center two-electron (2c–2e) σ bond. The WBIs of B–H bonds is 0.93, representing the normal single bond. The Be–K/K–K bonds with the nonnegligible WBIs of 0.21/0.13 have somewhat strong covalent interaction than B–Be bonds, the WBIs of latter is negligible (only 0.07), which leads to an integrally tetrahedral K₃Be ligands in two isomers. Furthermore, the Be–K and K–K bonds in K₃Be ligand have a collective WBIs of 1.02, being in line with one four-center two-electron (4c–2e) bond.

As for the natural atomic charges, the D_6h B₆H₆ rings in D_3d (¹A_1g) GM and 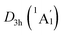LM have the same charge distribution (−0.91|e| for B and −0.02|e| for H, see Fig. S2(b and d), ESI†). Thus, the B₆H₆ rings exist in the [B₆H₆]⁶⁻ charged state, being isoelectronic with C₆H₆. The Be and K atom carries a positive charge of +0.94|e| and +0.63/0.62|e|, respectively. The tetrahedral K₃Be ligand has a collectively positive charge of +2.83/2.80|e|, being in line with [K₃Be]³⁺ species. Thus, both GM and LM could be viewed as the [K₃Be]³⁺[B₆H₆]⁶⁻[BeK₃]³⁺ ionic complexes, in which the electron-deficiency of B₆H₆ is reasonably compensated by two tetrahedral K₃Be ligands.

3.3. Chemical bonding

In order to interpret the unique geometries and stability of the D_3d GM (¹A_1g) and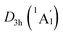 LM sandwiches, we performed the systematic chemical bonding analyses for them. The D_3d GM (¹A_1g) has 34 valence electrons in total, occupying 17 CMOs (Fig. 2). According to their constituent atomic orbitals (AOs), these occupied CMOs are reasonably sorted into four subsets. In subset (a), there are six σ CMOs composed by the B 2s/2p AOs, which can be directly recombined as six Lewis 2c–2e B–B σ bonds. The six CMOs in subset (b) originated from the radical B 2p AOs and H 1s AOs are shown one-to-one correspondence with those in subset (a), which describes the six Lewis 2c–2e B–H σ bonds in nature. The subset (c) exhibits a perfectly π sextet on the D_6h B₆H₆ ring, faithfully mimicking that in organic benzene, although the degenerated HOMO−3/HOMO−3′ π CMOs have slight hybridization with the HOMO−2/HOMO−2′ σ CMOs in subset (b). Thus, the B₆H₆ ring possesses 6π aromaticity according to the (4n + 2) Hückel rule. These 15 CMOs in subsets (a–c) with 30 occupying electrons are located on the B₆H₆ motif, supporting the assertation of [B₆H₆]⁶⁻ charge state of NBO results. Two CMOs in subset (d) are clearly located on the two tetrahedral K₃Be ligands, which can be directly recombined into two 4c–2e σ bonds, one on each K₃Be tetrahedron. Thus, the tetrahedral K₃Be ligand has the 2σ 3D aromaticity according to 2(n + 1)² electron counting rule.⁵⁸ It can also be viewed as a superatom.^59,60

Fig. 2 Occupied canonical molecular orbitals (CMOs) of D_3d (¹A_1g) GM for K₆Be₂B₆H₆ cluster. (a) Six σ CMOs for six B–B σ bonds. (b) Six σ CMOs for six B–H σ bonds. (c) Three delocalized π CMOs on B₆H₆ ring. (d) Two σ CMOs over two tetrahedral K₃Be ligands.

On the whole, the CMOs in subsets (a) and (b) describe the interactions of B–B and B–H of B₆H₆ ring, being in line with its six localized B–B and B–H σ bonds. The CMOs in subsets (c) and (d) represent the delocalized frameworks, including of the 6π aromaticity on B₆H₆ ring and 2σ aromaticity on two K₃Be tetrahedrons, which collectively renders the three-fold (2σ/6π/2σ) aromaticity for the [K₃Be]³⁺[B₆H₆]⁶⁻[BeK₃]³⁺ complex. The three-fold aromaticity underlies the stability of the GM structure. Moreover, the orbital component analysis suggests that HOMO-5 has a 14.2% Be 2s AOs contribution, in which two Be 2s AOs pretends to be the “p_z” style, taking part in the globally delocalized π bonding. As for the degenerated HOMO−3/HOMO−3′, there is a 12.0% Be 2p_x/2p_y AOs contribution, being bonding to the B 2p_z AOs of B₆H₆ ring. The minimal contribution of Be 2s/2p_x/2p_y AOs to three π CMOs is responsible for the extremely weak covalent interaction of B–Be bonds. The CMOs pattern of 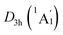LM is similar to that in D_3d (¹A_1g) GM, and its degenerated π CMOs with less hybridization are more elegant (Fig. S3, ESI†).

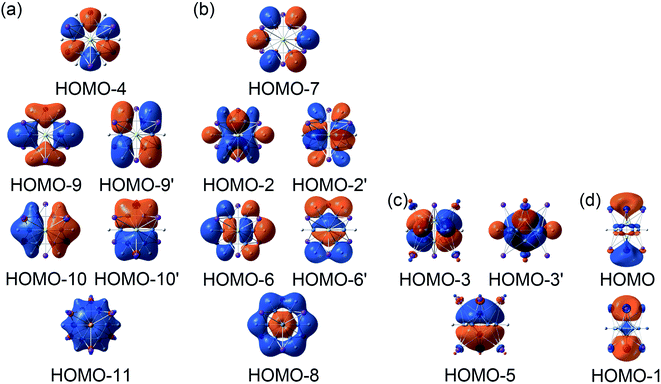
The above CMOs bonding images of D_3d (¹A_1g) GM and 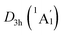LM are fully supported by the AdNDP analyses. As shown in Fig. 3, the AdNDP result for the D_3d (¹A_1g) GM clearly reproduces six localized 2c–2e B–B and B–H σ bonds, as well as two delocalized 4c–2e σ bonds on tetrahedral K₃Be ligands and three delocalized six-center two-electron (6c–2e) π bonds on B₆H₆ ring. All the occupation numbers (ONs) are ideal. The delocalized σ and π frameworks further confirm the three-fold (2σ/6π/2σ) aromaticity of the system. Note that the scheme of 4c–2e σ bond in K₃Be tetrahedron is more rational than the alternative three-center two-electron (3c–2e) σ bond on K₃ triangle, the latter gives rise to a rather low ON of 1.48|e|. It means that Be atom has a remarkable 20.4% contribution to the 4c–2e σ bond, being close to K atom (26.5%).⁴⁰ The identical AdNDP bonding pattern is observed in the 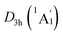LM (Fig. S4†).

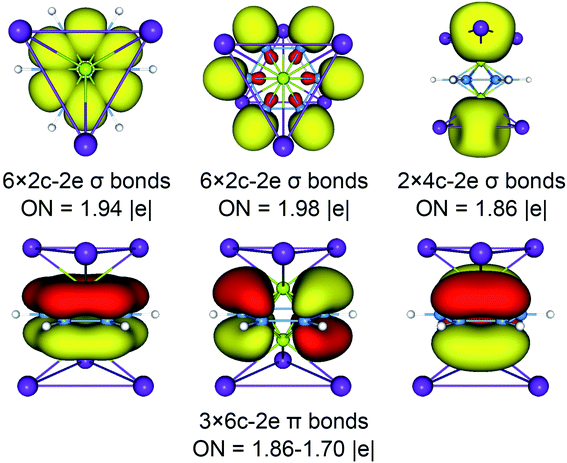Fig. 3 Adaptive natural density partitioning (AdNDP) bonding pattern of D_3d (¹A_1g) GM for K₆Be₂B₆H₆ cluster. Occupation numbers (ONs) are indicated.

3.4. Interaction between B₆H₆ ring and tetrahedral K₃Be ligands

As mentioned above, the B₆H₆ ring and two tetrahedral K₃Be ligands are viable in hexavalent anion [B₆H₆]⁶⁻ and trivalent cation [K₃Be]³⁺, respectively. The interaction between the B₆H₆ ring and tetrahedral K₃Be ligands should be mainly dominated by the robust electrostatic attraction. We qualitatively estimate the ionic interaction by manually expanding the distances of two Be atoms to 10 Å, and subsequently performing a single-point calculation at the same level of theory. In this case, the energy difference with respect to the ground state structure is mainly attributed to the electrostatic attraction. The calculated ionic interaction energies are as high as 18.35 eV for the D_3d (¹A_1g) GM and LM. Thus, the sandwiches are quite stable against dissociation. Alternatively, we also estimated the electrostatic attraction between the Be₂B₆H₆ inverse sandwich and the two K₃ rings by separating the K₃ rings to 10 Å distance, which are 5.09 eV for the GM and 5.01 eV for LM, respectively.

Furthermore, we calculated the dissociation energy of [K₃Be]³⁺ units in K₆Be₂B₆H₆ cluster according to the following formula, [K₃Be]³⁺[B₆H₆]⁶⁻[BeK₃]³⁺ (D_3d, ¹A_1g) = [K₃Be]³⁺[B₆H₆]⁶⁻[BeK₂]²⁺ (C_s, ¹A′) + K⁺. The [K₃Be]³⁺[B₆H₆]⁶⁻[BeK₂]²⁺ (C_s, ¹A′) is obtained from the GM structure by removing a K atom, and performing a fully optimization using its anion state at the same level. Such calculation can be used to evaluate quantitatively the energetics of the combination of [K₂Be]²⁺ and K⁺ with respected to the tetrahedral [K₃Be]³⁺ ligands in K₆Be₂B₆H₆ cluster. The result suggests that the dissociation energy of tetrahedral [K₃Be]³⁺ is as high as 4.90 eV, hinting the tetrahedral [K₃Be]³⁺ ligands is enough stable, and against disintegrating into the [BeK₂]²⁺ and K⁺ components.

3.5. The B₆H₆ ring in K₆Be₂B₆H₆ complex: a real borozene

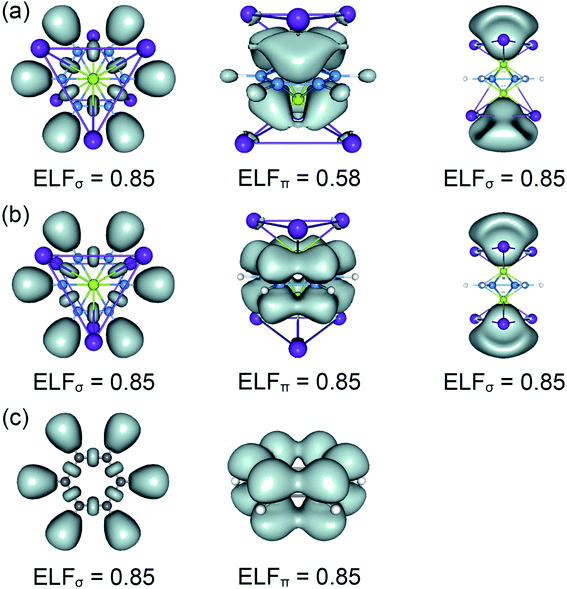
The real “borozene” should accurately imitate the C₆H₆ in both molecular structure and chemical bonding. Bonding analyses indicate that the K₆Be₂B₆H₆ cluster can be described as [K₃Be]³⁺[B₆H₆]⁶⁻[BeK₃]³⁺ complex. Here, the D_6h [B₆H₆]⁶⁻ ring is isoelectronic with C₆H₆, possessing the identical π sextet and Lewis B–B/B–H σ bond skeletons with the C₆H₆ (Fig. 2(c) and 3). Actually, it is an example of electronic transmutation, the boron atom acquiring an extra electron is transmutated into the carbon.⁶¹ Therefore, it truly occurs as a “borozene”. The ELFs data provide the further theoretical proof. As shown in Fig. 4, the D_6h [B₆H₆]⁶⁻ ring in the D_3d (¹A_1g) GM and LM exhibit the identical bonding patterns (ELF_σ and ELF_π) with the C₆H₆, despite the bifurcation value of ELF_π for the [B₆H₆]⁶⁻ ring in D_3d (¹A_1g) GM is somewhat lower (0.58) (Fig. 4(a)), which is mainly attributed to the weak hybridization of π CMOs (as indicated above). Interestingly, the [B₆H₆]⁶⁻ ring in LM presents an ideal bifurcation value (Fig. 4(b)), which positively confirms the 6π aromaticity of [B₆H₆]⁶⁻ ring. Compared with the C₆H₆ (Fig. 4(c)), the D_3d (¹A_1g) GM and LM have two additional 4c–2e σ bonds on tetrahedral [K₃Be]³⁺ ligands, being in line with their three-fold (2σ/6π/2σ) aromaticity, which are responsible for the stabilization for B₆H₆ and K₃Be components. The three-fold (2σ/6π/2σ) aromaticity in D_3d (¹A_1g) GM cluster is confirmed independently by the NICS calculation at the PBE0/6-311+G(d,p) level. The calculated NICS and NICS_zz values are enough negative: −19.8 and −25.4 ppm for the center of K₃Be ligand, and −16.0 and −22.8 ppm for 0.5 Å above the center of B₆H₆ ring.

Fig. 4 Electron localization functions (ELFs) of (a) D_3d (¹A_1g) GM and (b) LM for K₆Be₂B₆H₆ cluster, and (c) D_6h (¹A_1g) C₆H₆. The images support the three-fold (2σ/6π/2σ) aromaticity of K₆Be₂B₆H₆ cluster and the assertion of borozene for B₆H₆ ring.

3.6. The dynamic fluxionality

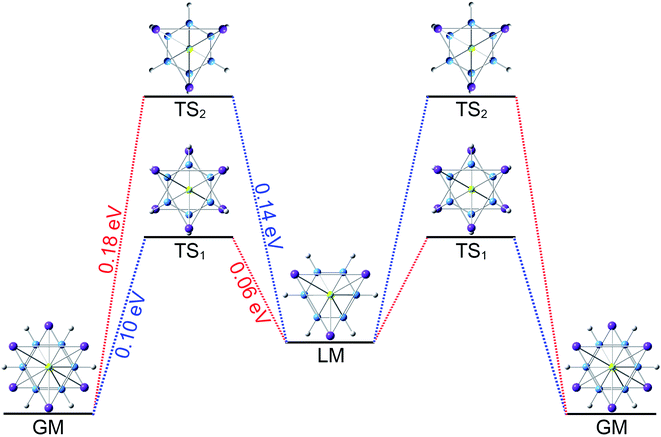
The three-fold (2σ/6π/2σ) aromaticity and robust electrostatic attraction in the [K₃Be]³⁺[B₆H₆]⁶⁻[BeK₃]³⁺ complex would facilitate interesting dynamic fluxionality of the cluster.^62–64 We obtained two TS structures (Fig. 5), D_3d (¹A_1g) TS₁ and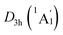 TS₂, along with the displacement vectors for two soft vibrational modes of 46.2 and 24.7 cm⁻¹ of the GM (Fig. S5(a)†). The TS₁ and TS₂ can be located from the GM by an independent rotation of 30° for B₆H₆ ring or an opposite rotation of 30° for each tetrahedral BeK₃ ligand with the B₆H₆ ring fixation, respectively. Alternatively, they also can be located from the LM by the similar operation. The LM structure has two soft vibrational modes of 58.8 and 8.9 cm⁻¹ (Fig. S5(b)†), relating to the intramolecular rotations. At the PBE0/6-311+G(d,p) level, the TS₁ and TS₂ structures are 0.10 and 0.18 eV above the GM with the ZPE corrections, which are refined to 0.14 and 0.23 eV at the single point CCSD(T) level. The small energy barriers imply that the clusters are dynamically fluxional at room temperature. The structural evolution process is illustrated in Fig. 5. Two pathways are demonstrated for the rotation of B₆H₆ ring (blue line) and the opposite rotation of two tetrahedral K₃Be ligands (red line). The BOMD simulation performed at the temperature of 300 K at the PBE0/6-31G* level faithfully confirm the above assessment (see the video in the ESI†), vividly demonstrating the fascinating dynamic structural fluxionality of the system. It should be noted that the structural integrity of K₆Be₂B₆H₆ cluster is maintained consistently even at the higher temperature of 600 K.

Fig. 5 Structural evolution of K₆Be₂B₆H₆ cluster during dynamic rotations. Two pathways are demonstrated for the rotation of B₆H₆ ring (blue curve) and the opposite rotation of two tetrahedral K₃Be ligands (red curve). The energy barriers of two transition state (TS) structures are 0.10 eV for TS₁ and 0.18 eV for TS₂ at the PBE0/6-311+G(d,p) level.

4. Conclusions

We have computationally designed a boron-based K₆Be₂B₆H₆ sandwich cluster, featuring a B₆H₆ ring being sandwiched by two tetrahedral K₃Be ligands. There is significant charge transfer from the K₃Be tetrahedrons to B₆H₆ ring (three electrons for each K₃Be), yielding the [K₃Be]³⁺[B₆H₆]⁶⁻[BeK₃]³⁺ complex. The [B₆H₆]⁶⁻ ring (with 6π delocalized electrons) precisely mimics the benzene in both geometry and chemical bonding, occurring as a real borozene. The tetrahedral [K₃Be]³⁺ ligand with 2σ delocalized electrons possesses the three-dimensional aromaticity, serving as a superatom in essence. Overall, the sandwich cluster is a three-fold 2σ/6π/2σ aromatic system. The multi-fold aromaticity and robust electrostatic attraction among three motifs facilitates interesting dynamic fluxionality.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (21873058), the Natural Science Foundation of Shanxi Province (2018103), the Top Science and Technology Innovation Teams of Xinzhou Teachers University and the Fund for Shanxi “1331 Project” Key Subjects Construction.

References

1. H. J. Zhai, B. Kiran, J. Li and L. S. Wang, Nat. Mater., 2003, 2, 827–833.
2. S. Pan, J. Barroso, S. Jalife, T. Heine, K. R. Asmis and G. Merino, Acc. Chem. Res., 2019, 52, 2732–2744.
3. A. N. Alexandrova, A. I. Boldyrev, H. J. Zhai and L. S. Wang, Coord. Chem. Rev., 2006, 250, 2811–2866.
4. T. Jian, X. Chen, S. D. Li, A. I. Boldyrev, J. Li and L. S. Wang, Chem. Soc. Rev., 2019, 48, 3550–3591.
5. E. Oger, N. R. M. Crawford, R. Kelting, P. Weis, M. M. Kappes and R. Ahlrichs, Angew. Chem., Int. Ed., 2007, 46, 8503–8506.
6. W. Huang, A. P. Sergeeva, H. J. Zhai, B. B. Averkiev, L. S. Wang and A. I. Boldyrev, Nat. Chem., 2010, 2, 202–206.
7. H. J. Zhai, Y. F. Zhao, W. L. Li, Q. Chen, H. Bai, H. S. Hu, Z. A. Piazza, W. J. Tian, H. G. Lu, Y. B. Wu, Y. W. Mu, G. F. Wei, Z. P. Liu, J. Li, S. D. Li and L. S. Wang, Nat. Chem., 2014, 6, 727–731.
8. Y. J. Wang, Y. F. Zhao, W. L. Li, T. Jian, Q. Chen, X. R. You, T. Ou, X. Y. Zhao, H. J. Zhai, S. D. Li, J. Li and L. S. Wang, J. Chem. Phys., 2016, 144, 064307.
9. W. N. Lipscomb, Science, 1977, 196, 1047–1055.
10. H. Braunschweig, R. D. Dewhurst and V. H. Gessner, Chem. Soc. Rev., 2013, 42, 3197–3208.
11. E. D. Jemmis, M. M. Balakrishnarajan and P. D. Pancharatna, Chem. Rev., 2002, 102, 93–144.
12. H. J. Zhai, A. N. Alexandrova, K. A. Birch, A. I. Boldyrev and L. S. Wang, Angew. Chem., Int. Ed., 2003, 42, 6004–6008.
13. Y. J. Wang, X. Y. Zhao, Q. Chen, H. J. Zhai and S. D. Li, Nanoscale, 2015, 7, 16054–16060.
14. A. P. Sergeeva, D. Y. Zubarev, H. J. Zhai, A. I. Boldyrev and L. S. Wang, J. Am. Chem. Soc., 2008, 130, 7244–7246.
15. A. P. Sergeeva, Z. A. Piazza, C. Romanescu, W. L. Li, A. I. Boldyrev and L. S. Wang, J. Am. Chem. Soc., 2012, 134, 18065–18073.
16. Z. A. Piazza, H. S. Hu, W. L. Li, Y. F. Zhao, J. Li and L. S. Wang, Nat. Commun., 2014, 5, 3113.
17. Q. Chen, G. F. Wei, W. J. Tian, H. Bai, Z. P. Liu, H. J. Zhai and S. D. Li, Phys. Chem. Chem. Phys., 2014, 16, 18282–18287.
18. A. N. Alexandrova, H. J. Zhai, L. S. Wang and A. I. Boldyrev, Inorg. Chem., 2004, 43, 3552–3554.
19. T. R. Galeev, C. Romanescu, W. L. Li, L. S. Wang and A. I. Boldyrev, J. Chem. Phys., 2011, 135, 104301.
20. P. W. Fowler and B. R. Gray, Inorg. Chem., 2007, 46, 2892–2897.
21. L. L. Pan, J. Li and L. S. Wang, J. Chem. Phys., 2008, 129, 024302.
22. T. T. Chen, W. L. Li, T. Jian, X. Chen, J. Li and L. S. Wang, Angew. Chem., Int. Ed., 2017, 56, 6916–6920.
23. W. L. Li, T. T. Chen, W. J. Chen, J. Li and L. S. Wang, Nat. Commun., 2021, 12, 6467.
24. N. G. Szwacki, V. Weber and C. J. Tymczak, Nanoscale Res. Lett., 2009, 4, 1085–1089.
25. W. L. Li, C. Romanescu, T. R. Galeev, Z. A. Piazza, A. I. Boldyrev and L. S. Wang, J. Am. Chem. Soc., 2012, 134, 165–168.
26. W. L. Li, T. T. Chen, D. H. Xing, X. Chen, J. Li and L. S. Wang, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E6972−E6977.
27. W. L. Li, T. Jian, X. Chen, T. T. Chen, G. V. Lopez, J. Li and L. S. Wang, Angew. Chem., Int. Ed., 2016, 55, 7358–7363.
28. W. L. Li, L. Xie, T. Jian, C. Romanescu, X. Huang and L. S. Wang, Angew. Chem., Int. Ed., 2014, 53, 1288–1292.
29. Z. H. Cui, W. S. Yang, L. Zhao, Y. H. Ding and G. Frenking, Angew. Chem., Int. Ed., 2016, 55, 7841–7846.
30. C. Romanescu, T. R. Galeev, W. L. Li, A. I. Boldyrev and L. S. Wang, Acc. Chem. Res., 2013, 46, 350–358.
31. D. Z. Li, H. Bai, Q. Chen, H. Lu, H. J. Zhai and S. D. Li, J. Chem. Phys., 2013, 138, 244304.
32. L. Y. Feng, R. Li and H. J. Zhai, Phys. Chem. Chem. Phys., 2019, 21, 20523–20537.
33. J. Aihara, J. Am. Chem. Soc., 1978, 100, 3339–3342.
34. A. N. Alexandrova, K. A. Birch and A. I. Boldyrev, J. Am. Chem. Soc., 2003, 125, 10786–10787.
35. A. N. Alexandrova and A. I. Boldyrev, Inorg. Chem., 2004, 43, 3588–3592.
36. L. F. Li, C. Xu, B. K. Jin and L. J. Cheng, J. Chem. Phys., 2013, 139, 174310.
37. L. F. Li, C. Xu and L. J. Cheng, Comput. Theor. Chem., 2013, 1021, 144–148.
38. J. Hou, Q. Duan, J. Qin, X. Shen, J. Zhao, Q. Liang, D. Jiang and S. Gao, Phys. Chem. Chem. Phys., 2015, 17, 9644–9650.
39. H. L. Yu, R. L. Sang and Y. Y. Wu, J. Phys. Chem. A, 2009, 113, 3382–3386.
40. Y. J. Wang, L. Y. Feng, L. Xu, X. R. Hou, N. Li, C. Q. Miao and H. J. Zhai, Phys. Chem. Chem. Phys., 2020, 22, 20043–20049.
41. B. P. T. Fokwa and M. Hermus, Angew. Chem., Int. Ed., 2012, 51, 1702–1705.
42. Y. J. Wang, C. Q. Miao, J. J. Xie, Y. R. Wei and G. M. Ren, New J. Chem., 2019, 43, 15979–15982.
43. Y. J. Wang, M. M. Guo, G. L. Wang, C. Q. Miao, N. Zhang and T. D. Xue, Phys. Chem. Chem. Phys., 2020, 22, 20362–20367.
44. M. Saunders, J. Comput. Chem., 2004, 25, 621–626.
45. P. P. Bera, K. W. Sattelmeyer, M. Saunders, H. F. Schaefer III and P. v. R. Schleyer, J. Phys. Chem. A, 2006, 110, 4287–4290.
46. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
47. R. J. Bartlett and M. Musial, Rev. Mod. Phys., 2007, 79, 291–352.
48. E. D. Glendening, C. Landis and F. Weinhold, NBO 6.0, Theoretical Chemistry Institute, University of Wisconsin, Madison, 2013.
49. B. Silvi and A. Savin, Nature, 1994, 371, 683–686.
50. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
51. D. Y. Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207–5217.
52. U. Varetto, Molekel 5.4.0.8, Swiss National Supercomputing Center, Manno, Switzerland, 2009.
53. P. v. R. Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. R. v. E. Hommes, J. Am. Chem. Soc., 1996, 118, 6317–6318.
54. T. Helgaker, E. Uggerud and H. J. A. Jensen, Chem. Phys. Lett., 1990, 173, 145–150.
55. M. J. Frisch, et al., Gaussian 09, revision D.01, Gaussian Inc., Wallingford, Connecticut, 2009.
56. S. Goedecker, J. Chem. Phys., 2004, 120, 9911–9917.
57. P. Pyykkö, J. Phys. Chem. A, 2015, 119, 2326–2337.
58. M. Bühl and A. Hirsch, Chem. Rev., 2001, 101, 1153–1183.
59. A. C. Reber and S. N. Khanna, Acc. Chem. Res., 2017, 50, 255–263.
60. P. Jena and Q. Sun, Chem. Rev., 2018, 118, 5755–5870.
61. X. Zhang, K. A. Lundell, J. K. Olson, K. H. Bowen and A. I. Boldyrev, Chem.–Eur. J., 2018, 24, 9200–9210.
62. J. O. C. Jiménez-Halla, R. Islas, T. Heine and G. Merino, Angew. Chem., Int. Ed., 2010, 49, 5668–5671.
63. Y. J. Wang, J. C. Guo and H. J. Zhai, Nanoscale, 2017, 9, 9310–9316.
64. J. C. Guo, L. Y. Feng, Y. J. Wang, S. Jalife, A. Vásquez-Espinal, J. L. Cabellos, S. Pan, G. Merino and H. J. Zhai, Angew. Chem., Int. Ed., 2017, 56, 10174–10177.

---

Footnote

† Electronic supplementary information (ESI) available: Supplementary Table S1 and Fig. S1–S5, as well as a short movie for dynamic fluxionality extracted from the BOMD simulation. See DOI: 10.1039/d2ra00692h

---