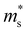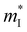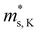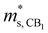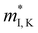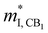Open Access Article
Open Access ArticleLarge improvement in thermoelectric performance of pressure-tuned Mg3Sb2†
Juan Li *,
Shuai Zhang,
Kai Han,
Bing Sun and
Lianzhen Cao
*,
Shuai Zhang,
Kai Han,
Bing Sun and
Lianzhen Cao
Department of Physics and Optoelectronic Engineering, Weifang University, Weifang 261061, China. E-mail: lj_wfu@163.com
First published on 5th January 2022
Abstract
The Mg3Sb2-based Zintl compound is a promising candidate for a high-performance thermoelectric material with the advantage of the component elements being low cost, non-toxic and earth-abundant. Here, we investigate the influence of pressure on the electronic structure and p-type and n-type thermoelectric transport properties of Mg3Sb2 by using density functional theory and Boltzmann transport theory. The energy gaps first increase and then decrease with the increasing of pressure, and a peak value of the valley degeneracy of conduction band occurs at 4 GPa. Based on the calculated band structures, the zT (figure of merit) values of p-type Mg3Sb2 under pressure are significantly enhanced, which predominantly originates from the boosted PF (power factor) contributed by the increased carrier's relaxation time. When the carrier concentration reaches 1 × 1020 cm−3, the PF of p-type Mg3Sb2 at 4 GPa is increased by 35% relative to that of the compound at 0 GPa, thus leading to a considerably improved zT of ∼0.62 at 725 K. Under the same conditions, due to the increased density of states effective mass, the n-type Mg3Sb2 exhibits a highest PF of ∼19 μW cm−1 K−2 and a peak zT of 1.7. Therefore, pressure tuning is an effective method to improve the p-type and n-type thermoelectric transport performance of Mg3Sb2-based Zintl compounds. This work on Mg3Sb2 under pressure may provide a new mechanism for the experimenters towards the enhancement of the thermoelectric performance of materials.
1. Introduction
More than half the energy content of the fuel is lost as waste heat. Thermoelectrics is an effective technology of directly interconverting heat and electrical energy without moving parts, which can be applied in power generation and solid-state refrigeration.1–5 Improving the energy conversion efficiency is the key factor influencing the extensive application of thermoelectric devices. The conversion efficiency is mainly governed by the performance of a thermoelectric material, which is quantified by the dimensionless figure of merit zT, zT = S2σT/κ, where S is the Seebeck coefficient, σ is the electrical conductivity, κ is the thermal conductivity and T is the absolute temperature.6–8 Therefore, increasing the power factor (S2σ) or decreasing the κ are significant ways to improve the zT and thereby to enhance the energy conversion efficiency of the thermoelectric devices.9–12In addition to the thermoelectric material's performance, the cost and properties of the constituent elements also have an important influence on the widespread application of the thermoelectric technology. The advantage of the constituent elements being low cost, non-toxic and earth-abundant make Mg3Sb2-based Zintl compounds promising candidates for high-performance thermoelectric materials.13–15 By controlling the growing condition, Mg3Sb2 can exhibit not only p-type transport performance but also n-type transport performance.16–21 Pure Mg3Sb2 is an intrinsic p-type semiconductor ascribed to the Mg vacancy responsible for the p-type carriers.19,20,22 Song et al.23 reported that through increasing the hole concentration, the zT value of 0.51 at 725 K can be achieved in p-type Mg2.985Ag0.015Sb2. Due to the conduction band complexity, Mg3Sb2 exhibits more outstanding n-type thermoelectric performance. Based on a defect chemistry approach, Tamaki et al.24 reported n-type Mg3.2Sb1.5Bi0.49Te0.01 with a high zT of 1.5 at 715 K, and similar results are reported by other groups.10,13,25–27
Pressure tuning28 is an effective strategy for designing high-performance thermoelectric materials through modifying the electronic structure. Under pressure, the lattice parameters and band gaps of materials will be significantly changed, which will result in some positive changes in the electronic structures.29,30 Because the key thermoelectric parameters (S and σ) are strongly dependent on the electronic structure, therefore, the strategy based on pressure tuning can be used to improve the thermoelectric performance of materials. Zhang et al.31 reported that the zT values of p-type SnSe along the b and c directions at 6 GPa and 700 K can be up to 2.5 and 1.7, respectively, and the zT of n-type sample at 600 K can reach 1.7. Polvani et al.32 reported that the zT value increased twofold in p-type Sb1.5Bi0.5Te3 upon pressure tuning. For improving the thermoelectric performance of Mg3Sb2, optimizing carrier concentration21,33–35 or tuning carrier scattering mechanism10,26 have been proved to be effective methods by a plenty of literatures, however, there are few theoretical reports about the method of pressure tuning. Therefore, it is necessary and important to investigate the effect of pressure on the thermoelectric properties of Mg3Sb2, which can provide significant guides for the experimental researchers.
The intention of this work is therefore to study the electronic structures and thermoelectric properties of Mg3Sb2 at hydrostatic pressure by using first-principles calculations and Boltzmann transport theory. It is found that pressure tuning has a great influence on the band gap and valley degeneracy of Mg3Sb2. Due to the positive changes in the electronic structure, the p-type and n-type thermoelectric properties of Mg3Sb2 are significantly improved. When the carrier concentration reaches 1 × 1020 cm−3, the zT of p-type Mg3Sb2 at 4 GPa and 725 K can be up to ∼0.62, ∼22% higher than the value of the sample at 0 GPa, which predominantly originates from the considerably enhanced PF contributed by the increased carrier's relaxation time. At the same temperature and carrier concentration, the n-type Mg3Sb2 at 4 GPa can exhibit a high PF of ∼19 μW cm−1 K−2 and a peak zT of 1.7, which is mainly due to the increased density of states effective mass. These results demonstrate that pressure tuning is an effective way to the enhancement of the p-type and n-type thermoelectric transport properties of Mg3Sb2-based Zintl compounds.
2. Computation methods
In this work, the density functional theory (DFT) combined with the projector augmented wave (PAW) method are carried out to calculate the electronic structures of Mg3Sb2 under different pressure, as implemented in the Vienna Ab initio Simulation Package (VASP).36–38 The optimized crystal parameters of Mg3Sb2 at 0 GPa can be obtained from our previous work.39,40 Under the pressure ranging from 1 to 10 GPa, the structural relaxation including the lattice constants and internal coordinates are allowed to relax into their equilibrium positions. The modified Becke Johnson functional of the Tran and Blaha (TB-mBJ) potential41,42 is adopted for obtaining the accurate electronic band structure. A 12 × 12 × 8 Monkhorst–Pack k mesh, a plane-wave cutoff energy of 400 eV and an energy convergence criterion of 10−4 eV are employed. Based on the calculated band structure, Effective Mass Calculator (EMC) program43 is applied to calculate the effective masses. Considering that the spin orbit coupling (SOC) has an influence on the valence band of Mg3Sb2,40 the calculated band structures with SOC are used for the following electronic transport calculations.The semi-classic Boltzmann transport theory is applied to calculate the electronic transport properties based on the calculated band structure with SOC, as implemented in the BoltzTraP2 code.44 The calculation results can directly present the temperature and carrier concentration dependence of S and σ/τ (where τ is the carrier's relaxation time). In order to obtain the σ, the deformation potential theory45 is employed to calculate the τ and carrier mobility (μ). The minimum lattice thermal conductivity are evaluated using the Cahill's expression.46
3. Results and discussion
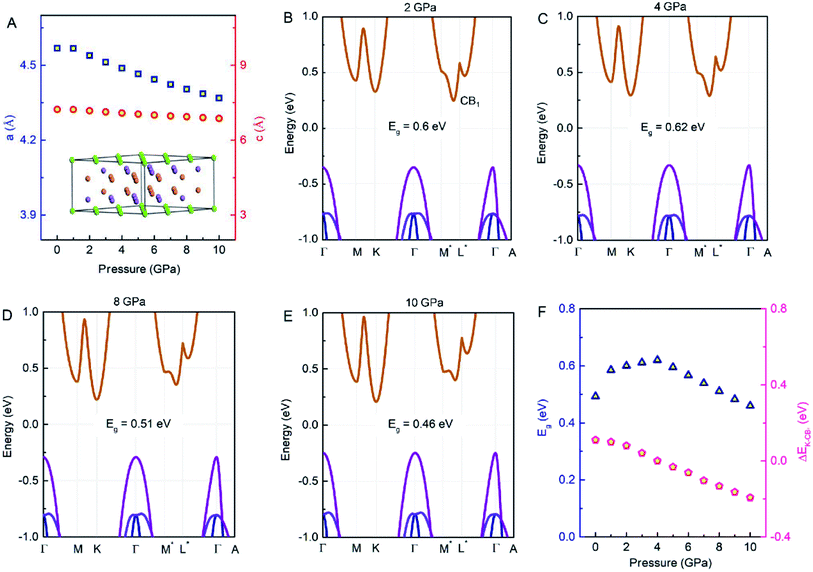
The layered Zintl compound Mg3Sb2 crystallizes in an inverse α-La2O3-type structure which belongs to the space group P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1, as displayed in Fig. 1A. This structure can be described as the cationic Mg2+ layers intercalated between the anionic [Mg2Sb2]2− layers. The Mg atoms in the ionic Mg2+ layers and in the covalently bonded [Mg2Sb2]2− layers are denoted as Mg1 and Mg2, respectively. The optimized lattice constants of Mg3Sb2 at 0 GPa from our previous work39,40 are a = 4.568 Å and c = 7.229 Å. Fig. 1A shows the pressure dependence of the lattice parameters of Mg3Sb2. In the pressure range of 0 to 10 GPa, the lattice parameters decrease as the pressure increases, and the decrease of a is larger than that of c. The changes of the lattice parameters may have a significant influence on the electronic structures, and further affect the thermoelectric properties of Mg3Sb2.
m1, as displayed in Fig. 1A. This structure can be described as the cationic Mg2+ layers intercalated between the anionic [Mg2Sb2]2− layers. The Mg atoms in the ionic Mg2+ layers and in the covalently bonded [Mg2Sb2]2− layers are denoted as Mg1 and Mg2, respectively. The optimized lattice constants of Mg3Sb2 at 0 GPa from our previous work39,40 are a = 4.568 Å and c = 7.229 Å. Fig. 1A shows the pressure dependence of the lattice parameters of Mg3Sb2. In the pressure range of 0 to 10 GPa, the lattice parameters decrease as the pressure increases, and the decrease of a is larger than that of c. The changes of the lattice parameters may have a significant influence on the electronic structures, and further affect the thermoelectric properties of Mg3Sb2.
The calculated band structures of Mg3Sb2 with pressure being 2, 4, 8 and 10 GPa are shown in Fig. 1B–E. With the pressure increasing, the valence band maximum at the Γ point move upward, and the conduction band minimum at the K point shift downward, whereas the conduction band minimum at the CB1 point along the M*–L* line show an upward shift. When the pressure is below 4 GPa, the conduction band minimum is located at the CB1 point, however, when the pressure continues to increase, the conduction band minimum is located at the K point. The energy gaps of Mg3Sb2 at 2, 4, 8 and 10 GPa are estimated to be 0.6, 0.62, 0.51 and 0.46 eV, respectively. In order to accurately describe the influence of pressure on the band gaps, the pressure dependence of the band gaps of Mg3Sb2 are shown in Fig. 1F. The band gaps present a first increase and then decrease trend with the increase of pressure. Changes in the band gaps may have an impact on the band effective mass. It is clearly that the pressure has a large effect on the conduction band energy difference ΔEK-CB1 between the K point in the band and CB1 band point. As can be seen from Fig. 1F, with the increase of pressure, the absolute value of ΔEK-CB1 decrease firstly and then increase. When the pressure increases to 4 GPa, ΔEK-CB1 approaches to nearly zero, giving rise to a peak in the valley degeneracy (Nv = 11). Because the thermoelectric parameters are closely associated with the band effective mass and valley degeneracy, pressure tuning may be an effective way to achieve high-thermoelectric properties of Mg3Sb2-based materials.
Fig. 2 shows the S, σ/τ, σ and PF as a function of carrier concentration for p-type Mg3Sb2 at 725 K with pressure being 0, 2, 4, 8 and 10 GPa, and the comparison with the experimental data of the reported Mg3−xAgxSb2 sample. The calculated S consistent with the experimental value verifies the accuracy of our computation methods. The S of p-type Mg3Sb2 under different pressure has a negative relationship with the carrier concentration in certain doping range. At the same carrier concentration, the S calculated at 2, 4, 8 and 10 GPa are smaller than the value calculated at 0 GPa, which indicates that pressure tuning has a detrimental influence on the S of p-type Mg3Sb2. In order to analyze the reason for the decrease of S under pressure, we calculate the single valley effective mass 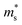 of the Γ valence band based on the electronic band structure (see Table 1). The relationship between S and
of the Γ valence band based on the electronic band structure (see Table 1). The relationship between S and 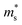 is given by:47
is given by:47
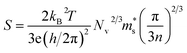 | (1) |
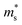 is the single valley effective mass, Nv is the valley degeneracy, n is the carrier concentration, T is the absolute temperature, h is the Planck constant and kB is the Boltzmann constant. According to the equation, the S is in positive correlation with the density of states effective mass
is the single valley effective mass, Nv is the valley degeneracy, n is the carrier concentration, T is the absolute temperature, h is the Planck constant and kB is the Boltzmann constant. According to the equation, the S is in positive correlation with the density of states effective mass 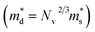 . The
. The 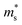 of the Γ valence band at 0, 2, 4, 8 and 10 GPa are estimated to be 0.433 me, 0.416 me, 0.414 me, 0.407 me and 0.402 me, respectively, which reveals that pressure tuning may lead to a decrease in the
of the Γ valence band at 0, 2, 4, 8 and 10 GPa are estimated to be 0.433 me, 0.416 me, 0.414 me, 0.407 me and 0.402 me, respectively, which reveals that pressure tuning may lead to a decrease in the 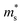 of the Γ valence band. Due to the negligible effect of the pressure on the valley degeneracy of the Γ valence band (Fig. 1B–E), the decreased S of p-type Mg3Sb2 by pressure tuning may be mainly ascribed to the decrease of the
of the Γ valence band. Due to the negligible effect of the pressure on the valley degeneracy of the Γ valence band (Fig. 1B–E), the decreased S of p-type Mg3Sb2 by pressure tuning may be mainly ascribed to the decrease of the 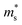 of the Γ valence band.
of the Γ valence band.
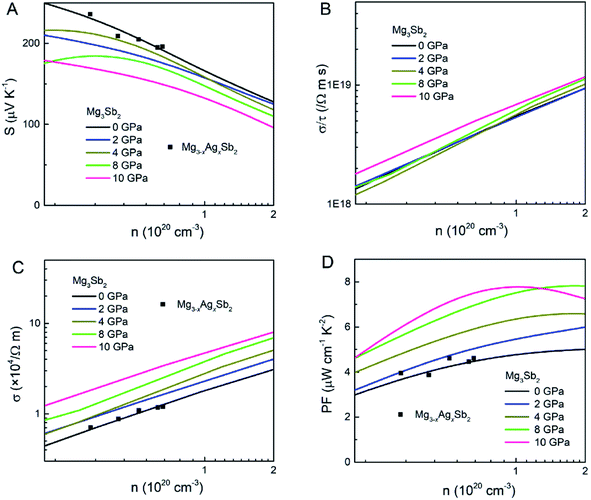 | ||
| Fig. 2 The calculated (A) Seebeck coefficient S, (B) electrical conductivity with respect to relaxation time σ/τ, (C) electrical conductivity σ and (D) power factor PF as a function of carrier concentration n for p-type Mg3Sb2 at 725 K with pressure being 0, 2, 4, 8 and 10 (unit: GPa). The black squares are the experimental values of the reported Mg3−xAgxSb2 from ref. 23. | ||
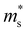 (me) of the Γ valence band, conductivity effective mass
(me) of the Γ valence band, conductivity effective mass 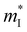 (me) of the Γ valence band, the deformation potential Ξ (eV) of the valence band, and the carrier mobility μ (cm2 V−1 s−1) and relaxation time τ (fs) at 725 K for p-type Mg3Sb2 with pressure being 0, 2, 4, 8 and 10 (unit: GPa)
(me) of the Γ valence band, the deformation potential Ξ (eV) of the valence band, and the carrier mobility μ (cm2 V−1 s−1) and relaxation time τ (fs) at 725 K for p-type Mg3Sb2 with pressure being 0, 2, 4, 8 and 10 (unit: GPa)
As shown in Fig. 2B, the σ/τ of p-type Mg3Sb2 at 0, 2, 4, 8 and 10 GPa show an increasing trend as the carrier concentration increases. The τ for determining the σ can be estimated by the deformation potential theory, as expressed as:40,48
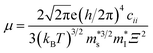 | (2) |
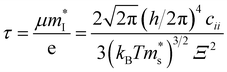 | (3) |
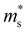 is the single valley effective mass,
is the single valley effective mass, 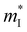 is the conductivity effective mass, Ξ is the deformation potential, cii is lattice elastic constant, h is the Planck constant and kB is the Boltzmann constant. The larger the value of cii and the smaller the values of
is the conductivity effective mass, Ξ is the deformation potential, cii is lattice elastic constant, h is the Planck constant and kB is the Boltzmann constant. The larger the value of cii and the smaller the values of 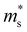 and Ξ, the better the performance of τ. Table 1 lists the input parameters and the calculated τ at 725 K for p-type Mg3Sb2 with pressure being 0, 2, 4, 8 and 10 GPa. With the increasing of pressure, the increased c11 and the decreased
and Ξ, the better the performance of τ. Table 1 lists the input parameters and the calculated τ at 725 K for p-type Mg3Sb2 with pressure being 0, 2, 4, 8 and 10 GPa. With the increasing of pressure, the increased c11 and the decreased 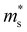 and Ξ are beneficial to the τ. The τ at 0, 2, 4, 8 and 10 GPa are estimated to be 3.29, 4.28, 4.96, 6.13 and 6.84 fs, respectively. Based on the calculated τ, the σ as a function of carrier concentration for p-type Mg3Sb2 with pressure being 0, 2, 4, 8 and 10 GPa are plotted in Fig. 2C. At the same carrier concentration, because of the enhanced τ, there is an improvement in the σ with the increase of pressure. As a result of the largely improved σ, the theoretical PF for p-type Mg3Sb2 is strongly enhanced as the pressure increases (Fig. 2D). Because there may exist phase transition in Mg3Sb2 at pressure above 5 GPa,49,50 therefore, pressure tuning on p-type thermoelectric properties require careful selection of the pressure. When the carrier concentration increases up to 1 × 1020 cm−3, p-type Mg3Sb2 at 4 GPa exhibits a high PF of ∼6.2 μW cm−1 K−2, 35% higher than the value of ∼4.6 μW cm−1 K−2 for the compound at 0 GPa. Therefore, pressure tuning can make a significant contribution to the excellent p-type electronic transports for Mg3Sb2-based compounds.
and Ξ are beneficial to the τ. The τ at 0, 2, 4, 8 and 10 GPa are estimated to be 3.29, 4.28, 4.96, 6.13 and 6.84 fs, respectively. Based on the calculated τ, the σ as a function of carrier concentration for p-type Mg3Sb2 with pressure being 0, 2, 4, 8 and 10 GPa are plotted in Fig. 2C. At the same carrier concentration, because of the enhanced τ, there is an improvement in the σ with the increase of pressure. As a result of the largely improved σ, the theoretical PF for p-type Mg3Sb2 is strongly enhanced as the pressure increases (Fig. 2D). Because there may exist phase transition in Mg3Sb2 at pressure above 5 GPa,49,50 therefore, pressure tuning on p-type thermoelectric properties require careful selection of the pressure. When the carrier concentration increases up to 1 × 1020 cm−3, p-type Mg3Sb2 at 4 GPa exhibits a high PF of ∼6.2 μW cm−1 K−2, 35% higher than the value of ∼4.6 μW cm−1 K−2 for the compound at 0 GPa. Therefore, pressure tuning can make a significant contribution to the excellent p-type electronic transports for Mg3Sb2-based compounds.
Fig. 3 shows the S, σ/τ, σ and PF as a function of carrier concentration for n-type Mg3Sb2 at 725 K with pressure being 0, 2, 4, 8 and 10 GPa, and the comparison with the experimental data of the reported Nd-, Pr-, Te- and Se-doped Mg3Sb2-based compounds. The discrepancy between the simulated results and the experimental data is mainly ascribed to the effect of Bi doping on the electrical transport properties of Mg3Sb2.39 At the same carrier concentration, compared to the samples at 0, 2, 8 and 10 GPa, the n-type Mg3Sb2 at 4 GPa possesses a higher S. As can be seen from Table 2, with the increase of pressure, the 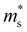 of the CB1 conduction band
of the CB1 conduction band 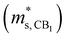 increases, whereas the
increases, whereas the 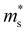 of the K conduction band
of the K conduction band 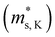 decreases. Because of the smaller absolute value of ΔEK-CB1 (below ∼0.11 eV) at 0, 2 and 4 GPa (Fig. 1F), the average
decreases. Because of the smaller absolute value of ΔEK-CB1 (below ∼0.11 eV) at 0, 2 and 4 GPa (Fig. 1F), the average 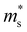 (0.252 me, 0.255 me and 0.257 me) of the both bands are used for calculating the τ. The increased
(0.252 me, 0.255 me and 0.257 me) of the both bands are used for calculating the τ. The increased 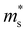 and the highest valley degeneracy (Fig. 2C) mainly contribute to the excellent S of n-type Mg3Sb2 at 4 GPa.
and the highest valley degeneracy (Fig. 2C) mainly contribute to the excellent S of n-type Mg3Sb2 at 4 GPa.
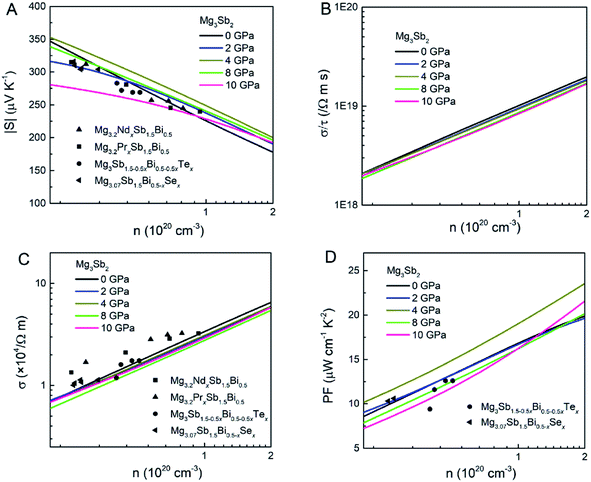 | ||
| Fig. 3 The calculated (A) Seebeck coefficient S, (B) electrical conductivity with respect to relaxation time σ/τ, (C) electrical conductivity σ and (D) power factor PF as a function of carrier concentration for n-type Mg3Sb2 at 725 K with pressure being 0, 2, 4, 8 and 10 (unit: GPa). The experimental data of the n-type Mg3.2NdxSb1.5Bi0.5,33 Mg3.2PrxSb1.5Bi0.5,25 Mg3Sb1.5−0.5xBi0.5−0.5xTex (ref. 14) and Mg3.07Sb1.5Bi0.5−xSex (ref. 13) samples are plotted for comparison. | ||
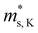 (me) of the K conduction band, single valley effective mass
(me) of the K conduction band, single valley effective mass 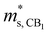 (me) of the CB1 conduction band, conductivity effective mass
(me) of the CB1 conduction band, conductivity effective mass 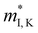 (me) of the K conduction band, conductivity effective mass
(me) of the K conduction band, conductivity effective mass 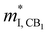 (me) of the CB1 conduction band, the deformation potential Ξ (eV) of the conduction band, and the carrier mobility μ (cm2 V−1 s−1) and relaxation time τ (fs) at 725 K for n-type Mg3Sb2 with pressure being 2, 4, 8 and 10 (unit: GPa), in comparison with the previously reported values at 0 GPa
(me) of the CB1 conduction band, the deformation potential Ξ (eV) of the conduction band, and the carrier mobility μ (cm2 V−1 s−1) and relaxation time τ (fs) at 725 K for n-type Mg3Sb2 with pressure being 2, 4, 8 and 10 (unit: GPa), in comparison with the previously reported values at 0 GPa
As shown in Table 2, the calculated τ for n-type Mg3Sb2 at 2, 4, 8 and 10 GPa are 3.16, 3.29, 3.42 and 3.45 fs, respectively. It is clearly that there is no obvious improvement in τ with the increasing of the pressure, which may be ascribed to the moderately changed μ according to the equation σ = neμ.39 Based on the calculated τ using the deformation potential theory, the σ as a function of carrier concentration for n-type Mg3Sb2 at 725 K with pressure being 0, 2, 4, 8 and 10 GPa are plotted in Fig. 3C. The σ shows an increasing trend as the pressure increases. Owing to the not remarkably increased τ, the contribution of the pressure tuning to the σ is not significant. Combined the calculated S and σ, Fig. 3D presents the PF as a function of carrier concentration for n-type Mg3Sb2 under different pressure. The synergistic effect of the increased S and the moderately changed σ at 4 GPa make the n-type Mg3Sb2 possess the highest PF of ∼19 μW cm−1 K−2 at the carrier concentration of 1 × 1020 cm−3. Therefore, further optimization of the electronic transport properties in n-type Mg3Sb2-based materials can be expected through pressure tuning.
The κ is generally composed of the electronic thermal conductivity (κe) and lattice thermal conductivity (κl). The observed κl of Mg3Sb2-based materials in the experiments can reach the minimum lattice thermal conductivity (κmin).24,25,51 In order to investigate the effect of the pressure on the thermal transport performance, the κmin for Mg3Sb2 at different pressure are calculated using the Cahill's formula:39,40
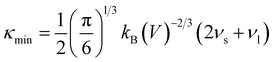 | (4) |
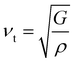 | (5) |
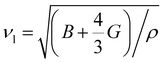 | (6) |
The experimental κe for p-type and n-type Mg3Sb2 at 725 K are in the range of 0.1–0.2 W m−1 K−1 and 0.14–0.36 W m−1 K−1, respectively.23,25,33,34,52 Here, the average κe (0.15 W m−1 K−1 and 0.25 W m−1 K−1 respectively for p-type and n-type sample) and the κmin are applied for estimating the κ. Based on the calculated PF and κ, Fig. 4 shows the simulated zT for p-type and n-type Mg3Sb2 at 725 K with pressure being 0, 2, 4, 8 and 10 GPa, and the comparison with the previously reported experimental data. As can be seen from Fig. 4A, the calculated zT of p-type Mg3Sb2 basically coincide with the experimental data, which demonstrates the correctness of the computational methods. It is found that the zT values of p-type Mg3Sb2 at 2, 4, 8 and 10 GPa are significantly improved compared to the value of the sample at 0 GPa. The largely enhanced thermoelectric performance of the sample by the pressure predominantly originates from the considerably increased PF. As a result, when the carrier concentration reaches 1 × 1020 cm−3, the p-type Mg3Sb2 at 4 GPa exhibits a peak zT of ∼0.62, ∼22% higher than the value of the sample at 0 GPa. Compared to the experimental data, the underestimated zT of n-type Mg3Sb2 calculated by the DFT method can be ascribed to the neglect of the contribution of the Bi doping on the κl and PF6,39 (Fig. 4B). Among all samples, the Mg3Sb2 at 4 GPa shows the best n-type performance with a zT of 1.7 at the carrier concentration of 1 × 1020 cm−3, which is mainly resulting from the increased PF. Based on the above analysis, a conclusion can be drawn that the pressure tuning is an effective method to achieve an enhancement of not only p-type but also n-type thermoelectric performance of Mg3Sb2-based Zintl compounds.
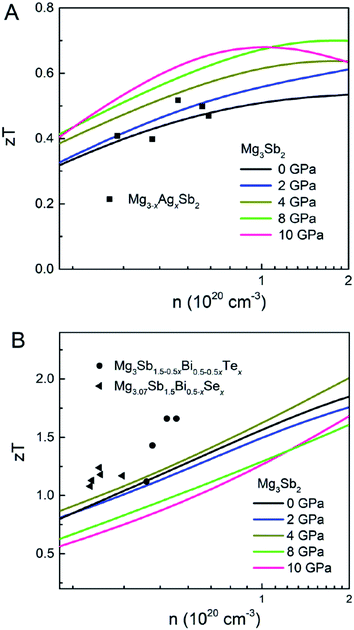 | ||
| Fig. 4 The calculated zT as a function of carrier concentration for (A) p-type and (B) n-type Mg3Sb2 at 725 K with pressure being 0, 2, 4, 8 and 10 (unit: GPa). In (A), the black squares represent the previously reported p-type Mg3−xAgxSb2.23 In (B), the black circles and triangles represent the previously reported n-type Mg3Sb1.5−0.5xBi0.5−0.5xTex and Mg3.07Sb1.5Bi0.5−xSex.13,14 | ||
4. Conclusion
In this work, we have investigated the influence of the pressure on the electronic band structures and p-type and n-type thermoelectric transport properties of Mg3Sb2 by using the density functional theory and semi-classic Boltzmann transport theory. According to the calculated results of the band structure, increasing pressure can lead the energy gaps to first increase and then decrease, and the pressure of 4 GPa can contribute to a peak value of the valley degeneracy of the conduction band. Because of the increased τ, the PF of p-type Mg3Sb2 at 4 GPa and 725 K is increased by ∼35 percent than that of the compound at 0 GPa, thus leading to a considerably enhanced zT of ∼0.62 at the carrier concentration of 1 × 1020 cm−3. Besides its impact on the p-type transports, pressure tuning can also influence the n-type transports of Mg3Sb2. When the pressure increases up to 4 GPa, the n-type sample at the carrier concentration of 1 × 1020 cm−3 can exhibit a high PF of ∼19 μW cm−1 K−2 and a peak zT of 1.7, resulting mainly from the increased density of states effective mass. Therefore, pressure tuning is an effective method to improve the p-type and n-type thermoelectric transport performance of Mg3Sb2-based Zintl compounds. This work on Mg3Sb2 under pressure may provide a new mechanism for experimenters to the enhancement of the thermoelectric performance of materials.Conflicts of interest
There are no conflicts to declare.References
- L. E. Bell, Science, 2008, 321, 1457–1461 CrossRef CAS PubMed.
- B. Jiang, Y. Yu, J. Cui, X. Liu, L. Xie, J. Liao, Q. Zhang, Y. Huang, S. Ning, B. Jia, B. Zhu, S. Bai, L. Chen, S. Pennycook and J. He, Science, 2021, 371, 830–834 CrossRef CAS PubMed.
- J. Mao, H. Zhu, Z. Ding, Z. Liu, G. A. Gamage, G. Chen and Z. Ren, Science, 2019, 365, 495–498 CrossRef CAS PubMed.
- S. Roychowdhury, T. Ghosh, R. Arora, M. Samanta, L. Xie, N. K. Singh, A. Soni, J. He, U. V. Waghmare and K. Biswas, Science, 2021, 371, 722–727 CrossRef CAS PubMed.
- K. Imasato, C. Fu, Y. Pan, M. Wood, J. Kuo, C. Felser and G. J. Snyder, Adv. Mater., 2020, 32, 1908218 CrossRef CAS PubMed.
- K. Imasato, S. D. Kang, S. Ohno and G. J. Snyder, Mater. Horiz., 2018, 5, 59–64 RSC.
- L. Zhao, G. Tan, S. Hao, J. He, Y. Pei, H. Chi, H. Wang, S. Gong, H. Xu, V. P. Dravid, C. Uher, G. J. Snyder, C. Wolverton and M. G. Kanatzidis, Science, 2016, 351, 141–145 CrossRef CAS PubMed.
- C. Chang, D. Wang, D. He, W. He, F. Zhu, G. Wang, J. He and L. Zhao, Adv. Energy Mater., 2019, 9, 1901334 CrossRef.
- Z. Bu, X. Zhang, B. Shan, J. Tang, H. Liu, Z. Chen, S. Lin, W. Li and Y. Pei, Sci. Adv., 2021, 7, eabf2738 CrossRef CAS PubMed.
- X. Chen, H. Wu, J. Cui, Y. Xiao, Y. Zhang, J. He, Y. Chen, J. Cao, W. Cai, S. J. Pennycook, Z. Liu, L. Zhao and J. Sui, Nano Energy, 2018, 52, 246–255 CrossRef CAS.
- Q. Zhu, S. Song, H. Zhu and Z. Ren, J. Power Sources, 2019, 414, 393–400 CrossRef CAS.
- J. Zhang, L. Song, G. K. H. Madsen, K. F. F. Fischer, W. Zhang, X. Shi and B. B. Iversen, Nat. Commun., 2016, 7, 10892 CrossRef CAS PubMed.
- J. Zhang, L. Song, S. H. Pedersen, H. Yin, L. T. Hung and B. B. Iversen, Nat. Commun., 2017, 8, 13901 CrossRef CAS PubMed.
- J. Zhang, L. Song, A. Mamakhel, M. R. V. Jørgensen and B. B. Iversen, Chem. Mater., 2017, 29, 5371–5383 CrossRef CAS.
- A. Bhardwaj, A. Rajput, A. K. Shukla, J. J. Pulikkotil, A. K. Srivastava, A. Dhar, G. Gupta, S. Auluck, D. K. Misra and R. C. Budhani, RSC Adv., 2013, 3, 8504 RSC.
- C. L. Condrona, S. M. Kauzlarich, F. Gascoin and G. J. Snyder, J. Solid State Chem., 2006, 179, 2252–2257 CrossRef.
- K. Imasato, S. D. Kang and G. J. Snyder, Energy Environ. Sci., 2019, 12, 965–971 RSC.
- K. Imasato, S. Ohno, S. D. Kang and G. J. Snyder, APL Mater., 2018, 6, 016106–016111 CrossRef.
- J. Li, S. Zhang, S. Zheng, Z. Zhang, B. Wang, L. Chen and G. Lu, J. Phys. Chem. C, 2019, 123, 20781–20788 CrossRef CAS.
- S. Ohno, K. Imasato, S. Anand, H. Tamaki, S. D. Kang, P. Gorai, H. K. Sato, E. S. Toberer, T. Kanno and G. J. Snyder, Joule, 2018, 2, 141–154 CrossRef CAS.
- Z. Ren, J. Shuai, J. Mao, Q. Zhu, S. Song, Y. Ni and S. Chen, Acta Mater., 2018, 143, 265–271 CrossRef CAS.
- X. Shi, X. Wang, W. Li and Y. Pei, Small Methods, 2018, 2, 1800022 CrossRef.
- L. Song, J. Zhang and B. B. Iversen, J. Mater. Chem. A, 2017, 5, 4932–4939 RSC.
- H. Tamaki, H. K. Sato and T. Kanno, Adv. Mater., 2016, 28, 10182–10187 CrossRef CAS PubMed.
- J. Li, F. Jia, S. Zhang, S. Zheng, B. Wang, L. Chen, G. Lu and L. Wu, J. Mater. Chem. A, 2019, 7, 19316–19323 RSC.
- J. Mao, J. Shuai, S. Song, Y. Wu, R. Dally, J. Zhou, Z. Liu, J. Sun, Q. Zhang, C. d. Cruz, S. Wilson, Y. Pei, D. J. Singh, G. Chen, C. W. Chu and Z. Ren, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 10548–10553 CrossRef CAS PubMed.
- X. Shi, T. Zhao, X. Zhang, C. Sun, Z. Chen, S. Lin, W. Li, H. Gu and Y. Pei, Adv. Mater., 2019, 31, 1903387 CrossRef PubMed.
- J. F. Meng, D. A. Polvani, C. D. W. Jones, F. J. DiSalvo, Y. Fei and J. V. Badding, Chem. Mater., 2000, 12, 197–201 CrossRef CAS.
- S. D. Guo and J. L. Wang, RSC Adv., 2016, 6, 31272–31276 RSC.
- L. Xu, Y. Zheng and J. C. Zheng, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 195102 CrossRef.
- Y. Zhang, S. Hao, L. D. Zhao, C. Wolverton and Z. Zeng, J. Mater. Chem. A, 2016, 4, 12073–12079 RSC.
- D. A. Polvani, J. F. Meng, N. V. C. Shekar, J. Sharp and J. V. Badding, Chem. Mater., 2001, 13, 2068–2071 CrossRef CAS.
- J. Li, S. Zhang, F. Jia, S. Zheng, X. Shi, D. Jiang, S. Wang, G. Lu, L. Wu and Z.-G. Chen, Mater. Today Phys., 2020, 15, 100269 CrossRef.
- X. Tang, B. Zhang, X. Zhang, S. Wang, X. Lu, G. Han, G. Wang and X. Zhou, ACS Appl. Mater. Interfaces, 2020, 12, 8359–8365 CrossRef CAS.
- J. Zhang, L. Song and B. B. Iversen, ACS Appl. Mater. Interfaces, 2021, 13, 10964–10971 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. Li, S. Zhang, B. Wang, S. Liu, L. Yue, G. Lu and S. Zheng, J. Mater. Chem. A, 2018, 6, 20454–20462 RSC.
- J. Li, S. Zheng, T. Fang, L. Yue, S. Zhang and G. Lu, Phys. Chem. Chem. Phys., 2018, 20, 7686–7693 RSC.
- D. J. Singh, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 205102 CrossRef.
- F. Tran and P. Blaha, Phys. Rev. Lett., 2009, 102, 226401 CrossRef PubMed.
- A. Fonari and C. Sutton, Effective Mass Calculator, 2012, http://github.com/afonari/emc Search PubMed.
- G. K. H. Madsen, J. Carrete and M. J. Verstraete, Comput. Phys. Commun., 2018, 231, 140–145 CrossRef CAS.
- J. Bardeen and W. Shockley, Phys. Rev., 1950, 80, 72–80 CrossRef CAS.
- D. G. Cahill, S. K. Watson and R. O. Pohl, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6131–6140 CrossRef CAS PubMed.
- R. Santos, S. A. Yamini and S. X. Dou, J. Mater. Chem. A, 2018, 6, 3328–3341 RSC.
- T. Fang, S. Zheng, T. Zhou, L. Yan and P. Zhang, Phys. Chem. Chem. Phys., 2017, 19, 4411–4417 RSC.
- M. Calderόn-Cueva, W. Peng, S. M. Clarke, J. Ding, B. L. Brugman, G. Levental, A. Balodhi, M. Rylko, O. Delaire, J. P. S. Walsh, S. M. Dorfman and A. Zevalkink, Chem. Mater., 2021, 33, 567–573 CrossRef.
- S. Ding, R. Su, W. Cui, J. Hao, J. Shi and Y. Li, ACS Omega, 2020, 5, 31902–31907 CrossRef CAS PubMed.
- S. W. Song, J. Mao, M. Bordelon, R. He, Y. M. Wang, J. Shuai, J. Y. Sun, X. B. Lei, Z. S. Ren, S. Chen, S. Wilson, K. Nielsch, Q. Y. Zhang and Z. F. Ren, Mater. Today Phys., 2019, 8, 25–33 CrossRef.
- J. Shuai, Y. Wang, H. S. Kim, Z. Liu, J. Sun, S. Chen, J. Sui and Z. Ren, Acta Mater., 2015, 93, 187–193 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra08930g |
| This journal is © The Royal Society of Chemistry 2022 |