Open Access Article
Open Access ArticleAn experimental and theoretical charge density study of theophylline and malonic acid cocrystallization†
Bryson A. Hawkins a,
Jonathan J. Du‡
a,
Jonathan J. Du‡
 a,
Felcia Laia,
Stephen A. Stantona,
Peter A. Williamsab,
Paul W. Groundwater
a,
Felcia Laia,
Stephen A. Stantona,
Peter A. Williamsab,
Paul W. Groundwater a,
James A. Platts
a,
James A. Platts c,
Jacob Overgaard
c,
Jacob Overgaard d and
David E. Hibbs
d and
David E. Hibbs *a
*a
aSydney Pharmacy School, Faculty of Medicine and Health, The University of Sydney, NSW 2006, Australia. E-mail: david.hibbs@sydney.edu.au
bSchool of Science and Health, Western Sydney University, Locked Bag 1797, Penrith, NSW 27513, Australia
cSchool of Chemistry, Cardiff University, Cardiff, CF10 3AT, UK
dDepartment of Chemistry and Centre for Integrated Materials Research (iMAT), Aarhus University, Langelandsgade 140, Aarhus C, DK-8000, Denmark
First published on 23rd May 2022
Abstract
The pharmaceutical agent theophylline (THEO) is primarily used as a bronchodilator and is commercially available in both tablet and liquid dosage forms. THEO is highly hygroscopic, reducing its stability, overall shelf-life, and therefore usage as a drug. THEO and dicarboxylic acid cocrystals were designed by Trask et al. in an attempt to decrease the hygroscopic behaviour of THEO; cocrystallisation of THEO with malonic acid (MA) did not improve the hygroscopic stability of THEO in simulated atmospheric humidity testing. The current study employed high-resolution X-ray crystallography, and Density Functional Theory (DFT) calculations to examine the electron density distribution (EDD) changes between the cocrystal and its individual components. The EED changes identified the reasons why the THEO:MA cocrystal did not alter the hygroscopic profile of THEO. The cocrystal was equally porous, with atomic packing factors (APF) similar to those of THEO 0.73 vs. 0.71, respectively. The THEO:MA (1) cocrystal structure is held together by an array of interactions; a heterogeneous synthon between the imidazole and a carboxylic fragment stabilising the asymmetric unit, a pyrimidine-imidazole homosynthon, and an aromatic cycle stack between two THEO moieties have been identified, providing 9.7–12.9 kJ mol−1 of stability. These factors did not change the overall relative stability of the cocrystal relative to its individual THEO and MA components, as shown by cocrystal (1) and THEO being equally stable, with calculated lattice energies within 2.5 kJ mol−1 of one other. The hydrogen bond analysis and fragmented atomic charge analysis highlighted that the formation of (1) combined both the EDD of THEO and MA with no net chemical change, suggesting that the reverse reaction — (1) back to THEO and MA — is of equal potential, ultimately producing THEO hydrate formation, in agreement with the work of Trask et al. These results highlight that a review of the EDD change associated with a chemical reaction can aid in understanding cocrystal design. In addition, they indicate that cocrystal design requires further investigation before becoming a reliable process, with particular emphasis on identifying the appropriate balance of synthon engineering, weak interactions, and packing dynamics.
Introduction
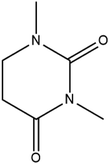
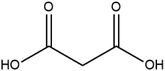
Cocrystal engineering is not a new concept, having been pioneered by Etter and Desiraju in the 1990s, but is steadily expanding in importance as it offers the ability to modify the molecular properties of active pharmaceutical ingredients (APIs).1–3 This is vital in drug development, with many pipeline pharmaceutical agents (99%) not reaching the consumer market due to poor dissolution and stability profiles.1–3 To overcome these undesirable properties, co-crystallisation is employed, informed by rational design techniques, such as, synthon generation, crystal packing modification and charge-transfer complex formation.4–7 All of these approaches include the simple design of relevant bonding networks.4–7 Cocrystals can be created in many ways, including the formation of salts, solvates and multi-component crystals of varied stoichiometry,4–7 but it can be difficult to choose the coformer (CF) required to produce the desired change in a particular physicochemical property. An example of this difficulty is highlighted by a study involving theophylline.8 Theophylline(1,3-dimethylxanthine) (THEO, Fig. 1(a)) is a bronchodilator, however the clinical use of the drug is limited due to issues with its storage and stability, caused by its sub-optimal hygroscopic behaviour and solubility in water.8–10 Trask et al. designed a series of cocrystals involving THEO and various dicarboxylic acids coformers (CFs) in an attempt to modify the hygroscopic profile of THEO.8 One of the dicarboxylic acids studied was malonic acid (MA, Fig. 1(b)), with the cocrystal THEO:MA, (1) found to undergo hydration at the same rate as anhydrous THEO in relative humidity (RH) stability studies.8 This finding differed from other cocrystals investigated in the study and other studies with alternative methylxanthines.8,11,12 For example, THEO:MA and THEO:GLU both form a hydrate but a different time points, THEO:MA failed testing within 1 day of 98% RH exposure while THEO:GLU survived for 3 days under the same conditions.8 It was noted that THEO:MA and the other combinations did not form a THEO:CF-hydrate during the hydration process, rather the dissociation of the THEO:CF crystals occurs at varied rates, followed by the formation of the THEO hydrate.8 As both THEO:MA and THEO:GLU share the designed synthons, and both eventually form a THEO:hydrate, it prompts the question why does THEO:GLU cocrystallization achieve the desired result while THEO:MA did not?8 One means of addressing this question is to review the chemical change between the reactant and products; this may offer greater insight into the failure of the THEO:MA cocrystal, and aid further design attempts involving methylxanthines and/or dicarboxylic acids. This is particularly useful as carboxylic, and dicarboxylic, acids are extensively employed in crystal engineering, for a variety of reasons: (1) they have the ability to act as both a hydrogen bond donor and acceptor, (2) the low pKa values that can create differences of less than 2–3 units from the selected API, this increases the chance for cocrystal formation, and (3) they also give rise to non-linear solubility profiles meaning that they can enhance stability, and also lead to better solubility.13,14 A further benefit is that some dicarboxylic acids are listed on the Food and Drug Authority's Generally Regarded as Safe (GRAS) list, meaning that their combinations with APIs have the potential to be fast-tracked to the clinic.15–18 These factors, and the work of Manallack, highlights the potential for MA and other carboxylic acids to coform with more than 50% of the APIs present in the Williams dataset (a dataset containing a large number of APIs), thus highlighting their potential for re-engineering APIs, to enhance their physicochemical profiles.19,20 However, as mentioned above there is significant variability between which dicarboxylic acid modifies which property, and this requires further investigation. One means of gaining greater understanding is through the investigation of electron density, which, can offer insights into the chemical changes that occur on the electronic level;21–23 understanding the electron density distribution (EDD) of each component of the crystallisation and the overall EDD changes between reactant and product will allow the determination of whether the designed bonds change the overall behaviour of the API.21–23 This will lead to a more detailed understanding of the API to CF relationship and allow a more predictable means of engineering crystals for specific purposes. In this study we explore how the EDD changes in the reaction of THEO(s) + MA(s) → THEO:MA(s) using high-resolution X-ray crystallographic analyses of THEO, MA and THEO:MA (1). The information presented here will aid in the understanding of how specific manipulation of physicochemical properties occurs or, in the case of THEO:MA, does not occur via crystal engineering. The results should aid in the pathway to a more reliable design process when selecting CFs based on EDD changes. | ||
| Fig. 1 Chemical structures of (a) theophylline(1,3-dimethylxanthine, THEO) and (b) malonic acid (MA). | ||
Methods
Experimental methods
For THEO and MA, single crystals suitable for X-ray diffraction were grown via slow evaporation from dry ethanol. The crystals were selected by hand on a rotating stage Olympus microscope and mounted onto a thin glass fibre. The crystals were analysed on a Supernova™ dual source diffractometer at the MoKα (λ = 0.71073) wavelength at The Sydney Pharmacy School, Faculty of Medicine and Health, University of Sydney. The full collection details for THEO and MA can be found in ESI† (Experimental collection details). For THEO:MA (1) single crystals were grown following the method of Trask et al.8 A crystal suitable for diffraction was selected and data was collected at the BL02B1 beamline at the SPring8 synchrotron in Japan. The full details on collection, data treatment and refinement models can be found in ESI† (Experimental collection details). For MA and (1), the resolution was limited to sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λmax = 1.00, this was due to inability to diffract to a higher resolution without introduction of significant radiation damage caused by prolonged exposure. Synchrotron radiation was used for (1) to limit radiation damage as well. The final multipole models reported in the manuscript are thermal diffuse scattering corrected data sets with anisotropic temperature factors (TDS + SHADE) applied to all atoms as previous utilised by our group. Selected crystallographic information can be found in Table 1.
θ/λmax = 1.00, this was due to inability to diffract to a higher resolution without introduction of significant radiation damage caused by prolonged exposure. Synchrotron radiation was used for (1) to limit radiation damage as well. The final multipole models reported in the manuscript are thermal diffuse scattering corrected data sets with anisotropic temperature factors (TDS + SHADE) applied to all atoms as previous utilised by our group. Selected crystallographic information can be found in Table 1.
| (THEO) | (MA) | (1) | |
|---|---|---|---|
| Formula | C7H8N4O2 | C3H4O4 | C7H8N4O2·C3H4O4 |
| Molecular mass | 168.7 | 104.1 | 284.2 |
| Crystal size (mm) | 0.82 × 0.43 × 0.25 | 0.36 × 0.62 × 0.74 | 0.10 × 0.09 × 0.08 |
| Temperature (K) | 150(0) | 150(0) | 20(0) |
| Crystal system | Orthorhombic | Triclinic | Monoclinic |
| Space group | Pna21 | P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) |
C2/c |
| a (Å) | 24.36(2) | 5.16(1) | 17.15(5) |
| b (Å) | 3.78(10) | 5.32(1) | 8.37(2) |
| c (Å) | 8.48(10) | 8.19(1) | 17.49(5) |
| α (°) | 90 | 108.09(1) | 90 |
| β (°) | 90 | 101.25(1) | 106.95(8) |
| γ (°) | 90 | 95.26(1) | 90 |
| Volume (Å3) | 780.51 | 206.77 | 2400.99 |
| Z | 4 | 2 | 2 |
| Refinement method | Full-matrix least-squares on F2 | Full-matrix least-squares on F2 | Full-matrix least-squares on F2 |
| No. of reflections collected | 54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 614 614 |
103![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 698 698 |
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 325 325 |
| No. unique | 9833 | 3476 | 9836 |
| Rint | 0.045 | 0.026 | 0.0243 |
| Completeness (%) | 99.6 | 100 | 97.9 |
| No. reflections used | 8913 | 3472 | 9836 |
| ρc (g cm−1) | 1.53 | 1.67 | 1.57 |
| F(000) | 376.0 | 108.0 | 1184.0 |
| μ (mm−1) | 0.117 | 0.162 | 0.006 |
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λmax θ/λmax |
1.110 | 1.000 | 1.000 |
| Index ranges | 0 ≤ h ≤ 54 | −10 ≤ h ≤ 9 | −34 ≤ h ≤ 32 |
| 0 ≤ k ≤ 8 | −10 ≤ k ≤ 10 | 0 ≤ k ≤ 16 | |
| −18 ≤ l ≤ 18 | 0 ≤ l ≤ 16 | 0 ≤ l ≤ 34 | |
| Thermal Diffuse Scattering (TDS) integration correction factors [a,b] | 0.05, 0.5 | −0.15, −0.05 | 0.05, 0.7 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| IAM refinement | |||
| Final R1, wR2 | 0.0530, 0.1283 | 0.0370, 0.108 | 0.036, 0.072 |
| Goodness of fit | 1.298 | 1.035 | 1.683 |
| Residual density (e Å−3) | −0.37, 0.62 | −0.7, 1.1 | −0.295, 0.813 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Multipole refinement (standard) | |||
| Nobs/Nvar | 26.32 | 18.21 | 17.95 |
| R(F), R(F2), all data | 0.0625, 0.0309 | 0.0242, 0.0869 | 0.0433, 0.0385 |
| Residual density (e Å−3) | −0.310, 0.319 | −0.474, 0.277 | −0.323, 0.406 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Multipole refinement (TDS) | |||
| Nobs/Nvar | 26.32 | 18.15 | 17.95 |
| R(F), R(F2), all data | 0.0578, 0.0245 | 0.0239, 0.0817 | 0.0407, 0.0322 |
| Residual density (e Å−3) | −0.290, 0.253 | −0.391, 0.342 | −0.234, 0.287 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Multipole refinement (SHADE) | |||
| Nobs/Nvar | 26.93 | 18.61 | 18.36 |
| R(F), R(F2), all data | 0.0621, 0.0300 | 0.0285, 0.0809 | 0.0436, 0.0392 |
| Residual density (e Å−3) | −0.305, 0.343 | −0.390, 0.391 | −0.341, 0.380 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Multipole refinement (TDS + SHADE) | |||
| Nobs/Nvar | 26.96 | 18.61 | 17.95 |
| R(F), R(F2), all data | 0.0583, 0.0256 | 0.0285, 0.0761 | 0.0433, 0.0385, 0.0406 |
| Residual density (e Å−3) | −0.223, 0.254 | −0.375, 0.431 | −0.323, 0.406 |
Computational methods
The Cartesian coordinates from the high-order refinements (sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ > 0.7) for each crystal were used as input geometries for the gas phase calculations. Both single-point (SP) and geometry optimisation (OPT) calculations were performed using the Gaussian 09 suite.24 All calculations used the long-range, gradient corrected hybrid exchange correlation three-parameter functional, CAM-B3LYP at the 6-311+G** level of theory.25–27 Topological analysis of the experimental (EXP) electron densities was performed using the XDPROP module of XD and the study the of theoretical electron densities was conducted using the AIMALL package.28,29
θ/λ > 0.7) for each crystal were used as input geometries for the gas phase calculations. Both single-point (SP) and geometry optimisation (OPT) calculations were performed using the Gaussian 09 suite.24 All calculations used the long-range, gradient corrected hybrid exchange correlation three-parameter functional, CAM-B3LYP at the 6-311+G** level of theory.25–27 Topological analysis of the experimental (EXP) electron densities was performed using the XDPROP module of XD and the study the of theoretical electron densities was conducted using the AIMALL package.28,29
Results and discussion
Residual density
The residual density analysis was performed on the MM refinements of all three crystals following the method of Meindl et al.30 The fractal dimensional plots generated from the studies can be found in ESI (Fig. S2–S4†). The results of the analysis were unremarkable, with the residual densities being Gaussian type distributions for all MMs, indicating that the residual densities can be attributed to random noise only.Geometry
The structure and asymmetric unit with bonding arrangements of THEO are depicted in Fig. 2(a) and 3(a), respectively. The asymmetric unit consists of a single molecule of THEO, the primary bond maintaining the unit cell is N(1)–H(1A)⋯N(2). THEO is a planar molecule with a packing system that resembles a parallelogram, which is the result of weak hydrogen bonds extending from the methyl group to the neighbouring carbonyl oxygen, C(7)–H(7C)⋯O(1). These two hydrogen bonds create a curved lattice structure (26.05°, in the 010 plane), which allows for the formation of the hydrogen bond C(1)–H(1)⋯O(2).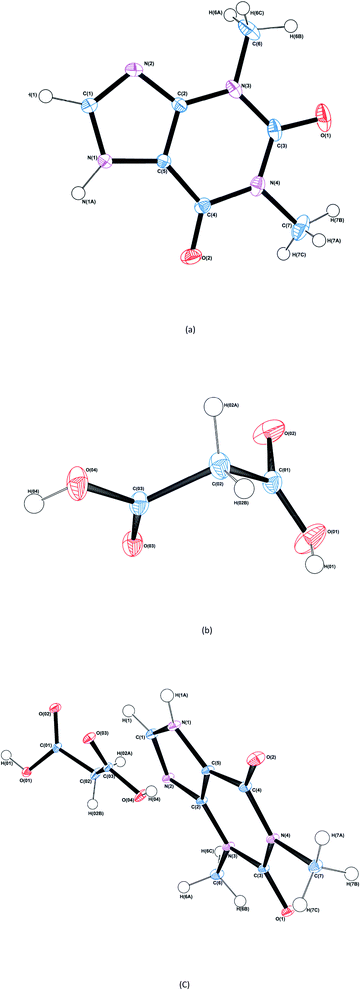 | ||
| Fig. 2 ORTEP diagrams of THEO, (a), MA, (b) and the THEO–MA cocrystal (1), (c). Thermal ellipsoids are shown at the 50% probability level.36 | ||
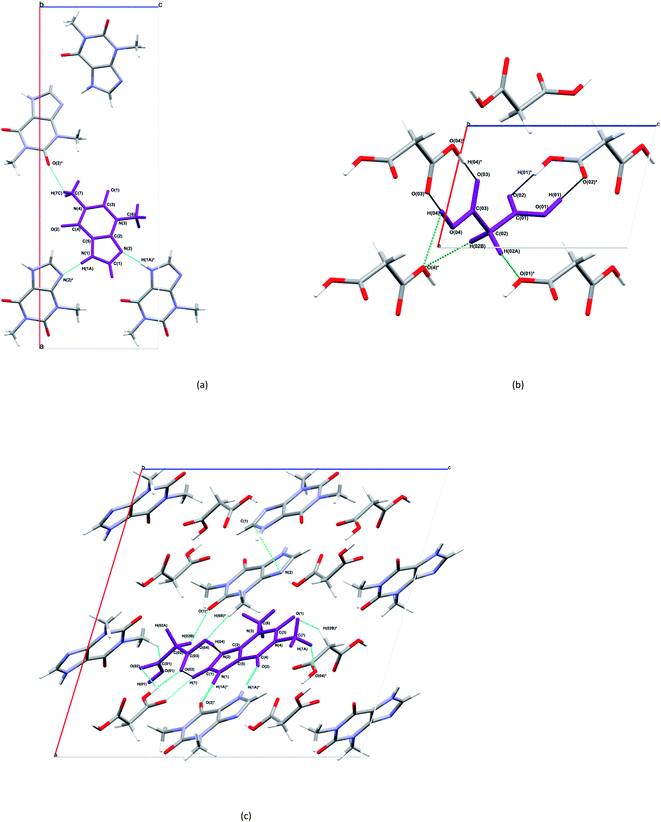 | ||
| Fig. 3 Selected bonding motifs for the asymmetric units of THEO, MA and (1), a,b,c, respectively. Asymmetric units are represented in purple, and non-bonding hydrogen atoms are not labelled for clarity. For THEO, (a), all hydrogen bonds are represented in teal. For MA, (b), the homosynthons are presented in black, and the remaining hydrogen bonds are in green. For (1), (c), the homosynthon is depicted in deep aqua, heterogeneous synthon in black, aromatic cycle stack light green (not on asymmetric unit for clarity), remaining hydrogen bonds are in aqua and hydrogen atoms of methyl groups of THEO moieties are unlabelled unless involved in a hydrogen bond.37 | ||
The structure and asymmetric unit with bonding arrangements of MA are shown in Fig. 2(b) and 3(b), respectively. Fig. 3(b) shows the seven hydrogen bonds that extend from the asymmetric unit of MA, with MA packing along the c-axis in an antiparallel manner, which is a result of MA having a single rotatable carbon C(02). The magnitude of the torsion angle around C(02) is maintained between MA and (1), with [O(04)–C(03)–C(02)–C(01)] of 172.34° and −172.87°, for MA and (1), respectively. This suggests that MA's rotational potential is limited in (1) and that it has limited ability to add flexibility as a CF in the cocrystal. This planar shape causes MA to act as a spacer between repeating THEO and MA molecules in the crystal lattice. This is in agreement with the recent work of Stanton et al., with the MA moiety in the triclinic THEO:MA polymorph having a near identical torsion angle (−172.18°). However, [O(01)–C(01)–C(02)–C(03)], the opposite direction torsion angle of MA's carbon chain is −167.47° in the triclinic form, compared −122.91° in (1) and −91.86° in MA, respectively.31 It is known that minor torsion angle differences can effect packing density by reducing the potential for weak hydrogen bond formation.7 This suggest that in (1) combining THEO and MA caused limited geometrical differences and limits the change in overall packing from THEO.7 It also suggests that the number of methylenes in dicarboxylic acid CFs is a crucial factor in the resultant hygroscopic stabilities between cocrystals, which has been seen previously in the caffeine glutaric acid (CAF:GLU) cocrystal.12
The structure and asymmetric unit with bonding arrangements of (1) are shown in Fig. 2(c) and 3(c), respectively. Fig. 2(c) shows that (1) contains a single molecule of THEO and MA, while Fig. 3(c) shows four hydrogen bonds that maintain the asymmetric unit of (1); two are the internal asymmetric unit intermolecular hydrogen bonds creating the heterogeneous synthon seen between the imidazole ring of THEO and MA; one hydrogen bond is O(04)–H(04)⋯N(2) and the remaining one is the C(1)–H(1)⋯O(03) bond, this synthon will be referred to as Synthon-1 for the remainder of the manuscript. A homosynthon forms between the protonated imidazole nitrogen N(1) and the oxygen of the pyrimidine moiety [N(1)–H(1A)⋯O(2) and vice versa], this will be referred to as Synthon-2. In (1), a bifurcated contact is created by the direction of the carbonyl oxygen from the carboxylic acid (O(03)⋯O(01) and O(02) ···O(01)). This is the result of the previously discussed torsional rotation of C(02) in MA giving direction to hydrogen bonds within the bifurcated hydrogen bond system; this feature is absent in the triclinic polymorph. Further details of the hydrogen bonds will be discussed in hydrogen bond topology.
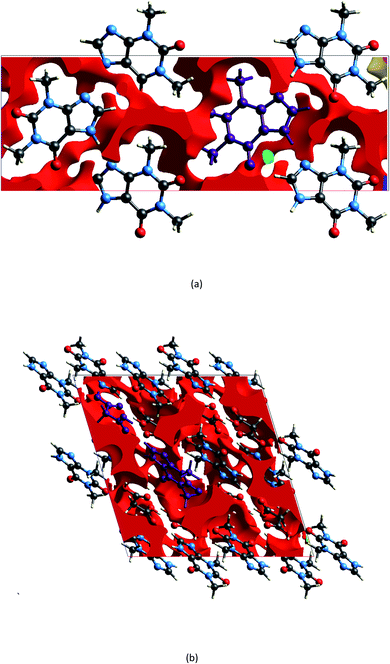
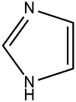
The geometry indicates that the combination of THEO and MA has limited effects on lattice manipulation, particularly for crystal packing dynamics. Although MA introduces a slight level of flexibility, it predominately acts as a spacer in the crystal lattice, limiting the branching of weak hydrogen bonds and the potential to alter the overall lattice stability. To review this further, the changes in geometrical parameters that give information on water penetration are assessed below. The hydration of the crystal phase relies on the intermolecular spaces becoming filled with incoming water molecules, which then outcompete the hydrogen bonding networks. One of the geometrical parameters which is related to hydration is the Atomic Packing Factor (APF), which provides an idea of the possible free atomic space both at the surface and within a crystal lattice.32 The APF for (1) and of THEO were calculated using PLATON.32,33 The APF of (1) was slightly higher than that of THEO, 0.73 vs. 0.71, respectively, but no solvent-accessible spaces were identified within the atomic space for either (1) or THEO.32 An alternative method which can be used to quantify the porosity and potential solvent-accessible space in a crystal lattice is to compare the EDD and promolecule density simultaneously. The promolecule space is that where the EDD ≤ 0, which will be defined as void space, this is the empty space within the crystal lattice that could possibly be penetrated in the hydration process.34 For most crystals this amount of space is limited, however, it can be useful in examining differences created by CF addition in order to limit this space in the solvation process. Turner et al. highlighted that non-porous crystals require an isovalue of 0.003 au for a realistic reflection of accessible space within the crystal, however, a further calculation at 0.0003 au will identify the permanent lattice cavities for solvent infiltration.34 The void volumes were calculated using CrystalExplorer at the isovalues of 0.003 and 0.0003 au; and a simple comparison of the void volume compared to total cell volume determines the void volume percentage, i.e. the proportion of empty space inside the lattice. The results of these calculations and graphical representations are shown in Table 2 and Fig. 4.34,35 It can be seen that both THEO and THEO:MA have very similar void volume to total cell volume percentages (17.22 vs. 15.28%, respectively), indicating once again that their porosities are almost identical. This corresponds to the geometry above, where MA did not change the packing dynamics significantly. As such, the geometrical solvation potential of THEO and (1) are nearly identical, in line with the findings of Trask et al.8 For the triclinic THEO:MA, the void at 0.003 au is 15.87%, indicating that the solvation rates between the polymorphs and THEO should be similar. The near identical geometric results seen in THEO, MA, (1) and the triclinic polymorph of (1) suggest that the individual weak interactions require review to identify the best polymorph of THEO:MA compared to THEO. Overall, the geometric findings suggest that the addition of MA does not decrease any void space between the API. This varies from longer length dicarboxylic acids, THEO:GLU, and CAF:GLU where GLU has more rotational centres on the aliphatic carbon chain increasing the variability of the weak hydrogen bonds.7 However, the caffeine and oxalic acid (CAF:OA) and THEO:OA cocrystals, which are both shorter CFs reduced the hygroscopic decay of the methylxanthines better than MA and GLU due to an increase in strong hydrogen bonds.8,11 This suggests that care is required for CF selection to ensure the requisite balance of weak interaction-mediated lattice staggering, and strong synthon design.11
| Isovalue/au | Volume/Å3 | Surface area/Å2 | % of cell volume | |
|---|---|---|---|---|
| (1) | 0.003 | 367.06 | 1136.51 | 15.28 |
| THEO | 137.84 | 397.24 | 17.22 | |
| (1) | 0.0003 | 0.55 | 5.49 | 0.023 |
| THEO | 0.25 | 3.52 | 0.03 |
Topology of the covalent systems
Bader's Quantum Theory of Atoms in Molecules (QTAIM) was used for topological analysis of both experimental (EXP) and theoretical (SP) models.38 Completeness of the analysis was verified by the satisfaction of Poincaré–Hopf theorem or the Morse relationship, for the SP and EXP models, respectively.21For THEO a reasonable agreement was seen between the SP and EXP models; the average difference of the ρbcp was −0.12 e Å−3 and ∇2ρbcp by 5.61 e Å−5 for all covalent bonds. The full list of the topology of covalent bonds can be found in ESI (Table S9†). The largest difference between the models was seen in the hydrogen bond donor system of N(1)–H(1A), where the EXP model underestimated the ∇2ρbcp by 25.52 e Å−5. This has been seen previously in electronegative bonding environments. A study by Hawkins et al. showed an underestimation of the EXP ∇2ρbcp compared to the theoretical value but this did not affect ρbcp of the internal covalent bond, hydrogen bond or synthon.12 As such the derived products of hydrogen bond strength were not affected in this environment.12 Similarly, the study of Wagner et al. which was at a higher level of experimental resolution found the ∇2ρbcp around the nitrogen species had near identical ρbcp but much lower ∇2ρbcp compared to the theoretical, which also did not affect the derived hydrogen bond strength.12,39
In MA, an overall good agreement was seen between the SP and EXP results. The EXP differing ρbcp by an average of −0.01 e Å−3 and ∇2ρbcp by 0.95 e Å−5 on all covalent bonds; the complete topology can be found in ESI (Table S10†). The largest difference was seen in the ∇2ρbcp of the carboxyl oxygen environments with the largest difference being 28.87 e Å−5 for O(03)–C(03) bond, which has been well reported on in the past.40
For (1), excellent agreement was found between the EXP and SP models. The EXP model subtly overestimating ρbcp by an average of 0.002 e Å−3 and ∇2ρbcp by 0.74 e Å−5 on all covalent bonds. The largest difference was observed in the O(04)–H(04) bond, where the EXP ρbcp was smaller by 0.32 e Å−3, this could be attributed to the lack of a crystal field in the SP models where the intermolecular hydrogen bonding is not considered. All other topological analyses are reported in ESI (Table S11†).
Hydrogen bond topology
In (1) there is a vast increase in the number of hydrogen bond present compared to THEO alone. The hydrogen bond count is more than double that in (1) compared to THEO after MA addition. It is common that an overall number of hydrogen bonds changing is responsible for a variation in physiochemical properties. For example, in CAF:GLU polymorphs there was a variation of just a single hydrogen bond and this was the cause of the slower hydration rates seen between polymorphs.12 This suggests that a comparison of the topological features in hydrogen bonding between reactants and products may reveal why THEO:MA formation did not enhance the hygroscopic profile of THEO. This review can be done in many ways, the ability to identify hydrogen bonds and other interactions is a now standard procedure, e.g. the use of the Hirshfeld surface analysis, which is documented in the ESI† (Hirshfeld Surface and fingerprint statistics ESI pg. 24–27). A less common approach is a topological analysis of EXP data, as performed below. However, prior to this method a good starting point in reviewing CF suitability is to assess the intermolecular bonding potential using the ‘UNI’ force field method developed by Gavezzotti et al., which is embedded in mercury.37,41,42 The ‘UNI’ method calculates the empirical intermolecular potential energy created by bonding throughout a 15 Å cluster.37,41,42 As mentioned in the introduction it is essential to review the overall chemical change for the process:| THEO(s) + MA(s) → THEO:MA(s) |
| −148.1 kJ mol−1 + −106.1 kJ mol−1 → −223.1 kJ mol−1 |
In which the change in energy from reactants to product indicates the stability change through the combination of THEO and MA to form (1). There is an overall change in energy is +31.1 kJ mol−1, indicating that (1) is less stable after cocrystal formation compared to THEO following Trask et al., experimental findings.8 Applying the same methods to the triclinic form by Stanton et al., the results are:
| −148.1 kJ mol−1 + −106.1 kJ mol−1 → −222.9 kJ mol−1 |
As there is also a 1:1 stoichiometry in this crystal the minimal energetic difference between THEO and the triclinic polymorph of (1) is +31.3 kJ mol−1. This is in line with the geometrical findings and previous accounts of stability differences between conformational polymorphs.12,43 For the THEO:GLU system;
| THEO(s) + GLU(s) → THEO:GLU(s) |
| −148.1 kJ mol−1 + −129.6 kJ mol−1 → −255.0 kJ mol−1 |
The overall change is +22.7 kJ mol−1.31 From this it can be presumed that THEO:GLU should not have improved stability from THEO, and it should have failed the humidity testing at a point in time prior to THEO. However, the energetic difference for THEO:GLU compared to THEO is less than (1), suggesting THEO:GLU is more stable than (1). This aligns with the experimental results of the humidity studies where it failed testing at day 3 compared to day 1 for THEO:MA.8 This indicates that the formation of the weak interactions, i.e. hydrogen bonding, in (1) do not slow down hydrate formation, compared to THEO and THEO:GLU from the same study.8 The topological analysis will allow the determination of the importance of each hydrogen bond and provide a better understanding of why the engineered synthons in (1) did not modify the hygroscopic profile of THEO. The topology of the hydrogen bonds in THEO, MA and (1) are discussed below and key parameters are summarised in Tables 3–5. The estimates of the hydrogen bond energies present in THEO, MA and (1) were obtained using methods established by Abramov and Espinosa, and categorised based upon the work of Hibbert et al.; hydrogen bonds classified as weak (EHB < 20 kJ mol−1), moderate (EHB = 20–40 kJ mol−1) and strong (EHB > 60 kJ mol−1).44–47
| Bond | ρ (e Å−3) | ∇2ρ (e Å−5) | ε | dH···bcp (Å) | dA···bcp (Å) | G/Eh (e Å−3) | V/Eh (e Å−3) | H/Eh (e Å−3) | EHB (kJ mol−1) |
|---|---|---|---|---|---|---|---|---|---|
| a G/Eh = kinetic energy density, V/Eh = potential energy density, H/Eh = enthalpy energy density, EHB = hydrogen bond energy a = −x + 3/2, y − 1/2, z − 1/2, b = −x + 3/2, y − 1/2, z + 1/2, c = −x + 1, −y + 1, z − 1/2. * infers symmetrical bond of equal magnitude in opposite direction. | |||||||||
| N(1)–H(1A)⋯N(2)a* | 0.40(5) | 4.48(6) | 0.08 | 0.548 | 1.232 | 0.38 | −0.46 | 0.07 | −88.54 |
| C(1)–H(1)⋯O(1)b | 0.025(3) | 0.04(1) | 0.38 | 1.628 | 1.401 | 0.02 | −0.01 | 0.76 | −2.35 |
| C(7)–H(7C)⋯O(2)c | 0.033(4) | 0.515(2) | 0.24 | 1.2122 | 1.5692 | 0.03 | −0.02 | 0.81 | −3.40 |
| Bond | ρ (e Å−3) | ∇2ρ (e Å−5) | ε | dH···bcp (Å) | dA···bcp (Å) | G/Eh (e Å−3) | V/Eh (e Å−3) | H/Eh (e Å−3) | EHB (kJ mol−1) |
|---|---|---|---|---|---|---|---|---|---|
| a G/Eh = kinetic energy density, V/Eh = potential energy density, H/Eh = enthalpy energy density, EHB = hydrogen bond energy. Symmetry operators: a = 1 − x,−y,−z. b = 1 − x, 2 − y, 1 − z. c = 2 − x,1 − y,−z. d = 2 − x,1 − y,−z. e = 2 − x,−y,−z. * infers symmetrical bond of equal magnitude in opposite direction. | |||||||||
| O(04)–H(04)···O(03)a* | 0.218(03) | 0.218(32) | 0.01 | 0.55 | 1.13 | 0.29 | −0.24 | 0.05 | −47.05 |
| O(01)–H(01)···O(02)b* | 0.230(02) | 5.408(40) | 0.06 | 0.55 | 1.11 | 0.32 | −0.27 | 0.06 | −51.56 |
| C(02)–H(02B)⋯O(04)c* | 0.023(7) | 0.570(2) | 0.74 | 1.0278 | 1.5986 | 0.03 | −0.02 | 0.01 | −3.17 |
| C(02)–H(02A)···O(01)d | 0.031(5) | 0.538(2) | 0.26 | 1.09 | 1.58 | 0.03 | −0.02 | 0.01 | −3.40 |
| O(04)–H(04)⋯O(04)e | 0.091(0) | 1.301(1) | 0.35 | 1.49 | 2.36 | 0.08 | −0.06 | 0.02 | −11.67 |
| Bond | ρ (e Å−3) | ∇2ρ (e Å−5) | ε | dH···bcp (Å) | dA···bcp (Å) | G/Eh (e Å−3) | V/Eh (e Å−3) | H/Eh (e Å−3) | EHB (kJ mol−1) |
|---|---|---|---|---|---|---|---|---|---|
| a G/Eh = kinetic energy density, V/Eh = potential energy density, H/Eh = enthalpy energy density, EHB = hydrogen bond energy. Symmetry operators: a = −x + 3/2, −y − 1/2, −z + 1; b = −x + 3/2, y − 1/2, −z + 1/2; c = −x + 3/2, y + 1/2, −z + 1/2; d = −x + 1, −y + 1, −z + 1. * infers symmetrical bond of equal magnitude in opposite direction. | |||||||||
| Interactions within the asymmetric unit | |||||||||
| O(04)–H(04)···N(2) | 0.36(23) | 4.68(33) | 0.06 | 0.52 | 1.11 | 0.36 | 0.40 | 0.04 | −77.9 |
| C(1)–H(1)⋯O(03) | 0.06(03) | 0.71(1) | 0.06 | 1.17 | 1.49 | 0.04 | −0.03 | 0.01 | −5.8 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||
| Interactions outside the asymmetric unit | |||||||||
| O(01)–H(01)⋯O(03)a | 0.17(23) | 4.66(29) | 0 | 0.55 | 1.18 | 0.26 | 0.19 | 0.07 | −37.2 |
| O(01)–H(01)⋯O(02)a | 0.08(2) | 0.99(1) | 0.24 | 1.15 | 1.41 | 0.06 | 0.04 | 0.1 | −8.7 |
| C(1)–H(1)⋯O(02)b | 0.07(12) | 1.68(3) | 0.12 | 0.81 | 1.35 | 0.09 | 0.06 | 0.03 | −11.7 |
| N(1)–H(1A)⋯O(2)a* | 0.21(22) | 4.35(22) | 0.02 | 0.59 | 1.15 | 0.26 | 0.22 | 0.04 | −43.2 |
| C(6)–H(6B)⋯O(04)c | 0.05(3) | 0.79(1) | 0.37 | 1.01 | 1.49 | 0.04 | −0.03 | 0.01 | −20.8 |
| C(02)–H(02B)⋯O(1)c | 0.05(1) | 0.70(1) | 0.13 | 1.07 | 1.49 | 0.04 | −0.03 | 0.01 | −5.2 |
| C(7)–H(7C)⋯O(01)d | 0.05(2) | 0.62(1) | 0.39 | 1.17 | 1.49 | 0.04 | −0.03 | 0.01 | −4.7 |
There are three hydrogen bonds present in THEO: two are carbon donated hydrogen bonds that are weak and ‘non-classical’ that fit the definitions of Munshi et al. and Koch et al.48,49 These bonds offer minimal packing stabilization to the system but create the curved packing arrangement, shown above in Fig. 3(a). The two carbon donated hydrogen bonds have minimal contribution to the overall stability of THEO. The remaining hydrogen bond N(1)–H(1A)⋯N(2) is ‘classical’ with a strong interaction energy (−88.54 kJ mol−1). It has previously been shown that nitrogen based hydrogen bond systems with near identical Donor-Atom–Hydrogen-atom–Acceptor-Atom-Angles (DHAA°) result in stronger hydrogen bond energies.50 To examine if this was the case in THEO, the ∇2ρ was analyzed to find the (3,−3) critical point for the N(2) lone pair of electrons (LP) and the coordinates of the critical point were then reviewed in mercury.37 It was found that the LP of N(2) are located at 177.36° from the D–H, N(1), and the bond is almost linear, with a DHAA° of 178.25°, in agreement with previous findings.12,51,52 The bond is represented below in Fig. 5, in which the −∇2ρbcp contour plot clearly shows the linear direction of the bond, with the trajectory of H(1A) aligning with the LP of N(2)*. For THEO, the summed total of the topologically-derived hydrogen bond strengths suggests that a further −34.7 kJ mol−1 of stabilisation occurs from hydrogen bonding in THEO compared to the ‘UNI’ energies.
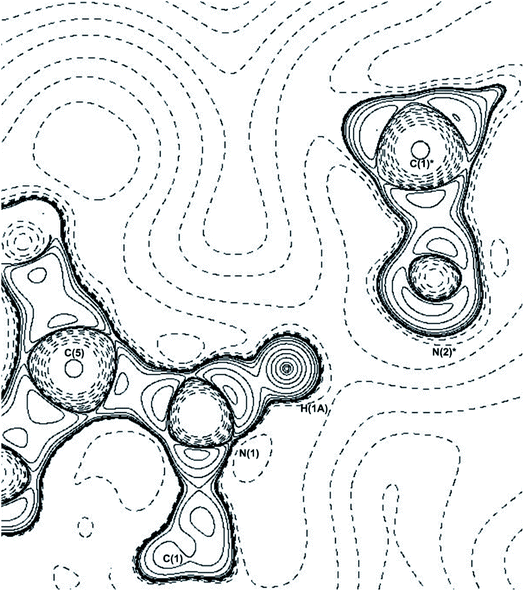 | ||
| Fig. 5 −∇2ρ contour plot of the N(1)–H(1A)⋯N(2)* hydrogen bond, * = symmetry operator: −x + 3/2, y − 1/2, z − 1/2. Plotted along C(5)–N(1)–C(1)* plane. | ||
In MA, seven hydrogen bonds were identified, in agreement with previous charge density studies.40 Three hydrogen bonds are weak, two of which are the ‘non-classical’ hydrogen bonds from the methylene group, H(02A) and H(02B). These bonds introduce approximately −3.0 kJ mol−1 to the stabilisation of MA.40 The remaining hydrogen bonds stem from the carboxyl regions alone; these four hydrogen bonds consist of two homosynthons, O(01)–H(01)⋯O(02) and vice versa, and O(04)–H(04)⋯O(03), and vice versa. These homosynthon bonds are strong, corresponding to the ‘classic’ nature of the hydrogen bonds, with topologically derived strengths of −51.56 and −47.05 kJ mol−1, for O(01)–H(01)⋯O(02) and O(04)–H(04)⋯O(03), respectively. The last hydrogen bond is O(04)–H(04)⋯O(04), in the 2 − x,−y,−z plane. This bond is weak compared to the homosynthon mentioned above, as it is formed in a charge depleted region on the oxygen atom. This bond provides −11.67 kJ mol−1 of stabilisation to the MA lattice. Overall, the summated strengths of these hydrogen bonds are close to the ‘UNI’ strengths above with the summed topological values being −10.75 kJ mol−1 higher.
For (1) all previously reported 10 hydrogen bonds were identified topologically.53 A triangular bifurcated hydrogen bond system was identified between MA moieties in (1) (Fig. 6(a)). The −∇2ρ contour plot shows the carbonyl oxygen of O(02)'s LP being repulsed to 108° by the adjacent MA's O(O1). The valence shell charge concentration (VSCC) indicates that both carbonyl oxygen atoms are charge deplete, (∇2ρ < 0). This creates the trajectory for the hydrogen bonds between O(03)⋯H(01)*–O(01)* and O(02)⋯H(01)*–O(01)*, making up two sides of the triangle. The last side of the triangle is created by a contact between the carbonyl oxygens of O(02) and O(03) of MA where the −∇2ρ collide with the positive curvature of the ∇2ρ from the perpendicular O(01)*. This creates a ring critical point (RCP) with the −x + 3/2, y + 1/2, −z + 1/2 MA. The gradient vector field of ρ plot, Fig. 6(b), indicates the direction of the maximum ρ leaving the nucleus of each atom. This is a useful feature here, as it clearly shows where the atomic boundaries collide with an alternative atoms' trajectory along the zero-flux surface. Fig. 6(b) clearly reveals the critical points between atoms forming the triangle as represented by the collision lines that resemble the cross sections of the triangle. The estimated hydrogen bond strengths are −37.2 kJ mol−1 and −8.7 kJ mol−1 for O(03)⋯H(01)*–O(01)* and O(02)⋯H(01)*–O(01)*, respectively. The variation in the hydrogen bond strengths are due to the direction of the LP elections to the BCP, in this case the O(03)⋯H(01)*–O(01)* bond forms the more direct BCP as clearly indicated in the −∇2ρ contour plot.
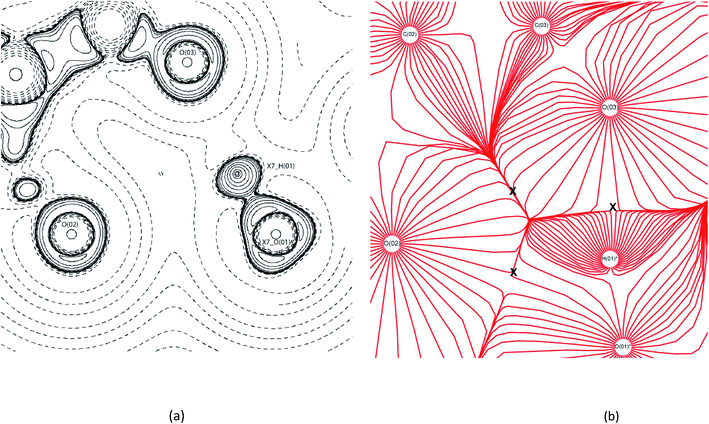 | ||
| Fig. 6 EXP contour (a) −∇2ρ and (b) trajectory gradient of ρ contour diagrams of bifurcated triangular bond formation in (1). X7_AtomLabel = symmetry operator: −x + 3/2, y + 1/2, −z + 1/2. In (b) the X indicates the locations of bond formation.54 | ||
An antiparallel aromatic cycle stack was identified topologically in (1). It is formed by the symmetrical contact between C(1)⋯N(2). This creates a RCP with two linking points, ρring 0.017e Å−3, and ∇2ρring 0.2 e Å−3. Waller et al. calculated validated energies for aromatic cycle stacking systems, based on the ρring and the number of linking points.55 Using these methods the interaction energy provided by the aromatic cycle stack in (1) is estimated to be 9.7–12.9 kJ mol−1.55
There are two synthons within the hydrogen bonds present in (1). Synthon-1 (defined above in geometry) between carboxylic acid of MA and the imidazole of THEO, and Synthon-2 between the imidazole and pyrimidine of THEO (defined above in geometry).8
Synthon-1 makes a ring system that is the primary hydrogen bonding arrangement maintaining (1). The hydrogen bonds making Synthon-1 are O(04)–H(04)⋯N(2) and C(1)–H(1)⋯O(03). O(04)–H(04)⋯N(2) is shorter and more linear compared to the C(1)–H(1)⋯O(03), (2.65 Å, 171.3°, and 3.2 Å, 116.2° respectively). Synthon-1 is formed by a strong and a weak bond, with strengths of −77.9 and −5.8 kJ mol−1 for O(04)–H(04)⋯N(2) and C(1)–H(1)⋯O(03), respectively. The hydrogen bond strengths in the Synthon-1 vary significantly, this is because they are different hydrogen bond types ‘classical’ and ‘non-classical’, respectively.56 Synthon-2 is created by symmetrical N(1)-H(1A)⋯O(2) hydrogen bonds. The synthon is stabilised by a near-linear DHAA° of 171.1° and bond length of 2.70 Å of N(1)–H(1A)⋯O(2). Synthon-2's hydrogen bonds are strong, with strengths of −43.2 kJ mol−1 for N(1)–H(1A)⋯O(2). The strength of the N(1)–H(1A)⋯O(2) is caused by the relationship of N(1)–H(1A)⋯O(2) and N(1)–H(1A)⋯LP angles, which are near linear. The DHAA° and DH-LP differ by only 2° (172° vs. 174°, respectively), this creates the two strong hydrogen bonds, aligning with previous topological experiments.1,12,39,52,57 Fig. 7 shows the −∇2ρ contour plots of the Synthon-1 and Synthon-2. For Synthon-1 the contour plot show the LP of N(2) being heavily polarised towards H(04), and in Synthon-2 the LP of O(2) is clearly being directed towards the H(1A). This makes it clear that the DHAA° and DH-LP relationship is a reliable indicator of potential hydrogen bond direction and strength.50,51,58
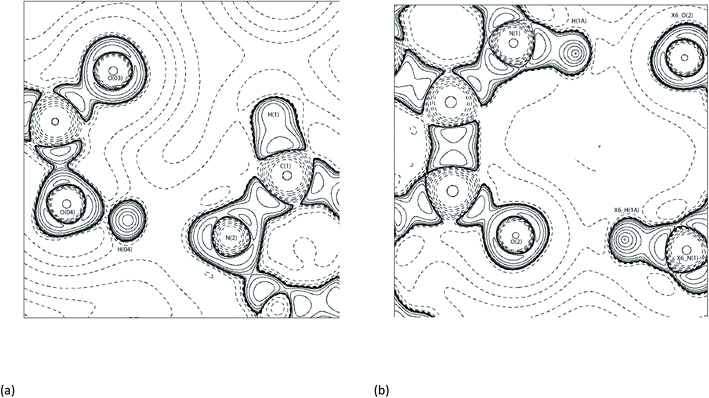 | ||
| Fig. 7 Contour −∇2ρ diagrams of (a) Synthon-1. Symmetry operator: x, y, z and (b) Synthon-2 in (1) with X6_AtomLabel is Symmetry operator: x + 3/2, y + 1/2, −z + 1/2.54 | ||
For (1) the remaining hydrogen bonds are all classified as weak ‘non-classical’ hydrogen bonds, with strengths ranging from −4.7 to −11.67 kJ mol−1.44 Although individually the hydrogen bonds are weak, when summed together they provide −26.96 kJ mol−1 stabilisation to the asymmetric unit. Bernstein et al. discussed the role of ‘non-classical’ hydrogen bonds in crystal packing, highlighting the importance of these bonds to create staggering of the hydrogen bonds throughout the crystal lattice.7 In (1), 22% of the hydrogen bonds are ‘non-classical’, this is less than what was seen in CAF:GLU (∼70%, in both polymorphs).12 In the case of CAF:GLU a single weak ‘non-classical’ hydrogen bond was the cause of the stability differences seen in the polymorphs noting the importance of the weak hydrogen bonds to give depth in the packing arrangement.12 As discussed in geometry, the planar shape of MA and THEO in (1) limits the number of these staggered hydrogen bonds able to form. Hence, it results in limited packing diversity, which is why THEO:MA did not improve the hygroscopic stability of THEO in (1). It also highlights that the minimal geometric change of MA in (1) results in the equal redistribution of the EDD in hydrogen bond formation between reactant and products. Lastly, the summed topological hydrogen bond strengths found for (1) were in good agreement with the values derived from the ‘UNI’ method. The topological summed hydrogen bond strengths were a further −35.1 kJ mol−1 more stable than the ‘UNI’ method (−258.3 and −223.1 kJ mol−1, respectively). Interestingly, the summed total of THEO and MA ‘UNI’ method intermolecular potential values correlate more closely (4.1 kJ mol−1) to the experimental topological findings (−254.2 and −258.3 kJ mol−1, respectively). This correlation of the ‘UNI’ method is useful for further crystal engineering as it is a simple way to predict whether the process of combining two compounds may form a better crystal. Reviewing the chemical reaction process with the values from the topological studies;
| THEO(s) + MA(s) → THEO:MA(s) |
| −182.83 kJ mol−1 + −116.85 kJ mol−1 → −258.3 kJ mol−1 |
Shows a net decrease in the stability of (1) by +41.38 kJ mol−1 on experimental hydrogen bond energies. This corresponds with the ‘UNI’ method, and the findings of Trask et al.8 It is probable that the number of hydrogen bonds remaining equal between the reactants (THEO and MA) and products [(1)] forces a net equal redistribution of the EDD, with no further enhancement of stability compared to THEO as seen experimentally in the hydration studies.8
Electrostatic potential and atomic charges
The electrostatic potential (ESP) mapped onto an isosurface of ρ (Fig. 8) can give vital information on intermolecular bonds. Fig. 8(a), shows THEO is neutral across the whole molecule with no electrostatic pooling in bonding regions. For Fig. 8(b), (1), the ESP isosurface indicates the high level of electrostatic complementarity within Synthon-1. It is clearly shows the electronegative N(2) and O(03) are involved the formation of the hydrogen bonds. For the THEO fragment in (1) the isosurface exhibits electronegative pooling around the carbonyl groups which is important in the formation of Synthon-2. The carbonyl of the pyrimidine ring (electronegative) and protonated hydrogen of the imidazole ring (electropositive) are visualised clearly. Also in Fig. 8(b) the triangular bifurcated arrangement is clearly visualised. The complementarity of both the carboxyl [O(02) and O(03)] is seen via the corresponding electropositive region of H(01), creating the hydrogen bonds O(03)···H(01)–O(01), and O(02)⋯H(01)–O(01). The methylene group of C(02) is significantly electropositive in Fig. 8(b). This facilitates its interaction with the electronegative O(1) of the pyrimidine ring, forming a hydrogen bond. This data reflects the fingerprint plots in ESI (Tables S16–S18†) that highlighted the hydrogen bond formed in (1) to mainly involve the carbonyl and carboxyl oxygens. This highlights the importance to carboxylic acids in crystal engineering, inclusive of MA as CFs because they provide an increased number of oxygen atoms to the system that raises the hydrogen bond formation propensity. However, overall the limited change in electrostatic charge for THEO in both systems, resembled by the net neutral isosurface further indicates why the two crystals hydrated at the same rate.8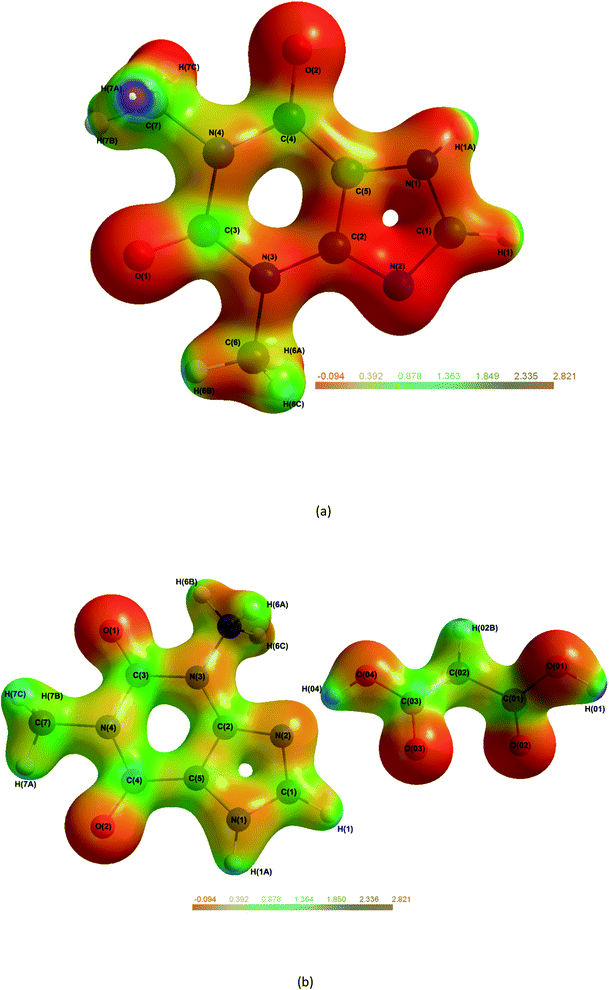 | ||
| Fig. 8 Molecular electrostatic potential maps of THEO, (a) and (1), (b) mapped on an isosurface of ρ. Plots generated at ±0.5e isoelectron density NB: in (1) H(02A) is out of plane.61 | ||
Another method to evaluate whether there was net equal EDD redistribution in the reaction of THEO(s) + MA(s) → THEO:MA(s) is to consider the atomic charges as fragments.62 This can be performed using the Bader charges found by integration of the zero-flux surface, and summing the charges for the atoms confined to a fragment. The fragments are defined by chemical components, i.e., a section that would have individual bonding abilities. This results in the imidazole and pyrimidine being separated for THEO, and MA remaining a single fragment due to its symmetrical structure, these fragments are summarised in Table 6.
From Table 6 it is evident that combining THEO with MA (1) results in a near identical magnitude of atomic charge in the imidazole fragment. However, it is in opposite directions, this charge shift occurs in (1) due to forming both Synthon-1 and -2. The total charges across the system follow the trend seen in the ESP plots and hydrogen bonding section indicating that overall, no net charge change occurs. This suggests two possible outcomes when water interacts with (1). (1), that both THEO and (1) have the same electronic potential to react with incoming water molecules and both hydrate at a similar rate or, (2) that upon water contact with (1) the weak interactions between THEO:MA are outcompeted causing the reverse reaction back to the reactants [THEO:MA → THEO + MA], resulting in the identical hydration rates seen experimentally as (1) is behaving as THEO.8
Lattice energies
Lattice energies reflect the amount of energy required to deconstruct the crystal lattice. As above discussed with the ‘UNI’ method it is vital to explore the process of THEO(s) + MA(s) → THEO:MA(s). For (1) the relative stability improvement caused by crystal engineering can be determined by the energy change in the above process. The lattice energies were calculated for THEO, MA and (1), and then relative stability is calculated by reviewing the chemical process. The lattice energies were calculated using CrystalExplorer (CE), this method summates the pairwise interaction energies between molecules in a 25 Å cluster from a DFT wavefunction following the methods of Thomas et al. and the results are shown in Table 7.35,43| Method | Functional and basis set | Lattice energy (kJ mol−1) | |
|---|---|---|---|
| THEO | CE | B3LYP/6-31G(d,p) pair-wise corrected | −139.7 |
| MA | CE | B3LYP/6-31G(d,p) pair-wise corrected | −125.4 |
| (1) | CE | B3LYP/6-31G(d,p) pair-wise corrected | −267.6 |
The lattice energies show that (1) is equally stable to THEO with an energy difference of −2.5 kJ mol−1. This difference is so small it could be attributed to experimental error in the wavefunction calculation. This data like the ‘UNI’ method indicates that the MA addition did not improve the stability of THEO to THEO:MA. The near identical lattice energies also follow the findings of Taylor et al., where most API:CF combinations have limited change in overall stability (average of 8 kJ mol−1).63 However, using this process it was noted that the reported lattice energies for the Triclinic polymorph of THEO:MA may not truly reflect the crystals relative stability. In turn, the new lattice energy for the Triclinic THEO:MA is −231.7 kJ mol−1, suggesting a decrease in the stability compared to THEO of 21.1 kJ mol−1, and it is less stable compared to (1) by 35.9 kJ mol−1.31 These results may suggest the Triclinic polymorph is a metastable intermediate of (1), which has been seen previously for methylxanthines in the case of CAF:GLU.11,12,64 Another method to review stability is comparing molecular dipole moments (MDMs). The MDM is enhanced in the crystal state and indicates the likely hood of reacting with a polar solvent (water in this case), the higher the MDM the more reactive the molecule is in presence of a polar solvent. Logically, to compare THEO to THEO:MA it is important to compare the MDM across THEO alone. In this case it is 9.19 D for THEO and 3.02 D in (1) (MA is 6.5 D and MA in (1) is 4.0 D). This suggests combining THEO with MA results in a subtle lowering of the MDM. This indicates that when (1) interacts with a polar solvent i.e. water it may react less rapidly, but physical testing would be required to confirm this.
The lattice energies alongside the MDMs above indicate that THEO when combined with MA did not change the stability of (1) compared to THEO. The results follow the findings from Trask et al. experiments, where the cocrystal of (1) responded in the same way as THEO throughout humidity testing.8
Conclusion
An EDD study of the monoclinic THEO:MA, (1) cocrystal originally identified by Trask et al. and the individual components, THEO, and MA, has been performed.8 It was found by examining the geometrical and EDD changes that there was no defining change between reactants to products. This explained why THEO hydrate formation occurs at an equal rate for THEO and (1).8 The cocrystal, (1), is constituted by one molecule of THEO and MA in the asymmetric unit. (1) was found to have a near identical APF in comparison to THEO, (0.73 and 0.71 respectively). Geometrically this was caused by the lack of torsional flexibility of MA. Although (1) is held together by a larger number of interactions, including synthons, an aromatic cycle stacking system, and a considerable number of strong hydrogen bonds (the most significant being; −77.97 kJ mol−1). These stabilising factors made no difference to the overall enhancement of (1) compared to THEO with the summed total of ‘UNI’ and topological hydrogen bond strengths for the THEO and MA components being more stable than (1). This was due to the change in the strong hydrogen bond EDD being equal between THEO, MA, and THEO:MA. The ESPs and atomic charges further showed that the formation of THEO:MA did not cause any defining charge movement from THEO to THEO:MA. This suggests that the potential to undergo hydration is equal in both THEO and THEO:MA. The lattice energies and stability factor review, showed (1) was slightly more stable than THEO alone when comparing lattice energies, (−2.5 kJ mol−1).63 This minor increase in stability really indicates that no improvement is made in (1) from THEO alone matching Trask et al. experimental finding.8 Overall, this study showed that the information provided from experimental charge density studies is able to review the chemical change process on an EDD level. This study also indicated that further work is required on selecting the best CF for crystallisation, where there is still large ambiguity. Further work should be performed by reviewing the experimental EDD of THEO:GLU and THEO:OA to formalise the results.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
The synchrotron experiment was performed on beamline BL02B1 at SPring-8 with the approval of the Japan Synchrotron Radiation Research Institute as a Partner User (proposal no. 2016B0078). This work was supported by the Danish National Research Foundation (DNRF-93). The authors would like to acknowledge the Gadigal people of the Eora Nation as traditional custodians of the land upon where we work, and where this research was conducted. All authors pay their respects to Elders past, present and emerging. S. A. S., F. L. and B. A. H. would like to thank The University of Sydney for scholarships.References
- M. C. Etter, Acc. Chem. Res., 1990, 23, 120–126 CrossRef CAS.
- G. R. Desiraju, Angew. Chem., Int. Ed., 1995, 34, 2311–2327 CrossRef CAS.
- N. Qiao, M. Li, W. Schlindwein, N. Malek, A. Davies and G. Trappitt, Int. J. Pharm., 2011, 419, 1–11 CrossRef CAS PubMed.
- C. C. Sun, Expert Opin. Drug Delivery, 2013, 10, 201–213 CrossRef CAS PubMed.
- L. Sun, Y. Wang, F. Yang, X. Zhang and W. Hu, Adv. Mater., 2019, 31, 1902328 CrossRef PubMed.
- D. J. Berry and J. W. Steed, Adv. Drug Delivery Rev., 2017, 117, 3–24 CrossRef CAS PubMed.
- J. Bernstein, M. C. Etter and L. Leiserowitz, Struct. Correl., 1994, 431–507 CAS.
- A. V. Trask, W. D. Motherwell and W. Jones, Int. J. Pharm., 2006, 320, 114–123 CrossRef CAS PubMed.
- S. Zhang and Å. C. Rasmuson, CrystEngComm, 2012, 14, 4644 RSC.
- S. Zhang and Å. C. Rasmuson, Cryst. Growth Des., 2013, 13, 1153–1161 CrossRef CAS.
- A. V. Trask, W. D. S. Motherwell and W. Jones, Cryst. Growth Des., 2005, 5, 1013–1021 CrossRef CAS.
- B. A. Hawkins, J. Han, J. J. Du, F. Lai, S. A. Stanton, S. S. Divakarla, P. W. Groundwater, J. A. Platts and D. E. Hibbs, Cryst. Growth Des., 2021, 21, 4456–4467 CrossRef CAS.
- D. J. Good and N. Rodriguez-Hornedo, Cryst. Growth Des., 2009, 9, 2252–2264 CrossRef CAS.
- D. P. McNamara, S. L. Childs, J. Giordano, A. Iarriccio, J. Cassidy, M. S. Shet, R. Mannion, E. O'Donnell and A. Park, Pharm. Res., 2006, 23, 1888–1897 CrossRef CAS PubMed.
- FDA, Alphabetical List of SCOGS Substances, https://www.fda.gov/Food/IngredientsPackagingLabeling/GRAS/SCOGS/ucm084104.htm, 2014 Search PubMed.
- O. Almarsson and M. J. Zaworotko, Chem. Commun., 2004, 1889–1896, 10.1039/b402150a.
- A. J. Cruz-Cabeza, CrystEngComm, 2012, 14, 6362–6365 RSC.
- S. Ebenezer and P. T. Muthiah, Cryst. Growth Des., 2012, 12, 3766–3785 CrossRef CAS.
- D. T. Manallack, Perspect. Med. Chem., 2007, 1, 25–38 Search PubMed.
- D. Williams and T. Lemke, pKa values for some drugs and miscellaneous organic acids and bases, Baltimore/Philadelphia, Lippincott Williams & Wilkins, 2002 Search PubMed.
- P. Coppens, X-Ray Charge Densities and Chemical Bonding, Oxford University Press, New York, 1997 Search PubMed.
- G. R. Desiraju, Chem. Commun., 1997, 1475–1482, 10.1039/a607149j.
- V. R. Hathwar, T. S. Thakur, T. N. G. Row and G. R. Desiraju, Cryst. Growth Des., 2011, 11, 616–623 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- Y. Tawada, T. Tsuneda, S. Yanagisawa, T. Yanai and K. Hirao, J. Chem. Phys., 2004, 120, 8425–8433 CrossRef CAS PubMed.
- A. Volkov, P. Macchi, L. J. Farrugia, C. Gatti, P. Mallinson, T. Richter, and T. Koritsanszky, XD2006-a computer program package for multipole refinement, topological analysis of charge densities and evaluation of intermolecular energies from experimental and theoretical structure factors, University at Buffalo, State University of New York, NY, USA, 2006 Search PubMed.
- T. A. Keith, "AIMAll." Version 19, 2017, p. 12 Search PubMed.
- K. Meindl and J. Henn, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 404–418 CrossRef CAS PubMed.
- S. A. Stanton, J. J. Du, F. Lai, G. Stanton, B. A. Hawkins, J. A. Ong, P. W. Groundwater, J. A. Platts and D. E. Hibbs, J. Phys. Chem. A, 2021, 125(45), 9736–9756 CrossRef CAS PubMed.
- A. Spek, Acta Crystallogr., Sect. A: Found. Crystallogr., 1990, 46, c34 Search PubMed.
- Y. Ebisuzaki, P. D. Boyle and J. A. Smith, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1997, 53, 777–779 CrossRef.
- M. J. Turner, J. J. McKinnon, D. Jayatilaka and M. A. Spackman, CrystEngComm, 2011, 13, 1804–1813 RSC.
- P. R. Spackman, M. J. Turner, J. J. McKinnon, S. K. Wolff, D. J. Grimwood, D. Jayatilaka and M. A. Spackman, J. Appl. Crystallogr., 2021, 54, 1006–1011 CrossRef CAS PubMed.
- L. J. Farrugia, J. Appl. Crystallogr., 1997, 30, 565 CrossRef CAS.
- C. F. Macrae, I. Sovago, S. J. Cottrell, P. T. A. Galek, P. McCabe, E. Pidcock, M. Platings, G. P. Shields, J. S. Stevens, M. Towler and P. A. Wood, J. Appl. Crystallogr., 2020, 53, 226–235 CrossRef CAS PubMed.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford Univ. Press, 1994 Search PubMed.
- A. Wagner, R. Flaig, B. Dittrich, H. Schmidt, T. Koritsánszky and P. Luger, Chem.–Eur. J., 2004, 10, 2977–2982 CrossRef CAS PubMed.
- R. Srinivasa Gopalan, P. Kumaradhas, G. U. Kulkarni and C. N. R. Rao, J. Mol. Struct., 2000, 521, 97–106 CrossRef CAS.
- A. Gavezzotti, Acc. Chem. Res., 1994, 27, 309–314 CrossRef CAS.
- A. Gavezzotti and G. Filippini, J. Phys. Chem., 1994, 98, 4831–4837 CrossRef CAS.
- S. P. Thomas, P. R. Spackman, D. Jayatilaka and M. A. Spackman, J. Chem. Theory Comput., 2018, 14, 1614–1623 CrossRef CAS PubMed.
- U. Koch and P. L. A. Popelier, J. Phys. Chem., 1995, 99, 9747–9754 CrossRef CAS.
- E. Espinosa, E. Molins and C. Lecomte, Chem. Phys. Lett., 1998, 285, 170–173 CrossRef CAS.
- E. Espinosa, M. Souhassou, H. Lachekar and C. Lecomte, Acta Crystallogr., Sect. B: Struct. Sci., 1999, 55, 563–572 CrossRef PubMed.
- Y. Abramov, Acta Crystallogr., Sect. A: Found. Crystallogr., 1997, 53, 264–272 CrossRef.
- U. Koch and P. L. A. Popelier, J. Phys. Chem., 1995, 99, 9747–9754 CrossRef CAS.
- P. Munshi and T. N. Guru Row, J. Phys. Chem. A, 2005, 109, 659–672 CrossRef CAS PubMed.
- P. A. Wood, F. H. Allen and E. Pidcock, CrystEngComm, 2009, 11, 1563–1571 RSC.
- T. H. Nguyen, P. W. Groundwater, J. A. Platts and D. E. Hibbs, J. Phys. Chem. A, 2012, 116, 3420–3427 CrossRef CAS PubMed.
- M. Schmidtmann, L. J. Farrugia, D. S. Middlemiss, M. J. Gutmann, G. J. McIntyre and C. C. Wilson, J. Phys. Chem. A, 2009, 113, 13985–13997 CrossRef CAS PubMed.
- I. S. C. F. Macrae, S. J. Cottrell, P. T. A. Galek, P. McCabe, E. Pidcock, M. Platings, G. P. Shields, J. S. Stevens, M. Towler and P. A. Wood, J. Appl. Crystallogr., 2020, 53, 226–235 CrossRef PubMed.
- B. Guillot, L. Viry, R. Guillot, C. Lecomte and C. Jelsch, J. Appl. Crystallogr., 2001, 34, 214–223 CrossRef CAS.
- M. P. Waller, A. Robertazzi, J. A. Platts, D. E. Hibbs and P. A. Williams, J. Comput. Chem., 2006, 27, 491–504 CrossRef CAS PubMed.
- F. Hibbert and J. Emsley, Adv. Phys. Org. Chem., 1990, 26, 255–279 CrossRef CAS.
- A. Ranganathan, G. U. Kulkarni and C. N. R. Rao, J. Mol. Struct., 2003, 656, 249–263 CrossRef CAS.
- T. H. Nguyen, D. E. Hibbs and S. T. Howard, J. Comput. Chem., 2005, 26, 1233–1241 CrossRef CAS PubMed.
- A. Ranganathan, G. Kulkarni and C. Rao, J. Mol. Struct., 2003, 656, 249–263 CrossRef CAS.
- E. Espinosa, E. Molins and C. Lecomte, Chem. Phys. Lett., 1998, 285, 170–173 CrossRef CAS.
- C. B. Hübschle and B. Dittrich, J. Appl. Crystallogr., 2011, 44, 238–240 CrossRef PubMed.
- J. J. Du, S. A. Stanton, P. A. Williams, J. A. Ong, P. W. Groundwater, J. Overgaard, J. A. Platts and D. E. Hibbs, Cryst. Growth Des., 2018, 18, 1786–1798 CrossRef CAS.
- C. R. Taylor and G. M. Day, Cryst. Growth Des., 2018, 18, 892–904 CrossRef CAS PubMed.
- N. Issa, P. G. Karamertzanis, G. W. A. Welch and S. L. Price, Cryst. Growth Des., 2009, 9, 442–453 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Crystallographic data, topological findings, atomic charges. The CIF data for (1). CCDC 2119968–2119969 and 2106513 for THEO, MA and (1). For ESI and crystallographic data in CIF or other electronic format see https://doi.org/10.1039/d1ra08389a |
| ‡ Current address: Biomedicine, School of Medicine, Emory University, Atlanta, Georgia, USA. |
| This journal is © The Royal Society of Chemistry 2022 |