The hidden aromaticity in borazine

Abstract

The aromaticity of borazine (B₃N₃H₆), also known as the inorganic benzene, is a controversial issue since this compound has several characteristics that could qualify it as an aromatic compound. However, recent studies using magnetic criteria indicate that this compound should be considered as a non-aromatic system. This assignment is mainly due to diatropic currents in the nitrogen atoms without observation of ring currents. The present work shows by means of the magnetic criteria that borazine has a ring current hidden by the local contributions of degenerate orbitals π₁ and π₂. Additionally, the study of borazine's first triplet state antiaromaticity using the magnetic and energetic criteria by means of isomerization stabilization energies (ISEs) together with Baird's and Hückel's rules suggests that borazine is best described as an (weakly) aromatic system.

---

Introduction

Aromaticity in borazine is a controversial issue, this compound is known as inorganic benzene,¹ is thermally stable,² possesses bond equalization and high protonation energies,³ is prone to electrophilic aromatic substitution reactions⁴ and has 6π-electrons, features that would primarily suggest that it is aromatic. Electron counting rules have been especially useful for aromaticity assignment in π-aromatic systems, the most important being Hückel's rule.⁵ This rule states that compounds with 4n + 2 (4n) π-electrons are aromatic (antiaromatic). However, electronegativity differences between B and N atoms have led to different aromaticity criteria – mainly the energetic and the magnetic – to present evidence that puts its aromatic nature in doubt, in fact, borazine has been used in recent works as a non-aromatic representative system.^6–8

In the case of energetic criteria, resonance energies are employed as a measure to determine whether a system is aromatic, anti-aromatic or non-aromatic.⁹ For classic aromatic benzene, these values may vary, due to this criteria employs homodesmotic reactions and therefore reference compounds may be different.⁹ Historical values such as those of Pauling–Wheland^10,11 and Kistiakowsky et al.¹² obtained empirically and experimentally give benzene a resonance value of 36 kcal mol⁻¹. More recently, several computational methods have been developed to determine the aromaticity of organic and inorganic compounds such as aromatic stabilization energy (ASE).⁹ For the case of borazine, Schleyer et al.¹³ show an ASE value of 10.0 kcal mol⁻¹ which is 29.3% the value of benzene.¹⁴ Additionally, Fernández and Frenking proposed an energy decomposition analysis based method¹⁵ to calculate aromatic stabilization (EDA-ASE)¹⁵ showing that borazine is less stabilized by aromaticity than benzene reporting that borazine has 27.3% the aromaticity of benzene.

From the magnetic point of view, recent studies suggest that borazine is non-aromatic,^6,7,16 according to the definition of magnetic aromaticity,¹⁷ it does not possess a diatropic ring current resulting from the external magnetic field perturbation. Monaco et al.^6,7 and Fowler et al.¹⁸ independently, show that the stronger diatropic currents are located in nitrogen atoms, these results are in agreement with popular indices such as NICS, magnetic susceptibility exaltation and interatomic magnetizabiliy reported in the literature.^19,20 In addition, Báez-Grez et al.²¹ and Islas et al.,²² employing dissected/total isolines/isosurfaces of the z-component of the induced magnetic field (B^ind_z), showed that the shielding cones in borazine ring are rather similar to those in benzene but weaker in magnitude, these results can be interpreted as indirect evidence of the existence of an aromatic ring current. Recently it has been shown that a strong aromaticity can be induced in borazine due not only to π contributions,²³ but also to σ.²⁴ On the other hand, quantification of aromaticity by ring current strength (RCS) calculations suggest that borazine has a weak aromatic behaviour. Several authors^7,24–27 report that the aromaticity of borazine is approximately 28% of the aromaticity of benzene according to RCS, however, their ring current patterns cannot be clearly identified. Other aromaticity criteria also present disagreements. The geometric criterion through the harmonic oscillator model of aromaticity (HOMA) indicates that the aromaticity of borazine is similar to that of benzene, while the delocalization criterion indicates a lower degree of aromaticity.²⁸ Surprisingly, Udagawa and Iwaki⁸ indicate that borazine exhibits an antiaromatic character according to multiconfigurational calculations. However, this method has not been well tested as an aromaticity criterion.

The question that arises is: should borazine be considered as an aromatic or non-aromatic system? The literature is diverse and both assertions seem to be valid. In present article, evidence will be shown that borazine presents a magnetic response and a “hidden” aromatic ring current similar to that in benzene. In addition, energetic criteria based on isomerization stabilization energies (ISEs)²⁹ supports the results obtained. Finally, it will be shown that the study of (anti)aromaticity in the first excited triplet state allows to complement the results in the fundamental state by combining Hückel's⁵ and Baird's rules.³⁰

Computational methods

Geometric optimizations were performed at the PBE0 (ref. 31)/def2-TZVP³² level using Gaussian 16 software.³³ Aromaticity was assessed by two criteria: the magnetic one through dissected magnetically induced current density (dMICD) maps^34–37 and the quantification via ring current strength (RCS)³⁸ performed with GIAO method.^39–43 Current density calculations were performed in the context of Quantum Theory of Atoms in Molecules (QTAIM)^{34–36,44,45} using the GIAOCD method⁴⁶ which is implemented in the AIMAll software.⁴⁷ RCS values were computed through the integration of current density passing through zero-flux interatomic surfaces. In order to obtain π contributions of RCS, the wfx files generated from the NMR calculations were modified removing the contributions of the σ-orbitals and preserving the π orbitals.^20,48,49 Vector maps were plotted using the VisIt program.⁵⁰ On the other hand, the energetic criteria was evaluated by obtaining the aromatic stabilization energies, based on the isomerization scheme (ISE) proposed by Schleyer.^29,51 In the case of borazine, we have computed the adiabatic T1 state, however, since there is a loss of ring planarity due to the destabilization effects caused by antiaromaticity, we have also calculated the ISE by keeping the atoms that compose the rings fixed. Negative ISE values indicate an aromatic character, while positive values represent anti-aromaticity.

Results and discussion

The hidden ring current in borazine

Dissected magnetically induced current density maps enable a detailed analysis of the orbital contributions to aromaticity. As example, left column in Fig. 1a show the π orbital contribution of the aromaticity of benzene which presents a diatropic (clockwise) ring current with a RCS value of 11.8 nA T⁻¹. In addition, Fig. 1c and e shown the contributions of the degenerated π₁, π₂ orbitals and π₃ orbitals respectively, both figures present diatropic ring currents. The computed RCS values for these contributions are 7.6 and 4.2 nA T⁻¹ respectively. As can be seen, each π orbital contributes approximately 33% to the aromaticity of benzene.

Fig. 1 Dissected magnetically induced current density maps and their π-contributions for benzene (a, c and e) and borazine (b, d and f) at the PBE0/def2-TZVP level.

Borazine has noticeable differences, Fig. 1b depicts diatropic currents located in nitrogen atoms and a weak ring current. In addition, a similar pattern is observed for degenerated orbitals (Fig. 1d), local diatropic currents are located in nitrogen atoms while the ring current is missing. RCS value for these orbitals is −0.2 nA T⁻¹. Results are in agreement with the calculations performed by Fowler et al.¹⁸ using the ipsocentric method.⁵² However, the π₃ orbital of borazine, presents a similar ring current compared to benzene as shown in Fig. 1e and f. In addition, this orbital possess a RCS value of 3.8 nA T⁻¹, differing only by 0.3 nA T⁻¹ to the contribution of the analogous molecular orbital in benzene. This evidence shows that borazine possess an aromatic character since it has a diatropic ring current pattern however, this is hidden by local diatropic currents located in the nitrogen atoms. The directions of the local diatropic currents cancel out the diatropic ring current due to their directions, as shown in Scheme 1. The explanation of aromatic patterns by the cancellation of ring currents has previously been used by Schleyer and coworkers to describe aromaticity patterns in polycyclic compounds such as porphyrinoids which have local and macrocyclic aromaticity.⁵³ These patterns have been recently identified through the study of the z-component of the induced magnetic field topology (B^ind_z).⁵⁴

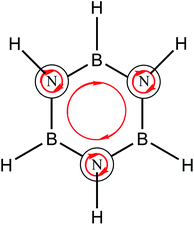Scheme 1 Local and ring diatropic currents in borazine. Red arrows represent the diatropic currents.

Nevertheless, it is possible to argue that antiaromatic compounds such as cyclobutadiene could present aromaticity since one of its π orbitals presents diatropicity as showed by Charistos et al.⁵⁵ However, when all π orbitals are taken into account, the final character is antiaromatic due to the strong paratropic response of the HOMO (see Fig. S1† for dissected ring current maps). The case of borazine it is different since, the ring magnetic response of this compound is related solely to the π₃ orbital, whereas the other π-orbitals hide the ring current due to the local currents in nitrogen atoms. Additionally, it has been shown that the frontier orbitals are the principal players in the assignment of aromaticity, but as shown for benzene, they do not contain 100% of the information.

Combining Hückel's and Baird's rules for proper aromaticity assignment

The combination of aromaticity rules has been recently reviewed and used for a complete understanding of this property.⁵⁶ As mentioned above, Hückel's rule states that compounds containing 4n + 2 (4n) π-electrons are considered aromatic (antiaromatic). Similarly, Baird's rule states that compounds with 4n (4n + 2) π-electrons will be aromatic (antiaromatic) in their lowest π–π* triplet state. The combination of both rules enables to state that a π-aromatic compound in the singlet state will be π-antiaromatic in its lowest π–π* triplet state.⁵¹

The antiaromaticity of benzene in their triplet state is widely known^30,57–59 and can be seen in Fig. 2a through the paratropic (anticlockwise) ring currents that confirm this feature, having a RCS_π value of −27.1 nA T⁻¹ for the first triplet state of benzene. For the case of borazine, the first vertical triplet state has been studied as a model since the optimized geometry is not planar, however, it allows to study the π–π* transition of borazine in ground state. In Fig. 2b a paratropic ring current can be seen which indicates that it is anti-aromatic, this is confirmed by the extremely high value of −6.4 × 10² nA T⁻¹, this result also explains its high instability and why borazine avoids a complete planarity in their adiabatic triplet state. The combination of Hückel's and Baird's rules allow to suggest that borazine is aromatic in its singlet state and antiaromatic in its triplet vertical π–π* state.

Fig. 2 π-Contribution to the magnetically induced current density for the triplet state of benzene (a) and vertical triplet state of borazine (b).

The energetic criteria confirm the results obtained using current density model. The aromatic stabilization energies based on isomerization reactions for benzene in ground and first triplet state are −34.86 and 33.54 kcal mol⁻¹ very similar to those obtained by Schleyer et al. confirming aromaticity in ground state and antiaromaticity in the first triplet state.^29,51 When the six-membered ring is kept fixed, the antiaromatic character is maintained, with a value of 26.22 kcal mol⁻¹. In the case of borazine, two reactions have been taken as reference, in such a way that the number of B–N bonds that can be observed in Fig. 3 are conserved. For the ground state, the values obtained are −12.41 and −6.55 kcal mol⁻¹, denoting a slightly aromatic character if compared to benzene. For reaction Fig. 3b, the aromaticity of borazine is approximately 36% the value of benzene. With respect to the adiabatic triplet state the values obtained are 0.15 and 5.79 kcal mol⁻¹, however the planarity of the ring is lost by additional effects to the aromaticity, so it is not a reliable method. To compensate for the influence of effects other than aromaticity, the atoms that conform the six-membered ring have been kept fixed. The values obtained are 12.51 and 21.72 kcal mol⁻¹ showing a remarkable antiaromatic character, fulfilling Baird's rule. It should also be noted that our results are in agreement with those published recently by Shoji et al.⁶⁰ who experimentally obtained a diazaboretidine ring (B₂N₂) derivative which is the isoelectronic analogue of cyclobutadiene. Authors indicate that B₂N₂ moiety is non-aromatic in the first triplet state, however, the B₂N₂H₄ ring present a conflicting aromatic Baird character in its planar (D_2h) triplet state. Magnetic criteria based on NICSzz(1) shown an Baird aromatic behaviour when compared to cyclobutadiene, whereas electronic criteria based on delocalization indices reveal a non-aromatic character. Although the magnetic criterion has been criticized for apparently overestimating the aromatic behavior of various compounds, especially those that present local currents (as occurs in nitrogen atoms),⁶¹ it is necessary to point out that this criterion can properly estimate the aromatic character of several compounds as long as different indices based on the same criterion are taken into account,^62,63 as occurs with the electronic indicators.

Fig. 3 Isomerization reactions for ISE computations for benzene (a) and borazine (b and c). Values in parentheses show the results with the fixed ring.

Conclusions

In the present article, evidence has been presented by means of the magnetic and energetic criteria which determines that borazine has an aromatic character, but less than benzene in the singlet state. The magnetic response shows that despite being approximately 30% of benzene, borazine has a “hidden” ring current where the contribution is only from the π₃ orbital, the results show that this orbital contributes in the same way as the π₃ orbital of benzene. The ring current of the degenerated π₁ and π₂ orbitals in borazine are responsible for the diatropic currents located in the nitrogen atoms that “hide” the aromatic ring current. Additionally, the antiaromaticity of borazine in its vertical triplet state confirms its aromatic nature in singlet state and moreover, due to high instability resulting from antiaromaticity, explains why borazine avoids planarity in adiabatic triplet state. Additionally, computed ISEs showed that borazine presents a degree of aromaticity in its singlet state and antiaromaticity in the triplet state with a value of 10.79 kcal mol⁻¹. The results confirm that borazine should be considered as a weakly aromatic system with a hidden ring current and that the combination of Hückel's and Baird's rules can be used in a complementary way for an appropriate assignment of aromaticity.

Author contributions

Rodrigo Báez-Grez: methodology, investigation, formal analysis; Ricardo Pino-Rios: conceptualization, methodology, investigation, formal analysis.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

R. B.-G. acknowledges the support of FONDECYT through Postdoctorado proyect no. 3210037. Powered@NLHPC: this research was partially supported by the supercomputing infrastructure of the NLHPC (ECM-02) of the Universidad de Chile. We thank the reviewers of this article for their valuable comments that have helped to improve the quality of this manuscript.

References

1. A. Stock and E. Pohland, Berichte der deutschen chemischen Gesellschaft (A and B Series), 1926, 59, 2215–2223.
2. M. V Kilday, W. H. Johnson and E. J. Prosen, J. Res. Natl. Bur. Stand., Sect. A, 1961, 65A, 101–104.
3. B. Kiran, A. K. Phukan and E. D. Jemmis, Inorg. Chem., 2001, 40, 3615–3618.
4. B. Chiavarino, C. ME and S. Fornarini, J. Am. Chem. Soc., 1999, 121, 2619–2620.
5. E. Hückel, Z. Phys., 1931, 70, 204–286.
6. G. Monaco and R. Zanasi, Phys. Chem. Chem. Phys., 2016, 18, 11800–11812.
7. R. Carion, B. Champagne, G. Monaco, R. Zanasi, S. Pelloni and P. Lazzeretti, J. Chem. Theory Comput., 2010, 6, 2002–2018.
8. R. A. Iwaki and T. Udagawa, Chem. Phys. Lett., 2020, 745, 137271.
9. M. K. Cyrański, Chem. Rev., 2005, 105, 3773–3811.
10. L. Pauling and G. W. Wheland, J. Chem. Phys., 1933, 1, 362–374.
11. L. Pauling and C. University and C. U. Press, The Nature of the Chemical Bond and the Structure of Molecules and Crystals: An Introduction to Modern Structural Chemistry, Cornell University Press, 1960.
12. G. B. Kistiakowsky, J. R. Ruhoff, H. A. Smith and W. E. Vaughan, J. Am. Chem. Soc., 1936, 58, 146–153.
13. P. von R. Schleyer, H. Jiao, N. J. R. v. E. Hommes, V. G. Malkin and O. L. Malkina, J. Am. Chem. Soc., 1997, 119, 12669–12670.
14. Y. Mo and P. von R. Schleyer, Chem.–Eur. J., 2006, 12, 2009–2020.
15. I. Fernández and G. Frenking, Faraday Discuss., 2007, 135, 403–421.
16. S. Pelloni, G. Monaco, P. Lazzeretti and R. Zanasi, Phys. Chem. Chem. Phys., 2011, 13, 20666–20672.
17. R. Gershoni-Poranne and A. Stanger, Chem. Soc. Rev., 2015, 44, 6597–6615.
18. A. Soncini, P. W. Fowler and L. W. Jenneskens, Struct. Bonding, 2005, 115, 57–79.
19. P. W. Fowler and E. Steiner, J. Phys. Chem. A, 1997, 101, 1409–1413.
20. C. Foroutan-Nejad, J. Phys. Chem. A, 2011, 115, 12555–12560.
21. R. Báez-Grez, L. Ruiz, R. Pino-Rios and W. Tiznado, RSC Adv., 2018, 8, 13446–13453.
22. R. Islas, E. Chamorro, J. Robles, T. Heine, J. C. Santos and G. Merino, Struct. Chem., 2007, 18, 833–839.
23. M. Baranac-Stojanović and M. Stojanović, RSC Adv., 2013, 3, 24108–24117.
24. R. Pino-Rios, A. Vásquez-Espinal, O. Yañez and W. Tiznado, RSC Adv., 2020, 10, 29705–29711.
25. W. A. Rabanal-León, W. Tiznado and L. Alvarez-Thon, Int. J. Quantum Chem., 2019, 119, e25859.
26. D. Du, D. Sundholm and H. Fliegl, J. Chin. Chem. Soc., 2016, 63, 93–100.
27. R. K. Jinger, H. Fliegl, R. Bast, M. Dimitrova, S. Lehtola and D. Sundholm, J. Phys. Chem. A, 2021, 125, 1778–1786.
28. K. Ota and R. Kinjo, RSC Adv., 2021, 11, 592–598.
29. P. v. R. Schleyer and F. Pühlhofer, Org. Lett., 2002, 4, 2873–2876.
30. N. C. Baird, J. Am. Chem. Soc., 1972, 94, 4941–4948.
31. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
32. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
33. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson and H. Nakatsuji, Gaussian, Inc., Wallingford CT, 2016.
34. T. A. Keith and R. F. W. Bader, J. Chem. Phys., 1993, 99, 3669–3682.
35. T. A. Keith and R. F. W. Bader, Chem. Phys. Lett., 1993, 210, 223–231.
36. T. A. Keith and R. F. W. Bader, Chem. Phys. Lett., 1992, 194, 1–8.
37. D. Sundholm, H. Fliegl and R. J. F. Berger, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 639–678.
38. J. Jusélius, D. Sundholm and J. Gauss, J. Chem. Phys., 2004, 121, 3952–3963.
39. F. London, J. Phys. Radium, 1937, 8, 397–409.
40. R. McWeeny, Phys. Rev., 1962, 126, 1028–1034.
41. R. Ditchfield, Mol. Phys., 1974, 27, 789–807.
42. K. Woliński and A. J. Sadlej, Mol. Phys., 1980, 41, 1419–1430.
43. K. Wolinski, J. F. Hinton and P. Pulay, J. Am. Chem. Soc., 1990, 112, 8251–8260.
44. R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Clarendon Press, 1994.
45. T. A. Keith and R. F. W. Bader, Can. J. Chem., 1996, 74, 185–200.
46. T. A. Keith, Chem. Phys., 1996, 213, 123–132.
47. T. A. Keith, AIMAll (Version 19.02.13), Overland Park KS, USA, 2019, http://aim.tkgristmill.com.
48. J. C. Santos, J. Andres, A. Aizman and P. Fuentealba, J. Chem. Theory Comput., 2005, 1, 83–86.
49. J. C. Santos, W. Tiznado, R. Contreras and P. Fuentealba, J. Chem. Phys., 2004, 120, 1670–1673.
50. High Performance Visualization: Enabling Extreme-Scale Scientific Insight, Chapman & Hall/CRC Computational Science, ed. E. Wes Bethel, H. Childs, C. Hansen, CRC Press, 2012, p. 520, ISBN1439875723, 9781439875728.
51. J. Zhu, K. An and P. von R. Schleyer, Org. Lett., 2013, 15, 2442–2445.
52. E. Steiner, P. W. Fowler and R. W. A. Havenith, J. Phys. Chem. A, 2002, 106, 7048–7056.
53. J. I. Wu, I. Fernández and P. v. R. Schleyer, J. Am. Chem. Soc., 2013, 135, 315–321.
54. R. Pino-Rios, G. Cárdenas-Jirón and W. Tiznado, Phys. Chem. Chem. Phys., 2020, 22, 21267–21274.
55. N. D. Charistos, A. G. Papadopoulos, T. A. Nikopoulos, A. Muñoz-Castro and M. P. Sigalas, J. Comput. Chem., 2017, 38, 2594–2604.
56. M. Solà, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, 9, e1404.
57. S. Zilberg and Y. Haas, J. Phys. Chem. A, 1998, 102, 10851–10859.
58. R. Papadakis and H. Ottosson, Chem. Soc. Rev., 2015, 44, 6472–6493.
59. M. Baranac-Stojanović, J. Org. Chem., 2020, 85, 4289–4297.
60. Y. Shoji, Y. Ikabata, I. Ryzhii, R. Ayub, O. El Bakouri, T. Sato, Q. Wang, T. Miura, B. S. B. Karunathilaka, Y. Tsuchiya, C. Adachi, H. Ottosson, H. Nakai, T. Ikoma and T. Fukushima, Angew. Chem., Int. Ed., 2021, 60, 21817–21823.
61. L. Zhao, R. Grande-Aztatzi, C. Foroutan-Nejad, J. M. Ugalde and G. Frenking, ChemistrySelect, 2017, 2, 863–870.
62. L. Arrué and R. Pino-Rios, Int. J. Quantum Chem., 2020, 120, e26403.
63. R. Báez-Grez, L. Arrué and R. Pino-Rios, Chem. Phys. Lett., 2021, 781, 138973.

---

Footnote

† Electronic supplementary information (ESI) available: Dissected magnetically induced current density maps, and Cartesian coordinates for all systems studied in this work. See DOI: 10.1039/d1ra06457f

---