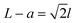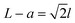DNA compaction and dynamic observation in a nanopore gated sub-attoliter silicon nanocavity

Abstract

Confinement of biopolymers inside volumes with micro- or nanoscale lateral dimensions is ubiquitous in nature. Investigating the behavior of biopolymers in a confined environment is essential to improve our basic understanding in life sciences. In this work, we present a nanopore gated sub-attoliter silicon nanocavity device, which allows DNA compaction similar to that in virus capsids. Single DNA molecules can be electrically driven into the nanocavity, and then get compacted inside the nanocavity under certain conditions. The dynamic fluctuations of the compacted DNA can be monitored via ionic current measurements. The mechanism for the DNA compaction is elucidated by varying the DNA length or concentration, voltage polarity, nanocavity dimensions and ionic strength. Furthermore, Brownian dynamics simulations reveal the dynamic fluctuations of the compacted DNA, which are reflected in the measured ionic current. Our nanocavity device is anticipated to provide a controlled environment in extremely small volumes for investigating the physics of confined biopolymers.

---

Introduction

A variety of biopolymers crucial to life are normally restricted to spatial constraints in vivo, due to either molecular crowding in the cellular medium or direct geometric confinement.¹ A typical example is DNA in living organisms. For instance, the human genome contains over 3 billion base pairs (bps) with a total length of about 1 meter if stretched out. However, it is tightly compacted in a cell nucleus with a size around 10 μm. A more extreme case is that of DNA inside viruses, where the DNA molecule is packed to nearly crystalline density inside a capsid with a diameter only around 50 nm.^2,3 DNA compaction in such a tight configuration is subject to extremely strong energetic and entropic penalties owing to the bending rigidity and electrostatic self-repulsion.⁴ Given the biological relevance and importance of DNA, there is a strong motivation to investigate the behavior of compacted DNA in such confined environments. Although the physics of unconfined DNA can be well-understood by the elegant theory of polymer models in textbooks,^5–8 studying confined DNA is much more challenging from both experimental and theoretical points of view. DNA in a confined environment behaves very differently from that in free space; computer simulations and sophisticated theories are required to understand its organization and conformation.^9–13 Extensive in vitro experiments using X-ray diffraction and cryo-electron microscopy have revealed the arrangement of DNA inside the virus capsid.^14–16 However, these in vitro experiments are static; therefore only a snapshot of the DNA conformation can be taken. Although DNA compaction can also be induced by introducing multivalent ions,^17,18 neutral polymers^19,20 or polycationic nanostructures²¹ in liquids, a lack of spatial confinement in these methods makes it difficult to mimic the in vivo scenario, such as that inside cell nuclei or virus capsids.

The development of nanotechnology has enabled observing, manipulating, assembling and manufacturing matter at the nanometer scale with high precision.²² Nanofabricated structures precisely generated one- or two-dimensional constraints on DNA molecules, and prompted in vitro single molecule studies to model the emergent features of confined DNA.^23–25 However, special nanofabricated structures that are capable of three-dimensional confinement of DNA still remain to be explored. In addition, measurement techniques to monitor the conformation changes of confined DNA are also desired to reveal the dynamics of the confined DNA. Among different nanofabricated structures, solid-state nanopore sensors have attracted great interest as a single-molecule detection tool for DNA sequencing,²⁶ protein profiling,^27,28 data storage²⁹ and study of protein aggregation.³⁰ The detection principle is monitoring the modulation of the ionic current induced by the blockage of the nanopore when an analyte molecule translocates through the nanopore.

In this work, we fabricated a nanopore gated sub-attoliter silicon (Si) nanocavity device for DNA compaction and analysis. This device is composed of three parts: a top silicon nitride (SiN_x) nanopore, a sub-attoliter Si nanocavity and a bottom Si nanopore. The top SiN_x nanopore and the nanocavity act as compartments to accommodate DNA, while the bottom Si nanopore acts as a readout unit of the ionic current measurement. Inspired by the micrometer sized cavity devices fabricated in bulk Si substrates (Pedone et al.^31,32), we significantly improved the process controllability by fabricating the Si cavity in an ultra-thin Si membrane and extended the dimensions of the cavity to nanoscale. DNA compaction was then realized by applying an electric field to drive the DNA into the nanocavity through the top SiN_x nanopore. The dynamic fluctuations of compacted DNA were monitored through an ionic current. The underlying mechanism of DNA compaction in the nanocavity was elucidated by varying the DNA length or concentration, voltage polarity, nanocavity dimensions and ionic strength. The dynamic fluctuations of the confined DNA were also studied with coarse-grained Brownian dynamics simulations. Our nanopore gated nanocavity device is anticipated to provide a controlled environment in extremely small volumes for investigating the physics of confined biopolymers.

Results and discussion

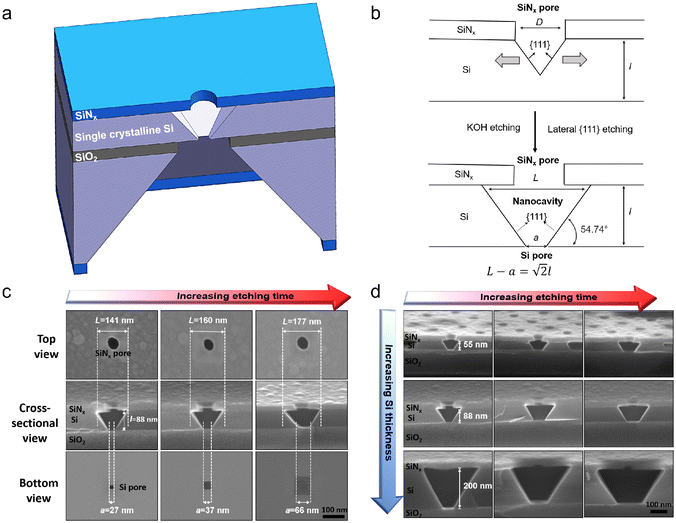
The fabrication process of our nanopore gated nanocavity device is schematically illustrated in Fig. S1.†Fig. 1(a) gives a three-dimensional cartoon illustration of a fabricated device. The dimensions of the nanocavities are determined jointly by the size of the top SiN_x nanopore, the Si membrane thickness in the silicon-on-insulator (SOI) substrate and the etching time of the nanocavity (Fig. 1(b)). Therefore, it can be fine-tuned by modifying these parameters. The controllability of the fabrication process can be inferred from the results in Fig. 1(c), where a series of top, cross-sectional and bottom view scanning electron microscopy (SEM) images of the fabricated nanocavities with different etching times are provided. These devices share almost the same top SiN_x pore size and are fabricated in the same 88 nm-thick Si membrane. The sizes of the top and bottom openings of the nanocavity, L and a, follow very well the relationship:
where l is the thickness of the Si membrane, as illustrated in Fig. 1(b). The lateral dimensions of the nanocavity and the Si pore can be extended by increasing the etching time. In addition, the dimensions of the nanocavity can also be modified by varying the thickness of the Si membrane as shown in Fig. 1(d). For easy sample preparation, the cross-sectional SEM images were obtained with the buried oxide layer and silicon substrate intact.

Fig. 1 Schematic illustration of the nanopore gated nanocavity device fabrication and structure analysis using SEM. (a) Three-dimensional cartoon illustration of the nanopore gated nanocavity device. (b) The fabricated nanocavity is composed of three parts: the top SiN_x pore, nanocavity and bottom Si pore. Its lateral dimensions are mainly controlled by the lateral etching of the {111} planes in Si. The top and bottom openings, L and a of the nanocavity, are determined by the etching time and governed by a relationship: where l is the thickness of the Si membrane. (c) SEM images of nanocavities fabricated in an 88 nm thick Si membrane from top, cross-sectional and bottom views. (d) Cross-sectional SEM images of the nanocavities fabricated with different Si membrane thicknesses ranging from 55 nm and 88 nm to 200 nm.

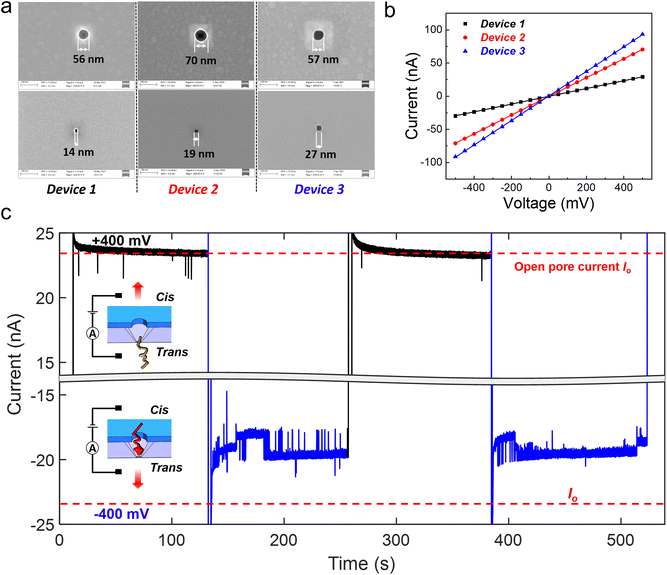
Three devices with different Si pore dimensions (14 nm, 19 nm and 27 nm; see Fig. 2(a) for the SEM images) were employed for the DNA compaction experiments. The corresponding volume of each device is 0.62 aL, 0.69 aL, and 0.81 aL, respectively. The devices were first characterized electrically with ionic current measurements, by sandwiching the nanocavity chip with top and bottom liquid reservoirs, and applying a voltage bias between the two reservoirs. Fig. 2(b) shows almost ideal Ohmic current–voltage (I–V) characteristics of these 3 devices in 4 M LiCl.

Fig. 2 Characterization of the three devices employed in the DNA compaction experiments and ionic current measurement results. (a) Top and bottom view SEM images of the three nanocavity devices that were employed for the DNA compaction experiments. (b) Ionic current measurements of the three nanocavity devices in 4 M LiCl. Almost ideal Ohmic current–voltage (I–V) characteristics of these 3 devices are observed. (c) Ionic current measurements of 20 kb DNA translocation through device 1 in 4 M LiCl. The concentration of added DNA is 100 pM. The applied bias is switched between +400 mV and −400 mV (remaining for 120 s at each bias polarity) twice. The baseline current at +400 mV always remains at the same level of the open pore current I_o (marked by the red dashed line), while the ionic current at −400 mV is greatly smaller than I_o and shows strong fluctuations.

When DNA molecules are added to the liquid reservoirs, they can be captured into the nanocavities by an electrophoretic force since DNA is highly negatively charged.³³ Individual spikes on a stable baseline were observed in the ionic current measurements on device 1, with a positive bias (Fig. 2(c)) and 100 pM, 20 kb double stranded DNA (dsDNA) molecules. The baseline current was in the same level as the open pore current (I_o). The individual spikes indicate normal trans-to-cis DNA translocation events. For completeness, different positive biases ranging from 300 mV to 500 mV were applied and the duration and relative amplitude of the translocation events at different biases are shown in Fig. S2(a and b†). However, when a negative 400 mV bias was applied to induce cis-to-trans DNA translocations, completely different behavior was observed in the ionic current trace (see Fig. 2(c)). The ionic current was smaller than I_o, and strong ionic current fluctuations with both upward and downward spikes were also observed. By reversing the applied bias from +400 mV to −400 mV (remaining for 120 s at each bias polarity) twice, similar phenomena were observed.

Since the bottom Si pore is the dominant constriction in the nanocavity device, it determines the measured ionic current. The ionic current reduction in the baseline can therefore be mainly attributed to a certain blockage of the Si pore constriction. However, normal DNA translocation events can only result in transient blockage of the nanopore and the baseline current should return to I_o when DNA exits the nanopore. This indicates that the baseline current reduction can be caused by the DNA molecule trapped inside the nanocavity, thus partially blocking the Si pore constriction for a long time. Similar current fluctuations with both upward and downward spikes have been reported for hairpin DNA molecules trapped inside a biological nanopore.^34,35 In our nanocavity device, the trapped DNA can be formed either by DNA compaction into a globule shape³⁶ or by multiple DNA strands residing in the Si pore constriction at the same time.^37,38 The dominating DNA trapping mechanism in our nanocavity will be discussed later. More evidence is shown in Fig. S2(c)† by switching the voltage 10 times. It can be explained that at +400 mV, the translocated DNA remained in the vicinity of the device, but out of the sensing zone of the Si pore; therefore the ionic current restored to the open pore current. When switching the voltage to a negative bias, the DNA could be quickly recaptured and trapped, leading to an immediate current drop.

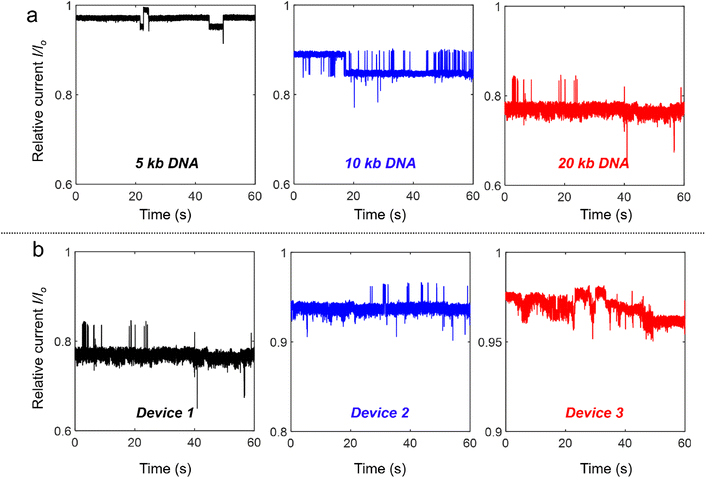
Similar experiments (100 pM DNA in 4 M LiCl under a −400 mV bias) were also performed with different DNA lengths from 5 kb and 10 kb to 20 kb. As shown in Fig. 3(a), all the relative current (I/I_o) traces measured through device 1 display strong fluctuations and the current levels are all smaller than the open pore current. Longer DNA shows stronger fluctuations, while normal translocation events were measured for these DNA molecules with different lengths at +400 mV (Fig. S3†). We also performed experiments at −400 mV in the three different devices shown in Fig. 2(a)† with 20 kb DNA, and similar ionic current fluctuation results were obtained as shown in Fig. 3(b). Device 1 with the smallest Si pore size displays the strongest fluctuations. These experiments demonstrated the generality of DNA trapping in our nanocavity devices.

Fig. 3 Relative current traces of DNA with different lengths and through the three nanocavity devices in 4 M LiCl at −400 mV. The concentration of added DNA is 100 pM. (a) Relative current traces of 5 kb, 10 kb and 20 kb DNA trapping in device 1 at −400 mV, respectively. (b) Relative current traces of 100 pM 20 kb DNA trapping in device 1, device 2 and device 3 at −400 mV, respectively.

Further DNA translocation experiments were performed with a ten times lower concentration (10 pM 20 kb DNA in 4 M LiCl), as shown in Fig. S4.† At −400 mV, similar DNA trapping signals were reproducibly observed. In addition, the sparse distribution of DNA translocation spikes at a positive bias (+400 mV) implies that the time interval between two DNA capture events is too long to result in multiple DNA molecules being captured in the nanocavity at the same time. If multiple DNA molecules are captured into the nanocavity sequentially, the ionic current would drop step by step, as shown in the measurements of Laohakunakorn et al.³⁸ The DNA trapping in our nanocavity is therefore highly plausible to be induced by the compaction of single DNA instead of multiple DNA molecules inside the device.

Several factors, including the electric field,^36,39 geometrical confinement^1,40 and ionic strength,⁴¹ can induce the conformation change of DNA molecules. In what follows, theoretical discussions and experimental verification of the contribution of these factors to the DNA compaction inside our nanocavity devices are provided. First, it is experimentally observed that a moderate electric field (∼2 × 10⁴ V m⁻¹) strongly compresses the isolated DNA polymer into isotropic globules,³⁶ while large electric fields may stretch already compacted DNA.³⁹ In our nanocavity devices, the electric field distribution is not uniform. In particular, the electric field intensity in the Si pore constriction at −400 mV is around 4.5 × 10⁶ V m⁻¹, which is much higher than the electric field (∼2 × 10⁵ V m⁻¹) in the cylindrical SiN_x pore region. Hence, in the cis-to-trans translocation at a −400 mV bias, the lower electric field around the cylindrical SiN_x pore region may induce DNA compression before entering the nanocavity. Yamazaki et al. discovered that the DNA at the vicinity of a nanopore could indeed be compressed by the electro-osmotic flow induced by the electric field.⁴² Second, to study the geometrical confinement effects induced by the top SiN_x pore, we also used bare Si nanocavities (without the top SiN_x pore) to translocate DNA with different lengths. As shown in Fig. S5,† all the experiments performed in 4 M LiCl showed normal translocation events with no evidence of DNA trapping and compaction inside the bare nanocavities. This demonstrated the critical role of the top SiN_x pore for DNA compaction inside the nanocavity device. In addition, the scatter plot of the translocation events through bare Si nanocavities shows that the duration at a negative bias is overall longer than that at a positive bias; see Fig. S5(c, e and g).† The gradually reduced dimensions near the bottom of the Si nanocavity poses increasing spatial confinement and further slowdown of the DNA translocation, as evidenced by the ultra-long translocation events (duration up to a few hundred microseconds) observed at a negative bias measured in the bare Si nanocavities. Third, the influence of ionic strength was studied by performing DNA translocation experiments with device 2 in 1 M LiCl. As shown in Fig. S6,† in 1 M LiCl, only normal translocation events were observed at both bias polarities (i.e. +400 mV and −400 mV) for different DNA lengths. The scatter plot of the distribution of amplitude and duration shows that the translocation of DNA with different lengths has almost the same amplitude but the duration of longer DNA is longer, which agrees well with the results reported by Wanunu et al.⁴³ Our experiments in 1 M LiCl show a direct contrast to the results in 4 M LiCl, and confirm the critical role of ionic strength for the observed DNA compaction. The MD simulations by Kowalczyk et al.³³ show that changing the ion concentration changes the number of bound ions per base along the DNA. As the LiCl concentration increases from 1 M to 4 M, the number of bound Li⁺ along the DNA molecules increases, which reduces the effective DNA charge and thus the repulsion force between neighboring segments.⁴⁴ As a result, DNA molecules can be more closely packed under 4 M LiCl. Overall, the DNA compaction inside our nanocavities could have resulted from the combined contributions from all the three aforementioned factors.

The interpretation of the observed different current signals of DNA in 4 M LiCl passing through the nanocavity device under different bias polarities is qualitatively illustrated in Fig. 4(a). Under a negative bias, DNA passes through the SiN_x pore first before entering the nanocavity. During this process, DNA is first compressed by the electric field around the top SiN_x pore, and then the geometrical confinement inside the nanocavity can locally compact the DNA to form self-entanglements and knots.^45–47 The entangled DNA can further form globules (similar to a DNA origami sphere⁴⁸), which cannot pass through the gradually reduced space near the bottom of the Si nanocavity, thus finally being compacted in the bottom Si pore constriction. However, the compacted DNA could only partially block the Si pore due to its permeable nanostructure to ions.^49,50 The rearrangement of such globules inside the nanocavity can lead to the current fluctuation. Under a positive bias, the bottom Si pore size is too small to allow a large bundle of DNA to pass through directly. Instead, DNA is driven through the Si pore either folded or unfolded in a linear fashion under the strong electric field, as demonstrated from the translocation events with a single level and multiple levels in Fig. S3(b).† Thus, the nanocavity can only be occupied by a few DNA threads that can be smoothly translocated through the SiN_x pore towards the cis side by the electric field. Hence, no DNA compaction is expected under a positive bias.

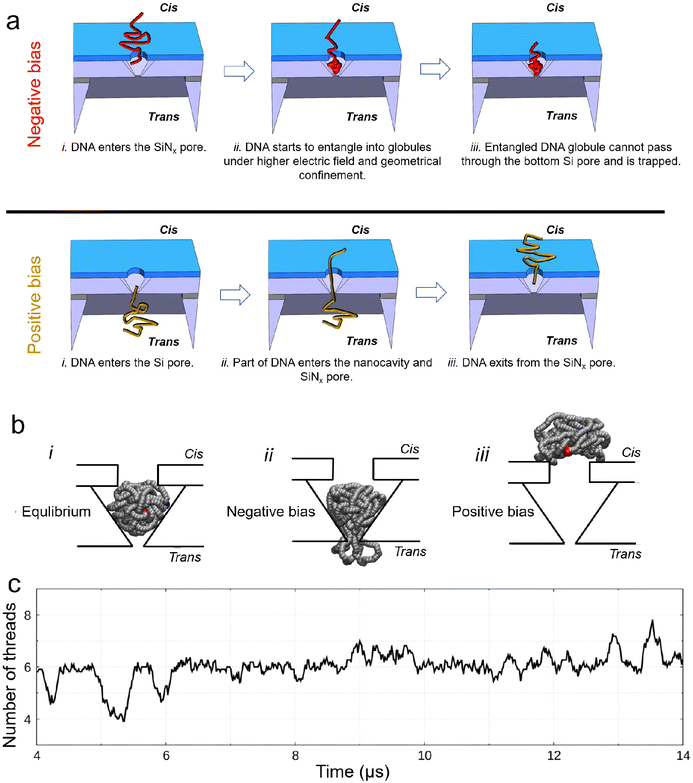Fig. 4 Explanation and simulation of the observed different current signals of DNA passing through the nanocavity under different bias polarities. (a) Schematic explanation for the observed phenomena under different bias polarities. (b) Brownian dynamics (BD) simulation of trapping and escape of an entangled 10 kb DNA inside device 1 under 4 M LiCl: the voltage is turned off (i), an electric field is applied from trans-to-cis, same as the negative bias in the experiments (ii) and the electric field is applied from cis-to-trans, same as the positive bias in the experiments (iii). Snapshots are obtained using the VMD software.⁵¹ (c) Number of threads in the Si pore constriction from BD simulations. The signal is obtained as a running average over a window of 1/100 of the entire simulation and, therefore, it is not an integer. Owing to the nature of coarse-grained simulations, the BD simulation can reflect the characteristics of the simulated process, but the timescale may not match the real process.

To further support our interpretation, we performed coarse-grained molecular dynamics simulations of a self-entangled DNA inside device 1 using a Brownian dynamics (BD) in-house code. The DNA is modelled as a sequence of beads and springs plus additional forces to induce a prescribed persistence length of 50 nm and steric exclusion. The external electrophoretic and electroosmotic actions were included using electric and velocity fields from preliminary continuum simulations of the Navier–Stokes Poisson–Nernst–Planck system for our device. In our BD simulations, we initially placed the DNA inside the nanocavity. The model DNA was first equilibrated inside the nanocavity without any external bias, Fig. 4(b)_i. When a negative bias of 400 mV was applied, the DNA attempted to exit the Si pore but was stuck. Multiple DNA segments may occupy the Si pore constriction dynamically (Fig. 4(b)_ii). This explains the experimentally measured ionic current fluctuations reported in Fig. 2 and 3 at a negative bias. In contrast, when applying a positive bias of 400 mV, the model DNA made a smooth exit from the top SiN_x pore (Fig. 4(b)_iii). Fig. 4(c) shows the time fluctuation of the number of DNA threads (N_t) in the Si pore constriction extracted from the simulation. Both upward and downward spikes resemble those observed in the measurements. More examples of the extracted signals are shown in Fig. S7.†

Inspired by the simulations, the upward spikes of the ionic current at a negative bias correspond to increased N_t in the Si pore constriction, while the downward spikes indicate the decreased N_t in the Si pore. By extracting both the upward and downward spikes from the measurements with the three different nanocavity devices in Fig. 3, the duration and relative amplitude of the spikes are statistically analyzed and shown in the box plot of Fig. 5(a and b). Fig. 5(a) shows that the characteristic time of the duration is on the order of milliseconds. Moreover, as the size of the Si pore increases (from device 1 to device 3), the duration of the observed spikes also increases. The volume increase of the nanocavity gives more freedom and relaxation time to the entangled DNA inside, resulting in a longer duration of the spikes. On the other hand, as the Si pore size increases, the relative amplitude of the extracted spikes decreases, as seen in Fig. 5(b). This is due to the fact that the percentage of the volume occupation of a fluctuating fraction of DNA in the Si pore constriction is smaller for a larger Si pore. For a simple calculation using the original size of the Si pore constriction measured from the SEM images in Fig. 2(a) and the diameter of dsDNA of 2 nm, the percentage of the cross-sectional occupation of a single folded DNA (two DNA threads) in the Si pore constriction is 4.1%, 2.2% and 1.1% for device 1, device 2 and device 3, respectively. The calculation results agree well with the data shown in Fig. 5(b), indicating that the upward and downward spikes might be generated by a single folded DNA fraction. Apart from simple upward and downward spikes, alternating spikes which switch quickly among upward and downward positions are also observed. Fig. 5(c) presents three examples of each type extracted from the measurement of 100 pM 20 kb DNA in device 1. The alternating spikes indicate that the entangled DNA is likely under high tension, which leads to fast conformation changes.

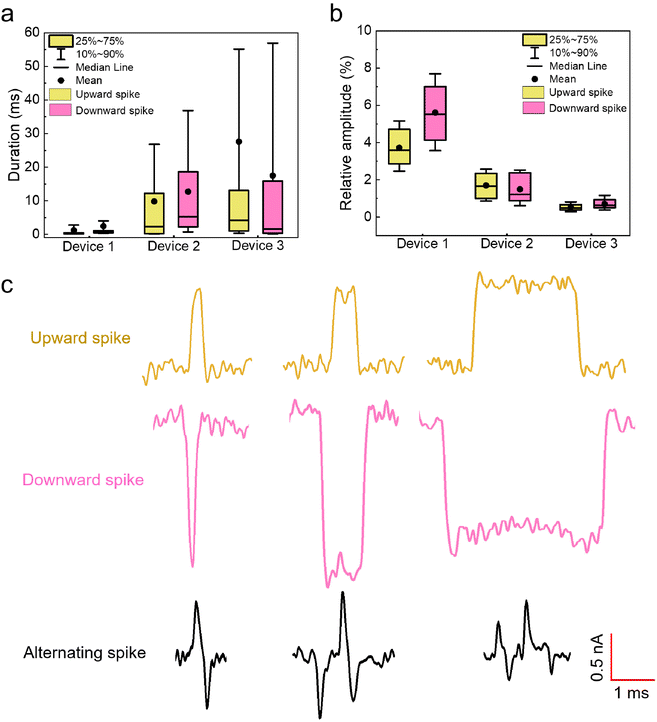Fig. 5 Box plot of extracted upward and downward spikes from the measurements of 100 pM 20 kb DNA with the three nanocavity devices in Fig. 3, and an exemplified view of different spikes extracted from the measurement with device 1. (a) Box plot of the duration of both upward and downward spikes extracted from the measurement in Fig. 3. (b) Box plot of the relative amplitude of both upward and downward spikes extracted from the measurement in Fig. 3. The relative amplitude is calculated as the extracted amplitude of the spikes with respect to the respective baseline current of the 3 devices at a negative bias. (c) Examples of different spikes from the measurements of 100 pM 20 kb DNA with device 1.

Conclusion

We demonstrated a nanopore gated sub-attoliter Si nanocavity device for DNA compaction. Reversible DNA compaction and release were repeatedly realized in this device by reversing the bias polarity. The dynamic fluctuations of the compacted DNA inside the nanocavity were monitored by the ionic current measurements. The DNA compaction process inside the nanocavities was explored by varying the DNA lengths, ionic strength, and nanocavity dimensions. Moreover, Brownian dynamics simulations confirmed that DNA compaction is induced by the DNA molecule self-entanglement in the nanopore gated nanocavity. Since the device fabrication is fully compatible with Si CMOS process technology, this demonstrated that the nanocavity device can be mass produced at the wafer scale with low cost, and the device dimensions can be fine-tuned with high controllability. It thus holds great potential for the study of confined biopolymer physics in extremely small volumes.

Materials and methods

The nanopore gated nanocavity fabrication

The nanopore gated nanocavity device fabrication process started with a double-side polished (100) silicon-on-insulator (SOI) wafer. The SOI wafer was composed of a top silicon (Si) layer, a buried oxide (BOX) layer and a 300 μm thick Si substrate. Three different top Si thicknesses including 55 nm, 88 nm and 200 nm were tested for the fabrication of nanocavities with different dimensions. Nanocavities used for DNA compaction were mainly fabricated with a 55 nm-thick top Si layer. The first step of the fabrication was to deposit a 30 nm-thick low-stress silicon nitride (SiN_x) layer on both sides of the SOI wafer by means of low-pressure chemical vapor deposition (Koyo Lindberg). Nanoscale holes were then patterned in the SiN_x layer on the top side by electron beam lithography (Nanobeam Ltd) and reactive ion etching (RIE). Square windows with a side length of 150 μm were opened on the bottom side of the SOI wafer by photolithography and RIE. Large cavities in the Si substrate were then etched by combining deep RIE and 80 °C KOH wet etching. The top Si layer was protected during this step and the BOX layer provided a good etch stop for the KOH etching. Nanocavities were finally formed by etching the top Si layer in 60 °C KOH and stripping the BOX layer. The formation of the nanocavities was mainly controlled by the lateral etching of the {111} planes in Si.

Electrical characterization

Prior to the electrical measurements, the nanocavity chip was cleaned in a freshly prepared piranha solution (V_H2SO4: V_H2O = 3 : 1) for 30 min, rinsed in deionized wafer and blow dried with nitrogen. The chip was then loaded in a custom-made polymethyl methacrylate (PMMA) flow cell equipped with a pair of Ag/AgCl electrodes (1 mm in diameter (Warner Instruments LLC.)). Two polydimethylsiloxane O-rings (inner diameter: 1 mm) were placed on the two sides between the chip and the cell. For the DNA compaction experiment, 100 pM DNA (NoLimits Individual DNA Fragments, Thermo Fisher Scientific) dispersed in LiCl solution (buffered with 1× Tris-EDTA, pH 8) was added to both sides of the reservoirs. A patch clamp amplifier (Axopatch 200 B, Molecular Devices) was used for current detection. The traces were sampled at 50 kHz and low-pass filtered at 5 kHz. Extraction of translocation events was performed with the Transalyzer package.⁵²

Brownian dynamics simulation

A coarse-grained Brownian approach is used to model the dsDNA motion in the nanopore. The DNA is modelled as a sequence of beads and springs. An angular potential is employed to enforce the prescribed persistence length. An in-house code, adapted from previous studies on protein translocation in nanopores,^53,54 is employed. Electrophoresis, electroosmosis, excluded volume interaction among the beads and steric confinement are included as external actions on the polymer beads. Electric and velocity fields were pre-calculated solving a stationary Navier–Stokes Poisson–Nernst–Planck (NS–PNP) system using COMSOL.^55,56 The details of the physical model and of the simulation methods are reported in the ESI.† The polymer was initially placed inside the pore in the absence of electrophoresis and electroosmosis (i.e. no bias was applied) and an equilibration of ∼2 μs was performed. Then, the electrophoretic and electroosmotic fields were turned on. Six replicas, starting from slightly different initial conditions and using different seeds for the random number generator, are performed for each condition.

Author contributions

S. Z. and Z. Z. designed the experiments. S. Z. fabricated and characterized the nanocavity devices and performed the DNA compaction experiments and finite element simulations. M. C. and F. C. performed the coarse-grained Brownian dynamics simulations. T. O. performed the theoretical calculations of DNA compaction inside the nanopore gated nanocavity devices. S. Z., M. C., F. C. and Z. Z. co-wrote the manuscript. All the authors analyzed the data, discussed the results and commented on the manuscript.

Conflicts of interest

The authors declare no competing financial interests.

Acknowledgements

This work was financially supported by the Olle Engkvist Foundation (196-0077), the Swedish Strategic Research Foundation (FFL15-0174), and the Wallenberg Academy Fellow Program (2020-0190). The authors thank Prof. Ulrich F. Keyser for useful discussions. S. Z. thanks Dr Chenyu Wen for fruitful discussions and help with the COMSOL simulations.

References

1. D. Marenduzzo, C. Micheletti and E. Orlandini, J. Phys.: Condens. Matter, 2010, 22, 283102.
2. K. E. Richards, R. C. Williams and R. Calendar, J. Mol. Biol., 1973, 78, 255–259.
3. W. M. Gelbart and C. M. Knobler, Science, 2009, 323, 1682–1683.
4. S. C. Riemer and V. A. Bloomfield, Biopolymers, 1978, 17, 785–794.
5. P. G. de Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, Ithaca, N.Y, 1979.
6. M. Doi and S. F. Edwards, The Theory of Polymer Dynamics, Clarendon Press, 1988.
7. A. R. Khokhlov, A. Y. Grosberg and V. S. Pande, Statistical Physics of Macromolecules, AIP-Press, 1994.
8. M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, Oxford, New York, 2003.
9. A. J. Spakowitz and Z.-G. Wang, Biophys. J., 2005, 88, 3912–3923.
10. A. S. Petrov, M. B. Boz and S. C. Harvey, J. Struct. Biol., 2007, 160, 241–248.
11. D. Marenduzzo, E. Orlandini, A. Stasiak, D. W. Sumners, L. Tubiana and C. Micheletti, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 22269–22274.
12. T. Odijk, Macromolecules, 1983, 16, 1340–1344.
13. T. Odijk, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 060901.
14. W. C. Earnshaw and S. C. Harrison, Nature, 1977, 268, 598–602.
15. F. P. Booy, W. W. Newcomb, B. L. Trus, J. C. Brown, T. S. Baker and A. C. Steven, Cell, 1991, 64, 1007–1015.
16. M. E. Cerritelli, N. Cheng, A. H. Rosenberg, C. E. McPherson, F. P. Booy and A. C. Steven, Cell, 1997, 91, 271–280.
17. R. W. Wilson and V. A. Bloomfield, Biochemistry, 1979, 18, 2192–2196.
18. P. G. Arscott, C. Ma, J. R. Wenner and V. A. Bloomfield, Biopolymers, 1995, 36, 345–364.
19. L. S. Lerman, Proc. Natl. Acad. Sci. U. S. A., 1971, 68, 1886–1890.
20. V. V. Vasilevskaya, A. R. Khokhlov, Y. Matsuzawa and K. Yoshikawa, J. Chem. Phys., 1995, 102, 6595–6602.
21. V. A. Kabanov, V. G. Sergeyev, O. A. Pyshkina, A. A. Zinchenko, A. B. Zezin, J. G. H. Joosten, J. Brackman and K. Yoshikawa, Macromolecules, 2000, 33, 9587–9593.
22. S. Bayda, M. Adeel, T. Tuccinardi, M. Cordani and F. Rizzolio, Molecules, 2020, 25, 112.
23. Y. Kim, K. S. Kim, K. L. Kounovsky, R. Chang, G. Y. Jung, J. J. dePablo, K. Jo and D. C. Schwartz, Lab-on-a-Chip, 2011, 11, 1721–1729.
24. J.-W. Yeh, A. Taloni, K. K. Sriram, J.-P. Shen, D.-Y. Kao and C.-F. Chou, Macromolecules, 2020, 53, 1001–1013.
25. W. Yang, B. Radha, A. Choudhary, Y. You, G. Mettela, A. K. Geim, A. Aksimentiev, A. Keerthi and C. Dekker, Adv. Mater., 2021, 33, 2007682.
26. G. F. Schneider and C. Dekker, Nat. Biotechnol., 2012, 30, 326–328.
27. E. C. Yusko, B. R. Bruhn, O. M. Eggenberger, J. Houghtaling, R. C. Rollings, N. C. Walsh, S. Nandivada, M. Pindrus, A. R. Hall, D. Sept, J. Li, D. S. Kalonia and M. Mayer, Nat. Nanotechnol., 2017, 12, 360–367.
28. I. M. F. Tanimoto, B. Cressiot, N. Jarroux, J. Roman, G. Patriarche, B. Le Pioufle, J. Pelta and L. Bacri, Biosens. Bioelectron., 2021, 183, 113195.
29. K. Chen, J. Kong, J. Zhu, N. Ermann, P. Predki and U. F. Keyser, Nano Lett., 2019, 19, 1210–1215.
30. N. Giamblanco, D. Coglitore, A. Gubbiotti, T. Ma, E. Balanzat, J.-M. Janot, M. Chinappi and S. Balme, Anal. Chem., 2018, 90, 12900–12908.
31. D. Pedone, M. Langecker, A. M. Münzer, R. Wei, R. D. Nagel and U. Rant, J. Phys.: Condens. Matter, 2010, 22, 454115.
32. D. Pedone, M. Langecker, G. Abstreiter and U. Rant, Nano Lett., 2011, 11, 1561–1567.
33. S. W. Kowalczyk, D. B. Wells, A. Aksimentiev and C. Dekker, Nano Lett., 2012, 12, 1038–1044.
34. S. Winters-Hilt, W. Vercoutere, V. S. DeGuzman, D. Deamer, M. Akeson and D. Haussler, Biophys. J., 2003, 84, 967–976.
35. X. Li, G. Song, L. Dou, S. Yan, M. Zhang, W. Yuan, S. Lai, X. Jiang, K. Li, K. Sun, C. Zhao and J. Geng, Nanoscale, 2021, 13, 11827–11835.
36. J. Tang, N. Du and P. S. Doyle, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 16153–16158.
37. Z. Liang, Z. Tang, J. Li, R. Hu, D. Yu and Q. Zhao, Nanoscale, 2015, 7, 10752–10759.
38. N. Laohakunakorn, S. Ghosal, O. Otto, K. Misiunas and U. F. Keyser, Nano Lett., 2013, 13, 2798–2802.
39. R. R. Netz, J. Phys. Chem. B, 2003, 107, 8208–8217.
40. J. M. T. Thompson and T. Odijk, Philos. Trans. R. Soc., A, 2004, 362, 1497–1517.
41. N. Borochov and H. Eisenberg, Biopolymers, 1984, 23, 1757–1769.
42. H. Yamazaki, T. Mizuguchi, K. Esashika and T. Saiki, Analyst, 2019, 144, 5381–5388.
43. M. Wanunu, J. Sutin, B. McNally, A. Chow and A. Meller, Biophys. J., 2008, 95, 4716–4725.
44. W. M. Gelbart, R. F. Bruinsma, P. A. Pincus and V. A. Parsegian, Phys. Today, 2000, 53, 38–44.
45. H. Isambert, A. Ajdari, J.-L. Viovy and J. Prost, Phys. Rev. Lett., 1997, 78, 971–974.
46. H. Isambert, A. Ajdari, J.-L. Viovy and J. Prost, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 56, 5688–5704.
47. D. M. Raymer and D. E. Smith, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 16432–16437.
48. I. Kopatz, R. Zalk, Y. Levi-Kalisman, E. Zlotkin-Rivkin, G. A. Frank and S. Kler, Nanoscale, 2019, 11, 10160–10166.
49. C. Plesa, A. N. Ananth, V. Linko, C. Gülcher, A. J. Katan, H. Dietz and C. Dekker, ACS Nano, 2014, 8, 35–43.
50. C.-Y. Li, E. A. Hemmig, J. Kong, J. Yoo, S. Hernández-Ainsa, U. F. Keyser and A. Aksimentiev, ACS Nano, 2015, 9, 1420–1433.
51. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
52. C. Plesa and C. Dekker, Nanotechnology, 2015, 26, 084003.
53. M. Bacci, M. Chinappi, C. M. Casciola and F. Cecconi, J. Phys. Chem. B, 2012, 116, 4255–4262.
54. F. Cecconi and M. Chinappi, Phys. Rev. E, 2020, 101, 032401.
55. S. Zeng, C. Wen, P. Solomon, S.-L. Zhang and Z. Zhang, Nat. Nanotechnol., 2019, 14, 1056–1062.
56. A. Gubbiotti, M. Baldelli, G. Di Muccio, P. Malgaretti, S. Marbach and M. Chinappi, Adv. Phys.: X, 2022, 7, 2036638.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2nr02260e

‡ Present address: Institute for Chemical and Bioengineering, ETH Zürich, 8093 Zürich, Switzerland.

---