Enhanced third harmonic generation in ultrathin free-standing β-Ga2O3 nanomembranes: study on surface and bulk contribution†
Gao
Yi
a,
Sangheon
Jeon
b,
Young Woo
Kwon
c,
Jongkyoon
Park
b,
Duy Anh
Nguyen
d,
C. S.
Suchand Sandeep
 a,
Wan Sik
Hwang
a,
Wan Sik
Hwang
 e,
Suck Won
Hong
e,
Suck Won
Hong
 *b,
Seungchul
Kim
*b and
Young-Jin
Kim
*b,
Seungchul
Kim
*b and
Young-Jin
Kim
 *ad
*ad
aSchool of Mechanical and Aerospace Engineering, Nanyang Technological University (NTU), 50 Nanyang Avenue 639798, Singapore. E-mail: yj.kim@kaist.ac.kr
bDepartment of Cogno-Mechatronics Engineering, Department of Optics and Mechatronics Engineering, Pusan National University (PNU), 30 Jangjeon-dong Geumjeong-gu, Busan 46241, Republic of Korea. E-mail: swhong@pusan.ac.kr; s.kim@pusan.ac.kr
cDepartment of Nano-Fusion Technology, College of Nanoscience and Nanotechnology, Pusan National University (PNU), 30 Jangjeon-dong Geumjeong-gu, Busan 46241, Republic of Korea
dDepartment of Mechanical Engineering, Korea Advanced Institute of Science and Technology (KAIST), 291 Daehark-ro, Yuseong-gu, Daejeon, 34141, Republic of Korea
eDepartment of Materials Science and Engineering, Korea Aerospace University, 76 Hanggongdaehak-ro, Deogyang-gu, Goyang 10540, Republic of Korea
First published on 9th December 2021
Abstract
Third harmonic generation (THG) has proven its value in surface and interface characterization, high-contrast bio-imaging, and sub-wavelength light manipulation. Although THG is observed widely in general solid and liquid substances, when laser pulses are focused at nanometer-level ultra-thin films, the bulk THG has been reported to play the dominant role. However, there are still third harmonics (TH) generated at the surface of the thin-films, not inside the bulk solid – so-called surface TH, whose relative contribution has not been quantitatively revealed to date. In this study, we quantitatively characterized the surface and bulk contributions of THG at ultra-thin β-Ga2O3 nanomembranes with control of both the laser and thin-nanomembranes parameters, including the laser peak power, polarization state, number of layers, and nanomembranes thicknesses. Their contributions were studied in detail by analyzing the TH from freestanding β-Ga2O3 nanomembranes compared with TH from β-Ga2O3 nanomembranes on glass substrates. The contribution of the TH field from the β-Ga2O3-air interface was found to be 5.12 times more efficient than that from the β-Ga2O3-glass interface, and also 1.09 times stronger than the TH excited at bulk 1-μm-thick β-Ga2O3. Besides, TH from the β-Ga2O3-air interface was found to be 20% more sensitive to the crystalline structure than that from the β-Ga2O3-glass interface. This research work deepens our understanding of surface and bulk THG from crystalline materials and provides new possibilities towards designing highly efficient nonlinear optical materials for bio-imaging, energy-harvesting, and ultrafast laser development.
1. Introduction
Nonlinear optical harmonic generation is an optical phenomenon that occurs when intensive incident photons interact with a nonlinear optical medium. During the formation and relaxation of the nonlinear electric dipoles excited by the incident electric field, several incident photons are combined into one photon with a higher energy level while maintaining its coherence with the incident laser field.1 High-order harmonics are known to convert near-infrared (NIR) laser photons even to extreme ultra-violet (EUV) regions, which makes them highly important in high-precision spectroscopy for atomic and molecular studies.2–4 Lower-order harmonic generations also have found their importance in different areas, including bio-molecular detection,5 nanoscale light manipulation,6 and interfacial studies due to their capabilities of non-invasive nature, sub-diffraction limit imaging, and high sensitivity to crystalline structures, nanostructures, and interfacial adhesion strength.7–9 Even-order harmonic generations are only excited in non-centrosymmetric materials or material interfaces where the bulk symmetry is broken;1,10 on the contrary, the odd-order harmonic generations (including THG) are not suppressed by the inversion symmetry,11 which makes them well suited to analyzing multi-crystalline samples12 and biological samples with complicated internal structures.13 Therefore, the relative contribution of third and odd-order harmonic generation from the surface and bulk part of the materials is important and should be understood in detail.Recent THG studies from bulk substrates, such as thin sapphire14,15 and silicon,9 revealed that TH could only be excited at a skin depth of ∼50 μm from the surface, whereas the bulk THG inside the substrates was quenched due to Guoy phase shift.16 When the sample gets thinner than the coherence length of the incident laser beam, however, bulk TH is reported to start to play a dominant role.17 By studying the THG from two-dimensional (2D) material, graphene, with different numbers of atomic layers, TH intensity was proven to be proportional to the square of the sample thickness, which matches well with the theoretically predicted behavior of pure bulk TH without the contribution of surface TH.18 Therefore, there are still uncleared conflicts and a lack of understanding of THG from bulk, surface, and nanomembranes samples, which requires more in-depth investigations. Recently, a study on the interplay between surface and bulk second harmonic generation (SHG) suggested that both surface and bulk contribution play important roles in the SHG process;19 their relative contribution was determined by analyzing the interference signal between surface and bulk SHG excited from 2D van der Waals crystals of different thicknesses ranging from nanometers to micrometers. Similar interference phenomena can take place between TH excited at the surface and bulk body of materials, and the composition of interfacial materials should have a significant impact on the surface THG; however, have not been addressed to date.
β-Ga2O3 is a novel class of nanomembrane material with a thickness of few to hundreds of nanometers in scale. They can be mechanically exfoliated from the bulk crystal, similar to the exfoliation of layered graphene or other transition-metal dichalcogenide crystals.20–24 Although β-Ga2O3 is a 3D single crystal, which has a monoclinic structure with a much larger lattice constant in the (100) direction in the conventional sense, it has been recently witnessed that mechanical exfoliation into layered nanomaterials could be possible due to unexpected highly anisotropic chemical bonding with strong in-plane covalent bonds and much weaker interlayer bonds.25,26 Thus, the ease of access for the exfoliation could be attributed to these unique chemical bonding features. In this Article, the ultra-thin β-Ga2O3 nanomembranes are currently being intensely explored as quasi-2D materials due to their intriguing physical properties that could have potential applications in optoelectronic and high-voltage switching devices.26–29 More importantly, β-Ga2O3 has been garnered great attention because of its intrinsic solar-blind region bandgap (Eg 4.7–4.9 eV) with high thermal and chemical stabilities. β-Ga2O3 nanomembranes have demonstrated outstanding high-performance solar-blind photodetectors among other nanomembranes based wide bandgap materials.30,31 Furthermore, the mechanically exfoliated β-Ga2O3 can also serve as deep ultraviolet (DUV) responsive ultra-thin nanomembranes-type materials built with 2D materials to form heterojunctions in the on-chip environmental surveillance and military applications such as ozone hole monitoring, satellites, missile tracking, security communication, and chemical/biological analysis applications.32,33 Despite there are intensive studies on the key figures of merit, there is still very little knowledge on the theoretical or experimental description of optical properties of β-Ga2O3 nanomembranes, for example, higher-order harmonic generation and distinct electro-optic effects under intense optical excitation.34
Here, we report an extra-ordinary TH emission collected from the recently discovered ultra-thin β-Ga2O3 nanomembranes in their freestanding and glass-support forms when pumped by mode-locked femtosecond laser pulses. β-Ga2O3 nanomembranes were mechanically exfoliated and transferred onto target substrates by precisely controlled contact printing with a high level of engineering sophistication. The resulting atomic-thick-layered nanomembranes have conformally contacted uniform layouts or slightly relief structures i.e., freestanding nanomembranes type with a high level of optical transparency; thereby, the sample characterization becomes versatile at both fundamental and TH wavelengths. Femtosecond laser excitation of THG makes this technique very unique because the optical properties of β-Ga2O3 nanomembranes were sensitive to the number of layers, bulk to freestanding structures, and physically formed interfaces. Characterization of THG reveals the key properties and provides preliminary insights into the physics and materials aspects of β-Ga2O3 nanomembranes associated with the dynamic changes of the interlayer interfaces. Under such conditions, TH field excited at the β-Ga2O3/air interface was determined to be 5.12 times stronger than at the β-Ga2O3-glass interface, TH field generated at the bulk β-Ga2O3 was linearly dependent on the thickness of β-Ga2O3. For a 1 μm thick β-Ga2O3 sample, bulk TH field strength was 4.70 times stronger than that at the β-Ga2O3-glass interface. The incident TH polarization dependence of freestanding and glass-supported samples resulted that the TH intensity is dependent on incident polarization states and sample thickness; the TH field was strengthened from 15 to 42% when the sample thickness increased from ∼330 to ∼990 nm. Besides, freestanding samples showed ∼20% higher sensitivity to incident polarization states than glass-supported samples. Our findings suggest that THG can be excited with the highest efficiency at β-Ga2O3/air interface, which can provide new possibilities in a highly efficient nonlinear optical conversion medium by stacking β-Ga2O3 nanomembranes to create multiple β-Ga2O3/air interfaces. Such highly efficient transparent nonlinear optical materials can be of great value in applications such as high-power ultrafast laser development, high-resolution surface characterization, and non-invasive biomolecular imaging.
2. Results and discussion
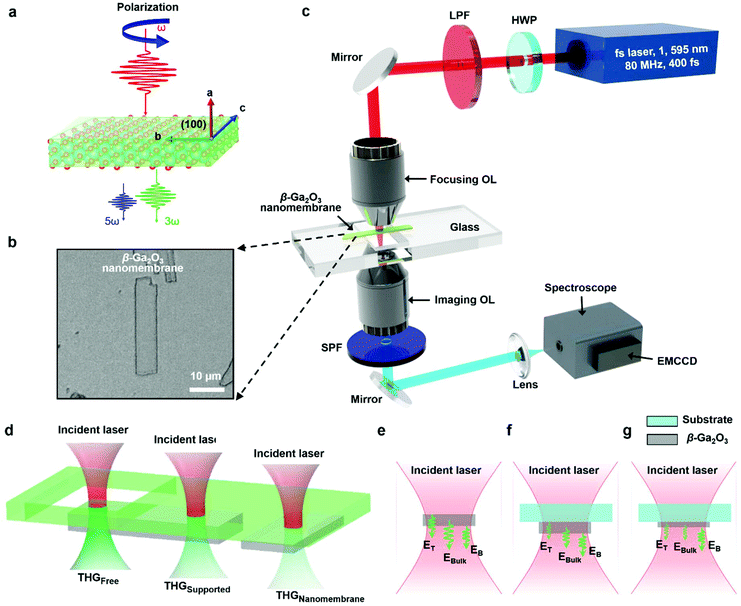
2.1. Surface and bulk optical HG: sample preparation and optical configuration
Fig. 1a shows schematic diagrams of a sequential process of the sample preparation; the micro-transfer printing process was used to produce β-Ga2O3 nanomembranes onto the target substrate. This simple micro-transfer printing process was developed with the firmly established method as sequentially presented (i–iv). First, bulk β-Ga2O3 was well cleaved from the crystal wafer to the initial substrate (i.e., SiO2/Si substrate) simply using water-soluble polyvinyl alcohol (PVA) or 3 M adhesive tape by multiple times contact/separation-based exfoliation with a thickness range of hundreds micrometer scale. Subsequently, this roughly prepared bulk β-Ga2O3 were re-exfoliated onto a donor substrate (i.e., glass substrate) by micromechanical cleavage in the process of the multiple transfer printing that sufficiently broke the van der Waals bonds of the interlayer of bulk β-Ga2O3 cleaving into the individual layers (i.e., β-Ga2O3 nanomembranes) (Fig. 1a(ii)).35–38 At this stage, the thickness range of the re-exfoliated β-Ga2O3 nanomembranes on the donor substrate varied from ∼300 nm up to ∼1 μm. Next, the randomly placed and perfectly prepared β-Ga2O3 nanomembranes were readily lifted up from this donor substrate by a pick-up plate module consisting of a load cell and polydimethylsiloxane (PDMS) elastomer (Fig. 1a(iii)). A key feature of this technique was the use of a force-gauge mounted pick-up plate, combined together with a viscoelastic PDMS stamp as an in-adhesive-free transfer medium, to efficiently transfer β-Ga2O3 nanomembranes by direct measuring the magnitude of the applied pressure when the micro-transfer printing process was performed in a precisely controllable manner (Fig. 1b). Thus, we controlled the accuracy of the compression force with a conformal contact and retracted velocity on the prepared β-Ga2O3 nanomembranes, maintaining the morphological integrity of the samples. In addition, the sample quality was identified in real-time using the equipped optical microscope (i.e., CCD camera), and thereby the desired samples were selectively transferred with high yield to a receiving substrate (i.e., BK7 glass substrate, t = 450 μm) for the optical measurements (Fig. 1a(iv)). The thickness of β-Ga2O3 nanomembrane transferred to the receiving substrate (i.e., BK7 glass substrate) was measured by scanning electron microscope (SEM) and atomic force microscope (AFM). Fig. 1c shows a representative SEM image of β-Ga2O3 nanomembrane and an optical height profile (Keyence VK-X250 K); the thickness was ∼990 nm without the blisters of contamination. To confirm this, we used AFM for the β-Ga2O3 nanomembrane as representing similar heights, ∼991 nm along the dotted white line (Fig. 1d). As is well known, the crystal structure of β-Ga2O3 is classified as a monoclinic with a large lattice constant in (100) direction; Fig. 1e shows the unit cell of the β-Ga2O3.39 Raman spectrum from the sample surface shows the quality of the β-Ga2O3 nanomembrane on a quartz substrate prepared by the micro-transfer process; there was no noticeable difference in the peak intensity between the bulk β-Ga2O3 and β-Ga2O3 nanomembranes. The structural properties of β-Ga2O3 nanomembranes were thoroughly investigated by a high-resolution transmission electron microscope (HRTEM), as shown in Fig. 1g. The surface HRTEM image of the exfoliated sample along with the (100) plane and the corresponding selected-area electron diffraction patterns (SAED) images (shown in Fig. 1h) revealed that the lattice parameters, such as the lattice symmetry, are highly consistent with the previously reported values of the monoclinic β-Ga2O3.The atomic structure of β-Ga2O3 excited by the femtosecond (fs) laser for optical HG is shown in Fig. 2a. As a monoclinic crystalline material, the nonlinear optical polarization tensor strength of β-Ga2O3 is dependent on the azimuthal angle between the crystalline axis of β-Ga2O3 and the polarization direction of the incident laser.1,14 This results in the reliance of the optical harmonic field on the polarization states of the incident laser. By rotating a half-wave plate, HG intensities at different incident polarization states can be obtained and utilized for the characterization of crystalline structures of materials. These will be thoroughly discussed in section 4. The optical image of a representative β-Ga2O3 nanomembrane is shown in Fig. 2b, displaying a smooth surface without visible defects. A few samples are carefully translocated to the hollow region of the customized glass substrate using a micro-transfer printing system for the study of HG from freestanding β-Ga2O3 nanomembranes, which will be discussed with more details in section 5. Nonlinear optical HG are excited and characterized using the optical setup in Fig. 2c. A NIR mode-locked Er-doped fiber femtosecond pulse laser (Toptica, FemtoFiber Pro NIR) having a central wavelength of 1595 nm is utilized as the excitation laser source considering its excellent transmission ratio for both β-Ga2O3 nanomembranes and glass substrate, as well as the high optical power required for the excitation of HG. The repetition rate and pulse duration of the fs laser are set to 80 MHz and 400 fs, respectively. The linear polarization state of the incident laser is controlled by a half-wave plate (Thorlabs WPH10M-1550), and a long-pass filter (FELH1200) is utilized to remove the short-wavelength noise generated during the power amplification in an Er-doped fiber amplifier and subsequent power delivery through the optical single-mode fiber. The filtered laser beam is then focused onto the sample using a 40× objective lens with a numerical aperture of 0.65 (Newport LI-40X); the focused beam has a power density of 1.1 × 109 W cm−2 and a beam diameter of 7.6 μm in full-width-half-maximum (FWHM). The objective lens itself supports a beam diameter of 1.5 μm in full-width-half-maximum (2.3 μm in 1/e2) for visible wavelength from 400 to 700 nm; however, because the input laser's wavelength is 1550 nm (out of the design specification), the optical aberration enlarged the laser beam to 7.6 μm. The power density was carefully adjusted so as not to exceed the damage threshold of β-Ga2O3, 1.4 × 109 W cm−2.40 In this regime, the TH signal was stable with a power fluctuation less than 5% without noticeable damage. Nonlinear optical HG is collected by another 40× objective lens with the same numerical aperture (Olympus UPlan 40X). They are then delivered to a broadband spectrometer (Andor's Shamrock 193i) with a susceptible electron-multiplying charge-coupled device (EMCCD; Andor's IXon Ultra) for the spectral analysis. Note that the emission in the wavelength of 360 nm is collected after short-pass-filtered by a 400 nm short-pass filter (Ruiqi Optoelectronics SPF-400) to suppress the relatively strong background noises at long wavelengths. A schematic of thickness-dependent TH intensities from freestanding and substrate-supported β-Ga2O3 nanomembranes is shown in Fig. 2d; the discrepancy of HG intensities from different samples is the result of changes in the top surface, bulk β-Ga2O3, bottom surface optical harmonic field, and the interference among them. The Ga2O3 film's physical characteristics, such as unexpected defects, cracks, dusts, grain boundaries as well as the strain, could make changes in TH output intensity. However, in this study, the Ga2O3 film is very thin (only one to a few layers thick) and light, so the strain level at the film should be extremely low. In addition, if there were any strain-induced TH intensity changes, the spatial TH intensity distribution should be observed in the optical microscope system due to the spatial strain distribution; however, the spatial TH intensity changes could not be observed. Therefore, the strain-induced TH signal change can exist but with very small amount, which did not contribute to the measurement. Fig. 2e–g show the amplitudes of surface and bulk optical harmonic field excited at the samples shown in Fig. 2d. Detailed characterization and explanation of surface and bulk contribution of optical harmonic fields will be given in the later sections.
2.2. Optical THG and FHG from β-Ga2O3 nanomembranes supported by glass substrates
The contributions of TH from glass/β-Ga2O3, air/β-Ga2O3 interfaces, and bulk β-Ga2O3 are characterized by using β-Ga2O3 nanomembranes with different thicknesses. The amplitude of TH field generated at bulk β-Ga2O3 is linearly related to the sample thickness, while the amplitudes of TH fields at interfaces are independent of the sample thickness,18 as illustrated in Fig. 2a and b. The variation of sample thickness also creates different optical path lengths for THG propagating in the samples, which results in the interference condition changes among TH generated at glass/β-Ga2O3, air/β-Ga2O3 interfaces, and bulk β-Ga2O3. To precisely describe TH generated from β-Ga2O3 nanomembranes, a model is developed considering both the change of third-order harmonic field amplitudes and the interference conditions. The TH field generated at glass/β-Ga2O3 (ET), air/β-Ga2O3 (EB) interfaces, and bulk β-Ga2O3 (EBulk), shown in Fig. 2(e)–(g), can be expressed as41,42| ET = a × eiφ1 | (1) |
| EB = b × eiφ2 | (2) |
| EBulk = f(l) × (eiφω − eiφ3ω) | (3) |
 and
and  describe the phases of THG fields as a function of the thickness of β-Ga2O3 nanomembranes (l) with the wavelength-dependent refractive indices (nf = 1.885 and nTH = 1.920).43 The amplitude of TH field at bulk β-Ga2O3 is proportional to sample thickness land can be described by f(l) = c × l.
describe the phases of THG fields as a function of the thickness of β-Ga2O3 nanomembranes (l) with the wavelength-dependent refractive indices (nf = 1.885 and nTH = 1.920).43 The amplitude of TH field at bulk β-Ga2O3 is proportional to sample thickness land can be described by f(l) = c × l. 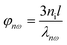 and (eiφω − eiφω) describes the phase of TH field at the bulk β-Ga2O3, where ni is the refractive index of β-Ga2O3 at corresponding wavelengths. The overall TH field excited at substrate-supported β-Ga2O3 nanomembranes can then be determined to be
and (eiφω − eiφω) describes the phase of TH field at the bulk β-Ga2O3, where ni is the refractive index of β-Ga2O3 at corresponding wavelengths. The overall TH field excited at substrate-supported β-Ga2O3 nanomembranes can then be determined to be| ESub-Ga2O3 = ET + EB + EBulk = a × eiφ1 + b × eiφ2 + f(l) × (eiφ1 − eiφ1). | (4) |
The intensity of TH excited at substrate-supported β-Ga2O3 nanomembranes can then be expressed as
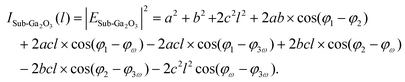 | (5) |
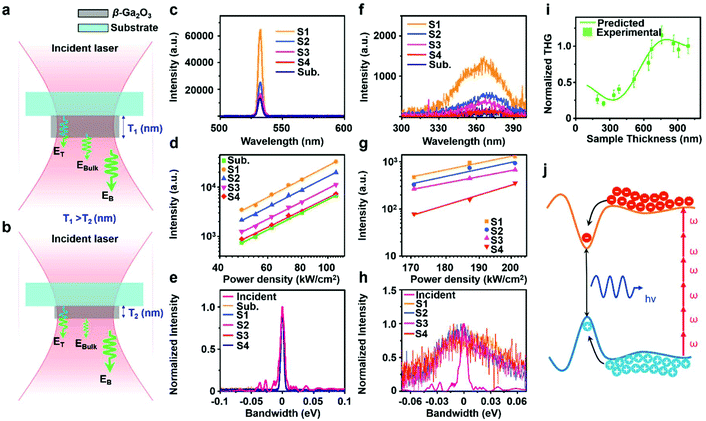
Based on this model, THs from 11 samples with different thicknesses are thoroughly characterized. The TH spectra, TH intensity plots with the different pump power density and photon energy spectra of four representative samples with thicknesses of 991 (noted as S1), 670 (noted as S2), 515 (noted as S3) and 334 nm (noted as S4) are shown in Fig. 2c–e. Clear THG peaks are observed at 531 nm for all the samples in Fig. 3c, which match well with the theoretical TH wavelength excited by a 1595 nm laser. Note that, although THG can be excited at bare glass/air interface, the contribution of THG from the bulk glass is negligible in the experiment due to the Guoy phase shift.16Fig. 3d shows the pump-power-dependent TH intensities for all the samples; the linear slope corresponds to 2.87, 2.81, 2.79, 2.69, and 2.78 for S1, S2, S3, S4, and a bare glass substrate, respectively. They are all close to 3.00 within 3% deviation, which agrees well with the nonlinear power dependence, ITHG ∝ PN in the nonlinear perturbative harmonic generation, where N is 3.0 for THG. The spectral bandwidth of TH was analyzed in Fig. 3e in the photon energy domain. The photon energy spectra of THs were normalized by the harmonic order, which is 3 for TH. The resulting spectra of TH agree well with the original spectrum of the incident laser at a fundamental wavelength of 1595 nm. Theoretically, the normalized TH bandwidth should be the same as that of the incident laser. The bandwidths of TH spectra with different samples are all ∼0.005 eV in full-width-half-maximum (FWHM), being slightly smaller than that of the fundamental laser spectrum of 0.008 eV. This smaller TH bandwidth is expected to come from the spectral characteristics of the optical components in the imaging path, spectrographs, and EMCCD. Besides TH at 531 nm, another weak but broad peak is detected at around 365 nm as in Fig. 3f, longer than the theoretical wavelength of FHG, which is 319 nm, while no emission is detected for bare glass substrate, it was named as ‘UV emission’. This red-shifted UV emission spectrum from the FH position indicates the contribution of other sources. One of the most likely sources is multi-photon luminescence. Considering the bandgap of β-Ga2O3, 4.8 eV, and the photon energy of the fundamental laser, the multi-photon absorption process should have been involved here at least. β-Ga2O3 nanomembranes have non-uniform potentials with the presence of local potential minimum in the material44 as illustrated in Fig. 3j. The potential fluctuation may come from the micro-inclusions of different phases45 and/or quantum well-like formation induced by structural defects, which was reported for similar 2-D materials like GaN.46 Under the intensive laser excitation, excited electrons and holes in the conduction and valence band would be localized to the minima/maxima potential levels for recombination, resulting in the offset of around 1 eV for the bandgap of β-Ga2O3 and therefore the emission at 365 nm. This can be further evidenced by the pumping power density vs. intensity plot (Fig. 3g), which shows slopes of 6.46, 5.75, 9.15, and 6.21 for S1, S2, S3, and S4, higher than the harmonic order of FH, indicating the involvement of higher-order multi-photon processes. The bandgap of β-Ga2O3 is 4.8 eV, 6.18 times higher than the photon energy of the fundamental laser, it means that more than 6 photons will be required for the excitation of electrons from the valence band to the conductive band for radiative recombination,1 which matches well with the slopes of pumping power density vs. TH intensity plot. The normalized photon-energy spectra for the emission in UV range were compared with that of the fundamental laser in Fig. 3h, showing a much wider FWHM (0.21 eV) than that of fundamental laser (0.08 eV), matches well with the nature of multi-photon luminescence.
After the characterization of TH and UV emission from β-Ga2O3, normalized TH intensities from 11 different samples are plotted against their thicknesses and compared with the curve predicted by the model in Fig. 3i. Due to the THG intensity measured by the EMCCD is of the arbitrary unit, theoretically modeled and experimentally measured THG intensities were normalized by the value of calculated and measured THG intensities of S1. The normalization of predicted and measured THG intensities allows us to prove the validity of the model. The experimental measure data points are then fitted by ISub-Ga2O3 (l) to determine the relationship between a, b, and c. It was found that the experimental data can be fitted well by ISub-Ga2O3 (l) with a chi-factor of 0.2 when b = 5.12a and f(l) = 4.70a for S1; this proves the reasonable validity of the theoretical model. This implies that the harmonic field at air/β-Ga2O3 is 5.12 times higher than that at glass/β-Ga2O3 interface in substrate-supported β-Ga2O3 nanomembranes, while the bulk TH field of a 991 nm-thick β-Ga2O3 nanomembrane is 4.70 times higher than that at glass/β-Ga2O3 interface.
2.3. Polarization and thickness dependence of TH and UV emission from β-Ga2O3 nanomembranes
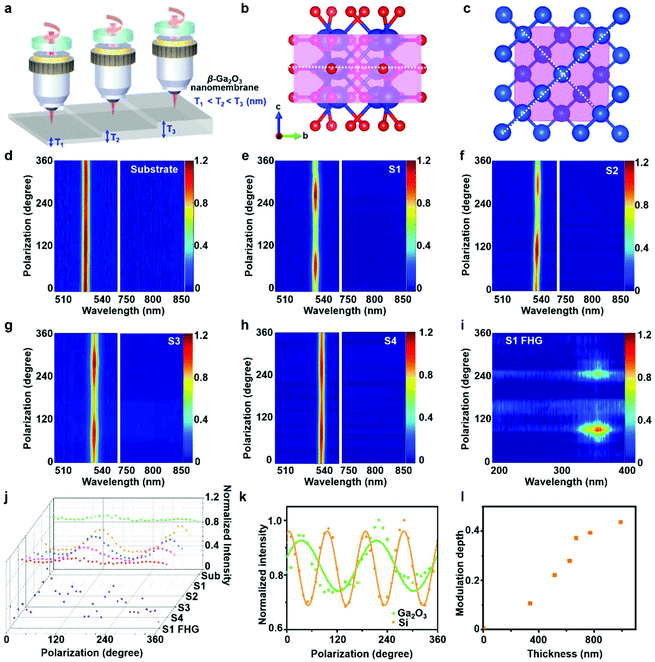
The incident polarization dependence of TH from β-Ga2O3 nanomembranes is investigated for six samples of different thicknesses utilizing the experimental setup shown in Fig. 4a. The input polarization state is controlled by a half-wave plate with a step size of 10 degrees. The conversion efficiency of the nonlinear perturbative harmonic generation process is strongly dependent on the crystalline structure due to the variation of energy bands at different electron oscillation directions,11,15 which enables the polarization dependence of HG to be a good indicator of the material's crystalline structure. As a monoclinic crystalline material, β-Ga2O3 shows a two-fold symmetric crystalline structure as pictured in Fig. 4b, with a black dotted line indicating the symmetric axis. Fig. 4d–h show the 2-D mapping of the polarization-dependent TH spectra from the glass substrate, S1, S2, S3, and S4. While THG from amorphous glass substrate shows no dependence on the input polarization state, THs excited at β-Ga2O3 nanomembranes show clear two-fold dependence on the polarization states of the incident laser, which matches well with the crystalline structure of β-Ga2O3. Similar polarization dependence is found for UV emission excited at S1, a high noise level is detected due to the low intensity of UV emission at 365 nm and the long integration time of over 60 s. In the measurement of polarization dependence of FHG from β-Ga2O3 nanomembranes thinner S1, the rotation of half-wave plate introduces noise higher than the intensity level, which makes it difficult to obtain the polarization dependence of UV emission excited at thin β-Ga2O3 samples. Fig. 4j summarized the sectional profile of the polarization dependence of TH from the glass substrate, representative β-Ga2O3 nanomembranes, and UV emission from S1. The TH intensities of S1 at different incident polarization states are fitted by a sine curve as in Fig. 4k with an adjacent R-square value of 0.716, suggesting a relatively large deviation from a typical sine curve. The deviation indicates the complicated atomic structure of β-Ga2O3 nanomembranes. Due to its monoclinic crystalline structure, nonlinear electric dipoles can be formed not only between atoms within the incident plane but also atoms out of the plane as in the ESI.† This induces the fluctuation of TH intensities when the incident polarization state is changed from 0 to 180°, and leads to the under-fitting of TH intensities to the sine curve. The polarization dependence of TH from β-Ga2O3 is then compared to that of a (100) single crystalline silicon wafer in Fig. 4k. Silicon has a standard cubic crystalline structure with two symmetric axes, as shown in Fig. 4c. The polarization-dependent normalized TH intensities of (100) silicon wafer are also fitted using a sine function with an adjacent R-square value of 0.96, which is much closer to 1, proving an obviously better fitting to the sine function thanks to the simple cubic crystalline structure of (100) silicon wafer. The differences between TH dependence on incident polarization states prove that polarization-dependent HG intensities can be a good characterization tool for the crystalline structures of materials.It can be found from Fig. 4j that the modulation depth of polarization-dependent TH from β-Ga2O3 nanomembranes is dependent on the nanomembranes thickness. The modulation depths of seven samples are plotted against their thicknesses, as in Fig. 4l. The modulation depth clearly increases with the thickness of β-Ga2O3 nanomembranes. This can be attributed to the different polarization dependence of surface and bulk contributed TH.47 TH excited at an interface of two materials is dependent on the atomic properties of both materials. As a result, its incident polarization dependence is also determined by the crystalline structures of both materials. For glass/β-Ga2O3 interface, while β-Ga2O3 has a monoclinic crystalline structure, glass is an amorphous material whose nonlinear optical polarization is independent of input polarization states; as a result, TH excited at glass/β-Ga2O3 interface is less dependent on input polarization than bulk β-Ga2O3. For air/β-Ga2O3 interface, the polarization dependence of TH is higher than that of glass/β-Ga2O3 interface due to the low atomic density of air. Since the polarization dependence of TH from bulk β-Ga2O3 is stronger than that from interfaces, the increase of β-Ga2O3 nanomembranes thickness leads to higher bulk contribution of bulk TH, which is more dependent on incident polarization states.
2.4. THG from freestanding and substrate-supported β-Ga2O3 nanomembranes
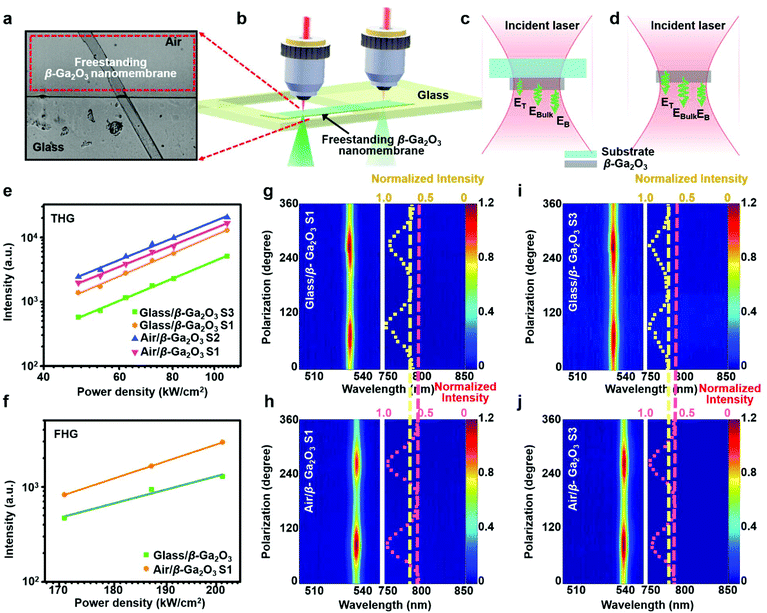
For the investigation of optical HGs from freestanding β-Ga2O3 nanomembranes, previous studies translocated the samples to the edge of the glass substrates, where the substrate partially supports them. This process makes it possible to focus the fundamental laser at freestanding β-Ga2O3 nanomembranes. The movement of the samples is achieved by using a microscope-based translocation system, which is detailly presented in Fig. 1b and ESI.† An optical micrograph of a representative freestanding β-Ga2O3 sample is shown in Fig. 5a and the experimental setup is schematically illustrated in Fig. 5b. Fig. 5c and d show the differences in surface and bulk contributed TH field from freestanding and substrate-supported β-Ga2O3 nanomembranes. Compared with substrate-supported samples, freestanding samples have two air/β-Ga2O3 interfaces which generated TH field 5.12 times higher than that excited at the glass/β-Ga2O3 interface. Besides, TH field generated at bulk β-Ga2O3 by a focused Gaussian beam is also dependent on the surrounding media based on the equation: | (6) |
 | (7) |
 | (8) |
Third-order nonlinear susceptibilities and dielectric constants of the materials are taken from literature as follows:1,48,49χ(3)Glass = 2.80 × 10−22 m2 V−2,  , χair(3) = 1.70 × 10−25 m2 V−2, εGlassω = 2.25, εGlass3ω = 2.31,
, χair(3) = 1.70 × 10−25 m2 V−2, εGlassω = 2.25, εGlass3ω = 2.31, 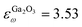 ,
,  , εairω = 1.00055, εairω = 1.00056. Taking the values in to eqs (7) and (8), it can be obtained that EBulk(free) = 1.59EBulk(supported). The result can then be substituted into eqn (5) and it is found that the TH intensity of freestanding S1 IFree-Ga2O3(S1) = 1.20ISub-Ga2O3(S1). For S3, it can be calculated that TH intensity of freestanding β-Ga2O3 nanomembranes is 2.78 folds higher than that of substrate-supported β-Ga2O3 nanomembranes. For separating the TH from β-Ga2O3 thin-film and other does from the glass substrate as well as validating the theoretical model, the experiments had been designed into two steps as shown in Fig. 5b–d, the first measurement with free-standing β-Ga2O3 nanomembrane only and the other measurement with β-Ga2O3 nanomembrane with the glass substrate. TH intensities at different pumping power densities are plotted in Fig. 5e. While the slopes of the pumping power density vs. TH intensity plot for freestanding samples and substrate-supported samples are similar (2.79, 2.87, 2.69, and 2.72 for substrate-supported S3, S1, and freestanding S3 and S1, respectively). The intensities of TH at freestanding S1 is 1.20 times higher than the substrate-supported one, which matches well with the value predicted by the theoretical model. The THG intensity ratio between freestanding and substrate-supported S3 is 3.00, which agrees well with the prediction as well. UV emission was also detected at the same wavelength of 365 nm from freestanding S1 as in Fig. 5f, the slope of pumping power density vs. UV emission intensity plot (7.78) is similar to that of the substrate-supported sample (6.21), with an intensity 2.29 times higher than UV emission generated at the substrate-supported sample. Note that UV emission from freestanding sample S2 is not detected due to the weak signal intensity, likely to be caused by the destructive interference among UV emission generated at the top, bottom interfaces and bulk β-Ga2O3 nanomembranes. Polarization dependence of THG from freestanding samples is also characterized and the 2-D mapping of the polarization-dependent THG spectra for freestanding samples are compared with substrate-supported ones in Fig. 5g–j. Similar two-fold symmetric polarization dependence is found for freestanding samples with modulation depths of 50% and 39% for S1 and S3, which are around 20% higher than substrate-supported samples. The higher dependence of incident polarization states of freestanding samples may come from the removal of the amorphous glass substrate. In substrate-supported samples, TH generated at the glass/β-Ga2O3 interface will be dependent on the nonlinear electric field dipole generated by the atoms in both glass and β-Ga2O3, due to the high atom density and the amorphous nature of glass, the polarization dependence of TH from glass/β-Ga2O3 will be weaker than bulk β-Ga2O3 and air/β-Ga2O3, which results in the relatively weak polarization dependence of substrate-supported sample. For freestanding samples with air/β-Ga2O3 interface, due to the extreme low atom density of air, the incident polarization dependence of nonlinear electric dipole generated at air/β-Ga2O3 interface remained the same as bulk β-Ga2O3, resulting in the higher polarization dependence of THG freestanding β-Ga2O3 nanomembranes.
, εairω = 1.00055, εairω = 1.00056. Taking the values in to eqs (7) and (8), it can be obtained that EBulk(free) = 1.59EBulk(supported). The result can then be substituted into eqn (5) and it is found that the TH intensity of freestanding S1 IFree-Ga2O3(S1) = 1.20ISub-Ga2O3(S1). For S3, it can be calculated that TH intensity of freestanding β-Ga2O3 nanomembranes is 2.78 folds higher than that of substrate-supported β-Ga2O3 nanomembranes. For separating the TH from β-Ga2O3 thin-film and other does from the glass substrate as well as validating the theoretical model, the experiments had been designed into two steps as shown in Fig. 5b–d, the first measurement with free-standing β-Ga2O3 nanomembrane only and the other measurement with β-Ga2O3 nanomembrane with the glass substrate. TH intensities at different pumping power densities are plotted in Fig. 5e. While the slopes of the pumping power density vs. TH intensity plot for freestanding samples and substrate-supported samples are similar (2.79, 2.87, 2.69, and 2.72 for substrate-supported S3, S1, and freestanding S3 and S1, respectively). The intensities of TH at freestanding S1 is 1.20 times higher than the substrate-supported one, which matches well with the value predicted by the theoretical model. The THG intensity ratio between freestanding and substrate-supported S3 is 3.00, which agrees well with the prediction as well. UV emission was also detected at the same wavelength of 365 nm from freestanding S1 as in Fig. 5f, the slope of pumping power density vs. UV emission intensity plot (7.78) is similar to that of the substrate-supported sample (6.21), with an intensity 2.29 times higher than UV emission generated at the substrate-supported sample. Note that UV emission from freestanding sample S2 is not detected due to the weak signal intensity, likely to be caused by the destructive interference among UV emission generated at the top, bottom interfaces and bulk β-Ga2O3 nanomembranes. Polarization dependence of THG from freestanding samples is also characterized and the 2-D mapping of the polarization-dependent THG spectra for freestanding samples are compared with substrate-supported ones in Fig. 5g–j. Similar two-fold symmetric polarization dependence is found for freestanding samples with modulation depths of 50% and 39% for S1 and S3, which are around 20% higher than substrate-supported samples. The higher dependence of incident polarization states of freestanding samples may come from the removal of the amorphous glass substrate. In substrate-supported samples, TH generated at the glass/β-Ga2O3 interface will be dependent on the nonlinear electric field dipole generated by the atoms in both glass and β-Ga2O3, due to the high atom density and the amorphous nature of glass, the polarization dependence of TH from glass/β-Ga2O3 will be weaker than bulk β-Ga2O3 and air/β-Ga2O3, which results in the relatively weak polarization dependence of substrate-supported sample. For freestanding samples with air/β-Ga2O3 interface, due to the extreme low atom density of air, the incident polarization dependence of nonlinear electric dipole generated at air/β-Ga2O3 interface remained the same as bulk β-Ga2O3, resulting in the higher polarization dependence of THG freestanding β-Ga2O3 nanomembranes.
3. Conclusion
In summary, we excited TH from freestanding and glass-supported ultrathin β-Ga2O3 nanomembranes of different thicknesses. The interference and polarization dependence of surface and bulk THG were thoroughly investigated at the β-Ga2O3-glass interface, β-Ga2O3-air interface, and bulk β-Ga2O3. For the surface THG, β-Ga2O3-air interface was found to be most efficient in comparison to the β-Ga2O3-glass interface and bulk β-Ga2O3. While adjusting the incident polarization states, THG intensity was modulated by 15 to 42% for the samples with thicknesses from 390 to 900 nm. TH excited from the freestanding sample showed 20% higher modulation depth than the glass-supported sample, which indicates that TH excited at β-Ga2O3-air interface is more sensitive to the crystalline lattice structure than that excited at β-Ga2O3-glass interface. These results deepen our understanding of THG, including their surface and bulk contribution, polarization sensitivity to their crystalline structures, surface and interfacial characteristics, and inter-layer interferences; all these can provide new possibilities in the development of ultrafast short-wavelength lasers, high-resolution surface characterization, and non-invasive biomolecular depth imaging.4. Experimental section
4.1. Cleaving of β-Ga2O3 nanomembranes and transfer printing process
The β-Ga2O3 nanomembranes were prepared by clipping large segments from the bulk β-Ga2O3 using well-known taping methods and then physically peeling off several times with adhesive tape.50,51 The viscoelastic PDMS stamp was prepared by mixing the prepolymer and curing agent in a ratio of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 by weight, removing the air bubbles in a vacuum desiccator, and pouring it onto a plastic Petri dish. This was placed in an oven and cured at 70 °C for 1 hour to prepare a viscoelastic PDMS stamp.
1 by weight, removing the air bubbles in a vacuum desiccator, and pouring it onto a plastic Petri dish. This was placed in an oven and cured at 70 °C for 1 hour to prepare a viscoelastic PDMS stamp.
4.2. Characterization of β-Ga2O3 nanomembranes
Raman spectrometer (UniNanoTech UniRAM-II) analyzed the structural characteristics of β-Ga2O3 nanomembranes using a 532 nm line. The surface and thickness of β-Ga2O3 nanomembranes were measured by SEM (Carl Zeiss AG-SUPRA 25, 0.5–20 kV) and AFM (Park System NX10). The atomic structure and crystal orientation were investigated by TEM (TALOSF200X, operated at 200 kV); the specimens were prepared using the plan-view lift-out technique of the focused ion beam (FIB, Scios-FEI).Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
This work was supported by the National Research Foundation of the Republic of Korea (NRF-2021R1A5A1032937, NRF2021R1A4A1031660, NRF-2012R1A3A1050386, NRF-2020R1A2C2102338, NRF-2020R1C1C1007691, NRF-2021R1A4A2001827) and KAIST UP Program. The authors thank Prof. Seung-Woo Kim for useful discussions and insightful suggestions.References
- R. W. Boyd, The Nonlinear Optical Susceptibility in Nonlinear Optics, Academic Press, 3rd edn, 2008, pp. 27–33 Search PubMed.
- N. L. Wagner, A. Wuest, I. P. Christov, T. Popmintchev, X. B. Zhou, M. M. Murnane and H. C. Kapteyn, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 13279–13285 CrossRef CAS PubMed.
- T. D. Scarborough, T. T. Gorman, F. Mauger, P. Sandor, S. Khatri, M. B. Gaarde, K. J. Schafer, P. Agostini and L. F. DiMauro, Appl. Sci., 2018, 8(7), 1129 CrossRef.
- Y. Q. He, L. X. He, P. F. Lan, B. N. Wang, L. Li, X. S. Zhu, W. Cao and P. X. Lu, Phys. Rev. A, 2019, 99, 053419 CrossRef CAS.
- Y. Birman, S. Khorsand, E. Tu, R. B. Mortensen and M. T. Butko, Methods, 2019, 167, 92–104 CrossRef CAS PubMed.
- W. Y. Tsai, T. L. Chung, H. H. Hsiao, J. W. Chen, R. J. Lin, P. C. Wu, G. Sun, C. M. Wang, H. Misawa and D. P. Tsai, Adv. Mater., 2019, 31, 1806479 CrossRef.
- J. I. Dadap, Z. Xu, X. F. Hu, M. C. Downer, N. M. Russell, J. G. Ekerdt and O. A. Aktsipetrov, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 13367–13379 CrossRef CAS.
- Y. R. Shen, Nature, 1989, 337, 519–525 CrossRef CAS.
- Y. Gao, H. Lee, J. N. Jiao, B. J. Chun, S. Kim, D. H. Kim and Y. J. Kim, Opt. Express, 2018, 26, 32812–32823 CrossRef CAS PubMed.
- N. Bloembergen, R. K. Chang, S. S. Jha and C. H. Lee, Phys. Rev., 1968, 174, 813–822 CrossRef CAS.
- T. Y. F. Tsang, Phys. Rev. A, 1995, 52, 4116–4125 CrossRef CAS PubMed.
- A. Antony, P. Poornesh, I. Kityk, G. Myronchuk, G. Sanjeev, V. Petwal, V. Verma and J. Dwivedi, J. Lumin., 2019, 207, 321–332 CrossRef CAS.
- B. Weigelin, G. J. Bakker and P. Friedl, J. Cell Sci., 2016, 129, 245–255 CAS.
- G. Yi, H. Lee, J. Jiannan, B. J. Chun, S. Han, H. Kim, Y. W. Kim, D. Kim, S. W. Kim and Y. J. Kim, Opt. Express, 2017, 25, 26002–26010 CrossRef CAS.
- H. Kim, S. Han, Y. W. Kim, S. Kim and S. W. Kim, ACS Photonics, 2017, 4, 1627–1632 CrossRef CAS.
- L. V. Doronina-Amitonova, A. A. Lanin, I. V. Fedotov, O. I. Ivashkina, M. A. Zots, A. B. Fedotov, K. V. Anokhin and A. M. Zheltikov, Appl. Phys. Lett., 2013, 103, 093701 CrossRef.
- P. N. Saeta and N. A. Miller, Appl. Phys. Lett., 2001, 79, 2704–2706 CrossRef CAS.
- N. Kumar, J. Kumar, C. Gerstenkorn, R. Wang, H. Y. Chiu, A. L. Smirl and H. Zhao, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 121406(R) CrossRef.
- S. Deckoff-Jones, J. J. Zhang, C. E. Petoukhoff, M. K. L. Man, S. D. Lei, R. Vajtai, P. M. Ajayan, D. Talbayev, J. Madeo and K. M. Dani, Sci. Rep., 2016, 6, 22620 CrossRef CAS PubMed.
- K. S. Novoselov, D. Jiang, F. Schedin, T. J. Booth, V. V. Khotkevich, S. V. Morozov and A. K. Geim, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 10451 CrossRef CAS.
- C. Lee, H. Yan, L. E. Brus, T. F. Heinz, J. Hone and S. Ryu, ACS Nano, 2010, 4, 2695–2700 CrossRef CAS PubMed.
- G. H. Lee, C. H. Lee, A. M. van der Zande, M. Y. Han, X. Cui, G. Arefe, C. Nuckolls, T. F. Heinz, J. Hone and P. Kim, APL Mater., 2014, 2, 092511 CrossRef.
- K. S. Novoselov, A. Mishchenko, A. Carvalho and A. H. C. Neto, Science, 2016, 353(6298), 903–906 CrossRef PubMed.
- A. K. Geim and I. V. Grigorieva, Nature, 2013, 499, 419–425 CrossRef CAS.
- H. J. Bae, T. H. Yoo, Y. Yoon, I. G. Lee, J. P. Kim, B. J. Cho and W. S. Hwang, Nanomaterials, 2018, 8(8), 594 CrossRef.
- W. S. Hwang, A. Verma, H. Peelaers, V. Protasenko, S. Rouvimov, H. Xing, A. Seabaugh, W. Haensch, C. G. Van de Walle, Z. Galazka, M. Albrecht, R. Fornari and D. Jena, Appl. Phys. Lett., 2014, 104, 203111 CrossRef.
- J. Kim, S. Oh, M. A. Mastro and J. Kim, Phys. Chem. Chem. Phys., 2016, 18, 15760–15764 RSC.
- E. Swinnich, M. N. Hasan, K. Zeng, Y. Dove, U. Singisetti, B. Mazumder and J.-H. Seo, Adv. Electron. Mater., 2019, 5, 1800714 CrossRef.
- M. Higashiwaki, K. Sasaki, A. Kuramata, T. Masui and S. Yamakoshi, Appl. Phys. Lett., 2012, 100, 013504 CrossRef.
- E. G. Víllora, K. Shimamura, T. Ujiie and K. Aoki, Appl. Phys. Lett., 2008, 92, 202118 CrossRef.
- Z. Galazka, R. Uecker, K. Irmscher, M. Albrecht, D. Klimm, M. Pietsch, M. Brützam, R. Bertram, S. Ganschow and R. Fornari, Cryst. Res. Technol., 2010, 45, 1229–1236 CrossRef CAS.
- W.-Y. Kong, G.-A. Wu, K.-Y. Wang, T.-F. Zhang, Y.-F. Zou, D.-D. Wang and L.-B. Luo, Adv. Mater., 2016, 28, 10725–10731 CrossRef CAS PubMed.
- S. Nakagomi, T. Sakai, K. Kikuchi and Y. Kokubun, Phys. Status Solidi A, 2019, 216, 1700796 CrossRef.
- M. Baldini, Z. Galazka and G. Wagner, Mater. Sci. Semicond. Process., 2018, 78, 132–146 CrossRef CAS.
- S. Kim, J. Wu, A. Carlson, S. H. Jin, A. Kovalsky, P. Glass, Z. Liu, N. Ahmed, S. L. Elgan, W. Chen, P. M. Ferreira, M. Sitti, Y. Huang and J. A. Rogers, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 17095 CrossRef CAS.
- F. Pizzocchero, L. Gammelgaard, B. S. Jessen, J. M. Caridad, L. Wang, J. Hone, P. Bøggild and T. J. Booth, Nat. Commun., 2016, 7, 11894 CrossRef CAS.
- A. Carlson, A. M. Bowen, Y. G. Huang, R. G. Nuzzo and J. A. Rogers, Adv. Mater., 2012, 24, 5284–5318 CrossRef CAS PubMed.
- M. A. Meitl, Z. T. Zhu, V. Kumar, K. J. Lee, X. Feng, Y. Y. Huang, I. Adesida, R. G. Nuzzo and J. A. Rogers, Nat. Mater., 2006, 5, 33–38 CrossRef CAS.
- J. Åhman, G. Svensson and J. Albertsson, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1996, 52, 1336–1338 CrossRef.
- J.-H. Yoo, S. Rafique, A. Lange, H. Zhao and S. Elhadj, APL Mater., 2018, 6, 036105 CrossRef.
- F. Kajzar, J. Messier and C. Rosilio, J. Appl. Phys., 1986, 60, 3040–3044 CrossRef CAS.
- F. Kajzar and J. Messier, Phys. Rev. A, 1985, 32, 2352–2363 CrossRef CAS.
- S. I. Stepanov, V. I. Nikolaev, V. E. Bougrov and A. E. Romanov, Rev. Adv. Mater. Sci., 2016, 44, 63–86 CAS.
- G. Pozina, M. Forsberg, M. A. Kaliteevski and C. Hemmingsson, Sci. Rep., 2017, 7, 42132 CrossRef CAS PubMed.
- X. T. Zhou, F. Heigl, J. Y. P. Ko, M. W. Murphy, J. G. Zhou, T. Regier, R. I. R. Blyth and T. K. Sham, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75 DOI:10.1103/PhysRevB.75.125303.
- S. Khromov, C. G. Hemmingsson, H. Amano, B. Monemar, L. Hultman and G. Pozina, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 075324 CrossRef.
- O. A. Aktsipetrov, A. A. Fedyanin, E. D. Mishina, A. A. Nikulin, A. N. Rubtsov, C. W. vanHasselt, M. A. C. Devillers and T. Rasing, Phys. Rev. Lett., 1997, 78, 46–49 CrossRef CAS.
- M. Thalhammer and A. Penzkofer, Appl. Phys. B: Lasers Opt., 1983, 32, 137–143 CrossRef.
- P. E. Ciddor, Appl. Opt., 1996, 35, 1566–1573 CrossRef CAS PubMed.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- H. Li, J. Wu, Z. Yin and H. Zhang, Acc. Chem. Res., 2014, 47, 1067–1075 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1nr06259j |
| This journal is © The Royal Society of Chemistry 2022 |