Alloying dichalcogenolate-protected Ag₂₁ eight-electron nanoclusters: a DFT investigation

Abstract

The isoelectronic doping of dichalcogenolato nanoclusters of the type [Ag₂₁{E₂P(OR)₂}₁₂]⁺ (E = S, Se) by any heteroatom belonging to groups 9–12 was systematically investigated using DFT calculations. Although they can differ in their global structure, all of these species have the same M@M₁₂-centered icosahedral core. In any case, the different structure types are all very close in energy. In all of them, three different alloying sites can be identified (central, icosahedral, peripheral) and calculations allowed the trends in heteroatom site occupation preference across the group 9–12 family to be revealed. These trends are supported by complementary experimental results. They were rationalized on the basis of electronegativity, potential involvement in the bonding of valence d-orbitals and atom size. TD-DFT calculations showed that the effect of doping on optical properties is sizable and this should stimulate research on the modulation of luminescence properties in the dithiolato and diseleno families of complexes.

---

Introduction

During recent decades, ligand-protected atom-precise noble metal nanoclusters have remained a subject of immense scientific interest, owing to their exceptional structural and bonding features as well as their chemical and physicochemical properties.^1–25 A way of tuning the properties of a homometallic nanocluster is to “alloy” it by substituting one or several metal atoms with those of another metal from the same or a close column.^18,19 It is necessary to control the number and position(s) of the heterometal atom(s) in the nanocluster molecular framework in order to achieve fine control of properties following alloying. This is not always an easy task experimentally, owing to the difficulties inherent in alloy characterization, such as the separation of alloys of different compositions and/or of positional isomers, as well as those caused by crystal disorder. This is why density functional theory (DFT) modeling has been used as a complementary tool to help determine the precise structure of alloys and rationalize their stabilities, peculiar electronic features and structure–property relationships.^6,25–40 So far, most of these theoretical investigations have been devoted to thiolate-protected alloys of gold or a limited number of their silver-equivalent alloyed homologues. With respect to silver alloys, the most comprehensive theoretical investigation was performed by Aikens and coworkers on the doping of [Ag₂₅(SR)₁₈]⁻, who found that group 10 atoms prefer a central location, whereas the other positions become preferable when doping with group 11–13 atoms.³⁹ During recent years, we developed an original idea of silver nanoclusters protected by dichalcogenolate ligands of the general formula [Ag₂₁{E₂P(OR)₂}₁₂]^+41,42 (E = S, Se). Their originality comes from the distinctive nature of the dichalcogenolate ligands, which differ from simple thiolates not only in their chelating nature but also in the fact they bear a different formal charge per coordinating atom (−1 for two chalcogens vs. −1 for one sulfur in the case of thiolates). As a result, dichalcogenolates stabilize species with nuclearities and compositions that are noticeably different from those of simple thiolates. Such compounds have no equivalent within gold nanocluster chemistry and their diseleno derivatives are the only examples of isolated Se-protected silver nanoclusters structurally characterized so far. They consist of a superatomic [Ag₁₃]⁵⁺-centered icosahedral core, protected by an outer passivating shell made up of 12 dichalcogenolate ligands and eight Ag(I) outer d¹⁰ metals. Isoelectronic alloys have also been characterized, namely [{Au@Ag₂₀}{Se₂P(OEt)₂}₁₂]⁺,⁴¹ [{Pt@Ag₂₀}{S₂P(OⁿPr)₂}₁₂],⁴³ [{Pt@Ag₂₀}{Se₂P(OⁿPr)₂}₁₂],⁴⁴ [{Pt@Ag₂₀}{Se₂P(OⁱPr)₂}₁₂],⁴⁴ [{Pt@Ag₂₀}{Se₂P(CH₂CH₂Ph)₂}₁₂],⁴⁴ [{Pd@Ag₂₀}{S₂P(OⁿPr)₂}₁₂],⁴⁵ [{Au@Ag₂₀}{S₂P(OⁱPr)₂}₁₂]⁺,⁴⁶ [{Au@Ag₂₀}{Se₂P(OⁱPr)₂}₁₂]⁺,⁴⁷ [{Au@Au₂Ag₁₈}{Se₂P(OⁱPr)₂}₁₂]⁺,⁴⁷ [{Ag@Ag₁₆Cu₄}{S₂P(OⁱPr)₂}₁₂]⁺⁴⁸ and [{Au@Ag₁₆Cu₄}{S₂P(OⁱPr)₂}₁₂].⁴⁸

Three structural types have so far been clearly shown to exist within this rather large family of homo- and heterometallic compounds (Fig. 1), all of them having the same M₁₃-centered icosahedral superatomic core, but differing in the topology of their outer passivating shell made up of 12 dichalcogenolate ligands and eight d¹⁰ outer metals (Fig. 2), which are distinctly different from the family of the [MAu₂₄(SR)₁₈]⁻ and [MAg₂₄(SR)₁₈]⁻ monothiolato alloys.³⁹ In this paper, we present a systematic and comprehensive theoretical investigation on the stability, structure and optical properties of such silver nanoclusters isoelectronically monosubstituted by a metal from group 9 (Co, Rh, Ir), 10 (Ni, Pd, Pt), 11 (Cu, Au) or 12 (Zn, Cd, Hg), together with some experimental X-ray and UV–vis results that support the computed results. All of the investigated species are isoelectronic to their [Ag₂₁{E₂P(OR)₂}₁₂]⁺ parent, i.e., they are eight-electron superatoms^{1,2,13,23,42,49,50} of configuration 1S² 1P⁶.

Fig. 1 Structurally characterized eight-electron [Ag₂₁{E₂P(OR)₂}₁₂]⁺ (E = S, Se) clusters and their isoelectronic alloys. The ideal symmetries are those of the whole cluster, assuming that all of the metal atoms are of the same nature.

Fig. 2 The octa-capped centered icosahedral metal frameworks ([M@M₁₂][μ₃-M₈]) of the three structural types defined in Fig. 1. They differ only by the position of the eight face-capping outer d¹⁰ (e.g. Ag(I)) atoms (in green). The positions of the 12 ligands (Fig. 1) ensue from those of these eight atoms. The specified T, C₃ and C₁ symmetries are those of the whole cluster (with ligands), considered as homometallic. They correspond to the T_h, D₃ and C₂ ideal symmetries for the naked M₂₁ framework, respectively (see Fig. 1).

Computational details

DFT calculations were carried out with the Gaussian 16 package⁵¹ on the various isomers of models [MAg₂₀(E₂PH₂)₁₂]^q (E = S, Se; M = Co, Rh, Ir: q = −1; M = Ni, Pd, Pt: q = 0; M = Cu, Ag, Au: q = +1; M = Zn, Cd, Hg: q = +2). The considered ligand simplification allows a huge amount of CPU time to be saved. On the other hand, its validity has been proved on many occasions.^41–48,52 The BP86 functional^53,54 was used together with the general triple-ζ polarized Def2-TZVP basis set from EMSL Basis Set Exchange Library,^55,56 in conjunction with effective core potentials (ECPs) for the eight heavier elements, thus permitting to somewhat account for scalar relativistic effects. All the optimized geometries were ascertained as true minima on the potential energy surface by carrying out vibrational frequency calculations. All of the investigated species were found to have a singlet ground state. The natural atomic orbital (NAO) charges were computed using the NBO 6.0 program on single-point calculations at the same level of theory.⁵⁷ The UV–vis transitions were calculated on the above-mentioned optimized geometries using time-dependent DFT (TD-DFT) calculations, with the CAM-B3LYP functional⁵⁸ and Def2-TZVP basis set. The UV–vis spectra were simulated from the computed TD-DFT transitions and their oscillator strengths using GaussView,⁵⁹ each transition being associated with a Gaussian function of half-height width equal to 1000 cm⁻¹.

Experimental details

The synthesis of [PtAg₂₀{S₂P(OⁿPr)₂}₁₂] was performed according to a previous report.⁴³ Whereas crystals containing the C₁-I isomer (P2₁/c space group) were obtained by diffusing n-hexane into dichloromethane solution at ambient temperature and contained solvated n-hexane molecules,⁴³ those of the C₃-I isomer (R3 space group) were grown in acetone at ambient temperature. A single crystal suitable for X-ray diffraction analysis was mounted on the tip of a glass fiber coated in paratone oil, then frozen. Data were collected on a Bruker APEX II CCD diffractometer using graphite monochromated Mo Kα radiation (λ = 0.71073 Å) at 100 K. Absorption corrections for area detector were performed using SADAB⁶⁰ and integration of the raw data frame was performed with SAINT.⁶¹ The structure was solved by direct methods and refined by least squares against F² using the SHELXL-2018/3 package,^62,63 incorporated in SHELXTL/PC V6.14.⁶⁴ All non-hydrogen atoms were refined anisotropically. One of the propyl groups (C10–C12) was found to be disordered over two positions with equal occupancy. Crystallographic data are provided in Table S1.† The structure reported herein has been deposited at the Cambridge Crystallographic Data Centre, CCDC no. 2091674.† UV–vis absorption spectra were measured on a PerkinElmer Lambda 750 spectrophotometer using quartz cells with a path length of 1 cm. All of the samples were recorded at ambient temperature in 2-MeTHF as a solvent.

Energetic and structural results

As reported above, the three different structures so far characterized are strongly related.⁶⁵ Not only do they all possess a formal eight-electron centered icosahedral M₁₃ core, but in all of them the 12 dichalcogenolate ligands are arranged in such a way that the 12 metal atoms occupying icosahedral vertices are coordinated to one sulfur/selenium atom in a radial orientation and the eight peripheral outer d¹⁰ centers are coordinated in a trigonal planar mode, thus making locally stable 16-electron complexes. These d¹⁰ metals cap icosahedral faces, but their interaction with the icosahedral core is weak^41–48,52 (being mainly of a metallophilic nature). Assuming a homometallic [Ag₂₁{E₂P(OR)₂}₁₂]⁺ cluster in any of the three structures defined above, the substitution of any of the Ag atoms by one hetero-metal generates several positional isomers that need to be calculated, the number of which becomes very large in the case of the structure of C₁ symmetry. In order to reduce the number of structures needing to be calculated, we first computed the homometallic [Ag₂₁{E₂PH₂}₁₂]⁺ (E = S, Se) in the three characterized structural types shown in Fig. 1 and 2. We thus assume that the role played by the nature of R in the structural choice of the [Ag₂₁{E₂P(OR)₂}₁₂]⁺ (E = S, Se) clusters and their alloys is negligible. This is supported, inter alia, by the fact that all of the known diselenolato species adopt the same structure type T, independently of the size and nature of R (Fig. 1). Selected computed results are given in Table 1. The dithiolato species have free energies lying in a range of less than 5 kcal mol⁻¹, whereas those of their diselenolato relatives are within 11 kcal mol⁻¹. In both cases, the C₁ structure is the least stable. All of the computed structures have related electronic structures, as exemplified by the nature of their HOMOs and LUMOs,⁴¹ HOMO–LUMO gaps and the NAO charges of the different types of Ag atoms (icosahedron center (type I), icosahedron vertices (type II) and outer capping Ag(I) centers (type III)). Owing to the similarities of the computed results for the three structures and their closeness in energy, we chose to focus on the two more stable and more symmetrical ones, namely T and C₃.

Table 1 Selected results obtained for the [Ag₂₁{E₂PH₂}₁₂]⁺ (E = S, Se) models in the three experimentally characterized structural types discussed in the text. HOMO–LUMO gaps (H–L) in eV and relative total (ΔE) and free (ΔG) energies in kcal mol⁻¹

Cluster	Symmetry	H–L	ΔE	ΔG	Ag NAO charges
[Ag21{S2(PH2)}12]^+	T	1.92	0.1	2.1	Center: −0.37
					Icosahedron: +0.23
					Outer capping: +0.63 (+0.61; +0.64)
	C 3	1.77	0	0	Center: −0.41
					Icosahedron: +0.23 (+0.21; +0.25)
					Outer capping: +0.63 (+0.60; +0.64)
	C 1	1.45	8.6	4.6	Center: −0.42
					Icosahedron: +0.23 (+0.07; 0.30)
					Outer capping: +0.63 (+0.61; +0.65)
[Ag21{Se2(PH2)}12]^+	T	1.73	0	0	Center: −0.29
					Icosahedron: +0.21
					Outer capping: +0.58 (+0.56; +0.60)
	C 3	1.52	4.6	0.2	Center: −0.34
					Icosahedron: +0.21 (+0.18; 0.23)
					Outer capping: +0.58 (+0.55; +0.59)
	C 1	1.29	15.6	10.3	Center: −0.34
					Icosahedron: +0.20 (+0.06; +0.29)
					Outer capping: +0.58 (+0.57; 0.60)

---

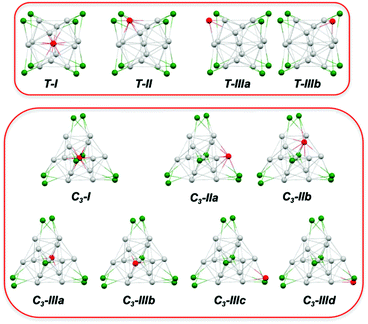
Substituting one of the Ag atoms in [Ag₂₁(E₂PH₂)₁₂]⁺ with a hetero-metal M generates four and seven different [MAg₂₀(E₂PH₂)₁₂]^q positional isomers for the T and C₃ structures, respectively, as illustrated in Fig. 3. Note that, because of the substitution, most of these isomeric structures have a symmetry that is lower than that of their T or C₃ [Ag₂₁(E₂PH₂)₁₂]⁺ progenitor. Thus, in the following, the T and C₃ labels designate a structure type, rather than a symmetry group.

Fig. 3 The different isomers generated by substituting one Ag atom with one hetero-metal M in the T and C₃ structure types of [Ag₂₁{E₂P(OR)₂}]⁺. Color code: Ag, grey (centered icosahedron), green (outer capping); M; red. Ligand not shown.

The relative energies and HOMO–LUMO gaps of the most stable isomers of the [MAg₂₀(E₂PH₂)₁₂]^q systems derived from structure types T and C₃ are given in Table 2. More detailed energetic results concerning all of the isomers defined in Fig. 3 are provided in Tables S2 and S3.† Starting with the thiolato (E = S) series, one can see that the C₃ structure type is always preferred over the T one, in both ΔE and ΔG, but in any case by less than ∼6 kcal mol⁻¹. These results are in line with those obtained for the homometallic [Ag₂₁{S₂PH₂}₁₂]⁺ cluster (see above). Moreover, except for M = Cd, the preferred substitution site (I, II or III) is the same for the T and C₃ structures. When M belongs to groups 9 and 10, there is a preference for type I, i.e. for M occupying the icosahedron center. This result is consistent with the X-ray structures of [{Pt@Ag₂₀}{S₂P(OⁿPr)₂}₁₂]⁴³ and [{Pd@Ag₂₀}{S₂P(OⁿPr)₂}₁₂].⁴⁵ The preference for type I is stronger for group 9 than for group 10 metals and within each group it increases when descending the triad (Table S2†). Type I is also clearly preferred for M = Au and this is corroborated by the X-ray structure of [{Au@Ag₂₀}{S₂P(OⁱPr)₂}₁₂]⁺.⁴⁶ However, this preference is somewhat less important than that for M = Pt. With M = Cu, type III, i.e. Cu occupying an outer capping position, is preferred. This is also the case for M = Zn. In the case of M = Cd, types III and II are almost isoenergetic, whereas for M = Hg, type II, i.e. Hg occupying an icosahedron vertex, is preferred.

Table 2 Computed HOMO–LUMO gaps (H–L) (in eV) and relative total (ΔE) and free (ΔG) energies (in kcal mol⁻¹) of the most stable isomers of clusters [MAg₂₀(L)₁₂]^q (L = E₂PH₂) found for structure types T and C₃, as defined in Fig. 3

		E = S
		T				C 3
		Isomer	H–L	ΔE	ΔG	Isomer	H–L	ΔE	ΔG
Group 9	[CoAg20(L)12]^−	T-I	1.46	3.3	4.7	C 3-I	1.36	0.0	0.0
	[RhAg20(L)12]^−	T-I	1.91	2.8	5.4	C 3-I	1.73	0.0	0.0
	[IrAg20(L)12]^−	T-I	2.04	4.2	6.0	C 3-I	1.84	0.0	0.0
Group 10	[NiAg20(L)12]	T-I	1.82	1.4	4.1	C 3-I	1.72	0.0	0.0
	[PdAg20(L)12]	T-I	1.92	1.0	3.6	C 3-I	1.81	0.0	0.0
	[PtAg20(L)12]	T-I	2.04	1.8	4.3	C 3-I	1.91	0.0	0.0
Group 11	[CuAg20(L)12]^+	T-IIIa	1.90	4.7	1.6	C 3-IIIc	1.75	0.0	0.0
	[AuAg20(L)12]^+	T-I	2.03	0.4	2.1	C 3-I	1.87	0.0	0.0
Group 12	[ZnAg20(L)12]^2+	T-IIIb	1.69	5.8	6.4	C 3-IIIa	1.50	0.0	0.0
	[CdAg20(L)12]^2+	T-II	1.76	2.7	4.7	C 3-IIIb	1.40	0.0	0.0
	[HgAg20(L)12]^2+	T-II	1.57	1.1	2.3	C 3-IIb	1.58	0.0	0.0

---

		E = Se
		T				C 3
		Isomer	H–L	ΔE	ΔG	Isomer	H–L	ΔE	ΔG
Group 9	[CoAg20(L)12]^−	T-I	1.75	0.0	2.0	C 3-I	1.53	0.7	0.0
	[RhAg20(L)12]^−	T-I	1.36	0.0	2.0	C 3-I	1.23	0.7	0.0
	[IrAg20(L)12]^−	T-I	1.86	0.0	2.5	C 3-I	1.62	0.1	0.0
Group 10	[NiAg20(L)12]	T-I	1.69	0.0	0.9	C 3-I	1.51	3.1	0.0
	[PdAg20(L)12]	T-I	1.73	0.0	0.7	C 3-I	1.54	3.3	0.0
	[PtAg20(L)12]	T-I	1.83	0.0	0.8	C 3-I	1.62	2.9	0.0
Group 11	[CuAg20(L)12]^+	T-IIId	1.70	0.0	0.0	C 3-IIIb	1.53	2.6	1.2
	[AuAg20(L)12]^+	T-I	1.83	0.0	0.1	C 3-I	1.59	4.3	0.0
Group 12	[ZnAg20(L)12]^2+	T-I	1.78	0.0	2.3	C 3-IIa	1.35	0.4	0.0
	[CdAg20(L)12]^2+	T-II	1.61	0.0	0.0	C 3-IIIa	1.27	3.1	1.0
	[HgAg20(L)12]^2+	T-II	1.45	0.0	5.3	C 3-IIb	1.42	3.4	0.0

---

The selenolato (E = Se) series exhibits quite similar trends, with some small differences. In particular, the energy differences between structure types T and C₃ are even smaller than in the E = S case and T is slightly preferred over C₃ in ΔE, whereas the opposite situation occurs in ΔG. One can simply note that all of the [MAg₂₀(Se₂PH₂)₁₂]^q X-ray structures determined so far adopt the T structure type. The other slight differences compared with the thiolato series concern the M = group 12 cases for which the energy differences between positional isomers are small. Zn balances between type II and type I and Cd and Hg slightly favor type II. The experimental structures of [MAg₂₀(Se₂PH₂)₁₂]^q species known so far, namely those of [{Pt@Ag₂₀}{Se₂P(OⁿPr)₂}₁₂],⁴⁵ [{Au@Ag₂₀}{Se₂P(OEt)₂}₁₂]⁺ (ref. 42) and [Au@Ag₂₀}{Se₂P(OⁱPr)₂}₁₂]⁺(ref. 47) support our computed results.

Finally, we would like to note additional support for the fact that the C₁ structure was not considered in the above calculations on alloys, based on the fact the three structural types of Fig. 1 are very close in energy, independent of the nature of M, and do not impact on the positional choice of M on the alloy metal framework (I, II or III). It turns out that we characterized the C₃ structure of [{Pt@Ag₂₀}{Se₂P(OⁿPr)₂}₁₂], whereas the C₁ structure of the same compound is already known (Fig. 1).⁴³ This is the first example of true isomerism (same R substituent) reported in the chemistry of silver or silver-rich nanoclusters. Both isomers are of type I, as predicted by the calculations. They were obtained from different crystallization conditions (see Experimental details). This new C₃-I X-ray structure is shown in Fig. 4 and has comparable metrical data with its C₁-I isomer (see ESI† for more details). Calculations on the C₃-I and C₁-I isomers of the [PtAg₂₀(E₂PH₂)₁₂] model found an energy difference of 5.6 kcal mol⁻¹ (C₃-I being more stable). The existence of true isomers also underpins the negligible role played by the nature of the R substituent in the preference for one of the structures of Fig. 1 over the others.

Fig. 4 The C₃-I X-ray molecular structure of [{Pt@Ag₂₀}{Se₂P(OⁿPr)₂}₁₂]. Left: total structure with n-propoxy groups omitted for clarity. Right: metal-framework. Color codes: orange: Pt; grey: Ag_ico: green, Ag_cap: yellow: S; pink: P.

Discussion

Assuming little energetic and bonding difference between structure types T, C₃ and C₁, the major discriminant factor in the [MAg₂₀(E₂PH₂)₁₂]^q structural choice is between types I, II and III, as stated in Table 3, which summarizes in a condensed way the data of Tables 2, S2 and S3.† There are several factors that interplay in the preference between the three types of site for M, the first one coming to mind being the size effect. The trends related to size effect are in fact not obvious, except that a small M atom (such as Zn) encapsulated within an Ag₁₂ icosahedron is likely not to be very favorable. Another factor is electronegativity. From this strict point of view, starting from an homometallic [Ag₂₁(E₂PH₂)₁₂]⁺ cluster and substituting one Ag atom with a more electronegative atom will favor the more electron-rich site, that is, type I (see the NAO charges in Table 1). Substituting Ag with a more electropositive atom will lead to the opposite choice, that is, type III (see the NAO charges in Table 1). The preference for type III is also related to the ability of M, when in an oxidation state corresponding to the valence d¹⁰ configuration, to stabilize trigonal planar coordination. Au(I) and Hg(II), for example, are more prone to di- rather than tri-coordination. In any case, probably the most important parameter is the availability of the M valence d orbitals when encapsulated within the Ag₁₃ icosahedron (structure type I). Whereas the role played by the occupied valence d-type AOs of M is negligible in structure types II and III, it can be different when structure type I is considered. As described in the Introduction, the superatomic electron configuration of the [Ag₂₁(E₂PH₂)₁₂]⁺ nanoclusters is 1S² 1P⁶ 1D⁰. The 1S, 1P and 1D superatomic orbitals are mainly combinations of the 4s(Ag) AOs (with some 4p(Ag) admixture). However, the “non-bonding” occupied valence d orbitals of the encapsulated M have the same symmetry as the vacant 1D orbitals, and can mix with them, resulting in a stabilizing effect.³⁵ This effect is weak in the case of M = Ag, but can be stronger when M has valence d-orbitals that are more diffuse and/or higher in energy. This is reflected by the NAO valence d populations of M (Table 4) computed for the T-I structure types. When M = Au or belongs to groups 9 and 10 (and especially with their heavier elements), lower d populations are found, indicating stronger valence d(M) bonding involvement and thus more favored type I structures. The opposite effect occurs when M = Cu or belongs to group 12. Such an effect has already been described when isoelectronically substituting with Os the central Au atom in the eight-electron superatom [Au₁₃(dppe)₅Cl₂]³⁺,⁶⁶ as well as in related doped Ag₂₅ isoelectronic thiolato nanoclusters.⁴⁰

Table 3 M site occupation preference in the computed [MAg₂₀(E₂PH₂)₁₂]^q species. Values in parentheses are Pauling electronegativities

Co (1.88)	Ni (1.91)	Cu (1.90)	Zn (1.65)
E = S, Se: I > III > II	E = S, Se: I > III > II	E = S, Se: III > I > II	E = S, Se: III > I > II
Rh (2.28)	Pd (2.20)	Ag (1.93)	Cd (1.69)
E = S, Se: I > III > II	E = S, Se: I > II ≈ III		E = S, Se: II ≈ III > I
Ir (2.20)	Pt (2.28)	Au (2.54)	Hg (2.00)
E = S: I > III > II	E = S: I > II > III	E = S, Se: I > II > III	E = S, Se: II > I > III
E = Se: I > II ≈ III	E = Se: I > II ≈ III

---

Table 4 Valence d NAO populations of M in the [M@Ag₂₀(E₂PH₂)₁₂]^q clusters of type T-I

Co	9.43	Ni	9.73	Cu	9.97	Zn	10.0
Rh	9.32	Pd	9.70	Ag	9.91	Cd	9.98
Ir	9.37	Pt	9.75	Au	9.92	Hg	9.92

---

Considering together both electronegativity and d-orbital effects allows understanding of most of the results in Table 3. From these data it is also possible to reasonably predict the structure of polysubstituted species. For example, in the case of M = Au, the unique central site (type I) will first be occupied, then additional Au atoms will occupy icosahedron vertices (type II), as exemplified by the X-ray structure of [{Au@Au₂Ag₁₈}{Se₂P(OⁱPr)₂}₁₂]⁺.⁴⁷ The preference for outer capping positions for Cu (type III) allows consideration of the theoretical limit of eight atoms in such positions. So far, up to four capping positions have been shown to be occupied by Cu in [{Ag@Ag₁₆Cu₄}{S₂P(OⁱPr)₂}₁₂]⁺ and [{Au@Ag₁₇Cu₃}{S₂P(OⁱPr)₂}₁₂].⁴⁸ The isoelectronic substitution of two Ag atoms by two Ni or two group 9 metals is likely to involve the central site (type I) and one of the capping sites (type III). The group 12 situation is less clear, but in any case it is likely not to involve the central site (type I).

With respect to their optical properties, all of the computed species have their lowest absorption energies associated with 1P → 1D transitions and it is possible to anticipate their variations with respect to the nature of M by looking at their HOMO–LUMO gaps (Table 2). In the case of the most symmetrical T-I structure type, the 1D level splits into two components (t and e) and the band of lowest energy has a 1P(t) → 1D(t) nature, while the next one is of a major 1P → 1D(e) character. The simulated spectra of the E = Se species with a T-I structure type favored are shown in Fig. 5a–c. They show a typical blue shift upon M descending a column and less variation within a given period. The experimental spectra of the [M@Ag₂₀{S₂P(OⁿPr)₂}₁₂] (M = Ag, Au, Pt) clusters are reported in Fig. 5c for comparison. Their λ_max values are 496, 472 and 470 nm (low energy band) and 414, 392 and 391 nm (high energy band) for M = Ag, Au, Pt, respectively. The corresponding computed values for the models [MAg₂₀{S₂PH₂}₁₂] (M = Ag, Au, Pt) are 474, 447 and 445 nm (low energy band) and 395, 376 and 370 nm (high energy band), respectively (Fig. 5c). Thus, with a small blue shift of ∼20 nm, the CAM-B3LYP-simulated spectra are in very good agreement with their available experimental counterparts.

Fig. 5 (a–c) TD-DFT-simulated UV–vis spectra of the most stable isomers of the [M@Ag₂₀(Se₂PH₂)₁₂]^q eight-electron species (T–I structure). (d) Experimental UV–vis spectra of [M@Ag₂₀{S₂P(OⁿPr)₂}₁₂] (M = Ag, Au, Pt) in 2-MeTHF solvent.

Conclusions

In summary, DFT calculations on eight-electron [MAg₂₀(E₂PH₂)₁₂]^q (E = S, Se) silver-rich nanoclusters indicate that if M = Au or belongs to group 9 or 10, M clearly prefers to occupy the central encapsulated site (type I). If M = Cu, the outer capping position, i.e. Cu(I) (type III), is favored. All of the known alloy species containing Au, Pt, Pd and/or Cu^41,43–48 follow our computed tends. These results are broadly consistent with those previously obtained by DFT calculations on eight-electron [MAg₂₄(SR)₁₈]^q models that also contain a centered icosahedral core,³⁵ and with most of the known X-ray structures of such species.^67–71 Although no [MAg₂₀(E₂PH₂)₁₂]^q alloy containing group 12 elements is known so far, our computed structures, HOMO–LUMO gaps and bonding parameters suggest that such species should be sufficiently stable to be isolated, with the preferred structure type being III, II/III and II for M = Zn, Cd and Hg, respectively. From the point of view of modulating optical properties, structure II, which impairs the superatomic core, would be particularly interesting to stabilize. Experimental attempts to synthesize such species are currently underway in our group.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the France–Taiwan ANR–MOST 2018 program (project Nanoalloys), the GENCI French National Computer Resource Center (grant A0030807367) and the Ministry of Science and Technology of Taiwan (MOST 109-2113-M-259-008; 108-2923-M-259-001).

Notes and references

1. M. Walter, J. Akola, O. Lopez-Acevedo, P. D. Jadzinsky, G. Calero, C. J. Ackerson, R. L. Whetten, H. Gronbeck and H. Häkkinen, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 9157–9162.
2. H. Häkkinen, Chem. Soc. Rev., 2008, 37, 1847–1859.
3. B. K. Teo, J. Cluster Sci., 2014, 25, 5–28.
4. R. Jin, C. Zeng, M. Zhou and Y. Chen, Chem. Rev., 2016, 116, 10346–10413.
5. I. Chakraborty and T. Pradeep, Chem. Rev., 2017, 117, 8208–8271.
6. G. Hu, Q. Tang, D. Lee, Z. Wu and D.-e. Jiang, Chem. Mater., 2017, 29, 4840–4847.
7. K. D. Weerawardene, H. Häkkinen and C. M. Aikens, Annu. Rev. Phys. Chem., 2018, 69, 205–229.
8. Q. Yao, T. Chen, X. Yuan and J. Xie, Acc. Chem. Rev., 2018, 51, 1338–1348.
9. N. A. Sakthivel and A. Dass, Acc. Chem. Rev., 2018, 51, 1774–1783.
10. Z. Lei, X.-K. Wan, S. F. Yuan, Z.-J. Guan and Q.-M. Wang, Acc. Chem. Rev., 2018, 51, 2465–2474.
11. T. Higaki, Q. Li, M. Zhou, S. Zhao, Y. Li, S. Li and R. Jin, Acc. Chem. Rev., 2018, 51, 2764–2773.
12. J. Yan, B. K. Teo and N. Zheng, Acc. Chem. Rev., 2018, 51, 3084–3093.
13. S. Sharma, K. K. Chakrahari, J.-Y. Saillard and C. W. Liu, Acc. Chem. Res., 2018, 51, 2475–2483.
14. C. A. Smith, M. R. Narouz, P. A. Lummis, I. Singh, A. Nazemi, C. H. Li and M. C. Crudden, Chem. Rev., 2019, 119, 4986–5056.
15. Y. Du, H. Sheng, D. Astruc and M. Zhu, Chem. Rev., 2019, 120, 526–622.
16. X. Kang and M. Zhu, Chem. Soc. Rev., 2019, 48, 2422–2457.
17. T. Omoda, S. Takano and T. Tsukuda, Small, 2020, 2001439.
18. X. Kang, Y. Li, M. Zhu and R. Jin, Chem. Soc. Rev., 2020, 49, 6443–6514.
19. H. Hirai, S. Ito, S. Takano, K. Koyasu and T. Tsukuda, Chem. Sci., 2020, 11, 12233–12248.
20. M. Kim, K. L. Dimuthu, M. Weerawardene, W. Choi, S. M. Han, J. Paik, Y. Kim, M.-G. Choi, C. M. Aikens and D. Lee, Chem. Mater., 2020, 32, 10216–10226.
21. K. Esma and T. Pradeep, ACS Omega, 2021, 6, 1–16.
22. S. Takano and T. Tsukuda, J. Am. Chem. Soc., 2021, 143, 1683–1698.
23. F. Gam, J. Wei, S. Kahlal, J.-Y. Saillard and J.-F. Halet, Struct. Bonding, 2021 DOI:10.1007/430_2021_81.
24. H. Yi, S. M. Han, S. Song, M. Kim, E. Sim and D. Lee, Angew. Chem., Int. Ed., 2021, 60, 22293–22300.
25. O. López-Estrada, E. Selenius, B. Zuniga-Gutierrez, S. Malola and H. Häkkinen, J. Chem. Phys., 2021, 154, 204303.
26. M. Walter and M. Moseler, J. Phys. Chem. C, 2009, 113, 15834–15837.
27. D.-e. Jiang and S. Dai, Inorg. Chem., 2009, 48, 2720–2722.
28. K. A. Kacprzak, L. Lehtovaara, J. Akola, O. Lopez-Acevedo and H. Häkkinen, Phys. Chem. Chem. Phys., 2009, 11, 7123–7129.
29. E. B. Guidez, V. Mäkinen, H. Häkkinen and C. M. Aikens, J. Phys. Chem. C, 2012, 116, 20617–20624.
30. H. Qian, D.-e. Jiang, G. Li, C. Gayathri, A. Das, R. R. Gil and R. Jin, J. Am. Chem. Soc., 2012, 134, 16159–16162.
31. D. R. Kauffman, D. Alfonso, C. Matranga, H. Qian and R. Jin, J. Phys. Chem. C, 2013, 117, 7914–7923.
32. T. Iwasa, K. Nobusada and A. Nakajima, J. Phys. Chem. C, 2013, 117, 24586–24591.
33. L. Liao, S. Zhou, Y. Dai, L. Liu, C. Yao, C. Fu, J. Yang and Z. Wu, J. Am. Chem. Soc., 2015, 137, 9511–9514.
34. K. Kwak, Q. Tang, M. Kim, D.-e. Jiang and D. Lee, J. Am. Chem. Soc., 2015, 137, 10833–10840.
35. S. Wang, Y. Song, S. Jin, X. Liu, J. Zhang, Y. Pei, X. Meng, M. Chen, P. Li and M. Zhu, J. Am. Chem. Soc., 2015, 137, 4018–4021.
36. K. R. Krishnadas, A. Baksi, A. Ghosh, G. Natarajan and T. Pradeep, ACS Nano, 2017, 11, 6015–6023.
37. F. Alkan, A. Muñoz-Castro and C. M. Aikens, Nanoscale, 2017, 9, 15825–15834.
38. M. G. Taylor and G. Mpourmpakis, J. Phys. Chem. Lett., 2018, 9, 6773–6778.
39. F. Alkan, P. Pandeya and C. M. Aikens, J. Phys. Chem. C, 2019, 123, 9516–9527.
40. W. Fei, S. Antonello, T. Dainese, A. Dolmella, M. Lahtinen, K. Rissanen, A. Venzo and F. Maran, J. Am. Chem. Soc., 2019, 141, 16033–16045.
41. W.-T. Chang, P.-Y. Lee, J.-H. Liao, K. K. Chakrahari, S. Kahlal, Y.-C. Liu, M.-H. Chiang, J.-Y. Saillard and C. W. Liu, Angew. Chem., Int. Ed., 2017, 56, 10178–10182.
42. R. S. Dhayal, J.-H. Liao, Y.-C. Liu, M.-H. Chiang, S. Kahlal, J.-Y. Saillard and C. W. Liu, Angew. Chem., Int. Ed., 2015, 54, 3702–3706.
43. T.-H. Chiu, J.-H. Liao, F. Gam, I. Chantrenne, S. Kahlal, J.-Y. Saillard and C. W. Liu, J. Am. Chem. Soc., 2019, 141, 12957–12961.
44. T.-H. Chiu, J.-H. Liao, F. Gam, I. Chantrenne, S. Kahlal, J.-Y. Saillard and C. W. Liu, Nanoscale, 2021, 13, 12143–12148.
45. B. S. Kumar, T.-H. Chiu, Y.-C. Liu, M.-H. Chiang, F. Gam, I. Chantrenne, S. Kahlal, J.-Y. Saillard and C. W. Liu, Nanoscale, 2019, 11, 14581–14586.
46. J.-H. Liao, S. Kahlal, Y.-C. Liu, M.-H. Chiang, J.-Y. Saillard and C. W. Liu, J. Cluster Sci., 2018, 29, 827–835.
47. W.-T. Chang, S. Sharma, J.-H. Liao, S. Kahlal, Y.-C. Liu, M.-H. Chiang, J.-Y. Saillard and C. W. Liu, Chem. – Eur. J., 2018, 24, 14352–14357.
48. Y.-J. Zhong, J.-H. Liao, T.-H. Chiu, F. Gam, S. Kahlal, J.-Y. Saillard and C. W. Liu, J. Chem. Phys., 2021, 155, 034304.
49. S. N. Khanna and P. Jena, Phys. Rev. Lett., 1992, 69, 1664–1667.
50. S. N. Khanna and P. Jena, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 13705–13716.
51. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Gaussian Inc., Wallingford, CT, 2016.
52. Y.-R. Lin, P. V. V. N. Kishore, J.-H. Liao, S. Kahlal, Y.-C. Liu, M.-H. Chiang, J.-Y. Saillard and C. W. Liu, Nanoscale, 2018, 10, 6855–6860.
53. A. D. Becke, Phys. Rev. A: Atom., Mol., Opt. Phys., 1988, 38, 3098–3100.
54. J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824.
55. A. Schaefer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577.
56. A. Schaefer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835.
57. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, C. R. Landis and F. Weinhold, NBO 6.0, Theoretical Chemistry Institute, University of Wisconsin, Madison, WI, 2013, http://nbo6.chem.wisc.edu.
58. T. Yanai, D. Tew and N. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
59. R. Dennington, T. A. Keith and M. Millam, GaussView, Version 6.1, Semichem Inc., Shawnee Mission, KS, 2016.
60. SADABS, version 2014-11.0, Bruker Area Detector Absorption Corrections, Bruker AXS Inc., Madison, WI, 2014.
61. SAINT, included in G. Jogl, V4.043: Software for the CCD detector system, Bruker Analytical, Madison, WI, ( 1995).
62. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122.
63. T. Gruene, H. W. Hahn, A. V. Luebben, F. Meilleur and G. M. Sheldrick, J. Appl. Crystallogr., 2014, 47, 462–466.
64. SHELXTL, version 6.14, Bruker AXS Inc., Madison, WI, 2003.
65. Another C₁ structure, slightly different from that of Fig. 1 and not considered here, was identified in a complex co-crystal structure: J.-H. Liao, S. Kahlal, Y.-C. Liu, M.-H. Chiang, J.-Y. Saillard and C. W. Liu, J. Cluster Sci., 2018, 29, 827–835.
66. J. Wei, P. L. Rodriguez-Kessler, J.-F. Halet, S. Kahlal, J.-Y. Saillard and A. Muñoz-Castro, Inorg. Chem., 2021, 60, 8173–8180.
67. J. Yan, H. Su, H. Yang, S. Malola, S. Lin, H. Häkkinen and N. Zheng, J. Am. Chem. Soc., 2015, 137, 11880–11883.
68. M. S. Bootharaju, C. P. Joshi, M. R. Parida, O. F. Mohammed and O. M. Bakr, Angew. Chem., Int. Ed., 2016, 55, 922–926.
69. X. Liu, J. Yuan, C. Yao, J. Chen, L. Li, X. Bao, J. Yang and Z. Wu, J. Phys. Chem. C, 2017, 121, 13848–13853.
70. L. He, Z. Gan, N. Xia, L. Liao and Z. Wu, Angew. Chem., Int. Ed., 2019, 58, 9897–9901.
71. M. Kim, K. L. D. M. Weerawardene, W. Choi, S. M. Han, J. Paik, Y. Kim, M.-G. Choi, C. M. Aikens and D. Lee, Chem. Mater., 2020, 32, 10216–10226.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2091674. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d1nr06019h

---