Nonlocal response of plasmonic core–shell nanotopologies excited by dipole emitters

Abstract

In light of the emergence of nonclassical effects, a paradigm shift in the conventional macroscopic treatment is required to accurately describe the interaction between light and plasmonic structures with deep-nanometer features. Towards this end, several nonlocal response models, supplemented by additional boundary conditions, have been introduced, investigating the collective motion of the free electron gas in metals. The study of the dipole-excited core–shell nanoparticle has been performed, by employing the following models: the hard-wall hydrodynamic model; the quantum hydrodynamic model; and the generalized nonlocal optical response. The analysis is conducted by investigating the near and far field characteristics of the emitter–nanoparticle system, while considering the emitter outside and inside the studied topology. It is shown that the above models predict striking spectral features, strongly deviating from the results obtained via the classical approach, for both simple and noble constitutive metals.

---

1. Introduction

Plasmonic structures that operate in a deep-nanometer regime,¹ such as metallic nanoparticles with the characteristic radii of only a few nanometers,^2,3 or dimer and nanoparticle-on-mirror structures with a sub-nanometer gap size,^4–6 cannot be fully and accurately described by employing the macroscopic Maxwell equations and constitutive relations. The reason is that the deep-nanometer regime manifests nonclassical effects, such as size-dependent surface plasmon resonance shift and linewidth broadening,^2,7 and electron spill-out,⁸ among others. Notably, these effects have been demonstrated to exist in several plasmonic applications, ranging from optoelectronics and metamaterials,^9,10 over information and communication technology,^11,12 to biochemical sensing.¹³

A semiclassical model, namely the hydrodynamic model (HDM),^7,14–18 has been extensively studied, in order to tackle the aforementioned nonclassical effects. Compared with more advanced theoretical treatments, e.g., the time-dependent density functional theory (TD-DFT),¹⁹ HDM employs the simplest possible approximation of the internal energy functional, according to the Thomas–Fermi description. However, the same model provides much higher computational efficiency and analytical solutions for some symmetrical structures, and can be applied to both deep-nanometer as well as larger, generic nanostructures.^16,17 More specifically, HDM studies the interaction between the external electromagnetic (EM) fields and metals with nonlocal material parameters. This interaction is described by a multiphysics approach, by coupling the electrodynamics of Maxwell equations with the linearized hydrodynamic equation of electronic motion. Moreover, the nonlocality introduces longitudinal waves that are associated with an additional boundary condition (ABC). This boundary condition is imposed, in general, on the induced hydrodynamic current, to provide a key component needed to solve the coupled equations.

Note, however, that several hydrodynamic models, supplemented by different ABCs, have been proposed in the literature. The performances of four hydrodynamic models, employing the corresponding ABCs, have been tested in ref. 20. Additionally, a more detailed analysis of the hydrodynamic models has revealed that only the hard-wall hydrodynamic model (HW-HDM) and the quantum hydrodynamic model (Q-HDM) are suitable for modeling the optical response of nanostructures.²¹ Another model, viz., the generalized nonlocal optical response (GNOR),^2,7 which introduces the diffusion term to the nonlocal material parameter of HW-HDM, has also been studied. It is worthwhile to note that the above works focus only on the case of plane wave excitation, and they do not deal with other excitation sources, such as a dipole emitter, which is of great interest for a number of experimental studies, e.g., the local density of states (LDOS), single molecule detection and fluorescence enhancement.^22–27 Nevertheless, the application of this source for the nonlocal features of deep-nanometer structures are yet to be investigated fully.

Numerous efforts have been reported, analyzing the radiative and nonradiative properties of a dipole emitter coupled with a single metallic nanosphere, within the framework of the local response approximation (LRA).^28–42 This topology has also been studied by using HW-HDM^22,43–45 and GNOR.^45,46 Additionally, TD-DFT^47,48 and the semiclassical infinite barrier approach^49–51 have been employed for the same topology.

Apart from a single nanosphere, in the context of the dipole excitation, several works have investigated within the classical response practically more important structures, namely metal core–dielectric shell^31,52,53 and dielectric core–metal shell^31,54–61 nanoparticles. These structures have attracted considerable attention, owing to their excellent tunability of optical properties that are highly desirable for several applications.^62–64 Additionally, an emitter may be placed inside the dielectric core or shell, which is of considerable experimental interest.^{23,26,27,65–67} Moreover, a dielectric core–metal shell nanoparticle has been investigated by a nonlocal response approach, and has been reported in ref. 68. While this work employs HW-HDM and GNOR, it does not take Q-HDM into account. Furthermore, the associated radiative and nonradiative decay rates have been computed for an emitter positioned outside the studied structure. However, the impact of the aforementioned models on the system in which an emitter is positioned inside the nanoparticle remains unknown.

The current work investigates the nonlocal response of metal core–dielectric shell and dielectric core–metal shell nanostructures, with wide range of sizes and constitutive materials, under the excitation of a dipole emitter. This is done by employing the following models: HW-HDM, Q-HDM, and GNOR. The analysis is performed for both radial and tangential emitters, which are located outside the nanoparticles and inside the dielectric core or shell. The following optical features are observed: the radiative decay rate, the nonradiative decay rate, and LDOS enhancements. We note that these features are also referred to as the Purcell factors in the literature.^33,34 To the best of our knowledge, the targeted computational study, including different nonlocal hydrodynamic models for the near and far field characteristics of a dipole emitter, considered both outside and inside the core–shell nanoparticles, has not yet been reported in the literature.

This work is organized as follows. Section 2 discusses the studied topologies. The underlying theoretical aspects of the dipole excitation of the core–shell nanoparticles are also explained. The associated numerical studies are performed in Section 3, and the results of these studies are presented in Section 4.

2. Theoretical and topological aspects

In this section, the considered topologies are discussed. More details on the dipole excitation of the studied structures are also provided.

2.1. Topology

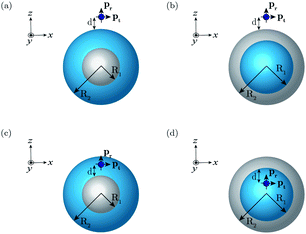
The geometry of the core–shell nanoparticles, investigated herein, is depicted in Fig. 1. The following constitutive metals are employed: sodium, silver, and gold, all of which are described by either Drude or experimental material models. The corresponding dielectric regions are comprised of silica, a commonly encountered material in core–shell topologies. The nanoparticles are embedded in vacuum. Furthermore, they are excited by an emitter, positioned along the z-axis, with its dipole moments oriented along the z- and the x-axes, referred to as the radial and tangential emitters, respectively. The following three scenarios of locations of the emitter are considered: (i) outside the structures; (ii) inside the shell of a metal core–dielectric shell structure; and (iii) inside the core of a dielectric core–metal shell structure.

Fig. 1 Studied topologies: metal core–dielectric shell and dielectric core–metal shell nanoparticles. An emitter with the dipole moments p_r and p_t, oriented along the radial and tangential directions, respectively, is positioned (a) and (b) outside and (c) and (d) inside the studied topologies, at the distance d from the corresponding metal (gray) and dielectric (blue) interfaces. The core and shell radii are denoted by R₁ and R₂, respectively.

2.2. Dipole excitation

Theoretically, the interaction between a dipole emitter and the core–shell nanoparticles can be dealt with by expanding the fields outside and inside the nanoparticles into vector spherical wave functions.^31,68 The scattering coefficients and the coefficients of the fields inside the structure-under-study are generated by implementing, on top of the classical boundary conditions, ABCs for a specific nonlocal response model. In general, these coefficients depend on the emitter position and orientation. First, considering the emitter outside the studied topologies, such coefficients have already been reported for a dielectric core–metal shell nanosphere, in the context of HW-HDM and GNOR.⁶⁸ We have extended the earlier approach, described in ref. 68, by including another model, viz., Q-HDM, and have performed the associated numerical calculations for both metal core–dielectric shell and dielectric core–metal shell nanospheres. Second, we have also computed the corresponding coefficients for an emitter positioned inside the dielectric core or shell, for the employed models. This has not been previously studied in the literature.

The following quantities have been investigated: (i) radiative decay rate; (ii) nonradiative decay rate; and (iii) orientation-averaged LDOS. The quantities have been normalized to the radiative decay rate and LDOS of an isolated emitter in vacuum. For a detailed mathematical description of the above analysis, see Sections 1 and 2 of the ESI.†

3. Numerical results

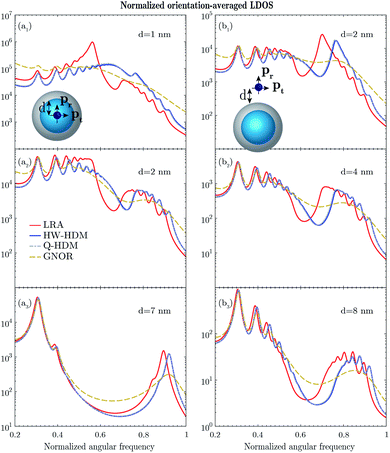
Motivated by the studies for a single nanosphere,^22,43 we begin by performing a detailed theoretical investigation of an extremely small core–shell geometry, with sodium as the constitutive free electron metal, described by the Drude model. As an example, we choose a core–shell nanoparticle with (R₁,R₂) = (1,2) nm, excited by an emitter located outside the nanoparticle. The studied geometry is analyzed for the entire spectral range, starting from the optical and going beyond the plasma frequency. More specifically, we study the surface and bulk plasmon modes, enabling us to provide a thorough survey of the possible experimental signatures of the nonlocal hydrodynamic response for the core–shell structures.²² The results of the normalized radiative and nonradiative decay rates, and orientation-averaged LDOS are depicted in Fig. 2 and 3 for a metal core–dielectric shell, and in Fig. 4 and 5 for a dielectric core–metal shell. On top, the associated surface plasmon modes and their spectral positions are tabulated in Tables 1 and 2, for the employed models.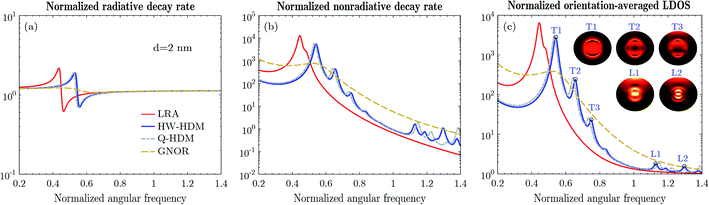

Fig. 2 Response of a sodium core–silica shell nanoparticle with (R₁,R₂) = (1,2) nm and a Drude material parameter. The angular frequency normalized to the plasma frequency is plotted on the horizontal axis. The following features: (a) radiative decay rate; (b) nonradiative decay rate; and (c) orientation-averaged LDOS, are computed for LRA, HW-HDM, Q-HDM, and GNOR. A log₁₀ scale is used to represent the magnitude of the studied features.

Fig. 3 Response of the sodium core–silica shell nanoparticle, studied in Fig. 2, for d = 2 nm: (a) radiative decay rate; (b) nonradiative decay rate; and (c) orientation-averaged LDOS. The insets illustrate the field patterns inside the studied structure, normalized to their maximum intensities, evaluated at the indicated surface and bulk plasmon resonances of HW-HDM, for the radial emitter.

Fig. 4 Response of a silica core–sodium shell nanoparticle with (R₁,R₂) = (1,2) nm and a Drude material parameter. The angular frequency normalized to the plasma frequency is plotted on the horizontal axis. The following features: (a) radiative decay rate; (b) nonradiative decay rate; and (c) orientation-averaged LDOS, are computed for LRA, HW-HDM, Q-HDM, and GNOR. A log₁₀ scale is used to represent the magnitude of the studied features.

Fig. 5 Response of the silica core–sodium shell nanoparticle, studied in Fig. 4, for d = 2 nm: (a) radiative decay rate; (b) nonradiative decay rate; and (c) orientation-averaged LDOS. The insets illustrate the field patterns inside the studied structure, normalized to their maximum intensities, evaluated at the indicated surface plasmon resonances of HW-HDM, for the radial emitter.

Table 1 Normalized spectral positions of the surface plasmon resonances, associated with the mode order n, for the sodium core–silica shell nanoparticle, studied in Fig. 3

Model	n = 1	n = 2	n = 3	n = 4
LRA	0.45	0.48	—	—
HW-HDM	0.54	0.66	0.75	0.83
Q-HDM	0.53	0.64	0.73	0.82
GNOR	0.52	—	—	—

---

Table 2 Normalized spectral positions of the surface plasmon resonances, associated with the bonding mode order n, for the silica core–sodium shell nanoparticle, studied in Fig. 5

Model	n = 1	n = 2	n = 3	n = 4	n = 5
LRA	0.48	0.56	0.59	—	—
HW-HDM	0.51	0.64	0.72	0.77	0.81
Q-HDM	0.51	0.63	0.71	0.76	0.81
GNOR	0.51	0.64	—	—	—

---

Then, within the same material model, we systematically investigate the impact of the nonlocal effects on the topologies with relatively larger size parameters, considering an emitter both outside and inside these topologies. Here, a metal core–dielectric shell with (R₁,R₂) = (5,10) nm and a dielectric core–metal shell with (R₁,R₂) = (8,10) nm are exemplified. The results of all these studies are demonstrated in Fig. 6 for the former, and in Fig. 7 for the latter topology.

Fig. 6 Response of a sodium core–silica shell nanoparticle with (R₁,R₂) = (5,10) nm and a Drude material parameter. The angular frequency normalized to the plasma frequency is plotted on the horizontal axis. The orientation-averaged LDOS is computed for the indicated distances, considering an emitter (a) inside and (b) outside the nanoparticle.

Fig. 7 Response of a silica core–sodium shell nanoparticle with (R₁,R₂) = (8,10) nm and a Drude material parameter. The angular frequency normalized to the plasma frequency is plotted on the horizontal axis. The orientation-averaged LDOS is computed for the indicated distances, considering an emitter (a) inside and (b) outside the nanoparticle.

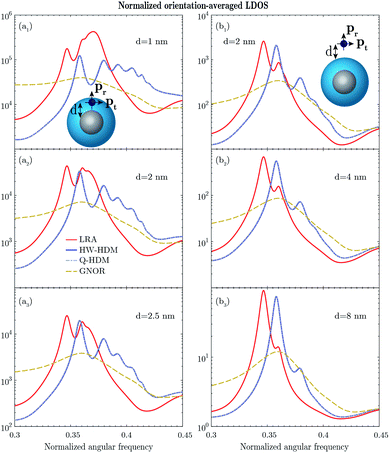
Our next step is to extend the above study by employing more practical, noble metals, namely silver and gold, that are of great importance for plasmonic experiments.⁴³ Contrary to sodium, the response of such metals in the studied frequency range is significantly modified by the contribution of bound electrons. The permittivity of bound electrons is obtained by subtracting the contribution of free electrons from the experimental material data.⁶⁹ In this context, we have investigated the following structures: a metal core–dielectric shell with (R₁,R₂) = (3,6) nm and a dielectric core–metal shell with (R₁,R₂) = (4,6) nm. The results of the orientation-averaged LDOS enhancement are plotted in Fig. 8 for the former, and in Fig. 9 for the latter structure. The associated surface plasmon modes and their spectral positions are shown in Tables 3 and 4.

Fig. 8 Response of a silver core–silica shell nanoparticle with (R₁,R₂) = (3,6) nm and an experimental material parameter. The angular frequency normalized to the plasma frequency is plotted on the horizontal axis. The orientation-averaged LDOS is computed for the indicated distances, considering an emitter (a) inside and (b) outside the nanoparticle.

Fig. 9 Response of a silica core–silver shell nanoparticle with (R₁,R₂) = (4,6) nm and an experimental material parameter. The angular frequency normalized to the plasma frequency is plotted on the horizontal axis. The orientation-averaged LDOS is computed for the indicated distances, considering an emitter (a) inside and (b) outside the nanoparticle.

Table 3 Normalized spectral positions of the surface plasmon resonances, associated with the mode order n, for the silver core–silica shell nanoparticle, studied in Fig. 8, with an emitter located inside the nanoparticle, at d = 1 nm

Model	n = 1	n = 2	n = 3	n = 4	n = 5	n = 6
LRA	0.35	0.36	—	—	—	—
HW-HDM	0.36	0.38	0.39	0.4	0.41	0.42
Q-HDM	0.36	0.38	0.39	0.4	0.41	0.42
GNOR	0.36	—	—	—	—	—

---

Table 4 Normalized spectral positions of the surface plasmon resonances, associated with the bonding mode order n, for the silica core–silver shell nanoparticle, studied in Fig. 9, with an emitter located inside the nanoparticle, at d = 1 nm

Model	n = 1	n = 2	n = 3	n = 4	n = 5
LRA	0.33	0.36	0.37	—	—
HW-HDM	0.33	0.37	0.38	0.39	0.4
Q-HDM	0.33	0.37	0.38	0.39	0.4
GNOR	0.36	0.37	—	—	—

---

Finally, we vary the sizes of the nanoparticles, while placing an emitter inside the dielectric core or shell, with a fixed distance to the metal interface. The results of the orientation-averaged LDOS enhancement are depicted in Fig. 10.

Fig. 10 Response of (a) silver core–silica shell and (b) silica core–silver shell nanoparticles, with variable size parameters, where R₂ = 2 × R₁ is chosen for the former, and R₂ = 1.25 × R₁ for the latter structure. The angular frequency normalized to the plasma frequency is plotted on the horizontal axis. An emitter is positioned inside the nanoparticles at a fixed distance from the metal interface, namely d = 1 nm. The observable higher-order (n = 3) resonance of HW-HDM, that is not captured by LRA, is denoted by the black circle, see (a₁).

The following parameters are used in the simulations: the plasma frequency ħω_P = 6.04 eV, the damping frequency ħγ = 0.16 eV, the Fermi velocity v_F = 1.07 × 10⁶ m s⁻¹, and the diffusion constant D = 2.67 × 10⁻⁴ m² s⁻¹ for sodium; ħω_P = 9.1 eV, ħγ = 0.02 eV, v_F = 1.39 × 10⁶ m s⁻¹, and D = 9.62 × 10⁻⁴ m² s⁻¹ for silver; and ħω_P = 9 eV, ħγ = 0.05 eV, v_F = 1.39 × 10⁶ m s⁻¹, and D = 8.62 × 10⁻⁴ m² s⁻¹ for gold.^7,69 Silica is weakly dispersive in the studied frequency range, with a permittivity of 2.25. In order to accurately characterize the interaction between the emitter and nanoparticles, the maximum mode order n of 50 is studied.

4. Discussion

Within the framework of the Drude model, the spectral features of a sodium core–silica shell nanoparticle with (R₁,R₂) = (1,2) nm are represented as a function of the emitter–nanoparticle distance and frequency in Fig. 2, and by selecting d = 2 nm in Fig. 3. Considering first the radiative decay rate, demonstrated in Fig. 2a and 3a, LRA shows a single surface plasmon resonance with a normalized spectral position of 0.44, corresponding to the dipolar mode (n = 1). Compared with LRA, the dipolar resonances of HW-HDM and Q-HDM experience a well-known blueshift,⁷ and their magnitudes are slightly lower. These resonances rapidly become indistinguishable, while increasing the distance. Moreover, GNOR generates a strongly attenuated spectral line, with no discernible resonance for the studied distance, see Fig. 3a.

Apart from the dipolar mode, the nonradiative decay rate, illustrated in Fig. 2b and 3b, manifests higher-order modes. The quadrupolar mode (n = 2) with a spectral position of 0.48, may be noticed for LRA. More importantly, in addition to the quadrupolar mode, HW-HDM and Q-HDM yield other higher-order modes, which do not arise in the case of LRA, as shown in Table 1, similar to the previous study for a single nanosphere.²² Below the plasma frequency, these models display four noticeable higher-order resonances, whose spectral positions and magnitudes vary slightly. However, these resonances are vanishing for larger distances, as depicted in Fig. 2b₂ and b₃. Next to the aforementioned blueshift, another essential hydrodynamic feature, namely the longitudinal mode, emerges above the plasma frequency.⁷ For d = 2 nm, HW-HDM predicts four distinguishable longitudinal peaks, indicating the confined dipolar and quadrupolar bulk plasmon modes,²² with spectral positions of 1.13 and 1.3, and 1.19 and 1.38, respectively. As argued for the plane wave response of the studied structure,²¹ Q-HDM introduces a shift of the longitudinal resonances, with respect to HW-HDM. As a result, for the aforementioned distance, the same model yields three observable longitudinal peaks, see Fig. 3b. For GNOR, a broader dipolar resonance clearly exists below the plasma frequency. Nevertheless, all other surface and bulk plasmon modes, that are present for the other studied models, are completely damped by the diffusion mechanism.⁴⁶

While the above analysis has been conducted for the radial emitter, we have also performed the study for the tangential emitter. The associated results of the decay rates for the sodium core–silica shell nanoparticle are depicted in Fig. S1 and explained in Section 3 of the ESI.† On top, based on the partial LDOS enhancements of both radial and tangential emitters, which may be related to the total decay rates,^57,70 we have computed the orientation-averaged LDOS enhancement, as plotted in Fig. 2c and 3c.

Next, the study has been performed for a silica core–sodium shell nanoparticle with the same size parameters, and the results are shown in Fig. 4 and 5. For the radiative decay rate, LRA reveals two dipolar resonances at 0.48 and 0.77, see Fig. 4a₁, representing the bonding and antibonding plasmon modes.^63,68 The blueshift, introduced by HW-HDM and Q-HDM, is much more pronounced for the second resonance, with respect to the classical solution, as in the case of the plane wave excitation.²¹ Compared with the above models, GNOR displays only the first resonance, see the peak at 0.51 in Fig. 5a. The associated nonradiative decay rate and LDOS spectra, illustrated in Fig. 4b, c, 5b and c, show multiple resonances. Apart from the quadrupolar and hexapolar (n = 3) components, emerging for LRA, additional higher-order surface plasmon modes are predicted by HW-HDM and Q-HDM, as demonstrated in Table 2. Furthermore, the longitudinal resonances with spectral positions of 1.16 and 1.31 appear for the former, and 1.18 and 1.4 for the latter model. On top of the dipolar peak, a quadrupolar component may be distinguished for GNOR, while the other aforementioned resonances do not emerge in the spectrum.

After studying extremely small nanoparticles, we focus on relatively larger core–shell structures, while considering emitters both outside and inside the same structures. The following features can be observed in Fig. 6, for a sodium core–silica shell nanoparticle (see also Fig. S2 of the ESI†). Compared with the previously studied topologies, the blueshifts between the corresponding local and nonlocal resonances are considerably lower. Additionally, the associated longitudinal resonances (not displayed here) are much more damped and indistinguishable in the spectrum. These features are caused by the fact that the size of the structure-under-study is relatively large, diminishing the impact of the nonlocality. For an emitter positioned inside the silica shell, see Fig. 6a, LRA shows, next to the attenuated dipolar and quadrupolar resonances, another more prominent peak at 0.53, for d = 1 nm, which is formed by the contributions of several higher-order modes. Such an observation has been previously reported for a single nanosphere, where the associated resonance, for a small emitter–nanoparticle distance, theoretically approaches the result for a planar interface.^22,43 In contrast, HW-HDM and Q-HDM may exceed this limit,²² and generate many more resonances, which experience strong damping by sodium. Notably, the same resonances do not arise in the spectrum for GNOR. While placing an emitter outside the studied nanoparticle, HW-HDM and Q-HDM produce fewer spectral components, thus providing a closer agreement with LRA, as illustrated in Fig. 6b. As in the case of the previously studied structures, the higher-order modes are suppressed and dominated by the dipolar one for larger distances, resembling the plane wave response.⁷¹

Similar observations also hold for a silica core–sodium shell structure, the results for which are shown in Fig. 7 (see also Fig. S3 of the ESI†). More interestingly, in the case of GNOR, several higher-order resonances may be noticed in the spectrum, contrary to the above topologies. While these resonances emerge in the frequency region below 0.6, they are completely vanishing outside this region, where the other studied models introduce additional spectral components. Note that as an emitter is positioned more closely to the core center, the number of higher-order modes is drastically reduced, as demonstrated in Fig. 7a. In the limiting case, where the emitter is located at the core center, only the dipolar mode can be excited.^55,72

We have so far performed the EM simulations using the Drude model. However, apart from the free electrons, incorporating the contribution of bound electrons in the material model is indispensable for noble metals, such as silver and gold, that are widely used in plasmonic experiments. In order to describe the response of the noble metals accurately, the Drude model has been extended by employing an experimental material model.⁶⁹ First, the analysis is conducted for a silver core–silica shell nanoparticle with (R₁,R₂) = (3,6) nm and a silica core–silver shell nanoparticle with (R₁,R₂) = (4,6) nm, in the optical frequency range, as depicted in Fig. 8 and 9 (see also Fig. S4 and S5 of the ESI†). Several spectral features, which have been previously observed and discussed for the Drude model, evidently arise for both structures. Essentially, despite introducing additional losses to the system through the presence of the bound electrons, HW-HDM and Q-HDM deliver striking higher-order resonances, which do not appear for LRA, as shown in Fig. 8a, for an emitter located inside the silver core–silica shell nanoparticle. According to Table 3, for d = 1 nm, on top of the quadrupolar mode that is also present for LRA, the other four higher-order components arise for HW-HDM and Q-HDM. Moreover, considering an emitter outside the nanoparticle, the same resonances may still be distinguished for smaller distances, although they are much less pronounced, see e.g., Fig. 8b₁. For the other studied structure, such resonances are evidently less apparent, regardless of the emitter position. By studying d = 1 nm in Fig. 9a₁ and d = 2 nm in Fig. 9b₁, one may observe attenuated higher-order peaks around a spectral position of 0.4 (see the corresponding modes in Table 4), vanishing for larger distances. On the contrary, the aforementioned resonances have been smeared out, while including the diffusion term of GNOR.

In order to substantiate our observations, we have also studied core–shell topologies with different size parameters, and the results are plotted in Fig. S6 and S7 of the ESI.† The generated features indicate that the nonlocal effects may be of great importance to correctly characterize the interaction between the emitter and core–shell nanoparticles, with silver as a constitutive metal. We emphasize that the results of HW-HDM (and Q-HDM), especially for an emitter located inside a silver core–silica shell nanoparticle, are in strong contrast to the ones in ref. 22 for a single silver nanosphere, demonstrating that the related higher-order modes are completely suppressed. Additionally, we have investigated the response of core–shell nanospheres, constituted of gold. The associated results, which are depicted in Fig. S8 and S9 of the ESI,† show that the higher-order resonances of the local and nonlocal response models are indistinguishable, due to the increased material losses in the desired frequency range.⁷³ To the best of our knowledge, no experimental results, concerning the studied configurations, have been previously reported in the literature. Nevertheless, the aforementioned features strongly suggest to perform the associated LDOS measurements.

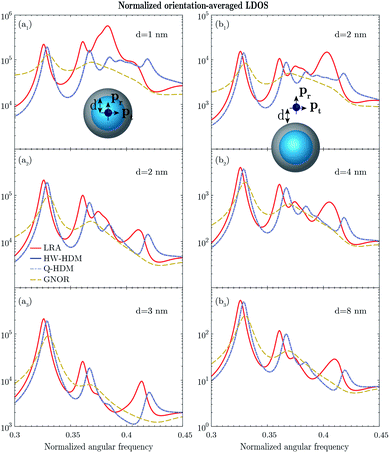
Finally, we study the possibility of exciting the above higher-order modes within the framework of HW-HDM for larger core–shell topologies, varying their size parameters, while placing an emitter inside the topologies, at d = 1 nm. By observing a silver core–silica shell structure with (R₁,R₂) = (6,12) nm, HW-HDM still generates a noticeable higher-order resonance with a spectral position of 0.38, see the black circle in Fig. 10a₁, which is captured neither by LRA nor GNOR. Nevertheless, for the increasing size parameters, the same resonance becomes indistinguishable. As for a silica core–silver shell structure, see Fig. 10b, the additional higher-order resonances introduced by HW-HDM are undiscernible.

5. Conclusions

This work studied the nonlocal features of spherical metal core–dielectric shell and dielectric core–metal shell nanoparticles, under the excitation of a dipole emitter. The investigation was carried out by employing the following models: HW-HDM, Q-HDM, and GNOR. Several size and material parameters were used. Both radial and tangential emitters were considered outside and inside the studied topologies. The radiative and nonradiative decay rates and orientation-averaged LDOS enhancements were analyzed. Different surface and bulk plasmon modes, generated by the models, were investigated. First, the study was conducted for core–shell nanoparticles with sodium as the constitutive metal, taking only the contribution of free electrons into account, as described by a Drude model. Then, more practical, noble metals, namely silver and gold, were employed, accounting for the contributions of both free and bound electrons through an experimental material model. It was demonstrated that the nonlocal effects may considerably influence the interaction between the emitter and core–shell nanoparticles. HW-HDM and Q-HDM generate multiple higher-order resonances, which do not arise within the classical approach. In addition to sodium, such resonances emerge prominently in core–shell structures constituted of silver, despite the additional losses caused by the bound electrons. Compared with HW-HDM and Q-HDM, the above resonances are completely damped by the diffusion mechanism for GNOR. Contrary to the aforementioned metals, in the case of gold, apart from the dipolar resonance, all other resonances are suppressed for the studied models.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors gratefully acknowledge the financial support from the Fund for Scientific Research Flanders (FWO) under the contract numbers 3E151025 and G090017N, and KU Leuven internal research funds under the contract numbers C14/19/083, C24/15/015, and IDN/20/014.

References

1. M. S. Tame, K. R. McEnery, Ş. K. Özdemir, J. Lee, S. A. Maier and M. S. Kim, Nat. Phys., 2013, 9, 329–340.
2. N. A. Mortensen, S. Raza, M. Wubs, T. Søndergaard and S. I. Bozhevolnyi, Nat. Commun., 2014, 5, 3809.
3. C. Tserkezis, J. R. Maack, Z. Liu, M. Wubs and N. A. Mortensen, Sci. Rep., 2016, 6, 28441.
4. R. Esteban, A. G. Borisov, P. Nordlander and J. Aizpurua, Nat. Commun., 2012, 3, 825.
5. M.-E. Kleemann, J. Mertens, X. Zheng, S. Cormier, V. Turek, F. Benz, R. Chikkaraddy, W. Deacon, A. Lombardi, V. V. Moshchalkov, G. A. E. Vandenbosch and J. J. Baumberg, ACS Nano, 2017, 11, 850–855.
6. A. Xomalis, X. Zheng, A. Demetriadou, A. Martinez, R. Chikkaraddy and J. J. Baumberg, Nano Lett., 2021, 21, 2512–2518.
7. S. Raza, S. I. Bozhevolnyi, M. Wubs and N. A. Mortensen, J. Phys.: Condens. Matter, 2015, 27, 183204.
8. G. Toscano, J. Straubel, A. Kwiatkowski, C. Rockstuhl, F. Evers, H. Xu, N. A. Mortensen and M. Wubs, Nat. Commun., 2015, 6, 7132.
9. P. Berini and I. De Leon, Nat. Photonics, 2012, 6, 16–24.
10. O. Hess, J. B. Pendry, S. A. Maier, R. F. Oulton, J. M. Hamm and K. L. Tsakmakidis, Nat. Mater., 2012, 11, 573–584.
11. W. A. Challener, C. Peng, A. V. Itagi, D. Karns, W. Peng, Y. Peng, X. Yang, X. Zhu, N. J. Gokemeijer, Y.-T. Hsia, G. Ju, R. E. Rottmayer, M. A. Seigler and E. C. Gage, Nat. Photonics, 2009, 3, 220–224.
12. D. Vercruysse, X. Zheng, Y. Sonnefraud, N. Verellen, G. Di Martino, L. Lagae, G. A. E. Vandenbosch, V. V. Moshchalkov, S. A. Maier and P. Van Dorpe, ACS Nano, 2014, 8, 8232–8241.
13. J. N. Anker, W. P. Hall, O. Lyandres, N. C. Shah, J. Zhao and R. P. Van Duyne, Nat. Mater., 2008, 7, 442–453.
14. N. A. Mortensen, Nanophotonics, 2021, 10, 2563–2616.
15. C. Ciracì, J. B. Pendry and D. R. Smith, ChemPhysChem, 2014, 14, 1109–1116.
16. X. Zheng, M. Kupresak, R. Mittra and G. A. E. Vandenbosch, IEEE Trans. Antennas Propag., 2018, 66, 4759–4771.
17. X. Zheng, M. Kupresak, V. V. Moshchalkov, R. Mittra and G. A. E. Vandenbosch, IEEE Trans. Antennas Propag., 2019, 67, 3948–3960.
18. X. Zheng, M. Kupresak, N. Verellen, V. V. Moshchalkov and G. A. E. Vandenbosch, Adv. Theory Simul., 2019, 2, 1900087.
19. A. Varas, P. García-González, J. Feist, F. J. García-Vidal and A. Rubio, Nanophotonics, 2016, 5, 409–426.
20. M. Kupresak, X. Zheng, G. A. E. Vandenbosch and V. V. Moshchalkov, Adv. Theory Simul., 2018, 1, 1800076.
21. M. Kupresak, X. Zheng, G. A. E. Vandenbosch and V. V. Moshchalkov, Adv. Theory Simul., 2020, 3, 1900172.
22. T. Christensen, W. Yan, S. Raza, A.-P. Jauho, N. A. Mortensen and M. Wubs, ACS Nano, 2014, 8, 1745–1758.
23. J. Xu, Y.-J. Zhang, H. Yin, H.-L. Zhong, M. Su, Z.-Q. Tian and J.-F. Li, Adv. Opt. Mater., 2018, 6, 1701069.
24. P. Reineck, D. Gómez, S. H. Ng, M. Karg, T. Bell, P. Mulvaney and U. Bach, ACS Nano, 2013, 7, 6636–6648.
25. O. Stranik, R. Nooney, C. McDonagh and B. D. MacCraith, Plasmonics, 2007, 2, 15–22.
26. O. G. Tovmachenko, C. Graf, D. J. van den Heuvel, A. van Blaaderen and H. C. Gerritsen, Adv. Mater., 2006, 18, 91–95.
27. P. Zhang and Y. Guo, J. Am. Chem. Soc., 2009, 131, 3808–3809.
28. H. Y. Chung, P. T. Leung and D. P. Tsai, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 155413.
29. R. Ruppin, J. Chem. Phys., 1982, 76, 1681–1684.
30. R. Carminati, J.-J. Greffet, C. Henkel and J. M. Vigoureux, Opt. Commun., 2006, 261, 368–375.
31. A. Moroz, Ann. Phys., 2005, 315, 352–418.
32. A. Moroz, Chem. Phys., 2005, 317, 1–15.
33. A. F. Koenderink, Opt. Lett., 2010, 35, 4208–4210.
34. A. E. Krasnok, A. P. Slobozhanyuk, C. R. Simovski, S. A. Tretyakov, A. N. Poddubny, A. E. Miroshnichenko, Y. S. Kivshar and P. A. Belov, Sci. Rep., 2015, 5, 12956.
35. H. Mertens, A. F. Koenderink and A. Polman, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 115123.
36. P. Anger, P. Bharadwaj and L. Novotny, Phys. Rev. Lett., 2006, 96, 113002.
37. P. Bharadwaj and L. Novotny, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 15, 14266–14274.
38. T. Härtling, P. Reichenbach and L. M. Eng, Opt. Express, 2007, 15, 12806–12817.
39. S. Sun, L. Wu, P. Bai and C. E. Png, Phys. Chem. Chem. Phys., 2016, 18, 19324–19335.
40. G. Sun and J. B. Khurgin, Phys. Rev. A: At., Mol., Opt. Phys., 2012, 85, 063410.
41. Y. Zhang, R. Zhang, Q. Wang, Z. Zhang, H. Zhu, J. Liu, F. Song, S. Lin and E. Yue Bun Pun, Opt. Express, 2010, 18, 4316–4328.
42. G. Colas des Francs, A. Bouhelier, E. Finot, J. C. Weeber, A. Dereux, C. Girard and E. Dujardin, Opt. Express, 2008, 16, 17654–17666.
43. C. Ciracì, R. Jurga, M. Khalid and F. Della Sala, Nanophotonics, 2019, 8, 1821–1833.
44. V. Datsyuk and O. M. Tovkach, J. Opt. Soc. Am. B, 2011, 28, 1224–1230.
45. R. Jurga, S. D'Agostino, M. Khalid, F. Della Sala and C. Ciracì, J. Phys. Chem. C, 2017, 121, 22361–22368.
46. T. Christensen, From classical to quantum plasmonics in three and two dimensions, PhD thesis, Technical University of Denmark, 2015.
47. P. A. D. Gonçalves, T. Christensen, N. Rivera, A.-P. Jauho, N. A. Mortensen and M. Soljačić, Nat. Commun., 2020, 11, 366.
48. T. Neuman, R. Esteban, D. Casanova, F. J. García-Vidal and J. Aizpurua, Nano Lett., 2018, 18, 2358–2364.
49. P. T. Leung, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 7622.
50. P. T. Leung and M. H. Hider, J. Chem. Phys., 1993, 98, 5019–5022.
51. J. Vielma and P. T. Leung, J. Chem. Phys., 2007, 126, 194704.
52. S. Sun, I. L. Rasskazov, P. Scott Carney, T. Zhang and A. Moroz, J. Phys. Chem. C, 2020, 124, 13365–13373.
53. I. L. Rasskazov, A. Moroz and P. S. Carney, J. Phys. Chem. Lett., 2021, 12, 6425–6430.
54. C. G. Khoury, S. J. Norton and T. Vo-Dinh, Nanotechnology, 2010, 21, 315203.
55. J. Enderlein, Phys. Chem. Chem. Phys., 2002, 4, 2780–2786.
56. J. Enderlein, Appl. Phys. Lett., 2001, 80, 315–317.
57. T. J. Arruda, R. Bachelard, J. Weiner, S. Slama and P. W. Courteille, Phys. Rev. A, 2017, 96, 043869.
58. T. Zhang, G. Lu, W. Li, J. Liu, L. Hou, P. Perriat, M. Martini, O. Tillement and Q. Gong, J. Phys. Chem. C, 2012, 116, 8804–8812.
59. R. Bardhan, N. K. Grady, J. R. Cole, A. Joshi and N. J. Halas, ACS Nano, 2009, 3, 744–752.
60. R. Bardhan, N. K. Grady and N. J. Halas, Small, 2008, 4, 1716–1722.
61. J.-W. Liaw, H.-C. Chen and M.-K. Kuo, J. Quant. Spectrosc. Radiat. Transfer, 2014, 146, 321–330.
62. P. Yu, Y. Yao, J. Wu, X. Niu, A. L. Rogach and Z. Wang, Sci. Rep., 2017, 7, 7696.
63. E. Prodan, C. Radloff, N. J. Halas and P. Nordlander, Science, 2003, 302, 419–422.
64. R. Ban, Y. Yu, M. Zhang, J. Yin, B. Xu, D.-Y. Wu, M. Wu, Z. Zhang, H. Tai, J. Li and J. Kang, ACS Appl. Mater. Interfaces, 2017, 9, 13564–13570.
65. M. A. Noginov, G. Zhu, A. M. Belgrave, R. Bakker, V. M. Shalaev, E. E. Narimanov, S. Stout, E. Herz, T. Suteewong and U. Wiesner, Nature, 2009, 460, 1110–1112.
66. C. Ayala-Orozco, J. G. Liu, M. W. Knight, Y. Wang, J. K. Day, P. Nordlander and N. J. Halas, Nano Lett., 2014, 14, 2926.
67. B. Ji, E. Giovanelli, B. Habert, P. Spinicelli, M. Nasilowski, X. Xu, N. Lequeux, J.-P. Hugonin, F. Marquier, J.-J. Greffet and B. Dubertret, Nat. Nanotechnol., 2015, 10, 170–175.
68. C. Tserkezis, N. Stefanou, M. Wubs and N. A. Mortensen, Nanoscale, 2016, 8, 17532–17541.
69. F. J. García de Abajo, J. Phys. Chem. C, 2008, 112, 17983–17987.
70. R. Regmi, A. A. Al Balushi, H. Rigneault, R. Gordon and J. Wenger, Sci. Rep., 2015, 5, 15852.
71. H. Chew, M. Kerker and D. D. Cooke, Phys. Rev. A: At., Mol., Opt. Phys., 1977, 16, 320–323.
72. H. Chew, J. Chem. Phys., 1987, 87, 1355–1360.
73. M. Kupresak, X. Zheng, G. A. E. Vandenbosch and V. V. Moshchalkov, Opt. Express, 2017, 25, 26760–26780.

---

Footnote

† Electronic supplementary information (ESI) available: Derivation of the governing equations for a dipole emitter positioned both outside and inside the core–shell nanoparticles for the employed nonlocal response models, expressions for the decay rates and LDOS, comparison of the decay rates of radial and tangential emitters, additional LDOS spectra for the core–shell topologies with different size and material parameters. See https://doi.org/10.1039/d1na00726b

---