A comprehensive picture of roughness evolution in organic crystalline growth: the role of molecular aspect ratio†
Jordan T.
Dull‡
 a,
Xiangyu
Chen‡
a,
Xiangyu
Chen‡
 b,
Holly M.
Johnson
a,
Maria Clara
Otani
a,
Frank
Schreiber
b,
Holly M.
Johnson
a,
Maria Clara
Otani
a,
Frank
Schreiber
 c,
Paulette
Clancy
c,
Paulette
Clancy
 *b and
Barry P.
Rand
*b and
Barry P.
Rand
 *ad
*ad
aDepartment of Electrical Engineering, Princeton University, Princeton, NJ 08544, USA. E-mail: brand@princeton.edu
bDepartment of Chemical and Biomolecular Engineering, Johns Hopkins University, Baltimore, MD 21218, USA. E-mail: pclancy3@jhu.edu
cInstitute for Applied Physics, University of Tubingen, 72076 Tubingen, Germany
dAndlinger Center for Energy and the Environment, Princeton University, Princeton, NJ 08544, USA
First published on 26th August 2022
Abstract
Exploiting the capabilities of organic semiconductors for applications ranging from light-emitting diodes to photovoltaics to lasers relies on the creation of ordered, smooth layers for optimal charge carrier mobilities and exciton diffusion. This, in turn, creates a demand for organic small molecules that can form smooth thin film crystals via homoepitaxy. We have studied a set of small-molecule organic semiconductors that serve as templates for homoepitaxy. The surface roughness of these materials is measured as a function of adlayer film thickness from which the growth exponent (β) is extracted. Notably, we find that three-dimensional molecules that have low molecular aspect ratios (AR) tend to remain smooth as thickness increases (small β). This is in contrast to planar or rod-like molecules with high AR that quickly roughen (large β). Molecular dynamics simulations find that the Ehrlich–Schwöbel barrier (EES) alone is unable to fully explain this trend. We further investigated the mobility of ad-molecules on the crystalline surface to categorize their diffusion behaviors and the effects of aggregation to account for the different degrees of roughness that we observed. Our results suggest that low AR molecules have low molecular mobility and moderate EES which creates a downward funneling effect leading to smooth crystal growth.
New conceptsWe demonstrate for the first time that thin film crystalline growth of bulky organic molecules – those with a low aspect ratio (i.e., 3D) – remains remarkably smooth. Past research has considered high aspect ratio molecules (rod or disc-like), which tend to grow rough films and thus have poor implications for device applications. Through molecular dynamic simulations, we uncover different step-edge barrier energies, diffusion behavior, and effects arising from aggregation, and follow this molecular aspect ratio metric. Applying this new understanding, we develop a more holistic model of film roughening that goes beyond the conventional step-edge barrier analysis to include molecular mobility and aggregation. We also introduce the concept of attempt frequency which quantifies the probability of smooth thin-film growth by combining the descent barrier and the binding energy at the edge. In this model, low aspect ratio molecules avoid rapid roughening because their geometry allows more direct π–π interaction which leads to kinetic and thermodynamic stability during thin film growth. |
Introduction
Commercial organic electronic devices typically have been forced to rely on disordered, amorphous films despite the superior charge transport properties of crystalline organic semiconductors.1,2 Much of the work on these crystalline organics has been done on single crystals, but progress has been made in growing these materials as crystalline thin films,3–11 a necessary step to mass-producing devices. A key component of device engineering is the ability to tune the thickness of each layer, which requires an understanding of growth mechanisms. This is particularly relevant for organic crystals where it is rather common for the roughness to evolve via more three-dimensional Stranski–Krastanov or Volmer–Weber island growth,12–14 rather than the desirable, two-dimensional, layer-by-layer outcome (Frank-van-der-Merwe growth). Rough interfaces should be avoided as they can lead to poor electrical properties in transistors15 and layer-inhomogeneities that can cause electrical shorts.16 So while films with poor crystallinity tend to grow very smooth in most cases,7,17 if crystalline organics are to be incorporated into devices, understanding and controlling the roughness of each layer is critical. Furthermore, understanding growth mechanics on a fundamental level is desirable beyond device applications in the form of uncovering the role step edge barriers,18–22 diffusion,23 or thickness-dependent strain release24 play in roughening behavior. From a non-equilibrium statistical mechanics perspective, there is less research on experimental and computation growth dynamics of bulky, anisotropic molecular systems compared to atomic or colloidal systems.25 Our work helps remedy this by focusing on different symmetries, compared to atomic (“spherical”) systems, which substantially changes the theoretical perspective.To investigate this, thin film organic crystals grown in a platelet-like morphology are used as templates for further growth of the same underlying material. This homoepitaxial technique has been used previously with rubrene to tune the thickness of the crystalline film26 and improve solar cell performance.27 At a more general level, homoepitaxy has the added benefit of not having to consider epitaxial strain as a key driving force.28 Here we use homoepitaxy to monitor the roughness evolution for a variety of organic crystals as a function of film thickness via atomic force microscopy (AFM). Many of the molecules considered here have multiple single bonds within their conjugated core, resulting in non-planar conformations. This is in contrast to the numerous roughness evolution studies of planar24,29–31 and rod-like12,19,32–36 conjugated molecules. Prior to this work, most roughness evolution research into more three-dimensional (3D) molecules with the ability to crystallize was limited to materials like C6020,37–39 and rubrene.26 For a comprehensive view, we analyze our growth results using a molecular aspect ratio (AR) metric and find that 3D molecules (with low AR) exhibit remarkably flat crystal growth in comparison to planar and rod-like molecules (with high AR). While categorizing the growth based solely on AR is obviously simplified, we find a surprisingly systematic behavior. We note that this is in the spirit of previous studies which have considered the orientation of rod-like molecules as a key parameter and indeed source of disorder.40,41 Molecular dynamics (MD) simulations show that low AR molecules have low molecular mobility and moderate energy barriers at step-edges, both of which lead to a downward funneling effect and smooth epitaxial growth. In addition, our MD results find qualitatively different diffusion behavior depending on the shape of a molecule directly impacting molecular mobility.
Methods
Materials
The materials used in this work include N,N′-bis(naphthalen-1-yl)-N,N′-bis(phenyl)-benzidine (NPB, Lumtec), 1,3,5-tris(1-phenyl-1-H-benzimidazol-2-yl)benzene (TPBi, Lumtec), 2,4,5,6-tetra(9H-carbazol-9-yl) isophthalonitrile (4CzIPN, Ossila), (±)-2,2′-bis(diphenylphosphino)-1,1′-binaphthyl (rac-BINAP, Alfa Aesar), C60 (nano-c), pentacene (iChemical) and α-sexithiophene (α-6T, Sigma Aldrich). All materials were purchased and used as received except NPB, C60, and pentacene, which were first purified via thermal gradient sublimation.Fabrication
All substrates were cleaned successively by sonication in deionized water with Extran soap in a 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio, deionized water, acetone, and isopropanol followed by an oxygen plasma treatment. Samples were deposited using thermal evaporation with a base pressure of ∼10−7 Torr. A quartz crystal microbalance was used to monitor the deposition rate. The template crystalline films are prepared by depositing the organic material as an amorphous film by physical vapor deposition followed by an annealing step on a pre-heated hotplate in a nitrogen filled glovebox, as described in ref. 11. For rac-BINAP, 60 nm of material is deposited on a glass/indium tin oxide (ITO) substrate and then annealed at 140 °C for 5 min. During the adlayer deposition, substrates were heated with a Julabo F32 Refrigerated/Heating Circulator.
1 ratio, deionized water, acetone, and isopropanol followed by an oxygen plasma treatment. Samples were deposited using thermal evaporation with a base pressure of ∼10−7 Torr. A quartz crystal microbalance was used to monitor the deposition rate. The template crystalline films are prepared by depositing the organic material as an amorphous film by physical vapor deposition followed by an annealing step on a pre-heated hotplate in a nitrogen filled glovebox, as described in ref. 11. For rac-BINAP, 60 nm of material is deposited on a glass/indium tin oxide (ITO) substrate and then annealed at 140 °C for 5 min. During the adlayer deposition, substrates were heated with a Julabo F32 Refrigerated/Heating Circulator.
Characterization
Images of the annealed samples were taken with a polarized optical microscope (Olympus BX60F5). Atomic force microscopy was conducted with a Veeco Digital Instruments Dimension 3100 in tapping mode and the data were analyzed with Gwyddion software.42 The X-ray diffraction (XRD) characterization was completed with a Bruker D8 Discover X-Ray Diffractometer with a copper source and a wavelength of 1.54 Å.Computational methodology
We used Sandia's molecular dynamics simulator, LAMMPS,43 to conduct all the MD simulations in this work. We used force field parameters for OPLS (optimized potentials for liquid simulations) developed by Jorgensen et al.44–46 for the molecules in the system. We used the steered molecular dynamics (SMD) method47 to find the step-edge descent trajectory and associated changes in free energy, including any near-step-edge energy barriers reminiscent of an Ehrlich–Schwöbel barrier (EES).21,22 The “production” stage of the simulations are conducted under NVT canonical ensemble conditions (constant number of particles, volume and temperature) at 300 K. For the diffusional studies of each molecular system, we ran MD simulations for 20 ns under an NVT ensemble at 300 K. We set up two systems to simulate diffusion: one that resembled the complementary SMD simulations that featured a monolayer terrace on top of a complete monolayer, thus allowing for the possibility of step-edge descent, and a second system configuration that featured only a complete monolayer (i.e. no step-edge present). More details on the SMD and diffusion simulations are provided in the ESI.†Results and discussion
A set of organic small molecules (identified in ref. 11) have the ability to grow into large-area, single-crystal domains, or platelets. These films exhibit molecularly smooth surfaces upon crystallization, making them ideal templates for the study of homoepitaxy. From this work, we prepare NPB, TPBi and 4CzIPN crystalline templates to study homoepitaxy. We also consider rac-BINAP, another platelet-forming material that was identified using the results of ref. 11. A polarized optical microscope (POM) image of a crystalline rac-BINAP film can be found in Fig. S1 (ESI†).In addition to these materials, we also grow films of C60, pentacene and α-6T because they are archetypal crystalline organic materials. For C60, a crystalline NPB template is used as its substrate because C60 will not easily crystallize upon deposition onto conventional substrates like SiO2 or ITO. Both pentacene and α-6T, on the other hand, readily crystallize during deposition on the smooth Si/SiO2 surface, as demonstrated here, eliminating the need for a template layer.
To investigate the roughness behavior of each material, the template crystals (or just SiO2 in the case of pentacene and α-6T) are reintroduced to the deposition chamber and various thicknesses of the test material are deposited. During deposition, the substrates are held at 80 °C, with the exception of 4CzIPN which is held at 100 °C due to its high crystallization temperature. A deposition rate of 0.1 Å s−1 was used for all materials except rac-BINAP which was deposited at 1 Å s−1. Table S1 (ESI†) summarizes these growth conditions.
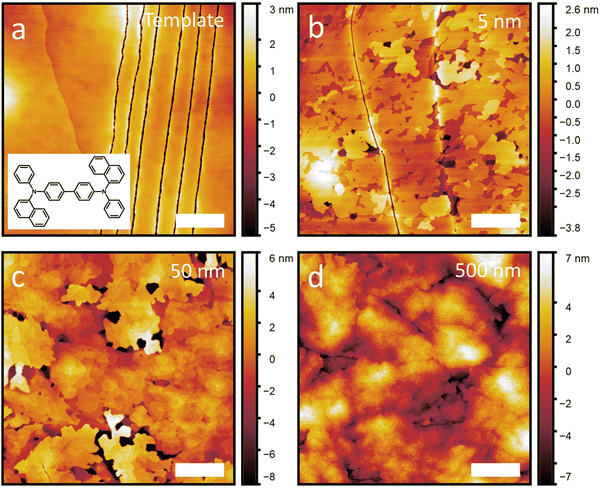
The films are then characterized by AFM shortly after growth. Fig. 1 shows a subset of the NPB samples including adlayer thicknesses of 0 nm (template), 5 nm, 50 nm and 500 nm. A full set of AFM scans and line profiles for NPB, as well as the other growth experiments included in this work, can be found in Fig. S2–S8 and S9 (ESI†), respectively. X-ray diffraction conducted on each template layer and each template with adlayer growth are shown in Fig. S10 (ESI†), proving the crystallinity of each film. The out-of-plane crystal orientation of each template is listed in Table S2 (ESI†). We observe that the diffraction peak intensity increases with increasing film thickness, illustrating that we are either propagating an existing crystal (through homoepitaxy) or growing a new crystal (as for C60, pentacene and α-6T).
From the AFM scans, we note that all template layers are smooth, occasional molecular steps notwithstanding. This provides an ideal surface on which to study epitaxial growth. In the case of the NPB template layer, we also observe series of narrow lines, possibly cracks, which likely arise from the mismatched thermal expansion of the glass/ITO substrate and the NPB crystal. Despite this, the NPB template remains smooth, with a root mean square (RMS) roughness (σ) value of 1.3 nm. The RMS roughness of the other templates are listed in Table S1 (ESI†).
Subsequent growth of NPB on its template crystal results in initial layer-by-layer growth (Fig. 1(b)) followed by island growth (Fig. 1(c) and (d)), illustrating that NPB grows following the Stranski–Krastanov designation. While this is a rather common growth mode for organic crystals (all materials but C60 in this work also exhibit this behavior), what appears uncommon is that at high thicknesses, NPB remains relatively smooth (see below) despite island growth usually leading to increased roughness.7,29
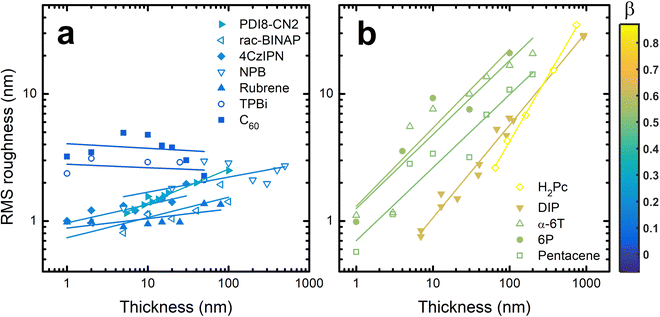
To quantify the roughness evolution, multiple AFM scans are taken at each thickness for each material and the σ values (extracted from the entire AFM scan) are averaged and plotted in Fig. 2. Also included in Fig. 2 are σ data from literature of other crystalline organic molecules grown at conditions similar to those used in this work; specifically, a growth rate of ∼0.1 Å s−1 and substrate temperature of ∼80 °C. These materials include rubrene,26N,N′-bis(n-octyl)-dicyanoperylene-3,4:9,10-bis(dicarboximide) (PDI8-CN2),48,49 free-base phthalocyanine (H2Pc),30 diindenoperylene (DIP),24 and para-sexiphenyl (6P).36 The growth conditions of these systems are also included in Table S1 (ESI†). We acknowledge that different materials will require different growth conditions to achieve near-equilibrium growth. Since the conditions used here are all similar, it is possible we are investigating different roughness evolution regimes between materials. However, the AFM and XRD data suggest ∼80 °C is warm enough to promote crystal growth, which nearly always transitions to 3D growth eventually,25 without being too hot to inhibit adsorption. Therefore, this substrate temperature, combined with a slow flux, allows these materials to grow near their equilibrium conditions such that we believe our results hold value in uncovering growth mechanics of homoepitaxy.
To compare the roughness evolution of these films, we employ a scaling theory used to describe growth-induced surface roughness.28,50 The scaling theory predicts a power law dependence for σ ∼ Tβ where T is the thickness of the film and β is the growth exponent. Therefore, fitting lines to the data in Fig. 2 allows us to extract β for each material system. For NPB, we find β = 0.12 ± 0.06 which is less than the random deposition limit of 0.5, proving the smooth growth of NPB. In some cases like PDI8-CN2,49σ oscillates at T < 6 nm or about 3 monolayers, a result of layer-by-layer growth. Since the scaling theory does not operate in this regime we do not include these data during fitting nor in Fig. 2. The fit lines are included in Fig. 2 and the β values are listed in Table S1 (ESI†).
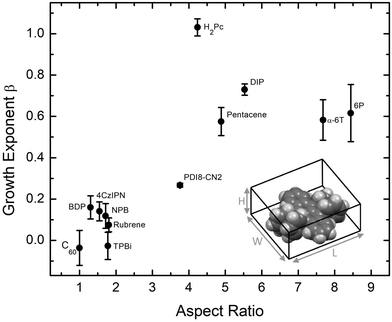
Examining the data in Fig. 2, there is a clear grouping of molecules that remain smooth versus those that significantly roughen as thickness increases. Notably, all of the molecules in Fig. 2(b) that grow rough are either rod-like or planar while most of those in Fig. 2(a) which remain smooth are 3D. To capture this idea quantitatively, the aspect ratio (AR) of each molecule is calculated. We define AR by drawing a box around a molecule in its crystal structure conformation, and divide the longest dimension of the box by the shortest dimension. We assume the molecule has a van der Waals surface enveloping it when determining the dimensions. An example is provided for rubrene in the inset of Fig. 3.
Plotting β against the molecular AR in Fig. 3 indeed shows a trend that molecules with higher AR (or more planar molecules) will grow rougher than low AR molecules (or 3D molecules). Importantly, we note that the low AR materials remain smooth despite showing a high degree of crystallinity via the XRD data taken in a Bragg–Brentano geometry (Fig. S10, ESI†) and AFM data in Fig. S2–S8 (ESI†). Organic materials grown highly crystalline tend to exhibit island growth leading to rough films,7,29 so the low AR materials considered here are rather unusual and warrant further explanation.
To understand the atomic-scale processes that underlie the relationship between roughness evolution and the AR of a molecule, we undertook molecular dynamics (MD) simulations of epitaxy for several of the systems tested experimentally. During deposition, when a molecule comes into contact with a crystalline substrate it has a variety of available options such as surface or edge diffusion, nucleation of a new layer, movement between layers, or desorption. In the context of β, it is customary to relate surface roughening primarily to the ability of molecules to traverse step-edges. The complete suppression of interlayer transport leads to β = 1/2. For a more quantitative analysis we define the Ehrlich–Schwöbel barrier (EES) as the additional energy (above that of surface diffusion barriers) required for a molecule to descend a molecular step-edge.21,22 In layer-by-layer growth, one expects EES to be small, indicating that molecules have little difficulty descending a terrace. On the other hand, if EES is large, molecules may find it difficult to traverse step-edges, resulting in them being “trapped” on the layer on which they were deposited. Such trapped molecules must then nucleate a new layer or attach to an existing terrace, often before the layer below completes its coverage. This leads to island growth and roughening of the surface. A good example of this phenomenon is pentacene in Fig. S7 (ESI†). However, it has been less appreciated that EES is likely only to be a factor if molecules are mobile enough to diffuse to and probe step-edges. Therefore, to investigate if a combination of EES and lateral molecular mobility can explain the smooth growth of low AR materials we applied MD simulations to a subset of the molecules considered in this study.
In our MD simulations, we selected rac-BINAP, NPB and TPBi to represent the low AR molecules, while α-6T was selected as a high AR molecule. The other high AR molecules like pentacene, 6P and DIP have been simulated in other work,20 making α-6T a natural choice. The MD simulations focused on two aspects of growth mechanics: estimating each material's EES value and determining molecular diffusion on the crystalline surface. The implementation of these simulations is described in the ESI.†
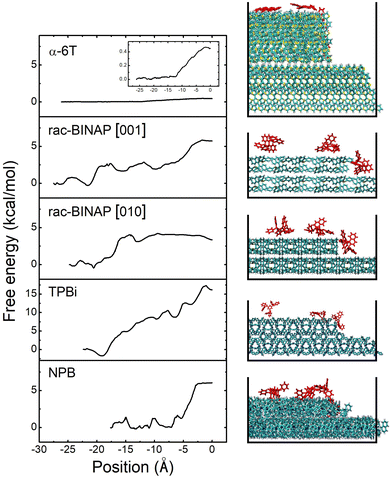
Estimating EES is done by applying steered molecular dynamics (SMD). Taking rac-BINAP as an example, we initially set up a molecular terrace composed of rac-BINAP in the out-of-plane crystal orientation determined by XRD (the (100) in this case). An ad-molecule is placed on top of the terrace and pulled along the [001] crystallographic direction toward the terrace's edge, assessing the barrier for it to descend the step-edge. A cross-sectional view of this process is shown in Fig. 4 illustrating the starting, intermediate, and final positions of the ad-molecule as defined in Fig. S11a (ESI†). A top-down view of the terrace is shown in Fig. S11b (ESI†) to visualize the direction in which the molecule was pulled.
Above the molecular crystal visualization in Fig. 4, we plot the free energy profiles produced by the SMD simulation. Traveling in the rac-BINAP [001] direction, the ad-molecule faces an energy barrier of 2.9 kcal mol−1 (0.13 eV) as it is pulled horizontally. The ad-molecule faces an energy barrier of 5.8 kcal mol−1 when it is pulled downwards and descends the step-edge in the [001] direction. In what follows, we define the free energy barrier associated with a horizontal pull across the terrace as E1 and the one associated with step-edge descent in a downward direction as E2. The overall lower EES barrier is defined as E2 − E1. In the case of rac-BINAP [001] direction, the EES is 2.9 kcal mol−1. It is worth noting that, in molecular systems such as these, due to the numerous orientations a molecule can take as it approaches a step-edge, there is not one EES for a given molecule but rather an ensemble of barriers.20 For instance, pulling rac-BINAP in the [010] direction produces a different free energy profile than the [001] direction. However, the SMD method used here allows us to calculate EES of the most probable step type among the ensemble of barriers.
We also conducted SMD simulations for α-6T, TPBi and NPB. Visualization of the trajectories and free energy profiles are shown in Fig. 4. The crystal plane used in these simulations match the experimental out-of-plane orientation determined by XRD and are listed in Table S2 (ESI†). A summary of the energy barriers for the four different systems associated with a horizontal pull across the terrace and a subsequent downward pull to the step below are shown in Table 1. These four systems clearly experience different energy barriers to traverse the terrace and to descend the step-edge. In α-6T, we only needed to conduct a horizontal pull across the terrace because the ad-molecule spontaneously descended the step-edge once it reached the edge of the terrace. This phenomenon is consistent with the free energy results for α-6T, in which the two free energies, E1 and E2, were both very small, under 1 kcal mol−1. A similar energy barrier and energy landscape is found in other high AR systems, such as pentacene, when incorporating entropic effects in calculating EES.19 The SMD trajectory and free energy profile thus indicate that, for α-6T, there was no significant thermodynamic barrier against step-edge descent.
| System | E 1 | E 2 | E ES |
|---|---|---|---|
| α-6T | Negligible | 0.5 | 0.5 |
| rac-BINAP [010] | 4.0 | 4.2 | 0.2 |
| rac-BINAP [001] | 2.9 | 5.8 | 2.9 |
| NPB | 1.4 | 6.2 | 4.8 |
| TPBi | 10.6 | 17.3 | 6.7 |
In contrast, the rac-BINAP, NPB and TPBi systems exhibit horizontal and descent energy barriers up to an order of magnitude higher than those for α-6T. The order of increasing size of the EES of these four systems is α-6T < rac-BINAP < NPB < TPBi. If EES is assumed to be the dominant factor that dictates the growth mode then the SMD results would suggest that α-6T should remain the smoothest during growth and TPBi would become the roughest. However, experimentally this is not observed, necessitating consideration of additional factors that may be responsible for contributing to the observed roughness order.
One consideration is the free energy barrier, Eedge, of a molecule breaking free from an island layer. We simulate this by pushing an already descended ad-molecule away from its equilibrated position at the step-edge. The free energy change of this process for α-6T is between −0.6 and −1.4 kcal mol−1. In contrast, the same process for rac-BINAP, NPB, and TPBi has a free energy barrier larger than 5 kcal mol−1 as shown in Table S3 (ESI†). The low, even negative free energy change indicates that α-6T can easily associate and dissociate from a molecular step-edge. The positive free energy barrier of the three low AR molecules indicates that the thin-film growth is thermodynamically stable after the ad-molecule descends over the step-edge and is unlikely to dissociate from it. Most importantly, we observe that when α-6T is pushed from the step-edge it is the only molecule observed to climb back up the step-edge while low AR molecules only have in-plane movement.
These energy barriers are only relevant if an ad-molecule has sufficient lateral (i.e. “on-terrace”) mobility to approach and probe descent over a step-edge. Therefore, we investigated the lateral diffusional properties of the four compounds tested above by simulating the trajectory of a single ad-molecule across a terrace for 20 ns. Fig. 5(a) shows the trace created by the trajectory of the center of mass of each ad-molecule. It is immediately obvious from Fig. 5(a) that the path traced by each molecule is qualitatively and quantitatively different in all four cases. We identify three categories to describe the diffusion properties of the four molecular systems. First, α-6T can be described as “freely roaming,” in which the ad-molecule essentially probes the entire terrace. Furthermore, the offshoot in the α-6T trace illustrates that the molecule spontaneously descended the terrace at approximately 14 ns. This high mobility likely arises from α-6T ad-molecules lying flat on a surface of upright molecules that compose the crystal. Since periodicity of the corrugations on the crystalline surface are far shorter than the length of an α-6T molecule, there is little commensurability, and the effective corrugation experienced by the ad-molecule is strongly reduced. Also, there may be little π–π interaction with the crystal which allows it to “skate” on the surface. The trace for α-6T might appear to indicate that the ad-molecule could not get near the edge of the terrace. However, this is because the trace follows the center of mass of the ad-molecule. If we consider the full area of the molecule (around 15–20 Å in diameter), we find that α-6T does, in fact, probe the entire terrace, as shown in Fig. S12 (ESI†).
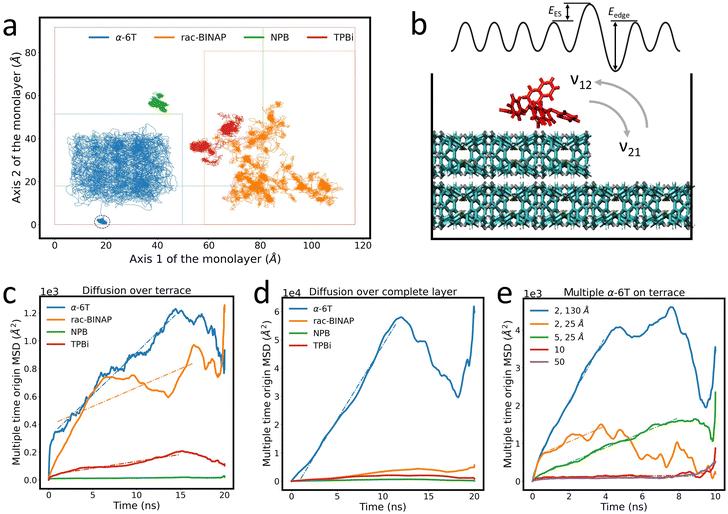 | ||
| Fig. 5 (a) Trace of the center of mass of ad-molecules traversing a molecular terrace. The dashed circle indicates the α-6T ad-molecule spontaneous descent over the island layer edge after 14 ns. The boundary of each terrace is marked as a dashed line of the same color as the molecular trajectory. Traces are shifted for clarity. (b) Illustration of the rates of ascent and descent as well as EES and Eedge in a simplified representation of a complex 3D molecular surface. Calculations of MSD for (c) diffusion over a terrace and (d) diffusion over a complete monolayer. (e) Calculations of MSD of 2, 5, 10 and 50 α-6T ad-molecules on an α-6T surface. The distance value in the legend indicates the initial center of mass distance between each ad-molecule. The initial distance is 5 Å if no specification is given. The 2 ad-molecules system with 130 Å initial distance formed an aggregate after 4 ns and 2 ad-molecules with 25 Å initial distance formed an aggregate shortly after the simulation started (i.e. within 0.5 ns). Dashed lines in (c)–(e) are fits to the MSD data to determine the diffusion coefficient and are listed in the ESI.† | ||
Secondly, rac-BINAP resembles a “run-and-tumble” motion,51 whereby the ad-molecule has periods when its diffusion is locally confined (“tumbling”), followed by “runs” to a different site on the terrace. Thirdly, trajectories for NPB and TPBi indicate that the ad-molecules are essentially “confined” to a local site during the 20 ns simulation period. It is possible that NPB and TPBi also exhibit “run-and-tumble” motion, but at timescales beyond the 20 ns window used in the simulation. Hence we did not observe any “runs,” but cannot determine if they exist at far longer timescales. These low AR molecules do not benefit from the “averaging out” of surface corrugations like α-6T does or other rod-like molecules typically do. There is more direct face-to-face overlapping between the ring structures of the ad-molecule and the ones in the thin film, hence stronger π–π interactions. On the contrary, the ring structures are perpendicular to each other between the ad-molecule and the thin film in high AR systems. This difference can be seen in the visualization included in Fig. 4. Although the OPLS force field does not have explicit π–π interactions, it is parameterized on the dispersion-corrected basis set46 and allows us to capture the interplay between the dispersion and electrostatic interactions. Based on a study on the naphthalene dimer, the most dominant interatomic interaction is the dispersion which destabilizes the perpendicular structure within high AR molecules, hence allowing higher mobility over the surface.52 Therefore, low AR molecules likely better conform to the surface and have high degrees of freedom to rearrange their ring structures resulting in the “run-and-tumble” and “confined” diffusion behaviors.
To capture the relative mobility of these molecules more quantitatively, we calculated the mean squared displacement (MSD) of each trace, as described in the ESI.† The resulting MSD values are shown in Fig. 5(c). Based on these results, the mobility of the ad-molecules decreases in the order: α-6T > rac-BINAP > TPBi > NPB. The “dips” in the MSD curve for α-6T are due to the spontaneous step-edge descent after approximately 14 ns which is consistent with the low EES in Table 1. The “dips” observed in the MSD curve for rac-BINAP reflect the molecule's “run-and-tumble” movement. On the other hand, the MSD curves for NPB and TPBi exhibit low mobility, consistent with their locally confined diffusion. To eliminate the possibility that the small area of the terrace was limiting the diffusion of the ad-molecule, we set up an additional system in which the ad-molecule is placed directly on top of a complete monolayer (i.e., effectively an infinitely large monolayer given the periodic boundary conditions). The MSD curves corresponding to this system configuration are shown in Fig. 5(d). The diffusion coefficient, D, of each molecule can be determined by the slope of the fit lines in Fig. 5(c) and (d) and are listed in Table S4 (ESI†). Note that D values are smaller when molecules are simulated on an island because the edges constrain their movement. Focusing on the unrestricted movement of the single monolayer case, we observe that D for α-6T is over an order of magnitude higher than those of rac-BINAP, NPB and TPBi when the area of the island is not a limiting factor.
The apparent capability of molecules like α-6T to probe large surface areas, mediated by high mobility and low energy barriers to descend and dissociate away from step-edges, increases the likelihood that these free molecules find one another and aggregate. Therefore, we turn the simulation focus onto the effects of aggregation. Importantly, we find that an aggregate of just two α-6T ad-molecules sharply reduces molecular mobility compared to the single molecule (between half and an order of magnitude) when the AR of the two-molecules aggregate decreases by half. The larger aggregates become even more immobile where the 5-molecule aggregate, with an AR that would rank it in the “low AR” group, possesses diffusivity of roughly the same magnitude as “low AR“ molecules (i.e., compared to rac-BINAP and TPBi). In fact, the mobility of the aggregate decreases as AR increases when multiple rod-like α-6T molecules form “bulky” (low AR-like) clusters. See Table S5 (ESI†) for a full list of D values associated with aggregation. Furthermore, aggregates of two α-6T molecules experience a significantly larger EES barrier to step-edge descent than a single molecule, as evidenced by no spontaneous descent of aggregates during a 50 ns simulation window. In effect, pairs of α-6T molecules behave more like solitary, low AR molecules. On the other hand, aggregation of low AR molecules like NPB, TPBi and rac-BINAP, does not dramatically increase the EES barrier. Because the molecular mobility and EES are correlated based on our earlier calculation in single ad-molecule system, we believe the aggregation does not decrease the mobility of low AR molecules either. Fig. 5(e) shows the MSD of aggregated α-6T molecules and Table S6 (ESI†) lists the energy barrier to step-edge descent of the four aggregated systems.
Results from simulating ad-molecule diffusion and the EES barrier are mutually consistent: α-6T has the highest mobility and the lowest EES; rac-BINAP has intermediate mobility and step-edge energy barrier height, while NPB and TPBi have the lowest mobility and highest EES.
To explain the roughness exponent order predicted by the simulations and our experimental observations, we consider a growth mechanism that relies on both molecular mobility across the terrace as well as considerations of the energy barriers, EES and Eedge, i.e. both intralayer and interlayer transport. First, we assume that smooth epitaxial growth arises from a net downward flux of molecules, from high terraces to lower ones. This has been well established through previous simulations that show that when molecules are allowed to proceed down step-edges, the resulting film is smooth with β < 0.5, where β = 0.5 is achieved in the random deposition limit.53–56 Therefore, we can consider the rate of population change of single, unaggregated molecules on an island, r. If r is negative, then the downward flux of molecules will produce smooth surfaces. We can express r with the rates of ascent (ν12) and descent (ν21) at molecular step-edges:
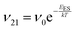 | (1) |
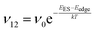 | (2) |
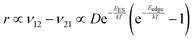 | (3) |
If we consider low AR molecules in the context of eqn (3), we find that since D is relatively small and EES is relatively large then the first two terms will be small. However, the expression in parentheses will be close to −1 because low AR molecules have a large Eedge as evident by their preference to reside at step-edges during growth. Therefore, low AR molecules have a negative r likely leading to smooth growth. Crucially, high AR molecules cannot only escape step-edges (due to small, even negative Eedge) but also ascend step-edges pushing r close to 0. Evidently, molecules like α-6T can explore much of a surface without being stuck on any given terrace. Eventually, they intersect with other ad-molecules and form aggregates that are not as mobile and experience larger EES, effectively trapping them on a terrace (see the ESI† for more detail). This allows new island formation to occur anywhere, even on top of other islands, which leads to a roughening effect. So while our consideration of this growth mechanism (and the dependence on the coarse-grained parameter AR) is somewhat simplified in the context of roughness evolution, it is able to obtain a comprehensive picture of a large number of compounds, proving its utility.
Bringing our discussion back to the more general picture of the aspect ratio as a key parameter, we can offer an explanation linking the shape of a molecule to the dynamics during epitaxy. High AR molecules tend to lie flat on their respective crystalline surface in order to maximize the number of nearest neighbor molecules and thereby minimize energy. However, since the molecules in the crystal tend to all stand upright, the periodicity of the resulting corrugations on the surface are far shorter than the length of the ad-molecule (see α-6T in Fig. 4). Therefore, the molecule bonds poorly with the crystal which allows it to “float” on the surface. This reduces the barrier to diffusion and increases its molecular mobility. The growth model above shows how this leads to rough surface evolution. Low AR molecules tend to have numerous degrees of freedom granted by branching, rotatable bonds, allowing them to conform to the crystalline surfaces, limiting their mobility. A similar argument can be made for the reason why these molecules bind well at molecular step-edges leading to large Eedge and therefore smooth growth. One exception, however, is C60, which does not have degrees of freedom from rotatable bonds yet is in the low AR class and exhibits a small β. For this case, we turn to atomic-like systems to understand why it remains smooth. In true atomic systems, the interaction range (normalized to the size of the atom) is comparatively large compared to C60,57 resulting in a strong bond to the crystal surface and a large energy penalty for attempting to descend a step-edge where there are fewer neighbors.38 For instance, both Ag/Ag(111) and Pt/Pt(111) exhibit roughening with increasing deposition thickness.14 For C60, the interaction range is relatively smaller so both diffusion and traversing a step-edge is easier than in atomic systems likely leading to smoother growth. We note, however, that this is only true for C60 at elevated substrate temperatures where ad-molecules have sufficient energy to migrate and of course where C60 can be considered effectively a sphere, since rotations are thermally excited.37
Conclusions
The surface roughness of a series of organic crystals is tracked as a function of film thickness. Comparing the growth exponent, β, to the aspect ratio of each molecule we find that low aspect ratio, bulky, molecules tend to remain smooth. Molecules with high aspect ratios lead to rough films. Molecular dynamic simulations of molecules from each class of material provide atomic-level insight that the conventional EES barrier alone is not sufficient to explain these trends. Indeed, we find that low aspect ratio molecules have large EES yet result in smooth growth. Conversely, we calculate a small EES for α-6T, a high AR molecule, despite experiments showing it develop rough surfaces. We propose a more holistic model of homoepitaxy that includes surface diffusion and aggregation affects along with energy barriers to dissociate from molecular step-edges. In addition to the relatively large step-edge barriers we calculate for low AR molecules, this class of material is also relatively immobile, prefers to attach to the crystal at step-edges, and is not negatively affected by aggregation. In the process of this work, we also found qualitatively distinct diffusion behavior apparently dictated by molecular shape. Taken together, these attributes allow low AR molecules to descend, but rarely ascend, step-edges, creating a downward flow of molecules leading to smooth epitaxial growth. These results point to the type of molecules, namely low aspect ratio molecules, that can form smooth crystalline surfaces, a key feature for their implementation in crystalline organic electronic devices.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank the Princeton SEAS Project X fund for partial support of this work. FS wishes to acknowledge financial support by the DFG. XC and PC thank Advanced Research Computing at Hopkins (ARCH) core facility (rockfish.jhu.edu) for the provision of the computation resources supported by the National Science Foundation (NSF) grant number OAC 1920103.References
- I. G. Lezama and A. F. Morpurgo, Progress in organic single-crystal field-effect transistors, MRS Bull., 2013, 38, 51–56 CrossRef CAS.
- H. Najafov, B. Lee, Q. Zhou, L. C. Feldman and V. Podzorov, Observation of long-range exciton diffusion in highly ordered organic semiconductors, Nat. Mater., 2010, 9, 938–943 CrossRef CAS PubMed.
- H. M. Lee, H. Moon, H. S. Kim, Y. N. Kim, S. M. Choi, S. Yoo and S. O. Cho, Abrupt heating-induced high-quality crystalline rubrene thin films for organic thin-film transistors, Org. Electron., 2011, 12, 1446–1453 CrossRef CAS.
- J. S. Bangsund, T. R. Fielitz, T. J. Steiner, K. Shi, J. R. Van Sambeek, C. P. Clark and R. J. Holmes, Formation of aligned periodic patterns during the crystallization of organic semiconductor thin films, Nat. Mater., 2019, 18, 725–731 CrossRef CAS PubMed.
- M. Shtein, J. Mapel, J. B. Benziger and S. R. Forrest, Effects of film morphology and gate dielectric surface preparation on the electrical characteristics of organic-vapor-phase-deposited pentacene thin-film transistors, Appl. Phys. Lett., 2002, 81, 268–270 CrossRef CAS.
- S. Verlaak, S. Steudel, P. Heremans, D. Janssen and M. Deleuze, Nucleation of organic semiconductors on inert substrates, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 195409 CrossRef.
- F. Schreiber, Organic molecular beam deposition: Growth studies beyond the first monolayer, Phys. Status Solidi A, 2004, 201, 1037–1054 CrossRef CAS.
- A. Hinderhofer, A. Gerlach, K. Broch, T. Hosokai, K. Yonezawa, K. Kato, S. Kera, N. Ueno and F. Schreiber, Geometric and electronic structure of templated C60 on diindenoperylene thin films, J. Phys. Chem. C, 2013, 117, 1053–1058 CrossRef CAS.
- A. O. F. Jones, B. Chattopadhyay, Y. H. Geerts and R. Resel, Substrate-induced and thin-film phases: Polymorphism of organic materials on surfaces, Adv. Funct. Mater., 2016, 26, 2233–2255 CrossRef CAS.
- M. A. Fusella, S. Yang, K. Abbasi, H. H. Choi, Z. Yao, V. Podzorov, A. Avishai and B. P. Rand, Use of an underlayer for large area crystallization of rubrene thin films, Chem. Mater., 2017, 29, 6666–6673 CrossRef CAS.
- J. T. Dull, Y. Wang, H. Johnson, K. Shayegan, E. Shapiro, R. D. Priestley, Y. H. Geerts and B. P. Rand, Thermal properties, molecular structure, and thin-film organic semiconductor crystallization, J. Phys. Chem. C, 2020, 124, 27213–27221 CrossRef CAS.
- T. L. Derrien, A. E. Lauritzen, P. Kaienburg, J. F. Hardigree, C. Nicklin and M. Riede, In situ observations of the growth mode of vacuum-deposited α-sexithiophene, J. Phys. Chem. C, 2020, 124, 11863–11869 CrossRef CAS.
- K. Vasseur, C. Rolin, S. Vandezande, K. Temst, L. Froyen and P. Heremans, A growth and morphology study of organic vapor phase deposited perylene diimide thin films for transistor applications, J. Phys. Chem. C, 2010, 114, 2730–2737 CrossRef CAS.
- J. W. Evans, P. A. Thiel and M. C. Bartelt, Morphological evolution during epitaxial thin film growth: Formation of 2D islands and 3D mounds, Surf. Sci. Rep., 2006, 61, 1–128 CrossRef CAS.
- S. E. Fritz, T. W. Kelley and C. Daniel Frisbie, Effect of dielectric roughness on performance of pentacene TFTs and restoration of performance with a polymeric smoothing layer, J. Phys. Chem. B, 2005, 109, 10574–10577 CrossRef CAS PubMed.
- C. H. Jonda, A. B. R. Mayer, U. Stolz, A. Elschner and A. Karbach, Surface roughness effects and their influence on the degradation of organic light emitting devices, J. Mater. Sci., 2000, 35, 5645–5651 CrossRef CAS.
- M. Möbus and N. Karl, The growth of organic thin films on silicon substrates studied by X-ray reflectometry, Thin Solid Films, 1992, 215, 213–217 CrossRef.
- M. Fendrich and J. Krug, Ehrlich–Schwoebel effect for organic molecules: Direct calculation of the step-edge barrier using empirical potentials, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 121302 CrossRef.
- O. M. Roscioni, G. D'Avino, L. Muccioli and C. Zannoni, Pentacene crystal growth on silica and layer-dependent step-edge barrier from atomistic simulations, J. Phys. Chem. Lett., 2018, 9, 6900–6906 CrossRef CAS PubMed.
- J. E. Goose, E. L. First and P. Clancy, Nature of step-edge barriers for small organic molecules, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 205310 CrossRef.
- G. Ehrlich and F. G. Hudda, Atomic view of surface self-diffusion: Tungsten on tungsten, J. Chem. Phys., 1966, 44, 1039 CrossRef CAS.
- R. L. Schwoebel and E. J. Shipsey, Step motion on crystal surfaces, J. Appl. Phys., 1966, 37, 3682 CrossRef CAS.
- A. Winkler, On the nucleation and initial film growth of rod-like organic molecules, Surf. Sci., 2016, 652, 367–377 CrossRef CAS PubMed.
- A. C. Dürr, F. Schreiber, K. A. Ritley, V. Kruppa, J. Krug, H. Dosch and B. Struth, Rapid roughening in thin film growth of an organic semiconductor (diindenoperylene), Phys. Rev. Lett., 2003, 90, 016104 CrossRef PubMed.
- E. Empting, M. Klopotek, A. Hinderhofer, F. Schreiber and M. Oettel, Lattice gas study of thin-film growth scenarios and transitions between them: Role of substrate, Phys. Rev. E, 2021, 103, 23302 CrossRef CAS.
- M. A. Fusella, F. Schreiber, K. Abbasi, J. J. Kim, A. L. Briseno and B. P. Rand, Homoepitaxy of crystalline rubrene thin films, Nano Lett., 2017, 17, 3040–3046 CrossRef CAS.
- B. Verreet, P. Heremans, A. Stesmans and B. P. Rand, Microcrystalline organic thin-film solar cells, Adv. Mater., 2013, 25, 5504–5507 CrossRef CAS PubMed.
- T. Michely and J. Krug, Islands, Mounds and Atoms, Springer Series in Surface Sciences, Springer Berlin Heidelberg, Berlin, Heidelberg, 2004, vol. 42 Search PubMed.
- P. Fenter, F. Schreiber, L. Zhou, P. Eisenberger and S. R. Forrest, In situ studies of morphology, strain, and growth modes of a molecular organic thin film, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 3046–3053 CrossRef CAS.
- S. Yim and T. S. Jones, Anomalous scaling behavior and surface roughening in molecular thin-film deposition, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 161305 CrossRef.
- S. Yim, K.-I. Kim and T. S. Jones, Growth morphology of perylene-3,4,9,10-tetracarboxylic dianhydride (PTCDA) thin films: Influence of intermolecular interactions and step-edge barriers, J. Phys. Chem. C, 2007, 111, 10993–10997 CrossRef CAS.
- R. Ruiz, D. Choudhary, B. Nickel, T. Toccoli, K. C. Chang, A. C. Mayer, P. Clancy, J. M. Blakely, R. L. Headrick and S. Iannotta, et al., Pentacene thin film growth, Chem. Mater., 2004, 16, 4497–4508 CrossRef CAS.
- H. Zhu, Q. L. Li, X. J. She and S. D. Wang, Surface roughening evolution in pentacene thin film growth, Appl. Phys. Lett., 2011, 98, 243304 CrossRef.
- H. L. Cheng, Y. S. Mai, W. Y. Chou, L. R. Chang and X. W. Liang, Thickness-dependent structural evolutions and growth models in relation to carrier transport properties in polycrystalline pentacene thin films, Adv. Funct. Mater., 2007, 17, 3639–3649 CrossRef CAS.
- S. D. Wang, X. Dong, C. S. Lee and S. T. Lee, Molecular orientation and film morphology of pentacene on native silicon oxide surface, J. Phys. Chem. B, 2005, 109, 9892–9896 CrossRef CAS PubMed.
- G. Hlawacek, P. Puschnig, P. Frank, A. Winkler, C. Ambrosch-Draxl and C. Teichert, Characterization of step-edge barriers in organic thin-film growth, Science, 2008, 321, 108–111 CrossRef CAS.
- A. F. Hebard, O. Zhou, Q. Zhong, R. M. Fleming and R. C. Haddon, C60 films on surface-treated silicon: Recipes for amorphous and crystalline growth, Thin Solid Films, 1995, 257, 147–153 CrossRef CAS.
- S. Bommel, N. Kleppmann, C. Weber, H. Spranger, P. Schäfer, J. Novak, S. V. Roth, F. Schreiber, S. H. L. Klapp and S. Kowarik, Unravelling the multilayer growth of the fullerene C 60 in real time, Nat. Commun., 2014, 5, 5388 CrossRef CAS PubMed.
- W. Janke and T. Speck, Modeling of epitaxial film growth of C60 revisited, Phys. Rev. B, 2020, 101, 125427 CrossRef CAS.
- M. Klopotek, H. Hansen-Goos, M. Dixit, T. Schilling, F. Schreiber and M. Oettel, Monolayers of hard rods on planar substrates. II. Growth, J. Chem. Phys., 2017, 146, 084903 CrossRef CAS PubMed.
- S. Kowarik, A. Gerlach, S. Sellner, F. Schreiber, L. Cavalcanti and O. Konovalov, Real-time observation of structural and orientational transitions during growth of organic thin films, Phys. Rev. Lett., 2006, 96, 181–188 CrossRef PubMed.
- D. Nečas and P. Klapetek, Gwyddion: An open-source software for SPM data analysis, Cent. Eur. J. Phys., 2012, 10, 181–188 Search PubMed.
- S. Plimpton, Fast parallel algorithms for short-range molecular dynamics, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- W. L. Jorgensen and J. Tirado-Rives, Potential energy functions for atomic-level simulations of water and organic and biomolecular systems, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 6665–6670 CrossRef CAS.
- L. S. Dodda, I. C. De Vaca, J. Tirado-Rives and W. L. Jorgensen, LigParGen web server: An automatic OPLS-AA parameter generator for organic ligands, Nucleic Acids Res., 2017, 45, W331–W336 CrossRef CAS PubMed.
- L. S. Dodda, J. Z. Vilseck, J. Tirado-Rives and W. L. Jorgensen, 1.14*CM1A-LBCC: Localized bond-charge corrected CM1A charges for condensed-phase simulations, J. Phys. Chem. B, 2017, 121, 3864–3870 CrossRef CAS.
- S. Izrailev, S. Stepaniants, B. Isralewitz, D. Kosztin, H. Lu, F. Molnar, W. Wriggers and K. Schulten, Steered Molecular Dynamics, Computational Molecular Dynamics: Challenges, Methods, Ideas, Springer, Berlin, Heidelberg, 1999, pp. 39–65 Search PubMed.
- F. Liscio, S. Milita, C. Albonetti, P. D'Angelo, A. Guagliardi, N. Masciocchi, R. G. D. Valle, E. Venuti, A. Brillante and F. Biscarini, Structure and morphology of PDI8-CN2 for n-type thin-film transistors, Adv. Funct. Mater., 2012, 22, 943–953 CrossRef CAS.
- F. Liscio, C. Albonetti, K. Broch, A. Shehu, S. D. Quiroga, L. Ferlauto, C. Frank, S. Kowarik, R. Nervo and A. Gerlach, et al., Molecular reorganization in organic field-effect transistors and its effect on two-dimensional charge transport pathways, ACS Nano, 2013, 7, 1257–1264 CrossRef CAS.
- J. Krug, Origins of scale invariance in growth processes, Adv. Phys., 1997, 46, 139–282 CrossRef CAS.
- F. Thiel, L. Schimansky-Geier and I. M. Sokolov, Anomalous diffusion in run-and-tumble motion, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 021117 CrossRef PubMed.
- T. R. Walsh, An ab initio study of the low energy structures of the naphthalene dimer, Chem. Phys. Lett., 2002, 363, 45–51 CrossRef CAS.
- F. Family, Dynamic scaling and phase transitions in interface growth, Phys. A, 1990, 168, 561–580 CrossRef.
- D. A. Kessler, H. Levine and L. M. Sander, Molecular-beam epitaxial growth and surface diffusion, Phys. Rev. Lett., 1992, 69, 100 CrossRef PubMed.
- H. Yan, Kinetic growth with surface diffusion: The scaling aspect, Phys. Rev. Lett., 1992, 68, 3048–3051 CrossRef CAS PubMed.
- G. W. Collins, S. A. Letts, E. M. Fearon, R. L. Mceachern and T. P. Bernat, Surface roughness scaling of plasma polymer films, Phys. Rev. Lett., 1994, 73, 708–711 CrossRef CAS PubMed.
- N. Kleppmann, F. Schreiber and S. H. L. Klapp, Limits of size scalability of diffusion and growth: Atoms versus molecules versus colloids, Phys. Rev. E, 2017, 95, 20801 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2mh00854h |
| ‡ Contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2022 |