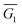Quantum interference dependence on molecular configurations for cross-conjugated systems in single-molecule junctions

Abstract

We report a combined experimental and computational study of seven cross-conjugated enediyne derivatives functionalised with a pendant group (diphenyl, 9-fluorenyl, 9-thioxanthene or cyclohexyl) at the central alkene site, and with thiomethyl (SMe) or thioacetate, as protected thiol, (SAc) groups as anchors. Measurements of the conductance (G) and Seebeck coefficient (S) of gold|single-molecule|gold junctions were obtained using a modified scanning tunnelling microscope-break junction (STM-BJ) technique. It is shown that most of the molecules give multiple conductance plateaus ascribed to different molecular configurations inside the junction. The higher conductance plateaus are consistent with the aryl pendant units interacting with one of the gold electrodes, thereby circumventing transmission of electrons through the enediyne system; the lower conductance plateaus are consistent with anchoring of both of the terminal SMe or S units to the electrodes. Most of the compounds show a positive value of S in the range 3.7–12.7 μV K⁻¹ indicating electronic transport through the HOMO, while one of them presents a negative value of S (−6.2 μV K⁻¹) indicating a predominance of the LUMO in the electronic transport. Theoretical calculations using density functional theory show a destructive quantum interference (DQI) feature in the gap between the highest occupied and lowest unoccupied molecular orbitals (the HOMO–LUMO gap) for the lower conductance plateaus, supporting the trends observed in the experimental data.

---

Design, System, Application

Thermoelectric materials have potential applications as large-area, flexible thermogenerators and Peltier coolers. Compared to traditional inorganic thermoelectric materials, organic counterparts are abundant, more environmentally friendly and can be processed from solution using low-temperature, high-throughput, lower-cost conditions. An efficient thermoelectric material should have a large Seebeck coefficient S, high electrical conductance G and low thermal conductivity κ. However, for organic molecules this combination of properties is difficult to obtain requiring optimised design of the molecular backbone, the anchor groups and the pendant groups. For example, the extent of π-electron conjugation in the molecular backbone can determine quantum interference effects which enhance or suppress conductance. The general utility of the present work lies in extending the range of molecules and conduction mechanisms that can be exploited to control thermoelectric properties. Measurements of the conductance and Seebeck coefficient of gold|single-molecule|gold junctions comprising enediyne molecules show that most of the molecules give multiple conductance plateaus ascribed to different molecular configurations inside the junction, which depend on the structure of the pendant groups. Theoretical calculations probe quantum interference features in the assembled system, supporting the trends observed in the experimental data. The application potential lies in the development of new organic thermoelectric materials.

Introduction

Experimental and theoretical studies of charge transport through single-molecules bridging two metallic electrodes (molecular junctions) are of fundamental importance in the development of molecular electronic devices such as switches, diodes, transistors, sensors and thermoelectric generators.^1–5 It is well established that the molecular backbone, the anchor groups and the pendant groups all play important roles in the molecular design in order to enhance electrical and thermoelectrical properties.^6–8 The extent of π-electron conjugation in the backbone is a crucial feature in determining the electronic properties of the device.^9,10 The tunnelling of an electron through the orbitals localised on the molecules can be described in terms of quantum interference (QI)¹¹ which can enhance or suppress conductance.^12,13

Research into organic thermoelectric materials is a rapidly expanding topic, driven by their potential applications as large-area, flexible thermogenerators and Peltier coolers. For many years, inorganic materials, such as Bi₂Te₃ and related compounds, have set the thermoelectric performance standards.¹⁴ However, they are brittle, toxic and require high temperatures to process. In contrast, organic thermoelectric materials are abundant, more environmentally friendly and can be processed from solution using low-temperature, high-throughput, lower-cost conditions.¹⁵ An efficient thermoelectric material should have a large Seebeck coefficient S, high electrical conductance G and low thermal conductivity κ. It has been shown that destructive quantum interference (DQI) creates an anti-resonance close to the Fermi energy (E_F),¹¹ leading to an increase in the value of S but compromising the enhancement of G. DQI is expected to appear for different molecular configurations, for example the meta connection of the anchoring groups or backbones^16,17 mechanosensitive molecules¹⁸ or specific π-conjugation pathways, as in cross-conjugated systems.^19,20

Y-shaped enediynes are classical cross-conjugated systems and their electronic and optical properties have been studied in previous reports.^21–25 We now present a combined experimental and theoretical study of seven cross-conjugated enediyne molecules (1–4) incorporating four different pendant groups (diphenyl, 9-fluorenyl, 9-thioxanthene or cyclohexyl) and two different anchor groups, thiomethyl (SMe) and thioacetate (SAc) as protected thiol groups that serve to assemble the molecules in gold|single-molecule|gold junctions. Note that the SAc gets deprotected once the molecule is deposited on the sample, by converting this anchor group into a thiol. The pendant groups diphenyl, 9-fluorenyl, 9-thioxanthene were chosen to provide variation in both the conjugation (and therefore energy) and rigidity of the pendant groups with the cyclohexyl group used as a non-conjugated reference. The results of scanning tunneling microscope-break junction (STM-BJ) experiments and density functional theory (DFT) calculations show the importance of these structural elements in tuning the values of the conductance and the Seebeck coefficient of the single-molecule junctions.

Molecule synthesis

Two series of cross-conjugated enediynes with anchor groups were synthesised with diphenyl, fluorene, and thioxanthene as aromatic pendant groups (Fig. 1). The thiomethyl anchored series (1a–3a) was synthesised using a modification of Treitel's approach²⁶ involving a Sonogashira coupling between the respective diaryl-2,2-dibromoethylene and 4-ethynylthioanisole. The thioacetate anchored compounds (1b–3b) were synthesised in an analogous fashion using (2-((4-ethynylphenyl)thio)ethyl)trimethylsilane as the alkyne to produce the ethyltrimethylsilane protected thiols that were, in turn, deprotected by tetrabutylammonium fluoride and treated with acetyl chloride to produce the thioacetate compounds. Compound 4 with a pendant cyclohexyl unit was prepared by a Sonogashira coupling between penta-1,4-diyn-3-ylidenecyclohexane and 4-iodothioanisole. 4 was chosen to exclude the possibility of the pendant aromatic group anchoring to one of the electrodes. The detailed procedures for the synthesis of compounds 1–4 are reported in the ESI,† along with their characterization by NMR spectroscopy, mass spectrometry and elemental analysis, including the single-crystal X-ray structure of 2a.

Fig. 1 Structures of compounds 1a–4 and 1b–3b used in this study.

Quantum transport measurements

G and S measurements of molecular junctions formed with compounds 1a–3a, 1b–3b and 4 were performed using a modified home-built scanning tunnelling microscope (STM) at ambient conditions and room temperature using the STM-BJ technique.²⁷ With this technique, the sample is contacted with the STM tip and, when the tip is retracted, atomic Au contacts form before the metallic contact breaks and a molecule may be trapped between both electrodes, forming a molecular junction. By recording the current during this whole process, current–distance (IZ) curves are obtained, showing a plateau in G values as a signature of molecular junction formation. G characterization was performed by collecting thousands of IZ traces and eliminating those without a clear molecular plateau by using a non-supervised clustering technique.^28,29

The 1D G histograms of the resulting IZ curves for 1a–3a and 1b–3b, performed with a V_bias = 100 mV, (shown in black in Fig. 2d–i) in general present multiple peaks, corresponding to different molecular configurations in the junction. We used the clustering technique to separate the traces corresponding to the different molecular configurations, grouping them in separate clusters. For all molecules except for 2a, two clusters (C₁ and C₂) were found, consisting in traces with a low- and a high-conductance plateaus. 2D histograms of G vs. distance (Z) of the compound 1a for all the traces and for the separated clusters C₁ and C₂ are shown in Fig. 2a–c, respectively, an example of individual IZ traces of C₁ and C₂ is included in black on top of the histograms. The corresponding 1D G histogram of each cluster is represented in Fig. 2d–i in red (C₁) and blue (C₂). Using a Gaussian fit we find the mean conductance value in each case, given in Fig. 2d–i as and .

Fig. 2 2D histograms of G vs. distance (Z) of molecule 1a, (a) all the traces, (b) cluster C₁ and (c) cluster C₂. A representative example of an individual trace (black line) is included in the corresponding 2D histogram for C₁ and C₂. (d–i) Conductance histograms for compounds 1a–3a (d–f), and 1b–3b (g–i), built with all the IZ traces with a molecular plateau (black). Red and blue lines represent the corresponding histograms for clusters C₁ and C₂; and are the corresponding mean values. The percentage of traces included in each cluster is given in the legend.

Considering the series with SMe anchor groups (Fig. 2d–f), compounds 1a and 3a present two clusters while in contrast, compound 2a exhibits only one cluster. To get further insight into the molecular configuration, we analysed the apparent stretching lengths (L_s)³⁰ of each cluster (see ESI† for further details and Table S3† for the values), and we found that C₁ of molecule 2a has a similar L_s as C₁ of molecules 1a and 3a, suggesting a similar molecular configuration with a slightly higher conductance in the case of 2a. Regarding the series with thiol anchor groups (1b, 2b and 3b) (Fig. 2g–i), similar mean conductance values both for and indicate a small effect of the pendant groups in the conductance of this series. Comparing L_s of all the compounds with two clusters (see Table S3†), we observe larger values in the case of the low-conductance cluster C₁. For this cluster the conductance values are lower and apparent molecular lengths are smaller in the case of compounds with SMe anchor groups compared with those with thiol anchor groups, in agreement with previously reported results.³¹

Fig. 3 Seebeck coefficient (S) of compounds 1a–3a (a–c), and 1b–3b (d–f). Linear regressions of all V_thvs. ΔT data points included in C₁ and C₂ (blue and red, respectively), separated using the clustering technique. Seebeck coefficients, obtained from the slope of the regressions, are given in each panel. Empty circles and error bars represent the mean value and standard deviation from a Gaussian fit to each set of V_th data measured for a given ΔT.

Complementary measurements of G for compound 4 (Fig. S24 of ESI†) showed a single low-conductance peak around 10⁻⁵G₀. Since the cyclohexyl pendant group of 4 would not be expected to interact with the electrodes, this result suggests that the formation of the high-conductance plateaus for the other compounds (1a–3a, and 1b–3b) is due to the interaction of the aromatic pendant groups with one of the electrodes.

To characterize the Seebeck coefficient, a temperature difference was established between the tip and the sample (ΔT) by heating up a 1 kΩ resistor placed onto the tip support and maintaining the sample at ambient temperature. While an IZ curve is performed, the thermoelectric response of the molecular junctions is measured using small current–voltage (IV) ramps of ±10 mV. G and the thermovoltage (V_th) can be simultaneously recorded from the slope and zero crossing point of each individual IV trace, respectively (see ESI† for more information). Measurements with different ΔT were performed to obtain a more robust statistical analysis. Note that the low-conductance values in C₁ of molecules 1a and 3a prevented a measurement of the V_th of this configuration.

Applying the above-mentioned clustering technique, the measured V_th values were separated into clusters C₁ and C₂, based on the IZ traces. The Seebeck coefficient of each cluster was then obtained from the slope of the linear regression of all V_thvs. ΔT points, as shown in Fig. 3, in red and blue for C₁ and C₂, respectively.

The difference between the S values of C₁ and C₂ for molecules with thiol anchor groups (1b–3b) (in Fig. 3d–f) reveals the small effect of these two different junction configurations on the thermopower. However, the different S values from molecule to molecule show the key role played by the pendant groups, with S of C₁ of 3b approximately 2.3 times larger than the value of 1b, for example. In contrast, the measured S values for compounds 1a and 3a (which have SMe anchor groups) are very similar (Fig. 3a and c), reflecting a smaller effect of the pendant groups.

The positive sign of S for all molecules, except 2a, indicates transport mainly through the HOMO.⁷ The negative sign of S for 2a is a signature of LUMO predominance in the electronic transport, as previously reported for SMe anchor groups.^16,32

To get further insight into the molecular configurations in the junction and the origin of the different signs of S for the different clusters we performed quantum transport calculations.

Theoretical calculations

The density functional code SIESTA³³ and transport code GOLLUM³⁴ were used to calculate the conductance and Seebeck coefficients of the molecules. First, the optimum geometry of each molecule was found and then the molecule was attached to gold electrodes. Assuming both types of anchor groups (SMe and thiol) attach to a surface adatom, two different binding configurations were investigated, namely, with one anchor group connected to each electrode (configuration 1) or with both anchor groups connected to the same electrode (configuration 2) (see Fig. 4a and b). This second configuration was considered based on the ‘bent’ backbone of the compounds.

Fig. 4 a) Molecular junction configuration 1, with one anchor group connected to each electrode, with tilt angle (θ = 40°) and rotation angle (Φ = 0°) for compound 1a. b) Molecular junction configuration 2, with both anchor groups connected to the same electrode, for compound 1a. c) Optimum binding geometry of compound 1a for configuration 1 with θ = 40° and Φ = 60°. d) Binding energy (E_Bind) of 1a on gold(111) surface as a function of rotation angle Φ for tilt angles θ between 0 and 50°.

Considering configuration 1, the optimal binding geometry with respect to the binding energy was calculated as a function of two different parameters, in addition to the Au–S distance (which was found to be 2.3 Å for S and 2.4 Å for SMe). These parameters are: (i) the tilt angle θ and (ii) the rotation about the axis of the molecule Φ (Fig. 4a). For example, in the case of a tilt angle of 90°, at Φ = 0° the molecule would lie parallel to the gold surface. The binding energy E_Bind of molecule 1a was then evaluated for these parameters in Fig. 4d which shows that as the molecule is tilted (θ > 20°) the binding energy increases in magnitude as the value of Φ is increased; this is due to the increased interaction between the pendant group and the gold surface. In the case of 1a the optimum binding geometry is θ = 40° and Φ = 60° with a binding energy of −0.92 eV. The binding energy of molecules 2–4 and 1–3b shows similar trends (Fig. S34–S40†).

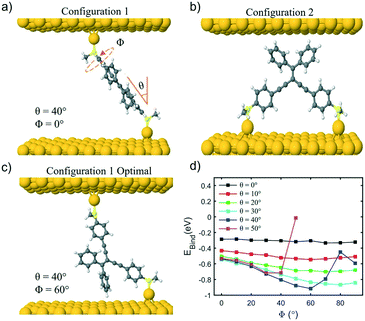
Cross-conjugation has been shown to lead to quantum interference in molecular junctions³⁵ and typically leads to destructive quantum interference (DQI) features. One simple method to determine the nature of the interference is the orbital product rule³⁶ which predicts that destructive interference will occur when the orbital products of the contact site have the same sign for the HOMO and LUMO, and constructive interference will occur when they have the opposite sign. The HOMO and LUMO of all compounds are shown in Fig. S27–S33 of ESI† (the sign of the wave function is denoted blue for negative, red for positive) and the wavefunction on both the contact atoms has the same sign, for both HOMO and LUMO, so the product is always positive, indicating destructive interference.

The electron transport through molecule 1a was then calculated to see if a DQI feature occurs. Fig. 5a and b shows the transmission coefficient T(E) for two different tilt angles (θ = 20° and 40°). In the case of θ = 20° the transmission shows a DQI feature in the HOMO–LUMO gap as predicted by the orbital product rule. Changing the rotation angle Φ at this tilt angle has only a small effect on the transmission. At a tilt angle of θ = 40° the transmission shows a DQI feature for Φ = 0°, at this rotation angle the pendant group is parallel to the gold surface (Fig. 4a) and so there is only a weak interaction between them. As the molecule is rotated the DQI feature in the transmission is suppressed (Φ > 60°); this is due to the increased interaction between the pendant group and the gold surface which causes the orbital product rule to break down as there are now multiple contact sites between the gold surface and the molecule. Fig. S41–S47† show the same general trend for molecules 1a, 2a, 4 and 1b–3b.

Fig. 5 Zero-bias transmission coefficient T(E) of 1a for values of Φ between 0 and 90°, for configuration 1, at tilt angle θ = 20° (a) and θ = 40° (b). (c) Zero-bias transmission coefficient T(E) of 1a for configuration 2.

The fact that the binding energy increases when the pendant group interacts with the gold suggests a contact geometry where the top electrode is attached to this substituent as shown in Fig. 4b (the so-called configuration 2). The optimum binding distance between the flat surface of the lead and the pendant group of 1a was calculated, then the transmission was calculated as shown in Fig. 5c (see Fig. S48–S52† for the corresponding transmissions for configuration 2 of compounds 2a–3a and 1b–3b; the cyclohexyl group of 4 is assumed not to bind to the gold surface). The transmission was found to be larger for configuration 2 than for configuration 1 in all cases and, together with the optimum binding energies, this allows us to associate molecular configuration 1 to cluster C₁ and configuration 2 to cluster C₂ (based on the experimental conductance and L_s values for each compound). The theoretical distance between the electrodes for configuration 1 and configuration 2 (Table S6†) follows the trends of the clusters C₁ and C₂ (Table S4†) with the separation of configuration 1 being larger than that of configuration 2.

The values of G and S of all compounds for configuration 1 were then evaluated (see Fig. S48–S54†) for several values of Φ and θ and at two values of the Fermi energy, namely, E_F⁰ and E_F¹, where E_F⁰ is the DFT predicted Fermi energy and E_F¹ is chosen to give the best agreement with the magnitude of the measured values. This correction is applied because the alignment of the frontier molecular energy levels in the junction relative to E_F⁰ can show significant errors in DFT.^37,38 For the SMe anchor groups (compounds 1a–4) the Fermi energy was chosen to be E_F¹ = E_F⁰ − 0.5 eV and for the S anchor (compounds 1b–3b), E_F¹ = E_F⁰ + 0.4 eV. Table 1 shows the comparison between experiment and theory for all the molecules studied, considering these values of E_F¹ (also applied to the transmissions of configuration 2). In general, G and S values show similar trends, however the differences in magnitude could be due to experimental conditions that have not been included in the theoretical model such as the junction environment. In the case of 2a the negative value of S can be attributed to the lower lying LUMO level for this molecule; the equivalent is not found for molecule 2b as the S anchors pin the HOMO resonance to the Fermi energy³⁹ Overall, the relatively small values of S observed in these molecules can be explained by the interaction of the pendant group with one of the gold electrodes suppressing the DQI feature which causes the high value of S at low tilt angles, as previously discussed.

Table 1 Comparison of the experimental and theoretical values for the conductance G and Seebeck coefficient S

Compound	log G1(G0)		log G2(G0)		S 1 (μV K^−1)		S 2 (μV K^−1)
	Exp	Theo	Exp	Theo	Exp	Theo	Exp	Theo
1a	−5.3	−4.2	−3.5	−3.9		5.1	4.2	3.0
2a	−4.9	−4.5		−3.7	−6.2	−10.2		−6.5
3a	−5.3	−4.2	−3.8	−3.5		4.1	5.1	4.3
4	−5.0	−5.2				5.7
1b	−4.9	−4.4	−3.7	−3.2	3.7	3.8	5.6	35.5
2b	−4.9	−4.0	−3.5	−3.2	8.3	11.5	5.0	23.0
3b	−4.9	−3.7	−3.5	−3.0	11.6	5.8	12.7	31.4

---

Finally, to explore the possibility of having fully stretched molecules in the junction, complementary conductance measurements with a bias voltage of 600 mV were also performed, allowing us to reach lower conductance ranges. Using again the clustering technique, for compounds 1a–3a we were able to identify only the clusters observed with 100 mV bias voltage (i.e., C₁ and C₂) while for molecules 1b–3b a third cluster, C₃, was also observed (see Fig. S25 of the ESI†). This new cluster presents a lower conductance mean value () and longer L_s than C₁ and C₂ (see Table S4 of the ESI†). This suggests that the molecular configuration in these cases might be, indeed, a completely stretched one, without interaction between the pendant groups and the electrodes. This is also in agreement with the theoretical G values for small tilt angles, which in the case of compounds 1b–3b (Fig. S55–S59†) is at least an order of magnitude lower than the value for configuration 1.

Conclusions

In summary, we have synthesized seven cross-conjugated enediyne derivatives that are functionalised with a pendant group (diphenyl, 9-fluorenyl, 9-thioxanthene or cyclohexyl) at the central alkene site, and with thiomethyl (SMe) or SAc (as protected thiol) groups attached as anchors. Their single-molecule conductance and Seebeck coefficient have been measured by STM-BJ techniques and corresponding theoretical calculations have been performed using DFT. Notably, two different conductance plateaus are observed for all the studied compounds, except for 2a. The high-conductance plateaus are consistent with anchoring of both of the terminal SMe or thiol units to a single gold electrode and the aryl pendant units interacting with the other electrode, thereby avoiding transmission of electrons through the enediyne system. On the other hand, the low-conductance plateaus are consistent with anchoring of one terminal SMe or thiol units to each electrode – a configuration that may lead to a destructive quantum interference (DQI) feature in the HOMO–LUMO gap, depending on the rotation angle of the molecule. The small difference between S of the different conductance plateaus suggests the suppression of the DQI in these molecular junctions as a consequence of the interaction of the pendant groups with the electrodes. Compound 2a with SMe anchors groups presents a different behavior in all the measurements, showing only a single plateau, with a conductance value and apparent stretching length consistent with the configuration with one terminal unit anchored to each electrode. Additionally, 2a shows a negative S value, indicating a LUMO predominance in the electronic transport; all the other compounds give a positive S value indicating HOMO-dominated transport. Overall, this study sheds new light on the range of molecules and mechanisms that can be exploited to control the Seebeck coefficient in single molecules, representing a step towards producing highly efficient thin-film thermoelectric devices for practical applications.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

J. H.-G., R. D., L. R.-G., C. J. L., M. R. B., and N. A. acknowledge funding from EC H2020 FET Open project grant agreement number 767187 “QuIET”. N. A. and L. R.-G. acknowledge funding from the Education and Research Council of the Comunidad de Madrid and the European Social Fund (ref. PEJD-2019-POST/IND-16353). N. A. acknowledge funding from the Comunidad de Madrid NANOMAGCOST-CM (P2018/NMT-4321) and from the Spanish Ministry of Science and Innovation, through grants MAT201788693-R and the “María de Maeztu” Programme for Units of Excellence in R&D (CEX2018-000805-M).

Notes and references

1. R. J. Nichols and S. J. Higgins, Annu. Rev. Anal. Chem., 2015, 8, 389–417.
2. P. T. Mathew and F. Fang, Engineering, 2018, 4, 760–771.
3. D. Xiang, X. Wang, C. Jia, T. Lee and X. Guo, Chem. Rev., 2016, 116, 4318–4440.
4. T. A. Su, M. Neupane, M. L. Steigerwald, L. Venkataraman and C. Nuckolls, Nat. Rev. Mater., 2016, 1, 16002.
5. J. Cuevas and E. Scheer, Molecular Electronics: An Introduction to Theory and Experiment, World Scientific, 2nd edn, 2017.
6. W. B. Chang, C. K. Mai, M. Kotiuga, J. B. Neaton, G. C. Bazan and R. A. Segalman, Chem. Mater., 2014, 26, 7229–7235.
7. L. Rincón-García, C. Evangeli, G. Rubio-Bollinger and N. Agraït, Chem. Soc. Rev., 2016, 45, 4285–4306.
8. L. Rincón-García, A. K. Ismael, C. Evangeli, I. Grace, G. Rubio-Bollinger, K. Porfyrakis, N. Agraït and C. J. Lambert, Nat. Mater., 2016, 15, 289–293.
9. L. J. O'Driscoll and M. R. Bryce, Nanoscale, 2021, 13, 10668–10711.
10. H. Valkenier, C. M. Guédon, T. Markussen, K. S. Thygesen, S. J. van der Molen and J. C. Hummelen, Phys. Chem. Chem. Phys., 2014, 16, 653–662.
11. C. J. Lambert, Chem. Soc. Rev., 2015, 44, 875–888.
12. D. M. Cardamone, C. A. Stafford and S. Mazumdar, Nano Lett., 2006, 6, 2422–2426.
13. X. Li, Z. Tan, X. Huang, J. Bai, J. Liu and W. Hong, J. Mater. Chem. C, 2019, 7, 12790–12808.
14. J. Wei, L. Yang, Z. Ma, P. Song, M. Zhang, J. Ma, F. Yang and X. Wang, J. Mater. Sci., 2020, 55, 12642–12704.
15. M. Lindorf, K. A. Mazzio, J. Pflaum, K. Nielsch, W. Brütting and M. Albrecht, J. Mater. Chem. A, 2020, 8, 7495–7507.
16. G. Yzambart, L. Rincón-García, A. A. Al-Jobory, A. K. Ismael, G. Rubio-Bollinger, C. J. Lambert, N. Agraït and M. R. Bryce, J. Phys. Chem. C, 2018, 122, 27198–27204.
17. I. M. Grace, G. Olsen, J. Hurtado-Gallego, L. Rincón-Garciá, G. Rubio-Bollinger, M. R. Bryce, N. Agraït and C. J. Lambert, Nanoscale, 2020, 12, 14682–14688.
18. D. Stefani, K. J. Weiland, M. Skripnik, C. Hsu, M. L. Perrin, M. Mayor, F. Pauly and H. S. J. van der Zant, Nano Lett., 2018, 18, 5981–5988.
19. A. Alanazy, E. Leary, T. Kobatake, S. Sangtarash, M. T. González, H. W. Jiang, G. R. Bollinger, N. Agräit, H. Sadeghi, I. Grace, S. J. Higgins, H. L. Anderson, R. J. Nichols and C. J. Lambert, Nanoscale, 2019, 11, 13720–13724.
20. S. Medina Rivero, P. García Arroyo, L. Li, S. Gunasekaran, T. Stuyver, M. J. Mancheño, M. Alonso, L. Venkataraman, J. L. Segura and J. Casado, Chem. Commun., 2021, 57, 591–594.
21. M. A. Christensen, E. A. della Pia, J. Houmøller, S. Thomsen, M. Wanko, A. D. Bond, A. Rubio, S. Brøndsted Nielsen and M. Brøndsted Nielsen, Eur. J. Org. Chem., 2014, 2014, 2044–2052.
22. L. O. Jones, M. A. Mosquera, B. Fu, G. C. Schatz, T. J. Marks and M. A. Ratner, Nano Lett., 2019, 19, 8956–8963.
23. D. Q. Andrews, G. C. Solomon, R. P. van Duyne and M. A. Ratner, J. Am. Chem. Soc., 2008, 130, 17309–17319.
24. A. Singh, A. K. Pati and A. K. Mishra, Phys. Chem. Chem. Phys., 2018, 20, 14889–14898.
25. A. A. Kocherzhenko, L. D. A. Siebbeles and F. C. Grozema, J. Phys. Chem. Lett., 2011, 2, 1753–1756.
26. N. Treitel, L. Eshdat, T. Sheradsky, P. M. Donovan, R. R. Tykwinski, L. T. Scott, H. Hopf and M. Rabinovitz, J. Am. Chem. Soc., 2006, 128, 4703–4709.
27. C. Evangeli, K. Gillemot, E. Leary, M. T. González, G. Rubio-Bollinger, C. J. Lambert and N. Agraït, Nano Lett., 2013, 13, 2141–2145.
28. L. A. Zotti, B. Bednarz, J. Hurtado-Gallego, D. Cabosart, G. Rubio-Bollinger, N. Agrait and H. S. J. van der Zant, Biomolecules, 2019, 9, 580–592.
29. D. Cabosart, M. el Abbassi, D. Stefani, R. Frisenda, M. Calame, H. S. J. van der Zant and M. L. Perrin, Appl. Phys. Lett., 2019, 114, 143102.
30. C. R. Arroyo, E. Leary, A. Castellanos-Gómez, G. Rubio-Bollinger, M. T. González and N. Agraït, J. Am. Chem. Soc., 2011, 133, 14313–14319.
31. R. Frisenda, S. Tarkuç, E. Galán, M. L. Perrin, R. Eelkema, F. C. Grozema and H. S. J. van der Zant, Beilstein J. Nanotechnol., 2015, 6, 1558–1567.
32. A. Ismael, X. Wang, T. L. R. Bennett, L. A. Wilkinson, B. J. Robinson, N. J. Long, L. F. Cohen and C. J. Lambert, Chem. Sci., 2020, 11, 6836–6841.
33. J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745–2779.
34. J. Ferrer, C. J. Lambert, V. M. García-Suárez, D. Z. Manrique, D. Visontai, L. Oroszlany, R. Rodríguez-Ferradás, I. Grace, S. W. D. Bailey, K. Gillemot, H. Sadeghi and L. A. Algharagholy, New J. Phys., 2014, 16, 093029.
35. L. J. O'Driscoll and M. R. Bryce, Nanoscale, 2021, 13, 1103–1123.
36. C. J. Lambert and S. X. Liu, Chem. – Eur. J., 2018, 24, 4193–4201.
37. J. B. Neaton, M. S. Hybertsen and S. G. Louie, Phys. Rev. Lett., 2006, 97, 216405.
38. S. Y. Quek, L. Venkataraman, H. J. Choi, S. G. Louie, M. S. Hybertsen and J. B. Neaton, Nano Lett., 2007, 7, 3477–3482.
39. R. Stadler and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 161405.

---

Footnotes

† Electronic supplementary information (ESI) available. CCDC 2141972. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2me00074a

‡ Juan Hurtado-Gallego, Ross Davidson and Iain M. Grace contributed equally.

---