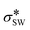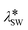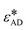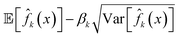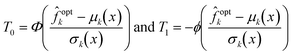Open Access Article
Open Access ArticleBayesian optimization for material discovery processes with noise†‡
Sanket
Diwale
 a,
Maximilian K.
Eisner
a,
Maximilian K.
Eisner
 b,
Corinne
Carpenter
a,
Weike
Sun
a,
Gregory C.
Rutledge
*a and
Richard D.
Braatz
b,
Corinne
Carpenter
a,
Weike
Sun
a,
Gregory C.
Rutledge
*a and
Richard D.
Braatz
 *a
*a
aDepartment of Chemical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139 USA. E-mail: rutledge@mit.edu; braatz@mit.edu
bDepartment of Electrical and Computer Engineering, Technical University of Munich, 80333 Munich, Germany
First published on 7th March 2022
Abstract
An augmented Bayesian optimization approach is presented for materials discovery with noisy and unreliable measurements. A challenging non-Gaussian, non-sub-Gaussian noise process is used as a case study for the discovery of additives for the promotion of nucleation of polyethylene crystals. NEMD (non-equilibrium molecular dynamics) data are used to validate and characterize the statistical outcomes of the candidate additives and the Bayesian optimization performance. The discovered candidates show nearly optimal performance for silicon for the class of tetrahedrally coordinated crystals and a material similar to graphene but more compliant for the class of hexagonally coordinated crystals. The Bayesian approach using a noise-augmented acquisition function and batched sampling shows a sub-σ level of median accuracy and an improved robustness against noise.
Design, System, ApplicationThe work addresses the data-driven discovery of materials using molecular dynamics and Bayesian optimization. Molecular dynamics provide an inherently stochastic environment for statistical characterization of material properties in simulation. However, the computational cost of such simulations makes it prohibitively expensive to include directly in an iterative learning or optimization scheme. Bayesian optimization addresses this challenge by providing a near-optimal strategy for minimizing the number of iterations required for such a data-driven scheme. We also use a united atomic force field model for material candidates that allows a low-dimensional parametric search space to be used both for molecular simulations and the Bayesian optimization scheme. A polymer melt crystallization process using nucleating agents serves as a case study for the materials discovery problem. A search for agents maximizing the expected nucleation rate is conducted using the Bayesian optimization scheme. A significant challenge in applying Bayesian optimization to noisy processes is that noise can behave as an adversary to the optimization scheme and lead to loss of convergence or significant performance degradation. The work presents a method to augment the Bayesian optimization scheme in the presence of such noise to improve convergence and robustness properties. When applied to the polymer crystallization problem, the algorithm shows a median convergence error of less than one standard deviation of the noise and a worst-case error of less than three standard deviations. A search within a class of tetrahedral nucleating agents suggests a close to optimal performance for silicon. In contrast, a search within a class of hexagonal agents shows that a crystal similar but more compliant than graphene would provide an optimal nucleation rate for polyethylene nucleation. |
1 Introduction
Global competitiveness in advanced materials depends on shortening the development cycles for the discovery of new materials. Given the vast monetary and time cost associated with experimental characterization and empirical discovery of new materials, data-driven and simulation-based techniques allow for the rapid discovery and development of promising new material candidates.Molecular simulations and finite-element methods have long been used for gaining insights into the characteristics and formation mechanics of new material candidates. Embedding these simulations within iterative learning and optimization schemes allows for a computational and data-driven approach to the discovery of new materials. This direct approach, however, faces several challenges.
Firstly, material formation mechanics are inherently stochastic, and thus multiple (stochastic) molecular simulations are required to obtain statistical material characteristics with sufficiently high confidence. Secondly, each molecular simulation incurs a high computational cost and can take anywhere from a few hours to a few days. Embedding such a simulation directly into an iterative learning or optimization scheme can become prohibitively expensive.
Another challenge posed from the numerical optimization perspective is that the number of potential degrees of freedom that define the class of potential molecular formulations is large and include both continuous and discrete variables. These optimizations become especially challenging to solve when the molecular simulations and the resulting objective functions are inherently stochastic. We show in this work that an atomic force field model can be effectively used to parameterize the search space for materials and used with a Bayesian optimization scheme to minimize the number of experiments or simulations required for a materials discovery problem in the presence of noise.
Bayesian optimization addresses the challenges of experimental sample minimization and noise modeling by using a stochastic model to assign information-theoretic value and confidence to the acquired experimental samples. A simultaneous learning and optimization approach is taken to address the exploration-exploitation tradeoff to minimize the number of samples required to discover optimal candidates reliably.
The work in Bayesian optimization may be divided into two parts. The first part considers optimization with noise-free observations of the objective values.1–6 The second considers optimization in the presence of noisy observations.7–17
The primary role of Bayesian uncertainty in such optimization algorithms is to serve as a surrogate for the information-theoretic uncertainty induced by the lack of observed data in the search space. The surrogate allows for the development of decision rules for sampling the objective in an iterative optimization scheme to balance between exploration (to reduce information-theoretic uncertainty) and exploitation (to optimize the intended objective value in the optimization).
By acquiring new samples of data to reduce information-theoretic uncertainty, the optimization scheme progressively learns a better model for the objective function while the exploitation terms in the decision rule bias the exploration towards the regions with good objective values.
The introduction of noise in the observations is known to significantly degrade the performance in Bayesian optimization12,17 and presents an active area of research.12–17 The degradation can be attributed to the fact that the Bayesian uncertainty in the presence of noise is used for the dual purpose of representing observation noise as well as information-theoretic uncertainty. The dual use of a single uncertainty model thus creates ambiguity for the decision rules where a high uncertainty value due to noise may obscure the knowledge of high information-theoretic uncertainty, leading to inefficient exploration and the loss of convergence properties.
In recent years, Bayesian optimization has been introduced to many fields, including in robotics,7–11 software testing,12 personalized medicine,18 automated machine learning,19 reinforcement learning,20,21 and materials discovery,22–25 where noisy measurements can significantly degrade the algorithm's performance12 and thus require further algorithmic and theoretical improvements to support practical applications.
In particular, works for materials discovery using Bayesian optimization22–25 have focused on the use of Bayesian optimization algorithms designed assuming either noise-free or Gaussian noise assumptions. We present here a practical materials discovery problem example, where such noise assumptions are invalidated and result in significant performance degradation of the previously used Bayesian optimization algorithms. We further show how simple modifications to the decision rules used in the algorithm may improve the robustness of the optimization to the observed noise.
For the materials discovery problem, we consider the process of polymer (polyethylene) nucleation in the presence of a nucleating agent. The process output, given as the observed nucleation time, follows an exponential probability distribution and presents a concrete, challenging, real-world example of a non-Gaussian and non-sub-Gaussian noise process to tackle by Bayesian optimization. Such a noise process falls outside the currently explored theoretical and empirical understanding of Bayesian optimization15,26–30 that has largely focused on noise-free, Gaussian noise, and sub-Gaussian noise. We highlight some of challenges posed to Bayesian optimization by such noise, and characterize and discuss convergence when dealing with such noise. A noise-augmented approach is shown to perform with a greater degree of robustness and better convergence performance than the traditional Bayesian optimization schemes designed for noise-free or Gaussian noise scenarios.
The type of stochastic models used for Bayesian optimization can be varied and includes probabilistic graphical models,31 Bayesian neural networks,32,33 Parzen tree estimators,34 and Gaussian process models.7–11 The use of Gaussian process models in Bayesian optimization is by far the most common, owing to the decades of empirical and theoretical exploration of their properties for Bayesian optimization.15,26–30,35 Gaussian process-based optimization also empirically offers the best performance in low-dimensional parameter spaces due to the higher degrees of freedom involved in training tree- or neural network-based models.33 For this reason, Gaussian processes are used as the underlying model in this work.
In the following, section 2 describes the polymer nucleation process, and the material discovery problem addressed in this work. Section 3 briefly introduces Bayesian optimization for noisy processes and section 4 discusses theoretical aspects of the algorithm. Section 5 hosts a discussion on the acquisition functions used as a sampling decision rule to choose iterates in Bayesian optimization and introduces the generalized noise-augmented acquisition function used in this work. Section 6 presents numerical results and discussion on the application of the noisy Bayesian optimization algorithm to the materials discovery problem in polymer nucleation. Section 7 highlights some key takeaways from the work and future directions for investigation.
The results show the robustness of the proposed algorithm to a non-Gaussian noise with a median convergence error of less than one standard deviation of the noise and a worst-case error of less than three standard deviations.
2 Polymer nucleation: a case study
In polymer crystallization from melts, additives referred to as nucleating agents are used to enhance the crystalline growth rate by lowering the activation energy for nucleation and subsequent crystallization. The nucleating agent's quantity and choice directly control the degree of crystallinity and morphology introduced into the polymer. The agent's effect in crystalline growth is characterized by the nucleation time (also called the induction time τ) that denotes the time instant at which heterogeneous nucleation occurs at the interface between the nucleating agent and the polymer precursor. The induction time at such an interface follows an exponential-like probability distribution36 of the form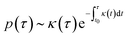 | (1) |
Under the simplifying assumption of time-invariant temperature and nucleation rate κ, (1) simplifies to a standard exponential distribution,
| p(τ) ∼ κe−κτ, | (2) |
The nucleation rate for a particular agent depends on its physical and chemical properties and has been studied for n-alkanes for tetrahedrally coordinated agents like silicon37 and for graphene-like materials.38 A united-atom force field (UAFF) model has been used37,38 to study the dependence of κ and the induction time on four parametric properties of nucleating agents:
1. σSW, the atomic diameter of the agent
2. εSW, the depth of two-body interaction potential
3. λSW, relative strength of three body interactions
4. εAD, the depth of interaction potential between the agent and crystallizing material.
The first three parameters refer to the Stillinger–Weber (SW) potential39 used to model the nucleating agent, where σSW provides a length scale, εSW is a cohesive energy scale, and εAD is an adhesive energy scale between the nucleating agent and the polymer. These properties are readily available for reference materials such as graphene and silicon from the literature, which have been used to normalize parameter values with respect to reference materials.37,38 We denote normalized values with a * superscript.
By considering the molecular design space to be parameterized by a vector of normalized UAFF parameters,
Using NEMD data,37,38 an estimate for the response surface is constructed using an elastic learning framework40 to predict the mean induction time τmean(x) as a function of x. This modeling step is not required for the Bayesian optimization scheme. However, this step allows us to define an underlying ground truth to compare convergence results in the Bayesian optimization approach. The model also acts as an inexpensive function evaluation substitute to the significantly more expensive NEMD simulation required to make predictions for an arbitrary candidate x. Using such a substitute allows faster function evaluations and enables running several variations of the Bayesian optimization scheme for a comparative study of their properties in a pragmatic time frame. In a real application, when such a comparative study of variants is not intended, the function evaluations would be directly computed from the output of the expensive NEMD run.
The elastic net provides an exponential indefinite quadratic model of the form (3) for the mean induction time estimate ![[small tau, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b8.gif) mean as a function of x,
mean as a function of x,
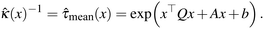 | (3) |
Bourque et al.37 restricts the data exploration to only three out of the four parameters, leaving out dependencies on 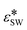 . To maintain consistency with the available NEMD data, we restrict the Bayesian optimization for the tetrahedral case to the same three parameters. Furthermore, the search space is restricted to the bounded domain of parameters considered in the NEMD data to avoid extrapolation from the data available. The bounded domain intervals are shown in Table 2.
. To maintain consistency with the available NEMD data, we restrict the Bayesian optimization for the tetrahedral case to the same three parameters. Furthermore, the search space is restricted to the bounded domain of parameters considered in the NEMD data to avoid extrapolation from the data available. The bounded domain intervals are shown in Table 2.
The mean induction time model (3) is then used with (2) to obtain an estimate for the probability distribution for induction time as a function of x. A random sample is drawn from this distribution to provide a noisy realization for the induction time measurement for a candidate x for the Bayesian optimization scheme.
In order to compare the results from Bayesian optimization to the estimate of the underlying ground truth, we run a numerical optimizer on the model (3) to find the minimizer for the mean induction time as
 | (4) |
 | (5) |
The Bayesian optimization is used in section 6 as an alternative method to find the optimal additive candidate x that minimizes the mean induction time without having the need to construct an a priori model of the form (3) or having access to an extensively gridded NEMD data set as obtained from Bourque et al.37,38 With a noisy measurement of induction times, the convergence error of the optimization scheme needs to be evaluated in relation to the variance of the measurement noise. We use the noise standard deviation at the estimated optimal candidate from (4) as a reference to compare the convergence error against. For an exponential distribution, the standard deviation is equal to the mean, and thus we assign the reference standard deviation
ση = ![[small tau, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b8.gif) optmean optmean | (6) |
The following sections describe the Bayesian optimization algorithm and its application to the noisy materials-discovery problem and the case studies described above.
3 Noisy Bayesian optimization
This section describes the Bayesian optimization approach to the noisy materials-discovery problem.Let ![[scr X, script letter X]](https://www.rsc.org/images/entities/char_e14a.gif) be a set of candidate materials, parameterized by a vector x. Let f(x) be a noisy process with an unknown distribution, which can be sampled via experiment for any given x. The Bayesian optimization seeks to find a minimizer to
be a set of candidate materials, parameterized by a vector x. Let f(x) be a noisy process with an unknown distribution, which can be sampled via experiment for any given x. The Bayesian optimization seeks to find a minimizer to
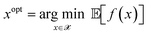 | (7) |
Since f(x) is an unknown stochastic process, a stochastic process model ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) k(x) is learned from a sampled data set of noisy observation tuples
k(x) is learned from a sampled data set of noisy observation tuples ![[scr D, script letter D]](https://www.rsc.org/images/entities/i_char_e523.gif) k = {(xi,yi): i = 1,…,k}, where yi is a noisy outcome of the distribution f(xi).
k = {(xi,yi): i = 1,…,k}, where yi is a noisy outcome of the distribution f(xi).
Several learning methods including probabilistic graphical models,31 Bayesian neural networks,32,33 Parzen tree estimators,34 and Gaussian process models7–11 have been used to construct a stochastic model ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) k(x) in Bayesian optimization. Gaussian process models are used in this work, due to the simplicity of the learning method, better empirical performance,33 and existing theoretical foundations15,26–30,35 that contextualize the convergence results.
k(x) in Bayesian optimization. Gaussian process models are used in this work, due to the simplicity of the learning method, better empirical performance,33 and existing theoretical foundations15,26–30,35 that contextualize the convergence results.
The Gaussian process model41 provides a Bayesian posterior mean and variance prediction at any query point x, conditioned on the evidence observed from the data set ![[scr D, script letter D]](https://www.rsc.org/images/entities/i_char_e523.gif) k and a prior mean function μ0(x) and prior covariance function K(xi,xj). The posterior mean prediction from the model is given by
k and a prior mean function μ0(x) and prior covariance function K(xi,xj). The posterior mean prediction from the model is given by
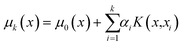 | (8) |
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) k vector,
k vector,α = [K(X,X) + σ2n![[Doublestruck I]](https://www.rsc.org/images/entities/char_e16c.gif) k]−1 (y − μ0(X)) k]−1 (y − μ0(X)) | (9) |
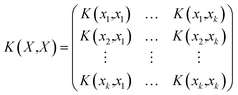 | (10) |
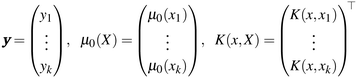 | (11) |
![[Doublestruck I]](https://www.rsc.org/images/entities/char_e16c.gif) k being an identity matrix of size k. The posterior covariance is given by
k being an identity matrix of size k. The posterior covariance is given by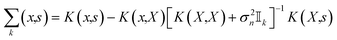 | (12) |
![[scr X, script letter X]](https://www.rsc.org/images/entities/char_e14a.gif) .
.
An additional step of selecting an optimized prior for the Gaussian process, by choosing a particular mean function μ0 and prior covariance function K within a parameterized space of mean and covariance functions, is often undertaken in Gaussian process learning, given the data set ![[scr D, script letter D]](https://www.rsc.org/images/entities/i_char_e523.gif) k. The parameters used to parameterize this space of function choices for μ0, K are called hyperparameters and are learned using a Bayesian or maximum likelihood approach.41
k. The parameters used to parameterize this space of function choices for μ0, K are called hyperparameters and are learned using a Bayesian or maximum likelihood approach.41
The optimization of hyperparameters based on ![[scr D, script letter D]](https://www.rsc.org/images/entities/i_char_e523.gif) k is, however, known to cause over-fitting problems and loss of convergence guarantees in Bayesian optimization.26,30 As a result, most Bayesian optimization schemes with convergence guarantees rely on either using fixed hyperparameters15,26 or a scheduling or error-based adaptive approach to hyperparameter selection.27–29
k is, however, known to cause over-fitting problems and loss of convergence guarantees in Bayesian optimization.26,30 As a result, most Bayesian optimization schemes with convergence guarantees rely on either using fixed hyperparameters15,26 or a scheduling or error-based adaptive approach to hyperparameter selection.27–29
The second element of Bayesian optimization is a decision rule, selecting the next batch of iterates to be sampled via experiment. Given the stochastic model ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) k, an acquisition function A(x|
k, an acquisition function A(x|![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) k) assigns a merit value to each potential sampling location x in the search space. This value is meant to trade off the value of exploring the search space against the value of exploiting current model knowledge based on
k) assigns a merit value to each potential sampling location x in the search space. This value is meant to trade off the value of exploring the search space against the value of exploiting current model knowledge based on ![[scr D, script letter D]](https://www.rsc.org/images/entities/i_char_e523.gif) k. Exploration allows finding new potential optimal candidates that the model
k. Exploration allows finding new potential optimal candidates that the model ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) k cannot yet predict due to the lack of relevant data in
k cannot yet predict due to the lack of relevant data in ![[scr D, script letter D]](https://www.rsc.org/images/entities/i_char_e523.gif) k while exploiting the existing model
k while exploiting the existing model ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) k allows choosing sample points that are most likely to provide optimal candidates within the limitations of model. Some examples of such acquisition functions are shown in Table 3 and discussed in detail in section 5.
k allows choosing sample points that are most likely to provide optimal candidates within the limitations of model. Some examples of such acquisition functions are shown in Table 3 and discussed in detail in section 5.
Let q be the batch size of candidates to be acquired at each iteration of the optimizer. The next batch of candidate samples for experiments are then selected as maximizers of the acquisition function A,
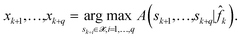 | (13) |
The sampled experimental data {(yk+i,xk+i): i = 1,…,q} acquired from the proposed candidates are appended to the data set to obtain ![[scr D, script letter D]](https://www.rsc.org/images/entities/i_char_e523.gif) k+q =
k+q = ![[scr D, script letter D]](https://www.rsc.org/images/entities/i_char_e523.gif) k ∪ {(yk+i,xk+i): i = 1,…,q} and the learned stochastic model is updated with the new data set to provide a model
k ∪ {(yk+i,xk+i): i = 1,…,q} and the learned stochastic model is updated with the new data set to provide a model ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) k+q. Estimates for the optimal value
k+q. Estimates for the optimal value ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) optk+q and optimal candidate xoptk+q are then obtained from the updated model
optk+q and optimal candidate xoptk+q are then obtained from the updated model ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) k+q within its trust region, typically chosen as the set of points where sufficient sampling has occurred. We consider the observed set of points {x1,…,xk+q} as the trust region for the model, and estimate optimal candidate as the point with the minimum expected value forthe stochastic model
k+q within its trust region, typically chosen as the set of points where sufficient sampling has occurred. We consider the observed set of points {x1,…,xk+q} as the trust region for the model, and estimate optimal candidate as the point with the minimum expected value forthe stochastic model ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) k+q,
k+q,
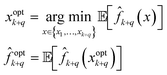 | (14) |
The updated model ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) k+q is then used to compute the next batch of candidate samples using the acquisition function as done in (13), and the iterations are repeated until convergence is detected.
k+q is then used to compute the next batch of candidate samples using the acquisition function as done in (13), and the iterations are repeated until convergence is detected.
Fig. 1 shows a flowchart for the Bayesian optimization algorithm described above with q = 1 chosen for simplicity. A termination condition (aka convergence) is said to be reached if a predefined maximum number of iterations is reached or if the maximum value for the acquisition function falls below a threshold value and no change in the optimal candidate value is observed over several iterations. The Bayesian optimization is then said to be complete, and the last updated optimal candidate xoptk+q is declared as the optimal candidate.
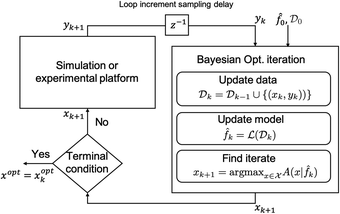 | ||
Fig. 1 Bayesian optimization flowchart. (![[script L]](https://www.rsc.org/images/entities/char_e144.gif) ( (![[scr D, script letter D]](https://www.rsc.org/images/entities/i_char_e523.gif) k) is used to denote the learning method of choice being applied to a data set k) is used to denote the learning method of choice being applied to a data set ![[scr D, script letter D]](https://www.rsc.org/images/entities/i_char_e523.gif) k). k). | ||
A few limitations to the Bayesian optimization approach may be kept in mind when designing such an algorithm. The first relates to the dimension of the search space. It is known from theory26 that near-optimal bounds for the convergence errors are on the order of 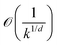 in a d-dimensional search space after k iterations of the algorithm. Thus, as the dimension of the search space d increases, the log of the error by a multiplicative factor d. This can make the application of the Bayesian optimization approach to large dimensional search spaces difficult in practice.
in a d-dimensional search space after k iterations of the algorithm. Thus, as the dimension of the search space d increases, the log of the error by a multiplicative factor d. This can make the application of the Bayesian optimization approach to large dimensional search spaces difficult in practice.
The second limitation relates to the increasing computational complexity ![[scr O, script letter O]](https://www.rsc.org/images/entities/i_char_e52e.gif) (n3) of kernel-based learning methods such as Gaussian process models with increasing size n of the training set. This limitation may be overcome by usinga parameterized model, such as a generalized linear model or a neural network with a fixed set of basic functions or feature mappings. The use of a generalized linear model may, however, limit the expressiveness of the model, and the use of a neural network may not be amenable to practical training with the small sizes of the training sets expected from a Bayesian optimization algorithm. A practical approach may be to use a randomized feature map that approximates a kernel, as proposed by Ueno et al.22
(n3) of kernel-based learning methods such as Gaussian process models with increasing size n of the training set. This limitation may be overcome by usinga parameterized model, such as a generalized linear model or a neural network with a fixed set of basic functions or feature mappings. The use of a generalized linear model may, however, limit the expressiveness of the model, and the use of a neural network may not be amenable to practical training with the small sizes of the training sets expected from a Bayesian optimization algorithm. A practical approach may be to use a randomized feature map that approximates a kernel, as proposed by Ueno et al.22
The third limitation is the lack of a priori bounds on the number of iterations required to find a good quality solution. The algorithm typically provides an asymptotic convergence bound, but the exact number of required iterations remains subject to trial and error and empirical observation. Section 4.1 presents a detailed discussion on characterizing the convergence error and provides a sketch for proof towards establishing a convergence bound in the presence of noise. An important insight that may be gained from the discussion is that obtaining a low convergence error with high probability requires repeated sampling at the observed candidates in the optimization algorithm. An acquisition function that promotes such repeated sampling is thus important for the reliable operation of the algorithm in the presence of noise. Section 4.2 discusses the empirical characterization of convergence in such noisy scenarios.
4 Convergence analysis
4.1 Theoretical analysis
Given a declaration of an optimal candidate xoptk and![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) optk after acquiring k data samples as in (14), the ability of the algorithm to converge to the true (but unknown) optimal values of xopttrue and fopttrue can be measured in terms of the convergence errors,
optk after acquiring k data samples as in (14), the ability of the algorithm to converge to the true (but unknown) optimal values of xopttrue and fopttrue can be measured in terms of the convergence errors,δfkopt = |![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) optk − fopttrue| & δxkopt = ‖xoptk − xopttrue‖. optk − fopttrue| & δxkopt = ‖xoptk − xopttrue‖. | (15) |
The convergence error δfkopt is called the instantaneous regret after acquiring k samples. Similarly, the cumulative sum 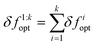 is called the cumulative regret. An algorithm is said to have the desirable asymptotic property of no-regret if the limit
is called the cumulative regret. An algorithm is said to have the desirable asymptotic property of no-regret if the limit 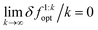 .
.
In most cases, the true optimal values are unknown. Thus the convergence errors in (15) cannot be directly measured. Instead, only a probabilistic bound on the expectation of these regrets can be made, based on the model assumptions and number of observed samples in the data set.
One such bound,26 for the noise-free case of Bayesian optimization in a d-dimensional search space is
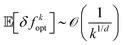 | (16) |
![[scr O, script letter O]](https://www.rsc.org/images/entities/i_char_e52e.gif) notation is used to describe the asymptotic behavior of the expected instantaneous regret. Eqn (16) shows that, if the underlying true function is at least twice differentiable and continuous (C2 function), with noise-free measurements, the expected regret asymptotically converges towards zero faster than the function k−1/d.
notation is used to describe the asymptotic behavior of the expected instantaneous regret. Eqn (16) shows that, if the underlying true function is at least twice differentiable and continuous (C2 function), with noise-free measurements, the expected regret asymptotically converges towards zero faster than the function k−1/d.
With noisy measurements, an additional challenge is encountered due to the errors incurred in learning the error-free true mean values. In the noise-free case, kernel-based learning methods like the Gaussian process learning, provide an error-free prediction of the mean value at the observed candidate points {x1,…,xk}. However, for the noisy case, the measurements yi are polluted with noise and the prediction error
ηf(x) = ![[Doublestruck E]](https://www.rsc.org/images/entities/char_e168.gif) [ [![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) k(x)] − k(x)] − ![[Doublestruck E]](https://www.rsc.org/images/entities/char_e168.gif) [f(x)] [f(x)] | (17) |
![[scr D, script letter D]](https://www.rsc.org/images/entities/i_char_e523.gif) k. An error in the mean value prediction directly affects the value computed by the acquisition function and causes an error in the optimal estimates obtained from (14). Thus noise in the measurement can act as an adversary in the Bayesian optimization scheme and lead to a loss of convergence properties.
k. An error in the mean value prediction directly affects the value computed by the acquisition function and causes an error in the optimal estimates obtained from (14). Thus noise in the measurement can act as an adversary in the Bayesian optimization scheme and lead to a loss of convergence properties.
The convergence of a Bayesian scheme in the presence of noise thus relies on drawing multiple samples around the already sampled locations in ![[scr D, script letter D]](https://www.rsc.org/images/entities/i_char_e523.gif) k to reduce the prediction error ηf. A significant degradation in the convergence properties for Bayesian optimization can be observed empirically13,42,43 with noisy measurements, when using the standard expected improvement (EI) or lower confidence bound (LCB) acquisition functions (Table 3). While convergence to the optimum can still be guaranteed with Gaussian noise,15 the convergence is shown empirically to be much slower with the standard EI or LCB acquisition functions.42 The noise-augmented EI and knowledge-gradient (KG) acquisition functions are known to have much better empirical convergence rates with noisy measurements.12,43
k to reduce the prediction error ηf. A significant degradation in the convergence properties for Bayesian optimization can be observed empirically13,42,43 with noisy measurements, when using the standard expected improvement (EI) or lower confidence bound (LCB) acquisition functions (Table 3). While convergence to the optimum can still be guaranteed with Gaussian noise,15 the convergence is shown empirically to be much slower with the standard EI or LCB acquisition functions.42 The noise-augmented EI and knowledge-gradient (KG) acquisition functions are known to have much better empirical convergence rates with noisy measurements.12,43
Furthermore, the convergence of Bayesian optimization schemes in the presence of a non-(sub) Gaussian noise distribution such as considered in section 2 is not yet established theoretically. The additional challenge posed by such distributions when using a Gaussian process model is the structural mismatch in the learned stochastic process (Gaussian) and the real underlying stochastic process (f). With finite repeated sampling at a given location x, the prediction error ηf(x) may still remain large, thus leading to slower convergence or adversarial effects of the noise in Bayesian optimization. These difficulties are shown empirically in section 6. However, Section 6 shows empirically that a combination of batched sampling and a generalized noise-augmented EI acquisition function can still be used to provide an improved convergence and robustness in Bayesian optimization with such structural mismatches.
A non-zero prediction error ηf(x) implies a non-zero expected error in the optimal candidate estimates,
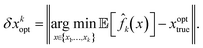 | (18) |
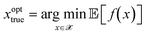 , a rearrangement of terms is be used to rewrite δxkopt as
, a rearrangement of terms is be used to rewrite δxkopt as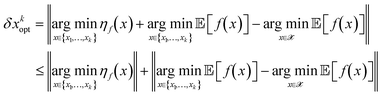 | (19) |
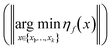 relates to the prediction error (17) in the model, while the second part relates to the exploratory error for the optimization arising from the limited trust region of the model ({x1,…,xk} ⊂
relates to the prediction error (17) in the model, while the second part relates to the exploratory error for the optimization arising from the limited trust region of the model ({x1,…,xk} ⊂ ![[scr X, script letter X]](https://www.rsc.org/images/entities/char_e14a.gif) ).
).
If the expectation of the true stochastic process ([![[Doublestruck E]](https://www.rsc.org/images/entities/char_e168.gif) f(x)]) is assumed to be Lipschitz continous with a Lipschitz bound L, then an error in optimal candidate estimation δxkopt leads to a worst-case estimation error in the optimal value δfkopt ≤ Lδxkopt. The effect of prediction and exploratory errors on δxkopt is then proportional to their effect on δxkopt.
f(x)]) is assumed to be Lipschitz continous with a Lipschitz bound L, then an error in optimal candidate estimation δxkopt leads to a worst-case estimation error in the optimal value δfkopt ≤ Lδxkopt. The effect of prediction and exploratory errors on δxkopt is then proportional to their effect on δxkopt.
For the noise-free case, Gaussian process learning can provide a zero prediction error 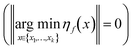 at the observed points, while the exploratory error follows an asymptotic convergence as shown in (16).
at the observed points, while the exploratory error follows an asymptotic convergence as shown in (16).
For the noisy case, we must rely on repeated sampling at the locations in {x1,…,xk} to drive the prediction error 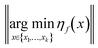 towards zero. The need for repeat sampling thus slows down the convergence rate for the exploratory error and may lead to a non-zero prediction error at termination due to the finite nature of repeated sampling in a practical algorithmic setting.
towards zero. The need for repeat sampling thus slows down the convergence rate for the exploratory error and may lead to a non-zero prediction error at termination due to the finite nature of repeated sampling in a practical algorithmic setting.
With repeated sampling at a given location, assuming negligible covariance to other locations, the worst-case convergence rate for the prediction error can be expected to follow a normal distribution ηf(x) ∼ ![[scr N, script letter N]](https://www.rsc.org/images/entities/i_char_e52d.gif) (0, σ2η(x)/n(x)) using the central limit theorem, where σ2η(x) is the noise variance at x and n(x) is the number of samples drawn at location x.
(0, σ2η(x)/n(x)) using the central limit theorem, where σ2η(x) is the noise variance at x and n(x) is the number of samples drawn at location x.
A Bayesian optimization scheme with the underlying assumptions and conditions of (16), taking N repeated samples for every location sampled in ![[scr D, script letter D]](https://www.rsc.org/images/entities/i_char_e523.gif) k, follows an exploratory error convergence rate of
k, follows an exploratory error convergence rate of ![[scr O, script letter O]](https://www.rsc.org/images/entities/i_char_e52e.gif) (1/(N−1k1/d)). The overall error in δxkopt can then be analyzed as an asymptotic convergence resulting from the sum of the two converging error components.
(1/(N−1k1/d)). The overall error in δxkopt can then be analyzed as an asymptotic convergence resulting from the sum of the two converging error components.
Repeated sampling at the optimal location xopttrue will lead to a prediction error ηf(xopttrue) ∼ ![[scr N, script letter N]](https://www.rsc.org/images/entities/i_char_e52d.gif) (0, σ2n(xopttrue)/N). The convergence error in the estimated optimal value δfkopt ∼ |ηf(xopttrue)| then has the expected value of the half-normal distribution,
(0, σ2n(xopttrue)/N). The convergence error in the estimated optimal value δfkopt ∼ |ηf(xopttrue)| then has the expected value of the half-normal distribution, 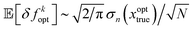 and variance Var[δfkopt] ∼ (1 − 2/π)σ2n(xopttrue)/N.
and variance Var[δfkopt] ∼ (1 − 2/π)σ2n(xopttrue)/N.
We can thus expect to see a non-zero convergence error on average in noisy Bayesian optimization with magnitude on the order of 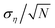 , (ση = σn(xopttrue)). We observe this phenomena in section 6 with ση for the case studies defined in section 2. We characterize the performance of achieving an expected error of less than one standard deviation of the noise (ση) with the name, sub-σ convergence or accuracy.
, (ση = σn(xopttrue)). We observe this phenomena in section 6 with ση for the case studies defined in section 2. We characterize the performance of achieving an expected error of less than one standard deviation of the noise (ση) with the name, sub-σ convergence or accuracy.
The above discussion is an outline of the arguments behind the convergence expected from a Bayesian optimization scheme in the presence of noise. A further formalization of the proof must take into account the effects of covariance between the data samples that are left out of the above discussion for simplicity.
Section 5 introduces some of the acquisition functions used in Bayesian optimization and introduces the generalized form of the noise-augmented Expected Improvement acquisition used in this work that promotes a data-dependent strategy for repeated sampling to selectively drive the prediction error ηf(x) down for the optimal candidates.
4.2 Empirical analysis
While the theoretical analysis of section 4.1 provides insights into the convergence rate statistics up to a proportionality factor, in practice, the factor is unknown and problem-dependent. Thus the theoretical bounds may not be amenable to characterize the number of samples required to guarantee convergence. Instead, one may empirically observe the rate of change of the optimal estimate with the iterations of the algorithm.Typically, a budget of N samples is decided beforehand for the optimization, and the optimization is terminated after the acquisition of N samples. The last Ntest samples of the N samples may be used as a test set to characterize the convergence.
The rate of change in the observed function value (![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) optk) is observed using the variance of the observed values over the test set. If the variance is smaller than a small threshold ε, the optimization is likely converged, if not, the budget for the samples N may need to be increased further.
optk) is observed using the variance of the observed values over the test set. If the variance is smaller than a small threshold ε, the optimization is likely converged, if not, the budget for the samples N may need to be increased further.
The convergence characteristics of the Bayesian optimization scheme vary from one run of the algorithm to another due to the randomized nature of acquired samples. The statistical characterization of the algorithm performance on a problem thus requires multiple independent runs. The algorithm's reliability is then evaluated by observing the variance in convergence characteristics across the multiple runs. Eqn (20) below proposes a quality metric (Q) for the algorithm across L independent multiple runs.
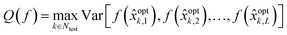 | (20) |
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) optk,i denotes the estimated optimal candidate at the kth iteration from the ith independent run of the algorithm. The variance Var[f(
optk,i denotes the estimated optimal candidate at the kth iteration from the ith independent run of the algorithm. The variance Var[f(![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) optk,1), f(
optk,1), f(![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) optk,2),…,f(
optk,2),…,f(![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) optk,L)] is taken across the L observed function values in the independent runs, at each iteration k in the test set. The quality metric Q then takes the worst case variance observed in the test set as a measure for the reliability or quality of the algorithm's design choices. A small value for Q, implies a small worst case variance and thus a higher reliability or quality for the algorithm.
optk,L)] is taken across the L observed function values in the independent runs, at each iteration k in the test set. The quality metric Q then takes the worst case variance observed in the test set as a measure for the reliability or quality of the algorithm's design choices. A small value for Q, implies a small worst case variance and thus a higher reliability or quality for the algorithm.
The worst-case variance observed in the test set indicates the worst-case convergence result that may be expected if any one of the independent runs was realized during the application of the algorithm to a problem and if the algorithm was randomly terminated at any iteration in the test set. Since the exact number of iterations required for reliable convergence is often unknown, such a worst-case characterization for the convergence result provides an important insight into the algorithm's reliability.
The function f in eqn (20) may be replaced by other functions such as the expected value of f or the regret function if the underlying ground truth for a problem is known, to provide additional insights into the convergence characteristics.
5 Acquisition functions
An acquisition function A(x|![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) k) evaluates the merit of choosing a candidate point x for sampling to drive down the prediction and exploratory errors (introduced in section 4) in a Bayesian optimization scheme. The next point to sample within a Bayesian optimization algorithm is then found as the point that maximizes the acquisition function, i.e.,
k) evaluates the merit of choosing a candidate point x for sampling to drive down the prediction and exploratory errors (introduced in section 4) in a Bayesian optimization scheme. The next point to sample within a Bayesian optimization algorithm is then found as the point that maximizes the acquisition function, i.e.,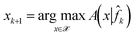 | (21) |
The simplest form of acquisition function is provided by the probability of improvement (POI),
APOI(x|![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) k) = k) = ![[Doublestruck P]](https://www.rsc.org/images/entities/char_e173.gif) ( (![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) k(x) ≤ k(x) ≤ ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) optk) optk) | (22) |
![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) optk−1 is the current best estimate for the optimal value. This kind of acquisition function represents the greedy approach to candidate sampling, where the sample showing the best probability of improvement according to the current model is chosen as the next candidate to acquire. While simple in formulation, the approach can suffer from non-convergence to the global (or even local) optimum of f, that is, the sampling scheme may fail to acquire samples improving model information and may converge to the optimum of an incorrect model
optk−1 is the current best estimate for the optimal value. This kind of acquisition function represents the greedy approach to candidate sampling, where the sample showing the best probability of improvement according to the current model is chosen as the next candidate to acquire. While simple in formulation, the approach can suffer from non-convergence to the global (or even local) optimum of f, that is, the sampling scheme may fail to acquire samples improving model information and may converge to the optimum of an incorrect model ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) N. In this scenario, the exploratory error component of the expected convergence error in (19) is left undiminished, leading to a large error.
N. In this scenario, the exploratory error component of the expected convergence error in (19) is left undiminished, leading to a large error.
This shortcoming of the greedy approach is overcome by the Expected Improvement (EI) metric1 which explicitly accounts for the information gained by sampling at a point x in addition to the improvement in the objective value. The metric is computed as the expectation of the objective value at x exceeding the previous best foptk,
AEI(x|![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) k) = k) = ![[Doublestruck E]](https://www.rsc.org/images/entities/char_e168.gif) [max( [max(![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) optk − optk − ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) k(x), 0)]. k(x), 0)]. | (23) |
![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) k in C2ν for any ν > 0.§ For a Gaussian process model
k in C2ν for any ν > 0.§ For a Gaussian process model ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) k(x) ∼
k(x) ∼ ![[scr N, script letter N]](https://www.rsc.org/images/entities/i_char_e52d.gif) (μk(x), σ2k(x)), the expected improvement can be written explicitly in terms of the predicted mean and variance as
(μk(x), σ2k(x)), the expected improvement can be written explicitly in terms of the predicted mean and variance as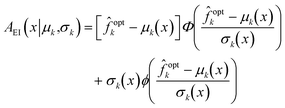 | (24) |
The expected improvement metric can be seen as a weighted sum between the improvement in mean (μk(x) − ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) optk) and standard deviation σk(x) weighted by cumulative probability and probability density functions respectively. The weighted standard deviation term in (24) provides the acquisition function some value in sampling points where σk(x) is large, thus promoting exploration in the parameter space, even when the corresponding point x has a low probability of improvement according to APOI. This exploratory quality is known to guarantee asymptotic convergence to the global optimum.26
optk) and standard deviation σk(x) weighted by cumulative probability and probability density functions respectively. The weighted standard deviation term in (24) provides the acquisition function some value in sampling points where σk(x) is large, thus promoting exploration in the parameter space, even when the corresponding point x has a low probability of improvement according to APOI. This exploratory quality is known to guarantee asymptotic convergence to the global optimum.26
A generalized version of the expected improvement3 is computed by using an integer power g of max (![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) optk −
optk − ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) k(x), 0) to compute the generalized expected improvement (gEI) as
k(x), 0) to compute the generalized expected improvement (gEI) as
AgEI(x|![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) k) = k) = ![[Doublestruck E]](https://www.rsc.org/images/entities/char_e168.gif) [[max( [[max(![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) optk − optk − ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) k(x), 0)]g] k(x), 0)]g] | (25) |
![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) k(x) ∼
k(x) ∼ ![[scr N, script letter N]](https://www.rsc.org/images/entities/i_char_e52d.gif) (μk(x), σ2k(x)), the generalized expected improvement can be computed recursively using
(μk(x), σ2k(x)), the generalized expected improvement can be computed recursively using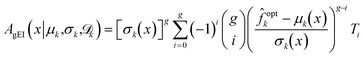 | (26) |
Another form of acquisition function used to tradeoff between exploration and exploitation is given by the lower confidence bound (LCB),44
| ALCB(x|μk, σk) = μk(x) − βkσk(x), | (27) |
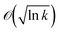 . The LCB acquisition function is motivated by its simplicity for use with Gaussian process models and is shown to perform at par with the expected improvement function.15,44
. The LCB acquisition function is motivated by its simplicity for use with Gaussian process models and is shown to perform at par with the expected improvement function.15,44
Unlike the above acquisition functions that are designed with asymptotic convergence in mind,45 introduced the knowledge gradient (KG) acquisition function to find a nearly optimal solution with only a limited budget for iterations. For AKG(x|![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) k), each new sample point is determined by assuming that it is the last available function evaluation in the budget of the Bayesian optimization algorithm. Thus the metric is designed to find the point that maximizes the best possible improvement expected by sampling a point x,
k), each new sample point is determined by assuming that it is the last available function evaluation in the budget of the Bayesian optimization algorithm. Thus the metric is designed to find the point that maximizes the best possible improvement expected by sampling a point x,
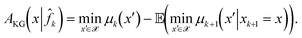 | (28) |
![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) k ∼
k ∼ ![[scr N, script letter N]](https://www.rsc.org/images/entities/i_char_e52d.gif) (μk(x), σ2k(x)) and the expectation is taken over this distribution. The closed-form expression of the updated mean after adding a point (xk+1 = x, y) for a Gaussianprocess model can be written as
(μk(x), σ2k(x)) and the expectation is taken over this distribution. The closed-form expression of the updated mean after adding a point (xk+1 = x, y) for a Gaussianprocess model can be written as| μk+1(x′|xk+1 = x) = μk(x′) + ∑(x′, x)(∑(x, x) + λI)−1 (y − μk(x)) | (29) |
![[scr N, script letter N]](https://www.rsc.org/images/entities/i_char_e52d.gif) (μk(x), σ2k(x)). This overall computation for the KG acquisition function can become computationally intractable and often requires some form of randomized Monte-Carlo approximation. The next point to acquire xk+1 is then obtained by maximizing AKG over the candidate sample space, each evaluation of which requires a Monte-Carlo approximation. This step makes the use of the KG acquisition function computationally expensive.
(μk(x), σ2k(x)). This overall computation for the KG acquisition function can become computationally intractable and often requires some form of randomized Monte-Carlo approximation. The next point to acquire xk+1 is then obtained by maximizing AKG over the candidate sample space, each evaluation of which requires a Monte-Carlo approximation. This step makes the use of the KG acquisition function computationally expensive.
In addition to the above, the acquisition functions can also be supplemented with additional trust-region constraints or penalties to enforce requirements such as model safety, safe exploration, or dynamical constraints7–11 leading to further variants.
The above acquisition functions focus on driving down the exploratory error in (19) and make no explicit attempts at repeated sampling to drive down prediction errors for noisy scenarios, which leads to poor convergence performance when working with noisy measurements.12
Latham et al.12 use a Monte-Carlo scheme of constructing multiple models ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) (i)k from artificially generated noise realizations from the model
(i)k from artificially generated noise realizations from the model ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) k. An averaged expected improvement using each model is then computed as
k. An averaged expected improvement using each model is then computed as
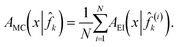 | (30) |
The averaged EI value over several noise realizations tries to capture a more realistic value of the expected improvement, not adversarially affected by any single noise realization. This approach promotes the repeated sampling required to improve the predictive error component of the convergence error and thus shows improved empirical performance.12
Huang et al.13 introduced the augmented EI acquisition function
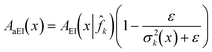 | (31) |
![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) k. The multiplicative augmentation to the expected improvement metric in (31) increases the value assigned to points with high variance prediction σ2k(x) given by the model. The variance prediction σ2k(x) asymptotically decreases to the noise variance σ2n hyperparameter value for a Gaussian process model with repeated sampling at x. The augmentation thus captures the amount of resampling at x as an internal state of the acquisition function and provides a way to enforce resampling at points with high noise variance in order to reduce predictive errors.
k. The multiplicative augmentation to the expected improvement metric in (31) increases the value assigned to points with high variance prediction σ2k(x) given by the model. The variance prediction σ2k(x) asymptotically decreases to the noise variance σ2n hyperparameter value for a Gaussian process model with repeated sampling at x. The augmentation thus captures the amount of resampling at x as an internal state of the acquisition function and provides a way to enforce resampling at points with high noise variance in order to reduce predictive errors.
We consider a generalized form of the augmentation in (31) and construct the generalized noise-augmented expected improvement as
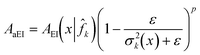 | (32) |
The maximization of the expected improvement or augmented expected improvement can be performed using a gradient-based numerical optimizer. The gradient computations, although tractable, increase the computational effort required. Also, gradient-based methods tend to get stuck in local optima for the acquisition functions, which tend to be multi-modal, i.e., have multiple local and global maxima. The multiple maxima can lead to the Bayesian optimizer getting stuck in a local exploration region. These limitations can be overcome by treating the acquisition function as a target probability distribution for a Markov Chain Monte Carlo (MCMC) sampler.46 The MCMC sampler can draw q samples for any integer q from a probability distribution proportional to the target acquisition function. Since AaEI(x|![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) k) ≥ 0 for all x, the acquisition function can be directly set as the target distribution and used to draw q samples from a probability distribution proportional to AaEI(x|
k) ≥ 0 for all x, the acquisition function can be directly set as the target distribution and used to draw q samples from a probability distribution proportional to AaEI(x|![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) k) with an MCMC sampler. This approach allows a simple and direct extension of the acquisition function to a batched sampling approach. Batched sampling further promotes repeated sampling and helps reduce prediction errors. Section 6 compares the convergence performances for different batch sizes q.
k) with an MCMC sampler. This approach allows a simple and direct extension of the acquisition function to a batched sampling approach. Batched sampling further promotes repeated sampling and helps reduce prediction errors. Section 6 compares the convergence performances for different batch sizes q.
6 Results
The Bayesian optimization algorithm from section 3 is run on the case studies for polymer nucleation described in section 2. The algorithm is run with a fixed budget of two thousand samples and compared across ten independent runs for statistical characterization of the convergence properties. A comparison is made using different choices for the generalized noise-augmented acquisition function (32), sample batch sizes q and with a prior-art algorithm for Bayesian optimization in material discovery from Ueno et al.22The performance of the algorithm is compared using metrics for optimality, convergence rate, and the quality metric Q to account for the reliability or expected variability in results across different runs. The optimality of the result is characterized by observing a normalized regret
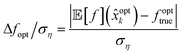 | (33) |
![[Doublestruck E]](https://www.rsc.org/images/entities/char_e168.gif) [f](x) as
[f](x) as ![[small tau, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b8.gif) mean(x) from (3), fopttrue as
mean(x) from (3), fopttrue as ![[small tau, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b8.gif) optmean from (4) and ση as the reference standard deviation from (6). The gridded NEMD data37,38 provides an estimate for the ground truth for the two case studies and are used to characterize the convergence of the algorithm using (33). The algorithm, however, is not provided any knowledge of this underlying ground truth.
optmean from (4) and ση as the reference standard deviation from (6). The gridded NEMD data37,38 provides an estimate for the ground truth for the two case studies and are used to characterize the convergence of the algorithm using (33). The algorithm, however, is not provided any knowledge of this underlying ground truth.
6.1 Bayesian optimization with noise-augmented acquisition applied to the polymer nucleation case studies
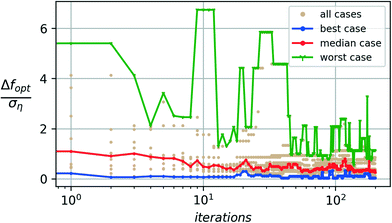
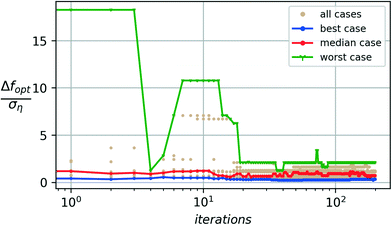
Fig. 2 and 3 show the typical convergence performance for the algorithm over the two case studies of polymer nucleation presented in section 2, using a batch size of 10 (q = 10) and a noise-augmented expected improvement acquisition function (p = 2).The noisy nature of the process implies that the Bayesian optimization cannot guarantee a zero convergence error to the noise-free optimal solution. Instead, the convergence error is compared to the standard deviation of the noise using the normalization.
The presence of noise also implies that different independent runs of the optimization see different realizations of the noise and thus lead to different convergence paths towards the optima. The algorithm's performance is thus characterized in terms of the observed distribution. Fig. 2 and 3 show the convergence error distribution over a group of 10 independent runs each for the tetrahedral and hexagonal additive groups respectively. The median case shows the median error across runs. The best- and worst-case performances show the minimum and maximum convergence error seen across the different runs at each iteration.
In both cases, we observe a median error of less than one standard deviation of the process noise and a worst-case deviation of less than three standard deviations. A sub-σ level of convergence for the algorithm shows the algorithm's effectiveness in estimating the optimal values with an accuracy level better than the underlying process noise. We observe that, on average, the algorithm performs at this sub-σ level. Even in the worst case, the error in the optimal estimate remains with a 3 − σ level of the noise. The corresponding estimates of the optimal candidate SW-parameters discovered are shown in Fig. 4a and b.
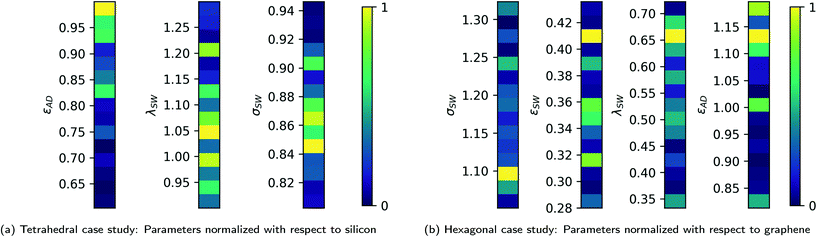
Fig. 4a and b show the distribution of optimal candidate estimates considered over 2000 sample acquisitions and ten runs for the tetrahedral and hexagonal additive case studies, respectively. Observing this distribution, as opposed to the final terminal value of the optimization, provides additional insight into the regions of the candidate space that the algorithm considers as likely locations to find an optimal candidate. Since the set of real, realizable crystals is only a subset of the continuous space described by the UAFF parameters, the collection of crystals with parameter values near or within this observed distribution provides the subset of candidates that are likely to achieve a close to optimal nucleation rate. The distribution also provides a way to account for any multi-modal nature in the optimal candidate solution space.
We use the normalized UAFF parameter space described in section 2 to parameterize the candidate search space, with SW potentials for the silicon and graphene crystals used as the normalization constants for the tetrahedral and hexagonal cases, respectively. The case study for tetrahedral additives is restricted to only three out of the four UAFF parameters ((εAD, λSW, σSW)) to maintain consistency with the ground truth data available.37 Fromthe results, the largest peak in the optimal candidate parameter distribution is observed to be around (0.98, 1.05, 0.85) for the tetrahedral case, with a larger spread of possible candidate values in the λSW parameters. A similar spread is observed in the optimal λSW candidate estimates for the hexagonal additive case as well from Fig. 4b, thus indicating a lower sensitivity of the optimal candidate to the λSW potential. The hexagonalcandidates distribution shows a peak at (1.1, 0.41, 0.66, 1.4) with secondary peaks for εSW and εAD at εSW = 0.36 and εAD = 1.
An optimal candidate normalized parameter of near 1 indicates the suitability of silicon and graphene respectively as optimal additive candidates for the two cases. Considering this distribution of optimal candidates with peaks around (0.98, 1.05, 0.85) and (1.1, 0.41, 0.66, 1.4) thus suggests nearly optimal performance of silicon and an optimal candidate away from graphene as a nucleating agent. Both εSW and λSW are proportional to the rigidity of the crystal and smaller values (0.41, 0.66) in the case for hexagonal crystals suggests a softer and more compliant material than graphene would perform well as a nucleating agent for poly-alkanes. This result is consistent with observations from Bourque et al.38 and crystal growth processes observed in semiconductors47 where a higher compliance substrate allows for better crystal growth despite relatively large substrate-semiconductor lattice mismatch. The search for crystals with these specific deviations in SW parameters is left as a direction for future exploration.
The results from Fig. 2 and 3 highlight the non-monotonic nature of convergence of the optimization algorithm in the presence of noisy measurements. This nonmonotonicity is expected as the underlying Gaussian process model evolves in its estimate of what it thinks the optimal value will be as more data and noise realizations are made available. An initial estimate of the optimum is based on far fewer observations of the data and noise realizations. It thus can easily be misguided by noise into creating an incorrect model of the underlying ground truth, i.e., suffers due to higher prediction errors. This occurrence results in a non-monotonic increase in deviation from the unknown optimum value. As further noise realizations are observed for any given candidate point, the model corrects itself and gains a better estimate for the statistics at the observed locations.
6.2 Comparison to prior-art and varying augmentation factors (p)
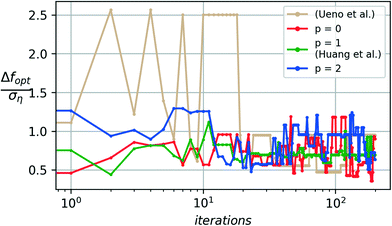
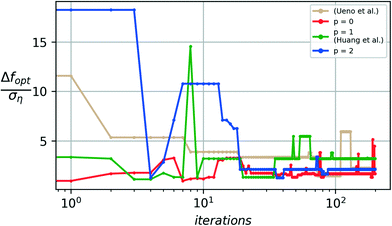
The noise-augmented acquisition function (32) is particularly designed to promote a higher degree of exploration in regions where fewer noise realizations have been observed to avoid getting trapped with an incorrect model of the underlying ground truth when a noise realization misguides the algorithm. This acquisition function may result in a slower convergence as the model focuses on additional exploration to combat noise and not only on the exploitation of the model, generated from initial noise realizations, to search for optimal candidates. The augmented acquisition function, however, provides higher overall stability with improved median and worst-case performance.Fig. 5 and 6 show a comparison of the median and worst-case performance obtained from the traditional expected improvement acquisition function (p = 0) to that of the augmented Expected Improvement function (p = 1, 2) in combating the noise-driven predictive errors from misleading of the optimization algorithm. A baseline comparison to the prior art using the toolbox from Ueno et al.22 is provided.
For p = 0, a non-monotonic increase is observed in the deviation away from optimum even after 2000 iterations of the algorithm have been completed, which occurs due to the insufficient exploration of noise realizations provided by the expected improvement metric.
As the power factor p is increased in the augmented acquisition function, increased weight is provided to the exploration of noise realizations. This exploration significantly improves the worst-case performance, with fewer and smaller non-monotonic deviations upon convergence for the p = 1 case and no observable deviations upon convergence from the p = 2 case, indicating that a sufficient exploration of the noise realizations is provided by the augmented case (p = 2) before converging to an optimal candidate. This improved stability in the algorithm prevents a misleading result from being declared as optimal when the algorithm is terminated in a run where the worst-case performance might have been realized. This notion of reliability or quality of the algorithm's design choices is quantified by the quality metric Q from (20).
Fig. 7 shows the comparison for the four cases considered above in terms of the quality metric Q(Δf/ση). The quality metric shows the worst-case variance in the regret obtained at any iteration in obtaining the test samples across the ten independent runs of the algorithm for each design choice. 35% of the sample budget, i.e., the last 700 samples of each run are reserved as the test set to quantify the quality metric.
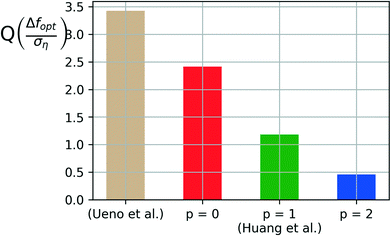 | ||
| Fig. 7 Comparing model quality (Q) for varying augmentation factors (p) obtained from the test iterations with 35% of the sample budget allotted for quality testing. | ||
The quality metric shows a clear improvement in the reliability of the algorithm as the augmentation factor (p) is increased from 0 to 2. The smaller the value of Q, the smaller the variability of results obtained from the algorithm, thus higher the reliability.
6.3 Comparison across varying batch size (q)
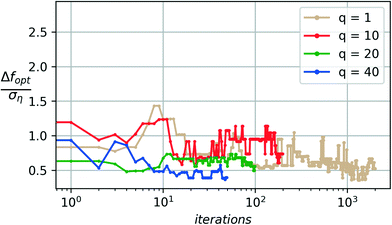
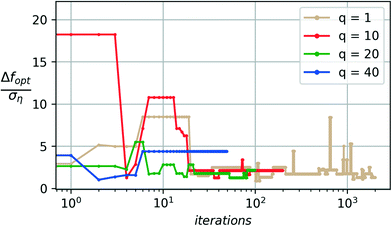
Another important aspect in dealing with noisy and expensive material discovery experiments is that experiments are typically performed in batches. Thus the optimizer must provide a batch of candidate samples at every iteration. The Bayesian optimization algorithm is run with the noise-augmented acquisition function with p = 2 for different choices of the sampling batch size q. Ten independent runs are used to characterize the statistical performance and quality (Q) of the algorithm for each choice of q. The total number of samples drawn is kept constant at 2000 (sample budget N = 2000) to keep the results comparable. The total number of iterations available to the optimizer is then given by 2000/q.Fig. 8 shows a comparison of the reliability or quality metric (Q) across the different choices for the batch sizes considered. The quality metric Q is evaluated over a test set containing the last 700 samples of each independent run for a given choice of q. The figure clearly shows a marginal improvement in the algorithm's reliability as the batch size is increased from 1 to 20. A significant loss in reliability is observed as the batch size is further increased to 40.
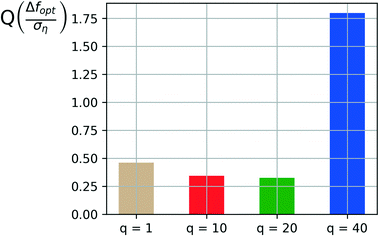 | ||
| Fig. 8 Comparing model quality (Q) for varying batch sizes (q) obtained from the test iterations with 35% of the sample budget allotted for quality testing. | ||
As the batch size increases, a larger number of samples are included in the model update at every iteration, which leads to a faster accumulation of data and noise realizations on every iteration. This makes the model updates less susceptible to noise on any given iteration. The downside of larger batch sizes is that there are fewer optimizer iterations (N/q) for a fixed budget of N samples. The selection of batch size (q) is thus a tradeoff between these two factors when the total samples budget is kept constant. Fig. 8 shows this tradeoff in action with the marginal improvement of reliability up to q = 20 and a significant drop of reliability with q = 40, which leaves the algorithm with too few (50) optimizer iterations.
Fig. 9 and 10 compare the median and worst-case performances of the algorithm with varying batch size q.
The median performance (Fig. 9) sees a nearly similar error (around 0.5ση) across the different choices for q. The small changes in median performance upon termination are within a small fraction of the noise standard deviation and are considered statistically insignificant.
The worst-case performance (Fig. 10) however, shows consistent convergence up to q = 20 and a significant degradation of performance by several multiples of the noise standard deviation for a batch size of 40. Such a degradation occurs due to an insufficient number of optimization steps available to the algorithm for q = 40.
In practice, it is often preferred to have experiments performed in batches and thus observing consistent convergence performance with the larger batch sizes such as q = 10 and q = 20 may thus be considered optimal, as quantified by the quality metric Q and the consistent results for the median and worst-case convergence.
6.4 Observations from the numerical studies
Using the comparisons from sections 6.2 and 6.3, a batch size of q = 10 or q = 20, with p = 2, is observed to provide an adequate tradeoff with good median and worst-case performance (sub-σ and sub-3σ respectively), with an improved reliability or quality metric Q.The numerical studies were performed using ten independent runs of the algorithm for each design choice, such as the choices for p and q. Furthermore, each independent run is initialized with an independent and randomly sampled initial training set which further contributes to the independent and randomized convergence paths taken by the algorithm across the different runs. The quality metric Q thus captures the worst-case variability of the results across all such independent runs for any given design choice of the algorithm and any sample in the last Ntest samples acquired by a run being declared as the optimal candidate.
The Bayesian optimization with batched sampling and a noise-augmented acquisition function thus provides an effective strategy to achieve a sub-σ level of median and best-case convergence in the presence of noise while maintaining a worst-case performance within three standard deviations of the noise level. The improved quality metric (Q) shows that the augmentation and batched sampling also lead to a lower sensitivity to factors such as the choice of initial training set or the choice of the termination iteration number.
7 Conclusions
This article explores the challenges in dealing with the process or measurement noise in materials discovery approaches using Bayesian optimization methods. The non-monotonic convergence and noise-driven variability of outcomes across different runs of the algorithm are shown to be significant factors to consider for the design of a Bayesian optimization approach that is robust to noise and a quality metric is introduced to quantify such variability. The use of an augmented acquisition function and a batched approach to sampling are both shown to be helpful in achieving improved robustness, and the median performance of the designed approach is shown to achieve a sub-σ level of accuracy in determining optimal candidates, while the worst-case performance shows better than 3σ level of accuracy in two case studies for additive discovery in polymer (polyethylene) nucleation.The case studies consider the search for optimal additive candidates using a united atomic force field model for search space parameterization in classes of tetrahedral and hexagonal additives, respectively. The results suggest nearly optimal performance for silicon in the class of tetrahedral crystals but suggest a candidate more compliant than graphene in their respective classes. With the deviations observed in optimal parameters from Si and graphene, a search for possibly better-matched crystals to the discovered candidates is a direction for further research.
The augmented Bayesian optimization approach for materials discovery in noisy processes is seen to be an effective approach to minimize the number of expensive experimental or MD simulation samples required while addressing the challenges of batched sampling and robustness to noise.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Science Foundation DMREF program under Grant No. CMMI-1729304.Notes and references
- J. Mockus, V. Tiesis and A. Zilinskas, in Towards Global Optimization, North-Holland, The Netherlands, 1978, vol. 2, pp. 117–129 Search PubMed.
- D. R. Jones, M. Schonlau and W. J. Welch, J. Glob. Optim., 1998, 13, 455–492 CrossRef.
- M. Schonlau, W. J. Welch and D. R. Jones, in New Developments and Applications in Experimental Design, ed. N. Flournoy, W. F. Rosenberger and W. K. Wong, Institute of Mathematical Statistics, Hayward, California, 1998, vol. 34, of IMS Lecture Notes-Monograh Series, pp. 11–25 Search PubMed.
- D. D. Cox and S. John, Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics, 1992, pp. 1241–1246 Search PubMed.
- J. Mockus, J. Glob. Optim., 1994, 4, 347–365 CrossRef.
- M. Locatelli, J. Glob. Optim., 1997, 10, 57–76 CrossRef.
- A. K. Akametalu, J. F. Fisac, J. H. Gillula, S. Kaynama, M. N. Zeilinger and C. J. Tomlin, Proceedings of the 53rd IEEE Conference on Decision and Control, 2014, pp. 1424–1431 Search PubMed.
- M. Turchetta, F. Berkenkamp and A. Krause, Adv. Neural Inf. Process. Syst., 2016, pp. 4312–4320 Search PubMed.
- M. O. Ahmed, S. Vaswani and M. Schmidt, Mach. Learn., 2020, 109, 79–102 CrossRef.
- F. Berkenkamp, A. P. Schoellig and A. Krause, Proceedings of the IEEE International Conference on Robotics and Automation, 2016, pp. 491–496 Search PubMed.
- S. S. Diwale, I. Lymperopoulos and C. N. Jones, Proceedings of IEEE Conference on Control Applications, 2014, pp. 1394–1399 Search PubMed.
- B. Letham, B. Karrer, G. Ottoni and E. Bakshy, Bayesian Anal., 2019, 14, 495–519 Search PubMed.
- D. Huang, T. T. Allen, W. I. Notz and N. Zeng, J. Glob. Optim., 2006, 34, 441–466 CrossRef.
- P. Auer, N. Cesa-Bianchi and P. Fischer, Mach. Learn., 2002, 47, 235–256 CrossRef.
- N. Srinivas, A. Krause, S. M. Kakade and M. W. Seeger, IEEE Trans. Inf. Theory, 2012, 58, 3250–3265 Search PubMed.
- J.-Y. Audibert, S. Bubeck and R. Munos, in Bandit View on Noisy Optimization, Optimization for Machine Learning edn., MIT Press, 2010, ch. 1 Search PubMed.
- S. R. Chowdhury and A. Gopalan, in Bayesian Optimization under Heavy-Tailed Payoffs, Curran Associates Inc., Red Hook, NY, USA, 2019 Search PubMed.
- Y. Zhao, D. Zeng, A. J. Rush and M. R. Kosorok, J. Am. Stat. Assoc., 2012, 107, 1106–1118 CrossRef CAS PubMed.
- J. Snoek, H. Larochelle and R. P. Adams, Proceedings of the 25th International Conference on Neural Information Processing Systems, 2012, pp. 2951–2959 Search PubMed.
- A. Wilson, A. Fern and P. Tadepalli, J. Mach. Learn. Res., 2014, 15, 253–282 Search PubMed.
- E. Brochu, V. M. Cora and N. de Freitas, A Tutorial on Bayesian Optimization of Expensive Cost Functions, with Application to Active User Modeling and Hierarchical Reinforcement Learning, 2010 Search PubMed.
- T. Ueno, T. D. Rhone, Z. Hou, T. Mizoguchi and K. Tsuda, Mater. Discov., 2016, 4, 18–21 CrossRef.
- P. I. Frazier and J. Wang, in Bayesian Optimization for Materials Design, ed. T. Lookman, F. J. Alexander and K. Rajan, Springer International Publishing, Cham, 2016, pp. 45–75 Search PubMed.
- Y. Zhang, D. W. Apley and W. Chen, Sci. Rep., 2020, 10, 4924 CrossRef CAS PubMed.
- A. Deshwal, C. M. Simon and J. R. Doppa, Mol. Syst. Des. Eng., 2021, 6(12), 1066–1086 RSC.
- A. D. Bull, J. Mach. Learn. Res., 2011, 12, 2879–2904 Search PubMed.
- D. Pati, A. Bhattacharya and G. Cheng, J. Mach. Learn. Res., 2015, 16, 2837–2851 Search PubMed.
- E. Contal, V. Perchet and N. Vayatis, International Conference on Machine Learning, 2014, pp. 253–261 Search PubMed.
- H. Tran-The, S. Gupta, S. Rana and S. Venkatesh, Proceedings of the Thirty-Fourth AAAI Conference on Artificial Intelligence, 2020, pp. 2425–2432 Search PubMed.
- F. Berkenkamp, A. P. Schoellig and A. Krause, J. Mach. Learn. Res., 2019, 20, 1–24 Search PubMed.
- P. Larrañaga and J. Lozano, Estimation of Distribution Algorithms: A New Tool for Evolutionary Computation, Springer, US, New York, 2012 Search PubMed.
- J. Snoek, O. Rippel, K. Swersky, R. Kiros, N. Satish, N. Sundaram, M. Patwary, M. Prabhat and R. Adams, Proceedings of the International Conference on Machine Learning, 2015, pp. 2171–2180 Search PubMed.
- J. T. Springenberg, A. Klein, S. Falkner and F. Hutter, Adv. Neural Inf. Process. Syst., 2016, 29, 4134–4142 Search PubMed.
- J. Bergstra, R. Bardenet, Y. Bengio and B. Kégl, Adv. Neural Inf. Process. Syst., 2011, 24, 2546–2554 Search PubMed.
- K. Kawaguchi, L. P. Kaelbling and T. Lozano-Pérez, Adv. Neural Inf. Process. Syst., 2015, 28, 2809–2817 Search PubMed.
- L. Goh, K. Chen, V. Bhamidi, G. He, N. C. S. Kee, P. J. A. Kenis, C. F. Zukoski and R. D. Braatz, Cryst. Growth Des., 2010, 10, 2515–2521 CrossRef CAS PubMed.
- A. J. Bourque, C. R. Locker and G. C. Rutledge, J. Phys. Chem. B, 2017, 121, 904–911 CrossRef CAS PubMed.
- A. J. Bourque and G. C. Rutledge, Eur. Polym. J., 2018, 104, 64–71 CrossRef CAS.
- F. H. Stillinger and T. A. Weber, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 5262–5271 CrossRef CAS PubMed.
- W. Sun and R. D. Braatz, Comput. Chem. Eng., 2020, 143, 107103 CrossRef CAS.
- C. E. Rasmussen and C. K. I. Williams, Gaussian Processes for Machine Learning, MIT Press, Cambridge, Massachusetts, 2006 Search PubMed.
- E. Vazquez, J. Villemonteix, M. Sidorkiewicz and E. Walter, J. Phys.: Conf. Ser., 2008, 135, 012100 CrossRef.
- V. Picheny, D. Ginsbourger and Y. Richet, Proceedings of the International Conference on Engineering Optimization, 2010, pp. 1–10 Search PubMed.
- N. Srinivas, A. Krause, S. Kakade and M. Seeger, Proceedings of the 27th International Conference on Machine Learning, 2010, pp. 1015–1022 Search PubMed.
- P. Frazier, W. Powell and S. Dayanik, INFORMS J. Comput., 2009, 21, 599–613 CrossRef.
- S. Theodoridis, Monte Carlo Methods, Academic Press, London, 2nd edn, 2020, pp. 731–769 Search PubMed.
- F. E. Ejeckam, Y. H. Lo, S. Subramanian, H. Q. Hou and B. E. Hammons, Appl. Phys. Lett., 1997, 70, 1685–1687 CrossRef CAS.
Footnotes |
| † The source code for the work presented in this article may be obtained from https://github.com/sanketdiwale/NoisyBayesianOptimization. |
| ‡ Electronic supplementary information (ESI) available. See DOI: 10.1039/d1me00154j |
| § C2ν denotes the space of real-valued functions that are differentiable 2ν times with continuous derivatives. |
| This journal is © The Royal Society of Chemistry 2022 |