Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Remediation of pharmaceuticals from wastewater via computationally selected molecularly imprinted polymers†
William
Battell
,
Gaël
Donval
,
Bernardo
Castro-Dominguez
 and
Carmelo
Herdes
and
Carmelo
Herdes
 *
*
Department of Chemical Engineering, University of Bath, Claverton Down, Bath, Somerset BA2 7AY, UK. E-mail: cehm21@bath.ac.uk
First published on 19th November 2021
Abstract
Pharmaceuticals are vital components of our daily life; however, as micropollutants, they also pose a significant wastewater treatment challenge. As the complete avoidance of pharmaceuticals is not a desired or viable solution, a targeted wastewater treatment must be implemented. Molecularly imprinted polymers can remove these contaminants from wastewater; however, determining their optimal constituents is a costly and lengthy experimental process. Here, we present a computational protocol used to design imprinted polymers for the targeted removal of fluoxetine, leveraging rigorous molecular models and simulation methods to study the crucial complexation step during the pre-polymerisation mixtures. Our molecular dynamics results validated with available experimental measurements correlate calculated radial distribution functions and predicted hydrogen bonding with experimental imprinting factors for various functional monomers. The simulated results are also analysed via Kirkwood–Buff integrals for the study of the role of functional monomers in the whole pre-polymerisation mixture. Marked dependencies of the functional monomer's carbonyl, hydroxyl and esters interactions are described, and functional monomer selection criteria using hydrogen bonding time and KBI initial slope and limiting value are proposed. This analysis offers further insights into why itaconic acid, amongst methacrylic acid, 2 (hydroxyethyl)methacrylate, acrylamide and acrylonitrile, is the optimal monomer for imprinting fluoxetine when ethylene glycol dimethacrylate is used as crosslinker and dimethylsulfoxide as solvent. Our computational protocol compiles off-the-shelf open-source software with well-established simulation methodologies to offer a viable alternative to the resource and time-consuming experimental task of choosing the best functional monomer for a given target molecule.
Design, System, ApplicationDevised decades ago, as man-made mimics of antibodies, molecularly imprinted polymers (MIPs) are still a promise. The development of MIPs capable of efficiently recognising, sensing, capturing or catalysing a target molecule is not without challenges. Some herculean experimental efforts are well known in the field in which the imprinted polymers have successfully achieved the molecular recognition capability of natural enzymes, where patents back up only a few with mature technology to sustain a commercial model, i.e., manufacturing MIPs or MIPs based devices. However, these efforts are overwhelmingly surpassed by studies in which expected results are not attained. The crux of the matter is often found in i) the enormous combinatory of reactants available or ii) our limited understanding of the complex molecular interactions during their synthesis, in fact, a combination of both. Here we compile a series of available molecular dynamic methodologies articulated as a step-by-step protocol for describing the molecular interactions of all relevant molecules in the MIPs' pre-polymerisation mixture. The design of an optimal MIP for the removal of the antidepressant Prozac from wastewater is showcased. |
Introduction
Over 3000 pharmaceuticals are currently available in Europe alone,1,2 with undeniable positive impact regarding their intended use; however, a high fraction of them constantly end up in wastewater, increasing concerns over potential risks to both ecosystems and human welfare.3–5 One such drug, investigated here, is the anti-depressant fluoxetine (FLX), more commonly known as Prozac. FLX is a selective serotonin reuptake inhibitor approved for use by the FDA since 1987,6 that by 2002 reached $22 billion in sales. FLX modern-day prescriptions are still very high, with over 25 million in the USA during 2018.7 The NHS monthly prescription cost analysis for England reports over 630 K prescription of FLX on March 2021.8 With such high quantities deployed, it is not surprising that FLX is found in surface waters, with typical concentrations in the microgram per litre level.9,10 Its bioaccumulation is also a problem, with trace levels moving through the food chain, eventually ingested by humans.11,12The complete avoidance of pharmaceuticals to protect water systems is not an attainable solution to the problem. While traditional wastewater treatment plants offer some reduction of these harmful micropollutants, their complete removal is currently not achievable via conventional methods.13 Therefore, our long-term goal is to offer a technology specifically designed to capture drugs at point sources e.g., at hospital wastewater systems,14 while our current focus is the fundamental understanding of this systems at the molecular level. With the foresee understanding, we envisage such technology to be based on molecularly imprinted polymers (MIPs) as core specific adsorbent layer in ultrafiltration membrane units for small organic molecules, such as FLX. A comprehensive review of MIP suitability in wastewater treatment can be found elsewhere.15
MIPs are a class of polymer that possess cavities with high affinities towards a chosen template molecule (TM) and have been shown to have a wide variety of applications, as biosensors,16 in the detection of small drugs molecules,17–21 antibiotics,22 and pesticides.23,24 Detection of small molecules lends itself well to wastewater treatment,15 and environmental analysis-based applications.25,26 Targeted design of adsorbents with optimal surface functional monomers (FM) is achievable if sound comprehension of the complex molecular interactions is gained. The idealised imprinting method is outlined in Fig. 1 with a) FM, b) crosslinker (CL) and c) TM, these compounds are homogenised in a given porogen solvent portrayed as a yellow background. Fig. 1 also shows the different stages of the MIP synthesis, 1) the TM and FM complexation step in the pre-polymerisation mixture, 2) the polymerisation of the CL molecules around the stabilised complex, 3) the extraction of the TM and solvent, and 4) the rebinding of the TM into the pristine imprinted cavity. All these steps are driven by intermolecular interactions, which are promoted or inhibited by the selection of the solvent, that also aid in the production of pores for the transport of the TM.
What is referred to as the pre-polymerisation mixture contains all MIP's components, namely TM, FM, CL and solvent molecules. How the entire system interacts before polymerisation has been one of the most important factors to consider for the generation of specific cavity sites.27 However, with so many possible compositions, the optimum system's determination is both a time-consuming and expensive experimental process. Computational modelling can leverage our understanding of molecular interactions in the pre-polymerisation mixtures efficiently, leading to narrow the choices for the MIP's constituents alongside their optimal composition.
A wide variety of computational techniques are applicable for MIPs, a comprehensive appraisal of computational technics in the field has been recently compiled by Nicholls et al.,28 and specifically for the detection of antibiotics in environmental and food samples by us and coworkers.29 One prevalent approach is functional monomer selection through screening via molecular mechanics, where the TM and FM interactions in vacuum are characterised by binding energies scores.30 Quantum mechanics methods, such as density functional theory (DFT), have become more widespread, as they offer a transferable approach to determine the TM and FM energy interactions at the cost of higher resource utilisation compared to classical methods.31,32 Mostly, DFT is limited to only one TM–FM interactions since larger systems are still computationally expensive. Classical methods are less transferable but much cheaper to use allowing for the implementation of advanced sampling techniques like molecular dynamics (MD) on larger systems.33,34 MD allows for the full pre-polymerisation mixture to be simulated. Similarly to MD, Monte Carlo (MC) methods also allow for these systems to be simulated using random sampling.35 The choice of MC over MD depends on the MIP's properties of interest.28
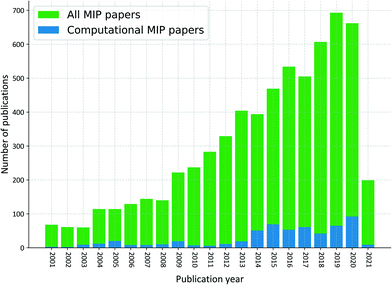
The tendency to use computational approaches to aid the design of MIPs has increased since 2001, however it is still marginal when compared to the total number of publications in the field, as shown in Fig. 2. It is our ambition that the compiled protocol presented here will assist the computational tasks, boosting this trend, as currently less than 5% of the experimental MIP synthesis are supported by insights gained from simulations.28,29
Computational methodology
Capitalising on our previous work on modelling MIP systems,36–39 in this work, the pre-polymerisation mixture for a FLX-MIP is simulated using MD. Methacrylic acid (MAA), itaconic acid (IA), 2 (hydroxyethyl)methacrylate (HEMA), acrylamide (ACA) and acrylonitrile (ACN) were selected as FM candidates. The CL and solvent are ethylene glycol dimethacrylate (EGDMA) and dimethylsulfoxide (DMSO), respectively. The validation of our predictions is done with available experimental data.40 To study the effect of FM selection (i.e., MAA, IA, HEMA, ACA and ACN), we propose the protocol depicted in Fig. 3.Setup molecular models/simulation cells
The optimised potentials for liquid simulations – all atom (OPLS-AA)41 force field was implemented for all MIPs components. The pre-polymerisation mixture is synthesised in the liquid phase; therefore, this force field offers a suitable starting point. The topology files for all molecules were obtained from the ATB repository,42 the specific MolID are given in the ESI.†Here, the protocol was initiated with MAA as it is the most commonly used FM for MIP synthesis. The pre-polymerisation mixture simulations cells were setup following the experimental ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50
50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 583 of FLX
583 of FLX![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MAA
MAA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EGDMA
EGDMA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
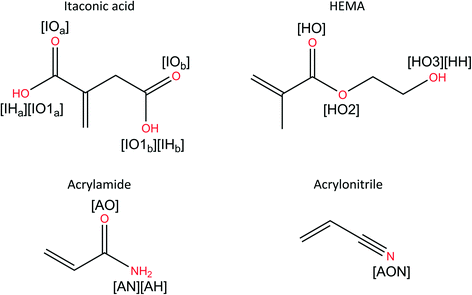
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO.40 As FLX offers two main hydrogen bonding sites (see Fig. 4), two FM per TM were chosen as an ideal start.
DMSO.40 As FLX offers two main hydrogen bonding sites (see Fig. 4), two FM per TM were chosen as an ideal start.
 | ||
| Fig. 4 2D schematic showing the chemical structure of all MIP's components, used here, including the atom (red) and names (in brackets) used for RDF and KBI analysis. | ||
To simulate the pre-polymerisation mixture an initial simulation cubic cell was populated with 10 molecules of FLX, 20 FM, 500 CL and 5830 solvent molecules. All components were randomly inserted in the simulation cell. This cell undergoes a sequence of energy minimisation, NVT and NpT ensemble simulations. The simulation sequence details, i.e., order, ensemble, time steps, cut-off, thermostat and barostat, can be found in Fig. S3 and Table S3 in the ESI.†
MD simulations
All simulations were conducted using open-source software GROMACS,43 version 2019. Force field validations are described in detail in the ESI,† including liquid densities of pure components, water surface tensions and water/octanol partition coefficients (KOW) calculations for FLX. The effect of different FM was investigated while all other components and ratios remained the same.Post simulation analysis
Analysis including radial distribution functions44 (RDFs, g(r)), Kirkwood–Buff integrals45,46 (KBI) and hydrogen bond (HB) formation47,48 were used to interrogate the simulations' trajectories.A g(r) is defined as the ratio between the average number density at any given distance, r, from any atom and the density at the same distance, r, from an atom in an ideal gas, with the same overall density.44 By definition g(r) = 1 for an ideal gas, for all r. Any deviation from this value is due to intermolecular interactions.44
The Kirkwood–Buff solution theory relates molecular interactions to macroscopic properties.45,46 This theory describes structural thermodynamics over the complete range of compositions for solvents using RDFs. The KBI (eqn (1)) can be related to many physical properties, including the interaction/binding energies of atoms. KBI represents the volume per number of atoms and allows a quantitative comparison between the RDFs for the various pair interactions.
 | (1) |
The specific atom pairs used here are those that are likely to give rise to HB, thus important for the FLX–FM complex formation in the pre-polymerisation step. The MIP's component chemical structures, the chosen atom pairs, and their labels are defined in Fig. 4 and 5. It is worth noticing that the calculations involving HB complexes with the FLX fluorine atoms (PF1-3, in Fig. 4) as the (trifluoromethyl)benzene HB has been proved to be too weak as measured and characterised by established and novel NMR methods,47 the calculated RDF for FLX fluorine atoms and HB analysis can be found in the ESI,† where their peaks and HB time% values are all outcompeted by the other relevant interactions.
The GROMACS subroutine hbond43 was used to calculate the HBs formed between the two specific atom pairs, namely the TM and FM atom pairs. HBs are determined by a specific cut-off distance and angle between donor hydrogen and acceptor, the common cut-off distance of 0.35 nm and angle of 30°, for energetically significant HBs were used here. HBs were determined at each frame of the simulation48 giving a percentage time spent by the FLX and FM as a complex (i.e., hydrogen bonding), allowing a comparisons between the systems.
Results and discussion
From unitary cell to production cell
We used seven different supercell sizes to determine an appropriate simulation box size (keeping the same ratios and density of elements). Out of all the simulations, Fig. 6a and b illustrates the RDFs between TM–CL (PH-EO1) and FM–CL (MH-EO1) in the ten-TM box and the 100-TM box (maximum size), both systems' peak positions and intensities are similar (disregarding the expected noise in the ten-TM case). This indicates that the smaller system is still representative of the physics generated in the larger one but at lower computing time/power for the simulations (see Table 1). | ||
| Fig. 6 RDFs for the ten-TM cell (blue) and the larger 100-TM cell (red), atom pairs between both a) FLX–CL and b) FM–CL. | ||
| Number of unit cells (TM) | Simulation time after 1 h run (ps) | Real time for 1 ns run (min) | Real time for 10 ns run (h) |
|---|---|---|---|
| 1 | 5344 | 11.23 | 1.87 |
| 8 | 1360 | 44.12 | 7.35 |
| 16 | 920 | 65.22 | 10.87 |
| 32 | 480 | 125.00 | 20.83 |
| 64 | 260 | 230.77 | 38.46 |
| 100 | 160 | 375.00 | 62.50 |
The smaller system shows more noise than that of the larger one: this is expected with only 10% the number of molecules. To improve the statistics of the ten-TM system, 18 duplicates were ran with the same parameters however each with a newly randomly generated starting configuration. The number of duplicates used was determined through time tests produced for the large system (Tables 1 and 2).
| Number of computer nodes | Simulation time after 1 h run (ps) | Real time for 1 ns run (min) | Real time for 10 ns run (h) |
|---|---|---|---|
| 1 | 40 | 1500.00 | 250.00 |
| 2 | 80 | 750.00 | 125.00 |
| 4 | 160 | 375.00 | 62.50 |
| 8 | 260 | 230.77 | 38.46 |
| 12 | 380 | 157.89 | 26.32 |
| 32 | 700 | 85.71 | 14.29 |
The wall time taken for a 10 ns simulation of the ten-TM cell using one node was 18 h. Based on this, running 18 duplicates of the ten-TM system is equivalent to the time/computing power of a single 100-TM box ran for the same 10 ns on 12 computer nodes (26 h – the most efficient for the 100-TM system). This then offers a larger overall simulation time and number of molecules/configurations analysed.
The pair interactions between FLX–FM are the result of considerably fewer molecules available for sampling during the simulation (compared to that of CL), therefore the variation between duplicates is more predominant. We used simulated annealing49 to solve this problem in a timely manner, the results for which can be seen in Fig. 7. The annealing temperature range was from 298–1000 K in 500 ps, this temperature maintained for 18 ns, then reduced back to 298 K at the same rate.
On Fig. 7a, without any special treatment, the two average RDFs happen to be much further away from each other than with simulated annealing, shown on Fig. 7b. The high temperature annealing step actually increases the likelihood for all molecules to interact with each other, therefore reducing variability in each RDF.
In passing, using duplicates (or here, duplicates of duplicates) improves configuration sampling: without them, we would have had no way to tell whether any of those RDFs were converged as smoothness is never a good convergence indicator for RDFs; only such repeats are. This suggests that using multiple smaller systems is better than using a single larger one. It is worth noticing that a FM–TM complex identified at higher annealing temperatures will persist for longer at the lower experimental synthesis temperature.
Considering all of the above, the annealing step was included in our protocol for all subsequent simulations, as presented in Fig. 3.
The effect of different FM
All FMs, their atom pair complex with the highest HB time and corresponding KBI limiting value are compared against the experimental imprinting factors (EIF)40 in Table 3. All HB time and corresponding KBI limiting values can be found in the ESI† (Table S4 and Fig. S9).| FM | Atom pair | HB time (%) | KBI limiting value (nm3) | EIF40 |
|---|---|---|---|---|
| IA | PH-IOa | 10.61 | −0.549 | 6.3 |
| PH-IOb | 10.31 | −0.935 | ||
| PH-IOa+b | 20.92 | −1.484 | ||
| ACA | PH-AO | 18.85 | 3.384 | 2.6 |
| HEMA | PH-HO2 | 16.90 | −1.475 | 2.8 |
| MAA | PH-MO1 | 13.47 | −1.290 | 2.2 |
| ACN | PH-AON | 7.76 | −2.940 | 1.1 |
The EIFs show the efficiency of the imprinting procedure,40 determined by the ratio between the rebinding capacity of the synthesised MIP and a NIP (non-imprinted polymer) made at the same conditions without the TM. Hence a NIP contains no specific cavity sites for the chosen TM; therefore it measures only generic surface binding, if any.
By comparing the HB times and EIFs, it can be seen that ACN offers the worse EIF at 1.1 and, significantly, the shortest HB time. MAA follows as the second-lowest EIF at 2.2, with the second short HB time. Both HEMA and ACA have similar HB times along with equivalent EIFs. Lastly, IA has the best EIF while producing the longest HB time as each carbonyl group contributes synergistically to the formation of HBs. These results indicate that the FLX complex with the longest HB time will convey the more favourable self-assembly pre-polymerisation system. Moreover, all systems' preferred atom pair for HB time consisted of FLX as the hydrogen donor and varying acceptors depending on the FM (see Table S4†). The carbonyl, as acceptor group, in IA, ACA and MAA can be ranked considering the number of carbonyl groups and substituents size attached to the carbonyl (see Fig. 4 and 5) as IA > ACA > MAA, which correlates with their EIFs. It is worth noticing that in HEMA, the preferred acceptor was the ester oxygen, even with a carbonyl group available. Finally, ACN only offers one acceptor group, a primary amine that ranked last in respect to EIF.
While the predicted HB time is a fingerprint of the quality of the TM–FM complex, the KBI analysis conveys information about the whole pre-polymerisation mixture, i.e. not only the TM–FM complex interactions. To facilitate the analysis, the full KBI curves as a function of r, the distance between the relevant atom pairs (from 0 to the maximum length of the simulation box), are plotted in Fig. 8a. The KBI value reported in Table 3 corresponds to the limiting value at rmax.
 | ||
| Fig. 8 a) The full KBI curves for the FM atom pairs in Table 3. b) Zoom into the KBI complexation region from 0 to 1 nm. | ||
For an open system, the KBI can be split into two main regions;46 the first is the excluded volume, Vex, which is defined as the region from the centre of the atoms in which the g(r) ≅ 0, hence KBI is always negative, for a spherical particle with hard-core diameter σ, Vex = 4πσ3/3.46 The second region, the remaining of the KBI excluding Vex, fluctuates between negative or positive values depending on the strength of the molecular interactions. The values of the KBIs for pure Lennard–Jones (LJ) particles46 can be used as references for the analysis of Fig. 8a. In general, the KBI limiting value for a LJ fluid with gas-like density and low interactions will be positive, while highly dense interactive fluids will be negative. The liquid densities of our studied MIP systems are similar; as such, the positive KBI limiting value for ACA implies the lowest level of interactions away from the complexation region. An ideal FM will have a high HB time, while its KBI limiting value is negative, as time will be expending exploring the complexation region rather than interacting with other molecules in the pre-polymerisation mixture, increasing the probability of an efficient TM–FM complex, this two factors once again points to IA as the best FM for this system.
Finally, focusing our attention into the KBI complexation region from 0 to 1 nm (Fig. 8b), where the attractive forces should overcome the repulsion of the atoms core in a good complex, we can notice that the KBIs' slopes, calculated between 0 to 0.5 nm are ranked as IA(a+b) = −1.36; IAa = −0.69; IAb = −0.67; ACN = −0.65; MAA = −0.64; HEMA = −0.62 and ACA = −0.60. This further characteristic is added to our FMs' computational selection criteria.
Conclusions
Fluoxetine molecularly imprinted polymers pre-polymerisation mixtures with variations on functional monomer were simulated using molecular dynamics to analyse self-assembly characteristics of the template molecule/functional monomer complex. The specific functional monomers used were methacrylic acid, itaconic acid, 2 (hydroxyethyl)methacrylate, acrylamide and acrylonitrile. Analysis on the simulated systems was completed through RDFs and hydrogen bonding time, as well as comparing KBI initial slopes and limiting values with the performance of the experimental systems. The computational analysis is validated by the previous experimental work in the same system, making itaconic acid the best functional monomer for fluoxetine removal from wastewater via molecularly imprinted polymers. Moreover, these results show that this computational method offers a general approach for the rational design of MIPs prior to experimental production, specifically with the difficult choice of functional monomer.Author contributions
William Battell: formal analysis, investigation, methodology, software, validation, visualisation, writing-original draft. Gaël Donval: software, writing – review & editing. Bernardo Castro-Dominguez: supervision, writing – review & editing. Carmelo Herdes: conceptualisation, formal analysis, methodology, project administration, resources, supervision, validation, visualisation, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Acknowledgement to the EPSRC for the PhD grant of William Battell. Access granted to Balena the High-Performance Computing facility at the University of Bath is also recognised.References
- K. Adamczak, noPills report 2012-2015, Kronprinzenstrasse 24, 45128 Essen, Germany. Edition June 2015, Accessed on 13 Sep. 21, http://www.no-pills.eu/conference/BS_NoPills_Final%20Report_summary_EN.pdf Search PubMed.
- A. Ginebreda, D. Barceló and S. Rodríguez-Mozaz, Environmental Risk Assessment of Pharmaceuticals in Wastewater Treatment, in The Handbook of Environmental Chemistry, Springer, Berlin, Heidelberg, 2020 Search PubMed.
- N. N. Koopaei and M. Abdollahi, J. Pharm. Sci., 2017, 25, 9 Search PubMed.
- L. F. Angeles, R. A. Mullen, I. J. Huang, C. Wilson, W. Khunjar, H. I. Sirotkin, A. E. McElroy and D. S. Aga, Environ. Sci.: Water Res. Technol., 2020, 6, 62 RSC.
- C. Gadipelly, A. Perez-Gonzalez, G. D. Yadav, I. Ortiz, R. Ibanez, V. K. Rathod and K. V. Marathe, Ind. Eng. Chem. Res., 2014, 53, 11571–11592 CrossRef CAS.
- D. T. Wong, K. W. Perry and F. P. Bymaster, Nat. Rev. Drug Discovery, 2005, 4, 764 CrossRef CAS PubMed.
- Medical Expenditure Panel Survey (MEPS) 2008-2018, Agency for Healthcare Research and Quality (AHRQ), Rockville, MD, Accessed on 13 Sep. 21, https://www.ahrq.gov/data/meps.html Search PubMed.
- NHS Business Services Authority, Prescription Cost Analysis (PCA) data, Accessed on 13 Sep. 21, https://www.nhsbsa.nhs.uk/prescription-data/dispensing-data/prescription-cost-analysis-pca-data Search PubMed.
- J. Corcoran, M. J. Winter and C. R. Tyler, Crit. Rev. Toxicol., 2010, 40, 287–304 CrossRef CAS PubMed.
- A. T. Ford, B. Hyett, D. Cassidy and G. Malyon, Ecotoxicology, 2018, 27, 477–484 CrossRef CAS PubMed.
- M. HedayatiRad, M. A. Nematollahi, M. N. Forsatkar and C. Brown, Ecotoxicol. Environ. Saf., 2017, 140, 84–88 CrossRef CAS PubMed.
- W. Brooks, C. M. Foran, S. M. Richards, J. Weston, P. K. Turner, J. K. Stanley, K. R. Solomon, M. Slattery and T. W. La Point, Toxicol. Lett., 2003, 142, 169–183 CrossRef PubMed.
- L. F. Angeles, R. A. Mullen, I. J. Huang, C. Wilson, W. Khunjar, H. I. Sirotkin, A. E. McElroy and D. S. Aga, Environ. Sci.: Water Res. Technol., 2020, 6, 62 RSC.
- O. Frédéric and P. Yves, Chemosphere, 2014, 115, 31–39 CrossRef PubMed.
- D. L. Huang, R. Z. Wang, Y. G. Liu, G. M. Zeng, C. Lai, P. Xu, B. A. Lu, J. J. Xu, C. Wang and C. Huang, Environ. Sci. Pollut. Res., 2015, 22, 963–977 CrossRef CAS PubMed.
- K. Haupt and K. Mosbach, Chem. Rev., 2000, 100, 2495–2504 CrossRef CAS PubMed.
- S. Ansari and M. Karimi, Talanta, 2017, 167, 470–485 CrossRef CAS PubMed.
- S. Ansari and M. Karimi, TrAC, Trends Anal. Chem., 2017, 89, 146–162 CrossRef CAS.
- E. Sari, R. Üzek, M. Duman and A. Denizli, J. Biomater. Sci., Polym. Ed., 2018, 11, 1302–1318 CrossRef PubMed.
- Z. Terzopoulou, M. Papageorgiou, G. Z. Kyzas, B. N. Bikiaris and D. A. Lambropoulou, Anal. Chim. Acta, 2016, 913, 63–75 CrossRef CAS PubMed.
- A. Adumitrăchioaie, M. Tertiş, A. Cernat, R. Săndulescu and C. Cristea, Int. J. Electrochem. Sci., 2018, 13, 2556–2576 CrossRef.
- T. Zhou, A. Halder and Y. Sun, Biosensors, 2018, 8, 82 CrossRef CAS PubMed.
- R. Wang, J. Pan, M. Qin and T. Guo, Eur. Polym. J., 2019, 110, 1–8 CrossRef CAS.
- Y. Saylan, S. Akgönüllü, D. Çimen, A. Derazshamshir, N. Bereli, F. Yilmaz and A. Denizli, Sens. Actuators, B, 2017, 241, 446–454 CrossRef CAS.
- A. Speltini, A. Scalabrini, F. Maraschi, M. Sturini and A. Profumo, Anal. Chim. Acta, 2017, 974, 1–26 CrossRef CAS PubMed.
- S. Ansari, TrAC, Trends Anal. Chem., 2017, 90, 89–106 CrossRef CAS.
- S. Shoravi, G. D. Olsson, B. C. G. Karlsson and I. A. Nicholls, Int. J. Mol. Sci., 2014, 15, 10622–10634 CrossRef CAS PubMed.
- I. A. Nicholls, K. Golker, G. D. Olsson, S. Suriyanarayanan and J. G. Wiklander, Polymer, 2021, 13(17), 2841 CAS.
- O. Jamieson, F. Mecozzi, R. D. Crapnell, W. Battell, A. Hudson, K. Novakovic, A. Sachdeva, F. Canfarotta, C. Herdes, C. E. Banks, H. Snyder and M. Peeters, Phys. Status Solidi A, 2021, 218, 2100021 CrossRef CAS.
- S. A. Piletsky, K. Karim, E. V. Piletska, C. J. Day, K. W. Freebairn, C. Legge and A. P. F. Turner, Analyst, 2001, 126, 1826–1830 RSC.
- B. Zhang, X. Fan and D. Zhao, Polymer, 2019, 11(1), 17 Search PubMed.
- T. F. D. Pereira, A. T. M. da Silva, K. B. Borges and C. S. Nascimento Jr, J. Mol. Struct., 2019, 1177, 101–106 CrossRef CAS.
- F. Bates, M. Busato, E. Piletska, M. J. Whitcombe, K. Karim and A. Guerreiro, Sep. Sci. Technol., 2017, 52, 1441–1453 CrossRef CAS.
- K. Golker, B. C. G. Karlsson, A. M. Rosengren and I. A. Nicholls, Int. J. Mol. Sci., 2014, 15, 20572–20584 CrossRef CAS PubMed.
- T. Curk, J. Dobnikar and D. Frenkel, Soft Matter, 2016, 12, 35–44 RSC.
- C. Herdes and L. Sarkisov, Langmuir, 2009, 25, 5352–5359 CrossRef CAS PubMed.
- E. Dourado, C. Herdes, P. R. V. Tassel and L. Sarkisov, Int. J. Mol. Sci., 2011, 12(18), 4781–4804 CrossRef CAS PubMed.
- L. Bird and C. Herdes, Mol. Syst. Des. Eng., 2018, 3, 89–95 RSC.
- E. Daniels, Y. L. Mustafa, C. Herdes and H. S. Leese, ACS Appl. Bio Mater., 2021, 4(9), 7243–7253 CrossRef CAS.
- A. D. Hudson, R. Mestres, J. Ueta, W. Battell, O. Jamieson, T. Dunbar, B. Macia and M. Peeters, Biomimetics, 2019, 4, 18 CrossRef CAS PubMed.
- W. L. Jorgensen, D. S. Maxell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- A. K. Malde, L. Zuo, M. Breeze, M. Stroet, D. Poger, P. C. Nair, C. Oostenbrink and A. E. Mark, J. Chem. Theory Comput., 2011, 7, 4026–4037 CrossRef CAS PubMed.
- H. J. C. Berendsen, D. van der Spoel and R. van Drunen, Comput. Phys. Commun., 1995, 91, 43–56 CrossRef CAS.
- D. Frenkel and S. Berend , Understanding Molecular Simulation: From Algorithms To Applications, Second, Elsevier, 2002 Search PubMed.
- J. G. Kirkwood and F. P. Buff, J. Chem. Phys., 1951, 19, 774 CrossRef CAS.
- A. Ben-Naim, J. Chem. Phys., 2008, 128, 234501 CrossRef PubMed.
- C. Dalvit, C. Invernizzi and A. Vulpetti, Chem. – Eur. J., 2014, 20, 11058–11068 CrossRef CAS PubMed.
- K. Golker, G. D. Olsson and I. A. Nicholls, Eur. Polym. J., 2017, 92, 137–149 CrossRef CAS.
- A. R. Leach, Molecular Modelling: Principles and applications, Prentice Hall, Pearson Education, 2nd edn, 2001 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1me00142f |
| This journal is © The Royal Society of Chemistry 2022 |