Deep learning neural network potential for simulating gaseous adsorption in metal–organic frameworks

Abstract

This study proposes ab initio neural network force fields with physically motivated features to offer superior accuracy in describing adsorbate–adsorbent interactions of nonpolar (CO₂) and polar (H₂O and CO) molecules in metal–organic frameworks with open-metal sites. Effects of the neural network architecture and features are also investigated for developing accurate models.

---

Metal–organic Frameworks (MOFs) have exhibited great potential in a variety of applications such as gas separation,^1,2 energy storage,³ and catalysis.⁴ Through combinations of metal clusters and organic linkers, a variety of MOFs can be synthesized with diverse topological and chemical properties. To identify optimal MOFs, molecular simulations play a critical role. A prerequisite of such materials exploration is the capability of the adopted molecular potential in accurately describing adsorbate–adsorbent interactions.⁵ Although generic force fields such as universal force field (UFF)⁶ have been shown to generally yield reasonable predictions,^7,8 failures are still frequently observed such as for MOFs with open-metal sites.⁹ Therefore, there has been a need to parameterize potentials using an approach often based on ab initio calculations such as density functional theory.¹⁰ As an example of such an effort, Sholl and co-workers^11–13 proposed a method that optimizes two global scaling factors applied to the Lennard-Jones potential with the aim of best representing DFT-computed reference energies. Accurate force fields were developed for describing CO₂ adsorption in zeolites¹¹ as well as H₂O in CuBTC,¹² although an extra empirical term was needed for the latter for satisfactory results. Smit and co-workers⁵ proposed an approach using so-called “approaching paths” to iteratively optimize the potential parameters for each pair of dissimilar atom types, and this approach was applied to study the adsorption of CO₂, N₂, and H₂O in M-MOF-74 (M = Mg, Zn, Mn, etc.). Considering the importance of polarizability,^14,15 Vlugt and co-workers¹⁶ developed a polarizable force field for CO₂ adsorption in M-MOF-74 using energies computed by DFT. While significant progress has been made to date, their fitting outcomes may also benefit from error cancellations. These approaches rely on a given set of potential formulae that may not faithfully describe molecular interactions; as reported in ref. 5, noticeable deviations between the force-field-computed energies and the DFT-calculated references still existed.⁵

Machine learning (ML) is a powerful means that can interpret data in complicated forms and make accurate predictions, which may show promise for describing highly complex intermolecular interactions for gaseous adsorption in porous materials. ML has been applied in a variety of applications such as image recognition,¹⁷ speech recognition,¹⁸ drug discovery and development,¹⁹ as well as chemistry and materials science.^20–23 The potential of ML for describing intermolecular interactions, however, has not yet been explored. To date, ML force fields using artificial neuron networks (ANN), the so-called Behler–Parrinello neural networks, have been reported to compute potential energy surfaces of systems by summing the atomic energies of each of the involved elements (i.e. one neural network (NN) per element type).^24,25 Using this NN framework, deep potential molecular dynamics was developed along with features that encode the atomic structures (configurations) using relative coordinates with respect to a reference atom.^26,27 Generally, the features (or descriptors) are global and local in scope.²⁸ The global features (ex: Coulomb matrix²⁹ and Ewald sum matrix³⁰) capture bulk structure information, while the local features (ex: atom-centered symmetry functions³¹ and smooth overlap of atomic positions³²) capture the regional information of the bulk. Applying Behler–Parrinello NNs to predict adsorbate–adsorbent interactions for gaseous adsorption may lead to an excess of parameters, given that host materials can involve chemically diverse environments (several NNs will be needed). In adsorption applications, porous materials are also generally treated as rigid such that the total energies of the adsorbents are not of interest. Besides, the adsorbate–adsorbent interactions are dominated by non-bonded forces and therefore the aforementioned features may not be well suited. Thus, new developments with a simplified architecture and a feature set designed for adsorption applications are needed.

Herein, we report a first-of-its-kind deep neural network (DNN) potential to describe adsorbate–adsorbent interactions for gaseous adsorption in MOFs. The adsorption of CO₂, H₂O, and CO in Mg-MOF-74 was focused on herein. DNN models were developed with features containing information regarding physical short- and long-range interactions, as schematically illustrated in Fig. 1. In these models, the distances (r_ij) between each distinct atom type of the adsorbate and that of the adsorbent were computed. Using H₂O in Mg-MOF-74 as an example, the adsorbate contains two distinct atom types (i.e., H and O) while the framework has nine different types (i.e., magnesium, three different oxygens, four distinct carbons, and hydrogen). This leads to a total of 18 different adsorbate–adsorbent atom-type pairs. For each pair, N smallest pair distances were adopted to represent the adsorption environment with N being a hyperparameter of the DNN model. Further, rather than directly using the pair distances as the inputs to the DNN model, the distances in forms of Born–Mayer³³ expression, Coulombic interaction, and dispersion multipoles were used to reflect the fundamental adsorption behaviors for the benefit of physics-assisted training. In this study, we set N = 4 and the DNN architecture comprised of 5 hidden layers and 50 neurons per layer, unless otherwise noted. The number of parameters involved in the resulting DNN model was more than 30,000. More details can be found in ESI.†

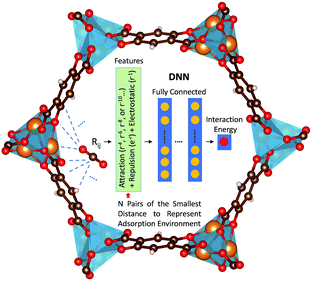Fig. 1 Illustration of the proposed features and DNN for modeling adsorbate–adsorbent interactions in MOFs. The blue dashed lines illustrate the atom pairs between the adsorbate and the adsorbent. More details can be found in ESI.†

We first investigated the capabilities of several common ML algorithms, including DNNs, random forests (RF), k-nearest neighbors (KNN), and support vector machines (SVM) in interpreting adsorbate–adsorbent interactions for both CO₂ and H₂O adsorbed in Mg-MOF-74. Their corresponding Henry coefficients (K_H) of adsorption were also calculated. Herein, the previously developed force fields using DFT by Lin et al.⁵ were utilized to generate reference energies for training and testing. A dataset consisting of random configurations was generated using Monte Carlo (MC) simulations in a canonical ensemble at a high temperature of 8,000 K. DNN was found capable of describing the interactions of CO₂ and H₂O with Mg-MOF-74 at a superior accuracy as compared to other ML algorithms (Fig. 2(a) and (b)). DNN-predicted values resemble those computed by the reference force field in a wide energy range from as small as −40 kJ mol⁻¹ for CO₂ and −65 kJ mol⁻¹ for H₂O to as large as 80 kJ mol⁻¹. By contrast, RF and KNN show considerable deviations. SVM overestimates interactions in the low energy region, while it underestimates energies above 0 kJ mol⁻¹. We note that, considering that it is rather computationally expensive to employ DFT or other quantum chemical methods to obtain reference energies, a small training set size of 2400 points was used. These results are also reflected in the computed K_H values at 300 K as shown in Fig. 2(c) and (d). Using merely 2400 data points for training the ML models, the developed DNN can yield Henry coefficients that are in excellent agreement with those by the force field of Lin et al.⁵ RF, KNN, and SVM underestimate the values, even with a size of training set to be as large as 80 000 points (Fig. 2(c) and (d)).

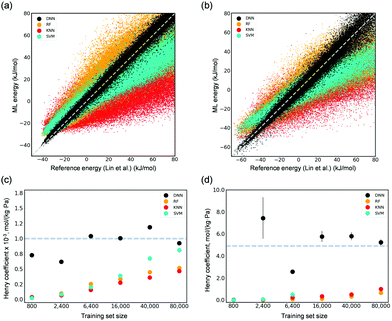Fig. 2 Parity plots of the ML-predicted (DNN, RF, KNN, and SVM models trained with 2400 points) energies and reference values computed by the force field of Lin et al.⁵ for 0.4 M unseen points regarding (a) CO₂ adsorption and (b) H₂O adsorption in Mg-MOF-74. Calculated Henry's coefficients of (c) CO₂ and (d) H₂O adsorbed in Mg-MOF-74 as a function of the training size from as small as 800 to as large as 80 000. The dotted lines in (c) and (d) represent the reference value (i.e., ∼1.0 × 10⁻³ mol (kg⁻¹ Pa⁻¹) for CO₂ and ∼5 mol (kg⁻¹ Pa⁻¹) for H₂O) computed by the force field of Lin et al.

The energy distribution of the training set was found critical in developing accurate ML models. Training datasets with a focus on different energy regions (i.e., randomly distributed vs. biased toward the low-energy region), obtained by MC at different temperatures (Fig. S1, ESI†), were used to train models for comparison. As shown in Fig. S2a and b (ESI†), DNN prefers a diverse training set, since DNN is based on the weights associated with neurons, so a diverse training set is anticipated to help train a robust model. RF, KNN, and SVM can also predict accurate K_H values with biased datasets. In RF regression, the trees are developed by asking questions regarding features to minimize the metrics (e.g., mean squared error). Therefore, a training set with more low-energy configurations helps in developing nodes with purity. However, when the query point is an unfavorable adsorption configuration but with similar configurational features to favorable configurations, it can be mis-predicted as a lower energy configuration. The same scenario also applies to KNN. These can be seen in Fig. S3 and S4 (ESI†) for their inaccuracy in predicting energies greater than 0 kJ mol⁻¹. A similar behavior was also observed for the SVM model. More details concerning the ML algorithms are presented in ESI.† Overall, DNN prevails among the common ML algorithms.

DFT-derived DNN force fields were developed for the adsorption of CO₂ and H₂O in Mg-MOF-74, and their accuracy was compared to existing force fields (i.e., UFF⁶ and the force field developed by Lin et al.⁵). The aforementioned scaling factor approach¹¹ was also employed herein for comparison. The DNN models and the scaling factors for these systems were trained using the DFT-computed reference energies from the work of Lin et al.⁵ that contains configurations of a wide spectrum of the energy (Fig. S5, ESI†). These DFT-computed reference data are made available in the ESI,† including both of their interaction energy and adsorption configuration. Our developed DNN models are shown in Fig. 3 to be much more accurate in representing adsorbate–adsorbent interactions, including configurations at both small (near the surface of the framework) and large distances (e.g., 3.0–5.0 Å) from the framework; using CO₂ as an example, the root mean squared error (RMSE) for the computed adsorption energies is as small as 1.15 kJ mol⁻¹, a value that is notably smaller than other classical potentials. The UFF-predicted energies are greatly overestimated with a large RMSE (CO₂) of 6.90 kJ mol⁻¹ because of the spuriously steep repulsive (i.e., r¹²) region of the potential.⁵ For the DFT-derived force field reported by Lin et al.,⁵ while it as expected decently predicts adsorption energy, noticeable deviations between the force field-computed energies and DFT-computed energies still exist, a RMSE (CO₂) of 2.25 kJ mol⁻¹. We note that, in Monte Carlo simulations for adsorption properties, configurations of lower energies (i.e., favorable adsorption) play a significantly more important role. While configurations with an energy greater than 10 kJ mol⁻¹ are included in the model training, they are excluded in the abovementioned RMSE calculations for the test set. The superior accuracy of the DNN model is even more pronounced for the case of H₂O (Fig. 3(c) and (d)). With respect to the scaling approach, employing only two scaling parameters appears to be too limited to succeed in accurately modeling this rather complex system. Overall, these results illustrate the inevitable limitation of force fields that employ a specific functional form. These limitations are additionally reflected in the computed K_H values. The CO₂ Henry coefficients computed by the DNN model, the force fields of Lin et al.,⁵ and the scaling approach are 3.0 × 10⁻³, 1.0 × 10⁻³, and 1.1 × 10⁻⁵ mol (kg⁻¹ Pa⁻¹), respectively, and the former two agree well with the experimental value³⁴ of 2.0 × 10⁻³ mol (kg⁻¹ Pa⁻¹). Both the DNN model and the potential by Lin et al.⁵ predicted comparable K_H values in the H₂O adsorption (i.e., 4.07 ± 0.50 and 4.81 ± 1.11 mol (kg⁻¹ Pa⁻¹), respectively). To extend this work to a system with electronic properties that could pose a challenge to conventional force fields, a DFT-derived DNN force field for CO adsorption was also developed using a total of 2000 CO adsorption configurations in the distance of 2.0–5.5 Å from the framework (Fig. S5, ESI†). The parity plot again shows outstanding description of CO adsorption in Mg-MOF-74 by DNN as compared to existing methods (Fig. 3(e) and (f)); a Henry coefficient of 5.5 × 10⁻⁵ mol (kg⁻¹ Pa⁻¹) was predicted.

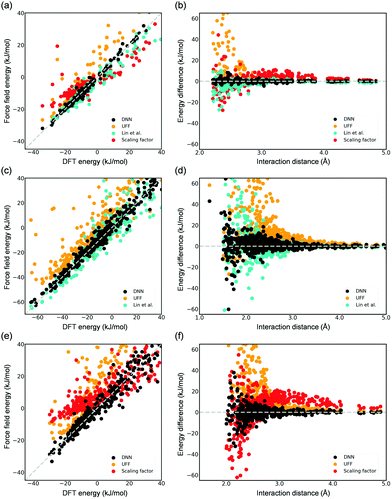Fig. 3 Parity plots of the DFT-computed energy (test sets) and those by the developed DNN force field, UFF, the force field reported by Lin et al.,⁵ or the parameterized potential using the scaling factor (a) CO₂ (1.15, 6.90, 2.25, 6.34), (c) H₂O (3.05, 18.58, 10.92), and (e) CO (5.64, 25.21, 13.46) adsorption in Mg-MOF-74. The values in the parentheses show the respective root mean square error (RMSE, kJ mol⁻¹) for each studied model following the order in the legends. Note that only configurations with DFT-computed energies to be less than 10 kJ mol⁻¹ are included in the RMSE values as mentioned in the text. (b), (d), and (f) are the corresponding energy deviation from the DFT references as a function of the shortest distance between the adsorbate and the Mg-MOF-74 framework. See Fig. S6 in the ESI† for the computed energy values as a function of interaction distance.

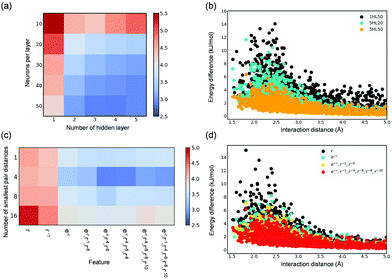
In the development of accurate NN potentials, two architecture parameters, i.e., the number of hidden layers and the number of neurons per hidden layer, can greatly affect their accuracy (i.e., RMSE of the test set). As shown in Fig. 4(a), deeper learning notably improves the overall description of the adsorbate–adsorbent interactions in a wide range of adsorption distance. This can also be seen from the energy deviation as a function of the shortest H₂O–MOF distance as shown in Fig. 4(b); using five hidden layers, relative to only one, offers a much more accurate energy prediction for configurations at distances ranging from 1.5 Å to 5.0 Å that are associated with both repulsive and attractive regions. Besides, to have a small RMSE, a sufficiently large number of neurons per hidden layer (≥20 in this case) is required. Particularly, the number of neurons per hidden layer was found to improve short-range interaction. By comparing the energy deviations of NNs (five hidden layers) with 50 neurons per hidden layer and with 20, the energy deviation largely diminishes primarily in the distance of approximately 2.5 Å, suggesting that the repulsive behavior is better described (Fig. 4(b)). Overall, employing deeper NN seems to improve the overall descriptions of interaction energies, while the number of neurons per hidden layer appears to facilitate predictions of adsorption energy for configurations at short distances from the framework.

Fig. 4 Average RMSE of NN-predicted energies vs. DFT-computed references for configurations of the test sets as a function of (a) the number of hidden layers and neurons per layer and (c) different features and the number of shortest pair distances. (b) and (d) average of the absolute difference between NN-computed energy and the DFT reference as a function of the shortest distance for selected combinations of the parameters. nHLm represents n hidden layers with m neurons per layer. Results shown in the figure are based on 100 different trained NN models for each combination of the model parameters. Configurations with interaction energies less than 10 kJ mol⁻¹ were considered in (a)–(d). 5HL50 was used for results presented in (c) and (d).

NN models presented so far have adopted features resembling of physical interactions-Pauli repulsion (e^−r), dispersion forces (r⁻⁴, r⁻⁶, r⁻⁸, r⁻¹⁰), and coulombic interactions (r⁻¹). As shown in Fig. 4(c), these physically motivated features indeed result in more accurate DNN force fields to better describe adsorbent–adsorbate interactions. Moreover, the behavior of resulting DNN models is directly reflected on the physical meaning of the adopted input features. As shown in Fig. 4(d), the energy predictions of DNN models with e^−r, which has been known to resemble the inter-atomic repulsive behavior, as compared to only the r term noticeably reduce the energy deviation for configurations with a short distance of less than 3.0 Å from the framework. Further, by adding features representing dispersive forces, energy deviation is overall reduced. Note incorporating more terms of dispersion multipole expansions as the input features does not lead to a better result (Fig. S7, ESI†), as the models are prone to overfitting and thus a higher RMSE of the test set was observed. This also explains the results regarding the choice of the number of the smallest pair distance (N); Fig. 4(c) shows an optimum value of 4, which justified the implementation of N = 4 in this study. It should be however noted that using more dispersion terms and more pair distances (i.e., larger N) may result in more accurate models when a larger training dataset is available.

Conclusions

This study demonstrates the great promise of DNN potentials in describing adsorbate–adsorbent interactions for simulating gaseous adsorption. With a few thousand reference points, the resulting first-principles DNN force fields can accurately predict a wide range of interaction energy for nonpolar (CO₂) and polar (H₂O and CO) molecules adsorbed in open-metal site MOFs and yield accurate Henry coefficients. Employing DNN models can also enable highly accelerated Monte Carlo simulations; compared to classical non-polarizable potentials, DNN can be as much as 100 times faster. We note that, while only Henry coefficients are computed in this work, the DNN model can be incorporated with classical potentials for adsorbate–adsorbate interactions such that a variety of other properties including adsorption isotherms can be computed. Besides, it is anticipated that this approach can be applied to a variety of other adsorbate and/or adsorbent systems. To facilitate the development of their DNN models, various techniques such as transfer learning may be used, particularly for similar systems, such that the required training size and time can be greatly reduced. For adsorption in flexible frameworks, accurate DNN models may also be developed with adsorption configurations in frameworks of different conformations as the training data. Overall, this work paves the ways for a paradigm shift in molecular potentials adopted in molecular simulations for gaseous adsorption.

Author contributions

C.-T. Y. and L.-C. L. conceived the proposed idea, performed machine learning, developed DNN models, conducted Monte Carlo calculations, and drafted the manuscript. I. P. and D. T. generated DFT dataset for training of CO DNN model. C.-C. C. supervised I. P. J. D. H. supervised I. P. and D. T., revised manuscript, and provided inputs to the result analysis.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

L.-C. L. greatly appreciates the support from the Yushan Young Scholar program (Ministry of Education in Taiwan, NTU-110VV009) and the Ministry of Science and Engineering in Taiwan (MOST 110-2222-E-002-011-MY3). We also gratefully acknowledge computational resources from the Ohio Supercomputer Center and the National Center for High-performance Computing (Taiwan). I. P., D. T., C.-C. C., and J. D. H. graciously acknowledge support in the form of computational resources from the Texas Tech University High Performance Computing Center.

References

1. J.-R. Li, J. Sculley and H.-C. Zhou, Chem. Rev., 2012, 112, 869–932.
2. C. A. Trickett, A. Helal, B. A. Al-Maythalony, Z. H. Yamani, K. E. Cordova and O. M. Yaghi, Nat. Rev. Mater., 2017, 2, 17045.
3. R. B. Getman, Y.-S. Bae, C. E. Wilmer and R. Q. Snurr, Chem. Rev., 2012, 112, 703–723.
4. M. Yoon, R. Srirambalaji and K. Kim, Chem. Rev., 2012, 112, 1196–1231.
5. L.-C. Lin, K. Lee, L. Gagliardi, J. B. Neaton and B. Smit, J. Chem. Theory Comput., 2014, 10, 1477–1488.
6. A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. Goddard III and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035.
7. A. Ö. Yazaydın, R. Q. Snurr, T.-H. Park, K. Koh, J. Liu, M. D. LeVan, A. I. Benin, P. Jakubczak, M. Lanuza, D. B. Galloway, J. J. Low and R. R. Willis, J. Am. Chem. Soc., 2009, 131, 18198–18199.
8. B. Liu and B. Smit, Langmuir, 2009, 25, 5918–5926.
9. R. Krishna and J. M. van Baten, Phys. Chem. Chem. Phys., 2011, 13, 10593–10616.
10. A. L. Dzubak, L.-C. Lin, J. Kim, J. A. Swisher, R. Poloni, S. N. Maximoff, B. Smit and L. Gagliardi, Nat. Chem., 2012, 4, 810–816.
11. H. Fang, P. Kamakoti, J. Zang, S. Cundy, C. Paur, P. I. Ravikovitch and D. S. Sholl, J. Phys. Chem. C, 2012, 116, 10692–10701.
12. J. Zang, S. Nair and D. S. Sholl, J. Phys. Chem. C, 2013, 117, 7519–7525.
13. H. Fang, R. Awati, S. E. Boulfelfel, P. I. Ravikovitch and D. S. Sholl, J. Phys. Chem. C, 2018, 122, 12880–12891.
14. J. Cirera, J. C. Sung, P. B. Howland and F. Paesani, J. Chem. Phys., 2012, 137, 054704.
15. P. Mishra, S. Edubilli, B. Mandal and S. Gumma, J. Phys. Chem. C, 2014, 118, 6847–6855.
16. T. M. Becker, J. Heinen, D. Dubbeldam, L.-C. Lin and T. J.-H. Vlugt, J. Phys. Chem. C, 2017, 121, 4659–4673.
17. G. E. Hinton, S. Osindero and Y.-W. Teh, Neural Comput., 2006, 18, 1527–1554.
18. G. Hinton, L. Deng, D. Yu, G. E. Dahl, A.-R. Mohamed, N. Jaitly, A. Senior, V. Vanhoucke, P. Nguyen, T. N. Sainath and B. Kingsbury, IEEE Signal Process. Mag., 2012, 29, 82–97.
19. J. Vamathevan, D. Clark, P. Czodrowski, I. Dunham, E. Ferran, G. Lee, B. Li, A. Madabhushi, P. Shah, M. Spitzer and S. Zhao, Nat. Rev. Drug Discovery, 2019, 18, 463–477.
20. J. Gasteiger and J. Zupan, Angew. Chem., Int. Ed. Engl., 1993, 32, 503–527.
21. K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Nature, 2018, 559, 547–555.
22. J. Schmidt, M. R.-G. Marques, S. Botti and M. A.-L. Marques, npj Comput. Mater., 2019, 5, 83.
23. S. Chong, S. Lee, B. Kim and J. Kim, Coord. Chem. Rev., 2020, 423, 213487.
24. J. Behler, J. Chem. Phys., 2016, 145, 170901.
25. J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401.
26. L. Zhang, J. Han, H. Wang, R. Car and E. Weinan, Phys. Rev. Lett., 2018, 120, 143001.
27. H. Wang, L. Zhang, J. Han and E. Weinan, Comput. Phys. Commun., 2018, 228, 178–184.
28. L. Himanen, M. O.-J. Jäger, E. V. Morooka, F. F. Canova, Y. S. Ranawat, D. Z. Gao, P. Rinke and A. S. Foster, Comput. Phys. Commun., 2020, 247, 106949.
29. M. Rupp, A. Tkatchenko, K.-R. Müller and O. A. von Lilienfeld, Phys. Rev. Lett., 2012, 108, 058301.
30. F. Faber, A. Lindmaa, O. A. von Lilienfeld and R. Armiento, Int. J. Quantum Chem., 2015, 115, 1094–1101.
31. J. Behler, J. Chem. Phys., 2011, 134, 074106.
32. A. P. Bartók, R. Kondor and G. Csányi, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 184115.
33. A. A. Abrahamson, Phys. Rev., 1969, 178, 76–79.
34. J. A. Mason, K. Sumida, Z. R. Herm, R. Krishna and J. R. Long, Energy Environ. Sci., 2011, 4, 3030–3040.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d1ma01152a

---