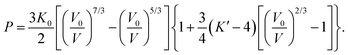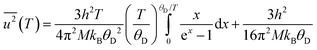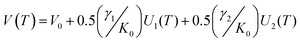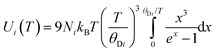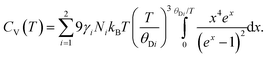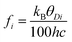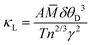Low-intermediate-temperature, high-pressure thermoelastic and crystallographic properties of thermoelectric clausthalite (PbSe-I)

Abstract

The thermoelastic properties of the rock-salt structured thermoelectric lead selenide (clausthalite, PbSe-I) have been determined using neutron powder diffraction techniques for the temperature interval 10–500 K at ambient pressure, and 0–5.2 GPa at 298, and 150 K. Within this temperature range, lead selenide can be described using the same self-consistent phenomenological model developed for the isostructural phases lead sulfide (PbS) and lead telluride (PbTe) in which the cations and anions behave as independent Debye oscillators (vibrational Debye temperatures of PbSe-I: Pb 111(1) K, Se 205(1) K). Simultaneous fitting of the unit cell volume and isochoric heat capacity to a two-term Debye internal energy function gives characteristic temperatures of 104(3) K and 219(5) K in excellent agreement with the two vibrational Debye temperatures derived from fitting the individual atomic displacement parameters. Grüneisen constants for the two term fits are 1.79 and 2.28 for the lower and upper characteristic temperature respectively. The calculated thermodynamic Grüneisen parameter increases monotonically from 2.03 at 10 K, to a maximum 2.22 at 100 K before decreasing back to 2.00 at 298 K and is broadly in agreement with the average of the two Grüneisen parameters associated with the two-term internal energy function. Despite the simplicity of the model, the calculated phonon density of states that is implicit within the two-term Debye model is found to show fair agreement with the full and partial vibrational densities of states derived from density functional theory (DFT). The bulk modulus and its pressure derivative at 298 K are 47.9(4) GPa and 5.4(2) respectively by fitting the pressure dependence of the unit cell volume to a 3rd order Birch-Murnaghan equation-of-state. For lower temperatures (T < 300 K) the high-pressure transition to PbSe-II is associated with a steep initial Clapeyron slope of 151 K GPa⁻¹.

---

Introduction

Lead chalcogenides of general formula PbX (X = S, Se, Te) crystallize in the rocksalt structure in space group Fm3̄m (phase I) at ambient temperature and pressure.^1,2 In PbSe, a structural phase transition to an orthorhombic phase, PbSe-II, has been identified by pressure-dependent resistivity and volumemtric measurements to occur at 4.2 GPa at ambient temperature.¹ The space group and crystal structure of this phase still remain contentious but do not form part of this submission which only concerns the thermoelastic properties of thermoelectric PbSe-I.

The narrow-band-gap PbX semiconductors have been intensively studied due to their electronic structure and properties^2–5 and the band gap behaviour under pressure.⁶ They have also attracted considerable interest as functional materials for a range of applications, which includes thin-film field-effect transistors⁷ thermophotovoltaic energy converters⁸ laser diodes⁹ and infra-red sensors.¹⁰

Much of the recent interest in lead chalcogenides and their derivatives arises from their promising thermoelectric properties.^11,12 The ability to convert otherwise waste heat directly into electrical power, afforded by a thermoelectric device, offers the potential to achieve efficiency savings across a range of industrial and transportation sectors.¹³ The efficiency of a device is determined by the performance of the component semiconductors, embodied in the figure of merit, ZT = S²σT/κ comprising the Seebeck coefficient (S), electrical conductivity (σ) and thermal conductivity (κ), where the last has contributions from lattice vibrations (κ_L) and charge carriers (κ_e).

Lead telluride, PbTe, is one of the most studied of thermoelectric materials as doping provides access to both n- and p-type semiconducting variants.¹⁴ Nanostructuring,¹⁵ using approaches that include the introduction of nanoinclusions in the LAST-m (lead–antimony–silver–tellurium) phases,¹⁶ solid-solution formation,¹⁷ hierarchical nanostructuring¹⁸ and the formation of nanoprecipitates of a second phase in the rocksalt matrix,¹⁹ has a beneficial impact on ZT. This arises principally from reductions in κ_L, due to increased scattering of heat-carrying phonons over a range of wavelengths. Maximum figures of merit that lie in the range ZT ≈ 1.4–1.7 have been attained in both n-^20,21 and p-type^22,23 nanostructured PbTe.

Concerns over relative scarcity of tellurium have led to renewed interest in the lighter chalcogen congeners of lead telluride,²⁴ since both selenium and sulfur are more abundant than tellurium. Parker and Singh first identified the possibility of high thermoelectric performance in optimally-doped PbSe on the basis of the presence of a flat heavy band with a high density of states, located near the top of the valence band.³ Subsequent synthetic studies have led to reports of figures of merit in excess of unity at relatively modest temperatures (673 ≤ T/K ≤ 873) for a range of hole and electron dopants^17,25–30 despite a lower valley degeneracy. Common to the electronic structure of PbTe and PbSe-I is the presence of a light upper valence band (L-band) and a second heavy hole band (Σ band), separated by an energy (ΔE) that is larger in the selenide (0.26 eV) than the telluride (0.15 eV). Tuning ΔE towards convergence of the L- and Σ-bands through band structure engineering³¹ has been shown to be an effective strategy to improve the thermoelectric performance of PbSe.

A significant factor in the unexpectedly high thermoelectric performance of PbSe-I is the low lattice thermal conductivity (κ_L 1.7–1.9 W m⁻¹ K⁻¹ at 300 K), which despite the lighter anion, is comparable with, or even slightly lower than, that of the corresponding telluride at 300 K.¹⁷ The origin of this unexpectedly low lattice thermal conductivity remains the subject of some debate. It has been suggested that the smaller unit cell of PbSe compared to PbTe¹⁷ or a weaker bond strength, and hence a reduction in the speed of sound³² may be the cause. Alternatively, an exceptionally strong anharmonicity reflected in a high Grüneisen parameter³³ resulting in an intrinsic localized mode,^34,35 or strong resonant bonding³⁶ resulting in the softening of phonons,³⁷ may play a role.

The thermal conduction properties of PbSe are therefore critically dependent on the bulk elastic properties. In our concluding article concerning the thermoelastic properties of the lead chalcogenides, we describe the results of neutron powder diffraction conducted as a function of both temperature and pressure, which provide new insights into the elastic properties of PbSe. These results are consistent with our previously published analysis of PbS and PbTe that cations and anions in rock-salt structured lead chacides can be modelled as independent Debye oscillators with a two-term internal energy function, leading to Grüneisen constants that are self-consistent and exhibit a high degree of anharmonicity.

Methods

High pressure

High pressure crystallographic data were collected at room temperature, 298 K, and at 150 K using the PEARL diffractometer³⁸ of the ISIS Facility of the Rutherford Appleton Laboratory. Approximately 60 mm³ of powdered PbSe-I (Sigma-Aldrich) was loaded into a null neutron coherent scattering Ti–Zr alloy capsule gasket.³⁹ A small pellet of lead was located in the centre of the sample to act as a pressure marker, and to enable hydrostatic conditions, the sample was moistened with a few drops of perdeuterated 4 : 1 methanol–ethanol pressure transmitting fluid. The capsule was placed in zirconia-toughened-alumina anvils³⁸ and loaded into a type V4 pentane driven Paris Edinburgh press. The press assembly was mounted into a liquid nitrogen cryostat tank and cooled by immersion of the cell body in liquid nitrogen, the sample temperature was maintained, and controlled by warming the press body against a liquid nitrogen reservoir using a pair of band heaters.³⁸ Temperature stability was ±1 K for both temperatures measured. Data were collected to a maximum load of 65 tonnes for both temperatures.

Neutron diffraction data for the d-spacing interval 0.46 < d/Å < 4.1 were collected using the main 2θ = 90° bank of the PEARL diffractometer. Data sets suitable for profile refinement^40,41 were obtained after electronically focusing the individual detector element spectra, normalizing the summed patterns with respect to the incident beam monitor and the scattering from a standard vanadium sample. Finally, a correction for the wavelength and scattering-angle dependence of the neutron attenuation by the anvil and gasket materials³⁷ was applied. Data were collected at 29 loads at 298 K, and 27 loads at 150 K.

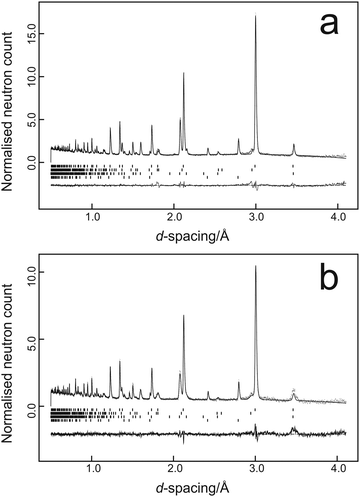
Data were fitted using the GSAS suite of programs^42,43 with typical results from the two temperatures being illustrated in Fig. 1a for the data collected at 37 tonnes load at 298 K and Fig. 1b for the data collected at 38 tonnes load at 150 K.

Fig. 1 Multiphase profile refinement fits to the high-pressure PEARL data; (a) 298 K at 37 tonnes load (4.0 GPa), (b) 150 K at 38 tonnes load (2.8 GPa). Observed data are shown as points, the full line shows the calculated pattern. Underneath the diffraction pattern is the difference plot (observed-calculated) and the reflection markers for the four phases in descending order PbSe-I, ZrO₂ (anvil), Al₂O₃ (anvil), and Pb (pressure marker). Profile refinement agreement factors were R_p = 0.054, R_wp = 0.048 for the 298 K data set and R_p = 0.082, R_wp = 0.065 for the 150 K data set.

Low temperature

Low temperature neutron powder diffraction data were collected using the high resolution neutron diffractometer HRPD at the ISIS neutron spallation source of the Rutherford Appleton Laboratory. Initial data were collected in the time-of-flight window 30–130 ms at 1.2 K using an AS Scientific ‘orange’ cryostat from an equimolar mixture of PbS/PbSe/PbTe powders to which NIST standard silicon reference powder SRM640c had been added as an internal calibrant.⁴⁴ These data permit direct comparison of the three lattice parameters at close to 0 K, which should be of value in athermal density functional calculations of the lead chalcogenides, and, in addition, provides a calibration base line for the data collections made at higher temperature. At 1.2 K the lattice parameters of the rock-salt structured lead chalcogenides are: PbS 5.907641(28) Å, PbSe 6.096764(20) Å, PbTe 6.429392(22) Å.

For the full low-intermediate temperature data collections (10–500 K), data were collected using a Sumitomo RDK-415D closed cycle refrigerator (CCR) from a 25.1 g sample of PbSe-I contained in a 1.5 cm thick aluminium slab can. Details of the configuration of the sample container are given in ref. 45–47 and diagrammatically in ref. 44. Data were collected at 11.5 K, the base temperature of the CCR on the first cooling cycle, for 80 μA h, approximately 2 hours, then at 20 K, and in 10 K steps to 500 K, for data collections of 17 μA h, approximately 24 minutes duration. The sample was then cooled to 10 K and measured for 80 μA h, heated to 15 K and measured at this temperature, and in 10 K intervals to 495 K for 17 μA h per temperature step. Finally, the sample was heated to 500 K and measured in 100 K intervals on cooling to 100 K for 80 μA h per temperature interval. To ensure thermal equilibrium was achieved at all temperatures, data collections were only commenced 5 minutes after the set point temperature was achieved; temperature stability was better than ±0.1 K of the set point temperature for all data collections.

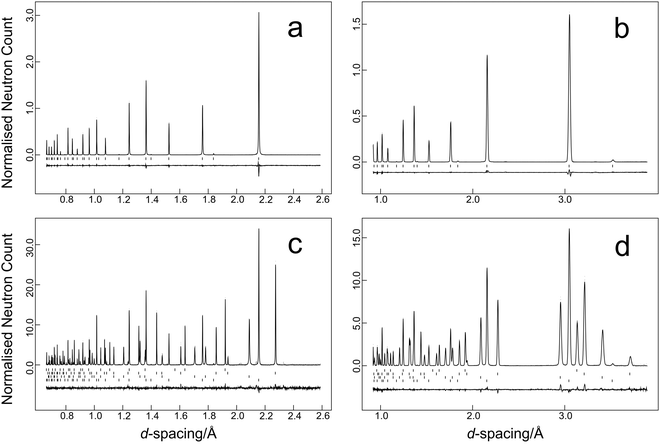
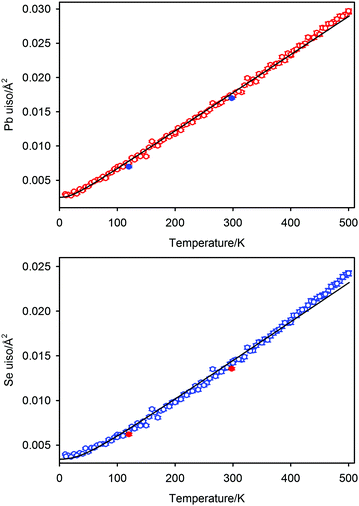
The time-of-flight data were focused, normalised to the incident flux distribution, and corrected for solid angle and detector efficiency variations. The data were finally corrected for self-shielding for a sample of number density 8.506 × 10²¹ cm⁻³ with scattering cross section of 11.871 b⁴⁸ and for the effects of wavelength-dependent absorption (absorption cross section 19.418 b⁴⁸ at a wavelength of 1.798 Å). Two data sets were generated for each temperature in the time-of-flight range 32–120 ms that corresponds to 0.64–2.40 Å in the high-resolution backscattering detector bank, and 0.9–3.4 Å in the high-count rate medium resolution detector bank. Data were fitted using the GSAS suite of programs.^42,43 Typical results from the temperature scan are illustrated in Fig. 2a and b for the data collected at 11.5 K and Fig. 2c and d for the multiphase sample collected at 1.2 K. Average estimated standard uncertainties for the short duration scans were 1 × 10⁻⁵ Å in the lattice parameter and 1.7 × 10⁻⁴ Ų for the isotropic atomic displacement parameters of both lead and selenium.

Fig. 2 Profile refinement fits to the HRPD data; (a and b) PbSe-I at 11.5 K, (c and d) PbSe, PbS, PbTe, SRM640c Si at 1.2 K. Data from the high resolution backscattering bank (2θ = 168.329°) are illustrated in a, c, data from the high count rate medium resolution bank (2θ = 90°) are illustrated in Fig. b, d. Observed data are shown as points, the full line shows the calculated pattern. Underneath the diffraction pattern is the difference plot (observed-calculated) and the reflection markers. For the multiphase refinement of the 1.2 K data set, the reflection markers are in the descending order SRM640c Si, PbTe, PbS, and PbSe. Profile refinement agreement factors were R_p = 0.040, R_wp = 0.039 for the PbSe data set, and R_p = 0.023, R_wp = 0.022 for the multiphase data set.

Crystallographic parameters for PbSe-I refined from the seven long duration data collections are listed in Table 1.

Table 1 Crystallographic parameters for PbSe-I derived from long duration scans

T/K	Lattice parameter/Å	Pb uiso/Å^2	Se uiso/Å^2
PbSe, Fm3̄m, Pb 1a (0.0, 0.0, 0.0), Se 1b (0.5, 0.5, 0.5).
10.0	6.096876(7)	0.00298(8)	0.00398(9)
11.5	6.096764(8)	0.00278(8)	0.00373(9)
100.0	6.103738(7)	0.00695(9)	0.00617(10)
200.0	6.115331(8)	0.01173(13)	0.00989(13)
300.0	6.127348(8)	0.01724(15)	0.01441(16)
400.0	6.139847(9)	0.02319(19)	0.01902(20)
500.0	6.152639(10)	0.02950(24)	0.02421(25)

---

Results and discussion

High pressure

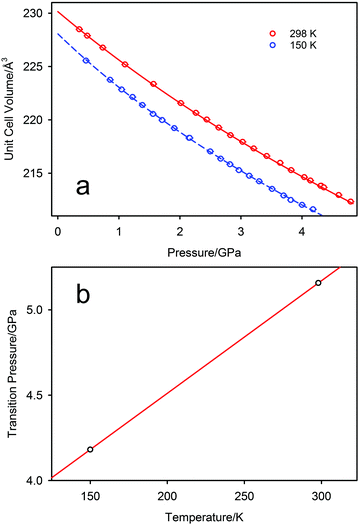
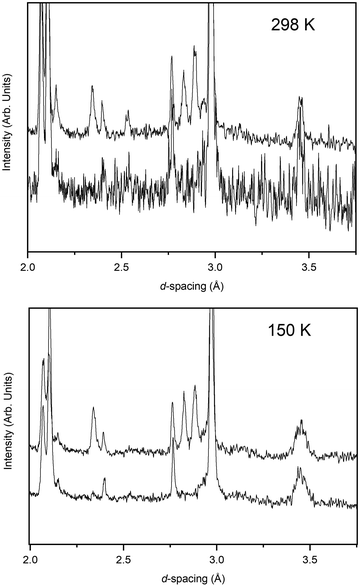
The pressure variation of the unit cell volume of PbSe-I at 298 K and 150 K are shown in Fig. 3a; the first appearance of the higher-pressure phase (PbSe-II) within the diffraction data was used to define the phase boundary PbSe-I–PbSe-II. At 298 K PbSe-II was first observed at 5.16(1) GPa, and, at the lower pressure of 4.18(1) GPa, at 150 K defining an initial steep phase boundary of ∼151 K GPa⁻¹ as shown in Fig. 3b. Data just below and just above the phase boundary for both temperatures is illustrated in Fig. 4 where the presence of PbSe-II may be observed as new Bragg peaks between 2.7 and 3.0 Å. The phase boundary does not cut the temperature axis at a physically realisable temperature (∼−481 K) and hence rock-salt-structured PbSe-I is the stable ground state phase.

Fig. 3 (a) Equation of state for PbSe-I at 298 K and 150 K and (b) the phase boundary for the phase transition PbSe-I–PbSe-II with Clapeyron slope of 151 K GPa⁻¹. 3rd order Birch-Murnaghan equations of state fits to the unit cell volume data are shown by the full and dashed lines in Fig a.

Fig. 4 Parts of the diffraction patterns collected at 298 K and 150 K at pressures just below and just above the phase boundary PbSe-I/PbSe-II where both phases coexist. New Bragg reflections corresponding to PbSe-II can be observed in the d-spacing range 2.75–3.0 Å.

The ambient-temperature bulk modulus (K₀) and its pressure derivative (K′) were calculated from fitting the pressure (P) – volume (V) data to a third order Birch-Murnaghan equation-of-state⁴⁹ with the fit being shown in Fig. 3a as the full line, and the equation-of-state being given by

Results from this investigation, V₀ = 230.14(3) ų, K₀ = 47.9(4) GPa, K′ = 5.5(2) are in good agreement with the recent equation-of-state determination by monochromatic synchrotron radiation (SXRD).⁵⁰ The energy dispersive synchrotron (EDXRD) study⁵¹ is in poor agreement with both the neutron diffraction study and the monochromatic synchrotron investigation due to the intrinsic poor resolution of the technique. Both synchrotron studies suffer from a paucity of experimental data in the phase field of PbSe-I, and hence have only been fitted to a second order Birch-Murnaghan equation-of-state⁴⁹ with the pressure derivative of the bulk modulus fixed at a value of 4. Our neutron diffraction determined bulk modulus is smaller than that derived from measurements of the elastic constants,⁵² or the fitting the experimental phonon dispersion curves to a shell model.⁵³ The bulk modulus derived from the elastic compliance results of Chudinov⁵⁴ are non-physical⁵⁵ and can be safely ignored as they imply the bulk modulus of PbSe-I at room temperature is two thirds that of diamond.

To our knowledge there are no experimental determinations of the third order elastic constants of PbSe-I at room temperature, and hence we have only ab initio calculations of K′ for comparison purposes (K′ = −(c₁₁₁ + 6c₁₁₂ + 2c₁₂₃)/(9K₀) for point group m3̄m⁵⁶). Calculations of the third order elastic constants for PbSe-I using a Born-Mayer potential^57,58 appear to be in conflict, quite possibly related to a typographical error in the quoted units of Raju.⁵⁷ The early work of Thakur⁵⁸ gives K′ = 338.1/K₀ whereas the most recent work of Raju⁵⁷ gives K′ a factor of 10 smaller, K′ = 34.03/K₀ (K₀ in GPa). The former relationship gives a reasonable order of magnitude for K′ (expectation value ∼4⁴⁹), whilst the latter gives a clearly non-physical result. A compendium of experimental and calculated bulk moduli and their pressure derivatives are listed in Table 2.

Table 2 Experimental and calculated bulk modulus and pressure derivative for PbSe-I

K 0/GPa	K′	Method	Ref.
a Physically implausible values.
47.9(4)	5.4(2)	Neutron diffraction (298 K)	This work
49	4 (fixed)	SXRD	50
45	4 (fixed)	EDXRD	51
54.1	—	Ultrasonic	52
54.9	—	Phonon dispersion	53
347^a	—	Ultrasonic	54
49.12	4.09	DFT	87
58.1	—	DFT LDA	33
49.2	—	DFT GGA	33
60.8	4.56	DFT LDA	88
44.5	—	DFT LDA/GGA	89
44.56	—	QHA	59
54.1	—	DFT LDA/GGA	90
	338.1/K0	Born-Mayer potential	58
	34.03/K0^a	Born-Mayer potential	57

---

For calculations of the isochoric heat capacity and the thermodynamic Grüneisen parameter it is necessary to evaluate the temperature-dependence of the bulk modulus. We have used the temperature variation of the second order elastic constants c₁₁ and c₁₂ determined from ultrasonic measurements⁵² and then fitted the calculated bulk modulus (c₁₁ + 2c₁₂)/3 to a saturating function of the form K₀(T) = K₀(0 K) + A/(exp(B/T) − 1). For consistency with our equation-of-state derived bulk modulus, we have retained the temperature dependence implied in the expression above but with K₀(0 K) scaled to fit our 298 K value (K₀(0 K) = 53 GPa, A = −22.11 GPa, B = 465 K). An experimental redetermination of the temperature variation of the second order elastic constants and a determination of the third order elastic constants of PbSe-I would be of great benefit to future thermoelastic investigations.

The nature of the high-pressure phase, PbSe-II, is still under investigation and will be reported elsewhere.

Low-intermediate temperature

Lattice parameter. The temperature-dependence of the lattice parameter and the calculated linear thermal expansion coefficient of PbSe-I between 1.2 K and 500 K is illustrated in Fig. 5 where it is compared to the results of the recent quasiharmonic approximation calculations (QHA).⁵⁹ The experimental data from the two short duration independent temperature scans are in excellent agreement, and, furthermore, also agree with the five long data collections indicating that the sample was indeed in equilibrium at all measured temperatures. The temperature variation of the lattice parameter of PbSe-I, saturation at low temperature, linear behaviour at higher temperatures, is as expected for an insulating or semiconducting compound in the absence of structural or magnetic phase transitions. The full black line and its extrapolation, shown as a dashed black line, are derived from weighted fitting of the entire lattice parameter data to a saturating function of the form a(T) = a₀ +k/(exp(E/T) − 1), where a₀ is the lattice parameter at 0 K and k and E are constants (a₀ = 6.097071(3) Å, k = 0.01453(1) Å, E = 117.24(9) K, r² ∼ 1.0). For these data, the maximum positive deviation (a_obs.–a_calc.) was 6.0 × 10⁻⁴ Å, the maximum negative deviation was −3.7 × 10⁻⁴ Å, and the deviation at 300 K was −3.7 × 10⁻⁴ Å. Adding the value of E for PbSe to our earlier experimental results made on PbS (E = 125 K)^45,46 and PbTe (E = 98 K)⁴⁷ shows that this term has an apparent linear dependence on the chalcogen atomic mass (M in atomic mass units); for the lead chalcogenides E/K = −0.283(63)M + 136(5) (r² = 0.952). The dot-dash line shows the calculated linear thermal expansion coefficient (α_L) of PbSe derived from the fitting coefficients for parameterising the lattice parameter. α_L is seen to rise rapidly from low temperatures and reaches approximate saturation by ∼200 K and has a high temperature limit within the harmonic approximation of ∼2.03 × 10⁻⁵ K⁻¹.

Fig. 5 The temperature dependence of the experimentally determined lattice parameter and the linear thermal expansion coefficient of PbSe-I compared to the results of calculations in the quasiharmonic approximation (QHA). The full line shows a fit to the experimental lattice parameter data using a saturating function described in the text. The associated linear thermal expansion coefficient was calculated from the fitting coefficients. For all temperatures in the interval 1.2 K ≤ T ≤ 500 K the QHA results for the lattice parameter and linear thermal expansion coefficient are significantly greater than those experimentally determined.

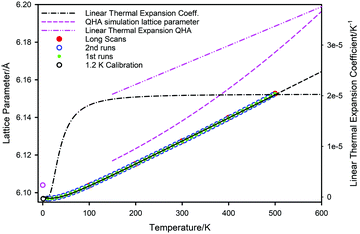
Consideration of Fig. 5 shows the results of the QHA calculations⁵⁹ slightly overestimates the 0 K lattice parameter, but at higher temperatures (T > 150 K) the simulated lattice parameter is significantly in error. This difference increases rapidly with increasing temperature and hence the calculated behaviour grossly overestimates the linear thermal expansion coefficient of PbSe; α_L = 3.8 × 10⁻⁵ K⁻¹ at 600 K by QHA calculation compared to 2.03 × 10⁻⁵ K⁻¹ by extrapolation of the experimental curve. According to the QHA calculations, strong anharmonic contributions apparently start at temperatures of approximately 300 K where the lattice parameter temperature variation begins to move away from linear behaviour. By contrast, non-linear effects are barely apparent in the experimental lattice parameter data even at 500 K. It is evident, therefore, that any deductions made from the QHA calculations that explicitly rely on distance measurements derived from the simulation of the lattice parameter are substantially in error.

Atomic displacement parameters. The temperature variation of the isotropic atomic displacement parameters for lead and selenium are shown in Fig. 6 where they are compared to single crystal results obtained by X-ray diffraction utilising Ag Kα radiation.⁶⁰ The results from the profile analysis are monotonically varying, with saturation at low temperatures, becoming linear at intermediate temperatures and therefore are consistent with Debye-like behaviour. For an atomic Debye oscillator of mass M, the temperature-dependence of the isotropic atomic displacement parameter is given by the expression
where h is Planck's constant, k_B is Boltzmann's constant and θ_D is the vibrational Debye temperature.⁶¹ In practice, for anything other than mono-elemental compounds, this expression is too restrictive, and the zero-point term is permitted to be an additional refinable variable, with the difference between the calculated and refined zero-point term being considered a measure of static disorder at the site under consideration.^62,63 The full lines on Fig. 6 are weighted fits to the atomic displacement parameters according to a harmonic Debye model including the free zero-point refinement with results, Pb: θ_D = 112.1(1) K, zero-point = 2.50(2) × 10⁻³ Ų, r² = 0.998, Se: θ_D = 205.3(3) K, zero-point = 3.41(2) × 10⁻³ Ų, r² = 0.995. The differences between the fitted zero-point terms from those calculated from the vibrational Debye temperatures are small for both cation and anion, 9.5 × 10⁻⁴ Ų in the former, and 1.18 × 10⁻³ Ų in the latter. Furthermore, noting the X-ray single crystal results are in good agreement with the neutron powder diffraction results, and further making the assumption that these data extend significantly above the vibrational Debye temperature, analysis of the X-ray diffraction results finds vibrational Debye temperatures of 109 K for the lead cation and 199 K for the selenium anion, consistent with our neutron powder diffraction results.

Fig. 6 The temperature dependence of the isotropic atomic displacement factors for lead and selenium compared with single crystal X-ray diffraction results shown as solid circles. The full lines are fits to the results from the neutron diffraction investigation using the modified Debye model described in the text. Vibrational Debye temperatures are 112.1(1) K for Pb, and 205.3(3) K for Se.

It is clear from the atomic displacement parameter data and their associated fits according to the modified Debye model that anharmonic effects are visible for temperatures greater than 400 K where the observed data are systematically higher than calculated. This is in marked contrast to the temperature dependence of the lattice parameter which shows no significant deviation from a harmonic model at the highest temperature measured. Root mean square atomic displacements calculated using QHA⁵⁹ are in fair agreement with the values calculated from the atomic displacement parameters of PbSe derived from the neutron diffraction data, however, as noted above, this agreement may be superficial considering the differences between the calculated and measured lattice parameters.

Unit cell volume, isochoric heat capacity and characteristic temperatures. Our earlier work has shown that the thermophysical properties of the isostructural lead chalcogenides, PbS, and PbTe may be simply approximated by assuming the cation and anion behave as independent Debye oscillators.^45–47 Characteristic temperatures derived from fitting calorimetric data to this model are found to agree with vibrational Debye temperatures refined by fitting atomic displacement parameters to the modified Debye model shown in the section above, and hence a self-consistent solution is found.

Within the first Grüneisen approximation that treats thermal expansion as equivalent to elastic strain, the molar volume at zero pressure, or equivalently the unit cell volume under the same conditions, is related to the internal energy by the equation of state V(T) = V₀ + (γ/K₀)U(T) where U(T) is the internal energy, V₀ the volume at 0 K, γ is a Grüneisen parameter and K₀ is the isothermal bulk modulus.^64,65 For a two-term Debye model, the unit cell volume is given by

where the internal energy for a Debye oscillator is given by
ref. 65 and N_i are the number of atoms of type i in volume V.

The isochoric heat capacity, C_V, is found by standard thermodynamic transformation to be related to the experimentally determined isobaric heat capacity C_P, by C_V = C_P–Tα_V²K₀V_m where α_V is the volume thermal expansion coefficient and V_m is the molar volume.⁶⁶ Noting that C_V = ∂U/∂T,⁶⁶ the isochoric heat capacity in the two-term Debye model is therefore

Hence, to deduce a self-consistent set of characteristic temperatures using the Debye internal energy function, it is necessary to simultaneously fit temperature dependent volumetric and calorimetric data to this model.^{45–47,67–69}

Concatenated isobaric heat capacity data for PbSe measured in the temperature interval 1.2–20 K,⁷⁰ and 20–260 K⁷¹ were converted to the isochoric form using the expression shown above, with the molar volume and volume expansivity calculated by an independent fit to the unit cell volume using a simpler, and adequate for the purpose, Einstein internal energy function. The temperature dependence of the bulk modulus was calculated assuming the 298 K value determined from the PEARL experiment complemented by the temperature variation implied from the measurements of the sound velocities as a function of temperature.⁵²

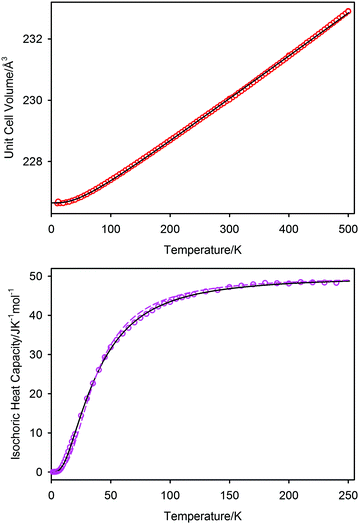
In Fig. 7 we show the unit cell volume and the isochoric heat capacity of PbSe; the simultaneous fit to these data using the two-term Debye model are shown as the full black lines. The inadequacy of a single Debye model to fit the isochoric heat capacity is shown as the dashed line in the lower graph of Fig. 7, where it can be seen to underestimate the heat capacity at low temperatures and overestimate it at intermediate temperatures. The two-term model can be seen to fit both sets of data well, with resultant characteristic temperatures of θ_D1 = 104(3) K and θ_D2 = 219(3) K; the unit cell volume at 0 K is 226.65(1) ų. The associated Grüneisen constants, assuming a bulk modulus of 47.9 GPa, are γ₁ = 1.79, and γ₂ = 2.28 with an average of 2.03. The single term Debye fit to the isochoric heat capacity gave a characteristic temperature of 153 K, and a Grüneisen constant of 2.01. A comparison of the characteristic temperatures and their associated Grüneisen constants for the three lead chalcogenides are listed in Table 3 where the quoted values are derived from re-refined data sets of PbS, and PbTe based on the new 1.2 K calibration shown earlier. Differences between the new values quoted here and the previously reported values^44–47 are within estimated standard deviations of the latter and do not affect the conclusions drawn in these works.

Fig. 7 Simultaneous fit to the unit cell volume and isochoric heat capacity of PbSe-I using a two-term Debye model in which the Pb cation and Se anion behave as independent Debye oscillators. The fit to the two-term model is shown as the full black line on both figures, the fit to a single Debye function for the isochoric heat capacity is illustrated as the dashed line. The single Debye function underestimates the low temperature isochoric heat capacity, whilst over-estimating the intermediate temperature heat capacity. Characteristic temperatures for the two-term model are 104(3) K and 219(3) K in close agreement with the vibrational Debye temperatures derived from fitting the atomic displacement parameters.

Table 3 Comparison of the thermoelastic and vibrational properties of rock-salt-structured PbX, X = S, Se, Te determined by neutron powder diffraction

Compound	V 0/Å^3	γ 1	θ D1/K	γ 2	θ D2/K	θ vib/K (Pb)	θ vib/K (X)
PbS	206.17(7)	3.09	110(3)	1.69	326(5)	120(1)	324(2)
Single Debye	206.23	2.40	202
PbSe	226.65(1)	1.79	104(3)	2.28	219(3)	111(1)	202(1)
Single Debye	226.63	2.01	153
PbTe	265.8(1)	1.83	92(3)	2.23	175(5)	99(1)	155(1)
Single Debye	265.8	2.01	128

---

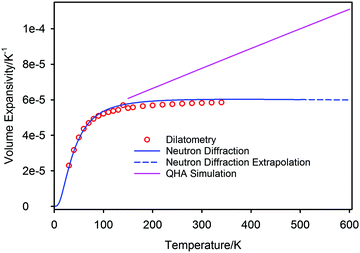
The volume thermal expansion coefficient (α_V) of PbSe, calculated from the unit cell volume and the temperature derivative of the fitted curve shown in Fig. 7, is illustrated in Fig. 8 where the results are compared to those determined experimentally from dilatometry⁷² and those calculated by QHA.⁵⁹ Extrapolation of the experimental volume expansivity using the fitted neutron diffraction results up to a temperature of 600 K is shown as the dashed line. There is gratifying agreement in the magnitude of the volume expansivity between the experimental dilatometry and the neutron diffraction results for PbSe, however, the QHA calculated volume expansivity significantly overestimates its magnitude and gradient for temperatures greater than 150 K.

Fig. 8 The temperature variation of the calculated volume expansivity of PbSe-I based on the two-term Debye model compared with values determined experimentally by dilatometry and those calculated in the quasiharmonic approximation.

The high temperature extrapolation of the unit cell volumes shows that within the harmonic approximation, the volume expansion coefficients of the three lead chalcogenides are remarkably similar; PbS α_V ∼ 6.12 × 10⁻⁵ K⁻¹,^45,46 PbSe α_V ∼ 6.09 × 10⁻⁵ K⁻¹, PbTe α_V ∼ 6.18 × 10⁻⁵ K⁻¹.⁴⁷

Phonon densities of states. The full and partial phonon densities-of-states (PPDOS) for PbSe-I, calculated from first-principles calculations in the local-density approximation, are shown graphically in Fig. 9.³³ Superimposed on these plots are the full and PPDOS calculated from the experimentally determined Debye characteristic temperatures derived from the temperature dependence of the unit cell volume and the isochoric heat capacity. The frequency of the Debye cut offs in wavenumbers is given by
where c is the speed of light. The position of the vibrational Debye temperatures determined from fitting the atomic displacement parameters are also included on this graph. Both the DFT calculated full vibrational density-of states (VDOS) and that from the two-term Debye model have been normalized to unit area. The assumption implicit within the Debye model that the frequency is a linear function of wave vector cannot replicate the fine structure of the DFT calculated vibrational density-of states (VDOS), however there is surprisingly good agreement between the two-term model and the theoretical calculation. The high frequency cut offs agree almost exactly; the mean frequencies of the lead PPDOS agree to within 3%; the agreement of the mean frequencies of the selenium (PPDOS), ∼10%. The position of the transverse optic mode at the Brillouin zone centre⁵³ is found to lie close to the positions of the mean lead (PPDOS).

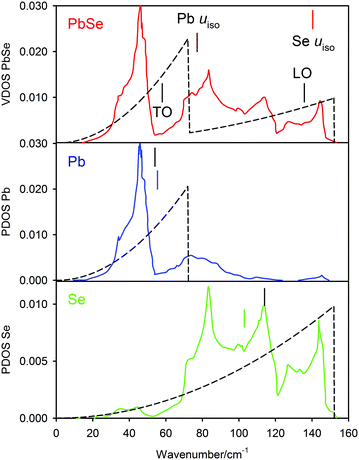Fig. 9 Upper figure, comparison of the vibrational density of states of PbSe-I calculated using first principles methods as the full line with that calculated from the two-term Debye model shown as the dashed line; both densities of states are normalized to unit area. The positions of the transverse optic and longitudinal optic modes derived from neutron inelastic scattering⁵³ are shown together with the positions of the vibrational Debye temperatures of the lead and selenium. The lower two figures show the calculated partial phonon density of states for the two atomic species where the mean frequencies are compared to those calculated from the two-term Debye model.

Thermodynamic Grüneisen parameter. The thermodynamic Grüneisen parameter γ_th, defined by γ_th(T) = (α_V(T)K₀(T)V_m(T))/c_V(T),⁶⁴ is shown plotted in Fig. 10, with the circles based on the fitting parameters for the isochoric heat capacity, the molar volume, the bulk modulus, and the volume expansivity. The triangles show the raw data derived from the experimentally derived isochoric heat capacity. With the exception of the very low temperature data, there is good agreement between the experimentally derived value of γ_th with that defined from the smooth fitted functions. γ_th increases from 2.03 at low temperature, monotonically increasing to 2.22 at 100 K, before decreasing to 2.00 at room temperature close to the average of the individual Grüneisen constants determined from the fitting of the unit cell volume and isochoric heat capacity (2.03). The physical basis for this behaviour is beyond the scope of this current work, however, the existence of long-ranged interactions such as first-, fourth-, eighth- and fourteenth-nearest neighbours in a chain along 〈100〉 is known to occur in PbTe. These interactions are related to the presence of delocalised, resonant bonded p-electrons that may have a marked temperature dependence and therefore influence the anharmonicity of some modes. All the PbX rock-salt structured phases exhibit a maximum in the thermodynamic Grüneisen parameter as a function of temperature^45–47 with the magnitude of the maximum over the average value correlating with the electronegativity of the anion species. Finally, the magnitude of γ_th for PbSe-I over the whole temperature interval studied is intermediate between that of PbS^45,46 and PbTe.⁴⁷

Fig. 10 The temperature dependence of the thermodynamic Grüneisen parameter of PbSe-I (γ_th). The circles indicate the behaviour of γ_th based on the fitting parameters for the isochoric heat capacity, the molar volume, the bulk modulus, and the volume expansivity. The triangles show the temperature variation of γ_th derived from the experimentally derived isochoric heat capacity.

Discussion

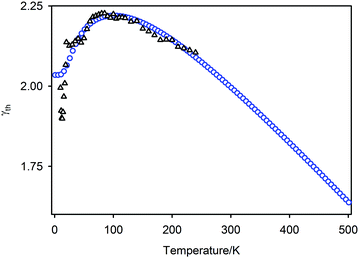
Neutron powder diffraction has shown that at low temperatures PbSe-I behaves crystallographically in the same way as the isostructural chalcogenides PbS, and PbTe, i.e. the temperature dependence of the unit cell volume and isochoric heat capacity within a two-term Debye model are consistent with the Debye-like behaviour of the individual atomic displacement parameters.^45–47 As only Bragg reflections are utilised in profile refinement, it is formally invalid to draw conclusions concerning pair correlations, and hence the contentious issue of emphanisis in the lead chalcogenides^73,74 cannot be commented on in the particular case of PbSe-I. The data presented in this submission, however, may be useful in any future total scattering or XAS study of PbSe-I.

Simple inorganic solids, such as the group 4 elemental solids and III–V semiconductors generally have Grüneisen parameters, γ, close to unity. High-performance thermoelectric materials frequently exhibit Grüneisen parameters in excess of 1, as exemplified by PbTe (γ = 1.45) and AgSbTe₂ (γ = 2.05)⁷⁵. The high values of γ for PbSe, determined from fitting the two-term Debye model to isochoric heat capacity and unit-cell volume data, indicate significant vibrational anisotropy. The calculated thermodynamic Grüneisen parameter of γ = 2.00, is broadly in line with the average of the two values determined from the two-term model and is consistent with previous reports of values in the range 1.5 ≤ γ ≤ 2.25. The QHA calculations of Skelton et al.⁵⁹ conclude that the mode softening seen in all lead chalcogenides leads to significant thermal motion, while the ab initio calculations of Shulumba et al.³⁵ reveal an anomalously large anharmonic interaction in PbSe. This is associated with a localised vibrational mode in the acoustic region. Calculation of the radial distribution function reveals that although this mode is asymmetric, it does not involve a change in the centre of mass.

The bulk modulus determined experimentally (K₀ 47.9(4) GPa) is somewhat higher than the value of 39.9 GPa at 300 K determined by Zhang et al.³³ from the lattice parameter dependence of the calculated free energy. This deviation may arise from the use in the energy calculations of the QHA, in which phonons are treated as harmonic but volume dependent. The average ([small theta, Greek, macron]_D = 161.5 K) of the Debye temperatures determined using a two-term model is comparable with those determined from speed of sound measurements by Wang et al.⁷⁶ (θ_D = 191 K) and Pei et al.²¹ (θ_D = 141 K).

Knowledge of the Debye temperature and Grüneisen parameter enable the lattice contribution to thermal conductivity to be estimated through⁷⁷

where A is a constant (ca. 3 × 10⁻⁸ for κ_L in W cm⁻¹ K⁻¹), albeit with a weak γ-dependence; M̄ is the average atomic mass in a.m.u; δ is the cube root of the average volume per atom in ų and n is the number of atoms in the primitive unit cell (Table 4). We have shown above that the Grüneisen parameter at room temperature determined from thermoelastic data is in good agreement with the mean of individual Grüneisen constants determined from the fitting of the unit cell volume and isochoric heat capacity. We use this mean value, [small gamma, Greek, macron], in estimating the thermal conductivity using the above expression. Similarly, we take the mean of the two Debye temperatures ([small theta, Greek, macron]_D) as approximating to the acoustic mode Debye temperature (θ_a = θ_Dn^−1/3). These assumptions lead to an estimate of κ_L = 0.028 W cm⁻¹ K⁻¹ for PbSe at 300 K. This compares with reported experimental values that span the range 0.016–0.021 W cm⁻¹ K⁻¹. While the estimated value of κ_L is slightly higher than experimentally determined values, it is consistent with the observation that the lattice contribution to the thermal conductivity of PbSe-I is lower than expected on the basis of atomic masses. The corresponding estimates of κ_L for the analogous telluride and sulfide, using data from Table 4, are respectively 0.020 and 0.040 W m⁻¹ K⁻¹. These are broadly in-line with experimental data which demonstrate the sulfide has a significantly larger lattice thermal conductivity than the selenide. The ratio of the estimated values, κ_L(PbS)/κ_L(PbSe) ≈ 1.4, is also similar to that of the experimentally-determined values (1.5), although the telluride/selenide ratio(κ_L(PbTe)/κ_L(PbSe) ≈ 0.7) is somewhat lower than expected. The low lattice thermal conductivity of PbSe may be traced to a Debye temperature that is relatively low for the average atomic mass and to a fairly large Grüneisen parameter that is comparable with that of the heavier telluride and consistent with anharmonic character of the vibrational modes.

Table 4 Parameters used for calculation of κ_L at 300 K

	PbTe	PbSe	PbS
A	3.029 × 10^−8	3.028 × 10^−8	2.95 × 10^−8
M̄/amu	167.4	143.08	119.63
δ/Å	3.23	3.06	2.97
n ^2/3	1.587	1.587	1.587
[small theta, Greek, macron] D/K	133.5	161.5	218
[small theta, Greek, macron] D ^3/K^3	2.379 × 10^6	4.212 × 10^6	10.36 × 10^6
[small gamma, Greek, macron]	2.03	2.035	2.39
[small gamma, Greek, macron] ^2	4.12	4.14	5.71
κ L/W cm^−1 K^−1 (calc.)	0.020	0.028	0.040
κ L/W cm^−1 K^−1 (exp.)	0.025	0.020	0.030

---

Finally, we note that the vibrational Debye temperatures of both the lead and the chalcogenide anion are approximately linear with the reduced mass of the compound PbX. On this basis, the calculated vibrational Debye temperatures for the potential thermoelectric phase PbPo are estimated as θ_D Pb = 91 K, and θ_D Po = 67 K. Verification of these estimates for PbPo we leave to more intrepid experimental investigators, or alternatively, the first principles calculations that are now being carried out on this phase.^78–86

Conclusions

The temperature dependence of the crystal structure and lattice parameter of PbSe-I, coupled with literature values of the isochoric heat capacity, show that the thermoelastic properties of this compound may be approximated by the two-term Debye oscillator model that was developed for the isostructural compounds PbS-I and PbTe-I. Fitting of the unit cell volume and isochoric heat capacity to this model finds two characteristic temperatures of 104(3) K and 219(5) K with associated Grüneisen constants of 1.79 and 2.28. Vibrational Debye temperatures derived from fitting the temperature variation of the atomic displacement parameters (Pb 111(1) K, Se 205(1) K) are in excellent agreement with the characteristic temperatures derived from the volume/heat capacity fitting. At 298 K the bulk modulus of PbSe-I is 47.9(4) GPa with pressure derivative 5.5(2) and a structural phase transition to PbSe-II is observed at a pressure of 5.16(1) GPa. At 150 K the identical transition is observed at the lower pressure of 4.18(1) GPa, and, in the absence of intermediate temperature data,defines an initial Clapeyron slope of 151 K GPa⁻¹.

Conflicts of interest

There are no conflicts top declare.

Acknowledgements

We are grateful to the two anonymous reviewers for their comments and improvements to the submission and to Prof. Ghim Wei Ho for editorial handling of the manuscript. We thank The Science and Technology Facilities Council for access to the HRPD and PEARL instruments of the ISIS neutron spallation source. KSK would like to thank Dr Paul F. Schofield (The Natural History Museum), Prof. Neil C. Hyatt (University of Sheffield) and Prof. Ian G. Wood (University College, London) for kindly arranging visiting positions.

Notes and references

1. E. Yu. Tonkov, High Pressure Phase Transformations, A Handbook, Vol. 2, Gordon and Breach, Philadelphia, 1988.
2. Y. I. Ravich, B. A. Efimova and I. A. Smirnov, Semiconducting Lead Chalcogenides, Springer, New York, 1970.
3. D. Parker and D. J. Singh, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 035204.
4. T. C. Chasapis, Y. Lee, E. Hatzikraniotis, K. M. Paraskevopoulos, H. Chi, C. Uher and M. G. Kanatzidis, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 085207.
5. D. Parker, D. J. Singh, Q. Zhang and Z. Ren, J. Appl. Phys., 2012, 111, 123701.
6. S. V. Ovsyannikov and V. V. Shchennikov, Chem. Mater., 2010, 22, 635.
7. D. V. Talapin and C. B. Murray, Science, 2005, 310, 86.
8. T. K. Chaudhuri, Int. J. Energy Res., 1992, 16, 481.
9. H. Preier, Appl. Phys., 1979, 20, 189.
10. H. Zogg, A. Fach, C. Maissen, J. Masek and S. Blunier, Opt. Eng., 1994, 33, 1440.
11. A. V. Powell and P. Vaqueiro in Thermoelectric Materials and Devices, ed. I Nandhakumar, N M White and S Beeby, RSC Energy & Environment Series No. 17, 2016, Chapter 2, pp. 27–59.
12. X. Shi, L. Chen and C. Uher, Int. Mater. Rev., 2016, 61, 379.
13. R. Freer and A. V. Powell, J. Mater. Chem. C, 2020, 8, 441.
14. C. Gayner and K. K. Kar, Prog. Mater. Sci., 2016, 83, 330.
15. M. G. Kanatzidis, Chem. Mater., 2010, 22, 648.
16. K. F. Hsu, S. Loo, F. Guo, W. Chen, J. S. Dyck, C. Uher, T. Horgan, E. K. Polychroniadis and M. G. Kanatzidis, Science, 2004, 303, 818.
17. H. Wang, A. D. LaLonde, Y. Pei and G. J. Snynder, Adv. Funct. Mater., 2013, 23, 1586.
18. K. Biswas, J. He, I. D. Blum, C.-I. Wu, T. P. Hogan, D. N. Seidman, V. P. Dravid and M. G. Kanatzidis, Nature, 2012, 489, 414.
19. Y. Pei, N. A. Heinz, A. LaLonde and G. J. Snyder, Energy Environ. Sci., 2011, 4, 3640.
20. J. Androulakis, C. H. Lin, H.-J. Kong, C. Uher, C.-I. Wu, T. Hogan, B. A. Cook, T. Caillat, K. M. Paraskevopoulos and M. G. Kanatzidis, J. Am. Chem. Soc., 2007, 129, 9780.
21. Y. Pei, J. Lensch-Falk, E. S. Toberer, D. L. Medlin and G. J. Snyder, Adv. Funct. Mater., 2011, 21, 241.
22. K. Biswas, J. He, Q. Zhang, G. Wang, C. Uher, V. P. Dravid and M. G. Kanatzidis, Nat. Chem., 2011, 3, 160.
23. P. F. P. Poudeu, J. D’Angelo, A. Downey, J. Short, T. Hogan and M. Kanatzidis, Angew. Chem., Int. Ed., 2006, 45, 3835.
24. T.-R. Wei, C.-F. Wu, F. Li and J.-F. Li, J. Materiomics, 2018, 4, 304.
25. C. Gayner, K. K. Kar and W. Kim, Mater. Today Energy, 2018, 9, 359.
26. S. Wang, G. Zheng, T. Luo, X. She, H. Li and X. Tang, J. Phys. D: Appl. Phys., 2011, 44, 475304.
27. Q. Zhang, F. Cao, W. Liu, K. Lukas, B. Yu, S. Chen, C. Opeil, D. Broido, G. Chen and Z. Ren, J. Am. Chem. Soc., 2012, 134, 10031.
28. Q. Zhang, H. Wang, W. Liu, H. Wang, B. Yu, Q. Zhang, Z. Tian, G. Ni, S. Lee, K. Esfarjani, G. Chen and Z. Ren, Energy Environ. Sci., 2012, 5, 5246.
29. Q. Zhang, E. K. Chere, K. McEnaney, M. Yao, F. Cao, Y. Ni, S. Chen, C. Opeil, G. Chen and Z. Ren, Adv. Energy Mater., 2015, 5, 1401977.
30. Y. Lee, S.-H. Lo, C. Chen, H. Sun, D.-Y. Chung, T. C. Chasapis, C. Uher, V. P. Dravid and M. G. Kanatzidis, Nat. Commun., 2014, 5, 3640.
31. H. Wang, Z. M. Gibbs, Y. Takagiwa and G. J. Snyder, Energy Environ. Sci., 2014, 7, 804.
32. Y.-F. Pei and Y. Liu, J. Alloys Compd., 2012, 514, 40.
33. Y. Zhang, X. Ke, C. Chen, J. Yang and P. R. C. Kent, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 024304.
34. M. E. Manley, O. Hellman, N. Shulumba, A. F. May, P. J. Stonaha, J. W. Lynn, V. O. Garlea, A. Alatas, R. P. Hermann, J. D. Budai, H. Wang, B. C. Sales and A. J. Minnich, Nat. Commun., 2019, 10, 1928.
35. N. Shulumba, O. Hellmann and A. J. Minnich, Phys. Rev. B, 2017, 95, 014302.
36. S. Lee, K. Esfarjani, T. Luo, J. Zhou, Z. Tian and G. Chen, Nat. Commun., 2014, 5, 3525.
37. M. Xu, S. Jakobs, R. Mazzarello, J.-Y. Cho, Z. Yang, H. Hollermann, D. Shang, X. Miao, Z. Yu, L. Wang and M. Wuttig, J. Phys. Chem. C, 2017, 121, 25447.
38. C. L. Bull, N. P. Funnell, M. G. Tucker, S. Hull, D. J. Francis and W. G. Marshall, High Pressure Res., 2016, 36, 493–511.
39. W. G. Marshall and D. J. Francis, J. Appl. Crystallogr., 2002, 35, 122–125.
40. B. O. Loopstra and H. M. Rietveld, Acta Crystallogr., Sect. B: Struct. Sci., 1969, 25, 787.
41. B. van Laar and H. Schenk, Acta Crystallogr., Sect. A: Found. Adv., 2018, 74, 88.
42. A. C. Larson and R. B. Von Dreele, General Structure Analysis System (GSAS), Los Alamos National Laboratory Report LAUR, pp. 86–748 ( 1986).
43. B. H. Toby, J. Appl. Crystallogr., 2001, 34, 210–213.
44. A. D. Fortes, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2018, 74, 196–216.
45. K. S. Knight, J. Phys.: Condens. Matter, 2014, 26, 385403.
46. K. S. Knight, Phys. Chem. Miner., 2015, 42, 235–242.
47. K. S. Knight, Can. Mineral., 2016, 54, 1–11.
48. V. F. Sears, Neutron News, 1992, 3, 26–37.
49. J. P. Poirier, Introduction to the Physics of the Earth's Interior, 2nd edition, Cambridge University Press, Cambridge, UK, 2000.
50. Y. Li, G. Li, C. Lin, X. Li and J. Liu, J. Appl. Phys., 2014, 116, 053502.
51. S. Wang, C. Zang, Y. Wang, L. Wang, J. Zhang, C. Childs, H. Ge, H. Xu, H. Chen, D. He and Y. Zhang, Inorg. Chem., 2015, 54, 4981–4989.
52. G. Lippmann, P. Kästner and W. Wanninger, Phys. Status Solidi A, 1971, 6, K159–K161.
53. P. R. Vijayaraghaven, S. K. Sinha and P. K. Iyengar, Proc. Nucl. Phys. Solid State Phys. Symp., 1963, 16C, 208–210.
54. A. A. Chudinov, Kristallografiya, 1963, 8, 473–475.
55. D. B. Sirdeshmukh and K. G. Subhadra, J. Appl. Phys., 1986, 59, 276–277.
56. S. Haussühl, Physical Properties of Crystals, An Introduction, Wiley-VCH, Weinheim, 2007.
57. K. M. Raju, Acta Phys. Pol., A, 2010, 118, 600–605.
58. K. P. Thakur, J. Phys. Chem. Solids, 1980, 41, 465–472.
59. J. M. Skelton, S. C. Parker, A. Togo, I. Tanaka and A. Walsh, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 205203.
60. Y. Noda, K. Masumoto, S. Ohba, Y. Saito, K. Toriumi, Y. Iwata and I. Shibuya, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1987, 43, 1443–1445.
61. R. W. James, The Optical Principles of the Diffraction of X-rays, G. Bell and Sons Limited, London, England, 1962.
62. I. G. Wood, K. S. Knight, G. D. Price and J. A. Stuart, J. Appl. Crystallogr., 2002, 35, 291–295.
63. B. C. Sales, D. G. Mandrus and B. C. Chakoumakos, Semiconduct. Semimet., 2001, 70, 1–36.
64. D. C. Wallace, Thermodynamics of Crystals, Wiley, New York, USA, 1972.
65. D. C. Wallace, Statistical Physics of Crystals and Liquids, World Scientific, Singapore, 2002.
66. F. Reif, Fundamentals of Statistical and Thermal Physics, McGraw-Hill, New York, USA, 1965.
67. K. S. Knight and N. Bonanos, Solid State Ionics, 2013, 232, 112–122.
68. K. S. Knight and C. L. Bull, Solid State Sci., 2016, 62, 90–104.
69. K. S. Knight, C. L. Bull and P. McIntyre, Mater. Chem. Phys., 2017, 199, 393–407.
70. S. N. Lykov and I. A. Chernik, Fiz. Tverd. Tela, 1982, 24, 3102–3105.
71. D. H. Parkinson and J. E. Quarrington, Proc. Phys. Soc., London, Sect. A, 1954, 67, 569–579.
72. S. I. Novikova and N. K. Abrikosov, Fiz. Tverd. Tela, 1963, 5, 1913–1916.
73. E. S. Božin, C. D. Malliakas, P. Souvatzis, T. Proffen, N. A. Spaldin, M. G. Kanazidis and S. J. Billinge, Science, 2010, 330, 1660.
74. T. Keiber, F. Bridges and B. C. Sales, Phys. Rev. Lett., 2013, 111, 095504.
75. D. T. Morelli, V. Jovovic and J. P. Heremans, Phys. Rev. Lett., 2008, 101, 035901.
76. H. Wang, Y. Pei, A. D. LaLonde and G. J. Snyder, Adv. Mater., 2011, 23, 1366.
77. D. T. Morelli and G. A. Slack ( 2006) High Lattice Thermal Conductivity Solids. in High Thermal Conductivity Materials, ed. Shindé S. L. and Goela J. S., Springer, New York, NY.
78. Y.-P. Wang, W.-X. Ji, C.-W. Zhang, P. Li and P.-J. Wang, J. Mater. Chem. C, 2016, 4, 8745.
79. D. C. Gupta and I. H. Bhat, J. Mol. Model., 2013, 19, 3481.
80. C.-J. Kang and B. I. Min, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 041104.
81. Y. Bencherif, A. Boukra, A. Zaoui and M. Ferhat, Phys. B, 2012, 407, 3520.
82. P. Bhardwaj and S. Singh, Phase Transit., 2015, 88, 859.
83. S. Rabii, Phys. Rev. B: Condens. Matter Mater. Phys., 1978, 10, 1876.
84. S. Nie, X. Y. Xu, G. Xu and Z. Fang, Chin. Phys. B, 2016, 25, 037311.
85. S. Rabii and R. H. Lasseter, Phys. Rev. Lett., 1974, 33, 703.
86. D. Singh, V. Bhalla, J. Bala and S. Wadhwa, Z. Naturforsch., A: Phys. Sci., 2017, 72, 977.
87. Y. Bencherif, A. Boukra, A. Zaoui and M. Ferhat, Infrared Phys. Technnol., 2011, 54, 39–43.
88. S.-H. Wei and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 13605–13610.
89. K. Hummer, A. Grüneis and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 195211.
90. E. A. Albanesi, C. M. I. Okoye, C. O. Rodriguez, E. L. Peltzer y Blanca and A. G. Petukhov, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 16589–16595.

---