Open Access Article
Open Access ArticleProgressive changes in crystallographic textures of biominerals generate functionally graded ceramics†
David
Wallis‡
a,
Joe
Harris‡
b,
Corinna F.
Böhm
b,
Di
Wang
c,
Pablo
Zavattieri
 c,
Patrick
Feldner
d,
Benoit
Merle
c,
Patrick
Feldner
d,
Benoit
Merle
 d,
Vitaliy
Pipich
e,
Katrin
Hurle
d,
Vitaliy
Pipich
e,
Katrin
Hurle
 f,
Simon
Leupold
g,
Lars N.
Hansen
h,
Frédéric
Marin
i and
Stephan E.
Wolf
f,
Simon
Leupold
g,
Lars N.
Hansen
h,
Frédéric
Marin
i and
Stephan E.
Wolf
 *bi
*bi
aDepartment of Earth Sciences, University of Cambridge, Cambridge, CB2 3EQ, UK
bDepartment of Materials Science and Engineering, Institute of Glass and Ceramics (WW3), Friedrich-Alexander University Erlangen-Nürnberg (FAU), Martensstrasse 5, 91058 Erlangen, Germany
cLyles School of Civil Engineering, Purdue University, West Lafayette, IN 47907-2051, Indiana, USA
dDepartment of Materials Science and Engineering, Institute I and Interdisciplinary Center for Nanostructured Films (IZNF), Friedrich-Alexander University Erlangen-Nürnberg (FAU), Cauerstr. 3, 91058 Erlangen, Germany
eJülich Centre for Neutron Science JCNS, Forschungszentrum Jülich GmbH, Outstation at MLZ, Lichtenbergstr. 1, 85747 Garching, Germany
fGeoZentrum Nordbayern – Mineralogy, Friedrich-Alexander University Erlangen-Nürnberg (FAU), Schlossgarten 5a, 91054 Erlangen, Germany
gDepartment of Earth and Environmental Sciences, University of Minnesota, Minneapolis, 55455, USA
hUMR CNRS 6282 Biogéosciences, Université de Bourgogne Franche-Comté, 6 Boulevard Gabriel, 21000 Dijon, France
iInterdisciplinary Center for Functional Particle Systems (FPS), Friedrich-Alexander University Erlangen-Nürnberg (FAU), Haberstrasse 9a, 91058 Erlangen, Germany. E-mail: stephan.e.wolf@fau.de
First published on 21st December 2021
Abstract
Biomineralizing organisms are widely praised for their ability to generate structural materials with exceptional crystallographic control. While earlier studies highlighted near-to single-crystalline biominerals, complex polycrystalline features are more widespread yet challenging to account for. Here, we propose that biominerals whose crystal texture varies with depth are functionally graded materials. Using the exemplary case of the nacro-prismatic pearl oyster Pinctada margaritifera, we demonstrate systematic textural changes in a biogenic ceramic. This bivalve employs three synergistic mechanisms to generate a texture gradient across its outer calcitic shell layer. This prismatic layer transitions from an initially weakly-textured to a strongly-textured material. Such changes in texture cause a variation in Young's modulus normal to the shell, owing to the anisotropic mechanical properties of the composing crystallites. Based on finite-element simulations and indentation experiments on the bivalve shell, we conclude that such graded bioceramics yield intrinsic toughening properties similar to those found in compositionally-graded synthetic materials. Notwithstanding, the gradation concept of Pinctada margaritifera is unparalleled among synthetic materials as it rests solely upon elastic anisotropy, making oyster shells potential blueprints for future bioinspired functional materials and damage-resistant ceramics.
I. Introduction
Biominerals are biogenic ceramic materials vital to the host organism's survival as they perform critical functions, such as in sensors,1,2 armor,3 or weaponry.4,5 Millions of years of selection pressure have optimized the designs of biominerals to the extent that conserved structural motifs can serve today as inspiration for designing functional materials.6 As structural materials, biominerals are evolutionarily optimized to attain both strength and toughness,7 combining two material traits that are typically mutually exclusive.8 Thus, biominerals are biologically generated ceramics that address a classic material-design challenge, how to generate hard but non-brittle materials.9 Nature's common solution to this challenge is blending stiff and soft components in a hierarchical architecture spanning several orders of length scale.10 This design trait of biominerals turns their mechanical response into a complex function of contributions from different length scales.11Damage evolution in a ceramic material is not solely governed by its microstructure (i.e., grain boundaries). It is affected by various phenomena, with toughening mechanisms ranging from crack tip interactions to crack tip shielding and crack bridging.12 Mechanisms impacting crack initiation and propagation operate both near and in the distance to the crack tip, in its front and its wake.13,14 In biominerals, intrinsic and extrinsic toughening mechanisms have been identified that synergistically contribute to its overall fracture toughness.8,15–17 Extrinsic mechanisms reduce the crack driving force and arise from microstructural elements located either behind or in the wake of the crack tip.8,14,15,18 Crack-bridging ligaments, micro-cracking, and crack deflection are extrinsic mechanisms common to biominerals.13–15,19–22 Intrinsic mechanisms work ahead of the crack tip, and they are inherent to the material and independent from discrete structural elements or interfaces.13,14 They increase the resistance against crack initiation and growth, hindering damage mechanisms.8,14,15,18 Uncoiling and fibrillar sliding in collagen are classic examples of intrinsic toughening mechanisms of biominerals.8,15
Biological materials often feature structural or compositional gradients imparting a progressive change in specific material properties.23 For example, such gradients were found to increase contact damage resistance4,5,23–28 or to confer interfacial strengthening and toughening.23,29,30 Stomatopods exemplify the efficacy of this design strategy.31 These mantis shrimps are noted for their hunting style since they employ their dactyl club as an ultrafast hammer to disrupt their preys’ shells and exoskeletons. Multiple compositional gradients have been identified that provide the club with the required impact and damage tolerance.4,5,26,28,32
The black-lipped Polynesian pearl oyster Pinctada margaritifera (Pterioida order) is a prey for stomatopods;31 it is a marine bivalve endemic to intertidal and subtidal habitats of coral reefs. The shell of P. margaritifera consists of an inner layer made from aragonitic nacre and an outer layer composed of calcitic columnar prisms. The oyster P. margaritifera is not the only specimen with a nacroprismatic shell design; a considerable number of molluscs feature a comparable shell organization.33,34 Nacroprismatic bivalves are found in various habitats and feature subtle differences in their shell structures while exhibiting remarkable mechanical properties. For instance, the biogenic and prismatic calcite layers of the bivalves Atrina rigida and Pinna nobilis are 50–70% harder than geologic calcite.35,36 This enhancement originates primarily from hindered dislocation motion, induced by effects such as solid-solution strengthening by Mg2+ incorporation37,38 or composite strengthening by incorporated bio(macro)-molecules.39–45 The shape of the tessellating prisms is not crystallographically controlled; it results from the shape-preserving transformation of an amorphous precursor.43,46,47 It has been further shown that the morphogenesis of nacroprismatic shells is guided by thermodynamic constraints, such as directional solidification or grain growth,48,49 and its crystallographic features by the mineralization kinetics.50
Biogenic calcite that appears to be nearly single-crystalline have attracted considerable attention.51–53 However, only a few species generate such uniform crystalline prisms, such as P. nobilis or A. rigida, with their [c]-axes parallel to the growth axis of the prisms and, thus, perpendicular to the shell surface.54–56 The calcite prisms of other species are crystallographically more complex, with various mapping experiments demonstrating their polycrystallinity. Thus, these prisms are composed of crystallographically iso-oriented subdomains (or crystallites) with distinct misorientation relative to their neighbors.53,57–60 In the present case of P. margaritifera, Checa et al. showed that prisms initially consist of only one crystallographic subdomain, which undergoes crystal lattice tilting and eventually splits into independent subdomains.61 These subdomains progressively align their [a]-axis with those of their neighbours’ subdomains, a process that was explained in terms of growth competition between individual crystallites within a single prism.62 Thus, these crystallographic features appear as a by-product of a biologically controlled crystal growth process63,64 with distinctly fast kinetics of mineralization.50
A comparative study65 on calcitic columnar prisms of seven mollusc shells suggested a biological function of crystal-lattice tilting beyond biomineral growth. It reported that calcite prisms of the two pearl oysters Pinctada fucata and P. margaritifera show the most pronounced crystal-lattice tilting and the highest hardness while also featuring the smallest crystallite sizes.65 It concluded that tilting crystal lattices are “the structural property that confers increased hardness to the prisms of the Pinctada species”.65 Macroscale crystal lattice tilting is microscopically caused by a larger number of small-angle crystal boundaries.66 Such crystallographic inhomogeneities are indeed well known to harden materials by impeding dislocation motion.8,35,67 However, substantial hardening can also be caused via the Hall–Petch effect, thus by smaller grain sizes, as demonstrated in avian eggshells.68
In this contribution, we fathom the peculiar crystallographic layout of the prismatic calcite layer of P. margaritifera, through electron backscatter diffraction (EBSD). We further apply a range of complementary techniques, including indentation experiments and stress-field simulations, to assess a potential impact on mechanical properties. We demonstrate a systematic crystallographic texture gradient across the entire prismatic calcite layer that arises from two complementary mechanisms: (i) a cross-over in the relative proportions of prisms with different preferential orientation and (ii) crystal-lattice tilting in individual prisms. The coaction of these two mechanisms contributes to a less obvious mechanism, (iii) gradual ordering of the entire prismatic layer by a transition from an initially non- or weakly textured material to a strongly textured material. The observed crystallographic texture gradient is a product of these three well-concerted processes, an observation that led us to conjecture that the textural changes are purposeful. Since a crystal's elastic modulus depends on its orientation, the texture gradient causes a gradual change in elastic properties that transforms the prismatic shell layer into a functionally graded material. Finite-element models predict that a gradient in Young's modulus improves the material's damage resistance by imparting significant stress delocalization. Indentation experiments on the prismatic layer of P. margaritifera indeed show that these elastically graded prisms are optimized for wear and contact damage and demonstrate a remarkable increase in fracture toughness, compared to elastically homogenous prisms of P. nobilis. Based on these observations, we conclude that biominerals with crystallographic texture gradients can be seen as functionally graded materials. If suitably oriented and of sufficient magnitude, their elastic gradation can impart stress delocalization, leading to a distinct enhancement of a bioceramic's fracture toughness and opening new bioinspired avenues to damage-resistant ceramics.
II. Results
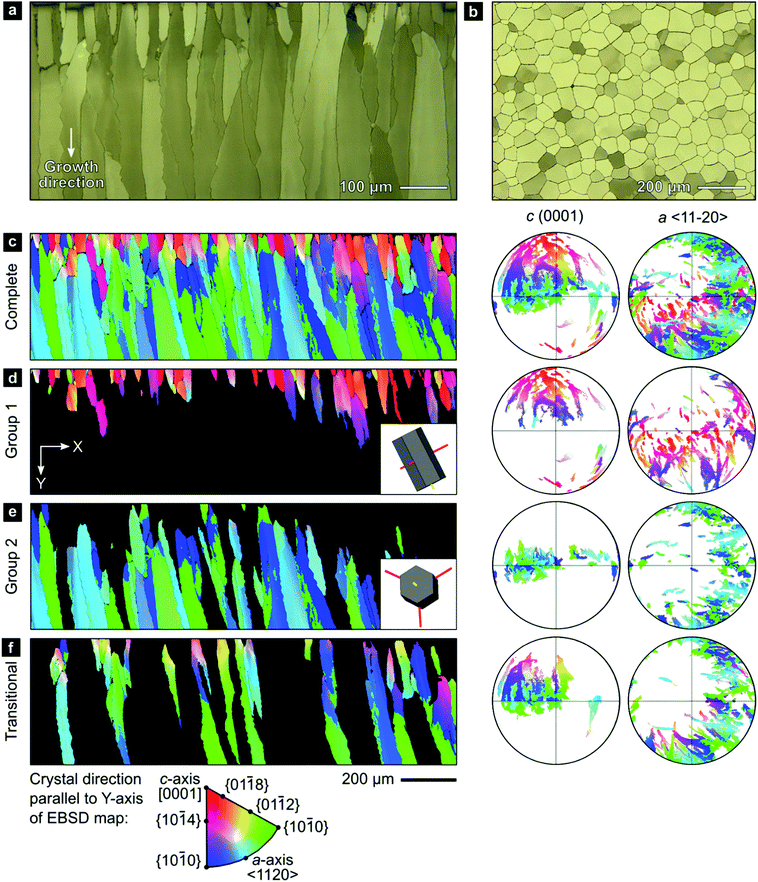
We employed a range of methods to investigate the outer calcitic layer of the bivalve shell Pinctada margaritifera (Fig. S1, ESI†), which consists only of calcite columns separated by a periprismatic organic matrix (Fig. 1a and b). Prisms are composed of crystallites, which form crystallographic subdomains if their mutual misorientation is small.61 As shell growth proceeds from the exterior to the interior by layer-by-layer deposition, the shell records a time series progressing from the outside to the inside of the shell (top to bottom in Fig. 1a and c–f).63II.1. Electron backscatter diffraction (EBSD) analyses reveal crystallographic texture gradients
Electron backscatter diffraction (EBSD) maps of the outer calcitic layer show systematic crystallographic texture gradients across its entire thickness, which arise from independent crystallographic changes across length scales, from the crystallite level up to the level of the entire prismatic layer.The EBSD map presented in Fig. 1c covers the complete cross-section of the prismatic layer between the exterior (top) and interior (bottom) boundaries. The crystallographic orientations of the prisms define two end-member groups, with some prisms being transitional between these end-members (Fig. 1d–f). Many prisms near the shell's exterior, Group 1, have [c]-axes typically at less than ∼50° to the growth direction (Fig. 1d). However, the largest area fraction consists of prisms, Group 2, with [c]-axes lying approximately within the plane of the shell (Fig. 1e). Our classification is in line with recent studies reporting on an unexpected growth direction of late prisms in P. margaritifera perpendicular to the [c]-axis, i.e., of Group 2 prisms in our terminology.69
A smaller set of prisms, termed ‘transitional’, have [c]-axes that start in similar orientations to those of Group 1. However, during progressive growth, the [c]-axes of their intraprismatic crystallites rotate by up to 68° to lie approximately within the plane of the shell (Fig. 1f); they represent a transmutation of Group 1 prisms into Group 2 prisms. All prisms contain significant orientation gradients, with [c]-axis orientations typically varying by several tens of degrees within a single prism, as illustrated in detail in Fig. 2. This phenomenon of crystal-lattice tilting has been first described by Checa and co-workers.61
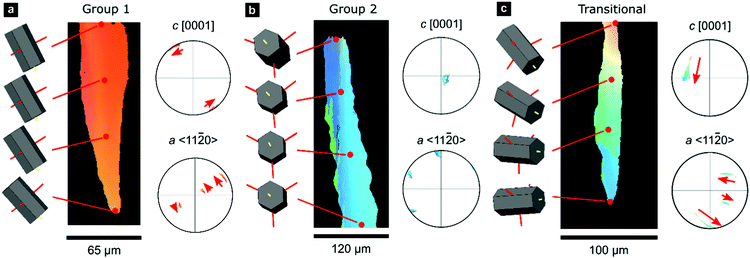 | ||
| Fig. 2 Gradients in crystallographic orientation within calcite prisms of P. margaritifera. Maps and pole figures of Group-1, Group-2, and transitional prisms colored according to the inverse pole figure for the Y-direction, inset in Fig. 1c. | ||
In all groups, the misorientation axes of domain boundaries with misorientation angles in the range 2–10° are parallel to either an 〈a〉-axis or {m}-pole, i.e., {11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0} or {10
0} or {10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0} However, these misorientation axes have different spatial orientations in each group of prisms (due to their different crystal orientations), leading to differing evolution of lattice orientation during prism growth (Fig. S2, ESI†). The axes of lattice rotation in Group-1 prisms are typically oblique to both the plane of the shell and to the growth direction (Fig. 2a and Fig. S2, ESI†). Thus, the crystal-lattice tilting in Group 1 prisms rotates the [c]-axis towards the plane of the shell during progressive growth, but their growth terminates before their [c]-axes reach the plane of the shell. In Group 2 prisms, out of the three symmetrical equivalents of both {m}-poles and/or 〈a〉-axes, rotation commonly occurs around the variant parallel to the growth direction (Fig. 2b). This constrains the [c]-axes of Group 2 prisms to remain within the plane of the shell during growth. In transitional prisms, the [c]-axes become aligned parallel to the plane of the shell and remain so during extensive further growth (Fig. 2c). Consequently, in all groups, [c]-axes either rotate toward and/or remain within the plane of the shell during progressive growth.
0} However, these misorientation axes have different spatial orientations in each group of prisms (due to their different crystal orientations), leading to differing evolution of lattice orientation during prism growth (Fig. S2, ESI†). The axes of lattice rotation in Group-1 prisms are typically oblique to both the plane of the shell and to the growth direction (Fig. 2a and Fig. S2, ESI†). Thus, the crystal-lattice tilting in Group 1 prisms rotates the [c]-axis towards the plane of the shell during progressive growth, but their growth terminates before their [c]-axes reach the plane of the shell. In Group 2 prisms, out of the three symmetrical equivalents of both {m}-poles and/or 〈a〉-axes, rotation commonly occurs around the variant parallel to the growth direction (Fig. 2b). This constrains the [c]-axes of Group 2 prisms to remain within the plane of the shell during growth. In transitional prisms, the [c]-axes become aligned parallel to the plane of the shell and remain so during extensive further growth (Fig. 2c). Consequently, in all groups, [c]-axes either rotate toward and/or remain within the plane of the shell during progressive growth.
Overall, we observe a texture gradient due to two apparent mechanisms: (i) changes in the relative proportions of prisms from Groups 1 and 2; and (ii) crystal-lattice tilting, i.e., systematic crystallite-to-crystallite rotations (thus of subdomains within prisms), progressively aligning the 〈a〉 and {m} directions with the growth direction and the [c]-direction with the plane of the shell.
The first mechanism can be easily explained by Grigor’ev crystal-growth competition on the prism level, in which crystals with their fastest growth axis oriented approximately perpendicular to the substrate outcompete others and dominate the late stage of prism growth.70 The crystallographic orientation of the prisms and their geometrical evolution indeed indicate that prism growth rates are crystallographically controlled and that 〈a〉 and/or {m} are the fastest growth directions in this mineralization system. For calcite, growth along the [c]-axis is commonly fastest during growth from solution. However, under diffusion-limited conditions, such as by the action of face-specific growth inhibitors or under spherulitic and pseudomorphic growth conditions, other growth directions may take over.66
The second mechanism, crystal lattice tilting, is well-documented in synthetic crystalline materials, such as calcite films generated via a nonclassical biomimetic crystallization route.66,71 In such materials, occluded impurities trigger largely uncontrolled autodeformation and non-crystallographic branching. Specialized intracrystalline biomineralization proteins possibly trigger the misorientations in P. margaritifera by comparable, but precisely controlled, mechanisms, as suggested by Checa and co-workers.53,61
The coaction of these two mechanisms enable a third mechanism: (iii) gradual crystallographic ordering. The combination of mechanisms (i) and (ii) yields both a textural gradient and an increasing texture strength. Prisms of Group 2 (Fig. 1f) have a stronger texture (evident as tighter clusters in the pole figures) than prisms of Group 1 (Fig. 1d). This effect can be quantified using the J-index,72 which provides a measure of texture strength. Group 1 has a J-index of 5.5, whereas Group 2 has a J-index of 8.9. This contrast in texture strength records a progressive disorder-to-order transition across the shell thickness.
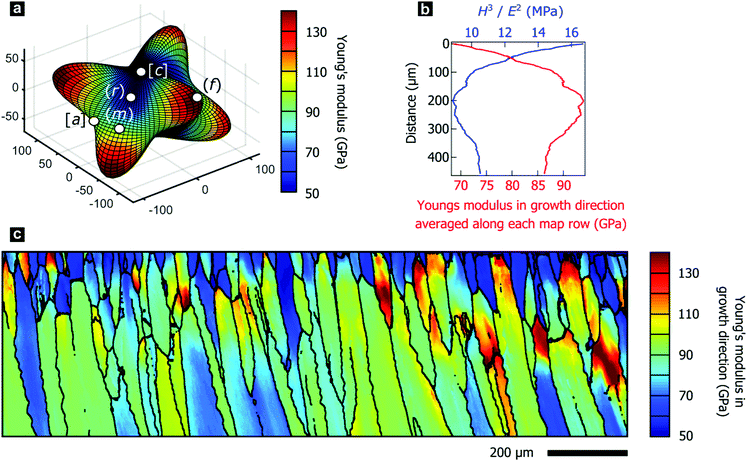
II.2. Crystallographic gradients modulate mechanical properties
The texture gradients inevitably change the directional mechanical properties of the entire prismatic layer as the constitutive crystallites have anisotropic mechanical properties. We demonstrate this effect using the directionality of Young's modulus in calcite, illustrated in Fig. 3a, as the anisotropic elastic properties of constituent crystallites control the effective stiffness of the prismatic layer. We employed effective-medium theory based on crystal orientation distributions and the anisotropic elastic stiffness tensor for calcite to estimate Young's modulus perpendicular to the shell surface.73,74 Mechanical properties in this direction are of particular interest as this is a likely direction of impacts to the shell.In P. margaritifera, the Young's modulus exhibits systematic gradients across the mapped area, both within individual prisms (Fig. 3c), and across the overall microstructure (Fig. 3b). Fig. 3b demonstrates that, in general, the Young's modulus normal to the shell surface increases with progressive growth. The initially low and heterogeneous Young's modulus is gradually transformed into a high and homogeneous Young's modulus during the first ∼0 μm of growth of the prismatic layer (Fig. 3b and c and Fig. S3, ESI†).
The variable elastic properties necessarily alter the macroscale mechanical performance of the prismatic layer, which is crucial for the mechanical resistance of the protective shell. We performed nano-indentation parallel to the growth direction at a range of depth positions within the prismatic layer, which revealed the hardness to be approximately constant at 4.28 ± 0.35 GPa. This value agrees well with the literature and is comparable to other nacroprismatic bivalves such as P. nobilis.36,75 As wear resistance scales with the relation Hm/En (m ≥ n ≥ 1), where H denotes the hardness and E the elastic modulus,76 wear resistance of the prismatic layer is highest at the exterior where the material is most compliant (Fig. 3b). Furthermore, we experimentally characterized intraprismatic crack initiation by nano-indentation, which probes length scales up to a few micrometers.77–79 Displacement bursts in the continuous load–displacement curves coincided with the appearance of visible cracks and therefore resulted from crack initiation (Fig. S4, ESI†). The probability distributions of crack initiation as a function of the indentation force demonstrate that the compliant prisms of Group 1, which dominate the shell exterior, consistently require greater indenter loads to initiate fracture than the stiffer prisms of Group 2 (Fig. S4e, ESI†). This shows that the mechanical properties of the prismatic layer of P. margaritifera are optimized for resistance to wear and surface damage.
II.3. Elastic gradients modulate a material's stress field
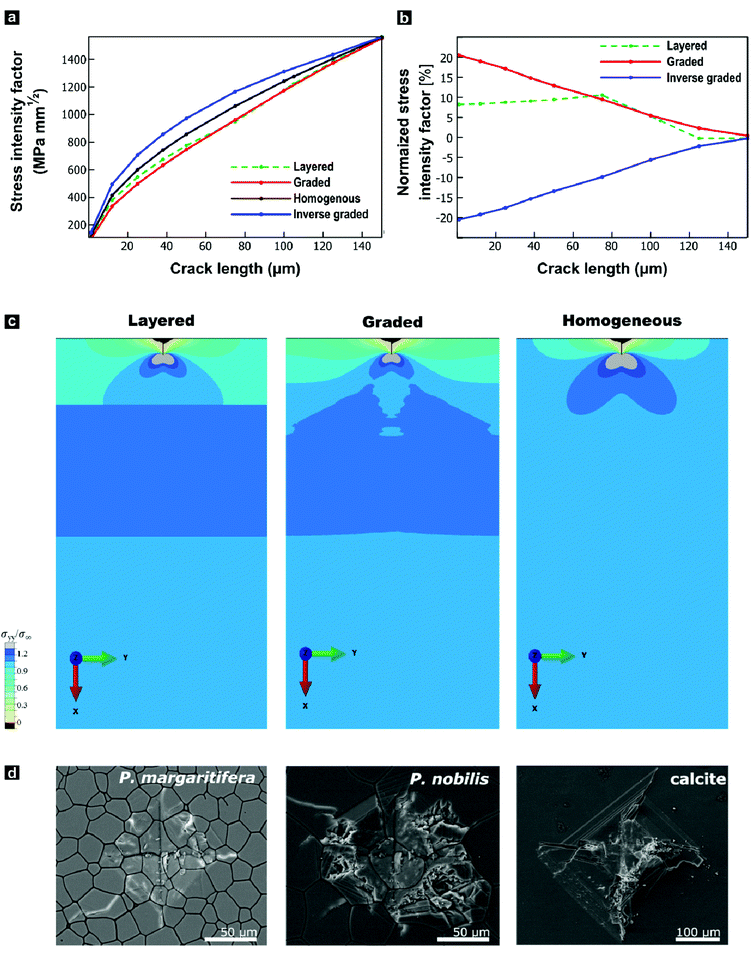
The progressively changing crystal texture, which imparts a change in stiffness normal to the shell surface, may thus transform the prismatic layer into a functionally graded material. Theoretical studies found that elastic gradients can confer distinct flaw-tolerance through their impact on stress distribution, albeit this effect is sensitive to other material characteristics, such as the Poisson's ratio.80–82 Only an elastic gradient that shows a suitable orientation and a sufficient elastic variation can reduce the stress at a crack tip and therefore intrinsically toughen a given material. Experimentally, Suresh and co-workers have impressively evidenced improved contact-damage tolerance for the case of compositionally-graded silicon nitrides.83–85 Such results could imply an additional biological function of graded textures in biominerals: crystallographic gradients may serve as a toughening motif increasing the contact-damage tolerance of mineralized armatures. However, this raises the question of whether the observed change in the elastic modulus is already sufficient and suitable to allow for similar toughening mechanisms.To address this question, we employed finite-element modelling simulations. In these simulations, we studied a surface crack under a tensile load by subjecting a notched strip of material to a pure remote mode I loading. We compared a reference model characterized by a homogenous Young's modulus with models that feature graded, inverse graded, or discrete multi-layered Young's moduli in vertical direction under identical loading conditions (Fig. S5, ESI†). The purpose of these simulations is to provide insights into the role of gradients on the local stress intensity factor. We surmise that resistance to crack propagation provides a local hardening mechanism that contributes to the delocalization of microcracks, and thus, contributing to the overall toughness of the material. We hypothesize that the effect of grain orientation and anisotropy has a lesser effect, where the resistance to crack propagation is mainly driven by the gradient in the stiffness. For each case, the fracture resistance was quantified in terms of the predicted stress-intensity factor (KI) as a function of crack length, plotted in Fig. 4a and b. In these simulations, the graded model outperforms all control materials by exhibiting the lowest stress intensity factor. The graded model experiences stress-intensity factors up to 20% lower than the homogenous material, and thus such a structure would lead to a notable improvement in fracture resistance. By distributing the stress widely across the bulk, the gradient improves the damage tolerance as it diminishes the stress intensity at the crack tip, as illustrated in Fig. 4c. In contrast and as a control, the opposite is true when the gradient is reversed. These simulations show that the observed elastic gradient is already sufficient to have a notable effect on the fracture toughness of a given material.
We undertook indentation experiments to validate these theoretical predictions. Based on these simulations, one would predict that the graded prismatic layer found in P. margaritifera features improved damage resistance compared to a non-graded counterpart. Such a non-graded control is essentially given by the prismatic calcite layer of P. nobilis: it is composed of co-oriented crystallites with [c]-axes normal to the plane of the shell, thus, with a crystallographic orientation similar to Group-1 prisms of P. margaritifera, see Fig. S6 (ESI†).46,86 We undertook indentation experiments, in which we compare P. margaritifera to P. nobilis, which can be seen as an elastically homogenous counterpart, along with geological calcite as a reference. Crack formation caused by the employed indentation experiments has been shown to occur under mode I loading, making these experiments comparable to our simulations.87,88 To probe the impact of the observed elastic gradient on the fracture toughness, we conducted Vickers microhardness tests. In the case of brittle solids, these tests probe depth ranges of approximately 75–100 μm, the scale over which Young's modulus of the oyster shell varies on the order of 25%. Vickers indentation under identical loading conditions resulted in an extended fracture, shattering, and disaggregation of both geological calcite and P. nobilis prisms in and around the indents, illustrated in Fig. 4d. In stark contrast, P. margaritifera endured the indentation with only minimal fracture. The Vickers tests further allowed for quantification of the materials’ fracture toughness. Geological calcite exhibited a fracture toughness of 0.34 ± 0.04 MPa m−1, whereas P. nobilis demonstrated a distinctly increased fracture toughness of 1.16 ± 0.49 MPa m−1, which we attribute to its hierarchical organization (see below). The crystallographically graded prismatic layer of P. margaritifera surpasses even P. nobilis, with a superior fracture toughness of 3.15 ± 1.86 MPa m−1. The superior mechanical performance of the prismatic layer of P. margaritifera demonstrates an optimized damage resistance.
Hardening and toughening may also arise by other, potentially unidentified structural features, such as changes in the hierarchical and ultrastructural organization or changes in the crystallite size, as discussed in the introduction. The typical size of prism of P. nobilis (Fig. S6 and Fig. 4d) appears to be larger than that Group I prisms of P. margaritifera (Fig. 2 and 4d) whereas Group 2 and transitional prisms (Fig. 1 and 2) are comparable in diameter. Our modelling does not capture this gradual increase in prism diameter, as the analysis of crack path deviation caused by the periprismatic sheaths are beyond the scope of this study. To assure that prisms of both species feature a similar internal ultrastructural organization and are thus indeed comparable, we employed both small-angle neutron scattering and anisotropic Scherrer analyses. Both, P. margaritifera and P. nobilis have been repeatedly reported to feature a similar ultrastructure with nanograins a few tens of nanometres in size,41,46,61,86,89 which similarly have been found in other calcareous biominerals, such as nacre.63,90–92 We probed the sub-prismatic crystallite morphology by anisotropic Scherrer analyses,93 which provided spatial dimensions of the coherently scattering domains. In the case of geological calcite, the crystallite sizes were beyond the range of this approach (>1000 nm), which demonstrates that this control calcite was well-crystalline. In contrast, we found that the crystallite morphologies in prisms of both bivalves feature a notable and comparable asymmetric layout. Their coherently scattering domains largely stretch out in the (hk0) directions (>1000 nm), but they are confined to some few hundreds of nanometres in the (001) direction. Thus, the crystalline domains of P. nobilis and P. margaritifera prisms have both a prolate shape with comparable aspect ratios and lateral dimensions of 200 ± 50 nm and 450 ± 200 nm, respectively. It should be noted that recent ptychography studies demonstrated that crystalline coherence also expand across a couple of granules.53
Small-angle neutron scattering (SANS) in the small- and very-small angle regime confirmed that the hierarchical organization of prisms extracted from both species is comparable, especially on the sub-micron length scale. Both types of calcite prisms are fractal materials characterized by a Porod exponent of 3, which suggests a three-dimensional network of particles.94 This inference is consistent with the observation that bivalve shell growth can proceed via the aggregation of nanosized particles.63,95 A multi-level Beaucage fit reveals further structural elements across scales; thus, a hierarchical order of building units, see Fig. S7 (ESI†).96 The powdered calcite prisms of P. nobilis are composed of three different units with diameters of approximately 0.55 μm, 45 nm, and 1.4 nm, respectively. In P. margaritifera, again, three structural units are found, with similar characteristic gyration radii of 0.87 μm, 40.8 nm, and 2.2 nm. We assume that the structural units with a diameter of 0.55 and 0.87 μm reflect the particle sizes of the powdered samples as no larger units are detected. The following structural elements with an approximate diameter of about 40 nm fit well with the reported size of the mineral nanogranules,41,46,61,86,89 whose self-assembly probably drives shell formation in these bivalves.63,95 The smallest component identified by SANS is in the low nanometre range. Their diameter is consistent with reports on the intergranular organic matrix, which can be described as a holey organic envelope of the nanogranules or an extended interstitial network with a 1–2 nm thickness.40,46,61,97 We also determined the mass fraction of this intracrystalline organic matrix by thermogravimetric analysis (TGA) and found a similar amount of about 0.5–1% in both species. The results obtained from two different scattering methods and TGA validate our assumption that the prismatic layer of P. nobilis represents a comparable but non-graded counterpart to the crystallographically graded prismatic layer of P. margaritifera.
III. Discussion and conclusions
Our results demonstrate that, concealed by the crystallographic complexity of its shell, the black-lipped pearl oyster employs three mechanisms to systematically generate a crystallographic texture gradient across its entire prismatic calcite layer. We identified two evident and complementary mechanisms that act on different length scales: (i) crystal-lattice tilting within prisms and (ii) a ratio cross-over of prisms with different preferred crystal orientations. The synergistic cooperation of these two phenomena gives rise to a rather concealed third mechanism: (iii) gradual ordering, i.e., a disorder-to-order transition from weak to strong texture. The gradual change in crystallographic texture is inevitably accompanied by a gradual change in directional elastic properties since the constituting crystallites are elastically anisotropic. We tested by finite-element modelling whether the elastic gradient observed in P. margaritifera would be suitably oriented and sufficient in magnitude to impart stress delocalization, as reported in the case of compositionally-graded synthetic ceramics. These simulations confirm that the observed gradients are suitable and can provide considerable intrinsic toughening.By employing nano-indentation and Vickers indentation, we validated that the mechanical performance of P. margaritifera is indeed commensurate with the expected mechanical behaviour of an elastically-graded material. Nano-indentation experiments showed that the prismatic layer is optimized concerning wear resistance, as it exposes its most compliant surface to the environment. This directional layout provides another beneficial effect; greater loads are needed to initiate fracture, further optimizing the shell's resistance against sharp contact damage. Based on the finite-element simulations, one would expect that an elastically graded prismatic layer features an increased fracture toughness compared to a non-graded, homogenous prismatic layer. Vickers indentation, which probes depth ranges commensurate with the dimensions of the observed gradient, found that the prismatic layer of P. margaritifera features a fracture toughness of 3.15 ± 1.86 MPa m−1. This value surpasses the fracture toughness of the elastically-homogenous prismatic layer of P. nobilis (1.16 ± 0.49 MPa m−1). However, this value cannot be quantitatively compared with our finite element predictions, which captures only the local toughening due to the elastic gradient. Such localized intrinsic toughening enables additional extrinsic mechanisms (i.e., microcracking), which promote the spread of damage to a greater volume, thereby increasing energy dissipation and toughness. Then, a collective behaviour of delocalization effects leads to the experimentally measured values exceeding those determined in our simulations. The spread of damage in the outer calcite layer of P. margaritifera supports our hypothesis that delocalization effects contribute to its toughness (Fig. 4d). Its behaviour in indentation experiments clearly deviates from the expected and observed brittle behaviour of geological calcite (Fig. 4d), which has a fracture toughness an order of magnitude lower than the calcitic prismatic layer of P. margaritifera. In the case of brittle calcite, damages highly localizes into major cracks that ultimately lead to catastrophic brittle failure—as expected for a brittle mineral. In stark contrast, biological materials typically exhibit widespread damage and flaw tolerance. Biological materials owe this distinctive trait to the presence of weak crack initiation sites (e.g., imperfections) that stimulate the nucleation and growth of additional and secondary cracks. In coaction with clever crack arrest mechanisms, these mechanisms give rise to delocalization, spread of damage and, as consequence, to enhanced energy absorption which contributes to the toughness.98 Our finite element simulations provide insights on how an elastic gradient can contribute to these local toughening mechanisms promoting crack arrest. Ultimately, the overall toughness of a material—as the one measured in our nanoindentation experiments—has to be seen as a representation of the collective behaviour of all microcracks. This explains the effect of delocalization and spread of damage on the fracture toughness of P. margaritifera.
Recent studies on nacre showed that nanogranular biominerals exhibit coherent and continuous stress contours in their mesoscale building units across nacre tablets.99 Nano-indentation experiments on nacre, followed in situ by high-resolution transmission electron microscopy, revealed those microstructural elements to interlock when loaded. Thus, strain contours can propagate across the microstructural elements in a relatively unhindered manner.90 Both experimental studies exemplified that mesoscale units cooperatively act when spreading the stress field,90,99 which allowed us to focus our simulations on the wider stress field by employing simplified structural models.
To exclude that the observed increase in fracture toughness results from unidentified structural differences between the two species, such as distinct changes in crystallite sizes, we performed small- to very-small angle neutron scattering and anisotropic Scherrer analyses. By thermogravimetric analyses (TGA), we also precluded that the observed mechanical differences originate in compositional differences, e.g., varying fractions of intracrystalline organics. With two different scattering methods in concert with TGA analyses, the prisms of P. nobilis turn out as suitable homogenous equivalents to the crystallographically-graded prisms of P. margaritifera.
Building on our cross-scale characterization of the prismatic layer of the oyster shell P. margaritifera summarized above and guided by the results of our finite-element simulations, we suggest that biominerals with crystallographic texture gradients are elastically-graded materials that feature distinctly modulated stress fields and stress intensity factors. These conclusions also imply that not only species with unidirectionally and near-single-crystalline bioarmor employ crystallographic control to optimize function.56 The functionally beneficial change of crystallite orientation during growth generates materials with complex and ostensibly unsystematic texture that stand out with excellent and complex mechanical properties. Such elastic gradients are potentially widespread in protective biomaterials, and we expect that other design principles, such as amorphous-to-crystalline or compositional changes, will also confer increased damage resistance. It should be stressed that the orientation of the elastic gradient determines the stress-field modulation, as shown by our simulation of an inverse elastic gradient.
We thus conclude that a functional gradient optimizes the molluscan body armour of P. margaritifera, which toughens the shell against catastrophic failure by spreading the stress field into the bulk, increasing its fracture toughness, and simultaneously optimizing the shell's resistance against wear and crack initiation at its exterior. In selected cross-lamellar shells, such as Charonia lampas lampas and Cypraea testudinaria, transverse texture gradients have been reported while near-to-no elastic gradients are present orthogonal to the shell surface.100,101 Such transverse gradients will have a notably different impact on the biomechanics of the shell, probably affecting its resistance against shear loading rather than impact damage.100,101 We thus anticipate that a wealth of seemingly poorly ordered biogenic materials (e.g., in Unionidae49,102) or bioceramics with changing textures (e.g., crustacean cuticles100 or even bone16,17,103) use comparable concepts to (additionally) generate elastic gradients. Therefore, complex but changing crystallographic textures of biominerals should be perceived as a functionally optimized motif rather than a mere non-functional outcome of an intricate biological control over crystal growth.
Using the example of P. margaritifera, we further suggest a novel design principle for the toughening of (bio-)ceramics based on graded textures. We demonstrated that a gradient in average crystallographic orientations, i.e., in crystallographic texture, can be an efficient way to modulate the mechanical properties of a (biogenic) ceramic. Synthetic materials or ceramics have not yet exploited the directionality of elastic properties in crystalline material and, thus, the black-lipped pearl oyster represents a blueprint for future bioinspired functional materials. This elegant concept applies to a wide range of material classes with anisotropic elasticity, heralding new design approaches towards architectured materials and novel non-brittle but tough ceramics.
Future work will focus on simulating large volumes to validate our hypothesis that the observed hardening results from local toughening stress delocalization. This mechanism, which is not captured in our simulations, involves the formation and growth of secondary microcracks, leading to increased energy dissipation and damage spreading.
Author contributions
D. W. conducted EBSD measurements, L. N. H. and D. W. analyzed the EBSD data; D. W., J. H., and S. E. W. interpreted the EBSD data; V. P. and S. E. W. analyzed and interpreted the SANS data; D. W. and P. Z. designed and conducted the F. E. M. modelling; C. F. B., J. H., P. F. conducted nano-indentation experiments under supervision of BM and analyzed the results; J. H., C. F. B., and S. L. conducted further characterization of the bivalve specimens; K. H. conducted anisotropic Scherrer analyses; F. M. provided specimens and biological context and contributed to the interpretation of the results; S. E. W. conceived the study. With the input of all other authors, D. W., J. H., and S. E. W. wrote the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
SEW acknowledges financial support by an Emmy Noether starting grant by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation), grant number 251939425. SEW and SL received further support by the Bavarian State Ministry of the Environment and Consumer Protection in the framework of the project network BayBionik, a collaborative research group (sub-project TUT01UT-73842, Grant holder SEW). DW and LNH acknowledge support from the Natural Environment Research Council Grant NE/M000966/1. DW and PZ acknowledge financial support from the Multi-University Research Initiative (AFOSR-FA9550-15-1-0009). BM and PF acknowledge financial support from DFG via the research training school GRK1896: “In Situ Microscopy with Electrons, X-rays and Scanning Probes” and the ‘Center for Nanoanalysis and Electron Microscopy’ (CENEM) at FAU. We thank J. Reiser and Dr J. Kaschta, and the Institute of Polymer Materials (LSP) at FAU for their support in TGA measurements.Notes and references
- B. A. Palmer, G. J. Taylor, V. Brumfeld, D. Gur, M. Shemesh, N. Elad, A. Osherov, D. Oron, S. Weiner and L. Addadi, Science, 2017, 358, 1172–1175 CrossRef CAS PubMed.
- J. Aizenberg, S. Weiner, A. Tkachenko, L. Addadi and G. Hendler, Nature, 2001, 412, 819–822 CrossRef CAS PubMed.
- L. Li and C. Ortiz, Nat. Mater., 2014, 13, 501–507 CrossRef CAS PubMed.
- J. C. Weaver, G. W. Milliron, A. Miserez, K. Evans-Lutterodt, S. Herrera, I. Gallana, W. J. Mershon, B. Swanson, P. Zavattieri, E. DiMasi and D. Kisailus, Science, 2012, 336, 1275–1280 CrossRef CAS PubMed.
- S. Amini, M. Tadayon, S. Idapalapati and A. Miserez, Nat. Mater., 2015, 14, 943–950 CrossRef CAS PubMed.
- M. E. Csete and J. C. Doyle, Science, 2002, 295, 1664–1669 CrossRef CAS PubMed.
- S. E. Naleway, J. R. A. Taylor, M. M. Porter, M. A. Meyers and J. McKittrick, Mater. Sci. Eng., C, 2016, 59, 1143–1167 CrossRef CAS PubMed.
- U. G. K. Wegst, H. Bai, E. Saiz, A. P. Tomsia and R. O. Ritchie, Nat. Mater., 2014, 14, 23–36 CrossRef PubMed.
- S. E. Naleway, M. M. Porter, J. McKittrick and M. A. Meyers, Adv. Mater., 2015, 27, 5455–5476 CrossRef CAS PubMed.
- M. A. Meyers, P.-Y. Chen, A. Y.-M. Lin and Y. Seki, Prog. Mater. Sci., 2008, 53, 1–206 CrossRef CAS.
- O. B. A. Agbaje, R. Wirth, L. F. G. Morales, K. Shirai, M. Kosnik, T. Watanabe and D. E. Jacob, R. Soc. Open Sci., 2017, 4, 170622 CrossRef CAS PubMed.
- D. J. Green, An introduction to the mechanical properties of ceramics, Cambridge University Press, Cambridge, UK, 1998 Search PubMed.
- T. Oh, J. Rödel, R. Cannon and R. Ritchie, Acta Metall., 1988, 36, 2083–2093 CrossRef CAS.
- R. O. Ritchie, Nat. Mater., 2011, 10, 817–822 CrossRef CAS PubMed.
- M. E. Launey, M. J. Buehler and R. O. Ritchie, Annu. Rev. Mater. Res., 2010, 40, 25–53 CrossRef CAS.
- T. A. Grünewald, M. Liebi, N. K. Wittig, A. Johannes, T. Sikjaer, L. Rejnmark, Z. Gao, M. Rosenthal, M. Guizar-Sicairos, H. Birkedal and M. Burghammer, Sci. Adv., 2020, 6, eaba4171 CrossRef PubMed.
- I. Silva Barreto, S. Le Cann, S. Ahmed, V. Sotiriou, M. J. Turunen, U. Johansson, A. Rodriguez-Fernandez, T. A. Grünewald, M. Liebi, N. C. Nowlan and H. Isaksson, Adv. Sci., 2020, 7, 2002524 CrossRef CAS PubMed.
- R. O. Ritchie, Philos. Trans. R. Soc., A, 2021, 379, 20200437 CrossRef CAS PubMed.
- B. Kahler, M. V. Swain and A. Moule, J. Biomech., 2003, 36, 229–237 CrossRef PubMed.
- S. Kamat, X. Su, R. Ballarini and A. H. Heuer, Nature, 2000, 405, 1036–1040 CrossRef CAS PubMed.
- F. Eltit, V. Ebacher and R. Wang, J. Struct. Biol., 2013, 183, 141–148 CrossRef CAS PubMed.
- D. Vashishth, K. Tanner and W. Bonfield, J. Biomech., 2000, 33, 1169–1174 CrossRef CAS PubMed.
- Z. Liu, M. A. Meyers, Z. Zhang and R. O. Ritchie, Prog. Mater. Sci., 2017, 88, 467–498 CrossRef CAS.
- B. J. F. Bruet, J. Song, M. C. Boyce and C. Ortiz, Nat. Mater., 2008, 7, 748–756 CrossRef CAS PubMed.
- Y. Politi, M. Priewasser, E. Pippel, P. Zaslansky, J. Hartmann, S. Siegel, C. Li, F. G. Barth and P. Fratzl, Adv. Funct. Mater., 2012, 22, 2519–2528 CrossRef CAS.
- S. Amini, A. Masic, L. Bertinetti, J. S. Teguh, J. S. Herrin, X. Zhu, H. Su and A. Miserez, Nat. Commun., 2014, 5, 3187 CrossRef PubMed.
- B. Bar-On, F. G. Barth, P. Fratzl and Y. Politi, Nat. Commun., 2014, 5, 3894 CrossRef CAS PubMed.
- N. Guarín-Zapata, J. Gomez, N. Yaraghi, D. Kisailus and P. D. Zavattieri, Acta Biomater., 2015, 23, 11–20 CrossRef PubMed.
- V. Imbeni, J. J. Kruzic, G. W. Marshall, S. J. Marshall and R. O. Ritchie, Nat. Mater., 2005, 4, 229–232 CrossRef CAS PubMed.
- S. Bechtle, T. Fett, G. Rizzi, S. Habelitz, A. Klocke and G. A. Schneider, Biomaterials, 2010, 31, 4238–4247 CrossRef CAS PubMed.
- J. H. Pit and P. C. Southgate, Aquacult. Int., 2003, 11, 545–555 CrossRef.
- Y. Zhang, O. Paris, N. J. Terrill and H. S. Gupta, Sci. Rep., 2016, 6, 26249 CrossRef CAS PubMed.
- O. B. A. Agbaje, I. Ben Shir, D. B. Zax, A. Schmidt and D. E. Jacob, Acta Biomater., 2018, 80, 176–187 CrossRef CAS PubMed.
- O. B. Bøggild, The shell structure of the mollusks, A.F. Høst & søn, København, 1930 Search PubMed.
- M. E. Kunitake, L. M. Mangano, J. M. Peloquin, S. P. Baker and L. A. Estroff, Acta Biomater., 2013, 9, 5353–5359 CrossRef CAS PubMed.
- C. F. Böhm, P. Feldner and B. Merle, Materials, 2019, 12, 1–9 Search PubMed.
- B. Pokroy, A. N. Fitch, F. F. Marin, M. Kapon, N. Adir and E. Zolotoyabko, J. Struct. Biol., 2006, 155, 96–103 CrossRef CAS PubMed.
- M. E. Kunitake, S. P. Baker and L. A. Estroff, MRS Commun., 2012, 2, 113–116 CrossRef CAS.
- J. Aizenberg, J. Hanson, T. F. Koetzle, S. Weiner and L. Addadi, J. Am. Chem. Soc., 1997, 119, 881–886 CrossRef CAS.
- H. Li, H. L. Xin, M. E. Kunitake, E. C. Keene, D. A. Muller, L. A. Estroff and A. Muller, Adv. Funct. Mater., 2011, 21, 2028–2034 CrossRef.
- Y. Dauphin, Mineral. Mag., 2008, 72, 243–246 CrossRef CAS.
- B.-A. Gotliv, N. Kessler, J. L. Sumerel, D. E. Morse, N. Tuross, L. Addadi and S. Weiner, ChemBioChem, 2005, 6, 304–314 CrossRef CAS PubMed.
- F. Nudelman, H. H. Chen, H. A. Goldberg, S. Weiner and L. Addadi, Faraday Discuss., 2007, 136, 9–25 RSC.
- F. Marin, B. Pokroy, G. Luquet, P. Layrolle and K. De Groot, Biomaterials, 2007, 28, 2368–2377 CrossRef CAS PubMed.
- Y. Dauphin, J. P. Cuif, J. Doucet, M. Salomé, J. Susini and C. T. Willams, J. Struct. Biol., 2003, 142, 272–280 CrossRef CAS PubMed.
- S. E. Wolf, I. Lieberwirth, F. Natalio, J.-F. Bardeau, N. Delorme, F. Emmerling, R. Barrea, M. Kappl and F. Marin, Faraday Discuss., 2012, 159, 433 RSC.
- S. Weiner and L. Addadi, Annu. Rev. Mater. Res., 2011, 41, 21–40 CrossRef CAS.
- B. Bayerlein, P. Zaslansky, Y. Dauphin, A. Rack, P. Fratzl and I. Zlotnikov, Nat. Mater., 2014, 13, 1102–1107 CrossRef CAS PubMed.
- V. Schoeppler, L. Gránásy, E. Reich, N. Poulsen, R. de Kloe, P. Cook, A. Rack, T. Pusztai and I. Zlotnikov, Adv. Mater., 2018, 30, 1803855 CrossRef PubMed.
- V. Schoeppler, D. Stier, R. J. Best, C. Song, J. Turner, B. H. Savitzky, C. Ophus, M. A. Marcus, S. Zhao, K. Bustillo and I. Zlotnikov, Adv. Mater., 2021, 2101358 CrossRef CAS PubMed.
- E. Weber and B. Pokroy, CrystEngComm, 2015, 17, 5873–5883 RSC.
- J. Villanova, S. Kozachkevich, P. Zaslansky, L. Kundanati, A. A. Bracha, I. Polishchuk, L. Bloch, D. Levy, A. Katsman, C. Giacobbe, Y. Etinger-Geller, P. Gilbert, B. Pokroy, A. J. Giuffre, M. A. Marcus, N. M. Pugno, Y. Kauffmann, G. Hendler, M. Burghammer and C.-Y. Sun, Science, 2017, 358, 1294–1298 CrossRef PubMed.
- F. Mastropietro, P. Godard, M. Burghammer, C. Chevallard, J. Daillant, J. Duboisset, M. Allain, P. Guenoun, J. Nouet and V. Chamard, Nat. Mater., 2017, 16, 946–952 CrossRef CAS PubMed.
- S. E. Wolf, N. Loges, B. Mathiasch, M. Panthöfer, I. Mey, A. Janshoff and W. Tremel, Angew. Chem., 2007, 119, 5716–5721 CrossRef.
- A. Berman, J. Hanson, L. Leiserowitz, T. F. Koetzle, S. Weiner and L. Addadi, Science, 1993, 259, 776–779 CrossRef CAS PubMed.
- Z. Deng, H. Chen, T. Yang, Z. Jia, J. C. Weaver, P. D. Shevchenko, F. De Carlo, R. Mirzaeifar and L. Li, Nat. Commun., 2020, 11, 5678 CrossRef CAS PubMed.
- P. Gilbert, A. Young and S. N. Coppersmith, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 11350–11355 CrossRef CAS PubMed.
- Y. Dauphin, J. Biol. Chem., 2003, 278, 15168–15177 CrossRef CAS PubMed.
- T. Okumura, M. Suzuki, H. Nagasawa and T. Kogure, Cryst. Growth Des., 2012, 12, 224–230 CrossRef CAS.
- T. Okumura, M. Suzuki, H. Nagasawa and T. Kogure, Micron, 2010, 41, 821–826 CrossRef CAS PubMed.
- A. G. Checa, J. T. Bonarski, M. G. Willinger, M. Faryna, K. Berent, B. Kania, A. González-Segura, C. M. Pina, J. Pospiech and A. Morawiec, J. R. Soc., Interface, 2013, 10, 20130425 CrossRef PubMed.
- A. G. Checa, F. J. Esteban-Delgado, J. Ramírez-Rico and A. B. Rodríguez-Navarro, J. Struct. Biol., 2009, 167, 261–270 CrossRef CAS PubMed.
- R. Hovden, S. E. Wolf, M. E. Holtz, F. Marin, D. A. Muller and L. A. Estroff, Nat. Commun., 2015, 6, 10097 CrossRef CAS PubMed.
- P. Gilbert, R. A. Metzler, D. Zhou, A. Scholl, A. Doran, A. Young, M. Kunz, N. Tamura and S. N. Coppersmith, J. Am. Chem. Soc., 2008, 130, 17519–17527 CrossRef CAS PubMed.
- I. C. Olson, R. Metzler, N. Tamura, M. Kunz, C. E. Killian and P. Gilbert, J. Struct. Biol., 2013, 183, 180–190 CrossRef CAS PubMed.
- A. G. Shtukenberg, Y. O. Punin, E. Gunn and B. Kahr, Chem. Rev., 2012, 112, 1805–1838 CrossRef CAS PubMed.
- Y.-Y. Kim, J. D. Carloni, B. Demarchi, D. Sparks, D. G. Reid, M. E. Kunitake, C. C. Tang, M. J. Duer, C. L. Freeman, B. Pokroy, K. Penkman, J. H. Harding, L. A. Estroff, S. P. Baker and F. C. Meldrum, Nat. Mater., 2016, 15, 903–910 CrossRef CAS PubMed.
- D. Athanasiadou, W. Jiang, D. Goldbaum, A. Saleem, K. Basu, M. S. Pacella, C. F. Böhm, R. R. Chromik, M. T. Hincke, A. B. Rodríguez-Navarro, H. Vali, S. E. Wolf, J. J. Gray, K. H. Bui and M. D. McKee, Sci. Adv., 2018, 4, 1–14 Search PubMed.
- Y. Dauphin, E. Zolotoyabko, A. Berner, E. Lakin, C. Rollion-Bard, J. P. Cuif and P. Fratzl, J. Struct. Biol., 2019, 205, 121–132 CrossRef CAS PubMed.
- D. P. Grigoriev, Otogeny of Minerals, Israel Programme for Scientific Translations, Jerusalem, 1965 Search PubMed.
- J. Harris, I. Mey, M. Hajir, M. Mondeshki and S. E. Wolf, CrystEngComm, 2015, 17, 6831–6837 RSC.
- H.-J. Bunge, Texture Analysis in Materials Science, Butterworth-Heinemann, Oxford, UK, 2013 Search PubMed.
- D. Mainprice, R. Hielscher and H. Schaeben, Geol. Soc. Spec. Publ., 2011, 360, 175–192 CrossRef.
- C. C. Chen, C. C. Lin, L. G. Liu, S. V. Sinogeikin and J. D. Bass, Am. Mineral., 2001, 86, 1525–1529 CrossRef CAS.
- M. Strąg, Ł. Maj, M. Bieda, P. Petrzak, A. Jarzębska, J. Gluch, E. Topal, K. Kutukova, A. Clausner, W. Heyn, K. Berent, K. Nalepka, E. Zschech, A. G. Checa and K. Sztwiertnia, Nanomaterials, 2020, 10, 634 CrossRef PubMed.
- S. Amini and A. Miserez, Acta Biomater., 2013, 9, 7895–7907 CrossRef CAS PubMed.
- G. M. Pharr, Mater. Sci. Eng., A, 1998, 253, 151–159 CrossRef.
- B. Merle, W. H. Higgins and G. M. Pharr, J. Mater. Res., 2020, 35, 343–352 CrossRef CAS.
- K. E. Johanns, J. H. Lee, Y. F. Gao and G. M. Pharr, Modell. Simul. Mater. Sci. Eng., 2014, 22, 015011 CrossRef.
- A. E. Giannakopoulos and S. Suresh, Int. J. Solids Struct., 1997, 34, 2357–2392 CrossRef.
- A. E. Giannakopoulos and S. Suresh, Int. J. Solids Struct., 1997, 34, 2393–2428 CrossRef.
- H. Yao and H. Gao, J. Comput. Theor. Nanosci., 2010, 7, 1299–1305 CrossRef CAS.
- D. C. Pender, N. P. Padture, A. E. Giannakopoulos and S. Suresh, Acta Mater., 2001, 49, 3255–3262 CrossRef CAS.
- D. C. Pender, S. C. Thompson, N. P. Padture, A. E. Giannakopoulos and S. Suresh, Acta Mater., 2001, 49, 3263–3268 CrossRef CAS.
- S. Suresh, Science, 2001, 292, 2447–2451 CrossRef CAS PubMed.
- J.-P. Cuif, M. Burghammer, V. Chamard, Y. Dauphin, P. Godard, G. Moullac, G. Nehrke and A. Perez-Huerta, Minerals, 2014, 4, 815–834 CrossRef.
- S. S. Chiang, D. B. Marshall and A. G. Evans, J. Appl. Phys., 1982, 53, 298–311 CrossRef CAS.
- X. Chen, J. W. Hutchinson and A. G. Evans, J. Am. Ceram. Soc., 2005, 88, 1233–1238 CrossRef CAS.
- S. E. Wolf, C. F. Böhm, J. Harris, B. Demmert, D. E. Jacob, M. Mondeshki, E. E. Ruiz-Agudo and C. Rodriguez-Navarro, J. Struct. Biol., 2016, 196, 260–287 CrossRef PubMed.
- J. Gim, N. Schnitzer, L. M. Otter, Y. Cui, S. Motreuil, F. Marin, S. E. Wolf, D. E. Jacob, A. Misra and R. Hovden, Nat. Commun., 2019, 10, 4822 CrossRef PubMed.
- M. Rousseau, E. Lopez, P. Stempflé, M. Brendlé, L. Franke, A. Guette, R. Naslain and X. Bourrat, Biomaterials, 2005, 26, 6254–6262 CrossRef CAS PubMed.
- C. Rodríguez-Navarro, E. Ruiz-Agudo, J. Harris and S. E. Wolf, J. Struct. Biol., 2016, 196, 260–287 CrossRef PubMed.
- D. Ectors, F. Goetz-Neunhoeffer and J. Neubauer, J. Appl. Crystallogr., 2015, 48, 189–194 CrossRef CAS.
- G. Porod, Kolloid-Z., 1951, 124, 108–122 CrossRef.
- G. Zhang and J. Xu, J. Struct. Biol., 2013, 182, 36–43 CrossRef CAS PubMed.
- G. Beaucage, J. Appl. Crystallogr., 1995, 28, 717–728 CrossRef CAS.
- A. Baronnet, J.-P. Cuif, Y. Dauphin, B. Farre and J. Nouet, Mineral. Mag., 2008, 72, 617–626 CrossRef CAS.
- W. Huang, D. Restrepo, J. Jung, F. Y. Su, Z. Liu, R. O. Ritchie, J. McKittrick, P. Zavattieri and D. Kisailus, Adv. Mater., 2019, 31, 1901561 CrossRef CAS PubMed.
- H. Loh, T. Divoux, B. Gludovatz, P. U. P. A. Gilbert, R. O. Ritchie, F. Ulm and A. Masic, Commun. Mater., 2020, 1, 77 CrossRef.
- R. Roer and R. Dillaman, Am. Zool., 1984, 24, 893–909 CrossRef CAS.
- D. Chateigner, C. Hedegaard and H. Wenk, in 11th International Conference on Textures of Materials, ed. Z. Liang, L. Zuo and Y. Chu, International Academic Publishers, 1996, vol. 2, pp. 1221–1226 Search PubMed.
- A. G. Checa and A. B. Rodríguez-Navarro, Proc. R. Soc. London, Ser. B, 2001, 268, 771–778 CAS.
- W. Wagermaier, H. S. Gupta, A. Gourrier, O. Paris, P. Roschger, M. Burghammer, C. Riekel and P. Fratzl, J. Appl. Crystallogr., 2007, 40, 115–120 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental details and supplementary figures: (S1) Macrophotograph of Pinctada margaritifera; (S2) Axes of 2–10° lattice rotations within Group 1, transitional, and Group 2 prisms; (S3) Stereoplots of Young's modulus for different portions of the prismatic layer; (S4) Nanoindentation analysis of compliant and stiff prisms of P. margaritifera; (S5) Details on the finite-element modelling; (S6) Micrographs and EBDS maps of the prismatic layer of Pinna nobilis; (S7) Small and very-small angle neutron scattering of powdered prisms. See DOI: 10.1039/d1ma01031j |
| ‡ D. W. and J. H. contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2022 |