Active single cell encapsulation using SAW overcoming the limitations of Poisson distribution

Abstract

We demonstrate the use of an acoustic device to actively encapsulate single red blood cells into individual droplets in a T-junction. We compare the active encapsulation with the passive encapsulation depending on the number of loaded cells as well as the created droplet volumes. This method overcomes the Poisson limitation statistical loading of cells for the passive encapsulation. In our experiments we reach a single cell encapsulation efficiency of 97.9 ± 2.1% at droplet formation rates exceeding 15 Hz.

---

Introduction

Microfluidics has emerged as a tool which enables the fast, efficient characterization of biological samples, whereby the size of the devices facilitates manipulation of suspended objects down to the single-cell and/or molecular level.^1,2 One sub-group of microfluidics for example is droplet microfluidics,^3–9 these are typically two-phase systems which can be used to produce monodisperse, surfactant-stabilized, aqueous droplets¹⁰ surrounded in an immiscible carrier fluid (e.g. fluorinated oil) at rates up to tens of kHz.¹¹ Consequently, reagent(s) and reaction products remain contained within a well-controlled microenvironment, meaning that sample variants can be screened at high- and even ultra-high throughput.^12–14

Within droplet microfluidic systems, with a few exceptions, the numbers of cells encapsulated per each droplet produced is governed by Poisson statistics.¹⁵ Since the number of encapsulated cells per drop can affect the viability of certain processes, it is often necessary to regulate this parameter. Despite that, the governing Poisson statistics serve to reduce the quantity of drops which contain the desired number of cells, and consequently, the rate at which single-cell encapsulation can possibly occur. Thus, single-cell encapsulation in droplet microfluidics generally remains challenging.

To date, the majority of published microfluidic single-cell cell encapsulation work has focused on the development and use of non-deterministic, passive encapsulation methods.¹⁵ Here, droplets are typically produced continuously at high rates by pumping fluids from external pressure-driven reservoirs through user-defined geometries, with biological cells contained within the aqueous phase being segmented at the drop producing region.¹⁶ The Poisson statistics, or average number of cells per droplet, can be regulated by changing the cell concentration within the aqueous phase or the size of the drops.

Active encapsulation methods, both non-deterministic and deterministic, present an alternative route to the production of droplets at similar rates but with the potential to improve the efficiency of single-cell encapsulation. The use of externally applied electric, magnetic, acoustic or optical forces can generate fields within microfluidics which actuate directly upon cells, thus facilitating efficient cell manipulation and potentially, controlled single-cell encapsulation.

Some novel non-deterministic, active encapsulation methods have been described in the literature, including: the use of a capillary tube with a fixed piezoelectric transducer which expels droplets from the tube exit, with some drops containing cells;¹⁷ and the use of traveling surface acoustic waves to concentrate particles in solution at the drop producing region, before ultimately producing droplets containing such particles.¹⁸ Generally, however, such non-deterministic, active methods have limited throughput, failing to exceed encapsulation rates in excess of 1 kHz and with low efficiencies of single cell encapsulation.

Alternatively, several researchers have reported the use of deterministic, single-cell encapsulation methods. The use of optical tweezers to bring cells or sub-cellular components to the water–oil interface before drop production was described by He et al.¹⁹ Here, 100% of drops contained a single cell, though the throughput was extremely limited (<1 Hz). Inertial microfluidic techniques^20,21 have been used to efficiently order cells into single file as they approach a drop making nozzle, thus enabling efficient single-cell encapsulation at throughputs up to 12 kHz, however only 77% of drops contained single cells.²⁰ Despite the advantages in cell ordering and throughput given by inertial microfluidics for single-cell encapsulation, experimentally this method can be difficult to implement, particularly when using a heterogenous mixture, since the size of each suspended cell/particle is an important physical characteristic influencing the spacing between suspended cells/particles.²⁰ Further, the arrival rate of the cells at the droplet-making nozzle must equal the droplet production rate to encapsulate single cells, meaning that the flow rates for aqueous and oil inlets must be precisely synchronized. However, such precise control of inlet flow rates is typically difficult to achieve in microfluidics, without a method of eliminating the effect of short-term oscillations and/or the effect of long-term drift in the flow system(s).²² Though, inertia microfluidics is limited to very high flow rates.

Another emerging methodology for single-cell encapsulation combines the electrical detection of flowing cells with on-demand droplet manipulation. For example, Schoendube et al.²³ used a set of electrodes to detect the local electrical impedance change induced by the presence of a cell in a continuous flow, which was used to trigger the pulsed actuation of a piezoelectric transducer. Consequently, after a user-defined delay time, the downstream ejection of a drop containing a single-cell was performed after it arrived at the microfluidic dispensing nozzle.

The use of surface acoustic waves (SAW) for the on demand manipulation of organic cells/molecules has been of recent interest to many researchers, due to the high degree of control over the force which can be applied locally on-chip along with the general biocompatibility of SAWs.^24,25 Using SAW, it is now possible to perform on demand actions such as triggered droplet sorting²⁶ trapping and releasing,^27,28 merging,^29,30 and splitting,³¹ based on detected fluorescence, optical, or electrical properties. Recently, the production of droplets using an on-chip pressure source arising from a SAW, which effectively operates as an acoustic micropump, was reported by Franke et al.^32,33 and Collins et al.¹⁸ In such work, droplet volume is a function of the applied SAW power, duration of the force and system geometry.

Recently two-step acoustic encapsulation devices have been introduced that encapsulate cells randomly obeying the Poisson distribution in the first step and in a second step discard empty drops. After encapsulation 10–15% of the drops are loaded with cells leaving 85–90% empty drops.^34,35 The purity after sorting is 85–90%, this includes empty drops and multiple cell-loaded drops. The fastest sorting rate they claim is 1 kHz with a cell recovery of 95%.

In this paper we present an active single step method to capture single red blood cells (RBCs) into individual droplets on demand using SAW achieving ∼98% single-cell encapsulation. Using this active acoustic method, we overcome the limitations of Poisson statistics and at the same time maintain high encapsulation rates. There are no empty drops, and therefore no wasted drops, produced when producing single-cell encapsulated drops. Also, all cells are recovered since we do not discard any cells. The small footprint of the system (4 mm²), consists of an IDT, surrounding channel from the first constriction point in the oil inlet to the T-junction and the SAW micropump.³³ This allows coupling with other microfluidic techniques^{28,30,36–39} that enable downstream actions, e.g. trapping, releasing, splitting, merging, sorting to be performed upon the droplet-encapsulated single cells. The method allows the encapsulation of all types of cells independent of size or composition, including highly deformable and/or soft cells, and can feasibly be used with heterogenous cell mixtures.

High purity of droplet-encapsulated single cells within a sample offers several advantages. Firstly, using cell-pairing applications where two droplets containing individual cells are merged as an example, assay time is reduced as there are limited numbers of empty droplets, potentially reducing labour costs. Since more single-cell-containing droplets can now be assayed in each single device, overall device throughput is increased which may lead to reduced manufacturing costs. Further, compared to systems with lower proportions of drops containing single cells, less reagent is required to perform an equivalent experiment, which lowers consumable costs. The device shown here uses a combination of standard drop-maker implemented into PDMS microfluidics and surface acoustic wave actuation on a planar substrate. We synchronize the drop formation with laser-based cell detection to trigger acoustical drop pinch-off upon cell occurrence. We achieve a highly-efficient encapsulation of single-cells at a rate of up to 97.9 ± 2.1% at droplet formation rates exceeding 15 Hz.

Results and discussion

Device design and drop formation

The cell encapsulation device consists of a microfluidic channel with a T-junction and an integrated surface acoustic wave micropump. The microchannel is replicated from a SU8-master with polydimethylsiloxane (PDMS, Sylgard™ 184 Silicone Elastomer Kit). We use a custom-designed plastic mounting to mechanically press the mold onto a piezoelectric substrate containing the structured interdigital transducer (IDT). Using this method, a microfluidic channel with a temporary fluidic seal is created, so that the IDT can be later removed from the device, cleaned and reused. The IDT generates bidirectional traveling surface acoustic waves (TSAW) which travel along the microchannel on either side of the IDT, constructively adding up the acoustic streaming effect of both counter propagating waves as shown in Fig. 1. Using a tapered geometry of the IDT (TIDT) allows us to fine tune the acoustic path and align it with the position of the small microchannel having a cross section of only 10 μm × 10 μm. To prevent damping of the acoustic wave in PDMS, the mould features an air gap above the TIDT of 10 μm height. As the continuous phase we use surfactant (FluoSurf 1.8 w/w% in HFE7500, Emulseo) stabilised fluorinated oil (HFE7500, 3M™ Novec) and for the dispersed phase a 1% diluted RBC suspension in phosphate buffered saline (PBS) is used. To generate the continuous flow in the system we use a custom-made pressure system. We drive the continuous and dispersed phase with separate adjustable pressures between the oil or sample inlet and the outlet, respectively. Drops form at the T-junction where the two immiscible fluids converge by a mechanism similar to the “squeezing regime” described earlier.⁴⁰ By controlling both inlet pressures, drop size and flow rate can be adjusted to make droplets from picolitre to nanolitre volumes and beyond.

Fig. 1 Schematic representation of the cell encapsulation device. The continuous phase (HFE-oil, yellow) from the oil inlet is actuated by the acoustics. The IDT operates as a micropump by generating travelling SAW in opposite directions (small dark red arrows at both sides of the TIDT). In this way we exploit the bidirectional excitation using an adapted channel design with fluid flow in the same direction of each of the antiparallel TSAWs. Using this channel design we double the acoustic effect on the fluid to enable more efficient operation at approximately half the IDT power compared to harnessing only one acoustic path. Adjusting the operating frequency of the TIDT, we control the position of the travelling SAW excitation to optimally couple into the microfluidic channel. The SAW generates a volume force on the continuous fluid along the propagation direction of SAW. The SAW amplitude is exponentially attenuated in the HFE oil with a damping length of 150 μm.²⁴ With the distance from the IDT to the T-junction being 600 μm the SAW amplitude at the junction has been decreased to ∼2% of the original value. Droplet formation and cell encapsulation occurring further downstream at the T-junction (see region of encapsulation). Cell encapsulated droplets exit the channel through the outlet and can be collected or used for further processing. Note: The SAW actuates only the continuous phase and is not in contact with the discontinuous phase containing the cell sample. Fluid flow directions are indicated by black arrows.

Cell encapsulation and cell triggered droplet formation

To overcome random loading of drops with cells and to ensure single cell encapsulation, we actively control the size of drops formed at the T-junction drop-maker one by one. We acoustically trigger the drop pinch-off by actuating a SAW pulse at the TIDT for a short period of time using a power of P = 29 dBm and a pulse length of t_pulse = 0.6 ms.^32,33 The acoustic pulse creates a temporary pressure increase at the T-junction that causes the drop to form.³³ At this power and pulse length the pinch-off takes t_pinch-off = 0.7 ± 0.1 ms. To synchronize droplet formation with the cell flow and check cell viability, we detect each cell flowing into the T-junction section. We focus a laser spot (488 nm, 10 mW, Omicron) at the T-junction to excite fluorescence of the red blood cell labelled with calcein-AM (Sigma Life Science, USA). The fluorescence signal is detected with a photomultiplier-tube (PMT, Hamamatsu) and the fluorescence level is analysed with custom-made software (LabView). If a cell is detected by the software, it electrically triggers the SAW to pulse and pinch-off the drop as shown in Fig. 2. Calcein-AM was used as it labels viable cells but not dead cells,⁴¹ ensuring that each drop has a viable cell in it. It has been demonstrated in similar setups that subjecting cells to acoustic fields up to powers of 1 Watt are not harmful to cells.^42–45 The software allows the application of various filters to analyse the signal and to control the output, such as controlling the threshold value for detection, SAW power P, pulse duration t_pulse and delay time t_delay.

Fig. 2 Active RBC encapsulation in droplet: series of micrographs showing the encapsulation mechanism and the pinch-off of a droplet actuated by a pressure increase in the continuous phase which is induced via surface acoustic waves. A cell flowing in the aqueous discontinuous phase approaching the T-junction (red circle) (a). The cell is detected by the laser focused at the T-junction and the fluorescence is detected by a photomultiplier tube (b). The fluorescence level is analysed in custom-made software. If the signal is above a fluorescence threshold, the SAW is triggered and the drop is cut-off (c). For this encapsulation experiment, we use a power of P = 29 dBm and a pulse of t_pulse = 0.6 ms. The yellow arrows indicate the flow direction of the continuous and dispersed phase. The scale bar in the micrograph is 50 μm. Refer to ESI† Movie S1 which shows the active encapsulation of single red blood cells into individual drops by surface acoustic wave induced pressure raise in the continuous phase.

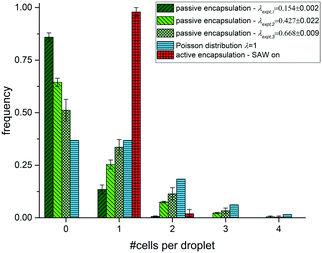
We evaluate the efficiency of active SAW cell encapsulation by comparing it with passive encapsulation into drops in the same microfluidic channel. For the passive cell encapsulation, different drop sizes were produced by variation of the pressure for the continuous oil phase p_oil, keeping the pressure for sample flow p_sample = 28.2 kPa constant. We use p_oil,V1 = 35.0 kPa, p_oil,V2 = 20.0 kPa and p_oil,V3 = 19.1 kPa that produce drops of different volumes, respectively. The smallest possible drop size in the squeezing regime is set by the geometry of the channel and has a drop with a length L equal to the channel width w, so that L/w ∼ 1. For the dimension of our channel with a square cross section w = h = 10 μm, this minimal volume can be estimated to be ∼1 pL. The smallest drop volume we use in our experiment is V₁ = 2.1 ± 0.1 pL, followed by larger volumes of V₂ = 10.5 ± 0.5 pL and V₃ = 18.9 ± 3.4 pL as shown in Fig. 3a–c. The drop rates are f₁ = 85.1 ± 1.1 Hz, f₂ = 39.4 ± 2.1 Hz and f₃ = 26.9 ± 1.4 Hz, respectively. Fitting the data with a Poisson fit we find λ_expt,V1 = 0.154 ± 0.002, λ_expt,V2 = 0.427 ± 0.022 and λ_expt,V3 = 0.668 ± 0.009, with small errors and coefficient of determination R-square close to 1, supporting the assumption of Poisson distributed RBCs.

Fig. 3 Micrographs of cell encapsulation and droplet formation: (a)–(c) passive encapsulation in drops of different volumes at constant sample pressure p_sample = 28.2 kPa and increasing oil pressures p_oil,V1 = 35.0 kPa, p_oil,V2 = 20.0 kPa and p_oil,V3 = 19.1 kPa. For the three pressure values we obtain drop volumes of V₁ = 2.1 ± 0.1 pL, V₂ = 10.5 ± 0.5 pL and V₃ = 18.9 ± 3.4 pL, respective drop rates for these drops are f_V1 = 85.1 ± 1.1 Hz, f_V2 = 39.4 ± 2.1 Hz and f_V3 = 26.9 ± 1.4 Hz. (d) Highly extended drops with large volumes and drop rates less than f_l < 0.015 Hz can be obtained with the pressure driven system to reduce the number of empty drops at the cost of extremely low drop rates. (e) For active encapsulation we achieve an average drop rate of f_a = 13.6 ± 2.10 Hz, with exactly one cell in a drop. In the image the first droplet on the right (only partly in the field of view) has a volume of V = 48.3 pL. The subsequent droplet in the middle is smaller V = 14.4 pL because the distance between entering RBCs at the T-junction were shorter and therefore a smaller drop was triggered to form. The next drop is the smallest with a volume of V = 5.5 pL. The yellow circles in the images highlight red blood cells. It demonstrates the random distribution of cells with many empty drops for (a)–(c), a cell in the long drop (d) and the single cell encapsulation in (e). The yellow arrows indicate the flow direction of the continuous and dispersed phase. The scale bar in the micrograph is 50 μm.

The use of pressure-driven flow is essential to generate highly extended drops with large volumes. As shown in Fig. 3d we can produce very long drops by decreasing the continuous flow to a limit below which no further drop breakup occurs. In this case, a remaining small amount of continuous fluid only flows along the four edges between the drop and the channel corner. In this regime, we can obtain extremely long drops and hence the drop generation rate is very low as depicted in Fig. 3d with drop formation times exceeding 1 min.

To achieve single cell loading of drops by SAW triggering, we operate the drop-maker in a regime whereby very long drops are formed. In this way, we can ensure that no drop is formed spontaneously before the next cell is detected and the number of empty drops can be minimized. This active cell encapsulation is depicted in Fig. 3e. In the experiment we firstly regulate the pressures to produce long drops and position the laser spot in the sample inlet close to the T-junction. We continuously interrogate and analyse the fluorescence signal and adjust the detection and output parameters in the software. If a cell is detected by the software, the SAW is actuated to pinch-off a single drop and then it continues to produce a drop until the next cell is detected. Therefore, eventually a polydisperse drop emulsion is formed with optimally each drop exactly containing one cell. In this encapsulation process we can distinguish cells which are 15 μm apart corresponding to a separation volume of 1.5 pL. This volume compared with a typical average drop volume of ∼80pL achieved using passive methods^34,35 is a factor of ∼50 times less. Therefore, the probability of multiple cell loading is greatly reduced.

Overcome Poisson distribution: single cell drop encapsulation in polydisperse drops/droplet loading by single cells

We analyse the data from the passive drop formation as shown in Fig. 3a–c by counting the number of cells per drop for the three different volumes tested.

The passive random loading of dispersed cells in a liquid into monodisperse droplets is expected to follow a discrete Poisson probability distribution as given by⁴⁶

with P_λ(k) the probability of finding k cells in a drop.

The non-dimensional parameter λ is the ratio of the drop volume V_drop and the average volume assigned per cell V̅_cell

V̅_cell is given by the inverse of the cell concentration c (number of cells per volume) V̅_cell = 1/c. It should not be confused with the volume of a cell itself, which is essentially the volume of its cytosol. λ is the experimental parameter that is varied in the experiment in two ways. The drop size V_drop that is controlled by the applied driving pressures in the inlet channels and the average volume per cell V̅_cell that is controlled by the cell concentration. The latter is related to the haematocrit (Ht) by c = Ht/V_RBC, with V_RBC being the volume of a RBC. For increasing drop size or increasing haematocrit the value of λ increases. Obviously, drops contain on average more cells if drop size or haematocrit increase.

We count the number of cells in each drop for the passive and active loading experiments and plot the frequency of cells depending on the number of cells per drop as shown in Fig. 4. With increasing drop volume for passive loading the average number of cells per drop increase as expected. Moreover, the frequency of drops with just one cell increases as well with increasing drop volume in these experiments and reaches a maximum of 33.6 ± 3.7% for the largest volume of V₃ = 18.9 pL. This value is already very close to the maximum loading efficiency expected from a Poisson distribution. However, for the active cell loading we even reach significantly higher single cell efficiencies. By analysing more than 300 drops, we find that 97.9% contain a single cell only. We have not observed any empty drops (without a cell) and only a 2.1% with two cells. Further, we have not observed any drop with more than two cells. In contrast, for passive cell loading the majority of drops are empty for all volumes tested. The frequency of empty drops, however, decrease with increasing drop volume in support of multiple loaded drops, many of which contain more than two cells. From eqn (2), we can determine the value of λ that maximizes the frequency of single cell loaded drops (k = 1) to be =1. This theoretical limit for the frequency yields P₁(1) = 0.368 and is depicted in Fig. 4. For comparison we fit the data for the different volumes using a Poisson distribution fit and find fitted values for λ to be λ_expt,V1 = 0.154 ± 0.002, λ_expt,V2 = 0.427 ± 0.022 and λ_expt,V3 = 0.668 ± 0.009, respectively. The errors of the fit are very small and suggest Poisson distributed cell loading. Hence, using SAW driven active encapsulation we not only outperform the passive loading experiment but also the theoretical limit for passive loading by a factor of 2.7.

Fig. 4 Histogram of frequency of drops (loading efficiency) depending on the number of RBCs per drop. Encapsulation is shown for the passive case for three volumes used (green shades), the active SAW encapsulation (red) and for reference the theoretical limit for Poisson encapsulation (blue). The loading efficiency E for single cell encapsulation for V₁ is E₁ = 13.5 ± 2.1%, for V₂ is E₂ = 25.4 ± 2.1% and for V₃ is E₃ = 33.6 ± 3.7%. The theoretical limit as given by the Poisson distribution is E_Poisson = P_λ=1(1) = 36.8%. Fitting the data with a Poisson fit we find λ_expt,V1 = 0.154 ± 0.002, λ_expt,V2 = 0.427 ± 0.022 and λ_expt,V3 = 0.668 ± 0.009, with small errors and coefficient of determination R-square close to 1, supporting the assumption of Poisson distributed RBCs. For the active encapsulation droplet loading efficiencies exceed the theoretical limit for passive encapsulation by a factor of 2.7 to be E_SAW = 97.9 ± 2.1%. Note, that no drop is empty and very few contain two cells in contrast to Poisson distributed loading.

The trade-off achieving such high loading efficiencies is a polydisperse droplet solution. We analyse the polydispersity of the droplet emulsion by determination of the size of each drop. Therefore, we processed the video data of the drops to produce a space–time plot. This spatio-temporal representation of the data simplifies drop volume determination in particular if drops are not fully in the field of view. We approximate the drop volume by the volume of a cuboid with cross-section of the channel and the length the resulting distance of a drop given by l_drop = (t₂ − t₁) × v_drop assuming a constant velocity of the drop v_drop propagating in x-direction in the channel. The drop volume is then calculated using V_drop = l_drop × A_cross as shown in Fig. 5.

Fig. 5 Micrographs showing how drop volumes using a reslice image of a video were analysed. Frames (a) and (b) are showing the same junction in the chip and are of the same drop at different times. (a) Is showing the anterior of the drop (front end) at the position x_r and at time t₁. (b) Shows the posterior of the drop (back end) of the same drop also at position x_r now at time t₂. (c) Shows the converted spatial data into temporal data around the fixed position x_r (shown in green). This resliced image (using ImageJ) is used to determine the length and hence the volume of the drop. Videos are captured with 10 000 fps. The scale bar in (a) and (b) is 50 μm and in (c) 10 ms. The flow directions are indicated by yellow arrows in (a).

The results of the drop volume analysis with space–time plots are shown in a histogram in Fig. 6a and in a box-and-whisker plot in Fig. 6b. The median of the distribution is at 25.2 pL, the lower quartile at 1.5 pL and the upper quartile at 86.6 pL. The scatter plot of the drop size distribution shows the volume of each drop with one cell. Clearly the sizes vary over a large range. The mean (or average) drop size is at 29.6 pL. Since almost all drops are loaded with one cell, one can conclude the cell concentration form this drop size by c = 1 cell/29.6 pL = 3.4 × 10¹⁰ cells per L. The haematocrit is then Ht_active = c × V_RBC = 0.3 ± 0.3%. We compare the found Ht from the active encapsulation with the Ht calculated from the fitted λ values from the passive loading for the Poisson distribution. The haematocrit is Ht_passive = 0.5 ± 0.2%. These two different Ht are in good agreement to each other but are slightly lower as the initial prepared Ht of the sample solution, which we estimate to be around 1%. This is likely to be due to sample-to-sample variability inherit with biological samples. Therefore, there may be different densities in the final concentrated RBC sample produced. Thus, leading to variations in sedimentation rate of cells during the experiment.

Fig. 6 Histogram of the droplet volumes for passive (green shades) and active (red) encapsulation in (a). For each volume for the passive and for the active encapsulation the droplet volumes are binned into 15 pL groups and plotted against the frequency. The volumes for the passive cases are monodisperse and results for volume 1–3 in the first and second bin. For the active encapsulation, the formed droplets are polydisperse with a maximum at 15 pL. A scatter and box plot of the droplet volumes produced during the active encapsulation grouped for the loading of cells in drop is shown in (b). For better visualisation data points are randomly scattered centred on the right within its bins on the left and the according box plot on the right. For the box plot of single loaded cell, we find the mean at 29.6 pL, the median at 25.2 pL, the lower quartile at 1.5 pL and the upper quartile at 86.6 pL. As can be derived from the box plot the distribution is right skewed.

Material and methods

Design and fabrication of hybrid chip

The microfluidic acoustic hybrid device consists of a single layer of PDMS assembled in between a piezoelectric substrate and a plastic cover. On the piezoelectric substrate (LiNbO₃, 128° Y-cut) gold electrodes are deposited. The tapered interdigital transducer (TIDT) consists of 60 finger pairs and the distance between the electrode fingers varies such that, the transducer wavelength is 23.0 to 24.2 μm and has an aperture width of 500 μm. According to the equation f = v_SAW × λ with f the frequency, v_SAW the speed of sound in the substrate and λ the transducer wavelength, which is given by the periodicity of the IDT, yields to excitation frequencies between 160 MHz and 167 MHz. The plastic cover mechanically presses the PDMS mould onto the substrate. Using screws, the contact pressure is controlled manually.

To fabricate the transducer, a whole 4′′ lithium niobate wafer is washed in each acetone and isopropanol sequentially for 5 min in an ultrasonic bath, followed by a 5 min rinse with RO water and dried with nitrogen. After cleaning, the wafer is centred in a spin coater and held by a vacuum. With a plastic pipette, a small volume of primer is dropped onto the surface of the wafer and spun for 5 s at 4000 RPM. S1818 photoresist (Microposit) is dropped onto the surface of the wafer and spun for 30 s at 4000 RPM, to give a film height of 1.8 μm. Then the wafer with resist is placed on a hotplate for 2 min at 120 °C to cure. After cooling down to room temperature, the wafer is exposed in a mask aligner (MA6, Süss MicroTec) using a chromium mask which contains the IDT design. The electrodes are aligned perpendicular to the x-direction of the crystal plane of the wafer before it is illuminated for 5 s. After exposing, the wafer is developed in a photo developer (Microposit, MF-319, Shipley) for 75 s. Subsequently, the wafer is rinsed with RO water for 5 min and is dried with nitrogen. The processed wafer is placed in an oxygen plasma for 2 min at 100 W to remove any remaining resist or dust particles. Then the wafer is put into a holder for metal deposition and is inserted into a metal deposition device (Plassys 15, Bestek, France) before a 10–100–10 nm layer of Ti–Au–Ti was deposited on the substrate. The Ti layers serve as adhesive layers between each deposited layer. Then a lift-off is performed using dimethyl sulfoxide (DMSO). After lift-off the wafer is diced (Alter Technology, UK) into 17.5 × 17.5 mm dies. The final step is a deposition of a 200 nm SiO₂ protective layer on top the IDT structures using a dry etch device (Plasmafab 505).

The PDMS microchannels are fabricated using standard soft lithography procedures.^47,48 The channel structure is designed in CAD program (AutoCAD 2019, Autodesk) and printed on a plastic foil (JD-Photo data, UK). The microfluidic channel consists of a T-junction geometry and a gap for the IDT directing to the SAW-pump. SU8-3010 photoresist (Microchem, SU8 3000 series) is spin coated on a silicon wafer substrate to a final height of 10 μm as stated on the data sheet (Microchem, S1800 series). The mask is exposed onto the SU8 layer using a mask aligner. After developing, the structured SU8 acts as a mold for a plurality of identical microchannels. This allows us to use the SU8 master for rapid prototyping. PDMS is filled into the mold and heat cured. The ratio of elastomer base to curing agent is 10 : 1. Inlets and outlet holes are created with a biopsy puncher.

Red blood cell preparation

Whole blood was obtained from healthy donors with informed consent and washed three times in phosphate buffered saline solution (PBS 1×, pH 7.4, 330 mOsm L⁻¹, Gibco life technologies). After each washing step, we centrifuge the sample for 5 min at 2500 RPM (mini spin plus centrifuge, Eppendorf) and remove the white buffy coat and supernatant. After the last centrifugation step, we take 80 μl of concentrated RBC from the bottom of the reaction tube and incubate in 1 ml green-fluorescent calcein-AM solution (5 μM) for 30 min at 37 °C, followed by three times washing with PBS. To avoid sedimentation of cells during the experiment we suspend the cells in a density matched solution using a density gradient solution (OptiPrep Density Gradient Medium, Sigma Life Science). Optiprep is a sterile non-ionic solution of 60% (w/v) iodixanol in water. Additionally, we use bovine serum albumin (BSA, Ameresco) to prevent adhesion of cells to each other and the microchannel walls. Therefore, we use 533 μL OptiPrep solution and mix with 1407 μL PBS/BSA (14 mg ml⁻¹) and suspend 60 μL of concentrated fluorescent-labelled RBC solution. The final density of this solution is ρ = 1.080 g mL⁻¹. The cell solution is stored at room temperature and is degassed for at least 15 min in the desiccator to remove smaller bubbles before use. We estimate the hematocrit (Ht) of this solution to be 1%.

Conclusions and outlook

In this article, we have described a droplet microfluidic system with integrated SAW, which enables the ∼98% efficient encapsulation of single cells within droplets at rates exceeding 15 Hz. By utilizing laser-based cell detection which triggers rapid SAW-actuated droplet pinch-off, we have overcome the limitations of the Poisson distribution to continuously encapsulate single cells in individual droplets on demand. This microfluidic chip can perform efficient encapsulation of single cells on a relatively small device footprint (4 mm²), which offers easy integration into droplet-based microfluidic lab on a chip (LoC) devices having low sample availability. Further, this droplet microfluidic device is especially suitable for use with small sample volumes, heterogenous cell samples and operates in a low to mid velocity flow rate regime of up to several mm s⁻¹. This is out of the range used in inertial microfluidics to order cell separation (0.1 m s⁻¹). Thus, this system can be of use in a range of biomedical or manufacturing applications that involve rapid, low-cost, continuous single-cell encapsulation. The range of drops we use is 1–135 pL which is a typical drop size used in this field.^49,50 Therefore, we do not expect any additional issues concerning the stability or the manipulation of droplets other than those reported in the literature.

Additional enhancements to this system could involve the detection of an individual cell which triggers the actuation of two SAW pulses, in contrast to the current single SAW pulse. The time interval between each pulse will be tuneable and is to be varied depending on the flow velocity within the detection region of the chip. Assuming a constant flow velocity, such a system should hypothetically enable the repeatable encapsulation of cells in droplets of a user-defined volume, thus consistently providing samples of single-cell encapsulated drops (i.e., limited empty droplets or drops containing more than one cell) and high droplet mono-dispersity.

The integration of this chip with other microfluidic techniques that perform other droplet actions (e.g. trapping, merging, sorting) will help to develop a functional LoC device.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is part of a project that has received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 813786 (EVOdrops). Additionally, AL and TF acknowledge support from the UK Engineering and Physical Sciences Research Council (EPSRC) via grant EP/P018882/1. The authors thank Raymond Sparrow for assistance and discussion with preparation of the manuscript.

References

1. H. A. Stone, A. D. Stroock and A. Ajdari, Annu. Rev. Fluid Mech., 2004, 36, 381–411.
2. K. Ino, M. Okochi, N. Konishi, M. Nakatochi, R. Imai, M. Shikida, A. Ito and H. Honda, Lab Chip, 2008, 8, 134–142.
3. Y.-J. Eun, A. S. Utada, M. F. Copeland, S. Takeuchi and D. B. Weibel, ACS Chem. Biol., 2011, 6, 260–266.
4. P. C. Blainey, FEMS Microbiol. Rev., 2013, 37, 407–427.
5. C. E. Stanley, R. C. R. Wootton and A. J. DeMello, Chimia, 2012, 66, 88–98.
6. S.-Y. Teh, R. Lin, L.-H. Hung and A. P. Lee, Lab Chip, 2008, 8, 198.
7. L. Mazutis, J. Gilbert, W. L. Ung, D. A. Weitz, A. D. Griffiths and J. A. Heyman, Nat. Protoc., 2013, 8, 870–891.
8. M. T. Guo, A. Rotem, J. A. Heyman and D. A. Weitz, Lab Chip, 2012, 12, 2146.
9. E. Brouzes, M. Medkova, N. Savenelli, D. Marran, M. Twardowski, J. B. Hutchison, J. M. Rothberg, D. R. Link, N. Perrimon and M. L. Samuels, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 14195–14200.
10. J.-C. Baret, Lab Chip, 2012, 12, 422–433.
11. I. C. Clark and A. R. Abate, Lab Chip, 2018, 18, 3598–3605.
12. T. Stuart and R. Satija, Nat. Rev. Genet., 2019, 20, 257–272.
13. N. Wen, Z. Zhao, B. Fan, D. Chen, D. Men, J. Wang and J. Chen, Molecules, 2016, 21, 881.
14. X. Zhang, T. Li, F. Liu, Y. Chen, J. Yao, Z. Li, Y. Huang and J. Wang, Mol. Cell, 2019, 73, 130–142.e5.
15. D. J. Collins, A. Neild, A. DeMello, A.-Q. Liu and Y. Ai, Lab Chip, 2015, 15, 3439–3459.
16. J. Hong, A. J. DeMello and S. N. Jayasinghe, Biomed. Mater., 2010, 5, 021001.
17. H. Wang, W. Zhang and Z. Dai, Anal. Methods, 2014, 6, 9754–9760.
18. D. J. Collins, T. Alan, K. Helmerson and A. Neild, Lab Chip, 2013, 13, 3225.
19. M. He, J. S. Edgar, G. D. M. Jeffries, R. M. Lorenz, J. P. Shelby and D. T. Chiu, Anal. Chem., 2005, 77, 1539–1544.
20. J. F. Edd, D. Di Carlo, K. J. Humphry, S. Köster, D. Irimia, D. A. Weitz and M. Toner, Lab Chip, 2008, 8, 1262.
21. E. W. M. Kemna, R. M. Schoeman, F. Wolbers, I. Vermes, D. A. Weitz and A. van den Berg, Lab Chip, 2012, 12, 2881.
22. D. F. Crawford, C. A. Smith and G. Whyte, Sci. Rep., 2017, 7, 10545.
23. J. Schoendube, D. Wright, R. Zengerle and P. Koltay, Biomicrofluidics, 2015, 9, 014117.
24. M. Wiklund, Lab Chip, 2012, 12, 2018–2028.
25. D. J. Collins, B. Morahan, J. Garcia-Bustos, C. Doerig, M. Plebanski and A. Neild, Nat. Commun., 2015, 6, 8686.
26. L. Schmid, D. A. Weitz and T. Franke, Lab Chip, 2014, 14, 3710–3718.
27. J. H. Jung, G. Destgeer, J. Park, H. Ahmed, K. Park and H. J. Sung, Anal. Chem., 2017, 89, 2211–2215.
28. R. W. Rambach, P. Biswas, A. Yadav, P. Garstecki and T. Franke, Analyst, 2018, 143, 843–849.
29. M. Sesen, T. Alan and A. Neild, Lab Chip, 2014, 14, 3325–3333.
30. V. Bussiere, A. Vigne, A. Link, J. McGrath, A. Srivastav, J.-C. Baret and T. Franke, Anal. Chem., 2019, 91, 13978–13985.
31. J. H. Jung, G. Destgeer, B. Ha, J. Park and H. J. Sung, Lab Chip, 2016, 16, 3235–3243.
32. L. Schmid and T. Franke, Lab Chip, 2013, 13, 1691.
33. L. Schmid and T. Franke, Appl. Phys. Lett., 2014, 104, 133501.
34. P. Li, Z. Ma, Y. Zhou, D. J. Collins, Z. Wang and Y. Ai, Anal. Chem., 2019, 91, 9970–9977.
35. R. Zhong, S. Yang, G. S. Ugolini, T. Naquin, J. Zhang, K. Yang, J. Xia, T. Konry and T. J. Huang, Small, 2021, 2103848, 1–9.
36. R. W. Rambach, K. Linder, M. Heymann and T. Franke, Lab Chip, 2017, 17, 3422–3430.
37. J. H. Jung, G. Destgeer, B. Ha, J. Park and H. J. Sung, Lab Chip, 2016, 16, 3235–3243.
38. K. Mutafopulos, P. Spink, C. D. Lofstrom, P. J. Lu, H. Lu, J. C. Sharpe, T. Franke and D. A. Weitz, Lab Chip, 2019, 19, 2435–2443.
39. W. L. Ung, K. Mutafopulos, P. Spink, R. W. Rambach, T. Franke and D. A. Weitz, Lab Chip, 2017, 17, 4059–4069.
40. P. Garstecki, M. J. Fuerstman, H. A. Stone and G. M. Whitesides, Lab Chip, 2006, 6, 437.
41. T. Franke, S. Braunmüller, L. Schmid, A. Wixforth and D. A. Weitz, Lab Chip, 2010, 10, 789.
42. D. Bazou, W. T. Coakley, A. J. Hayes and S. K. Jackson, Toxicol. In Vitro, 2008, 22, 1321–1331.
43. M. Evander, L. Johansson, T. Lilliehorn, J. Piskur, M. Lindvall, S. Johansson, M. Almqvist, T. Laurell and J. Nilsson, Anal. Chem., 2007, 79, 2984–2991.
44. T. Franke, S. Braunmüller, L. Schmid, A. Wixforth and D. A. Weitz, Lab Chip, 2010, 10, 789–794.
45. I. Leibacher, P. Hahn and J. Dual, Microfluid. Nanofluid., 2015, 19, 923–933.
46. D. J. Collins, A. Neild, A. DeMello, A.-Q. Liu and Y. Ai, Lab Chip, 2015, 15, 3439–3459.
47. Y. Xia and G. M. Whitesides, Annu. Rev. Mater. Sci., 1998, 28, 153–184.
48. D. Qin, Y. Xia and G. M. Whitesides, Nat. Protoc., 2010, 5, 491–502.
49. A. Suea-Ngam, P. D. Howes, M. Srisa-Art and A. J. Demello, Chem. Commun., 2019, 55, 9895–9903.
50. S. Mashaghi, A. Abbaspourrad, D. A. Weitz and A. M. van Oijen, TrAC, Trends Anal. Chem., 2016, 82, 118–125.

---

Footnote

† Electronic supplementary information (ESI) available: Movie S1 showing the active encapsulation of single red blood cells into individual drops by surface acoustic wave induced pressure raise in the continuous phase. See DOI: 10.1039/d1lc00880c

---