Characterization of a high-sensitivity ICP-TOFMS instrument for microdroplet, nanoparticle, and microplastic analyses

Abstract

We report the capabilities of an inductively coupled plasma time-of-flight mass spectrometry (ICP-TOFMS) instrument for single-droplet and single-particle analysis. The icpTOF-S2 (TOFWERK AG) is a high-sensitivity version of the icpTOF instrument series that features a shorter flight distance, which allows highly time resolved single-particle measurements (down to 12 μs/spectrum). The mass resolving power of the icpTOF-S2 is ∼850 at full-width half maximum and the instrument can record quasi-simultaneous full-element mass spectra—from mass-to-charge (m/z) 6 to 254. The icpTOF-S2 provides absolute sensitivities of up to 564 counts per fg and detection efficiencies of 1 ion per 6100 atoms for ¹⁷⁵Lu. These sensitivities enable single-digit attogram detection limits and theoretical particle-size detection below 10 nm in diameter for most sensitive elements, such as U, Th, and Lu. We demonstrate accurate size distribution measurement for gold nanoparticles with a mean diameter of 15 nm. With the instrument tuned for low-m/z sensitivity, we demonstrate the detection and quantification of carbon in polystyrene bead microparticles that have an average diameter of 3.1 μm. The determined critical mass for ¹²C detection is 3.2 pg and the critical diameter is 1.8 μm. Linear dynamic range for single-particle and single-droplet analysis spans 4 orders of magnitude, from 1 to 20 000 count(s) per particle event. The instrument's abundance sensitivity is around 2000 ppm, and this abundance sensitivity shows time-dependent variability as a function of intense ion spikes from microdroplets or large particles.

---

Introduction

The use of nanomaterials across a wide variety of industries has increased over the past several decades; however, the human health and environmental impact of nanoparticles (NPs)—both natural and anthropogenic—is not yet well understood.¹ Inductively coupled plasma mass spectrometry (ICP-MS) is an established high-throughput technique for NP quantification.^2,3 In single-particle (sp) ICP-MS, nanoparticle signals are measured above a dissolved element background. The measurement of small nanoparticles is therefore limited by the instrument sensitivity and the dissolved analyte background. There are methods to reduce the dissolved fraction of a nanoparticle containing sample, such as sample filtration to separate dissolved elements from particle fractions,⁴ sample dilution,⁵ and the use of an ion exchange resin.⁶ Despite efforts to remove the dissolved analyte background, the measurement of small particles is often still limited by instrument sensitivity, which has brought about the need for more sensitive ICP-MS instrumentation.

Single-particle ICP-MS measurements are made by introducing dilute particle suspensions into the plasma; these particles produce discrete ion clouds that are registered as transient signal spikes in the time-resolved MS data. spICP-MS enables quantification in terms of the mass amounts of element(s) in individual particles and the particle number concentration (PNC). Through assuming a known density, stoichiometry, and shape, measured mass amounts of elements in a single particle can be converted to particle diameter, i.e., size. Single-particle ICP-MS is commonly used for the detection of metal containing NPs or cells;^7,8 however, recently it has been demonstrated that spICP quadrupole mass spectrometry (spICP-QMS) can be used for the detection of carbon in microplastics.^9–11 Quadrupole mass spectrometry (QMS) instruments are most commonly used for spICP-MS; however, since the quadrupole is a scanning type mass filter, it is not capable of measuring more than one nuclide simultaneously.¹² With sufficiently short dwell times and settling times, it is possible to rapidly switch between (at most 2 m/z) channels to measure multi-element particles with QMS. However, even with this fast switching, the quantification of multiple elements in a single particle is limited by spectral intensity skew error.^13,14

In contrast to QMS instruments, full-spectrum mass analyzers such as the Mattauch–Herzog geometry sector-field mass spectrograph (MHMS)^15–17 and time-of-flight (TOF) mass spectrometer^18–21 can be used to (quasi) simultaneously record signals from multiple nuclides from transient events. Of these full-mass-spectrum analyzers, TOFMS instruments are particularly well suited for single particle analysis because they are capable of short spectral averaging times.^22,23 Current detector technology limits the use of MHMS for recording very fast transient signals.^16,17 Recent reports have provided figures of merit of the various ICP-TOFMS instruments available.^21,24,25 Three instrumentation companies—TOFWERK, Nu Instruments, and Standard BioTools (formerly Fluidigm)—currently make ICP-TOFMS instruments with sufficient time resolution for single-particle analysis.^21,26,27 Of these instruments, those from TOFWERK (icpTOF® series) and Nu Instruments (Vitesse®) provide complete elemental mass range measurements. The CyTOF® instruments (Standard BioTools) record ions across a truncated m/z range from 75–209 m/z, though otherwise offer similar performance characteristics as the icpTOF-S2 instrument reported here. For the untargeted detection of diverse multi-element nanoparticles, full-mass spectrum acquisition is required; in addition, low-m/z detection allows for the analysis of essential elements in biological systems, such as in single cells^28–30 or tissue samples.³¹

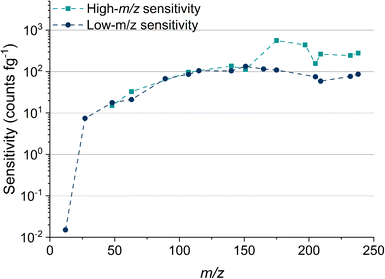
Recently, the icpTOF-S2 instrument has become available from Tofwerk AG (Thun, Switzerland) and has been used extensively in our lab for the last 2.5 years. The icpTOF-S2 operates at a TOF extraction frequency of 83.3 kHz and can provide burst-mode spectral collection at a time resolution of 12 μs for up to ∼1.2 ms (100 mass spectra) or continuous averaged mass spectral collection at 1000 Hz (83 mass spectra averaged). The icpTOF-S2 offers the highest sensitivity of the icpTOF series instruments, with absolute sensitivities in the tens to hundreds of counts per fg for most elements. Fast data acquisition, together with high sensitivity, are ideal for single-particle analysis. Here, we characterize the performance of the icpTOF-S2 in terms of absolute sensitivity, linear dynamic range, and abundance sensitivity for nanoparticle and microplastic detection using online microdroplet calibration.

Experimental

Instrumentation

An icpTOF-S2 instrument (Tofwerk AG, Thun, Switzerland) was used for all experiments. Experiments were performed using two different tune settings: one optimized for high-m/z sensitivity for general instrument characterization and another tuned for low-m/z sensitivity to allow for the detection of carbon in microplastics. Typical operating conditions are listed in Table 1; however, because the instrument was tuned daily, the actual parameters of a given experiment may differ slightly from those reported in the table. As seen in Table 1, the most prominent differences between the high-m/z and low-m/z tune settings are the voltage on the collision cell flat pole quadrupole (CCT) and the bias voltage on the quadrupole RF notch filter. Both of these quadrupoles act as bandpass m/z filters, and so must be adjusted to optimize transmission of ions with low-m/z values. Also, introduction of a collision gas in the CCT causes sensitivity loss for ions with low-m/z values due to scattering, and so a collision gas is not recommended for low-m/z operation of the instrument. Nanoparticle suspensions were introduced using a cyclonic spray chamber (Glass Expansion, Hawthorn, Victoria, Australia) and a Meinhard high-efficiency quartz nebulizer (Meinhard, Golden, CO, USA). For the microplastic measurements, a microFAST MC syringe based autosampler (Elemental Scientific, Omaha, NE, USA) was used to introduce sample into the pneumatic nebulizer. A flow rate of 45 μL min⁻¹ was used in combination with the same cyclonic spray chamber and nebulizer.

Table 1 Instrument settings for the icpTOF-S2

Parameter	Unit	High-m/z	Low-m/z
a Additional gasses are added to the falling tube around the microdroplet dispenser tip.
Mass-spectral acquisition time	ms	0.048 & 1	0.036 & 1.2
Nebulizer flow rate	L min^−1	0.75	0.88
Auxiliary flow rate	L min^−1	0.9	1.2
Cool gas flow rate	L min^−1	14	14.6
Sampling depth	mm	5.5	5.5
Plasma power	W	1586	1586
He additional gas^a flow rate	mL min^−1	370	300
Ar additional gas^a flow rate	mL min^−1	12	13
CCT mass	V	275	107
CCT bias	V	−4	−0.5
CCT H2 flow rate	mL min^−1	5.6	0
Notch filter RF amplitude	V	380	150
Reference potential	V	66	55

---

For online microdroplet calibration experiments, ICP-TOFMS data were acquired continuously at spectral acquisition rates of 1000 Hz (83 spectra averaged/time point) or 833 Hz (100 spectra averaged/time point). For highly time resolved analysis, “trigger mode” spectral acquisition was used. In trigger mode, batches of up to 100 mass spectra (averaged or not) are recorded continuously and then there is a dead-time while the data is transferred to the hard drive. In trigger mode, full mass spectra can be recorded at a time resolution down to 12 μs, though only for up to 1.2 ms at a time. As the name suggests, trigger mode ion collection is actuated when signal crosses a defined threshold, i.e. the signal “triggers” the spectral collection. Trigger-mode collection allows detailed investigation of signal structure from a microdroplet or particle. For determination of instrument figures of merit, TOF spectral acquisition was triggered off ¹³³Cs⁺ signal. Carbon-12 signal was used to trigger signal collection for the microplastic bead analysis.

Chemicals

Monodisperse gold nanoparticle suspensions (10.4 ± 0.7 nm, 15.5 ± 1.0 nm, 28.0 ± 0.9 nm, 50.3 ± 2.3 nm) were purchased from nanoComposix, now Fortis Life Sciences (San Diego, CA, USA). Spherical silver NPs (nominally 30, 50, 70, and 80 nm in diameter) were also purchased from nanoComposix. Dilute suspensions of NP analytes were prepared gravimetrically (ML204T/A00 Analytical Balance, Mettler-Toledo, Switzerland) in 18.2 MΩ cm water (PURELAB flex, Elga LabWater, United Kingdom) spiked with Cs at a concentration between 1 and 10 ng mL⁻¹. The NP suspensions were prepared to have PNCs between 1 × 10⁶ and 1 × 10⁵ NPs mL⁻¹. The standards used for the microdroplet calibration solutions were C, Al, Ti, Cu, Y, Ag, In, Ce, Eu, Ho, Lu, Au, Tl, Bi, Th, U, and they were chosen to encompass a wide range of m/z values. Calibration solutions were prepared to concentrations ranging from 0.001 to 300 ng mL⁻¹ from single-element standards (High-Purity Standards, South Carolina, USA), except for the carbon standard, which was prepared from tartaric acid (Fisher Scientific, Waltham, MA, USA) to a concentration of 170 μg mL⁻¹. Standards were diluted gravimetrically using either 1% (v/v) sub-boiled HNO₃, 1% (v/v) HCl (TraceSelect Grade, Honeywell-Fluka, Charlotte, NC, USA), or a mixture of 0.5% (v/v) HNO₃/2.4% (v/v) HCl in ultrapure water. Multi-element doped polystyrene (PS) beads (EQ Four Element Calibration Beads) were purchased from Standard BioTools Inc., formerly Fluidigm (San Francisco, California, USA).

Microdroplet introduction

A commercially available piezoelectric microdroplet dispenser head (AD-KH-501-L6 with control unit MD-E-3011-131, Microdrop Technologies, Norderstedt, Germany) was used to produce monodisperse microdroplets composed of a multi-element solution. A dual sample introduction system was used to introduce the microdroplets into the plasma. This system has been described in detail elsewhere.³² Microdroplets with diameters from 67–75 μm were introduced at 40 or 50 Hz into a 30 cm length of stainless-steel tubing. The microdroplets were sized using a Ximea xiQ microscope camera (XIMEA GmbH, Münster, Germany). The camera was calibrated using a positive USAF1951 test target (ThorLabs, USA), and an ImageJ macro was used to measure the diameter of the droplets from a recorded video. A helium/argon mixture was added to a port at the top of the tube to aid in droplet desolvation. The dried droplet residue particles were mixed with aerosols from the spray chamber in a quartz tee piece at the base of the steel tube.³³ With this system, microdroplets and the nebulized sample are introduced simultaneously into the plasma.^34,35

For the measurement of analyte NPs and microplastics beads, online microdroplet calibration³⁶ was used, and a minimum of 750 droplets were introduced into the plasma in a burst at the beginning and end of each measurement. Cesium was used as a tracer to identify the droplet signals, and the absolute sensitivities (counts per g) for each element were calculated using the median signal of each analyte in the droplets. The signals from first 100 droplets at the beginning of each burst were omitted for median signal calculation to account for solvent evaporation in the tip of the microdroplet generator. This solvent evaporation happens before and between bursts of droplets and causes the first droplets to be more concentrated with trace elements and so produce elevated signals. To determine instrument figures of merit, microdroplets were introduced continuously at a rate of 40 or 50 Hz; at this frequency, no signal enhancement due to solvent evaporation was observed.

Data processing

All data was collected in TofDAQ Recorder, and mass spectral peak integrations were done using TofDAQ viewer (Tofwerk AG, Thun, Switzerland). Data was processed by our in-house “TOF Single-Particle Investigator” (TOF-SPI) program, written in LabVIEW (LabVIEW 2018, National Instruments Corp., TX, USA). TOF-SPI is a batch analysis program designed for online microdroplet calibration. The program is used to calculate average background signals and single-particle critical values for each user-define analyte nuclide(s), determine absolute element sensitivities, background subtract data, correct split-particle events, quantify element masses in single particles, and determine particle number concentrations. Single-particle critical values (L_C,sp) are calculated according to compound Poisson distributed ICP-TOFMS data, as previously described.³⁷L_C,sp is the detection threshold used to separate particle-derived signals from steady-state dissolved element background signals; above the L_c,sp, all detected signals are considered to come from NPs. The critical value is calculated as one-sided detection decision with element-specific false-positive (α) rates from 1 × 10⁻⁵ to 1 × 10⁻⁷ and the calculation is done in the same manner as developed by Currie and recommended by the IUPAC.³⁸ However, the L_c,sp for spICP-TOFMS is determined using compound-Poisson statistics because the dispersion of low-count icpTOF data is not adequately described by Normal or Poisson distributions. With spICP-TOFMS, we routinely measure >100 000 data points per nuclide per analysis; with this large data set, low alpha values are required to reduce the chance of background signal being registered as a particle events (i.e. above L_C,sp).

Results and discussion

The performance of the icpTOF-S2 was evaluated for the purpose of single-particle measurements in terms of linear dynamic range, absolute sensitivities, detectable mass, and abundance sensitivity. The high-m/z detection capabilities of the TOF were characterized using multi-element containing microdroplets and Au and Ag nanoparticles. The low-m/z detection abilities were explored through the analysis of carbon and metals in both microdroplets and uniform polystyrene (PS) beads.

Linear dynamic range

A broad linear dynamic range (LDR) is an essential characteristic of ICP-MS instruments. In spICP-MS analysis, the LDR range is truncated because fast transient signals produce high count rates (counts per second, cps) even with fairly low absolute signals. For example, a particle with a signal of 1000 counts, a Gaussian shape, and a full-width half maximum (FWHM) time width of 250 μs, will produce an average of 3.2 million cps across the central ±1σ of the peak. At the peak apex, the count rate will be even higher. Most pulse-counting ion detectors start experiencing pulse-pileup effects at around 2 million cps, which can lead to under-counting signals and non-linear response.^12,39,40 Pulse-pileup effects can be overcome in spICP-MS by measuring analog signals from the ion detector via a fast analog-to-digital converter (ADC).^41,42 On the icpTOF instrument, ion detection is achieved with a fast ADC system that enables measurement from single ions to the saturation limit of the microchannel plate (MCP) detector stack used to amplify ion strikes. The measured voltage per unit time (i.e. mV × ns) is then converted to estimated counts based on a detector calibration factor that is updated daily.³⁷ A major advantage of TOF over scanning mass spectrometers is that TOF provides a full mass spectrum for every extraction, which enables quantitative detection of multi-element particles.

To examine the LDR of the instrument, a multi-element calibration was done using microdroplets with a diameter of 75 μm and concentrations ranging from 0.001 ng mL⁻¹ to 300 ng mL ⁻¹. Because the discrete element mass introduced via the microdroplets mimics single particles, microdroplets can be used to test the LDR of the ICP-TOFMS instrument for measurement of particles. Linear response was observed across four orders of magnitude for m/z values ≥ 107 (i.e., Ag, Ce, Eu, Tl, Bi, Th, and U) (Fig. 1), and ranged from ∼1 count to ∼20 000 counts per droplet. In terms of cps, this translates to a linear range from ∼1000 to 20 million cps averaged over the 1 ms acquisition window; at the peak apex, the cps rate would be even higher. A signal below 1000 cps isn't possible to record from a single particle because at least one ion must be detected to find a particle event. Signals of less than 1 count/droplet may be detectable from the average of many droplets; however, as seen in Fig. 1, linear response was not achieved below ∼1 count/droplet. The LDR determined for ⁴⁸Ti and ⁶³Cu are truncated because of lower sensitivity for these nuclides compared to heavier nuclides. The LDR could likely be extended for ⁴⁸Ti and ⁶³Cu through measuring droplets made from more concentrated solutions or tuning the instrument for low-m/z values.

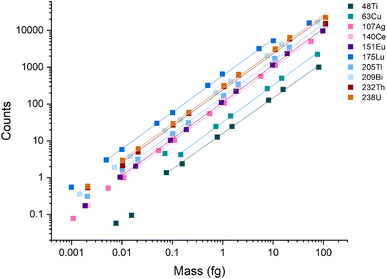Fig. 1 Calibration curves for the icpTOF-S2 with microdroplet introduction. During these measurements, the instrument was tuned for high-m/z sensitivity.

Table 2 lists the absolute sensitivities, critical masses (X^mass_C,sp), and calculated critical diameters (X^diameter_C,sp) for a range of elements that were measured using microdroplet calibration. The critical mass is the mass threshold above which detected signals are considered nanoparticles. For a given nuclide, the critical mass is calculated by dividing the critical value (L_C,sp) in counts by the sensitivity in counts per g. This critical mass can then be converted to a critical diameter (X^diameter_C,sp) by assuming a particle stoichiometry, density, and spherical shape. ICP-TOFMS data is compound-Poisson distributed, rather than Gaussian or Poisson.^37,43 For this reason, critical values reported here are determined using compound Poisson statistics^37,43,44 with an alpha value of 0.001%. The critical value for any given m/z channel depends on the background level at that m/z channel and is the minimum ion signal required to say whether a signal is particle-derived, i.e., that the signal is above the background. Critical values were determined using two separate tune settings: one optimized for high-m/z sensitivity and the other for low-m/z sensitivity. In Fig. 2, we report the abundance-corrected absolute sensitivities for nuclides with atomic mass from 12 to 238 u with both the high- and low-m/z settings. By tuning the instrument for ¹²C detection, the sensitivities for the heaviest nuclides decreases by ∼70%, though critical masses are still in the tens of attograms range. Without tuning for low-m/z values, the ¹²C⁺ signal cannot be measured. In the icpTOF-S2, there is a steep cutoff in the transmission of ions through the CCT and RF notch filter quadrupoles for low-m/z values with the “normal” high-m/z tune settings. Here, we made a conscientious effort to tune for detection of ¹²C⁺ along with the rare-earth elements (REEs). From experience, we know that critical masses down to ∼750 fg are possible for carbon detection, though this comes at the expense of high-m/z sensitivity. Sensitivity for ¹²C⁺ is much lower than other analyte nuclides due to instrument mass bias and the high first ionization potential of carbon (11.3 eV).^45,46

Table 2 Critical masses and estimated critical diameters determined with microdroplet introduction

Element	X ^massC,sp (ag) High m/z	X ^massC,sp (ag) Low m/z	Model particle	Density (g cm^−1)	X ^diameterC,sp (nm) High m/z	X ^diameterC,sp (nm) Low m/z
C	—	3.2 × 10^6	(C8H8)n	1.05	—	1800
Al	—	876	Al2O3	3.95	—	75
Ti	95	472	TiO2	4.23	35	60
Cu	88	418	CuO	5.61	31	52
Y	—	76	Y2O3	5.01	—	31
Ag	10	106	Ag	10.49	12	27
In	—	42	In2O3	7.18	—	22
Ce	6.1	35	CeO2	7.22	12	21
Eu	6.9	49	Eu2O3	7.4	12	23
Ho	—	26	Ho2O2	8.795	—	18
Lu	1.3	28	Lu2O3	9.42	6.5	18
Au	13	—	Au	19.3	11	—
Tl	4.9	77	Tl2O3	10.19	9.7	24
Bi	2.9	68	Bi2O3	8.9	8.5	24
Th	3.5	52	ThO2	10	8.8	21
U	2.6	46	UO2	10.97	7.7	20

---

Fig. 2 Abundance-corrected sensitivities for the icpTOF-S2 tuned for both high- and low-m/z values.

Abundance sensitivity

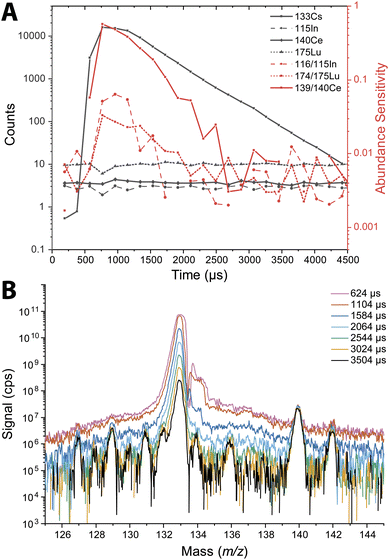
The abundance sensitivity of a mass spectrometer is typically given as a ratio of S_M±1 to S_M, where S_M±1 is the signal intensity of the one mass unit away from an analyte peak at m/z M.⁴⁷ Lower abundance sensitivity values indicate that there is less baseline elevation and peak tailing into adjacent m/z channels. TOFMS is particularly prone to elevated baselines that can dramatically affect the signal level of low abundance nuclides. Previous work by Hendriks et al. demonstrated that baseline modelling and subtraction can be an effective way to correct for elevated baselines from high-intensity signals.²¹ However, for short transient signals, baseline subtraction is not effective because many zero-count time bins impede accurate baseline estimation, and baseline correction based on an average mass spectrum is inadequate. In the case of nanoparticle measurements, the baseline is not stable across the whole measurement, so it is not easily modeled for baseline subtraction.

We probed the long-range effects on abundance sensitivity that can occur when a high-intensity transient signal is measured with the icpTOF-S2. In this experiment, microdroplets composed of a solution of 5 μg mL⁻¹ of Cs were introduced at the same time that a solution of containing 1 ng mL⁻¹ of In, Ce, and Lu was introduced continuously through the pneumatic nebulizer and cyclonic spray chamber. Signals were recorded in trigger mode to enable mass spectral measurement at a time resolution of 48 μs. These highly time resolved mass spectra were collected across 4.5 ms, which allowed for complete measurement of the intense ¹³³Cs⁺ signal pulse from the microdroplet. Fig. 3 shows the average time-resolved signals for In, Ce, Lu, and Cs from 264 droplet events. As seen in Fig. 3B, the ¹³³Cs⁺ signal from the microdroplets is very intense with a peak height of 16 000 counts (333 million cps). At this signal level, the MCP detection system is saturated and will produce a non-linear response. On the other hand, the continuous signals from ¹¹⁵In⁺, ¹⁴⁰Ce⁺, and ¹⁷⁵Lu⁺ remain relatively flat at count rates from 83 000 to 200 000 cps across the droplet profile, indicating that the detector sufficiently recovers to provide quantitative detection of these elements. We would expect a flat response for the continuously introduced analyte. With constant analyte signals, we also would expect the abundance sensitivities recorded at m/z values adjacent to these analyte nuclides to be constant; however, as seen in Fig. 3A, the abundance sensitivities are correlated to the ¹³³Cs⁺ signal peak. The steady-state abundance sensitivities at m/z 115, 140, and 175 are between 2 × 10⁻³ to 5 × 10⁻³. As the Cs signal increases, the spectral background elevates, which causes the off-m/z signals to increase and elevate (i.e. worsen) the abundance sensitivity across the whole mass range. The effect is most severe for the m/z closest to the intense signal, as demonstrated by the more than 100× increase in abundance sensitivity at m/z 139 at the apex of the microdroplet-derived signal. For m/z further away, the abundance sensitivity can still increase up to an order of magnitude.

Fig. 3 (A) Average signal from individually detected droplets containing 5 μg mL⁻¹ Cs and a nebulized solution containing 1 ng mL⁻¹ In, Ce, and Lu (black). Average abundance sensitivity of In, Ce, and Lu across the Cs droplet profile (red). Data was recorded with a 48 μs time resolution. (B) Mass spectrum at different time intervals across the droplet profile. This demonstrates the transient long range baseline elevation from an intense particle signal.

Long-range baseline elevation can be a challenge for single particle measurements. A large particle signal in a heterogeneous particle mixture may temporarily obscure the signals of less abundant species by elevating the baseline. Likewise, the baseline elevation caused by intense signals can cause single-particle data processing software to falsely register the elevated baseline as particle events. In practice, we find that single-particle events with total signal above ∼20 000 counts can lead to the detection of spurious single-particle events at adjacent mass channels due to baseline elevation. A conservative approach is to remove all signals concomitant with such intense particle events. In addition, the steady-state abundance sensitivities of 2 × 10⁻³ to 5 × 10⁻³ that are typical of the icpTOF-S2 instrument are significantly higher than that achieved with other, longer flight tube geometry, ICP-TOFMS instruments. For reference, typical abundance sensitivities on the icpTOF-R, icpTOF-2R, and Vitesse instruments are reported to be 3 × 10⁻⁴, 3 × 10⁻⁵, and 3 × 10⁻⁵, respectively.

Nanoparticle detection

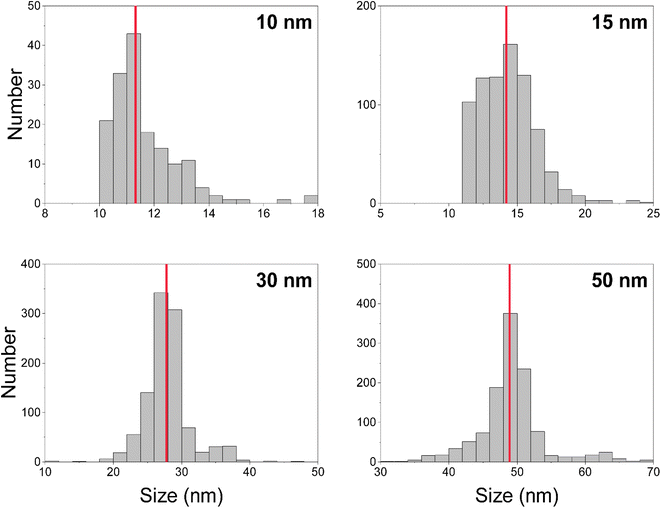
We measured Au nanoparticles with nominal diameters of 50, 30, 15, and 10 nm using online microdroplet calibration (Fig. 4). The icpTOF-S2 provides a sensitivity of 331 counts per fg for ¹⁹⁷Au and, combined with the background, a critical diameter of 11 nm. As seen in Fig. 4, AuNPs from all suspensions are measurable; however, for the 10 nm AuNPs, only the upper portion of the size distribution is recorded. Truncation of the 10 nm AuNP distribution causes the median determined diameter to be over-estimated at 11.8 nm. However, with the icpTOF-S2, the 15, 30, and 50 nm Au particles are accurately sized, which indicates measurement of the complete size distribution.⁴⁸ We also measured Ag NPs of nominal sizes of 30, 50, 70, and 80 nm, and provide results in Fig. S2.† To improve the sensitivity for the measurement of small NPs, we reduced the plasma sampling depth. When the torch is moved closer to the sampler orifice of the mass spectrometer, atoms and ions from particles have less time to diffuse in the plasma, which can enhance the sensitivity.⁴⁹ Moving the ICP torch from a sampling depth of 5.5 mm to 4 mm increased the sensitivity for ¹⁹⁷Au from 331 to 439 counts per fg. Results for the measurement of 10 nm AuNPs at reduced sampling depths is provided in Fig. S3.†

Fig. 4 Size (i.e. diameter) distributions for nominally 10, 15, 30, and 50 nm gold nanoparticles. Median measured diameters are indicated by the red lines and are as follows (left to right, top to bottom): 11.8 nm, 14.2 nm, 27.8 nm, 48.9 nm.

Measurement of ¹²C in polystyrene microspheres

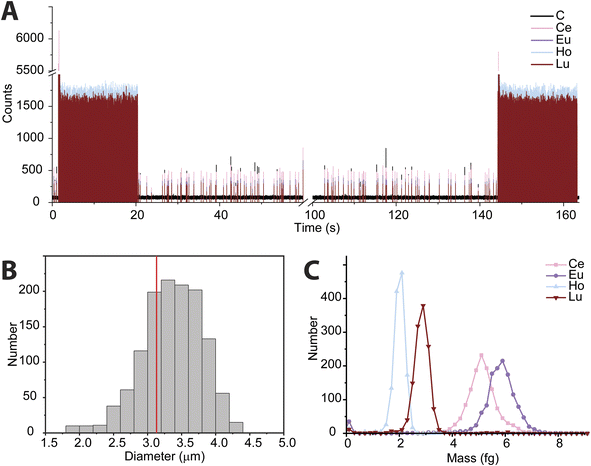
In recent years, the measurement of microplastics by detection of carbon via spICP-MS has emerged as an area of research.^9–11 To date, these proof-of-principle studies have been accomplished with quadrupole-based ICP-MS instruments. Here, we tuned the icpTOF-S2 instrument for the measurement of low-m/z ions to enable the measurement of ¹²C⁺ and heavier nuclides quasi-simultaneously. In Fig. 5, we present results from the use of online microdroplet calibration to quantify the mass of carbon in polystyrene (PS) microspheres, i.e. “beads.” The PS beads are doped with four REEs: Ce, Eu, Ho, and Lu. By carefully tuning the CCT, a single-particle critical mass for carbon (X^mass_c,sp,C) of 3.3 pg was attained while still maintaining sufficient sensitivity for higher-m/z ions to detect the REEs in the microplastic beads. The critical diameter for PS beads is 1.8 μm. The critical mass for ¹²C is elevated by the high background of 76 counts per data point; this background likely comes predominantly from dissolved CO₂ in nebulized samples and as an impurity in the Ar gas. As seen in Fig. 5B, we recorded a median diameter of 3.4 ± 0.45 μm for the PS spherical beads (error is reported as the standard deviation). We also measured the beads via scanning electron microscopy (see ESI†) and found an average diameter of 3.1 ± 0.1 μm. REE metal signals were measured simultaneously with carbon in the polystyrene beads; histograms of the determined mass amounts of the doped REEs in the beads is provided in Fig. 5C. The relative REE mass amounts match previously reported results for the doped PS beads.⁵⁰

Fig. 5 (A) Time trace of REE-doped polystyrene beads. Microdroplets used for calibration were introduced at the beginning and end of the measurement. (B) Distribution of polystyrene beads as measured by spICP-TOFMS. The red line indicates the average bead size from scanning electron microscopy measurements. (C) REE mass distributions from polystyrene beads.

While the mean determined diameter via spICP-TOFMS for the PS beads matches within uncertainty with the SEM sizing results, the particle diameter distribution in Fig. 5B is broader than would be expected from Poisson statistics alone. The carbon signal from the PS beads has an average signal of 304 ± 120 counts (relative standard deviation (RSD) = 39%), which is substantially higher than the 304 ± 17 counts (RSD = 5.8%) predicted by Poisson statistics alone. When uncertainty from background subtraction of the elevated ¹²C⁺ background signal (76 ± 11 counts) is also considered, the expected RSD for measurement of the PS beads increases to 6.7%, which is still much lower than the measured RSD of the ¹²C⁺ signal from the PS beads. The elevated RSD of the ¹²C⁺ beads is also substantially higher than the RSD obtained from ¹²C⁺ signal in the microdroplet standards (410 ± 82 counts, RSD = 20%) and that of the REE signals in the PS beads, which have RSD values of ∼15% and average signals per PS bead from 250 to 500 counts. In Table S2,† the average signals and standard deviations of all nuclides measured from the PS beads are reported. Size distribution of the PS beads is insufficient to account for the large RSD in spICP-TOFMS signals. The elevated RSD values found for nuclides detected by spICP-TOFMS indicates that sources of noise other than counting statistics, such as plasma flicker noise, are dominant components to the noise.⁵¹ The detected signals from ¹²C⁺ from the PS beads is particularly noisy; a likely source of this noise could be incomplete vaporization and variable ionization efficiency of carbon as a function of PS bead introduction position into the ICP. Signals from the REEs in the PS beads also have RSDs that are two to three times higher than predicted by counting statistics. The two-fold lower RSD for ¹²C⁺ signals from microdroplet signals compared to that from the PS beads suggests that microdroplet sample introduction is more repeatable than PS bead introduction and that the interaction of the PS bead and the plasma is a critical parameter affecting the RSD. In future work, we will investigate these sources of noise for carbon detection and quantification via spICP-TOFMS.

In Fig. 6, we present high time resolution measurements of the PS beads and microdroplets containing 100 ng mL⁻¹ of metals and 170 μg mL⁻¹ carbon. These measurements were made using trigger mode with a spectral averaging time of 36 μs (3 mass spectra averaged per data point). While all elements in the REE-doped polystyrene beads are detected, the average profiles (Fig. 6A) clearly show a shift in arrival times between the ¹²C⁺ and REE nuclides. This shift was also observed when measuring carbon-containing multi-element microdroplets. The time shift in arrival times is mostly due to m/z-dependent velocities of ions in the optics upstream of the TOF extraction region. Lighter ions travel faster through the ion-optics path and so enter the extraction region ahead of heavier ions. This has been reported previously;⁵² however, here we show that the large mass difference between ¹²C⁺ and ²³⁸U⁺, which is almost 20-fold, leads to an extended time shift of up to ∼180 μs. At this time shift the maximum intensity from ²³⁸U ions is detected 15 TOF extractions after that of ¹²C ions.

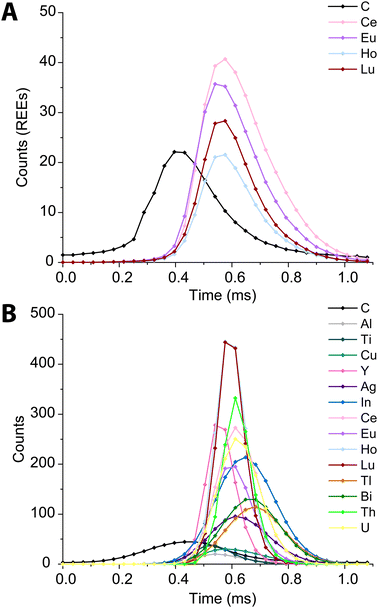Fig. 6 Average time trace profiles for 1200 REE-doped polystyrene beads (A) and 2000 microdroplets containing 100 ng mL⁻¹ metals and 100 μg mL⁻¹ carbon (B) acquired with a time resolution of 36 μs.

There is a clear m/z-dependence in the detection time shifts of the analytes; however, the time shifts cannot be fully explained by differences in m/z value. For example, ions from ⁸⁹Y arrive at the TOF extraction region before those from ⁶³Cu; likewise, ions from ¹⁷⁵Lu are time-shifted ahead of those from ¹¹⁵In⁺. There are also clear element-specific peak widths, such as the narrow peak width obtained for ⁸⁹Y⁺. The times shifts are likely a combination of m/z-dependent ion transport in the ion optics of the mass spectrometer and element-dependent spatial distribution of ions in the ICP.^20,53,54 While these time shifts appear rather extreme, routine spICP-TOFMS measurements are typically achieved with a time-resolution of 1 ms or greater. At this time resolution, most single-particle signals will have accurate coincidence of signals from low-mass and heavy-mass elements present in single particles. Nonetheless, time-shifted signals will cause split-element particle events be more common, and so accurate split-event correction procedures are required.⁴⁴ In our online microdroplet calibration spICP-TOFMS analysis of the microspheres, less than 1% of signals had spuriously split C-REE signals after split-event correction.

Conclusion

We characterized the performance of the icpTOF-S2 for single-particle analysis with online microdroplet calibration. The fast data acquisition and full-mass-range detection of the instrument along with detection limits down to the single-digit attograms make it a useful tool for high-sensitivity single-particle analysis. This sensitivity is important for the detection of nanoparticles as it enables the detection of both small single element nanoparticles as well as the presence of minor elements in multi-element particles. The high instrument sensitivity does come at the cost of poor abundance sensitivity (2 × 10⁻³ to 5 × 10⁻³), which is still suitable for applications where the measurement of low abundance isotopes is not critical. Similar ICP-TOFMS instruments are available (i.e. the icpTOF-R, icpTOF-2R, and Vitesse) that have longer drift tube lengths. Use of a longer drift tube significantly improves mass resolution and abundance sensitivity but comes at the cost of lower absolute sensitivities.⁵² We also demonstrate that the abundance sensitivity has time-dependent variability. For intense transient signals from microdroplets or nanoparticles, elevated baseline effects can cause abundance sensitivity to decrease more than 100×. We demonstrate that the icpTOF-S2 can accurately measure 15 nm gold nanoparticles. Additionally, we demonstrate for the first time the detection and sizing microplastics with ICP-TOFMS using carbon-12 in concert with the detection of metal dopants in the microplastic particles. Such an approach could be useful in the combined analysis of carbon in microplastic or nanoplastic particles and metal additives used as tracing agents⁵⁵ or endogenous metals used in plastics as heat stabilizers, pigments or catalysts.⁵⁶

Conflicts of interest

The authors have no conflicts of interest to declare.

Acknowledgements

The authors would like to acknowledge funding from an Iowa State University (ISU) Faculty start up grant. Additionally, thanks to Trond Forre from the ISU Chemistry Department glass shop and Bruce Erickson and Reid Jenson from the ISU Machine Shop for their aid in constructing the microdroplet introduction system. Lastly, thank you to Sarah Szakas for her aid in sizing the polystyrene microspheres with SEM.

References

1. M. D. Montaño, G. V. Lowry, F. von der Kammer, J. Blue and J. F. Ranville, Environ. Chem., 2014, 11, 351–366.
2. D. Mozhayeva and C. Engelhard, J. Anal. At. Spectrom., 2020, 35, 1740–1783.
3. C. Degueldre and P. Y. Favarger, Colloids Surf., A, 2003, 217, 137–142.
4. L. G. Jahn, G. D. Bland, L. W. Monroe, R. C. Sullivan and M. E. Meyer, Aerosol Sci. Technol., 2021, 55, 571–585.
5. D. M. Schwertfeger, J. R. Velicogna, A. H. Jesmer, R. P. Scroggins and J. I. Princz, Anal. Chem., 2016, 88, 9908–9914.
6. M. Hadioui, C. Peyrot and K. J. Wilkinson, Anal. Chem., 2014, 86, 4668–4674.
7. M. v. d. Au, M. Schwinn, K. Kuhlmeier, C. Büchel and B. Meermann, Anal. Chim. Acta, 2019, 1077, 87–94.
8. W. Qin, H.-J. Stärk and T. Reemtsma, Analyst, 2021, 146, 6753–6759.
9. E. Bolea-Fernandez, A. Rua-Ibarz, M. Velimirovic, K. Tirez and F. Vanhaecke, J. Anal. At. Spectrom., 2020, 35, 455–460.
10. R. Gonzalez de Vega, S. Goyen, T. E. Lockwood, P. A. Doble, E. F. Camp and D. Clases, Anal. Chim. Acta, 2021, 1174, 338737.
11. F. Laborda, C. Trujillo and R. Lobinski, Talanta, 2021, 221, 121486.
12. I. Strenge and C. Engelhard, J. Anal. At. Spectrom., 2016, 31, 135–144.
13. K. Ding, S. Liang, C. Xie, Q. Wan, C. Jin, S. Wang, Y.-T. Tang, M. Zhang and R. Qiu, Anal. Chem., 2022, 94, 10745–10753.
14. S. Naasz, S. Weigel, O. Borovinskaya, A. Serva, C. Cascio, A. K. Undas, F. C. Simeone, H. J. P. Marvin and R. J. B. Peters, J. Anal. At. Spectrom., 2018, 33, 835–845.
15. D. A. Solyom, O. A. Gron, J. H. Barnes Iv and G. M. Hieftje, Spectrochim. Acta, Part B, 2001, 56, 1717–1729.
16. M. Resano, K. S. McIntosh and F. Vanhaecke, J. Anal. At. Spectrom., 2012, 27, 165–173.
17. D. Ardelt, A. Polatajko, O. Primm and M. Reijnen, Anal. Bioanal. Chem., 2013, 405, 2987–2994.
18. P. P. Mahoney, S. J. Ray and G. M. Hieftje, Appl. Spectrosc., 1997, 51, 16A–28A.
19. S. J. Ray and G. M. Hieftje, J. Anal. At. Spectrom., 2001, 16, 1206–1216.
20. O. Borovinskaya, B. Hattendorf, M. Tanner, S. Gschwind and D. Günther, J. Anal. At. Spectrom., 2013, 28, 226–233.
21. L. Hendriks, A. Gundlach-Graham, B. Hattendorf and D. Günther, J. Anal. At. Spectrom., 2017, 32, 548–561.
22. T. Erhardt, C. M. Jensen, O. Borovinskaya and H. Fischer, Environ. Sci. Technol., 2019, 53, 13275–13283.
23. A. Praetorius, A. Gundlach-Graham, E. Goldberg, W. Fabienke, J. Navratilova, A. Gondikas, R. Kaegi, D. Günther, T. Hofmann and F. von der Kammer, Environ. Sci.: Nano, 2017, 4, 307–314.
24. A. Gundlach-Graham, in Comprehensive Analytical Chemistry, ed. R. Milačič, J. Ščančar, H. Goenaga-Infante and J. Vidmar, Elsevier, 2021, vol. 93, pp. 69–101.
25. X. Tian, H. Jiang, L. Hu, M. Wang, W. Cui, J. Shi, G. Liu, Y. Yin, Y. Cai and G. Jiang, TrAC, Trends Anal. Chem., 2022, 157, 116746.
26. A. Azimzada, J. M. Farner, I. Jreije, M. Hadioui, C. Liu-Kang, N. Tufenkji, P. Shaw and K. J. Wilkinson, Front. Environ. Sci., 2020, 8, 91.
27. Y.-S. S. Yang, P. U. Atukorale, K. D. Moynihan, A. Bekdemir, K. Rakhra, L. Tang, F. Stellacci and D. J. Irvine, Nat. Commun., 2017, 8, 14069.
28. M. von der Au, O. Borovinskaya, L. Flamigni, K. Kuhlmeier, C. Büchel and B. Meermann, Algal Res., 2020, 49, 101964.
29. T. Vonderach and D. Günther, J. Anal. At. Spectrom., 2021, 36, 2617–2630.
30. S. Theiner, A. Schweikert, S. J. M. Van Malderen, A. Schoeberl, S. Neumayer, P. Jilma, A. Peyrl and G. Koellensperger, Anal. Chem., 2019, 91, 8207–8212.
31. S. Theiner, A. Schweikert, C. Haberler, A. Peyrl and G. Koellensperger, Metallomics, 2020, 12, 1246–1252.
32. S. Harycki and A. Gundlach-Graham, Anal. Bioanal. Chem., 2022, 414, 7543–7551.
33. J. Koch, L. Flamigni, S. Gschwind, S. Allner, H. Longerich and D. Günther, J. Anal. At. Spectrom., 2013, 28, 1707–1717.
34. B. Ramkorun-Schmidt, S. A. Pergantis, D. Esteban-Fernandez, N. Jakubowski and D. Gunther, Anal. Chem., 2015, 87, 8687–8694.
35. L. Hendriks, B. Ramkorun-Schmidt, A. Gundlach-Graham, J. Koch, R. N. Grass, N. Jakubowski and D. Günther, J. Anal. At. Spectrom., 2019, 34, 716–728.
36. K. Mehrabi, D. Günther and A. Gundlach-Graham, Environ. Sci.: Nano, 2019, 6, 3349–3358.
37. A. Gundlach-Graham, L. Hendriks, K. Mehrabi and D. Gunther, Anal. Chem., 2018, 90, 11847–11855.
38. L. A. Currie, Pure Appl. Chem., 1995, 67, 1699–1723.
39. W.-W. Lee and W.-T. Chan, J. Anal. At. Spectrom., 2015, 30, 1245–1254.
40. M. D. Montano, J. W. Olesik, A. G. Barber, K. Challis and J. F. Ranville, Anal. Bioanal. Chem., 2016, 408, 5053–5074.
41. J. W. Olesik and P. J. Gray, J. Anal. At. Spectrom., 2012, 27, 1143–1155.
42. S. Gschwind, L. Flamigni, J. Koch, O. Borovinskaya, S. Groh, K. Niemax and D. Günther, J. Anal. At. Spectrom., 2011, 26, 1166–1174.
43. L. Hendriks, A. Gundlach-Graham and D. Günther, J. Anal. At. Spectrom., 2019, 34, 1900–1909.
44. A. Gundlach-Graham and K. Mehrabi, J. Anal. At. Spectrom., 2020, 35, 1727–1739.
45. H. Niu and R. S. Houk, Spectrochim. Acta, Part B, 1996, 51, 779–815.
46. E. T. Luong and R. S. Houk, J. Am. Soc. Mass Spectrom., 2003, 14, 295–301.
47. A. A. Rubinshtein, G. D. Schilling, S. J. Ray, R. P. Sperline, M. B. Denton, C. J. Barinaga, D. W. Koppenaal and G. M. Hieftje, J. Anal. At. Spectrom., 2010, 25, 735–738.
48. A. C. Gimenez-Ingalaturre, K. Ben-Jeddou, J. Perez-Arantegui, M. S. Jimenez, E. Bolea and F. Laborda, Anal. Bioanal. Chem., 2022 DOI:10.1007/s00216-022-04215-z.
49. I. Kálomista, A. Kéri and G. Galbács, Talanta, 2017, 172, 147–154.
50. J. Liu, J. Jarzabek, D. Majonis, J. Watson, V. Baranov and M. A. Winnik, Anal. Chem., 2020, 92, 999–1006.
51. G. Cornelis and M. Hassellöv, J. Anal. At. Spectrom., 2014, 29, 134–144.
52. M. Burger, L. Hendriks, J. Kaeslin, A. Gundlach-Graham, B. Hattendorf and D. Günther, J. Anal. At. Spectrom., 2019, 34, 135–146.
53. J. W. Olesik, Appl. Spectrosc., 1997, 51, 158A–175A.
54. K.-S. Ho, W.-W. Lee and W.-T. Chan, J. Anal. At. Spectrom., 2015, 30, 2066–2073.
55. D. M. Mitrano, A. Beltzung, S. Frehland, M. Schmiedgruber, A. Cingolani and F. Schmidt, Nat. Nanotechnol., 2019, 14, 362–368.
56. M. Velimirovic, B. Teunkens, H. Ghorbanfekr, B. Buelens, T. Hermans, S. Van Damme, K. Tirez and F. Vanhaecke, Sci. Total Environ., 2022, 851, 158226.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ja00295g

---