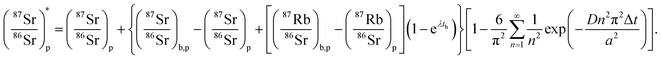In situ
87Rb–87Sr analyses of terrestrial and extraterrestrial samples by LA-MC-ICP-MS/MS with double Wien filter and collision cell technologies†
Received
23rd April 2022
, Accepted 22nd August 2022
First published on 10th October 2022
Abstract
The advent of double-Wien filter-selection-aperture and hexapole-collision-cell technologies coupled to laser ablation multicollector inductively coupled plasma mass spectrometry (LA-MC-ICP-MS/MS) enables in situ analysis of 87Sr variations produced by the decay of radioactive 87Rb (t1/2 = 49.61 ± 0.16 Ga). We present methodologies to acquire in situ87Rb–87Sr data using a Thermo Scientific™ Neoma™ MC-ICP-MS coupled to a laser ablation system. The ions first pass through a mass filter that blocks ions outside of the Rb–Sr mass region. The ions then travel through a hexapole collision cell filled with SF6, inducing the fluorination of Sr+ to form SrF+. Strontium isotopes are measured as SrF+ free of interferences, while rubidium isotopes are measured as Rb+. Formulas are presented to calculate the error ellipses of 87Rb/86Sr and 87Sr/86Sr ratios corrected for instrumental fractionation by standard bracketing. While LA-MC-ICP-MS/MS is not as precise as Thermal Ionization Mass Spectrometry (TIMS), it is less destructive and sample throughput is higher. It is therefore particularly well suited to analyze small and precious samples, or to examine population characteristics. We have analyzed several terrestrial and extraterrestrial materials to showcase the unique capabilities of LA-MC-ICP-MS/MS in Sr isotopic analyses: (1) an orthoclase megacryst and other minerals from the 397 Ma Shap granite, (2) feldspar grains from the 26.5 ka Oruanui supereruption in New Zealand, (3) Durango apatite, (4) highly refractory hibonite inclusions from the Murchison meteorite, and (5) the martian meteorite NWA 7034 also known as Black Beauty. Black Beauty is a polymict breccia that contains zircons as old as 4.4 Ga but whose 40Ar/39Ar age was partially reset at 1.4 Ga. All K-feldspar grains analyzed in Black Beauty give an 87Rb–87Sr age of 2.189 ± 0.059 Ga. Most likely, the 2.2 Ga 87Rb–87Sr age represents the age of lithification. This study demonstrates the great potential of in situ87Rb–87Sr dating for analyzing samples returned by planetary exploration missions, such as those currently collected by the Perseverance rover on Mars, or those that will be returned from Phobos by the MMX mission.
1. Introduction
Rubidium is a monovalent alkali metal that chemically very closely follows potassium, while strontium is a divalent alkaline-earth metal more similar to other group II elements like calcium. Many of the processes that have shaped planetary bodies have fractionated Rb from Sr, which over time produced variations in the 87Sr/86Sr ratio from the decay of radioactive 87Rb (t1/2 = 49.61 ± 0.16 Ga1,2). The more straightforward application of 87Rb–87Sr systematics is dating of rocks,3 but this system has found applications in very diverse fields, covering for example: (1) the history of continental crust extraction and emergence, oceanic crust recycling, mantle mixing, and the nature of Hadean crust,4–9 (2) magma mixing and assimilation of country rocks,10–15 (3) the timing of depletion in moderately volatile elements in Earth, the Moon, and other planetary bodies,16–18 (4) correlation between rock strata during periods of Earth's history that saw rapid changes in the Sr isotopic composition of seawater,19,20 (5) animal and hominid origin and migration,21–27 and (6) past exchanges of cultural artifacts and commercial goods between different regions.28–30 The materials targeted in those studies are diverse and comprise K-rich minerals such as alkali feldspars and micas, bulk silicate and carbonate rocks, phosphates of igneous and biological origins, surface and underground water, and man-made materials.
Strontium isotopic analysis can be readily done by thermal ionization mass spectrometry (TIMS) as Sr is efficiently ionized using this technique (ref. 31 and references therein). Such measurements, however, are not always possible when high Rb/Sr grains are too small to be separated. When such measurements are possible, they still require sampling, digestion, Sr purification by chromatography in a clean laboratory setting, Sr loading on a filament, and analysis by TIMS. In situ Sr isotopic analysis can expand the range of applicability of 87Rb–87Sr studies to new targets and provide a higher sample throughput, whilst minimizing sample destruction of precious samples such as human remains, meteoritic samples, or cultural artifacts. The difficulty of such measurements lies, however, in the presence of isobaric interferences on Sr isotopes, in particular 87Rb on 87Sr which requires a mass resolving power of about 3 × 105 to effectively separate. Strategies have been developed to minimize these interferences, the most notable being (1) focusing on low Rb samples such as carbonate, apatite or plagioclase and correcting for possible isobaric interferences via measurement of the 85Rb and peak-stripping assuming a constant value for 85Rb/87Rb,32–39 (2) using resonant ionization mass spectrometry (RIMS) to only ionize Sr by using lasers with wavelengths tuned to a specific electronic transition of Sr such that Rb is not ionized,4,40–43 and (3) using a reactive gas such as N2O, O2, CH3F, or SF6 in a collision/reaction cell (CRC) to react Sr+ but not Rb+, with the former analyzed as molecular ions SrO+ or SrF+.44–53
The latter approach often involves the use of a pre-cell quadrupole mass filter to remove the ions in the mass range that would otherwise interfere with molecular Sr ions (e.g.,106Cd+ interfering with 87Sr19F+). Such measurements are usually performed on a single collector ICP-MS, which has limited precision due to inherent changes in beam intensity of transient laser ablation signals. A prototype instrument named Proteus was developed that combines a quadrupole mass-filter and collision/reaction cell with a MC-ICP-MS, permitting the measurement of all Sr isotopes in multicollection.51 The precision of Sr isotopic analyses was improved compared to single collector mass spectrometers and demonstration was made that this approach could be used for in situ87Rb–87Sr dating of geological materials. The design of Proteus, however, suffered from low sensitivity compared to other MC-ICP-MS and the fact that instrumental mass bias did not follow mass-dependent fractionation, rendering accurate corrections problematic. More recently, another prototype instrument was developed called Vienna that addressed the shortcomings of Proteus.52 It relied on a novel mass-filter and collision/reaction cell module that has now been implemented on the commercially available Neoma MC-ICP-MS from Thermo Fisher Scientific™. The Vienna MC-ICP-MS/MS was built around an earlier generation Thermo Scientific™ Neptune™ MC-ICP-MS while the Neoma MS/MS is based on a new, more sensitive, user-friendly, and electronically stable MC-ICP-MS platform. Both Vienna and the Neoma MS/MS use (1) a double Wien filter separated by an adjustable aperture for mass selection and (2) a hexapole collision/reaction cell. The operation of the Neoma MS/MS as applied to in situ Sr isotopic analyses is detailed in Sect. 2. While the Vienna and Neoma MS/MS rely on the same technology, the hardware and software of the two instruments differ. Both Proteus51 and Vienna52 were prototype instruments that paved the way for the development of the commercially available Neoma MS/MS. We report here tests of in situ Sr analyses with the Neoma MS/MS coupled to a 193 nm excimer laser ablation system. All laser ablation data reported below are compiled in a .xlsx file provided as ESI.†
2. Materials and methods
Laser ablation was performed using a NWR193-UC 193 nm excimer laser ablation system (ESI Lasers). The mass spectrometer used was a precommercial version of the Thermo Scientific Neoma MC-ICP-MS with MS/MS option (Fig. 1) operated under the Qtegra ISDS™ software (v2.12). Below, we start with a description of the Neoma MS/MS hardware, with focus on the double Wien filter-hexapole collision cell as applied to Sr isotopic analyses.52 We then give details on the measurement conditions. Finally, we explain how the data reduction was done, including handling of transient laser ablation data with a Mathematica-based software (LASr) and error propagation.
 |
| | Fig. 1 Simplified schematics of the Neoma MC-ICP-MS/MS. After ionization in the plasma (1), the ions are accelerated by an extraction voltage (2). They then enter a first Wien filter (3). The opposite magnetic and electric forces are balanced when the entrance velocity is v = E/B. The ratio E/B is adjusted to let ions in the mass region of Sr pass. Heavier (e.g., Cd+) and lighter (e.g., Ar+) ions enter the Wien filter with lower and higher velocities than Sr and are deflected, resulting in their collision with an adjustable slit aperture (4). This slit aperture effectively acts as a mass filter. The ions that pass through the slit then go through an inversion lens (5) and are recollimated using a second Wien filter (6). The Sr+ and Rb+ ions then pass through a hexapole collision/reaction cell where SF6 is injected (7). Sr+ ions readily react with SF6 to make SrF+ while Rb+ ions do not react. Rb+ and SrF+ then pass through an electrostatic analyzer (8), which is part of the double-focusing geometry to compensate for the spread in ion velocities generated by the plasma source. The ions are then separated according to their mass-to-charge m/q ratio in a magnetic sector (9). The separated ion intensities are measured on Faraday collectors (10), with 85Rb and 87Rb measured at m/q = 85 and 87, while 86Sr, 87Sr, and 88Sr are measured as fluorides at m/q = 105, 106, and 107, respectively. | |
2.1. Prefilter and collision/reaction cell technology
The Neoma MS/MS uses the same ICP technology as the Thermo Scientific™ iCAP™ Qnova series of ICP-MS and ICP-OES instruments. The interface between the ICP and the mass spectrometer is an update of the Jet Interface, first introduced on the Thermo Scientific™ Neptune Plus™ MC-ICP-MS. After acceleration by an extraction voltage of −2 kV, the ions enter a novel ion optics Prefilter module composed primarily of two Wien filters separated by an inversion lens and adjustable aperture. The Wien velocity filter/mass spectrograph was developed in 1898 and provided the first hint for the existence of the proton,54 which was later discovered by Ernest Rutherford. This filter consists of near-uniform orthogonal magnetic (intensity Bw) and electrostatic (intensity Ew) fields that pull charged particles in opposite directions. Putting aside the dispersion in energy and velocity of ions in the plasma source, the ions accelerated by the extraction voltage enter the first Wien filter with a velocity  , where q is the charge (1.6 × 10−19 C for singly charged ions), U is the acceleration voltage (−2000 V), and m is the isotopic mass (1.4 × 10−25 kg for 87Sr). The electrostatic force in the Wien filter is qEw, while the magnetic force is qvBw. When the magnetic and electrostatic forces are balanced (Ew = vBw), the ion trajectory remains undisturbed, which happens for ions of mass-to-charge ratio m/q = 2U(Bw/Ew)2. Ions with a different mass-to-charge ratio will fan out and collide with the adjustable aperture that separates the two Wien filters. By adjusting the ratio of Bw/Ew in the first Wien filter and the aperture opening, it is thus possible to permit the transmission of ions within a certain mass range. Those that pass through the aperture are bent back towards the central axis by the inversion lens and are recollimated using the second Wien filter (the values of Bw and Ew are the same as the first Wien filter). For Rb–Sr isotopic analyses, the ratio Bw/Ew and the aperture are adjusted to remove Ar+ and all atomic and molecular ion interferences in the SrF+ mass region (Fig. 1).
, where q is the charge (1.6 × 10−19 C for singly charged ions), U is the acceleration voltage (−2000 V), and m is the isotopic mass (1.4 × 10−25 kg for 87Sr). The electrostatic force in the Wien filter is qEw, while the magnetic force is qvBw. When the magnetic and electrostatic forces are balanced (Ew = vBw), the ion trajectory remains undisturbed, which happens for ions of mass-to-charge ratio m/q = 2U(Bw/Ew)2. Ions with a different mass-to-charge ratio will fan out and collide with the adjustable aperture that separates the two Wien filters. By adjusting the ratio of Bw/Ew in the first Wien filter and the aperture opening, it is thus possible to permit the transmission of ions within a certain mass range. Those that pass through the aperture are bent back towards the central axis by the inversion lens and are recollimated using the second Wien filter (the values of Bw and Ew are the same as the first Wien filter). For Rb–Sr isotopic analyses, the ratio Bw/Ew and the aperture are adjusted to remove Ar+ and all atomic and molecular ion interferences in the SrF+ mass region (Fig. 1).
After exiting the Prefilter, the ions enter a hexapole CRC where SF6 is injected. Collisions with gaseous SF6 induce some scatter and the role of the hexapole is to keep the ions focused. Upon colliding with the gas, almost all (>85%) strontium is fluorinated to make SrF+ ions, while rubidium remains as Rb+.49 Fluorine has only one stable isotope 19F, therefore the proportions of SrF+ ion isotopologues are those of Sr isotopes. The ions then pass through a standard double-focusing geometry electrostatic analyzer (ESA) and magnetic sector, where they are separated according to their mass-to-charge ratios. The ion intensities are measured in Faraday collectors. The Neoma MS/MS is equipped with 11 Faraday collectors that can all be connected to amplifiers with 1013, 1011, and 1010 Ω feedback resistors. Deflection plates in front of the axial Faraday can deflect the signal to a discrete dynode secondary electron multiplier (not used in this study).
The Prefilter removes atomic and molecular ions outside of the Rb–Sr mass region. The CRC fluorinates Sr through the ion–molecule reaction Sr+ + SF6 → SrF+ + SF5, while Rb remains unchanged. The Prefilter and CRC module enable precise and accurate in situ87Sr/86Sr ratio analyses in Rb-rich samples by measuring Sr isotopes as SrF+ at a mass where interferences have been eliminated by the Prefilter.51,52
2.2. Measurement conditions
The mass spectrometer and laser ablation system were controlled using the Qtegra ISDS and ActiveView2 software, respectively. The laser ablation system had a TwoVol2 two-volume laser ablation cell that was flushed with 1200 mL min−1 He. N2 was added after the ablation cell at a rate of 4 mL min−1. All measurements were made with a 100 μm spot size, laser fluence of 5 J cm−2, with a repetition rate of 20 Hz, unless stated. We used two laser ablation/data acquisition schemes depending on whether Sr isotopic analysis was the sole focus, or Rb/Sr ratio measurements were also needed (Sr-only and Rb + Sr hereafter). For Sr-only measurements, the data were acquired over 2 minutes comprising 120 measurement cycles of 1 s each. Laser ablation lasted for 60 s. Data acquisition was started 30 seconds prior to ablation and measurable signal was sustained for ∼45 s. The maximum signal achieved on SRM®610 (Sr = 515.5 ppm) at the beginning of the ablation was ∼4.7 × 107 cps on 88Sr19F+. We give all ion intensities in cps, which can easily be converted to a voltage measured on a 1011 Ω amplifier by dividing by 6.24 × 107 (4.7 × 107 cps corresponds to ∼0.75 V). The intensity of the transient signal on SRM610 decayed from the maximum by a factor of ∼0.97 per second of ablation. The Rb + Sr analyses were performed in peak jumping mode. An issue in the precommercial instrument software prevented us from reducing the settling time between peak jumps below 3 s, which is the value that we used (a 0.5 s settling time would have been sufficient to accommodate the response time of the 1011 Ω amplifiers51). The Rb + Sr measurements consisted of 20 cycle measurements in a sequence 2 s Sr–3s settling time–0.5 s Rb–3s settling time. The arrival and departure times of Rb+ and SrF+ ion signals are the same as those in the Sr-only acquisition scheme.
All instrument conditions are tabulated in Table 1. The cooling and intermediate Ar gas flows were set at 14 and 0.8 L min−1, respectively. The plasma power was set at 1200 W. The z-distance was fixed to 6.5 mm. Previous studies have shown that it can be advantageous to increase the distance between the sampler cone and the torch to reduce instrumental fractionation between Rb and Sr.51,55 Because this is done at the expense of sensitivity and our acquisition time was already penalized by a long settling time, we decided against that option and the torch position was tuned for sensitivity. Nickel Jet sampler and X skimmer cones were used. The three adjustable parameters for the Prefilter module are Bw/Ew which defines the pass-through mass, Bw which influences how ions of different mass-to-charge ratios fan out in the Wien filter, and the opening of the aperture separating the two Wien filters. The Bw/Ew ratio was adjusted to let Sr+ and Rb+ ions through, the magnetic field was then adjusted with the aperture partially closed to trim ions with m/q ratios lower or higher than Sr+ and Rb+, and the aperture was finally adjusted to close the mass window more finely without encroaching on Sr+ and Rb+ masses. The Prefilter parameters used were Bw/Ew = 0.030, Bw = 0.315T (Bw setting of 50%; 100% magnetic field strength corresponds to 0.63T) and the aperture 60% closed. Adjustment of these parameters was done by scanning ion masses with the magnetic field of the magnetic sector. Peak scans of a multielement solution containing Rb, Sr, Rh, Ag and many other elements are shown in Fig. 2 with the Prefilter set to full transmission without SF6 in the CRC (left panel) and with the Prefilter closed to the mass range 82–94 with SF6 injected in the CRC (right panel; this corresponds to the operating conditions under which we measured Sr isotopic ratios). As shown, Sr isotopes can be measured as SrF+ where isobaric interferences have been removed by mass selection in the Prefilter.
Table 1 Instrumental conditions
| Parameter |
Value |
Unit |
Parameter |
Value |
Unit |
|
ESI Apex Omega Q desolvating nebulizer system
|
ESI NWR193 UC laser ablation system with TwoVol2 cell
|
| Argon |
3.8 |
L min−1 |
Helium |
1.2 |
L min−1 |
| Nitrogen |
3 |
mL min−1 |
Nitrogen |
4 |
mL min−1 |
| Spray chamber |
140 |
°C |
Spot size |
100 |
μm |
| Peltier |
3 |
°C |
Fluence |
5 |
J cm−2 |
| Desolvator |
155 |
°C |
Repetition rate |
20 |
Hz |
| Peripump |
17 |
rpm |
Dwell time |
60 |
s |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
Thermo Scientific Neoma MC-ICP-MS with MS/MS option
|
Thermo Scientific Neoma MC-ICP-MS with MS/MS option
|
| Cool gas flow |
14 |
L min−1 |
Cool gas flow |
14 |
L min−1 |
| Auxiliary gas flow |
0.8 |
L min−1 |
Auxiliary gas flow |
0.8 |
L min−1 |
| Nebulizer gas flow |
0.9 |
L min−1 |
Nebulizer gas flow |
0.89 |
L min−1 |
| Torch horizontal position |
−1.4 |
mm |
Torch horizontal position |
−1.35 |
mm |
| Torch vertical position |
−1.05 |
mm |
Torch vertical position |
−0.95 |
mm |
| Sampling depth |
5 |
mm |
Sampling depth |
6.5 |
mm |
| Plasma power |
1200 |
W |
Plasma power |
1200 |
W |
| Resolving power |
2100 |
MRP |
Resolving power |
2100 |
MRP |
| Focus |
52 |
% |
Focus |
52 |
% |
|
X Deflection |
−14.8 |
% |
X Deflection |
−14.8 |
% |
|
Y Deflection |
−3 |
% |
Y Deflection |
-3 |
% |
| Shape |
46.4 |
% |
Shape |
46.4 |
% |
| Wien filter magnetic field |
50 |
% |
Wien filter magnetic field |
50 |
% |
| Wien filter electric field |
320 |
V |
Wien filter electric field |
320 |
V |
| Wien focus 1 |
−440 |
V |
Wien focus 1 |
−440 |
V |
| Wien focus 1 X symmetry |
0 |
V |
Wien focus 1 X symmetry |
0 |
V |
| Wien focus 1 Y symmetry |
15 |
V |
Wien focus 1 Y symmetry |
15 |
V |
| Slit angle |
60 |
° |
Slit angle |
60 |
° |
| Wien focus 2 |
−395 |
V |
Wien focus 2 |
−395 |
V |
| Wien focus 3 |
−370 |
V |
Wien focus 3 |
−370 |
V |
| Wien focus 3 X symmetry |
0 |
V |
Wien focus 3 X symmetry |
0 |
V |
| Wien focus 3 Y symmetry |
−13 |
V |
Wien focus 3 Y symmetry |
−13 |
V |
| CCT entry |
−50 |
V |
CCT entry |
−50 |
V |
| CCT bias |
0 |
V |
CCT bias |
0 |
V |
| CCT RF amplitude |
100 |
% |
CCT RF amplitude |
100 |
% |
| CCT exit 1 |
−85 |
V |
CCT exit 1 |
−85 |
V |
| CCT exit 2 |
−100 |
V |
CCT exit 2 |
−100 |
V |
| CCT SF6 |
36 |
μL min−1 |
CCT SF6 |
36 |
μL min−1 |
 |
| | Fig. 2 Illustration of mass window selection for in situ Sr isotopic analysis using the Prefilter and CRC of the Neoma MS/MS.52 The left panel shows the mass spectrum of a tune solution with the aperture wide open and the magnetic field of the prefilter set at 0.06T and the aperture opened (even in pass-through mode, the Prefilter magnetic field is set to a non-zero value to allow ion transmission). The right panel shows the same mass scan after the Prefilter is tuned to allow ions between mass 82 and 94 to pass (magnetic field of 0.315T and aperture closed to 60%). The same solution was used but interferences in the mass range of SrF+ (e.g., Ag+) were removed by the MS/MS module. After reaction with SF6 >85% of Sr is transmitted to the ESA-magnetic sector as Sr19F+ for isotopic analysis. | |
After passage through the Prefilter, the ions pass through the CRC. The flow rate of SF6 in the collision cell was set to ∼0.05 mL min−1 (after conversion from the measured value of 0.2 mL min−1 on a H2 mass flow controller). Due to the low amount of SF6 gas required, a gas mix of SF6 in He51 would be preferred for this application. The conditions of the collision/reaction cell were tuned for maximum sensitivity on SrF+. When switching from Sr+ to SrF+ measurement conditions, the sensitivity decreased by 45%. The ions then pass through the ESA and the magnetic sector. Two acquisition schemes were used depending on whether both Rb and Sr were analyzed, or only Sr was measured (Table 2). In the Sr-only configuration, we set the magnetic field of the magnetic sector to measure 83Kr19F+, 84Sr19F+, 85Rb19F+, 86Sr19F+, 87Sr19F+, and 88Sr19F+ on L3, L2, L1, C, H1, and H2. In the Rb + Sr configuration, we measured SrF+ using the same collector array, but a line was added to the sequence to measure 85Rb+, 86Sr+, 87Sr+, and 88Sr+ on L3, L2, L1, and C via peak jumping. All Faraday collectors were connected to 1011 Ω amplifiers. These amplifiers saturate at 100 V (6.24 × 109 cps). The reason why we had to do Rb–Sr analyses in peak jumping mode is that on the precommercial instrument available, the outermost Faraday collectors were not properly positioned to allow simultaneous measurement of Rb+ and SrF+ ions in static mode.
Table 2 Cup configuration
|
|
L5 |
L4 |
L3 |
L2 |
L1 |
C |
H1 |
H2 |
H3 |
H4 |
H5 |
| Rb |
|
|
85Rb |
86Sr |
87Rb |
88Sr |
89Y |
90Zr |
|
|
|
| SrF |
|
|
83KrF |
84SrF |
85RbF |
86SrF |
87SrF |
88SrF |
|
|
|
| Amplifier assignment |
|
|
1011 Ω |
1011 Ω |
1011 Ω |
1011 Ω |
1011 Ω |
1011 Ω |
|
|
|
The mass spectrometer was tuned first using a multielement solution and an Apex Omega Q desolvating nebulizer. The mass spectrometer was tuned again before each laser ablation sequence by running spot analyses on the SRM610 glass standard. With a flow rate of 100 μL min−1, using a 20 ppb Sr solution, we obtained ∼9.4 × 108 cps (∼15 V) on 88Sr19F+, which corresponds to a sensitivity of 700 V ppm−1 and a useful yield for Sr of ∼0.0025 ion at the collector per Sr atom injected (∼0.25%). Overall, the Neoma MS/MS has similar sensitivity to the Neptune Series MC-ICP-MS in dry plasma conditions (using a desolvating nebulizer or laser ablation system) and is a factor of ∼2 more sensitive than the Neptune in wet plasma conditions.
2.3. Data reduction and error propagation with LASr
Laser ablation data were exported from the Qtegra ISDS software as xml files that were then converted to xlsx files. The first step in the data reduction involved the use a Mathematica-based software called LASr (Fig. 3 and ESI†). Note that this is a purpose-developed program that we plan to continue developing in the future. The software uses a graphical user interface (GUI) that takes the user through several steps. First, a file is selected in a GUI file/directory navigator, after which the user selects which approach is used for handling the transient LA signal. Three options are available: (i) “Average counts”, which uses the average counts for all isotopes in the acquisition window. (ii) “Peak integration”, which involves integrating the signal over a user-set acquisition window, where the signal is linearly interpolated between adjacent data points (or linearly extrapolated if the boundary of the acquisition window does not coincide with a data point). This is the method that we adopted in our data reduction as Rb and Sr were measured in peak jumping mode and the integration method minimizes bias associated with spectral skew. (iii) “Extrapolation to time zero” extrapolates the data to the start of the acquisition window. The user then chooses, using dropdown menus, the entries in the data table where the header entries are located for index, timestamp, and label, together with ion intensities for Rb, Sr, RbF, and SrF. For Sr-only measurements, the ion masses that need to be selected are 84SrF, 85RbF, 86SrF, 87SrF + 87RbF, and 88SrF. For Rb + Sr measurements, the same ion masses are selected, together with 85Rb, 87Rb + 87Sr, and 88Sr. The user then proceeds to another GUI window where the column header is selected, which will be trimmed during data reduction. The next step in the data reduction involves sequentially examining the intensity vs. time profile for each sample to define with a slider menu the time l1 immediately before the signal starts rising, time l2 when the laser ablation signal reaches its maximum, and time l3 when the signal drops precipitously at the end of ablation. The program takes the average count-per-second signal in the blank time interval 0 to l1 and subtracts it from the signal in the acquisition window l2 to l3. The signal in the intervals l1 − l2 and l3-end is not used for any purpose.
 |
| | Fig. 3 LASr Mathematica software for reduction of 87Rb–87Sr LA-MC-ICP-MS/MS data. The GUI software imports LA-MC-ICP-MS/MS data generated from Qtegra as an .xlsx file and exports another .xlsx file that contains the reduced data for each sample. (A) The user selects the reduction scheme to handle the transient laser ablation signal (average counts = average cps in the acquisition window; extrapolation to time zero = extrapolation of the data in the acquisition window to the start of the acquisition window; peak integration = the interpolated cps are integrated over the acquisition window). (B) Using dropdown menus, the user selects the lines where sample index, timestamp, label, and ion intensities are. (C) The user defines the entries that correspond to the table header. (D) Definition of the “blank” and “acquisition” windows. Sliders allow the user to move the three vertical lines in the bottom figure (red = l1, left blue = l2, right blue = l3). Everything that is at the left of the red vertical line is used to define the blank (blank window), which is subtracted from the signal. The two blue vertical bars bracket the transient sample signal (acquisition window), which is used to calculate 87Rb/86Sr and 87Sr/86Sr ratios after blank subtraction. The actions taken in (D) are repeated for each laser analysis. | |
The program then proceeds to calculate raw 87Rb+/86Sr+ and internally normalized 87Sr+/86Sr+ ratios using data in the acquisition window that have been blank-subtracted. Here, raw refers to ion ratios that have not been fully corrected for instrumental fractionation. This correction is done via standard bracketing and is discussed further below. The program first removes known isobaric interferences. No significant 83Kr19F+ was observed and no correction to subtract 84Kr19F+ and 86Kr19F+ from 84Sr19F+ and 86Sr19F+ was applied. The corrected interferences are from 87Rb19F+ on 87Sr19F+, and from 87Sr+ on 87Rb+. The later correction was used as a check that the 87Rb+/85Rb+ ratio corresponded to the expected isotopic ratio for Rb, meaning that 85Rb+ does not suffer from additional interferences. The raw 87Rb+/86Sr+ ratio was simply calculated from the raw 85Rb+/86Sr19F+ ratio using the formula,
| |  | (1) |
where the factor 0.278346/0.721654 corresponds to the
87Rb/
85Rb ratio recommended by the IUPAC.
56 Instrumental and natural isotopic mass bias is assumed to follow the exponential law, which can be written as
a2/
a1 = (
A2/
A1)(
m2/
m1)
β with
a2/
a1 the measured (fractionated) isotopic ratio,
A2/
A1 the true (reference) isotopic ratio,
m2/
m1 the ratio of isotopic masses, and
β the coefficient of natural and instrumental mass bias. The coefficient of natural and instrumental mass bias is calculated using the interference-free
88Sr/
86Sr ratio,
| | 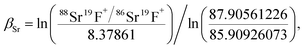 | (2) |
where 8.375209 is the
88Sr/
86Sr ratio conventionally used for internal normalization of Sr isotopic ratios. This value was measured by Nier in 1938 in Sr metal
57 and differs from the value of 8.37861 measured in the SRM987 carbonate standard.
58 Because we use standard bracketing, the value of the
88Sr/
86Sr ratio used for internal normalization has no consequence for the final value of the
87Sr/
86Sr ratio that we report.
Eqn (2) implicitly assumes that the isotopic fractionation acted on Sr isotopes rather than SrF isotopologues, as the masses used are those of Sr rather than SrF. This is a reasonable assumption to make because the coefficient of mass bias is dominated by instrumental fractionation (natural isotopic variations are small for Sr; ∼±0.3‰ on the
88Sr/
86Sr ratio
59) and much of the isotopic fractionation in MC-ICP-MS takes place in the torch–cone interface. We use this coefficient of mass bias to calculate (i) a fractionated
87RbF
+/
85RbF
+ ratio used to subtract the
87RbF
+ interference on
87SrF
+, and (ii) correct the
87SrF
+/
86SrF
+ ratio for mass-dependent isotopic fractionation,
| |  | (3) |
The program applies eqn (1) and (3) to both the integrated peaks and individual data points in the integration window. With the latter, the ion intensities measured during the Rb sequence are interpolated to the times of the SrF sequence to minimize bias associated with spectral skew. The values of 87Rb+/86Sr+ and 87Sr+/86Sr+ calculated from the integrated peaks in the acquisition window are the values that the program reports for each sample. The values of 87Rb+/86Sr+i and 87Sr+/86Sr+i for each cycle (i denotes the SrF cycles, of which there are n in total in the acquisition window) are used to estimate the standard deviations of the mean,
| | 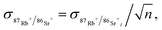 | (4) |
| | 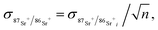 | (5) |
as well as the correlation coefficient
| |  | (6) |
Once the user has cycled through all the laser ablation measurements, the software exports an xlsx file that contains the reduced data for each sample.
Silicate glass standards SRM610 and feldspar glass H (FGH) from Davidson et al. (2001)33 were used to bracket the sample measurements. The major element composition of SRM610 is ∼72 wt% SiO2, 14 wt% Na2O, 12 wt% CaO, and 2 wt% Al2O3, which is not representative of chemical compositions encountered in nature. It contains 425.7 ppm Rb and 515.5 ppm Sr. It was used here because its 87Rb/86Sr and 87Sr/86Sr ratios are well known (2.3894 and 0.709699, respectively60), it was used previously in in situ87Rb–87Sr studies, and it has near homogeneous composition. We also used a plagioclase glass standard (FGH) that had been prepared by Davidson et al. (2001)33 by melting plagioclase grains extracted from a sample from Mt Pelée (M8230 from ref. 61) and doping the sample with Rb. It contains ∼262 ppm Rb and ∼506 ppm Sr. Its 87Rb/86Sr and 87Sr/86Sr ratios are 1.500986 and 0.704193, respectively.33 The matrix composition of this standard is a better match for the rocks and minerals that we measured here, but its level of homogeneity is unknown, especially for the 87Rb/86Sr ratio. We adopted SRM610 normalization as our preferred normalization scheme for reasons that are discussed below, notably because the secondary correction to the Shap granite is smaller with SRM610, but the data reduced using bracketing by FGH are also compiled in data tables and plotted in some figures for comparison, and the results agree within uncertainty.
Most of the measurements were performed in sequences of 5 sample laser spot measurements bracketed by spot measurements of FGH and SRM610 in a sequence FGH–SRM610–spot1–spot2–spot3–spot4–spot5–FGH–SRM610. The 87Rb+/86Sr+ and internally normalized 87Sr+/86Sr+ ratios were further corrected by bracketing with the standards using the formulas,
| | 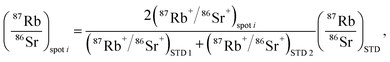 | (7) |
| |  | (8) |
where STD 1 and STD 2 denote the two standard spot measurements (either SRM610 or FGH) that bracket the sample spot measurement, while (
87Rb/
86Sr)
STD and (
87Sr/
86Sr)
STD are the recommended values for either SRM610 or FGH.
Both the sample and standard spot analyses are affected by uncertainties that need to be propagated in eqn (7) and (8). For 87Rb–87Sr dating, it is particularly important to evaluate the extent to which the errors are correlated, as this affects calculated ages and goodness-of-fit estimates. The errors in 87Rb/86Sr and 87Sr/86Sr could be correlated for two reasons: (i) during a spot analysis of heterogeneous material, different minerals or mineral domains ablated at one spot can have variable 87Rb/86Sr, associated with some spread in 87Sr/86Sr from 87Rb decay that should fall along the isochron. (ii) The two ratios 87Rb/86Sr and 87Sr/86Sr ratios share the same denominator isotope (86Sr), which can induce some statistical correlation between the two ratios (see the Appendix in ref. 62).
In the following, S denotes 87Sr/86Sr ratios, while R denotes 87Rb/86Sr ratios. The sample measurements (subscript 1) are bracketed by two standard measurements (subscripts 2 and 3) with know 87Sr/86Sr and 87Rb/86Sr ratios (noted s and r respectively). The 87Sr/86Sr and 87Rb/86Sr ratios of the sample corrected by standard bracketing are given by,
| |  | (9) |
| |  | (10) |
We note g the function that gives the corrected ratios from the measured ratios,
| |  | (11) |
To calculate the uncertainties on the ages and intercepts of 87Sr/86Sr and 87Rb/86Sr isochrons, we need to propagate the uncertainties on S1, S2, S3, R1, R2, and R3 onto  and
and  . This is done using the delta method. The gradient matrix of g is,
. This is done using the delta method. The gradient matrix of g is,
| |  | (12) |
Because S1–R1, S2–R2, and S3–R3 are the only dependent variable pairs, the covariance matrix for (S1,S2,S3,R1,R2,R3) is,
| |  | (13) |
The delta method gives an approximation of the covariance matrix V for 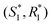 ,
,
| |  | (14) |
and we have,
| |  | (15) |
| |  | (16) |
| |  | (17) |
The IsoplotR program uses standard deviations  and correlation coefficients ρX,Y = Cov(X,Y)/(σXσY) as inputs in isochron calculations. The equations above can be reformulated with those notations and we have,
and correlation coefficients ρX,Y = Cov(X,Y)/(σXσY) as inputs in isochron calculations. The equations above can be reformulated with those notations and we have,
| |  | (18) |
| | 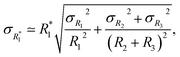 | (19) |
| |  | (20) |
| |  | (21) |
The IsoplotR program was used to calculate the intercepts (initial 87Sr/86Sr ratios) and slopes (ages) of the 87Rb–87Sr isochrons.63 We have also calculated model ages for individual spot measurements by calculating the slope of two-point isochrons connecting a particular spot analysis and the isochron intercept defined by all the points,
| | 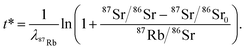 | (22) |
where
λ87Rb is the decay constant of
87Rb of 0.000013972 per million year.
1,2 To calculate the uncertainty on this model age, it is again important to consider the correlation between the
87Rb/
86Sr and
87Sr/
86Sr errors and we have,
| |  | (23) |
3. Results
3.1. Analysis of reference materials with known compositions
We applied the method outlined above to several reference materials with known 87Rb/86Sr and 87Sr/86Sr ratios: Durango apatite,64 SRM612,60 feldspar glasses I and L2.33 Durango apatite contains ∼475 Sr with an 87Sr/86Sr ratio of 0.70633 and 87Rb/86Sr ∼ 0.64 FGI was made from the same Mt Pelée plagioclase as FGH described above, but it contains different amounts of Rb (∼142 ppm) and Sr (∼501 ppm). Its 87Rb/86Sr and 87Sr/86Sr ratios are 0.82234 and 0.704137 ± 12, respectively.33 FGL2 was made from plagioclase separated from a volcanic rock from El Chichón (DT-5), which was doped with Rb. The Rb and Sr concentrations in that glass are ∼75 and ∼2058 ppm with 87Rb/86Sr and 87Sr/86Sr ratios of 0.10550 and 0.704335 ± 17, respectively.33 The degree of homogeneity in FGI and FGL2 are unknown. SRM612 has the same major element composition as SRM610 (∼72 wt% SiO2, 14% Na2O, 12% CaO, and 2% Al2O3) but lower trace element content (31.4 ppm Rb and 78.4 ppm Sr). Its 87Rb/86Sr and 87Sr/86Sr ratios are 1.15766 and 0.709063, respectively.60 We plot in Fig. 4 the measured 87Rb/86Sr and 87Sr/86Sr ratios against previously published values using both SRM610 and FGH bracketing normalizations. Depending on the standard used, we find small departures in 87Sr/86Sr ratios from recommended values (Fig. 4B) but the 87Sr/86Sr data remain accurate within ∼±0.001. This level of accuracy is sufficient for most applications as natural variations in 87Sr/86Sr span a large range. The reason for the small observed departures is difficult to establish but could be due to (i) inadequate correction of mass-dependent fractionation using the exponential law, or (ii) a small isobaric interference on Sr isotopes. The first explanation is unlikely because the predicted effect would be smaller than what is measured given the range of mass-dependent fractionation affecting Sr isotopes in MC-ICP-MS/MS.65 We find no correlation between Rb/Sr and departure of 87Sr/86Sr from recommended values, suggesting that the presence of an interference from 87RbF+ on 87SrF+ is unlikely. We cannot exclude, however, the presence of a yet unidentified interference on Sr isotopes. Evaluating the accuracy of 87Rb/86Sr ratio measurements is more difficult as the homogeneity of FGI and FGL2 has not been tested but we find reasonable agreement between published and measured values.
 |
| | Fig. 4 Comparison between previously published and measured 87Rb/86Sr (A) and 87Sr/86Sr (B) ratios in Durango apatite (DA), feldspar glass I and L2 (FGI, FGL2), and SRM612. The black filled circles use SRM610 for correction of instrumental fractionation. The red filled circles use feldspar glass H (FGH) for correction. The solid lines are 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 correlations. The reference values for SRM612, Durango apatite, Feldspar glasses I and L2 are from Woodhead and Hergt,60 Yang et al.,64 and Davidson et al.33 1 correlations. The reference values for SRM612, Durango apatite, Feldspar glasses I and L2 are from Woodhead and Hergt,60 Yang et al.,64 and Davidson et al.33 | |
3.2. Comparison between measurement uncertainties and theoretical limit from counting statistics and Johnson noise
In Sr isotopic analysis by MC-ICP-MS, instability in instrumental mass bias is the main source of variation in raw isotopic ratios, but it is corrected for by internal normalization using the 88Sr/86Sr ratio. The remaining uncertainty in internally normalized 87Sr/86Sr ratios can be due to counting statistics, Johnson noise associated with thermal agitation of free electrons, variations in the law describing mass fractionation in the mass spectrometer, and unresolved isobaric interferences. Errors arising from counting statistics and Johnson noise are unavoidable and represent the foundation of what precision is theoretically achievable. Below, we compare the measured precision of isotopic analyses with the theoretical limit from counting statistics and Johnson noise by adapting the formulas derived by Dauphas et al.62 to a transient signal with blank subtraction. The blank is measured at the beginning of the laser ablation over Nb cycles (index p) of duration Δt each. The sample is measured as a transient signal after the blank over Ns cycles (index j) of duration Δt each. The total number of counts ni for isotope i is obtained by subtracting from the sample counts the blank counts scaled to the same analysis duration as the sample,| |  | (24) |
where Ui,q is the voltage (in V) measured for isotope i during cycle q (j and p correspond to sample and blank cycle measurements), Ri is the value of the resistor (in Ω) used to measure isotope i, e is the elementary charge (1.602 × 10−19 C), ts = NsΔt, tb = NbΔt,  , and
, and  . The uncertainties associated with counting statistics and Johnson noise during a cycle (blank or sample) are,
. The uncertainties associated with counting statistics and Johnson noise during a cycle (blank or sample) are,| | | σcounting,i,q2 = ni,q = Ui,qΔt/eRi, | (25) |
| | | σJohnson,i,q2 = 4kTΔt/e2Ri, | (26) |
where k is Boltzmann constant (1.380649 × 10−23 m2 kg s−2 K−1) and T is the temperature of the resistor in K. There uncertainties add up quadratically over all cycles and we have,| |  | (27) |
We use the following notations,
| |  | (28) |
The relative uncertainties on internally normalized ratios (the star superscript in 84Sr/86Sr* and 87Sr/86Sr* indicates that those ratios are internally normalized) from counting statistics and Johnson noise are,62
| |  | (30) |
| |  | (31) |
| |  | (32) |
| |  | (33) |
We have calculated the precision achieved during Sr-only isotopic analysis of standards SRM610, SRM612, and Durango apatite. This was done in two manners: (i) all standards were analyzed on 5 to 10 spots each, and we calculated the standard deviation of those analyses (spot-level uncertainty). (ii) Each spot analysis is divided into cycles, and we calculated the standard deviation of the mean of all cycles for each spot analysis (cycle-level uncertainty). We also applied eqn (28) and (31) to calculate the theoretical limit on precision for conditions relevant to our Sr isotopic analyses (blank measured over 28 cycles of 1 s each with 0.0025 V on 86, 0.00030 V on 87, and 0.003 V on 88; sample measured over 56 cycles of 1 s each, all isotopes measured on 1011 Ω resistors; the temperature of the resistors set to 42 °C). We calculated the theoretical error with (eqn (28)) or without (the last two terms dropped from eqn (28)) the blank error included. This calculation shows that for those conditions, Johnson noise should become the dominant source of uncertainty when 88Sr is at less than ∼1.2 V, which corresponds to 0.14 V on 86Sr and 0.10 V on 87Sr. We compare in Fig. 5 the theoretical limit with the precisions achieved. As shown, there is excellent agreement between the blank-free theoretical limit and the precision calculated from the standard deviation of the mean of the cycle-level analyses. The precision calculated from the standard deviation of the spot-level analyses is also close but is slightly higher. Adding the uncertainty arising from the blank brings the theoretical expectation in closer agreement with the spot-level uncertainty. This makes sense as the main difference between the cycle-level and spot-level uncertainties is blank subtraction. The same blank is subtracted from all cycles measured at one spot, so blank subtraction is not a source of scatter at the cycle level. In spot analyses a different blank is subtracted for each analysis, so it contributes to the scatter. Overall, our standard measurements have precisions that are close to the theoretical limit.
 |
| | Fig. 5 Comparison between actual measurement precision on internally normalized 87Sr/86Sr for SRM610, SRM612, and Durango apatite, with theoretical limit from Johnson noise and counting statistics (eqn (31)62). The dashed grey lines are the theoretical limits for Johnson noise (dominant below ∼1.2 V on 88Sr) and counting statistics (dominant above ∼1.2 V) when the blank uncertainty is not included (excluding the last two terms in eqn (28)). The red line combines those errors quadratically. The dashed red line shows the effects of Johnson noise and counting statistics when the blank uncertainty is included (eqn (28); the added uncertainty arises primarily from Johnson noise on the blank). The light red filled squares were calculated from the standard deviation of the mean of cycle analyses. The dark red filled circles were calculated from 5 to 10 repeat analyses of the same standard. The main difference between cycle- and spot-level dispersion is removal of a different blank for each spot analysis. The precision on 87Sr/86Sr achievable by LA-MC-ICP-MS/MS is close to the theoretical limit. | |
3.3. Secondary calibration to the Shap granite isochron
A significant difficulty in in situ87Rb–87Sr analysis by LA-MC-ICP-MS/MS is the fractionation of Rb/Sr induced by the laser ablation and plasma torch. While we apply a first-order correction for this fractionation by bracketing the sample laser ablation analyses by standard analyses (SRM610 and FGH) of known compositions, inaccuracy can persist due to mismatch in matrix composition/structure and possible heterogeneity for FGH. Bevan et al.51 used the approach of measuring isochrons in materials of known ages and similar mineralogy/composition to apply a correction factor on the 87Rb/86Sr ratio. As discussed below, we have applied in situ87Rb–87Sr dating to Martian meteorite NWA 7034, where the isochron slope is determined by K-rich feldspars, which match neither SRM610 nor FGH chemically. The K-rich feldspar in NWA 7034 has a composition Or77Ab21An3 (Meteoritical Bulletin), well within the field of K-feldspar polymorphs orthoclase, sanidine, and microcline. To appropriately correct for matrix effects on 87Rb–87Sr, we have measured the Shap granite, with emphasis on orthoclase which has a bulk composition Or75.0Ab24.6An0.4 (ref. 66) that is very close to the composition of alkali-feldspars in NWA 7034. A second reason why we decided to study Shap granite is that it was previously dated by in situ87Rb–87Sr using the Proteus instrument51 and by micromilling followed by TIMS.67 The Shap granite has an 87Rb/86Sr isochron age of ∼397 Ma.68 The measurements presented here were acquired on the very same specimen analyzed by Davidson et al.,67 who obtained an age of 405 ± 2 Ma and an initial 87Sr/86Sr ratio of ∼0.7072. The mount analyzed by Davidson et al.67 contains a large megacryst with an orthoclase core and a plagioclase (albite) rim, and a groundmass of biotite, plagioclase, and quartz. Davidson et al.67 milled four locations in the megacryst: inner orthoclase core, outer orthoclase core, inner plagioclase rim, outer plagioclase rim. We ran a transect along those previously milled spots (Fig. 6). The 87Rb/86Sr and 87Sr/86Sr ratios measured by LA-MC-ICP-MS/MS along this transect are plotted in Fig. 6A together with the previous TIMS measurements. As shown, there is excellent agreement between the TIMS and LA-MC-ICP-MS/MS. The 87Rb/86Sr and 87Sr/86Sr ratios follow parallel trends, which is the result of in situ decay of 87Rb into 87Sr in the megacryst. We also measured several minerals in the groundmass (see Fig. 6B for the locations of the laser spots), including several high Rb/Sr biotite crystals. The data points for the Shap granite are plotted in 87Rb–87Sr isochron diagrams in Fig. 7. The two normalizations to FGH and SRM610 are used in those plots. We plot the isochrons using only the megacryst data and using all data including the high Rb/Sr biotite data. Using FGH normalization, the ages obtained are 277 ± 19 Ma (megacryst only) and 338 ± 7 Ma (all data including biotite). This is much lower than the known age of the sample of 397 Ma, indicating either that FGH is a poor matrix match for orthoclase or that FGH is heterogeneous and the shard that we mounted has different 87Rb/86Sr ratio than the value measured by Davidson et al.67 Using SRM610 normalization, we obtain ages of 326 ± 10 Ma (megacryst only) and 369 ± 12 Ma (all data including biotite). Although the difference is smaller than when FGH is used for normalization, this is still lower than the independently know age of 397 Ma. As discussed below, for dating Martian meteorite Black Beauty, we are primarily interested in the bias associated with analyzing 87Rb/86Sr in K-rich feldspar, so the isochron constructed using the megacryst alone is the one most relevant. To obtain the correct age for the Shap granite megacryst, one must divide the FGH normalized 87Rb/86Sr ratio by 1.43 and the SRM610 normalized 87Rb/86Sr ratio by 1.21. Because the bias associated with SRM610 is smaller than with FGH, we adopt this normalization and use the correction factor of 1.21 to correct 87Rb/86Sr ratios on K-feldspar calculated based on SRM610 bracketing,| |  | (34) |
 |
| | Fig. 6
87Rb/86Sr (right axis; orange symbols) and 87Sr/86Sr (left axis; blue symbols) ratios (A) along a transect in a K-feldspar megacryst from the Shap granite (B). The small, filled circles and lines are LA-MC-ICP-MS/MS data, while the large symbols are measurements from Davidson et al.67 acquired by TIMS on micromilled samples along the same transects (black holes in panel (B) for the inner core, outer core, inner rim, and outer rim). Panel (B) shows a false color image generated by data acquired on an SEM. Yellow is orthoclase, green is albite, blue is quartz, and red is biotite. The 87Sr/86Sr variations stem primarily from 87Rb-decay after crystallization (Fig. 7, ref. 67). The 100 μm laser ablation spots inside (transects) and outside the megacryst are shown as white-filled circles. | |
 |
| | Fig. 7
87Rb–87Sr in situ isochron diagrams for the Shap granite, which is independently dated at ∼397 Ma.68 Isochron slopes and intercepts were calculated using the IsoplotR program. The measurements presented here were acquired on the same specimen analyzed by Davidson et al.67 using micromilling and TIMS analyses. Davidson et al.67 obtained an age of 405 Ma and an initial 87Sr/86Sr ratio of ∼0.7072. In panels (A) and (C), the 87Sr/86Sr and 87Rb/86Sr ratios were corrected for instrumental fractionation by normalization to feldspar glass H (FGH) from Davidson et al.,33 while panels (B) and (D) were corrected by normalization to SRM610. Panels (A) and (B) use all data, including spots analyzed on biotite with extreme 87Rb/86Sr ratios. Panels (A) and (D) only use data from a single orthoclase megacryst. All ages reported here are too young relative to expectations.67,68 The reason for the too young ages is the inadequacy of the FGH and SRM610 standards to correct for fractionation of the Rb/Sr ratio induced by laser ablation and plasma-ionization.51 To obtain the correct age for the Shap granite megacryst (orthoclase), one must divide the FGH- and SRM610-normalized 87Rb/86Sr ratios by 1.43 and 1.21, respectively. | |
Bevan et al.51 calculated correction factors based on analysis of the Dartmoor granite DG-1 isochron and obtained values that ranged between 0.975 and 1.007. Although our correction is significant, the Shap granite megacryst is an excellent matrix match for K-feldspar in NWA 7034 and the correction is likely to be accurate. Bevan et al.51 obtained a precision of ±2.5 Ma on their isochron of the Shap granite, which reflects in part the fact that they measured many more feldspar spots (n = 135) than we did on the Shap megacryst (n = 40) and their 87Rb/86Sr feldspar measurements span a much wider range (0–50) than those measured by us in the megacryst (0–4). Our best estimate for the initial 87Sr/86Sr ratio of 0.70821(27) is slightly higher than the values of ∼0.7072 and 0.70755(4) reported by Davidson et al.67 and Bevan et al.51 As discussed in Sect. 2.4, our SRM610-normalized 87Sr/86Sr ratios are expected to be accurate to within ∼±0.001, so there is no obvious discrepancy with previous studies.
The Shap granite biotite that we measured has extremely high 87Rb/86Sr ratio, which provides us with an opportunity to assess the extent to which Rb can form fluorides and the size of the effect that this induces on 87Sr19F+. One of the biotite that we analyzed has SRM610-normalized 87Rb/86Sr and 87Sr/86Sr ratios of 817 ± 114 and 4.871 ± 0.238, with a correlation coefficient of ∼0.6 between the two. If we artificially set 85Rb19F+ to 0, the 87Sr/86Sr ratio shifts to 4.879, which is well within error. Even during laser ablation of this extremely Rb-rich mineral, the 85Rb19F+ does not rise above the blank, corresponding to a conservative upper limit 85Rb19F+/85Rb+ < 10−5. To summarize, Rb does not form fluorides and the 87RbF+ correction is always negligible.
4. Discussion
The 87Rb–87Sr decay system produces isotopic variations in rocks and minerals that can be used to (1) date rocks, (2) tease out the history of crustal growth on Earth, (3) trace assimilation of country rock and mixing in magmas, (4) correlate strata through isotope chemostratigraphy, (5) trace animal and human migration, and (6) trace the past exchanges of goods and artifacts. TIMS analyses of Sr isotopic compositions after Sr purification and Rb/Sr determinations by isotope dilution are the gold standards for such measurements due to their unrivalled accuracies and precisions (Sect. 3). TIMS analyses however suffer from two main limitations: 87Rb–87Sr dating typically involves destructive rock disaggregation (crushing, mineral separation, and powdering), and throughput is limited by rock preparation, clean laboratory work, and isotopic data acquisition. The novel technique of LA-MC-ICP-MS/MS is minimally destructive, preserves petrographic context for the minerals analyzed, and is rapid. It opens many exciting avenues of research to study precious and small extraterrestrial samples and cultural artifacts, or to characterize many samples rapidly. Below, we show three examples of Sr isotopic analyses in natural samples where LA-MC-ICP-MS/MS data complement or even supersede TIMS data.
4.1. The age of NWA 7034 (Black Beauty)
The Martian meteorite NWA 7034 (and associated paired meteorites) is a unique polymict impact breccia.69–73 Its alkali element content is much higher than that of SNC meteorites and it contains differentiated igneous lithologies, including trachyandesite and basaltic andesite clasts. It is composed of a fine-grained matrix that hosts several types of clasts (melt clasts probably formed by impact, igneous clasts, and protobreccia, which is thought to be recycled from more ancient breccia). A fascinating aspect of Black Beauty is the chronology of its components and what it tells us about Mars' history. U–Pb dating of zircon and baddeleyite revealed concordia ages of ∼4.4 Ga and partial resetting at 1.4 Ga (also seen with U–Pb in phosphate).69,72,74–77 U–Pu–Xe,78146Sm–142Nd and 147Sm–143Nd79 also point to very early formation of some components within Black Beauty. Chronometers more prone to thermal disturbance indicate much more recent resetting, with most 40Ar–39Ar ages clustering around 1.4 Ga.78,80,81 U + Th + Sm/He systematics point to even more recent resetting within the last ∼150 Ma.78,80–82 The 1.4 Ga age has been interpreted as the age of lithification (formation of the breccia)81 or resetting by protracted heating associated with plume magmatism.78 The 87Rb–87Sr system complicates chronological inferences even further as the isochron obtained by Agee et al.70 on mineral separates yielded an age of 2.089 ± 0.081 Ga. The mineral separates analyzed by Agee et al.70 are mixtures of minerals comprising dark (Fe,Mg-rich) and light (apatite, feldspar) colored minerals. Nyquist et al.79 also studied 87Rb–87Sr in Black Beauty fragments and found evidence of disturbance in plagioclase. The samples measured by Nyquist et al.79 spanned a narrower range of 87Rb/86Sr ratio (up to ∼0.6) than the samples measured by Agee et al.70 (up to ∼1.8) but the reason for the discrepancy between the two studies is unclear as Agee et al.70 found no evidence for disturbance in their 4-point isochron.
The diversity of ages recorded by the various components and chronometers in Black Beauty shows that this meteorite had a complex history punctuated by major thermal disturbances. A major question that is largely unaddressed is the significance of the 2.1 Ga 87Rb–87Sr age measured by Agee et al.70 Is this age reliable? Does it reflect the time of lithification of the breccia, in which case 1.4 Ga 40Ar–39Ar ages could reflect later impact resetting?
Black Beauty is ideally suited for in situ87Rb–87Sr dating by LA-MC-ICP-MS/MS as it contains K-rich feldspars that are old enough to have accumulated significant radiogenic 87Sr and the question addressed can be easily resolved with the precision attainable with this technique. K-rich feldspars are found both within larger igneous clasts and as individual grains dispersed in the matrix. An advantage of in situ87Rb–87Sr dating is that one can measure ages on individual crystals of various sizes and compositions to evaluate whether some have experienced resetting, which could help refine our understanding of the thermal history of Black Beauty. The sample analyzed here (FMNH ME 6118.2) is ∼2.5 cm across and composed of diverse clasts of igneous and impact-ejecta origins (Fig. 8). Its most striking feature is the presence of a large olivine-rich clast (oc in Fig. 8; named Valentine due to its resemblance to a heart in false color image), which to our knowledge has not been documented before in other sections of NWA 7034 and paired meteorites. Our focus here are K-rich feldspars, as K and Rb have nearly identical behaviors in igneous systems.83 To identify these grains, we acquired high-resolution (∼4.656 μm per pixel) quantitative chemical maps (Oxford Instruments AZTec QuantMap) of our section using a TESCAN LYRA3 field emission scanning electron microscope equipped with two Oxford Instrument XMax 80 silicon drift energy dispersive X-ray spectroscopy (EDS) detectors. A lower resolution QuantMap was generated by binning the pixels in batches of 4 × 4 corresponding to a resolution of ∼18.624 μm per pixel. The chemical maps were then imported in Mathematica for further processing. The maps were convoluted with a circular flat kernel of 100 μm diameter to simulate analysis with a 100 μm laser ablation spot size. The convoluted K2O and CaO chemical maps are shown in Fig. 9. We used these maps to estimate 87Rb/86Sr ratios in potential laser ablation spots as Rb and K have very similar geochemical behaviors, and Sr and Ca also have somewhat similar behaviors. To calculate the “87Rb/86Sr” ratio map in Fig. 9, we take the K2O/CaO ratio and multiply it by an empirical factor relating the 87Rb/86Sr ratio measured by laser ablation and the K2O/CaO ratio measured by EDS either before (by relocation of the LA spots) or after (by analysis of the LA pit) laser ablation (Fig. 10). A Mathematica script was used to detect grains that were at least 5 wt% K and have an equivalent diameter of at least 30 μm. By grain, we mean contiguous pixels that fulfill the criterion of K > 5 wt%. The map of K-rich grains was superposed on an optical image of the Black Beauty section (Fig. 8). The K2O/CaO ratio (“87Rb/86Sr”) and K-rich grain maps were used to identify the grains that were targeted for Sr isotopic analyses. We also measured K-poor and Ca-rich minerals to precisely define the isochron intercept.
 |
| | Fig. 8 Petrography the NWA 7034 (Black Beauty) sample used in this study. Right: False-color Mg–Ca–Al image of Black Beauty. The Al-rich, Mg-poor grains are alkali feldspars. This map was calculated from EDS QuantMap quantitative maps acquired on a TESCAN LYRA3 field emission scanning electron microscope. Left: Reflected light image. Different clast types described in previous studies71–73 are indicated with labels (sp = dark melt spherules, m = dark melt clasts, cm = crystallized melt clasts, f = angular mineral fragments). Olivine-rich clasts (oc) are also present in the sample that to our knowledge have not been described before. As a guide for the analysis of alkali-rich phases we used the K concentration map to mark grains of at least 30 μm equivalent diameter that contain 5 wt% K or more (in red on the left panel). | |
 |
| | Fig. 9 False color maps of K2O, CaO, and “87Rb/86Sr” for Black Beauty generated from QuantMap data. The third map was calculated based on an observed correlation between K2O/CaO measured by EDS and 87Rb/86Sr ratio measured by ICP-MS at the laser spots (87Rb/86Sr ≃ 1.4 K2Owt%/CaOwt%; Fig. 10). The black spots in the third panel (log10[“87Rb/86Sr”]) correspond approximately to the positions of the laser beam spots. The resolution of the original EDS map was downgraded by convoluting the original data by a flat circular kernel of 100 μm diameter to simulate signal averaging under the laser beam. | |
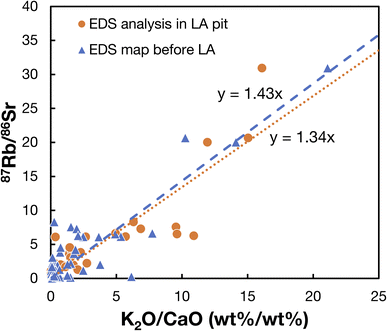 |
| | Fig. 10 Relationship between the 87Rb/86Sr ratio measured by laser ablation in Black Beauty and the K2O/CaO ratio measured in (1) the laser ablation pit by EDS analysis on a SEM or (2) through EDS mapping before laser ablation by locating the places where the measurements were made on a chemical map acquired before LA analysis. The Martian K/Rb ratio of 298 g g−1 (ref. 83) and Ca/Sr ratio of 1170 g g−1 (ref. 111) would yield a slope of 13, which is steeper than the slope measured here. K and Rb behave very similarly, but Ca and Sr can have different geochemical behaviors. | |
In Fig. 11, we plot the data in an 87Rb/87Sr–87Sr/86Sr isochron diagram. Calculation of the isochron parameters was done using IsoplotR. As shown, the K-rich feldspars have 87Rb/86Sr ratios that extend to much higher values (∼37) than what had been measured previously by Agee et al.70 (∼1.8) and Nyquist et al.79 (∼0.6). We find a clear correlation between 87Rb/87Sr–87Sr/86Sr, defining an age of 2.190 ± 0.059 Ga. This age is identical within error to the age of 2.089 ± 0.081 Ga obtained by Agee et al.70 on a 4-point mineral separate isochron. We obtain an intercept of 0.71188 ± 0.0169, which agrees within error with the intercept of 0.71359 ± 0.00054 obtained by Agee et al.70 for dark–light mineral separates. The isochron age and intercept were calculated using the method “maximum likelihood regression with overdispersion” of IsoplotR. The reason for the overdispersion (∼0.008 in 87Sr/86Sr) is unclear and could result from geological scatter or underestimation of the analytical uncertainty. As discussed in Section 2.4, we estimate the accuracy of our 87Sr/86Sr measurements to be ∼±0.001, but the level of accuracy of 87Rb/86Sr ratio measurements is more difficult to assess. We do not find evidence for large disturbance in 87Rb–87Sr systematics in K-rich feldspars, as had been seen before by Nyquist et al.79 in plagioclase. A possible explanation for this discrepancy could be a difference in the closure temperatures of plagioclase and K-rich feldspars.
 |
| | Fig. 11
87Rb–87Sr in situ isochron diagrams for Martian meteorite NWA 7034 (also known as Black Beauty). The 87Sr/86Sr and 87Rb/86Sr ratios were corrected based on the ratio in the bracketing SRM610 standard. The 87Rb/86Sr ratio was further divided by 1.21 based on the Rb–Sr data acquired on the Shap granite (Fig. 7), following the approach of Bevan et al.51 The data points define an age 2190 ± 60 Ma (±95% CI) and an intercept of 0.7119 ± 0.0017 (±95% CI). The age and intercept do not change significantly when the three most radiogenic spot analyses are excluded from the regression (2235 ± 72 Ma and 0.71148 ± 0.00170, respectively). The same data corrected using the FGH glass standard and a secondary normalization using the Shap granite give an age and intercept of 2347 ± 61 Ma and 0.7107 ± 0.0023 (not shown), which are close to the values calculated from SRM610 + Shap. The high Rb/Sr spots in Black Beauty are alkali-rich feldspars. | |
Of the 108 laser spots analyzed, 30 have 87Rb/86Sr > 1 and well resolved excesses in their 87Sr/86Sr ratios. We examined the section using an SEM after laser ablation analysis to (i) measure the K2O/CaO in the laser ablation pits (Fig. 10) and (ii) estimate the grain size and petrographic context (Fig. S1†). The 30 high-Rb/Sr spots were measured on 13 distinct grains as some larger grains were measured multiple times. The surface area of the grains was calculated based on SEM imaging, allowing us to compute equivalent diameters (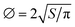 with S the surface area). The grains range in equivalent diameter between 111 and 460 μm. We calculated model ages for each grain by taking the slope of the lines defined by individual data points and the all-points isochron intercept (eqn (22) and (23)). This allows us to test if smaller grains have been more easily disturbed and give a different age than larger grains. We plot in Fig. 12 the 2-point model age for each spot against the diameter of the target grain. As shown, there is no relationship between the two and the data define a slope dt/da = −1.6 ± 2.2 Ma μm−1 (a is the radius in μm) that is indistinguishable from 0. Individual spot analyses are consistent with an 87Rb–87Sr age of ∼2.2 Ga and there is no indication of resetting at 1.4 Ga even for the smaller grains. Lindsay et al.81 calculated the temperature–time conditions needed for radiogenic 40Ar to be lost and 40Ar/39Ar ages to be reset at 1.4 Ga in K-rich feldspar. Their estimate that heating was short-lived, ranging between ∼5 h at 1000 °C and 10 year at 500 °C is likely to be a minimum as they did not account for the discrete distribution of diffusion domain sizes apparent in the degassing of virtually all their samples. We can estimate the effect that such heating events would have on Sr isotopes by modeling diffusive Sr isotope exchange between the interior of feldspar grains containing radiogenic 87Sr and the surrounding medium. For each grain, we model that process as diffusion in a sphere starting with uniform composition, with the composition at its surface kept at a constant value set by the surrounding medium. All nonradiogenic Sr isotopes are assumed to remain unchanged during the transient heating event. The equation governing the evolution of the 87Sr/86Sr ratio in the grain with time is,84
with S the surface area). The grains range in equivalent diameter between 111 and 460 μm. We calculated model ages for each grain by taking the slope of the lines defined by individual data points and the all-points isochron intercept (eqn (22) and (23)). This allows us to test if smaller grains have been more easily disturbed and give a different age than larger grains. We plot in Fig. 12 the 2-point model age for each spot against the diameter of the target grain. As shown, there is no relationship between the two and the data define a slope dt/da = −1.6 ± 2.2 Ma μm−1 (a is the radius in μm) that is indistinguishable from 0. Individual spot analyses are consistent with an 87Rb–87Sr age of ∼2.2 Ga and there is no indication of resetting at 1.4 Ga even for the smaller grains. Lindsay et al.81 calculated the temperature–time conditions needed for radiogenic 40Ar to be lost and 40Ar/39Ar ages to be reset at 1.4 Ga in K-rich feldspar. Their estimate that heating was short-lived, ranging between ∼5 h at 1000 °C and 10 year at 500 °C is likely to be a minimum as they did not account for the discrete distribution of diffusion domain sizes apparent in the degassing of virtually all their samples. We can estimate the effect that such heating events would have on Sr isotopes by modeling diffusive Sr isotope exchange between the interior of feldspar grains containing radiogenic 87Sr and the surrounding medium. For each grain, we model that process as diffusion in a sphere starting with uniform composition, with the composition at its surface kept at a constant value set by the surrounding medium. All nonradiogenic Sr isotopes are assumed to remain unchanged during the transient heating event. The equation governing the evolution of the 87Sr/86Sr ratio in the grain with time is,84
| |  | (35) |
where (
87Sr/
86Sr)
th+Δt, (
87Sr/
86Sr)
th, and (
87Sr/
86Sr)
b,th are the Sr isotopic compositions in the grain (i) after the heating event, which lasted a time Δ
t, (ii) right before the heating event, and (iii) of the surrounding medium (bulk),
a is the grain radius and
D is the diffusivity. Strontium self-diffusion experiments give the temperature dependence of the diffusivity:
D =
D0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
e
−E/(RT), with
R the gas constant (8.3145 J K
−1 mol
−1),
D0 = 10 μm
2 s
−1 and
E = 167
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
000 J mol
−1.
85 We use the diffusivity measured by Giletti
et al.85 rather than the one measured by Cherniak and Watson,
86 as the former were self-diffusion experiments relying on Sr isotopic analyses as opposed to chemical diffusion. Self-diffusion data should be more relevant to the
87Rb–
87Sr resetting scenario investigated here. We calculate below how the heating event that reset the
40Ar/
39Ar system at a time
th before present, could have influenced the isochron relationship if the Sr isotopic compositions of the grains were partially equilibrated with the surrounding medium but the Rb/Sr remained unaffected.
 |
| | Fig. 12 Two-point model 87Rb–87Sr age for individual K-feldspar Rb-rich grains (eqn (22) and (23)) as a function of grain size (equivalent diameter). The solid horizontal line is the isochron calculated using all in situ data (∼2.2 Ga; Fig. 11), while the dashed horizontal line is the 40Ar/39Ar plateau age obtained for K-rich grains by Lindsay et al.81 As shown, the grains show no obvious sign of resetting at 1.4 Ga. | |
Knowing present 87Rb/86Sr and 87Sr/86Sr ratios measured in the grains and the bulk meteorite at present (subscript p), we can calculate the 87Sr/86Sr ratios at the time of the heating event, (87Sr/86Sr)th = (87Sr/86Sr)p + (87Rb/86Sr)p(1 − eλth). For example, the present bulk rock 87Rb/86Sr and 87Sr/86Sr ratios of NWA 7034 are 0.4275 and 0.726229, respectively,70 corresponding to a bulk (87Sr/86Sr)b ratio of 0.717784 at 1.4 Ga. The same calculation can be done to estimate (87Sr/86Sr)i for each grain. We can then use eqn (35) to calculate how the thermal event could have partially reset the Sr isotopic composition of the grain to a new value (87Sr/86Sr)Δt. We then calculate what the present Sr isotopic composition would be if the system had been disturbed but the 87Rb/86Sr ratio had not changed. The present 87Sr/86Sr isotopic composition of a grain disturbed at th would be,
| | 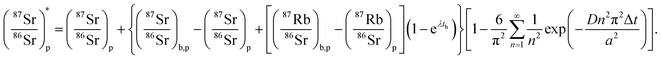 | (36) |
We used this formula to calculate the shift in 87Sr/86Sr associated with heating for 5 h at 1000 °C, or for 10 year at 500 °C. In both cases, the effect is negligible for all Rb-rich grains analyzed here. Available data therefore suggests that the thermal event that reset 40Ar/39Ar systematics did not reset 87Rb–87Sr. Most likely, the 87Rb–87Sr age of ∼2.2 Ga (Fig. 11) represents the lithification time for the breccia and the 40Ar/39Ar system was reset by a later impact event.
This example shows that in situ87Rb–87Sr analysis by LA-MC-ICP-MS/MS could be well suited to date samples that will hopefully be returned to Earth from Mars' Jezero crater around 2033.87,88 The Perseverance rover has identified a possible microgabbro in the Cf-fr (Crater floor-fractured rough) or Máaz formation on the floor of the Jezero crater.89 This rock shares similarities with differentiated basaltic martian meteorite Los Angeles,90 which was dated using 87Rb–87Sr.91 It is therefore likely that some rocks returned from the Jezero crater will be datable by LA-MC-ICP-MS/MS. The MMX mission will return samples from Mars' moon Phobos in 2029.92,93 Spectroscopic observations hint at the presence of phyllosilicate and feldspar at the surface of Phobos,94 which could possibly be dated by LA-MC-ICP-MS/MS. The surface of Phobos could also contain fragments ejected from Mars95 that might be datable by LA-MC-ICP-MS/MS. Use of LA-MC-ICP-MS/MS rather than TIMS for 87Rb–87Sr analyses of returned samples will limit sample consumption and enable studies of minerals or fragments with different ages and geological histories.
4.2. Magma sources in the 26.5 ka Oruanui supereruption
The 26.5 ka Oruanui supereruption was the largest eruption to occur at Taupo Volcano in New Zealand, releasing 530 km3 of primarily rhyolitic magma in a period of weeks to months.96 It has been the subject of numerous studies aimed at understanding how such a large volume of differentiated magma could form, examining the roles of magmatic differentiation, partial melting, and assimilation. Based on 87Sr/86Sr ratio analyses of plagioclase crystals, Charlier et al.11 showed that the Oruanui magma body had a complex history. Through micromilling, they studied a plagioclase population characterized by the presence of rutile-rich cloudy cores. The crystal fraction of pumice clasts is ∼10%, ∼2/3 of which are plagioclase. Among those plagioclase crystals, ∼3% contain sub-rounded bluish-grey cloudy cores. While these crystals represent a small portion of the total volume of magma erupted (∼0.2%), they are ubiquitous and bear witness of the processes of magma differentiation and crystal inheritance in the Oruanui magma body. These crystals contain three zones:11 (i) a cloudy core (c) characterized by variable and elevated anorthite (An) content and slightly elevated 87Sr/86Sr (∼0.7055–0.7065) relative to the bulk rocks, (ii) an overgrowth rim (o) with significantly higher An content and often more radiogenic 87Sr/86Sr reaching ∼0.7076, and (iii) a euhedral rim (e) with an An content that decreases outwards to bulk rock values and a 87Sr/86Sr ratio that also decreases outwards from radiogenic to bulk rock values. The age of the samples and their low Rb/Sr ratios mean that the variations in 87Sr/86Sr are not due to in situ87Rb decay but rather reflect the contributions of three different magma sources. The cloudy core, overgrowth rim, and euhedral rim are thought to be derived from assimilation of intermediate-composition crustal rocks, melts produced by melting of ancient greywacke basement, and bulk rock magma composition, respectively.11 Measurement of micromilled samples by TIMS is time consuming, limiting the number of analyses that can be performed. The precision achieved on 87Sr/86Sr isotopic analyses by Charlier et al.11 is on the order of ∼±0.0001, which is more than sufficient to detect 0.7055–0.7076 (∼0.0020 span) variations in 87Sr/86Sr ratios. With LA-MC-ICP-MS/MS on the same samples, we achieved precisions of ∼±0.0007 on 100 μm spots, which is worse than TIMS but is still more than sufficient to resolve the isotopic variations previously documented, especially given that many laser spots can be measured on a single sample, which can help improve statistics. We have analyzed several transects along two single plagioclase crystals (a cloudy core grain and a clear grain) from the 26.5 ka Oruanui supereruption (Fig. 13). The cloudy core grain shows the same An profile as those previously documented by Charlier et al.11 The 87Sr/86Sr ratio shows limited variation, but this could be a matter of grain selection as previous data showed significant grain-to-grain variability. In the grain that we analyzed, the cloudy core has an 87Sr/86Sr ratio that is close to the bulk rock value (∼0.7054), while the overgrowth and euhedral rims extend to more radiogenic values of around (∼0.7060). This is not readily visible when plotting the two transects on the cloudy core grain individually, as one transect contains mostly cloudy core data points (t3–t4; Fig. 13F), while the other contains primarily overgrowth rim data points (t5–t6; Fig. 13G). This is clearly seen, however when plotting the distribution of 87Sr/86Sr ratios in each zone in the form of a kernel density estimate (Fig. 13C). In the clear plagioclase grain, we see no resolvable 87Sr/86Sr variation (Fig. 13H). Overall, this study shows that while the precision of LA-MC-ICP-MS/MS is not as good as TIMS, which has a better useful yield than LA-MC-ICP-MS/MS for Sr (1.5% (ref. 97) vs. 0.25%), the precision is still sufficient to detect magma mixing and assimilation based on in situ87Sr/86Sr isotopic analyses.
 |
| | Fig. 13
In situ Sr isotopic analysis of a cloudy core (A and B) and a clear (D) plagioclase grains from the 26.5 ka Oruanui eruption, New Zealand. Similar grains were previously studied by Charlier et al.11 using micromilling followed by TIMS isotopic analysis. c, o, and e in the various panels correspond to cloudy core, overgrowth rim, and euhedral rim, respectively. The cloudy core in (A) and (B) contains exsolved rutile. The overgrowth rim has higher An content than the euhedral rim and much of the cloudy core (E). Two transects measured across the cloudy feldpar (t3–t4 in panel (F) and t5–t6 in panel (G)) give 87Sr/86Sr isotopic compositions that are almost uniform but in detail, the 87Sr/86Sr ratio of the cloudy core seems to be more tightly clustered than the overgrowth and euhedral rims, which extend to more radiogenic values ((C) PDF stands for probability density function, calculated using a kernel density estimate). The clear feldspar grain has uniform 87Sr/86Sr isotopic composition (H). The grey bars in (C), (F), and (H) represents the range of 87Sr/86Sr values determined from individual pumice clasts in the Oruanui rhyolite.112 Given the young ages and relatively low 87Rb/86Sr ratios of the grains, radiogenic ingrowth of 87Sr after eruption can be neglected. | |
4.3. Meteoritic hibonite inclusions
Hibonite is a highly refractory mineral found as inclusions in primitive meteorites (nominally CaAl12O19 but with some minor element substitutions, predominantly 2Al3+ ↔ Mg2+ + Ti4+), notably in the CM carbonaceous chondrite group.98–100 These hibonite inclusions are classified into several subgroups depending on their morphologies and mineral associations (PLAty-hibonite Crystals = PLACs, Spinel-HIBonite inclusions = SHIBs, Blue AGgregates = BAGs). Hibonite inclusions have unusual isotopic traits among meteoritic materials. Those of the PLACs variety often display large 48Ca and 50Ti anomalies, yet did not incorporate any of the short-lived nuclide 26Al (t1/2 = 0.7 Ma).98,101–105 SHIBs are less exotic in their compositions and are more akin to large refractory inclusions also found in some carbonaceous chondrites, with absent or more subdued isotopic anomalies and near canonical initial 26Al/27Al ratio of 5 × 10−5.98,101,104,106,107 We analyzed the Sr isotopic composition of seven hibonite-rich and spinel-hibonite inclusions that were separated from the CM2 chondrite Murchison and were previously investigated for their O, Ti, and Ca isotopic compositions as well as 26Al–26Mg systematics.105,106 They range in size between ∼40 and 100 μm and comprise 5 PLAC-like samples and 2 SHIBs. All the 5 PLAC-like samples have nondetectable initial 26Al/27Al ratios, consistent with their formation either (i) early in a region of the solar nebula that had not incorporated 26Al, or (ii) less likely late after 26Al-decay. Most samples have normal (near-terrestrial) 48Ca and 50Ti isotopic compositions except for one (HIB1-5-3) that shows anomalous deficits for these isotopes of ∼−0.4% (40 ε-units).105 PLACs and SHIBs contain ∼20–100 and 50–200 ppm Sr, respectively99,100 and are devoid of Rb. Our motivation for measuring the Sr isotopic compositions of hibonite inclusions was to search for possible isotopic anomalies108 and compare the 87Sr/86Sr ratios with the known solar system initial ratio (0.69876 ± 0.00002;109 0.69883 ± 0.00002;110 0.698784 ± 0.000076 (ref. 97)). Given the small size and refractory nature of hibonite inclusions, we changed the laser beam spot to 35 μm and the repetition rate to 12 Hz. The signal remained approximately constant during the ablation, suggesting that the laser did not couple well with the sample and no laser-spot deepening effect happened. All hibonite inclusions have 87Sr/86Sr ratios close to the solar system initial (Fig. 14). Platy hibonite HIB1-5-3, which has 0.4% excesses in 48Ca and 50Ti has a 1.4% excess in 87Sr relative to the solar initial. Similar 87Sr excesses are found in other hibonite grains with normal 48Ca and 50Ti. Examination of the BSE image of HIB1-5-3 shows that it is somewhat porous and appears to have some Rb-bearing Murchison matrix in the pores, which might explain its high 87Sr/86Sr ratio. The 1.4% 87Sr excess in HIB1-5-3 is therefore unlikely to be of nucleosynthetic origin.
 |
| | Fig. 14
87Sr/86Sr isotopic compositions of hibonite inclusions extracted from the Murchison CM carbonaceous chondrite. The solid horizontal line is the solar system initial value (0.69876 ± 0.00002 (ref. 109) 0.69883 ± 0.00002 (ref. 110)). Hibonite inclusions are ultra-refractory and formed at the birth of the solar system with very low Rb/Sr. As expected, we find that they have 87Sr/86Sr ratios close to the solar system initial. The slightly more radiogenic compositions in some of them are most likely due to incorporation of Rb from the matrix of Murchison. | |
5. Conclusion
We present methodologies for in situ analysis and reduction of 87Rb–87Sr data acquired by LA-MC-ICP-MS/MS. The use of a double Wien mass filter combined with fluorination in a hexapole collision/reaction cell make it possible to measure 87Sr/86Sr ratios in samples with elevated 87Rb/87Sr ratios. Laser ablation data reduction is done with a Mathematica-based graphical user interface software named LASr. Instrumental fractionation is dealt with by bracketing sample by standard measurements. We derive formulas to propagate all uncertainties and their correlations for 87Rb/86Sr and 87Sr/86Sr ratios. We have measured several standards (Durango apatite, SRM610, SRM612, feldspar glasses) to show that the data were accurate. Measurement uncertainty calculated from repeat laser ablation data agrees with expectations for Johnson noise and counting statistics. For the same amount of Sr consumed, the data generated by LA-MC-ICP-MS/MS are less precise than those obtainable by TIMS, but the measurements are less destructive and sample throughput is higher. LA-MC-ICP-MS/MS is thus very well suited to analyze small and precious samples, to tackle questions that require knowledge and preservation of petrographic context, and to examine population characteristics. We have used the Neoma MS/MS on several applications to showcase its unique capabilities. We present in situ87Rb–87Sr data of the Martian polymict breccia NWA 7034 (Black Beauty) that resolve a long-standing problem in the chronology of this sample. We show that K-rich feldspar define a clear 2.2 Ga age, which most likely reflects the age of lithification for this sample. The younger 1.4 Ga 40Ar/39Ar ages most likely reflect later resetting by an impact that was too short-lived or did not reach a sufficient temperature to reset the 87Rb–87Sr chronometer. This result demonstrates the usefulness of this technique for dating precious extraterrestrial samples, such as the ones that will be collected from Phobos by the MMX mission,92,93 or those that are now being collected by the Perseverance rover on Mars in the Jezero crater.87,88
Conflicts of interest
The authors declare the following competing financial interest(s): Dr Grant Craig, Dr Claudia Bouman, Dr Nicholas Lloyd, Dr Darren Tollstrup, Dr Johannes Schwieters are employed by Thermo Fisher Scientific (Bremen) GmbH.
Acknowledgements
The section of NWA 7034 was provided by the Robert A. Pritzker Center for Meteoritics and Polar Studies of the Field Museum of Natural History enabled by a generous donation from Jay Piatek. We thank the TAWANI Foundation for funding the Robert A. Pritzker Center that enabled part of this work. Constructive criticisms from four anonymous reviewers helped improve the quality of the manuscript. We thank Frank Vanhaecke for his support during editorial handling. This work was supported by NASA grants NNX17AE86G (LARS), 80NSSC17K0744 (HW), 000306-002 (HW), 80NSSC21K0380 (EW), 0995GXB174 (EW), NSF grant EAR-2001098 (CSEDI), and funding from DOE to N. D.
References
- P. Boehnke and T. M. Harrison, Int. Geol. Rev., 2014, 56, 905–914 CrossRef.
- I. M. Villa, P. De Bièvre, N. Holden and P. Renne, Geochim. Cosmochim. Acta, 2015, 164, 382–385 CrossRef CAS.
-
A. P. Dickin, Radiogenic Isotope Geology, Cambridge University Press, 2018 Search PubMed.
- P. Boehnke, E. A. Bell, T. Stephan, R. Trappitsch, C. B. Keller, O. S. Pardo, A. M. Davis, T. M. Harrison and M. J. Pellin, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 6353–6356 CrossRef CAS PubMed.
- R. B. Emo, M. A. Smit, M. Schmitt, E. Kooijman, E. E. Scherer, P. Sprung, W. Bleeker and K. Mezger, Geochim. Cosmochim. Acta, 2018, 235, 450–462 CrossRef CAS.
- A. Zindler and S. R. Hart, Annu. Rev. Earth Planet. Sci., 1986, 14, 493–571 CrossRef CAS.
- N. Flament, N. Coltice and P. F. Rey, Precambrian Res., 2013, 229, 177–188 CrossRef CAS.
- J. Veizer and W. Compston, Geochim. Cosmochim. Acta, 1976, 40, 905–914 CrossRef CAS.
- M. T. McCulloch and V. C. Bennett, Geochim. Cosmochim. Acta, 1994, 58, 4717–4738 CrossRef CAS.
- D. J. DePaolo, J. Petrol., 1985, 26, 925–951 CrossRef CAS.
- B. L. Charlier, C. J. Wilson and J. P. Davidson, Contrib. Mineral. Petrol., 2008, 156, 799–813 CrossRef CAS.
- F. Tepley, J. Davidson, R. Tilling and J. G. Arth, J. Petrol., 2000, 41, 1397–1411 CrossRef CAS.
- H. P. Taylor Jr, Earth Planet. Sci. Lett., 1980, 47, 243–254 CrossRef.
- D. J. DePaolo, Earth Planet. Sci. Lett., 1981, 53, 189–202 CrossRef CAS.
- T. L. Grove, D. C. Gerlach and T. W. Sando, Contrib. Mineral. Petrol., 1982, 80, 160–182 CrossRef CAS.
- A. N. Halliday and D. Porcelli, Earth Planet. Sci. Lett., 2001, 192, 545–559 CrossRef CAS.
- U. Hans, T. Kleine and B. Bourdon, Earth Planet. Sci. Lett., 2013, 374, 204–214 CrossRef CAS.
- L. E. Borg, G. A. Brennecka and T. S. Kruijer, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2115726119 CrossRef CAS PubMed.
- J. Veizer, Annu. Rev. Earth Planet. Sci., 1989, 17, 141–167 CrossRef CAS.
- J. M. McArthur, R. Howarth and T. Bailey, J. Geol., 2001, 109, 155–170 CrossRef CAS.
- B. P. Kennedy, A. Klaue, J. D. Blum, C. L. Folt and K. H. Nislow, Can. J. Fish. Aquat. Sci., 2002, 59, 925–929 CrossRef.
- B. L. Beard and C. M. Johnson, J. Forensic Sci., 2000, 45, 1049–1061 CAS.
- A. J. E. Pryor, T. Insoll and L. Evis, Sci. Technol. Archaeol. Res., 2020, 6, 113–136 Search PubMed.
- K. J. Knudson, T. D. Price, J. E. Buikstra and D. E. Blom, Archaeometry, 2004, 46, 5–18 CrossRef CAS.
- T. D. Price, G. Grupe and P. Schröter, Appl. Geochem., 1994, 9, 413–417 CrossRef CAS.
- K. J. Knudson, S. R. Williams, R. Osborn, K. Forgey and P. R. Williams, J. Anthropol. Archaeol., 2009, 28, 244–257 CrossRef.
- E. K. Thornton, S. D. DeFrance, J. Krigbaum and P. R. Williams, Int. J. Osteoarchaeol., 2011, 21, 544–567 CrossRef.
- K. H. Wedepohl and A. Baumann, Naturwissenschaften, 2000, 87, 129–132 CrossRef CAS PubMed.
- I. C. Freestone, K. Leslie, M. Thirlwall and Y. Gorin-Rosen, Archaeometry, 2003, 45, 19–32 CrossRef CAS.
- S. Seman, L. Dussubieux, C. Cloquet and T. O. Pryce, Archaeometry, 2021, 63, 88–104 CrossRef CAS.
- B. L. Charlier, C. Ginibre, D. Morgan, G. M. Nowell, D. Pearson, J. P. Davidson and C. Ottley, Chem. Geol., 2006, 232, 114–133 CrossRef CAS.
- J. N. Christensen, A. N. Halliday, D.-C. Lee and C. M. Hall, Earth Planet. Sci. Lett., 1995, 136, 79–85 CrossRef CAS.
- J. Davidson, F. Tepley III, Z. Palacz and S. Meffan-Main, Earth Planet. Sci. Lett., 2001, 184, 427–442 CrossRef CAS.
- M. Bizzarro, A. Simonetti, R. K. Stevenson and S. Kurszlaukis, Geochim. Cosmochim. Acta, 2003, 67, 289–302 CrossRef CAS.
- F. C. Ramos, J. A. Wolff and D. L. Tollstrup, Chem. Geol., 2004, 211, 135–158 CrossRef CAS.
- J. Woodhead, S. Swearer, J. Hergt and R. Maas, J. Anal. At. Spectrom., 2005, 20, 22–27 RSC.
- P. Z. Vroon, B. Van Der Wagt, J. M. Koornneef and G. R. Davies, Anal. Bioanal. Chem., 2008, 390, 465–476 CrossRef CAS PubMed.
- J. Fietzke, V. Liebetrau, D. Günther, K. Gürs, K. Hametner, K. Zumholz, T. H. Hansteen and A. Eisenhauer, J. Anal. At. Spectrom., 2008, 23, 955–961 RSC.
- J. Irrgeher, P. Galler and T. Prohaska, Spectrochim. Acta, Part B, 2016, 125, 31–42 CrossRef CAS.
- S. F. Anderson, J. Levine and T. J. Whitaker, Rapid Commun. Mass Spectrom., 2015, 29, 1457–1464 CrossRef PubMed.
- S. F. Anderson, J. Levine and T. J. Whitaker, Rapid Commun. Mass Spectrom., 2015, 29, 191–204 CrossRef PubMed.
- G. K. Nicolussi, M. J. Pellin, R. S. Lewis, A. M. Davis, R. N. Clayton and S. Amari, Phys. Rev. Lett., 1998, 81, 3583 CrossRef CAS.
- T. Stephan, R. Trappitsch, A. M. Davis, M. J. Pellin, D. Rost, M. R. Savina, R. Yokochi and N. Liu, Int. J. Mass Spectrom., 2016, 407, 1–15 CrossRef CAS.
- T. Zack and K. J. Hogmalm, Chem. Geol., 2016, 437, 120–133 CrossRef CAS.
- L. Gorojovsky and O. Alard, J. Anal. At. Spectrom., 2020, 35, 2322–2336 RSC.
- L. Balcaen, E. Bolea-Fernandez, M. Resano and F. Vanhaecke, Anal. Chim. Acta, 2015, 894, 7–19 CrossRef CAS PubMed.
- L. J. Moens, F. F. Vanhaecke, D. R. Bandura, V. I. Baranov and S. D. Tanner, J. Anal. At. Spectrom., 2001, 16, 991–994 RSC.
- E. Bolea-Fernandez, S. J. M. Van Malderen, L. Balcaen, M. Resano and F. Vanhaecke, J. Anal. At. Spectrom., 2016, 31, 464–472 RSC.
- K. J. Hogmalm, T. Zack, A. K. O. Karlsson, A. S. L. Sjöqvist and D. Garbe-Schönberg, J. Anal. At. Spectrom., 2017, 32, 305–313 RSC.
- P. Cheng, G. K. Koyanagi and D. K. Bohme, Anal. Chim. Acta, 2008, 627, 148–153 CrossRef CAS PubMed.
- D. Bevan, C. D. Coath, J. Lewis, J. Schwieters, N. Lloyd, G. Craig, H. Wehrs and T. Elliott, J. Anal. At. Spectrom., 2021, 36, 917–931 RSC.
- G. Craig, H. Wehrs, D. G. Bevan, M. Pfeifer, J. Lewis, C. D. Coath, T. Elliott, C. Huang, N. S. Lloyd and J. B. Schwieters, Anal. Chem., 2021, 93, 10519–10527 CrossRef CAS PubMed.
- D. Rösel and T. Zack, Geostand. Geoanal. Res., 2021, 46, 143–168 CrossRef.
- W. Wien, Ann. Phys., 1898, 301, 440–452 CrossRef.
- I. Kroslakova and D. Günther, J. Anal. At. Spectrom., 2007, 22, 51–62 RSC.
- J. Meija, T. B. Coplen, M. Berglund, W. A. Brand, P. De Bièvre, M. Gröning, N. E. Holden, J. Irrgeher, R. D. Loss and T. Walczyk, Pure Appl. Chem., 2016, 88, 293–306 CrossRef CAS.
- A. O. Nier, Phys. Rev., 1938, 54, 275 CrossRef CAS.
- L. J. Moore, T. J. Murphy, I. L. Barnes and P. J. Paulsen, J. Res. Natl. Bur. Stand., 1982, 87, 1 CrossRef CAS PubMed.
- F.-Z. Teng, N. Dauphas and J. M. Watkins, Rev. Mineral. Geochem., 2017, 82, 1–26 CrossRef CAS.
- J. D. Woodhead and J. M. Hergt, Geostand. Newsl., 2001, 25, 261–266 CrossRef CAS.
- J. Davidson and M. Wilson, J. Petrol., 2011, 52, 1493–1531 CrossRef CAS.
- N. Dauphas, J. H. Chen, J. Zhang, D. A. Papanastassiou, A. M. Davis and C. Travaglio, Earth Planet. Sci. Lett., 2014, 407, 96–108 CrossRef CAS.
- P. Vermeesch, Geosci. Front., 2018, 9, 1479–1493 CrossRef CAS.
- Y.-H. Yang, F.-Y. Wu, J.-H. Yang, D. M. Chew, L.-W. Xie, Z.-Y. Chu, Y.-B. Zhang and C. Huang, Chem. Geol., 2014, 385, 35–55 CrossRef CAS.
- H. Tang and N. Dauphas, Earth Planet. Sci. Lett., 2012, 359, 248–263 CrossRef.
- M. R. Lee, K. A. Waldron and I. Parsons, Mineral. Mag., 1995, 59, 63–78 CrossRef CAS.
- J. Davidson, B. Charlier, J. M. Hora and R. Perlroth, Geology, 2005, 33, 29–32 CrossRef CAS.
-
C. Rundle, Review and Assessment of Isotopic Ages from the English Lake District, British Geological Survey, 1992 Search PubMed.
- M. Humayun, A. Nemchin, B. Zanda, R. H. Hewins, M. Grange, A. Kennedy, J. P. Lorand, C. Göpel, C. Fieni and S. Pont, Nature, 2013, 503, 513–516 CrossRef CAS PubMed.
- C. B. Agee, N. V. Wilson, F. M. McCubbin, K. Ziegler, V. J. Polyak, Z. D. Sharp, Y. Asmerom, M. H. Nunn, R. Shaheen and M. H. Thiemens, Science, 2013, 339, 780–785 CrossRef CAS PubMed.
- A. R. Santos, C. B. Agee, F. M. McCubbin, C. K. Shearer, P. V. Burger, R. Tartèse and M. Anand, Geochim. Cosmochim. Acta, 2015, 157, 56–85 CrossRef CAS.
- F. M. McCubbin, J. W. Boyce, T. Novák-Szabó, A. R. Santos, R. Tartèse, N. Muttik, G. Domokos, J. Vazquez, L. P. Keller and D. E. Moser, J. Geophys. Res.: Planets, 2016, 121, 2120–2149 CrossRef CAS.
- A. Wittmann, R. L. Korotev, B. L. Jolliff, A. J. Irving, D. E. Moser, I. Barker and D. Rumble III, Meteorit. Planet. Sci., 2015, 50, 326–352 CrossRef CAS.
- M. M. Costa, N. K. Jensen, L. C. Bouvier, J. N. Connelly, T. Mikouchi, M. S. Horstwood, J.-P. Suuronen, F. Moynier, Z. Deng and A. Agranier, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 30973–30979 CrossRef CAS PubMed.
-
Q.-Z. Yin, F. M. McCubbin, Q. Zhou, A. R. Santos, R. Targese, X. Li, Q. Li, Y. Liu, G. Tang, J. W. Boyce, Y. Lin, W. Yang, J. Zhang, J. Hao, S. M. Elardo, C. K. Shearer, D. J. Rowland, M. Lerche and C. B. Agee, 45th Lunar and Planetary Science Conference, 2014, abstract #1320 Search PubMed.
- S. Hu, Y. Lin, J. Zhang, J. Hao, W. Xing, T. Zhang, W. Yang and H. Changela, Meteorit. Planet. Sci., 2019, 54, 850–879 CrossRef CAS.
- L. C. Bouvier, M. M. Costa, J. N. Connelly, N. K. Jensen, D. Wielandt, M. Storey, A. A. Nemchin, M. J. Whitehouse, J. F. Snape and J. J. Bellucci, Nature, 2018, 558, 586–589 CrossRef CAS PubMed.
- W. S. Cassata, B. E. Cohen, D. F. Mark, R. Trappitsch, C. A. Crow, J. Wimpenny, M. R. Lee and C. L. Smith, Sci. Adv., 2018, 4, eaap8306 CrossRef PubMed.
- L. E. Nyquist, C. Y. Shih, F. M. McCubbin, A. R. Santos, C. K. Shearer, Z. X. Peng, P. V. Burger and C. B. Agee, Meteorit. Planet. Sci., 2016, 51, 483–498 CrossRef CAS.
- J. A. Cartwright, U. Ott, S. Herrmann and C. B. Agee, Earth Planet. Sci. Lett., 2014, 400, 77–87 CrossRef CAS.
- F. N. Lindsay, J. S. Delaney, C. Göpel, G. F. Herzog, R. Hewins, M. Humayun, K. Nagao, L. E. Nyquist, J. Park and J. B. Setera, Meteorit. Planet. Sci., 2021, 56, 515–545 CrossRef CAS.
- P. C. Stephenson, Y. Lin and I. Leya, Meteorit. Planet. Sci., 2017, 52, 2505–2520 CrossRef CAS.
- N. Dauphas, N. X. Nie, M. Blanchard, Z. J. Zhang, H. Zeng, J. Y. Hu, M. Meheut, C. Visscher, R. Canup and T. Hopp, Planet. Sci. J., 2022, 3, 29 CrossRef.
-
J. Crank, The Mathematics of Diffusion, Oxford University Press, 1979 Search PubMed.
- B. J. Giletti, Geochim. Cosmochim. Acta, 1991, 55, 1331–1343 CrossRef CAS.
- D. J. Cherniak and E. B. Watson, Earth Planet. Sci. Lett., 1992, 113, 411–425 CrossRef CAS.
- K. A. Farley, K. H. Williford, K. M. Stack, R. Bhartia, A. Chen, M. de la Torre, K. Hand, Y. Goreva, C. D. Herd and R. Hueso, Space Sci. Rev., 2020, 216, 1–41 CrossRef.
- G. Kminek, M. A. Meyer, D. W. Beaty, B. L. Carrier, T. Haltigin and L. E. Hays, Astrobiology, 2022, 22, S-1–S-4 CrossRef PubMed.
- R.C. Wiens, A. Udry, O. Beyssac, C. Quantin-Nataf, N. Mangold, A. Cousin, L. Mandon, T. Bosak, O. Forni, S.M. McLennan and V. Sautter,
et al., Compositionally and density stratified igneous terrain in Jezero crater, Mars, Science Advances, 2022, 8(34), eabo3399 CrossRef CAS PubMed.
- A. E. Rubin, P. H. Warren, J. P. Greenwood, R. S. Verish, L. A. Leshin, R. L. Hervig, R. N. Clayton and T. K. Mayeda, Geology, 2000, 28, 1011–1014 CrossRef CAS.
- L. Nyquist, Y. Reese, H. Wiesmann, C.-Y. Shih and C. Schwandt, Meteorit. Planet. Sci. Suppl., 2000, 35, A121 Search PubMed.
- K. Kuramoto, Y. Kawakatsu, M. Fujimoto, A. Araya, M. A. Barucci, H. Genda, N. Hirata, H. Ikeda, T. Imamura and J. Helbert, Earth, Planets Space, 2022, 74, 1–31 CrossRef.
- T. Usui, K.-I. Bajo, W. Fujiya, Y. Furukawa, M. Koike, Y. N. Miura, H. Sugahara, S. Tachibana, Y. Takano and K. Kuramoto, Space Sci. Rev., 2020, 216, 1–18 CrossRef.
- M. Giuranna, T. Roush, T. Duxbury, R. Hogan, C. Carli, A. Geminale and V. Formisano, Planet. Space Sci., 2011, 59, 1308–1325 CrossRef.
- K. R. Ramsley and J. W. Head III, Planet. Space Sci., 2013, 87, 115–129 CrossRef.
- C. J. Wilson, J. Volcanol. Geotherm. Res., 2001, 112, 133–174 CrossRef.
- B. L. Charlier, F. L. Tissot, H. Vollstaedt, N. Dauphas, C. J. Wilson and R. T. Marquez, Sci. Adv., 2021, 7, eabf6222 CrossRef CAS PubMed.
- T. R. Ireland, Geochim. Cosmochim. Acta, 1988, 52, 2827–2839 CrossRef CAS.
- T. R. Ireland, A. Fahey and E. Zinner, Geochim. Cosmochim. Acta, 1988, 52, 2841–2854 CrossRef CAS.
- R. W. Hinton, A. M. Davis, D. E. Scatena-Wachel, L. Grossman and R. J. Draus, Geochim. Cosmochim. Acta, 1988, 52, 2573–2598 CrossRef CAS.
- T. R. Ireland, A. J. Fahey and E. K. Zinner, Geochim. Cosmochim. Acta, 1991, 55, 367–379 CrossRef CAS.
- M.-C. Liu, K. D. McKeegan, J. N. Goswami, K. K. Marhas, S. Sahijpal, T. R. Ireland and A. M. Davis, Geochim. Cosmochim. Acta, 2009, 73, 5051–5079 CrossRef CAS.
- M.-C. Liu, M. Chaussidon, C. Göpel and T. Lee, Earth Planet. Sci. Lett., 2012, 327, 75–83 CrossRef.
- A. J. Fahey, J. N. Goswami, K. D. McKeegan and E. K. Zinner, Astrophys. J., 1987, 323, L91–L95 CrossRef CAS.
- L. Kööp, A. M. Davis, D. Nakashima, C. Park, A. N. Krot, K. Nagashima, T. J. Tenner, P. R. Heck and N. T. Kita, Geochim. Cosmochim. Acta, 2016, 189, 70–95 CrossRef.
- L. Kööp, D. Nakashima, P. R. Heck, N. T. Kita, T. J. Tenner, A. N. Krot, K. Nagashima, C. Park and A. M. Davis, Geochim. Cosmochim. Acta, 2016, 184, 151–172 CrossRef.
- M.-C. Liu, J. Han, A. J. Brearley and A. Hertwig, Sci. Adv., 2019, 5, eaaw3350 CrossRef CAS PubMed.
- N. Dauphas and E. A. Schauble, Annu. Rev. Earth Planet. Sci., 2016, 44, 709–783 CrossRef CAS.
- C. M. Gray, D. A. Papanastassiou and G. J. Wasserburg, Icarus, 1973, 20, 213–239 CrossRef CAS.
- G. Wasserburg, F. Tera, D. Papanastassiou and J. Huneke, Earth Planet. Sci. Lett., 1977, 35, 294–316 CrossRef CAS.
- T. Yoshizaki and W. F. McDonough, Geochim. Cosmochim. Acta, 2020, 273, 137–162 CrossRef CAS.
- C. J. Wilson, S. Blake, B. Charlier and A. Sutton, J. Petrol., 2006, 47, 35–69 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Mathematica program for reduction of Rb–Sr laser ablation data (LASr). Excel spreadsheet containing all the laser ablation data reported here. Supplementary Fig. S1. See https://doi.org/10.1039/d2ja00135g |
| ‡ Now at Max Planck Institute for Solar System Research, Justus-von-Liebig-Weg 3, 37077 Göttingen, Germany. |
|
| This journal is © The Royal Society of Chemistry 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ab,
Timo
Hopp‡
*ab,
Timo
Hopp‡
 a,
Grant
Craig
a,
Grant
Craig
 c,
Zhe J.
Zhang
a,
Maria C.
Valdes
de,
Philipp R.
Heck
c,
Zhe J.
Zhang
a,
Maria C.
Valdes
de,
Philipp R.
Heck
 de,
Bruce L. A.
Charlier
de,
Bruce L. A.
Charlier
 f,
Elizabeth A.
Bell
g,
T. Mark
Harrison
g,
Andrew M.
Davis
be,
Laure
Dussubieux
h,
Patrick R.
Williams
h,
Michael J.
Krawczynski
i,
Claudia
Bouman
c,
Nicholas S.
Lloyd
f,
Elizabeth A.
Bell
g,
T. Mark
Harrison
g,
Andrew M.
Davis
be,
Laure
Dussubieux
h,
Patrick R.
Williams
h,
Michael J.
Krawczynski
i,
Claudia
Bouman
c,
Nicholas S.
Lloyd
 c,
Darren
Tollstrup
c and
Johannes B.
Schwieters
c
c,
Darren
Tollstrup
c and
Johannes B.
Schwieters
c
 , where q is the charge (1.6 × 10−19 C for singly charged ions), U is the acceleration voltage (−2000 V), and m is the isotopic mass (1.4 × 10−25 kg for 87Sr). The electrostatic force in the Wien filter is qEw, while the magnetic force is qvBw. When the magnetic and electrostatic forces are balanced (Ew = vBw), the ion trajectory remains undisturbed, which happens for ions of mass-to-charge ratio m/q = 2U(Bw/Ew)2. Ions with a different mass-to-charge ratio will fan out and collide with the adjustable aperture that separates the two Wien filters. By adjusting the ratio of Bw/Ew in the first Wien filter and the aperture opening, it is thus possible to permit the transmission of ions within a certain mass range. Those that pass through the aperture are bent back towards the central axis by the inversion lens and are recollimated using the second Wien filter (the values of Bw and Ew are the same as the first Wien filter). For Rb–Sr isotopic analyses, the ratio Bw/Ew and the aperture are adjusted to remove Ar+ and all atomic and molecular ion interferences in the SrF+ mass region (Fig. 1).
, where q is the charge (1.6 × 10−19 C for singly charged ions), U is the acceleration voltage (−2000 V), and m is the isotopic mass (1.4 × 10−25 kg for 87Sr). The electrostatic force in the Wien filter is qEw, while the magnetic force is qvBw. When the magnetic and electrostatic forces are balanced (Ew = vBw), the ion trajectory remains undisturbed, which happens for ions of mass-to-charge ratio m/q = 2U(Bw/Ew)2. Ions with a different mass-to-charge ratio will fan out and collide with the adjustable aperture that separates the two Wien filters. By adjusting the ratio of Bw/Ew in the first Wien filter and the aperture opening, it is thus possible to permit the transmission of ions within a certain mass range. Those that pass through the aperture are bent back towards the central axis by the inversion lens and are recollimated using the second Wien filter (the values of Bw and Ew are the same as the first Wien filter). For Rb–Sr isotopic analyses, the ratio Bw/Ew and the aperture are adjusted to remove Ar+ and all atomic and molecular ion interferences in the SrF+ mass region (Fig. 1).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)


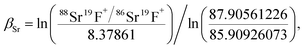

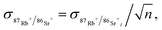
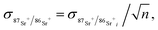

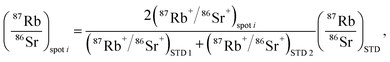




 and
and  . This is done using the delta method. The gradient matrix of g is,
. This is done using the delta method. The gradient matrix of g is,

 ,
,



 and correlation coefficients ρX,Y = Cov(X,Y)/(σXσY) as inputs in isochron calculations. The equations above can be reformulated with those notations and we have,
and correlation coefficients ρX,Y = Cov(X,Y)/(σXσY) as inputs in isochron calculations. The equations above can be reformulated with those notations and we have,
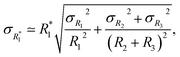


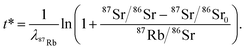


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 correlations. The reference values for SRM612, Durango apatite, Feldspar glasses I and L2 are from Woodhead and Hergt,60 Yang et al.,64 and Davidson et al.33
1 correlations. The reference values for SRM612, Durango apatite, Feldspar glasses I and L2 are from Woodhead and Hergt,60 Yang et al.,64 and Davidson et al.33
 , and
, and  . The uncertainties associated with counting statistics and Johnson noise during a cycle (blank or sample) are,
. The uncertainties associated with counting statistics and Johnson noise during a cycle (blank or sample) are,













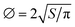 with S the surface area). The grains range in equivalent diameter between 111 and 460 μm. We calculated model ages for each grain by taking the slope of the lines defined by individual data points and the all-points isochron intercept (eqn (22) and (23)). This allows us to test if smaller grains have been more easily disturbed and give a different age than larger grains. We plot in Fig. 12 the 2-point model age for each spot against the diameter of the target grain. As shown, there is no relationship between the two and the data define a slope dt/da = −1.6 ± 2.2 Ma μm−1 (a is the radius in μm) that is indistinguishable from 0. Individual spot analyses are consistent with an 87Rb–87Sr age of ∼2.2 Ga and there is no indication of resetting at 1.4 Ga even for the smaller grains. Lindsay et al.81 calculated the temperature–time conditions needed for radiogenic 40Ar to be lost and 40Ar/39Ar ages to be reset at 1.4 Ga in K-rich feldspar. Their estimate that heating was short-lived, ranging between ∼5 h at 1000 °C and 10 year at 500 °C is likely to be a minimum as they did not account for the discrete distribution of diffusion domain sizes apparent in the degassing of virtually all their samples. We can estimate the effect that such heating events would have on Sr isotopes by modeling diffusive Sr isotope exchange between the interior of feldspar grains containing radiogenic 87Sr and the surrounding medium. For each grain, we model that process as diffusion in a sphere starting with uniform composition, with the composition at its surface kept at a constant value set by the surrounding medium. All nonradiogenic Sr isotopes are assumed to remain unchanged during the transient heating event. The equation governing the evolution of the 87Sr/86Sr ratio in the grain with time is,84
with S the surface area). The grains range in equivalent diameter between 111 and 460 μm. We calculated model ages for each grain by taking the slope of the lines defined by individual data points and the all-points isochron intercept (eqn (22) and (23)). This allows us to test if smaller grains have been more easily disturbed and give a different age than larger grains. We plot in Fig. 12 the 2-point model age for each spot against the diameter of the target grain. As shown, there is no relationship between the two and the data define a slope dt/da = −1.6 ± 2.2 Ma μm−1 (a is the radius in μm) that is indistinguishable from 0. Individual spot analyses are consistent with an 87Rb–87Sr age of ∼2.2 Ga and there is no indication of resetting at 1.4 Ga even for the smaller grains. Lindsay et al.81 calculated the temperature–time conditions needed for radiogenic 40Ar to be lost and 40Ar/39Ar ages to be reset at 1.4 Ga in K-rich feldspar. Their estimate that heating was short-lived, ranging between ∼5 h at 1000 °C and 10 year at 500 °C is likely to be a minimum as they did not account for the discrete distribution of diffusion domain sizes apparent in the degassing of virtually all their samples. We can estimate the effect that such heating events would have on Sr isotopes by modeling diffusive Sr isotope exchange between the interior of feldspar grains containing radiogenic 87Sr and the surrounding medium. For each grain, we model that process as diffusion in a sphere starting with uniform composition, with the composition at its surface kept at a constant value set by the surrounding medium. All nonradiogenic Sr isotopes are assumed to remain unchanged during the transient heating event. The equation governing the evolution of the 87Sr/86Sr ratio in the grain with time is,84
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e−E/(RT), with R the gas constant (8.3145 J K−1 mol−1), D0 = 10 μm2 s−1 and E = 167
e−E/(RT), with R the gas constant (8.3145 J K−1 mol−1), D0 = 10 μm2 s−1 and E = 167![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 J mol−1.85 We use the diffusivity measured by Giletti et al.85 rather than the one measured by Cherniak and Watson,86 as the former were self-diffusion experiments relying on Sr isotopic analyses as opposed to chemical diffusion. Self-diffusion data should be more relevant to the 87Rb–87Sr resetting scenario investigated here. We calculate below how the heating event that reset the 40Ar/39Ar system at a time th before present, could have influenced the isochron relationship if the Sr isotopic compositions of the grains were partially equilibrated with the surrounding medium but the Rb/Sr remained unaffected.
000 J mol−1.85 We use the diffusivity measured by Giletti et al.85 rather than the one measured by Cherniak and Watson,86 as the former were self-diffusion experiments relying on Sr isotopic analyses as opposed to chemical diffusion. Self-diffusion data should be more relevant to the 87Rb–87Sr resetting scenario investigated here. We calculate below how the heating event that reset the 40Ar/39Ar system at a time th before present, could have influenced the isochron relationship if the Sr isotopic compositions of the grains were partially equilibrated with the surrounding medium but the Rb/Sr remained unaffected.