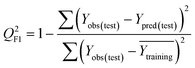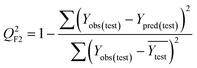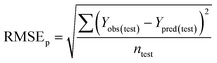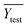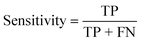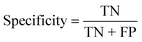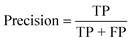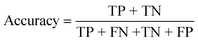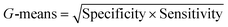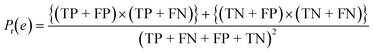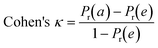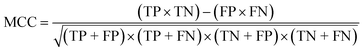A novel quantitative read-across tool designed purposefully to fill the existing gaps in nanosafety data†
Mainak
Chatterjee
a,
Arkaprava
Banerjee
a,
Priyanka
De
a,
Agnieszka
Gajewicz-Skretna
 b and
Kunal
Roy
b and
Kunal
Roy
 *a
*a
aDrug Theoretics and Cheminformatics Laboratory, Department of Pharmaceutical Technology, Jadavpur University, Kolkata 700032, India. E-mail: kunalroy_in@yahoo.com; kunal.roy@jadavpuruniversity.in; Fax: +91 33 2837 1078; Tel: +91 98315 94140
bLaboratory of Environmental Chemometrics, Faculty of Chemistry, University of Gdansk, Wita Stwosza 63, 80-308 Gdansk, Poland
First published on 25th November 2021
Abstract
In the current time, the number of various engineered nanomaterials (NMs) and nanoparticles (NPs) is increasing at a steady pace due to the new developments in the field of nanotechnology. These rapid uses of NPs are allowing their entry into the environment and human body also. The small size and large surface area of these materials enhance the potential to pass through the living plasma membrane and hence create possibilities to interact with various intracellular materials. The negative impact of NPs towards human health and environmental safety has already been established. The laboratory experimentations are troublesome and ethically complicated; thus, various computational techniques (e.g., quantitative read-across predictions) are very crucial for data gap filling and risk assessments, especially in view of the limited experimental data being available. In the current study, we propose a new quantitative read-across methodology for predicting the toxicity (biological activity in general) of newly synthesized NPs based on the similarity (Euclidean distance-based similarity, Gaussian kernel function similarity, Laplacian kernel function similarity) with structural analogues. These new methods are successfully validated against three published nanotoxicity datasets. The quality of predictions depends on the selection of the distance threshold, similarity threshold, and the number of most similar training compounds. In the current study, best predictions were obtained after selecting 0.4–0.5 as the distance threshold, 0.00–0.05 as the similarity threshold, and 2–5 as the number of most similar training compounds. After toxicity prediction of test set compounds, the external validation metrics such as Q2ext_F1, Q2ext_F2, RMSEP were calculated. The computed metric values clearly indicate the efficiency of the new read-across method and accuracy of the generated data by the proposed algorithm. A java based program (available at https://sites.google.com/jadavpuruniversity.in/dtc-lab-software/home) has also been developed based on the proposed algorithm which can effectively predict the toxicity of unknown NPs after providing the structural information of chemical analogues. Therefore, the new algorithm and the program can be used for the data gap filling, prioritizing existing and new NPs, and in a nutshell for the risk assessments of NPs.
Environmental significanceThe widespread use of nanoparticles in various fields of the society enhances the quality of human life; however, at the same time, the nanoparticle contaminants penetrate into the environment also. Various scientific communities are working on the risk assessment of nanoparticles in order to control their negative impacts on human health and environmental safety. Experimental toxicity studies are costly and troublesome; thus, the use of in silico approaches is increasing. In this study, a read-across based algorithm has been developed and proved to be an efficient method for nanotoxicity prediction for small datasets. A java based computer program has also been developed and reported. The proposed algorithm and the program are providing more accurate predictions than previously published reports, and hence can be an efficient tool for better risk assessment of nanoparticles. |
Introduction
Driven by a desire for efficient and sustainable strategies aimed at filling data and knowledge gaps on occupational safety and health risks associated with manufacturing and using engineered nanomaterials, in recent years, research institutions across academia and industry, as well as policy-making authorities, have made collaborative multi-sectoral efforts to develop and implement new approach methodologies (NAMs) for assessing nanoparticle toxicity.1 NAMs by definition include in vitro, in chemico, or in silico methods that aim to support hazard assessment, improve understanding of toxic effects and reduce animal tests or replace them entirely with advanced animal-free testing approaches. NAMs can be used individually, but they may also be used in combination with other NAMs and/or in vivo data forming so-called multi-modal NAMs (so-called integrated approaches).1–3Among a wide range of alternative non-testing approaches for safety evaluation of chemicals (including nanoparticles), the in silico modeling NAMs are viewed as a promising starting point for filling the existing gaps in (nano)safety data. These computer-aided methods comprise structural alerts, grouping, read-across and quantitative structure–activity relationship (QSARs) approaches. QSAR being a statistical fitting approach requires a considerable number of data points for acceptable degrees of freedom. In case, the number of experimental data points is limited, the derived QSAR models may be statistically unreliable. As recently pointed out by the European Chemicals Agency4 and some authors,5 read-across is one of the most widely used alternative tools for hazard assessment, aimed at filling data gaps. Read-across not being a hardcore statistical approach, read-across based predictions appear to be more appropriate for small data sets. This is mainly (although not exclusively) because read-across methods, unlike the QSAR approach, require less empirical data to perform reliable and accurate predictions used for filling data gaps. This is particularly important in the area of nanosafety, given that limited amount of high-quality nanotoxicological data are currently available. Some previous studies on prediction of nanotoxicity have been enlisted in Table 1 from which the readers can get an idea about the predictive methods used for nanotoxicity predictions nowadays.| Author | Method | System | Data points | End points | Application |
|---|---|---|---|---|---|
| QSAR: quantitative structure–activity relationship; QRAPC: quantitative read-across based on principal component analysis; MeOx NPs: metal oxide nanoparticles; EC50: median effective concentration; LC50: median lethal concentration. | |||||
| Cao, J. et al.6 | QSAR | MeOx NPs | 21 | LC50 | Assessment of cytotoxicity against human lung adenocarcinoma (A549) |
| Kotzabasaki, M. et al.7 | Classification based nano-QSAR | Superparamagnetic iron oxide nanoparticles (SPIONs) | 16 | Cell viability | Prediction of toxicological properties of superparamagnetic iron oxide nanoparticles (SPIONs) |
| Roy, K. et al.8 | QSAR | MeOx NPs (hydroxide) | 25 | Release of lactate dehydrogenase (ldhR) from the cell | Assessment of cytotoxicity of MeOx NPs |
| Sifonte, E. P. et al.9 | QSAR | MeOx NPs | 16 | 1/LC50 | Assessment of toxicity of MeOx NPs against human keratinocyte cell |
| Varsou, D.-D. et al.10 | Read-across based classification model | MeOx NPs | 11 | Acute toxicity | Predicting acute toxicity of freshly dispersed versus medium-aged NMs |
| Gajewicz, A. et al.11 | QRAPC | MeOx NPs | <20 | LC50, EC50 | Environmental hazard and risk assessment |
The basic idea behind the read-across concept is the extrapolation of the outcome of hazard identification from one or more data-rich source chemical(s) to other – one or more – target chemical(s) that are considered similar to the source and for which safety data are missing.12 To date, several strategies and a variety of read-across algorithms, models, and tools have been devised.11–20 Current trends in read-across methodology comprise using one of the following schemes: (1) the worst-case scenario by taking the most conservative value among the source chemicals; (2) averaging approach; (3) similarity-weighted activity of nearest neighbors; (4) filtering approach and (5) search expansion approach.21–25 The plurality of the existing approaches might be rationalized by the fact that read-across at a first glance may seem relatively straightforward, even simple. However, as recently pointed out by Ball et al.,12 the application of read-across is often subjective. Consequently, the reliability and reproducibility of read-across models, and thereby the uncertainties associated with model predictions strongly depend on the choice of modeling scheme and the expert's experience and expertise in performing the in silico modeling.20 In recent years, several initiatives have been launched to identify the opportunities for making read-across approaches more robust (i.e. less uncertainty sensitive), and more available to a wider array of stakeholder bodies, including experts and decision-makers.21–25 Unfortunately, despite broad consultations at the international level, the existing guidance documents for NAMs-based read-across do not provide clear support and tailored recommendations on how to use and report read-across predictions, or how to address the various facets of uncertainty for read-across. The lack of transparency in currently available algorithms and practical examples remain the largest obstacles and bottlenecks hindering the implementation and regulatory acceptance of read-across approach. Hence, the next step towards the widespread public acceptance and regulatory approval of read-across as an alternative technique to animal testing for (nano)toxicity evaluation would be to build confidence in the use of a well-justified, appropriately validated, and scientifically sound read-across approach.1
In view of this, the aims of this study are two-fold: firstly, it formulates the basis of a new prediction-oriented quantitative read-across approach that would guarantee the repeatability of the modeling results and addressing uncertainty evaluation in read-across, thus promoting its widespread acceptance. Secondly, it verifies the utility of the newly developed read-across algorithm for filling nanosafety data gaps by using three high-quality literature datasets. Further, to facilitate the implementation of the developed approach for quantitative read-across, this study offers a fully automated, user-friendly, and freely available java based program. The program is available from https://sites.google.com/jadavpuruniversity.in/dtc-lab-software/home. The tool allows the users to optimize different hyper-parameters of similarity kernel functions and distance and similarity thresholds so that the users may get the best quality of quantitative predictions. Although the kernel functions are already known, their use in nanotoxicity predictions and optimization of different hyper-parameters using the openly accessible tool is the novelty of the present work. Among all currently produced materials that explicitly claim nanoscale properties, most are metals or metal oxides.26 This forms the basis of using the toxicity data of MeOx NPs for the present case studies.
Materials and methods
Toxicity data
Engineered nanoparticles can grossly be classified into 5 groups, such as metal oxide nanoparticles (MeOx NPs), carbon nanomaterials, zero valence metal nanoparticles, quantum dots (QDs), and dendrimers, based on their chemical compositions.27 Among all groups, MeOx NPs are of utmost importance; the current work is designed and performed using the toxicity data of MeOx NPs. The utilization of various metal oxides as bulk materials has been observed for many years but recently the nanoforms of metal oxides are being circulated in the market as various consumer products. Titanium dioxide NPs are utilized extensively in various sectors. It has widespread applications in solar cells and cosmetic industries along with zinc oxide NPs due to their photolytic nature and UV ray blocking effect.28 Al2O3 NPs are used in materials science and cement industries. Besides these, other important MeOx NPs are CuO, CoO, Fe2O3, NiO, SnO2, Bi2O3, Cr2O3, etc. which are used randomly. Apart from the applications, MeOx NPs are produced more than other classes. A 15.4% global market growth is forecasted between year 2017 to 2022 for MeOx NPs, and the Asia-Pacific region (Japan, China, India, South Korea, and Vietnam) is expected to be the fastest-growing market of this class of NPs according to an industry report.29 The easy availability of toxicity data in the literature was also a reason behind the selection of MeOx NPs in this study, although the data is limited in number. Therefore, this study designed on metal oxide nanoparticles will help to validate the proposed methodology based on a quantitative read-across algorithm, and in the near future, the methodology could be used for the prediction of toxicity (biological activity in general) of various other classes of nanoparticles and other small datasets also.Three different nanotoxicity datasets have been employed to validate the proposed algorithm in the current study. The toxicity data of metal oxides have been collected against (1) a human keratinocyte cell line (HaCaT) as dataset 1, (2) Escherichia coli as dataset 2, and (3) Escherichia coli in absence of light as dataset 3 from the literature.30–32 Datasets 1, 2, and 3 contain 18, 17, and 16 data points, respectively. In dataset 1, the experimental in vitro toxicity data was expressed in terms of 1/log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LC50i.e., the negative logarithm of molar concentration of MeOx NPs which caused a 50% reduction of HaCaT cells after 24 h of exposure. In contrary, the experimental toxicity data of datasets 2 and 3 were expressed in terms of 1/log
LC50i.e., the negative logarithm of molar concentration of MeOx NPs which caused a 50% reduction of HaCaT cells after 24 h of exposure. In contrary, the experimental toxicity data of datasets 2 and 3 were expressed in terms of 1/log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EC50, i.e., the negative logarithmic molar concentration of MeOx NPs which caused the bacteria 50% less viable after 24 h of exposure in the presence and absence of light respectively. The toxicity data of three datasets are enlisted in Tables S1–S3 respectively in the ESI† section.
EC50, i.e., the negative logarithmic molar concentration of MeOx NPs which caused the bacteria 50% less viable after 24 h of exposure in the presence and absence of light respectively. The toxicity data of three datasets are enlisted in Tables S1–S3 respectively in the ESI† section.
Molecular descriptors
Molecular descriptors are the numeric representations of various structural features of molecules which are essentially utilized to develop a mathematical relationship between the biological activity (toxicity) and the molecular structures.33 Calculation and selection of the most relevant descriptors towards the biological activity are the integral parts of various computational techniques such as QSARs and read-across.34 However, in the current study, most relevant descriptors/features were chosen based on the previous works on the datasets and the literature reports.According to the previously published literature reports, it has been found out that the toxicity of nanoparticles occurs due to the fast dissolution of active species and formation of reactive oxygen species (ROS) from the surface redox reaction of NPs.35,36 For dataset 1, two different descriptors – namely, the Mulliken electronegativity of the cluster (χc) and the enthalpy of formation of a MeOx nanocluster representing a fragment of the surface (ΔHcf) were used in the present work. Selected descriptors (χc and ΔHcf) are the factors affecting dissolution of metal oxide from the surfaces of NPs and the surface redox reaction.11 In some recently published articles, the mechanistic interpretation of the selected descriptors was discussed in detail.30,37 The enthalpy of formation of gaseous cations (ΔHMe+) and the molecular charge of metal cations (Me+) are the descriptors of interest for dataset 2 which were chosen based on the previously published work.11 Both of the descriptors (ΔHMe+ and Me+) were identified as the important factors affecting the dissolution of MeOx and the formation of ROS and hence to the toxicity of MeOx NPs towards Escherichia coli. Molecular charge of metal cations (Me+) is inversely proportional to the release of metal ions from the surface of NPs; smaller charge on metal cations will enhance the release of metal ions and vice versa. For dataset 3, ΔHMe+ (enthalpy of formation of gaseous cations) and LZELEHHO (absolute electronegativity of metal oxide) were already proven as two important structural features for the induced nanotoxicity against bacteria Escherichia coli in absence of light and were used in the present study.11 The descriptor values of three datasets are enlisted in Tables S1 (dataset 1), S2 (dataset 2), and S3 (dataset 3) in the ESI† section.
Dataset division
For any read-across prediction, there are some source compounds (chemical analogues with known toxicity) from which the toxicity of new or unknown analogues (target compounds) are predicted. In the present work, each of the datasets was divided into a training set (source compounds) and a test set (target compounds). The toxicity of test set compounds has been predicted from the structural information and experimental toxicity data of the training set compounds. There is no such rule of thumb for size of training and test sets in dataset division. In the conventional practice of QSARs, 70–80% compounds are kept in the training set while 20–30% compounds are kept in the test set. These 70/30 or 80/20 divisions are reasonable for datasets with sufficient number of data points (n > 50); however, all the datasets of this study were relatively small (n < 20). Thus, 70/30 or 80/20 divisions were not suitable. Another aspect of the dataset division is “bias-variance dilemma”, which should be kept in mind. A comparatively bigger training set can produce a biased model while from a small test set, the variance of predicted response can be increased.38 After considering the above-mentioned conditions and to get a balanced division, datasets 1 and 3 were divided into training and test sets in equal proportions (dataset 1: 9 training compounds, 9 test compounds; dataset 3: 8 training compounds, 8 test compounds), and dataset 2 was divided with 47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 53 ratio (8 training compounds, 9 test compounds) into training and test sets. All the datasets have been divided randomly multiple times, because the random division ensures an unbiased selection.39
53 ratio (8 training compounds, 9 test compounds) into training and test sets. All the datasets have been divided randomly multiple times, because the random division ensures an unbiased selection.39
Methodology or the algorithm
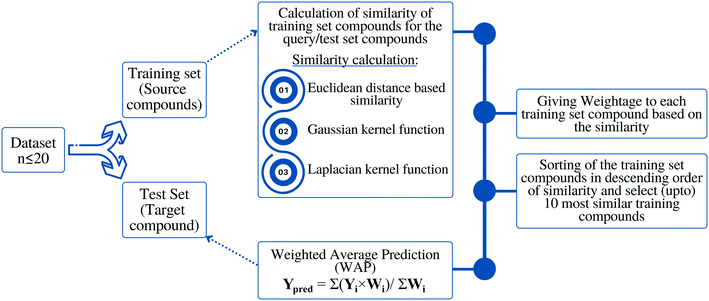
The algorithm is based on two consecutive steps – (1) finding up to 10 most similar training compounds for each query or test compound, and (2) the weighted average prediction of test set compounds from the most similar training set compounds. Among two compounds (chemical analogues) in the chemical space, the existing structural similarity can be measured and expressed with a numerical value ranging from 0 to 1. The measured similarity value increases with simultaneous increment of structural similarity. Computed similarity value of ‘1’ represents absolutely similar, i.e., identical compounds while ‘0’ represents completely dissimilar compounds. In this study, the similarity among test compounds and training compounds were measured using Euclidean distance-based measure, Gaussian kernel function, and Laplacian kernel function. For preprocessing of the data, the descriptor values of both training and test sets were scaled using the mean and standard deviation of the training set compounds to avoid the inter-descriptor variability40 using the following eqn (1):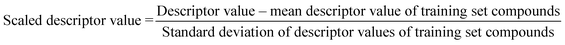 | (1) |
Euclidean distance (ED) has been used here as one of the ways to find most similar training compounds for each test set compound. ED is the distance between two points (here two compounds) in the Euclidean space or vector space (here descriptor space) which is calculated using the Pythagorean theorem41 as the following eqn (2):
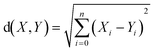 | (2) |
 | (3) |
We proposed to calculate the similarity from ED by subtracting the rescaled ED from 1. Distance is inversely proportional to similarity; thus, most similar compounds must have least distance among them. In this study, 1 is the maximum similarity value possible and hence distance will be 0 (= 1–1) among the most similar compounds.
Gaussian kernel function is another approach which is employed to find out the most similar training compounds for each test set compound. Gaussian kernel function is a radial basis kernel function41 which is defined by the following eqn (4):
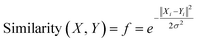 | (4) |
Laplacian kernel function is another radial basis function which is used for the similarity estimation is this study. The Laplacian kernel function43 is defined as following eqn (5):
| κ(X, Y) = e(−γ‖X−Y‖1) | (5) |
Based on the measured similarity of a test compound with different training compounds, the training set was sorted in descending order and up to 10 (9 or 8 in this study) most similar training compounds were selected as read-across source compounds. Weightage was given to every selected training compound based on the measured similarity as following eqn (6):
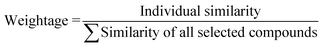 | (6) |
The sum of weightage of all selected compounds always would be one. Finally, the toxicity values of test compounds (the weighted average toxicity) were calculated from the training set experimental data and given weightage as following eqn (7):
 | (7) |
Validation metrics
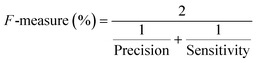
To confirm the efficiency and reliability of the proposed algorithm, it was validated according to the OECD validation recommendations. In this study, nanotoxicity of test set compounds was quantitatively predicted from training set compounds without development of a statistical model. Hence, unlike QSAR models, no internal validation metric was used to determine the goodness-of-fit and robustness of the algorithm. To check the predictive ability of the new algorithm, rigorous external validation was carried out for all the datasets. As the nanotoxicity values were quantitatively predicted, we have used regression based validation metrics for checking the quality of predictions. External validation metrics such as external validation coefficients (Q2F1 and Q2F2) and error based parameter-root mean square error of prediction (RMSEP) were calculated from test set data. The external validation coefficient value of 1 indicates best possible prediction and any deviation from 1 indicates departure from the ideal value. As per the conventions in the QSAR literature, values of Q2F1 and Q2F2 ≥ 0.6 and a small RMSEP value (near zero) signify efficient and less erroneous predictions.45 Various classification-based metrics were also measured from the predictions of test set data. To calculate the classification-based metrics, the test set compounds were classified into toxic and non-toxic compounds (toxic: toxicity value > mean of training set response values; non-toxic: toxicity value < mean of training set response values) based on the test set experimental data. A two-by-two confusion matrix was then constructed from the true positive (correctly predicted as toxic), true negative (correctly predicted as non-toxic), false positive (non-toxic but erroneously predicted as toxic), and false negative (toxic but erroneously predicted as non-toxic) predictions for calculating the sensitivity, specificity, accuracy, F-measure, precision, G-means, Cohen's κ, and Matthews correlation coefficient, which are the measures of classifier performance. Higher values (near 100%) of these indicate better classification. G-Means is a combination of sensitivity and specificity by their geometric mean, which signifies a balanced performance of an algorithm between active and inactive classes. Kohen's κ metric indicates the agreement between predicted classification and observed classification and this analysis can measure values in the range of −1 (no agreement) to 1 (complete agreement). Any value of Cohen's κ more than 0.6 signifies an acceptable prediction whereas more than 0.8 signifies highly predictive algorithm. The Matthews correlation coefficient (MCC) indicates the quality of binary classification. Coefficient values 1, 0, −1 signify perfect prediction, average prediction, and inverse prediction respectively.44 All the quantitative external validation metric and classification based metric values are enlisted in Table 2. These metrics are discussed in detail in the cited reference43 and the readers may go through this for better understanding.Software development
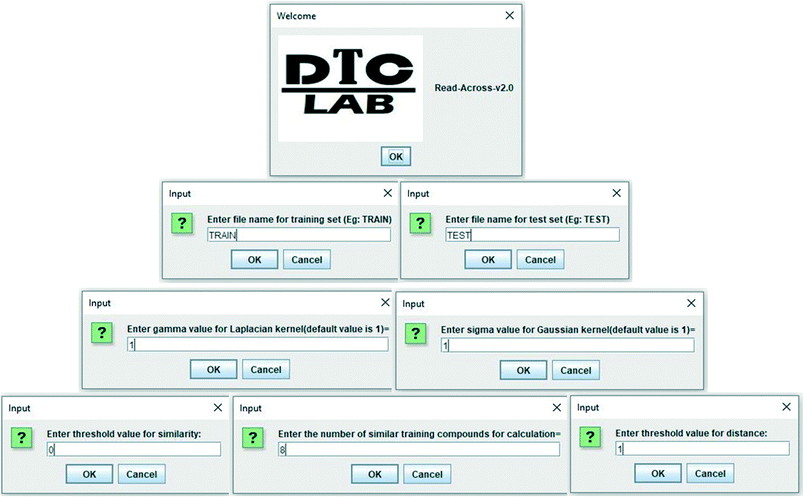
In the current study, a java based computer program “Read-Across-v2.0” has been developed, which is able to quantitatively predict the toxicity (biological activity in general) of nanomaterials (chemicals in general). The program also shows the quality of predictions in terms of different external validation metrics if the experimental data of test set compounds are supplied. The software tool is easy to handle, free, and can be downloaded from the following link https://sites.google.com/jadavpuruniversity.in/dtc-lab-software/home. The program files have also been made available in the ESI† section. The current version can be executed from the Windows as in Fig. 2 where the operator has to supply the separate Excel files (.xlsx format) for the training data (containing serial numbers, descriptors, and experimental data), and test data (containing serial numbers, descriptors, and experimental data, if available). The values of sigma and gamma (the suggested value being 1), number of similar training compounds for calculation (ranging between 2 and 10), distance and similarity thresholds are the determinants of predictions, and these should be supplied as user input. The user should provide the optimum values of the above-mentioned determinants for better quality of predictions. All input files (.xlsx format) have been supplied in ESI† for better understanding.Program output
After successful execution of the program, it generates two output files – namely: “Biological activity” and “Sort”. Both the files are in Excel format (.xlsx) and are briefly discussed here.1. “Biological Activity.xlsx”: It is the main output of the program which contains the predictions from three different methods (Euclidean distance-based similarity, Gaussian kernel function similarity, and Laplacian kernel function similarity). The program also prints the values of determinants (sigma value, gamma value, number of similar training compounds, distance threshold, similarity threshold) provided by the operator in this output file. The quantitative external validation metrics i.e., Q2F1, Q2F2, and RMSEP are also computed and displayed in the “Biological Activity.xlsx” if the experimental data of test set compounds have been provided. The number of selected close training compounds for calculation may differ after applying the distance and similarity thresholds in three methods, and these numbers of selected compounds in each method are also displayed in the “Biological Activity.xlsx”. All the biological activity output files generated during the study have been supplied in the ESI† section for better understanding.
2. “Sort.xlsx”: This file contains the sorted training compounds in a particular order (Euclidean distance: ascending order; similarities: descending order) based on the distance and similarities (both Gaussian kernel function, and Laplacian kernel function) for each test compound. The experimental data of training compounds are also sorted accordingly with the distance and similarities and displayed in “Sort.xlsx”. This file helps the operator to crosscheck the correctness of the algorithm.
Result and discussion
The nanotoxicity of three above mentioned datasets (dataset 1, dataset 2, and dataset 3) was predicted separately by employing three similarity estimation techniques (Euclidean distance similarity, Gaussian kernel function similarity, Laplacian kernel function similarity). Optimum values of sigma (σ) and gamma (γ) for Gaussian kernel function, and Laplacian kernel function, respectively were computed for all studied datasets. All the three similarity estimation methods were optimized. The effect of various thresholds such as, distance threshold, similarity threshold, and optimum number of close training compounds for predictions were also evaluated. The detailed results of the study have been discussed in the following sections.Toxicity prediction by Euclidean distance-based similarity estimation
The Euclidean distance-based similarity estimation was the 1st technique used in the present study for the selection of close training compounds against each query compound. The similarity was estimated from the computed Euclidean distance by employing the proposed algorithm, which has been discussed earlier. For the Euclidean distance calculation, the descriptors of both training and test sets were scaled as per eqn (1). After distance calculation, the distances were rescaled into 0 to 1 range for the similarity estimation. The similarity of training compounds with query compound was calculated and sorted in descending order. It has been observed from the estimated similarity data that two most similar compounds were placed closer in descriptor space and vice versa.In the dataset 1, two descriptors (χc and ΔHcf) were used for the structural similarity estimation. Dataset 1 contains 18 MeOx nanoparticles, and was divided into equal proportion between training and test sets. The nanotoxicity data of test compounds (target chemicals) were predicted from the experimental toxicity data and structural information of the training compounds (source compounds). After prediction, quantitative external validation metrics such as – Q2F1, Q2F2, and RMSEP were computed to check the quality of predictions. In dataset 1, the values of Q2F1, Q2F2, and RMSEP were 0.63, 0.62, and 0.14 respectively, which validate the algorithm. The descriptors ΔHMe+ and Me+ were used for the similarity estimation in dataset 2, which contains 17 MeOx NPs. The toxicity of 9 test compounds of dataset 2 was predicted from the biological (1/log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EC50) and structural data (descriptor values) of 8 training compounds. The calculated validation metric values of dataset 2 (Q2F1 = 0.45, Q2F2 = 0.45, and RMSEP = 0.42) do not indicate sufficient concordance between the experimental and predicted response values. Toxicity of the test compounds of dataset 3 was also predicted by the Euclidean distance-based similarity estimation. Dataset 3 contains 16 MeOx NPs and two descriptors (ΔHMe+ and LZELEHHO) for similarity estimation. The dataset compounds were divided in equal proportions into training and test sets. After prediction, the external validation was performed, and the values of metrics are: Q2F1 = 0.77, Q2F2 = 0.69, and RMSEP = 0.60. The results indicate sufficient correlation among the experimental and predicted data, though the prediction error (RMSEP) was in the higher side. So, from the prediction quality of Euclidean distance-based similarity estimation, we can conclude that the method is working to some extent for selected datasets. To improve the quality of predictions, distance threshold has been applied. The results are discussed later in this communication.
EC50) and structural data (descriptor values) of 8 training compounds. The calculated validation metric values of dataset 2 (Q2F1 = 0.45, Q2F2 = 0.45, and RMSEP = 0.42) do not indicate sufficient concordance between the experimental and predicted response values. Toxicity of the test compounds of dataset 3 was also predicted by the Euclidean distance-based similarity estimation. Dataset 3 contains 16 MeOx NPs and two descriptors (ΔHMe+ and LZELEHHO) for similarity estimation. The dataset compounds were divided in equal proportions into training and test sets. After prediction, the external validation was performed, and the values of metrics are: Q2F1 = 0.77, Q2F2 = 0.69, and RMSEP = 0.60. The results indicate sufficient correlation among the experimental and predicted data, though the prediction error (RMSEP) was in the higher side. So, from the prediction quality of Euclidean distance-based similarity estimation, we can conclude that the method is working to some extent for selected datasets. To improve the quality of predictions, distance threshold has been applied. The results are discussed later in this communication.
Toxicity prediction by Gaussian kernel function similarity estimation
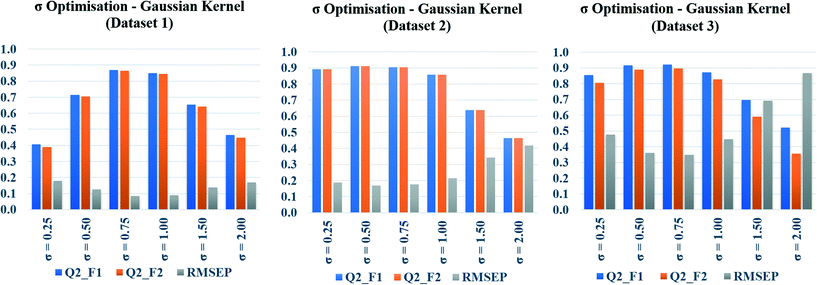
In the present communication, Gaussian kernel function similarity estimation has been used to find out the order of similar training compounds for each test compound. After arranging the training compounds in descending order of similarity, toxicity data of query compounds were predicted by the previously discussed weighted average prediction method. The scaled or normalized descriptor values were used for the L2 norm (Euclidean distance) calculation followed by similarity estimation. For Gaussian kernel function similarity estimation, sigma (σ) is an important determinant which affects the performance of the kernel and it never becomes zero. The value of σ was optimized for three studied datasets (dataset 1, dataset 2, and dataset 3) separately. The toxicity was predicted with six different σ values (0.25, 0.50, 0.75, 1.0, 1.5, 2.0), and the quality of predictions was adjudged by external validation metrics such as, Q2F1, Q2F2, and RMSEP.The calculated metric values are represented graphically in Fig. 3, where the metric values (Y axis) have been plotted as bars against the values of σ (X axis). Taller Q2F1, Q2F2 bars, and a smaller RMSEP bar represent better predictions. In the diagram, tallest Q2F1, Q2F2 bars (towards 1), and smallest RMSEP bar (towards 0) have been observed at 0.75 as the value of sigma for datasets 1 and 3. In dataset 2, the best observation has been seen when σ = 0.5. So, we can conclude here that 0.75 is the best selected value of sigma for datasets 1 and 3, whereas 0.5 is the best selected value for dataset 2. The above-mentioned values of σ have been used in remaining parts of the study for Gaussian kernel function similarity estimation. The computed values of validation metrics at different σ have been shown at Table S4 in the ESI† section.
Toxicity prediction by Laplacian kernel similarity estimation
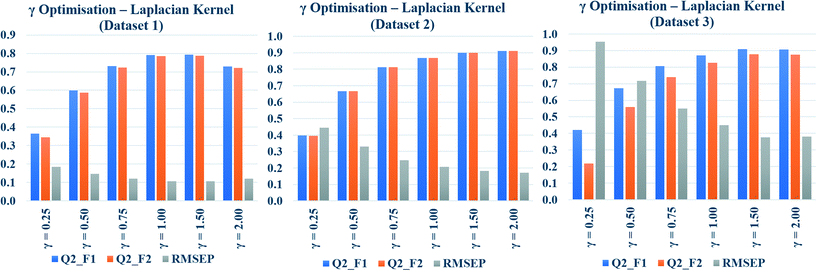
The Laplacian kernel function was another important method used in this study for similarity estimation followed by toxicity prediction. In this method, the Manhattan distance (L1 norm) was calculated from the previously scaled descriptors, and then the similarity among each test compound and various training compounds was estimated by employing eqn (5). Just like σ in Gaussian kernel function, gamma (γ) in eqn (5) is a non-zero number, which determines the performance of Laplacian kernel function. The values of γ have been optimized for three datasets and tabulated in Table S5 in the ESI† section. Various numerical values of γ (0.25, 0.50, 0.75, 1.0, 1.5, 2.0) were used for the similarity calculation followed by toxicity prediction. The quality of perditions was judged by the external validation.The data have been graphically represented (Fig. 4) as bar diagram, where the validation metrics are plotted in Y axis against different values of γ (X axis). It is evident from the diagram that the best results of Laplacian kernel function can be obtained at γ = 1 for dataset 1, γ = 2 for dataset 2, and γ = 1.5 for dataset 3. For further studies, the optimized γ values (specific for the datasets) have been used for the best results in the following sections.
Effects of number of close training compounds on the toxicity prediction in new algorithm
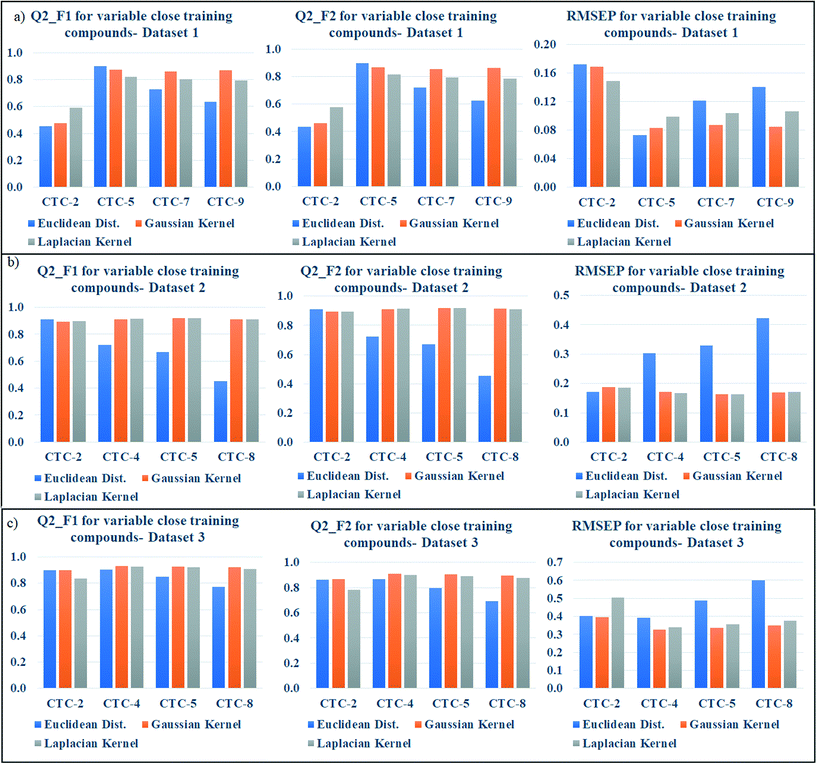
According to the proposed algorithm, the weighted average predictions should be calculated with most similar training compounds (up to 10). After dataset division, the number of test compounds in each studied dataset was less than 10 (dataset 1: 9 test compounds; dataset 2: 9 test compounds; dataset 3: 8 test compounds); thus, in the preliminary prediction, all test compounds for each dataset were taken into account. But we have then optimized the number of close training compounds for efficient predictions. For this optimization study using Gaussian and Laplacian kernel function based read-across, the previously optimized σ values (dataset 1 = 0.75, dataset 2 = 0.5, dataset 3 = 0.75) and γ values (dataset 1 = 1.0, dataset 2 = 2.0, dataset 3 = 1.5) were used. After similarity estimation and sorting the training compounds in descending order of similarity, the weighted average value has been computed by changing the number of training compounds from 2 to 9 (2 to 8 for dataset 3). The validation metrics have been computed for judging the quality of predictions and are enlisted in Tables S6 (dataset 1), S7 (dataset 2), and S8 (dataset 3) in the ESI† section.For better understanding, the optimization data has been graphically represented as bar diagram where the metrics have been plotted as bars in Y axis against the number of close training compounds in X axis (Fig. 5: dataset 1; Fig. 5b: dataset 2; Fig. 5c: dataset 3). Taller Q2F1 and Q2F2 bars (value towards 1), and smaller RMSEP bars (value towards 0) represent better predictions. In dataset 1, all the three similarity-based predictions showed the best results with 5 close training compounds. The graphical representation also validates the result. In dataset 2, the best Euclidean distance-based prediction was obtained with 2 close training compounds (Q2F1 = 0.91, Q2F2 = 0.91, RMSEP = 0.17) whereas the best Gaussian kernel (Q2F1 = 0.92, Q2F2 = 0.92, RMSEP = 0.16) and Laplacian kernel (Q2F1 = 0.92, Q2F2 = 0.92, RMSEP = 0.16) predictions were obtained with 5 close training compounds. For dataset 3, the prediction quality has deteriorated after taking more than 5 close training compounds for prediction. The best Euclidean distance-based prediction (Q2F1 = 0.91, Q2F2 = 0.88, RMSEP = 0.37) was obtained with 3 close training compounds, whereas the best Gaussian kernel (Q2F1 = 0.93, Q2F2 = 0.91, RMSEP = 0.33) and Laplacian kernel predictions (Q2F1 = 0.93, Q2F2 = 0.90, RMSEP = 0.34) were obtained with 4 close training compounds. So, the insights of this optimization study suggest predicting the toxicity of query chemicals by taking 2–5 close training compounds for the best results.
Distance and similarity threshold optimization for the new similarity based read-across algorithm
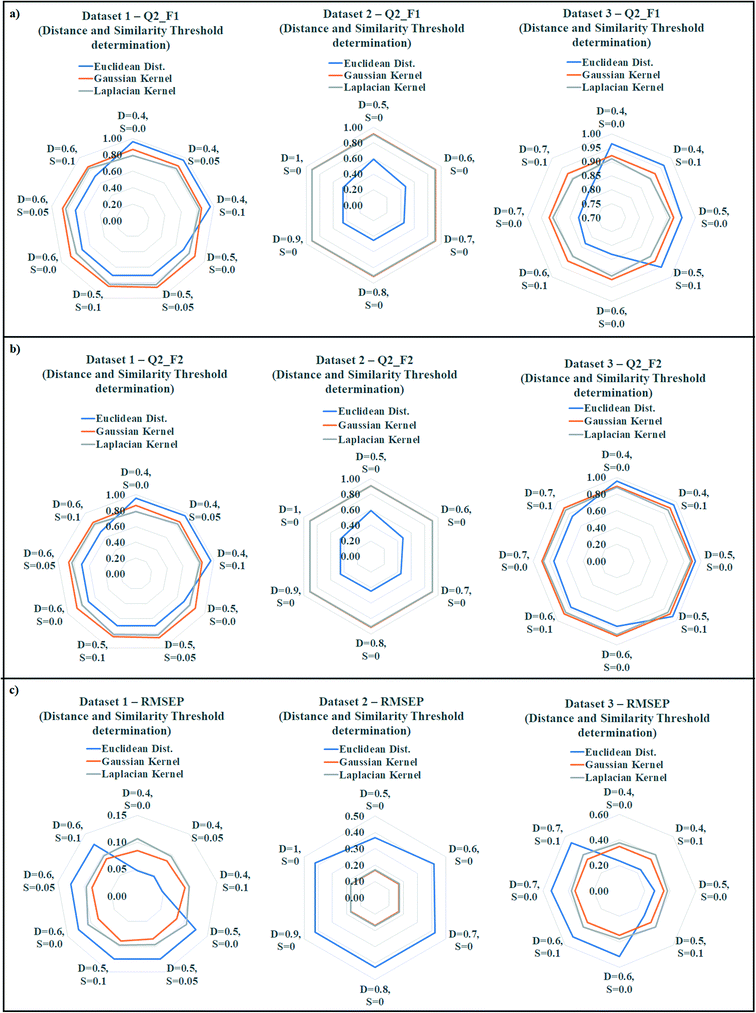
The quality of predictions can be compromised due to presence of less similar compounds in the training set. According to the proposed similarity based read-across algorithm, the most similar training analogues for a query chemical are able to predict the toxicity more efficiently. If the training compounds are not structurally similar up to a certain range, then it must affect the prediction quality. To find out the best training compounds for the prediction, we have tried to establish a suitable distance and similarity cut-off value (threshold) in the present communication. It should be noted that whenever the distance and similarity thresholds were applied for the prediction, all training compounds were taken into account. The distance and similarity threshold along with the number of training compound threshold were not applied simultaneously during optimization. The distance threshold was applied for the Euclidean distance based read-across, whereas the similarity threshold was applied for the Gaussian and Laplacian kernel function read-across. We have applied various distance thresholds from 1 to 0, and various similarity thresholds from 0 to 1 in the optimization. The validation results of this optimization were enlisted in Tables S9 (dataset 1), S10 (dataset 2), and S11 (dataset 3) in the ESI† section. Only the acceptable predictions (in terms of validation metrics) with different distance and similarity thresholds were presented.The observed data was graphically represented in Fig. 6 (Fig. 6a: dataset 1; Fig. 6b: dataset 2; Fig. 6c: dataset 3) where the radar plots were used for presenting the validation metrics. The radar plots are used to represent a multivariate data in 2-dimensional format.44 These plots are constructed from a center point from which various axes are drawn. It should be noted that minimum 3 axes are necessary to construct a radar plot. Each axis represents a variable with a defined name (distance and similarity values were presented). The angular axes represent the magnitude of the variables (metric values were presented) in a radar plot. All the three methods of similarity estimation were represented using different colors (blue = Euclidean, orange = Gaussian, gray = Laplacian). For the Q2F1, and Q2F2 plots, the higher angular magnitude represents better prediction whereas the opposite is applicable for RMSEP plot.
In datasets 1 and 3, Euclidean distance read-across performed well (dataset 1: Q2F1 = 0.96, Q2F2 = 0.96, RMSEP = 0.05; dataset 3: Q2F1 = 0.96, Q2F2 = 0.95, RMSEP = 0.23) after applying a distance threshold 0.4. On the contrary, a distance threshold 0.5 produced the best observation in dataset 2 (Q2F1 = 0.59, Q2F2 = 0.59, RMSEP = 0.37). A similarity threshold value 0.05 was optimum for the prediction of toxicity using Gaussian kernel and Laplacian kernel read-across in dataset 1 (Gaussian: Q2F1 = 0.87, Q2F2 = 0.86, RMSEP = 0.09; Laplacian: Q2F1 = 0.83, Q2F2 = 0.82, RMSEP = 0.10). In datasets 2 and 3, the best Gaussian kernel (dataset 2: Q2F1 = 0.91, Q2F2 = 0.91, RMSEP = 0.17; dataset 3: Q2F1 = 0.92, Q2F2 = 0.90, RMSEP = 0.35) and Laplacian kernel function (dataset 2: Q2F1 = 0.91, Q2F2 = 0.91, RMSEP = 0.17; dataset 3: Q2F1 = 0.91, Q2F2 = 0.88, RMSEP = 0.38) based predictions were obtained after applying 0.0 as the similarity threshold value. So, the above observations indicate the optimum distance threshold ranges from 0.4 to 0.5 in the Euclidean distance based read-across, and optimum similarity threshold ranges from 0.0 to 0.05 for Gaussian kernel and Laplacian kernel read-across.
Evaluation of similarity-based read-across algorithm by classification-based metrics
From the distance and similarity threshold optimization, we have seen that the Euclidean distance read-across algorithm at a distance threshold (D) 0.4 predicts the toxicity of datasets 1 and 3 most efficiently. On the other hand, Gaussian and Laplacian kernel read-across are the most efficient algorithms for the prediction of toxicity of dataset 2 at a similarity threshold (S) 0.0. In the present communication, the best possible predicted toxicity from the studied datasets have been classified into toxic and non-toxic classes and compared with the experimental toxicity data. Various classification-based metrics have been computed (as mentioned in Table 2) to evaluate the classification capability of the prediction, and in a nutshell, the efficiency of prediction of the new similarity based read-across algorithm. The computed metric values have been enlisted in Table 3. The Kohen's κ value of 0.68, higher F-measure (85.71%), and the MCC value of 0.79 for dataset 1 indicate an acceptable classification of the predicted values. In datasets 2 and 3, the maximum possible metric values are obtained from the best predictions which indicate perfect correspondence of the toxic and non-toxic compounds between the experimental and predicted data. So, it is very evident from the result that the newly developed read-across algorithm can efficiently predict the toxicity of small datasets and are able to classify the data into toxic and non-toxic classes also.| Classification based metrics | Dataset 1 | Dataset 2 | Dataset 3 |
|---|---|---|---|
| Euc (D = 0.4) | GK and LK (S = 0.0) | Euc (D = 0.4) | |
| TP: true positive, FN: false negative, FP: false positive, TN: true negative, Euc: Euclidean distance based read-across, GK: Gaussian kernel read-across, LK: Laplacian kernel read-across, D: distance threshold, S: similarity threshold, MCC: Matthews correlation coefficient. | |||
| TP | 3 | 5 | 1 |
| FN | 0 | 0 | 0 |
| FP | 1 | 0 | 0 |
| TN | 5 | 4 | 7 |
| Sensitivity (%) | 75 | 100 | 100 |
| Specificity (%) | 100 | 100 | 100 |
| Accuracy (%) | 84.62 | 100 | 100 |
| Precision (%) | 100 | 100 | 100 |
| F-Measure (%) | 85.71 | 100 | 100 |
| G-Means | 0.87 | 1 | 1 |
| Cohen's κ | 0.68 | 1 | 1 |
| MCC | 0.79 | 1 | 1 |
Comparison of performance of new similarity-based algorithm with previously published in silico models
The performance of the new similarity based read-across approach developed in this study has been compared with the prediction quality of QRAPC and nano-QSAR models reported previously in the literature.12,19–21 The prediction quality of all in silico models (i.e., similarity-based read-across, QRAPC, nano-QSAR) are summarized in Table 4. It should be noted that the results have been compared by means of the external validation metrics – Q2F2 and RMSEP, because the authors of previous communications (QRAPC, nano-QSAR) reported the above-mentioned metrics only. Q2F2 is an external validation coefficient which indicates the correlation among experimental and predicted data, and its measured value is affected by the number of test compounds. So, for direct comparison with the previously published work, the number of test set compounds in each case has also been enlisted in Table 4. The best predictions of individual dataset obtained after employing three similarity based estimations with suitable distance and similarity thresholds are reported here for comparison.| Ref. | Test set (target compounds) | ||
|---|---|---|---|
| Q 2F2 | RMSEP | n* | |
| Euca: Euclidean distance-based similarity; GKb: Gaussian kernel function similarity; LKc: Laplacian kernel function similarity; D: distance threshold; S: similarity threshold; n*: no. of compounds in test set; the most efficient algorithms/models for the prediction of toxicity are indicated in bold. | |||
| Dataset 1 | |||
| Euca (D = 0.4) | 0.96 | 0.05 | 9 |
| GKb (S = 0.05) | 0.86 | 0.09 | 9 |
| LKc (S = 0.05) | 0.82 | 0.10 | 9 |
| QRAPC11 | 0.74 | 0.20 | 11 |
| Nano-QSAR29 | 0.83 | 0.13 | 8 |
| Dataset 2 | |||
| Euca (D = 0.5) | 0.59 | 0.37 | 9 |
| GKb (S = 0.0) | 0.91 | 0.17 | 9 |
| LKc (S = 0.0) | 0.91 | 0.17 | 9 |
| QRAPC11 | 0.80 | 0.19 | 10 |
| Nano-QSAR30 | 0.83 | 0.19 | 7 |
| Dataset 3 | |||
| Euca (D = 0.4) | 0.95 | 0.23 | 8 |
| GKb (S = 0.0) | 0.90 | 0.35 | 8 |
| LKc (S = 0.0) | 0.88 | 0.38 | 8 |
| QRAPC11 | 0.91 | 0.33 | 7 |
| Nano-QSAR31 | −0.20 | 0.53 | 4 |
The data for dataset 1 shows that the Euclidean distance-based read-across and Gaussian kernel function based read-across have achieved better quality than the QRAPC and nano-QSAR models. The Laplacian kernel read-across has achieved better performance than the QRAPC model (Laplacian kernel read-across provided less erroneous result than nano-QSAR). For dataset 2, better quality of prediction has been obtained by both Gaussian and Laplacian kernel read-across. The performance of Euclidean distance read-across was inferior to the previously published reports but the method met the cut-off criteria for acceptance reported in Table 2. For dataset 3, the Euclidean distance-based read-across was the best performer among all other methods. The Gaussian and Laplacian kernel read-across have also provided good results and are comparable with the QRAPC model. All these datasets favor the new similarity based read-across algorithm over the previous methods; the new method is able to predict the toxicity of nanoparticles with the least error. Therefore, from the comparative literature study, it can be concluded that the newly developed read-across algorithm provides reasonably accurate predictions and can be used for small datasets.
Conclusion
In the present communication, a new quantitative read-across algorithm based on various similarity estimation techniques was introduced. Euclidean distance, Gaussian kernel function, and Laplacian kernel function were employed here for the similarity estimation. The algorithm developed in this study was properly validated using three small (n ≤ 20) nanotoxicity data sets. The research insights of this contribution have clearly demonstrated the efficiency of the algorithm and accuracy of predicted data. The sigma and gamma values of Gaussian and Laplacian kernel function, respectively, have been successfully optimized for each dataset used. The effect of number of close training compounds to the prediction quality has been assessed. 2–5 close training compounds can efficiently predict the toxicity of query compounds. The best results can also be achieved by applying a distance threshold for the Euclidean distance similarity estimation and a similarity threshold for the Gaussian and Laplacian kernel function similarity estimations. The threshold values (suitable distance threshold = 0.4 to 0.5; suitable similarity threshold = 0.00 to 0.05) have been optimized successfully for the studied datasets. The new method is able to predict toxicity with better efficiency than the previously reported methods. Unlike the conventional read-across methods, the new methods are eligible to use any number of descriptors. Simple linear algebraic calculations have been used in the new method, so it is computationally less exhaustive. A simple java based computer program has also been developed (available at: https://sites.google.com/jadavpuruniversity.in/dtc-lab-software/home) in this study, which can efficiently predict the toxicity using the new algorithm. Finally, we can conclude here that the new similarity-based read-across algorithm and the designed software are easy to use, efficient, and an expert independent alternative method for the toxicity prediction of MeOx nanoparticles. Hence, the algorithm may serve as a complementary technique for the data-gap filling, prioritization, and in a nutshell for better risk assessment of nanoparticles.Author contributions
MC: computation and validation, initial draft. AB: software development. PD: computation and validation. AGS: editing, supervision. KR: conceptualization, supervision, editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research is funded by Science and Engineering Research Board (SERB), New Delhi under the MATRICS scheme. MC conveys his sincere gratitude to All India Council for Technical Education (AICTE), New Delhi for financial assistance during Ph.D. in the form of National Doctoral Fellowship (NDF). PD thanks Indian Council of Medical Research, New Delhi for senior research fellowship. AB thanks Jadavpur University for a scholarship. This research has been partially funded by the European Union's Horizon 2020 research and innovation program under grant agreement No. 953183 (HARMLESS project).References
- European Chemicals Agency (ECHA), in New Approach Methodologies in Regulatory Science, 2016 Search PubMed.
- J. C. Madden, S. J. Enoch, A. Paini and M. T. D. Cronin, A Review of In Silico Tools as Alternatives to Animal Testing: Principles, Resources and Applications, ATLA, Altern. Lab. Anim., 2020, 48, 146–172 CrossRef PubMed.
- P. Nymark, M. Bakker, S. Dekkers, R. Franken, W. Fransman, A. García-Bilbao, D. Greco, M. Gulumian, N. Hadrup, S. Halappanavar, V. Hongisto, K. S. Hougaard, K. A. Jensen, P. Kohonen, A. J. Koivisto, M. D. Maso, T. Oosterwijk, M. Poikkimäki, I. Rodriguez-Llopis, R. Stierum, J. B. Sørli and R. Grafström, Toward Rigorous Materials Production: New Approach Methodologies Have Extensive Potential to Improve Current Safety Assessment Practices, Small, 2020, 16, 1904749 CrossRef CAS PubMed.
- European Chemical Agency (ECHA), in The use of alternatives to testing on animals for the REACH Regulation, 2020 Search PubMed.
- S. E. Escher, H. Kamp, S. H. Bennekou, A. Bitsch, C. Fisher, R. Graepel, J. G. Hengstler, M. Herzler, D. Knight, M. Leist, U. Norinder, G. Ouédraogo, M. Pastor, S. Stuard, A. White, B. Zdrazil, B. van de Water and D. Kroese, Towards grouping concepts based on new approach methodologies in chemical hazard assessment: the read-across approach of the EU-ToxRisk project, Arch. Toxicol., 2019, 93, 3643–3667 CrossRef CAS.
- J. Cao, Y. Pan, Y. Jiang, R. Qi, B. Yuan, Z. Jia, J. Jiang and Q. Wang, Computer-aided nanotoxicology: risk assessmentof metal oxide nanoparticles via nano-QSAR, Green Chem., 2020, 22, 3512–3521 RSC.
- M. I. Kotzabasaki, I. Sotiropoulos and H. Sarimveis, QSAR modeling of the toxicity classification ofsuperparamagnetic iron oxide nanoparticles(SPIONs) in stem-cell monitoring applications: an integrated study from data curation to modeldevelopment, RSC Adv., 2020, 10, 5385–5391 RSC.
- J. Roy and K. Roy, Assessment of toxicity of metal oxide andhydroxide nanoparticles using the QSAR modeling approach, Environ. Sci.: Nano, 2021, 8, 3395–3407, 10.1039/d1en00733e.
- E. P. Sifonte, F. A. Castro-Smirnov, A. A. S. Jimenez, H. R. G. Diez and F. G. Martínez, Quantum mechanics descriptors in a nano-QSAR model to predict metal oxide nanoparticles toxicity in human keratinous cells, J. Nanopart. Res., 2021, 23, 161, DOI:10.1007/s11051-021-05288-0.
- D. D. Varsou, L. J. A. Ellis, A. Afantitis, G. Melagraki and I. Lynch, Ecotoxicological read-across models for predicting acute toxicity of freshly dispersed versus medium-aged NMs to Daphnia magna, Chemosphere, 2021, 285, 131452 CrossRef CAS PubMed.
- A. Gajewicz, Development of valuable predictive read-across models based on “real-life” (sparse) nanotoxicity data, Environ. Sci.: Nano, 2017, 4, 1389–1403 RSC.
- N. Ball, M. T. D. Cronin, J. Shen, K. Blackburn, E. D. Booth, M. Bouhifd, E. Donley, L. Egnash, C. Hastings, D. R. Juberg, A. Kleensang, N. Kleinstreuer, E. D. Kroese, A. C. Lee, T. Luechtefeld, A. Maertens, S. Marty, J. M. Naciff, J. Palmer, D. Pamies, M. Penman, A.-N. Richarz, D. P. Russo, S. B. Stuard, G. Patlewicz, B. van Ravenzwaay, S. Wu, H. Zhu and T. Hartung, Toward Good Read-Across Practice (GRAP) Guidance, ALTEX, 2016, 33, 149 CrossRef PubMed.
- V. Stone, S. Gottardo, E. A. J. Bleeker, H. Braakhuis, S. Dekkers, T. Fernandes, A. Haase, N. Hunt, D. Hristozov, P. Jantunen, N. Jeliazkova, H. Johnston, L. Lamon, F. Murphy, K. Rasmussen, H. Rauscher, A. S. Jiménez, C. Svendsen, D. Spurgeon, S. Vázquez-Campos, W. Wohlleben and A. G. Oomen, A framework for grouping and read-across of nanomaterials- supporting innovation and risk assessment, Nano Today, 2020, 35, 100941 CrossRef CAS.
- A. Mech, K. Rasmussen, P. Jantunen, L. Aicher, M. Alessandrelli, U. Bernauer, E. A. J. Bleeker, J. Bouillard, P. D. P. Fanghella, R. Draisci, M. Dusinska, G. Encheva, G. Flament, A. Haase, Y. Handzhiyski, F. Herzberg, J. Huwyler, N. R. Jacobsen, V. Jeliazkov, N. Jeliazkova, P. Nymark, R. Grafström, A. G. Oomen, M. L. Polci, C. Riebeling, J. Sandström, B. Shivachev, S. Stateva, S. Tanasescu, R. Tsekovska, H. Wallin, M. F. Wilks, S. Zellmer and M. D. Apostolova, Insights into possibilities for grouping and read-across for nanomaterials in EU chemicals legislation, Nanotoxicology, 2019, 13, 119–141 CrossRef CAS.
- A. Gajewicz, K. Jagiello, M. T. D. Cronin, J. Leszczynski and T. Puzyn, Addressing a bottle neck for regulation of nanomaterials: quantitative read-across (Nano-QRA) algorithm for cases when only limited data is available, Environ. Sci.: Nano, 2017, 4, 346–358 RSC.
- D.-D. Varsou, G. Tsiliki, P. Nymark, P. Kohonen, R. Grafström and H. Sarimveis, toxFlow: A Web-Based Application for Read-Across Toxicity Prediction Using Omics and Physicochemical Data, J. Chem. Inf. Model., 2018, 58, 543–549 CrossRef CAS PubMed.
- C. Helma, M. Rautenberg and D. Gebele, Nano-Lazar: Read across Predictions for Nanoparticle Toxicities with Calculated and Measured Properties, Front. Pharmacol., 2017, 8, 377, DOI:10.3389/FPHAR.2017.00377.
- D.-D. Varsou, A. Afantitis, G. Melagraki and H. Sarimveis, Read-across predictions of nanoparticle hazard endpoints: a mathematical optimization approach, Nanoscale Adv., 2019, 1, 3485–3498 RSC.
- A. Gajewicz, What if the number of nanotoxicity data is too small for developing predictive Nano-QSAR models? An alternative read-across based approach for filling data gaps, Nanoscale, 2017, 9, 8435–8448 RSC.
- A. Hasse and F. Klaessig, EU US Roadmap Nanoinformatics 2030, 2018 Search PubMed.
- R. Santana, R. Zuluaga, P. Gañán, S. Arrasate, E. Onieva and H. González-Díaz, Predicting coated-nanoparticle drug release systems with perturbation-theory machine learning (PTML) models, Nanoscale, 2020, 12, 13471–13483 RSC.
- B. Ortega-Tenezaca and H. González-Díaz, IFPTML mapping of nanoparticle antibacterial activity: Vs. pathogen metabolic networks, Nanoscale, 2021, 13, 1318–1330 RSC.
- V. V. Kleandrova, F. Luan, H. González-Díaz, J. M. Ruso, A. Melo, A. Speck-Planche and M. N. D. S. Cordeiro, Computational ecotoxicology: Simultaneous prediction of ecotoxic effects of nanoparticles under different experimental conditions, Environ. Int., 2014, 73, 288–294 CrossRef CAS.
- R. Santana, R. Zuluaga, P. Gañán, S. Arrasate, E. Onieva and H. González-Díaz, Designing nanoparticle release systems for drug-vitamin cancer co-therapy with multiplicative perturbation-theory machine learning (PTML) models, Nanoscale, 2019, 11, 21811–21823 RSC.
- F. Luan, V. V. Kleandrova, H. González-Díaz, J. M. Ruso, A. Melo, A. Speck-Planche and M. N. D. S. Cordeiro, Computer-aided nanotoxicology: Assessing cytotoxicity of nanoparticles under diverse experimental conditions by using a novel QSTR-perturbation approach, Nanoscale, 2014, 6, 10623–10630 RSC.
- M. S. Chavali and M. P. Nikolova, Metal oxide nanoparticles and their applications in nanotechnology, SN Appl. Sci., 2019, 1, 607, DOI:10.1007/s42452-019-0592-3.
- M. Farré and D. Barceló, in Comprehensive Analytical Chemistry, ed. M. Farré and D. Barceló, Elsevier, 2012, vol. 59, pp. 1–32 Search PubMed.
- J. P. Best and D. E. Dunstan, Nanotechnology for photolytic hydrogen production: Colloidal anodic oxidation, Int. J. Hydrogen Energy, 2009, 34, 7562–7578 CrossRef CAS.
- Metal Nanoparticles Market by metal (Platinum, Gold, Silver, Iron, Titanium, Copper, Nickel), End-use industry (Pharmaceutical & healthcare, Electrical & electronics, Catalyst, Personal care & cosmetics), and Region - Global Forecast to 2022, https://www.marketsandmarkets.com/Market-Reports/metal-nanoparticle-market-138262033.html, (accessed 5 August 2021).
- A. Gajewicz, N. Schaeublin, B. Rasulev, S. Hussain, D. Leszczynska, T. Puzyn and J. Leszczynski, Towards understanding mechanisms governing cytotoxicity of metal oxides nanoparticles: Hints from nano-QSAR studies, Nanotoxicology, 2015, 9, 313–325 CrossRef CAS.
- T. Puzyn, B. Rasulev, A. Gajewicz, X. Hu, T. P. Dasari, A. Michalkova, H.-M. Hwang, A. Toropov, D. Leszczynska and J. Leszczynski, Using nano-QSAR to predict the cytotoxicity of metal oxide nanoparticles, Nat. Nanotechnol., 2011, 6, 175–178 CrossRef CAS PubMed.
- K. Pathakoti, M. J. Huang, J. D. Watts, X. He and H. M. Hwang, Using experimental data of Escherichia coli to develop a QSAR model for predicting the photo-induced cytotoxicity of metal oxide nanoparticles, J. Photochem. Photobiol., B, 2014, 130, 234–240 CrossRef CAS.
- K. Roy, S. Kar and R. N. Das, in Understanding the Basics of QSAR for Applications in Pharmaceutical Sciences and Risk Assessment, Academic Press (Elsevier), London, 2015, pp. 47–80 Search PubMed.
- K. Roy, S. Kar and R. N. Das, in Understanding the Basics of QSAR for Applications in Pharmaceutical Sciences and Risk Assessment, Academic Press (Elsevier), London, 2015, pp. 81–102 Search PubMed.
- A. Nel, T. Xia, L. Mädler and N. Li, Toxic Potential of Materials at the Nanolevel, Science, 2006, 311, 622–627 CrossRef CAS PubMed.
- K. Unfried, C. Albrecht, L.-O. Klotz, A. Von Mikecz, S. Grether-Beck and R. P. F. Schins, Cellular responses to nanoparticles: Target structures and mechanisms, Nanotoxicology, 2007, 1, 52–71 CrossRef CAS.
- C. Oksel, D. A. Winkler, C. Y. Ma, T. Wilkins and X. Z. Wang, Accurate and interpretable nanoSAR models from ge- netic programming-based decision tree construction approaches, Nanotoxicology, 2016, 10, 1001–1012 CrossRef CAS.
- I. Kononenko and M. Kukar, in Machine Learning and Data Mining, Horwood Publishing Limited, Chichester, 2007 Search PubMed.
- K. K. Dobbin and R. M. Simon, Optimally splitting cases for training and testing high dimensional classifiers, BMC Med. Genomics, 2011, 4, 31 CrossRef.
- K. Roy, S. Kar and R. N. Das, in Understanding the Basics of QSAR for Applications in Pharmaceutical Sciences and Risk Assessment, 2015, pp. 191–229 Search PubMed.
- J. Tabak, Geometry: The Language of Space and Form, Infobase Publishing, 2014 Search PubMed.
- K. Roy, P. Chakraborty, I. Mitra, P. K. Ojha, S. Kar and R. N. Das, Some case studies on application of “rm2” metrics for judging quality of quantitative structure–activity relationship predictions: Emphasis on scaling of response data, J. Comput. Chem., 2013, 34, 1071–1082 CrossRef CAS.
- J. Chen, C. Wang, Y. Sun and X. Shen, Semi-supervised Laplacian regularized least squares algorithm for localization in wireless sensor networks, Comput. Netw., 2011, 55, 2481–2491 CrossRef.
- K. Roy, S. Kar and R. N. Das, in Understanding the Basics of QSAR for Applications in Pharmaceutical Sciences and Risk Assessment, Academic Press (Elsevier), London, 2015, pp. 231–289 Search PubMed.
- M. J. Saary, Radar plots: a useful way for presenting multivariate health care data, J. Chronic Dis., 2008, 61, 311–317 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Supplementary Tables (Tables S1–S11). Software and input and output files. See DOI: 10.1039/d1en00725d |
| This journal is © The Royal Society of Chemistry 2022 |