The low overpotential regime of acidic water oxidation part II: trends in metal and oxygen stability numbers

Abstract

The operating conditions of low pH and high potential at the anodes of polymer electrolyte membrane electrolysers restrict the choice of catalysts for the oxygen evolution reaction (OER) to oxides based on the rare metals iridium or ruthenium. In this work, we investigate the stability of both the metal atoms and, by quantitative and highly sensitive ¹⁸O isotope labelling experiments, the oxygen atoms in a series of RuO_x and IrO_x electrocatalysts during the OER in the mechanistically interesting low overpotential regime. We show that materials based on RuO_x have a higher dissolution rate than the rate of incorporation of labelled oxygen from the catalyst into the O₂ evolved (“labelled OER”), while for IrO_x-based catalysts the two rates are comparable. On amorphous RuO_x, metal dissolution and labelled OER are found to have distinct Tafel slopes. These observations together lead us to a full mechanistic picture in which dissolution and labelled OER are side processes to the main electrocatalytic cycle. We emphasize the importance of quantitative analysis and point out that since less than 0.2% of evolved oxygen contains an oxygen atom originating from the catalyst itself, lattice oxygen evolution is at most a negligible contribution to overall OER activity for RuO_x and IrO_x in acidic electrolyte.

---

Broader context

Water electrolysis, which produces hydrogen (H₂) and oxygen (O₂) from water and electricity, is a central technology for decarbonization of industry and transport. Polymer electrolyte membrane electrolysis cells have several advantages over other electrolysis technologies but require the rare element iridium to catalyze water oxidation in the high-potential, low-pH environment of the anode. Iridium is produced as a byproduct of platinum mining in only ∼10 tons per year, far short of what is needed at present electrolyser loadings to supply the TW-level H₂ demand predicted in the coming decades. The most studied alternative, ruthenium, is almost as rare. The demand for iridium or ruthenium can be lowered by improving their activity or lowering their degradation rates, both of which necessitate a fundamental understanding of the mechanistic relationship between oxygen evolution and material degradation. ¹⁸O isotope-labelling studies provide a way to investigate this relationship, but to be insightful we argue that the isotopic labelling study must be quantitative and be combined with quantitative measurements of metal dissolution. In this article, we do just that for a range of iridium and ruthenium-based catalysts and use the results to create a combined mechanistic picture of water oxidation and material degradation.

Introduction

A major bottleneck in technologies essential to enabling society's transition away from fossil fuels looms in the requirement of the extremely rare noble metal iridium (Ir) in the anode of polymer electrolyte membrane electrolysis cells (PEMEC) for production of H₂ by water electrolysis with renewable electricity.^1–6 The most-studied alternatives to Ir-based PEMEC anode electrocatalysts are oxides based on ruthenium (Ru), which show lower stability, but slightly higher OER activity, than Ir-based oxides.^7,8 However, Ru is, like Ir, a platinum mining biproduct with only ∼3 times the annual global production of Ir (ref. 9), and so is also insufficiently scalable. Continued research in Ru- and Ir-based oxides is nonetheless valuable because: (i) modest improvements in stability and activity improve the scalability of Ir or Ru-based PEMEC technology by enabling electrolyser devices to run at the same efficiency with lower catalytic loading; and (ii) a better understanding of why these two materials are relatively active and stable helps guide the discovery of new acid-stable OER catalysts based on more abundant elements.

Stability and catalytic activity of metal oxides for the OER are linked through the reactivity of oxygen atoms: metal–oxygen bonds are formed and broken during the electrocatalytic cycle oxidizing water, and metal–oxygen bonds are also what holds the material together. A way to probe this interplay is by isotope labelling of the oxygen in the electrocatalyst with ¹⁸O and determining whether this labelled oxygen is incorporated in the O₂ released and/or unlabelled oxygen from the electrolyte is incorporated in the electrocatalyst during operation. In acidic electrolyte (the focus of our study) incorporation of labelled oxygen in O₂ has previously been detected from amorphous oxides of iridium formed by thermal decomposition of HIrCl₆ (ref. 10) potential cycling^11,12 or leaching of SrIrO₃ (ref. 11) as well as RuO_x sputter-deposited on a porous membrane¹³ and doped nanocrystalline RuO₂ (ref. 14), but not on smooth crystalline IrO₂ (ref. 11 and 12) or RuO₂ (ref. 15). In alkaline electrolyte, incorporation of labelled oxygen in O₂ was detected from perovskite electrocatalysts with oxygen vacancies (La_0.5Sr_0.5, CoO_3−δ, and Pr_0.5Ba_0.5CoO_3−δ, and SrCoO_3−δ) (ref. 16) and spinel Co₃O₄ (ref. 17), but not LaCoO₃ (ref. 16) or NiFeO_xH_y (ref. 18). Fig. 1 compiles these results from prior isotope-labelling studies: Studies that showed labelled oxygen evolution are above the x-axis. Of these, studies where the amount of labelled oxygen evolution was shown to be more than one monolayer are further located in one of the top two sectors (I or II). studies where the amount of labelled oxygen evolution was shown to be more than the amount of metal dissolution during the same measurement are further located in one of the two left sectors (I or III).

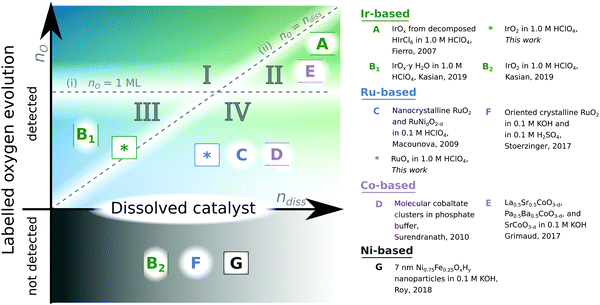Fig. 1 Summary of results of ¹⁸O isotope-labelling studies. The y-axis indicates the amount of labelled oxygen detected in the O₂ evolved. If no labelled oxygen is detected from the electrocatalyst, it is placed below the x-axis. If the labelled oxygen evolution exceeded one monolayer, the study is placed above the horizontal line labelled n_O = 1 ML in either sector I or II. The x-axis indicates the amount of metal dissolved from the catalyst. If the labelled oxygen evolution exceeded metal dissolution, the study is placed above the 45° line labelled n_O = n_diss, in either sector I or III. The two dashed lines thus divide the space into four sectors with the following implied meanings: (I) true lattice oxygen evolution, (II) degradative lattice oxygen evolution, (III) surface bound oxygen evolution, and (IV) labelled oxygen evolution of unknown origin. A is ref. 10; B is ref. 12; C is ref. 14; D is ref. 24; E is ref. 16; F is ref. 15; and G is ref. 18.

Comparison of results in isotope-labeling OER studies is complicated by the use of varying experimental procedures, which are compiled in Table S1 (ESI†). To summarize the variety of experimental procedures: isotopic signals (or lack thereof) in the evolved O₂ have been detected by several in situ electrochemistry – mass spectrometry (EC-MS) techniques including differential EC-MS (DEMS),^{10,13,14,17,19} on-line EC-MS (OLEMS),^15,16,20 scanning flow cell (SFC) OLEMS,^11,12 and chip EC-MS.^18,21 The isotopic composition of the oxygen in the electrocatalyst has been measured by ex situ isotope-sensitive techniques including Raman spectroscopy,²² atomic probe tomography (APT)²³ and low-energy ion scattering spectrometry (LEIS).¹⁸ While most studies use various methods to isotopically label the electrocatalyst,^{11,12,21–24} some instead label the electrolyte.^10,18

When the isotopic label of the electrocatalyst has been detected in the evolved O₂, it has often been attributed to a “lattice oxygen evolution mechanism” (LOM), of which several have been proposed.^{7,11,16,25,26} In both acidic and alkaline electrolytes, observation of a LOM has been proposed to be associated with increased activity compared to catalysts which only produce oxygen through the conventional mechanism involving sequential adsorption and deprotonation of water,^11,27 while in acidic electrolytes it has also been correlated with electrocatalyst dissolution.^11,12 None of these works, however, provides an explicit definition of “lattice oxygen”, implicitly equating it with the “labelled oxygen” that the experiment is able to measure. The distinction is however important: labelled oxygen can include water intercalated in an electrocatalyst, and at the surface of the electrocatalyst it is not trivial to categorize oxygen atoms as “adsorbed oxygen” vs. “lattice oxygen”, nor is it trivial to know for sure if they can be labelled or will exchange spontaneously with oxygen atoms in the electrolyte.

We propose, in line with previous work,^16,27,28 that lattice oxygen should be defined as oxygen atoms with the same coordination environment as is experienced by oxygen in the bulk of a crystalline material. Loosely adsorbed water molecules or oxygen adsorbed on secondary oxide phases are not considered lattice oxygen by this definition, and can also not easily be isotopically labelled since they are in equilibrium with the bulk electrolyte. Tightly coordinated oxygen atoms on the surface can be borderline cases. For instance, on the (110) surface of rutile RuO₂ or IrO₂, our definition of “lattice oxygen” includes three-fold coordinated surface oxygen but excludes any oxygen adsorbed on metal coordinatively unsaturated (CUS) sites as well as bridging oxygen atoms, even though bridging oxygen atoms do not exchange spontaneously with the electrolyte at the open-circuit potential²⁹ and can thereby retain an isotopic label from synthesis to the start of OER. See Fig. S1 of the (ESI†) for further discussion of this definition.

To test a lattice oxygen evolution mechanism according to this definition of lattice oxygen, two conditions need to be met: (i) an experiment should show that the amount of labelled oxygen from the electrocatalyst which is incorporated in the O₂ evolved (n_O) exceeds one monolayer equivalent (1 ML), as otherwise the labelled oxygen could come from tightly bound surface adsorbed oxygen such as bridging oxygen. Furthermore, to examine that lattice oxygen evolution is a catalytic mechanism and not part of a degradation process, (ii) an experiment should also show that the amount of lattice oxygen evolved exceeds the amount of metal dissolved (n_diss), which can be measured by inductively coupled plasma – mass spectrometry (ICP-MS). We indicate the studies that satisfy either of these two criteria by the divisions in Fig. 1: if criterion (i) is met, a study lies above the n_O = 1 ML line; and if criterion (ii) is met, it lies above the n_O = n_diss line. Unfortunately, most prior studies were qualitative in nature and did not measure the electrochemically active surface area, and/or did not measure metal dissolution. To the best of our knowledge, sector I of Fig. 1 is empty, i.e., no isotope-labelling study of oxygen evolution electrocatalysis has conclusively shown a lattice oxygen evolution mechanism according to these criteria.

Quantitative results are also needed to gauge the potential importance of a lattice oxygen evolution mechanism if it does occur. To this end, with inspiration from the “stability number” introduced by Geiger and Kasian et al.,¹¹ we introduce the oxygen stability number as the total number of O₂ molecules evolved divided by the number of labelled oxygen atoms from the electrocatalyst incorporated in the O₂. Like the original stability number¹¹ (here referred to as the metal stability number to avoid confusion), which is the number of O₂ evolved divided by the number of metal atoms dissolved, the oxygen stability number of an electrocatalyst material is in general a function of the electrolysis conditions such as the applied current density.

In this article, we present an extensive dataset of labelled oxygen evolution and metal dissolution for a range of ruthenium and iridium based oxides prepared with ¹⁸O during electrolysis in acidic electrolyte in the mechanistically interesting low-overpotential regime. We use chip EC-MS to detect oxygen evolved during OER, LEIS to characterize the isotopic label on the electrocatalytic surface before and after OER, and ICP-MS to measure metal dissolution; and the results are organized in a homemade relational database accompanying this article. In addition to being fully quantitative, these are by far the most sensitive isotope labelling experiments in OER to date: while, for example, SFC-OLEMS has a detection limit of ∼4 nmol s⁻¹ cm⁻² (ref. 30) chip EC-MS has a detection limit of <1 pmol s⁻¹ cm⁻² (ref. 31). It is this sensitivity which enables us to quantify labelled oxygen evolution in a low current regime where depletion of the isotopic label can be ruled out, allowing us to determine conclusively the oxygen stability numbers, and thus the relative importance of the adsorbate oxidation and lattice oxygen oxidation mechanisms to the OER activity. By comparing trends in metal stability number and oxygen stability number across materials and applied current densities, we are able to sketch a general mechanistic picture relating water oxidation, lattice oxygen evolution, and metal dissolution in Ru- and Ir-based catalysts for water oxidation in acid.

Results

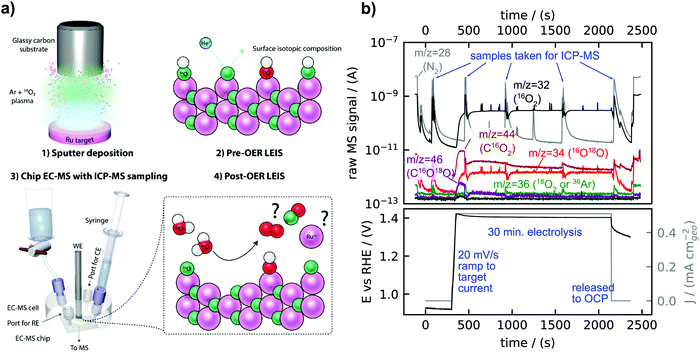
Fig. 2a is a sketch of the experimental procedure, described in detail in the Experimental section. Briefly, isotopically labelled Ru¹⁸O_x and Ir¹⁸O_x catalysts were synthesized, usually by reactive sputter deposition in a plasma including ¹⁸O₂, and the initial surface isotopic composition was characterized by LEIS. Samples were tested at constant current in the chip EC-MS setup modified to collect electrolyte samples for ICP-MS measurements of metal dissolution before post-reaction LEIS characterization. The dissolution of OER catalysts is known to be dependent on the flow characteristics of the setup³² – in this regard, the stagnant thin layer of electrolyte in the EC-MS setup resembles more the environment experienced by an OER catalyst in a PEMEC than do most aqueous model systems.

Fig. 2 (a) Experimental setup and procedure. Samples are synthesized with ¹⁸O by reactive sputter deposition and characterized by low-energy ion scattering (LEIS), which is sensitive to the surface isotopic ratio. They are then tested for OER activity, lattice oxygen evolution, and dissolution in a chip electrochemistry – mass spectrometry cell modified for collecting electrolyte samples during the experiment, and characterized again by LEIS afterwards. (b) Example EC-MS experiment on s-25 °C Ru¹⁸O_x annotated with m/z ratios and special events. The raw mass spectrometry signals are shown in the top panel on a log scale and the concurrent electrochemical potential and current density are shown in the bottom panel. The data shown starts with air in the cell (m/z = 28 and 32 signals for N₂ and O₂, respectively), and electrolyte is inserted in the first few seconds. The electrochemical measurement was started at open circuit potential at t = 0, and at t ∼ 300 s, the potential was scanned at 20 mV s⁻¹ until the current reached 0.5 mA cm⁻²_geo. This current density was held for 30 minutes. At the five times indicated, electrolyte was extracted for later analysis by ICP-MS, causing a spike in the m/z = 28 signal as fresh air-saturated electrolyte enters the cell.

Fig. 2b shows raw EC-MS data from a typical experiment, here for a catalyst of amorphous ruthenium oxide created by reactive sputter deposition at room temperature (s-25 °C Ru¹⁸O_x). Signals associated with O₂ at m/z = 32 (¹⁶O₂) and m/z = 34 (¹⁶O¹⁸O) and with CO₂ at m/z = 44 (C¹⁶O₂) and m/z = 46 (C¹⁶O¹⁸O) increased at the start of the electrolysis period. There was a detectable amount of C¹⁸O₂ at m/z = 48 but ¹⁸O₂ at m/z = 36 was not detectable; the small m/z = 36 signal observed moves together with N₂ (m/z = 28) and ⁴⁰Ar (m/z = 40) and is therefore attributed to ³⁶Ar in air. The detected CO₂ decreased with time and can be attributed to the oxidation of adventitious carbon species adsorbed on the catalyst surface. The isotopic analysis of CO₂ formed electrochemically was the subject of two recent works,^21,33 and will not be evaluated in detail in the present work, where we focus on isotopic signals of O₂. The four electrolyte sampling events during electrolysis were visible in the m/z = 28 signal, as the fresh electrolyte drawn into the cell is air-saturated. Each sample of the electrolyte involves collecting ∼200 μL to ensure that the entire working electrolyte of 2 μL is collected and replenished with fresh electrolyte. However, electrolyte sampling did not cause a change in the electrochemical potential or steady state O₂ signals at m/z = 32 (¹⁶O₂) and m/z = 34 (¹⁶O¹⁸O), which indicates that the electrolyte flow did not influence the electrochemical kinetics.

Careful analysis of the data in Fig. 2b reveals that some labelled oxygen from the amorphous RuO_x catalyst was incorporated into the O₂ evolved. In order to understand whether the m/z = 34 signal can be fully accounted for by the natural 0.20% abundance of H₂¹⁸O in the electrolyte, corresponding to a natural ¹⁶O¹⁸O/¹⁶O₂ ratio of 0.40%, we re-plot the O₂ signals of Fig. 2b in Fig. 3a as an “isotope-tracking plot”.²¹ In the middle panel of Fig. 3a, calibrated and background-subtracted O₂ signals are plotted vs. time on two separate linearly scaled y-axes, with the ¹⁶O¹⁸O flux plotted in red on a left y-axis and the ¹⁶O₂ flux plotted in black on a right y-axis. The two axes are scaled according to the natural ¹⁶O¹⁸O/¹⁶O₂ ratio of 0.40%. The natural ¹⁶O¹⁸O/¹⁶O₂ ratio was confirmed regularly by OER with un-labelled samples, consistently resulting in 0.400% ± 0.005%. Plotted this way, whenever ¹⁸O from the labelled oxide electrocatalysts is incorporated in the O₂ evolved, the red trace will deviate from the black trace. In this experiment (Fig. 3a), the red trace exceeds the black trace by about 0.5 pmol s⁻¹ cm⁻²_geo of ¹⁶O¹⁸O flux, easily discernible due to the sensitivity of the method. This is the rate at which labelled oxygen from the electrocatalyst was incorporated into the O₂ evolved. In comparison, the total OER rate was 1300 pmol s⁻¹ cm⁻²_geo; only ∼50 ppm of the total oxygen evolved contained a labelled oxygen atom. The integrated excess ¹⁸O in the O₂ was about 750 pmol cm⁻²_geo.

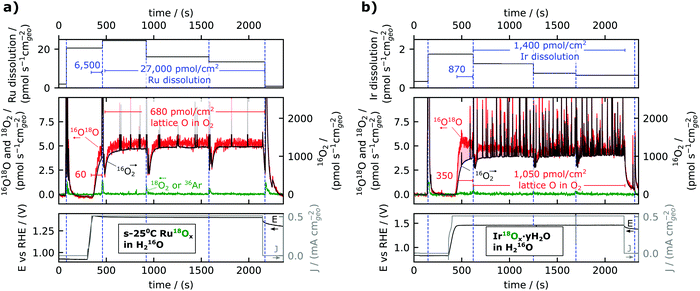Fig. 3 Dissolution (top panels) and lattice oxygen reactivity (middle panels) during stability experiments (electrochemistry data in bottom panel) for (a) s-25 °C Ru¹⁸O_x and (b) electrochemically cycled Ir¹⁸O_x (Ir¹⁸O_x·yH₂¹⁸O). Dissolution is shown as a time-averaged rate between electrolyte sampling periods. Lattice oxygen reactivity is shown by plotting the MS data with ¹⁶O¹⁸O on the left y-axis and ¹⁶O₂ on the right y-axis, and the axes are scaled according to the natural isotopic ratio so that any incorporation of lattice oxygen in the O₂ evolved causes the red trace (¹⁶O¹⁸O) to lie above the black trace (¹⁶O₂). (a) Represents the same experimental data as is shown raw in Fig. 2b. The noisy oxygen signals in (b) are presumably due to the formation of small bubbles.

The ruthenium dissolution rate was about 20 pmol s⁻¹ cm⁻²_geo; this is about a factor 60 smaller than the rate of oxygen evolution (1300 pmol s⁻¹ cm⁻²_geo), consistent with Roy et al.,³⁴ but at the same time about a factor 40 larger than the rate of labelled oxygen incorporated in the O₂ evolved (0.5 pmol s⁻¹ cm⁻²_geo). This result is shown in the top panel of Fig. 3a as the normalized rate of ruthenium dissolution indicated in pmol s⁻¹ cm⁻²_geo for each electrolyte sample taken during electrolysis. The average ruthenium dissolution rate was the highest at the start of the electrolysis period and slowly decreased with time. Note the dissolution rate plotted in the top panel is averaged over the time interval between the taking of electrolyte samples, but that this value underestimates the dissolution rate at the start of the electrolysis period. To further facilitate the quantitative comparison between the amounts of dissolution and labelled oxygen evolution, their integral values in pmol cm⁻²_geo are displayed as annotations with blue font in Fig. 3a. Two timespans are used for the integral values: one for the ramp-up and first ∼2 minutes of electrolysis, during which capacitive charging makes up a significant portion of the current;³⁵ and the other for the remainder of the electrolysis in steady-state. Taking into account that the Ru dissolution commences with the onset of applied current, the ramp-up to 0.5 mA cm⁻²_geo (∼1.4 V_RHE) was found to have more than 100 Ru atoms dissolved per labelled oxygen in the evolved O₂ (6500 pmol cm⁻²_geo dissolved Ru compared to 60 pmol cm⁻²_geo labelled OER), in contrast to the reduced dissolution rate of ∼40 Ru atoms dissolved per labelled oxygen atom evolved during steady state electrolysis (27 000 pmol cm⁻²_geo dissolved Ru compared to 680 pmol cm⁻²_geo labelled OER).

The labelled oxygen evolved during 30 minutes of electrolysis was ∼2% of a monolayer, using the capacitive charging current to determine the surface area, whereas the ruthenium dissolution approximately corresponded to one monolayer. In the first article of this series,³⁵ we showed that ruthenium oxides sputter-deposited at a series of temperatures ranging from 25 °C to 400 °C had widely varying activity on a geometric basis, but that activity converges when normalizing by capacitive charging current, motivating capacitive charging current as a measure of the electrochemically active surface area (ECSA) on these catalysts. To determine the number of moles in a monolayer equivalent, we further use a specific capacitance of 115 μF cm⁻²_geo from ref. 35 and an active site density of 5 nm⁻², which is the density of coordinatively unsaturated sites on RuO₂(110). The fact that the amount of labelled oxygen evolution is much lower than a monolayer equivalent implies that it is likely limited to oxygen atoms at the surface of the catalyst, such as bridging oxygen atoms.

The experiment described in Fig. 2 and 3 was performed on a range of ¹⁸O labelled electrocatalysts (see Experimental section and ESI†), most with multiple repetitions on separate samples of the same electrocatalyst type, and all details are included in the ESI† and in the online repository. As an illustrative comparison, a measurement for hydrous iridium oxide (Ir¹⁸O_x·yH₂O) is shown in Fig. 3b. This catalyst was prepared by the method described in ref. 11: an Ir¹⁸O₂ film was prepared by reactive sputter deposition with ¹⁸O₂ in the plasma and then electrochemically cycled (200 times at 50 mV s⁻¹ from 0 V_RHE to 1.5 V_RHE) in 0.1 M HClO₄ electrolyte made with H₂¹⁸O; a procedure known to form an amorphous hydrous surface layer.^36,37 Ir¹⁸O_x·yH₂O evolved a significant amount of labelled oxygen at the beginning of the measurement, peaking at about ∼3 pmol s⁻¹ cm⁻²_geo, but the labelled OER rate decreased to about 1 pmol s⁻¹ cm⁻²_geo within the first five minutes at 0.5 mA cm⁻²_geo. Compared to a crystalline sputter-deposited Ir¹⁸O₂ film (Fig. S2, ESI†), Ir¹⁸O_x·yH₂O showed higher activity (1.46 V_RHE instead of 1.51 V_RHE to reach 0.5 mA cm⁻²_geo), higher dissolution (∼1 pmol s⁻¹ cm⁻²_geo instead of 0.1), and higher labelled oxygen evolution (∼1 pmol s⁻¹ cm⁻²_geo instead of 0.2). This is all in agreement with previous results reported at higher overpotentials,^11,12,23 except that previous measurements were not sensitive enough to measure the labelled oxygen evolved from Ir¹⁸O₂. All iridium samples were much more stable against dissolution than RuO_x. Dissolution of Ir from Ir¹⁸O_x·yH₂O exceeded evolution of labelled oxygen by a factor 2.5 in the ramp-up (870 pmol cm⁻²_geo Ir compared to 350 pmol cm⁻²_geo¹⁸O) and only by a factor 1.3 at steady state (1400 pmol cm⁻²_geo Ir compared to 1050 pmol cm⁻²_geo¹⁸O). On several other iridium-based samples, labelled oxygen incorporation into O₂ modestly exceeded metal dissolution (Fig. 4 and Fig. S2, ESI†).

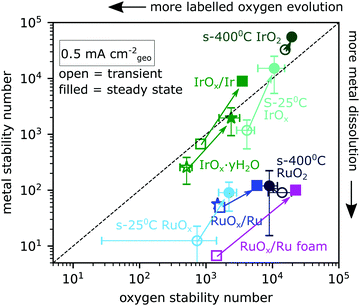Fig. 4 The number of O₂ evolved per metal atom dissolved (metal stability number) is plotted against the number of O₂ evolved per labelled oxygen evolved (oxygen stability number) for Ru- and Ir-based catalysts. Data come from 30 minute constant-current electrolysis experiments at 0.5 mA cm⁻²_geo (e.g.Fig. 3) and are divided into transient data (open symbols, t ≤ ∼2 minutes) and steady state data (filled symbols, t > ∼2 min). Sputter-deposited oxides are indicated as circles, electrochemically oxidized metallic films as squares, and electrochemically cycled films as stars. Error bars are standard deviation for at least two samples.

By correlating the labelled oxygen evolution rate with the metal dissolution rate in Fig. 4, distinct groupings emerge for Ir-based and Ru-based catalysts. The y-axis shows the metal stability number, which is the number of O₂ molecules evolved per metal atom dissolution.¹¹ The x-axis shows the oxygen stability number, defined in the introduction and which we in practice equate with the total number of O₂ molecules evolved per included ¹⁸O atom in excess of that expected from the natural isotope ratio. The labelled oxygen evolution rate increases to the left in the plot and the metal dissolution rate increases downwards. Both stability numbers were calculated for the first ∼2 minutes of electrolysis at 0.5 mA cm⁻²_geo and for steady state, as indicated by the integral values in Fig. 3. This enables us to plot each catalyst type as if it were two distinct surfaces – a transient surface during the ramp-up period (open symbols) and the stable surface of steady state electrolysis (filled symbols). Error bars represent the standard deviation of the respective value of at least two independently prepared samples and are included for most sample types. All samples show lower stability numbers (more dissolution and more lattice oxygen evolution) at the onset of electrolysis than at steady state. The steady-state metal stability numbers we measured for Ru-based catalysts are comparable to those reported in ref. 34. The stability we measure for s-400 °C IrO₂ (crystalline Ir¹⁸O₂ sputter-deposited at 400 °C) is lower than some previously reported values (∼7 × 10⁴ in our case compared to 10⁵–10⁶).³⁸ The difference might be due to the stability number being lower at the low current densities probed by chip EC-MS or due to imperfect electrolyte exchange in the cell when the electrolyte was sampled, which could cause some of the metal dissolution from the ramp-up period to remain in the cell and cross-contaminate the steady-state electrolyte samples. Ruthenium-based samples lie well below the y = x line, meaning that they lose ruthenium atoms to dissolution much faster than they incorporate lattice oxygen into the O₂ evolved. On the other hand, all iridium-based oxides lie close to the y = x line, meaning that lattice oxygen is incorporated into the O₂ at a rate comparable to metal dissolution.

Some iridium-based samples exhibit more labelled oxygen evolution than metal dissolution, i.e. n_O > n_diss. This list includes s-400 °C Ir¹⁸O₂ (crystalline Ir¹⁸O₂ sputter-deposited at 400 °C), where the isotopic signal is one labelled oxygen atom per ∼20 000 O₂ molecules evolved, which was only detectable due to the high sensitivity and careful integration and background subtraction in comparison with control measurements. The dissolution rate was even lower, at one dissolved iridium atom per ∼50 000 O₂ molecules evolved. The labelled oxygen evolution from the samples for which n_O > n_diss was, however, always below one monolayer: for example, O₂ from s-400 °C Ir¹⁸O₂ during 30 min at 0.5 mA cm⁻²_geo contained ∼100 pmol cm⁻²_geo¹⁸O (Fig. S2, ESI†), compared to 230 pmol cm⁻²_geo of Ir_CUS sites on flat IrO₂(110). They thus fit in sector III of Fig. 1 for which n_O > n_diss is demonstrated but not n_O > 1 ML, and may accordingly represent “surface lattice oxygen evolution reaction (surface LOER)”, i.e., some of the labelled oxygen on the surface enters the OER catalytic cycle as if it were an adsorbate. In contrast to OER, electrochemical CO oxidation on s-25 °C Ir¹⁸O_x, first described in ref. 21, exhibited unambiguous lattice oxygen incorporation in the CO₂ evolved with n_O > n_diss and n_O > 1 ML as shown in Fig. S3 (ESI†).

It is informative to compare films that differ only in their sputter deposition temperature. As described in the first article of this series, for RuO_x a higher sputter deposition temperature results in a more crystalline film and lower geometric activity, but the same activity when normalized to capacitance, indicating a difference only in the geometric density of accessible surface sites. However, this cannot by itself explain the higher oxygen stability number observed in s-400 °C RuO₂ compared to s-25 °C RuO_x, which we would expect to be the same if the surfaces had the same intrinsic activity and stability and stability numbers did not change as a function of potential. Nor would lower geometric density of accessible surface sites by itself be able to explain the higher metal and oxygen stability numbers seen in s-400 °C IrO₂ compared to s-25 °C IrO_x. In both cases it must be related either to the intrinsic stability of surface sites (though not necessarily the same surface sites as for oxygen evolution) or to the difference potential required to reach the 0.5 mA cm⁻² applied current density used in these measurements.

For RuO_x, dissolution always exceeded labelled oxygen evolution, but the two processes did not follow the same trend with applied current density (Fig. 5a) or potential (Fig. 5b). Since n_O < n_diss for all ruthenium-based samples (Fig. 4), the additional experiments in Fig. 5 were needed to determine whether labelled oxygen evolution from ruthenium-based oxides is “surface LOER”, “degradative LOER”, or both. If the labelled oxygen evolving mechanism shared a rate-determining step with water oxidation, we should expect labelled O₂ evolution to be proportional to total O₂ production and thus for the lattice oxygen stability number to be constant with respect to total current density. On the other hand, if the labelled oxygen evolving mechanism is a bi-product of degradation, we should expect it to be proportional to the metal dissolution, and thus for the lattice oxygen stability number to show the same dependence on overall current density as the metal stability number. Fig. 5a shows the result for s-25 °C Ru¹⁸O₂. The steady-state metal stability number for s-25 °C Ru¹⁸O₂ increases with current density, indicating that dissolution increases more slowly with potential (has a higher Tafel slope) than oxygen evolution. On the other hand, the lattice oxygen stability number remains steady at about 3000 O₂ molecules evolved for each inclusion of a labelled oxygen atom. The different trends indicate that lattice oxygen evolution on RuO₂ is mechanistically distinct from dissolution, i.e. that it is more likely to be “surface LOER” than “degradative LOER”. The same analysis was not repeated on IrO₂ since labelled oxygen evolution and metal dissolution do not significantly exceed the respective detection limits at lower current densities than 0.5 mA cm⁻²_geo.

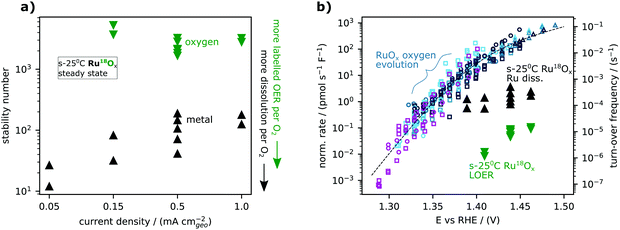Fig. 5 Trends in lattice oxygen and metal steady-state stability for labelled ruthenium oxide sputter-deposited at room temperature (s-25 °C Ru¹⁸O_x). (a) The metal stability number (black) and oxygen stability number (green) are plotted against the applied geometric current density. Each point at a given current density is from an independently prepared sample. (b) The same results shown as molar rate normalized by electrode capacitance and plotted against potential. The activity measurements (small symbols) and model (dashed line) from the accompanying manuscript³⁵ are included for context. The right y-axis indicates the corresponding turn-over frequency estimated using a specific capacitance of 115 μF cm⁻²_ECSA (from single crystal measurements [ref. 39 and DOI: 10.1039/D1EE03914H]) and a site density of 5 nm⁻²_ESCA (that of CUS sites on RuO₂(110)) for the conversion.

It is illustrative to think of (electrolyte) oxygen evolution, metal dissolution, and labelled (lattice) oxygen evolution as three processes occurring simultaneously at different rates as a function of potential. Fig. 5b shows the capacitance-normalized molar rates for the exchange and dissolution data in Fig. 5a against potential together with the activity dataset for sputter-deposited RuO_x films and Ru foam introduced in the first article of this series (DOI: 10.1039/D1EE03914H). The intrinsic activity of all three processes can also be expressed as approximate turn-over-frequencies by normalizing to the number of active sites, as indicated by the right y-axis of Fig. 5b. While labelled oxygen evolution follows the same trend vs. potential as water oxidation on RuO_x, metal dissolution follows a different trend. Specifically, in the range studied, lattice oxygen evolution has a Tafel slope of <∼60 mV per decade which decreases (higher potential dependence) with decreasing overpotential, following the overall OER activity, while metal dissolution has a Tafel slope of ∼120 mV per decade.

Low-energy ion scattering spectrometry (LEIS) characterization after electrolysis experiments revealed that more oxygen from the electrolyte was incorporated into the surface of both ruthenium-based and iridium-based catalysts than could be explained by exchange through lattice oxygen evolution. Fig. 6a and b show the spectra for the s-25 °C RuO₂ and IrO_x·yH₂O catalysts following the EC-MS experiments shown in Fig. 3a and b, respectively. The ¹⁶O in the as-prepared samples (lower spectra) may come from impurities in the sputter chamber during sample synthesis or strong adsorption of water (surface hydration) during air exposure between synthesis and characterization. After OER (middle spectrum in Fig. 6a), the portion of ¹⁶O on the as-prepared s-25 °C Ru¹⁸O₂ catalyst had increased from ∼13% to ∼30%, implying a small degree of either oxygen exchange or hydration during the electrolysis experiment. The difference, ∼20% of a monolayer, is much greater than the ∼2% of a monolayer of ¹⁸O from the sample that was evolved as O₂, but less than the amount of Ru dissolution (∼1 ML) during the OER measurement. After sputtering (upper spectrum), the isotopic ratio of oxygen at the surface is close to the pre-electrolysis ratio, implying that any exchange of oxygen atoms was confined to the outer surface. Similarly, electrochemical labelling by oxidizing or electrochemically cycling a Ru¹⁶O_x electrocatalyst in ¹⁸O-containing electrolyte only incorporated the ¹⁸O in the outer monolayer (Fig. S4, ESI†), highlighting why reactive sputter deposition with ¹⁸O₂ was necessary to produce labelled samples.

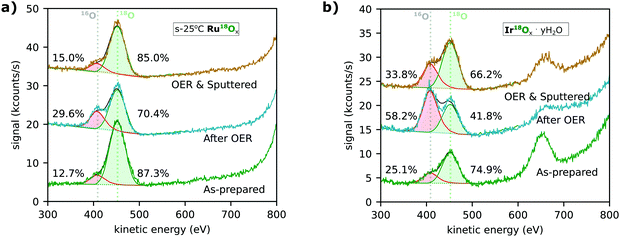Fig. 6 Low-energy ion scattering (LEIS) measurements of (a) s-25 °C Ru¹⁸O_x and (b) electrochemically cycled Ir¹⁸O_x (Ir¹⁸O_x·yH₂¹⁸O). The spectra shown were taken before (“As-prepared”, green trace) and after (“After OER”, blue trace) the respective EC-MS experiments shown in Fig. 2. An additional spectrum was taken after sputtering approximately one monolayer of material away to determine if any change in isotopic composition was confined to the surface. The centers of the ¹⁸O and ¹⁶O peaks and the isotopic distribution of O on the surface, determined by fitting of the peaks, are indicated. The Ru and Ir peaks are >800 eV and not in the window shown. The peak at ∼650 eV in (b) is chlorine from the 0.1 M HClO₄ electrolyte used in the catalyst preparation.

Ir¹⁸O_x·yH₂O formed by electrochemical cycling treatment shows significant ¹⁶O incorporation (Fig. 6b). Ir¹⁸O_x·yH₂O contains ∼25% ¹⁶O before electrolysis, possibly due to easy exchange of intercalated water with water vapor in the air; ∼58% ¹⁶O on the surface after electrolysis, implying a large degree of oxygen exchange during electrolysis; and ∼34% ¹⁶O even after the surface atomic layer is sputtered off. This result again implies more oxygen exchange than can be explained by lattice oxygen evolution. Ir¹⁸O₂ which has not been electrochemically cycled before OER shows less incorporation (Fig. S4, ESI†), but still more than labelled oxygen evolution. Note that LEIS is only sensitive to the outermost atomic layer, so even in this catalyst, the surface layer retained about ∼42% of its original oxygen atoms during 30 minutes of OER at 0.5 mA cm⁻². These results are in good agreement with the atomic probe tomography results by Schweinar et al.²³

LEIS spectra were taken before and after OER for most classes of sample included in Fig. 4. The fitting results for all spectra are summarized in Fig. S4 (ESI†). For all sample classes, ¹⁸O remained the dominant oxygen isotope on the surface after OER, but with the modest increase in ¹⁶O nonetheless consistently exceeding that expected based on the amount of ¹⁸O in the O₂ evolved. This indicates that the main mechanism of oxygen exchange is not a lattice oxygen evolution mechanism, but something else. Possibilities include hydration and exchange of water or exchange of tightly bound surface adsorbates. Note that both of these explanations involve oxygen atoms which we exclude from our definition of lattice oxygen. After argon sputtering, the spectra consistently returned to a ¹⁶O/¹⁸O ratio close to, but slightly higher than, the pre-OER ratio. We hypothesize that, rather than implying bulk activity, this slight increase is due to the rough and in some cases porous surface of the catalyst casting shadows where the post-OER surface is not uniformly sputtered away.

Discussion

The portion of O₂ produced by Ru- and Ir-based catalysts during OER in acid at 0.5 mA cm⁻²_geo that contained an oxygen atom originating from the electrocatalyst ranged from about one in 500 (s-25 °C Ru¹⁸O_x and Ir¹⁸O_x·yH₂O at the start of electrolysis) to less than one in 10 000 (s-400 °C Ru¹⁸O₂ and s-400 °C Ir¹⁸O₂ at steady-state). These “oxygen stability numbers” are the x-axis of Fig. 4. In other words, for all materials studied here, the vast majority of O₂ molecules consisted of two oxygen atoms originating from the water of the electrolyte. This means that a water oxidation mechanism dominates over any lattice oxidation mechanism by multiple orders of magnitude. That the majority of O₂ evolved does not contain an oxygen molecule from the catalyst is consistent with prior isotope labelling studies: For instance, Kasian et al. (ref. 12), measuring at 10–25 mA cm⁻²_geo (much higher than the 0.5 mA cm⁻²_geo used in our present study), also observe an oxygen stability number of ∼500 for IrO_x·yH₂O.

In principle, for an OER electrocatalyst with activity dominated by a lattice oxygen evolution mechanism, the isotopic signal would return to the natural baseline once the isotopic label of the oxygen in the active portion of the electrocatalyst was depleted, and so a transient isotopic signal has often been interpreted as evidence of a dominant lattice oxygen evolution mechanism. However, unlike most previous studies, our experiments can rule out ¹⁸O depletion for two reasons: (i) the ¹⁸O isotopic label remains at the surface of all catalysts tested as measured by LEIS. With the exception of the hydrous catalyst IrO_x·yH₂O, the majority of the oxygen at the surface, and the vast majority below the surface atomic layer, remains ¹⁸O (Fig. 6 and Fig. S4, ESI†). Furthermore, (ii) the total amount of labelled oxygen from the catalysts incorporated into the O₂ evolved was less than one atomic layer equivalent in all experiments. This is an advantage of chip EC-MS: the high sensitivity of the system enables us to quantify labelled oxygen evolution even at low applied current densities where it amounts to well under a picomole of O₂ per second.

We can therefore decisively conclude that the dominant oxygen evolution mechanism on Ru- and Ir-based oxides in acidic electrolyte does not incorporate lattice oxygen into O₂. Labelled oxygen evolution instead results from a minor side process, but one that could nonetheless provide insight into the oxygen evolution and degradation pathways. Even though lattice oxygen is not directly involved in the dominant OER mechanism, lattice oxygen is of course still important for holding the electrocatalyst together and for defining the coordination environment of the active sites.

Referring to Fig. 1 and our definition of lattice oxygen as oxygen atoms with the same coordination environment as oxygen in the bulk of a crystalline material, we briefly comment on whether the observed labelled oxygen evolution represents lattice oxygen evolution. The metal dissolution rate far exceeds the labelled oxygen evolution rate for ruthenium-based catalysts (collectively, Ru¹⁸O_x) while the two rates are similar on iridium-based catalysts (collectively, Ir¹⁸O_x), resulting in two groupings when Ru¹⁸O_x and Ir¹⁸O_x surfaces are mapped out according to metal stability number and oxygen stability number (Fig. 4). This seemingly implies that labelled oxygen evolution on Ru¹⁸O_x could result from the generation of undercoordinated surface oxygen atoms, which enter the electrocatalytic cycle as metal atoms dissolve; but that this is not a likely explanation for Ir¹⁸O_x. However, on no catalyst tested in our work does the amount of labelled oxygen evolved during the experiment exceed one monolayer equivalent based on capacitance measurements. This implies that the evolved ¹⁸O, including on Ru¹⁸O_x, could all be strongly bound surface oxygen such as bridging oxygen. Thus, our studies place Ru¹⁸O_x in sector IV of Fig. 1 (“labelled oxygen evolution of unknown origin”) and Ir¹⁸O_x in sector III of Fig. 1 (“surface bound oxygen evolution”). It is likely that lattice oxygen does occur to some extent for IrO_x based on previous studies^10–12 done at higher current density, which show amounts of labelled oxygen evolution likely exceeding a monolayer equivalent.^10,12

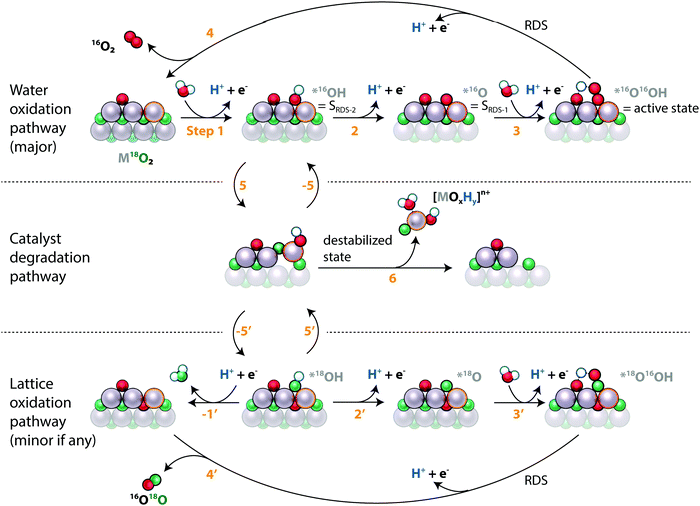
Fig. 4 also reveals that metal dissolution and labelled oxygen evolution are correlated across different catalytic surfaces for both metals, implying that the underlying mechanisms are linked for RuO_x and IrO_x in acidic electrolyte. This correlation can be explained by the two processes occurring through a common intermediate. As both dissolution and lattice oxygen evolution involve the breaking of metal oxygen bonds, this shared intermediate could be a destabilized surface state, i.e. a surface metal atom that partially leaves its coordination environment. This hypothesis is illustrated in the proposed combined reaction scheme in Fig. 7. The electrocatalyst is indicated as a surface layer and subsurface layer of metal atoms interspersed with labelled oxygen atoms, and the surface site that reacts in the pathways is emphasized with a highlighted outline. Note that the states are drawn for conceptual clarity rather than structural accuracy.

Fig. 7 Suggested mechanisms for OER (top track), catalyst degradation (middle track), and OER with lattice oxygen evolution (lower track) sketched for a labelled (¹⁸O, green atoms) electrocatalyst in unlabelled (¹⁶O, red atoms) electrolyte. Each row in the sketch includes a surface and near-surface region of the electrocatalyst and follows the reaction on one active site, indicated by an outline of the metal atom. The name of the state of the active site (*, *¹⁶OH, etc.) is indicated in gray. A spectator surface oxygen atom is included to the left of the active site. The lattice oxygen evolving mechanism is identical to the main OER mechanism except for the exchange of two oxygen atoms while the surface is especially reactive, here suggested to be when the adsorbate is *OH. That process also makes the catalyst prone to degradation.

The main oxygen evolution pathway, indicated in the top row, is in essence the conventional “metal peroxide” pathway⁴⁰ involving four concerted proton-electron transfers, labelled steps 1–4 in Fig. 7. The only difference is that we have drawn the peroxide intermediate, *OOH, with the hydrogen atom abstracted to a neighboring surface-bound oxygen atom, as has been proposed to take place on Ru(110), stabilizing this intermediate and lowering the OER overpotential.^29,41,42 We have labelled the peroxide intermediate as the “active state” or S_RDS, *O as S_RDS-1, and *OH as S_RDS-2 based on the analysis in the first article of this series.³⁵ The destabilized state that we propose as the link between labelled oxygen evolution and metal dissolution is indicated at the start of the middle row. It is reached from a state in the OER catalytic cycle by step 5. From the destabilized state we propose one of three things can happen: the metal atom can fall back into its original coordination environment, reversing the destabilization (step −5); the metal atom can leave its coordination environment further, leading to dissolution (6); or it can return to its original coordination environment but with two oxygen atoms switched such that a lattice oxygen atom ends on the surface (−5′). The last possibility results in lattice oxygen evolution, i.e. the evolution of a lattice oxygen molecule and the incorporation of an unlabelled oxygen atom into the catalyst, as indicated on the bottom row of Fig. 7 (steps 2′, 3′, and 4′), which are equivalent to the corresponding steps for surface bound oxygen evolution. Significantly, this arrangement of the steps implies that lattice oxygen evolution starts by taking a step down the degradation pathway.

The fact that rates of labelled oxygen evolution are similar on RuO_x and IrO_x catalysts but that dissolution occurs at a much higher rate on RuO_x catalysts indicates that the important difference between the two metal elements is the branching between steps 6 (dissolution) and −5′ (labelled oxygen evolution): the ratio k_−5′/(k_−5′ + k₆) is much higher for IrO_x than for RuO_x. In other words, a destabilized iridium atom is much more likely to restabilize than a destabilized ruthenium atom. This may be related to the ability of Ru to oxidize beyond the 4+ state that it has in RuO₂: the thermodynamically stable state of Ru appearing in the Pourbaix diagram at typical OER conditions of pH = 1 and U = 1.6 V_RHE is volatile RuO₄, where for Ir at the same conditions it is rutile IrO₂ (ref. 43 and 44).

Fig. 5b shows that on s-25 °C Ru¹⁸O_x (amorphous labelled ruthenium oxide sputter-deposited at room temperature), the labelled oxygen rate was proportional to the total oxygen evolution rate as a function of potential whereas the dissolution rate decreased in proportion to oxygen evolution rate with increasing potential. One possible explanation is that oxygen evolution with and without lattice exchange have equivalent rate-determining steps (RDS; steps 4 and 4′ in Fig. 7) whereas dissolution has a rate-determining step (step 6) with a weaker potential-dependence (higher Tafel slope). Note that 4′ can be the effective RDS for lattice oxygen evolution even without 5 and −5′ being in equilibrium if lattice oxygen evolution is one of two competing pathways down which *¹⁸OH can go once formed. The fact that ¹⁶O is incorporated in the catalysts at a higher rate than ¹⁸O is incorporated into the O₂ evolved, as shown by LEIS (Fig. 6) and in agreement with Schweinar et al.'s results for IrO₂ (ref. 23), implies that this is the case: *¹⁸OH can likely exchange with water to form *¹⁶OH (step −1′ followed by 1) if it does not react down 2′, 3′, and 4′ fast enough, so the potential dependence of labelled oxygen evolution comes from the RDS of the OER.

The choice of *OH as the intermediate from which the dissolution and lattice oxygen evolution mechanisms branch out is motivated by two factors: first, we provide evidence in our previous work³³ and in Fig. S3 (ESI†) that CO reacts with lattice oxygen via *OH, indicating that the surface is prone to expose lattice oxygen when covered by *OH. Second, the fact that the metal stability number increases with increasing potential hints at the branching point being a state with higher coverage at lower overpotential, namely S_RDS-2, which we tentatively assigned to *OH in the first article of this series.³⁵ This implies that the Tafel slopes for oxygen evolution, metal dissolution, and labelled oxygen evolution should converge (i.e., both oxygen and metal stability numbers should become constant with potential) at higher overpotentials, when *OH coverage is negligible at equilibrium but *OH is formed transiently as an intermediate of the OER electrocatalytic cycle, consistent with the previously reported results for IrO_x (ref. 12). We should point out that the explanations provided by Fig. 7 are not exclusive – another possible explanation for the differing Tafel behavior of labelled oxygen evolution and metal dissolution is that the dissolution mechanism changes as a function of potential, as suggested by Kasian et al. in ref. 25, whereas the lattice oxygen mechanism remains constant.

This result in Fig. 5 also rules out electrochemical potential as an explanation for the difference in oxygen stability number between s-400 °C RuO₂ and s-25 °C RuO_x observed in Fig. 4, since oxygen stability number apparently does not change as a function of potential alone on s-25 °C RuO_x. Thus, we can conclude that there is an intrinsic difference in the surfaces of s-400 °C RuO₂ and s-25 °C RuO_x. Though we cannot determine the precise difference from the present data, we hypothesize that the rougher surface of RuO_x has more highly undercoordinated Ru sites that are able to bring a labeled oxygen atom into the OER catalytic cycle. In contrast, the overall OER activity converges when normalized to capacitance, indicating the same intrinsic activity of the dominant sites. An implication is that labelled oxygen evolution might come primarily from sites that differ from the sites which dominate the overall OER activity. This interpretation, that there are different sites associated with activity and catalyst degradation, is promising as it implies that an electrocatalyst can be optimized for activity without necessarily compromising stability.

As a last discussion point, we wish to comment on the implications of our methods and results on future ¹⁸O isotope-labelling studies in oxygen evolution catalysis. Quantitative results are essential. Firstly, quantification of (i) the labelled oxygen evolution rate, (ii) the metal dissolution rate, and (iii) the number of active sites is necessary to determine whether labelled oxygen evolution is a surface phenomenon, a degradative processes, or a true catalytic mechanism involving lattice oxygen (see Fig. 1). Secondly, the quantified labelled oxygen evolution rate has to be compared to the total oxygen evolution rate to gauge the importance of a possible lattice oxygen evolution mechanism to the overall activity. Finally, isotopic composition of the oxygen in the catalytic surface should also be quantified both before and after oxygen evolution to determine whether labelled oxygen evolution matches oxygen exchange in the catalyst. Because data analysis interpretation can be quite difficult, we encourage the use of public repositories to enable groups to see exactly how the analysis was done and replot each other's data. This will benefit from open-source analysis tools. In this article, we presented quantitative data for a range of RuO_x and IrO_x catalysts at low overpotential, but the study was far from exhaustive. It would be especially interesting to see labelled oxygen studied as described above for alkaline electrocatalysts, where the mechanism and relation to degradation might be quite different.¹⁶ On the other hand, since our results indicate that labelled oxygen evolution seems to be largely a proxy for instability, at least for RuO_x and IrO_x in acidic electrolyte (Fig. 4), researchers may wish to prioritize careful measurements of activity and stability in the search for better acid-stable OER electrocatalysts. The challenge, based on this and the accompanying article,³⁵ is to optimize the metal–oxygen binding energy for catalytic intermediates at sites on the surface while making the bulk metal–oxygen binding as strong as possible to stabilize the catalyst. Promising strategies towards scalable acid-stable OER electrocatalysis include bulk alloying with more stable elements^38,45–47 and stabilization of optimally coordinated surface sites^29,48 to complement engineering techniques that lower the required loading.^49,50

Conclusion

In this study, we introduced the oxygen stability number in the oxygen evolution reaction (OER) as the ratio of the total number of O₂ molecules generated to the number of oxygen atoms from the catalyst incorporated into the O₂. Using a highly sensitive chip EC-MS setup, we showed that the oxygen stability number in acidic electrolyte at 0.5 mA cm⁻²_geo ranges from ∼500 (0.2% labelled oxygen evolution on amorphous Ru¹⁸O_x and hydrous Ir¹⁸O_x·yH₂O at the start of electrolysis) to ∼10 000 (0.01% labelled oxygen evolution on crystalline Ru¹⁸O₂ and Ir¹⁸O₂ at steady-state). On this basis, and by ruling out depletion of the isotopic label at the surface using LEIS, we conclude that lattice oxygen evolution is at most a negligible contribution to overall OER activity for Ru- and Ir-based catalysts in acidic electrolyte. For RuO_x, metal dissolved at a higher rate than labelled oxygen was evolved, i.e. the oxygen stability number was always significantly higher than the metal stability number, while the two rates were similar for IrO_x. Between different catalytic surfaces within these two classes of catalysts, labelled oxygen evolution rate increased with metal dissolution rate. These results are consistent with a picture in which lattice oxygen evolution on RuO_x and IrO_x in acidic electrolyte is mechanistically related to dissolution – that, put simply, to get to the lattice oxygen evolution pathway, you have to cross through the dissolution pathway. We highlight the need to report quantitative results and to quantitatively compare the isotopic signal to both degradation rate and overall catalytic rate when performing isotope labelling mechanistic studies in electrocatalysis. Our results indicate that future studies in acid-stable OER electrocatalysis should focus on understanding, controlling, and optimizing the reactivity of catalytic surface sites while maximizing the stability of the bulk electrocatalyst.

Experimental

Sample synthesis

Most samples were synthesized by reactive sputter deposition of ruthenium or iridium in a plasma of 20% ¹⁸O₂ (99% isotopic purity). Some included a subsequent electrochemical step in their preparation. We studied the following samples based on previous work:

– s-25 °C Ru¹⁸O₂ sputter deposited at room temperature (XRD-amorphous)

– s-400 °C Ru¹⁸O₂ sputter deposited at 400 °C (rutile)

– Ru¹⁸O_x/Ru formed by oxidation of sputter deposited metallic Ru in 97% H₂¹⁸O electrolyte

– Ru¹⁸O_x/Ru-foam formed by oxidation of ruthenium foam (see the first article of this series³⁵) in 97% H₂¹⁸O electrolyte

– s-25 °C Ir¹⁸O₂ sputter deposited at room temperature

– s-400 °C Ir¹⁸O₂ sputter deposited at 400 °C

– Ir¹⁸O_x/Ir formed by oxidation of sputter deposited metallic Ir in 97% H₂¹⁸O electrolyte

– Ir¹⁸O_x·yH₂O, an amorphous hydrous iridium layer formed by potential cycling of sputter deposited Ir¹⁸O₂ samples in 97% H₂¹⁸O electrolyte^16,27,29

The isotopic composition of the surface of each sample was characterized by LEIS before testing in chip EC-MS in 1.0 M HClO₄ of the natural isotopic composition.

EC-MS and ICP-MS

The chip EC-MS technique and setup have been described in detail elsewhere.^26,30,45,46 The only addition to the setup in this work was the capability for extracting samples of electrolyte. The cell, which held the sample, had four electrolyte channels – two were used for the reference and counter electrodes, while the other two were used as an inlet and an outlet, see Fig. 2a. The outlet was connected to a syringe for controlled collection of electrolyte samples, which diluted the initial ∼2 μL working volume between the sample and the membrane chip (the mass spectrometer inlet) by a factor of about ∼100. The extracted electrolyte sample was later further diluted to exactly 10 ML in 2% nitric acid for ICP-MS measurement, where the sub-ppb sensitivity of ICP-MS corresponded to ∼3 pmol of Ru or ∼1 pmol of Ir per sample (see the ICP-MS calibration curves in Fig. S5, ESI†). While the electrolyte sample was collected, a valve on the inlet was opened to an electrolyte reservoir, so that the working volume was not subjected to a significant pressure fluctuation as the syringe for the electrolyte was withdrawn.

Each EC-MS experiment included a potential ramp and a 30 minute electrolysis period at constant current (0.5, 0.15, or 0.05 mA cm⁻²_geo) with helium (He) gas making up the pressure in the chip. Electrolyte samples were taken without interrupting the electrochemical program after approximately 2, 10, 20, and 30 minutes of electrolysis, after which the experiment was ended. The sample was then rinsed in pure isotopically natural H₂O before being transferred to the vacuum chamber for LEIS. Priority was taken to do post-OER LEIS as quickly as possible after EC-MS (usually a few hours) to reduce the possible effect of slow exchange of oxygen with air.

Low-energy ion scattering (LEIS)

LEIS spectra were acquired on two different ultra high vacuum instruments: a ThetaProbe surface analysis system from Thermo Scientific with an EX05 ion gun producing He⁺ ions at 980 eV; and, a Multiscan Lab XP surface analysis system from Scienta Omicron equipped with a NanoSAM detector and ISE100 Fine Focus ion gun for producing He⁺ ions at 1000 eV. The analysis is described more in the ESI† and all the scripts converting the raw data into figures are included in the accompanying repository. Briefly, the ¹⁶O and ¹⁸O isotope peaks were fitted to reference spectra, and the area for each peak was compared to the total oxygen signal to quantify the ratio of each oxygen isotope on the surface. For the spectra acquired on the ThetaProbe system, there was a tendency for the spectra to be arbitrarily shifted – presumably due to charging of the sample. This was handled by shifting the entire spectrum such that the oxygen isotope with the highest signal was aligned with the expected peak position.

Data analysis

All data was analyzed and organized with the open-source “In situ Experimental Data Tool” (ixdat, https://ixdat.readthedocs.org) and a homemade database, all available at https://github.com/ixdat/LowOverpotentialRegime.

Conflicts of interest

The authors do not have any conflicts of interest to declare.

Acknowledgements

We gratefully acknowledge the funding by Villum Fonden, part of the Villum Center for the Science of Sustainable Fuels and Chemicals (V-SUSTAIN grant 9455), and the European Research Council (ERC) CLUNATRA under the European Union’s Horizon 2020 research and innovation program (grant agreement no. 741860).

References

1. M. Carmo, D. L. Fritz, J. J. Mergel and D. Stolten, A Comprehensive Review on PEM Water Electrolysis, Int. J. Hydrogen Energy, 2013, 38, 4901–4934.
2. A. Buttler and H. Spliethoff, Current Status of Water Electrolysis for Energy Storage, Grid Balancing and Sector Coupling via Power-to-Gas and Power-to-Liquids: A Review, Renewable Sustainable Energy Rev., 2018, 82, 2440–2454.
3. Energy X, Research Needs towards Sustainable Production of Fuels and Chemicals, ed. J. K. Nørskov, Energy-X, Brussels, Belgium, 2019.
4. C. Budischak, D. Sewell, H. Thomson, L. Mach, D. E. Veron and W. Kempton, Cost-Minimized Combinations of Wind Power, Solar Power and Electrochemical Storage, Powering the Grid up to 99.9% of the Time, J. Power Sources, 2013, 225, 60–74.
5. O. Schmidt, A. Gambhir, I. Staffell, A. Hawkes, J. Nelson and S. Few, Future Cost and Performance of Water Electrolysis: An Expert Elicitation Study, Int. J. Hydrogen Energy, 2017, 42, 30470–30492.
6. A. Sgobbi, W. Nijs, R. De Miglio, A. Chiodi, M. Gargiulo and C. Thiel, How Far Away Is Hydrogen? Its Role in the Medium and Long-Term Decarbonisation of the European Energy System, Int. J. Hydrogen Energy, 2016, 41, 19–35.
7. L. An, C. Wei, M. Lu, H. Liu, Y. Chen, G. G. Scherer, A. C. Fisher, P. Xi, Z. J. Xu and C. Yan, Recent Development of Oxygen Evolution Electrocatalysts in Acidic Environment, Adv. Mater., 2021, 33, 2006328.
8. T. Reier, H. N. Nong, D. Teschner, R. Schlögl and P. Strasser, Electrocatalytic Oxygen Evolution Reaction in Acidic Environments - Reaction Mechanisms and Catalysts, Adv. Energy Mater., 2017, 7, 1601275.
9. P. C. K. Vesborg and T. F. Jaramillo, Addressing the Terawatt Challenge: Scalability in the Supply of Chemical Elements for Renewable Energy, RSC Adv., 2012, 2, 7933–7947.
10. S. Fierro, T. Nagel, H. Baltruschat and C. Comninellis, Investigation of the Oxygen Evolution Reaction on Ti/IrO2 Electrodes Using Isotope Labelling and on-Line Mass Spectrometry, Electrochem. Commun., 2007, 9, 1969–1974.
11. S. Geiger, O. Kasian, M. Ledendecker, E. Pizzutilo, A. M. Mingers, W. T. Fu, O. Diaz-Morales, Z. Li, T. Oellers and L. Fruchter, et al., The Stability Number as a Metric for Electrocatalyst Stability Benchmarking, Nat. Catal., 2018, 1, 508–515.
12. O. Kasian, S. Geiger, T. Li, J. Grote, K. Schweinar, S. Zhang, C. Scheu, D. Raabe, S. Cherevko and B. Gault, et al., Degradation of Iridium Oxides via Oxygen Evolution from the Lattice: Correlating Atomic Scale Structure with Reaction Mechanisms, Energy Environ. Sci., 2019, 12, 3548–3555.
13. M. Wohlfahrt-Mehrens and J. Heitbaum, Oxygen Evolution on Ru and RuO2 Electrodes Studied Using Isotope Labelling and On-Line Mass Spectrometry, J. Electroanal. Chem., 1987, 237, 251–260.
14. K. Macounova, M. Makarova and P. Krtil, Oxygen Evolution on Nanocrystalline RuO2 and Ru_0.9Ni_0.1O₂ Electrodes – DEMS Approach to Reaction Mechanism Determination, Electrochem. Commun., 2009, 11, 1865–1868.
15. K. A. Stoerzinger, O. Diaz-Morales, M. Kolb, R. R. Rao, R. Frydendal, L. Qiao, X. R. Wang, N. B. Halck, J. Rossmeisl and H. A. Hansen, et al., Orientation-Dependent Oxygen Evolution on RuO2 without Lattice Exchange, ACS Energy Lett., 2017, 2, 876–881.
16. A. Grimaud, O. Diaz-Morales, B. Han, W. T. Hong, Y. Lee, L. Giordano, K. A. Stoerzinger, M. T. M. Koper and Y. Shao-Horn, Activating Lattice Oxygen Redox Reactions in Metal Oxides to Catalyse Oxygen Evolution, Nat. Chem., 2017, 9, 457–465.
17. H. M. A. Amin and H. Baltruschat, How Many Surface Atoms in Co3O4 Take Part in Oxygen Evolution? Isotope Labeling Together with Differential Electrochemical Mass Spectrometry, Phys. Chem. Chem. Phys., 2017, 19, 25527–25536.
18. C. Roy, B. Sebok, S. B. Scott, E. M. Fiordaliso, J. E. Sørensen, A. Bodin, D. B. Trimarco, C. D. Damsgaard, P. C. K. K. Vesborg and O. Hansen, et al., Impact of Nanoparticle Size and Lattice Oxygen on Water Oxidation on NiFeOxHy, Nat. Catal., 2018, 1, 820–829.
19. J. Willsau, O. Wolter and J. Heitbaum, In the Oxygen Evolution Reaction on Platinum?, J. Electroanal. Chem., 1985, 195, 299–306.
20. O. Diaz-Morales, F. Calle-Vallejo, C. de Munck and M. T. M. Koper, Electrochemical Water Splitting by Gold: Evidence for an Oxide Decomposition Mechanism, Chem. Sci., 2013, 4, 2334.
21. S. B. Scott, J. Kibsgaard, P. C. K. Vesborg and I. Chorkendorff, Tracking Oxygen Atoms in Electrochemical CO Oxidation - Part II: Lattice Oxygen Reactivity in Oxides of Pt and Ir, Electrochim. Acta, 2021, 374, 137844.
22. S. Lee, K. Banjac, M. M. Lingenfelder and X. Hu, Oxygen Isotope Labelling Experiments Reveal Different Reaction Sites for the Oxygen Evolution Reaction on Nickel and Nickel Iron Oxides, Angew. Chem., Int. Ed., 2019, 1–6,  DOI:10.1002/anie.201903200.
23. K. Schweinar, B. Gault, I. Mouton and O. Kasian, Lattice Oxygen Exchange in Rutile IrO 2 during the Oxygen Evolution Reaction, J. Phys. Chem. Lett., 2020, 11, 5008–5014.
24. Y. Surendranath, M. W. Kanan and D. G. Nocera, Mechanistic Studies of the Oxygen Evolution Reaction by a Cobalt-Phosphate Catalyst at Neutral PH, J. Am. Chem. Soc., 2010, 132, 16501–16509.
25. O. Kasian, J. Grote, S. Geiger, S. Cherevko and K. J. J. Mayrhofer, The Common Intermediates of Oxygen Evolution and Dissolution Reactions during Water Electrolysis on Iridium, Angew. Chem., Int. Ed., 2018, 57, 2488–2491.
26. L. Giordano, B. Han, M. Risch, W. T. Hong, R. R. Rao, K. A. Stoerzinger and Y. Shao-Horn, PH Dependence of OER Activity of Oxides: Current and Future Perspectives, Catal. Today, 2016, 262, 2–10.
27. A. Grimaud, A. Demortière, M. Saubanère, W. Dachraoui, M. Duchamp, M. Doublet and J. Tarascon, Activation of Surface Oxygen Sites on an Iridium-Based Model Catalyst for the Oxygen Evolution Reaction, Nat. Energy, 2017, 2, 16189.
28. E. Mutoro, E. J. Crumlin, M. D. Biegalski, H. M. Christen and Y. Shao-Horn, Enhanced Oxygen Reduction Activity on Surface-Decorated Perovskite Thin Films for Solid Oxide Fuel Cells, Energy Environ. Sci., 2011, 4, 3689–3696.
29. R. R. Rao, M. J. Kolb, N. B. Halck, A. F. Pedersen, A. Mehta, H. You, K. A. Stoerzinger, Z. Feng, H. A. Hansen and H. Zhou, et al., Towards Identifying the Active Sites on RuO2(110) in Catalyzing Oxygen Evolution, Energy Environ. Sci., 2017, 10, 2626–2637.
30. J. Grote, A. R. Zeradjanin, S. Cherevko and K. J. J. Mayrhofer, Coupling of a Scanning Flow Cell with Online Electrochemical Mass Spectrometry for Screening of Reaction Selectivity, Rev. Sci. Instrum., 2014, 85, 104101.
31. D. B. Trimarco, S. B. Scott, A. H. Thilsted, J. Y. Pan, T. Pedersen, O. Hansen, I. Chorkendorff and P. C. K. K. Vesborg, Enabling Real-Time Detection of Electrochemical Desorption Phenomena with Sub-Monolayer Sensitivity, Electrochim. Acta, 2018, 268, 520–530.
32. J. Knöppel, M. Möckl, D. Escalera-lópez, K. Stojanovski, S. Thiele, M. Rzepka, M. Bierling, T. Böhm, S. Thiele, M. Rzepka and S. Cherevko, On the Limitations in Assessing Stability of Oxygen Evolution Catalysts Using Aqueous Model Electrochemical Cells, Nat. Commun., 2021, 12, 2231.
33. S. B. Scott, J. Kibsgaard, P. C. K. Vesborg and I. Chorkendorff, Tracking Oxygen Atoms in Electrochemical CO Oxidation – Part I: Oxygen Exchange via CO2 Hydration, Electrochim. Acta, 2021, 374, 137842.
34. C. Roy, R. R. Rao, K. A. Stoerzinger, J. Hwang, J. Rossmeisl, I. Chorkendorff, Y. Shao-Horn and I. E. L. Stephens, Trends in Activity and Dissolution on RuO2 under Oxygen Evolution Conditions: Particles versus Well-Defined Extended Surfaces, ACS Energy Lett., 2018, 3, 2045–2051.
35. S. B. Scott, R. R. Rao, C. Moon, J. E. Sørensen, J. Kibsgaard, Y. Shao-Horn and I. Chorkendorff, The Low Overpotential Regime of Acidic Water Oxidation Part I: The Importance of O2 Detection, Energy Environ. Sci., 2022 10.1039/D1EE03914H.
36. V. Pfeifer, T. E. Jones, J. J. Velasco Vélez, R. Arrigo, S. Piccinin, M. Hävecker, A. Knop-Gericke and R. Schlögl, In Situ Observation of Reactive Oxygen Species Forming on Oxygen-Evolving Iridium Surfaces, Chem. Sci., 2017, 8, 2143–2149.
37. D. N. Buckley and L. D. Burke, The Oxygen Electrode. Part 5.—Enhancement of Charge Capacity of an Iridium Surface in the Anodic Region, J. Chem. Soc., Faraday Trans. 1, 1975, 71, 1447.
38. O. Kasian, T. Li, A. M. Mingers, K. Schweinar, A. Savan, A. Ludwig and K. Mayrhofer, Stabilization of an Iridium Oxygen Evolution Catalyst by Titanium Oxides, J. Phys. Energy, 2021, 3, 034006.
39. N. Yoshida, Y. Yamada, S. I. Nishimura, Y. Oba, M. Ohnuma and A. Yamada, Unveiling the Origin of Unusual Pseudocapacitance of RuO 2·n H2O from Its Hierarchical Nanostructure by Small-Angle X-Ray Scattering, J. Phys. Chem. C, 2013, 117, 12003–12009.
40. I. C. Man, H.-Y. Su, F. Calle-vallejo, H. A. Hansen, J. I. J. I. Martínez, N. G. Inoglu, J. Kitchin, T. F. Jaramillo, J. K. Nørskov and J. Rossmeisl, Universality in Oxygen Evolution Electrocatalysis on Oxide Surfaces, ChemCatChem, 2011, 3, 1159–1165.
41. R. R. Rao, M. J. Kolb, L. Giordano, A. F. Pedersen, Y. Katayama, J. Hwang, A. Mehta, Y. Hoydoo, J. R. Lunger and H. Zhou, et al., Operando Identification of Site-Dependent Water Oxidation Activity on Ruthenium Dioxide Single Crystal Surfaces, Nat. Catal., 2020, 3, 516–525.
42. S. Divanis, A. M. Frandsen, T. Kutlusoy and J. Rossmeisl, Lifting the Discrepancy between Experimental Results and the Theoretical Predictions for the Catalytic Activity of RuO2(110) towards Oxygen Evolution Reaction, Phys. Chem. Chem. Phys., 2021, 23, 19141–19145.
43. M. Pourbaix, Atlas of Electrochemical Equilibria in Aqueous Solutions, Pergamon Press, Oxford, New York, 1966.
44. Pourbaix Diagram App by the Materials Project, available at https://materialsproject.org/#apps/pourbaixdiagram.
45. R. Frydendal, E. A. Paoli, I. Chorkendorff, J. Rossmeisl and I. E. L. Stephens, Toward an Active and Stable Catalyst for Oxygen Evolution in Acidic Media: Ti-Stabilized MnO2, Adv. Energy Mater., 2015, 5, 1500991.
46. G. T. K. K. Gunasooriya and J. K. Nørskov, Analysis of Acid-Stable and Active Oxides for the Oxygen Evolution Reaction, ACS Energy Lett., 2020, 5, 3778–3787.
47. Y.-R. Zheng, J. Vernieres, Z. Wang, K. Zhang, D. Hochfilzer, K. Krempl, T.-W. Liao, F. Presel, T. Altantzis, J. Fatermans, S. B. Scott, N. M. Secher, C. Moon, P. Liu, S. Bals, S. V. Aert, A. Cao, M. Anand, J. K. Nørskov, J. Kibsgaard and I. Chorkendorff, Monitoring Oxygen Production on Mass-Selected Iridium–Tantalum Oxide Electrocatalysts, Nat. Energy, 2022, 7, 55–64.
48. C. F. Dickens and J. K. Nørskov, A Theoretical Investigation into the Role of Surface Defects for Oxygen Evolution on RuO2, J. Phys. Chem. C, 2017, 121, 18516–18524.
49. M. Ledendecker, S. Geiger, K. Hengge, J. Lim, S. Cherevko, A. M. Mingers, D. Göhl, G. V. Fortunato, D. Jalalpoor and F. Schüth, et al., Towards Maximized Utilization of Iridium for the Acidic Oxygen Evolution Reaction, Nano Res., 2019, 12, 2275–2280.
50. Y. N. Regmi, E. Tzanetopoulos, G. Zeng, X. Peng, D. I. Kushner, T. A. Kistler, L. A. King and N. Danilovic, Supported Oxygen Evolution Catalysts by Design: Toward Lower Precious Metal Loading and Improved Conductivity in Proton Exchange Membrane Water Electrolyzers, ACS Catal., 2020, 10, 13125–13135.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ee03915f

‡ Present address: Department of Materials, Imperial College London, London, UK.

§ Present address: Department of Chemistry, Imperial College London, London, UK.

¶ Present address: Korean Advanced Institute of Science and Technology, Republic of Korea.

---