Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The low overpotential regime of acidic water oxidation part I: the importance of O2 detection†
Soren B.
Scott‡§
 a,
Reshma R.
Rao¶§
a,
Reshma R.
Rao¶§
 *b,
Choongman
Moon||
a,
Jakob E.
Sørensen
*b,
Choongman
Moon||
a,
Jakob E.
Sørensen
 a,
Jakob
Kibsgaard
a,
Jakob
Kibsgaard
 a,
Yang
Shao-Horn
a,
Yang
Shao-Horn
 b and
Ib
Chorkendorff
b and
Ib
Chorkendorff
 *a
*a
aSurfCat Section for Surface Physics and Catalysis, Department of Physics, Technical University of Denmark, Kgs. Lyngby, Denmark. E-mail: ibchork@fysik.dtu.dk
bDepartment of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, Massachusetts, USA. E-mail: reshma.rao@imperial.ac.uk
First published on 19th March 2022
Abstract
The high overpotential required for the oxygen evolution reaction (OER) represents a significant barrier for the production of closed-cycle renewable fuels and chemicals. Ruthenium dioxide is among the most active catalysts for OER in acid, but the activity at low overpotentials can be difficult to measure due to high capacitance. In this work, we use electrochemistry – mass spectrometry to obtain accurate OER activity measurements spanning six orders of magnitude on a model series of ruthenium-based catalysts in acidic electrolyte, quantifying electrocatalytic O2 production at potential as low as 1.30 VRHE. We show that the potential-dependent O2 production rate, i.e., the Tafel slope, exhibits three regimes, revealing a previously unobserved Tafel slope of 25 mV decade−1 below 1.4 VRHE. We fit the expanded activity data to a microkinetic model based on potential-dependent coverage of the surface intermediates from which the rate-determining step takes place. Our results demonstrate how the familiar quantities “onset potential” and “exchange current density” are influenced by the sensitivity of the detection method.
Broader contextHalving net CO2 emissions by 2030 and eliminating them by 2050, as is necessary to limit global warming to 1.5 °C, will require hundreds of gigawatts capacity of renewable energy storage and conversion of electrical to chemical energy, most of which is expected to rely on water electrolysis. The slow kinetics of the oxygen evolution reaction (OER) is a main source of energy loss in polymer electrolyte membrane (PEM) and alkaline water electrolysis as well as emerging electrochemical technologies such as CO2 reduction and metal–air batteries, and thus a hindrance in their uptake. Catalyzing OER is a particular challenge in the acidic electrolyte of the otherwise most advantageous PEM electrolyzers, where only oxides of scarce elements iridium and ruthenium are sufficiently stable and active as OER catalysts. Attempts to design more active OER catalysts rely on understanding the electrocatalytic mechanism to enhance the kinetics. However, uncertainties remain about the electrocatalytic mechanism, particularly the activity at low overpotential, since quantitatively probing sub monolayers of evolved oxygen is a challenge. In this work, we use ultrasensitive O2 detection to accurately measure OER activity of ruthenium oxides at overpotentials down to 70 mV and thus provide new insights into the OER mechanism. |
Introduction
Electrochemical water oxidation is a key enabler to the renewable production of energy carriers such as hydrogen1–3 and chemicals such as ethanol and ethylene from carbon dioxide reduction4,5 and ammonia from nitrogen reduction.6–8 However, the slow kinetics of water oxidation is limiting the large-scale uptake of electrosynthesis of fuels and chemicals.9–11 Particularly, in proton exchange membrane electrolyzers that operate at low pH, only oxides of the rare noble metals iridium and ruthenium exhibit reasonable activity3,12,13 and stability.14–16 Design of oxygen evolution catalysts with enhanced stability and specific activity is needed,10,17,18 which would lower the noble metal loading required for water oxidation and reduce the capital cost of electrolyzers. This need in turn requires more knowledge of the mechanisms of water oxidation electrocatalysis. In this work, we focus on ruthenium oxide electrocatalysts because they are the most active in acidic electrolyte19,20 and because RuO2 has been extensively studied as a model electrocatalyst.21–23Computational methods have been used extensively to predict trends in the electrocatalytic activity by calculating the energies of electrocatalytic intermediates.24–26 In a highly influential work,27 Rossmeisl and coworkers assumed a metal peroxide pathway involving adsorbate oxidation via the electrocatalytic intermediates *, *OH, *O, and *OOH (where * represents a metal atom at the surface of the metal oxide). In this model, the correlation (scaling) of the adsorption energies of *OH and *OOH is used to explain why an overpotential of ∼200–300 mV relative to the nominal equilibrium potential of 1.23 VRHE (RHE as reversible hydrogen electrode) is required to drive the OER on the theoretically predicted optimal catalyst.27 The lowest theoretical overpotential at which no steps are uphill in free energy is called the limiting overpotential.27 Specifically for RuO2 surfaces, the limiting overpotential ranges from 380 mV for the (110) facet to 340 mV for the (100) facet.22
Unfortunately, the direct correspondence of the limiting potential to experimental observations has been elusive28–30 because of several factors. On the theoretical side, translating the limiting potential to an actual OER rate requires the development of kinetic models of the OER, which rely on identifying and accurately computing reaction barriers in the complex multi-step reaction, a computationally challenging task.31–33 On the experimental side, determining the physical origin of anodic current at low oxygen-evolution overpotentials (<1.45 VRHE), and thus the true oxygen evolution activity, is challenging, not least on ruthenium oxides, for three reasons: First, RuOx-based materials have large capacitance, which contributes significantly to the oxidation current.34 The capacitance is further amplified for amorphous RuOx and hydrous RuOx,35,36 which can show larger gravimetric oxygen evolution activity compared to crystalline oxides.37 Secondly, recent studies by Cherevko et al.38 and Hodnik et al.39 have alluded to the possibility of electrochemical dissolution of Ru ions in solution preceding the onset of OER, further raising questions about the onset of oxygen evolution. These observations highlight that the concept of “onset potential”, measured experimentally, is ambiguous because it depends on the ability to reliably measure OER activity among other possible sources of anodic current. Thirdly, detection of O2 has not been sensitive or quantitative enough to provide an accurate independent measurement of the OER rate at low overpotentials. On single crystal RuO2(110) in acid at potentials lower than 1.5 VRHE, OER current densities of ∼5 μA cm−2oxide and lower have been observed, which corresponds to an oxygen flux of ∼10−10 mol s−1 cm−2oxide and lower, which is below the detection limit of conventional electrocatalytic O2 detection by differential electrochemistry mass spectrometry (DEMS).40 An emerging, fundamental question is whether OER can be observed at overpotentials less than 1.5 VRHE.
The dependence of OER activity on electrochemical potential is often evaluated as the Tafel slope, defined as the change in overpotential required to produce an order of magnitude increase in water oxidation current density. Microkinetic models predict potential-dependent Tafel slopes for metal oxides due to an increase in the coverage of species participating in the rate-determining step with increasing potential.31,41–43 A recent theoretical study on RuO2(110) has suggested that the rate-determining step is the O–O bond formation, *O + H2O → *OOH + H+ + e−, from which a Tafel slope of ∼39 mV decade−1 can be obtained at potentials lower than ∼1.5 VRHE, where the active coordinatively unsaturated Ru sites (*) is filled with *OH.31 The Tafel slope was proposed to transition to 120 mV decade−1 at potentials higher than ∼1.5 VRHE where the *O covered surface was thermodynamically stable.31 Experimentally, at potentials greater than ∼1.55 VRHE, a Tafel slope of ∼120 mV decade−1 has been noted on RuO2 nanoparticles19 and oriented thin films, and from ∼1.45 to ∼1.55 VRHE,44,45 a Tafel slope of ∼60 mV decade−1 has been observed. Therefore, corroborating theoretical predictions31 of possible Tafel slopes lower than 60 mV decade−1 at potentials lower than ∼1.5 VRHE is challenging. Accurate measurement of OER activity at low overpotential could be extremely valuable in informing the computational results, considering that this potential dependence of the activity is dependent on the computed energetics of the reaction intermediates.22,41,42,46
Recent developments in microchip-based electrochemistry-mass spectrometry (chip EC-MS) technology40 has for the first time enabled real time, quantitative detection of gases in amounts as low as ∼10−12 mol s−1. This enables the ultra-sensitive detection of electrochemically produced O2 and thus accurate measurement of OER activity in spite of the challenges highlighted above. This EC-MS setup allows for 100% collection efficiency and well-characterized reproducible mass transport, allowing quantitative real-time detection of gaseous electrochemical desorption products at sub-picomol per second sensitivity,47,48 contributing to the unravelling of the mechanisms of electrocatalytic hydrogen evolution,48 CO reduction,49 propene oxidation,50,51 and CO oxidation.47,52,53 It has been used previously for isotope-labeling experiments in the OER,53,54 but its sensitivity has not previously been utilized to push the limits of accurate activity measurements. In this work, we use chip EC-MS to study the kinetics of water oxidation on RuO2 surfaces at potentials <1.50 VRHE. The lowest overpotential at which we could consistently detect sustained O2 production (at about 0.25 pmol s−1) was 1.30 VRHE, only 70 mV above the standard thermodynamic potential for water oxidation. RuO2 films sputter deposited at temperatures ranging from room temperature to 400 °C were found to have a Tafel slope of ∼25 mV decade−1 below 1.45 VRHE, which increased to 60 mV decade−1 up to 1.55 VRHE and transitioned to 120 mV decade−1 at higher potentials. We demonstrate that improving sensitivity towards oxygen generation can bypass the so-called “onset potential” observed in less sensitive methods, enabling accurate study of the mechanistically interesting low-overpotential regime by actually measuring the O2 evolution. This article is the first in a two-part series, where the second addresses electrocatalyst stability and employs isotope-labeling to address remaining mechanistic questions.
Results and discussion
Detecting oxygen evolution at low overpotentials
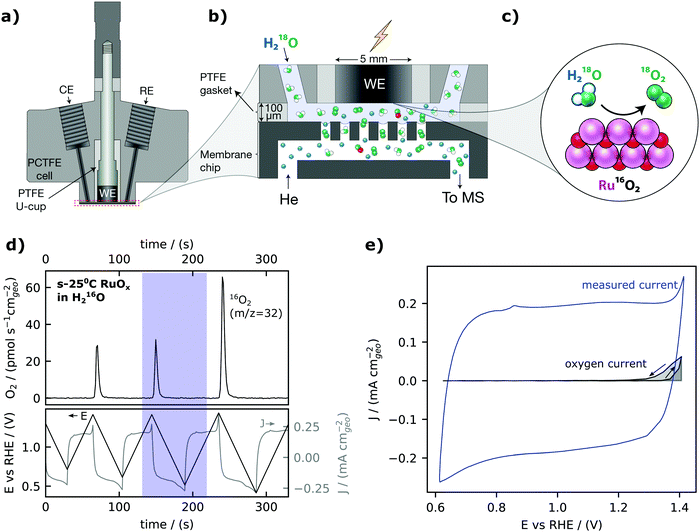
Our electrochemistry – mass spectrometry (EC-MS) setup for detection of electrochemically generated O2 is sketched in Fig. 1a–c and described in detail in reference.40 We used a cell made from a resistive polymer, PTCFE, to hold a working electrode disk, reference electrode (RE) and counter electrode (CE) in place. The interface to the mass spectrometer, which is at ∼10−6 mbar high vacuum, is formed in a silicon microchip: a perforated membrane allows the external electrochemical environment to equilibrate with an internal volume etched into the chip which functions as a nanoscopic head-space, saturating the electrolyte with inert gas (helium, He) and carrying gaseous electrochemical products through a capillary fabricated into the chip to the vacuum chamber. A gasket of Teflon is used together with the cell to define a 100 μm thick layer of electrolyte between the electrode and the chip. Sputter-deposited RuOx films, as the working electrode, were prepared by reactive magnetron sputtering from a Ru target under a 3 mTorr pressure (80% argon and 20% oxygen) on a glassy carbon electrode at room temperature, 200 °C, 300 °C and 400 °C– hereafter also referred to as s-25 °C RuOx, s-200 °C RuOx, s-300 °C RuOx and s-400 °C RuOx respectively. The crystallinity increases with increasing deposition temperature, with the room temperature films being XRD-amorphous and the 400 °C films showing the rutile structure (Fig. S1, ESI†). The surface roughness is comparable across all films from Table S1 (ESI†).The calibrated mass spectrometer signal for O2 (m/z = 32) and corresponding current and voltage collected from cyclic voltammetry of a room-temperature sputter-deposited RuOx film are shown in Fig. 1d. At potentials less than 1.40 VRHE, the current expected from the rate of OER measured from mass spectrometry (in grey, Fig. 1e) is much smaller than the measured current from cyclic voltammetry (in blue, Fig. 1e). The large difference can be attributed to faradaic pseudocapacitive currents, RuOx(OH)y + δH+ + δe− ↔ RuOx−δ(OH)y+δ,55,56 which highlights the challenges of detecting OER at low overpontentials using electrochemical techniques alone. Therefore, the small magnitude of the water oxidation currents relative to the capacitive currents in the cyclic voltammogram illustrate that oxygen detection is essential when measuring OER at low overpotential on high-capacitive materials such as RuO2.
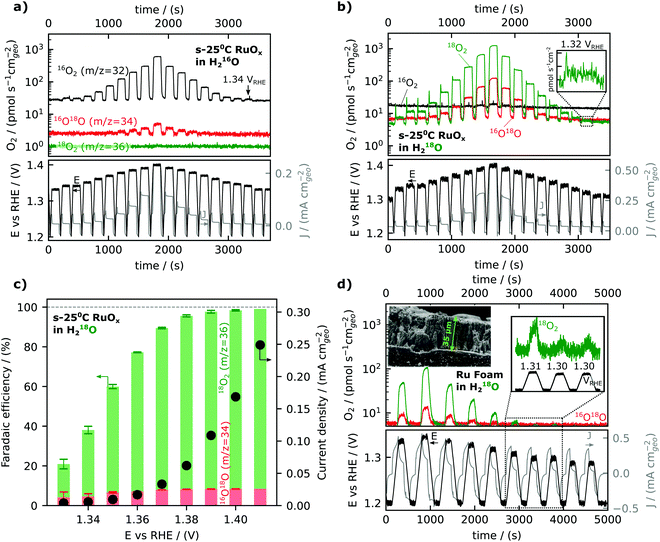
We will now turn to steady-state oxygen generation measured by mass signal at m/z = 32 detected in He-saturated 0.1 M HClO4 electrolyte as low as 1.34 VRHE, as shown in Fig. 2a. The potential was scanned at 5 mV s−1 in 0.1 M HClO4 from open circuit (∼0.8–0.9 VRHE) to a resting potential of 1.2 VRHE. The potential was then ramped to the working potential at which potentiostatic measurements were conducted for 2 minutes. Following the 2 minutes at the working potential, the potential was ramped backed down to the resting potential of 1.2 VRHE The mass signal observed for m/z = 32 and m/z = 34 (due to the natural abundance of 18O) on a representative film sputter deposited at room temperature is shown to track the potential step change in Fig. 2a, demonstrating the detection of oxygen generation as a function of voltage. The reproducibility of data and analogous data for films prepared at different temperatures can be found in the ESI† and accompanying database. Oxygen was detected at each working potential, down to 1.34 VRHE, and the oxygen signal became masked by the background of the 16O2 (m/z = 32) at potentials lower than 1.34 VRHE.
An equivalent experiment in an isotopically labelled electrolyte (He-saturated 0.1 M HClO4 in 97% H218O labelled water) is shown in Fig. 2b, showing a clear oxygen signal at 1.32 VRHE or a nominal overpotential of 90 mV. Isotopically labeling the water in the electrolyte with oxygen-18 can achieve higher sensitivity and allow the detection of oxygen evolution at lower overpotentials, due to the lower background of m/z = 36 (18O2) compared to m/z = 32 (16O2). The 16O18O/18O2 ratio is not significantly different than the expected value of ∼6% due to the 16O impurity in the labelled electrolyte at any potential, i.e., no significant lattice oxygen evolution, involving 16O of the oxides, was observed in this experiment. Small lattice oxygen evolution signals (<0.1% of the total O2 evolved) were observed in more sensitive experiments using labelled Ru18Ox films, which is the subject of the second article of this series (DOI: 10.1039/D1EE03915F).
The faradaic efficiency for oxygen evolution was found to be ∼100% at potentials greater than 1.40 VRHE but dropped at lower overpotential, reaching ∼ 20% at 1.33 VRHE, as shown in Fig. 2c. The faradaic efficiency is here defined as the ratio of the OER-related current density obtained by converting the oxygen flux detected by EC-MS to the total current density measured. The oxygen flux is averaged over the final 30 seconds of the 2-minute potentiostatic measurements at the working potential. The exponential decrease in the current density of oxygen evolution (black dots in Fig. 2c) from ∼1.42 VRHE to ∼1.32 VRHE was accompanied with significant reduction in the faradaic efficiency for OER from ∼1.42 VRHE to ∼1.32 VRHE, during which the residual capacitance current became dominant. Notably, at potentials greater than 1.40 VRHE, the oxidation current comes from OER (faradaic efficiency ∼100%), and thus we can use current alone to compare OER activity.
While the activity measurements exemplified in Fig. 2a and b were conducted in electrolyte saturated with He, and thus differed from the standard equilibrium condition of 1 bar O2, separate experiments showed that this did not affect the measured activity. In chip EC-MS, the electrolyte is saturated through the chip with a carrier gas, here He, while product gases such as O2 diffuse through the working volume of the electrolyte and escape through the chip. The concentration profile of a light gas such as O2 in the electrolyte can be estimated by Fick's first law of diffusion, and so depends on the production rate.47 At our detection limit of about 1 pmol s−1 cm−2, the concentration at the electrode surface is about 50 pM, or 4 × 10−8 of the saturation concentration, resulting in a Nernst equilibrium potential of 1.12 VRHE (calculation details in Section 2 of the ESI†). Thus, the actual thermodynamic overpotential for OER is larger than the nominal overpotential based on the standard equilibrium potential of 1.23 VRHE. However, using isotopically labeled electrolyte, we are able to directly probe the effect of O2 saturation on OER rate. Fig. S2 (ESI†) shows EC-MS data for the oxidation of H218O in (a) He-saturated and (b) 16O2-saturated 18O-labeled electrolyte. The presence of 16O2 makes no difference to the OER rate, measured via the 18O2 signal at m/z = 36. This is consistent with results by Marc Koper and coworkers, showing that the saturation of the electrolyte with O2 makes no difference to activity in alkaline OER.57
In order to further lower the potential limit for oxygen detection, Ru foam samples with a roughness factor of ∼3000 (see below) were synthesized on glassy carbon substrates by cathodic electrodeposition at −6 VRHE of ruthenium from a solution of 10 mM RuCl3 under vigorous hydrogen evolution conditions.50 The synthesized Ru “foam” was porous as shown by the scanning electron microscope image in the inset of Fig. 2d. Using the porous Ru foam, oxygen was observed at potentials as low as 1.30 VRHE, only 70 mV above the standard thermodynamic potential for water oxidation, 1.23 VRHE, Fig. 2d (and possibly 1.29 VRHE, see Fig. S3, ESI†). Notably, the current response as a function of time in Fig. 2d shows a steady decay in the current over the entire potential hold, which can be attributed to the large capacitative charge for the high surface area foam samples, in contrast to the O2 signal, which rises only slightly during the potential hold. Thus the direct detection of oxygen at potentials lower than the observable onset of current can be reliably distinguished from charging current and enables the mechanistic investigation of oxygen evolution reaction kinetics closer to the equilibrium conditions.
The detection of oxygen at such low nominal overpotentials may seem surprising given density functional theory calculations that suggest an OER limiting potential of ∼1.43 VRHE27,58,59 (∼200 mV overpotential) on the optimal catalyst, following the linear scaling relationships between the *O, *OH and *OOH intermediates. Here, we experimentally show that this value does not correspond to the lowest measurable experimental onset potential. This is because, while the rate of the reaction decreases exponentially with applied potential, the exponential function never reaches zero. At low overpotentials, the reaction can still proceed, although at a slower rate than high potentials where all steps are predicted to be energetically favorable. Thus, the measurable onset of OER is only limited by the sensitivity of the oxygen detection system.
Oxygen evolution activity on RuOx
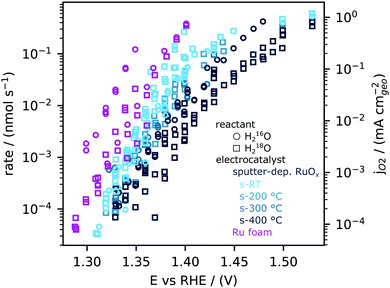
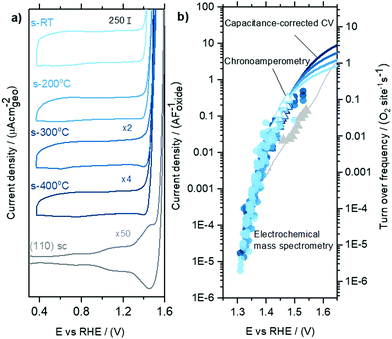
We next quantitatively compare the oxygen flux measured as a function of potential for the sputtered RuOx films and the high surface area Ru foam measured in labelled and unlabelled electrolyte, as shown in Fig. 3. The flux of oxygen generated at any given potential is about an order of magnitude higher on the room temperature sputtered films compared to those sputtered at 400 0C. All samples were measured in a potential range that makes use of the ∼5 orders of magnitude dynamic range of the EC-MS setup (∼10−5 to ∼ 1 nmol s−1 cm−2). All of these measurements and more activity data are available in the database of the accompanying repository. The corresponding OER current density, obtained by converting the moles of oxygen to a current using Faraday's law of electrolysis is shown on the right y axis of Fig. 3. The current densities obtained per geometric surface area at 1.45 VRHE for the sputtered films ranges from ∼0.1 mA cm−2geo for the 400 °C sputtered film to ∼1 mA cm−2geo for the room temperature sputtered film. These current densities are at least two orders of magnitude larger than that observed on single crystal RuO2(110), where ∼5 μA cm−2geo was observed at similar potentials. Considering surface X-ray diffraction studies on single crystal RuO2(110) have demonstrated that the surfaces are atomically smooth with only the top monolayer contributing to OER,21,22,60 we hypothesize that the sputtered films have a larger electrochemically active surface area per geometric area (roughness factor) compared to single crystals.Cyclic voltammetry of sputter-deposited films between 0.4 VRHE and 1.3 VRHE show that the capacitance decreases from the room temperature sputtered samples to those sputtered at 200 °C, 300 °C and 400 °C, Fig. 4a and Fig. S4 (ESI†). There was no effect of O2 saturation of the electrolyte on the parts of the CV relevant to OER (Fig. S5, ESI†). Interestingly, the capacitance of sputter-deposited films, which could be estimated from normalizing the current density by the scanning rate, are greater than single crystals by approximately one order of magnitude. The specific capacitance normalized to electrochemically active surface area (ECSA) of amorphous RuOx has been estimated to be a bit higher at 200 μF cm−2ECSA,35,36 but its measurement is challenging due to the difficulty of independently measuring the ECSA. In this work, we will use our value for the capacitance of RuO2(110), 115 μF cm−2ECSA (Fig. S6, ESI†), to estimate roughness factors of the other films. The specific capacitance of 400 °C-sputter-deposited films is ∼15–20 times larger (2100 μF cm−2geo) than that of RuO2 single crystal surfaces, implying a roughness factor of 15–20. The specific capacitance of sputter deposited films decreases with increasing deposition temperature from room temperature, with ∼6 times greater capacitance (12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 μF cm−2geo) for RuOx deposited at room temperature compared to that sputter-deposited at 400 °C, implying a roughness factor of ∼100. The Ru foam's roughness factor of ∼3000 was calculated based on its specific capacitance of ∼400
500 μF cm−2geo) for RuOx deposited at room temperature compared to that sputter-deposited at 400 °C, implying a roughness factor of ∼100. The Ru foam's roughness factor of ∼3000 was calculated based on its specific capacitance of ∼400![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 μF cm−2geo (see Fig. S3, ESI†). We attribute this difference in capacitance to the larger density of accessible sites in the films deposited at lower temperature, possibly owing to the formation of less compact films.
000 μF cm−2geo (see Fig. S3, ESI†). We attribute this difference in capacitance to the larger density of accessible sites in the films deposited at lower temperature, possibly owing to the formation of less compact films.
The geometric OER activity of sputter deposited films is 2–3 orders of magnitude higher (∼20 mA cm−2geo at 1.53 VRHE for room temperature sputter deposited RuO2) than that of the RuO2(110) (∼0.015 mA cm−2geo at 1.53 VRHE), measured from CV and potentiostatic measurements. This difference is partly explained by electrochemically active surface area (ECSA) as measured by capacitance. Notably, however, the activity of the sputter deposited RuOx films normalized to the capacitance is still ∼5 times higher than the RuO2(110) single crystal surface (Fig. 4b). While the OER activity normalized to geometric surface area for the sputter deposited films decrease with increasing sputtering temperature, the activity normalized to the average capacitance found between 0.4 VRHE and 1.3 VRHE, and consequently the turnover frequency, are similar for the sputtered films and ∼1 order of magnitude higher than RuO2(110), as shown in Fig. 4b. Other single-crystal surfaces RuO2(100) and (101) have activities only slightly higher than RuO2 (110),22,61,62 and so the sputter-deposited films have significantly higher ECSA-normalized activity than any single crystal facet. This observation suggests that the differences in activity between the single crystal surfaces and the sputter deposited films is not only a result of differences in accessibility of active sites alone, but also possibly from the intrinsic activity of these sites for OER. Differences in the activity between single crystal and sputter deposited films can originate from different coordination environments of the active Ru sites, which has been shown to significantly impact binding energy of reaction intermediates and OER activity.22,61,62 Recent experimental data on well-defined single crystals of RuO2 (110), (100) and (101) surfaces demonstrates that a change in the coordination environment of oxygen atoms surrounding the active Ru site and the predicted Ru–O–Ru bond angle can result in a weakening in binding energy between the most active RuO2(100) surface and the thermodynamically stable RuO2(110) surface of ∼0.04 eV22 and consequently an increase in OER activity of ∼5 times per active Ru site, based on a Tafel slope of 60 mV decade−1.22 Theoretical work by Nørskov and coworkers. considered a diverse range of active Ru sites on kinked RuO2(121) surfaces61,62 and showed that the oxygen binding energetics, ΔGO − ΔGOH on different surface sites can vary by ∼0.7 eV. In summary, while these sputter deposited oxides can produce larger OER activity compared to single crystal surfaces at a given potential, their OER mechanism at low potential is not understood.
Tafel slope at low overpotential
By co-plotting the OER partial current density determined from the oxygen flux along with the electrochemical activity measurements, we find that all the four sputter deposited films exhibit a new Tafel regime with a slope of ∼25 mV decade−1 at low potentials, which has not been previously experimentally detected on Ru-based oxides. Three distinct Tafel regimes have been observed on all the sputter deposited films (Fig. 4b and Fig. S7, ESI†). First, in the low overpotential regime (<1.40 VRHE) the newly revealed Tafel slope is ∼25 mV decade−1. Second, the next regime has a Tafel slope of 60 mV decade−1 and lasts till ∼1.47 VRHE on the room temperature sputter deposited film, and till ∼1.52 VRHE on the high temperature sputter deposited film. A Tafel slope of ∼60 mV decade−1 has also been found in previous work on oriented RuO2 single crystals,21,22,45 epitaxial thin films44,63,64 and nanoparticles19 at potentials greater than 1.50 VRHE. Finally, at potentials above ∼1.55 VRHE and ∼1.60 VRHE for the room temperature and 400 °C sample respectively, the Tafel slope increases to ∼120 mV decade−1.Potential-dependent Tafel slope can be attributed to one or more of several reasons. First, changes in the surface coverage of intermediates as a function of potential22,42,65 can result in different Tafel slopes across a range of potential for the same rate determining step as elucidated by the microkinetic analysis in the seminal work of Bockris46,65 and more recently by Shinagawa et al.42 and Mefford et al.41 Second, changes in the Tafel slope can be attributed to a change in the reaction mechanism with potential. Third, the superposition of different sites contributing to the overall activity could also result in different Tafel slopes, depending on which site dominates the activity at a given potential. From the Butler Volmer equation:
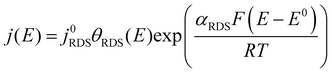 | (1) |
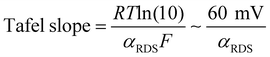 | (2) |
This cannot explain a Tafel slope of 25 mV decade−1, considering the value of αRDS can only be between 0 and 1. This is the case even if the mechanism changes as a function of potential, or multiple active sites with different j0RDS and αRDS contribute. In the latter case, furthermore, the Tafel slope should decrease at higher potential as the site with the larger αRDS increasingly dominates the current, opposite to the observed behavior. Therefore, we conclude that θRDS has a potential dependence.
Based on the changes in the Tafel slope, we can also rule out a purely chemical rate-determining step. Recent measurements of X-ray adsorption and discharge current on IrOx indicated that the rate-determining step may not be directly coupled to an electron transfer.66 In this case, the potential dependence comes only from the coverage of the active state, θRDS, which would eventually reach 1 at high overpotentials, resulting in an infinitely large Tafel slope. Instead, on the sputtered films, we observe a Tafel slope approaching 120 mV s−1 with increasing overpotential as expected with αRDS = 1/2. A chemical nature of the rate-determining step would imply a steep rise in the Tafel slope once a surface coverage of 1 is reached. We attempted to fit the results with both modifications to eqn (1) but they resulted in worse fits with much higher mean square errors.
Here, we propose that the changing Tafel slope comes from the potential dependence of the coverage of surface species that can participate in the rate-determining step (SI under “Kinetic model”). From the microkinetic rate equation, one can incorporate this coverage dependence in an “effective transfer coefficient”,42,46α*. The effective transfer coefficient, unlike the symmetry factor of the rate-determining step, is not restricted to be between 0 and 1. As demonstrated in the ESI† (eqn (S39), ESI†), the effect of surface coverage on the effective transfer coefficient can be explained by:
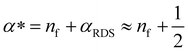 | (3) |
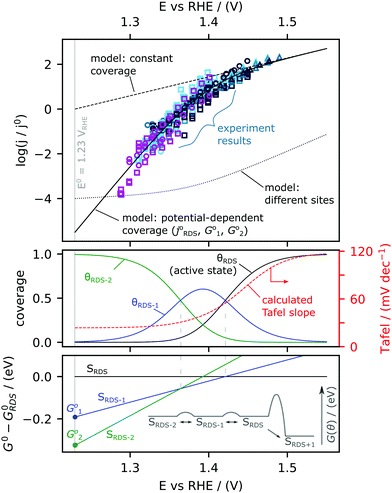
The Tafel slope at the lowest nominal overpotentials measured in this study was about 25 mV decade−1, implying that at these potentials, α* = 2.5 (by eqn (2) with α* replacing αRDS) and nf = 2 (by eqn (3)). In other words, our data indicate the equilibrium coverage of intermediates at low potentials is such that there needs to be two electron transfers per site before reaching the RDS. Therefore, we model the reaction assuming three distinct surface termination states, denoted SRDS, SRDS-1 and SRDS-2, where SRDS is the active state from which the rate-determining step takes place, and SRDS-1 and SRDS-2 precede it by one and two electron transfers, respectively. We assume that SRDS, SRDS-1 and SRDS-2 are in equilibrium. Consequently, at any given potential, the surface coverage of these states θRDS, θRDS-1 and θRDS-2 can be obtained based on the relative standard free energies of these three states at a given potential, shown in Fig. 5. For mathematical details of the model, see the ESI.†
We do not consider the back reaction, the oxygen reduction reaction (ORR) in this model. Equilibrium concepts are discussed in detail in the ESI.† Briefly, in the potential range spanned by our data (E > 1.29 VRHE), we predict that any ORR current would be at least 5 orders of magnitude lower than the OER current, and thus negligible, as illustrated in Fig. S8 of the ESI.† An insignificant ORR contribution is consistent with the lack of any effect of O2 partial pressure on the measured OER rate (Fig. S2 and S5, ESI†) and by the fact that the scatter in the normalized activity data increases if plotted against Nernst-adjusted overpotential rather than against potential on the RHE scale (Fig. S8a and b, ESI†). Note that with ORR left out of the model, the concept of overall equilibrium does not come into play, and E0 = 1.23 VRHE serves only as a reference potential.
The physical nature of SRDS, SRDS-1 and SRDS-2 can be hypothesized based on DFT calculations and in situ surface diffraction measurements in previous works21,22 on single crystal RuO2(110) surface, where it has been proposed that the rate-determining step is the final deprotonation step, *OO—H → O2 + (H+ + e−) + *. In this case, the RDS-active state (SRDS) corresponds to active coordinatively unsaturated sites (CUS) filled with *OO—H, SRDS-1 corresponds to all CUS sites filled with *O since one electron transfer is required to reach the RDS (*O + H2O → *OO –H + (H+ + e−), ΔG01) and SRDS-2 corresponds to all CUS sites filled with *OH since two electron transfers are required to reach the RDS (*OH + H2O → *OO—H + 2(H+ + e−), ΔG02). We reproduce the experimentally observed changes in Tafel slope by fitting the expanded version of Eqn 1 (eqn (S44) of the ESI†) with three parameters: j0RDS, ΔG01 and ΔG02 and find that the best fit is given by j0RDS = 0.9 mA F−1 (TOF0 = 3 × 10−4 s−1), ΔG01 = −0.19 eV, and ΔG02 = −0.33 eV. Details of fitting procedure are in ESI.† The result of the fitting is shown in Fig. 5. In the top panel, the model current density is co-plotted with the experimental data. The modeled coverages are shown in the middle panel, and the modeled standard free energies of the states relative to the active state are plotted in the lower panel. The redox transition from SRDS-2 to SRDS-1 occurs at 1.35 VRHE and the redox transition from SRDS-1 to SRDS occurs at 1.41 VRHE. These values are in fairly good agreement with the theoretically constructed Pourbaix diagram constructed for the ideal surface of RuO2(110)21 where the transition from *OH to *O species (*OH → *O + (H+ + e−)) occurs at 1.22 VDFT-RHE and the subsequent transition from *O to *OOH species (*O + H2O → *OO—H − (H+ + e−)) occurs at 1.42 VDFT-RHE. The discrepancies between the numerical values can be attributed to differences in the binding energetics of oxygenated intermediates on the sputter-deposited films relative to the CUS sites on the (110) surface. Notably, based on this model, at low overpotential, the rate of the reaction is strongly dependent on the coverage of species that can participate in the RDS. Therefore, at potentials <1.35 VRHE, a factor-10 improvement in activity would require stabilizing the RDS state with respect to the state dominating the surface (SRDS-2) by only 30 meV, which results in an increase in density of species that can be involved in the RDS. In contrast, if the energetics of SRDS and SRDS-2 were unchanged, the activation barrier for the rate-determining step would have to be reduced by 120 meV to achieve the same improvement (see ESI† for details: eqn (S45), ESI†). These results thus highlight the importance of optimising the energetics of pre-OER surface species to improve kinetics in the low-overpotential regime.
The identification of a new Tafel regime at potentials lower than 1.40 VRHE calls into question the determination of exchange current density for oxygen evolution reaction. The exchange current is defined as the magnitude of the current density of the forward reaction at zero overpotential and serves as a metric to compare the activity of different catalysts. The value is typically extracted by extrapolating the kinetics observed at potentials >∼1.50 VRHE to the equilibrium potential, assuming a constant Tafel slope. Based on our results, extrapolating data from ∼1.5 VRHE, results in an exchange current density of 0.9 mA F−1 (TOF of 3 × 10−4 s−1). However if we extrapolate instead from the low-overpotential regime <∼1.4 VRHE, the exchange current density is six orders of magnitude lower, ∼1 nA F−1 (TOF ∼ 3 × 10−10 s−1). This corresponds to a value of ∼2 × 10−10 mA cm−2ECSA, or ∼10−8 mA cm−2geo for s-25 °C RuOx, which has a roughness factor of ∼50. The ECSA-normalized exchange current density for OER on RuO2 is thus about 10 orders of magnitude lower than the exchange current density obtained for hydrogen evolution on low-index single crystal Pt surfaces, ∼1 mA cm−2ECSA.68 Clearly, both the experimental onset potential and the exchange current density are ambiguous metrics for OER activity, with an accuracy depending on the measurement sensitivity for oxygen. Therefore, we recommend using turn-over frequency for O2 production at a given nominal overpotential as the best fundamental metric whenever it is possible to estimate the number of active sites.
Conclusions
In this work, we used highly sensitive mass spectrometric O2 detection to measure the OER activity of RuOx at low overpotentials. Direct detection of O2 at low overpotentials is necessary because the electrocatalytic current can be small compared to other currents such as the capacitive charging current. Using 18O isotopic labeling to improve sensitivity, we detect oxygen from 1.32 V vs. RHE on sputter deposited amorphous RuOx and 1.30 V vs. RHE on Ru foam, nominal overpotentials of only 90 mV and 70 mV, respectively. To our knowledge, this sets the record for the lowest overpotential at which electrocatalytic O2 evolution has been measured. Complementing the dynamic range of mass spectrometry by synthesizing samples with a wide range of roughness factors, we obtained quantitative data spanning more than six orders of magnitude, revealing a new Tafel regime of 25 mV decade−1 below ∼1.4 VRHE. We attribute this strong potential dependence to a potential-dependent coverage of the surface state active in the rate-determining step, in line with recent kinetic and spectroscopic insight. Using these ultrasensitive activity measurements as inputs to a mechanistic model, we provide evidence for an electron transfer coupled rate-determining step from an active surface state in equilibrium with two other surface states more stable by energies of −0.19 eV and −0.32 eV at 1.23 VRHE. In addition to challenging the conventional notion of onset potential and exchange current density in water oxidation electrocatalysis, this data and technique opens a new window through which to probe the energetics of electrocatalytic intermediates and inform rational catalyst design of better and more scalable acid–electrolyte oxygen evolution catalysts.Experimental methods
Sample preparation and characterization
RuOx films were prepared by reactive sputtering on glassy carbon substrates. The substrates (0.196 cm2) were polished before the deposition process with 0.25 μm diamond paste. A thin layer (∼5 nm) of Ti was first sputter deposited and pressure of 10 mTorr from a Ti target to facilitate adhesion of the RuOx on the substrate. RuOx films were then deposited from a metallic Ru target at the noted temperature in a pressure of 3 mTorr with an Ar:O2 flow ratio of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. A 50 W power source was used. The target for sputtering was purchased from Kurt J. Lesker. For isotopically labelled oxides, the oxygen gas in the chamber was 18O2 (manufacturer) with a purity of 99%.
2. A 50 W power source was used. The target for sputtering was purchased from Kurt J. Lesker. For isotopically labelled oxides, the oxygen gas in the chamber was 18O2 (manufacturer) with a purity of 99%.
The Ru foam sample was synthesized by cathodic electrodeposition using a glassy carbon substrate. The deposition potential used was −6 VRHE (in the potential region for vigorous hydrogen generation) and deposition solution was 10 mM RuCl3. The deposition time was 2500 seconds. X-ray diffraction spectra were collected using a PANanalytical X’pert PRO machine with an X-ray wavelength of 1.54 Å for the CuKα line. AFM images collected using a Veeco Nanoscope IV. The XRD data collected was normalized to the noise level.
Electrochemical measurements
Electrochemical measurements were performed using a Biologic SP-300 potentiostat in a four-neck glass cell with a three-electrode configuration. ∼150 mL of 0.1 M HClO4 (70% Veritas® double distilled) was prepared using deionized water (Millipore, >18.2 MΩcm). A 4 M saturated Ag/AgCl reference electrode was used, which was calibrated to the RHE scale in the 0.1 M HClO4 solution. A large Pt wire was used as the counter electrode. The pH of the solution was measured using a pH meter. The electrolyte was bubbled with Ar (for cyclic voltammetry measurements) or O2 (for activity measurements). Electrical impedance spectroscopy was performed under open circuit with an amplitude of 10 mV. The high frequency intercept of the real resistance obtained from the Nyquist plot was used as the solution resistance.EC-MS
Electrochemistry-mass spectrometry measurements were performed using an interface system purchased from Spectro Inlets A/S. The setup is described in reference.47 An internal volume fabricated into a silicon-on-insulator microchip functions as a microscopic headspace which equilibrates with the working volume and delivers electrochemical products to the vacuum chamber without differential pumping. The mass spectrometer was a QMG electronics system and QMA 125 mass analyzer from Pfeiffer Vacuum, and the potentiostat was a Biologic SP 150. The electrolyte was 0.1 M HClO4 in either deionized water (Millipore) or 97% H218O isotope-labelled water (Medical Isotopes). The working electrode was connected through a 100 Ohm resistor to stabilize the potential, and all reported potentials are corrected by subtracting the current times this resistance. (This makes a negligible difference at the lowest over-potentials of interest, where the current is on the order of a microampere.)Data and modelling
Fitting was done by minimizing the mean square error on the logarithm of the modeled current density, with each activity point measured by potential hold in EC-MS (<1.45 VRHE) or conventional RDE electrochemistry (>1.4 VRHE).
Conflicts of interest
The authors do not have any conflicts of interest to declare.Acknowledgements
We gratefully acknowledge the funding by Villum Fonden, part of the Villum Center for the Science of Sustainable Fuels and Chemicals (V-SUSTAIN grant 9455), and the European Research Council (ERC) CLUNATRA under the European Union’s Horizon 2020 research and innovation program (grant agreement no. 741860)References
- H. B. Gray, Nat. Chem., 2009, 1, 7 CrossRef CAS PubMed.
- I. Roger, M. A. Shipman and M. D. Symes, Nat. Rev. Chem., 2017, 1, 1–13 CrossRef.
- M. Bernt, A. Siebel and H. A. Gasteiger, J. Electrochem. Soc., 2018, 165, F305–F314 CrossRef CAS.
- F. P. G. de Arquer, C.-T. Dinh, A. Ozden, J. Wicks, C. McCallum, A. R. Kirmani, D.-H. Nam, C. Gabardo, A. Seifitokaldani, X. Wang, Y. C. Li, F. Li, J. Edwards, L. J. Richter, S. J. Thorpe, D. Sinton and E. H. Sargent, Science, 2020, 367, 661–666 CrossRef PubMed.
- C.-T. Dinh, T. Burdyny, M. G. Kibria, A. Seifitokaldani, C. M. Gabardo, F. P. G. de Arquer, A. Kiani, J. P. Edwards, P. D. Luna, O. S. Bushuyev, C. Zou, R. Quintero-Bermudez, Y. Pang, D. Sinton and E. H. Sargent, Science, 2018, 360, 783–787 CrossRef CAS PubMed.
- G. Soloveichik, Nat. Catal., 2019, 2, 377–380 CrossRef CAS.
- S. Z. Andersen, V. Čolić, S. Yang, J. A. Schwalbe, A. C. Nielander, J. M. McEnaney, K. Enemark-Rasmussen, J. G. Baker, A. R. Singh, B. A. Rohr, M. J. Statt, S. J. Blair, S. Mezzavilla, J. Kibsgaard, P. C. K. Vesborg, M. Cargnello, S. F. Bent, T. F. Jaramillo, I. E. L. Stephens, J. K. Nørskov and I. Chorkendorff, Nature, 2019, 570, 504 CrossRef CAS PubMed.
- H. Iriawan, S. Z. Andersen, X. Zhang, B. M. Comer, J. Barrio, P. Chen, A. J. Medford, I. E. L. Stephens, I. Chorkendorff and Y. Shao-Horn, Nat. Rev. Methods Primers, 2021, 1, 1–26 CrossRef.
- W. T. Hong, M. Risch, K. A. Stoerzinger, A. Grimaud, J. Suntivich and Y. Shao-Horn, Energy Environ. Sci., 2015, 8, 1404–1427 RSC.
- C. Wei, R. R. Rao, J. Peng, B. Huang, I. E. L. Stephens, M. Risch, Z. J. Xu and Y. Shao-Horn, Adv. Mater., 2019, 31, 1806296 CrossRef PubMed.
- J. H. Montoya, L. C. Seitz, P. Chakthranont, A. Vojvodic, T. F. Jaramillo and J. K. Nørskov, Nat. Mater., 2017, 16, 70–81 CrossRef PubMed.
- M. Bernt and H. A. Gasteiger, J. Electrochem. Soc., 2016, 163, F3179–F3189 CrossRef CAS.
- T. Reier, H. N. Nong, D. Teschner, R. Schlögl and P. Strasser, Adv. Energy Mater., 2017, 7, 1601275 CrossRef.
- S. Geiger, O. Kasian, M. Ledendecker, E. Pizzutilo, A. M. Mingers, W. T. Fu, O. Diaz-Morales, Z. Li, T. Oellers, L. Fruchter, A. Ludwig, K. J. J. Mayrhofer, M. T. M. Koper and S. Cherevko, Nat. Catal., 2018, 1, 508–515 CrossRef CAS.
- M. Carmo, D. L. Fritz, J. Mergel and D. Stolten, Int. J. Hydrogen Energy, 2013, 38, 4901–4934 CrossRef CAS.
- N. Danilovic, R. Subbaraman, K.-C. Chang, S. H. Chang, Y. J. Kang, J. Snyder, A. P. Paulikas, D. Strmcnik, Y.-T. Kim, D. Myers, V. R. Stamenkovic and N. M. Markovic, J. Phys. Chem. Lett., 2014, 5, 2474–2478 CrossRef CAS PubMed.
- E. A. Paoli, F. Masini, R. Frydendal, D. Deiana, C. Schlaup, M. Malizia, T. W. Hansen, S. Horch, I. E. L. Stephens and I. Chorkendorff, Chem. Sci., 2014, 6, 190–196 RSC.
- R. Frydendal, E. A. Paoli, B. P. Knudsen, B. Wickman, P. Malacrida, I. E. L. Stephens and I. Chorkendorff, ChemElectroChem, 2014, 1, 2075–2081 CrossRef CAS.
- Y. Lee, J. Suntivich, K. J. May, E. E. Perry and Y. Shao-Horn, J. Phys. Chem. Lett., 2012, 3, 399–404 CrossRef CAS PubMed.
- K. A. Stoerzinger, L. Qiao, M. D. Biegalski and Y. Shao-Horn, J. Phys. Chem. Lett., 2014, 5, 1636–1641 CrossRef CAS PubMed.
- R. R. Rao, M. J. Kolb, N. B. Halck, A. F. Pedersen, A. Mehta, H. You, K. A. Stoerzinger, Z. Feng, H. A. Hansen, H. Zhou, L. Giordano, J. Rossmeisl, T. Vegge, I. Chorkendorff, I. E. L. Stephens and Y. Shao-Horn, Energy Environ. Sci., 2017, 10, 2626–2637 RSC.
- R. R. Rao, M. J. Kolb, L. Giordano, A. F. Pedersen, Y. Katayama, J. Hwang, A. Mehta, H. You, J. R. Lunger, H. Zhou, N. B. Halck, T. Vegge, I. Chorkendorff, I. E. L. Stephens and Y. Shao-Horn, Nat. Catal., 2020, 3, 516–525 CrossRef CAS.
- H. Over, Chem. Rev., 2012, 112, 3356–3426 CrossRef CAS PubMed.
- Z. W. Seh, J. Kibsgaard, C. F. Dickens, I. Chorkendorff, J. K. Nørskov and T. F. Jaramillo, Science, 2017, 355, eaad4998 CrossRef PubMed.
- L. C. Seitz, C. F. Dickens, K. Nishio, Y. Hikita, J. Montoya, A. Doyle, C. Kirk, A. Vojvodic, H. Y. Hwang, J. K. Norskov and T. F. Jaramillo, Science, 2016, 353, 1011–1014 CrossRef CAS PubMed.
- X. Zheng, B. Zhang, P. De Luna, Y. Liang, R. Comin, O. Voznyy, L. Han, F. P. García de Arquer, M. Liu, C. T. Dinh, T. Regier, J. J. Dynes, S. He, H. L. Xin, H. Peng, D. Prendergast, X. Du and E. H. Sargent, Nat. Chem., 2018, 10, 149–154 CrossRef CAS PubMed.
- I. C. Man, H.-Y. Su, F. Calle-Vallejo, H. A. Hansen, J. I. Martínez, N. G. Inoglu, J. Kitchin, T. F. Jaramillo, J. K. Nørskov and J. Rossmeisl, ChemCatChem, 2011, 3, 1159–1165 CrossRef CAS.
- M. T. M. Koper, J. Solid State Electrochem., 2013, 17, 339–344 CrossRef CAS.
- K. S. Exner, J. Phys. Chem. C, 2019, 123, 16921–16928 CrossRef CAS.
- K. S. Exner and H. Over, Acc. Chem. Res., 2017, 50, 1240–1247 CrossRef CAS PubMed.
- C. F. Dickens, C. Kirk and J. K. Nørskov, J. Phys. Chem. C, 2019, 123, 18960–18977 CrossRef CAS.
- Y.-H. Fang and Z.-P. Liu, J. Am. Chem. Soc., 2010, 132, 18214–18222 CrossRef CAS PubMed.
- Y. Ping, R. J. Nielsen and W. A. Goddard, J. Am. Chem. Soc., 2017, 139, 149–155 CrossRef CAS PubMed.
- K. Naoi and P. Simon, Electrochem. Soc. Interface, 2008, 4 Search PubMed.
- N. Yoshida, Y. Yamada, S. Nishimura, Y. Oba, M. Ohnuma and A. Yamada, J. Phys. Chem. C, 2013, 117, 12003–12009 CrossRef CAS.
- W. Dmowski, T. Egami, K. E. Swider-Lyons, C. T. Love and D. R. Rolison, J. Phys. Chem. B, 2002, 106, 12677–12683 CrossRef CAS.
- E. Tsuji, A. Imanishi, K. Fukui and Y. Nakato, Electrochim. Acta, 2011, 56, 2009–2016 CrossRef CAS.
- S. Cherevko, S. Geiger, O. Kasian, N. Kulyk, J.-P. Grote, A. Savan, B. R. Shrestha, S. Merzlikin, B. Breitbach, A. Ludwig and K. J. J. Mayrhofer, Catal. Today, 2016, 262, 170–180 CrossRef CAS.
- N. Hodnik, P. Jovanovič, A. Pavlišič, B. Jozinović, M. Zorko, M. Bele, V. S. Šelih, M. Šala, S. Hočevar and M. Gaberšček, J. Phys. Chem. C, 2015, 119, 10140–10147 CrossRef CAS.
- D. B. Trimarco, Real-time detection of sub-monolayer desorption phenomena during electrochemical reactions: Instrument development and applications, Department of Physics, Technical University of Denmark, 2017.
- J. Tyler Mefford, Z. Zhao, M. Bajdich and W. C. Chueh, Energy Environ. Sci., 2020, 13, 622–634 RSC.
- T. Shinagawa, A. T. Garcia-Esparza and K. Takanabe, Sci. Rep., 2015, 5, 13801 CrossRef PubMed.
- C. P. Plaisance, S. D. Beinlich and K. Reuter, J. Phys. Chem. C, 2019, 123, 8287–8303 CrossRef CAS.
- K. A. Stoerzinger, L. Qiao, M. D. Biegalski and Y. Shao-Horn, J. Phys. Chem. Lett., 2014, 5, 1636–1641 CrossRef CAS PubMed.
- P. Castelli, S. Trasatti, F. H. Pollak and W. E. O’Grady, J. Electroanal. Chem. Interfacial Electrochem., 1986, 210, 189–194 CrossRef CAS.
- J. O. Bockris, J. Chem. Phys., 1956, 24, 817–827 CrossRef CAS.
- D. B. Trimarco, S. B. Scott, A. H. Thilsted, J. Y. Pan, T. Pedersen, O. Hansen, I. Chorkendorff and P. C. K. Vesborg, Electrochim. Acta, 2018, 268, 520–530 CrossRef CAS.
- S. B. Scott, A. K. Engstfeld, Z. Jusys, D. Hochfilzer, N. Knøsgaard, D. B. Trimarco, P. C. K. Vesborg, R. J. Behm and I. Chorkendorff, Catal. Sci. Technol., 2020, 10, 6870–6878 RSC.
- D. Hochfilzer, J. E. Sørensen, E. L. Clark, S. B. Scott, I. Chorkendorff and J. Kibsgaard, ACS Energy Lett., 2021, 6, 1879–1885 CrossRef CAS.
- A. Winiwarter, L. Silvioli, S. B. Scott, K. Enemark-Rasmussen, M. Sariç, D. B. Trimarco, P. C. K. Vesborg, P. G. Moses, I. E. L. Stephens, B. Seger, J. Rossmeisl and I. Chorkendorff, Energy Environ. Sci., 2019, 12, 1055–1067 RSC.
- A. Winiwarter, M. J. Boyd, S. B. Scott, D. C. Higgins, B. Seger, I. Chorkendorff and T. F. Jaramillo, ChemElectroChem, 2021, 8, 250–256 CrossRef CAS.
- S. B. Scott, J. Kibsgaard, P. C. K. Vesborg and I. Chorkendorff, Electrochim. Acta, 2021, 374, 137842 CrossRef CAS.
- S. B. Scott, J. Kibsgaard, P. C. K. Vesborg and I. Chorkendorff, Electrochim. Acta, 2021, 374, 137844 CrossRef CAS.
- C. Roy, B. Sebok, S. B. Scott, E. M. Fiordaliso, J. E. Sørensen, A. Bodin, D. B. Trimarco, C. D. Damsgaard, P. C. K. Vesborg, O. Hansen, I. E. L. Stephens, J. Kibsgaard and I. Chorkendorff, Nat. Catal., 2018, 1, 820–829 CrossRef CAS.
- P. Simon and Y. Gogotsi, Nat. Mater., 2020, 19, 1151–1163 CrossRef CAS PubMed.
- M. Salanne, B. Rotenberg, K. Naoi, K. Kaneko, P.-L. Taberna, C. P. Grey, B. Dunn and P. Simon, Nat. Energy, 2016, 1, 1–10 Search PubMed.
- A. C. Garcia and M. T. M. Koper, ACS Catal., 2018, 8, 9359–9363 CrossRef CAS PubMed.
- J. Rossmeisl, Z.-W. Qu, H. Zhu, G.-J. Kroes and J. K. Nørskov, J. Electroanal. Chem., 2007, 607, 83–89 CrossRef CAS.
- J. H. Montoya, A. D. Doyle, J. K. Nørskov and A. Vojvodic, Phys. Chem. Chem. Phys., 2018, 20, 3813–3818 RSC.
- R. R. Rao, M. J. Kolb, J. Hwang, A. F. Pedersen, A. Mehta, H. You, K. A. Stoerzinger, Z. Feng, H. Zhou, H. Bluhm, L. Giordano, I. E. L. Stephens and Y. Shao-Horn, J. Phys. Chem. C, 2018, 122, 17802–17811 CrossRef CAS.
- C. F. Dickens and J. K. Nørskov, J. Phys. Chem. C, 2017, 121, 18516–18524 CrossRef CAS.
- C. F. Dickens, J. H. Montoya, A. R. Kulkarni, M. Bajdich and J. K. Nørskov, Surf. Sci., 2019, 681, 122–129 CrossRef CAS.
- D.-Y. Kuo, H. Paik, J. Kloppenburg, B. Faeth, K. M. Shen, D. G. Schlom, G. Hautier and J. Suntivich, J. Am. Chem. Soc., 2018, 140, 17597–17605 CrossRef CAS PubMed.
- K. A. Stoerzinger, R. R. Rao, X. R. Wang, W. T. Hong, C. M. Rouleau and Y. Shao-Horn, Chem, 2017, 2, 668–675 CAS.
- J. O. Bockris and T. Otagawa, J. Phys. Chem., 1983, 87, 2960–2971 CrossRef CAS.
- H. N. Nong, L. J. Falling, A. Bergmann, M. Klingenhof, H. P. Tran, C. Spöri, R. Mom, J. Timoshenko, G. Zichittella, A. Knop-Gericke, S. Piccinin, J. Pérez-Ramírez, B. R. Cuenya, R. Schlögl, P. Strasser, D. Teschner and T. E. Jones, Nature, 2020, 587, 408–413 CrossRef CAS PubMed.
- A. J. Bard, L. R. Faulkner, J. Leddy and C. G. Zoski, Electrochemical methods: fundamentals and applications, Wiley, New York, 1980, vol. 2 Search PubMed.
- N. M. Marković, B. N. Grgur and P. N. Ross, J. Phys. Chem. B, 1997, 101, 5405–5413 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ee03914h |
| ‡ Present affiliation: Department of Materials, Imperial College London, London, United Kingdom. |
| § SBS and RRR contributed equally. |
| ¶ Present affiliation: Department of Chemistry, Imperial College London, London, United Kingdom. |
| || Present affiliation: Korean Advanced Institute of Science and Technology, Republic of Korea. |
| This journal is © The Royal Society of Chemistry 2022 |