The origin of capacity fluctuation and rescue of dead Mn-based Zn–ion batteries: a Mn-based competitive capacity evolution protocol†
Hang
Yang
a,
Wanhai
Zhou
b,
Duo
Chen
 *ac,
Jiahao
Liu
b,
Zeyu
Yuan
a,
Mengjie
Lu
a,
Laifa
Shen
*ac,
Jiahao
Liu
b,
Zeyu
Yuan
a,
Mengjie
Lu
a,
Laifa
Shen
 c,
Valerii
Shulga
a,
Wei
Han
c,
Valerii
Shulga
a,
Wei
Han
 *a and
Dongliang
Chao
*a and
Dongliang
Chao
 *b
*b
aCollege of Physics, the State Key Laboratory of Inorganic Synthesis and Preparative Chemistry, International Center of Future Science, Jilin University, Changchun 130012, China. E-mail: whan@jlu.edu.cn
bLaboratory of Advanced Materials, Shanghai Key Laboratory of Molecular Catalysis and Innovative Materials, State Key Laboratory of Molecular Engineering of Polymers, and School of Chemistry and Materials, Fudan University, Shanghai, 200433, China. E-mail: chaod@fudan.edu.cn
cJiangsu Key Laboratory of Electrochemical Energy Storage Technologies, College of Materials Science and Technology, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China. E-mail: chenduo@nuaa.edu.cn
First published on 23rd December 2021
Abstract
Although Mn2+ additives alleviate the dissolution issue of Mn-based cathodes in aqueous zinc–ion batteries (ZIBs), problems including complex side reactions and abnormal capacity fluctuation pose new challenges for their large-scale applications. In virtue of manganese oxide based on preeminent cation-pillar engineering, we elaborate the origin of capacity fluctuation, which is found to be correlated with the unique Mn2+ behavior. For the first time, we figure out new metrics such as effective cycling percentage (η) and maximum Mn2+ contribution ratio (ε) to reappraise the electrochemical performance of the current Mn-based ZIBs via a new capacity evaluation protocol, i.e., Mn-based competitive capacity evolution (Mn-CCE). The universality of the protocol and its metrics were further verified via quantitative analyses of the reported Mn-based ZIBs. More significantly, the failure of Mn-based electrodes is demonstrated to be rescuable via facile acid treatment, which is expected to quintuple the lifespan of batteries. The findings can provide new insights to understand the electrochemical behaviors, serve as the assessment criteria, and further guide the development of Zn/Mn-related devices for practical applications.
Broader contextMn-Based aqueous zinc–ion batteries (ZIBs) have triggered a great research upsurge in safe energy storage systems due to decent output voltage, environmental friendliness, and scalable manufacturing. However, the use of essential Mn2+ additives in Mn-based ZIBs, with an original purpose to alleviate dissolution issues, gives rise to complex side reactions and abnormal performance fluctuation, which impedes the development toward commercialization. In addition, the foreseeable massive battery waste after its scalable application in the near future will also induce new pressure on the environment. In this work, we comprehensively analyzed the origin of capacity fluctuation, and propose herein a Mn-based competitive capacity evolution (Mn-CCE) protocol to reappraise the electrochemical behavior of Mn-based ZIBs. Simultaneously, a facile rescue method was developed for dead cathodes, which is expected to achieve quintuple lifespan. These findings provide new insights into the electrochemical behavior of the Mn-based ZIBs, paving a promising way to facilitate the scalable application of aqueous energy storage devices. |
1. Introduction
Considering the increasing concerns of security and scarcity of Li and Co reserves in lithium–ion batteries, exploring alternative energy storage systems is becoming the spotlight of worldwide research to cope with the astounding development of diversified electronic devices.1,2 Aqueous rechargeable Zn–ion batteries (ZIBs) stand out among the various energy storage techniques due to the natural advantages of safety, low cost, high energy density, and environmental friendliness.3–7 However, it is difficult to design a robust and high-efficiency cathode material and further implement the commercialization of ZIBs. MnO2-based materials have been widely studied as active cathodes for their superiority in specific capacity and output voltage.8–12 However, MnO2-based polymorphs suffer from the serious phase transition, resulting in the disappointing electrochemical reversibility. Thereinto, δ-phase MnO2 with a peculiar layered structure, compared with the channel-like structure, is theoretically more reliable for the storage and release of ions, which is supposed to be more suitable for Zn2+ insertion/extraction and high-efficiency electrochemical kinetics.13–18 However, in practice, the desired charge storage advantages of the layered structure have not been materialized, which instead embody low specific capacity and poor structural stability.18–21Dissolution of manganese oxide in the discharge/charge process has been considered to be another critical factor for the unsatisfactory electrochemical performance of ZIBs. In order to address this issue, adding a certain amount of Mn2+ ions into the electrolyte has been widely demonstrated as an effective approach to suppress the Jahn–Teller effect of manganese oxides.22–26 Nonetheless, the side reactions introduced by Mn2+ ion additives increase the complexity of aqueous ZIB chemistry. On the one hand, the Mn2+ electrolyte additive may positively contribute to extra capacity. On the other hand, the induced parasitic reaction may negatively obscure the electrochemical behaviors of the raw cathode, and the accumulation of the by-product could result in battery degradation and even failure.23,24 Thus far, many strategies such as controlling the morphology and phase, forming conductive framework hybrids, and introducing vacancies and doping have been developed to enhance the structural stability and electrochemical reversibility of Mn-based ZIBs.27,28 To the best of our knowledge, all the above-mentioned strategies are passive to alleviate some specific issues of the original MnO2 cathode. However, the batteries would ultimately go into decline, especially when cycled at a small current density, and one can only discard the battery after the performance failure. Consequently, it is desirable to shed additional light on the failure analysis of the running Mn-based ZIBs, eliminate the adverse effects proactively, and rescue the failed battery to prolong its lifetime. In this respect, a comprehensive consideration is necessary to clarify the electrochemical behavior of Mn2+ from both active materials and electrolytes.
Herein, we first regulate the interlayer spacing of layered δ-MnO2 theoretically and experimentally via cation-pillar engineering. Taking Ba2+-pillared layered δ-MnO2 as a model, the charge storage mechanism for Mn-based ZIBs is comprehensively corroborated. Its degradation mechanism is elaborated, where the Mn2+ behavior dominates the process. Through quantitative analyses of capacity contribution ratio from Mn2+, a new charge storage evaluation protocol named Mn-based competitive capacity evolution (Mn-CCE) is proposed. This protocol aims to incisively comprehend the activity of electrode materials and electrolytes during the charge storage process. More importantly, it is demonstrated for the first time that the MnO2-electrode failure can be rescued proactively via tuning the dead Mn behavior by facile acid treatment, which is expected to quintuple the lifetime of batteries. The findings would be of great significance for understanding the electrochemistry and classifying the Mn-based ZIBs rationally to cope with the potential complex usage scenarios in the future.
2. Results and discussion
2.1 Characterizations
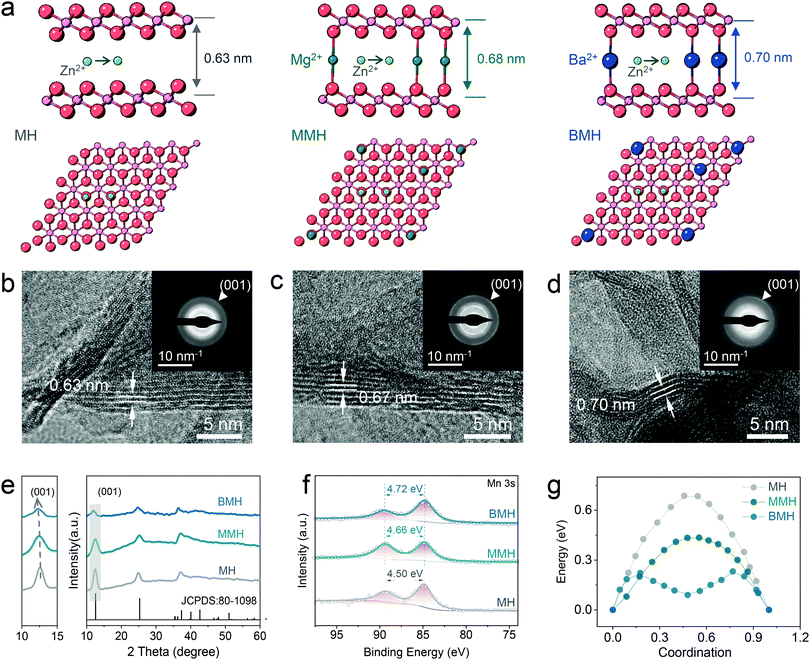
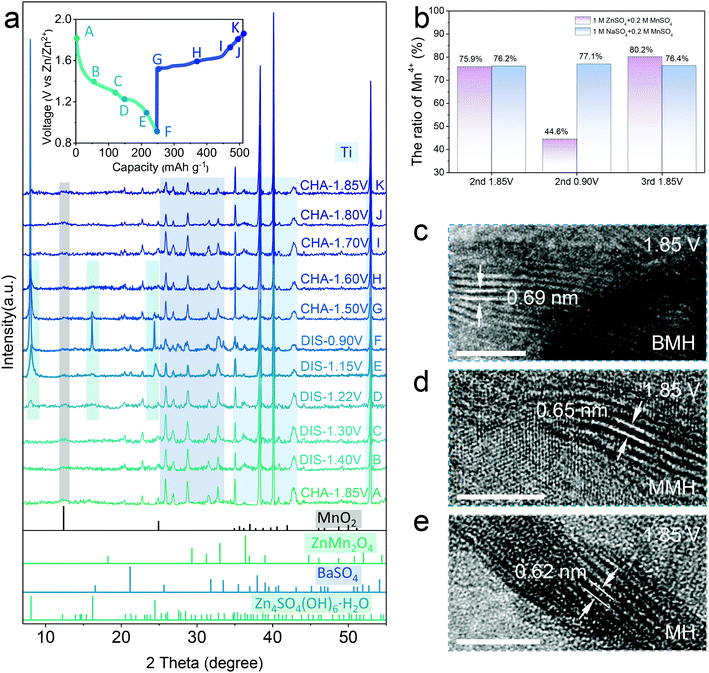
The distinguished effect of the enlarged interlayer via cation-pillar engineering is demonstrated using the DFT calculation. The potential migration pathways of the three samples are given in Fig. 1a, where Zn2+ is found to tend to diffuse along with the sites close to oxygen atoms in the interlayer. Moreover, the calculated interlayer spacing was determined as 0.63, 0.68, and 0.70 nm for δ-MnO2 (MH), Mg2+-pillared δ-MnO2 (MMH), and Ba2+-pillared δ-MnO2 (BMH), respectively, which is in good agreement with the high-resolution TEM (HRTEM) images, shown in Fig. 1b–d, where the corresponding lattice spacings in the (001) crystal plane for MH, MMH, and BMH are observed as 0.63, 0.67 and 0.70 nm, respectively. It can also be verified by the results of selected area electron diffraction (SAED) patterns, indicating the key role of the pre-inserted metal ions in interlayer chemistry engineering. Fig. 1e presents the X-ray diffraction (XRD) pattern of obtained BMH, MMH, and MH. The characteristic diffraction peaks are well indexed to pure δ-phase MnO2 (JCPDS 97-006-8916) with a layered structural birnessite framework. No obvious impurity peak is detected. Note that the (001) peaks of BMH and MMH shift to a lower degree than that of MH to varying degrees, suggesting the expansion of the (001) plane caused by the insertion of Ba2+/Mg2+. The intercalated Ba2+/Mg2+ ions serve as interlayer pillars that may ensure expedite ion diffusion channels for rapid electrochemical kinetics.12,14,15,29 Furthermore, the X-ray photoelectron spectroscopy (XPS) results (Fig. 1f) indicate that BMH and MMH exhibit a lower spin-energy separation for the Mn 3s doublet, suggesting a slight reduction in the Mn oxidation state due to ion pre-intercalation.8,30–32 More importantly, the corresponding migration energy barrier between the adjacent sites for Zn2+ was computed to be 0.21, 0.43, and 0.68 eV for BMH, MMH, and MH, respectively (Fig. 1g). The low Zn diffusion energy barrier endows BMH with rapid Zn2+ diffusion kinetics, revealing its excellent electrochemical performance. Assisted with the inductively coupled plasma-optical emission spectroscopy (ICP-OES), thermogravimetric analysis (TGA, Fig. S1, ESI†), scanning electron microscopy (SEM, Fig. S2, ESI†), and XPS (Fig. S3, ESI†), the successful design and synthesis of the three samples are further demonstrated, and the stoichiometry formulae for BMH, MMH, and MH were determined to be Ba0.17MnO2·0.46H2O, Mg0.13MnO2·0.65H2O, and MnO2·0.54H2O, respectively. Taking BMH as an example, the pH monitoring for the electrolyte shows the reversible fluctuation in the discharge/charge process (Fig. S4a, ESI†), implying reversible consumption/release of H+ at different electrochemical states. Furthermore, ex situ XRD patterns in Fig. 2a show the reversible formation of basic zinc sulfate (Zn4SO4(OH)6·5H2O, noted as ZHS, JCPDS 39-0688), which originated from the precipitation between ZnSO4 and accumulated OH− after the H+ insertion in the discharge process.8,30,33 It can be described using the following reaction:| 4Zn2+ + 6OH− + SO24− + 5 H2O ↔ Zn4SO4(OH)6·5H2O | (1) |
The typical diffraction peak of (001) for δ-MnO2 is well maintained at various discharge/charge states. Note that the BaSO4 phase (JCPDS 24-1035) appears in the electrode, which might be caused by the precipitation of the extracted Ba2+ ions at the initial charging process (Fig. S5 and Table S1, ESI†).15 In addition, the XPS spectra attributed to Zn 2p (Fig. S4b, ESI†) show reversible enhancement and decrease in discharge/charged state caused by the Zn2+ insertion/extraction in the BMH.15 It is in good agreement with the STEM-EDX observation in the BMH nanosheets, where Zn signals at the discharge state are more significant than that after charging (Fig. S4c and d, ESI†), substantiating the reversible insertion/extraction chemistry of Zn2+ in the layered BMH cathode. Besides, the valence state evolution of Mn elements in the cathode was also analyzed via XPS spectra (Fig. S4c and d, ESI†). As shown in Fig. 2b, an obvious change in the ratio of Mn4+ in BMH was observed at different discharge/charge states, while similar phenomena were not obtained in the cells using 1 M Na2SO4 + 0.2 M MnSO4 electrolyte without Zn2+ and less H+, demonstrating that the reversible intercalation of Zn2+ and/or H+ is the main cause for the valence change of Mn in the discharge/charge process.34–36 Additionally, the interlayer distance of the (001) plane remains a large value of 0.69 nm at the fully charged state, which further illustrates the superiority of pre-intercalation cation engineering (Fig. 2c–e). It should be pointed out that the lattice spacing of the cathode materials becomes smaller after cycling, which might be ascribed to the partial deintercalation of pre-inserted cations at the initial charging process.15,37
2.2 Electrochemical behavior
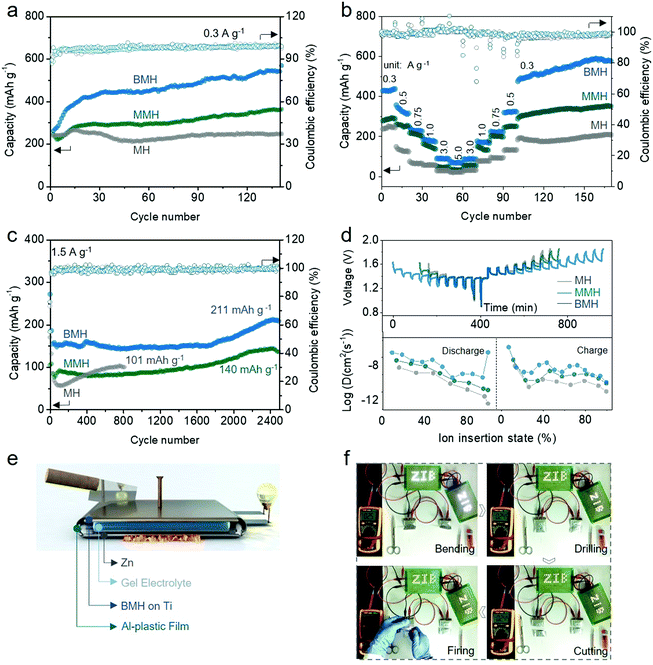
To verify the feasibility of the interlayer-engineering strategy, the electrochemical performances of the BMH, MMH, and MH cathodes were assessed using the typical CR2032 coin-type cells, which are coupled with a Zn foil anode, a glass fiber separator, and 1 M ZnSO4 + 0.2 M MnSO4 as the electrolyte. Fig. S6 (ESI†) presents the cyclic voltammetry (CV) curves for BMH, MMH, and MH at a scan rate of 0.3 mV s−1 in the second cycle. Two pairs of reversible redox peaks can be observed for the three samples, which correspond to H+ and Zn2+ (de)intercalation in different discharge/charge stages.30 Obviously, BMH and MMH exhibit a higher current response in the CV curves than MH, demonstrating better electrochemical reactivity benefiting from the pre-insertion of Ba2+/Mg2+. As displayed in Fig. 3a, BMH, MMH and MH deliver corresponding relatively steady capacities of 534, 358, and 205 mA h g−1, respectively, at a current density of 0.3 A g−1 after 140 cycles. The larger layered distance of the BMH endows it with facilitated ion diffusion and robust crystal stability, thereby showing superior electrochemical properties to MMH and MH, which was further confirmed by the following comprehensive tests. As shown in Fig. 3b, BMH cathode realizes a higher capacity than those of MMH and MH at all the current densities from 0.3 to 5.0 A g−1 (detailed results are shown in Table S2, ESI†), indicating a better rate capability. The prominent rate property might be ascribed to the enlarged gallery spacing for the rapid ion (de)intercalation. Moreover, BMH delivers a decent capacity of 211 mA h g−1 at 1.5 A g−1 after 2500 cycles (Fig. 3c), demonstrating excellent long-term cycling durability. Owing to the narrow interlayer distance, MMH and MH can only exhibit inferior capacities of 140 mA h g−1 after 2500 cycles and 101 mA h g−1 after 820 cycles, respectively. Notably, an evident capacity rise emerges in the later cycling stage due to the Mn2+ additive in the electrolyte, which will be explained in the following parts.To further demonstrate the intrinsic influence of the incorporation of Ba2+ and Mg2+ on the electrochemical behavior of δ-phase MnO2, the galvanostatic intermittent titration technique (GITT, the details of the calculation are available in the ESI†) was employed to evaluate the ion diffusion coefficient D of Zn2+ in three materials.38,39 As shown in Fig. 3d, the D values determined by GITT for BMH are higher than those for MMH and MH, which validate its superior diffusion kinetics among the three samples. As shown in Fig. S7a–c (ESI†), two pairs of reversible redox peaks of Peak 1/Peak 4 and Peak 2/Peak 3 were detected at the initial scan stage, which was attributed to the insertion/extraction of H+/Zn2+ ions. It should be mentioned that a new Peak 5 gradually appears as the scan proceeds, which is supposed to be related to the emerging conversion reaction from Mn2+ to ZnMn2O4, which occurred on the electrode surface.23,24,40–43 The peak current (i, mA) and scan rate (ν, mV s−1) of the CV curves follow a power law i = avb, where the constant b = 1.0 corresponds to the surface-induced faradaic controlled process, and b = 0.5 suggests a diffusion-controlled process.44,45 The relatively low b values of BMH for Peak 1–4 indicate that the (de)intercalation process of H+/Zn2+ ions is inclined to be a diffusion-dominated process (Fig. S7d–f, ESI†). Meanwhile, the b values for all the three electrodes for Peak 5 approach 1.0, indicating that the enhanced conversion reaction of Mn2+ is due to the surface-induced faradaic behavior. In addition, the quantified capacity contribution ratio (Fig. S7g–I, ESI†) presents a high diffusion contribution for the BMH cathode, manifesting the unimpeded ion diffusion and fast kinetics in the enlarged layered crystal structure.
The flexible quasi-solid-state (QSS) pouch-type Zn/BMH battery was assembled using a BMH cathode, a Zn plate anode, and a PAM/ZnSO4/MnSO4 gel electrolyte for probing the practical potential in safe and flexible devices (Fig. 3e). The QSS pouch-type battery could not only deliver outstanding electrochemical performances (Fig. S8, ESI†), but also possess promising application prospects toward flexible and safe electronics. The LED light arrays can be easily powered by the two prototype batteries with a stabilized voltage at about 2.44 V. The flexible Zn/BMH battery can ensure stable energy output even under a series of extreme working conditions, such as bending, drilling, cutting, and firing, as shown in Fig. 3f and Video S1 (ESI†), indicating the superb reliability to resist various extreme conditions in the practical application as a flexible energy storage device.
2.3 The origin of capacity fluctuation and new capacity evaluation protocol.
The structural evolution of BMH is presented in Fig. 4a for an entire discharge/charge cycle (the original SEM images are available in Fig. S9, ESI†). Significantly, the original morphology of BMH is well reserved at various states; meanwhile, a few of the nanoparticles reversibly appear on the surface of BMH nanosheets during the cycling process. From the SEM images of BMH after 180 cycles (the inset in Fig. 4b), the nanoparticles were found to increase and agglomerate apparently. The nanoparticles were testified as ZnMn2O4 from the XRD patterns (Fig. 4b), and the atom ratios of Zn, Mn, and O were confirmed by EDS analysis (Fig. S10, ESI†).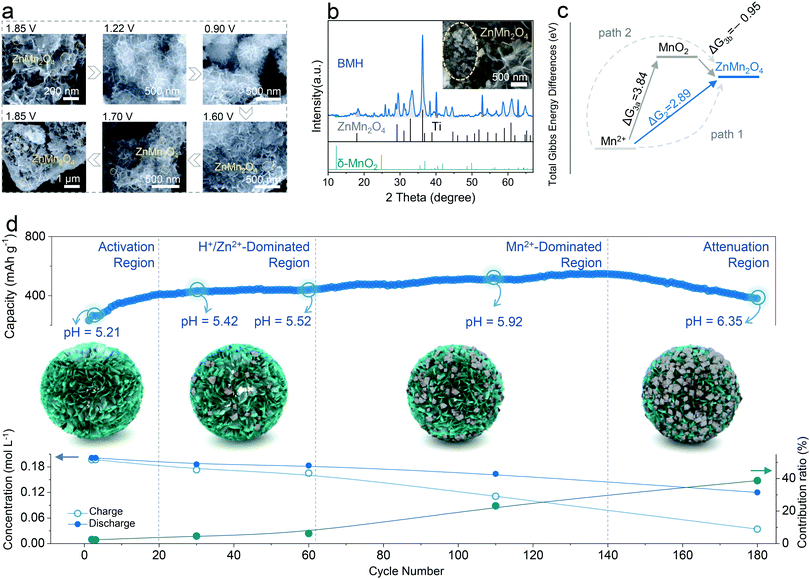 | ||
| Fig. 4 The origin of capacity fluctuation and Mn-based competitive capacity evolution (Mn-CCE) protocol. (a) Evolution of SEM images at different dis/charged states for BMH cathode from the 2nd cycle. (b) XRD patterns and SEM (inset) of BMH after 180 cycles at 0.3 A g−1. (c) Total Gibbs energy differences at 300 K for two possible reaction paths, i.e., Path 1 and Path 2, corresponding with eqn (2) and (3), respectively. (d) Mn-based competitive capacity evolution protocol: upper is the partition of the cycle profile and the pH value at 1.85 V for different stages, the middle is the micromechanism schematic in four different regions, and the bottom is the concentration and contribution ratio of the Mn2+. | ||
In order to elucidate the origin of ZnMn2O4, two cells fabricated with BMH cathodes in different electrolytes were studied. In the galvanostatic charge–discharge (GCD) profiles shown in Fig. S11a (ESI†), an obvious shift for the initial charging voltage from ca. 1.5 V (in the first 30th) to ca. 1.4 V (light blue mark) with the increase in the cycling number can be observed, which is in line with gradually emerging Peak 5 in the CV curves (Fig. S7a, ESI†). However, a similar phenomenon cannot be detected in the cell using pure 1 M ZnSO4 electrolyte (Fig. S11b, ESI†), and the XRD pattern of the cycled electrode shows no diffraction peak for ZnMn2O4 (Fig. S12, ESI†). Therefore, the ZnMn2O4 nanoparticles can be determined to have generated from the Mn2+-containing electrolyte. According to the previous reports, this electrochemical reaction could proceed along the following two possible paths:41–43,46
Charge process: 2Mn2+ + Zn2+ + 8OH− → ZnMn2O4 + 4H2O + 2e− E = 1.320![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V vs. Zn/Zn2+ V vs. Zn/Zn2+ | (2) |
| Charge process: Mn2+ + 2H2O → MnO2 (↓) + 4H+ + 2e− E = 1.869V vs. Zn/Zn2+ | (3a) |
Discharge process: MnO2 (↓) + 0.5Zn2+ + e− → 0.5ZnMn2O4 E = −1.230![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V vs. Zn/Zn2+ V vs. Zn/Zn2+ | (3b) |
By comparing the voltages and the total Gibbs energy differences (Fig. 4c) for both paths, Path 1 is the favored alternative to form ZnMn2O4. Moreover, the formation energy of ZnMn2O4 is lower than that of MnO2, as shown by the theoretical calculation (as shown in Fig. S13, ESI†), which further demonstrates that Mn2+ in our case is more prone to form ZnMn2O4 irrespective of the reaction path.
The Mn2+ additive in the electrolyte can provide extra capacity because of the reversible formation and disappearance of ZnMn2O4 nanoparticles (Fig. 4a), therefore its capacity contribution can be estimated by analyzing the evolution of the ion concentration in the electrolyte at different cycling stages by ICP-OES. The calculation details of capacity contribution are available in Table S3 (ESI†). As shown in Fig. 4d, the cycle curve can be divided into four parts according to its fluctuation characteristics in various cycling stages and the corresponding contribution ratio from Mn2+ (CfM). The details are discussed as follows:
Region I is the activation region, where the cycling curve shows an evident and rapid capacity increase at first and then levels off. In this region, the concentration variation trend of Zn2+ (Fig. S14, ESI†) is similar to that of Mn2+, whilst the former exhibits a higher variation magnitude, indicating that the capacity contribution from Zn2+ insertion/exaction predominates in comparison with the conversion reaction of Mn2+. Besides, the monitoring of pH values confirms the intercalation/deintercalation reaction of H+ in this region (Fig. S14, ESI†). By calculating the amount of charge transferred in the Mn2+ reaction, the contribution ratio of Mn2+ to the total capacity was found to be at a low level (CfM < 5%) in the initial stage. Thus, similar to the previous reports, the capacity increase in this region is associated with the wetting of the electrode rather than the influence of Mn2+.47 Note that the Zn2+ content is no longer considered in the later stages due to the interference in determining the Zn2+ contribution from side reactions, including the formation of zinc hydroxyl sulfate, corrosion, and passivation of Zn anodes.
Region II is the H+/Zn2+-dominated region, in which the capacity curve exhibits a flat or mildly ascending shape after the Activation Region. Although the amount of Mn2+ deposition increases slightly in this region, the deposited Mn-species can be reversibly reduced in the discharged process as the Mn2+ content in the 60th cycle is approximately equal to that in the 30th cycle. Therefore, this region can be considered as the reversible region, where the reversible intercalation/deintercalation reaction of H+/Zn2+ plays a dominant role.
Region III is the Mn2+-dominated region, where the cycling curve presents an obvious capacity climbing trend. In this region, the CfM increases obviously compared with the first two regions, accompanied by the decline in the Mn2+ content of the electrolyte. The results give a rational explanation for the total capacity rise. Specifically, to elucidate the reason for the formation of the Mn2+-dominated region, a commercial MnO2 cathode with a bulk morphology (SEM images as shown in Fig. S15a, ESI†) was designedly selected to construct a ZIB system using the 1 M ZnSO4 + 0.2 M MnSO4 electrolyte. As shown in Fig. S15b (ESI†), the cycling curve presents a superposition state of the first three regions and starts immediately from the Mn2+-dominated stage. This might be attributed to the suppression of the intercalation chemistry by the attenuated nanoscale effect in bulk MnO2, and Mn2+ is prone to be deposited directly onto the large-sized bulk material. Therefore, the emergence of the Mn2+-dominated region could be triggered by the successive accumulation of ZnMn2O4 nanoparticles on the δ-MnO2 surface, which intensifies the further Mn2+ conversion reaction.
How to rationally divide Region II and III is also a critical issue. According to the above-mentioned description, the distinction of Region III from Region II is that the Mn2+ conversion reaction dominates the electrochemical process, thereby making related contribution changes. As shown in Fig. 4d, the Mn2+ contribution exhibits a rapid rise from the 60th cycle, indicating the entry into the Mn2+-dominated region. However, this differentiation method is not convenient in practice because it requires a lot of additional tests, e.g., ICP-OES analyses. Herein, we propose a facile qualitative way of comparing the slopes of the performance curve to assess the boundary between region II and III. An inflection point would be determined that separates the effective region into two parts, i.e., Zn2+/H+-dominated region with a lower overall slope k1 and the Mn2+-dominated region with a higher slope k2. As shown in Fig. S16 and Note S1 in the ESI,† the maximum specific value of k2/k1 was found at the 62th cycle, which is consistent with the aforementioned analysis about Mn2+-reaction contribution, implying its good feasibility.
The last region IV is the Attenuation Region, where the cycling curve turns to a steep downward trend of capacity from the upward stage. In this region, the Mn2+ content continues to decrease, implying the successive irreversible deposition of ZnMn2O4. However, the total capacity decreases rapidly as the CfM increases, which is due to the dramatic increase in resistance accompanied by the extensive accumulation of the irreversible ZnMn2O4 nanoparticles (Fig. S17, ESI†). It can be corroborated by the Nyquist plot at different cycling stages, as shown in Fig. S18 (ESI†), in which the impedance of the cathode rises observably in the Attenuation Region.24,41,46 The reason the CE is still close to 100% is that the undissolved ZnMn2O4 nanoparticles also undergo (de)intercalation of H+/Zn2+, which supplies a small amount of capacity.48,49
The assessment method of Mn-CCE proposed herein will provide a new sight to comprehensively understand the dynamic evolution of the different capacity contributors in the cycling process for aqueous Mn-based ZIBs, because the insertion/extraction of H+/Zn2+ and conversion reaction of Mn2+ are considered to occur concurrently in the whole stage. Their contribution ratios in various stages depend on the nanostructural evolution of the electrode and the local pH environment at the electrode/electrolyte interface. In the initial H+/Zn2+-dominated region, the deposition of ZnMn2O4 is quasi-reversible but sluggish due to the low pH environment (Fig. S14, ESI†). As the cycle proceeds, the precipitation reaction of ZnMn2O4 is facilitated owing to the increase in the localized pH, according to eqn (2) and (3). Besides, the accumulated irreversible ZnMn2O4 nanoparticles form adequate nucleation sites, triggering the intensified Mn2+-deposition reaction and providing enhanced CfM capacity, which formed the Mn2+-dominated region. Furthermore, in the attenuation region, a large amount of spinel ZnMn2O4 accumulate due to the raised pH environment, which obstructs the ion/charge transfer of the electrode, leading to rapid performance degradation, even the failure of the battery.
To unravel the concern on whether the battery failure is caused by the exhaustion of the electrolyte, another cell was assembled using a dead BMH electrode with a fresh electrolyte and a Zn anode. As shown in Fig. S19 (ESI†), the extremely low discharge capacity in the initial stage indicates that the disabled cathode can no longer serve as an effective active cathode. With the increase in the cycling number, the capacity rises gradually due to the contribution from Mn2+ in the electrolyte. The cyclic performance also exhibits a typical Mn2+-dominated behavior, as the intercalation chemistry of H+/Zn2+ is suspended for the dead BMH electrode, which further confirms the feasibility of the Mn-CCE protocol.
It should be pointed out that the deposition reaction of Mn2+ in the charging process differs at different charging voltages or electrolyte environments; therefore, the deposition product might be MnO2 in some other reported Mn-based Zn-battery systems instead of ZnMn2O4 due to the promoted MnO2 deposition kinetics.9,50 In fact, these Mn-precipitation reactions could render extra discharge capacity no matter in which form, for the fact that Mn2+ contribution is actually from the electrolyte. Moreover, the deposited tunnel MnO2 tends to turn into a ZnMn2O4 spinel upon cycling, especially when the pH value increases in the later period.23,24,40,46 Although the detailed procedure in other reports is slightly distinct from our BMH-cell, the evolution of the cyclic capacity can conform well to the proposed Mn-CCE protocol, demonstrating the universality of the protocol in Mn2+-contained aqueous battery systems.
The cyclic performance at high current rates also conforms to the as-proposed Mn-CCE protocol on the whole. Taking BMH as an example, it can be divided into 4 regions (as shown in Fig. S20, ESI†). Its overall tendency is similar to the low current rate, except for the initial activation process, in which it first exhibits high capacity for several cycles and then a capacity fluctuation owing to the change in the kinetics condition at the high current density. The fresh BMH electrode possesses abundant active sites exceeding the reversible discharge/charge demand enabled at a high rate, thereby causing the irreversible capacity. Combined with the progressive wetting of the electrode, it shows a special fluctuant activation process. The kinetics limitation and the enhanced polarization in the high current rate might be the key influence factors on the competition between Zn2+/H+- and Mn2+-based reactions. Considering that the deposition reaction of Mn2+ requires electric energy according to eqn (2), the amount of deposited ZnMn2O4 at the high current rate would be less than that at a low rate. Meanwhile, the accumulation of ZnMn2O4 would be slower, revealing the later arrival of the Mn2+-dominated region. Thus, the cycling curve at 1.5 A g−1 exhibits the longer stable H+/Zn2+-dominated region.
The Mn-CCE protocol provides new insights to understand the internal electrochemical behaviors of the Mn-based ZIBs, and could further serve as an assessment criterion for Mn-based cathodes. The significance can be concluded in the following aspects:
It can define the valid cycling numbers by calculating the length of H+/Zn2+-dominated and Mn2+-dominated regions, which can eliminate the abnormal cycles in the activation and attenuation region. In addition, the proportion of the stable operation for an electrode can also be determined by the metrics of effective cycling percentage as follows:
| η = (nII + nIII)/(nI + nII + nIII + nIV) × 100% | (4) |
The capacity for Mn2+-conversion reaction originates from the electrolyte rather than the cathode; thus it should not be counted in evaluating the capacity of original active materials. Via analyzing the electrochemical process in these four cycling regions, the real capacity from the original cathode (Cc) can be easily estimated as the initial capacity of the H+/Zn2+-Dominated Region, which includes few Mn2+ contributions. Meanwhile, we can also define metrics of a maximum Mn2+ contribution ratio as follows:
| ε = (CM − Cc)/CM × 100% | (5) |
We are now capable of selecting different types of Mn-based ZIB devices to accommodate a variety of practical requirements. The device with H+/Zn2+-dominated behavior possesses outstanding reversibility and long-term lifespan, which is suitable for devices such as mobile phones and smartwatches that need to repeat charge/discharge cycles. We suggest that the mass of the electrolyte and its capacity contribution should be simultaneously considered for the Mn2+-dominated materials. Under the condition with an equal amount of electrolyte, the battery with Mn2+-dominated behaviors might deliver a higher capacity, which fits devices such as electronic toys that require long-time power output after a single charge and not sensitive to the total quality of the cell. Therefore, different types of Mn-based materials could be selected according to the consumer demands, providing a universal guideline for the commercialization of Mn-based ZIBs in the future. Furthermore, selecting a suitable crystal structure, adjusting the electric conductivity, and modulating the appropriate microstructure might be expected to design advanced Mn-based cathodes with specific demands.12,46,47,51
It is worth noting that the capacity fluctuation phenomenon is ubiquitous in previously reported Mn-based ZIBs (Table S4, ESI†).12,15,23,30,47,49,51–60 For example, MnOx−2 reported by Liu and co-workers was found to exhibit a Mn2+-dominated behavior (ε > 50%) due to the extensive Mn2+ contribution from the electrolyte and successive upward performance curves,56 while the Ca0.28MnO2·0.5H2O cathode reported by Sun et al. showing a flat cycling profile can be regarded as exhibiting a H+/Zn2+-dominated behavior (ε < 50%).15 Therefore, the understanding of capacity fluctuation and the proposed universal capacity evaluation protocol for Mn-based ZIBs is of great significance to guide the development of Zn/Mn electrochemistry-related devices in future practical applications.
2.4 Rescue of dead Mn-based cathodes.
According to the above-mentioned discussion, the failure of Mn-based Zn–ion batteries could be ascribed to the accumulation of ZnMn2O4. Therefore, we intend to develop a proactive methodology to rescue the battery by a strategy of tuning dead-Mn behavior, that is, wiping off the spinel nanoparticles on the surface of δ-MnO2. By soaking the dead electrode in a 0.1 M H2SO4 solution for 24 h, ZnMn2O4 on the failed BMH cathode can be wiped off via disproportionation, according to the following reaction:| ZnMn2O4 + 4H+ → MnO2 + Mn2+ + Zn2++ 2H2O | (6) |
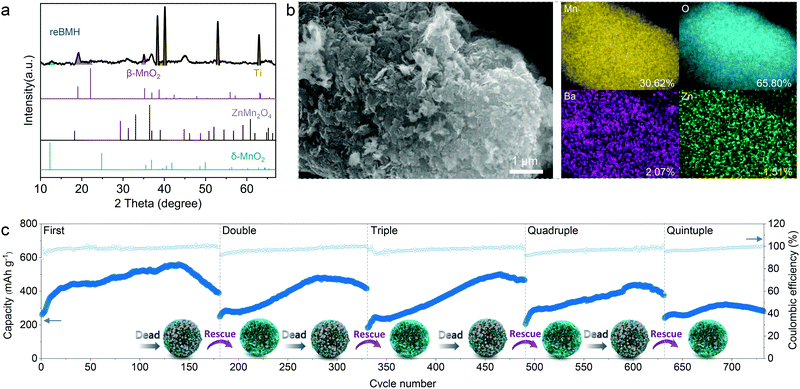
The treated sample is defined as rescued BMH (reBMH). The XRD patterns shown in Fig. 5a suggest that the ZnMn2O4 nanoparticles are successfully dissolved with only the δ-phase MnO2 remains. Note that a new set of characteristic peaks indexed a β-phase MnO2 (JCPDS 72-1983) appear for reBMH, which is the product of the disproportionation reaction. Thus, the nanoparticles observed in the SEM image of reBMH are in accordance with the new-formed MnO2 (Fig. 5b). The EDS results also indicate that the ratio of Mn and O is close to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, while the Zn content in reBMH is extremely low, which confirms the successful elimination of ZnMn2O4. From the magnified SEM image in Fig. S22 (ESI†), the nanoflower-like structure is well reserved in reBMH, indicating no damage to the pristine BMH after the acid treatment. To prove this concept, we also synthesized pure ZnMn2O4 for the acid treatment.61 A similar transformation from spinel ZnMn2O4 to β-phase MnO2 can be observed, further demonstrating the abovementioned conversion in eqn (6) (see Fig. S23, ESI†).
2, while the Zn content in reBMH is extremely low, which confirms the successful elimination of ZnMn2O4. From the magnified SEM image in Fig. S22 (ESI†), the nanoflower-like structure is well reserved in reBMH, indicating no damage to the pristine BMH after the acid treatment. To prove this concept, we also synthesized pure ZnMn2O4 for the acid treatment.61 A similar transformation from spinel ZnMn2O4 to β-phase MnO2 can be observed, further demonstrating the abovementioned conversion in eqn (6) (see Fig. S23, ESI†).
The reBMH electrode is reassembled into a coin cell with a fresh electrolyte. As shown in Fig. 5c, the reBMH is capable of resuming a high capacity of 470 mA h g−1 after 140 cycles at 0.3 A g−1 in the 2nd recycle. Surprisingly, the electrode can be repeatedly treated after failure and the reBMH renders impressive capacities of 490, 430, and 300 mA h g−1 when it undergoes the 3rd, 4th, and 5th revival, respectively. Furthermore, the reBMH exhibits the remarkable capacities of 306.9, 304.7, 225.2, 176.7, and 123.7 mA h g−1 at current densities of 0.3, 0.5, 0.75, 1.0, and 2.0 A g−1, respectively, implying the rate recoverability via resuming the Mn2+-behavior (Fig. S24a, ESI†). At a relatively high current density of 1.0 A g−1 (Fig. S24b, ESI†), the reBMH also exhibits excellent stability and rate capability, which retains 177.4 mA h g−1 after 600 cycles.
It suggests that via this facile, low-cost, and scalable rescue strategy, the recycling manufacture of the battery could be achieved in industries, considering that the resumable electrode still possesses competitive electrochemical capacity. These results prove the feasibility of the facile proactive strategy of tuning the dead-Mn behavior, realizing more than a quintuple lifespan of Mn-based ZIBs, which is helpful for resource recovery, pollution reduction, and cost curtailment.
Moreover, the performance curves in the 2nd, 3rd, and 4th revival can also be divided into four regions. As shown in Fig. 5c, the activation region shrinks obviously, which might be caused by the activation of a small amount of newly formed MnO2. Considering that the formed MnO2 nanoparticles would weaken the proportion of δ-MnO2 nanoflowers and provide nucleation sites for Mn2+ deposition, the H+/Zn2+-dominated region therewith shortens, and Mn2+-dominated region is triggered in advance for the reBMH-based batteries. The evolution of the cycling profiles for reBMH further demonstrates the as-proposed electrochemical mechanism for Mn-based ZIBs.
3. Conclusions
In summary, via mechanism analysis of the designed Mn-based cathodes based on the prominent cation pre-intercalated engineering, the energy storage mechanism of H+/Zn2+ intercalation chemistry accompanied by a Mn2+ conversion reaction has been confirmed by the synergetic first-principles calculation, electrochemical kinetics analyses, and various ex situ characterizations. What counts is that we have unraveled the fact that Mn2+ additives can impact the charge/discharge curve thoroughly, and thus, proposed a more comprehensive and objective Mn-CCE protocol for the Mn-based ZIBs (Scheme 1), which illustrates the electrochemical behavior at different cycle stages, aiming to comprehend the more profound and real electrochemical mechanism of the real Mn-based oxide distinctly. In addition, a recycling method for the failed cathode has been demonstrated after analyzing the degradation mechanism of the manganese oxide cathode, and the dead Mn-based ZIBs are rescued four times with remarkable electrochemical performances (Scheme 1). This work provides a new protocol for understanding and evaluating the electrochemical behavior of Mn-based ZIBs, and paves a recoverable and environmentally friendly commercialization path.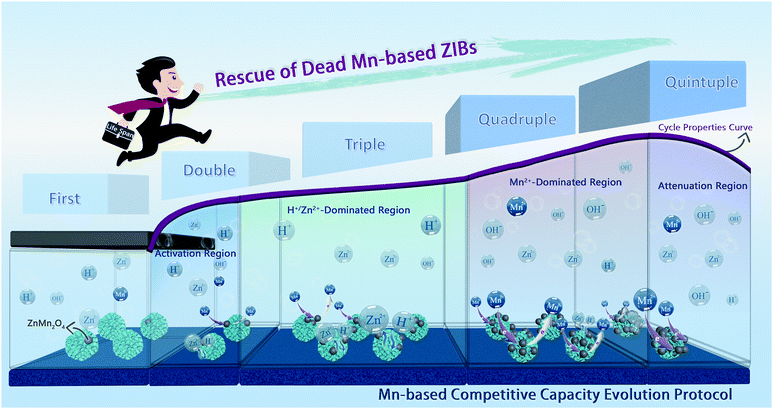 | ||
| Scheme 1 Schematic diagram of the Mn-based competitive capacity evolution protocol and the extension of lifetime for the dead Mn-based ZIBs. | ||
4. Experimental section
4.1 Materials
Three samples were synthesized by a simple hydrothermal method. Typically, KMnO4 (Beijing Chemical Works), BaCl2/MgCl2, and MnCl2 (Sinopharm Chemical Reagent Co., Ltd) in a molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6
6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 were added into 80 mL deionized water. This solution was transferred into a 100 mL Teflon-lined stainless steel autoclave and maintained at 160 °C for 12 h. Finally, the BMH and MMH were obtained after the product was thoroughly washed with deionized water and dried under vacuum at 60 °C for 12 h. MH was synthesized without BaCl2/MgCl2.
1 were added into 80 mL deionized water. This solution was transferred into a 100 mL Teflon-lined stainless steel autoclave and maintained at 160 °C for 12 h. Finally, the BMH and MMH were obtained after the product was thoroughly washed with deionized water and dried under vacuum at 60 °C for 12 h. MH was synthesized without BaCl2/MgCl2.
4.2 Sample characterization
The XRD patterns were recorded using a Rigaku Smart-Lab X-ray diffractometer. Scanning electron microscopy (SEM, Regults 8100) and transmission electron microscopy (TEM, JEOL JSM-2010![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) F) were employed to investigate the morphology. X-Ray photoelectron spectroscopy (XPS) was conducted using a Thermo Escalab 250Xi electron spectrometer. A pH measuring instrument was supported by INESA Scientific Instrument Co., Ltd (pHSJ-3F). Inductively coupled plasma-optical emission spectrometer (ICP-OES, Agilent ICPOES730) was used to monitor the evolution of electrolyte ions.
F) were employed to investigate the morphology. X-Ray photoelectron spectroscopy (XPS) was conducted using a Thermo Escalab 250Xi electron spectrometer. A pH measuring instrument was supported by INESA Scientific Instrument Co., Ltd (pHSJ-3F). Inductively coupled plasma-optical emission spectrometer (ICP-OES, Agilent ICPOES730) was used to monitor the evolution of electrolyte ions.
4.3 Electrochemical measurements
Electrochemical measurements were performed using CR2032 coin-type cells in the potential range of 0.9–1.85 V (vs. Zn2+/Zn). The cells were assembled using a zinc foil (φ = 15 mm, 50 μm thick) as the anode, a BMH/MMH/MH electrode as the cathode, a 1 M ZnSO4 + 0.2 M MnSO4 aqueous solution (∼100 μL) as the electrolyte, and a glass fiber paper (φ = 16 mm) as the separator. The electrode was fabricated by compressing a mixture of active materials of δ-MnO2-based composites, conductive materials (carbon nanotubes, CNTs), and binders (polyvinylidene fluoride, PVDF) in a weight ratio of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 onto a Ti foil (φ = 12 mm), and dried in a vacuum oven at 60 °C overnight. The areal loading density of the active materials was 1.5 mg cm−2. The cyclic voltammetry (CV) curves and electrochemical impedance spectroscopy (EIS) spectra were recorded using a CHI760E electrochemical working station. The cycling and charge–discharge behavior was investigated utilizing a multichannel battery test system LAND CT-2001A in the coin cell. The pH test was carried out in a beaker-type cell using a zinc flake (2 × 2 cm) as the anode, a BMH electrode (2 × 2 cm) as the cathode, and 1 M ZnSO4 + 0.2 M MnSO4 as the electrolyte. The diffusion coefficient D of Zn2+ was obtained by a series of galvanostatic charge/discharge pulses of 600 s at 0.3 A g−1 followed by a 0.5 h rest. The calculation method is based on the following equation:
1 onto a Ti foil (φ = 12 mm), and dried in a vacuum oven at 60 °C overnight. The areal loading density of the active materials was 1.5 mg cm−2. The cyclic voltammetry (CV) curves and electrochemical impedance spectroscopy (EIS) spectra were recorded using a CHI760E electrochemical working station. The cycling and charge–discharge behavior was investigated utilizing a multichannel battery test system LAND CT-2001A in the coin cell. The pH test was carried out in a beaker-type cell using a zinc flake (2 × 2 cm) as the anode, a BMH electrode (2 × 2 cm) as the cathode, and 1 M ZnSO4 + 0.2 M MnSO4 as the electrolyte. The diffusion coefficient D of Zn2+ was obtained by a series of galvanostatic charge/discharge pulses of 600 s at 0.3 A g−1 followed by a 0.5 h rest. The calculation method is based on the following equation: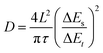 | (7) |
4.4 Preparation of flexible quasi-solid-state ZIBs
The quasi-solid-state battery was packaged with a PAM/ZnSO4/MnSO4 gel electrolyte, a BMH cathode (2 × 3 cm), and a flexible Zn anode (2 × 3 cm). For the gel electrolyte, the monomer mixture was composed of a monomer (4 g of acrylamide), an initiator (30 mg of K2S2O8), and a cross-linker (4 mg of N,N′-methylenebis-(acrylamide)) in 20 mL of deionized water. Then, after a polymerization reaction at 40 °C for 4 h, the PAM/ZnSO4/MnSO4 electrolyte was obtained by soaking the as-prepared PAM film in 2 M ZnSO4 and 0.2 M MnSO4 solution for 48 h.4.5 Rescue of dead Mn-based cathode.
The dead BMH electrode disassembled from the corrupted coin cell was directly soaked in 0.1 M H2SO4 solution for 24 h at room temperature. After rinsing with deionized water, the reBMH electrode was obtained. Then, the reBMH could serve as an active cathode to reassemble into a new coin cell.4.6 Computational methods
We performed the first-principles density functional calculations using the Perdew–Burke–Ernzerhof (PBE) functional within the spin-polarized GGA+U approximation as implemented in the Cambridge serial total energy package (CASTEP) code.62,63 The Vanderbilt ultrasoft pseudopotential was used with a cutoff energy of 450 eV.64 The norm-conserving pseudopotentials were used with a cutoff energy of 820 eV. Geometric convergence tolerances were set for a maximum force of 0.03 eV Å−1, a maximum energy change of 10−5 eV per atom, a maximum displacement of 0.001 Å, and a maximum stress of 0.5 GPa. Density mixing electronic minimization was implemented and the self-consistent field (SCF) tolerance was set to ‘fine’ with high accuracy of 10−6 eV per atom for energy convergence. The Hubbard U correction was introduced to describe the effect of localized d electrons of the transition metal ions. The applied effective U value given to Mn ions is 4 eV, consistent with earlier work.65–67 The migration barriers of the Zn–ion in the material were calculated using the NEB method as implemented in CASTEP.The diffusion of Zn was investigated by searching the possible diffusion route and identifying the migration transition state with the lowest diffusion energy barrier. The diffusion energy barrier is the energy difference between the total energies of the transition state and the initial structure. The transition state was searched by the generalized synchronous transit (LST/QST) method implemented in the CASTEP code.65 The algorithm starts from linear synchronous transit (LST) optimization and continues with a quadratic synchronous transit (QST) maximization process. Thereafter, the conjugate gradient (CG) minimization was conducted from the obtained LST/QST structure to refine the geometry of the transition state. The LST/QST/CG calculations were repeated till a stable transition state was obtained.
The first-principles investigations of the phonon dispersion relations and phonon modes were performed within the linear response theory.68,69 The phonon-related thermodynamic properties such as enthalpy and entropy were calculated in a quasiharmonic approximation. The Gibbs free energies (eqn (8)) were employed to discuss the relative stability of ZnMn2O4 and δ-MnO2.
| GT = Etotal + HT − TST + EZPE | (8) |
Gibbs free energy change (ΔG) was evaluated based on the computational hydrogen electrode model, which takes one-half of the chemical potential of gaseous hydrogen under standard conditions as the free energy of the proton–electron pairs. Gibbs free energy changes were calculated using the following equation:
| ΔGT = +ΔEZPE − TΔST + neU | (9) |
The reaction potential V vs. Zn/Zn2+ can then be calculated using the following expression:70
| V = −(E1 − E2)/ne | (10) |
Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
The authors sincerely acknowledge financial support from the National Natural Science Foundation of China (NSFC Grant No. 21571080 and 22109029). The authors thank the financial support from Fudan University (No. JIH2203010 and IDH2203008/003). The authors thank the financial support from International Center of Future Science, Jilin University, Changchun, P. R. China (ICFS Seed Funding for Young Researchers). The authors would like to acknowledge the facility of Instrument and equipment sharing platform, college of physics, Jilin University, Changchun, P. R. China.Notes and references
- S. Chu and A. Majumdar, Nature, 2012, 488, 294–303 CrossRef CAS PubMed.
- M.-S. Balogun, H. Yang, Y. Luo, W. Qiu, Y. Huang, Z.-Q. Liu and Y. Tong, Energy Environ. Sci., 2018, 11, 1859–1869 RSC.
- Z. Liu, Y. Huang, Y. Huang, Q. Yang, X. Li, Z. Huang and C. Zhi, Chem. Soc. Rev., 2020, 49, 180–232 RSC.
- D. Chao, W. Zhou, F. Xie, C. Ye, H. Li, M. Jaroniec and S.-Z. Qiao, Sci. Adv., 2020, 6, 21 Search PubMed.
- M. Song, H. Tan, D. Chao and H. J. Fan, Adv. Funct. Mater., 2018, 28, 1802564 CrossRef.
- B. F. Cui, X. P. Han and W. B. Hu, Small Struct., 2021, 2, 2000128 CrossRef.
- Z. Liu, X. Luo, L. Qin, G. Fang and S. Liang, Adv. Powder Mater., 2021 DOI:10.1016/j.apmate.2021.10.002.
- H. Pan, Y. Shao, P. Yan, Y. Cheng, K. S. Han, Z. Nie, C. Wang, J. Yang, X. Li, P. Bhattacharya, K. T. Mueller and J. Liu, Nat. Energy, 2016, 1, 16039 CrossRef CAS.
- D. Chao, W. Zhou, C. Ye, Q. Zhang, Y. Chen, L. Gu, K. Davey and S. Z. Qiao, Angew. Chem., Int. Ed., 2019, 58, 7823–7828 CrossRef CAS PubMed.
- D. Chao and S.-Z. Qiao, Joule, 2020, 4, 1846–1851 CrossRef.
- S. Guo, J. Li, B. Zhang, W. Chen, G. Fang, M. Long and S. Liang, Sci. Bull., 2021 DOI:10.1016/j.scib.2021.10.016.
- J. Huang, Z. Wang, M. Hou, X. Dong, Y. Liu, Y. Wang and Y. Xia, Nat. Commun., 2018, 9, 2906 CrossRef PubMed.
- M. Zhang, R. Liang, T. Or, Y.-P. Deng, A. Yu and Z. Chen, Small Struct., 2020, 2, 2000064 CrossRef.
- H. Peng, H. Fan, C. Yang, Y. Tian, C. Wang and J. Sui, RSC Adv., 2020, 10, 17702–17712 RSC.
- T. Sun, Q. Nian, S. Zheng, J. Shi and Z. Tao, Small, 2020, 16, 2000597 CrossRef CAS PubMed.
- D. Chen, M. Lu, D. Cai, H. Yang and W. Han, J. Energy Chem., 2021, 54, 712–726 CrossRef.
- M. Han, L. Qin, Z. Liu, L. Zhang, X. Li, B. Lu, J. Huang, S. Liang and J. Zhou, Mater. Today Energy, 2021, 20, 100626 CrossRef CAS.
- M. H. Alfaruqi, S. Islam, D. Y. Putro, V. Mathew, S. Kim, J. Jo, S. Kim, Y.-K. Sun, K. Kim and J. Kim, Electrochim. Acta, 2018, 276, 1–11 CrossRef CAS.
- X. Chen, W. Li, Z. Zeng, D. Reed, X. Li and X. Liu, Chem. Eng. J., 2021, 405, 126969 CrossRef CAS.
- S. Chen, D. Zhao, L. Chen, G. Liu, Y. Ding, Y. Cao and Z. Chen, Small Struct., 2021, 2, 2100082 CrossRef.
- N. Qiu, H. Chen, Z. Yang, S. Sun and Y. Wang, Electrochim. Acta, 2018, 272, 154–160 CrossRef CAS.
- N. Zhang, F. Cheng, J. Liu, L. Wang, X. Long, X. Liu, F. Li and J. Chen, Nat. Commun., 2017, 8, 405 CrossRef PubMed.
- V. Soundharrajan, B. Sambandam, S. Kim, S. Islam, J. Jo, S. Kim, V. Mathew, Y.-K. Sun and J. Kim, Energy Storage Mater., 2020, 28, 407–417 CrossRef.
- C. Qiu, X. Zhu, L. Xue, M. Ni, Y. Zhao, B. Liu and H. Xia, Electrochim. Acta, 2020, 351, 136445 CrossRef CAS.
- X. Shen, X. Wang, Y. Zhou, Y. Shi, L. Zhao, H. Jin, J. Di and Q. Li, Adv. Funct. Mater., 2021, 31, 2101579 CrossRef CAS.
- H. Chen, S. Cai, Y. Wu, W. Wang, M. Xu and S. J. Bao, Mater. Today Energy, 2021, 20, 100646 CrossRef CAS.
- T. Xiong, Y. Zhang, W. S. V. Lee and J. Xue, Adv. Energy Mater., 2020, 10, 2001769 CrossRef CAS.
- Y. Zhao, Y. Zhu and X. Zhang, InfoMat, 2019, 2, 237–260 CrossRef.
- C. Liu, Z. Neale, J. Zheng, X. Jia, J. Huang, M. Yan, M. Tian, M. Wang, J. Yang and G. Cao, Energy Environ. Sci., 2019, 12, 2273–2285 RSC.
- W. Sun, F. Wang, S. Hou, C. Yang, X. Fan, Z. Ma, T. Gao, F. Han, R. Hu, M. Zhu and C. Wang, J. Am. Chem. Soc., 2017, 139, 9775–9778 CrossRef CAS PubMed.
- M. C. Biesinger, B. P. Payne, A. P. Grosvenor, L. W. M. Lau, A. R. Gerson and R. S. C. Smart, Appl. Surf. Sci., 2011, 257, 2717–2730 CrossRef CAS.
- W. Chen, G. Li, A. Pei, Y. Li, L. Liao, H. Wang, J. Wan, Z. Liang, G. Chen, H. Zhang, J. Wang and Y. Cui, Nat. Energy, 2018, 3, 428–435 CrossRef CAS.
- F. Wan, L. Zhang, X. Dai, X. Wang, Z. Niu and J. Chen, Nat. Commun., 2018, 9, 1656 CrossRef PubMed.
- J. Hou, Y. Li, M. Mao, L. Ren and X. Zhao, ACS Appl. Mater. Interfaces, 2014, 6, 14981 CrossRef CAS PubMed.
- W. Yang, Y. Zhu, F. You, L. Yan, Y. Ma, C. Lu, P. Gao, Q. Hao and W. Li, Appl. Catal., B, 2018, 233, 184 CrossRef CAS.
- T. Xiong, Z. G. Yu, H. Wu, Y. Du, Q. Xie, J. Chen, Y. W. Zhang, S. J. Pennycook, W. S. V. Lee and J. Xue, Adv. Energy Mater., 2019, 9, 1803815 CrossRef.
- X. Liu, X. Hu, S. Hou, W. He, Z. Liang, L. Meng, Q. Guo, T. Liu, Q. Ru and L. Zhao, J. Mater. Chem. A, 2021, 9, 21209–21218 RSC.
- Y. Yang, Y. Tang, G. Fang, L. Shan, J. Guo, W. Zhang, C. Wang, L. Wang, J. Zhou and S. Liang, Energy Environ. Sci., 2018, 11, 3157–3162 RSC.
- D. Chen, M. Lu, B. Wang, H. Cheng, H. Yang, D. Cai, W. Han and H. J. Fan, Nano Energy, 2021, 83, 105835 CrossRef CAS.
- S. Islam, M. H. Alfaruqi, D. Y. Putro, S. Park, S. Kim, S. Lee, M. S. Ahmed, V. Mathew, Y. K. Sun, J. Y. Hwang and J. Kim, Adv. Sci., 2021, 8, 2002636 CrossRef CAS PubMed.
- S. J. Kim, D. Wu, N. Sadique, C. D. Quilty, L. Wu, A. C. Marschilok, K. J. Takeuchi, E. S. Takeuchi and Y. Zhu, Small, 2020, 16, 2005406 CrossRef CAS PubMed.
- L. Li, T. K. A. Hoang, J. Zhi, M. Han, S. Li and P. Chen, ACS Appl. Mater. Interfaces, 2020, 12, 12834–12846 CrossRef CAS PubMed.
- S. Ding, L. Liu, R. Qin, X. Chen, A. Song, J. Li, S. Li, Q. Zhao and F. Pan, ACS Appl. Mater. Interfaces, 2021, 13, 22466–22474 CrossRef CAS PubMed.
- Y. Jin, L. Zou, L. Liu, M. H. Engelhard, R. L. Patel, Z. Nie, K. S. Han, Y. Shao, C. Wang, J. Zhu, H. Pan and J. Liu, Adv. Mater., 2019, 31, e1900567 CrossRef PubMed.
- D. Chao, C. Zhu, P. Yang, X. Xia, J. Liu, J. Wang, X. Fan, S. V. Savilov, J. Lin, H. J. Fan and Z. X. Shen, Nat. Commun., 2016, 7, 12122 CrossRef CAS PubMed.
- R. Liang, J. Fu, Y.-P. Deng, Y. Pei, M. Zhang, A. Yu and Z. Chen, Energy Storage Mater., 2021, 36, 478–484 CrossRef.
- Y. Fu, Q. Wei, G. Zhang, X. Wang, J. Zhang, Y. Hu, D. Wang, L. Zuin, T. Zhou, Y. Wu and S. Sun, Adv. Energy Mater., 2018, 8, 1801445 CrossRef.
- J. C. Knight, S. Therese and A. Manthiram, J. Mater. Chem. A, 2015, 3, 21077–21082 RSC.
- N. Zhang, F. Cheng, Y. Liu, Q. Zhao, K. Lei, C. Chen, X. Liu and J. Chen, J. Am. Chem. Soc., 2016, 138, 12894–12901 CrossRef CAS PubMed.
- L. Dai, Y. Wang, L. Sun, Y. Ding, Y. Yao, L. Yao, N. E. Drewett, W. Zhang, J. Tang and W. Zheng, Adv. Sci., 2021, 8, 2004995 CrossRef CAS PubMed.
- G. Fang, C. Zhu, M. Chen, J. Zhou, B. Tang, X. Cao, X. Zheng, A. Pan and S. Liang, Adv. Funct. Mater., 2019, 29, 1808375 CrossRef.
- X. Wu, Y. Xiang, Q. Peng, X. Wu, Y. Li, F. Tang, R. Song, Z. Liu, Z. He and X. Wu, J. Mater. Chem. A, 2017, 5, 17990–17997 RSC.
- B. Wu, G. Zhang, M. Yan, T. Xiong, P. He, L. He, X. Xu and L. Mai, Small, 2018, 14, e1703850 CrossRef PubMed.
- K. Sada, B. Senthilkumar and P. Barpanda, J. Mater. Chem. A, 2019, 7, 23981–23988 RSC.
- F. W. Fenta, B. W. Olbasa, M.-C. Tsai, M. A. Weret, T. A. Zegeye, C.-J. Huang, W.-H. Huang, T. S. Zeleke, N. A. Sahalie, C.-W. Pao, S.-H. Wu, W.-N. Su, H. Dai and B. J. Hwang, J. Mater. Chem. A, 2020, 8, 17595–17607 RSC.
- J. Huang, J. Zeng, K. Zhu, R. Zhang and J. Liu, Nano-Micro Lett., 2020, 12, 110 CrossRef CAS PubMed.
- N. Liu, X. Wu, Y. Yin, A. Chen, C. Zhao, Z. Guo, L. Fan and N. Zhang, ACS Appl. Mater. Interfaces, 2020, 12, 28199 CrossRef CAS PubMed.
- X. Pu, B. Jiang, X. Wang, W. Liu, L. Dong, F. Kang and C. Xu, Nano-Micro Lett., 2020, 12, 152 CrossRef CAS PubMed.
- Q. Tan, X. Li, B. Zhang, X. Chen, Y. Tian, H. Wan, L. Zhang, L. Miao, C. Wang, Y. Gan, J. Jiang, Y. Wang and H. Wang, Adv. Energy Mater., 2020, 10, 2001050 CrossRef CAS.
- J. Wang, J.-G. Wang, H. Liu, Z. You, C. Wei and F. Kang, J. Power Sources, 2019, 438, 226951 CrossRef CAS.
- Z. Zhao, G. Tian, A. Sarapulova, V. Trouillet, Q. Fu, U. Geckle, H. Ehrenberg and S. Dsoke, J. Mater. Chem. A, 2018, 6, 19381–19392 RSC.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- M. D. Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, J. Phys.: Condens. Matter, 2002, 14, 2717–2744 CrossRef CAS.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895 CrossRef PubMed.
- S. P. Ong, V. L. Chevrier, G. Hautier, A. Jain, C. Moore, S. Kim, X. Ma and G. Ceder, Energy Environ. Sci., 2011, 4, 3680–3688 RSC.
- A. I. Liechtenstein, V. Anisimov and J. Zaanen, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, R5467 CrossRef CAS PubMed.
- D. Lee, J. Xu and Y. Meng, Phys. Chem. Chem. Phys., 2013, 15, 3304–3312 RSC.
- D. Y. Kim, R. H. Scheicher, H.-K. Mao, T. W. Kang and R. Ahuja, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 2793 CrossRef CAS PubMed.
- K. Refson, P. R. Tulip and S. J. Clark, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 155114 CrossRef.
- A. Urban, D.-H. Seo and G. Ceder, npj Comput. Mater., 2016, 2, 16002 CrossRef CAS.
- S. P. Ong, V. L. Chevrier, G. Hautier, A. Jain, C. Moore, S. Kim, X. Ma and G. Ceder, Energy Environ. Sci., 2011, 4, 3680–3688 RSC.
- M. S. Islam and C. A. Fisher, Chem. Soc. Rev., 2014, 43, 185 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ee03547a |
| This journal is © The Royal Society of Chemistry 2022 |