 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
CO2 capture by pumping surface acidity to the deep ocean†
Michael D.
Tyka
 *,
Christopher
Van Arsdale
*,
Christopher
Van Arsdale
 and
John C.
Platt
and
John C.
Platt

Google Inc., 601 N 34th St, Seattle, WA 98103, USA. E-mail: mike.tyka@gmail.com
First published on 3rd January 2022
Abstract
To remain below 2 °C of warming, most IPCC pathways call for active CO2 removal (CDR). On geological timescales, ocean uptake regulates atmospheric CO2 concentration, with two homeostats driving CO2 uptake: dissolution of deep ocean carbonate deposits (1 ka timescales) and terrestrial weathering of silicate rocks (100 ka timescales). Many current ocean-based CDR proposals effectively act to accelerate the latter. Here we present a method which relies purely on the redistribution and dilution of acidity from a thin layer of the surface ocean to a thicker layer of deep ocean, in order to reduce surface acidification and accelerate carbonate homeostasis. This downward transport could be seen analogous to the action of the natural biological carbon pump. The method offers advantages over other ocean alkalinity and CO2-stripping methods: the conveyance of mass is minimized (acidity is pumped in situ to depth), and expensive mining, grinding and distribution of alkaline material is eliminated. No dilute substance needs to be concentrated, reducing the quantity of seawater to be processed. Finally, no terrestrial material is added to the ocean, avoiding significant alteration of seawater ion concentrations or issues with heavy metal toxicity (encountered in mineral-based alkalinity schemes). The artificial transport of acidity accelerates the natural deep ocean compensation by calcium carbonate. It has been estimated that the total compensation capacity of the ocean is on the order of 1500 GtC. We show through simulation that pumping of ocean acidity could remove up to 150 GtC from the atmosphere by 2100 without excessive increase of local pH. The permanence of the CO2 storage depends on the depth of acid pumping. At >3000 m, ∼85% is retained for at least 300 years, and >50% for at least 2000 years. Shallow pumping (<2000 m) offers more of a stop-gap deferral of emissions for a few hundred years. Uptake efficiency and residence time also vary with the location of acidity pumping. Requiring only local resources (ocean water and energy), this method could be uniquely suited to utilize otherwise-unusable open ocean energy sources at scale. We present a brief techno-economic estimate of 130–250$ per tCO2 at current prices and as low as 93$ per tCO2 under modest learning-curve assumptions.
Broader contextIn addition to near-total decarbonization of the world economy it is increasingly clear that already emitted CO2 will also need to be actively removed from the atmosphere in order to stabilize the Earth's temperature. Due to their natural role in regulating CO2 over geological periods of time, the weathering of alkaline minerals and the subsequent flow of alkalinity into the oceans are an attractive candidate for CO2 sequestration with the potential to store many hundreds of gigatonnes of CO2. With the aim of accelerating such dissolution most prior work has focused on terrestrial minerals, while less attention has been paid to the alkaline carbonate sediments in the deep ocean. Our electrochemical approach of pumping surface acidity into deeper ocean layers could provide a means to induce the dissolution of alkaline mineral deposits (calcite) in the deep ocean while accelerating CO2 uptake at the surface. The approach is uniquely suited for open ocean energy sources since no terrestrial material is needed and could thus provide an interesting new technology in the overall portfolio of negative emissions that will be needed in the latter half of this century. |
1 Introduction
Stabilizing the earth's climate into the next centuries will require a near total decarbonization of the world energy supply, i.e. reducing emissions from their current peak levels. However, some industrial processes, such as industrial heat and concrete manufacturing as well as emissions from land use changes, air travel, or livestock are very difficult to decarbonize.1 Further, even if future emissions were curbed, enough historical CO2 has already accumulated in the atmosphere to cause problematic warming and could trigger tipping points. Thus, the vast majority of IPCC RCP2.6 scenarios which remain under 2 °C of warming require negative emissions on the order of 150 GtC before 21002,3 in addition to rapid decarbonization. On geological timescales several mechanisms act to regulate the atmospheric CO2 concentration: over periods of hundreds of years the oceans will absorb the majority of the excess CO2 leading to very significant surface acidification.4 Subsequent downward transport of the CO2 brings the acidity in contact with CaCO3 deposits, dissolving them and releasing alkalinity, and thus stabilizing the pH.5 On even longer timescales (100 ka), weathering of terrestrial silicate rocks releases new alkalinity to the oceans and allows the previously dissolved CaCO3 to be redeposited while the lysoclines return to their original depths. The consecutive transfer of the excess CO2 along these three sinks acts to keep the temperature of the earth within relatively stable bounds over long periods of time.6,7 Unfortunately, the response time of even the first of these two buffers is too slow to keep up with the rate of human emissions,8,9 leading to a temporary but dangerous spike in atmospheric CO2 concentrations, warming and surface ocean acidification.The primary limiting step is the net transport of CO2 into the deep ocean due to the action of the biological pumps.9,10 Anthropogenic CO2 has not yet penetrated deeply into the ocean, because most of the remineralization of sinking organic matter occurs in the first 500 m beyond the euphotic zone, with peak acidification at about 250 m depth.4 Anthropogenic CO2 has acidified mostly surface waters, impacting carbonate-shell-forming organisms, while staying out of reach of inorganic CaCO3 deposits located well below the euphotic zone.11 Positive feedbacks are also present in this system, where CO2-saturated surface waters oppose further CO2 uptake, reduce the ocean buffering ability and accelerate future pH changes due to the nonlinearity of the carbonate system12; these issues are further compounded under increasing stratification and a weakened biological pump predicted for a warming ocean.
While many methods have been proposed to accelerate terrestrial mineral weathering,2,13 by mechanical14,15 or electrochemical means,16,17 accelerating dissolution of sedimentary carbonate minerals has not yet been explored. Here, we examine the feasibility of artificially transporting acidity to the deep ocean, in order to accelerate both the natural carbonate compensation mechanism and the ensuing flux of carbon from the atmospheric reservoir into the ocean (bi)carbonate reservoir. Such an action cannot replace the need for total decarbonization of the economy, but could contribute to blunt the ecological impact of past emissions by dilution in spatial and temporal dimensions. The inventory of erodible CaCO3 on the ocean floor is estimated to be ∼1600 GtC,8 theoretically more than sufficient to compensate for the ∼640 GtC that humanity has released since preindustrial times.
1.1 Accelerating deep water equilibration
We envision a method to artificially increase the downward transport of acidity from the surface ocean to the deep ocean that first involves electrochemically splitting seawater into acid and base. The weakly alkaline effluent would be released at the surface, while the weakly acidic water would be pumped into the deep ocean (see Fig. 1). In the surface water the alkalinity would thus be raised and the pH stabilized. This maintains an increased flux of CO2 into the ocean and reduces atmospheric CO2, helping to alleviate immediate radiative forcing. The increased pH (decreased acidity) would also help stabilize the health of coral reefs18–20 and Coccolithophores and help preserve these ecosystems past the anthropogenic CO2 spike. Synthesis and subsequent sinking of coccoliths plays a vital role in ballast formation in the biological pump and indirectly aids the downward transport of organic carbon in the ocean21. These surface-ocean effects would be the same as those of ocean liming proposals13, i.e. surface dissolved inorganic carbon (DIC) would increase together with an equally increased alkalinity and the carbonate equilibrium would remain stable. A common approximation10 for the concentration of carbonate ions is [CO32−] ≈ Alk−DIC, which makes this immediately apparent. Meanwhile the acidic, low-pH effluent could be diluted across a large section of the deep water column using perforated, flexible, deep vertical pipes. As the deep water column contains much more water than the thin surface water layer that the acidity originated in, such redistribution of surface-ocean acidity dilutes the surface acidity and its ecological effects. Isopycnal deep water circulation would then spread and dilute this acidity horizontally, bringing it in contact with calcite sediments. The precise impact of such a redistribution on pH and calcite saturation is complex and will be explored through ocean simulation in this paper.Comparison with mineral alkalinization
A great variety of methods have been proposed to increase ocean capacity for CO2, without raising ocean acidity, by dissolving terrestrial minerals.13 These proposals aim to accelerate the total terrestrial weathering rate and subsequent ocean influx by 1–2 orders of magnitude.2 In practice, the mining, grinding, transport and distribution of gigatonnes of rock per year poses significant challenges. If the material is ground to ∼100 μm, the dissolution of these minerals is on the order of many decades14,15 and particles would sink out of the mixed layer long before dissolution,22 limiting applicability to shallow coastal areas.23 Grinding down to 1 μm would enable open ocean distribution, but significantly increase grinding energy costs.24 Iron, abundant in most olivine minerals, would inadvertently fertilize the ocean leading to significant ecological disruption2,14 and changes in silicate concentration would shift the phytoplankton species composition towards diatoms.22 Nickel, also found in olivines,25,26 is biologically both an essential co-factor and toxic at high concentration with different concentrations optimal for different marine species.27 Chromium is present in flood-basalts and ultra-basic rocks in similar quantities to nickel.25This proposal shares many properties with the above ocean alkalinity enhancement proposals, with some advantages. Firstly there is no need for large mass transport of alkaline rocks to the ocean13 or transport of products away from electrolysers.28 The only matter transport needed is the pumping of a small amount of water a few kilometers downwards. This locality makes the method uniquely suitable for open ocean deployment and provides a way to use otherwise unusable renewable energy resources. Open waters offer greater scalability at reduced ecological impact as dilution over large areas is trivial. The proposed method also avoids the severe impacts of creating a gigatonne-scale mining operation on terrestrial ecosystems. The net cation composition of the ocean is not changed, avoiding introduction of iron, silicate or toxic trace metals into ocean ecosystems, a major concern with most mineral-based alkalinization approaches.2 The redistribution of alkalinity dilutes the already occurring anthropogenic acidification of the surface ocean into the deeper ocean. Due to these advantageous ecological properties, the proposed method may find it easier to gain social license, as it aims to mitigate human impact by spatial and temporal dilution. In general, all ocean alkalinity methods are currently regulated by international maritime laws such as the London Convention29 which would have to reviewed and possibly amended before deployment could begin at scale.30
We note also that widely discussed biological ocean CDRs31 which propose increasing primary biological productivity and sinking of biological matter, such as ocean fertilization, could be seen as equivalent to the acidity pumping proposed here. This is because the vast majority of sunk soft tissue is remineralized in the water column or on the ocean floor, thus acidifying deep waters.32 Only 0.4% of the originally fixed carbon is buried in sediments and permanently removed from circulation.10 Thus efforts increasing primary biological production likewise rely on the dissolution of deep CaCO3 deposits to prevent the transported carbon from being re-emitted to the atmosphere on the timescales of ocean circulation. Thus, these methods also ultimately aim to accelerate deep carbonate dissolution, albeit indirectly. The same can be said for efforts to directly inject CO2 into the deep sea, as the resulting CO2 lakes or hydrates gradually dissolve.33
In this paper we present ocean circulation simulations to examine the effects and limitations of large-scale acidity pumping as well as techno-economic arguments which suggest that the cost per tonne of CO2 could potentially be competitive with terrestrial direct air capture (DAC) and other negative emissions technologies while avoiding the ecological impacts of accelerated mineral weathering.2
2 Methods
2.1 Global circulation model of acid–base pumping
To simulate the effect of acid–base pumping on surface and deep water pH, as well as net ocean CO2 uptake, and evaluate the return time of acidity, we used a full ocean circulation model in a 128 × 64 worldwide spherical polar grid using MITgcm.34 The simulation had cell sizes of 2.8° × 2.8° divided into 20 exponentially spaced depth levels, from 10 m thick at the surface to 690 m thick at depth. The simulation was initialized and forced as detailed in Dutkiewicz et al. (2005).35 The MITgcm GEOM and DIC modules were used to simulate the soft tissue and carbonate pumps, as well as ocean-atmosphere gas exchange. A number of studies36,37 have simulated addition of alkalinity to the ocean in the context of realistic emission scenarios with increasing atmospheric pCO2. Here we chose to focus instead on the efficiency of CO2 uptake and the circulation aspects of acidity return, and thus the atmospheric concentration of CO2 was simply held constant at 415 ppm similar to work by Köhler et al.22| r = k*([CO32−]sat − [CO32−]) | (1) |
| k* = Ksβ/(Ks + β) | (2) |
3 Results
3.1 Uniform pumping
In our initial simulations alkalinity was pumped uniformly over the entire ocean, wherever the respective depth was available to pump acidity to. The amount of alkalinity pumped was 0.25 Pmol per year, the equivalent to a maximum uptake of 3 GtCeq per year, roughly the same amount as was used by Köhler et al.22 Note that throughout this paper we will use units of 1 GtCeq = 0.833 Tmol to provide a better intuitive sense for the quantities involved (relative to human emissions of ∼10 GtC per year). Pumping proceeded for 50 years which would yield roughly the required amount of negative emissions called for by most RCP2.6 pathways.We also investigated lower and higher pumping rates up to 10 GtCeq per year to examine the effect on pH and carbonate saturation and to provide context for assessing a reasonable level of alkalinization without excessively affecting marine ecology. Previous work37 examined alkalinity addition as high as ∼22 GtCeq per year although such a high rate may not be practical or ecologically safe. After the 50 year pumping period was over the simulation was allowed to continue up to the 5000 year mark to investigate carbonate compensation and the longevity of the stored carbon. To identify the role of carbonate compensation a control run was performed with sediment compensation turned off. A positive control run was also performed to compare to the case where alkalinity is added at the surface but no compensating acid is deposited at depth, effectively simulating the addition of a fast dissolving alkaline material.
Fig. 2a shows that alkalinity pumping results in rapid uptake of CO2, virtually indistinguishable from simple net alkalinity addition to the surface for the first 50 years. In the subsequent period, the depth of acid release strongly determines the return time and the eventual re-emission of any previously captured CO2. Injection of acidity in too shallow waters causes reemission within a few hundred years, an insufficient amount of time for any significant amount of carbonate compensation to occur. However, for acid depths greater than 3200 m the CO2 absorbed does not begin to be re-emitted for at least 300 years, retaining 85–95% of the absorbed CO2. For an acidity release below 2250 m, the relaxation half-life of CO2 return to the atmosphere is found to be ∼2000 years. This time provides sufficient contact time for deep carbonate dissolution to occur as shown in Fig. 2b, with the global calcite dissolution rate increasing by as much as 0.25 GtCeq per year. We note that the system relaxation time is significantly increased due to this dissolution, as the half life for CO2 return in the reference simulations without carbonate dissolution was much shorter (∼1000 years), depending solely on ocean circulation. We note that because carbonate compensation is a bidirectional homeostat, simply balancing net dissolution with net deposition, the proportion of CO2 which will be permanently removed depends on the future emissions scenarios and the eventual equilibrium point of the ocean. The method proposed here simply allows the homeostat to respond much more quickly than it would have otherwise done.
 | ||
| Fig. 2 Shown is the total excess CO2 uptake and total excess calcite dissolution at the seafloor with respect to time (logarithmic scale past the 100 year mark). Alkalinity and acidity are separated and acidity is pumped to depth, wherever possible, with a total rate of 3 GtC equivalent per year. Different colors represent different depths at which acidity was injected. The solid lines represent simulations including carbonate compensation, whereas the dashed lines are simulations ignoring carbonate compensation. The grey shading indicates the period for which pumping was active (the first 50 years). (a) Shows the total excess carbon (in GtC) absorbed by the ocean due to alkalinity pumping, relative to a reference simulation without any perturbation. Note that the maximal CO2 uptake reaches ∼85% of the total amount of alkalinity moved (150 GtCeq over 50 years), in agreement with the compensation behavior of the carbonate system shown in Fig. S0 (ESI†) (see also Renforth et al.13). As long as acidity is moved below 2000 m, even in the absence of carbonate compensation, the absorbed carbon is retained well beyond 300 years. (b) Shows the relative increase in global sedimentary carbonate dissolution. When acidity is transported below 3280 m about 40% of the absorbed CO2 is compensated by calcite. Note that the total excess dissolved calcite begins to drop again at ∼1000 years. This is due to the fact that our simulation kept the atmospheric CO2 concentration constant at 418 ppm, and thus the system begins to return to an equilibrium point where sedimentation rate and dissolution rate balance. The true long-term equilibrium point of the carbonate homeostat will depend strongly on future anthropogenic CO2 emissions, which are highly uncertain. | ||
Fig. 3 tracks median and 95%ile changes in surface and ocean floor pH. See Fig. S1 (ESI†) for the corresponding change in calcite saturation. The median surface ΔpH rises rapidly for the first 1–2 years (0.03 per year) but slows within 10 years to a steady rate of 2 × 10−4 per year, reaching a maximum median ΔpH of 0.022 after 50 years. The increased rate of CO2 dissolution is mostly able to buffer the increase in surface alkalinity. The seafloor pH however continues to decrease throughout the pumping period due to the considerably slower calcite dissolution rate. Despite this, the perturbation is at most −0.15 pH units at its most extreme point. Varying the global pumping rate between 0.3 and 10 GtCeq per year we found a roughly linear dependence of pH and Omega perturbation and pumping rate (Fig. 4). The sensitivity of benthic ecosystems to pH perturbation is poorly understood and requires further research. However, seasonal changes in open-ocean pH can be up to 0.2 pH units43 while diurnal changes in coastal areas can reach as much as a full pH unit.44 Using this as a guide we suggest that alkalinity pumping at global rates of 1–3 GtCeq per year may be feasible without excessive stress on marine systems, though this is a critical area in need of further research.45
 | ||
| Fig. 3 Median and 95%ile changes in pH at the surface (a and b) (increase in pH) and at the seafloor (c and d) (decrease in pH) for the same runs. It can be seen that even in locations of most extreme pH change, the localized pH changes are not excessive. The changes at the surface are smaller than at depth (despite originating in a much thinner slice of water) because the lowered partial pressure of CO2 immediately pulls in more carbon due to the relatively fast equilibration time. At depth the compensation with carbonate deposits proceeds much more slowly and therefore the pH response to acidity pumping is larger over time. Fig. S1 (ESI†) shows the equivalent plots of median and 95%ile changes in calcite saturation (Ω). | ||
3.2 Location dependence
Uniform pumping is neither practical nor efficient. From a practical perspective, the location of pumping will depend strongly on the mode of deployment (see Discussion). From an oceanographic perspective, both the efficiency of alkalinity compensation at the surface and the timescales of return of acidity from deep waters vary substantially depending on the location in the ocean. The former varies due to differences in the uptake efficiency factor and surface currents, while the latter depends on how soon deep waters are returned to the surface with the global overturning circulation.The carbonate equilibrium in seawater responds to an increase in alkalinity by shifting towards the carbonate ion. The concomitant reduction in the partial pressure pCO2 causes an uptake of CO2 from the atmosphere until equilibrium is restored. The number of moles of CO2 absorbed for every mole of alkalinity added, the uptake efficiency ηCO2, can be expressed as the ratio of the partial pressure sensitivities of pCO2 with respect to total alkalinity (Alk) and total inorganic carbon (DIC).13,38 This compensation ratio presents a fundamental inefficiency that needs to be taken into account when calculating potential CO2 uptake of any ocean alkalinization method in addition to any process inefficiencies. The commonly used approximations DIC ≈ [HCO3−] + [CO32−] and Alk ≈ [HCO3−] + 2[CO32−] at typical ocean pH yield a good approximation for the uptake factor: (derivation in ESI†).
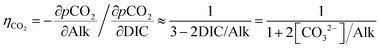 | (3) |
We thus performed a grid scan of the ocean, where in each simulation an amount of 100 Tmol per year of alkalinity (0.12 GtCeq per year) was pumped at any one grid point only. Altogether ∼1000 independent simulations were conducted, one for every gridpoint with sufficient depth to inject acidity. In each case the entire ocean biogeochemistry was monitored compared to a reference simulation with no pumping.
Fig. 5 and Fig. S3 (ESI†) show the normalized total uptake of CO2, such that a value of 1.0 represents an ocean uptake equimolar to the amount of alkalinity pumped. Previous work that examined alkalinity addition in different coarse latitude bands22 found not all areas are equally efficient at CO2 uptake or retention. We extend this work with a finegrained map and find that on short timescales the efficiency is dominated by the local surface efficiency and atmospheric pCO2. However, after some time surface currents spread the excess surface alkalinity and the effect becomes less pronounced. For the case of alkalinity addition (rather than pumping) most of the locations eventually reach close to the full average efficiency of 0.85 except areas of significant downwelling in the polar regions (see Fig. S3, ESI†). The alkalinity is pulled downwards and removed from the surface as is evident in depth plots of calcite saturation (Fig. S5, ESI†). In the case of acidity pumping the behaviour is very similar, but on longer timescales, uptake efficiency becomes dominated by the rate of acid return. Since deep return currents generally move southwards, injection of acidity in the northern hemisphere appears to be significantly more efficient in the long run, with some small areas as notable exceptions. Two large areas in the southern ocean appear to return acidity faster than others and are inefficient locations for alkalinity pumping (Fig. 5). Fig. S3 (ESI†) gives detailed plots of the total excess absorbed CO2 due to pumping at a selected number of locations. We compared our computed CO2 retention times with results from a multi-model comparison48 which used models of comparable resolution to simulate direct CO2 injection (see Fig. S7, ESI†). We find, in general, good agreement for almost all locations and depths with the model ensemble.
 | ||
| Fig. 5 Efficiency of alkalinity pumping (ηCO2) as a function of latitude and longitude. Here (ηCO2) is the number of moles of excess CO2 absorbed by the ocean normalized by the number of moles of alkalinity pumped. Each point on the grid represents an entire ocean simulation in which 1 Tmol per year were pumped at that point only (a total of ∼1000 simulations). Mapped is the relative increase in total oceanic dissolved inorganic carbon (relative to the reference), normalized by the amount of acidity pumped. Three different timepoints are shown: (a) uptake of CO2 at the end of the 50 year pumping period. Significant differences in the effective ηCO2 are observed, depending on where the alkalinity was pumped, varying from 0.5 to 0.85. The differences during this period are driven primarily by the efficiency of CO2 uptake, as the distribution closely matches that of simple alkalinity addition (cf. Fig. S6, ESI†). In particular the northern Atlantic exhibits poor CO2 uptake. (b) CO2 uptake 100 years after the end of pumping. Alkalinity pumping in most northern hemisphere areas has caught up to an uptake efficiency of 0.85 with equatorial regions exhibiting the best retention. (c) 200 years after the end of pumping. The apparent CO2 uptake is fully dominated by the acid return kinetics (cf. Fig. S6 (ESI†), where alkalinity was added instead of pumped). It is apparent that acidity pumping in the southern hemisphere is less efficient, likely due to the fact that ventilation of deep water occurs in the Southern Ocean and thus acidity returns to the surface more rapidly. Conversely the North Pacific retains pumped acidity the best. | ||
3.3 Impact on surface and deep water pH
Understanding the pH sensitivity of different locations allows optimization of the alkalinization strategy to minimize ecological effects and costs while maximizing CO2 uptake.At the surface, the pH increase will be highest right at the injection site, decreasing exponentially with distance. The alkalinity will be compensated by CO2 uptake, but depending on the local currents and eddies which transport and distribute the alkalinity, as well as wind speeds, surface agitation and local atmospheric CO2 concentration, we can expect different sensitivities at different injection sites. It is important to avoid too large a pH change both for ecological reasons as well as needing to avoid triggering inorganic precipitation49 of CaCO3. At depth, the injection of acidity must also be considered against an ecological safety margin. We propose that the acidity is injected no closer than 500 m to the seafloor and at least 2000 m from the surface. This area of the ocean is the least populated by marine species and thus gives ample time for the acidity to dilute horizontally away from the diffuser pipes. Fig. 6 shows the sensitivity of surface and deep water pH on the pumping location from ∼1000 individual simulations of single-point alkalinity pumping. The sensitivity (m2 s mol−1) was calculated by dividing the maximal ΔpH observed for any given simulation by the pumping rate density (mol m−2 s−1). As expected, areas with stronger surface currents spread surface alkalinity most efficiently, reducing the pH impact at the release location. This effect would be less pronounced if the release stations were free floating with these bulk water movements; however, the horizontal eddy diffusivity is considerably larger in these currents, which would make them preferential release sites nevertheless. Another factor reducing surface pH impact are wind speeds, which reduce the ocean-atmosphere CO2 equilibration time. The circumpolar wind band likely accounts for the low surface sensitivities observed in the southern ocean (Fig. 6 and Fig. S4, ESI†).
 | ||
| Fig. 6 Local surface pH sensitivity in s km2 mol−1 obtained by injection at each grid point only (each grid point represents an entire independent simulation). The sensitivity was calculated by dividing the globally maximal ΔpH in either direction observed for any given simulation by the pumping rate density (mol km−2 s−1). Panel (a) reflects pH changes in the alkaline direction (typically found at the surface release site). The surface sensitivity represents the efficiency with which a stationary addition of alkalinity at any given location with some constant rate is distributed and neutralized by CO2 invasion. Larger values indicate slower spreading from the release site and/or slower neutralization by CO2 invasion. Areas with stronger surface currents can spread surface alkalinity most efficiently and are least sensitive to surface pH changes. Panel (b) reflects pH changes in the acidic direction (found in deep water where the acidity is pumped to). The crosses mark the location of the individual plots in Fig. S4 (ESI†). | ||
4 Discussion
4.1 Deployment possibilities
The proposed method is only reliant on local resources (seawater) and power and could be implemented in a variety of locations with varying power sources, as shown in Fig. 1. Specifically, it would be uniquely matched for untethered power generators, obviating the otherwise arising problem of energy storage or transmission and material transport encountered in other offshore methods,50 thus providing a productive use of open-ocean power sources in situ. Open-ocean stations could operate on wave, wind or ocean thermal (OTEC51–54) power and could be scaled with a large number of untethered, identical units. Open-ocean photovoltaics have been investigated55 and trial projects are underway.56 All of these technologies are still in early development and have not yet benefited from commercial efficiencies of scale and are thus currently relatively expensive. Part of the reason for the lack of wide scale adoption is the need for energy transmission in one form or another. Ocean acidity pumping could thus be a perfect match for these technologies. The lack of need for power transmission or transport can further reduce costs compared to current estimates. Alkalinity release in open waters, rather than coastal waters, might be less impactful to marine biology permitting deployment at larger scale.An alternative approach could involve near-coast operation; larger sized plants could tap into cheap terrestrial energy, especially daytime excess solar. Acid/base generators could potentially be located just-off-coast with a grid connection to land – transportation of electricity being considerably cheaper than transport of matter, i.e. the pumping of seawater onto land and back should be avoided.57 Decommissioned oil rigs may offer an ideal platform for such deployment.
Coastal locations where the continental slope is close to the coast and strong surface currents occur would be preferred, because they shorten the distance acid and base need to be transported, and currents would be able to distribute the excess surface alkalinity effectively. A potential intermediate deployment would consist of near-shore wind farms. Where possible, especially in areas where deep waters are not accessible, the acid stream could also be injected underground, into basalt formations58–60 or depleted oil wells where it would react with silicate rocks and be neutralized.16 Injection of hydrochloric acid into rock formations is conceptually similar to the CarbFix process58 and more generally to carbon capture and storage approaches (CCS).61 However experimental studies of injectivity, the ensuing in situ chemistry and the storage capacities for such acid injections are needed to assess the viability of this approach. Injection into depleted oil reservoirs might be appropriate for example for the North Sea although such areas may be limited to smaller amounts of alkalinity that can be safely released while keeping pH changes below ecological thresholds. However, this could present a feasible method to stabilize ocean pH in localized areas to counteract ecological damage from acidification.18–20
4.2 Techno-economic estimation
Although a full techno-economic analysis is beyond the scope of this paper, we conduct a rough estimation of potential costs of electrodialysing seawater using published data from other methods which create pH gradients. Acid/base production could be implemented using either electrolysis or bipolar membrane electrodialysis. Electrolysis was among the first methods suggested for negative emissions technology,16 though the generation of gases is energetically inefficient and has to be either recouped using a fuel cell, adding complexity and cost, or recouped by selling the products,28 which necessitates mass transport of the products.50 The use of electrolysis on seawater at gigatonne scale may also produce significant quantities of volatile halogenated organics which are ozone depleting, such as bromo- and chloromethane.17 Here we choose to focus on electrodialysis methods, which have been proposed and tested for seawater CO2 extraction.62–67 However, even if colocated with desalination plants, costs are high (373–604$ per tCO2,63 540$ per tCO266) in part due to very large quantities of seawater needing to be processed (about 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 m3 tCO2−1). In contrast, releasing the alkalinity to the ocean for passive CO2 absorption and storage is conceptually and technologically simpler, consisting only of the acid/base generator. The quantity of seawater needing to be processed is greatly reduced (100–500 m3 tCO2−1 depending on the exact concentration of effluent acid and base). There is no CO2 extraction, thus saving capital and operational costs of membrane contactors63. Indeed Digdaya et al. found membrane contactors and vacuum pumps accounted for 90% of the equipment cost.66 Instead, leveraging the ocean as a sorbent surface obviates the need for air contactors as well as additional storage, as the CO2 is stored as relatively benign bicarbonate ions. From a capital and operational cost perspective, alkalinity pumping is a strict subset of electrodialysis-driven CO2 extraction and should thus always be cheaper, whether the acidity is moved to deep ocean or underground. The three largest contributors to overall levelized cost would be the cost of electricity to drive the electrodialysis stack, the cost of pre-treating seawater to prevent fouling of the membrane stack and the cost and lifetime of the membranes themselves. Minor contribution costs are the pumping of acidified water to depth. In the open ocean scenario we assume that the cost of the structure are implicit in the assumed levelized costs for open-ocean electricity, and that the electrodialysis apparatus is generally much smaller than the structure. In the following we discuss the likely current ranges of these costs and likely learning curve improvements into the future. However it should be noted that in order to further narrow these estimates, construction of medium-size prototypes63 is essential.
000 m3 tCO2−1). In contrast, releasing the alkalinity to the ocean for passive CO2 absorption and storage is conceptually and technologically simpler, consisting only of the acid/base generator. The quantity of seawater needing to be processed is greatly reduced (100–500 m3 tCO2−1 depending on the exact concentration of effluent acid and base). There is no CO2 extraction, thus saving capital and operational costs of membrane contactors63. Indeed Digdaya et al. found membrane contactors and vacuum pumps accounted for 90% of the equipment cost.66 Instead, leveraging the ocean as a sorbent surface obviates the need for air contactors as well as additional storage, as the CO2 is stored as relatively benign bicarbonate ions. From a capital and operational cost perspective, alkalinity pumping is a strict subset of electrodialysis-driven CO2 extraction and should thus always be cheaper, whether the acidity is moved to deep ocean or underground. The three largest contributors to overall levelized cost would be the cost of electricity to drive the electrodialysis stack, the cost of pre-treating seawater to prevent fouling of the membrane stack and the cost and lifetime of the membranes themselves. Minor contribution costs are the pumping of acidified water to depth. In the open ocean scenario we assume that the cost of the structure are implicit in the assumed levelized costs for open-ocean electricity, and that the electrodialysis apparatus is generally much smaller than the structure. In the following we discuss the likely current ranges of these costs and likely learning curve improvements into the future. However it should be noted that in order to further narrow these estimates, construction of medium-size prototypes63 is essential.
| ΔG = 2.303RTΔpH | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 72). This represents process efficiencies of only 20–45%, suggesting that there is potential for learning curves and technological improvements. Many of the above studies aim to valorize reject brines and are optimized to produce both concentrated (>1 M) and pure acids and bases for industrial use and thus require deionized water to feed acid and base tanks in feed-and-bleed flow schemes. For purposes of acidity pumping the effluent can be more impure and dilute than in the above studies, affording potentially lower costs. The levelized cost of electricity for free floating power generation is highly variable, and likely suboptimal due to the lack of current economies. Wind power has been estimated at $30–80 per MWh.54 OTEC is estimated to provide energy at a cost of $150–200 per MWh.50,53 Wave power generators levelized costs are highly uncertain and maybe in the range of $120–470 per MWh.73 Even though transmission costs can be saved in our case, the present-day costs are likely too high for economical carbon capture, but have considerable potential for reduction with economies of scale. As an alternative, land-base power could be used in near-coast applications where strong currents allow for nearby alkalinity distribution. Examples include the Agulhas, the Kuroshio, the Gulfstream and the North Brazilian current. However deep-water acid disposal becomes more limited as bottom currents are much slower and it may be better to instead pump the acidified stream underground if suitable underground formations are available. Utility scale solar is likely the cheapest land-based energy source with unsubsidized levelized costs as cheap as $32–44 per MWh and wind at $28–54 per MWh.74 It is thought that there will be a considerable excess of this power during daytime hours, for which finding a carbon negative use would be desirable to help with load leveling.
72). This represents process efficiencies of only 20–45%, suggesting that there is potential for learning curves and technological improvements. Many of the above studies aim to valorize reject brines and are optimized to produce both concentrated (>1 M) and pure acids and bases for industrial use and thus require deionized water to feed acid and base tanks in feed-and-bleed flow schemes. For purposes of acidity pumping the effluent can be more impure and dilute than in the above studies, affording potentially lower costs. The levelized cost of electricity for free floating power generation is highly variable, and likely suboptimal due to the lack of current economies. Wind power has been estimated at $30–80 per MWh.54 OTEC is estimated to provide energy at a cost of $150–200 per MWh.50,53 Wave power generators levelized costs are highly uncertain and maybe in the range of $120–470 per MWh.73 Even though transmission costs can be saved in our case, the present-day costs are likely too high for economical carbon capture, but have considerable potential for reduction with economies of scale. As an alternative, land-base power could be used in near-coast applications where strong currents allow for nearby alkalinity distribution. Examples include the Agulhas, the Kuroshio, the Gulfstream and the North Brazilian current. However deep-water acid disposal becomes more limited as bottom currents are much slower and it may be better to instead pump the acidified stream underground if suitable underground formations are available. Utility scale solar is likely the cheapest land-based energy source with unsubsidized levelized costs as cheap as $32–44 per MWh and wind at $28–54 per MWh.74 It is thought that there will be a considerable excess of this power during daytime hours, for which finding a carbon negative use would be desirable to help with load leveling.
Assuming an efficiency range of 160–250 kJ mol−1, energy prices of $30–80 per MWh and an ocean uptake efficiency ηCO2 of 0.8 we obtain a range for the energy costs of $38–158 per tCO2. It is interesting to compare these energy requirements to other CDR approaches. Electrolytic approaches require about ∼300 kJ mol−1.28 Direct air capture (DAC) had been estimated at 312–524 kJ mol−1.75 A comprehensive analysis of recent DAC methods reported 371–546 kJ mol−1 for liquid solvent approaches and 174–260 kJ mol−1 for solid sorbents,76 however much of the energy required is heat rather than electrical.
Energy requirements for methods involving mafic or ultramafic rocks to the ocean, likely needing to be ground to 1 μm for open ocean application,22 vary substantially from15,49 175–315 kWh t−1 to24 500–1000 kWh t−1. Depending on the rock type, with a net uptake efficiency of 0.3–0.8 tCO2 per tonne of rock, one obtains an energy requirement of 35–528 kJ per mol of CO2 absorbed.
 | (5) |
| Ppump = hfγwQ | (6) |
| PED = cHEspQ | (7) |
If alkalinity is generated near shore at scale it will need to be dispersed away far from the shore to avoid local pH spikes. However, because the alkalinity is relatively dilute (0.1–1 mol kg−1) compared to dry solid alkaline materials (∼25 mol kg−1) bulk transportation is considerably less efficient. For example, at η = 0.8, 28.4 tonnes of 1 mol kg−1 hydroxide solution are required for every tonne of CO2 absorbed. Large-scale maritime shipping costs are around $0.0016–0.004 per t per km and produce about 7 gCO2 per t per km.49 Assuming alkalinity to be dispersed in a 150 km strip around the coast, i.e. well within the exclusive economic zone of any bordering country, and typical tanker speeds of 14 knots (7.2 m s−1), the 300 km roundtrip (150 km zone) could be completed in 12 hours, with a daily turnaround. Assuming a factor of 2 inefficiency compared to ordinary shipping, due to the very frequent loading, we obtain a cost of $13–33 per tCO2. Furthermore, as tankers are hard to decarbonize, ∼57 kgCO2 are emitted for every tonne of CO2 absorbed, about a 5% reduction in efficiency. The additional costs and the additional CO2 impact of transport limit alkalinity release to coastal areas and thus limit the total scaling of land-based alkalinity production.
Overall for open-ocean deployment we obtain a minimum cost per tonne of CO2 captured of ∼$93–297 per tCO2. This estimate is quite close to estimations obtained by a recent study57,63 (110–325$ per tCO2) for the BPMED portion of their process, which conducted a much more detailed technoeconomic analysis for CO2 extraction. As expected the costs are much lower than estimates for CO2 extraction (373–604$ per tCO263, 540$ per tCO266)
At the lower end, the total cost estimate has similar-sized cost contributions from energy cost, membrane cost and water treatment cost. Thus to drive down overall costs development and cost reduction is needed in all three areas. We note that the dialysis membrane industry is currently very small and very significant cost savings could be expected at scale.79 Furthermore, as with all ocean CDRs, working with ocean water and in marine environments in general poses significant challenges in terms of corrosion and longevity of the equipment which will need to be addressed for a practical, scalable application.
For comparison, costs for direct air capture have been reported at $89–407 per tCO2 for solid sorbent systems and $156–506 per tCO2 for liquid solvent systems.76 The operational costs of enhanced weathering has been estimated at $70–578 per tCO2 and $24–123 per tCO2 for basic and ultrabasic rocks respectively49 and ocean liming falls in the $72–159 per tCO2 range.13
5 Conclusions
We have explored the feasibility of accelerating the natural compensation of ocean acidification by CaCO3 deposits by artificially pumping excess acidity towards the abyssal CaCO3 sediments. The subsequent alkalinization of the surface would counteract anthropogenic acidification and increase the uptake of significant quantities of atmospheric CO2. Thus alkalinity pumping could meaningfully contribute to a portfolio of negative emissions technologies. Based on our simulation we estimate 1–3 GtC per year could be removed over a 50 year period, without lowering deep water pH by more than 0.2. For acid injection depth >3000 m we show that carbonate compensation is significantly engaged, permanently removing up to 40% of the absorbed CO2. Reemission of the remainder occurs only after 300 years and slowly over several millenia of gradual outgassing, effectively flattening the curve of the anthropogenic CO2 shock to the atmosphere. In theory up to 150 GtC could be removed this way before the end of the century, satisfying requirements for negative emissions laid out by RCP2.6 pathways. What might a scaled up deployment look like? Modern offshore 10 MW wind turbines can generate on the order of 50 GWh of energy per year, which could be used to sequester on the order of10 ktC per year. Thus for a total scale of 1 GtC per year about 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 of such units would be necessary (i.e. about 1000 GW of total capacity). For comparison current global offshore wind capacity is already expected to reach about 500 GW by 2050, thus a goal of 1 GtC per year negative emissions could be feasible before the end of the century.
000 of such units would be necessary (i.e. about 1000 GW of total capacity). For comparison current global offshore wind capacity is already expected to reach about 500 GW by 2050, thus a goal of 1 GtC per year negative emissions could be feasible before the end of the century.
The pumping of ocean acidity presented in this paper avoids many of the environmental issues with mineral-adding alkalinity methods both in terms of impurity dissolution in the ocean and mining impacts on land. It is conceptually simple and requires only locally available resources (seawater and energy), and is thus uniquely suited to openwater deployment. While in the short term, on-shore electrochemical alkalinization is likely more economical due to the inherent engineering challenges of marine engineering, it is also inherently limited in scale. We have shown that transport of dilute acid or base is not economical beyond 150 km away from the production site. Disposal of dilute acid into deep basalt aquifers provides a partial solution but its scaling limits are not well understood. Therefore open-water production of acid and base could supplement terrestrially powered CDR and is an interesting avenue of research despite the usual challenges of marine engineering. Open-water CDR also provides a route to make use of otherwise unusable renewable energy, an area of CDR research that has been underexplored. In general, manipulation of acidity/alkalinity as a proxy for CO2 may be technologically simpler and/or more efficient than manipulation of CO2 directly, whether the acidity is moved into deep ocean or underground. We also presented a fine-grained analysis of location dependence of surface alkalinization and show that in the short term there is substantial variation in CO2 uptake efficiency which will need to be considered in any ocean alkalinization plan, mineral-based or not. As with all ocean-based CDR methods, simulations have inherent limits and the ecological parameters and limitations require substantial further research of natural analogues45 and experimentation in meso-scale pilot programs.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Matt Eisaman, Ben Saenz, Rob Dunbar, Joel Atwater, Will Regan, Eli Patten, Daniel Rosenfeld and Kevin McCloskey for many helpful discussions and comments on the manuscript.Notes and references
- S. J. Davis, N. S. Lewis, M. Shaner, S. Aggarwal, D. Arent, I. L. Azevedo, S. M. Benson, T. Bradley, J. Brouwer, Y.-M. Chiang, C. T. M. Clack, A. Cohen, S. Doig, J. Edmonds, P. Fennell, C. B. Field, B. Hannegan, B.-M. Hodge, M. I. Hoffert, E. Ingersoll, P. Jaramillo, K. S. Lackner, K. J. Mach, M. Mastrandrea, J. Ogden, P. F. Peterson, D. L. Sanchez, D. Sperling, J. Stagner, J. E. Trancik, C.-J. Yang and K. Caldeira, Science, 2018, 360, eaas9793 CrossRef PubMed.
- L. T. Bach, S. J. Gill, R. E. M. Rickaby, S. Gore and P. Renforth, Front. Clim., 2019, 1, 7 CrossRef.
- G. P. Peters, Nat. Clim. Change, 2016, 6, 646–649 CrossRef.
- J. E. Dore, R. Lukas, D. W. Sadler, M. J. Church and D. M. Karl, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 12235–12240 CrossRef CAS PubMed.
- D. Archer, M. Eby, V. Brovkin, A. Ridgwell, L. Cao, U. Mikolajewicz, K. Caldeira, K. Matsumoto, G. Munhoven, A. Montenegro and K. Tokos, Annu. Rev. Earth Planet. Sci., 2009, 37, 117–134 CrossRef CAS.
- D. Archer, H. Kheshgi and E. Maier-Reimer, Geophys. Res. Lett., 1997, 24, 405–408 CrossRef CAS.
- D. Archer, H. Kheshgi and E. Maier-Reimer, Global Biogeochem. Cycles, 1998, 12, 259–276 CrossRef CAS.
- D. Archer, J. Geophys. Res., 2005, 110, C9 CrossRef.
- N. S. Lord, A. Ridgwell, M. C. Thorne and D. J. Lunt, Global Biogeochem. Cycles, 2016, 30, 2–17 CrossRef CAS.
- J. L. Sarmiento and N. Gruber, Ocean biogeochemical dynamics, Princeton University Press, Princeton, 2006 Search PubMed.
- O. Sulpis, B. P. Boudreau, A. Mucci, C. Jenkins, D. S. Trossman, B. K. Arbic and R. M. Key, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 11700–11705 CrossRef CAS PubMed.
- L.-Q. Jiang, B. R. Carter, R. A. Feely, S. K. Lauvset and A. Olsen, Sci. Rep., 2019, 9, 18624 CrossRef CAS PubMed.
- P. Renforth and G. Henderson, Rev. Geophys., 2017, 55, 636–674 CrossRef.
- F. Montserrat, P. Renforth, J. Hartmann, M. Leermakers, P. Knops and F. J. R. Meysman, Environ. Sci. Technol., 2017, 51, 3960–3972 CrossRef CAS PubMed.
- S. J. Hangx and C. J. Spiers, Int. J. Greenhouse Gas Control, 2009, 3, 757–767 CrossRef CAS.
- K. Z. House, C. H. House, D. P. Schrag and M. J. Aziz, Environ. Sci. Technol., 2007, 41, 8464–8470 CrossRef CAS PubMed.
- G. H. Rau, S. A. Carroll, W. L. Bourcier, M. J. Singleton, M. M. Smith and R. D. Aines, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 10095–10100 CrossRef CAS PubMed.
- M. Mongin, M. E. Baird, A. Lenton, C. Neill and J. Akl, Environ. Res. Lett., 2021, 16, 064068 CrossRef CAS.
- R. Albright, L. Caldeira, J. Hosfelt, L. Kwiatkowski, J. K. Maclaren, B. M. Mason, Y. Nebuchina, A. Ninokawa, J. Pongratz and K. L. Ricke, et al. , Nature, 2016, 531, 362–365 CrossRef CAS PubMed.
- E. Y. Feng, D. P. Keller, W. Koeve and A. Oschlies, Environ. Res. Lett., 2016, 11, 074008 CrossRef.
- P. Ziveri, B. de Bernardi, K.-H. Baumann, H. M. Stoll and P. G. Mortyn, Deep Sea Res., Part II, 2007, 54, 659–675 CrossRef.
- P. Köhler, J. F. Abrams, C. Völker, J. Hauck and D. A. Wolf-Gladrow, Environ. Res. Lett., 2013, 8, 014009 CrossRef.
- Project Vesta, https://www.projectvesta.org/.
- J. J. Li and M. Hitch, Int. J. Min., Metall. Mater., 2015, 22, 1005–1016 CrossRef CAS.
- D. J. Beerling, J. R. Leake, S. P. Long, J. D. Scholes, J. Ton, P. N. Nelson, M. Bird, E. Kantzas, L. L. Taylor and B. Sarkar, et al. , Nat. Plants, 2018, 4, 138–147 CrossRef PubMed.
- T. Simkin and J. V. Smith, J. Geol., 1970, 78, 304–325 CrossRef CAS.
- J. B. Glass and C. L. Dupont, Oceanic Nickel Biogeochemistry and the Evolution of Nickel Use, Royal Society of Chemistry, 2019, ch. 2, pp. 12–26 Search PubMed.
- G. H. Rau, H. D. Willauer and Z. J. Ren, Nat. Clim. Change, 2018, 8, 621–625 CrossRef.
- Convention on the Prevention of Marine Pollution by Dumping of Wastes and Other Matter, 1972.
- R. M. Webb, K. Silverman-Roati and M. B. Gerrard, Removing Carbon Dioxide Through Ocean Alkalinity Enhancement: Legal Challenges and Opportunities, https://climate.law.columbia.edu/sites/default/files/content/Webb.
- IPCC special report on carbon dioxide capture and storage, ed. B. Metz and Intergovernmental Panel on Climate Change, Cambridge University Press, for the Intergovernmental Panel on Climate Change, Cambridge, 2005 Search PubMed.
- P. W. Boyd, A. J. Watson, C. S. Law, E. R. Abraham, T. Trull, R. Murdoch, D. C. E. Bakker, A. R. Bowie, K. O. Buesseler, H. Chang, M. Charette, P. Croot, K. Downing, R. Frew, M. Gall, M. Hadfield, J. Hall, M. Harvey, G. Jameson, J. LaRoche, M. Liddicoat, R. Ling, M. T. Maldonado, R. M. McKay, S. Nodder, S. Pickmere, R. Pridmore, S. Rintoul, K. Safi, P. Sutton, R. Strzepek, K. Tanneberger, S. Turner, A. Waite and J. Zeldis, Nature, 2000, 407, 695–702 CrossRef CAS PubMed.
- S. A. Rackley, Carbon Capture and Storage, Elsevier, 2010, pp. 267–286 Search PubMed.
- Massachusetts Institute of Technology General Circulation Model, https://mitgcm.org/.
- S. Dutkiewicz, A. Sokolov, J. Scott and P. Stone, A three-dimensional ocean-seaice-carbon cycle model and its coupling to a two dimensional atmospheric model: Uses in climate change studies. Report 122, MIT Joint Program on the Science and Policy of Global Change, 2005, http://mit.edu/globalchange/www/MITJPSPGC_Rpt122.pdf [Online; accessed 20-April-2021].
- A. Lenton, R. J. Matear, D. P. Keller, V. Scott and N. E. Vaughan, Earth Syst. Dynam., 2018, 9, 339–357 CrossRef.
- M. F. González and T. Ilyina, Geophys. Res. Lett., 2016, 43, 6493–6502 CrossRef.
- J. J. Middelburg, K. Soetaert and M. Hagens, Rev. Geophys., 2020, 58, e2019RG000681 CrossRef PubMed.
- W. M. Berelson, W. M. Balch, R. Najjar, R. A. Feely, C. Sabine and K. Lee, Global Biogeochem. Cycles, 2007, 21, GB1024 CrossRef.
- B. P. Boudreau, J. J. Middelburg and F. J. R. Meysman, Geophys. Res. Lett., 2010, 37, L03603 CrossRef.
- B. P. Boudreau, Geophys. Res. Lett., 2013, 40, 744–748 CrossRef CAS.
- Download: https://gresearch.storage.googleapis.com/climate-energy/acidity/CO2_Capture_by_pumping_acidity.tgz.
- M. Hagens and J. J. Middelburg, Geophys. Res. Lett., 2016, 43, 12528–12537 CrossRef CAS.
- C. E. Cornwall, C. D. Hepburn, C. M. McGraw, K. I. Currie, C. A. Pilditch, K. A. Hunter, P. W. Boyd and C. L. Hurd, Proc. R. Soc. B, 2013, 280, 20132201 CrossRef PubMed.
- L. T. Bach and P. W. Boyd, Seeking natural analogs to fast-forward the assessment of marine CO2 removal, 2021 DOI:10.1073/pnas.2106147118.
- M. P. Humphreys, L. Gregor, D. Pierrot, S. M. A. C. van Heuven, E. R. Lewis and D. W. R. Wallace, PyCO2SYS: marine carbonate system calculations in Python, 2020, https://zenodo.org/record/3744275 Search PubMed.
- E. R. Lewis and D. W. R. Wallace, Program Developed for CO2 System Calculations, 1998 Search PubMed.
- J. C. Orr, O. Aumont, A. Yool, K. Plattner, F. Joos, E. Maier-Reimer, M.-F. Weirig, R. Schlitzer, K. Caldeira, M. E. Wickett and R. J. Matear, Ocean CO2 sequestration efficiency from 3-d ocean model comparison, 2001 Search PubMed.
- P. Renforth, Int. J. Greenhouse Gas Control, 2012, 10, 229–243 CrossRef CAS.
- G. H. Rau and J. R. Baird, Renewable Sustainable Energy Rev., 2018, 95, 265–272 CrossRef CAS.
- J. R. Chiles, The Other Renewable Energy, 2009, https://www.inventionandtech.com/content/other-renewable-energy-0 [Online; accessed 20-April-2021].
- F. Kreith and D. Bharathan, J. Heat Transfer, 1988, 110, 5–22 CrossRef CAS.
- L. Liu, New J. Phys., 2014, 16, 123019 CrossRef.
- A. Babarit, J.-C. Gilloteaux, G. Clodic, M. Duchet, A. Simoneau and M. F. Platzer, Int. J. Hydrogen Energy, 2018, 43, 7266–7289 CrossRef CAS.
- S. Z. Golroodbari and W. Sark, Prog. Photovoltaics, 2020, 28, 873–886 Search PubMed.
- B. Willis, The Race Is On for Commercial Deployment of Solar in Open Seas, 2021, https://www.greentechmedia.com/articles/read/race-on-for-commercial-deployment-of-solar-in-open-seas [Online; accessed 20-April-2021].
- M. D. Eisaman, Joule, 2020, 4, 516–520 CrossRef.
- J. M. Matter, W. Broecker, M. Stute, S. Gislason, E. Oelkers, A. Stefánsson, D. Wolff-Boenisch, E. Gunnlaugsson, G. Axelsson and G. Björnsson, Energy Procedia, 2009, 1, 3641–3646 CrossRef CAS.
- B. P. McGrail, H. T. Schaef, A. M. Ho, Y.-J. Chien, J. J. Dooley and C. L. Davidson, J. Geophys. Res., 2006, 111, B12201 CrossRef.
- D. S. Goldberg, T. Takahashi and A. L. Slagle, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 9920–9925 CrossRef CAS PubMed.
- M. Bui, C. S. Adjiman, A. Bardow, E. J. Anthony, A. Boston, S. Brown, P. S. Fennell, S. Fuss, A. Galindo, L. A. Hackett, J. P. Hallett, H. J. Herzog, G. Jackson, J. Kemper, S. Krevor, G. C. Maitland, M. Matuszewski, I. S. Metcalfe, C. Petit, G. Puxty, J. Reimer, D. M. Reiner, E. S. Rubin, S. A. Scott, N. Shah, B. Smit, J. P. M. Trusler, P. Webley, J. Wilcox and N. Mac Dowell, Energy Environ. Sci., 2018, 11, 1062–1176 RSC.
- M. D. Eisaman, J. L. Rivest, S. D. Karnitz, C.-F. de Lannoy, A. Jose, R. W. DeVaul and K. Hannun, Int. J. Greenhouse Gas Control, 2018, 70, 254–261 CrossRef CAS.
- C.-F. de Lannoy, M. D. Eisaman, A. Jose, S. D. Karnitz, R. W. DeVaul, K. Hannun and J. L. Rivest, Int. J. Greenhouse Gas Control, 2018, 70, 243–253 CrossRef CAS.
- H. D. Willauer, F. DiMascio, D. R. Hardy and F. W. Williams, Energy Fuels, 2017, 31, 1723–1730 CrossRef CAS.
- B. D. Patterson, F. Mo, A. Borgschulte, M. Hillestad, F. Joos, T. Kristiansen, S. Sunde and J. A. van Bokhoven, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 12212–12219 CrossRef CAS PubMed.
- I. A. Digdaya, I. Sullivan, M. Lin, L. Han, W.-H. Cheng, H. A. Atwater and C. Xiang, Nat. Commun., 2020, 11, 362–365 CrossRef PubMed.
- F. Sabatino, M. Mehta, A. Grimm, M. Gazzani, F. Gallucci, G. J. Kramer and M. van Sint Annaland, Ind. Eng. Chem. Res., 2020, 59, 7007–7020 CrossRef CAS.
- J. R. Davis, Y. Chen, J. C. Baygents and J. Farrell, ACS Sustainable Chem. Eng., 2015, 3, 2337–2342 CrossRef CAS.
- J. Farrell and S. Snyder, Bipolar Membrane Electrodialysis for Zero Liquid Discharge Water Softening and Wastewater Reclamation, https://west.arizona.edu/sites/default/files/data/3_Research_Jim.
- M. Reig, S. Casas, C. Valderrama, O. Gibert and J. Cortina, Desalination, 2016, 398, 87–97 CrossRef CAS.
- Y. Wang, A. Wang, X. Zhang and T. Xu, Ind. Eng. Chem. Res., 2011, 50, 13911–13921 CrossRef CAS.
- J. Shen, J. Huang, L. Liu, W. Ye, J. Lin and B. V. der Bruggen, J. Hazard. Mater., 2013, 260, 660–667 CrossRef CAS PubMed.
- Annual Report Ocean Energy Systems, 2015, https://report2015.ocean-energy-systems.org/ [Online; accessed 20-April-2021].
- Lazards Levelized Cost of Energy Analysis, 2019, https://www.lazard.com/media/451086/lazards-levelized-cost-of-energy-version-130-vf.pdf [Online; accessed 20-April-2021].
- M. Broehm, J. Strefler and N. Bauer, Techno-Economic Review of Direct Air Capture Systems for Large Scale Mitigation of Atmospheric CO2, 2015 DOI:10.2139/ssrn.2665702.
- National Academies of Sciences Engineering and Medicine, Negative Emissions Technologies and Reliable Sequestration: A Research Agenda, The National Academies Press, Washington, DC, 2019 Search PubMed.
- M. Hansima, M. Makehelwala, K. Jinadasa, Y. Wei, K. Nanayakkara, A. C. Herath and R. Weerasooriya, Chemosphere, 2021, 263, 127951 CrossRef CAS PubMed.
- A. Alsheghri, S. A. Sharief, S. Rabbani and N. Z. Aitzhan, Energy Procedia, 2015, 75, 319–324 CrossRef CAS.
- H. Tsuchiya and O. Kobayashi, Int. J. Hydrogen Energy, 2004, 29, 985–990 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ee01532j |
| This journal is © The Royal Society of Chemistry 2022 |


