Open Access Article
Open Access ArticleApplication of machine learning and statistical modeling to identify sources of air pollutant levels in Kitchener, Ontario, Canada†
Wisam
Mohammed
 a,
Adrian
Adamescu
a,
Lucas
Neil
a,
Adrian
Adamescu
a,
Lucas
Neil
 b,
Nicole
Shantz
ab,
Tom
Townend
c,
Martin
Lysy
b,
Nicole
Shantz
ab,
Tom
Townend
c,
Martin
Lysy
 *d and
Hind A.
Al-Abadleh
*d and
Hind A.
Al-Abadleh
 *a
*a
aDepartment of Chemistry and Biochemistry, Wilfrid Laurier University, 75 University Ave West, Waterloo, ON N2L 3C5, Canada. E-mail: halabadleh@wlu.ca; Tel: +1 519-884-0710 ext. 2873
bAusenco, 100–1016B Sutton Dr, Burlington, Ontario L7L 6B8, Canada
cAQMesh, Environmental Instruments Ltd, Unit 5, The Mansley Centre, Timothy's Bridge Road, Stratford-upon-Avon, CV37 9NQ, UK
dDepartment of Statistics and Actuarial Science, University of Waterloo, 200 University Ave West, Waterloo, ON N2L 3G1, Canada. E-mail: mlysy@uwaterloo.ca; Tel: +1 519-888-4567 ext. 45503
First published on 6th October 2022
Abstract
Machine learning is used across many disciplines to identify complex relations between outcomes and numerous potential predictors. In the case of air quality research in heavily populated urban centers, such techniques were used to correlate the impacts of Traffic-Related Air Pollutants (TRAP) on vulnerable members of communities, future pollutant levels, and potential solutions that mitigate adverse effects of poor air quality. However, machine learning tools have not been used to assess the variables that influence measured pollutant levels in a suburban environment. The objective of this study is to apply a novel combination of Random Forest (RF) modeling, a machine learning algorithm, and statistical significance analysis to assess the impacts of anthropogenic and meteorological variables on observed pollutant levels in two separate datasets collected during and after the COVID-19 lockdowns in Kitchener, Ontario, Canada. The results highlight that TRAP levels studied here are linked to meteorology and traffic count/type, with relatively higher sensitivity to the former. Upon taking statistical significance into account when assessing relative importance of variables affecting pollutant levels, our study found that traffic variables had a more discernible influence than many meteorological variables. Additional studies with a larger dataset and spread throughout the year are needed to expand upon these initial findings. The proposed approach outlines a “blueprint” method of quantifying the importance of traffic in mid-size cities experiencing fast population growth and development.
Environmental significanceAssessing air quality at the neighborhood scale provides information on pollutant levels and sources that is often missed by regional stations. Since natural variability and human activities factors affect pollutant levels used in communicating air quality to the public, quantifying the relative importance of these factors would guide strategic urban planning and regulations aimed creating healthy air for all. Here we employ innovative mathematical tools that analyze data from a network of low-cost air quality stations in Kitchener, Ontario, Canada for correlation with meteorology and traffic counts/type during after COVID-19 related lockdowns. Our findings show that pollutant levels are sensitive to traffic changes even when meteorology plays the dominant role in their levels. |
1. Introduction
The application of machine learning algorithms to analyze air quality data is increasing in “smart cities” that utilize numerous air monitoring sensors to collect near real-time information accessible by both the government and citizens alike.1 These machine learning algorithms have a multitude of uses such as predicting future pollutant levels,2 determining the impacts of pollutants on the development in adolescents,3 and quantifying the impacts of anthropogenic sources and meteorology on local air quality.4 Recent studies explored the use of machine learning to predict spatial- and size-resolved particle concentrations downwind from roadside vegetation barriers that serve as a layer of protection against traffic-related air pollutants (TRAP) to better understand mitigation strategies.5,6 Other studies employed machine learning as a forecasting tool to predict future smog events caused by TRAP.7The air pollutants that are routinely measured due to their known health impacts include nitric oxide (NO), nitrogen dioxide (NO2), ground-level ozone (O3), fine particulate matter (PM2.5), carbon monoxide (CO), and carbon dioxide (CO2). The combustion of fossil fuels in automotive vehicles is known to be a major contributor to levels of nitrogen oxides (NOx, x = 1, 2),8–10 CO,11 and volatile organic compounds (VOCs). The photochemical decomposition of NO2 in the troposphere gives rise to oxygen radicals, which react with atmospheric oxygen and VOCs to form ground-level ozone, a secondary pollutant.12,13 Primary sources of PM2.5 include wind-blown dust particles, biomass burning, industrial activity,14,15 and non-exhaust emissions stemming from the wear and tear of automotive breaks, tires, and roads.16 Secondary PM2.5 form in the atmosphere from complex atmospheric multiphase reactions involving VOCs and other chemicals in the gas and condensed phases.8,14
Prolonged exposure to the aforementioned pollutants results in adverse health effects in local communities, with a larger impact on vulnerable members with pre-existing conditions such as heart disease and asthma.17 Long periods of exposure to these pollutants can worsen asthmatic symptoms, increase chances of genetic defects in unborn children,18 impact adolescent health,19 increase the risk of cardiovascular diseases, and cause organ failure.9,14,20 Recent studies on the impacts of TRAP on cardiovascular health highlighted that even at lower levels, TRAP is a significant contributor to pollution-induced diabetes mellitus,21 myocardial infarction,22 and cancer development in the respiratory tract.23 In 2016, the United Nations Children's Fund (UNICEF) reported 600![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 deaths in adolescents globally as a direct result of exposure to unfavorable air quality conditions.24 Hence, air quality continues to be a major concern among governmental bodies worldwide, particularly in urban communities, despite decades since enacting pollution control regulations.25
000 deaths in adolescents globally as a direct result of exposure to unfavorable air quality conditions.24 Hence, air quality continues to be a major concern among governmental bodies worldwide, particularly in urban communities, despite decades since enacting pollution control regulations.25
With the rapid expansion of urban communities comes the increase in industrialization and automotive use, both of which serve to emit harmful pollutants that pose a hazard to both human health and the environment.26,27 Over the past several decades, the World Health Organization (WHO) had been gradually lowering exposure limits of TRAP deemed as “safe” to provide countries with realistic targets to reach over a specified time interval. The most recent air quality guidelines (AQG) released by the WHO in 2021 lowered the exposure limits once again for NO2, O3 and PM2.5 to 13 ppb (24 h), 50 ppb (8 h), and 15 μg m−3 (24 h), respectively.28
The first step in mitigating the negative impacts of air pollution is enhancing monitoring at multiple scales, from regional to hyperlocal, to better identify “hot-spots”. For example, in July 2018, the Breathe London Blueprint project was launched in London, UK with over 100 AQMesh air quality monitoring multisensor pods.29 Similar projects were also launched in Glasgow,30 San Francisco,31 Paris,32 and Mongolia.33 More recently, our research group launched a pilot project in Kitchener, Ontario (ON), Canada using five AQMesh multisensor pods distributed near different elementary schools to assess local air quality across different locations in the network relative to the provincial reference station located in a city park.34 Our first published study highlighted the difference in pollutant levels among different locations relative to the reference station and analyzed the effect of the wildfires season on local air quality.34 One major conclusion from our study was the need for additional measurements of traffic count, vehicle and fuel type, and local meteorology that account for the effect of the built environment on wind speed and direction, and temperature.
The objective of this study is to apply a combination of machine learning and statistical significance modeling to isolate the variables that influence pollutant levels collected using the AQMesh multisensor pods in Kitchener, ON during a two-week period in fall 2020 and 2021. This analysis allowed for the identification of the most probable traffic-related emission sources and the sensitivity of pollutant levels to meteorology. Our analysis also investigated the impact that lockdowns may have had on traffic-related emission sources of air pollutants.
2. Methods and data analysis
2.1. Location of AQMesh multisensor pods
Five stationary multisensor pods (model version 2020) developed by AQMesh were installed in Kitchener, ON. These multisensory pods use the most recent gas sensing algorithm (v5.3.1), which allows for more accurate conversions of detection signals to pollutant concentrations. Four pods were distributed near elementary schools, with the fifth pod co-located within 30 meters of an air quality monitoring station run by the Ministry of the Environment, Conservation and Parks (MECP; see ESI Fig. S1 and Table S1† for details). We conducted extensive analyses to assess the performance of these multisensor pods in addition to highlighting the variability of pollutant levels at each location.34 The pods of interest for the analysis here are the ones located near a major highway (highway 8) (Pod 1) and near a main suburban road (Pod 2).342.2. Acquisition of data
All pollutant data used in this study were obtained from the open access dashboard for the multisensor air quality pods network in Kitchener, ON.35 The raw data were subjected to rigorous quality assurance protocols. First, the raw data was manually reviewed and any erroneous datapoints, such as abnormally elevated PM2.5 levels originating from increased relative humidity, were omitted. Second, the manually reviewed dataset was subjected to long distance scaling analysis. This “long distance scaling” refers to sensors far beyond the co-location range of 1 meter, where accurate scaling can take place. Briefly, this analysis works by identifying comparable datapoints between the AQMesh instrument and the local reference, where hyperlocal events are redacted, and the regional response to each target pollutant are scaled accordingly. This method has been used and validated across many similar projects, most notably in the Breathe London pilot study.29 A more thorough explanation can be found in the ESI section† of our previous publication.34 Meteorological data were collected from two separate sources: (1) variables such as wind speed, relative humidity, temperature, and atmospheric pressure were collected from the solid-state sensors in each AQMesh pod, and (2) precipitation and solar irradiance were obtained from the National Climate Archives website.36 Wind speed data was collected from the regional-run station near the airport located approximately 9 kilometers from our multisensory pods network.Raw traffic data were obtained from the city of Kitchener, which were collected on an hourly basis and contained traffic counts classifications of thirteen separate categories in compliance with the Federal Highway Administration (FWHA) protocols.37 This data allowed for more detailed observations regarding the size and frequency of each classification type. Rigorous quality assurance protocols were also conducted on the traffic counts to ensure the validity of the data. Significant outliers were investigated comprehensively through a combination of reviewing recent documents pertaining to construction-driven detours, communication with the staff in the city of Kitchener, and physical observations of traffic flow prior to incorporating manual adjustments.
The traffic count data were provided by the city of Kitchener for only two locations: Pod 1 and Pod 2. Furthermore, the data collected was further limited to the following periods: (1) October 20–November 10, 2020, and (2) October 7–October 18, 2021. There were concerns that this small dataset of to 477 and 287 for 2020 and 2021, respectively, would present challenges with the machine learning algorithm. This concern was found to be less of an issue for accurately predicting levels than for quantifying the statistical significance of the predictive importance of the meteorological and traffic variables, as discussed in Section 3.3.
2.3. Machine learning model: Random Forest
The Random Forest (RF) model is a machine learning algorithm which may be used to identify complex dependence patterns between pollutant levels and the underlying meteorological variables and traffic counts. RF operates by subsetting the meteorological and traffic predictor variables – or features – using decision trees and taking the predicted pollutant level as the average in each subset. The output of many such trees is analyzed, and a final prediction model is obtained by pooling the trees together.38–40 Scheme S1† shows an illustration of the procedure followed by the sample code used in the model. When the number of features compared to the number of data points is relatively small, RF has prediction accuracy typically far superior to that of multiple linear regression modeling.41–44 We present similar findings for our data and other predictive assessments of the RF model in Section 3.3.One benefit of the RF model is that it can rank the importance of the feature variables in predicting pollutant levels. This ranking is done for each feature variable by calculating the percent increase in mean square error (MSE) between the RF model fit to the original dataset (MSEoriginal) and to a dataset with the values of the given feature variable randomly permuted (MSEpermute), relative to the variance of the pollutant levels (var(pollutant)) as shown in eqn (1):
 | (1) |
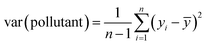 , yi is the pollutant level for observation i, and ȳ is the average pollutant level. The MSE for the RF model is defined as the sum of squared differences between the observed pollutant level (yi) and the pollutant level predicted by the RF model (ŷRF(xi)), given the feature vector (xi).45 This value is then multiplied by the reciprocal of the total number (n) of considered values as shown in eqn (2):
, yi is the pollutant level for observation i, and ȳ is the average pollutant level. The MSE for the RF model is defined as the sum of squared differences between the observed pollutant level (yi) and the pollutant level predicted by the RF model (ŷRF(xi)), given the feature vector (xi).45 This value is then multiplied by the reciprocal of the total number (n) of considered values as shown in eqn (2):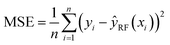 | (2) |
By considering the square of the differences, the MSE is very sensitive to drastic changes. Since the correlation between the permuted feature variable and pollutant levels is effectively zero, the higher the calculated %IncMSE for a given variable, the higher its importance when it comes to predicting pollutant concentration.
3. Results and discussion
3.1. Statistical significance analysis of meteorological data between fall 2020 and 2021
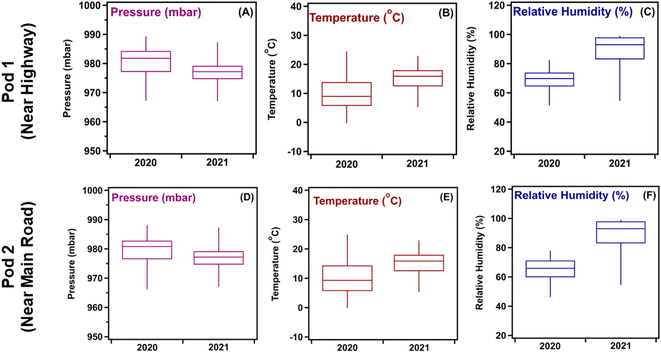
With the lockdown measures put in place in fall 2020, statistically significant reductions in overall pollutant levels were observed across Southern Ontario in Canada.46 The installation of AQMesh multisensor pods network in Kitchener, ON allowed for a large volume of data to be collected before, during, and after the COVID-19 lockdown restrictions. Our previous publication on quantifying the statistical significance of these reductions highlighted that they were likely due to less congestion and traffic in suburban communities.34,46Fig. 1 compares the observed meteorological variables for the two-week period studied in 2020 and 2021 for Pods 1 and 2. Upon visual inspection, there are notable variations between the two datasets, indicating that the influence of meteorology on pollutant levels may vary between the two years, as shown later in Section 3.3. These visual observations were further validated by the method of statistical quantification used in our previous publication46 (see R code in ESI†), i.e., by calculating the p-value against the null hypothesis that the median of each variable in question is the same in 2020 and 2021. When the p-value is greater than 0.05, the difference in medians is not deemed to be statistically significant, i.e., cannot be distinguished from natural day-to-day variations. In contrast, a p-value less than 0.05 indicates that there is a significant difference between the medians in 2020 and 2021, which could potentially account for the difference in pollutant levels. The p-value for each variable in question is reported in Table 1, which are all close to zero, meaning that any of these variables could potentially account for the difference in pollutant levels between 2020 and 2021. Additional comparisons between precipitation, wind speed, and solar irradiance were also conducted using hourly data (ESI Fig. S2 and S3†). Statistical analyses for these variables highlighted no significant variations, indicating that the influence they had on pollutant levels should remain consistent over the two years compared.
| Variable | Median 2020 | Median 2021 | p-Value calculated |
|---|---|---|---|
| a Calculated p-values >0.05 indicate no significant variations between the two compared years. Values of 0.00 are in fact very small numbers <5 × 10−6. | |||
| Pod 1 | |||
| Pressure (mbar) | 981.8 | 977.2 | 0.00 |
| Temperature (°C) | 9.00 | 15.9 | 0.00 |
| Relative humidity (RH%) | 69.8 | 93.0 | 0.00 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Pod 2 | |||
| Pressure (mbar) | 980.8 | 977.2 | 0.00 |
| Temperature (°C) | 9.30 | 15.9 | 0.00 |
| Relative humidity (RH%) | 65.9 | 93.0 | 0.00 |
3.2. Statistical significance analysis of pollutant levels between fall 2020 and 2021
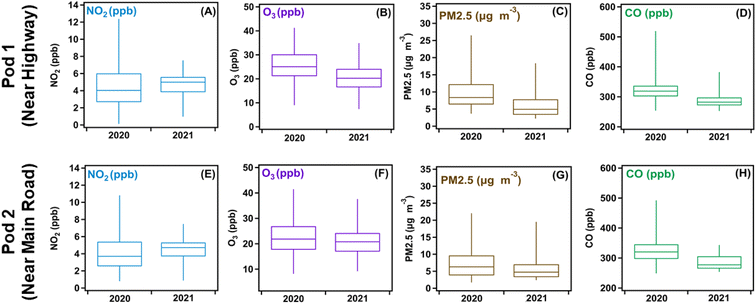
Pollutant levels collected using the multisensor pods network during fall 2020 and 2021 were also analyzed for statistical significance. Visual inspection of the box plots in Fig. 2 show differences in the distribution of pollutant levels and median for the same pollutant over the two years. Table 2 lists the calculated p-values for each pollutant, which were all well below 0.05, indicating statistically significant differences between the two years studied. An interesting observation is that all pollutants, excluding NO2, showed a decline in the median value between 2020 and 2021. Lockdowns in 2020 resulted in shutting down in-person learning at the schools close to the pods location and forced the closure of non-essential businesses. In 2021, the lockdown restrictions were relaxed, and students were allowed to partially return to in-person learning. Non-essential businesses were allowed to operate once more, and companies were beginning to adapt to a hybrid in-person/remote system for their employees. These factors were thought to have impacted traffic flow near the two pod locations studied, which would explain the NO2 and O3 trends seen in Fig. 2. The next section expands on this hypothesis and shows results from the RF model that quantifies the influence that each metrological and traffic variable has on the overall pollutant levels for the time periods studied.| Pollutant | Median 2020 | Median 2021 | p-Value calculated |
|---|---|---|---|
| a Calculated p-values >0.05 indicate no significant variations between the two compared years. Values of 0.00 are in fact very small numbers <5 × 10−6. | |||
| Pod 1 | |||
| NO2 (ppb) | 4.03 | 4.99 | 0.00 |
| O3 (ppb) | 25.1 | 20.3 | 0.00 |
| PM2.5 (mg m−3) | 8.36 | 4.92 | 0.00 |
| CO (ppb) | 319 | 282 | 0.00 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Pod 2 | |||
| NO2 (ppb) | 3.63 | 4.77 | 0.00 |
| O3 (ppb) | 22.7 | 20.8 | 0.00 |
| PM2.5 (mg m−3) | 6.72 | 4.72 | 0.00 |
| CO (ppb) | 320 | 277 | 0.00 |
3.3. Relative importance of variables for observed pollutant levels from RF model
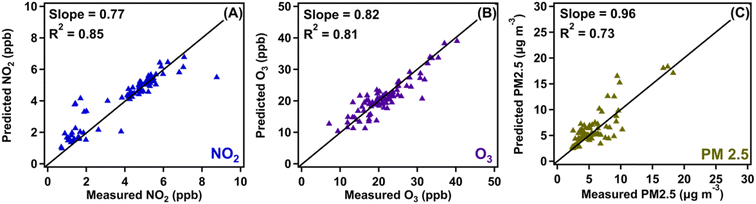
The RF model was fit to the data using 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 random trees and with hyperparameters (the number of features to try at each split, and the size of each tree) tuned to minimize the out-of-sample MSE using the R package RandomForestSRC.47 To test the performance of the RF model and its predictive power using our dataset, we divided our data into a 70–30 split, where 70% of our observed data was used to train the model and the remaining 30% was used to test the quality of the model predictions.48,49Fig. 3 shows regression plots that compare the out-of-sample predictions of the RF model on the 30% hold-out data to the actual pollutant levels during the October 07–18, 2021 period. These plots can be used to visually assess the bias and variance of the RF model. For example, the models for NO2 and O3 have little variance relative to that of PM2.5, with the predictions for NO2 and O3 being closer to the 1
000 random trees and with hyperparameters (the number of features to try at each split, and the size of each tree) tuned to minimize the out-of-sample MSE using the R package RandomForestSRC.47 To test the performance of the RF model and its predictive power using our dataset, we divided our data into a 70–30 split, where 70% of our observed data was used to train the model and the remaining 30% was used to test the quality of the model predictions.48,49Fig. 3 shows regression plots that compare the out-of-sample predictions of the RF model on the 30% hold-out data to the actual pollutant levels during the October 07–18, 2021 period. These plots can be used to visually assess the bias and variance of the RF model. For example, the models for NO2 and O3 have little variance relative to that of PM2.5, with the predictions for NO2 and O3 being closer to the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 lines relative to those for PM2.5. In contrast, the RF model for NO2 exhibits the highest bias, with large values being systematically underestimated. However, though the datasets used were small, this did not significantly undermine the ability of the RF model to accurately predict pollutant levels, as evident in the large values of R2 obtained for NO2, O3, and PM2.5, respectively. These R2 values are similar to those reported in a much larger study50 using a similar methodology. When the RF model was fed with the combined fall 2020 and 2021 datasets, which increased the dataset size to 762 from 477 for 2020 and 287 for 2021, the out-of-sample predictive ability of the model was very similar for O3, but slightly worse for NO2 and PM2.5 (ESI Fig. S4†). This is because of a few large values of the pollutant levels for these two pollutants which the RF model underestimated. Predictions of the RF model were far superior to those of a multiple linear regression model trained and tested on the same data (ESI Table S2†).
1 lines relative to those for PM2.5. In contrast, the RF model for NO2 exhibits the highest bias, with large values being systematically underestimated. However, though the datasets used were small, this did not significantly undermine the ability of the RF model to accurately predict pollutant levels, as evident in the large values of R2 obtained for NO2, O3, and PM2.5, respectively. These R2 values are similar to those reported in a much larger study50 using a similar methodology. When the RF model was fed with the combined fall 2020 and 2021 datasets, which increased the dataset size to 762 from 477 for 2020 and 287 for 2021, the out-of-sample predictive ability of the model was very similar for O3, but slightly worse for NO2 and PM2.5 (ESI Fig. S4†). This is because of a few large values of the pollutant levels for these two pollutants which the RF model underestimated. Predictions of the RF model were far superior to those of a multiple linear regression model trained and tested on the same data (ESI Table S2†).
Predictions in less clustered areas of the plots in Fig. 3 were shown to reduce the performance of the model's ability to predict pollutant levels, which is shown most prominently in Fig. 3C. This is believed to be caused by two main factors: (1) the data presented are below the limit of confidence (20 μg m−3 for PM 2.5, 10 ppb for NO2 and O3) for the sensors. This means that the data collected below these thresholds cannot be taken with 100% certainty, an assumption that the model does not make when predicting values, (2) the model was trained with most of the data having very low concentrations of PM2.5 (<10 μg m−3). This resulted in greater accuracy when making predictions in the clusters, and less accuracy in the “scattered” sections (10 μg m−3 ≤ PM 2.5 ≤ 20 μg m−3). Both factors influencing the model's accuracy can be rectified with a dataset exceeding the limit of confidence of the sensor and with a larger dataset to provide a reference for a wider range of pollutant levels.
Table 3 lists the traffic counts provided by the city of Kitchener near Pods 1 and 2. Results indicate that traffic volume did not change significantly (p-value >0.05) between the two years at the two locations. With that said, for Pod 1 there were cases when traffic counts were higher in 2021 (when lockdowns were relaxed) than the 2020 period, and for Pod 2 (located near a main road), there were instances where the traffic counts were higher in 2020 than 2021. While evidence from the p-values alone cannot distinguish these differences from normal day-to-day variation in traffic flow, upon further examination of the local context provided by the city of Kitchener, we found that a construction project had been launched near Pod 2 during the lockdown in 2020. Hence, the observed counts for 2020 in Table 3 originate from a combination of construction vehicles traversing through the roadside maintenance site and residents. This construction project was for the long-term and evolved as time progressed. In fall 2021, the project expanded to nearby roads, resulting in certain routes being closed off, causing vehicles and buses to deviate from their regular routes via detours, ultimately resulting in missed traffic counts at that location.
| Variable | Median 2020 | Median 2021 | p-Value calculated |
|---|---|---|---|
| a Calculated p-values >0.05 indicate no significant variations between the two compared years. Variations in the total counts are attributed to rounding medians to whole numbers. | |||
| Pod 1 | |||
| Cars | 25 | 29 | 0.34 |
| Vans/pickups | 2 | 2 | 1 |
| Buses/trucks | 1 | 1 | 1 |
| Motorcycles | 0 | 0 | 1 |
| Total traffic | 28 | 32 | 0.36 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Pod 2 | |||
| Cars | 26 | 23 | 0.41 |
| Vans/pickups | 3 | 2 | 0.65 |
| Buses/trucks | 3 | 3 | 1 |
| Motorcycles | 0 | 0 | 1 |
| Total traffic | 32 | 29 | 0.44 |
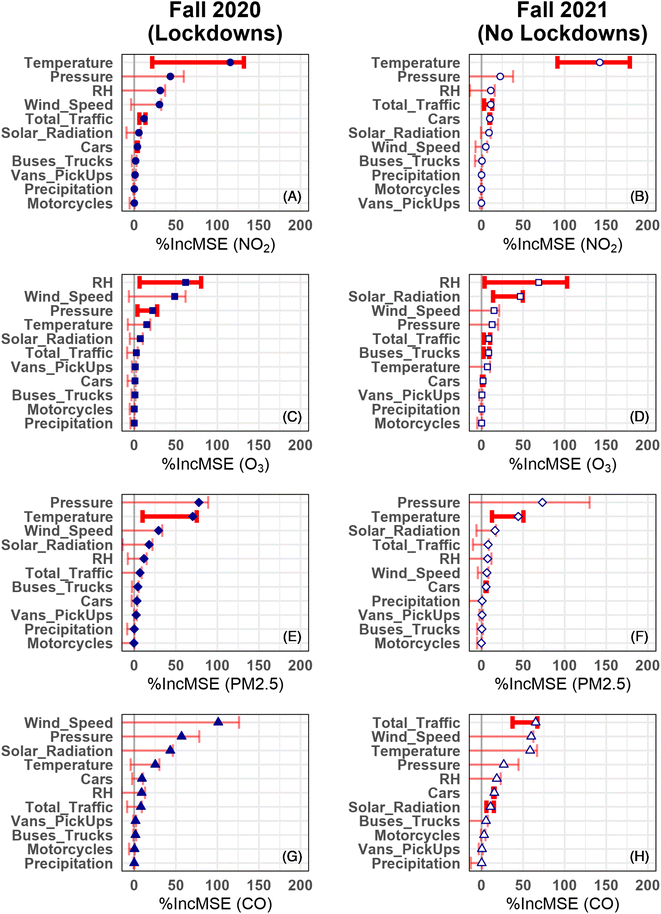
The RF model was used to determine the importance of meteorological factors and traffic on pollutant concentrations. The model relayed this importance through the calculation of %IncMSE, where higher percentages indicate a greater importance attributed to the influence of the variable under study.39 The %IncMSE are shown for each meteorological and traffic variable for years 2020 and 2021 on each pollutant concentration for Pod 1 in Fig. 4 and Pod 2 in ESI Fig. S5.† Also displayed are 95% confidence intervals for %IncMSE.51 Both pod locations used in this study showed several similarities. For example, large values of %IncMSE often come with the largest 95% confidence intervals, and these error bars are usually skewed towards lower values. This is because %IncMSE is very sensitive to how well the RF model performs on the extreme observations it has most difficulty predicting. Therefore, large values of %IncMSE can often be due to a handful of extreme values. However, since the error bars are obtained via subsampling,51 these extreme values become much harder to predict, leading to a drop in %IncMSE. While the sample sizes obtained were sufficiently large to justify the calculation of error bars via subsampling,51 the asymmetry issue is mitigated with larger sample sizes, thus underscoring the need to obtain larger datasets in future studies. Accounting for only the statistically significant %IncMSE values (those with error bars above zero), Fig. 4 shows that the most important meteorological variables are temperature, relative humidity, pressure, and solar irradiance. This result seems to be in line with the literature review,52,53 where both temperature and pressure play a significant role in facilitating the formation of secondary pollutants.
Fig. 4A and B show the calculated %IncMSE for NO2 in fall 2020 and 2021, respectively for Pod 1. There were significant variations in meteorological values between the two years as shown in Table 1, and hence they remain the dominant variables affecting NO2 levels. However, aside from temperature, the only statistically significant %IncMSE values are for total traffic and cars. While the %IncMSE value for these traffic variables is small compared to that of pressure, relative humidity, and wind speed, the fact that the error bars are also small and above zero indicates that the influence of these variables is not merely driven by predictions on a handful of extreme observations, as the large error bars on the aforementioned meteorological variables would suggest. Also, for the NO2 data, the %IncMSE calculated for solar radiation was very close to those calculated for traffic-related variables in Fig. 4 and ESI Fig. S5.† This observation is likely due to the influence of solar radiation on the photochemical decomposition of NO2 to form nitric oxide and free oxygen radicals,34,54 the latter of which goes on to form O3.55
Fig. 4C and D show the calculated %IncMSE for each meteorological and traffic-related variable to assess its importance for O3 levels recorded by Pod 1 in fall 2020 and 2021, respectively. It appears that O3 levels are mainly dependent on meteorology, namely relative humidity, solar radiation, and pressure. As mentioned earlier, the formation of ground level O3 is mainly driven by the photochemical decomposition and reaction of NO2 and VOCs.20,54,55 As for %IncMSE values for Pod 2 (Fig. S5†), the only significant meteorological variable for predicting O3 is solar radiation. For the traffic variables, small but statistically significant %IncMSE values for total traffic, cars, and buses/trucks are found in Pod 1, and buses/trucks in Pod 2, again suggesting that the importance metric for these variables is not merely driven by a handful of extreme observations.
Fig. 4E and F show the calculated %IncMSE for each meteorological and traffic-related variable to assess its importance in predicting PM2.5 levels recorded by Pod 1 in fall 2020 and 2021, respectively. In this case, the most significant meteorological variable by %IncMSE is temperature. However, this result does not mean that temperature is the only variable responsible for the elevated levels of PM2.5, but rather interacts with one or more other variables to have a synergetic effect on the measured data. PM2.5 has primary and secondary sources (see Introduction above), where vehicles emit PM2.5 from the incomplete combustion of fuel, and the precursors, namely VOCs, react in the atmosphere to form fine particulates. Furthermore, the chemical and physical properties of these particulates are influenced by relative humidity,56 which has a statistically significant value of %IncMSE at Pod 2 in 2021 (Fig. S5†). While total traffic is significant at Pod 1 in 2020 and cars are significant at Pod 2 in 2021, it remains unclear as to how influential traffic variables are on the measured values of PM2.5. Additional studies using different time periods are needed prior to making any definite conclusions.
Fig. 4G and H show the calculated %IncMSE for each meteorological and traffic-related variable to assess its importance in predicting CO levels recorded by Pod 1 in fall 2020 and 2021, respectively. Carbon monoxide is directly emitted from the combustion of fuel from vehicles much like NO, a precursor to NO2.57,58 This pollutant is relatively short-lived in the atmosphere and participates in atmospheric reactions to form CO2. The lower CO levels in fall 2021 relative to 2020 listed in Table 2 suggest additional sinks for CO becoming important such as reactions with hydroxyl radical,12,13 which in the presence of light and NOx can lead to O3 formation. An interesting observation in Fig. 4G andH is that %IncMSE for total traffic and cars is larger and more significant in 2021 than 2020. However, this is not due to a statistically significant increase in the corresponding traffic counts, according to the p-value calculation of Table 3. Rather, it is due to the fact that CO has far more extreme values in 2020 than 2021 (Fig. 2D). To explain this in more detail, ESI Fig. S6† plots the CO measurements against total traffic and car counts for 2020 and 2021. Also pictured in each plot is the LOESS curve of the RF model predictions against the given variable. In Fig. S6I and M† (Pod 1, 2020), there are several extreme values of CO (around 25 total traffic and 20 car counts, respectively) which are far above the LOESS curve. Those extreme values still exist in Fig. S6J and N† (Pod 1, 2021), but they are much closer to the LOESS curve. Thus, the predictions attributable to these traffic variables were better in 2021 than 2020, hence the larger %IncMSE. More interesting still is that the story in Pod 2 is essentially reversed. That is, cars drop significantly in %IncMSE from 2020 to 2021. At first, it might seem that it is due to changes in important meteorological variables between 2020 and 2021 such as temperature and wind speed, which affect the relative importance of cars. A more fulsome explanation is offered by Fig. S6.† Once again, the extreme values of CO are much closer to the LOESS curves in 2021 than 2020, as shown when comparing Fig. S6L and P to K and O, respectively.† This explains the increase in %IncMSE for temperature. However, %IncMSE is a combined measure of distance from the mean trend and departure of the mean trend from zero (if the mean trend of a variable is zero, then it cannot have a predictive effect on the outcome). Thus, for cars and wind speed, it appears that the smaller distances from the LOESS curve in 2021 are offset by the larger variation in the curve in 2020, resulting in an overall decrease in %IncMSE. Additional studies during high pollution events where traffic counts are more varied between the periods of study are needed to better understand the significance of traffic on CO levels.
A recent study50 conducted in Los Angeles used a similar RF model to quantify the impacts that TRAP and meteorology have on pollutant levels during the early days of the COVID-19 lockdown period. This RF model was more comprehensive, and included higher specificity for vehicle types, fuel used, miles travelled, etc. The results highlighted that pollutant levels showed a significant decline during the studied period compared to previous years. Furthermore, “heavy-duty trucks”, or vehicles used to transport resources, were the biggest contributor to pollutant levels during the lockdown period. When comparing this study, which took place in a large city, to the findings presented here (a medium-sized city), there was some overlap in the findings: (1) traffic appears to play a statistically significant role in the levels of NO2, O3, and PM2.5, and (2) meteorology has the biggest influence on all pollutants, evident in the high ranking of importance for its variables in both studies. While direct variable importance rankings are not possible since the Los Angeles study used a different importance metric from ours, the main methodological difference between our studies is that ours computes the statistical significance (via error bars containing zero) on the variable importance metric, whereas the Los Angeles study does not. This allowed us to conclude that even the relatively small %IncMSE for several traffic variables was statistically significant, whereas much large %IncMSE values for a number of meteorological variables was not. Upon taking statistical significance into account, our study found that traffic variables had a more discernible influence than many meteorological variables, whereas in the Los Angeles study, based on the magnitude of variable importance metrics alone, the meteorological variables were almost always the dominant factors for predicting pollutant levels.
4. Summary and implications
The use of machine learning algorithms on meteorology and traffic datasets allowed for a comprehensive assessment of which factors impact pollutant levels. Meteorological variables were found to be the most influential variables on pollutant levels, with a number of traffic variables having smaller but statistically significant influences as well. There were statistically significant differences in the meteorological variables between the two years studied (Table 1), but no such significant differences between traffic counts (Table 3). The latter finding precludes any assessment of the effect of lockdowns on pollutant concentrations as a direct result of changes in traffic counts. However, upon taking statistical significance into account when assessing relative importance of variables affecting pollutant levels, our study found that traffic variables had a more discernible influence than many meteorological variables. While the small sample size did not seriously undermine the accuracy of the RF model (Fig. 3 and ESI Table S2†), it did lead to large error bars on the variable importance metrics (Fig. 4 and ESI Fig. S5†). For this reason, it is difficult to draw any definite conclusions from this study alone. Additional studies with a larger traffic dataset and spread throughout the year are needed to expand upon these initial conclusions.Machine learning algorithms offer a new way to analyze air pollution data in relation to meteorology and traffic. Scaling up the project presented here would be feasible, as the computational power required to run the machine learning code and p-value calculations is fairly low. Future studies with traffic data that run over a longer time frame would be beneficial and could be used to predict pollution levels based on changes to meteorological and traffic data. Additionally, a larger dataset will not only improve the accuracy of the model but also allow for more definite conclusions to be made regarding pollutants and variable metrics that hover near the statistical significance threshold. The analysis presented here also examines the contrast between the variables that influence air quality in large and mid-size cities. This contrast suggests that local contexts matter in drafting bylaws and regulations to lower emissions and minimize exposure of citizens to air pollutants. Electrifying the transport system in mid-size cities experiencing population growth would ensure that TRAP would have lower importance than meteorology. Continuous monitoring is highly recommended for regular assessment of seasonal and human influences.
Data availability
The data presented in this study are available on request from the corresponding authors. The scaled data are publicly available on the Kitchener Air Quality Dashboard: https://Kitchenergis.maps.arcgis.com/apps/das-boards/fddc1fd0c5e84b459d7c04f5e4db1a7c (accessed on 06 June 2022).Author contributions
HAA conceived the idea and planned the research with the co-authors. ML conceived of and implemented the statistical analysis. WM wrote the first draft of the manuscript and made the figures. WM and TT did the quality control/quality assurance of the sensor data followed by the LDS analysis. NS analyzed the traffic data. AA and ML did the machine learning analysis. LN provided input on the interpretation of the results. All authors contributed to the writing of the manuscript.Conflicts of interest
T. T. works at AQMesh. The authors declare that they have no other conflict of interest.Acknowledgements
The authors acknowledge funding from the City of Kitchener, NSERC Alliance Program for COVID-19 related research, and the Canadian Foundation for Innovation Exceptional Opportunities Fund. The authors thank Courtney Zinn in the Digital Lab of the City of Kitchener for facilitating the acquisition of traffic data. ML acknowledges funding from NSERC Discovery Grant RGPIN-2020-04364. WM acknowledges funding from the MS2Discovery Institute Student Researcher Award.References
- Organization for Economic Co-operation and Development, Smart Cities and Inclusive Growth, accessed March 16, 2022, https://www.oecd.org/cfe/cities/OECD_Policy_Paper_Smart_Cities_and_Inclusive_Growth.pdf Search PubMed.
- H. K. S. Doreswamy, K. M. Yogesh and I. Gad, Forecasting Air Pollution Particulate Matter (PM2.5) Using Machine Learning Regression Models, Porcedia Comput. Sci., 2020, 171, 2057–2066 CrossRef.
- S. Oskar and J. A. Stingone, Machine Learning Within Studies of Early-Life Environmental Exposures and Child Health: Review of the Current Literature and Discussion of Next Steps, Curr. Environ. Health Rep., 2020, 7, 170–184 CrossRef PubMed.
- Y. Liu, P. Wang, Y. Li, L. Wen and X. Deng, Air quality prediction models based on meteorological factors and real-time data of industrial waste gas, Sci. Rep., 2022, 12(1), 1–15 CrossRef PubMed.
- K. Hashad, J. Gu, B. Yang, M. Rong, E. Chen, X. Ma and M. K. Zhang, Designing roadside green infrastructure to mitigate traffic-related air pollution using machine learning, Sci. Total Environ., 2021, 773, 1–9 CrossRef PubMed.
- I. Jarvis, H. Sbihi, Z. Davis, M. Brauer, A. Czekajlo, H. Davies, W. S. Gergel, E. M. Guhn, M. Jerrett, M. Koehoorn, L. Nesbitt, T. Oberlander, F. J. Su and M. van den Bosch, The influence of early-life residential exposure to different vegetation types and paved surfaces on early childhood development: A population-based birth cohort study, Environ. Int., 2022, 163, 1–10 CrossRef PubMed.
- J. Wang, H. Li, Y. Wang and H. Yang, A novel assessment and forecasting system for traffic accident economic loss caused by air pollution, Environ. Sci. Pollut. Res., 2020, 28, 1–20 Search PubMed.
- D. R. Gentner, S. H. Jathar, T. D. Gordon, R. Bahreini, D. A. Day, I. El Haddad, P. L. Hayes, S. M. Pieber, S. M. Platt, J. de Gouw, A. H. Goldstein, R. A. Harley, J. L. Jimenez, A. S. H. Prevot and A. L. Robinson, Review of Urban Secondary Organic Aerosol Formation from Gasoline and Diesel Motor Vehicle Emissions, Environ. Sci. Technol., 2017, 51, 1074–1093 CrossRef CAS PubMed.
- USEPA, Nitrogen Dioxide (NO2) Pollution, accessed June 21, 2021, https://www.epa.gov/no2-pollution/basic-information-about-no2 Search PubMed.
- N. Al-Naimi, P. Balakrishnan and I. Gotkepe, Measurement and modelling of nitrogen dioxide (NO2) emissions: a marker for traffic-related air pollution in Doha, Qatar, Ann. GIS, 2015, 21, 249–259 CrossRef.
- R. K. Angatha and A. Mehar, Impact of Traffic on Carbon Monoxide Concentrations Near Urban Road Mid-Block, J. Inst. Eng. (India): Ser. A, 2020, 101, 713–722 CAS.
- Atmospheric Chemistry at Night, accessed November 24, 2021, https://www.rsc.org/images/environmental-brief-no-3-2014_tcm18-237724.pdf Search PubMed.
- H. Akimoto. and J. Hirokawa, Atmospheric Multiphase Chemistry: Fundamentals of Secondary Aerosol Formation, Wiley, 2020 Search PubMed.
- J. H. Kroll and J. H. Seinfield, Chemistry of secondary organic aerosol: formation and evolution of low volatility organics in the atmosphere, Atmos. Environ., 2008, 42, 3593–3624 CrossRef CAS.
- S. Philip, R. V. Martin, G. Snider, C. L. Weagle, A. van Donkelaar, M. Brauer, D. K. Henze, Z. Kilmont, C. Venkataraman, S. K. Guttikunda and Q. Zhang, Anthropogenic fugitive, combustion and industrial dust is a significant, underrepresented fine particulate matter source in global atmospheric models, Environ. Res. Lett., 2017, 12, 1–7 Search PubMed.
- R. M. Harrison, J. Allan, D. Carruthers, M. R. Heal, A. C. Lewis, B. Marner, T. Murrells and A. Williams, Non-exhaust vehicle emissions of particulate matter and VOC from road traffic: A review, Atmos. Environ., 2021, 262, 1–20 CrossRef.
- Environmental Climate Change Canada, The Air Quality Health Index: How Air Pollution Affects Your Health Fact Sheet, accessed February 12, 2021, https://www.ec.gc.ca/ae-ve/default.asp?lang=En%26n=9918CDC7-1 Search PubMed.
- É. Lavigne, M. A. Bélair, M. T. Do, D. Steib, P. Hystad, A. van Donelaar, R. V. Martin, D. L. Crouse, E. Crighton, H. Chen, J. R. Brook, R. T. Burnett, S. Weichenenthal, P. J. Villeneuve, T. To, S. Cakmak, M. Johnson, A. S. Yaseen, K. Johnson, M. Ofner, L. Xie and M. Walker, Maternal exposure to ambient air pollution and risk of early childhood cancers: A population-based study in Ontario, Canada, Environ. Int., 2017, 100, 139–147 CrossRef PubMed.
- T. To, J. Zhu, E. Terebessy, K. Zhang, I. Fong, L. Pinault, M. Jerrett, A. Robichaud, R. Menard, A. van Donkelaar, R. V. Martin, P. Hystad, J. Brook, R. S. Dell and D. Steib, Does exposure to air pollution increase the risk of acute care in young children with asthma? An Ontario, Canada study, Environ. Res., 2021, 199, 1–7 CrossRef PubMed.
- USEPA, Ground-level Ozone Basicshttps://www.epa.gov/ground-level-ozone-pollution/ground-level-ozone-basics, accessed August 02, 2021.
- M. Johnson, J. R. Brook, R. D. Brook, T. H. Oiamo, I. Luginaah, P. A. Peters and J. D. Spence, Traffic-Related Air Pollution and Carotid Plaque Burden in a Canadian City With Low-Level Ambient Pollution, J. Am. Heart Assoc., 2020, 9, 1–14 Search PubMed.
- E. Alexeeff, S. A. Roy, J. Shan, X. Liu, K. Messier, J. Apte, S. C. Portier, S. Sidney and S. K. Van Den Eeden, High-resolution mapping of traffic related air pollution with Google street view cars and incidence of cardiovascular events within neighborhoods in Oakland, CA, J. Environ. Health, 2018, 17, 1–13 CrossRef PubMed.
- A. G. Ribeiro, G. S. Downward, C. U. de Freitas, F. Ciaravalloti Neto, M. R. A. Cardoso, M. R. D. O. Latorre, P. Hystad, R. Vermeulen and A. C. Nardocci, Incidence and mortality for respiratory cancer and traffic-related air pollution in São Paulo, Brazil, Environ. Res., 2019, 170, 1–9 CrossRef PubMed.
- United Nations Childrens Fund. Pollution: 300 million children breathing toxic air - UNICEF report, accessed November 02, 2021, https://www.unicef.org/press-releases/pollution-300-million-children-breathing-toxic-air-unicef-report Search PubMed.
- A. Carlson and D. Burtraw, Lessons from the Clean Air Act: Building Durability and Adaptability into US Climate and Energy Policy., Cambridge University Press, Cambridge, United Kingdom, 2019 Search PubMed.
- C. J. Matz, M. Egyed, R. Hocking, S. Seenundun, N. Charman and N. Edmonds, Human health effects of traffic-related air pollution (TRAP): a scoping review protocol, Syst. Rev., 2019, 8(223), 1–5 Search PubMed.
- I. Rivas, M. Viana, T. Moreno, M. Pandolfi, F. Amato, C. Reche, L. Bouso, M. Alvarez-Pedrerol, A. Alastuey, J. Sunyer and X. Querol, Child exposure to indoor and outdoor air pollutants in schools in Barcelona, Spain, Environ. Int., 2014, 69, 200–212 CrossRef CAS PubMed.
- BreatheLife, What are the WHO Air Quality Guidelines, accessed October 16th, 2021, https://breathelife2030.org/news/w-h-o-air-quality-guidelines/ Search PubMed.
- Environmental Defence Fund, Breathe London Blueprint, EDF, accessed November 21, 2020, https://www.globalcleanair.org/blueprint/ Search PubMed.
- D. Mumovic, J. M. Crowther and Z. Stevanovic, Integrated air quality modelling for a designated air quality management area in Glasgow, Build. Environ., 2006, 41, 1–10 CrossRef.
- J. S. Apte, K. P. Messier, S. Gani, M. Brauer, T. W. Kirchstetter, M. M. Lunden, J. D. Marshall, C. J. Portier, R. C. H. Vermeulen and S. P. Hamburg, High-Resolution Air Pollution Mapping with Google Street View Cars: Exploiting Big Data, Environ. Sci. Technol., 2017, 51(12), 6999–7008 CrossRef CAS PubMed.
- A. Baron, P. Chazette and J. Totems, Remote sensing of two exceptional winter aerosol pollution events and representativeness of ground-based measurements, Atmos. Chem. Phys., 2020, 20, 1–17 CrossRef.
- T. Soyol-Erdene, G. Ganbat and B. Baldorj, Urban Air Quality Studies in Mongolia: Pollution Characteristics and Future Research Needs, Aerosol Air Qual. Res., 2021, 21, 1–22 CrossRef.
- W. Mohammed, N. Shantz, L. Neil, T. Townend, A. Adamescu and H. A. Al-Abadleh, Air Quality Measurements in Kitchener, Ontario, Canada Using Multisensor Mini Monitoring Stations, Atmosphere, 2022, 13(1), 1–17 CrossRef.
- Air quality monitoring in Kitchener, ON dashboard, accessed January, 2022, https://kitchenergis.maps.arcgis.com/apps/dashboards/fddc1fd0c5e84b459d7c04f5e4db1a7c Search PubMed.
- Environment and Climate Change Canada, Historical Data - Climate - Environment and Climate Change Canada, accessed March, 2022, https://climate.weather.gc.ca/historical_data/search_historic_data_e.html Search PubMed.
- M. E. Hallenbeck, O. I. Selezneva and R. Quinley, Verification, Refinement, and Applicability of Long-Term Pavement Performance Vehicle Classification Rules, accessed April 16, 2022, https://www.fhwa.dot.gov/publications/research/infrastructure/pavements/ltpp/13091/index.cfm Search PubMed.
- L. Brieman, Random Forests, Mach. Learn, 2001, 45, 5–32 CrossRef.
- A. Liaw and M. Wiener, Classification and regression by Random Forest, accessed Feb 22, 2022, https://cogns.northwestern.edu/cbmg/LiawAndWiener2002.pdf Search PubMed.
- K. Guo, X. Wan, L. Liu, Z. Gao and M. Yang, Fault Diagnosis of Intelligent Production Line Based on Digital Twin and Improved Random Forest, J. Appl. Sci., 2021, 11(5), 1–18 Search PubMed.
- I. Ouedraogo, P. Defourny and M. Vanclooster, Application of random forest regression and comparison of its performance to multiple linear regression in modeling groundwater nitrate concentration at the African continent scale, Hydrogeol. J., 2019, 27, 1081–1098 CrossRef CAS.
- P. T. Noi, J. Dengener and M. Kappas, Comparison of multiple linear regression, cubist regression, and random forest algorithms to estimate daily air surface temperature from dynamic combinations of MODIS LST data, Remote Sens., 2017, 9(5), 1–23 Search PubMed.
- G. Biau and E. Scornet, A Random Forest Guided Tour, TEST, 2016, 25, 197–227 CrossRef.
- R. Couronné, P. Probst and A. L. Boulesteix, Random forest versus logistic regression: a large-scale benchmark experiment, BMC Bioinf., 2018, 19, 1–14 CrossRef PubMed.
- D. Bhalla, Splitting Data into Training and Test Sets With R, accessed March 26, 2022, https://www.listendata.com/2015/02/splitting-data-into-training-and-test.html Search PubMed.
- Z. Bobbitt, How to Split Data into Training & Test Sets in R (3 Methods), accessed January 12, 2022, https://www.statology.org/train-test-split-r/ Search PubMed.
- G. James, D. Witten, T. Hastie and R. Tibshirani, An Introduction to Statistical Learning with Applications in R, 2nd edn, 2021 Search PubMed.
- H. A. Al-Abadleh, M. Lysy, L. Neil, P. Patel, W. Mohammed and Y. Khalaf, Rigorous quantification of statistical significance of the COVID-19 lockdown effect on air quality: The case from ground-based measurements in Ontario, Canada, J. Hazard. Mater., 2021, 413, 1–17 CrossRef PubMed.
- H. Ishwaran and U. B. Kogalur. Fast Unified Random Forests for Survival, Regression, and Classification (RF-SRC), R Package Version 3.1.0, 2022 Search PubMed.
- J. Yang, Y. Wen, Y. Wang, S. Zhang, J. P. Pinto, E. A. Pennington, Z. Wang, Y. Wu, S. P. Sander, J. H. Jiang, J. Hao, Y. L. Yung and J. H. Seinfield, From COVID-19 to future electrification: Assessing traffic impacts on air quality by a machine-learning model, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, 1–8 Search PubMed.
- H. Ishwaran and M. Lu, Standard errors and confidence intervals for variable importance in random forest regression, classification, and survival, Stat. Med., 2019, 38, 558–582 CrossRef PubMed.
- B. Duo, L. Chu, Z. Wang, R. Li, L. Zhang, H. Fu, J. Chen, H. Zhang and A. Qiong, Observations of atmospheric pollutants at Lhasa during 2014–2015: Pollution status and the influence of meteorological factors, J. Environ. Sci., 2017, 63, 1–18 Search PubMed.
- C. M. Nussbaumer and R. C. Cohen, The Role of Temperature and NOx in Ozone Trends in the Los Angeles Basin, Environ. Sci. Technol., 2020, 54, 1–8 CrossRef PubMed.
- S. Sillman, Overview: Tropospheric ozone, smog and ozone-NOx-VOC sensitivity, accessed April 06, 2022, http://www-personal.umich.edu/%7Esillman/ozone.htm.
- NO2 – Nitrogen dioxide, accessed March 19, 2022, https://wordpress71133.wordpress.com/no2-nitrogen-dioxide/.
- C. Lou, L. Hongyn, Y. Li and Y. Peng, Relationships of relative humidity with PM2.5 and PM10 in the Yangtze River Delta, China, Environ. Monit. Assess., 2017, 189, 1–16 CrossRef CAS PubMed.
- Ministry of the Environment, Conservation, and Parks (MECP), Air Quality in Ontario 2014, accessed January 04, 2022, https://www.ontario.ca/page/air-quality-ontario-2014-report.
- I. Suryati and H. Khair, Mapping Air Quality Index of Carbon Monoxide (CO) in Medan City, IOP Conf. Ser.: Mater. Sci. Eng., 2017, 180, 1–7 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Detailed experimental procedures, and figures and tables showing data analysis. See DOI: https://doi.org/10.1039/d2ea00084a |
| This journal is © The Royal Society of Chemistry 2022 |