 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Slow magnetic relaxation in Fe(II) m-terphenyl complexes†
Andrew J.
Valentine
 a,
Ana M.
Geer
a,
Ana M.
Geer
 b,
Toby J.
Blundell
c,
Will
Tovey
a,
Matthew J.
Cliffe
b,
Toby J.
Blundell
c,
Will
Tovey
a,
Matthew J.
Cliffe
 a,
E. Stephen
Davies
a,
Stephen P.
Argent
a,
E. Stephen
Davies
a,
Stephen P.
Argent
 a,
William
Lewis
a,
William
Lewis
 d,
Jonathan
McMaster
a,
Laurence J.
Taylor
d,
Jonathan
McMaster
a,
Laurence J.
Taylor
 *a,
Daniel
Reta
*a,
Daniel
Reta
 *e and
Deborah L.
Kays
*e and
Deborah L.
Kays
 *a
*a
aSchool of Chemistry, University Park, University of Nottingham, Nottingham, NG7 2RD, UK. E-mail: laurence.taylor@nottingham.ac.uk; deborah.kays@nottingham.ac.uk
bDepartamento de Química Inorgánica, Instituto de Síntesis Química y Catálisis Homogénea (ISQCH), CSIC Universidad de Zaragoza, Pedro Cerbuna 12, 50009 Zaragoza, Spain
cDepartment of Chemistry, Durham University, South Road, Durham, DH1 3LE, UK
dSchool of Chemistry, The University of Sydney, F11, Eastern Ave, Sydney, NSW 2006, Australia
eKimika Fakultatea, Euskal Herriko Unibertsitatea UPV/EHU & Donostia International Physics Center (DIPC), Euskadi, IKERBASQUE, Basque Foundation for Science, Bilbao, Spain. E-mail: daniel.reta@ehu.eus
First published on 8th November 2022
Abstract
Two-coordinate transition metal complexes are exciting candidates for single-molecule magnets (SMMs) because their highly axial coordination environments lead to sizeable magnetic anisotropy. We report a series of five structurally related two-coordinate Fe(II) m-terphenyl complexes (4-R-2,6-Xyl2C6H2)2Fe [R = tBu (1), SiMe3 (2), H (3), Cl (4), CF3 (5)] where, by changing the functionalisation of the para-substituent (R), we alter their magnetic function. All five complexes are field-induced single-molecule magnets, with relaxation rates that are well-described by a combination of direct and Raman mechanisms. By using more electron donating R groups we were able to slow the rate of magnetic relaxation. Our ab initio calculations predict a large crystal field splitting (>850 cm−1) and sizeable zero-field splitting parameters (ca. −60 cm−1, |E| < 0.2 cm−1) for 1–5. These favourable magnetic properties suggest that m-terphenyl ligands have untapped potential as chemically versatile ligands able to impose highly axial crystal fields.
Introduction
Single-Molecule Magnets (SMMs) are molecules that display slow magnetic relaxation without long-range magnetic ordering.1,2 As such, SMMs have attracted significant interest due to their potential applications in spintronics, quantum computing, and nanotechnology.3,4 SMM behaviour was first observed in the polynuclear cluster [MnIV4MnIII8O12(O2CCH3)16(H2O)4],5 and later the mononuclear [nBu4N][Pc2TbII] (Pc = phthalocyaninato) demonstrated that SMM behaviour could occur in species containing a single lanthanide centre6,7 due to their inherently strong spin–orbit coupling and anisotropy. This facilitated the rational design of mononuclear SMMs, converging upon highly axial dysprosium-based systems.8–11 Building upon this, mixed-valence dilanthanide complexes with strong magnetic exchange have recently shown record coercive fields at liquid nitrogen temperatures.12While the first mononuclear SMMs incorporated lanthanide ions, the 3d metals have also received significant attention.13 The challenge for mononuclear 3d SMMs is that the crystal fields exerted on the metal centre by the ligands tend to quench the orbital angular momentum. This can be avoided through careful ligand design, and there have been a number of reports of Fe(I),14,15 Fe(II),16–27 Co(II),28–34 Ni(II),35 and Mn(III)36 complexes that display slow magnetic relaxation. Among these, two-coordinate metal centres in linear or near-linear geometries, most notably [Co{C(SiMe2O-1-naphthyl)3}2],34 have shown the best performance in terms of magnetic blocking temperature and open hysteresis15,24,28,34 as their large magnetic anisotropy inhibits quenching of the orbital angular momentum. Thus, to realise the potential of 3d SMMs, one promising pathway is to explore ligands which impose strong axial fields and are sufficiently bulky to achieve linear coordination.
To that end, m-terphenyl ligands stand out as potential candidates. These are a class of bulky, monoanionic ligands that have proven useful in the stabilisation of highly reactive or unusual d-block and main group species.37–39 Several two-coordinate 3d species have been reported,40–46 and have found applications in catalysis44–47 and small molecule activation41,43,48 due to the high reactivity of the coordinatively unsaturated metal centre. In addition, the para-substituent on the central aryl ring can be functionalised, making them amenable to tuning of their electronic properties.49–52
Whilst the related m-terphenoxide ligands have been investigated for Dy(III) SMMs,53m-terphenyl carbanions have not been studied for SMM synthesis, despite imposing a near-linear coordination environment. Here, we report the synthesis and characterisation of five m-terphenyl Fe(II) complexes (1–5), four of which are novel, that all display field induced SMM behaviour. We show that, while 1–5 display similar molecular geometries in the solid state, their relaxation profiles are strongly influenced by the nature of the para-substituent R.
Results and discussion
Synthesis and structural characterisation
Reaction of the organolithium complexes [4-R-2,6-Xyl2C6H2Li]2 (R = tBu, SiMe3, H, Cl, CF3)51 in solution with FeCl2·(thf)1.5 resulted in the formation of the corresponding Fe(II) m-terphenyl complexes (4-R-2,6-Xyl2C6H2)2Fe [R = tBu (1), SiMe3 (2), H (3), Cl (4), CF3 (5); Scheme 1]. Note that these complexes are numbered in order of the electron donating/withdrawing power of the R group (as quantified by their Hammet constant, σpara)54 with 1 (tBu) being the most electron donating, and 5 (CF3) the most electron withdrawing. For 1–4, the reaction was carried out in a mixture of toluene and THF (ca. 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). For complex 5 (R = CF3), carrying the reaction out in diethyl ether gave significantly better yields (57% vs. 36%). The complexes were purified by recrystallisation from hexane (1, 2, 5) or toluene (3, 4) in moderate to good yields (42–58%). Complexes 1–5 are highly air- and moisture-sensitive, but stable over long periods (>1 year) at room temperature under inert atmosphere. Complex 5 is noted to be particularly sensitive, with crystalline samples undergoing rapid surface decomposition (from yellow to orange/dark brown) upon exposure to trace amounts of air.
1). For complex 5 (R = CF3), carrying the reaction out in diethyl ether gave significantly better yields (57% vs. 36%). The complexes were purified by recrystallisation from hexane (1, 2, 5) or toluene (3, 4) in moderate to good yields (42–58%). Complexes 1–5 are highly air- and moisture-sensitive, but stable over long periods (>1 year) at room temperature under inert atmosphere. Complex 5 is noted to be particularly sensitive, with crystalline samples undergoing rapid surface decomposition (from yellow to orange/dark brown) upon exposure to trace amounts of air.
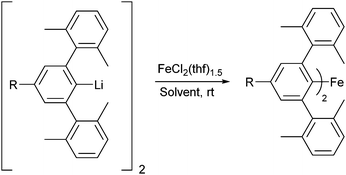 | ||
Scheme 1 Synthesis of diaryl complexes (4-R-2,6-Xyl2C6H2)2Fe 1–5 [R = tBu (1), SiMe3 (2), H (3), Cl (4), CF3 (5)]. Solvent = toluene/THF (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) for 1–4; diethyl ether for 5. 1) for 1–4; diethyl ether for 5. | ||
Complex 3 (R = H) has been reported previously, and its characterisation matched that of the literature.48 The novel complexes 1, 2, 4 and 5 have been characterised by X-ray crystallography, mass spectrometry, elemental analysis; and IR, UV/Vis, and 1H NMR spectroscopy. These complexes crystallise as yellow-green or yellow solids, dissolving to give bright yellow solutions with broad UV/Vis absorptions (λmaxca. 370 nm; ε = 830–1550 dm3 mol−1 cm−1; Fig. S9†).
The crystal structures for 1–5 determined by X-ray diffraction (Fig. 1, Fig. S10–S13†) show the iron is two-coordinate and the complexes are all monomeric in the solid state, with bent C–Fe–C bond angles over a range of 167.71(9)–174.9(2)° and a narrow range of Fe–C bond lengths [2.019(4)–2.041(4) Å] (Table 1). All structures feature large Fe⋯Fe separations of >9 Å and, despite displaying similar molecular geometries, they crystallise in different space groups (Table S2†) with different numbers of symmetry independent molecules in the unit cell (Z′ = 1 for 1, 3, 5; 1.5 for 2; 3 for 4). Additionally, the crystal structure of 5 contains 0.5 co-crystallised iso-hexane molecules per formula unit (ESI, section S4.1†), which is also observed in the 1H NMR spectrum of 5 (Fig. S6†).
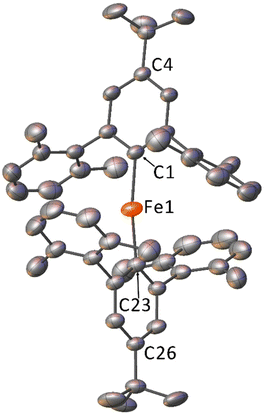 | ||
| Fig. 1 Crystal structure of 1 with displacement ellipsoids set to 30%. Hydrogen atoms and minor disorder components omitted for clarity. | ||
| Compound | Fe1–C1 | Fe1–C23 | C1–Fe1–C23 | Fe1–C1⋯C4 | Fe1–C23⋯C26 |
|---|---|---|---|---|---|
| 1 | 2.034(4) | 2.022(4) | 170.0(1) | 174.6(2) | 167.8(2) |
| 21 | 2.026(4) | 2.018(4) | 172.2(2) | 169.4(2) | 170.4(2) |
| 22 | 2.019(4) | 2.019(4) | 174.9(2) | 170.7(2) | 170.7(2) |
| 3 | 2.027(2) | 2.029(2) | 167.71(9) | 167.4(1) | 174.9(1) |
| 41 | 2.031(2) | 2.030(2) | 170.50(8) | 169.0(1) | 171.5(1) |
| 42 | 2.023(2) | 2.034(2) | 170.74(8) | 175.7(1) | 165.1(1) |
| 43 | 2.041(2) | 2.033(2) | 168.30(8) | 165.7(1) | 170.99(9) |
| 5 | 2.039(1) | 2.034(1) | 170.04(5) | 168.77(7) | 172.99(7) |
Notably, the structures with Z′ > 1 (2 and 4) show relatively broad variation in C–Fe–C bond angles and C–Fe bond lengths (Table 1). This suggests that changing the electronic character of the R group has little effect on the solid-state structures, with the variations in bond length and angle likely dominated by crystal packing effects. This is in line with our previous work on these ligands with lithium and Group 12 metal ions.51,52 The bond lengths and angles about the Fe centres are similar to those observed for the related m-terphenyl carbanion complex, (2,6-Mes2C6H3)2Fe.40 However, the C–Fe–C bond angles are less acute than those seen in the more sterically demanding m-terphenyl carbanion complex, (2,6-Dipp2C6H3)2Fe [C–Fe–C = 159.34(6) Å].41 These non-linear structures can be contrasted with the field-induced SMMs Fe[N(H)Ar]2 [Ar = C6H3-2,6-(C6H3-2,6-iPr2)2; C6H3-2,6-(C6H2-2,4,6-iPr2)2], which also feature m-terphenyl moieties in their amide ligands, but which display a linear coordination environment around iron.24
The 1H NMR spectroscopic signals of these complexes are broad and occur over a wide range of chemical shifts (+181.6 to −59.5 ppm) owing to their paramagnetism (Fig. S3–S6†). Despite this, it is possible to assign protons based on integration of the signals. For 1–5, a linear correlation is observed between σpara54 of the R group and some of the 1H NMR signals; with the C6H2m-H signals shifting upfield and the methyl signals for the xylyl substituents shifting downfield with increasing σpara (Table S1, Fig. S1†). Both trends bring the signals closer to 0 ppm (i.e. reduce the magnitude of the pseudocontact shift) as the R group becomes more electron withdrawing (Fig. S2†). These data suggest that the degree of spin delocalisation onto the ligand can be controlled by varying the electronics of R.55 It should be noted, however, that no correlation is observed between σpara and the computed zero-field splitting (ZFS) parameters of 1–5 (see below).
Electrochemistry
Cyclic voltammetry (CV) studies on THF solutions of 1–5 revealed that all complexes undergo a reduction at negative potentials (Fig. 2). Previous CV studies on related Group 12 m-terphenyl complexes [(4-R-2,6-Xyl2C6H3)2Hg, R = tBu, CF3] indicated that these ligands are not redox active in this potential range,52 so it is likely that the process corresponds to a Fe(II) to Fe(I) reduction. Cyclic voltammograms recorded at 100 mV s−1 show a redox couple for complexes 2 and 4, with properties characteristic of a diffusion controlled process,56 but little to no return wave for 1, 3, and 5 (Fig. 2, Fig. S15–S19, Table S3†). At higher scan rates (>200 mV s−1), more pronounced return waves for 1, 3, and 5 are observed, suggesting that the reduced complexes are prone to decomposition. A linear relationship between the cathodic peak current (Ip,c) and the square-root of the scan rate (ν1/2) is observed for 1–5 (Fig. S20†), which suggests the reduction is diffusion controlled for all complexes.56 It is unclear why certain R groups better stabilise the reduced species since there is no obvious correlation with the steric bulk or electron withdrawing capability of the substituent. However, the cathodic peak potentials (Ep,c) of 1–5 do correlate with σpara54 (Fig. S14†) such that more electron donating groups shift Ep,c to more negative voltages, indicative of a linear free energy relationship across the series.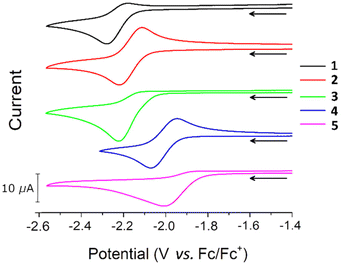 | ||
| Fig. 2 Cyclic voltammograms for 1–5. All voltammograms recorded in 0.5 M [nBu4N][BF4] solution in THF at ν = 100 mV s−1. | ||
Electronic structure calculations
The electronic structures of 1–5 were studied with complete active space self-consistent field spin–orbit (CASSCF-SO) calculations using OpenMolcas57 on the geometries determined by X-ray crystallography (see ESI, section S6.1† for details). The first four electronic states are grouped as two pseudo-doublets, with an energy separation that ranges between 159 and 173 cm−1 (Table S5†). These are well-isolated from the fifth electronic state, which is consistently predicted at ca. 250 cm−1. Assuming a ground multiplet with an effective S = 2 spin, the anisotropy of the complexes can be modelled as a second-order effect via a ZFS Hamiltonian according to eqn (1):58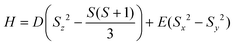 | (1) |
Static magnetic characterisation
Magnetisation curves at 2, 3, 5 and 10 K up to 40 kOe (Fig. S24†), together with variable temperature magnetic susceptibility data under a 1000 Oe applied field (Fig. 3), were collected on ground, polycrystalline samples of 1–5. Complexes 1–5 show χmT values at 300 K (Table 2) far in excess of the predicted spin-only values for Fe(II) (3.00 cm3 K mol−1 for S = 2, g = 2.00). While 1 and 5 give the lowest and highest values for χmT at 300 K respectively (4.07 and 5.03 cm3 K mol−1), there is not a clear correlation between χmT and σpara (R2 = 0.370, Fig. S21†). The χmT data for the 1–5 bear strong similarities to a previously reported series of linear and near-linear 2-coordinate Fe(II) complexes,24 particularly the presence of a maximum in χmT at ca. 75 K (Fig. 3). This maximum indicates that the orbital angular momentum is unquenched due to the axiality of the systems (Table 1). This agrees with previous studies in which only markedly non-linear two-coordinate Fe(II) complexes failed to display this maximum, i.e. the bent Fe[N(H)Dmp]2 (Dmp = 2,6 Mes2C6H3; N–Fe–N = 140.9(2)°).24 For 1–5, starting at 300 K, the increase of χmT on cooling suggests depopulation of states with a lower magnetic moment due to anisotropy,24,60 followed by a decrease in χmT at the lowest temperatures.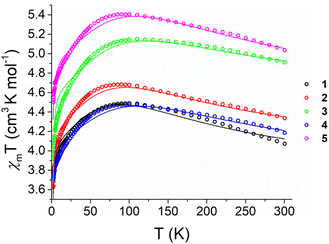 | ||
| Fig. 3 Temperature dependence of χmT values for powdered polycrystalline samples of 1–5 measured under a 1000 Oe field between 1.8 and 300 K (circles) with calculated fittings (fit1) according to eqn (2) (lines). | ||
| Sample | χ m T (cm3 K mol−1) | M sat (μB) |
|---|---|---|
| 1 | 4.07 | 2.7 |
| 2 | 4.34 | 2.8 |
| 3 | 4.91 | 2.9 |
| 4 | 4.19 | 2.6 |
| 5·(C6H14)0.5 | 5.03 | 3.3 |
Assuming a ground multiplet with an effective S = 2 spin, the anisotropy of the complexes can be described as a second-order effect. As such, the magnetic data can be modelled through a combination of a crystal field and a Zeeman Hamiltonian (eqn (2)),58 as implemented in PHI:61
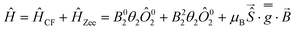 | (2) |
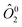 the operator equivalent, and
the operator equivalent, and 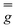 the g-tensor. Within this formalism, D = 3B02θ2 and E = B02θ2 describe the axial and rhombic terms of a zero-field splitting Hamiltonian, respectively.
the g-tensor. Within this formalism, D = 3B02θ2 and E = B02θ2 describe the axial and rhombic terms of a zero-field splitting Hamiltonian, respectively.
Initially, a global fitting of both the susceptibility and magnetisation was attempted for 1–5.62 To avoid over-parameterisation, the CASSCF-SO values were used as a starting point, with gx = gy ≠ gz and B22 fixed to the CASSCF-SO value (see above and Table S6†). However, the obtained fit was biased towards the magnetisation curves, which drastically worsened the model's agreement with the susceptibility traces. This is tentatively assigned to the way residuals are calculated in a global fitting. Further data analysis revealed that both the high temperature susceptibility and magnetisation curves tend towards an anisotropic model, whereas low temperature susceptibility suggested otherwise. To overcome this apparent inconsistency, χmT was first fit using D and gx = gy ≠ gz as parameters, biasing toward the high temperature susceptibility data with PHI's “Residual” keyword. Next, both the χmT and M vs. H data were fit, fixing the previously optimised parameters, and allowing E to vary as well as a introducing a mean-field parameter (zJ) to model intermolecular interactions. This was needed to reproduce the drop in χmT at low temperatures. The values obtained from this fit are labelled as fit1 (Table 3, Fig. 3). Finally, a global fitting without any constraints was performed, labelled fit2 (Table S10†). Both approaches predict small antiferromagnetic interactions for all complexes, compatible with the reported intermolecular interactions. A comparison between experimental and fitted values with both models is presented in Fig. S24 and S25,† highlighting that a sizeable change in parameters between fit1 and fit2 leads to a very modest improvement in M vs. H but no significant improvement in χmT. Based on this, and because the values obtained from fit1 are much closer to the CASSCF-SO values than fit2 (Table S6†), we conclude that the much more anisotropic values of fit1 are the most representative. Still, it is worth mentioning that the so-obtained E values are at least one order of magnitude larger than the CASSCF-SO ones, significantly reducing the E/D ratio, and one obtains the same fitting regardless of its sign. Fitting with gx ≠ gy or including magnetic impurities does not improve the fittings.
| Compound | g x = gy | g z | D (cm−1) | E (cm−1) | zJ (cm−1) |
|---|---|---|---|---|---|
| 1 | 1.80 | 2.87 | −59.14 | 2.94 | −1.6 × 10−2 |
| 2 | 1.90 | 2.91 | −59.91 | −6.13 | −7.3 × 10−3 |
| 3 | 2.08 | 3.03 | −68.54 | 7.19 | −2.1 × 10−3 |
| 4 | 1.82 | 2.86 | −73.07 | 2.69 | −1.7 × 10−2 |
| 5 | 1.98 | 3.15 | −72.39 | 4.69 | −9.9 × 10−3 |
It should be noted that while the simulated (fit1) M vs. H curves match the experimental data well for 2, 3, and 5; the agreement is less good for 1 and 4 (Fig. S24†). The reason for this is unclear, but could arise from small errors in the mass (a ca. 7% error in the mass of 1 would give good agreement between the simulated and experimental curves) or from structural variations, as indicated by the large α values from the generalised Debye model.63 Nevertheless, the experimental profile of the M vs. H curves is reproduced for all simulations, and the shape of the χmT plots is well captured.
Plots of M vs. H/T for 1–5, recorded at 10, 20, 30, and 40 kOe over a temperature range of 1.8–5.0 K, show similar behaviour to other reported 2-coordinate 3d complexes24,28,34 with data that are non-superimposable on a single Brillouin curve (Fig. S26–S30†). This provides further evidence of strong magnetic anisotropy in 1–5.24,64Msat values for 1–5 of 2.6–3.3μB (Table 2) are far lower than the spin-only 4.0μB expected for a S = 2 centre, however, these values are comparable to those obtained for other linear Fe(II) complexes.24
Dynamic magnetic characterisation
AC magnetic susceptibility measurements were performed on 1–5 to investigate their low temperature magnetic relaxation. For all AC susceptibility measurements, magnetic relaxation times (τ) were determined by a global fitting of the in phase (χ′) and out-of-phase susceptibilities (χ′′) vs. frequency using a generalised Debye model65 as implemented in the CC-FIT2 software package.63For 1–5, no out-of-phase susceptibility signal (χ′′) was detected at zero-field over the frequency range 1–1400 Hz. This is likely due to rapid quantum tunnelling of magnetisation (QTM), which is commonly observed in mononuclear Fe(II) species.20–24,26,27 However, 1–5 exhibit slow magnetic relaxation under an applied DC field. To determine the dependence of τ on field strength, AC susceptibility measurements were performed on 1–5 at 2 K (1–1400 Hz switching frequency) over a range of applied DC fields (H = 100–5000 Oe). For 1–5, τ initially increases with increasing applied field as QTM is reduced, reaches a maximum at a certain field strength (Hmax), and then decreases (Fig. S36 and S37†) following the onset of a direct process. This behaviour is similar to that observed for previously reported Fe(II) field induced SMMs.20–24,26,27 Estimates of Hmax for 1–5 are provided in Table 4, and fall in the range 1000–2000 Oe. At 2 K and an applied field of 1500 Oe, τ is observed to increase in the order 5 < 4 < 2 < 3 ≪ 1. This trend approximately parallels the electron donating/withdrawing power of the R group on the m-terphenyl ligand, with the electron-donating tBu (1) showing by far the longest relaxation time (Fig. S36†), and the electron-withdrawing CF3 (5) the shortest (Fig. S37†). It should be noted that τ values were not determined for 1 at H = 100–500 Oe or 3 at H = 100–200 Oe as the χ′ vs. χ′′ data could not be well fit to the generalised Debye model.
| Compound | H max (Oe) | log10[C/(s−1 K−n)] | n | log10[A/(s−1 Oe−1 K−1)] |
|---|---|---|---|---|
| 1 | 1000 | −1.12(2) | 4.98(2) | 0.839(6) |
| 2 | 1750 | −0.58(7) | 5.19(9) | 2.062(9) |
| 3 | 1000 | −0.73(2) | 4.74(2) | 1.712(4) |
| 4 | 2000 | −0.1(1) | 4.6(1) | 2.22(1) |
| 5 | 2000 | −1(1) | 5(1) | 2.82(2) |
Subsequently, AC susceptibility measurements were performed for 1–5 at a fixed DC field (Hmax, Table 4) over a range of temperatures (1.8–16.0 K) and frequencies (1–1400 Hz) to determine the temperature dependence of τ. Fig. 4a shows the out-of-phase susceptibility (χ′′) of 1 as a function of frequency, while plots of χ′′ as a function of frequency (Fig. S38–S42†), temperature (Fig. S43–S47†) and Cole–Cole plots (Fig. S48–S52†) for 1–5 are provided in the ESI. 1–5 all show a maximum in χ′′ which shifts to higher frequencies with increasing temperature. These data were fit to the general Debye model (Tables S11–S15†) and log10–log10 plots of τ−1vs. T, henceforth referred to as relaxation profiles, were constructed. The relaxation profiles for 1–5 are presented in Fig. 4b. Note that for 2, 4, and 5 relaxation rates are not given below 2.4 K; this is because the Cole–Cole plots for these complexes (Fig. S49, S51 and S52†) could not be well fit to the general Debye model due to the presence of a low frequency process. There were insufficient low frequency data points to satisfactorily model these according to a 2-process equation.
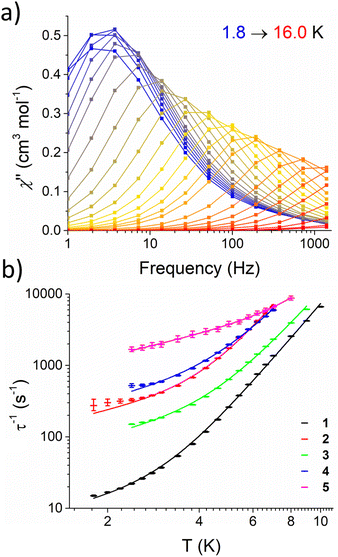 | ||
| Fig. 4 (a) Frequency dependence of χ′′ for 1 over the temperature range 1.8–16.0 K, recorded on a MPMS magnetometer at 1000 Oe applied field. Lines are intended as guides for eyes. (b) Relaxation profile for 1–5 under an applied field (Hmax, Table 4) with fittings (solid lines) according to eqn (3). Error bars represent error in the fitting of τ from Cole–Cole plots. | ||
Given that the data has been collected in field, the relaxation profiles for 1–5 were fit by considering a combination of Raman and direct terms, according to eqn (3).63
| τ−1 = 10RTn + 10AT | (3) |
Nevertheless, the optimised parameters for a given compound are virtually identical with and without considering ESDs (see Fig. S53–S62, Table S7†). The relaxation parameters (C, n, A) for 1–5 are presented in Table 4. The parameters associated to the Raman process are in agreement with those found for other Fe(II) complexes26 and, importantly, the characteristic n term is consistently close to 5. The data was also fitted considering an Orbach process, but this model was discarded as it led to effective barriers one order of magnitude smaller than the CASSCF predicted first excited state (see above). While this model affords a satisfactory fit of the data, recent studies have shown that spin–phonon coupling mediated by low energy phonons can be important for rationalising under-barrier relaxation processes in SMMs.68–70 We thus considered two different models which account for spin–lattice relaxation published by Wu (eqn (S1)†),69 and Lunghi (eqn (S2)†).68 In both cases, a reasonable fit of the data for complex 1 (Wu and Lunghi models, Fig. S63 and S65†) and 2 (Wu model only, Fig. S64†) could only be obtained through the use of physically unreasonable parameters, with spin phonon couplings several orders of magnitude larger than the expected values of 0.1–1.0 cm−1 (Tables S17 and S18†). We thus concluded that eqn (3) is the most appropriate model for the relaxation rates of 1–5.
Fig. 4b shows that magnetic relaxation rates increase in order 1 < 3 < 2 < 4 < 5 over the direct-dominated temperature range (1.8–5.0 K), and that 1 and 5 remain the slowest and fastest relaxing across the whole temperature range, respectively. This is likely because the direct mechanism dominates at T < 5 K; with 5, 4, and 2 being measured under the largest external fields. Nonetheless, for molecules measured under the same external field (Table 4), more electron withdrawing groups lead to faster relaxation rates: i.e.5 relaxes ca. 2× faster than 4 and 3 relaxes ca. 10× faster than 1. At higher temperatures (T > 6.0 K) the relaxation profiles begin to converge and the difference in their relaxation rates becomes less pronounced. This indicates that, despite a change in the phonon density of states associated with the different R groups, the Raman mechanism remains largely unaffected in the studied temperature range. This is somewhat surprising, as 1–5 crystallise in different structure types with different space groups, and one might expect to observe different low-energy phonon modes, changing the efficacy of the Raman mechanism.
Hysteresis measurements were also performed on 1–5 at 1.8 K and a sweep rate of 67 Oe s−1. Under these conditions, slight open hysteresis was observed for complexes 1 and 3 (Fig. S31 and S33†), but not for 2, 4, or 5 (Fig. S32, S34, and S35†). This is in line with the AC susceptibility data, which shows that 1 and 3 have the slowest rates of magnetic relaxation.
Conclusions
The reaction of the m-terphenyl lithium salts [4-R-2,6-Xyl2C6H2Li]2 (R = tBu, SiMe3, H, Cl, CF3) and FeCl2·(thf)1.5 affords Fe(II) complexes 1–5 as yellow-green crystalline solids. Single crystal X-ray diffraction demonstrates that 1–5 all feature two-coordinate Fe(II) ions in near-linear geometries. DC magnetometry measurements on 1–5 show maxima in the χmT plots at ca. 75 K, χmT values which exceed the spin-only value, and discontinuity in plots of M vs. H/T at low temperatures, indicating substantial orbital angular momentum contributions leading to large magnetic anisotropy. These observations are corroborated by the highly axial values obtained from fitting the magnetic data to the ZFS Hamiltonian. Ab initio calculations on the crystal structures afford computed ZFS Hamiltonian parameters which are also indicative of a highly axial ligand field. Complexes 1–5 all display field-induced SMM behaviour, with the rate of relaxation dependent upon the identity of the R group. The relaxation profiles were fit to a combination of direct and Raman relaxation processes and show that the most electron donating group (1) relaxes considerably slower than the most electron withdrawing counterpart (5) across the whole investigated temperature range.While 1–5 exhibit modest SMM properties, this work demonstrates that the m-terphenyls are a tuneable and versatile class of ligand capable of inducing highly axial ligand fields upon a metal centre. These ligands have not been explored in this context, and this study opens exciting opportunities to apply them to other metal ions and thus establish magneto-structural correlations for the development of SMMs with improved relaxation behaviour.
Author contributions
AJV developed the synthesis and characterisation for 1, 2, 4, and 5, which was continued by LJT and WT. AMG and TJB performed synthesis and initial magnetic measurements on complex 3. MJC helped to perform MPMS measurements and assisted with data analysis and interpretation. ESD performed CV measurements on 1–5. SPA and WL helped with the solution and refinement of single-crystal X-ray diffraction data for 1–5. JM provided guidance and support to AJV and LJT throughout the project. LJT performed the MPMS measurements on 1–5 presented in this manuscript, analysed the magnetic data, prepared the initial draft of the manuscript, and coordinated with other authors. DR performed CASSCF calculations and fittings of the magnetic data and wrote these sections for the manuscript. He also helped interpret the magnetic data and with the development of the manuscript. DLK was the PI for this research, conceived of the project, helped with writing, and provided input throughout.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We acknowledge the EPSRC [grant number EP/R004064/1]; the Leverhulme Trust [grant numbers RPG-2014-317; RF-2021-102]; and the University of Nottingham [Hobday Bequest] for financial support of this research. We would also like to thank the National Mass Spectrometry Facility at Swansea University for mass spectrometry measurements and the Microanalysis Service at London Metropolitan University for elemental microanalysis measurements. We thank Dr María Giménez López (University of Santiago de Compostela) for preliminary discussions, and Prof. Mark Murrie and Dr Emma Regincós Martí (University of Glasgow) for helpful discussions about AC susceptibility data.References
- D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, Oxford University Press, 2006 Search PubMed.
- M. J. Giansiracusa, G. K. Gransbury, N. F. Chilton and D. P. Mills, in Encyclopedia of Inorganic and Bioinorganic Chemistry, John Wiley & Sons, Ltd., 2021, p. eibc2784 Search PubMed.
- M. Shiddiq, D. Komijani, Y. Duan, A. Gaita-Ariño, E. Coronado and S. Hill, Nature, 2016, 531, 348–351 CrossRef CAS.
- R. Vincent, S. Klyatskaya, M. Ruben, W. Wernsdorfer and F. Balestro, Nature, 2012, 488, 357–360 CrossRef CAS PubMed.
- R. Sessoli, H. Tsai, A. R. Schake, S. Wang, J. B. Vincent, K. Folting, D. Gatteschi, G. Christou and D. N. Hendrickson, J. Am. Chem. Soc., 1993, 115, 1804–1816 CrossRef CAS.
- N. Ishikawa, M. Sugita, T. Ishikawa, S. Y. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694–8695 CrossRef CAS PubMed.
- N. Ishikawa, M. Sugita, T. Okubo, N. Tanaka, T. Iino and Y. Kaizu, Inorg. Chem., 2003, 42, 2440–2446 CrossRef CAS.
- C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439–442 CrossRef CAS PubMed.
- K. R. McClain, C. A. Gould, K. Chakarawet, S. J. Teat, T. J. Groshens, J. R. Long and B. G. Harvey, Chem. Sci., 2018, 9, 8492–8503 RSC.
- F. S. Guo, B. M. Day, Y. C. Chen, M. L. Tong, A. Mansikkamäki and R. A. Layfield, Science, 2018, 362, 1400–1403 CrossRef CAS.
- V. S. Parmar, D. P. Mills and R. E. P. Winpenny, Chem. – Eur. J., 2021, 27, 7625–7645 CrossRef CAS PubMed.
- C. A. Gould, K. R. McClain, D. Reta, J. G. C. Kragskow, D. A. Marchiori, E. Lachman, E. S. Choi, J. G. Analytis, R. D. Britt, N. F. Chilton, B. G. Harvey and J. R. Long, Science, 2022, 375, 198–202 CrossRef CAS.
- G. A. Craig and M. Murrie, Chem. Soc. Rev., 2015, 44, 2135–2147 RSC.
- P. P. Samuel, K. C. Mondal, N. Amin Sk, H. W. Roesky, E. Carl, R. Neufeld, D. Stalke, S. Demeshko, F. Meyer, L. Ungur, L. F. Chibotaru, J. Christian, V. Ramachandran, J. Van Tol and N. S. Dalal, J. Am. Chem. Soc., 2014, 136, 11964–11971 CrossRef CAS.
- J. M. Zadrozny, D. J. Xiao, M. Atanasov, G. J. Long, F. Grandjean, F. Neese and J. R. Long, Nat. Chem., 2013, 5, 577–581 CrossRef CAS.
- W. M. Reiff, A. M. LaPointe and E. H. Witten, J. Am. Chem. Soc., 2004, 126, 10206–10207 CrossRef CAS PubMed.
- W. M. Reiff, C. E. Schulz, M. H. Whangbo, J. I. Seo, Y. S. Lee, G. R. Potratz, C. W. Spicer and G. S. Girolami, J. Am. Chem. Soc., 2009, 131, 404–405 CrossRef CAS.
- P. Wang, M. R. Saber, P. E. Vannatta, G. P. A. Yap, C. V. Popescu, C. C. Scarborough, M. T. Kieber-Emmons, K. R. Dunbar and C. G. Riordan, Inorg. Chem., 2021, 60, 6480–6491 CrossRef CAS PubMed.
- Y. Li, J. Xi, J. Ferrando-Soria, Y. Q. Zhang, W. Wang, Y. Song, Y. Guo, E. Pardo and X. Liu, Dalton Trans., 2022, 51, 8266–8272 RSC.
- D. E. Freedman, W. H. Harman, T. D. Harris, G. J. Long, C. J. Chang and J. R. Long, J. Am. Chem. Soc., 2010, 132, 1224–1225 CrossRef CAS PubMed.
- D. Weismann, Y. Sun, Y. Lan, G. Wolmershäuser, A. K. Powell and H. Sitzmann, Chem. – Eur. J., 2011, 17, 4700–4704 CrossRef CAS PubMed.
- X. Feng, C. Mathonière, I. R. Jeon, M. Rouzières, A. Ozarowski, M. L. Aubrey, M. I. Gonzalez, R. Clérac and J. R. Long, J. Am. Chem. Soc., 2013, 135, 15880–15884 CrossRef CAS PubMed.
- C. Mathonière, H. J. Lin, D. Siretanu, R. Clérac and J. M. Smith, J. Am. Chem. Soc., 2013, 135, 19083–19086 CrossRef.
- J. M. Zadrozny, M. Atanasov, A. M. Bryan, C. Y. Lin, B. D. Rekken, P. P. Power, F. Neese and J. R. Long, Chem. Sci., 2013, 4, 125–138 RSC.
- M. Atanasov, J. M. Zadrozny, J. R. Long and F. Neese, Chem. Sci., 2013, 4, 139–156 RSC.
- T. Bodenstein and A. Eichhöfer, Dalton Trans., 2019, 48, 15699–15712 RSC.
- Q. Q. Su, Q. Yuan, X. F. Wu, S. H. Chen, J. Xiang, X. X. Jin, L. X. Wang, B. W. Wang, S. Gao and T. C. Lau, Chem. Commun., 2021, 57, 781–784 RSC.
- X. N. Yao, J. Z. Du, Y. Q. Zhang, X. B. Leng, M. W. Yang, S. Da Jiang, Z. X. Wang, Z. W. Ouyang, L. Deng, B. W. Wang and S. Gao, J. Am. Chem. Soc., 2017, 139, 373–380 CrossRef CAS.
- T. Jurca, A. Farghal, P. H. Lin, I. Korobkov, M. Murugesu and D. S. Richeson, J. Am. Chem. Soc., 2011, 133, 15814–15817 CrossRef CAS.
- V. V. Novikov, A. A. Pavlov, Y. V. Nelyubina, M. E. Boulon, O. A. Varzatskii, Y. Z. Voloshin and R. E. P. Winpenny, J. Am. Chem. Soc., 2015, 137, 9792–9795 CrossRef CAS PubMed.
- S. Gómez-Coca, A. Urtizberea, E. Cremades, P. J. Alonso, A. Camón, E. Ruiz and F. Luis, Nat. Commun., 2014, 5, 1–8 Search PubMed.
- F. Habib, O. R. Luca, V. Vieru, M. Shiddiq, I. Korobkov, S. I. Gorelsky, M. K. Takase, L. F. Chibotaru, S. Hill, R. H. Crabtree and M. Murugesu, Angew. Chem., Int. Ed., 2013, 52, 11290–11293 CrossRef CAS.
- S. Gomez-Coca, E. Cremades, N. Aliaga-Alcalde and E. Ruiz, J. Am. Chem. Soc., 2013, 135, 7010–7018 CrossRef CAS PubMed.
- P. C. Bunting, M. Atanasov, E. Damgaard-Møller, M. Perfetti, I. Crassee, M. Orlita, J. Overgaard, J. Van Slageren, F. Neese and J. R. Long, Science, 2018, 362, 1378 CrossRef.
- R. Ruamps, R. Maurice, L. Batchelor, M. Boggio-Pasqua, R. Guillot, A. L. Barra, J. Liu, E. E. Bendeif, S. Pillet, S. Hill, T. Mallah and N. Guihéry, J. Am. Chem. Soc., 2013, 135, 3017–3026 CrossRef CAS PubMed.
- J. Vallejo, A. Pascual-Álvarez, J. Cano, I. Castro, M. Julve, F. Lloret, J. Krzystek, G. De Munno, D. Armentano, W. Wernsdorfer, R. Ruiz-García and E. Pardo, Angew. Chem., Int. Ed., 2013, 52, 14075–14079 CrossRef CAS.
- B. Twamley, S. T. Haubrich and P. P. Power, in Advances in Organometallic Chemistry, ed. R. West and A. F. Hill, Academic Press, 1999, vol. 44, pp. 1–65 Search PubMed.
- J. A. C. Clyburne and N. McMullen, Coord. Chem. Rev., 2000, 210, 73–99 CrossRef CAS.
- D. L. Kays, in Organometallic Chemistry, ed. I. J. S. Fairlamb and J. S. Lynam, Royal Society of Chemistry, Cambridge, 2010, vol. 36, pp. 56–76 Search PubMed.
- D. L. Kays and A. R. Cowley, Chem. Commun., 2007, 1053–1055 RSC.
- C. Ni and P. P. Power, Chem. Commun., 2009, 5543–5545 RSC.
- C. Ni, T. A. Stich, G. J. Long and P. P. Power, Chem. Commun., 2010, 46, 4466–4468 RSC.
- C. Ni, H. Lei and P. P. Power, Organometallics, 2010, 29, 1988–1991 CrossRef CAS.
- H. R. Sharpe, A. M. Geer, T. J. Blundell, F. R. Hastings, M. W. Fay, G. A. Rance, W. Lewis, A. J. Blake and D. L. Kays, Catal. Sci. Technol., 2018, 8, 229–235 RSC.
- H. R. Sharpe, A. M. Geer, W. Lewis, A. J. Blake and D. L. Kays, Angew. Chem., Int. Ed., 2017, 56, 4845–4848 CrossRef CAS PubMed.
- A. J. South, A. M. Geer, L. J. Taylor, H. R. Sharpe, W. Lewis, A. J. Blake and D. L. Kays, Organometallics, 2019, 38, 4115–4120 CrossRef CAS.
- H. R. Sharpe, A. M. Geer, H. E. L. Williams, T. J. Blundell, W. Lewis, A. J. Blake and D. L. Kays, Chem. Commun., 2017, 53, 937–940 RSC.
- H. R. Sharpe, A. M. Geer, L. J. Taylor, B. M. Gridley, T. J. Blundell, A. J. Blake, E. S. Davies, W. Lewis, J. McMaster, D. Robinson and D. L. Kays, Nat. Commun., 2018, 9, 3757 CrossRef.
- R. Wolf, C. Ni, T. Nguyen, M. Brynda, G. J. Long, A. D. Sutton, R. C. Fischer, J. C. Fettinger, M. Hellman, L. Pu and P. P. Power, Inorg. Chem., 2007, 46, 11277–11290 CrossRef CAS.
- Y. Peng, R. C. Fischer, W. A. Merrill, J. Fischer, L. Pu, B. D. Ellis, J. C. Fettinger, R. H. Herber and P. P. Power, Chem. Sci., 2010, 1, 461–468 RSC.
- A. J. Valentine, A. M. Geer, L. J. Taylor, A. M. Teale, K. E. Wood, H. E. L. Williams, W. Lewis, S. P. Argent, J. McMaster and D. L. Kays, Dalton Trans., 2021, 50, 722–728 RSC.
- A. J. Valentine, L. J. Taylor, A. M. Geer, C. D. Huke, K. E. Wood, W. Tovey, W. Lewis, S. P. Argent, A. M. Teale, J. McMaster and D. L. Kays, Organometallics, 2022, 41, 1426–1433 CrossRef CAS PubMed.
- Y. S. Meng, L. Xu, J. Xiong, Q. Yuan, T. Liu, B. W. Wang and S. Gao, Angew. Chem., Int. Ed., 2018, 57, 4673–4676 CrossRef CAS.
- C. Hansch, A. Leo and R. W. Taft, Chem. Rev., 1991, 91, 165–195 CrossRef CAS.
- G. Parigi, E. Ravera and C. Luchinat, Prog. Nucl. Magn. Reson. Spectrosc., 2019, 114–115, 211–236 CrossRef CAS.
- N. Elgrishi, K. J. Rountree, B. D. McCarthy, E. S. Rountree, T. T. Eisenhart and J. L. Dempsey, J. Chem. Educ., 2018, 95, 197–206 CrossRef CAS.
- I. F. Galván, M. Vacher, A. Alavi, C. Angeli, F. Aquilante, J. Autschbach, J. J. Bao, S. I. Bokarev, N. A. Bogdanov, R. K. Carlson, L. F. Chibotaru, J. Creutzberg, N. Dattani, M. G. Delcey, S. S. Dong, A. Dreuw, L. Freitag, L. M. Frutos, L. Gagliardi, F. Gendron, A. Giussani, L. González, G. Grell, M. Guo, C. E. Hoyer, M. Johansson, S. Keller, S. Knecht, G. Kovačević, E. Källman, G. Li Manni, M. Lundberg, Y. Ma, S. Mai, J. P. Malhado, P. Å. Malmqvist, P. Marquetand, S. A. Mewes, J. Norell, M. Olivucci, M. Oppel, Q. M. Phung, K. Pierloot, F. Plasser, M. Reiher, A. M. Sand, I. Schapiro, P. Sharma, C. J. Stein, L. K. Sørensen, D. G. Truhlar, M. Ugandi, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, O. Weser, T. A. Wesołowski, P. O. Widmark, S. Wouters, A. Zech, J. P. Zobel and R. Lindh, J. Chem. Theory Comput., 2019, 15, 5925–5964 CrossRef.
- A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of Transition Ions, Oxford University Press, 1970 Search PubMed.
- M. Atanasov, D. Ganyushin, D. A. Pantazis, K. Sivalingam and F. Neese, Inorg. Chem., 2011, 50, 7460–7477 CrossRef CAS.
- M. Kotani, J. Phys. Soc. Jpn., 1949, 4, 293–297 CrossRef CAS.
- N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, J. Comput. Chem., 2013, 34, 1164–1175 CrossRef CAS.
- S. Mugiraneza and A. M. Hallas, Commun. Phys., 2022, 5, 95 CrossRef.
- D. Reta and N. F. Chilton, Phys. Chem. Chem. Phys., 2019, 21, 23567–23575 RSC.
- C. Benelli and D. Gatteschi, Introduction to Molecular Magnetism: From Transition Metals to Lanthanides, Wiley-VCH, 2015 Search PubMed.
- K. S. Cole and R. H. Cole, J. Chem. Phys., 1941, 9, 341–351 CrossRef CAS.
- A. Cornia, A. L. Barra, V. Bulicanu, R. Clérac, M. Cortijo, E. A. Hillard, R. Galavotti, A. Lunghi, A. Nicolini, M. Rouzières, L. Sorace and F. Totti, Inorg. Chem., 2020, 59, 1763–1777 CrossRef CAS PubMed.
- J. Acharya, A. Sarkar, P. Kumar, V. Kumar, J. Flores Gonzalez, O. Cador, F. Pointillart, G. Rajaraman and V. Chandrasekhar, Dalton Trans., 2020, 49, 4785–4796 RSC.
- A. Lunghi, F. Totti, R. Sessoli and S. Sanvito, Nat. Commun., 2017, 8, 14620 CrossRef PubMed.
- L. Gu and R. Wu, Phys. Rev. Lett., 2020, 125, 117203 CrossRef CAS.
- M. Briganti, F. Santanni, L. Tesi, F. Totti, R. Sessoli and A. Lunghi, J. Am. Chem. Soc., 2021, 143, 13633–13645 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Full experimental details for the synthesis, characterization, and analysis. CCDC 2184650–2184653. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2dt03531f |
| This journal is © The Royal Society of Chemistry 2022 |
