The crystal structure and luminescence properties of the first lithium oxonitridolithosilicate Li₃SiNO₂:Eu²⁺

Abstract

The compound Li₃SiNO₂:Eu²⁺ was synthesized in high temperature solid-state reactions in weld shut tantalum ampules and the crystal structure of Li₃SiNO₂ has been determined by single-crystal X-ray diffraction. It crystallizes in the monoclinic space group C2/c (no. 15) with the lattice parameters a = 1049.01(3), b = 1103.42(3), c = 511.86(2) pm, β = 116.14(1)°, and a volume of V = 0.53187(2) nm³. This compound is built up from two different layers, which are arranged alternately along the crystallographic a-axis. The results from single-crystal diffraction were confirmed by the Rietveld analysis of bulk samples. Moreover, Li₃SiNO₂ could be successfully doped with the activator ion Eu²⁺ and the luminescence spectroscopy of single-crystals revealed broad band emission at λ_max = 601 nm (fwhm = 90 nm).

---

Introduction

Although the field of lithium oxonitridosilicates has been known for quite a long time and the first compound Li₄Si_0.8N_2.4(Li₂O)_1.6 was published by Juza, Weber, and Meyer-Simon in 1953,¹ only a few more representatives are known today. A few years later (1981), the well-known LiSiON was synthesized by Laurent, Guyader, and Roult and analyzed by time-of-flight neutron diffraction.² Ma et al. were able to successfully dope the compound LiSiON with the activator ion Eu²⁺ in 2012, which resulted in emission with a maximum of λ_max = 426–478 nm (fwhm = 142–193 nm) depending on the activator ion concentration.³ Based on X-ray phase analysis and classical quantitative analysis, compounds such as Li₄SiN₂O, Li₃SiNO₂ or Li₇SiN₃O were predicted by Kraśnicka and Podsiadlo at the same time.^4,5 The structure of the last compound, Li₇SiN₃O, was then elucidated by Casas-Cabanas and Palacín in 2014 using Rietveld refinement.⁶ All lithium oxonitridosilicates, whose structures are known to date, contain lithium ions exclusively in tetrahedral coordination. This results in structures that consist only of the combined network of tetrahedrally coordinated silicon and lithium ions. In the following, lithium oxonitridolithosilicate compounds shall be referred to as structures, which are built up by the aforementioned (Li/Si)–(O/N) tetrahedral network but additionally with lithium as a completing cation which occupies the cavities. Although no luminescent lithium oxonitridolithosilicate is known yet, there are already some established phosphors in the field of alkali lithosilicates.^7–10 The best common examples are Na[Li₃SiO₄]:Eu²⁺ (NLSO:Eu²⁺) (λ_max = 469 nm; fwhm = 32 nm), K[Li₃SiO₄]:Eu²⁺ (KLSO:Eu²⁺) (λ_max = 604 nm; fwhm = 150 nm), NaK₇[Li₃SiO₄]₈:Eu²⁺ (NKLSO:Eu²⁺) (λ_max = 515 nm and 598; fwhm = 49 nm and 138 nm),^11–14 RbNa₃[Li₃SiO₄]₄:Eu²⁺ (λ_max = 471 nm; fwhm = 22.4 nm),^8,15,16 RbNa[Li₃SiO₄]₂:Eu²⁺ (λ_max = 523 nm; fwhm = 41 nm),¹⁷ RbLi[Li₃SiO₄]₂:Eu²⁺ (RLSO:Eu²⁺) (λ_max = 530 nm; fwhm = 42 nm),¹⁸ RbNa₂K[Li₃SiO₄]₄:Eu²⁺ (λ_max = 480 nm; fwhm = 26 nm),¹⁹ CsNa₂K[Li₃SiO₄]₄:Eu²⁺ (λ_max = 485 nm; fwhm = 26 nm),¹⁹ LiK₇[Li₃SiO₄]₈:Eu²⁺ (LKLSO:Eu²⁺) (λ_max = 511 nm; fwhm = 45 nm),²⁰ Na₂K₂[Li₃SiO₄]₄:Eu²⁺ (λ_max = 486 nm; fwhm = 20.7 nm),^21,22 RbKLi₂[Li₃SiO₄]₄:Eu²⁺ (λ_max = 474 nm and 532; fwhm = 24.8 nm and 43.5 nm),^7,23 and Cs_{4−x−y−z}Rb_xNa_yLi_z[Li₃SiO₄]:Eu²⁺ (CRNLLSO:Eu²⁺) (λ_max = 473 nm and 531 nm; fwhm = 25.2 nm and 58 nm).²⁴ These compounds exhibit interesting luminescence properties and some of them are characterized by their narrow single band emission in the blue and green spectral range.

In this article, we present the structure of Li₃SiNO₂ based on single-crystal X-ray data refinement. Additionally, the title phase was doped with the activator ion Eu²⁺ and, in comparison with the well-known alkali lithosilicates, nitrogen was successfully incorporated into the crystal structure resulting in a shift of the emission band to higher wavelengths compared to the aforementioned oxosilicates.^25–27 The here presented compound can be seen as the first example in the field of lithium oxonitridolithosilicates and additionally it exhibits single band emission in the orange spectral region, which is a novelty even for the substance class of oxonitridolithosilicates.

Results and discussion

Crystal structure

The compound Li₃SiNO₂ crystallizes in the monoclinic space group C2/c with the lattice parameters a = 1049.01(3), b = 1103.42(3), c = 511.86(2) pm, β = 116.14(1)°, and a volume of V = 0.53187(2) nm³. Details on the crystal-structure refinement are given in Table 1. Atomic coordinates, displacement parameters, and interatomic distances are listed in Tables 2–4.

Table 1 Crystal data and structure refinement of Li₃SiNO₂

Empirical formula	Li3SiNO2
Molar mass/g mol^−1	94.92
Crystal system	Monoclinic
Space group	C2/c
Powder data
Powder diffractometer	STOE Stadi P
Radiation	Mo-Kα1 (λ = 70.93 pm)
a/pm	1054.82(8)
b/pm	1102.96(7)
c/pm	512.56(4)
β/°	116.66(1)
V/nm^3	0.53293(6)
Single-crystal data
Single-crystal diffractometer	Bruker D8 Quest Kappa
Radiation	Mo-Kα (λ = 71.073 pm)
a/pm	1049.01(3)
b/pm	1103.42(3)
c/pm	511.86(2)
β/°	116.14(1)
V/nm^3	0.53187(2)
Formula units per cell Z	8
Calculated density/g cm^−3	2.371
Crystal size/mm^3	0.200 × 0.070 × 0.070
Temperature/K	297(2)
Detector distance/mm	40
Exposure time	0.5° per frame; 40 s per frame
Absorption coefficient/mm^−1	0.604
F(000)/e	368
θ-Range/°	2.84–40.25
Range in hkl	±19, ±20, ±9
Reflections total/independent	24 474/1622
R int	0.0318
Reflections with I ≥ 2σ(I)	1579
Data/ref. parameters	1622/66
Absorption correction	Multi-scan
Final R1/wR2 [I ≥ 2σ(I)]	0.0222/0.0591
Final R1/wR2 (all data)	0.0226/0.0594
Goodness of fit on F^2	1.147
Largest diff. peak/hole/e Å^−3	0.516/−0.640

---

Table 2 Wyckoff positions, atomic coordinates, and equivalent isotropic displacement parameters U_eq (Ų) of Li₃SiNO₂ (standard deviations in parentheses)

Atom	Wyckoff-position	x	y	z	U eq	Occ.
Si1	8f	0.22086(2)	0.43007(2)	0.25806(3)	0.00621(6)	1
Li1	4e	½	0.2978(2)	¼	0.0101(2)	1
Li2	4e	½	0.4746(2)	¾	0.0153(3)	1
Li3	4e	0	0.4338(2)	¾	0.0205(4)	1
Li4	4e	0	0.3190(3)	¼	0.0188(4)	0.76
Li4A	4e	0	0.275(2)	¼	0.019(2)	0.24
Li5	8f	0.2769(2)	0.1976(2)	0.2176(3)	0.0198(3)	1
O1	8f	0.12887(4)	0.31224(3)	0.05472(8)	0.00791(8)	1
O2	8f	0.38906(4)	0.39292(5)	0.3760(2)	0.01470(9)	1
N1	8f	0.17022(5)	0.44522(4)	0.5324(2)	0.00872(8)	1

---

Table 3 Anisotropic displacement parameters U_ij (Ų) of Li₃SiNO₂ (standard deviations in parentheses). The displacement parameters of the atoms Li4 and Li4A were refined isotropically

Atom	U 11	U 22	U 33	U 23	U 13	U 12
Si1	0.00646(8)	0.00652(8)	0.00580(7)	−0.00072(3)	0.00283(5)	0.00006(4)
Li1	0.0103(6)	0.0084(5)	0.0133(6)	0	0.0068(5)	0
Li2	0.0161(7)	0.0172(7)	0.0098(6)	0	0.0031(5)	0
Li3	0.0180(8)	0.0129(7)	0.0179(8)	0	−0.0039(7)	0
Li5	0.0255(6)	0.0191(6)	0.0205(6)	0.0106(4)	0.0154(5)	0.0119(5)
O1	0.0082(2)	0.0068(2)	0.0081(2)	−0.00118(9)	0.0031(2)	−0.0003(2)
O2	0.0077(2)	0.0199(2)	0.0150(2)	−0.0062(2)	0.0035(2)	0.0019(2)
N1	0.0129(2)	0.0072(2)	0.0076(2)	0.0002(2)	0.0059(2)	0.0008(2)

---

Table 4 Interatomic distances (Å) in Li₃SiNO₂ (standard deviations in parentheses)

Si1–O2	1.6453(4)	Li3–O1	2.050(2) 2×	Li4A–O1	2.047(2) 2×
Si1–O1	1.6792(4)	∅ Li3–O	2.050(2)	Li4A–O2	2.544(8) 2×
∅ Si1–O	1.6668(4)			∅ Li4A–O	2.296(8)
		Li3–N1	2.189(2) 2×
Si1–N1	1.7146(5)	Li3–N1	2.4894(5) 2×	Li4A–N1	2.558(8) 2×
Si1–N1	1.7231(5)	∅ Li3–N	2.339(2)	∅ Li4A–N	2.558(8)
∅ Si1–N	1.7189(5)
		Li4–O1	2.0058(4) 2×	Li5–O1	1.889(2)
Li1–O2	1.880(2)	∅ Li4–O	2.0058(4)	Li5–O1	2.036(2)
Li1–O1	1.969(2) 3×			Li5–O2	2.418(2)
∅ Li1–O	1.947(2)	Li4–N1	2.223(2) 2×	∅ Li5–O	2.114(2)
		∅ Li4–N	2.223(2)
Li2–O2	1.967(2) 2×			Li5–N1	1.950(2)
Li2–O2	2.138(2) 2×			∅ Li5–N	1.950(2)
∅ Li2–O	2.053(2)

---

The three-dimensional framework in the structure of Li₃SiNO₂ is built up from two different layers, which are stacked alternately along the crystallographic a-axis. As shown in Fig. 1, the first layer, named layer A, consists of condensed SiO₂N₂ and LiO₃N tetrahedra, where the vertex-sharing SiO₂N₂ tetrahedra form unbranched zweier single chains²⁸ along the crystallographic c-axis via bridging N^[2]3− anions. The structural feature of such unbranched zweier single chains was found for the first time in nature in the mineral diopside CaMgSi₂O₆, which belongs to the mineral group of pyroxenes and, according to the silicate classification by Liebau, it is an inosilicate.^28–30 SiO₂N₂ tetrahedra can also be found in compounds such as Ca₃SiO₄N₂,³¹ where these tetrahedra are also connected to each other via N³⁻ anions. The Si–O distances, which vary from 164.53(4) to 167.92(4) pm, and the Si–N distances with values from 171.46(5) to 172.31(5) pm are in good agreement with the sum of the ionic radii.^23,24,32,33 The occupation of the N1 site with O instead of N leads to a significant under-occupation, indicating the presence of N at this position. These unbranched zweier single chains are then connected to each other via LiO₃N tetrahedra, which form Li₂O₄N₂ dimer units, when only layer A is considered.³⁴ Hereby two LiO₃N tetrahedra share a common edge via the O²⁻ anions. Although the dimer units are not connected to each other, they connect the unbranched zweier single chains in such a way that they are corner-sharing via the N³⁻ anions and edge-sharing via two O²⁻ anions. In the LiO₃N tetrahedra, the Li–O distances range from 188.9(2) to 241.8(2) pm and the Li–N distance is 195.0(2) pm. Since one Li–O distance is quite elongated, the corresponding coordination polyhedra can also be described as elongated trigonal pyramids exhibiting a 3 + 1 coordination, where the Li⁺ cations are slightly displaced from the centers (see Fig. 1).^12,33,35

Fig. 1 Layer A of Li₃SiNO₂. In the upper left, the LiO₃N tetrahedra (orange) with the Li–N and Li–O distances and the dimer units formed from them are shown. In the upper right, the SiO₂N₂ tetrahedron (blue) is illustrated, including the Si–N and Si–O distances, and the unbranched zweier single chains built up from it. In the lower half, layer A, which is formed from LiO₃N and SiO₂N₂ tetrahedra, is represented along [1̄00].

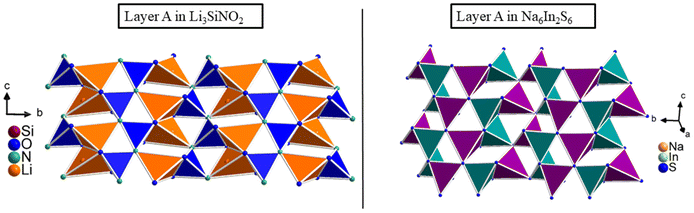
The connectivity within layer A in the structure of Li₃SiNO₂ is related to that in the compounds Na₂Mn₂S₃³⁶ and Na₆In₂S₆,³⁷ where the SiO₂N₂ tetrahedra correspond to the MnS₄ tetrahedra (Mn1 site) and NaS₄ tetrahedra, respectively, and the LiO₃N tetrahedra correspond to the MnS₄ tetrahedra (Mn2 site) and InS₄ tetrahedra, respectively (see Fig. 2).

Fig. 2 On the left, layer A of Li₃SiNO₂ is shown compared to layer A of the compound Na₆In₂S₆, which is represented on the right. The LiO₃N tetrahedra are displayed in orange, SiO₂N₂ tetrahedra are displayed in blue, the NaS₄ tetrahedra are displayed in violet and the InS₄ tetrahedra are displayed in teal.

The second layer, named layer B, is built up from three different coordination polyhedra consisting of LiO₄ tetrahedra, LiO₂N₄ octahedra, and LiO₄N₂ octahedra, whereby within the latter dynamic positional disorder occurs. In this layer, there are five crystallographically distinguishable lithium sites. The Li1 and Li2 sites form LiO₄ tetrahedra with Li1–O and Li2–O distances ranging from 188.0(2) to 196.9(2) pm and 196.7(2) to 213.8(2) pm, respectively, which are in good agreement with the sum of the ionic radii.^20,23 The Li3 site is coordinated by four N³⁻ and two O²⁻ anions and constitutes a distorted octahedral arrangement, where the Li3–O distances are 205.0(2) pm and the Li3–N distances are between 218.9(2) and 248.94(5) pm. Since two of the Li3–N distances are slightly longer and are located opposite to each other, this can also be described as an elongated octahedron. For Li4/4A, dynamic positional disorder occurs in the LiO₄N₂ octahedra, where the blurred electron density can be described by two partially occupied Li⁺ positions (Li4 and Li4A). The two sites are coordinated by four O²⁻ anions and two N³⁻ anions, where the Li4–O distances range from 200.58(4) to 292.0(3) pm and the Li4–N distance is 222.3(2) pm. The Li4A–O distances range from 204.7(2) to 254.4(8) pm and the Li4A–N distance is 255.8(8) pm, implying a highly distorted octahedron. Due to the spatial proximity, only one of the two positions (Li4 and Li4A) can be occupied at the same time and due to a strong correlation between the two sites, only an isotropic refinement of the displacement parameters in the structure solution was applied. For comparison, the displacement ellipsoids of the asymmetric unit of Li₃SiNO₂ are shown in the ESI (see Fig. S1†). The asymmetric units are illustrated for the cases where the Li4 site is described by only one fully occupied Li site and by two partially occupied Li sites, respectively. The occupation of the two sites was approximated in such a way that the two isotropic displacement parameters were approximately equal in size and then fixed manually at this value. The crystal structure refinement results in occupations of Li4 = 0.76 and Li4A = 0.24 implying that the Li4 site is statistically preferred. To confirm the occupations of these sites, five crystals from four different syntheses were measured by single-crystal X-ray diffraction at room temperature. All crystal structure refinements showed the same results with minimal deviations. Single-crystal X-ray measurements at low temperatures (−90 °C) have shown that the occupation of the Li4 and Li4A sites changes by 8% (Occ. of Li4 = 0.84 and Li4A = 0.16) and the Li4 site is more preferred. This indicates dynamic positional disorder between the two sites, which is temperature dependent. The results of the single-crystal measurements at low temperature are shown in the ESI,† listed in Tables S2–S5.† One reason for the dynamic positional disorder could be that the volume of the LiO₄N₂ octahedron (V = 16.73 ų) is larger than that of the LiO₂N₄ octahedron (V = 14.19 ų) and thus the Li⁺ cation has more space to displace, which becomes higher with increasing temperature (see Fig. 3). The program Vesta 3³⁸ was used to calculate the polyhedron sizes.

Fig. 3 The different coordination polyhedra of layer B are shown. On the upper half, the LiO₄ tetrahedra of the Li1 and Li2 sites are displayed in orange including the Li–O distances. On the lower left, the LiO₂N₄ octahedron is displayed in green including the Li–O and Li–N distances and the polyhedron size, respectively. On the lower right, the LiO₄N₂ octahedron with the two partially occupied Li⁺ positions is represented in bright green including the Li–O and Li–N distances and the polyhedron size. The Li–O and Li–N distances of the Li4 site are shown in red.

The four different coordination polyhedra around the four Li sites, as mentioned before, form an interconnected tetrahedra and octahedra band spanning the condensed layer B (see Fig. 4). The LiO₂N₄ and LiO₄N₂ octahedra built up the octahedra band, named band X, along the crystallographic c-axis, where the LiO₂N₄ octahedra are double edge-sharing to each other by two common N³⁻ anions on each edge. The LiO₄N₂ octahedra, on the other hand, are not connected to each other, but share common edges with the LiO₂N₄ octahedra within the octahedra band X. The LiO₂N₄ and LiO₄N₂ octahedra are connected in such a way that one LiO₄N₂ octahedron shares common edges with three LiO₂N₄ octahedra once via two N³⁻ anions and twice via one O²⁻ and one N³⁻ anions. Considering the cb-plane, the LiO₄N₂ octahedra are arranged alternately to the right and to the left of the LiO₂N₄ octahedra. A similar connection pattern is formed by the LiO₄ tetrahedra within the tetrahedra band, named band Y. The LiO₄ tetrahedra of the Li2 site are connected to each other along the crystallographic c-axis by double edge-sharing via two common O²⁻ anions on each edge. The LiO₄ tetrahedra of the Li1 site, which are not connected to each other within the tetrahedral band Y, always arrange themselves alternately to the left and right of the LiO₄ tetrahedra of the Li2 site from the viewpoint perpendicular to the cb-plane. The LiO₄ tetrahedra of the Li1 and Li2 sites share a common edge via two O²⁻ anions. Along the crystallographic b-axis, the bands X and Y are arranged alternately. The bands X and Y are connected in such a way that the LiO₄ tetrahedra of the Li1 site share a common edge with the LiO₂N₄ octahedra and two common edges with the LiO₄N₂ octahedra, each via two O²⁻ anions. Additionally, the LiO₄N₂ octahedra and the LiO₄ tetrahedra of the Li2 site are edge-sharing via two O²⁻ anions. Furthermore, the c glide plane, derived from the space group C2/c, is visible when the mirror plane is placed perpendicular to the crystallographic b-axis through the center of the octahedral band X (see Fig. 4). Since the Li⁺ cations are not only part of the tetrahedral substructure, we assign this compound to the substance class of lithium oxonitridolithosilicates.

Fig. 4 The highly condensed layer B. In the upper half, the construction of the two different bands (X and Y) are presented. In the lower half, the arrangement and interconnection of the two different bands (X and Y), that build up layer B, are shown. The LiO₄ tetrahedra of the Li1 and Li2 sites are displayed in orange, the LiO₂N₄ octahedra are displayed in green, and the LiO₄N₂ octahedra including the dynamic positional disorder of the Li4 and Li4A sites are represented in bright green.

The entire structure of Li₃SiNO₂ is built up from the two layers A and B by stacking them alternately along the crystallographic a-axis with the characteristic pattern BAB′A′ (see Fig. 5). Although layers A and B are equivalent in construction to layers A′ and B′, they are differently orientated due to the most favorable arrangement in terms of energy. Layers A and A′ are related via a two-fold rotation axis that runs along the crystallographic b-axis through layer B. Layers B and B′ are connected via a 2₁ screw axis, which is additionally caused by the space group C2/c and runs along the crystallographic b-axis through layers A and A′. The two layers A and B are connected in such a way that the LiO₃N tetrahedra of the Li5 site share a common edge with the LiO₄ tetrahedra of the Li1 site via two O²⁻ anions, and are edge-shared to the LiO₄N₂ octahedra and the LiO₂N₄ octahedra via an O²⁻ and N³⁻ anion. In addition, the LiO₄ tetrahedra of the Li5 site are also corner-shared to the LiO₄ tetrahedra of the Li2 site via an O²⁻ anion. The SiO₂N₂ tetrahedra of the unbranched zweier single chains show a similar connection pattern. The SiO₂N₂ tetrahedra share common corners with the LiO₄ tetrahedra of the Li2 sites via O²⁻ anions. They share a common edge with the LiO₂N₄ octahedra via two N³⁻ anions as well as via one N³⁻ and one O²⁻ anion. In addition, it is edge-shared to the LiO₄N₂ octahedra via an O²⁻ and N³⁻ anion.

Fig. 5 The entire structure of Li₃SiNO₂ built up from layers A and B. The LiO₄ tetrahedra of the Li1 and Li2 sites and the LiO₃N tetrahedra are displayed in orange, the SiO₂N₂ tetrahedra are displayed in blue, the LiO₂N₄ octahedra are displayed in green and the LiO₄N₂ octahedra including the dynamic positional disorder of the Li4 and Li4A sites are represented in bright green.

The compound Li₃SiNO₂ could be successfully doped with the activator ion Eu²⁺ and the resulting luminescence properties are discussed in the Luminescence section.

MAPLE, CHARDI, and BLBS

The electrostatic consistency of the crystal structure is proved by MAPLE (Madelung Part of Lattice Energy),^39–41 BLBS (bond length–bond strength),^42,43 and CHARDI (Charge Distribution method)^44,45 calculations. In the latter method, the charge distribution is calculated using the concept of effective coordination numbers in combination with bond strength based on Pauling's concept. The BLBS calculations predict the formal oxidation state of an atom by correlating the bond strengths (bond valences) and bond lengths, where the sum of all bond valences should add up to the oxidation state of the respective atom. The MAPLE and CHARDI calculations were performed for the cases where either the Li4 or the Li4A site is fully occupied. The results of the CHARDI and BLBS calculations are shown in Table 5. The partial MAPLE values and MAPLE sums of Li₃SiNO₂ are listed in Table 6.

Table 5 Charge distribution in Li₃SiNO₂ calculated via CHARDI (∑Q) and BLBS (∑V). ∑Q1 are the values where the Li4 site is fully occupied and ∑Q2 are the values where the Li4A site is fully occupied

	Si1	Li1	Li2	Li3	Li4	Li4A	Li5	O1	O2	N1
∑V	4.10	1.10	1.00	1.02	0.89	0.68	1.01	−2.09	−1.85	−3.07
∑Q1	4.15	0.92	1.01	0.98	0.93	—	0.93	−2.50	−1.97	−2.52
∑Q2	4.21	0.98	0.99	0.99	—	0.83	0.94	−2.59	−2.02	−2.40

---

Table 6 Partial MAPLE values and MAPLE sums (kJ mol⁻¹ of Li₃SiNO₂)^a

Li3SiNO2	Li4 fully occupied	Li4A fully occupied	Model
a Typical partial MAPLE values (kJ mol^−1): Si^4+ 9000–10 200; Li^+ 600–860; O^2− 2000–2800; N^3− 5000–6200.^47 The MAPLE sums of LiSiON and Li2O were calculated from the published single-crystal data.
Si1	9200	9261
Li1	808	780
Li2	678	635
Li3	637	696
Li4	667	—
Li4A	—	644
Li5	653	648
O1	2573	2549	+1	LiSiON^2
O2	2529	2592	+1	Li2O^46
N1	5783	5646
	Σ = 22 133	Σ = 22 106	Σ = 22 191
	Δ = 0.26%	Δ = 0.38%

---

The results from the BLBS method show the expected charge for the atoms with the exception of the Li4A atom and are in good accordance with the oxidation states based on crystallographic criteria. The outcome of the BLBS method is supported by the CHARDI calculations, where only the atoms O1 and N1 show larger deviations. The deviations of the N1 and O1 atoms could be explained by the fact that they are spatially very close to the dynamic positional disordered Li4 and Li4A sites and thus interact with them more strongly than the O2 atom. The deviation of the Li4A atom with respect to the BLBS calculation could be due to the fact that the position could describe the blurred electron density very well, but does not correspond to a “typical” Li position in relation to the coordination and the partially longer Li–O/N distances, so the description of a dynamic process with a static model is limited. Furthermore, the partial MAPLE values and the MAPLE sums are compared to the reference values to verify the refined crystal structure. The partial MAPLE values of all individual atoms are in good agreement with the reference values known from the literature and confirm the assignment of the different atoms and the incorporation of N and O into the structure. The results of the calculations are consistent with those from the SCXRD refinement, and the assignment of the N and O atoms to the corresponding sites seems plausible. Comparing the MAPLE sums of LiSiON and Li₂O with the calculated MAPLE sums of Li₃SiNO₂, the values were found to deviate by only 0.26 and 0.38% depending on the full occupation of the Li4 or Li4A site, which indicates the validity of the crystal structure.

Luminescence

The luminescence properties of Li₃SiNO₂:Eu²⁺ were investigated on single-crystals and powder samples, where the latter was used to determine the excitation spectrum and the thermal quenching behavior.

The powder sample of Li₃SiNO₂ could not be synthesized in the pure phase and contains 3 wt% of LiSi₂N₃. The results of the Rietveld refinement can be found in the ESI (see Fig. S2 and Table S1†). Li₃SiNO₂ with a nominal activator concentration of 2 mol% Eu²⁺ based on the content of lithium can be excited with near-UV to blue light (e.g. λ_exc = 448 nm) and the single-crystals exhibit broad band emission at λ_max = 601 nm with a full width at half maximum (fwhm) of 90 nm (0.32 eV, 2597 cm⁻¹). In comparison, the powder sample (λ_exc = 400 nm) exhibits broad band emission at λ_max = 606 nm with a full width at half maximum (fwhm) of 100 nm (0.33 eV, 2695 cm⁻¹). In the CIE-xy color space, this corresponds to the values x = 0.564(1) and y = 0.433(1) for the measured single-crystal emission band and to x = 0.562(1) and y = 0.436(1) for the powder sample. Furthermore, an excitation spectrum of the powder sample was recorded exhibiting a maximum at 376 nm (see Fig. 6a and b). The first lab samples without any systematic engineering regarding the emission properties already yielded quantum efficiencies (QE) above 30%. The compound has a brown to gray body color under daylight and is stable under atmospheric conditions for several months.

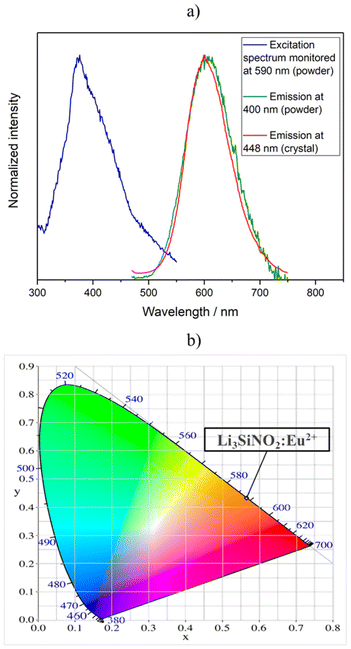Fig. 6 (a) The red line represents the luminescence spectrum of a Li₃SiNO₂:Eu²⁺ crystal recorded at an excitation wavelength of 448 nm. The green line shows the luminescence spectrum of a powder sample of Li₃SiNO₂:Eu²⁺ recorded at an excitation wavelength of 400 nm. The blue line represents the excitation spectrum of the powder sample of Li₃SiNO₂:Eu²⁺ monitored at λ_em = 590 nm (based on raw data maximum). (b) It shows the color point of the Li₃SiNO₂:Eu²⁺ single-crystals in the CIE-xy color space.⁴⁸

The thermal quenching behavior (TQ) of Li₃SiNO₂:Eu²⁺ was examined on a powder sample (see Fig. 7).

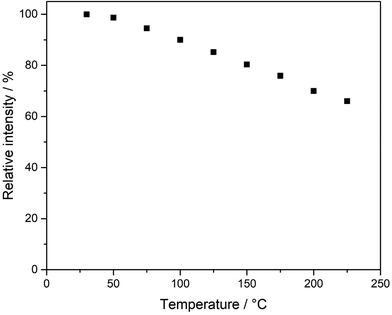Fig. 7 Representation of the thermal quenching behavior of Li₃SiNO₂:Eu²⁺ as the relative integral photoluminescence intensity to that at 25 °C measured in steps of 25 °C up to 225 °C.

As can be seen in Fig. 7, the relative integral photoluminescence intensity decreases with increasing temperature and drops to 66% of the initial value at a temperature of 225 °C. At a typical operating temperature of 125 °C for a pc-LED, the relative integral intensity is still above 85%. Nevertheless, QE and TQ would have to be improved for any industrial use.

Since the compound shows only one emission band, it would indicate that only one position in the structure is suitable for incorporating the activator ion Eu²⁺. One possible position would be the Li3 site, which forms an octahedral coordination to two O²⁻ anions with Li–O distances of 205.0(2) pm and to four N³⁻ anions with Li–N distances between 218.9(2) and 248.94(5) pm resulting in a polyhedron size of 14.19 ų. Although the distances are too short regarding typical Eu–O/N coordination (Eu–O distances range from 240 to 300 pm and Eu–N distances range from 260 to 325 pm),^49–51 local spatial distortion or enlargement of the octahedron could occur in contrast to the average structure. To maintain charge neutrality, the inclusion of a divalent Eu²⁺ cation may be compensated by Li-vacancies in the surroundings or by local O/N substitution. In comparison with the LiO₂N₄ octahedron of the Li3 site, the LiO₄N₂ octahedron including the dynamic positional disordered Li4 and Li4A sites is slightly larger and would also be a possible position to host the Eu²⁺ cation. The Li4/Li4A site is coordinated octahedrally by four O²⁻ anions with Li–O distances between 200.58(4) and 292.0(3) pm and two N³⁻ anions with Li–N distances between 222.3(2) and 255.8(8) pm resulting in a polyhedron size of 16.73 ų. Due to the two short Li–O distances, this would also lead to an enlargement or spatial distortion of the octahedron. Compared to compounds such as Li₂CaSi₂N₄:Eu²⁺,⁵² Mg₃GaN₃:Eu²⁺,⁵³ and Li-α-SiAlON:Eu²⁺,⁵⁴ the polyhedron size and Li–O/N distances of the Li3 and Li4/Li4A sites in Li₃SiNO₂:Eu²⁺ are in a similar range and it seems possible that one of them hosts the activator ion Eu²⁺. In the former compound, there are two crystallographically distinguishable Ca sites, which are octahedrally coordinated by six N³⁻ anions and the compound exhibits an emission maximum at λ_max = 583–585 nm. The Ca1 site has Ca1–N distances between 248.9(3) and 250.9(3) pm resulting in a polyhedron size of 16.54 ų and the Ca2 site with a Ca2–N distances of 258.6(3) pm has a polyhedron size of 18.95 ų, whereby the author supposed that both Ca sites are suitable to host the activator ion Eu²⁺. In Mg₃GaN₃:Eu²⁺, it was assumed that the activator ion Eu²⁺ is located in octahedral voids, where the possible observed Eu–N distances are between 232.0 and 248.9 pm resulting in an estimated polyhedron sizes between 14.5 and 16.5 ų exhibiting an emission maximum at 578 nm with a fwhm of 132 nm. In Eu²⁺ doped Li-α-SiAlON, it was supposed that the activator ion Eu²⁺ occupies a Li site, which is sevenfold coordinated by N³⁻/O²⁻ anions with Li–O/N distances ranging from 205.2 to 276.7 pm. Depending on the Eu²⁺ concentration, the compound Li-α-SiAlON exhibits an emission maximum in the range λ_max = 563–586 nm.

It would also be possible that the activator ion Eu²⁺ is situated on the Li2 site. As illustrated in Fig. 8, a lithium channel is formed in the structure of Li₃SiNO₂ along the crystallographic c-axis, which consists of an edge-shared LiO₄ tetrahedral band (Li2 site) and corresponds to band Y. This band Y is connected to two unbranched zweier single chains of SiO₂N₂ tetrahedra by corner-sharing via the O²⁻ anion, respectively. Due to this special arrangement of the unbranched zweier single chains of SiO₂N₂ tetrahedra, there would also be two N³⁻ anions in close spatial proximity to the Li2 site, whose Li–N distance would be 314.9 pm. Although this Li–N distance is too large for a Li⁺ cation's first coordination sphere, it would be a permissible Eu–N distance for the activator ion Eu²⁺. Considering these two N³⁻ anions, an octahedral coordination would also result for the Eu²⁺ cation on the Li2 site and is consequently a possible position hosting the Eu²⁺ cation. Due to the additional tetrahedral coordination of the O²⁻ anions of the Li2 site, this would form a distorted octahedron with a polyhedron size of 12.52 ų and, due to the short Li–O distances, there would also be an enlargement or spatial distortion of the octahedron. The incorporation of the activator ion Eu²⁺ into lithium channels or domains has already been observed in other compounds known from the literature, such as RbKLi₂[Li₃SiO₄]₄:Eu²⁺,^7,23 Cs_{4−x−y−z}Rb_xNa_yLi_z[Li₃SiO₄]:Eu²⁺,²⁴ and LiK₇[Li₃SiO₄]₈:Eu²⁺.²⁰ However, it should be considered that in these compounds the Li⁺ cations form an approximately square planar coordination to four O²⁻ anions instead of a tetrahedral one.

Fig. 8 On the left, the position of one of the lithium channels in the structure of Li₃SiNO₂ is shown. In the middle, the connection of two unbranched zweier single chains of SiO₂N₂ tetrahedra (blue) with the LiO₄ tetrahedra of the Li2 site (orange, band Y) is represented. On the right, the Li2 site including the possible octahedral coordination to four O²⁻ and two N³⁻ anions is illustrated.

Due to the special arrangement of the various polyhedra, unoccupied distorted octahedral voids are formed in the structure, which could also be a possible position hosting the activator ion Eu²⁺. A similar behavior was observed in the compound Mg₃GaN₃:Eu²⁺, as mentioned before. The unoccupied distorted octahedral void is coordinated by five O²⁻ anions and one N³⁻ anion, resulting in a MO₅N octahedron with an O1–O2 distance of 465.1, an O2–O2 distance of 511.9, and a N1–O2 distance of 430.6 pm (see Fig. 9). Comparing the anion–anion distances with those of the LiO₂N₄ octahedron (two times a N1–O1 distances of 421.1, and a N1–N1 distance of 497.2 pm) and the dynamic positional disordered LiO₄N₂ octahedron ( two times a O2–N1 distances of 501.8, and an O1–O1 distance of 400.9 pm), it is found to be similar in size to the last one and the MO₅N octahedron would result in a polyhedron size of 16.46 ų. The polyhedron size of the MO₅N octahedron was calculated by placing a dummy atom in the center of the octahedral void without considering any structural relaxation. Considering these anion–anion distances of the MO₅N octahedron, a spatial distortion or enlargement of the octahedral void could occur, when an Eu²⁺ cation is incorporated.

Fig. 9 On the left, the unoccupied distorted octahedral void (OV) in the structure of Li₃SiNO₂ is shown by the labeled O²⁻ anions and the N³⁻ anion, which is constructed by the special arrangement of the various polyhedra. On the right, the corresponding anions of the unoccupied MO₅N octahedron are shown including the specific anion–anion distances. In the middle, the resulting MO₅N octahedron (gray) with hypothetical M–O/N distances including the polyhedron size is illustrated. The LiO₄ and LiO₃N tetrahedra are displayed in orange, the LiO₂N₄ octahedron is displayed in green, the SiO₂N₂ tetrahedra are displayed in blue and the LiO₄N₂ octahedron including the dynamic positional disordered Li4 and Li4A sites is displayed in bright green.

All four positions could act as doping sites for the activator ion Eu²⁺ that explain the observed single band emission. Presumably, however, it is assumable that only one of these sites is preferred, otherwise a split or broad emission profile should be observed. It seems most likely that the activator ion Eu²⁺ is incorporated into the Li2 site building up the lithium channel or in the center of the LiO₄N₂ octahedron including the dynamic positional disordered Li4 and Li4A sites. One possible reason for the latter is that, compared to the octahedrally coordinated Li3 site, it has larger cation–anion distances, which partially correspond to the observed Eu–N and Eu–O distances, therefore resulting in a larger polyhedron size. In the case of the Li2 site, an increased electron density could be observed at this site in the Eu²⁺ doped crystals, which roughly corresponds to the 2 mol% activator ion Eu²⁺ concentration used in the syntheses. In addition, the residual electron density near this site was also found to be aligned towards the N³⁻ anions and the resulting distance to the N³⁻ anions is around 250 pm, which is approximately in the range of Eu–N distances. Considering the unoccupied distorted octahedral void as a possible position hosting the Eu²⁺ cation, it should be possible to detect low electron density at this position in the single-crystal data. However, no electron density could be observed around this position and consequently the unoccupied distorted octahedral void is presumably not occupied by the activator ion Eu²⁺. Based on SCXRD, an unambiguous localization of the luminescence center in Li₃SiNO₂:Eu²⁺ was not possible.

Compared to other luminescent lithium (oxo)nitride silicates such as LiSi₂N₃:Eu²⁺ (ref. 55) or LiSiON:Eu²⁺,³ the Li–O/N distances of Li₃SiNO₂:Eu²⁺ are in a similar range. LiSi₂N₃:Eu²⁺ crystallizes in the orthorhombic space group Cmc2₁ and has one Li site tetrahedrally coordinated by four N³⁻ anions with Li–N distances between 202(2) and 264(2) pm. The compound exhibits broadband emission with a maximum at λ_max = 572–584 nm. The compound LiSiON:Eu²⁺, which crystallizes in the orthorhombic space group Pca2₁, also has one Li site. The Li⁺ cation has a coordination sphere to three O²⁻ and one N³⁻ anions, whose Li–O distances are between 191.8 and 206.8 pm and the Li–N distance is 225.2 pm resulting in an emission maximum at λ_max = 426–478 nm (fwhm = 142–193 nm). In the publication of LiSi₂N₃:Eu²⁺ and LiSiON:Eu²⁺, no possible positions for the activator ion Eu²⁺ were discussed. In relation to LiSi₂N₃:Eu²⁺ and LiSiON:Eu²⁺, a blue shift in luminescence due to the partial substitution of N³⁻ anions by O²⁻ anions cannot be observed for Li₃SiNO₂:Eu²⁺. Since the structures have fundamental differences regarding the coordination of the Li⁺ cations, a comparison of these compounds is not possible. Other compounds such as Sr[LiAl₃N₄]:Eu²⁺ (SLA:Eu²⁺) (λ_max = 654 nm; fwhm = 50 nm)⁵⁶ and Sr[Li₂Al₂O₂N₂]:Eu²⁺ (SALON:Eu²⁺) (λ_max = 614 nm; fwhm = 48 nm),⁵⁷ for example, have comparable structures, where a partial substitution of N³⁻ anions by O²⁻ anions leads to a blue shift in the observed emission bands. The nephelauxetic effect is stronger for the activator ion Eu²⁺ when it is coordinated by N³⁻ anions rather than by O²⁻ anions due to the higher formal charge of N³⁻ anions. Consequently it leads to a lowering of the 5d energy levels resulting in a red-shift of the Eu²⁺ emissions induced from the d to f transitions.⁵⁸

Conclusion

In this study, a new orange-emitting phosphor Li₃SiNO₂:Eu²⁺ has been successfully prepared by a solid-state reaction in tantalum ampules. The compound can be excited effectively by near-UV to blue light and the single-crystals of Li₃SiNO₂:Eu²⁺ exhibit an emission maximum at λ_max = 601 nm with a full width at half maximum (fwhm) of 90 nm (0.32 eV, 2597 cm⁻¹). The crystal structure with its 3D-network can be described as a condensed layered structure consisting of two different layers A and B, which arrange alternately along the crystallographic a-axis. Although layer A has structural similarities to other compounds such as Na₂Mn₂S₃ and Na₆In₂S₆ and zweier single chains can basically also be found in phosphors such as MSi₂O₂N₂ (M = Sr, Ba, Eu),^26,59–73 the structural motif and connection pattern in layer B are still unknown. The latter consists of pure Li⁺ cations, which build up a dense network of corner- and edge-shared tetrahedra and octahedra with the O²⁻ and N³⁻ anions. Furthermore, we discussed four possible positions in the structure hosting the activator ion Eu²⁺, which include two different octahedral coordination spheres, one octahedral void spanned by a special arrangement of different polyhedra and a tetrahedrally coordinated Li-channel. In comparison with other compounds known from the literature such as α- and β-SiALON,^74–76 we see that heavy cations are not necessarily required as counterions in the structure that can be substituted by the activator ion Eu²⁺ resulting in interesting luminescence properties. Although the new phosphor can be synthesized by low-cost educts and shows relatively good stability against moisture and atmospheric conditions, a further optimization of the material's optical properties must be achieved for possible applications as a phosphor material for example in pc-LEDs.

Experimental section and theoretical methods

Synthesis

Since it is crucial to maintain control over the amount of oxygen for synthesizing oxonitrides, all preparations were carried out using an inert gas (Ar 5.0, Messer Austria GmbH) filled glovebox (MBraun, O₂ < 1 ppm, H₂O < 1 ppm). The starting materials Si₃N₄ (UBE SN-E10, >99%) and Li₂O (Sigma Aldrich, >97%) with a stoichiometric ratio of 1 : 4 were weighed and mixed with 5 wt% LiF (Sigma Aldrich, >99.99%) as a flux and 2mol% EuF₂ (Alfa Aesar, >99.9%) using an agate mortar. Afterwards, the powder mixture was filled into a tantalum ampule and sealed via arc welding under an argon atmosphere. The reaction vessel was then placed inside a silica-glass ampule containing a 400 mbar inert gas atmosphere (Ar 5.0, Messer Austria GmbH). The temperature profile of the synthesis consists of a heating ramp with 4 °C min⁻¹ up to 960 °C, a dwelling time of 4 h, and subsequently a cooling ramp of −0.3 °C min⁻¹ to 300 °C. Once cooled down to room temperature, the ampules could be opened and the samples were further examined under atmospheric conditions without detectable decomposition within several months. The product shows intense yellow to orange luminescence under UV-light (see Fig. 10).

Fig. 10 Left: optical appearance of the 2 mol% Eu²⁺-doped compound Li₃SiNO₂ under daylight. Right: optical appearance of the 2 mol% Eu²⁺-doped compound Li₃SiNO₂ under UV-light (365 nm).

Single-crystal X-ray diffraction

Under a polarization microscope, suitable single-crystals of Li₃SiNO₂ were isolated and subsequently investigated with a Bruker D8 Quest diffractometer (Mo-Kα radiation, λ = 0.7107 Å) equipped with a Photon 300 CMOS detector. The programs Saint⁷⁷ and Sadabs⁷⁸ were used for data processing and multi-scan absorption correction. For the structure solution and parameter refinement, ShelXS⁷⁹ using Direct Methods and ShelXL⁸⁰ using the least squares method, both implemented in the program WinGX,⁸¹ were applied. The structural data were standardized employing Structure Tidy⁸² as implemented in Platon (version 170613).⁸³ Further details on the crystal structure investigation of the single-crystal of Li₃SiNO₂ can be obtained from The Cambridge Crystallographic Data Centre viahttps://www.ccdc.cam.ac.uk/structures/under the deposition number 2208257.†

Powder X-ray diffraction

Powder X-ray diffraction (PXRD), equipped with a STOE Stadi P powder diffractometer with Ge(111)-monochromatized Mo-Kα₁ (λ = 70.93 pm) radiation and a Mythen 1K detector operated in Debye–Scherrer geometry across a 2θ range of 2°–40°, was used for phase analysis. The experimental powder pattern was compared with the calculated powder pattern derived from the single-crystal data of Li₃SiNO₂. The secondary phase identification was carried out with the ICDD PDF-2 database and the program Topas 4.2⁸⁴ was applied for Rietveld refinements.

Luminescence

The emission spectra of representatives from Li₃SiNO₂ were recorded by a setup of a blue laser diode (λ = 448 nm, THORLABS, Newton, NJ, USA) in combination with a CCD detector (AVA AvaSpec 2048, AVANTES, Apeldoorn, The Netherlands). A tungsten–halogen calibration lamp was used for the previous spectral radiance calibration of the setup. The software AVA AvaSoft (version 7) was used for the data preparation. The analysis of the luminescence properties of powder samples was carried out using a Fluoromax 4 spectrophotometer (Horiba). The emission spectrum was recorded in the wavelength range between 470 and 750 nm (step size 1 nm) using an excitation wavelength of 400 nm. The same method was used to record the excitation spectra monitored at the corresponding maximum intensity and for the thermal-quenching analysis.

Author contributions

All the authors have accepted responsibility for the entire content of this submitted manuscript and approved submission.

Conflicts of interest

The authors declare no conflict of interest regarding this article.

Acknowledgements

A part of this work is funded by the German Federal Ministry of Economic Affairs and Climate Action (Bundesministerium für Wirtschaft und Klimaschutz) in the frame of the “Important Project of Common European Interest (IPCEI) on microelectronics”. The authors would like to thank Christiane Stoll for her support in the single-grain and powder luminescence as well as single-crystal X-ray diffraction measurements (ams-OSRAM International GmbH).

References

1. R. Juza, H. H. Weber and E. Meyer-Simon, Z. Anorg. Allg. Chem., 1953, 273, 48–64.
2. Y. Laurent, J. Guyader and G. Roult, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1981, B37, 911–913.
3. Y. Ma, F. Xiao, S. Ye, Q. Zhang, Z. Jiang and Y. Qian, ECS J. Solid State Sci. Technol., 2012, 1, R1.
4. A. Kraśnicka and S. Podsiadlo, J. Therm. Anal. Calorim., 1988, 34, 305–310.
5. S. Podsiadło, J. Therm. Anal., 1987, 32, 771–775.
6. M. Casas-Cabanas, H. Santner and M. Palacín, J. Solid State Chem., 2014, 213, 152–157.
7. K. Bernet and R. Hoppe, Z. Anorg. Allg. Chem., 1991, 592, 93–105.
8. J. Hoffmann, R. Brandes and R. Hoppe, Z. Anorg. Allg. Chem., 1994, 620, 1495–1508.
9. B. Nowitzki and R. Hoppe, Chem. Inf., 1986, 17, 217–230.
10. D. Baumann, M. Seibald, T. Fiedler, S. Lange, H. Huppertz, D. Dutzler, T. Schröder, D. Bichler, G. Plundrich, S. Peschke, G. Hoerder, G. Achreiner and K. Wurst, WO/2018/029304, 2018.
11. R. Werthmann and R. Hoppe, Z. Anorg. Allg. Chem., 1984, 509, 7–22.
12. D. Dutzler, M. Seibald, D. Baumann and H. Huppertz, Angew. Chem., Int. Ed., 2018, 57, 13676–13680.
13. M. Iwaki, S. Kumagai, S. Konishi, A. Koizumi, T. Hasegawa, K. Uematsu, A. Itadani, K. Toda and M. Sato, J. Alloys Compd., 2019, 776, 1016–1024.
14. B. Nowitzki and R. Hoppe, Rev. Chim. Minér., 1986, 23, 217–230.
15. H. Liao, M. Zhao, M. S. Molokeev, Q. Liu and Z. Xia, Angew. Chem., Int. Ed., 2018, 57, 11728–11731.
16. H. Liao, M. Zhao, M. S. Molokeev, Q. Liu and Z. Xia, Angew. Chem., 2018, 130, 11902–11905.
17. H. Liao, M. Zhao, Y. Zhou, M. S. Molokeev, Q. Liu, Q. Zhang and Z. Xia, Adv. Funct. Mater., 2019, 29, 1901988.
18. M. Zhao, H. Liao, L. Ning, Q. Zhang, Q. Liu and Z. Xia, Adv. Mater., 2018, 30, 1802489.
19. M. Zhao, Y. Zhou, M. S. Molokeev, Q. Zhang, Q. Liu and Z. Xia, Adv. Opt. Mater., 2019, 7, 1801631.
20. D. S. Wimmer, M. Seibald, D. Baumann, S. Peschke, K. Wurst, G. Heymann, D. Dutzler, A. Garcia-Fuente, W. Urland and H. Huppertz, Eur. J. Inorg. Chem., 2021, 2021, 4470–4481.
21. M. Zhao, H. Liao, M. S. Molokeev, Y. Zhou, Q. Zhang, Q. Liu and Z. Xia, Light: Sci. Appl., 2019, 8, 1–9.
22. F. Ruegenberg, A. García-Fuente, M. Seibald, D. Baumann, S. Peschke, W. Urland, A. Meijerink, H. Huppertz and M. Suta, Adv. Opt. Mater., 2021, 9, 2101643.
23. D. Dutzler, M. Seibald, D. Baumann, F. Philipp, S. Peschke and H. Huppertz, Z. Naturforsch., B: J. Chem. Sci., 2019, 74, 535–546.
24. F. Ruegenberg, M. Seibald, D. Baumann, S. Peschke, P. C. Schmid and H. Huppertz, Chem. – Eur. J., 2020, 26, 2204–2210.
25. H.-W. Wei, X.-M. Wang, H. Jiao and X.-P. Jing, J. Alloys Compd., 2017, 726, 22–29.
26. V. Bachmann, C. Ronda, O. Oeckler, W. Schnick and A. Meijerink, Chem. Mater., 2009, 21, 316–325.
27. H. A. Höppe, H. Lutz, P. Morys, W. Schnick and A. Seilmeier, J. Phys. Chem. Solids, 2000, 61, 2001–2006.
28. According to F. Liebau, polysilicate units (e.g. chains according to the term “dimensionality” = 1) are classified according to the lowest number of SiO₄ tetrahedra per identity period (“periodicity” of the chain) as the chains of zwei, drei, vier etc. tetrahedra. The terms derive from German numerals zwei (2, two), drei (3, three), vier (4, four), etc. by adding the suffix “er” to the numeral. F. Liebau, Structural Chemistry of Silicates, Springer, Berlin, Heidelberg, 1985. Furthermore, according to the number of polysilicate chains connected to each other via Si–O–Si bridges to form bands (“multiplicity” of the chains), a distinction is made between single, double, triple, etc. chains.
29. J. Zussman, Earth-Sci. Rev., 1968, 4, 39–67.
30. B. Warren and W. L. Bragg, Z. Kristallogr.-Cryst. Mater., 1929, 69, 168–193.
31. X.-M. Wang, C.-H. Wang, M. Wu, Y. Wang and X.-P. Jing, J. Mater. Chem., 2012, 22, 3388–3394.
32. S. Schmiechen, P. Strobel, C. Hecht, T. Reith, M. Siegert, P. J. Schmidt, P. Huppertz, D. Wiechert and W. Schnick, Chem. Mater., 2015, 27, 1780–1785.
33. P. Strobel, V. Weiler, C. Hecht, P. J. Schmidt and W. Schnick, Chem. Mater., 2017, 29, 1377–1383.
34. P. Strobel, S. Schmiechen, M. Siegert, A. Tücks, P. J. Schmidt and W. Schnick, Chem. Mater., 2015, 27, 6109–6115.
35. D. Wilhelm, D. Baumann, M. Seibald, K. Wurst, G. Heymann and H. Huppertz, Chem. Mater., 2017, 29, 1204–1209.
36. K. Klepp, P. Böttcher and W. Bronger, J. Solid State Chem., 1983, 47, 301–306.
37. B. Eisenmann and A. Hofmann, Z. Kristallogr., 1991, 197, 151–152.
38. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.
39. R. Hoppe, Angew. Chem., Int. Ed. Engl., 1966, 5, 95–106.
40. R. Hoppe, Angew. Chem., Int. Ed. Engl., 1970, 9, 25–34.
41. M. v. R. Hübenthal, Maple, version 4, University of Gießen, Gießen (Germany), 1993.
42. I. Brown and D. Altermatt, Acta Crystallogr., Sect. B: Struct. Sci., 1985, 41, 244–247.
43. N. Brese and M. O'keeffe, Acta Crystallogr., Sect. B: Struct. Sci., 1991, 47, 192–197.
44. R. Hoppe, Z. Kristallogr.-Cryst. Mater., 1979, 150, 23–52.
45. R. Hoppe, S. Voigt, H. Glaum, J. Kissel, H. P. Müller and K. Bernet, J. Less-Common Met., 1989, 156, 105–122.
46. T. Farley, W. Hayes, S. Hull, M. Hutchings and M. Vrtis, J. Phys.: Condens. Matter, 1991, 3, 4761.
47. M. Zeuner, S. Pagano and W. Schnick, Angew. Chem., Int. Ed., 2011, 50, 7754–7775.
48. CIE-Diagram: https://de.wikipedia.org/wiki/Datei:Cie_chromaticity_diagram_wavelength.png#/media/Datei:CIExy1931.png (04.08.2021).
49. C. Funk, J. r. Köhler, I. Lazar, D. Kajewski, K. Roleder, J. r. Nuss, A. Bussmann-Holder, H. Bamberger, J. van Slageren and D. Enseling, Cryst. Growth Des., 2018, 18, 6316–6325.
50. M. Zeuner, S. Pagano, P. Matthes, D. Bichler, D. Johrendt, T. Harmening, R. Pöttgen and W. Schnick, J. Am. Chem. Soc., 2009, 131, 11242–11248.
51. J. Felsche, Sci. Nat., 1971, 58, 218–219.
52. M. Zeuner, S. Pagano, S. Hug, P. Pust, S. Schmiechen, C. Scheu and W. Schnick, Eur. J. Inorg. Chem., 2010, 2010, 4945–4951.
53. F. Hintze, N. W. Johnson, M. Seibald, D. Muir, A. Moewes and W. Schnick, Chem. Mater., 2013, 25, 4044–4052.
54. R.-J. Xie, N. Hirosaki, M. Mitomo, K. Sakuma and N. Kimura, Appl. Phys. Lett., 2006, 89, 241103.
55. Y. Li, N. Hirosaki, R. Xie, T. Takeka and M. Mitomo, J. Solid State Chem., 2009, 182, 301–311.
56. P. Pust, V. Weiler, C. Hecht, A. Tücks, A. S. Wochnik, A.-K. Henß, D. Wiechert, C. Scheu, P. J. Schmidt and W. Schnick, Nat. Mater., 2014, 13, 891–896.
57. G. J. Hoerder, M. Seibald, D. Baumann, T. Schröder, S. Peschke, P. C. Schmid, T. Tyborski, P. Pust, I. Stoll, M. Bergler, C. Patzig, S. Reißaus, M. Krause, L. Berthold, T. Höche, D. Johrendt and H. Huppertz, Nat. Commun., 2019, 10, 1824.
58. J. L. Leaño, M.-H. Fang and R.-S. Liu, ECS J. Solid State Sci. Technol., 2017, 7, R3111.
59. O. Oeckler, F. Stadler, T. Rosenthal and W. Schnick, Solid State Sci., 2007, 9, 205–212.
60. F. Stadler, O. Oeckler, H. A. Höppe, M. H. Möller, R. Pöttgen, B. D. Mosel, P. Schmidt, V. Duppel, A. Simon and W. Schnick, Chem. – Eur. J., 2006, 12, 6984–6990.
61. K. Park, D. Kim, Y. Jeong, J. Kim and T. Kim, J. Nanosci. Nanotechnol., 2016, 16, 1700–1702.
62. V. Bachmann, T. Jüstel, A. Meijerink, C. Ronda and P. J. Schmidt, J. Lumin., 2006, 121, 441–449.
63. X. Song, H. He, R. Fu, D. Wang, X. Zhao and Z. Pan, J. Phys. D: Appl. Phys., 2009, 42, 065409.
64. M. Seibald, T. Rosenthal, O. Oeckler, C. Maak, A. Tücks, P. J. Schmidt, D. Wiechert and W. Schnick, Chem. Mater., 2013, 25, 1852–1857.
65. J. Botterman, K. Van den Eeckhout, I. De Baere, D. Poelman and P. F. Smet, Acta Mater., 2012, 60, 5494–5500.
66. X. Song, R. Fu, S. Agathopoulos, H. He, X. Zhao and X. Yu, J. Am. Ceram. Soc., 2011, 94, 501–507.
67. J. A. Kechele, O. Oeckler, F. Stadler and W. Schnick, Solid State Sci., 2009, 11, 537–543.
68. C. H. Hsu, B. M. Cheng and C. H. Lu, J. Am. Ceram. Soc., 2011, 94, 2878–2883.
69. R. Fu, S. Agathopoulos, X. Song, X. Zhao, H. He and X. Yu, Opt. Mater., 2010, 33, 99–102.
70. H. A. Höppe, F. Stadler, O. Oeckler and W. Schnick, Angew. Chem., Int. Ed., 2004, 43, 5540–5542.
71. J. Botterman, K. Van den Eeckhout, A. J. Bos, P. Dorenbos and P. F. Smet, Opt. Mater. Express, 2012, 2, 341–349.
72. M. Seibald, T. Rosenthal, O. Oeckler and W. Schnick, Crit. Rev. Solid State Mater. Sci., 2014, 39, 215–229.
73. M. Seibald, T. Rosenthal, O. Oeckler, F. Fahrnbauer, A. Tücks, P. J. Schmidt and W. Schnick, Chem. – Eur. J., 2012, 18, 13446–13452.
74. K. Kimoto, R.-J. Xie, Y. Matsui, K. Ishizuka and N. Hirosaki, Appl. Phys. Lett., 2009, 94, 041908.
75. N. Hirosaki, R.-J. Xie, K. Kimoto, T. Sekiguchi, Y. Yamamoto, T. Suehiro and M. Mitomo, Appl. Phys. Lett., 2005, 86, 211905.
76. R.-J. Xie, N. Hirosaki, M. Mitomo, Y. Yamamoto, T. Suehiro and K. Sakuma, J. Phys. Chem. Lett., 2004, 108, 12027–12031.
77. Saint, version 8.34a, Bruker AXS Inc., Madison, Wisconsin (USA), 2014.
78. Sadabs, version 2014/5, Bruker AXS Inc., Madison, Wisconsin (USA), 2001.
79. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112.
80. G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3.
81. L. J. Farrugia, J. Appl. Crystallogr., 2012, 45, 849–854.
82. L. Gelato and E. Parthé, J. Appl. Crystallogr., 1987, 20, 139–143.
83. A. L. Spek, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2009, 65, 148–155.
84. Topas, version 4.2, Bruker AXS Inc., Madison, Wisconsin (USA), 2009.

---

Footnotes

† Electronic supplementary information (ESI) available. CCDC 2208257. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2dt03064k

‡ D. W. and K. R. contributed equally to this work.

---