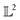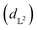Open Access Article
Open Access ArticleAutonomous retrosynthesis of gold nanoparticles via spectral shape matching†
Kiran
Vaddi
 *a,
Huat Thart
Chiang
*a,
Huat Thart
Chiang
 a and
Lilo D.
Pozzo
a and
Lilo D.
Pozzo
 *ab
*ab
aDepartment of Chemical Engineering, University of Washington, Seattle, WA, USA. E-mail: kiranvad@uw.edu; dpozzo@uw.edu
bDepartment of Material Science and Engineering, University of Washington, Seattle, WA, USA
First published on 8th June 2022
Abstract
Synthesizing complex nanostructures and assemblies in experiments involves careful tuning of design factors to obtain a suitable set of reaction conditions. In this paper, we study the application of Bayesian optimization (BO) to achieve autonomous retrosynthesis of a specific nanoparticle or nano-assembly structure, shape, and size starting from a set of reagents selected a priori. We formulate the BO as a shape matching problem given target spectra as a structural proxy with a goal to minimize the shape discrepancy. The proposed framework is grounded in analyzing the spectra as belonging to function spaces and a Riemannian metric defined on them. The metric decomposes spectral similarity into amplitude and phase components. It provides a shape matching distance to optimize as opposed to purely intensity similarity obtained from the commonly used mean squared error (MSE). Applying the framework to experimental and simulated spectra, we demonstrate the advantage of shape matching over MSE and other generic functional distance measures.
1 Introduction
The application of machine learning (ML) based methods to scientific data has improved significantly with both data and tools becoming available in an easy-to-use and open-source format. Predictions based on computational and experimental datasets enabled the accelerated discovery of materials and their developments. Adaptation of high-throughput experimentation for laboratory synthesis and characterization of materials played a key role in enabling screening large design spaces to find materials of interest. This effort is not paralleled through the prediction of laboratory synthesis procedures themselves with few exceptions using language processing to predict potential synthesis routes (given the previously reported synthesis procedures1) and computer-assisted retrosynthesis2 (to evaluate pathways for given reactant product pair). One area of research that has attracted significant interest to address predictive laboratory synthesis is the use of probability-based optimization methods for material discovery starting from a target property provided in spectral form.Black-box optimization such as Bayesian Optimization (BO) is commonly used to optimize a black-box function using a surrogate model and a utility function that is used to guide sequential decisions about evaluation points. Application of BO to structure optimization of nanoparticles has recently been studied in problems that involve optimizing a characteristic response collected through experiments such as UV-Vis spectroscopy incorporated into high-throughput frameworks.3–5 Oftentimes, the characteristic responses collected as a spectrum (i.e., a signal over a discrete sample of a stimulus e.g.: wavelength) are not suited for direct usage in BO. Researchers have looked at defining score functions that return a scalar similarity between a query and target spectra (e.g.: Euclidean distance,4 Cosine distance,3etc.). However, the similarity functions are heavily based on expert knowledge about analyzing the signal and only consider differences on the intensity scale using vector-space distance measures. One way to overcome the limitations (or bottlenecks created from the need for expert knowledge) is to optimize the shape of the spectra i.e., match the query spectra shape to target spectra such that both the local and global features are optimized simultaneously.
Shape matching is advantageous over Euclidean distance in many characterization techniques of interest and provides a natural way to evaluate similarities based on semantic and scientific meaning. For example, in UV-Vis spectroscopy, the shape of the spectra, which is defined by the molar attenuation coefficient, generally gives information on the intrinsic properties of the nanoparticle such as the particle shape or size,6 while the intensity of the spectra gives information on extrinsic properties, such as the concentration. In addition, the intensity of the spectra can be influenced by the particle shape and size distribution, the dielectric properties of the solvent, and the surface chemistry of the nanoparticles, which may introduce further parameters for optimization.7 Because the objective of many optimization campaigns in inorganic nanoparticle retrosynthesis is to obtain particles of desired shapes or sizes, we hypothesize that having a similarity metric that primarily accounts for the structure would be advantageous in the optimization. Given that complex spectra provide information about phenomena occurring over multiple length scales, spectral shape matching provides a viable option for simultaneously matching the relevant patterns of multi-scale phenomena without over-emphasizing variations on the y-scale.
In this paper, we study BO in combination with shape matching on function spaces and the underlying Riemannian manifold structure. We provide a generic framework that considers spectral data as points on function spaces and use differential geometry-based approaches to define similarity measures. These similarity measures are then compared with other, more commonly used approaches, such as Euclidean distance, or peak positions of UV-Vis spectra. The rest of the paper is arranged as follows: we first introduce and review various mathematical frameworks such as Bayesian optimization, function spaces, and Riemannian metrics used in this paper before applying them to a case study of simulated Gaussian spectra and a high-throughput gold nanorod synthesis experiment. We then conclude and provide directions for future usage and applications of interest.
2 Methods
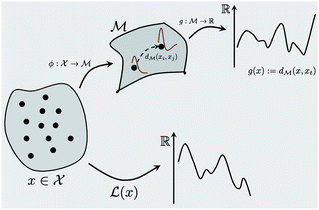
This section provides details about various machine learning and mathematical methods we use to build our framework (see Fig. 1). We first introduce the Bayesian optimization framework in Section 2.1 and highlight its various important components in the context of the spectra-based structure optimization studied in this paper. We then introduce the core idea of the paper in Section 2.3 that represents spectral data as belonging to function space and various manifold and Riemannian metric structures one can use for that representation. Making use of the function space representation, we provide a practical solution to using BO for shape matching in Section 2.2 and derive the required Riemannian metric in Section 2.4. The advantages of using a Riemannian metric are then demonstrated in Section 2.5.2.1 Bayesian optimization
Bayesian optimization (BO) is an iterative algorithm of finding the maximum of a function h whose closed-form expression is unknown.8 Such functions often arise in experimental sciences where the exact mechanism (i.e. a closed-form expression) governing a particular response is unknown thus a forward model does not exist. BO provides a methodology to fit a probabilistic model as a surrogate between the inputs (e.g.: compositional variates) and the outputs (e.g.: similarity of query and target spectra) while simultaneously trying to find the maximum of h using x* = argmaxxh(x). If we denote the set of inputs (i.e. search space or design space) as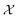 , the function h takes a
, the function h takes a 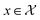 and returns an output we try to maximize. When the output is a scalar value i.e.
and returns an output we try to maximize. When the output is a scalar value i.e.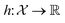 , one common approach to select batch of samples X to query next is to first define a measure of improvement (to the maximum value of h) using an acquisition function
, one common approach to select batch of samples X to query next is to first define a measure of improvement (to the maximum value of h) using an acquisition function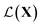 (see eqn (1)) and select points that maximize it. In a Bayesian approach, value of querying X is determined by a utility
(see eqn (1)) and select points that maximize it. In a Bayesian approach, value of querying X is determined by a utility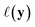 of unknown outcomes y using posterior belief
of unknown outcomes y using posterior belief 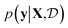 given observed data
given observed data 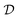 .9 Given a utility in
.9 Given a utility in 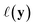 , the acquisition value for points X is defined as expectation over sample draws (or evaluations)
, the acquisition value for points X is defined as expectation over sample draws (or evaluations) 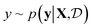 given a probabilistic surrogate model for
given a probabilistic surrogate model for 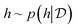 .
.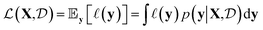 | (1) |
As an example, expected improvement10 computes utility using eqn (2) measuring the improvement given a threshold α as:
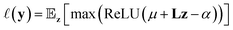 | (2) |
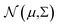 with mean μ and covariance Σ = LL⊤ as the surrogate for h.‡ The parameter z is introduced to make the (stochastic)gradient-based optimization of
with mean μ and covariance Σ = LL⊤ as the surrogate for h.‡ The parameter z is introduced to make the (stochastic)gradient-based optimization of 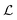 for batch selection tractable using the reparameterization trick i.e.y = μ + Lz (see ref. 9 for more information).
for batch selection tractable using the reparameterization trick i.e.y = μ + Lz (see ref. 9 for more information).
2.2 Utility function for optimization of spectra
In this work, we are interested in solving the optimization problem where at each x, we observe spectra such as the absorption measurement from UV-Vis over a specific wavelength range. We would like to optimize for a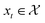 that results in a particular shape of the spectra defined as the target. Thus, the acquisition functions
that results in a particular shape of the spectra defined as the target. Thus, the acquisition functions 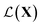 defined for the scalar functions above are not applicable. For example, it is unclear how to define improvement of h(x) when
defined for the scalar functions above are not applicable. For example, it is unclear how to define improvement of h(x) when 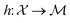 where
where 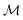 is the space of functions (see Section 2.3). To overcome this, we define h(x) = g(ϕ(x)) i.e. h = g◦ϕ where
is the space of functions (see Section 2.3). To overcome this, we define h(x) = g(ϕ(x)) i.e. h = g◦ϕ where 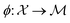 and
and 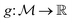 . ϕ is a black-box function that takes an input x and returns a spectrum as a point in the space of functions such as
. ϕ is a black-box function that takes an input x and returns a spectrum as a point in the space of functions such as 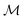 . Function g is defined as a measure of similarity between a target spectra ft = ϕ(λ; xt) at the unknown target location xt and spectra at a query location xq as fq = ϕ(λ; xq). One choice for g is to define it in closed form using the distance function or simply compute distance in its ambient space
. Function g is defined as a measure of similarity between a target spectra ft = ϕ(λ; xt) at the unknown target location xt and spectra at a query location xq as fq = ϕ(λ; xq). One choice for g is to define it in closed form using the distance function or simply compute distance in its ambient space 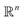 :
: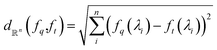 | (3) |
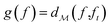 using the distances on space of functions
using the distances on space of functions 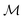 . The utility
. The utility 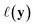 can now be defined as a measure of improvement in the geodesic distance between the model's best estimate and the target spectra.
can now be defined as a measure of improvement in the geodesic distance between the model's best estimate and the target spectra.
2.3 Spectra as points in function spaces
In chemistry and material sciences, spectral data (e.g.: spectroscopy, X-ray diffraction, small-angle X-ray scattering, etc.) are ubiquitous and provide a faster way to characterize the samples often at multiple length scales. As an example, in optical spectroscopy, the wavelength of incident light with known intensity is varied and the scattered intensity from the sample is collected as the output. Mathematically, a spectrum can be described as an evaluation of a function at discrete stimuli to the sample.11 The notion of function spaces allows us to perform standard data analysis and gradient computation of spectral data using differential geometric methods. For example, to collect a UV-Vis spectrum, the wavelength of the incident light is varied in a region of interest, and the optical extinction efficiency of the sample after the light of a particular wavelength passes through it is reported. The collected spectrum can now be considered as discrete evaluations of the function f(λ) where λ is the wavelength. For data analysis purposes, each spectrum can be considered as belonging to a space of functions denoted as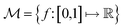 defined on a domain mapped to the unit interval. A differential geometric perspective on functions can now be used to consider functions as points on differentiable manifolds. A manifold for the purposes of this paper is a set of points with a notion of a neighborhood for any given point and is locally similar to the Euclidean space with flat geometry.§ To compute distances on manifolds, we make use of the manifold tangent space
defined on a domain mapped to the unit interval. A differential geometric perspective on functions can now be used to consider functions as points on differentiable manifolds. A manifold for the purposes of this paper is a set of points with a notion of a neighborhood for any given point and is locally similar to the Euclidean space with flat geometry.§ To compute distances on manifolds, we make use of the manifold tangent space 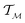 , the space of tangent vectors at all points on the manifold. By definition, the tangent space is a vector space and can be equipped with an inner product called Riemannian metric 〈·, ·〉 that can be used to measure lengths and angles between the tangent vectors. Specifically, the set
, the space of tangent vectors at all points on the manifold. By definition, the tangent space is a vector space and can be equipped with an inner product called Riemannian metric 〈·, ·〉 that can be used to measure lengths and angles between the tangent vectors. Specifically, the set 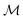 is a Hilbert manifold i.e. a vector space¶ with norm ‖.‖ related to the inner product by
is a Hilbert manifold i.e. a vector space¶ with norm ‖.‖ related to the inner product by 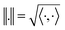 . The Riemannian metric structure allows us to define a distance between two points on manifolds as path lengths connecting them. Given a parametric path
. The Riemannian metric structure allows us to define a distance between two points on manifolds as path lengths connecting them. Given a parametric path 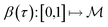 , the instantaneous velocity of the path
, the instantaneous velocity of the path 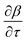 is a tangent vector in
is a tangent vector in 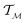 . The length of the path β is given by integrating the lengths of instantaneous velocity vectors over the parametric path using:
. The length of the path β is given by integrating the lengths of instantaneous velocity vectors over the parametric path using: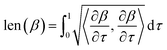 | (4) |
The shortest path on any given manifold between two points is called a geodesic and the corresponding path length as geodesic distance 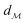 . A generic form of geodesic distance is thus an optimization problem itself (eqn (5)) but for particular manifolds and choice of a metric, there are closed-form expressions.
. A generic form of geodesic distance is thus an optimization problem itself (eqn (5)) but for particular manifolds and choice of a metric, there are closed-form expressions.
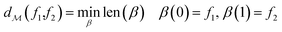 | (5) |
Many choices for the inner product exist with the most commonly used 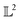 -inner product given by eqn (6) and the resulting function space is called a
-inner product given by eqn (6) and the resulting function space is called a 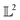 -space. For any two functions
-space. For any two functions 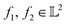 we first map its domain to an unit interval [0, 1] and compute inner product using eqn (6).
we first map its domain to an unit interval [0, 1] and compute inner product using eqn (6).
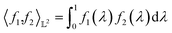 | (6) |
The tangent space 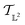 is the entire
is the entire 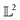 -space thus allows us to define geodesics in a closed form given by a straight line τf1 + (1 − τ)f2 and the geodesic distance is a simple vector norm:
-space thus allows us to define geodesics in a closed form given by a straight line τf1 + (1 − τ)f2 and the geodesic distance is a simple vector norm:
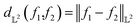 | (7) |
Note that the distance in eqn (7) is different from the commonly used mean-squared error (MSE) between two functions as it involves the integration of functions over the domain. More importantly, MSE is simply a similarity measure between the intensities (or y-scale of one-dimensional function) while eqn (7) provides a geodesic distance between the functions. For more details on the differential geometry of functions, readers are referred to ref. 12 and 13.
2.4 A Riemannian metric for functions shape matching
Although the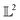 -inner product provides a Riemannian structure to the function spaces, it is very generic and not useful in practice. This is best explained by an example. Consider, the function space of Gaussian's|| with mean μ and variance σ2 evaluated at λ given by:
-inner product provides a Riemannian structure to the function spaces, it is very generic and not useful in practice. This is best explained by an example. Consider, the function space of Gaussian's|| with mean μ and variance σ2 evaluated at λ given by: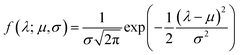 | (8) |
 given by f0 = f(3, 0.5), f1 = f(−2, 0.5), f2 = f(−3, 0.5), f3 = f(−2, 0.8) depicted as a solid-blue curve, solid-black curve, dotted-black curve and dot-dashed-black curve respectively in Fig. 2.
given by f0 = f(3, 0.5), f1 = f(−2, 0.5), f2 = f(−3, 0.5), f3 = f(−2, 0.8) depicted as a solid-blue curve, solid-black curve, dotted-black curve and dot-dashed-black curve respectively in Fig. 2.
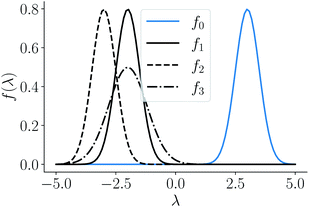 | ||
Fig. 2 Example functions from eqn (8). The functions drawn in dotted and solid black lines are at an equal distance from the function drawn in solid-blue line when compared using an MSE distance and the 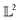 metric but not through the amplitude–phase distance. Similarly, the dash-dot black curve is rightly classified as further than the solid black curve from the solid blue curves using amplitude–phase distance but not others Table 1. metric but not through the amplitude–phase distance. Similarly, the dash-dot black curve is rightly classified as further than the solid black curve from the solid blue curves using amplitude–phase distance but not others Table 1. | ||
When measured using an MSE similarity both the solid and dotted black curves in Fig. 2 are equidistant at 3.34 units from the solid blue curve. This is expected as the MSE only considers the variation along the y-scale thus unable to distinguish between the two functions that are distinct only along the x-axis (i.e. f2 can be obtained by linearly shifting the f1 along the x-axis) where its y-scale variation w.r.to f0 is invariant. This behavior also occurs with the 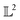 metric (equidistant at 0.34 units) as the value of f0 is zero where the variation of x-axis between f1 and f2 occur. To account for this, we consider another Riemannian metric defined on function spaces by first decoupling the total variation/distance between functions as amplitude (i.e. variation along the y-axis) and phase (i.e. variation along the x-axis).
metric (equidistant at 0.34 units) as the value of f0 is zero where the variation of x-axis between f1 and f2 occur. To account for this, we consider another Riemannian metric defined on function spaces by first decoupling the total variation/distance between functions as amplitude (i.e. variation along the y-axis) and phase (i.e. variation along the x-axis).
The amplitude and phase variations are defined by considering a warping function γ of the domain that continuously maps any given function f1 to f2 without changing the relative amplitudes. More precisely, γ: [0, 1] ↦ [0, 1] is a boundary preserving diffeomorphism (i.e. a smooth function with an inverse) with γ(0) = 0 and γ(1) = 1. The set of warping functions denoted as Γ forms a mathematical structure called the group (i.e. a set with an inverse and identify properties under an associated action) and it can be understood by how it acts on functions f. For example, if we define the group action of a γ ∈ Γ as simply warping the domain using (f, γ) = f◦γ, we can compute γ that optimally warps f1 to f2 by solving 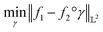 . The
. The 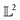 norm, however, is known to suffer from pinching effect among others thus a square-root slope function (SRSF) metric is used instead,13,14 details of which are out of the scope of this paper. SRSF transforms a function f using:
norm, however, is known to suffer from pinching effect among others thus a square-root slope function (SRSF) metric is used instead,13,14 details of which are out of the scope of this paper. SRSF transforms a function f using:
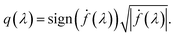 | (9) |
The resulting function representation q is again a differential manifold and 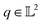 . We can once again use the differential geometry of the
. We can once again use the differential geometry of the 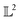 -space to compute the inner product as described below. If v is a tangent vector in the tangent space
-space to compute the inner product as described below. If v is a tangent vector in the tangent space 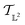 , then its corresponding tangent vector using SRSF is given by
, then its corresponding tangent vector using SRSF is given by 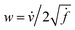 . The required inner product for
. The required inner product for 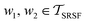 is defined as described in Section 2.3:
is defined as described in Section 2.3:
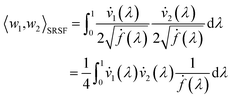 | (10) |
The required warping function γ is now computed by solving for 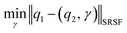 where the group action is
where the group action is 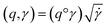 . The warping function γ allows us to define: (i) the amplitude – that doesn't change with the action of γ, (ii) the phase – that only changes with the action of γ. We can now use γ to decompose the function space into the amplitude space and the phase space and assign separate metrics to compute relevant distances. The amplitude space will comprise of “orbits”
. The warping function γ allows us to define: (i) the amplitude – that doesn't change with the action of γ, (ii) the phase – that only changes with the action of γ. We can now use γ to decompose the function space into the amplitude space and the phase space and assign separate metrics to compute relevant distances. The amplitude space will comprise of “orbits” 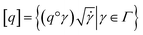 as functions that can be obtained interchangeably by warping their domain alone.** These orbits are not vector spaces thus we need to define a notion of distance. For any given pair of SRSF's q1, q2 in the amplitude space, we define their distance using the orbits as:
as functions that can be obtained interchangeably by warping their domain alone.** These orbits are not vector spaces thus we need to define a notion of distance. For any given pair of SRSF's q1, q2 in the amplitude space, we define their distance using the orbits as:
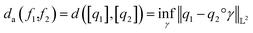 | (11) |
Intuitively, the amplitude distance measures the minimum distance between two functions after alignment. The phase space of the functions is defined by the set of warping functions Γ. Phase distance between two functions f1, f2 is equivalent to function distance between the corresponding warping function γ and the identity warping function γ(t) = t, t ∈ [0, 1]. Warping functions attain a well-known spherical geometry (the infinite dimensional Hilbert spheres 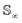 i.e. points with unit norm in infinite dimensions required to fully represent a function space) upon representing them using the SRSF transformation i.e.
i.e. points with unit norm in infinite dimensions required to fully represent a function space) upon representing them using the SRSF transformation i.e.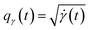 (since
(since ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (t) > 0). This is because,
(t) > 0). This is because,
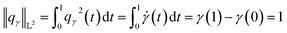 | (12) |
Since qγ uniquely maps a given γ, we can conclude that 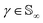 with the geodesics given by the great circles
with the geodesics given by the great circles 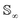 . Thus the required phase distance between the functions f1, f2 is given by arc length of the great circle:
. Thus the required phase distance between the functions f1, f2 is given by arc length of the great circle:
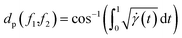 | (13) |
The total (un-weighted) distance between functions f1, f2 can now be computed using:
| dap(f1,f2) = da(f1,f2) + dp(f1,f2) | (14) |
Using the distance in eqn (14), we can now successfully differentiate between the solid and dotted black curves in Fig. 2 where both curves have zero amplitude distance to the reference blue curve but are at a phase distance of 0.55 and 0.62 respectively. We refer to the distance function in eqn (14) as the amplitude–phase distance to differentiate it from the SRSF distance function obtained using eqn (5) under the SRSF inner product in eqn (10) (i.e. dSRSF = ‖f1 − f2‖SRSF). The SRSF distance function suffers from a similar problem as that of the 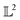 distance and considers both the solid and dotted black curves to be equidistant at 1.78 units from the solid blue curve. The effectiveness of shape matching can be inferred from the distances each metric assigns to f3 relative to f1. We observe that functions f1, f3 are a very similar to each other as their peaks are perfectly aligned (at λ = −2) but f1 is similar to f0 in shape than f3. While all the metrics successfully differentiate f1, f3 to be distinct (see Table 1), the amplitude–phase distance measures the distance to f3 as 4% longer than f1 which is in agreement with our intuition while other metrics consider it to be ≈10% shorter. The amplitude–phase distance, therefore, is a suitable measure for shape matching. Note that, alternatively, we can define total shape matching distance to be a weighted combination of da and dp to better capture the retrosynthesis target. For example, if we want to prioritize matching nanoparticle size than concentration as our retrosynthesis target, we can weigh phase distance more to better match the peak position.
distance and considers both the solid and dotted black curves to be equidistant at 1.78 units from the solid blue curve. The effectiveness of shape matching can be inferred from the distances each metric assigns to f3 relative to f1. We observe that functions f1, f3 are a very similar to each other as their peaks are perfectly aligned (at λ = −2) but f1 is similar to f0 in shape than f3. While all the metrics successfully differentiate f1, f3 to be distinct (see Table 1), the amplitude–phase distance measures the distance to f3 as 4% longer than f1 which is in agreement with our intuition while other metrics consider it to be ≈10% shorter. The amplitude–phase distance, therefore, is a suitable measure for shape matching. Note that, alternatively, we can define total shape matching distance to be a weighted combination of da and dp to better capture the retrosynthesis target. For example, if we want to prioritize matching nanoparticle size than concentration as our retrosynthesis target, we can weigh phase distance more to better match the peak position.
2.5 Advantage of SRSF over MSE and other function distances
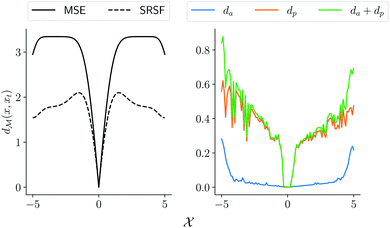
MSE or Euclidean distance are commonly used as a measure of similarity for optimizing spectral data. In this section, we provide a simple example to demonstrate the advantages of the SRSF framework over the standard metrics and similarity measures such as MSE. We first note that MSE, and Euclidean distance in n-dimensions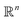 are identical and require all the functions to have the same evaluation points in the domain. However, SRSF is a metric on the vector space of function spaces and can be computed irrespective of the domain sampling rate used to represent them. The general SRSF distance based on the metric provided in eqn (10) varies smoothly as opposed to MSE that measures effective “overlap” resulting in numerically-flat regions away from the target spectra as shown in Fig. 3. In Fig. 3, we plot the distance from a target Gaussian function centered at zero with a fixed variance = 0.5 to all other curves with different mean values on the x-axis. We observe that MSE results in distance functions with extended flat regions in addition to a sharp minimum also observed with SRSF distance. The amplitude–phase distance on the other hand results in a distance measure shown in the right panel of Fig. 3 that monotonically decreases towards the target. The amplitude–phase distance function is noisy as the internal working of eqn (14) involves optimizing for γ using a dynamic-programming algorithm.13 The noisy distance function is not going to be problematic in practice as we use a surrogate model defined by smooth Gaussian processes for BO with a Gaussian likelihood noise (see Section 3.1).
are identical and require all the functions to have the same evaluation points in the domain. However, SRSF is a metric on the vector space of function spaces and can be computed irrespective of the domain sampling rate used to represent them. The general SRSF distance based on the metric provided in eqn (10) varies smoothly as opposed to MSE that measures effective “overlap” resulting in numerically-flat regions away from the target spectra as shown in Fig. 3. In Fig. 3, we plot the distance from a target Gaussian function centered at zero with a fixed variance = 0.5 to all other curves with different mean values on the x-axis. We observe that MSE results in distance functions with extended flat regions in addition to a sharp minimum also observed with SRSF distance. The amplitude–phase distance on the other hand results in a distance measure shown in the right panel of Fig. 3 that monotonically decreases towards the target. The amplitude–phase distance function is noisy as the internal working of eqn (14) involves optimizing for γ using a dynamic-programming algorithm.13 The noisy distance function is not going to be problematic in practice as we use a surrogate model defined by smooth Gaussian processes for BO with a Gaussian likelihood noise (see Section 3.1).
Measures of similarity such as MSE, do not perform well in high-dimensional data sets such as the ones we are interested in (i.e., spectra or scattering profiles), and quantifying the amount of similarity between two functions using them may not be meaningful. One reason for this is the curse of dimensionality,15 where trends in data become counter-intuitive as the number of dimensions increases. One aspect of the curse of dimensionality is that in higher-dimensional vector spaces, almost all the points are equidistant thus the notion of similarity is not well defined. Some of the recent works in machine learning and deep learning address this problem by formulating learning as a geometric problem defined by symmetry groups and differential manifolds.16 Our current approach for functions belongs to a similar category where we exploit the underlying symmetries (i.e. invariance of inner-product under domain warping encoded via group structure on the warping functions) along with their underlying geometry (given by infinite-dimensional Hilbert sphere).
3 Results and discussion
We apply the Bayesian optimization framework for spectra based retrosynthesis in two different case studies. In the first case study, we use simple Gaussian functions as the space of spectra to explore and optimize in and compare the performance of different distance measures for optimization problems. We then apply the framework to an experimental synthesis case study with user-defined UV-Vis spectrum as a target and again compare the performances of different metrics. Both the case studies presented here are run in a batch fashion to account for the optimization of the acquisition function updates using the stochastic gradient ascent. In both the case studies, we model the surrogate GP using the commonly used Matérn Kernel (see ref. 17, ch. 4, p. 84) with the default hyperparameter priors and optimization algorithms in the botorch package. The best estimate at any given batch iteration is obtained by maximizing the surrogate GP which is equivalent to finding the maximum of trained GP mean function. We solve the maximization problem with a goal to maximize the negative distance therefore the similarity to target.3.1 Case study 1: comparing the performance of MSE and amplitude–phase distance
In this case study, we compare the performance of the MSE and our proposed amplitude–phase distance within the BO framework of Section 2.1. We try to optimize the mean μ and standard deviation σ parameters of a target Gaussian function using the BO framework presented in Section 2.1. The Gaussian function is computed over a uniform interval λ ∈ [−5, 5] using eqn (8). The search space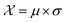 is bounded on μ ∈ [−5, 5] and σ ∈ [0, 1]. We arbitrarily pick a target location in
is bounded on μ ∈ [−5, 5] and σ ∈ [0, 1]. We arbitrarily pick a target location in 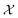 to be xt = (−2, 0.1) and the spectral target is given by ϕ(λ; xt). The goal in this task is to obtain a
to be xt = (−2, 0.1) and the spectral target is given by ϕ(λ; xt). The goal in this task is to obtain a 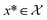 that results in minimum distance between ϕ(λ; xt) and ϕ(λ; x*). In Fig. 4, we plot the optimization trace with distance between current best estimate
that results in minimum distance between ϕ(λ; xt) and ϕ(λ; x*). In Fig. 4, we plot the optimization trace with distance between current best estimate 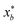 at batch iteration b of the target and the ground truth denoted
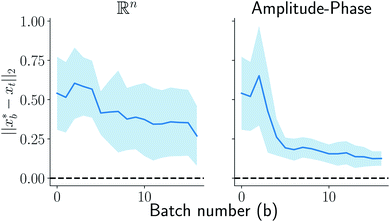
at batch iteration b of the target and the ground truth denoted 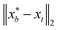 on y-axis over the batch iteration number on x-axis. Both the MSE and amplitude–phase distances start the optimization process with the same set of randomly selected data and are allowed a budget of 16 batch iterations with a batch size of 4 samples. The optimization is repeated 10 times each time starting with different random samples in
on y-axis over the batch iteration number on x-axis. Both the MSE and amplitude–phase distances start the optimization process with the same set of randomly selected data and are allowed a budget of 16 batch iterations with a batch size of 4 samples. The optimization is repeated 10 times each time starting with different random samples in 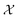 . We can observe from the mean trace in Fig. 4 (solid-blue curve) that on average amplitude–phase distance obtains ≈0.1 units gain over MSE. We also observe that MSE provides more noisy estimates of the best location even towards the end of the campaign (batch number ≈10) in comparison to the amplitude–phase distance. Amplitude–phase distance also converges much faster (batch number ≈10) to its best estimate while the MSE has not converged at the budget expiry. We attribute the success of the amplitude–phase distance to its convexity as described earlier.
. We can observe from the mean trace in Fig. 4 (solid-blue curve) that on average amplitude–phase distance obtains ≈0.1 units gain over MSE. We also observe that MSE provides more noisy estimates of the best location even towards the end of the campaign (batch number ≈10) in comparison to the amplitude–phase distance. Amplitude–phase distance also converges much faster (batch number ≈10) to its best estimate while the MSE has not converged at the budget expiry. We attribute the success of the amplitude–phase distance to its convexity as described earlier.
3.2 Case study 2: comparison of similarity metrics for the retrosynthesis of gold nanorods
In this case study, a high-throughput experimental retrosynthesis campaign of a gold nanorod structure is performed starting with a target UV-Vis spectra. Retrosynthesis campaigns were performed in parallel, with a different similarity metric in a two-dimensional reaction space. We describe and discuss results for two retrosynthesis campaigns: (a) using the Euclidean distance between the raw spectra, (b) using the amplitude–phase distance (eqn (14)). Retrosynthesis campaigns for two other metrics (peak-wavelength distance and SRSF distance (eqn (10))) are included in the ESI.† Following the synthesis procedure described in ref. 18, gold nanorods were synthesized with five chemicals: gold(III) chloride trihydrate, hexadecyltrimethylammonium bromide (CTAB), ascorbic acid (AA), silver nitrate (AgNO3), and gold seeds. An arbitrary nanorod was synthesized by pipetting a pre-specified volume of the five solutions and its UV-Vis spectrum was used as the target for the optimization.Each optimization had a batch size of 4 samples and the iterative process continued until a total of 7 batches had been synthesized. The concentrations of CTAB, gold(III) chloride trihydrate, and gold seeds were kept constant and equal to those that were used to synthesize the target sample (see the column target concentration in Table 2). The search space for the autonomous retrosynthesis is then defined as the two-dimensional reaction space of the concentrations of silver nitrate ([AgNO3]) and ascorbic acid ([AA]). An OT2 liquid handling robot was used to autonomously synthesize the samples using an in-house developed control software OT2-DOE,†† and a Biotek plate reader was used to characterize the samples using UV-Vis spectroscopy with wavelengths of 400–900 nm in increments of 5 nm. The samples were made in 96-well polystyrene microplates, which were heated to around 30 °C during the synthesis using a hot plate. After the synthesis, the samples were kept at the same temperature for 50 minutes, so that the nanoparticles could fully grow, before being characterized by UV-Vis spectroscopy. All the retrosynthesis campaigns had identical initial conditions (i.e., the first batch had the same concentrations and measured spectra).
| Reagent | Stock solution concentration (M) | Target concentration (M) | Concentration range (M) |
|---|---|---|---|
| CTAB | 2.0 × 10−1 | 6.40 × 10−2 | 6.40 × 10−2 |
| Gold(III) chloride trihydrate | 1.0 × 10−3 | 1.96 × 10−4 | 1.96 × 10−4 |
| Silver nitrate | 6.4 × 10−4 | 6.20 × 10−5 | 0 to 7.38 × 10−5 |
| Ascorbic acid | 6.3 × 10−3 | 3.60 × 10−4 | 0 to 7.27 × 10−4 |
| Gold seeds | 1.8 × 10−5 | 1.44 × 10−6 | 1.44 × 10−6 |
Results from the retrosynthesis of gold nanorods using the amplitude–phase distance are shown in Fig. 5. Each panel in Fig. 5 represents the surrogate at a particular stage of the optimization (annotated by the iteration) along with the data the model has ‘seen’ or been trained on. The surrogate is plotted as continuous contours using the colorbar shown on the far right in Fig. 5. We obtain a best composition estimate (i.e. location in the design space whose spectra best matches the target spectra ut shown in aqua colored star in Fig. 5) in the design space by querying for the maximum of surrogate 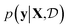 .
.
 | ||
| Fig. 5 Optimization trace for a gold nanorod target using the amplitude–phase distance. Each panel shows the surrogate model as a contour plot, data points collected/queried from the experiment in circles, the current best estimate using an aqua-colored star, and the retrosynthesis target using a green-colored star. The x-axis of each plot represents the concentration of silver nitrate (M × 10−5) and the y-axis represents the concentration of ascorbic acid (M × 10−4). All the compositions are annotated with the respective spectra obtained from the experiment. We observe gradual changes to the surrogate approximation with an increase in data collected and the optimization mainly focuses on improving the region with a lot of ‘target-like’ spectra. As argued in the text, the surrogate obtained around iteration 6 and 7 appear closer to an underlying phase diagram of nano-structural geometry obtained from a coarse grid sampling of the design space shown in Fig. 7. | ||
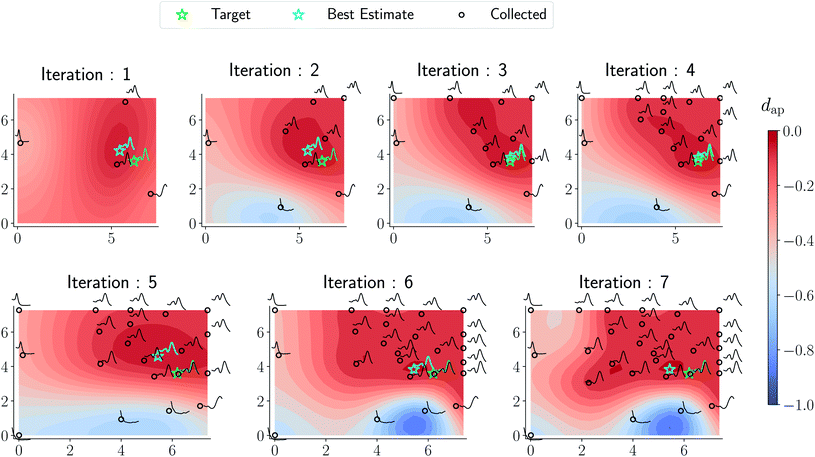
In Fig. 6 we visualize the optimization campaign for a gold nanorod target structure using a Euclidean distance for spectral similarity similar to Fig. 5.
 | ||
| Fig. 6 Optimization trace for a gold nanorod target using a Euclidean distance similar to Fig. 5. As argued in the text, the surrogate obtained from the optimization is not reflective of the underlying phase diagram in Fig. 7 although the target approximation is relatively similar to that of the amplitude–phase distance. | ||
As can be seen from Fig. 5 and 6, both the retrosynthesis campaigns result in a fairly similar approximation to the target spectra but do so with distinctly different surrogate models at the end of respective campaigns (see Fig. S2 and S3 in ESI† for other metrics). To understand which surrogate model better captures the true shape-based phase diagram of nano-structural geometries, we performed a coarse grid sampling of the two-dimensional design space shown in Fig. 7. We observe three broad classes of nanostructures in the design space 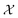 : (a) nanorods – spanning the upper right corner of
: (a) nanorods – spanning the upper right corner of 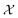 in orange; (b) nanospheres – spanning left-most part of
in orange; (b) nanospheres – spanning left-most part of 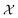 in blue and (c) space with no nanostructures at the bottom in red. Based on the classes we observe in Fig. 7, we hypothesize that the underlying phase diagram would be a function (assuming continuous, mapping concentrations to the type of nano-structure classes mentioned above) with nearly flat regions representing the three classes. The surrogate model learned during the optimization campaign should at least identify the critical points/regions of the phase diagram function in order to provide trustworthy approximations of the retro-synthesized target. Based on our observations in Fig. 7, for a nanorod target, we note that the surrogate obtained from amplitude–phase distance is a better representation of the underlying phase diagram as it clearly identifies that the top right corner of
in blue and (c) space with no nanostructures at the bottom in red. Based on the classes we observe in Fig. 7, we hypothesize that the underlying phase diagram would be a function (assuming continuous, mapping concentrations to the type of nano-structure classes mentioned above) with nearly flat regions representing the three classes. The surrogate model learned during the optimization campaign should at least identify the critical points/regions of the phase diagram function in order to provide trustworthy approximations of the retro-synthesized target. Based on our observations in Fig. 7, for a nanorod target, we note that the surrogate obtained from amplitude–phase distance is a better representation of the underlying phase diagram as it clearly identifies that the top right corner of 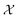 to contain nanorods with minimal changes to similarity w.r.to target spectra. In contrast, the surrogate from Euclidean distance has a sharp peak near the best estimate followed by a sharp decrease in the space comprising only nanorods effectively only capturing similarity closer to the target not anywhere else. This does not capture the underlying phase diagram structure in terms of flat regions and the nature of function transitions, but it may indicate that the Euclidean distance metric is suitable when differentiating between structures of the same class (e.g., nanorods). We also observe that BO with Euclidean distance metric prioritizes exploitation, as seen by a high number of samples near the target in iteration 7 of Fig. 6, while the one using amplitude–phase prioritizes exploration, as seen by the more dispersed samples in iteration 7 of Fig. 5. Moreover, the Euclidean distance surrogate is highly dependent on samples collected during the exploration phase being close to the target as the true function approximation has a sharp peak that needs to be modeled by the surrogate for the optimization to find the true global maximum.
to contain nanorods with minimal changes to similarity w.r.to target spectra. In contrast, the surrogate from Euclidean distance has a sharp peak near the best estimate followed by a sharp decrease in the space comprising only nanorods effectively only capturing similarity closer to the target not anywhere else. This does not capture the underlying phase diagram structure in terms of flat regions and the nature of function transitions, but it may indicate that the Euclidean distance metric is suitable when differentiating between structures of the same class (e.g., nanorods). We also observe that BO with Euclidean distance metric prioritizes exploitation, as seen by a high number of samples near the target in iteration 7 of Fig. 6, while the one using amplitude–phase prioritizes exploration, as seen by the more dispersed samples in iteration 7 of Fig. 5. Moreover, the Euclidean distance surrogate is highly dependent on samples collected during the exploration phase being close to the target as the true function approximation has a sharp peak that needs to be modeled by the surrogate for the optimization to find the true global maximum.
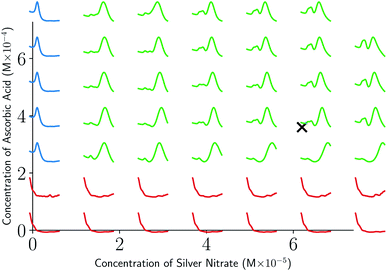 | ||
| Fig. 7 Spectra obtained from a coarse grid sampling of the two-dimensional design space in Table 2. Observe that the space is continuous in terms of nano-structural geometries with three broad classes: no nano-structures (red), nanospheres (blue), and nanorods (green). Retrosynthesis target spectrum location is highlighted with a black cross mark. | ||
4 Conclusion
In this paper, we introduced a practical framework for autonomous retrosynthesis of nanoscale structures using a combination of Bayesian optimization and Riemannian geometry. Our framework is designed for structure optimization using spectral data such as optical extinction, scattering as structural proxies. We proposed a differential geometry-based approach for analyzing and comparing spectral data that result in a near-convex function to be optimized and outperforms the commonly used similarities measures (MSE) and distances (Euclidean). The proposed use of amplitude–phase distance allows us to run material retrosynthesis campaigns to match the shape of spectra as opposed to matching expert-defined or hand-engineered features. We anticipate that the generic framework proposed in this paper would provide a powerful framework to optimize over complex synthesis spaces and spectral characterization beyond the case studies presented here. Specifically, we anticipate that this approach would be useful in optimizing for spectra where the scientifically interesting features are complex, occurring over a span of the domain (e.g.: small-angle X-ray scattering) as opposed to point-wise (such as peak intensity or position) or when the spectra are closed curves (e.g.: cyclic voltammetry).Data availability
All the data and code to reproduce the case studies presented in this paper is available at https://github.com/pozzo-research-group/HEAD/tree/BO. We use botorch19 for Bayesian optimization routines, GPyTorch20 for Gaussian processes, geomstats21 and fdasrsf22 for differential geometry based computation. All the code is implemented in python with reliance on numpy,23 scipy24 for numerical computing and matplotlib25 for plotting routines.Author contributions
All the authors contributed equally to conceptualization, problem formulation, manuscript writing, and reviews. K. V. developed the theoretical and algorithmic framework for optimization, and distance metric computations and performed theoretical case studies. H. T. C. developed the experimental pipeline, wrote code for high-throughput experimentation, and performed all the experimental synthesis and data collection. K. V. and H. T. C. contributed equally in integrating the optimization algorithm with the experimental pipeline and data analysis.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This material is based upon work supported by the US Department of Energy (DOE), Office of Science, Office of Basic Energy Sciences (BES), as part of the Energy Frontier Research Centers program: CSSAS – The Center for the Science of Synthesis Across Scales – under Award Number DE-SC0019288. Part of this work was conducted with instrumentation provided by the Joint Center for Deployment and Research in Earth Abundant Materials (JCDREAM).Notes and references
- E. Kim, Z. Jensen, A. van Grootel, K. Huang, M. Staib, S. Mysore, H.-S. Chang, E. Strubell, A. McCallum and S. Jegelka, et al. , J. Chem. Inf. Model., 2020, 60, 1194–1201 CrossRef CAS PubMed.
- C. W. Coley, D. A. Thomas, J. A. Lummiss, J. N. Jaworski, C. P. Breen, V. Schultz, T. Hart, J. S. Fishman, L. Rogers, H. Gao and R. W. Hicklin, Science, 2019, 365(6453), eaax1566 CrossRef CAS PubMed.
- F. Mekki-Berrada, Z. Ren, T. Huang, W. K. Wong, F. Zheng, J. Xie, I. P. S. Tian, S. Jayavelu, Z. Mahfoud and D. Bash, et al. , npj Comput. Mater., 2021, 7, 1–10 CrossRef.
- D. Salley, G. Keenan, J. Grizou, A. Sharma, S. Martín and L. Cronin, Nat. Commun., 2020, 11, 1–7 CrossRef PubMed.
- H. Tao, T. Wu, S. Kheiri, M. Aldeghi, A. Aspuru-Guzik and E. Kumacheva, Adv. Funct. Mater., 2021, 31, 2106725 CrossRef CAS.
- X. Liu, M. Atwater, J. Wang and Q. Huo, Colloids Surf., B, 2007, 58, 3–7 CrossRef CAS PubMed.
- T. Hendel, M. Wuithschick, F. Kettemann, A. Birnbaum, K. Rademann and J. Polte, Anal. Chem., 2014, 86, 11115–11124 CrossRef CAS PubMed.
- J. R. Gardner, M. J. Kusner, Z. E. Xu, K. Q. Weinberger and J. P. Cunningham, ICML, 2014, pp. 937–945 Search PubMed.
- J. T. Wilson, R. Moriconi, F. Hutter and M. P. Deisenroth, 2017, arXiv preprint arXiv:1712.00424.
- J. Močkus, Optimization techniques IFIP technical conference, 1975, pp. 400–404 Search PubMed.
- K. Vaddi and O. Wodo, ChemRxiv, 2021 DOI:10.26434/chemrxiv.14569035.v1.
- X. Pennec, S. Sommer and T. Fletcher, Riemannian geometric statistics in medical image analysis, Academic Press, 2019 Search PubMed.
- A. Srivastava and E. P. Klassen, Functional and shape data analysis, Springer, 2016, vol. 1 Search PubMed.
- A. Srivastava, E. Klassen, S. H. Joshi and I. H. Jermyn, IEEE Trans. Pattern Anal. Mach. Intell., 2010, 33, 1415–1428 Search PubMed.
- C. C. Aggarwal, A. Hinneburg and D. A. Keim, International conference on database theory, 2001, pp. 420–434 Search PubMed.
- M. M. Bronstein, J. Bruna, T. Cohen and P. Veličković, 2021, arXiv preprint arXiv:2104.13478.
- C. K. Williams and C. E. Rasmussen, Gaussian processes for machine learning, MIT Press, Cambridge, MA, 2006, vol. 2 Search PubMed.
- B. Nikoobakht and M. A. El-Sayed, Chem. Mater., 2003, 15(10), 1957–1962 CrossRef CAS.
- M. Balandat, B. Karrer, D. R. Jiang, S. Daulton, B. Letham, A. G. Wilson and E. Bakshy, 2019, arxiv e-prints, arXiv-1910.
- J. R. Gardner, G. Pleiss, D. Bindel, K. Q. Weinberger and A. G. Wilson, 2018, arXiv preprint arXiv:1809.11165.
- N. Miolane, N. Guigui, A. Le Brigant, J. Mathe, B. Hou, Y. Thanwerdas, S. Heyder, O. Peltre, N. Koep and H. Zaatiti, et al. , J. Mach. Learn. Res., 2020, 21, 1–9 Search PubMed.
- J. D. Tucker, W. Wu and A. Srivastava, Comput. Stat. Data Anal., 2013, 61, 50–66 CrossRef.
- C. R. Harris, K. J. Millman, S. J. van der Walt, R. Gommers, P. Virtanen, D. Cournapeau, E. Wieser, J. Taylor, S. Berg and N. J. Smith, et al. , Nature, 2020, 585, 357–362 CrossRef CAS PubMed.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser and J. Bright, et al. , Nat. Methods, 2020, 17, 261–272 CrossRef CAS PubMed.
- J. D. Hunter, Comput. Sci. Eng., 2007, 9, 90–95 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2dd00025c |
| ‡ ReLU is a rectified linear unit non-linearity. |
| § This notion is more generic than the commonly known low-dimensional manifold concept in the (applied)machine learning community. |
¶ Because given 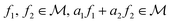 , where , where 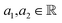 . . |
| || Gaussian's are selected both for its simplicity and relevance to poly-dispersity related effects on spectral characterizations of nanoparticles. |
| ** Orbits w.r.to the warping function group and its associated action. |
| †† https://github.com/pozzo-research-group/OT2-DOE/tree/Shape_Matching_Paper. |
| This journal is © The Royal Society of Chemistry 2022 |