Open Access Article
Open Access ArticleSelf-learning entropic population annealing for interpretable materials design†
Jiawen
Li
a,
Jinzhe
Zhang
a,
Ryo
Tamura
*abcd and
Koji
Tsuda
 *acd
*acd
aGraduate School of Frontier Sciences, The University of Tokyo, 5-1-5 Kashiwanoha, Kashiwa 2778561, Japan. E-mail: tsuda@k.u-tokyo.ac.jp
bInternational Center for Materials Nanoarchitectonics (WPI-MANA), National Institute for Materials Science, 1-1 Namiki, Tsukuba, Ibaraki 305-0044, Japan. E-mail: tamura.ryo@nims.go.jp
cResearch and Services Division of Materials Data and Integrated System, National Institute for Materials Science, 1-1 Namiki, Tsukuba, Ibaraki 305-0044, Japan
dRIKEN Center for Advanced Intelligence Project, 1-4-1 Nihonbashi, Chuo-ku, Tokyo 103-0027, Japan
First published on 4th April 2022
Abstract
In automatic materials design, samples obtained from black-box optimization offer an attractive opportunity for scientists to gain new knowledge. Statistical analyses of the samples are often conducted, e.g., to discover key descriptors. Since most black-box optimization algorithms are biased samplers, post hoc analyses may result in misleading conclusions. To cope with the problem, we propose a new method called self-learning entropic population annealing (SLEPA) that combines entropic sampling and a surrogate machine learning model. Samples of SLEPA come with weights to estimate the joint distribution of the target property and a descriptor of interest correctly. In short peptide design, SLEPA was compared with pure black-box optimization in estimating the residue distributions at multiple thresholds of the target property. While black-box optimization was better at the tail of the target property, SLEPA was better for a wide range of thresholds. Our result shows how to reconcile statistical consistency with efficient optimization in materials discovery.
Introduction
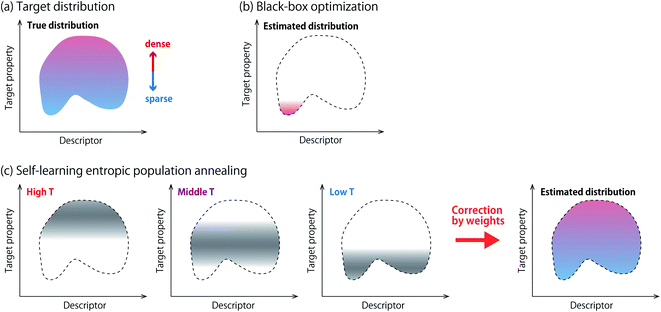
Automatic design of materials based on black-box optimization1 has shown tremendous success in developing functional materials including organic chemical compounds,2 inorganic materials3 and biopolymers such as peptides4 and proteins.2 Popular methods of black-box optimization include Bayesian optimization,5 and evolutionary algorithms.6,7 Given a candidate material, an experiment is regarded as a black-box function that returns its property value such as bioactivity,8 thermal conductivity9 or electron gain energy.10 Black-box optimization is an iterative procedure that recommends one material or a batch of materials for experiments at a time. It is expected to find a material with a favorable property with a minimum number of experiments. Notice that an experiment is often replaced with a simulator or a prediction model.Samples obtained from black-box optimization offer an attractive opportunity for scientists to gain new knowledge. Statistical analyses of the samples are often conducted to discover new structure–property relationships,10 or key descriptors that explain their favorable property.11 However, such analyses have to be done with caution, because most of the existing black-box optimizers are biased samplers. Fig. 1a and b show a schematic picture about this issue. This paper aims to develop algorithmic methods that achieve efficient optimization and statistical consistency at the same time.
Density-of-states (DoS) refers to the probability distribution of observables of a physical system such as spin glass.12 Observables may include energy, pressure and other physical parameters. If DoS is obtained, the free energy of the target physical system can be evaluated and the system is regarded as understood. Exact estimation of DoS requires enumeration of all possible physical configurations which involves prohibitive computational cost. Estimation of DoS is nevertheless possible with sampling methods including the Wang–Landau method13 and stochastic approximation Monte Carlo.14 These methods are known under the umbrella term entropic sampling. They have mechanisms to obtain samples from low energy regions, which are hardly found by naive sampling procedures due to the small occurrence probability. In this paper, we use entropic sampling in the context of interpretable materials design. The target property and a descriptor are designated as the energy of the system and an additional observable, respectively, and the joint distribution is estimated as DoS.
Among several methods of entropic sampling, we employ entropic population annealing (EPA)15 as our base method, and extend it to self-learning EPA (SLEPA) by incorporating a machine learning model. In both methods, Boltzmann distributions at multiple temperatures are introduced and some samples are obtained from each distribution using Markov chain Monte Carlo (MCMC) (Fig. 1c). As the temperature is decreased, the samples are gradually concentrated towards optimal solutions. Then, DoS is estimated from the samples using the multiple histogram method (MHM).16 The difference between EPA and SLEPA is that EPA accesses the energy (i.e., target property) whenever a new sample is created, while SLEPA uses a predicted value from the surrogate machine learning model. SLEPA tends to be more cost effective, but the distribution shift made by the prediction error has to be corrected eventually in DoS estimation.
In computational experiments, SLEPA and EPA were evaluated in a peptide design problem, where scientists are interested in finding sequential signatures that determine the properties.17 We are thus committed to estimating the residue distributions of qualified sequences that correspond to a small percentile in the target property. Multiple qualification thresholds ranging from 0.01 to 10 percentiles were used. When an evolution strategy (ES),6 a pure black-box optimizer, was applied, its estimation accuracy was best for the tightest thresholds. Simple random sampling was best for the loosest thresholds. For a wide range of thresholds, however, SLEPA and EPA were better than them. SLEPA showed better estimation accuracies than EPA, indicating that the use of a surrogate model enhances sample efficiency. This result illustrates how to reconcile statistical consistency with efficient optimization and shows the usefulness of our approach when acquiring knowledge is more important than optimization.
Method
Observables and density of states
Let X denote the set of all possible materials. In black-box optimization, we aim to find x ∈ X that minimizes the target property e(x). Obtaining e(x) for x incurs certain cost, because it is done via an experiment or numerical simulation. In the following, e(x) is referred to as energy and the acquisition of e(x) is called observation. In this paper, we deal with the research tasks where the relationship between e(x) and d(x), a descriptor, is of interest. More specifically, we need to find the expectation value of an observable O(d(x), e(x)), i.e., a function depending on e(x) and d(x),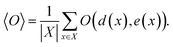 | (1) |
The observable is determined according to users' interest. Let us suppose that one is interested in the descriptor value to yield a favorable target property, e(x) ≤ δ, where δ is a qualification threshold. The observable should then be set as O(d(x), e(x)) = d(x)I(e(x) ≤ δ), where I(·) is the indicator function which is one if the condition in the parentheses is satisfied, zero otherwise. Also, if one needs to draw a two dimensional distribution as in Fig. 1, the density at the grid el ≤ e(x) ≤ eh, dl ≤ d(x) ≤ dh can be obtained by setting O(d(x), e(x)) = I(dl ≤ d(x) ≤ dh, el ≤ e(x) ≤ eh).
In understanding our method, it is beneficial to reformulate 〈O〉 from another viewpoint, i.e., histogram-based view. Let E and D denote all possible values of e(x) and d(x), respectively. The observable expectation of eqn (1) can be rewritten as
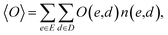 | (2) |
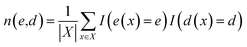 | (3) |
Multicanonical sampling
In multicanonical sampling,12 we consider a family of distributions parameterized by inverse temperature β,| Pβ(x) = exp(−βe(x) + f), | (4) |
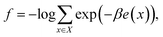 | (5) |
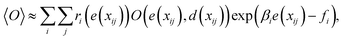 | (6) |
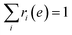 , and fi is the normalization factor at βi. The weights are determined so that the estimation error of DoS with respect to e, n(e), is minimized.16 By using MHM which will be explained later, ri(e) and n(e) are estimated. A consistent estimate of 〈O〉 can be obtained via correction by weights ri(e) (see Fig. 1c).
, and fi is the normalization factor at βi. The weights are determined so that the estimation error of DoS with respect to e, n(e), is minimized.16 By using MHM which will be explained later, ri(e) and n(e) are estimated. A consistent estimate of 〈O〉 can be obtained via correction by weights ri(e) (see Fig. 1c).
Population annealing
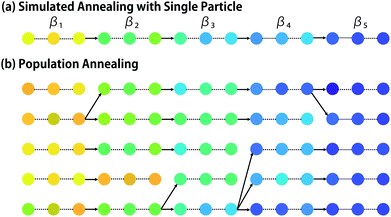
Population annealing (PA) was developed by Hukushima and Iba19 as an improved form of simulated annealing.20 In recent years, it has been applied to various problems in physics.21,22 In the simplest form of simulated annealing, an initial particle x is randomly chosen, and the increasing sequence of β = β1, …, βτ is given (see Fig. 2a). Hereinafter, the maximum and minimum inverse temperatures are denoted as βmax = βτ and βmin = β1, respectively. At the i-th iteration, Ki samples by Pβi(x) are generated by applying the MCMC method. One can apply any MCMC method including Metropolis sampling and Gibbs sampling.12 When Metropolis sampling is employed, particle x is randomly perturbed to x′ and it is accepted with probability min(1, Pβ(x′)/Pβ(x)). If rejected, the particle stays the same. In population annealing, M particles {xm}m=1,…,M are used. At i-th iteration, Ki samples by Pβi(x) are generated for each particle by MCMC steps with fixed βi, and Ni = M × Ki. Then, the particles are resampled to fit to the next canonical distribution Pβi+1(x). In this resampling, the probability for xm is determined as| qm ∝ exp(−(βi+1 − βi)e(xm)). | (7) |
The particle set is updated by drawing M particles with replacement. As a result, a particle may vanish or multiply (see Fig. 2). Reweighting is similar to natural selection in evolution algorithm,7 because poor particles with high e are more likely to vanish. It is known that, when the temperature difference |βi+1 − βi| is too large, resampling may lead to loss of diversity, i.e., all particles end up having the same ancestor.23
Multiple histogram method
MHM is a numerical algorithm for estimating the DoS from the samples of Boltzmann distributions at multiple temperatures.16 Let us assume that Ni samples are obtained at temperature βi by PA, and denote the number of samples with energy e as hi(e). In MHM, using weight parameters ri(e), DoS is obtained as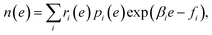 | (8) |
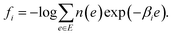 | (9) |
The weights ri(e) are determined to minimize the estimation error of n(e). MHM assumes that hi(e) is subject to Poisson distribution whose mean is Nin(e)exp(−βie + fi). Since the variance of a Poisson distribution is equal to its mean, the variance of hi(e) is described as V[hi(e)] = Nin(e)exp(−βie + fi). So the variance of pi(e) ≈ hi(e)/Ni is derived as
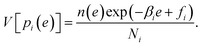 | (10) |
Due to the statistical independence of samples at different temperatures, we obtain the estimation error of n(e), i.e., the variance of n(e) as
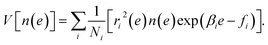 | (11) |
The optimization problem for the weights ri(e) is then defined as
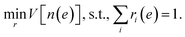 | (12) |
Using a Lagrange multiplier, we obtain
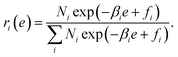 | (13) |
Substituting it to eqn (8), we obtain the optimized representation of n(e),
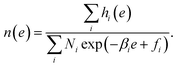 | (14) |
The DoS n(e) and free energy fi are obtained by solving the nonlinear system consisting of eqn (14) and (9) by fixed point iteration. When fi is obtained, ri(e) and 〈O〉 can be estimated.
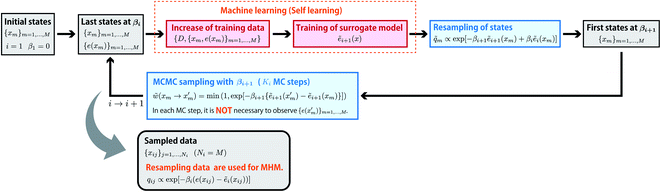
Self-learning entropic population annealing
Like EPA, self-learning entropic population annealing (SLEPA) uses M particles and alternates MCMC steps and resampling. The difference is that the energy e(x) is replaced by the prediction by a machine learning model ẽi(x) (see Fig. 3). In our experiments, we used Gaussian process regression24 as the machine learning model. The model is updated as more and more training examples are available. The first model ẽ1(x) is trained by initial M particles and their energies. The i-th model corresponding to βi is trained by iM examples obtained up to the point. Notice that the number of MCMC steps Ki does not affect the number of observations in SLEPA. So Ki can be set to a reasonably large value to ensure the convergence of MCMC steps. Populations of samples obtained from SLEPA are based on the Boltzmann distributions of predicted energies. Before applying MHM, these populations are corrected by resampling. The weight of the j-th particle obtained at βi is described as| qij ∝ exp[−βi(e(xij) − ẽi(xij))]. | (15) |
Results
Estimation of residue distribution
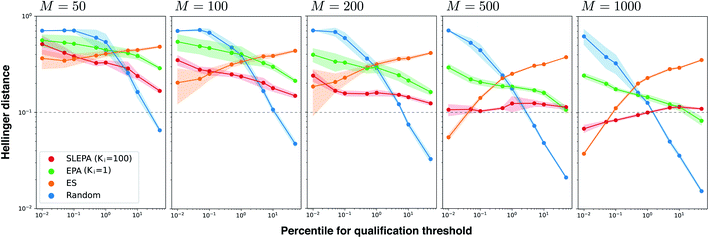
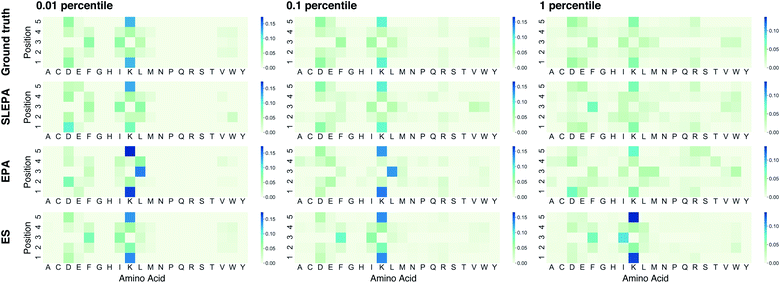
To illustrate how SLEPA can be used in practice, short peptides of length five are designed. Recently, antimicrobial peptides have been of increasing interest to address the threat of multidrug-resistant pathogens.17 Strong hydrophobic moment25 is a distinct feature of antimicrobial peptides.17 Motivated by this fact, the target property e(x) is designated as hydrophobic moment which is computed using a prediction model implemented in python library modlAMP.17 Given a budget on the number of observations, our goal is to estimate the residue distribution for qualified sequences e(x) ≤ δ, where δ is a qualification threshold. In SLEPA and EPA, the number of iterations is set to τ = 20, and the inverse temperatures are set between βmin = 0 and βmax = 10 with equal interval. In an MCMC step, a residue at a randomly chosen position is changed to a random residue (i.e., one residue flip). The number of MCMC steps of SLEPA is determined as Ki = 100, while that of EPA is set to one to save the number of observations. As the surrogate model of SLEPA, we use Gaussian process regression implemented in PHYSBO.24 To train the surrogate model, each residue is encoded to a seven dimensional feature vector called Tscale.26 As baselines, we employ simple random sampling and (μ, λ) evolution strategy (ES).6 In the ES, λ particles are retained. In each step, the energies of all particles are observed and top μ particles are chosen. A new generation of λ particles are generated by applying one residue flip to the chosen ones. The number of particles λ and the number of iterations are aligned with SLEPA and EPA, and μ is fixed to 10% of λ. For simple random sampling and ES, the residue distribution is constructed by counting.Fig. 4 shows the Hellinger distance of the residue distribution obtained by each method to the ground truth distribution obtained by complete enumeration. The Hellinger distance is defined as the Euclidean distance of square roots of probabilities. It is robust against zero probabilities. In all methods, the distance gets smaller as the number of particles M is increased. In all ranges of M, the performance of ES, one of our baseline methods, deteriorates as the qualification threshold is relaxed. This is intelligible, because ES performs pure optimization and does not have a mechanism to keep statistical consistency. Simple random sampling, on the other hand, performs poorly when the qualification threshold is small due to lack of any optimization mechanism. SLEPA and EPA show stably good results at all qualification thresholds, reflecting the fact that these methods are designed to optimize while maintaining statistical consistency. SLEPA exhibits better results than EPA in most cases. This result indicates that the use of machine learning is effective in increasing the number of MCMC steps to improve distribution estimation. The best distribution estimates (M = 200) by SLEPA, EPA, and ES are shown in Fig. 5.
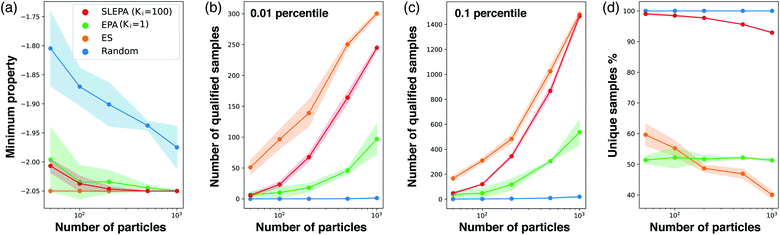
Quality of samples
Fig. 6a shows the best target property against the number of particles. In addition, Fig. 6b and c show the number of unique samples qualifying the threshold. While ES, a pure optimization algorithm, is the best, SLEPA shows a competitive performance when the number of particles is relatively large. EPA is clearly behind SLEPA, indicating that the surrogate model improves optimization substantially. To get an idea about sample diversity, Fig. 6d shows the ratio of the number of unique samples to the total number. The ratio of ES is particularly low, because the samples are concentrated around the optimal point and duplications are likely to happen. Comparing SLEPA and EPA, the ratio of SLEPA is much higher due to the difference in the number of MCMC steps. Since the samples of SLEPA are well mixed by MCMC, there is a smaller chance to create duplications.Number of MCMC steps
So far, the number of MCMC steps of EPA was set to one to keep the number of observations equal. In Fig. 7, we compared SLEPA and EPA with the same number of MCMC steps. When the number of MCMC steps of EPA is increased to 100, it was better than SLEPA in terms of the accuracy in distribution estimation and the number of qualified samples. This result shows the advantage of EPA that it can always make use of the correct energy instead of the predicted one. Although EPA was not performing well under a budget on observations, it is still a viable choice, if observation can be done cost effectively with fast simulation or a certain prediction model. See the ESI† for experimental results with other parameter settings.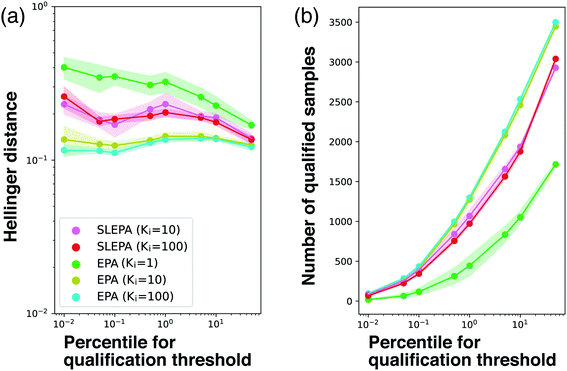 | ||
| Fig. 7 (a) Hellinger distance to the ground truth distribution at M = 200. SLEPA (Ki = 10 and 100) and EPA (Ki = 1, 10, and 100) are compared. (b) Number of qualified samples. | ||
Discussion
We have presented how automatic materials design can be made interpretable by introducing ideas from statistical physics and machine learning. In a benchmarking problem, it is confirmed that EPA and SLEPA have the desired property of accurate distribution estimation. So far, algorithmic methods for automatic materials design have been developed towards better optimization efficiency, paying minimum attention to statistical bias. Hopefully this paper sheds light on statistical consistency that is crucially important in correct understanding of materials.In our experiments, SLEPA with a Gaussian process was better than EPA, but the performance of SLEPA depends on the choice of the surrogate model and its prediction ability. The use of a surrogate model can be disadvantageous in the occasions where the model works poorly.
While SLEPA can reveal correlations between variables, it is well known that correlation does not necessarily mean causation.27 According to multiple studies, however, if the joint distribution satisfies certain criteria, it is possible to identify the causal direction from it.28,29 The combination of SLEPA and such causal discovery methods may detect causal relationships among variables about materials properties.
The parameters of SLEPA consist of the number of MCMC steps Ki, the number of particles M, the inverse temperature array βi and the hyperparameters of the adopted machine learning model. First of all, the number of MCMC steps should be set as large as possible to ensure the convergence in each iteration, but setting it over 1000 would be meaningless. For accurate DoS estimation, the number of particles M should be large too, but it is also affected by the capacity of the evaluator. For example, if SLEPA is used together with a simulator that can evaluate z materials in parallel, setting M to a value larger than z may result in unwanted latency. The inverse temperature array is determined first by setting the range [βmin, βmax] and dividing it into τ equally spaced points. As mentioned, a small τ leads to a large change of temperature that is harmful to resampling, while a large τ causes slow optimization. As in most black-box optimizers, we start from uniformly random samples, thus βmin = 0. Setting βmax would be the trickiest part, because, if too high, the probability is concentrated on one particle in almost all iterations and, if too low, the accuracy of DoS would be poor. To set βmax appropriately, we recommend computation of the unnormalized probability exp(−βmaxe(x)) for all initial examples to check if the probability is concentrated or scattered too much. Finally, the hyperparameters should be set according to the guideline of the machine learning model. In our experiments, we used the automatic hyperparameter initialization and update functions of PHYSBO.24
The integration of statistical physics, machine learning, and materials design offers a great opportunity of algorithmic development. When SLEPA is applied in the latent space of variational autoencoders,2 highly structural objects such as chemical compounds30 and crystal structures31 can be generated. To solve multiobjective optimization problems, SLEPA can be extended to estimate multidimensional DoS.32 In addition, other entropic samplers such as replica-exchange Monte Carlo,18 broad histogram33 and transition matrix Monte Carlo34 may find their own advantages in the context of materials design.
Data availability
Additional experimental results are summarized in the ESI.† An implementation of SLEPA is available at https://github.com/tsudalab/SLEPA and https://doi.org/10.5281/zenodo.6339987. The code to reproduce the results in this paper is available at https://doi.org/10.5281/zenodo.6374926.Author contributions
R. T. and K. T. conceived the idea and designed the research. All authors developed the algorithm, performed computational experiments, and wrote the manuscript.Conflicts of interest
The authors declare no competing interests.Acknowledgements
This work is supported by AMED JP20nk0101111, NEDO P15009, SIP (Technologies for Smart Bio-industry and Agriculture, “Materials Integration” for Revolutionary Design System of Structural Materials), JSPS Grant-in Aid for Scientific Research (Grant Number 21H01008), and JST ERATO JPMJER1903 and CREST JPMJCR21O2.References
- K. Terayama, M. Sumita, R. Tamura and K. Tsuda, Acc. Chem. Res., 2021, 54, 1334–1346 CrossRef CAS PubMed.
- B. Sanchez-Lengeling and A. Aspuru-Guzik, Science, 2018, 361, 360–365 CrossRef CAS PubMed.
- N. Szymanski, Y. Zeng, H. Huo, C. Bartel, H. Kim and G. Ceder, Mater. Horiz., 2021, 8, 2169–2198 RSC.
- D. P. Tran, S. Tada, A. Yumoto, A. Kitao, Y. Ito, T. Uzawa and K. Tsuda, Sci. Rep., 2021, 11, 10630 CrossRef CAS PubMed.
- D. R. Jones, M. Schonlau and W. J. Welch, J. Glob. Optim., 1998, 13, 455–492 CrossRef.
- I. Rechenberg, Comput. Methods Appl. Mech. Eng., 2000, 186, 125–140 CrossRef.
- P. C. Jennings, S. Lysgaard, J. S. Hummelshøj, T. Vegge and T. Bligaard, npj Comput. Mater., 2019, 5, 1–6 CrossRef.
- A. Zhavoronkov, Y. A. Ivanenkov, A. Aliper, M. S. Veselov, V. A. Aladinskiy, A. V. Aladinskaya, V. A. Terentiev, D. A. Polykovskiy, M. D. Kuznetsov and A. Asadulaev, et al. , Nat. Biotechnol., 2019, 37, 1038–1040 CrossRef CAS PubMed.
- S. Ju, T. Shiga, L. Feng, Z. Hou, K. Tsuda and J. Shiomi, Phys. Rev. X, 2017, 7, 021024 Search PubMed.
- Y. Zhang, J. Zhang, K. Suzuki, M. Sumita, K. Terayama, J. Li, Z. Mao, K. Tsuda and Y. Suzuki, Appl. Phys. Lett., 2021, 118, 223904 CrossRef CAS.
- H. Sahu, W. Rao, A. Troisi and H. Ma, Adv. Energy Mater., 2018, 8, 1801032 CrossRef.
- K. Binder and D. W. Heermann, Monte Carlo simulation in statistical physics: an introduction, Springer, Heidelberg, 5th edn, 2010 Search PubMed.
- F. Wang and D. P. Landau, Phys. Rev. Lett., 2001, 86, 2050–2053 CrossRef CAS PubMed.
- F. Liang, C. Liu and R. J. Carroll, J. Am. Stat. Assoc., 2007, 102, 305–320 CrossRef CAS.
- L. Barash, J. Marshall, M. Weigel and I. Hen, New J. Phys., 2019, 21, 073065 CrossRef CAS.
- A. M. Ferrenberg and R. H. Swendsen, Phys. Rev. Lett., 1989, 63, 1195–1198 CrossRef CAS PubMed.
- A. T. Müller, G. Gabernet, J. A. Hiss and G. Schneider, Bioinformatics, 2017, 33, 2753–2755 CrossRef PubMed.
- K. Hukushima and K. Nemoto, J. Phys. Soc. Jpn., 1996, 65, 1604–1608 CrossRef CAS.
- K. Hukushima and Y. Iba, AIP Conf. Proc., 2003, 200–206 CrossRef CAS.
- S. Kirkpatrick, C. D. Gelatt and M. P. Vecchi, Science, 1983, 220, 671–680 CrossRef CAS PubMed.
- H. Christiansen, M. Weigel and W. Janke, Phys. Rev. Lett., 2019, 122, 060602 CrossRef CAS PubMed.
- W. Wang, J. Machta and H. G. Katzgraber, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 013303 CrossRef PubMed.
- T. Li, T. P. Sattar and S. Sun, Signal Process., 2012, 92, 1637–1645 CrossRef.
- Y. Motoyama, R. Tamura, K. Yoshimi, K. Terayama, T. Ueno and K. Tsuda, 2021, arXiv: 2110.7900.
- G. Zhao and E. London, Protein Sci., 2006, 15, 1987–2001 CrossRef CAS PubMed.
- M. Cocchi and E. Johansson, Quant. Struct.-Act. Relat., 1993, 12, 1–8 CrossRef CAS.
- J. Pearl, Causality, Cambridge University Press, 2009 Search PubMed.
- D. Janzing, J. Mooij, K. Zhang, J. Lemeire, J. Zscheischler, P. Daniušis, B. Steudel and B. Schölkopf, Artif. Intell., 2012, 182, 1–31 CrossRef.
- S. Shimizu, T. Inazumi, Y. Sogawa, A. Hyvärinen, Y. Kawahara, T. Washio, P. O. Hoyer and K. Bollen, J. Mach. Learn. Res., 2011, 12, 1225–1248 Search PubMed.
- R. Gómez-Bombarelli, J. N. Wei, D. Duvenaud, J. M. Hernández-Lobato, B. Sánchez-Lengeling, D. Sheberla, J. Aguilera-Iparraguirre, T. D. Hirzel, R. P. Adams and A. Aspuru-Guzik, ACS Cent. Sci., 2018, 4, 268–276 CrossRef PubMed.
- C. J. Court, B. Yildirim, A. Jain and J. M. Cole, J. Chem. Inf. Model., 2020, 60, 4518–4535 CrossRef CAS PubMed.
- M. K. Fenwick, J. Chem. Phys., 2008, 129, 09B619 CrossRef PubMed.
- M. Kastner, M. Promberger and J. Munoz, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 7422 CrossRef CAS PubMed.
- J.-S. Wang and R. H. Swendsen, J. Stat. Phys., 2002, 106, 245–285 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d1dd00043h |
| This journal is © The Royal Society of Chemistry 2022 |