Ab initio molecular dynamics with enhanced sampling in heterogeneous catalysis
GiovanniMaria
Piccini
 *ab,
Mal-Soon
Lee
a,
Simuck F.
Yuk
*ab,
Mal-Soon
Lee
a,
Simuck F.
Yuk
 ac,
Difan
Zhang
a,
Greg
Collinge
ac,
Difan
Zhang
a,
Greg
Collinge
 a,
Loukas
Kollias
a,
Loukas
Kollias
 a,
Manh-Thuong
Nguyen
a,
Vassiliki-Alexandra
Glezakou
*a and
Roger
Rousseau
a,
Manh-Thuong
Nguyen
a,
Vassiliki-Alexandra
Glezakou
*a and
Roger
Rousseau
 *a
*a
aBasic & Applied Molecular Foundations, Physical and Computational Sciences Directorate, Pacific Northwest National Laboratory, Richland, WA 99352, USA. E-mail: giovannimaria.piccini@gmail.com; vanda.glezakou@pnnl.gov; roger.rousseau@pnnl.gov
bIstituto Eulero, Università della Svizzera italiana, Via Giuseppe Buffi 13, Lugano, Ticino, Switzerland
cDepartment of Chemistry and Life Science, United States Military Academy, West Point, NY 10996, USA
First published on 12th October 2021
Abstract
Ab initio molecular dynamics simulations combined with enhanced sampling techniques are becoming widespread methods to investigate chemical phenomena in catalytic systems. These techniques automatically include finite temperature effects, anharmonicity, and collective dynamics in their robust description of enthalpic and entropic contributions, which can have significant impact on reaction free energy landscapes. This contrasts with standard ab initio static approaches that are based on assessing reaction free energies from various coarse-grained descriptions of the reaction potential energy surface. Enhanced sampling ab initio molecular dynamics opens the way to first principles simulations of systems of increasing complexity like solid/liquid catalytic interfaces. In this work, we aim at guiding the reader through the basis of these techniques, summarizing their fundamental theoretical and practical aspects, and reviewing the relevant literature in the field. After a brief introduction to the problem, we will illustrate the advantage of using molecular simulations to include finite temperature effects, examine the most common ab initio techniques currently in use, describe their application to solid state heterogeneous catalysts, and finally critically review the most popular enhanced sampling techniques used in computational catalysis.
Introduction
Modeling the reactivity of heterogeneous catalytic systems is nontrivial and poses significant challenges.1–7 At low temperature and coverage and for systems with well-defined catalytic sites, ab initio static calculations deliver many important results allowing interpretation of experimental evidence.8–19 However, such conditions are often largely ideal, as catalytic processes at realistic experimental conditions imply dealing with a much higher level of complexity. Common catalytic production processes work at high temperatures and pressures where conditions are far from ideal. Moreover, modern heterogeneous catalytic systems are often characterized by complex interfaces between the solid catalyst and a substrate from the liquid phase (pure or in solution) at room temperature, or by confined environments and soft mater scaffolds such as enzymes or liquid catalysts at elevated temperatures. In these scenarios, dynamic and entropic effects play a fundamental role in determining the reactivity of the systems and static ab initio methods face severe limitations in describing their activity.2 In this context, molecular dynamics (MD) simulations become a fundamental tool for modelling and describing catalytic chemical reactions at realistic experimental conditions.2,20–30By integrating the classical equations of motions of the nuclei, MD simulations provide one the most accurate approaches to account for finite temperature effects, i.e., entropy. In MD simulations, the time evolution of a chemical system is propagated by numerically integrating Newton's second principle of dynamics F = −∇V, where V is the potential energy function. For sufficiently long MD trajectories one can estimate the Boltzmann distribution of a system at a given temperature and thus its free energy. In most of its successful applications, MD simulations rely on the definition of empirical classic potentials that parametrize forces arising from bond stretching, angles bends, torsions, electrostatic, and van der Waals interactions. For a broad variety of systems ranging from biological molecules31 to materials,32 these potentials have shown great capabilities and allow the exploration of the dynamics of systems exhibiting incredible complexity with unprecedented atomistic detail. However, by construction, these potentials do not allow bond breaking or formation, a feature that lies at the core of chemical reactivity arising from the quantum mechanical electronic properties of the molecular system.
In order to model the type of problems that deal with the electronic properties of molecular systems, one must solve the electronic Schrödinger equation. This produces energies and forces (potentials) that allow one to describe the dynamics of a reaction according to its explicit electronic structure. This approach is termed ab initio molecular dynamics (AIMD).33–36 Unfortunately, this comes at a great expense in terms of computational cost, as the solution of the Schrödinger equation is usually performed iteratively and scales exponentially with the total number of electrons in the system. Density functional theory (DFT) has provided the computational chemistry community with an immensely versatile and efficient tool to reduce the computational cost of electronic structure calculations since its computational cost scales cubically with the total number of electrons in the systems (N3). This allows calculating up to several hundreds of atoms in the simulation unit cell with reasonable accuracy. Despite its lower computational cost compared to other more accurate quantum chemical methods, DFT still requires much more computational power than classical potentials, hindering significantly its use in MD simulations. The first example of a combination of DFT and MD simulations has been provided by the Car–Parrinello method,35 where the solution of the electronic problem is handled by integrating the nuclei and electronic orbitals coupled equations of motions simultaneously, thus avoiding expensive iterative matrix diagonalizations. Subsequently, the increase of computational power and the enhanced performances of ab initio algorithms allowed the direct use of Born–Oppenheimer potentials to propagate the dynamics (BOMD).36,37 If the system's size is overwhelmingly large, one can use hybrid methods to calculate, under specific conditions, the total energy and potential of a system. In such cases, the reactive region is treated at the quantum mechanical level (QM) and the remainder is described by a classical molecular mechanics potential (MM). These approaches are commonly referred to as QM/MM methods.38–40 These last two methods have become nowadays the most used approaches to ab initio molecular dynamics and are playing an increasingly significant role in computational catalysis. More recently, it has been shown how reactive force fields can be obtained ad hoc for specific systems by training deep neural networks or other machine learning schemes on ab initio data. Given the availability of efficient GPU41,42 based architectures and algorithms, the applications of these methods are increasing in the simulation community, providing energy and gradients with ab initio accuracy at a cost comparable to classical force fields.
Ab initio methods alone, however, are not sufficient to simulate reactive events in catalysis, particularly those with high free energy barriers i.e., those that are rate limiting or rate controlling. It is well known that chemical reactions are activated processes. This means that relevant metastable states of a reaction (reactants, products, and intermediates) are separated by high free energy barriers. For this reason, the probability of transition between states is very low and these events are rare compared to low-energy or unactivated events. In the field of molecular simulations this is a well-known issue, commonly referred to as the “time-scale problem”.43–45 Typically, to ensure energy conservation in a MD simulation one needs to integrate the equations of motion with a time step on the order of fractions of femtoseconds. A chemical reaction usually takes place in a time scale that is orders of magnitude larger than 10−15 s. For example, for a reaction at 300 K with a free energy barrier of 75 kJ mol−1, the average escape time to reach the products state is 2 seconds. Covering this time span with a femtosecond time step several times to collect sufficient statistics on the event is simply intractable.
To mitigate or circumvent this problem, several methods have been proposed to accelerate sampling of rare events. These are denoted enhanced sampling methods. Starting from the seminal work of Torrie and Valleau on non-Boltzmann sampling known as Umbrella sampling,46 a plethora of methods appeared in the literature like parallel tempering,47,48 hyperdynamics,49 transition path sampling,50 metadynamics,51 and many others.52 These methods allow sampling of rare events, enabling control and investigation of reaction mechanisms and estimates of the free energy profiles of the reaction. What differentiates these approaches from more standard methods in quantum chemistry, e.g., the nudged elastic band (NEB) method,53 is that they automatically include with great accuracy the entropic effects that are fundamental in processes like chemical catalysis. As such, there is no need to approximate the free energy of stationary and transition states using models like the rigid roto-translator/harmonic oscillator. In addition, the free energy, ΔG (ΔA), can be decomposed into an enthalpic component, ΔH = ΔU + PΔV (energetic component, ΔU), and an entropic component, ΔS, thereby enabling one to understand temperature effects upon reaction barriers and rates.
Furthermore, as data science has evolved rapidly in recent years, data-driven methods such as machine learning (ML) and artificial neural networks (NN) have drawn more attention in a variety of fields such as materials science,54,55 catalysis,56–58 and separations.59 Since conventional AIMD simulations have been challenged due to the multiscale complexity of catalytic reactions, their data-driven methods have helped scientists to improve computational modeling and better understanding fundamental insights of catalysis in AIMD simulations. Therefore, we also discuss the application of these methods in the aspects of improving AIMD for studying catalytic reactions. Other applications of ML and NNs to static quantum calculations, computational screening, or pathway exploration in catalysis are beyond our scope and readers can refer to other resources.56,58,60–64
The overall purpose of this review is to discuss AIMD combined with enhanced sampling for the study of catalysis. There is currently a rise in the number of studies in catalysis using these tools, and it is the feeling of the authors that it is highly appropriate to provide: (i) an overview of the most commonly encountered methods in the field, (ii) a discussion of the strengths, weaknesses and pitfalls of the various approaches, and (iii) a series of examples that demonstrate what one can learn from these types of studies. This article is a complement to the recent perspective article published by the authors in ACS Catalysis2 which emphasizes areas in catalysis where entropy and correlated dynamical motion necessitate a statical mechanics based approach which goes beyond the simulations based on static models (ex. elevated temperatures, confined spaces and solid–liquid interfaces). In contrast, the current article focuses specifically on AIMD/enhanced sampling method and how they have been employed in catalysis. In this article we will review the fundamental theoretical and practical aspects of heterogeneous catalysis modeling using AIMD simulations for problems in catalysis as well as highlight some of the most recent developments and applications of enhanced sampling techniques to relevant problems in catalytic reactivity.
Entropy from unconstrained MD
Molecular dynamics offers the most accurate way to include finite temperature effects in modeling realistic systems at operando conditions. In recent years, ab initio molecular dynamics (AIMD) have also become one of the commonly used tools to calculate free-energy changes and their deconvoluted enthalpic and entropic components in not only heterogeneously catalyzed systems2,6,26 but also in homogeneously catalyzed systems, as well.65–70 The changes in free energy can quickly be estimated based on the distribution of states extracted from the AIMD trajectory through ΔG = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(p/p0), where p and p0 represent the probabilities of being in the state of interest and the reference state, respectively. One of the more well-received approaches to accounting for anharmonicity is to employ the quasi-harmonic approximation (QHA) using AIMD data. Alternatively, enhanced sampling methodologies with constrained MD, such as metadynamics71–73 or the Blue-Moon approach,74–76 can be applied to calculate entropies with the relationships, ΔS = −dΔG/dT or ΔS = (ΔU − ΔG)/T, using the free energy (ΔG) and internal energy (ΔU) obtained from the simulation as discussed in detail later. It is noteworthy that unconstrained AIMD only enables us to calculate ΔS of the end point states, i.e., initial and final states of elementary reactions, while the enhanced sampling methods furthermore allow us to determine ΔS of transition states. In the QHA approach,25,26,77 the vibrational density of states (VDOS) is obtained from the Fourier transform of the velocity autocorrelation function using extracted velocities from the equilibrated AIMD data, as follows:
ln(p/p0), where p and p0 represent the probabilities of being in the state of interest and the reference state, respectively. One of the more well-received approaches to accounting for anharmonicity is to employ the quasi-harmonic approximation (QHA) using AIMD data. Alternatively, enhanced sampling methodologies with constrained MD, such as metadynamics71–73 or the Blue-Moon approach,74–76 can be applied to calculate entropies with the relationships, ΔS = −dΔG/dT or ΔS = (ΔU − ΔG)/T, using the free energy (ΔG) and internal energy (ΔU) obtained from the simulation as discussed in detail later. It is noteworthy that unconstrained AIMD only enables us to calculate ΔS of the end point states, i.e., initial and final states of elementary reactions, while the enhanced sampling methods furthermore allow us to determine ΔS of transition states. In the QHA approach,25,26,77 the vibrational density of states (VDOS) is obtained from the Fourier transform of the velocity autocorrelation function using extracted velocities from the equilibrated AIMD data, as follows: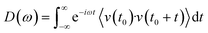 | (1) |
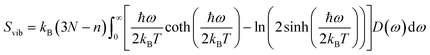 | (2) |
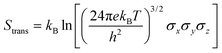 | (3) |
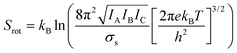 | (4) |
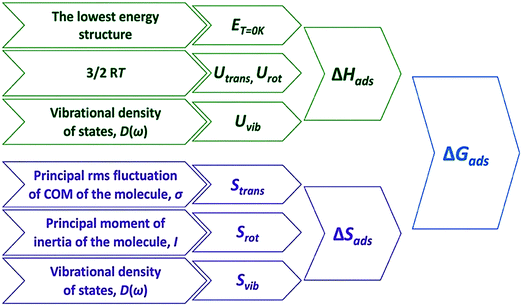 | ||
| Fig. 1 Overall scheme of adsorption free energies derivation based on the QHA. Reprinted with permission from ref. 2. Copyright 2020 American Chemical Society. | ||
The computational determination of enthalpic and entropic contributions is a crucial step for understanding the detailed free energy landscape of complex catalyzed systems. Unlike enthalpic contributions to the free energy change which can be qualitatively predicted from the “0 K” DFT energy of a few well-defined minima on the potential energy surface, the entropic component cannot be directly deduced from static DFT calculations. Instead, the harmonic approximation (HA) is frequently applied for studying strongly bound adsorbates at low temperatures where the surface-adsorbate bonding are minimally perturbed. HA depends on the second-order derivative of the Born-Oppenheimer energy surface around the equilibrium. The resulting vibrational modes are associated with high vibrational frequencies, which are adequately described within the limits of HA. In contrast, the influence of anharmonicity as well as collective dynamics in catalytic systems leads to inaccuracy in calculating the entropic contribution using the standard HA approach alone.80 The atomic fluctuations, shifting away from equilibrated positions, induce atoms and molecules to access the anharmonic regions of the potential energy surface. Such effects become prominent for many adsorbates that are weakly bound, solvated, confined, or at high temperatures. Thus, the determination of entropy via anharmonic consideration is important to gain precise thermodynamic and kinetic perspectives of complex catalytic systems at finite temperatures.2Table 1 and Fig. 2 show calculated entropies of gas-phase ethanol at high temperatures using HA and QHA which are compared with absolute entropies obtained from NASA polynomials, evidencing the importance of anharmonic effect on entropy even for simple molecules.25Table 1 clearly shows strong overestimation of translational entropy but underestimation of vibrational entropy with HA leading to larger difference of entropy from NASA polynomials than QHA.
| T (K) | QHA | HA | NASA polynomials | % diff for QHA(HA) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| S trans | S rot | S vib | S tot | S trans | S rot | S vib | S tot | |||
| 300 | 114 | 96 | 67 | 277 | 157 | 94 | 22 | 273 | 282 | −1.8 (−3.2) |
| 700 | 133 | 107 | 125 | 365 | 174 | 104 | 73 | 351 | 359 | +1.6 (−2.2) |
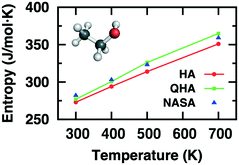 | ||
| Fig. 2 Computed entropies for gas-phase ethanol as a function of temperature using HA and QHA compared with those from NASA polynomials. Adapted with permission from ref. 25. Copyright 2016 American Chemical Society. | ||
It is not surprising that multiple approaches have been developed to properly account for anharmonic effects and their influences on entropy.79,81–83 For instance Campbell and Seller found an interesting relationship to derive the entropy of adsorbed molecules, including methanol and alkanes, based on their gas-phase entropy.84 The entropies of such molecules were calculated to be higher than those estimated by HA and can be better described by their gas-phase entropy, as shown below:
| Soads(T) = 0.70Sogas(T) − 3.3R | (5) |
In our previous studies of 2D and 3D zeolitic systems, we were able to properly account for the anharmonic effect through the usage of QHA. Fig. 3 shows a comparison of Gibbs free energies of adsorbed ethanol over 3D H-ZSM-5 computed with QHA and compared against HA and calorimetric measurements.25,26 Here anharmonic effects are large and can lead to errors of several 10s of kJ mol−1 as compared with experiment as shown in Fig. 3. The authors showed a good quantitative agreement between the experimental and theoretical adsorption energies of ethanol. We also showed that the change of entropy from first to second ethanol adsorption on H-ZSM-5 cannot be reproduced with HA.25
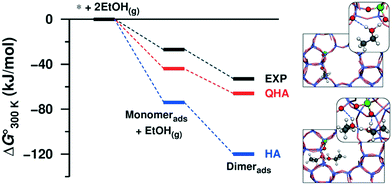 | ||
| Fig. 3 Standard Gibbs free energy of ethanol adsorption obtained from HA and QHA compared with experiments and the most stable structures (at 0 K) of the adsorbed ethanol monomer and dimer on the Brønsted acid site of H-ZSM-5. Reprinted with permission from ref. 25. Copyright 2016 American Chemical Society. | ||
For low-coverage systems, QHA gives very compatible results with the more rigorous approach of Piccini and Sauer which more readily incorporates more accurate electronic structure calculations and explicitly accounts for quantum chemical anharmonicity and mode counting from hybrid QM/QM methods.85 Compared to QHA, this approach accounts correctly for the unequal spacing of the vibrational quantum states. To be certain, QHA accurately estimates the anharmonic fundamental frequencies by integrating the velocity–velocity correlation functions in the time domain. However, when it comes to estimates of the thermodynamic functions from a statistical mechanics point of view, the thermal contribution of each normal mode is calculated using a harmonic model, where the spacing between vibrational states is equally spaced. Conversely, in terms of computing the thermodynamic functions, the approach proposed by Piccini and Sauer uses a numerical sum-over-the-states partition function for each anharmonic normal mode, which accounts for the uneven spacing (see Fig. 4 for this comparison). For each single normal mode, this represents a moderate contribution in terms of entropy, and for small systems, it is usually irrelevant. However, for condensed phase systems containing hundreds of atoms, each single anharmonic normal mode contribution can quickly sum up to a non-negligible quantity that may affect the estimation of the thermodynamic functions. Nonetheless, the method proposed by Piccini and Sauer relies on a static picture of the problem under study, where referenced molecular geometries (reactants, products, intermediates, and transition structures) represent well the fundamental thermodynamic states. For these reasons, such a method could be difficult to apply when collective molecular and thermal phenomena become relevant like in the presence of a solid–liquid interface or very high temperatures.
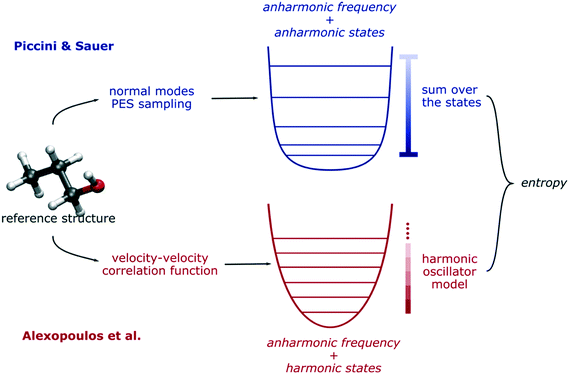 | ||
| Fig. 4 Schematic comparison of the Piccini & Sauer method for thermal anharmonic correction85 and the QHA by Alexopoulos et al.25 | ||
In extended or confined systems where adsorption phenomena are relevant, the effects of anharmonicity in the estimation of the entropic term are very large. QHA is able to capture these effects, especially in highly fluxional systems for which it is not possible to identify single reference structures. Such systems include those at high temperatures, solid–liquid interfaces, and porous materials such as zeolites or metal–organic frameworks (MOFs). As previously mentioned, the main limitations of the QHA method reside in the statistical mechanical treatment of the vibrations. Namely, these limitations are (i) all the modes are considered as harmonic fundamental frequencies and no corrections for overtones or combination bands are possible (in most cases, these contributions are often not very large when estimating entropy but may be more substantial for zero-point energies (ZPE), (ii) depending on the size of the system, rather long trajectories are needed to correctly extract the anharmonic contributions from the integration of the velocity–velocity correlation function, (iii) nuclear quantum effects are accounted for at a semiclassical level and are included only in the ZPE, and (iv) QHA can only sample minima that are separated by small energy barriers.
Dynamics on ab initio potentials
In catalytic processes where chemical bonds between atoms are broken or formed, we must account for explicit electronic contributions to the interaction between atoms to correctly predict their thermodynamics/kinetics. On this basis, methods based on electronic structure calculations are commonly used. Keep in mind that while reactive force fields (like ReaxFF86) have been used to simulate bond forming and bond breaking processes,87 they do have problems that can badly affect the accuracy of simulations such as their lack of transferability88,89 and unreasonable charge distributions of structures that are far from equilibrium.90 Semi-empirical methods like tight-binding based approaches are also used by the catalysis community,91 but they also have significant limitations arising from the parametrization of their Hamiltonians.92 First principles-based methods, largely based on gradient corrected DFT, are most widely used in computational catalysis. In this section, we will summarize in detail the two most common AIMD techniques for direct simulations of (classical) trajectories, namely, Born–Oppenheimer (BO) approximation36,37 and (extended Lagrangian) Car–Parrinello (CP) molecular dynamics.35BO molecular dynamics
At the heart of electronic structure theory of a system consisting of N electrons and M nuclei is the Schrodinger equation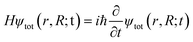 | (6) |
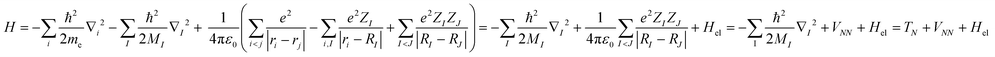 | (7) |
Because of the significant mass difference between the electron and nuclei (the latter are almost 2000 times heavier than the former), we can assume that the electronic wavefunction responds instantaneously to nuclear variation. The nuclei can be treated as “fixed” while the electrons move in their electrostatic field. The electronic wavefunction is then obtained by solving the following equation.
Helψel(r,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R) = Eel(R)ψel(r, R) = Eel(R)ψel(r,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R) R) | (8) |
MI![[R with combining umlaut]](https://www.rsc.org/images/entities/i_char_0052_0308.gif) I(t) = −∇I[VNN + Eel(R)] I(t) = −∇I[VNN + Eel(R)] | (9) |
To this end, we need to determine the BO potential energy surface. To do that, one can apply several electronic structure methods. BO AIMD, based on DFT, is probably the most widely used AIMD approach. The availability of DFT codes and the easy combination of a DFT code and a MD routine are amongst the reasons for this. Serval codes provide BOMD. The ONETEP,98 FHI-aims,99 CP2K100,101 CASTEP102 and VASP103 are amongst the most popular BOMD codes.
CP molecular dynamics
In BO MD, the electronic wavefunctions are obtained from the solution of the time-independent Schrodinger equation, the time evolution (dynamics) of the electrons is therefore not considered.104 In CPMD, a “fictitious” dynamics for orbitals is introduced and incorporated in the form of the following extended Lagrangian: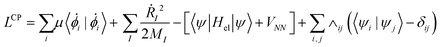 | (10) |
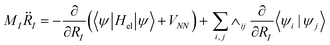 | (11) |
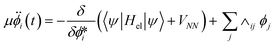 | (12) |
As localized basis sets significantly add complexity to the implementation of the CP algorithm, plane-wave basis functions are usually used.105 CPMD106 and Quantum ESPRESSO107 are popular CPMD codes.
Comparatively, the CPMD and BOMD approaches should give comparative results when both are conducted carefully. The relative choice between the two thus depends on the system under investigation. In general, the CPMD approach requires smaller time steps than BOMD but does not require any iterations of the SCF wavefunction and are fully time revisable unlike BOMD.109 However, care must be chosen in determining the fictious electron mass as to not destroy the underlaying adiabatic decoupling of nucleic and fictious election degrees of freedom required for the CP approximation to work.108,110 Accounting for the errors in CPMD forces is not a trivial task since they cannot be refined simply based on a constant correction to the masses of the ions, as shown in Fig. 5.
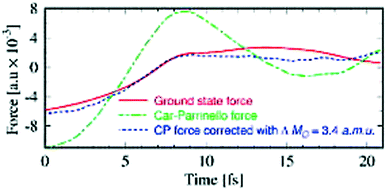 | ||
| Fig. 5 Samples of force components on D2O molecules based on a 21 fs segment of CPMD trajectory. The Car–Parrinello force (green) and the Car–Parrinello force corrected with constant mass corrections at three points along the trajectory (blue) is compared against the ground-state force at the same ionic positions. Adapted from ref. 108, with the permission of AIP Publishing. | ||
Enhancing the sampling of catalytic reactions
As discussed above, MD is a very powerful tool for simulating several properties of many chemical systems. A catalytic reaction is an activated processes that transforms reactants to products (i.e., chemical reactions) that are of interest to chemistry—and to heterogenous catalysis in particular. From a thermodynamic perspective, reactants, products, and intermediates of a reaction are local free energy minima separated by free energy barriers. One can directly observe catalytic elementary steps using unconstrained AIMD only when the free energy barriers are less than about a Boltzmann factor, kBT, which is typically quite low and thus rarely associated with a rate controlling step. For this reason, the probability of observing a kinetically-relevant transition event is very low within AIMD-accessible time scales. For a long time, this limitation has hindered the application of MD to problems of interest in chemistry and catalysis.One strategy for circumventing this problem is the application of an external fictitious bias potential to the system in order to discourage the simulation from sampling already visited regions of phase space. The first example of this technique can be found in the landmark paper of Torrie and Valleau46 in which umbrella sampling (US) was introduced. There, the authors proposed to add an external bias along a designated collective variable (CV)—i.e., a function s(R) of the Cartesian atomic coordinates, R, of the system—that describes the thermodynamic process of interest. A bond distance in a chemical bond breaking or a dihedral angle in a conformational isomerization are examples of CVs. In such a way, US achieves a non-Boltzmann sampling of the problem at a given temperature, as the bias potential that prevents the system from exploring already visited regions of the free energy landscape modifies the probability distribution function, reducing the effective height of the barriers in the biased ensemble.
Since the US method was introduced, a large variety of methods have been proposed to overcome limitations related to high free energy barriers in MD simulation and thereby permit the study of rare events (see, e.g., ref. 52). Here, we will focus only on methods based on biasing along a CV to obtain a free energy profile since these methods are the most appropriate to high precision studies of specific chemical reactions. Namely, we will focus on two families of CV-based methods: gradient-based ones, like the blue-moon ensemble method, and non-Boltzmann sampling, like US metadynamics (MetaD). The latter will be described in a bit more detail as it has become one of the most popular and widely applied methods in chemical simulations and also allows for the calculation of reaction rates. Other methods involving many replicas of the systems at different conditions like parallel tempering,47,48 or free energy perturbation methods111,112 are powerful tools as well but are not the most commonly used in AIMD for studying chemical reactivity due to prohibitively large number of configurations required to converge the statistics.
Collective variables for chemical reactions
Collective variables (CVs), s = s(R) are functions of the atomic coordinates R and are meant to describe the progress of a reaction from reactants to products. Ideally, the best collective variable is the reaction coordinate, i.e., the line that follows the minimum free energy path from reactants to products. In practice, this function is not known a priori, and its identification is completely non-trivial. Thus, approximations are made in terms of simpler chemical parameters such as bond lengths, angles, torsions, coordination numbers, taken alone or combined in lower dimensional forms, e.g., in linear or non-linear combinations. The fundamental requirement for a CV is to discriminate between the relevant states of a reaction and it must include all the slow degrees of freedom that are relevant to the process. These are fundamental requirements to ensure proper sampling and, thus, convergence of the free energy estimation.Typical examples can be found in organic SN2 reactions, where the distances between the central carbon atom and the leaving group, and the one between the carbon atom and the nucleophile discriminate well between reactants and products.113,114 Often, complex chemical reactions involve several degrees of freedom and the use of these degrees of freedom as independent collective variables implies dealing with large multidimensional free energy surfaces. This comes with several disadvantages. First, the physical and chemical interpretation of the results is compromised since high dimensional surfaces are not easily readable and projection onto lower dimensions is needed. Second, from a technical point of view, the convergence rate and efficiency of most CV-based free energy methods drops dramatically when many degrees of freedom are treated independently (see, e.g., ref. 71). A practical solution is to combine the most relevant CVs into low dimensional, possibly 1D, using, e.g., linear or non-linear combinations.115 For simple reactions, chemical intuition can be used straightforwardly to determine the optimal coefficients of the combination. However, for systems of increasing complexity this may be a daunting task. Recently, it has been shown that low dimensional CVs in the form of simple linear combinations can be obtained through automating the concept of chemical intuition.116–118 Starting from the statistical information provided by the fluctuations of the system in the reference free energy basins, i.e., reactants and products, one can use simple classification rules and algorithms to obtain linear combinations of several chemical descriptors, like distances, angles, coordination numbers etc., to be used as optimal CVs. Later, this approach has been further developed beyond its linear formulation using neural networks to introduce non-linearity, providing an even more flexible tool to obtain low dimensional CVs.119
If one has access not only to the information provided by the local basins of attraction but also to the dynamics of the rare event it is possible, in principle, to obtain even more accurate CVs. If this information is available from unbiased simulations (usually only for conformational changes in biomolecular systems120) or from biased ones, one can extract optimal collective variables from the transition dynamics. It is not our purpose to dig deep into the details of these specialized methods first developed by Noè and Pande and later applied to the enhanced sampling problems,117,121,122 but they represent a very promising and efficient solution to approximate the reaction coordinates.
Alternatively, if one knows a priori the mechanism of a reaction, i.e. can approximate a reaction path through a series of plausible molecular structures, special CVs, commonly referred to as path collective variables (PathCVs) can be used to sample the chemical reaction.123 The development of these CVs does not differ substantially to the grounding ideas of the nudged elastic band (NEB) method124 and PathCVs can be seen as the finite temperature version of it. In simple terms, having a series of images (molecular structures) representing the change from reactants to products, one can build two PathCVs, s (path function value) and z (distance function value), that describe the progress of a reaction and the distance from the minimum free energy path, respectively (see Fig. 6).
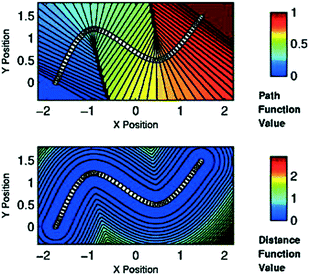 | ||
| Fig. 6 Top: Surface plot of variable s for sixty points in two dimensions (white dots). Note that isolines are perpendicular to the path in its neighborhood. Bottom: Contour plot of variable z in two-dimensional space shows that its definition can be approximately considered as a measure of the distance from the path itself. Reprinted from ref. 123, with the permission of AIP Publishing. | ||
PathCVs are a very powerful method but require the knowledge of the reaction mechanism beforehand, which is often not available. A very promising variant of this method, based on coordination numbers metrics, is way more robust for sampling chemical reactions and does not require the knowledge of intermediate structures.125 Topology-based methods such as Social PeRmutation INvarianT (SPRINT) coordinates represent a third alternative to the problem and have been used for chemical reaction problems, as well.126 However, despite their great flexibility, SPRINT coordinates may suffer from a limited resolving power in the case of homogeneous bulk systems with uniform coordination patterns. In this context, Pietrucci et al. used these path and SPRINT CVs to investigate the formation of fullerene from graphene flakes using biased AIMD simulations (see Fig. 7).
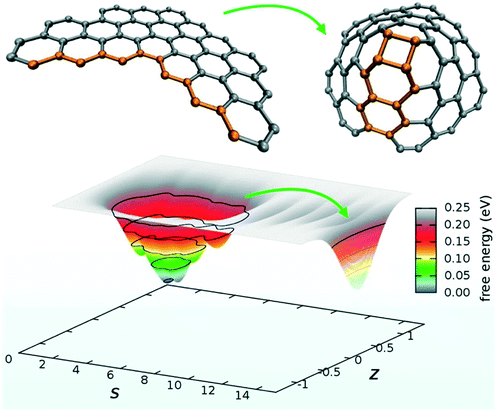 | ||
| Fig. 7 Graphene nanoflake: zipping into a nanocone and free-energy landscape as a function of the path collective variables. Reprinted with permission from ref. 127. Copyright 2014 American Chemical Society. | ||
Methods to enhance sampling along collective variables
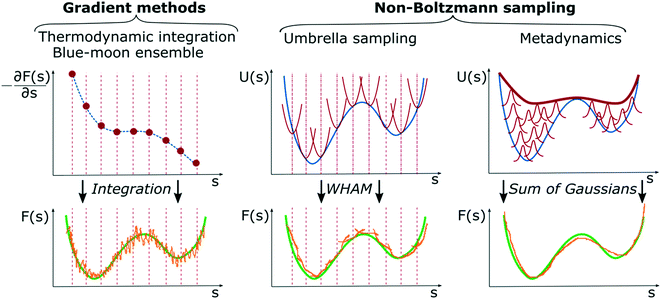
As previously mentioned, enhanced sampling techniques can be divided into two major families, one based on sampling along collective variables and one based on tempering techniques. Here, we focus only on CV-based methods as they are the most commonly used in chemical reaction sampling and have led to major results in computational catalysis. The reason for this is that catalysis is often associated with large changes in the entropy of the system and CV-based methods increase the probability of crossing entropic barriers in CV space; hence exploring configurations of largely different entropy. Such a family can be further subdivided into two complementary approaches: gradient methods like thermodynamic integration (TI),128,129 blue-moon ensemble,74 or adaptive biasing force algorithm,130 and non-Boltzmann sampling like umbrella sampling46 or metadynamics.51Fig. 8 summarizes the main features of the two method families.Gradient methods
Gradient methods aim at reconstructing the free energy along a designated CV by integrating its gradient (∂F/∂s). The first example of this technique is represented by thermodynamic integration, where one calculates the mean force (average gradient) of the free energy at specific points of the CVs and subsequently reconstruct the free energy by numerical integration as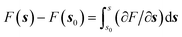 . Often, in order to estimate the mean force at a point, si, of the CV space, one needs to constrain the value of the CV to sample a proper ensemble of configurations of the system. This is usually done by using holonomic constraints but introduces fictitious forces that must be “weighed out” to reconstruct the equilibrium free energy. This method, proposed originally by Ciccotti et al.,74 is referred to as the Blue-Moon ensemble, as it aims at observing events so rare they occur “once every blue moon”. Choosing ahead of time the quadrature points, {si}, for integrating the free energy may be rather cumbersome for complex systems and more practical solutions that do not depend dramatically on this choice are desirable. This is the essence of adaptive methods like the adaptive-biasing force74,131 which allow for a more flexible choice of the initial configurations and, thus, make life easier when it comes to converging the free energy estimate along the CV.
. Often, in order to estimate the mean force at a point, si, of the CV space, one needs to constrain the value of the CV to sample a proper ensemble of configurations of the system. This is usually done by using holonomic constraints but introduces fictitious forces that must be “weighed out” to reconstruct the equilibrium free energy. This method, proposed originally by Ciccotti et al.,74 is referred to as the Blue-Moon ensemble, as it aims at observing events so rare they occur “once every blue moon”. Choosing ahead of time the quadrature points, {si}, for integrating the free energy may be rather cumbersome for complex systems and more practical solutions that do not depend dramatically on this choice are desirable. This is the essence of adaptive methods like the adaptive-biasing force74,131 which allow for a more flexible choice of the initial configurations and, thus, make life easier when it comes to converging the free energy estimate along the CV.
Non-Boltzmann sampling
These methods aim at reconstructing the equilibrium free energy profile of a specific activated process from a non-Boltzmann probability distribution. To achieve this goal, sampling is performed adding a bias potential to the underlying potential energy surface along a designated CV. By doing so, one prevents the system from sampling already visited regions of the configurational space, thus, eventually favoring transition between metastable states, i.e., the local minima of the free energy along the CV. By changing the potential energy landscape along a CV, Vb(s) = V(s) + ΔV(s), one modifies the ensemble in which the sampling occurs, and equilibrium properties can be reconstructed by statistical reweighting procedures. In the seminal work introducing US, Torrie and Valleau proposed that non-Boltzmann sampling can be achieved by adding a static bias potential in the form ΔV(s) = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) w where w is a trial function that aims at flattening the probability distribution over the CV space, thus removing high free energy barriers separating metastable states. The function w is thought of as an “umbrella” covering both easy and hard to sample regions of the configurational space and must be found by trial-and-error procedures.52 This technique represents a big step forward in terms of free energy sampling. However, its application to complex systems is largely hindered by the trial-and-error procedure to determine the bias potential. To overcome these technical limitations, a more practical solution has been proposed, where a series of local restrain potentials (windows) are placed along fixed points over the CV space, similarly to TI methods, and different replicas of the simulations are performed for each window. The final Boltzmann equilibrium distribution is then reconstructed by the weighted histogram analysis method (WHAM)132 that combines properly all the information collected from the replicas in one single statistical ensemble.
w where w is a trial function that aims at flattening the probability distribution over the CV space, thus removing high free energy barriers separating metastable states. The function w is thought of as an “umbrella” covering both easy and hard to sample regions of the configurational space and must be found by trial-and-error procedures.52 This technique represents a big step forward in terms of free energy sampling. However, its application to complex systems is largely hindered by the trial-and-error procedure to determine the bias potential. To overcome these technical limitations, a more practical solution has been proposed, where a series of local restrain potentials (windows) are placed along fixed points over the CV space, similarly to TI methods, and different replicas of the simulations are performed for each window. The final Boltzmann equilibrium distribution is then reconstructed by the weighted histogram analysis method (WHAM)132 that combines properly all the information collected from the replicas in one single statistical ensemble.
As mentioned, the main difficulty of US lies in the choice and design of a proper bias potential or, in the case of multi-replica simulations, in the large number of calculations required to ensure convergence. A great alternative to this approach is represented by metadynamics.51,133 The fundamental idea behind MetaD can be found in previous formulations like “local elevation”,134 where an on-the-fly and time-dependent bias in the form of sum of Gaussian functions is deposited along some order parameters, e.g. dihedral angles of a protein, to push the system away from its free energy basins of attraction. The great advancement of MetaD is the possibility of reconstructing the unbiased free energy landscape of the process under study, and thus allowing for quantitative measurement of thermodynamic and kinetic properties. Given its popularity and wide application range in the field of computational catalysis, here will follow a more detailed section on this method in its well-tempered variant (WT-MetaD),133 clarifying the fundamental theoretical and practical aspects.
Well-tempered metadynamics in a nutshell
In WT-MetaD, a history dependent biased potential is deposited along one or more CVs {s} at fixed time intervals. Such a bias takes the form of a sum of Gaussian kernels whose height decreases as long as the simulation proceeds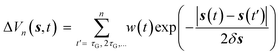 | (13) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−ΔV(s,t)/kBΔT, where ω0 is the initial “deposition rate”, with units in Gaussian height per time, and ΔT is a parameter controlling the excursion velocity of the system from free energy minima. It can be demonstrated133 that WT-MetaD converges smoothly to the true free energy times a multiplicative constant and has the advantage that only specific barriers are crossed by tuning the ΔT parameter.
exp(−ΔV(s,t)/kBΔT, where ω0 is the initial “deposition rate”, with units in Gaussian height per time, and ΔT is a parameter controlling the excursion velocity of the system from free energy minima. It can be demonstrated133 that WT-MetaD converges smoothly to the true free energy times a multiplicative constant and has the advantage that only specific barriers are crossed by tuning the ΔT parameter.
During a MetaD simulation the system is stochastically pushed away from already visited regions of the CV space. In this way, the fluctuations within the basin of attraction are enhanced and transition to other metastable states are accelerated. This gives access not only to a full exploration of the desired chemical rare event but allows one to determine the shape of the free energy landscape and calculate free energy differences including all the relevant entropic contributions without the need of approximations, e.g., harmonic or anharmonic frequency calculations, to estimate the thermodynamics of the process. As a general rule, the quality of the results must be supported by a convergence test of the free energy landscape obtained. This can be done by simply integrating the free energy within the basins of attraction corresponding to reactants and products and calculate the difference ΔF every N time steps during the simulation. In such a way, one can monitor the oscillating behavior of the free energy difference between the two refence basins which should approach a specific value asymptotically. The oscillations are due to the system being pushed forth and back among the free energy basins. Therefore, to converge a free energy surface, one needs several recrossing of the barriers separating them. Only when such oscillations are small within a specific range (optimally ±1kBT) the simulation can be considered converged.
From the free energy profile, one may also derive an approximate estimation of the free energy barrier although this quantity is strongly related to the quality of the CV used to sample and project the free energy process. A more quantitative approach that gives access to reaction rates is provided by a variant of MetaD referred to as infrequent metadynamics,72 a method inspired by Voter's hyperdynamics approach.49 In this method one starts with N independent replicas of the system from a reference metastable state configuration, say the reactants state, initialized with different velocities and properly equilibrated. Then, a MetaD bias is applied on each replica independently using very long deposition intervals (long τG) and the simulations are stopped when the system has escaped the initial metastable state. The slow deposition rate ensures a rather low probability of depositing a bias on the transition state. In such a way, using transition state theory one can calculate for each replica the physical (unbiased) escape time t* simply by reweighting the MetaD simulation time tMetaD by the ensemble average of the bias as t* = tMetaD 〈exp(βΔV(s)〉V, where β = 1/kBT is the inverse temperature. From the collected escape time of each replica, one can obtain a cumulative distribution probability function, fit it to a Poisson-like distribution, and calculate reaction rates as kR→P = 1/〈t*〉 where the term in angular brackets is the mean escape time for all the N replicas obtained from the Poisson fit.135 In this context, Xie and Barton used infrequent metadynamics simulations (InMetaD) to calculate the activation energy of glucose 6-phosphate hopping between association states in electrolytes (see Fig. 9).
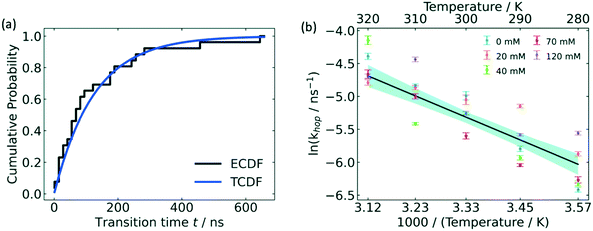 | ||
| Fig. 9 Hopping activation energy by InMetaD. (a) Cumulative probability distribution of transition time from independent InMetaD simulations at IS = 0 mM, 310 K. Theoretical cumulative probability distribution (TCDF) is in blue, and the stepwise empirical cumulative probability distribution (ECDF) in black was fitted from the unbiased transition times, t. (b) Arrhenius plot of the hopping rate at varying ionic strength. The black line represents an Arrhenius fit for all ionic strengths. The shaded area in blue is the 95% confidence interval. Reproduced from ref. 136 (under a Creative Commons Attribution-NonCommercial 3.0 Unported Licence) with permission from the Royal Society of Chemistry. | ||
Data-driven methods for improving AIMD simulations
As mentioned above, data-driven methods such as machine learning and neural networks have been applied to the study of molecular simulations in catalytic reactions.137–141 However, directly employing these methods to AIMD simulations is still under-developed, and their benefits could generally be considered in three categories. First is that these approaches have directly accelerated AIMD simulations where the expensive and repetitive energy and force computations required in AIMD simulations have resulted in significant bottlenecks.142,143 These ML-based algorithms have been proposed to learn past configurations of AIMD on-the-fly and predict energy and force of new configurations faster than conventional AIMD simulations.144 The second categorical advantage is that these methods enable the generation of force field parameters with quantum accuracy based on established AIMD simulations for catalytic systems.56,145,146 The reactive dynamics on catalysts can be explored under conditions comparable to experiments.147 They can also push the AIMD simulations to longer time scales and larger simulated system sizes within acceptable simulation times.148 Similarly, conventional AIMD simulations have difficulty exploring solvent and particle size effects in catalysis due to the need for enough statistical sampling, but the neural network force field derived from AIMD data can provide a powerful tool, e.g., for complicated structure and composition identification under real reaction conditions.149,150 Lastly but not least, these methods can provide some insights by the in-depth analysis of the large amount of AIMD-produced data in catalysis simulations. For instance, ML is applied to interpret AIMD simulations to extract relevant information in chemical reactions with minimal prior input of knowledge on these reactions.151,152Applications of enhanced sampling AIMD in computational catalysis
Here, we review the most relevant applications of different CV based enhanced sampling techniques in catalysis to provide a better understanding of when it is appropriate to use this method and what can be learned from this approach. We focus on nanoporous materials and solid–liquid interfaces where these methods are the most ubiquitously encountered due the nature of confinement effects which challenge simple harmonic approximations. Here, we review the application of enhanced sampling techniques to the study of the reactivity in three important classes of catalytic systems, namely zeolites, metal organic frameworks (MOFs), and solid–liquid interfaces.Zeolites
Acidic zeolites are among the most widely used materials in catalysis and play an important role in the petrochemical industry153 and more recently in the conversion of biomasses.154–158 The catalytic activity in these materials is locally concentrated in the proximity of the Brønsted acid site (BAS), where a bridging OH group is shared by an aluminum and a silicon atom belonging to the material framework (see Fig. 10).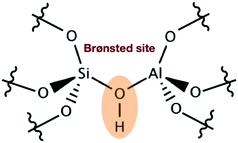 | ||
| Fig. 10 Schematic representation of a BAS showing the bridging hydroxyl group embedded in the zeolite framework. | ||
This specific structural feature of acidic zeolites is a great advantage in terms of computational modelling as not many heterogeneous systems are as well characterized. This gave rise to a large research effort to describe from first principles the reactivity inside these materials, shedding light on the mechanistic aspects as well as their thermodynamics and kinetics. One of the most relevant industrial reactions that is catalyzed efficiently by zeolites is the methanol to hydrocarbons (MTH) process, where a new carbon–carbon bond is formed between a light alkene molecule and a zeolite-activated methanol (see Fig. 11). This reaction is very challenging from a computational point of view as its reactivity is driven by the adsorption of methanol at the BAS as well as the supramolecular complex formed with the physiosorbed alkene.
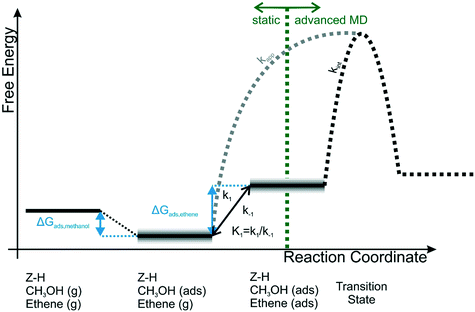 | ||
| Fig. 11 Schematic representation of the relation between apparent and intrinsic kinetics. For the calculation of ΔGads,ethene various schemes are used, shown by the grey uncertainty in the co-adsorption step of ethene. The value of kint is obtained dynamically in this work.159 Reprinted from Journal of Catalysis, vol. 388, Bailleul, S., Dedecker, K., Cnudde, P., Vanduyfhuys, L., Waroquier, M., & Van Speybroeck, V., Ab initio enhanced sampling kinetic study on MTO ethene methylation reaction, pp. 38–51, Copyright 2020, with permission from Elsevier. | ||
From the point of view of enhanced sampling simulations, the group of van Speybroek has provided important methodological and application advancements in modeling the MTO reaction in zeolites. In a series of articles,159–163 they use different CV-based enhanced sampling techniques to study the methylation of different olefinic and aromatic substrates in acidic zeolites. Using TI, US, MetaD and variationally enhanced sampling (VES)164 – a variational approach to metadynamics – the authors provided a dynamical picture of the reaction mechanisms162,163 and qualitative estimates and trends over olefinic chemical series of the reaction barriers159–161 along the CV. The use of enhanced sampling techniques combined with MD simulations allows one to describe the complex reactivity of these processes at real experimental conditions, where in static approaches one may face limitations.
Zeolites are also used very frequently at the industrial level for alkene cracking to optimize the size of hydrocarbons. It is generally assumed that the mechanism of the reaction proceeds via protonation of the olefinic C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond by means of the BAS of the zeolite generating a carbeniun ion intermediate that subsequently undergo to β-scission leading to shorter carbon chains. Recently, Bučko, Chizallet and coworkers investigated the zeolites catalyzed acidic cracking of alkenes focusing on the skeletal isomerization165,166 and β-scission mechanisms167 using AIMD in combination with blue moon ensemble calculations. Some of these computational demonstrations of unique chemistry over zeolites can be seen in Fig. 12. In such a way, they have sampled the possible reaction pathways leading to different products involving carbenium ion intermediates, shedding light on the mechanistic aspects driving the catalytic reaction acceleration and the selectivity induced by the material confinement. Van Speybroek et al. used ab initio MetaD to additionally investigate the stability of cracking intermediates in zeolite H-ZSM-5, which confirmed that carbenium ions are cracking intermediates rather than alkoxides.168
C bond by means of the BAS of the zeolite generating a carbeniun ion intermediate that subsequently undergo to β-scission leading to shorter carbon chains. Recently, Bučko, Chizallet and coworkers investigated the zeolites catalyzed acidic cracking of alkenes focusing on the skeletal isomerization165,166 and β-scission mechanisms167 using AIMD in combination with blue moon ensemble calculations. Some of these computational demonstrations of unique chemistry over zeolites can be seen in Fig. 12. In such a way, they have sampled the possible reaction pathways leading to different products involving carbenium ion intermediates, shedding light on the mechanistic aspects driving the catalytic reaction acceleration and the selectivity induced by the material confinement. Van Speybroek et al. used ab initio MetaD to additionally investigate the stability of cracking intermediates in zeolite H-ZSM-5, which confirmed that carbenium ions are cracking intermediates rather than alkoxides.168
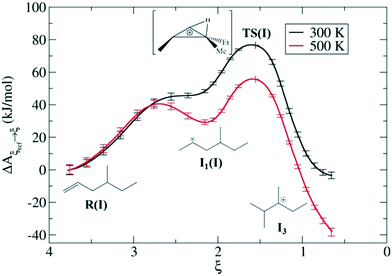 | ||
| Fig. 12 Dynamic features of transition states for isomerization of alkenes over chabazite at two different temperatures based on enhanced sampling AIMD simulations—in this case the blue moon ensemble method. Reprinted with permission from ref. 163. Copyright 2019 American Chemical Society. | ||
More recently, the application of zeolites in the conversion of alcohols have been studied at large. Alcohols are very abundant compounds in lignocellulosic biomass streams.169,170 In order to be useful for other chemical processes involving synthesis steps like carbon–carbon bond formation, they must be converted into olefins. Acidic dehydration followed by Friedel–Crafts alkylation with aromatic compounds leads to useful supplements for non-fossil fuels. It has been shown experimentally that zeolites/water interfaces are able to catalyze efficiently alcohol dehydration171,172 and Friedel–Crafts alkylation,173–175 leading to high-performance industrial production of heavier substrates. The group of Lercher at the Technical University of Munich – TUM (Germany) and Pacific Northwest National Laboratory – PNNL (USA) has pioneered the field shedding light on the fundamental experimental details of these reactions.
From a computational point of view, these alcohol conversion systems represent a further challenge as the reaction takes place at the solid/liquid interface between the zeolite and the alcohol aqueous solution.176–178 In this case, the catalytic site is not a well-defined Brønsted site but a dynamic molecular interface where the acidic proton is delocalized in the solution confined in the pores of the zeolite (see Fig. 13). Despite the intense experimental characterization of these processes, a detailed and comprehensive mechanistic understanding at the molecular level is still lacking.
First, one needs to characterize the mobility of the Brønsted proton in the water cluster confined in the tight hydrophobic zeolite walls. In this regard, Grifoni et al. have recently published a comprehensive study correlating two fundamental aspects, namely zeolite framework structure and water loading.179 They investigated the acidic deprotonation and diffusion process of four different zeolites of increasing pore size in the presence of 1 up to 8 adsorbed water molecules around the catalytic site using full ab initio periodic MetaD simulations. The results of the calculations provide evidence that at low water loadings, the standard free energy of the formed complexes is dominated by enthalpy and is associated with the acid strength of the Brønsted acidic site and the space around it. Conversely, the entropy increases linearly with the concentration of water in the pores and favors proton solvation which is independent of the pore size/shape.
One of the first insights into the dehydration mechanism of ethanol/water mixtures in zeolite has been proposed by Gounder et al. where they used MetaD to explore the mechanism of the reaction.180 At lower water pressure, the inhibition effects of water leads the formation of transition states around the periphery of H2O clusters. At higher water pressure, the extended hydrogen-bonded networks are presented within the water–ethanol cluster, which is accompanied by strengthening water inhibition effects. Such interesting dynamic phenomena were captured due to the combined works of AIMD and MetaD simulations. Fois et al. also used blue-moon sampling to study Ti-based zeolites. They identified kinetically vs. thermodynamically favorable structures resulting from the interactions of water and hydrogen peroxide with the metal center in Ti-based zeolites and explained their relevance to the catalytic properties of zeolites.181 Recently, Hack et al. found that the excess charge is transferred from the zeolite lattice to highly coordinated water molecules within the water cluster using the combined approach of 2D IR spectroscopy and AIMD simulation.182 This study provided valuable understandings on the dynamic natures of H-bond switching and reorientation within water clusters under the tight confinement environment of zeolites.
Metal–organic frameworks (MOFs)
MOFs are novel materials with remarkable porosity and surface area. This makes them excellent candidates for separations and catalysis.184–188 Nevertheless, their complex hybrid structure of metal clusters connected by organic ligands makes them difficult to model due to the rich chemistry of inorganic–organic interactions. In this respect, recent studies have used AIMD with enhanced sampling methods to investigate catalytic processes involving MOFs.More precisely, Caratelli et al. studied UiO-66 (see Fig. 14) and postulated that Lewis acid sites can be formed due to ligands temporarily detaching after interacting with protic solvents.183 This dynamic behavior is of particular interest as these sites can be the active sites in catalytic processes.183 Caratelli et al. used coordination number CVs in order to study this process using AIMD with metadynamics. Heshmat investigated CO2 hydrogenation catalyzed by a frustrated Lewis pair bonded to UiO-66. In this work, the use of metadynamics provides new insights into the reaction mechanism. More precisely, a previously undiscovered stepwise mechanism that is kinetically similar to the concerted mechanism suggested by static DFT calculations is identified using biased AIMD simulations.189
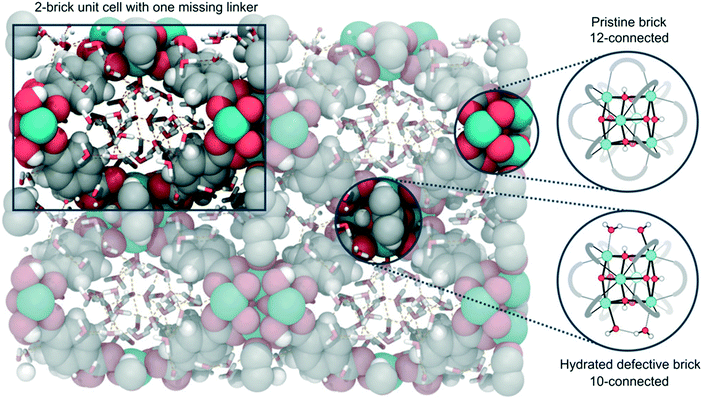 | ||
| Fig. 14 Representation of the defective 2-brick unit cell of UiO-66 used in the simulations, with solvent in the pores of the material. The unit cell is composed by one 12-connected pristine brick and one 10-connected hydrated defective brick, which are displayed on the right. Reprinted from ref. 183 under a creative commons license: https://creativecommons.org/licenses/by-nc-nd/4.0/legalcode). | ||
Haigis et al. used AIMD simulation with metadynamics bias acting on a bond distance CV in order to evaluate the free energy landscape of interactions between MIL-53(Ga) and water.190 The organic linker detaches from the metal center in the presence of water following the cleavage of a gallium – carboxylic oxygen bond. Also, water inside MOF channels lowers the free energy barrier substantially, thus facilitating the process.190 Consequently, this work explains how framework stability is deteriorated in presence of water and suggests ways to overcome this issue.191,192
Defects are also known to affect their mechanical stability; hence mechanistic studies are needed to understand their formation and regulate their emergence during MOF synthesis. Large system sizes and long-time scales are needed to study the thermodynamics and kinetics of growth and understand defect formation. Recently, we investigated the role of solvent and spectator ions in the formation of defects based on microsecond-long metadynamics simulations relying on classical potentials.192 In this context, we used AIMD to simulate the formation of building units in order to derive the classical potential (see Fig. 15).191,192
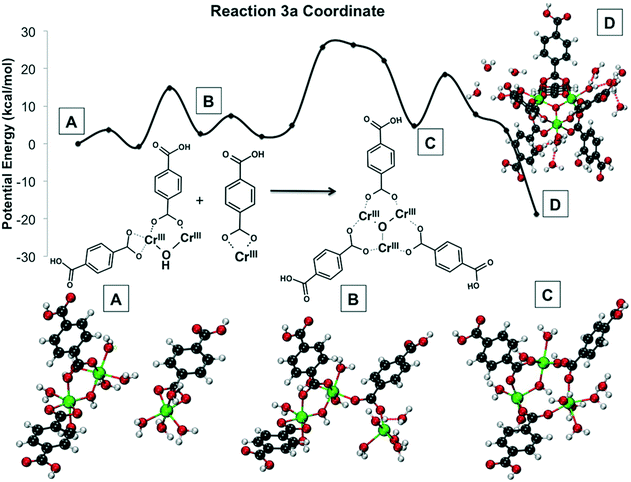 | ||
| Fig. 15 Reaction 3 coordinates and energy profile. In (A), the relative orientation of the reactants is shown. In (B), a Cr–O bond is formed, after a coordination site opens because a water molecule is dissociated from chromium. In (D) the central bridging oxygen joining the three chromiums is formed, whereas in (C) an OH group joins two chromium atoms. Not all water molecules shown explicitly for clarity. Green is Cr(III), red is O, gray is C, and white is H. All Cr atoms are Cr(III). Reprinted with permission from ref. 191. Copyright 2014 American Chemical Society. | ||
Although metadynamics is a powerful tool that can improve sampling during AIMD simulations in the field of catalysis, other enhanced sampling methods have been successfully employed in this context. For instance, Hajek et al. used AIMD simulations with umbrella sampling in order to investigate structural changes during activation processes. They focused on UiO-66 and biased the coordination number between the Zr atoms of the metal center and the bridging hydroxyl oxygen. Through these findings, they explained how linkers can be much more mobile than metal centers as they detach and reattach to hydroxyl groups inside the MOF. This results in a dynamic acidity, observed inside the MOF, that can have an important role in catalysis.193 Ming et al. used thermodynamic integration to estimate the free energy barrier of water insertion in MOF-5.194 Above a threshold of adsorbed water molecules in the MOF, these facilitate the insertion of more water molecules as the free energy barrier for this process is rather low due to the cleavage of Zn–O bonds. Demuynck et al. used both classical and ab initio MD as well as various enhanced sampling methods to study the MIL-53(Al) breathing behavior.195 They highlighted the necessity for AIMD simulations due to dispersion corrections and anharmonic effects contributing to the free energy profile relevant to the breathing process. In a later study, the same group used time-structure based independent component analysis (tICA) on information gained from replica exchange (RE) simulations, namely the tICA-RE protocol.196 This helps the identification of slow modes in the replica exchange trajectories that can be biased using enhanced sampling methods. This way they could formulate CVs which characterize breathing of MOFs. This analysis showed that internal dihedral angles are better CVs than volume as they reveal a stepwise breathing mechanism and identify metastable states in this process.
Enhanced sampling is ordinarily used to study catalytic processes, but there are also unbiased AIMD simulations of MOFs in catalysis. For example, Vandichel et al. studied the stability of UiO-66 in presence of water that is important for its use in catalytic processes.197 In this work, they explain how the presence of linker defects facilitates dehydroxylation and water removal (when defects occur in neighboring linkers for the latter) and how defects affect mechanical stability. Zhang et al. assessed the catalytic properties of TMOF-1. They studied the energetics of CO2 diffusion using AIMD simulations. They postulate that CO2 can easily diffuse through the channels of this renewable heterogeneous catalyst as the free energy landscape of CO2 diffusion is rather flat.198 Bellarosa et al. investigated structural changes within IRMOF-1 using Born-Oppenheimer MD.199 Zn-IRMOF-1 degrades more easily than Mg-IRMOF-1 as the latter maintains its structure due to the strong coordination between Mg and the oxygen of water. More elaborately, this strong interaction hinders additional water molecules approaching the same metal center.199
Chen et al. used AIMD simulations in conjunction with experiments to investigate the effect of temperature and CO2 adsorption on MIL-53(Sc) breathing, hence characterizing the change in pore geometry caused by external stimuli.200 At last, Xue et al. used AIMD simulations to investigate interactions between HKUST-1 and water.201 This MOF has attracted interest in heterogeneous catalysis, but its low stability in humid environments limits its use in applications; hence interactions between the MOF and water need further investigation. Simulations revealed that strong vibrations are induced by water molecules in the pores of HKUST-1. Also, framework stability is affected by temperature and water concentration.201
Heterogeneous catalysis at solid/liquid interfaces
Sitting at an opposite side of nanoporous catalytic materials like zeolites or MOFs we find catalytic surfaces. Here, a much larger variety of materials in terms of composition, structure, and physico-chemical properties is available, ranging from insulating or semiconducting metal oxides to metallic systems, from clean surfaces in vacuum to multifaceted nanoparticles in solution. This great experimental versatility, however, often comes with a great disadvantage in terms of computational modelling. First of all, in most cases such surfaces are not characterized by well-defined catalytic sites, whereas the active part of the material is delocalized all over the surface or situated ambiguously on structural defects of the surface like vacancies or color centers up to kinks or terraces. In such a situation modeling the reaction may be rather cumbersome and could take a lot of work for screening the possible reactive sites. Furthermore, nanoparticles or large catalytic surfaces including catalytic defect sites often constitute several thousands of atoms which hampers the application of ab initio methods for sampling long trajectories. In such cases, one often needs to reduce the complexity of the problem using a slab surface model, where the first surface layer and a number of sublayers sufficient to simulate the bulk properties of the material are used to mimic the real material. However, even under such reduced complexity conditions, the model may require up to hundreds of atoms, often including transition or post-transition metals of the d or f block.Despite modelling challenges, AIMD simulations have been employed to study structural and dynamic properties as well as adsorption/desorption of organic molecules at the solid–liquid interface. Gaigeot et al. employed DFT-based MD simulations to study properties of water orientation and hydrogen bonding at solid oxide/liquid water interfaces.202 They showed that different chemical properties such as acidity of oxide surfaces differentiate water organization at the interfaces. Cheng and Sprik investigated a compact electric double layer at the rutile TiO2–water interface by adding protons to bridging oxygens or removing oxygens from H2O molecules adsorbed on terminal Ti cation sites from DFT-based MD simulations.203 Yuk et al. investigated the hydrogenation of benzaldehyde on Pt-group metals in aqueous phase using AIMD simulations, where they show that the site competition between H and benzaldehyde is dependent on the metal surface.204 They also observe the strong effect of water on the hydrogenation.
Several researchers successfully used enhanced sampling techniques to simulate reactivity at catalytic surfaces. Among many examples, oxide surfaces have been largely studied for their application in sustainable energy conversion catalysis. Different crystalline phases of titanium oxide have attracted a lot of attention as they can play a relevant role in the photocatalytic water splitting205 and CO2 reduction.206 Recently, Andrade et al. (see Fig. 16) used US in combination with ab initio derived neural network potentials to investigate the proton transfer process of bulk liquid water and surface hydroxylation of TiO2 anatase (101).207
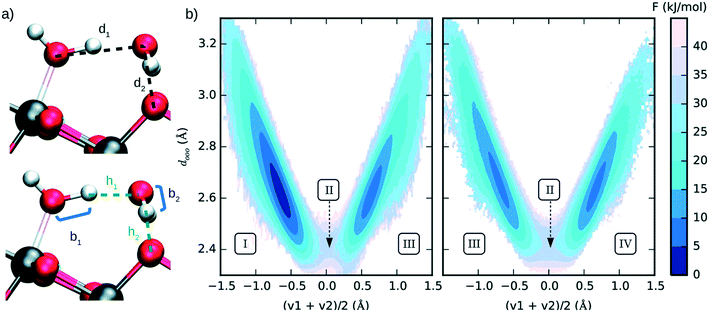 | ||
| Fig. 16 (a) Interatomic distances used to define the two collective variables (CVs) describing proton transfer reactions. The first CV, dooo = (d1 + d2)/2, represents the average distance between hydrogen-bonded oxygen atoms connecting proton-donor and proton-acceptor sites. The second CV, (v1 + v2)/2 (vi = bi − hi), describes the progress of the proton transfer reaction, with positive and negative values corresponding to the dissociated and the molecular states, respectively. (b) Free energy surface of water dissociation (left) and proton transport (right) at the anatase (101)–water interface. Roman numerals indicate the adsorption state of water at specific regions in the free energy plot, I: molecular adsorption; II: transition state; III and IV: equivalent configurations of the dissociated water. Molecular water is more stable than the dissociated state by 8.0 ± 0.9 kJ mol−1, with a free energy barrier of 32 ± 4 kJ mol−1 separating these states. Reproduced from ref. 207 (under a Creative Commons Attribution-NonCommercial 3.0 Unported Licence) with permission from the Royal Society of Chemistry. | ||
The complexity of the molecular motions at solid/liquid interfaces may often lead to very slow converge of the unbiased AIMD sampling due to the large number of degrees of freedom that are relevant to the solvent rearrangements. This is often practically impossible from a simulation point of view given the prohibitive computational demand. In such cases, it is mandatory to enhance the sampling to include all solvent degrees of freedom. In another work, Li et al. studied the dissociation of water on defective rutile TiO2 (110) surfaces using ab initio MetaD simulations.208 Zinc oxide can also be used to reduce and convert CO into more profitable products like methanol. Marx et al. used ab initio MetaD to investigate the mechanism and reaction pathways of this process over the ZnO (000![[1 with combining low line]](https://www.rsc.org/images/entities/char_0031_0332.gif) ) surface.209 Michel et al. used a combination of experimental observations and ab initio metadynamics to understand the stability of reactive alumina surfaces in water.210 Fabris et al. used a combination of ab initio MetaD and US to investigate the hydroxylation and reduction of ceria surfaces.211 Lee et al. studied water film formation, cation mobilization and carbonation at sc-CO2/anorthite interfaces by combining AIMD simulations and blue-moon ensemble simulations. They showed that a water monolayer can be formed even at the low water concentrations at the interface. Furthermore, the presence of water monolayer accelerates the formation of cation vacancies followed by carbonation reaction at electron-rich terminal oxygen sites.212
) surface.209 Michel et al. used a combination of experimental observations and ab initio metadynamics to understand the stability of reactive alumina surfaces in water.210 Fabris et al. used a combination of ab initio MetaD and US to investigate the hydroxylation and reduction of ceria surfaces.211 Lee et al. studied water film formation, cation mobilization and carbonation at sc-CO2/anorthite interfaces by combining AIMD simulations and blue-moon ensemble simulations. They showed that a water monolayer can be formed even at the low water concentrations at the interface. Furthermore, the presence of water monolayer accelerates the formation of cation vacancies followed by carbonation reaction at electron-rich terminal oxygen sites.212
Catalysis at metallic surfaces is often more demanding from a computational point of view due to the fact that the small band gap restricts the use of linear scaling DFT methods and necessitates the use of either small cells or short simulation times—both factors that limit the reliability of the results. Nonetheless, examples of the application of enhanced sampling techniques can also be found in this field. Yang et al. studied the adsorption of hydrogen at water/Pt(111) interface through a combination of AIMD/Blue-Moon ensemble simulations and kinetics.213 They discovered that H2 adsorption is strongly suppressed in the presence of the liquid as a result of both enthalpic (change in work function of Pt(111)) and entropic (restructuring of the interface) drivers. Sun and Jiang reported an AIMD study of the CH2 CH + H reaction on Ni(111)214 using integrated tempering.215 Okumura et al. studied the reactive adsorption of hydrogen on a Pt surface using MetaD on a neural network derived potential. Very recently, de Pablo et al. reported the investigation of the free energy landscape for nitrogen dissociation on Ru(0001)216 using a neural-network-based enhanced sampling method called combined-force frequency (CFF),217 a ML gradient-based method.
CH + H reaction on Ni(111)214 using integrated tempering.215 Okumura et al. studied the reactive adsorption of hydrogen on a Pt surface using MetaD on a neural network derived potential. Very recently, de Pablo et al. reported the investigation of the free energy landscape for nitrogen dissociation on Ru(0001)216 using a neural-network-based enhanced sampling method called combined-force frequency (CFF),217 a ML gradient-based method.
Conclusions
The combination of ab initio molecular dynamics with enhanced sampling methods provides the computational catalysis community with a powerful and flexible tool to study reactivity in complex and structured reaction environments from first principles. Through these molecular simulations, one can examine catalysts in a holistic manner accounting for both the active site and its environment. This contribution to the understanding of the atomistic and molecular aspects of catalysis enables us to move beyond simple models (which are designed for rapid screening of materials) to models that better reflect the innate complexity of catalysts under operating conditions, including elevated temperatures and a mixture of products, reactants, and inhibiters/co-catalysts. In this respect, AIMD and other statistical methods are slowly becoming vital to complementing experimental evidence, refining our understanding of reactivity in complex environments, and ultimately using this knowledge to design better catalytic materials/processes. In parallel, the entrance of machine learning and data science techniques in the mainstream of molecular simulations is boosting the applicability of modeling techniques to a wide variety of problems and improving in silico materials design. It is the hope of the authors that this review will help researchers in the computational catalysis community in orienting themselves in this vast field as well as guiding experimental scientists in understanding the immense potential that these techniques possess to improve process understanding with atomistic detail.Conflicts of interest
There are no conflicts to declare.Acknowledgements
GMP, MSL, MTN, LK, and VAG acknowledge support from the US Department of Energy (DOE), Office of Science, Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences, and Biosciences. SFY, DZ, GC, and RR were supported by funding from US-DOE, Office of Energy Efficiency and Renewable Energy, Biotechnology Office's Consortium for Computationally Physics and Chemistry. Pacific Northwest National Laboratory is operated by Battelle for DOE under contract DE-AC05-76RL01830.References
- L. Grajciar, C. J. Heard, A. A. Bondarenko, M. V. Polynski, J. Meeprasert, E. A. Pidko and P. Nachtigall, Towards operando computational modeling in heterogeneous catalysis, Chem. Soc. Rev., 2018, 47(22), 8307–8348 RSC.
- G. Collinge, S. F. Yuk, M.-T. Nguyen, M.-S. Lee, V.-A. Glezakou and R. Rousseau, Effect of Collective Dynamics and Anharmonicity on Entropy in Heterogenous Catalysis: Building the Case for Advanced Molecular Simulations, ACS Catal., 2020, 10(16), 9236–9260 CrossRef CAS.
- M. Stamatakis and D. G. Vlachos, Unraveling the Complexity of Catalytic Reactions via Kinetic Monte Carlo Simulation: Current Status and Frontiers, ACS Catal., 2012, 2(12), 2648–2663 CrossRef CAS.
- M. Jørgensen and H. Grönbeck, Perspectives on Computational Catalysis for Metal Nanoparticles, ACS Catal., 2019, 9(10), 8872–8881 CrossRef.
- J. K. Nørskov, T. Bligaard, J. Rossmeisl and C. H. Christensen, Towards the computational design of solid catalysts, Nat. Chem., 2009, 1(1), 37–46 CrossRef.
- B. W. J. Chen, L. Xu and M. Mavrikakis, Computational Methods in Heterogeneous Catalysis, Chem. Rev., 2021, 121(2), 1007–1048 CrossRef CAS.
- A. Asthagiri and M. J. Janik, Computational Catalysis, Royal Society of Chemistry, Cambridge, 2013 Search PubMed.
- A. Alavi, P. Hu, T. Deutsch, P. L. Silvestrelli and J. Hutter, CO Oxidation on Pt(111): An Ab Initio Density Functional Theory Study, Phys. Rev. Lett., 1998, 80(16), 3650–3653 CrossRef CAS.
- M. Saeys, M.-F. Reyniers, G. B. Marin and M. Neurock, Density Functional Study of Benzene Adsorption on Pt(111), J. Phys. Chem. B, 2002, 106(30), 7489–7498 CrossRef CAS.
- Z.-P. Liu, P. Hu and A. Alavi, Catalytic Role of Gold in Gold-Based Catalysts: A Density Functional Theory Study on the CO Oxidation on Gold, J. Am. Chem. Soc., 2002, 124(49), 14770–14779 CrossRef CAS PubMed.
- M. Digne, P. Sautet, P. Raybaud, P. Euzen and H. Toulhoat, Use of DFT to Achieve a Rational Understanding of Acid–basic Properties of γ-Alumina Surfaces, J. Catal., 2004, 226(1), 54–68 CrossRef CAS.
- D. A. Hansgen, D. G. Vlachos and J. G. Chen, Using First Principles to Predict Bimetallic Catalysts for the Ammonia Decomposition Reaction, Nat. Chem., 2010, 2(6), 484–489 CrossRef CAS PubMed.
- F. Tao, S. Dag, L.-W. Wang, Z. Liu, D. R. Butcher, H. Bluhm, M. Salmeron and G. A. Somorjai, Break-Up of Stepped Platinum Catalyst Surfaces by High CO Coverage, Science, 2010, 327(5967), 850 CrossRef CAS.
- L. C. Grabow and M. Mavrikakis, Mechanism of Methanol Synthesis on Cu through CO2 and CO Hydrogenation, ACS Catal., 2011, 1(4), 365–384 CrossRef CAS.
- M. Behrens, F. Studt, I. Kasatkin, S. Kühl, M. Hävecker, F. Abild-Pedersen, S. Zander, F. Girgsdies, P. Kurr, B.-L. Kniep, M. Tovar, R. W. Fischer, J. K. Nørskov and R. Schlögl, The Active Site of Methanol Synthesis over Cu/ZnO/Al<sub>2</sub>O<sub>3</sub> Industrial Catalysts, Science, 2012, 336(6083), 893 CrossRef CAS PubMed.
- E. W. McFarland and H. Metiu, Catalysis by Doped Oxides, Chem. Rev., 2013, 113(6), 4391–4427 CrossRef CAS.
- W. Thiel, Computational Catalysis—Past, Present, and Future, Angew. Chem., Int. Ed., 2014, 53(33), 8605–8613 CrossRef CAS PubMed.
- J. Saavedra, H. A. Doan, C. J. Pursell, L. C. Grabow and B. D. Chandler, The Critical Role of Water at the Gold-titania Interface in Catalytic CO Oxidation, Science, 2014, 345(6204), 1599 CrossRef CAS PubMed.
- A. Kulkarni, S. Siahrostami, A. Patel and J. K. Nørskov, Understanding Catalytic Activity Trends in the Oxygen Reduction Reaction, Chem. Rev., 2018, 118(5), 2302–2312 CrossRef CAS.
- D. Frenkel and B. Smit, Understanding Molecular Simulation: From Algorithms to Applications, Elsevier Science, 2001 Search PubMed.
- X. Liu, X. Wen and R. Hoffmann, Surface Activation of Transition Metal Nanoparticles for Heterogeneous Catalysis: What We Can Learn from Molecular Dynamics, ACS Catal., 2018, 8(4), 3365–3375 CrossRef CAS.
- M. Boero, M. Parrinello and K. Terakura, First Principles Molecular Dynamics Study of Ziegler−Natta Heterogeneous Catalysis, J. Am. Chem. Soc., 1998, 120(12), 2746–2752 CrossRef CAS.
- V. Termath, F. Haase, J. Sauer, J. Hutter and M. Parrinello, Understanding the Nature of Water Bound to Solid Acid Surfaces. Ab Initio Simulation on HSAPO-34, J. Am. Chem. Soc., 1998, 120(33), 8512–8516 CrossRef CAS.
- V. van Speybroeck and R. J. Meier, A recent development in computational chemistry: chemical reactions from first principles molecular dynamics simulations, Chem. Soc. Rev., 2003, 32(3), 151–157 RSC.
- K. Alexopoulos, M.-S. Lee, Y. Liu, Y. Zhi, Y. Liu, M.-F. o. Reyniers, G. B. Marin, V.-A. Glezakou, R. Rousseau and J. A. Lercher, Anharmonicity and confinement in zeolites: structure, spectroscopy, and adsorption free energy of ethanol in H-ZSM-5, J. Phys. Chem. C, 2016, 120(13), 7172–7182 CrossRef CAS.
- S. F. Yuk, M.-S. Lee, G. Collinge, J. Zhang, A. B. Padmaperuma, Z. Li, F. Polo-Garzon, Z. Wu, V.-A. Glezakou and R. Rousseau, Mechanistic Understanding of Catalytic Conversion of Ethanol to 1-Butene over 2D-Pillared MFI Zeolite, J. Phys. Chem. C, 2020, 124(52), 28437–28447 CrossRef CAS.
- Y.-G. Wang, D. Mei, V.-A. Glezakou, J. Li and R. Rousseau, Dynamic formation of single-atom catalytic active sites on ceria-supported gold nanoparticles, Nat. Commun., 2015, 6(1), 6511 CrossRef CAS.
- Y.-G. Wang, Y. Yoon, V.-A. Glezakou, J. Li and R. Rousseau, The Role of Reducible Oxide–Metal Cluster Charge Transfer in Catalytic Processes: New Insights on the Catalytic Mechanism of CO Oxidation on Au/TiO2 from ab Initio Molecular Dynamics, J. Am. Chem. Soc., 2013, 135(29), 10673–10683 CrossRef CAS.
- C.-Q. Xu, M.-S. Lee, Y.-G. Wang, D. C. Cantu, J. Li, V.-A. Glezakou and R. Rousseau, Structural Rearrangement of Au–Pd Nanoparticles under Reaction Conditions: An ab Initio Molecular Dynamics Study, ACS Nano, 2017, 11(2), 1649–1658 CrossRef CAS PubMed.
- Y.-G. Wang, D. C. Cantu, M.-S. Lee, J. Li, V.-A. Glezakou and R. Rousseau, CO Oxidation on Au/TiO2: Condition-Dependent Active Sites and Mechanistic Pathways, J. Am. Chem. Soc., 2016, 138(33), 10467–10476 CrossRef CAS.
- S. A. Hollingsworth and R. O. Dror, Molecular Dynamics Simulation for All, Neuron, 2018, 99(6), 1129–1143 CrossRef CAS.
- J. A. Harrison, J. D. Schall, S. Maskey, P. T. Mikulski, M. T. Knippenberg and B. H. Morrow, Review of force fields and intermolecular potentials used in atomistic computational materials research, Appl. Phys. Rev., 2018, 5(3), 031104 Search PubMed.
- D. Marx, In Ab initio molecular dynamics: Theory and Implementation, 2000 Search PubMed.
- M. E. Tuckerman, Ab initio molecular dynamics: basic concepts, current trends and novel applications, J. Phys.: Condens. Matter, 2002, 14(50), R1297–R1355 CrossRef CAS.
- R. Car and M. Parrinello, Unified Approach for Molecular Dynamics and Density-Functional Theory, Phys. Rev. Lett., 1985, 55(22), 2471–2474 CrossRef CAS PubMed.
- M. C. Payne, M. P. Teter, D. C. Allan, T. A. Arias and J. D. Joannopoulos, Iterative minimization techniques for ab initio total-energy calculations: molecular dynamics and conjugate gradients, Rev. Mod. Phys., 1992, 64(4), 1045–1097 CrossRef CAS.
- M. Born and R. Oppenheimer, Zur Quantentheorie der Molekeln, Ann. Phys., 1927, 389(20), 457–484 CrossRef.
- T. Laino, F. Mohamed, A. Laio and M. Parrinello, An Efficient Real Space Multigrid QM/MM Electrostatic Coupling, J. Chem. Theory Comput., 2005, 1(6), 1176–1184 CrossRef CAS.
- A. Laio, J. VandeVondele and U. Rothlisberger, A Hamiltonian electrostatic coupling scheme for hybrid Car–Parrinello molecular dynamics simulations, J. Chem. Phys., 2002, 116(16), 6941–6947 CrossRef CAS.
- T. K. Woo, P. M. Margl, P. E. Blöchl and T. Ziegler, A Combined Car−Parrinello QM/MM Implementation for ab Initio Molecular Dynamics Simulations of Extended Systems: Application to Transition Metal Catalysis, J. Phys. Chem. B, 1997, 101(40), 7877–7880 CrossRef CAS.
- D. Lu, H. Wang, M. Chen, L. Lin, R. Car, W. E, W. Jia and L. Zhang, 86 PFLOPS Deep Potential Molecular Dynamics simulation of 100 million atoms with ab initio accuracy, Comput. Phys. Commun., 2021, 259, 107624 CrossRef CAS.
- I. S. Ufimtsev and T. J. Martinez, Quantum Chemistry on Graphical Processing Units. 3. Analytical Energy Gradients, Geometry Optimization, and First Principles Molecular Dynamics, J. Chem. Theory Comput., 2009, 5(10), 2619–2628 CrossRef CAS.
- A. F. Voter, F. Montalenti and T. C. Germann, Extending the Time Scale in Atomistic Simulation of Materials, Annu. Rev. Mater. Res., 2002, 32(1), 321–346 CrossRef CAS.
- O. Valsson, P. Tiwary and M. Parrinello, Enhancing Important Fluctuations: Rare Events and Metadynamics from a Conceptual Viewpoint, Annu. Rev. Phys. Chem., 2016, 67(1), 159–184 CrossRef CAS PubMed.
- B. Peters, Introduction in Reaction Rate Theory and Rare Events Simulations, ed. B. Peters, Elsevier, Amsterdam, 2017, ch. 1, pp. 1–17 Search PubMed.
- G. M. Torrie and J. P. Valleau, Nonphysical Sampling Distributions in Monte Carlo Free-energy Estimation: Umbrella Sampling, J. Comput. Phys., 1977, 23(2), 187–199 CrossRef.
- D. J. Earl and M. W. Deem, Parallel tempering: Theory, applications, and new perspectives, Phys. Chem. Chem. Phys., 2005, 7(23), 3910–3916 RSC.
- R. H. Swendsen and J.-S. Wang, Replica Monte Carlo Simulation of Spin-Glasses, Phys. Rev. Lett., 1986, 57(21), 2607–2609 CrossRef PubMed.
- A. F. Voter, Hyperdynamics: Accelerated Molecular Dynamics of Infrequent Events, Phys. Rev. Lett., 1997, 78(20), 3908–3911 CrossRef CAS.
- C. Dellago, P. G. Bolhuis and P. L. Geissler, Transition Path Sampling, in Advances in Chemical Physics, 2002, pp. 1–78 Search PubMed.
- A. Laio and M. Parrinello, Escaping free-energy minima, Proc. Natl. Acad. Sci. U. S. A., 2002, 99(20), 12562 CrossRef CAS PubMed.
- C. Abrams and G. Bussi, Enhanced Sampling in Molecular Dynamics Using Metadynamics, Replica-Exchange, and Temperature-Acceleration, Entropy, 2014, 16(1), 163–199 CrossRef.
- H. Jonsson, G. Mills and K. W. Jacobsen, Nudged elastic band method for finding minimum energy paths of transitions, in Classical and Quantum Dynamics in Condensed Phase Simulations, World Scientific, 1998, pp. 385–404 Search PubMed.
- C. Chen, Y. Zuo, W. Ye, X. Li, Z. Deng and S. P. Ong, A Critical Review of Machine Learning of Energy Materials, Adv. Energy Mater., 2020, 10(8), 1903242 CrossRef CAS.
- G. R. Schleder, A. C. M. Padilha, C. M. Acosta, M. Costa and A. Fazzio, From DFT to machine learning: recent approaches to materials science–a review, JPhys Mater., 2019, 2(3), 032001 CrossRef CAS.
- Y. Li, H. Li, F. C. Pickard, B. Narayanan, F. G. Sen, M. K. Y. Chan, S. K. R. S. Sankaranarayanan, B. R. Brooks and B. Roux, Machine Learning Force Field Parameters from Ab Initio Data, J. Chem. Theory Comput., 2017, 13(9), 4492–4503 CrossRef CAS PubMed.
- J. M. Serra, A. Corma, A. Chica, E. Argente and V. Botti, Can artificial neural networks help the experimentation in catalysis?, Catal. Today, 2003, 81(3), 393–403 CrossRef CAS.
- W. Yang, T. T. Fidelis and W.-H. Sun, Machine Learning in Catalysis, From Proposal to Practicing, ACS Omega, 2020, 5(1), 83–88 CrossRef CAS.
- J. Jawad, A. H. Hawari and S. Javaid Zaidi, Artificial neural network modeling of wastewater treatment and desalination using membrane processes: A review, Chem. Eng. J., 2021, 419, 129540 CrossRef CAS.
- J. R. Kitchin, Machine learning in catalysis, Nat. Catal., 2018, 1(4), 230–232 CrossRef.
- Z. Li, S. Wang and H. Xin, Toward artificial intelligence in catalysis, Nat. Catal., 2018, 1(9), 641–642 CrossRef.
- P. Schlexer Lamoureux, K. T. Winther, J. A. Garrido Torres, V. Streibel, M. Zhao, M. Bajdich, F. Abild-Pedersen and T. Bligaard, Machine Learning for Computational Heterogeneous Catalysis, ChemCatChem, 2019, 11(16), 3581–3601 CrossRef CAS.
- S. Ma and Z.-P. Liu, Machine Learning for Atomic Simulation and Activity Prediction in Heterogeneous Catalysis: Current Status and Future, ACS Catal., 2020, 10(22), 13213–13226 CrossRef CAS.
- T. Toyao, Z. Maeno, S. Takakusagi, T. Kamachi, I. Takigawa and K.-I. Shimizu, Machine Learning for Catalysis Informatics: Recent Applications and Prospects, ACS Catal., 2020, 10(3), 2260–2297 CrossRef CAS.
- M.-S. Lee, B. P. McGrail and V.-A. Glezakou, Microstructural Response of Variably Hydrated Ca-rich Montmorillonite to Supercritical CO2, Environ. Sci. Technol., 2014, 48(15), 8612–8619 CrossRef CAS.
- C. S. Praveen, A. Comas-Vives, C. Copéret and J. VandeVondele, Role of Water, CO2, and Noninnocent Ligands in the CO2 Hydrogenation to Formate by an Ir(III) PNP Pincer Catalyst Evaluated by Static-DFT and ab Initio Molecular Dynamics under Reaction Conditions, Organometallics, 2017, 36(24), 4908–4919 CrossRef CAS.
- R. Rousseau, G. K. Schenter, J. L. Fulton, J. C. Linehan, M. H. Engelhard and T. Autrey, Defining Active Catalyst Structure and Reaction Pathways from ab Initio Molecular Dynamics and Operando XAFS: Dehydrogenation of Dimethylaminoborane by Rhodium Clusters, J. Am. Chem. Soc., 2009, 131(30), 10516–10524 CrossRef CAS PubMed.
- P. Vidossich, A. Lledós and G. Ujaque, First-Principles Molecular Dynamics Studies of Organometallic Complexes and Homogeneous Catalytic Processes, Acc. Chem. Res., 2016, 49(6), 1271–1278 CrossRef CAS PubMed.
- M. O'Hagan, W. J. Shaw, S. Raugei, S. Chen, J. Y. Yang, U. J. Kilgore, D. L. DuBois and R. M. Bullock, Moving Protons with Pendant Amines: Proton Mobility in a Nickel Catalyst for Oxidation of Hydrogen, J. Am. Chem. Soc., 2011, 133(36), 14301–14312 CrossRef PubMed.
- T. K. Woo, P. M. Margl, T. Ziegler and P. E. Blöchl, Static and Ab Initio Molecular Dynamics Study of the Titanium(IV)-Constrained Geometry Catalyst (CpSiH2NH)Ti-R+. 2. Chain Termination and Long Chain Branching, Organometallics, 1997, 16(15), 3454–3468 CrossRef CAS.
- A. Barducci, M. Bonomi and M. Parrinello, Metadynamics, WIREs Comput. Mol. Sci., 2011, 1(5), 826–843 CrossRef CAS.
- P. Tiwary and M. Parrinello, From Metadynamics to Dynamics, Phys. Rev. Lett., 2013, 111(23), 230602 CrossRef.
- P. Tiwary and M. Parrinello, A Time-Independent Free Energy Estimator for Metadynamics, J. Phys. Chem. B, 2015, 119(3), 736–742 CrossRef CAS.
- G. Ciccotti and M. Ferrario, Blue Moon Approach to Rare Events, Mol. Simul., 2004, 30(11–12), 787–793 CrossRef CAS.
- E. A. Carter, G. Ciccotti, J. T. Hynes and R. Kapral, Constrained reaction coordinate dynamics for the simulation of rare events, Chem. Phys. Lett., 1989, 156(5), 472–477 CrossRef CAS.
- M. Sprik and G. Ciccotti, Free energy from constrained molecular dynamics, J. Chem. Phys., 1998, 109(18), 7737–7744 CrossRef CAS.
- R. L. De Sousa and H. W. Leite Alves, Ab Initio Calculation of the Dynamical Properties of PPP and PPV, Braz. J. Phys., 2005, 36, 501–504 CrossRef.
- A. Sediki, L. C. Snoek and M.-P. Gaigeot, N–H+ vibrational anharmonicities directly revealed from DFT-based molecular dynamics simulations on the Ala7H+ protonated peptide, Int. J. Mass Spectrom., 2011, 308(2), 281–288 CrossRef CAS.
- G. Piccini and J. Sauer, Effect of Anharmonicity on Adsorption Thermodynamics, J. Chem. Theory Comput., 2014, 10(6), 2479–2487 CrossRef CAS PubMed.
- C. J. Cramer, Essentials of Computational Chemistry: Theories and Models, John Wiley & Sons, 2005 Search PubMed.
- C. T. Campbell, L. H. Sprowl and L. Arnadottir, Equilibrium Constants and Rate Constants for Adsorbates: Two-Dimensional (2D) Ideal Gas, 2D Ideal Lattice Gas, and Ideal Hindered Translator Models, J. Phys. Chem. C, 2016, 120(19), 10283–10297 CrossRef CAS.
- M. Jorgensen and H. Gronbeck, Adsorbate Entropies with Complete Potential Energy Sampling in Microkinetic Modeling, J. Phys. Chem. C, 2017, 121(13), 7199–7207 CrossRef.
- B. Njegic and M. S. Gordon, Predicting accurate vibrational frequencies for highly anharmonic systems, J. Chem. Phys., 2008, 129(16), 164107 CrossRef PubMed.
- C. T. Campbell and J. R. V. Sellers, The Entropies of Adsorbed Molecules, J. Am. Chem. Soc., 2012, 134(43), 18109–18115 CrossRef CAS.
- G. Piccini, M. Alessio and J. Sauer, Ab initio study of methanol and ethanol adsorption on Brønsted sites in zeolite H-MFI, Phys. Chem. Chem. Phys., 2018, 20(30), 19964–19970 RSC.
- A. C. T. van Duin, A. Strachan, S. Stewman, Q. Zhang, X. Xu and W. A. Goddard, ReaxFFSiO Reactive Force Field for Silicon and Silicon Oxide Systems, J. Phys. Chem. A, 2003, 107(19), 3803–3811 CrossRef CAS.
- K. Chenoweth, A. C. T. van Duin and W. A. Goddard Iii, The ReaxFF Monte Carlo Reactive Dynamics Method for Predicting Atomistic Structures of Disordered Ceramics: Application to the Mo3VOx Catalyst, Angew. Chem., Int. Ed., 2009, 48(41), 7630–7634 CrossRef CAS.
- D. Furman and D. J. Wales, Transforming the Accuracy and Numerical Stability of ReaxFF Reactive Force Fields, J. Phys. Chem. Lett., 2019, 10(22), 7215–7223 CrossRef CAS PubMed.
- T. P. Senftle, S. Hong, M. M. Islam, S. B. Kylasa, Y. Zheng, Y. K. Shin, C. Junkermeier, R. Engel-Herbert, M. J. Janik, H. M. Aktulga, T. Verstraelen, A. Grama and A. C. T. van Duin, The ReaxFF Reactive Force-Field: Development, Applications and Future Directions, npj Comput. Mater., 2016, 2(1), 15011 CrossRef CAS.
- Y. Han, D. Jiang, J. Zhang, W. Li, Z. Gan and J. Gu, Development, applications and challenges of ReaxFF reactive force field in molecular simulations, Front. Chem. Sci. Eng., 2016, 10(1), 16–38 CrossRef CAS.
- H. L. Woodcock, M. Hodošček and B. R. Brooks, Exploring SCC-DFTB Paths for Mapping QM/MM Reaction Mechanisms, J. Phys. Chem. A, 2007, 111(26), 5720–5728 CrossRef CAS.
- M. Elstner, D. Porezag, G. Jungnickel, J. Elsner, M. Haugk, T. Frauenheim, S. Suhai and G. Seifert, Self-consistent-charge density-functional tight-binding method for simulations of complex materials properties, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58(11), 7260–7268 CrossRef CAS.
- L. Verlet, Computer “Experiments” on Classical Fluids. I. Thermodynamical Properties of Lennard-Jones Molecules, Phys. Rev., 1967, 159(1), 98–103 CrossRef CAS.
- R. W. Hockney, The potential calculation and some applications, Methods Comput. Phys., 1970, 9, 136 Search PubMed.
- C. Costentin, M. Robert and J.-M. Savéant, Electrochemical concerted proton and electron transfers. Potential-dependent rate constant, reorganization factors, proton tunneling and isotope effects, J. Electroanal. Chem., 2006, 588(2), 197–206 CrossRef CAS.
- J. T. Fermann and S. Auerbach, Modeling proton mobility in acidic zeolite clusters: II. Room temperature tunneling effects from semiclassical rate theory, J. Chem. Phys., 2000, 112(15), 6787–6794 CrossRef CAS.
- S. Hammes-Schiffer, Hydrogen Tunneling and Protein Motion in Enzyme Reactions, Acc. Chem. Res., 2006, 39(2), 93–100 CrossRef CAS.
- C.-K. Skylaris, P. D. Haynes, A. A. Mostofi and M. C. Payne, Introducing ONETEP: Linear-scaling density functional simulations on parallel computers, J. Chem. Phys., 2005, 122(8), 084119 CrossRef.
- V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Ab initio molecular simulations with numeric atom-centered orbitals, Comput. Phys. Commun., 2009, 180(11), 2175–2196 CrossRef CAS.
- J. VandeVondele, U. Borštnik and J. Hutter, Linear Scaling Self-Consistent Field Calculations with Millions of Atoms in the Condensed Phase, J. Chem. Theory Comput., 2012, 8(10), 3565–3573 CrossRef CAS PubMed.
- J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Quickstep: Fast and accurate density functional calculations using a mixed Gaussian and plane waves approach, Comput. Phys. Commun., 2005, 167(2), 103–128 CrossRef CAS.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, First principles methods using CASTEP, Z. Kristallogr. Cryst. Mater., 2005, 220(5–6), 567–570 CrossRef CAS.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47(1), 558–561 CrossRef CAS.
- D. K. Remler and P. A. Madden, Molecular dynamics without effective potentials via the Car-Parrinello approach, Mol. Phys., 1990, 70(6), 921–966 CrossRef CAS.
- J. Hutter, Car–Parrinello molecular dynamics, WIREs Comput. Mol. Sci., 2012, 2(4), 604–612 CrossRef CAS.
- CPMD http://www.cpmd.org/.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials, J. Phys.: Condens. Matter, 2009, 21(39), 395502 CrossRef PubMed.
- P. Tangney, On the theory underlying the Car-Parrinello method and the role of the fictitious mass parameter, J. Chem. Phys., 2006, 124(4), 044111 CrossRef PubMed.
- T. D. Kühne, M. Krack, F. R. Mohamed and M. Parrinello, Efficient and Accurate Car-Parrinello-like Approach to Born-Oppenheimer Molecular Dynamics, Phys. Rev. Lett., 2007, 98(6), 066401 CrossRef PubMed.
- G. Galli and M. Parrinello, Ab-Initio Molecular Dynamics: Principles and Practical Implementation, in Computer Simulation in Materials Science: Interatomic Potentials, Simulation Techniques and Applications, ed. M. Meyer and V. Pontikis, Springer Netherlands, Dordrecht, 1991, pp. 283–304 Search PubMed.
- W. L. Jorgensen and L. L. Thomas, Perspective on Free-Energy Perturbation Calculations for Chemical Equilibria, J. Chem. Theory Comput., 2008, 4(6), 869–876 CrossRef CAS.
- R. W. Zwanzig, High-Temperature Equation of State by a Perturbation Method. I. Nonpolar Gases, J. Chem. Phys., 1954, 22(8), 1420–1426 CrossRef CAS.
- J. K. Hwang, G. King, S. Creighton and A. Warshel, Simulation of free energy relationships and dynamics of SN2 reactions in aqueous solution, J. Am. Chem. Soc., 1988, 110(16), 5297–5311 CrossRef CAS.
- C. D. Fu, L. F. L. Oliveira and J. Pfaendtner, Assessing Generic Collective Variables for Determining Reaction Rates in Metadynamics Simulations, J. Chem. Theory Comput., 2017, 13(3), 968–973 CrossRef CAS PubMed.
- M. Sultan and V. S. Pande, tICA-Metadynamics: Accelerating Metadynamics by Using Kinetically Selected Collective Variables, J. Chem. Theory Comput., 2017, 13(6), 2440–2447 CrossRef PubMed.
- D. Mendels, G. Piccini and M. Parrinello, Collective Variables from Local Fluctuations, J. Phys. Chem. Lett., 2018, 9(11), 2776–2781 CrossRef PubMed.
- M. M. Sultan and V. S. Pande, Automated design of collective variables using supervised machine learning, J. Chem. Phys., 2018, 149(9), 094106 CrossRef PubMed.
- G. Piccini, D. Mendels and M. Parrinello, Metadynamics with Discriminants: A Tool for Understanding Chemistry, J. Chem. Theory Comput., 2018, 14(10), 5040–5044 CrossRef CAS PubMed.
- L. Bonati, V. Rizzi and M. Parrinello, Data-Driven Collective Variables for Enhanced Sampling, J. Phys. Chem. Lett., 2020, 11(8), 2998–3004 CrossRef CAS PubMed.
- K. Lindorff-Larsen, S. Piana, R. O. Dror and D. E. Shaw, How Fast-Folding Proteins Fold, Science, 2011, 334(6055), 517 CrossRef CAS PubMed.
- J. McCarty and M. Parrinello, A variational conformational dynamics approach to the selection of collective variables in metadynamics, J. Chem. Phys., 2017, 147(20), 204109 CrossRef PubMed.
- G. Piccini, D. Polino and M. Parrinello, Identifying Slow Molecular Motions in Complex Chemical Reactions, J. Phys. Chem. Lett., 2017, 8(17), 4197–4200 CrossRef CAS PubMed.
- D. Branduardi, F. L. Gervasio and M. Parrinello, From A to B in free energy space, J. Chem. Phys., 2007, 126(5), 054103 CrossRef PubMed.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, A climbing image nudged elastic band method for finding saddle points and minimum energy paths, J. Chem. Phys., 2000, 113(22), 9901–9904 CrossRef CAS.
- F. Pietrucci and A. M. Saitta, Formamide Reaction Network in Gas Phase and Solution via a Unified Theoretical Approach: Toward a Reconciliation of Different Prebiotic Scenarios, Proc. Natl. Acad. Sci. U. S. A., 2015, 112(49), 15030 CrossRef CAS PubMed.
- F. Pietrucci, Novel Enhanced Sampling Strategies for Transitions Between Ordered and Disordered Structures, in Handbook of Materials Modeling: Methods: Theory and Modeling, ed. W. Andreoni and S. Yip, Springer International Publishing, Cham, 2020, pp. 597–619 Search PubMed.
- F. Pietrucci and W. Andreoni, Fate of a Graphene Flake: A New Route toward Fullerenes Disclosed with Ab Initio Simulations, J. Chem. Theory Comput., 2014, 10(3), 913–917 CrossRef CAS PubMed.
- D. Frenkel and B. Smit, Chapter 1 – Introduction, in Understanding Molecular Simulation, ed. D. Frenkel and B. Smit, Academic Press, San Diego, 2nd edn, 2002, pp. 1–6 Search PubMed.
- J. G. Kirkwood, Statistical Mechanics of Fluid Mixtures, J. Chem. Phys., 1935, 3(5), 300–313 CrossRef CAS.
- E. Darve and A. Pohorille, Calculating free energies using average force, J. Chem. Phys., 2001, 115(20), 9169–9183 CrossRef CAS.
- J. Comer, J. C. Gumbart, J. Hénin, T. Lelièvre, A. Pohorille and C. Chipot, The Adaptive Biasing Force Method: Everything You Always Wanted To Know but Were Afraid To Ask, J. Phys. Chem. B, 2015, 119(3), 1129–1151 CrossRef CAS PubMed.
- S. Kumar, J. M. Rosenberg, D. Bouzida, R. H. Swendsen and P. A. Kollman, THE weighted histogram analysis method for free-energy calculations on biomolecules. I. The method, J. Comput. Chem., 1992, 13(8), 1011–1021 CrossRef CAS.
- A. Barducci, G. Bussi and M. Parrinello, Well-Tempered Metadynamics: A Smoothly Converging and Tunable Free-Energy Method, Phys. Rev. Lett., 2008, 100(2), 020603 CrossRef PubMed.
- T. Huber, A. E. Torda and W. F. van Gunsteren, Local elevation: A method for improving the searching properties of molecular dynamics simulation, J. Comput.-Aided Mol. Des., 1994, 8(6), 695–708 CrossRef CAS PubMed.
- K. L. Fleming, P. Tiwary and J. Pfaendtner, New Approach for Investigating Reaction Dynamics and Rates with Ab Initio Calculations, J. Phys. Chem. A, 2016, 120(2), 299–305 CrossRef CAS PubMed.
- Y. Xie and S. Calabrese Barton, Infrequent metadynamics study of rare-event electrostatic channeling, Phys. Chem. Chem. Phys., 2021, 23(23), 13381–13388 RSC.
- F. Noé, A. Tkatchenko, K.-R. Müller and C. Clementi, Machine Learning for Molecular Simulation, Annu. Rev. Phys. Chem., 2020, 71(1), 361–390 CrossRef PubMed.
- S. Lorenz, A. Groß and M. Scheffler, Representing high-dimensional potential-energy surfaces for reactions at surfaces by neural networks, Chem. Phys. Lett., 2004, 395(4), 210–215 CrossRef CAS.
- S. Lorenz, Reactions on Surfaces with Neural Networks, Doctoral Thesis, Technische Universität Berlin, Berlin, 2001 Search PubMed.
- S. Lorenz, M. Scheffler and A. Gross, Descriptions of surface chemical reactions using a neural network representation of the potential-energy surface, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73(11), 115431 CrossRef.
- S. Lorenz, M. Scheffler and A. Gross, Surface physics, nanoscale physics, low-dimensional systems-Descriptions of surface chemical reactions using a neural network representation of the potential-energy surface, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73(11), 115431 CrossRef.
- S. J. Ang, W. Wang, D. Schwalbe-Koda, S. Axelrod and R. Gómez-Bombarelli, Active learning accelerates ab initio molecular dynamics on reactive energy surfaces, Chem, 2021, 7(3), 738–751 CAS.
- R. Jinnouchi, F. Karsai and G. Kresse, Making free-energy calculations routine: Combining first principles with machine learning, Phys. Rev. B, 2020, 101(6), 060201 CrossRef CAS.
- V. Botu and R. Ramprasad, Adaptive machine learning framework to accelerate ab initio molecular dynamics, Int. J. Quantum Chem., 2015, 115(16), 1074–1083 CrossRef CAS.
- S. Chmiela, A. Tkatchenko, H. E. Sauceda, I. Poltavsky, K. T. Schütt and K.-R. Müller, Machine learning of accurate energy-conserving molecular force fields, Sci. Adv., 2017, 3(5), e1603015 CrossRef PubMed.
- T. Gao and J. R. Kitchin, Modeling Palladium Surfaces with Density Functional Theory, Neural Networks and Molecular Dynamics, Catal. Today, 2018, 312, 132–140 CrossRef CAS.
- K. Shakouri, J. Behler, J. Meyer and G.-J. Kroes, Accurate Neural Network Description of Surface Phonons in Reactive Gas–Surface Dynamics: N2 + Ru(0001), J. Phys. Chem. Lett., 2017, 8(10), 2131–2136 CrossRef CAS PubMed.
- W. Jia, H. Wang, M. Chen, D. Lu, L. Lin, R. Car, E. Weinan and L. Zhang, in Pushing the Limit of Molecular Dynamics with Ab Initio Accuracy to 100 Million Atoms with Machine Learning, SC20: International Conference for High Performance Computing, Networking, Storage and Analysis, 9–19 Nov. 2020, 2020, pp. 1–14 Search PubMed.
- N. Artrith and A. M. Kolpak, Grand canonical molecular dynamics simulations of Cu–Au nanoalloys in thermal equilibrium using reactive ANN potentials, Comput. Mater. Sci., 2015, 110, 20–28 CrossRef CAS.
- N. Artrith and A. M. Kolpak, Understanding the Composition and Activity of Electrocatalytic Nanoalloys in Aqueous Solvents: A Combination of DFT and Accurate Neural Network Potentials, Nano Lett., 2014, 14(5), 2670–2676 CrossRef CAS PubMed.
- F. Häse, I. F. Galván, A. Aspuru-Guzik, R. Lindh and M. Vacher, Machine learning for analysing ab initio molecular dynamics simulations, J. Phys.: Conf. Ser., 2020, 1412, 042003 CrossRef.
- F. Häse, F. I. Galván, A. Aspuru-Guzik, R. Lindh and M. Vacher, How machine learning can assist the interpretation of ab initio molecular dynamics simulations and conceptual understanding of chemistry, Chem. Sci., 2019, 10(8), 2298–2307 RSC.
- W. Vermeiren and J. P. Gilson, Impact of Zeolites on the Petroleum and Petrochemical Industry, Top. Catal., 2009, 52(9), 1131–1161 CrossRef CAS.
- Y. Li, L. Li and J. Yu, Applications of Zeolites in Sustainable Chemistry, Chem, 2017, 3(6), 928–949 CAS.
- C. G. S. Lima, N. M. Moreira, M. W. Paixão and A. G. Corrêa, Heterogenous green catalysis: Application of zeolites on multicomponent reactions, Curr. Opin. Green Sustain. Chem., 2019, 15, 7–12 CrossRef.
- T. Ennaert, J. Van Aelst, J. Dijkmans, R. De Clercq, W. Schutyser, M. Dusselier, D. Verboekend and B. F. Sels, Potential and challenges of zeolite chemistry in the catalytic conversion of biomass, Chem. Soc. Rev., 2016, 45(3), 584–611 RSC.
- D. P. Serrano, J. A. Melero, G. Morales, J. Iglesias and P. Pizarro, Progress in the design of zeolite catalysts for biomass conversion into biofuels and bio-based chemicals, Catal. Rev.: Sci. Eng., 2018, 60(1), 1–70 CrossRef CAS.
- C. Perego, A. Bosetti, M. Ricci and R. Millini, Zeolite Materials for Biomass Conversion to Biofuel, Energy Fuels, 2017, 31(8), 7721–7733 CrossRef CAS.
- S. Bailleul, K. Dedecker, P. Cnudde, L. Vanduyfhuys, M. Waroquier and V. Van Speybroeck, Ab initio enhanced sampling kinetic study on MTO ethene methylation reaction, J. Catal., 2020, 388, 38–51 CrossRef CAS.
- S. L. C. Moors, K. De Wispelaere, J. Van der Mynsbrugge, M. Waroquier and V. Van Speybroeck, Molecular Dynamics Kinetic Study on the Zeolite-Catalyzed Benzene Methylation in ZSM-5, ACS Catal., 2013, 3(11), 2556–2567 CrossRef CAS.
- J. Van der Mynsbrugge, M. Visur, U. Olsbye, P. Beato, M. Bjørgen, V. Van Speybroeck and S. Svelle, Methylation of benzene by methanol: Single-site kinetics over H-ZSM-5 and H-beta zeolite catalysts, J. Catal., 2012, 292, 201–212 CrossRef CAS.
- K. De Wispelaere, B. Ensing, A. Ghysels, E. J. Meijer and V. Van Speybroeck, Complex Reaction Environments and Competing Reaction Mechanisms in Zeolite Catalysis: Insights from Advanced Molecular Dynamics, Chem. – Eur. J., 2015, 21(26), 9385–9396 CrossRef CAS PubMed.
- K. De Wispelaere, S. Bailleul and V. Van Speybroeck, Towards molecular control of elementary reactions in zeolite catalysis by advanced molecular simulations mimicking operating conditions, Catal. Sci. Technol., 2016, 6(8), 2686–2705 RSC.
- O. Valsson and M. Parrinello, Variational Approach to Enhanced Sampling and Free Energy Calculations, Phys. Rev. Lett., 2014, 113(9), 090601 CrossRef CAS PubMed.
- J. Rey, P. Raybaud, C. Chizallet and T. Bučko, Competition of Secondary versus Tertiary Carbenium Routes for the Type B Isomerization of Alkenes over Acid Zeolites Quantified by Ab Initio Molecular Dynamics Simulations, ACS Catal., 2019, 9(11), 9813–9828 CrossRef CAS.
- J. Rey, A. Gomez, P. Raybaud, C. Chizallet and T. Bučko, On the origin of the difference between type A and type B skeletal isomerization of alkenes catalyzed by zeolites: The crucial input of ab initio molecular dynamics, J. Catal., 2019, 373, 361–373 CrossRef CAS.
- J. Rey, C. Bignaud, P. Raybaud, T. Bučko and C. Chizallet, Dynamic Features of Transition States for β-Scission Reactions of Alkenes over Acid Zeolites Revealed by AIMD Simulations, Angew. Chem., Int. Ed., 2020, 59(43), 18938–18942 CrossRef CAS PubMed.
- P. Cnudde, K. De Wispelaere, J. Van der Mynsbrugge, M. Waroquier and V. Van Speybroeck, Effect of temperature and branching on the nature and stability of alkene cracking intermediates in H-ZSM-5, J. Catal., 2017, 345, 53–69 CrossRef CAS.
- F. H. Isikgor and C. R. Becer, Lignocellulosic biomass: a sustainable platform for the production of bio-based chemicals and polymers, Polym. Chem., 2015, 6(25), 4497–4559 RSC.
- S. Fatma, A. Hameed, M. Noman, T. Ahmed, M. Shahid, M. Tariq, I. Sohail and R. Tabassum, Lignocellulosic Biomass: A Sustainable Bioenergy Source for the Future, Protein Pept. Lett., 2018, 25(2), 148–163 CrossRef CAS PubMed.
- Y. Liu, A. Vjunov, H. Shi, S. Eckstein, D. M. Camaioni, D. Mei, E. Baráth and J. A. Lercher, Enhancing the catalytic activity of hydronium ions through constrained environments, Nat. Commun., 2017, 8(1), 14113 CrossRef CAS PubMed.
- P. H. Hintermeier, S. Eckstein, D. Mei, M. V. Olarte, D. M. Camaioni, E. Baráth and J. A. Lercher, Hydronium-Ion-Catalyzed Elimination Pathways of Substituted Cyclohexanols in Zeolite H-ZSM5, ACS Catal., 2017, 7(11), 7822–7829 CrossRef CAS.
- Y. Liu, E. Baráth, H. Shi, J. Hu, D. M. Camaioni and J. A. Lercher, Solvent-determined mechanistic pathways in zeolite-H-BEA-catalysed phenol alkylation, Nat. Catal., 2018, 1(2), 141–147 CrossRef CAS.
- C. Zhao, D. M. Camaioni and J. A. Lercher, Selective catalytic hydroalkylation and deoxygenation of substituted phenols to bicycloalkanes, J. Catal., 2012, 288, 92–103 CrossRef CAS.
- C. Zhao and J. A. Lercher, Selective Hydrodeoxygenation of Lignin-Derived Phenolic Monomers and Dimers to Cycloalkanes on Pd/C and HZSM-5 Catalysts, ChemCatChem, 2012, 4(1), 64–68 CrossRef CAS.
- N. Pfriem, P. H. Hintermeier, S. Eckstein, S. Kim, Q. Liu, H. Shi, L. Milakovic, Y. Liu, G. L. Haller, E. Baráth, Y. Liu and J. A. Lercher, Role of the ionic environment in enhancing the activity of reacting molecules in zeolite pores, Science, 2021, 372(6545), 952 CrossRef CAS PubMed.
- M. Wang, N. R. Jaegers, M.-S. Lee, C. Wan, J. Z. Hu, H. Shi, D. Mei, S. D. Burton, D. M. Camaioni, O. Y. Gutiérrez, V.-A. Glezakou, R. Rousseau, Y. Wang and J. A. Lercher, Genesis and Stability of Hydronium Ions in Zeolite Channels, J. Am. Chem. Soc., 2019, 141(8), 3444–3455 CrossRef CAS.
- Y. Zhi, H. Shi, L. Mu, Y. Liu, D. Mei, D. M. Camaioni and J. A. Lercher, Dehydration Pathways of 1-Propanol on HZSM-5 in the Presence and Absence of Water, J. Am. Chem. Soc., 2015, 137(50), 15781–15794 CrossRef CAS PubMed.
- E. Grifoni, G. Piccini, J. A. Lercher, V.-A. Glezakou, R. Rousseau and M. Parrinello, Confinement effects and acid strength in zeolites, Nat. Commun., 2021, 12(1), 2630 CrossRef CAS PubMed.
- J. S. Bates, B. C. Bukowski, J. Greeley and R. Gounder, Structure and solvation of confined water and water–ethanol clusters within microporous Brønsted acids and their effects on ethanol dehydration catalysis, Chem. Sci., 2020, 11(27), 7102–7122 RSC.
- E. Fois, A. Gamba and E. Spanó, Competition between Water and Hydrogen Peroxide at Ti Center in Titanium Zeolites. An ab Initio Study, J. Phys. Chem. B, 2004, 108(28), 9557–9560 CrossRef CAS.
- J. H. Hack, J. P. Dombrowski, X. Ma, Y. Chen, N. H. C. Lewis, W. B. Carpenter, C. Li, G. A. Voth, H. H. Kung and A. Tokmakoff, Structural Characterization of Protonated Water Clusters Confined in HZSM-5 Zeolites, J. Am. Chem. Soc., 2021, 10203–10213 CrossRef CAS PubMed.
- C. Caratelli, J. Hajek, E. J. Meijer, M. Waroquier and V. Van Speybroeck, Dynamic Interplay between Defective UiO-66 and Protic Solvents in Activated Processes, Chem. – Eur. J., 2019, 25(67), 15315–15325 CrossRef CAS PubMed.
- V. Pascanu, G. González Miera, A. K. Inge and B. Martín-Matute, Metal–Organic Frameworks as Catalysts for Organic Synthesis: A Critical Perspective, J. Am. Chem. Soc., 2019, 141(18), 7223–7234 CrossRef CAS PubMed.
- M. S. Alhumaimess, Metal–organic frameworks and their catalytic applications, J. Saudi Chem. Soc., 2020, 24(6), 461–473 CrossRef CAS.
- Q. Wang and D. Astruc, State of the Art and Prospects in Metal–Organic Framework (MOF)-Based and MOF-Derived Nanocatalysis, Chem. Rev., 2019, 120(2), 1438–1511 CrossRef PubMed.
- Y.-B. Huang, J. Liang, X.-S. Wang and R. Cao, Multifunctional metal–organic framework catalysts: synergistic catalysis and tandem reactions, Chem. Soc. Rev., 2017, 46(1), 126–157 RSC.
- M. Ali, E. Pervaiz, T. Noor, O. Rabi, R. Zahra and M. Yang, Recent advancements in MOF-based catalysts for applications in electrochemical and photoelectrochemical water splitting: A review, Int. J. Energy Res., 2021, 45(2), 1190–1226 CrossRef CAS.
- M. Heshmat, Alternative Pathway of CO2 Hydrogenation by Lewis-Pair-Functionalized UiO-66 MOF Revealed by Metadynamics Simulations, J. Phys. Chem. C, 2020, 124(20), 10951–10960 CrossRef CAS PubMed.
- V. Haigis, F.-X. Coudert, R. Vuilleumier, A. Boutin and A. H. Fuchs, Hydrothermal Breakdown of Flexible Metal–Organic Frameworks: A Study by First-Principles Molecular Dynamics, J. Phys. Chem. Lett., 2015, 6(21), 4365–4370 CrossRef CAS PubMed.
- D. C. Cantu, B. P. McGrail and V.-A. Glezakou, Formation Mechanism of the Secondary Building Unit in a Chromium Terephthalate Metal–Organic Framework, Chem. Mater., 2014, 26(22), 6401–6409 CrossRef CAS.
- L. Kollias, D. C. Cantu, M. A. Tubbs, R. Rousseau, V.-A. Glezakou and M. Salvalaglio, Molecular Level Understanding of the Free Energy Landscape in Early Stages of Metal–Organic Framework Nucleation, J. Am. Chem. Soc., 2019, 141(14), 6073–6081 CrossRef CAS PubMed.
- J. Hajek, C. Caratelli, R. Demuynck, K. De Wispelaere, L. Vanduyfhuys, M. Waroquier and V. Van Speybroeck, On the intrinsic dynamic nature of the rigid UiO-66 metal–organic framework, Chem. Sci., 2018, 9(10), 2723–2732 RSC.
- Y. Ming, N. Kumar and D. J. Siegel, Water Adsorption and Insertion in MOF-5, ACS Omega, 2017, 2(8), 4921–4928 CrossRef CAS PubMed.
- R. Demuynck, S. M. J. Rogge, L. Vanduyfhuys, J. Wieme, M. Waroquier and V. Van Speybroeck, Efficient Construction of Free Energy Profiles of Breathing Metal–Organic Frameworks Using Advanced Molecular Dynamics Simulations, J. Chem. Theory Comput., 2017, 13(12), 5861–5873 CrossRef CAS PubMed.
- R. Demuynck, J. Wieme, S. M. J. Rogge, K. D. Dedecker, L. Vanduyfhuys, M. Waroquier and V. Van Speybroeck, Protocol for Identifying Accurate Collective Variables in Enhanced Molecular Dynamics Simulations for the Description of Structural Transformations in Flexible Metal–Organic Frameworks, J. Chem. Theory Comput., 2018, 14(11), 5511–5526 CrossRef CAS PubMed.
- M. Vandichel, J. Hajek, A. Ghysels, A. De Vos, M. Waroquier and V. Van Speybroeck, Water coordination and dehydration processes in defective UiO-66 type metal organic frameworks, CrystEngComm, 2016, 18(37), 7056–7069 RSC.
- G. Zhang, G. Wei, Z. Liu, S. R. J. Oliver and H. Fei, A Robust Sulfonate-Based Metal–Organic Framework with Permanent Porosity for Efficient CO2 Capture and Conversion, Chem. Mater., 2016, 28(17), 6276–6281 CrossRef CAS.
- L. Bellarosa, S. Calero and N. López, Early stages in the degradation of metal–organic frameworks in liquid water from first-principles molecular dynamics, Phys. Chem. Chem. Phys., 2012, 14(20), 7240–7245 RSC.
- L. Chen, J. P. S. Mowat, D. Fairen-Jimenez, C. A. Morrison, S. P. Thompson, P. A. Wright and T. Düren, Elucidating the Breathing of the Metal–Organic Framework MIL-53(Sc) with ab Initio Molecular Dynamics Simulations and in Situ X-ray Powder Diffraction Experiments, J. Am. Chem. Soc., 2013, 135(42), 15763–15773 CrossRef CAS PubMed.
- W. Xue, Z. Zhang, H. Huang, C. Zhong and D. Mei, Theoretical Insights into the Initial Hydrolytic Breakdown of HKUST-1, J. Phys. Chem. C, 2019, 124(3), 1991–2001 CrossRef.
- M.-P. Gaigeot, M. Sprik and M. Sulpizi, Oxide/water interfaces: how the surface chemistry modifies interfacial water properties, J. Phys.: Condens. Matter, 2012, 24(12), 124106 CrossRef.
- J. Cheng and M. Sprik, The electric double layer at a rutile TiO2water interface modelled using density functional theory based molecular dynamics simulation, J. Phys.: Condens. Matter, 2014, 26(24), 244108 CrossRef CAS PubMed.
- S. F. Yuk, M.-S. Lee, S. A. Akhade, M.-T. Nguyen, V.-A. Glezakou and R. Rousseau, First-principle investigation on catalytic hydrogenation of benzaldehyde over Pt-group metals, Catal. Today, 2020 Search PubMed , in press.
- A. Fujishima and K. Honda, Electrochemical Photolysis of Water at a Semiconductor Electrode, Nature, 1972, 238(5358), 37–38 CrossRef CAS PubMed.
- J. L. White, M. F. Baruch, J. E. Pander, Y. Hu, I. C. Fortmeyer, J. E. Park, T. Zhang, K. Liao, J. Gu, Y. Yan, T. W. Shaw, E. Abelev and A. B. Bocarsly, Light-Driven Heterogeneous Reduction of Carbon Dioxide: Photocatalysts and Photoelectrodes, Chem. Rev., 2015, 115(23), 12888–12935 CrossRef CAS PubMed.
- M. F. Calegari Andrade, H.-Y. Ko, L. Zhang, R. Car and A. Selloni, Free energy of proton transfer at the water–TiO2 interface from ab initio deep potential molecular dynamics, Chem. Sci., 2020, 11(9), 2335–2341 RSC.
- H.-L. Wang, Z.-P. Hu and H. Li, Dissociation of liquid water on defective rutile TiO2 (110) surfaces using ab initio molecular dynamics simulations, Front. Phys., 2018, 13(3), 138107 CrossRef.
- J. Kiss, J. Frenzel, N. N. Nair, B. Meyer and D. Marx, Methanol synthesis on ZnO(000
![[1 with combining overline]](https://www.rsc.org/images/entities/char_0031_0305.gif) ). III. Free energy landscapes, reaction pathways, and mechanistic insights, J. Chem. Phys., 2011, 134(6), 064710 CrossRef PubMed.
). III. Free energy landscapes, reaction pathways, and mechanistic insights, J. Chem. Phys., 2011, 134(6), 064710 CrossRef PubMed. - R. Réocreux, É. Girel, P. Clabaut, A. Tuel, M. Besson, A. Chaumonnot, A. Cabiac, P. Sautet and C. Michel, Reactivity of shape-controlled crystals and metadynamics simulations locate the weak spots of alumina in water, Nat. Commun., 2019, 10(1), 3139 CrossRef PubMed.
- F. R. Negreiros, M. F. Camellone and S. Fabris, Effects of Thermal Fluctuations on the Hydroxylation and Reduction of Ceria Surfaces by Molecular H2, J. Phys. Chem. C, 2015, 119(37), 21567–21573 CrossRef CAS.
- M.-S. Lee, B. Peter McGrail, R. Rousseau and V.-A. Glezakou, Structure, dynamics and stability of water/scCO2/mineral interfaces from ab initio molecular dynamics simulations, Sci. Rep., 2015, 5(1), 14857 CrossRef CAS PubMed.
- G. Yang, S. A. Akhade, X. Chen, Y. Liu, M.-S. Lee, V.-A. Glezakou, R. Rousseau and J. A. Lercher, The Nature of Hydrogen Adsorption on Platinum in the Aqueous Phase, Angew. Chem., Int. Ed., 2019, 58(11), 3527–3532 CrossRef CAS PubMed.
- G. Sun and H. Jiang, Ab initio molecular dynamics with enhanced sampling for surface reaction kinetics at finite temperatures: CH2⇌ CH + H on Ni(111) as a case study, J. Phys. Chem. C, 2015, 143(23), 234706 CrossRef PubMed.
- Y. Q. Gao, An integrate-over-temperature approach for enhanced sampling, J. Phys. Chem. C, 2008, 128(6), 064105 CrossRef PubMed.
- E. M. Y. Lee, T. Ludwig, B. Yu, A. R. Singh, F. Gygi, J. K. Nørskov and J. J. de Pablo, Neural Network Sampling of the Free Energy Landscape for Nitrogen Dissociation on Ruthenium, J. Phys. Chem. Lett., 2021, 12(11), 2954–2962 CrossRef CAS PubMed.
- E. Sevgen, A. Z. Guo, H. Sidky, J. K. Whitmer and J. J. de Pablo, Combined Force-Frequency Sampling for Simulation of Systems Having Rugged Free Energy Landscapes, J. Chem. Theory Comput., 2020, 16(3), 1448–1455 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2022 |