Challenges of modeling nanostructured materials for photocatalytic water splitting

Abstract

Understanding the water splitting mechanism in photocatalysis is a rewarding goal as it will allow producing clean fuel for a sustainable life in the future. However, identifying the photocatalytic mechanisms by modeling photoactive nanoparticles requires sophisticated computational techniques based on multiscale modeling. In this review, we will survey the strengths and drawbacks of currently available theoretical methods at different length and accuracy scales. Understanding the surface-active site through Density Functional Theory (DFT) using new, more accurate exchange–correlation functionals plays a key role for surface engineering. Larger scale dynamics of the catalyst/electrolyte interface can be treated with Molecular Dynamics albeit there is a need for more generalizations of force fields. Monte Carlo and Continuum Modeling techniques are so far not the prominent path for modeling water splitting but interest is growing due to the lower computational cost and the feasibility to compare the modeling outcome directly to experimental data. The future challenges in modeling complex nano-photocatalysts involve combining different methods in a hierarchical way so that resources are spent wisely at each length scale, as well as accounting for excited states chemistry that is important for photocatalysis, a path that will bring devices closer to the theoretical limit of photocatalytic efficiency.

---

Bipasa Samanta

Top row, from left to right: Bipasa Samanta, Post-Doctoral Fellow at Technion, Israel Institute of Technology. Ángel Morales-García, Junior Group Leader Jóven Investigador (JIN) Researcher at the University of Barcelona (UB) & Institute of Theoretical and Computational Chemistry of the UB. Francesc Illas, Professor at the University of Barcelona, member of European Academy of Sciences and Academia Europeae. Nicolae Goga, Professor at University Politehnica of Bucharest and Associate Senior Researcher at the University of Groningen, the Netherlands. Juan A. Anta, Professor of Physical Chemistry in Universidad Pablo de Olavide de Sevilla. Sofia Calero, full Professor and Chair of the Materials Simulation and Modeling Group, Department of Applied Physics, Eindhoven University of Technology (TU/e), The Netherlands. Bottom row, from left to right: Anja Bieberle-Hütter, Head of the Solar Fuels department and leading the group “Electrochemical Materials and Interfaces” at the Dutch Institute for Fundamental Energy Research (DIFFER) in Eindhoven, the Netherlands. Florian Libisch, Associate Professor for Theoretical Solid State Physics at the TU Wien, Vienna, Austria. Ana Belen Muñoz García, Associate Professor of Physical Chemistry at the University of Naples Federico II. Michele Pavone, Associate Professor of Physical Chemistry at University of Naples Federico II and Vice-Chair of the EU-COST Action CA18234. Maytal Caspary Toroker, Associate Professor of the Department of Materials Science and Engineering at the Technion – Israel Institute of Technology and Chair of the EU-COST Action CA18234.

1. Introduction: solar energy conversion requires functional photocatalytic materials

Improving the quality of human life while living within the carrying capacity of supporting ecosystems is one of the key challenges to modern society. The route to becoming truly sustainable affects many aspects of everyday and commercial life, from household energy consumption to transport and food production. The International Energy Agency (IEA)¹ shows that 80% of the worldwide energy demand is supplied by the combustion of natural resources² such as coal and petroleum. This has significant detrimental effects on local urban environments (e.g., air quality) but, more importantly, is leading to global warming and abnormal climatic changes.³ As a result, a central mission of several administrations, including the European Commission, is to accelerate global clean energy innovation towards a sustainable balance.

Hydrogen (H₂) is an alternative fuel that can be produced by a variety of methods.⁴ It emerges as one of the most suitable green fuels for tackling the triple issues of exhaustion, pollution, and climatic change. In this context, one of the most attractive technologies for H₂ production is photocatalytic water splitting, since it only requires solar energy, the most abundant and inexhaustible energy source. This is an interesting strategy, as well as a tremendous challenge, for the conversion of solar energy into chemical energy.⁵ Solar-based H₂ generation by photocatalysis has almost no effect on global warming, produces no air pollutants and can be stored easily.⁶ Therefore, the global energy demand should move progressively towards H₂-based technologies since they can produce a high energy content from natural resources such as sunlight and water, thereby promoting clean, friendly, long-lasting energy sources and renewable resources.⁷ Hydrogen can then be stored for use in hydrogen fuel cells to generate electricity for further transformation to higher hydrocarbons that can be stored well or for heating houses and buildings.

The idea to achieve photo-assisted electrolytic water splitting comes from the pioneering work of Fujishima and Honda⁸ in 1972, who used UV light to irradiate a titanium dioxide (TiO₂) anode coupled to a platinum cathode. This study was responsible for initiating modern heterogeneous photocatalysis with TiO₂ as the workhorse along with several other suitable materials and triggered extensive efforts to design efficient heterogeneous water splitting photocatalysts. Although this breakthrough opened a new avenue for solar fuel production,^9–11 splitting water to molecular hydrogen and oxygen has remained elusive thus far. One of the main drawbacks of the approach of Fujishima and Honda⁸ comes from the intrinsic properties derived from the electronic structure of TiO₂, which has an optical band gap larger than 3 eV, and a concomitant requirement to use UV radiation, which constitutes only 5% of the total sunlight reaching the Earth's surface.¹² Other materials, such as Fe₂O₃, WO₃, or BiVO₄, are promising but also face intrinsic challenges.¹³ Neither high throughput experiments^14–16 nor combinatorial studies^17–20 have up to now succeeded in identifying new promising catalytic materials for industrial applications. Hence, alternative strategies are urgently needed to realize an efficient interaction between light, a catalyst and reactants; in summary, key challenges have yet to be solved to fully exploit the enormous potential of solar-produced hydrogen as efficient, clean chemical energy storage.²¹

2. Photocatalytic water splitting: a complicated sequence of events

A key stumbling block for practical applications of the experiments by Fujishima and Honda was the requirement for UV radiation. A much more promising approach is to use sunlight as a renewable energy source; however, finding alternative semiconductor photocatalysts with appropriate band gaps within the spectral range of sunlight energy is a challenging task. Other requirements of a good water splitting material are its abundance, chemical stability, nontoxicity, low cost and, obviously, excellent photocatalytic activity. This strategy synergizes perfectly with the green chemistry concept and with the imperative challenges regarding clean energy and a decarbonized society proposed for the near future. The number of published papers dealing with photocatalytic water splitting has soared, with more than 14 000 references appearing in the Web of Science in just the last 5 years. The majority of investigations have focused on TiO₂-, Fe₂O₃-, ZnO-, and WO₃-derived photocatalysts. While many alternative materials have also been investigated,¹³ no single material that can fulfill all requirements has been identified thus far. These numbers highlight the many efforts to develop optimal photocatalysts for overall water splitting with visible light. However, it is difficult to understand what factor(s) dominate the net photocatalytic activity because photocatalytic reactions proceed through a complicated sequence of competing multistep processes, as sketched in Fig. 1.²²

Fig. 1 Scheme of a general photocatalytic water splitting process including the relevant steps involved during sunlight activation of the photocatalyst. Black arrows show favorable steps, while red arrows show unfavorable steps.

The principle of photocatalysis in semiconductors relies on the generation of excitons: electron–hole pairs bound by Coulomb forces. They are created by the absorption of a photon with an energy of at least the semiconductor band gap minus the exciton binding energy E_exc determined by the intrinsic electronic structure of the photoactive material (step 1 in Fig. 1) and E_exc can be significant for 2D materials.²³ In a simple single-body picture, the photo-excited electron is promoted from the valence band (VB) or the highest occupied molecular orbital (HOMO) to the conduction band (CB) or the lowest unoccupied molecular orbital (LUMO) of the photoactive crystalline solid or the nanostructure, respectively (step 2 in Fig. 2). For photo-excitation energies larger than the band gap, electronic relaxation to the bottom of the CB occurs quickly by electron–electron or electron–phonon coupling on short timescales (fs). Spontaneous optical (radiative) relaxation of the photo-excited charge carriers into the ground state occurs by spontaneous emission, with typical decay rates in the nano- to picosecond time scale and, hence, this process competes with the creation of new excitons. Moreover, even maintaining continuous irradiation of the sample, the majority of the created electron–hole pairs simply recombine or deexcite non-radiatively, for example at defects, also preventing the desired catalytic process. Fortunately, enough excitons decay into free charge carriers which requires just overcoming the exciton binding energy. This key charge-separation process (step 3 in Fig. 1) yields photogenerated electrons and holes moving independently, their motion governed by their effective masses, temperature, and concentration. Provided a long-enough mean-free path, these charge carriers eventually trigger the photocatalytic redox reaction at the photocatalysts surface (step 4 in Fig. 1). The diffusion of the charge carriers towards the surface takes place at a picosecond (ps) time scale and requires concentration gradients to move them adequately. The photocatalytic process finishes with the consumption of the surviving charge carriers by a redox reaction (steps 5 and 6 in Fig. 1) that takes place on a longer time scale. Unfortunately, these large asymmetries in the time scale between spontaneous emission, exciton creation, charge carrier diffusion and redox reaction may cause charge carrier accumulations resulting in enhanced recombination losses (steps 7 and 8 in Fig. 1).

Fig. 2 Key properties analyzed by the DFT method that are relevant to the photocatalytic water splitting process.

In addition, several parameters also affect the photocatalytic activity of the abovementioned inorganic photocatalysts, including their surface chemistry, surface and junction defects, crystallinity, doping and deep traps, band edge positions, particle size, and morphology.²⁴ The above observations demonstrate the importance of understanding the kinetics and dynamics of a photocatalytic reaction to establish rational strategies for the immediate development of a new generation of photocatalysts for future practical applications.²⁵

Experimentally, it is difficult to determine the influence of the different factors mentioned above on photocatalytic activity. Here, computational modeling provides an unbiased approach to analyze in detail the influence on photocatalytic water splitting and design new catalytic nanomaterials. To complement experiments and design new ones, theoretical models can be used to investigate the relation among structure, morphology, surface chemistry, and catalysis, as well as the role of composition. A large amount of useful information has been gathered from electronic structure calculations of extended models of TiO₂,^26–29 ZnO,^30–32 and WO₃.^33–35 However, these models neglect the effects arising from the finite size and shape of TiO₂, ZnO, and WO₃ nanoparticles.^36–38 Taking these effects into account requires explicit modeling of realistic nanoparticles by using top-down and bottom-up protocols.^39–42

3. Modeling of photocatalysis: advances versus challenges

Modeling the complicated sequence of events occurring during photocatalysis by nanoparticles requires insight into the processes occurring at atomistic scales. The available computational methods either face incomplete information about microscopic details of the system or are computationally too demanding for the size of the system considered. For example, semiclassical methods such as molecular dynamics or Monte Carlo, while computationally less expensive, are based on parametrized force fields and lack a complete atomistic picture. Conversely, sophisticated methods such as couple cluster, configuration interaction, or many-body perturbation theory can provide very accurate description of a single electronic problem, yet quickly become overwhelmed by the size of the system involved. Accurately describing the several length scales involved in photocatalytic processes therefore requires sophisticated computational techniques connected by multiscale modeling.

In the following sections, we provide a brief overview of currently available methods used for modeling photocatalytic water splitting catalysts, each focused on a particular approach and length scale. For solving the electronic problem, we focus on DFT-based methods as the current workhorse of ab initio material modeling in Section 3.1, the most widely used approaches for the atomistic modeling of photocatalytic water splitting. A less accurate method capable of treating a much larger number of atoms is molecular dynamics (MD), as presented in Section 3.2. Monte Carlo (MC) simulations achieve even larger scale sampling (Section 3.3). However, to approach the length scales of an experimental catalytic system, one must rely on the use of continuum modeling methods (Section 3.4). Finally, we discuss how to link these different length and accuracy scales, which involves using multiscale approaches (Section 3.5).

3.1 Atomistic modeling

Atomistic modeling involves the study of materials at the atomic scale using the concepts of quantum mechanics and relying on appropriate algorithms and codes running on powerful supercomputers. Density functional theory (DFT) provides an excellent compromise between cost and accuracy that can reasonably handle the various steps of the photocatalytic process for systems up to a few hundred atoms. This methodology is useful for understanding the material chemistry and for predicting the properties of new materials. Atomic-scale quantum mechanical modeling is particularly important for modeling water splitting since the chemical reaction intermediates need to be adsorbed and released from the crystal surface at an atomically arranged active site. Intimate knowledge of this reactivity process is crucial for both fundamental understanding as well as quantitative modeling. Beyond DFT, there is a broad array of other ab initio methods that improve on either the accuracy issues of DFT (post DFT methods such as using time-dependent DFT for excited states, coupled-cluster approaches or Green's function methods,⁴³ quantum-chemical approaches for excited states⁴⁴ or Monte-Carlo approaches⁴⁵) as well as frameworks to reduce computational cost by machine learning⁴⁶ or smart parametrization such as density-functional theory tight binding,⁴⁷ to name a few. These approaches all address the atomistic electronic problem, and are therefore distinct from approaches suitable for larger scales discussed in the following Sections. To keep the discussion of atomistic approaches focused, we mostly restrict our considerations here to DFT-based methods.

3.1.1 Methods. Computational methods based on Density Ffunctional Theory (DFT) are almost universally used to approach the properties of materials in different forms, from nanoparticles to bulk and surfaces.⁴⁸ Several computational codes are currently routinely used to predict many physical–chemical properties. Commonly used DFT codes include VASP,^49–51 Gaussian,⁵² wien2K,⁵³ DMol3,^54,55 GPAW,⁵⁶ ABINIT,⁵⁷ CASTEP,⁵⁸ CP2k,⁵⁹ ORCA,^60,61 or the Atomistix Toolkit.⁶² All of these software toolkits include a basic Kohn–Sham equations solver—many various further post-DFT methods. We refer the interested reader to the respective code documentations for details. Using a starting guess for the electron density one calculates the effective Kohn–Sham potential V_eff as where , and E_XC[ρ(r⃑)] is the (approximate) exchange–correlation functional and is the electron–ion interaction. Then the Kohn–Sham eigenvalue equation
is solved. One obtains a new density using the eigenfunctions as , with occupation numbers f_i. For this density, the total energy functional E[ρ] yields an estimate for the ground state energy. Reinserting the new density into the expression for V_eff defines a self-consistency cycle that can be iterated until convergence is reached, i.e., until changes in the density or energy become smaller than a desired threshold. Note that convergence is not guaranteed: modern codes use several tricks to accelerate or even achieve convergence. After converging the electronic system, forces on the atoms can be evaluated and the atoms can be moved accordingly to also converge atomic positions. DFT thus provides physical–chemical properties including factors particularly relevant for water splitting, including photon adsorption energies, transport of electrons and holes, determination of band energies, and surface properties (Fig. 2).

Furthermore, DFT can also predict with sufficient accuracy many kinetic and thermodynamic parameters e.g., transition states, reaction barrier heights, overpotentials, entropy and solvent effects for the oxygen evolution reaction (OER) and hydrogen evolution reaction (HER) mechanisms.^63–66

However, methods beyond standard DFT are often needed: accurately describing charge-transfer processes critical to many catalytic processes is challenging for standard exchange–correlation functionals.⁶⁷ Furthermore, the first step in the water splitting reaction is excitation by a photon which is beyond a ground state method like DFT. To treat excited states, methods such as many-body perturbation theory (MBPT) and time-dependent DFT (TD-DFT) are used.⁶⁸ When a material interacts with external electronic or magnetic fields, electrons become excited and the ground state method of DFT no longer applies. Time-dependent TD-DFT is the extension of traditional DFT to the time domain, which may include time dependent potentials such as external fields. Because of this time dependent potential there is an extra contribution of the exchange correlation kernel to the energy expression, which makes TD-DFT better adapted for excitation energy calculations than DFT.

MBPT includes electronic correlation as perturbation in the Hamiltonian and solves the resulting problem perturbatively. Since it is a wave function-based method, MBPT more properly describes the excitation energy, but it is computationally more costly, especially compared to TD-DFT. Other than TD-DFT and MBPT, various other methods like the Bethe–Salpeter equation (BSE) and GW were developed to study excitation energies. For example, surface reaction intermediates for water splitting with Fe₂O₃ were calculated by means of the GW⁶⁹ and BSE⁷⁰ methods, demonstrating the important role of the surface excited state on the O-terminated surface, which behaves as a reaction bottleneck. While TD-DFT and DFT are density-based and MBPT is a wavefunction based method, GW is the approximation to Hedin's equation,⁷¹G is the time ordered Green function and W is the dynamically screened interaction. Thus, in the GW approximation one can calculate the exact self-energy of a many body system by expanding in terms of G and W. It is computationally faster than MBPT and gives better results than TD-DFT. BSE is an improvement over GW where excitations are handled by a two particle propagator. Thus, with a compromise of accuracy and computational time, GW–BSE are better methods to be applied for excited state calculations. Another method to crudely approximate excited states is the ΔSCF method: the difference between DFT energies for neutral and charged systems provides an estimate for the first electron affinity or first ionization potential. Kazaryan et al.⁷² studied both the ground state and excited state of Ti(OH)₄ for the water splitting reaction. Employing various DFT methods, both the ground state (B3LYP⁷³/TZ2P, BP86^74,75/TZ2P, CAM-B3LYP⁷⁶) and excited states at the ΔSCF level show that hydrogen abstraction for water splitting was an excited state surface phenomenon with low to moderate activation barriers.

3.1.2 State-of-the-art. Improving the performance of a catalyst requires several steps, starting from the identification of its active sites and ending on increasing their effectiveness without compromising the remaining features. When considering a catalytic material, certain facets of the surface⁷⁷ may be more reactive than others. Surface reconstructions, terraces or defects require even larger cells, yet often constitute the most active catalytic sites⁷⁸ due to their chemical surroundings or unsaturation. Bader charge⁷⁹ or Fukui function⁸⁰ calculations help to identify potential active sites. For example, if the surface atom has both positive or negative charge, and the reactant is negative, the reaction is predicted to take place at the positively charged atom. Further parameters like adsorption energies also explain where the incoming reactant will get adsorbed and how strongly. If the reactant does not get adsorbed or adsorbs weakly, the chance that the reaction will proceed at that site is strongly reduced. In addition to the importance of purposely tuning the bulk electronic structure features (band gap and absolute band edge potentials), various strategies have been explored to enhance the physical and chemical features of catalysts, such as introducing active sites, doping,⁸¹ codoping,⁸² alloying⁸³ and defect engineering.^81,84 Since most of the catalysts considered are nanomaterials, these can be deposited on a supporting material and connected to an electrochemical device for studying the water splitting reaction. Thus many of the computational methods meant for studying photocatalytic properties may also be used for modeling photoelectrocatalysis as they are closely related. Since the nanocrystals can be incorporated into an electrochemical cell, this Section will also discuss additional properties relevant for electrochemistry, including contribution of bias.
3.1.2.1 Adsorption free energy as a basic parameter for electrocatalytic water splitting. Even if not directly related to photocatalytic water splitting, it is convenient to mention the electrochemical process as it offers some interesting insights, especially because of its relationship to photoelectrocatalysis. Two main easily computable descriptors have emerged to assess the potential of a material to work as a HER/OER electrocatalyst: (a) the Gibbs free energy of atomic hydrogen at the catalytic active center should be close to zero for efficient HER catalysis,⁸⁵ and (b) for efficient OER catalysis, the max ΔG of all the reaction steps involved should be close to 1.23 eV.⁸⁶

The Gibbs free energy of atomic hydrogen is approximately ∼3.43 eV, yet the Gibbs free energy of atomic hydrogen at the catalytically active center strongly depends on the catalytic surface considered. For example, Anantharaj et al.⁸⁷ reported in their paper (see Fig. 2D–F in ref. 87) volcanic plots for various transition metal phosphides using different activity parameters such as geometrical-area-normalized current, ECSA-normalized current, and average TOF per surface site. Their data shows how the Gibbs free energy for atomic hydrogen depends on different catalytic surface. High variations in the Gibbs free energy of atomic hydrogen were also shown by Seh et al.⁸⁶ They also showed a volcanic plot of the OER (Fig. 3 in ref. 86), and the dependence of the overpotential on the difference of the Gibbs free energy of O and OH intermediates. Recently Jang et al.⁸⁸ have also reported variations in ΔG of atomic hydrogen on Bi, Sb and BiSb alloy and showed that the value depends on the catalytic surface. Thus, although the value should be zero, the Gibbs free energy of atomic hydrogen at the catalytic active center is highly dependent on the surface being used.

Pt has been the focus of attention for the HER in water splitting reactions owing to the zero value of the Gibbs free adsorption energy of hydrogen. Thus, Fajin et al.⁸⁹ investigated platinum surfaces to study the effect of surface structure on catalysis. They reported that low coordinated Pt atoms strongly adsorb water molecules and that corners and edges were the active sites for water dissociation. A similar study on the adsorption of water to low coordinated Pt atoms was also reported for different Pt_n nanoparticles (NPs).⁹⁰ They concluded that dissociation was easier on small particles (13 atoms) than on large particles (up to 140 atoms), whose activity tended toward that of infinite surfaces. The particle size effects on water dissociation on various surfaces were theoretically investigated by Phatak et al.⁹¹

Furthermore, Kibsgaard et al.⁹² determined the efficiency of various transition metal phosphide catalysts by determining the free energy of hydrogen adsorption against the current, normalized by the geometrical and electrochemical surface area and turnover frequency. They observed that mixed metal phosphide (Fe_0.5Co_0.5P) showed the highest HER activity. Similarly, metallic transition metal dichalcogenides were theoretically proven to be potential HER catalysts for the water splitting reaction based on their lower values of the Gibbs free energy of adsorption.⁹³ Rossmeisl et al.⁹⁴ investigated the OER activity on rutile-type surfaces by calculating the oxygen binding energies as a function of −ΔG associated with the elementary steps of the OER reaction. The authors found that the reaction was limited by the oxide and peroxide formation step. Man et al.⁹⁵ performed similar investigations on binary metal oxides and perovskites for the OER. They provided a volcano plot on the basis of HO* and HOO* adsorption energies on the surfaces. The calculations suggested a fundamental limitation on the maximum oxygen evolution activity of planar oxide catalysts. Friebel et al.⁹⁶ further highlight the importance of the Gibb's free energy by comparing their calculated over potential with the shift of the α-Ni(OH)₂/γ-NiOOH redox potential to higher values with increasing Fe content.

3.1.2.2 Study of active sites. To effectively understand the importance of active sites involved in photocatalytic water splitting, Qiao et al.⁹⁷ performed a DFT study to identify them in a PdSeO₃ monolayer. They observed that the selenium atoms are good for water oxidation and the oxygen1 atoms are good for hydrogen reduction half reaction. The free energy of atomic hydrogen adsorption was reported to be 0.98 eV. Further DFT-based calculations by Zhang et al.⁹⁸ predict the possible active sites of GO–SiC–MoS₂ composite. Due to stronger interaction between SiC and MoS₂, the catalytic activity is concentrated at this interface rather than at the GO or MoS₂ interfaces. Luo et al.⁹⁹ identified that ruthenium atoms act as active sites for the reduction of protons, and when doped with nitrogen, the active site changes from Ru to nitrogen and the hydrogen evolution activity is comparable to that of Pd. There is also an increase in the photocatalytic activity of the TiO₂, due to the presence of impurity band in the bandgap which results in a red shift. Wu et al.¹⁰⁰ investigate the catalytic active site of Pt loaded graphitic carbon nitride (g-C₃N₄) They showed that Pt atoms are the active sites and the anchoring of Pt atoms increases by formation of cyano defects. They also observed that divalent atomic Pt provides more active sites than Pt metal nano particles. A very detailed analysis of active site for photocatalytic water splitting was done by Zhao et al.¹⁰¹ on titania where they showed that rutile 110 surface (Ti 5 coordinated) is more active than anatase 101 surface.
3.1.2.3 Band energy positions. Since the water splitting reaction includes a charge transfer, the study of the band energy positions is also important for determining the catalytic activity of the catalyst. Band energy position refers to the position of the Valence Band Maxima (VBM) and Conduction Band Minima (CBM). In order for the charge transfer (and thereby the desired catalytic process) to occur, the valence band should be at more positive potential than 1.23 V (vs. NHE) and conduction band should be at negative potential than 0 V (vs. NHE). Necessarily, the band gap required for water splitting should be less than 2.5 eV and the photon energy should be greater than 1.23 eV. Wei and Zunger¹⁰² showed through band structure calculations that p–d repulsion in group II–VI semiconductors modified the charge distribution of pristine crystals and their corresponding alloys, lowering the band gaps and increasing the valence band onset. On the other hand, Lee et al.¹⁰³ studied in detail the structure of Zn–Ge–oxynitride materials, focusing on the effects on the electronic bands after doping the catalyst with oxygen. The presence of oxygen orbitals in the valence band and nitrogen orbitals in the conduction band caused large band dispersion, which resulted in uplifting the valence band, narrowing the band gap, and, consequently, facilitating enhanced optical absorption across the band gap in the visible region.
3.1.2.4 Doping, codoping and alloying. Another principal strategy to improve the performance of a catalyst is doping. Appropriate doping promotes changes in the electronic structure of the material by strengthening or weakening the bonding of intermediates, modifying the bandgap, shifting the bands, and changing the electronic charge on each element. Conversely, doping also introduces local defects, that may adversely affect mean free paths. Both results affect the catalytic activity, making accurate microscopic modeling key for understanding and optimizing the effect of doping. For example, Deng et al.¹⁰⁴ doped MoS₂ with Co and reported that with a moderate Co content, the HER activity reached an optimal value due to a change in the electron count and in the Bader charge of the sulfur atoms, which in turn resulted in an optimal value of the free energy of hydrogen adsorption. Shimodaira et al.¹⁰⁵ substituted Mo⁶⁺ with Cr⁶⁺ in lead molybdate and observed that charge transfer occurred from the valence band of Pb to the acceptor band of Cr, thus inducing a decrease in the band gap. Wang et al.¹⁰⁶ showed that doping Ru in Ru–RuP_x–Co_xP increased the density of states (DOS) at the Fermi level and decreased the intermediate adsorption energy of the OER, thereby increasing the potential of the catalyst for OER activity. In addition, Wang et al.¹⁰⁷ doped WO₃ with Hf and observed that the conduction band shifted to higher energies, promoting the HER reaction. The concept of codoping was demonstrated by Zheng et al.¹⁰⁸ with graphene: they observed that some dopants (nitrogen and oxygen) acted as acceptors, while others (fluorine, sulfur, boron and phosphorus) acted as donors. They also showed that N and P codoped graphene featured the lowest HER potential compared to pristine or singly doped graphene. In the study by Liang et al.,¹⁰⁹ two dimensional monolayers (AlN and GaN) doped with transition metal ions were investigated in regard to their OER activity. A low overpotential with Ni doping was found and related to the stabilization of the OOH adsorbent which was correlated with a switch from a high-spin to a low-spin state of the dopant atom.

Along with doping, alloys between oxides have been investigated to improve the catalytic activity of photoactive water splitting catalysts. Through DFT calculations, Kanan and Carter⁸² showed that the band gap of MnO was reduced by alloying with ZnO. Similarly, Toroker and Carter¹¹⁰ showed through calculations that the large band gap of materials unsuitable for water splitting could be narrowed by doping with iron oxide. Furthermore, Zheng et al.¹¹¹ coupled graphitic carbon nitride with nitrogen-doped graphene, and the hybrid system showed high activity for the HER. The reasons for the increased activity were that G–C₃N₄ provided highly active hydrogen adsorption sites while n-doped graphene facilitated the electron transfer process for proton reduction.

3.1.2.5 Defect formation. Creating defects, such as vacancies, may also significantly enhance catalytic activity. Vacancies can help to localize charges to locally drive a desired catalytic process and also alter charge transport properties, which can enhance OER or HER activity. Conversely, badly-placed defects may trap the photo-excited charge carriers, preventing them from reaching the relevant catalytic sites. Ab initio modeling of the electronic structure of defects is thus key for improving device efficiency and for avoiding undesired effects. DFT calculations¹¹² show that the creation of oxygen vacancies in Co₃O₄ resulted in a higher degree of electron delocalization and that these delocalized electrons can be easily excited to facilitate water oxidation. In another example, Wu et al.¹¹³ studied the effect of oxygen vacancies in WO₂–carbon mesoporous nanowires for the HER. The vacancies shifted the Fermi level into the conduction band, creating a metal with high electron mobility, which is a requirement for the water splitting reaction. However, it is not only creating vacancies that is important for enhancing the electrical conductivity but also optimizing the defect amount. Indeed, Du et al.¹¹⁴ showed that in a perovskite catalyst, having one oxygen vacancy per unit cell yielded a much better conductor than having no vacancies or two oxygen vacancies.

Vacancies can directly change the reaction activation energies and intermediate adsorption energies. Thus, Peng et al.¹¹⁵ further demonstrated that the reduction in the activation energy barrier of the HER/OER reactions was due to the reduction of adsorption energies caused by oxygen vacancies that were created by reducing with NaBH₄. In a different kind of study of oxygen vacancies, Mefford et al.¹¹⁶ reported reaction pathway switching due to vacancy creation in a La_1−xSr_xCoO_3−d/SrCoO_2.7 perovskite electrocatalyst. Zhao et al.¹¹⁷ verified that dual Co doping and oxygen vacancies in MnO₂ nanosheets increased the conductivity, decreased the adsorption energies, and thus increased the catalytic activity for the OER.

3.1.2.6 Determining the mechanism and the rate-limiting step. DFT is a powerful tool for determining the rate-limiting (or potential-determining) step in the reaction mechanisms, which is critical for optimizing a water splitting electrocatalyst. Many studies use the approach first introduced by Rossmeisl et al.⁹⁴ to determine the potential determining step and the overpotential. The authors have provided a detailed descriptions of methods to be used to calculate the thermochemistry of the entire process including how to determine ΔG for each step, which intermediates to involve, which extra factors to include such as pH and potential, etc. and how to calculate them. Rossmeisl et al. also identifies the step with the largest ΔG as the rate determining step and outline the use of the rate-limiting potential and this ΔG_max for calculating the overpotential. Optimizing the intermediate energy or calculating the zero-point energy or TΔS provides access to the overall thermodynamics. Finally, Rossmeisl et al. showed that, based on linear binding energy relationship, the volcano plot as a function of binding energy of O can describe the oxygen evolution activity of a catalytic surface. Zhang et al.^118–122 performed several studies on Fe₂O₃ and WO₃ to investigate the impact of the structure (orientation, nanocluster) and chemistry (doping, vacancies, cocatalyst). Chen et al.¹²³ performed a first principles DFT study of the chemical dynamics of first proton-coupled energy transfer (PCET) on a TiO₂ surface. They observed that the PCET was sequential, e.g., first, the proton was transferred, and then the electron was transported in an inner sphere process. Additionally, Valdes et al.¹²⁴ showed through computational studies the universal applicability of the four-step coupled proton–electron transfer reaction mechanism for the OER on metal oxides and the photooxidation of water.
3.1.2.7 Charge transport. Successful charge transport to proper redox sites is important for efficient water splitting. Viswanathan et al.¹²⁵ performed DFT-based calculations of charge transport and reported that with an increasing thickness of TiO₂, the electrical conductivity decreased. To this end, Liao et al.¹²⁶ reported that along with optimizing the thickness, methods to improve charge transport with dopants are necessary. They addressed electron transport due to n-type doping in hematite and concluded that zirconium, silicon, and germanium were better for doping, as they did not act as electron trapping sites. Similarly, Toroker and Carter¹²⁷ studied hole transport in doped wurtzite and reported that vacancies created stronger traps for electrons than dopants. Aside from local doping, nanostructuring can alter charge transport. For example, Xie et al.¹²⁸ calculated the high charge density distribution on MoN nanosheets and identified them as potential candidates for catalysis because they can effectively facilitate electron transport through sheets compared to their bulk counterparts. In addition to charge transfer towards the surface, charge carriers need to overcome the interface at the back contact between the electrode and the metal behind it. To model charge transport across oxide/metal interfaces, a high-throughput screening method was developed based on wave packet dynamics.¹²⁹
3.1.2.8 Excited state properties. Since the non-equilibrium transfer of charges, i.e., holes and electrons, is a key step in photocatalysis, it is important to study excited state properties of the photocatalyst to estimate charge recombination possibilities and to improve the rational design of the catalyst. In this regard, Valero et al.¹³⁰ studied the character of excited states in TiO₂ nanoparticles using TDDFT calculations. They observed that for excited states, the charge separation depends on the nanocluster shape and size. They studied the character of the electronic excitations by using canonical Kohn–Sham molecular orbitals (MOs) and from natural transition orbitals (NTOs). A similar work was done by Martynow et al.¹³¹ where they have studied molecular photocatalysts of the type [(tbbpy)₂M1(tpphz)M2X₂]²⁺ (M1 = Ru, Os; M2 = Pd, Pt; X = Cl, I). They used TDDFT to calculate the oscillator strengths and orbital characters of the singlet and triplet excited states. They showed through their calculations that the first absorption bands consist mainly of a superposition of six to eight MLCT states matching the experimental values. Further a wide and strong optical adsorption spectrum is important for generating electron hole pair. In this regard, Liu et al.¹³² calculated the optical spectrum of a two-dimensional As/BlueP heterostructure, and reported a broadening of the optical absorption spectrum in the visible light region upon in-plane strain of 4.5%, improving photocatalytic efficiency. Ma et al.¹³³ studied the optical spectra of Ag₃PC^VI₄ (C = O, S, Se) and reported that absorption coefficients of sulfides and selenides are much larger than those of oxides. Also, sulfides and selenides have direct band gap character which is favourable for electronic transitions making them better photocatalysts.

3.1.3 Limitations and perspective. From the literature survey described above, we see that DFT studies on surface defects or vacancies elucidate how the created charges may successfully reach the adsorbed water molecule or may be trapped in these defects, although detailed studies focusing on the charge transfer dynamics are still missing. Furthermore, to optimize the catalytic activity of a catalyst, one needs to optimize its active sites. Establishing design rules through computational modeling provides possible routes towards optimizing the active sites, for example by selecting new material compositions, surface defect engineering or facet selection.⁷⁷ Thus, addressing surface properties via DFT plays an important role here. Suitable surface engineering to favor certain types of reconstruction⁴¹ can then increase the number of active sites.

However, when modeling catalytic reactions on nanostructure surfaces using DFT, there are many challenges and open issues. Although DFT is sufficiently accurate in many cases, there are problems where the approximations used in standard exchange–correlation functionals fail, particularly when considering band gaps of oxides and charge transfer processes.⁶⁷ The former can be handled by relying on hybrid functionals that include a fraction of exact, nonlocal Fock exchange but the latter require more accurate post-DFT approaches such as DFT+U, HSE, GW + BSE, TD-DFT, etc. or correlated wavefunction techniques, which are often too costly for realistic geometries.

As a second drawback, despite its decent accuracy DFT cannot guarantee that it describes the physics involved in the suggested mechanisms with sufficient accuracy or that the predicted nature of oxygen evolution is the actual one. Even if the predicted reaction path is handled perfectly accurately, there might be an additional configuration which should be lower in energy but is not, due to the shortcomings of DFT for, e.g., charge transfer processes. In addition, kinetic energy barrier calculations are typically performed at constant charge rather than constant potential. One scheme to circumvent this limitation involves extrapolation to the limit of an infinite unit cell, where a single charge transfer has negligible impact on the simulated potential; thus, the reaction barrier is obtained at constant potential. A second scheme was addressed by Chan and Nørskov,¹³⁴ who presented a method based on a constant potential correction obtained by charge extrapolation rather than previous cell extrapolation. Furthermore, DFT strongly depends on the choice of exchange–correlation potential; this is the level of theory (local, gradient corrected, kinetic energy, hybrid) used to define the exchange–correlation potential, which in turn affects the reduction potential. This is especially serious in cases where a solvent is involved. To circumvent this difficulty one has to include solvent effects by either implicit or explicit (e.g., quantum mechanics/molecular mechanics QM/MM)¹³⁵ methods that combine quantum mechanical techniques for a cluster of interest with a surrounding environment handled by classical molecular mechanics. Solvation models are used for this. In implicit solvation models, atomistic species are considered as a continuum. We therefore discuss such models later in this review under the Section “Continuum modeling”. Moreover, standard static quantum mechanical methods relying on the Born–Oppenheimer approximation, either within DFT or wavefunction approaches, cannot provide a realistic description of ionic dynamics. For some properties, dynamics involve only the ground state potential energy surface, and molecular dynamics provides a way to approach these phenomena, as outlined below.

3.2 Molecular dynamics simulations

Molecular dynamics (MD) is a branch of computerized chemistry and its primary purpose is analyzing the dynamics (time evolution) of molecular systems either in the electronic ground state or involving nonradiative transitions between several electronic states. The first is usually referred to as Born–Oppenheimer MD (BOMD) or simply MD. The second is termed nonadiabatic MD (NAMD) and is especially relevant in photocatalysis, although the methodology is still being developed with very few applications in this particular field.¹³⁶ BOMD depends on the classical physics equations of motion, where the nuclei move on a given potential energy surface. For every simulation step an update of the forces (resulted from potential interactions), velocities and positions of all particles happens. Depending on the level of approximation, the particles interact through different types of potentials – bonded and nonbonded. In water splitting, this is central for describing the intimate details of the catalytic reaction in a material environment. Particularly, water splitting was analyzed using molecular dynamics through the means of photosynthesis, semiconductors, and dye-sensitized photoelectrochemical cells (PECs)—see Section 3.2.2.

3.2.1 Methods. Molecular dynamics (MD) is defined as an approach that is used to analyze and simulate the time evolution of particles systems at the ground electronic state of a potential energy surface, which is obtained or approximated in some way. MD depends on the classical physics (Newtonian) equations of motion. At each step of the simulation, the velocities, forces (coming from interaction potentials) and positions of particles are updated. Using statistical ensembles, properties such as particle number, pressure and temperature are controlled. Some common use cases of MD are in chemistry, material sciences, biophysics, etc., for systems of 10⁵–10⁶ atoms per particles for time scales in the range of nanoseconds to microseconds. Given the current computational power available, on large supercomputers these numbers can be larger (e.g., molecular systems between 10⁹ or 10¹² atoms can been simulated). Through methods such as coarse-grained MD, time scales smaller than 1 microsecond can also be achieved.

There are many computational ingredients to consider before carrying out an MD simulation. In short, a global MD algorithm can be described as follows. As a first step, the initial conditions and some inputs must be set – as an example, the potential V that is calculated in function of atom positions r and velocities v, etc. – are mandatory. New potentials and corresponding forces are calculated in a number of MD steps. The potentials that are acting on the nuclei can be determined usually from empirical potentials. Then an updated configuration depending on classical physics equations of motion is done. New positions of particles, temperature of the system, velocities and other properties are computed in this updated algorithm.

Here are the above steps described in more detail. First, the forces acting on the atoms (most often parameters of an empirical force field) have to be read in. A force field in molecular modeling is defined as a set of parameters that are used to efficiently calculate the energy of potentials of an MD system. Physical or chemical experimental data, quantum mechanics, or both, can be used to create force fields. Another input that is required, besides the parameters of the force fields, is the coordinates, velocities and the size of the box. The basis vectors of the periodic box determine the shape and size of the box.

After that, the corresponding forces and the energy of the potential of the atomistic system are calculated together with the forces, velocities and new positions.

Data of interest (e.g. molecular trajectories) is saved at certain intervals while the simulation takes place. Given the substantial volume of data, it is not mandatory to save every step but only at some wanted intervals. Saved data can contain velocities and/or positions, forces and helpful information about the integration time step and the dimensions of the simulation volume, etc.

3.2.2 Different types of MD. Next to the classical MD, there are different types of MD. In this paragraph we mention some of them that are relevant for water splitting. When the potentials are determined from electronic structure calculation, this is usually referred to as ab initio MD (AIMD). Some other variants come from the computation of potentials. The computation of potentials¹³⁷ can be done with:

• (reactive) force fields, which means that we are discussing about a classical, standard MD simulation.

• the Schrödinger equation, in which case an AIMD simulation is performed and ionic motion is still treated classically, but the potential they feel is calculated via quantum mechanics on the fly; and.

• a mixed quantum/molecular dynamics approach, in which a quantum/MD mechanics is executed.

3.2.3 State-of-the-art. Atomistic modeling from first principles can be used to understand the physical–chemical nature of active sites to engineer strategies to improve properties. By contrast, MD focuses on characterizing complex systems such as solid/liquid interfaces for a variety of applications. Particularly, the following were analyzed by using MD simulations:

Photosynthesis: (1) the diffusion coefficient making use of coarse-grained schemes, (2) radial distribution functions, and (3) the velocity of a particle in the vicinity of the surface that is active;

Semiconductors: (1) for the conduction position it has been studied the surface adsorbate exact nature (2) the relative alignment of the conduction PBE and valence with respect to potentials of water redox;

Titanium-based simulations for water splitting: (1) understanding of cell structures, solid–water interfaces, volume thermal expansivity and bulk modulus and (2) titanium dioxide-based catalysts; and.

Dye-sensitized PECs: catalytic mechanism of water oxidation.

3.2.3.1 MD simulations for photosynthesis. Classical MD have been used successfully for enhancing artificial photosynthesis processes¹³⁸ by understanding and simulating how the reactants flow over active sites surfaces (e.g. the study of interfacial phenomena at surfaces which are reactive and catalytic reactive). A characterization method has been developed¹³⁹ to accurately describe the flow of reactants over a site that is active (e.g. a “metal ion”). By using particle trajectory data, the dynamic and structural characteristics of the system are studied. In addition, Lennard-Jones (LJ) repulsive potentials together with Yukawa potentials (electrostatic screened ones) for the absorption modeling of sites that are active were used. The MD simulations were done with LAMMPS tooling.¹⁴⁰ Using CG scheme for diffusion coefficient profiling,¹⁴¹ the radial distribution functions and the velocity of a particle in the vicinity of the surface that is active were obtained.
3.2.3.2 Molecular dynamics simulations of semiconducting materials for water splitting. Calibration of the valence and conduction band related to the water redox potentials is one of the main properties that helps in determining whether a material with semiconducting properties is good for water splitting. In a first approximation, the vacuum level of the frequent energy reference can be used for the computation of the band alignment. Nonetheless, this procedure can lead to faulty results as it does not take into account the arrangement of dipole layers in a liquid/solid interface. Even though methods that could lead to appropriate vacuum computations have been researched, those methods do not consider material characteristics that are related to the material and surface termination.

Wu et al.,^142,143 has done one of the earliest studies to add to the band edge alignment at the liquid/solid interface. His attempt combined molecular dynamics based on the force field TIP4P with DFT computations with the help of the semilocal functional PBE. The correction of the band edge alignment was done using the electrostatic potential profile across the interface. A principal hypothesis was that the error of the DFT computations in finding the conduction band of the inspected semiconductors (TiO₂, WO₃, GaAs, GaP, GaAs and ZnSe) compensated the error for the forecast level of the H₂O acceptor that is the unoccupied and lowest orbital of a solvated H₃O⁺ ion. This approach seemed to be a good one for these particular materials, but no similar success was noticed for the rest.¹⁴⁴ In a similar way, the alignment of the conduction band with the NHE (Normal Hydrogen Electrode) potential was well predicted by the AIMD simulations of interfaces of TiO₂/water using the PBE functional. Broad discrepancies were shown by the same simulations for the potential of ionization or the position of the valence band.¹⁴⁵ This outcome had its source in the usual underestimation of the band edge using PBE functional for the TiO₂ band gap.

The free energy integration with the use of a dummy proton with fluctuating charge determined the change of free energy of the titanium dioxide reduction at the normal hydrogen electrode together with the proton solvation. The DFT-MD simulations looked at the importance of surface adsorbates nature for the position of valence band and conduction band using PBE.¹⁴⁶ These simulations indicates that the relative positions of the PBE at the {101} and {001} facets of titanium dioxide anatase alter with the state of the absorbed H₂O particles. Accumulation of electrons on {001} facets is advantaged by the deprotonation of the H₂O adsorption while holes rather accumulate at the {101} facets. Oppositely, the relative positions of PBE near the surfaces are inverted with reference to the anatase bulk when no deprotonation happens under acidic circumstances. Consequently, the oxidative facets {101} become reductive and similarly the reductive {001} facets turn oxidative.

Note that we focused here on the positions of band edges, which are more relevant to electrocatalysis than to photocatalysis, since the hot electrons/holes used in photocatalysis have usually energies beyond those band edges. However, due to the limited amount of MD simulations for photocatalysis, we nevertheless discuss them as a possible starting point for MD simulations for water splitting using photocatalysis.

3.2.3.3 Semiconductor photocatalysis^147,148 simulations based on Titania for water splitting^149,150. Molecular dynamics simulations (classical ones) were used for looking at the catalysts of TiO₂¹⁵¹ (for example Pt/TiO₂ with two polymorphs – rutile and anatase) as water splitting photocatalysts^152–156 by the use of the LAMMPS. For accounting the interactions between titanium dioxide surfaces and water the “universal force field” (UFF) parameters were used.

The effect which water has on surfaces like Pt-loaded titania were intensely studied by the authors and the following valuable properties were noted: the radial distribution function, density profile, diffusion coefficient, residence time and dipole angles. Furthermore, the results showed that the dipoles of H₂O for the Pt/rutile system does not havea preferrential orientation and presented a long inhabitation period of more than 30 ps. Diverse research have focused on understanding solid–water interfaces.^157–162

It is essential to look at the atomistic potential that is used to characterize solid/water interface and the solid itself. Several materials and their potentials have been examined in this area. Different force fields are used in the example of TiO₂ to clarify the O and Ti atomistic interaction in various stoichiometries and morphologies. For TiO₂ polymorphs such as brookite, anatase, and TiO₂ II, Matsui and Akaogi¹⁶³ and coworkers created a pairwise potential. The sum of the Coulomb, dispersion, and repulsion interactions was taken into account by these authors in a typical interatomic potential.¹³ Kim et al.,¹⁶⁴ on the other hand, designed a different interatomic potential for rutile that included additional conditions to the initial Matsui potential, such as short-range repulsion, Coulomb, Morse and van der Waals, and Morse interactions. The proposed potential mimics mass modulus, cellular structure and thermal expansion in volume and can be used also for other polymorphs.¹⁶⁴ The potential was able to match different experimental properties combining the relationships between volume thermal expansion crystal structures, enthalpy and volume compressibility. This potential is widely used for molecular dynamics simulations.^165,166 However, the relative anisotropic static permeability of rutile is not well described, which is the major downside of this potential. A question remains open as to whether interatomic potentials are applicable to chemical reactions in general and to photocatalytic water splitting in particular.

3.2.3.4 Dye-sensitized PECs. The use of dye-sensitized PEC is another approach to photocatalytic water splitting.^167,168 It has been shown that constrained AIMD are good to be used for the catalytic mechanism in water oxidation study.¹⁶⁹ Further, the authors studied the injection of the photoinduced electron into the conduction band of anode of titanium dioxide using a atomistic complex with a mononuclear fully organic DiNM dye and a Ru-based WOC. DS-PEC devices can be integrated successfully with the chosen dye through AIMD simulations.

3.2.4 Limitations and perspective. Few studies have been conducted on water splitting through MD, and there are few or none on water splitting through photocatalysis. Simulations of photosynthesis in semiconducting materials as well as water splitting were the focus of the first set of simulations. Another review was conducted on simulations that examined water splitting processes based on titanium. Some MD simulations studied dye-sensitized PECs. As an open gap there should be more simulations that are looking for more materials (not only titanium-based materials, which is mostly the case) that can be used for water splitting.

Looking at the properties that are studied with MD, some of the limitations are due to the lack of accurate force fields for different materials and the prohibitive computational cost of AIMD simulations. Since force fields are difficult to develop since they are mostly done manually, the study of more materials and their properties becomes more difficult. One possible further direction is the development of force fields for more materials and extensions of current force fields to make it possible to study more materials, parameters and phenomena related to water splitting.

3.3 Mesoscale modeling

The Monte Carlo (MC) method, based on the massive generation of random numbers, has been extensively applied in nuclear physics, condensed-matter physics and theoretical chemistry.¹⁷⁰ MC numerical simulations take advantage of the law of great numbers to avoid the calculation of large multidimensional integrals, such as those associated with the basic laws of quantum physics and statistical mechanics. Thus, it can be applied to systems containing 10⁷–10⁹ atoms per system.

The MC method has not been extensively used to simulate water splitting systems. However, three main areas of application of MC simulations to solve issues related to catalysis and photocatalysis can be identified:

(1) Studies of charge transport and electron dynamics in nanostructured photoelectrodes are described in Fig. 3;

Fig. 3 Illustration of Monte Carlo methods for electron transport in nanomaterials. Hopping times are calculated via a stochastic expression (R being a random number between 0 and 1) that depends on the energies of the traps with respect to a certain transport level. This way energetic and morphological disorder can be considered.

(2) Calculation of material properties using classical force fields; and.

(3) Simulation of reaction paths in photocatalytic processes.

A considerable effort in methodology development is needed before the application of the MC method to photoelectrochemical water splitting reactions. The state-of-the-art is outlined below.

3.3.1 Methods. MC methods for electron dynamics in nanostructured electrodes are also known as random walk simulations.^171–173 This technique is based on the generation of random rates for the transfer of electronic carriers (electrons, holes, excitons) between localized electronic states in the material, commonly referred to as traps. Three models have most commonly been used to do this: the multiple-trapping model,¹⁷⁴ the hopping model¹⁷⁵ and Marcus transfer rates.¹⁷⁶

The first assumes that electron transport occurs by a succession of trapping/detrapping events between the localized states and a transport level (usually identified with the electronic band edge). The second considers direct jumps between traps, taking into account probabilities that decay exponentially with the distance between traps. Both models include a Boltzmann factor that multiplies the jumping rate and depends on temperature and the energy difference of the electronic transition: exp[−(E_final − E_initial)/k_BT]. The third uses the well-known Marcus theory and reorganization energies for electrons to calculate the probability of transfer between localized states in a semiconductor.

MC methods applied to the calculation of material properties make use of the well-known Metropolis algorithm.¹⁷⁰ The implementation of this algorithm requires the availability of a classical force field, a real handicap, that feeds the procedure with the required lattice energy for a given atomic configuration. A Markov chain of configurations is then generated from the computation of transitional Boltzmann factors for different atomic “moves”, hence providing structural and thermodynamic properties of the material by averaging along the produced trajectory. This trajectory can resemble the true trajectory as determined by Newtonian dynamics under certain conditions.¹⁷⁷

A similar strategy is employed to simulate reaction paths. In this case, the Boltzmann factors of transitional free energies (computed by DFT) and the Metropolis algorithm are applied to statistical trials to move forward in alternative reaction pathways. This strategy helps to discriminate between alternative mechanisms, even for very slow reactions.

3.3.2 MC applications. MC (random walk) approaches applied to diffusive transport are by far the ones with the most literature.^{171,172,175,176,178} They have been applied in a variety of situations involving transport in random media, such as Brownian motion.¹⁷⁷ In fact, this approach is a natural way to investigate electronic processes in nanostructured and disordered systems. The nature of transport and recombination in this type of material is quite stochastic, so the use of the MC method is particularly well suited to study the relevant mechanisms from “first principles” with a reasonable numerical effort. The use of random walk methods in nanostructured solar cells and water splitting systems is especially appealing due to the key role of the interplay between transport and recombination to achieve an efficient device. Applications to solar cell modeling were pioneered in 1999 by Nelson,¹⁷⁹ who adapted the continuous time random walk theory of Scher and Montrol.¹⁸⁰ Random walk simulation has been employed to describe diffusion-limited recombination,^181–183 morphological and percolation effects,^184–186 photoconductivities,^187,188 electron diffusion coefficients,^189–191 and photocurrent and photovoltage transients¹⁹² in dye-sensitized solar cells (DSSC) and dye-sensitized photoelectrolytic cells (PECs). These studies have recently been extended to describe charge separation in water splitting systems with the same type of photoanodes.¹⁹³

In the second class of applications, the MC method has been applied to obtain material properties in water splitting systems such as titania¹⁹⁴ and ceria.^195,196 Amft et al.¹⁹⁴ used the MC method to simulate the adsorption of molecules of water on the titania surface. Grieshammer et al.¹⁹⁵ started from DFT calculations to obtain lattice energies and then developed a classical interaction potential that fit the resulting energetic landscapes. The classical potential made it possible to run calculations on larger systems, thus saving computational time. This method has been used for describing the clustering of defects¹⁹⁶ and of phase separations in metal oxide alloys for water splitting.¹⁹⁷

In the third class of applications, simulation of reaction paths and rare events using the MC method has been introduced by van Erp and coworkers.^198,199Ab initio quantum calculations are used as input to produce transition energies. Then, an MC sampling procedure with various types of trajectory moves is employed. This strategy allows actual reaction rates to be efficiently obtained, even for very slow reactions. This method has been successfully applied to the modeling of the water dissociation reaction.¹⁹⁸ An analogous procedure has been used by Hareli and Toroker²⁰⁰ to simulate the predominant reaction path for water oxidation by nickel oxyhydroxide. DFT calculations are run to calculate the reaction free energies of alternative reaction paths. These free energies are fed to a traditional Metropolis algorithm to calculate the transition probabilities from one intermediate to another, hence estimating the probability that the chemical reaction takes place via a particular reaction path. In water splitting with hematite, a kinetic MC (kMC) approach was used by Kerisit and Rosso²⁰¹ to model charge transport. Sinha et al.²⁰² used kMC to model the surface coverages of different intermediates as a function of time and applied potential. Two different mechanisms were simulated, and it was found that the coverage of OOH and O was negligible for both mechanisms, whereas H₂O and OH dominated the surface.

3.3.3 Limitations and perspective. MC techniques boast the great advantage of being less computationally demanding than DFT and MD techniques. However, the produced trajectories only approximately reproduce the true dynamics of the system.^177,189 In addition, the predictive power of MC simulations relies on the availability of suitable models: transport mechanisms in the case of random walk simulations and classical force fields in the case of the computation of material properties. In any case, fully exploiting the potential of MC techniques for photocatalytic water splitting remains an open challenge.

3.4 Continuum modeling

Continuum modeling (CM) is defined as a mathematical way of applying a model to continuous data, e.g., data that have a potentially infinite number and divisibility. In this way, CM is the opposite of discrete modeling, where a mathematical set of equations is fit to discrete data, e.g., data that take on a countable set of values, such as integers, and which are not infinitely divisible. CM models are typically described by differential equations. In a typical plot in multiscale modeling, CM is at the upper end with long time and long length scales. This is the step between kinetic MC modeling and experiments. Thus, CM is a main bridge for connecting modeling with experiments.

CM modeling was first used in the field of continuum mechanics, where typically the behavior of materials is modeled as a continuous mass rather than individual atoms.²⁰³ In fluid dynamics, CM is used to model fluid flow using a continuous liquid instead of single liquid molecules, such as water.²⁰⁴ CM is also increasingly employed to simulate traffic by replacing single cars or pedestrians with a continuum description.^205,206 Recently, CM has become popular for applications in solid-state ionics, electrochemistry, and catalysis, particularly fuel cell,^207–209 electrolyzers, and water splitting applications.^210–216 The reason is the strong need to bridge modeling and experiments to better analyze experimental measurements and to identify the limiting processes in electrochemical applications, thereby improving performance. In general, we can identify three levels where CM is used for electrochemical and catalytic applications: the atomistic level, the interface level, and the component/device level. All levels are discussed in more detail in the following sections.

3.4.1 Methods. Different methods and software are used for the different levels of CM. At the atomistic level, e.g., solvation models, commercial software packages exist, such as VASPsol,^217,218 Quantum-ESPRESSO,²¹⁹ CANDLE²¹⁸ and SaLSA,^212,220 COSMO, or linearized Poisson–Boltzmann/polarizable continuum models (LPB-PCM).^221–230

At the interface level, usually in-house codes are developed, mostly in MATLAB and/or SIMULINK. The main reasons for this are that this branch of CM modeling is rather new and the reactions taking place at the interface strongly depend on the application. Hence, general models cannot be set up or would require large databases. In addition, different chemical and physical phenomena are required depending on the application. The models can be implemented using methods from control theory and system identification. An example is provided in the study by George et al.^210,211 The advantage here is that any chemical or physical phenomenon can be modeled and no restrictions toward theory or application exist. A disadvantage is that knowledge of coding is required for developing these models. Thus, the modeling effort is more time consuming and complex.

At the component/device level, finite element modeling software and multiphysics modeling packages, such as COMSOL or ANSYS, are typically used. The advantage is that these software packages are ready to use, and many physical and chemical equations and theories have already been implemented that can be directly used with the addition of respective boundary conditions and the chemical and physical parameters of a specific system. The disadvantage is that theories that are not included in the software cannot be easily added. Therefore, the use of such software packages is usually limited to certain fields and applications where the respective chemistry and physics are already implemented.

3.4.2 State-of-the-art.
3.4.2.1 Atomistic level. The first level in CM is the atomistic level. In typical atomistic modeling, each atom is modeled individually. This is difficult when considering a solid–liquid interface, where many solid and liquid molecules interact. A fully ab initio approach, e.g., an explicit solvation model, represents the most detailed system but requires averaging many atoms and molecules. This makes an atomistic approach computationally very expensive and often not possible to handle even with large supercomputers. Thus, CM modeling using a continuum for the liquid phase at the solid–liquid interface is therefore attractive. CM is used in the form of solvation models. The solvent molecules are replaced with a continuum dielectric, and the simulation result is averaged over molecular configurations embedded in a solvent model. Such models are called implicit solvation models. The advantage is the considerably lower complexity and cost. Typical problems that are solved with solvation models are electronic structure calculations at solid–liquid interfaces. Ping et al.²¹² studied solvation effects on the band positions of surfaces, such as Si(111), TiO₂(110), IrO₂(110), and WO₃(001). The solvation model predictions were in excellent agreement (within approximately 0.1 eV) with ab initio molecular dynamics (AIMD) results and in good agreement (within approximately 0.2–0.3 eV) with experimental measurements. Additionally, the energetics for surface oxygen vacancies and their effect on the band positions were calculated. The study demonstrates that the solvation calculations are closer to experimental values than vacuum calculations and agree well with explicit AIMD simulations, which are, however, computationally much more expensive. Sinha et al.²⁰² used an implicit solvation model to calculate the free energy steps in the OER of water splitting over hematite. The results were compared to a model without solvation. It was found that the overall impact of the solvation model on the free energy steps was rather small (a difference smaller than 0.1 eV on the electrochemical overpotential and <0.2 eV on the relative stabilities of intermediates).²⁰² Hence, if the difference between explicit and implicit solvents is not large, solvation models that only assume implicit solvents are sufficient for modeling solid–liquid interfaces. Even though implicit models are beneficial regarding computational costs, there are several challenges that are related to the physical description of the solvent and ion distribution and to the determination of the reaction energetics at constant potential.²²¹
3.4.2.2 Interface level. The second level in CM is the interface level. The interface level is defined as the area where the electrochemical and catalytic reactions take place. Hence, the entire reaction mechanism taking place at the interface is considered. For different applications, such as fuel cells, electrolyzers, and water splitting, the research field currently has the following challenge: identifying the limitations at the interface, whether electrochemical or structural. However, to increase efficiency and performance, it is of utmost importance to know these limitations. The fact that these limitations are unknown is related to experimental measurement and analysis methods. On the one hand, surface species cannot be easily measured during the operation of a device even though they are the key for identifying the reaction mechanism that limits performance.^86,231,232 On the other hand, electrochemical interfaces are usually experimentally characterized by current–voltage curves and electrochemical impedance spectroscopy. These are mainly measurements of physical properties, such as currents, voltages, and resistances. The data are then fitted to physical models. For example, in Electrochemical Impedance Spectroscopy (EIS), the data are fitted to so-called equivalent circuit models consisting of resistances, capacitances, and inductances. However, the interface is an electrochemical system. In water splitting, particularly on the oxygen evolution reaction (OER) side, oxygen is produced by splitting water through a four-step mechanism with several intermediates, such as OH, O, and OOH.⁹⁴ Hence, the relation between the physical model and electrochemical interface is missing in typical data analysis from the experimental side.

Due to this problem, which appears not only for water splitting but also for fuel cells, electrolyzers, and corroded materials, studies have focused on so-called microkinetic modeling. Microkinetic modeling is actually known from its use in catalysis (e.g., Filo)²³³ and is usually used for determining surface species and concentrations in catalytic systems. Microkinetic modeling electrochemical systems is more difficult due to additional charge carriers and the production of current, which creates a multiple input–output system. A general approach to simulate this is known from control theory and system identification.^234,235 Modeling can be carried out in the form of state-space approaches. Such modeling was performed in the field of solid oxide fuel cells (SOFCs) by Mitterdorfer and Gauckler^207,208 and by Bieberle and Gauckler.²⁰⁹ EIS data similar to experimental data were simulated and compared to actual experimental data. These studies were extended by Vogler et al.,²³⁶ showing that one of 6 mechanisms on the anode side of the SOFC could be identified; in this manner, hydrogen spillover was finally found as the limiting process at the Ni–YSZ interface of an SOFC anode.

Microkinetic modeling was recently also presented by Dickens et al.²³⁷ for the OER on metallic oxide surfaces. Volcano plots and current–voltage plots were simulated, and coverage regimes for different surface intermediates were identified. George et al.^210,211 even went a step further and simulated the semiconductor–electrolyte interface of the OER. In the first study,²¹⁰ a general model was set up step-by-step, and a case study for the hematite–water interface was presented using a nonlinear state-space approach, which is shown schematically in Fig. 4. Current–voltage curves and EIS data were simulated from the typical OER mechanism as suggested by Rossmeisl et al.⁹⁴ and with DFT input data from Zhang et al.¹¹⁹ The simulation followed experimental conditions, and the results compared favorably to experimental data. In addition, the model allowed for modeling surface coverage data that are very challenging to obtain experimentally and currently unavailable.^238,239 In the next step, George et al.²¹¹ added illumination and charge carrier dynamics in the model to simulate chopped light measurements. Such studies offer the possibility to simulate electrochemical data that can be directly compared to electrochemical measurements and in this way contribute to identifying the reaction mechanism at electrochemical interfaces (intermediate species, comparison of different reaction mechanisms, materials scanning, parameter scanning, etc.). In this way, such studies fill the gap of experimental challenges, such as the measurement of surface species and concentrations.

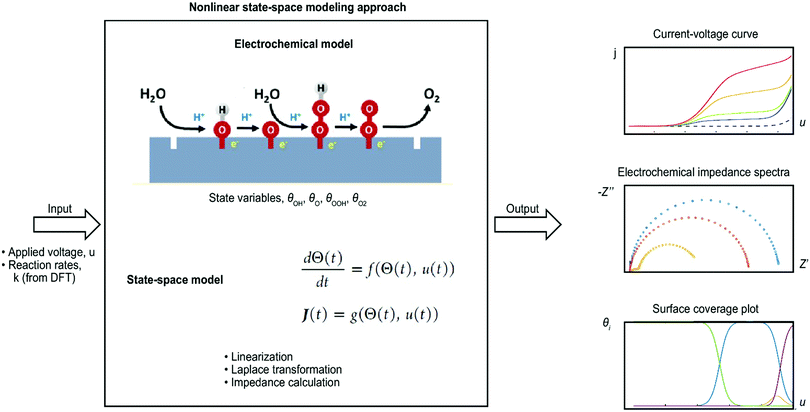Fig. 4 Nonlinear state-space approach for simulating electrochemical data of the oxygen evolution reaction (OER) (approach is explained in detail in ref. 210 and 211).

3.4.2.3 Component/device level. The third level in CM is the component/device level. CM modeling is used to simulate the characteristic data that are used for performance and quality control of entire systems. CM is used to perform accelerated simulations, which can prevent the need for many experiments or to predict performance and degradation data to avoid too many experiments. In contrast, such simulations can be used to compare real experiments and interpret experimental findings with chemical and physical models. Furthermore, so-called multiphysics models are used. Bove and Ubertini²⁴⁰ simulated the current density distribution in SOFCs by considering the entire electrode–electrolyte component, including the flow in the gas distribution channels. In this simulation, the implemented physics laws were Ohm's law and the Butler–Volmer equation for the electrodes and Fick's law, the Navier–Stokes equation, and the Poisson equation for simulating the channel flow. Yuan and Sunden²⁴¹ calculated the temperature distribution on a PEMFC membrane using gas flow and heat transport equations. Regarding thermochemical water splitting, Haussener et al.²¹³ implemented heat and mass transfer models with fluid flow and respective chemistry to simulate a sulfur–iodine-based thermochemical cycler for water splitting. Regarding photoelectrochemical systems, several papers by Haussener et al.^213,214 and Singh et al.²¹⁵ implemented multiphysics models that accounted for charge and species conversation, fluid flow, heat transfer, and electrochemical processes. Current densities, linear sweep voltammograms, and STH efficiencies were provided as well as overpotential curves that allowed differentiation between different types of losses in the system.²¹³

3.4.3 Limitations and perspective. CM is a widespread modeling technique for different fields and applications. In the field of water splitting, it is still at the beginning stage, and few studies have been carried out thus far. The advantage of CM is its close proximity to experiments and the feasibility of simulating the same data under the same conditions as experimental measurements. Typical data that can be simulated are current–voltage curves or impedance spectra. In addition, entire systems can be simulated, in which modular simulation approaches are very helpful. Simulations are usually not computationally expensive and most of the time do not need high-performance supercomputing infrastructures. In contrast to these advantages, CM relies on input data that usually depend on the output of other modeling approaches in a multiscale modeling chain (see Section 3.5). Therefore, the quality of the simulation results depends on the quality of simulations with other time and length scales. CM does not have atomic accuracy. This is countered by the possibility of using fitting procedures that allow for direct comparison to experiments.

In general, CM is not a prominent path for modeling water splitting. However, interest is growing, particularly from experimental groups, since it allows the simulation of real systems, such as solid–liquid interfaces and systems, under actual operating conditions. This is highly required for increasing the performance of energy devices; therefore, a high impact is expected in the future.

3.5 Multiscale approaches for the catalysis of water adsorption/oxygen desorption

3.5.1 Defining multiscaling. Modeling realistic devices for catalytic water splitting involves the use of several different length scales with varying accuracy requirements. The different regimes involved—from highly accurate quantum mechanical approaches to continuum modeling—have been discussed separately in the previous sections of the present review. Arriving at a comprehensive theoretical model requires combining these different methods with their individual length, time, and accuracy scales in a meaningful way to produce a multiscale approach.

There is no general one-size-fits-all approach to multiscaling: different techniques allow for combining a plethora of methods in different ways. The essential quality of a multiscale approach is the treatment of multiple scales in space or time. Multi-scaling approaches are meanwhile applied in a variety of different fields, ranging from protein folding²⁴² or meteorology²⁴³ to biology.²⁴⁴ The recent rise in the popularity of multiscale approaches is carried out by the availability of experimental and theoretical approaches providing structural information down to the atomic level and the enormous increase in computational power.²⁴⁵ However, given the complexity of the accurate simulation of heterogeneous catalysis even at a specific length scale—e.g., the atomistic description of the catalyst surface using quantum mechanical methods—performing accurate interconnected calculations at several scales seems daunting. To meet the challenge of simulating catalysis for water splitting, we first have to combine expertise at several scales to develop multiscale approaches in a coordinated research effort.

3.5.2 Multiscaling for photocatalytic water splitting. Multiscale approaches are essential to capture the complexities of heterogeneous catalysis: the charge-transfer reactions and excited states are the center of many photocatalytic processes and they require highly accurate treatment of the electronic system, beyond even the accuracies of conventional density functional theory. Conversely, mesoscopic-scale approaches, such as microkinetic modeling or solvation models, are required to describe the surrounding environment, the dynamic concentration of different reactants and to identify rate-limiting processes. On the scale of a catalytic reactor, flow equations or state-space modeling provide valuable insight and ways to improve device efficiency or reduce cost. Although progress for these individual methods has been considerable, we do not yet have a complete, unified picture of a general catalyst under varying conditions. A true multiscale framework will bring us closer to finding an abundant, efficient, safe, and affordable photocatalyst for water splitting.

To date, parameter-free multiscale approaches for catalytic reactions on the atomic scale are still hampered by simplifications in describing the reactive site. While steps, defects and terraces are likely to host highly active catalytic sites, their description is much more challenging than those of pristine cleaved surfaces. In fact, state-of-the-art microkinetic modeling often neglects the effect of the shape of the catalyst on reactivity and selectivity.^246–249 Indeed, the need for ab initio kinetic models not only for pristine surfaces but also for different facets, terraces and defects quickly leads to an explosion of complexity, although scaling relations may help to quickly identify specific sites of interest.²⁵⁰ Modern approaches aim to predict nanoparticle growth and reactive sites under operating conditions²⁵¹ or resort to semiempirical methods to provide acceptable parametrizations for different facets.^252,253

A true multiscale framework to describe heterogeneous photocatalysis for water splitting could interrelate phenomena at relevant time and length scales,²⁵⁴ bringing devices closer to the theoretical limit of photocatalytic efficiency.²⁵⁵ This was suggested for the first time by Zhang and Bieberle-Hütter together with a literature review on the modeling of photoelectrochemical water splitting.²¹⁶ Most results to date concern the combination of two levels of theory. For example, to describe water splitting at titania surfaces in aqueous solution, one can use DFT-derived optimized force fields (ReaxFF)²⁵⁶ that can then be used for kinetic modeling.²⁵⁷ The obtained complex distribution of water on these surfaces hints at the importance of a true multiscale description. Similar approaches for iron oxides,²⁵⁸ aluminum nanoclusters²⁵⁹ or ZnO²⁶⁰ demonstrate the robustness and versatility of kinetic modeling in heterogeneous catalysis. In particular, the effect of water molecules at surfaces is easily missed in DFT calculations. Along similar lines, kMC approaches first obtain electron transfer rates by DFT and then employ kinetic models to describe the transport processes of, for example, hematite²⁶¹ or Pt(111).²⁶² The combination of more than two methods and scales is still rare. A multiscale approach to investigate the mechanism of the OER was recently demonstrated by Sinha et al.²⁰² These authors used DFT, DFT-MD, and kMC to study a hematite Fe₂O₃(110) water system. DFT calculations indicated that the formation of O* species was a potential limiting step. DFT-MD simulations determined a transition state barrier of 0.35 eV for proton transfer. The DFT and DFT-MD results were combined to create a reaction path model for the OER. Rate constants for the elementary steps were estimated and used as input for the kMC simulations. The surface coverages of the different intermediates in the OER were calculated by kMC as a function of time and applied potential. This work was the first to show a multiscale model for the OER by coupling DFT, DFT-MD, and kMC. The beauty of the above approach is that data that are experimentally unavailable but highly needed can be calculated, such as surface coverages. The multiscale model now needs to be refined to further improve the mechanistic picture of the interface and the electrochemical model.

In a separate study, the same group also coupled DFT with continuum modeling.²¹⁰ In this study, DFT simulations were used to estimate reaction rate constants for the different single steps in the multistep OER process on a hematite surface. This input was then used in a nonlinear state-space approach to calculate electrochemical data, such as current voltage curves and electrochemical impedance data. In addition to these data, which are typical experimental data, surface coverages can be calculated—data which is experimentally unavailable.

Coupling DFT calculations for transition energies with a combined microkinetic-and-reactor model allows for a multiscale description of propane dehydrogenation on Pt.²⁶³ Very recent results for ethylene epoxidation on Ag catalysts realize a true multiscale description from the atomistic level all the way to a description of the reactor.²⁶⁴ A similar approach for water splitting would be very useful as a benchmark for current multiscale methods.

3.5.3 Multiscaling methods. Given the number of different multiscaling techniques, we will restrict ourselves to the most important approaches to describe catalytic processes. The major challenge in modeling heterogeneous catalysis is the different scales involved: catalysts feature active sites—often edges between different facets or even single atoms embedded on a surface—that are already challenging to simulate in a fully quantum-mechanical approach.²⁵⁰ Reaction rates or selecting specific reaction products depend on the local chemical environment, which, in turn, is a function of temperature, pressure or surface coverage. Predicting and optimizing the macroscopic functionality of a catalyst requires addressing these different length and time scales.

Multiscale modeling needs to provide the solution to two distinct aspects of the problem:²⁶⁵ complications and complexity. Regarding complications, we refer to the need to accurately describe phenomena at different scales and to seamlessly couple the results. Complexity refers to the vast parameter space still required to model a realistic catalyst after having established a multiscale description: providing all parameters for every conceivable local reaction via ab initio approaches remains unfeasible. We discuss strategies to solve both problems below.

Beyond the need for connecting theories at different length scales—from ab initio modeling at the atomic scale to large-scale descriptions for reactor chambers—multiscaling also involves bridging accuracy scales, especially concerning different levels of ab initio theories; notably, electron–electron interaction renders an exact analytical treatment of the many-body Schrödinger equation impossible for more than two electrons, while brute-force numerical solutions are unfeasible due to the unfavorable scaling of the Schrödinger equation with the number of electrons. Approximate methods, such as DFT, have proven exceptionally successful at providing very accurate results that fit experimental benchmarks for many problems. Indeed, the development of more advanced exchange–correlation functionals is an active area of research. However, there are a few noteworthy cases where the approximations employed in DFT prove critical. Of particular interest for photocatalysis are excited states, which are challenging to treat using ground state approaches, such as DFT, and charge transfer processes, which are at the heart of many important catalytic reactions but unfortunately poorly described by exchange–correlation functionals.

A promising alternative to treat large, complex systems is to further partition on the atomic scale, obtaining a cluster of a few atoms that should be treated with high accuracy (e.g., with higher accuracy than even DFT) and the surrounding atomic environment. This cluster is then embedded in the surrounding environment described by a less accurate method. In contrast to QM/MM approaches,²⁶⁶ we consider here cases where DFT is the less accurate method used for treating the immediate environment. The cluster of interest is typically handled using quantum-chemical approaches such as correlated wavefunction techniques or highly accurate yet expensive post-DFT methods such as GW²⁶⁷ or the random phase approximation.²⁶⁸ Several embedding schemes have been proposed.^269–272 Density-based embedding approaches allow the seamless combination of different methods, since the only communication happens via the electron density, a quantity accessible via many different methods.^272–275 More elaborate approaches require embedding operators instead of potentials,^{269,276–278} but they also reduce the margin of error. While several implementations in popular codes exist, these are rarely included in the basic package and typically require substantial user input.

Given the methods laid out in the previous sections of this review, all the tools needed to arrive at a true multiscale model are available. On the atomic scale, ab initio approaches, such as DFT, can provide input for effective parametrized models to estimate bond dissociation energies and reaction kinetics even if achieving this level of description in excited states and nonadiabatic phenomena involved in photocatalytic water splitting remain a formidable challenge. On the mesoscale, we aim to predict the reaction rates of elementary events (single steps in the required chain of reactions toward the desired product). A Markovian master equation allows for simulating the different reaction rates, either using the mean-field approximation,^278–280 or more accurately by kMC algorithms that account for the correct and site-resolved statistical interplay among the elementary steps of the microkinetic model.^279,281 Reaction path analysis then allows for determining the dominant elementary reaction steps under given operating conditions.^249,282 Regarding electrochemical systems, Melander et al.²⁸³ recently presented a general DFT framework for modeling electrochemical interfaces at given potentials and finite temperatures that even allows for selective coarse graining as needed. On the macroscale, CM allows for a seamless comparison to experiment: one introduces concepts from statistical mechanics such as chemical potential or temperature and simulates their change in time and space.²⁸⁴ For example, predicting the catalytic rate of a proposed reactor would involve the hydrodynamic flow of a solvent through its 3D geometry.²⁸⁵ State-space modeling provides rate equations for reactants and products,^286–288 and has been proposed as a key ingredient for one level of a true multiscale description of photoelectrochemical systems.²¹⁶

Once the description at each scale is established, we then have to connect the individual models.²⁸⁹ Direct coupling is obviously impractical. Instead, interdependencies are decoupled by appropriate approximations at each scale. For example, quantum-mechanical approaches provide effective interaction potentials or force fields that serve as input for microkinetic modeling.²⁹⁰ Likewise, kMC simulations provide estimates for local reaction rates at different catalytic sites.²⁹¹ Balancing the number of kMC simulations required to arrive with an acceptable timestep at the macroscale requires approximations such as the instantaneous steady-state to allow the tabling of steady-state reactivity data.²⁹² A full multiscale model could thus encompass five levels of scale (see Fig. 5):²¹⁶

Fig. 5 A general approach to multiscale modeling.

• On the atomistic level, DFT (potentially including embedded more accurate quantum-chemical corrections) provides fundamental parameters, such as geometries, reaction barriers or overpotentials, including excited states involved in the photocatalytic process;

• Molecular mechanics can then describe the emerging chemical environment and reconstruction of nanocatalysts, while NAMD is still needed to describe the physics involved in the nonradiative deexcitation of the photogenerated hole-electron pair;

• Coarse-grained approaches for mesoscale modeling, such as kMC, provide the dynamics of reactions and allow for identifying rate-limiting reactions, but generalizing these approaches to involve one or several excited states remains a pending task;

• Continuum approaches that allow up to device-scale simulations, can provide the hydrodynamic flow of solvents, temperature distribution in a device, or electrochemical data, such as current–voltage curves or impedance spectra (using state-space models); and

• Process simulation models describe the operation of the reactor in an industrial setting.

These five tiers provide a clear path toward a multiscale approach: a treatable system size and timescales that increase with every step, as does the level of approximation. In principle, each level could provide the effective parameters needed for a reasonable description at the next scale (top row of arrows in Fig. 5). However, realizing descriptions at these different scales is not enough: we next have to face the issue of complexity. First-principles methods, especially those required to accurately describe breaking bonds, require considerable numerical effort. Consequently, initially parametrizing all possible interactions of reactants requires an unfeasible number of DFT calculations, even if each one of them is treatable. Thus, the hierarchical multiscale approach outlined above needs to wisely spend computational resources on the key rate-limiting steps at each level.^293,294 Identifying those contributions on the fly and then dispatching more accurate first-principles calculations to accurately determine those contributions is key for arriving at a tractable multiscale approach (see bottom row of arrows in Fig. 5).²⁹⁵ A brief outline²⁶⁵ is provided below:

(1) Treat the full problem by a low-accuracy method at affordable cost;

(2) Compare predictions for the dominant reaction parts with selected experiments or benchmark high-level results to identify inconsistencies and determine the responsible approximations;

(3) Selectively improve the accuracy of the description for those reactions identified as problematic; and.

(4) Include the improved description in the full model, while reevaluating step 2 until sufficient accuracy is obtained.

Machine learning approaches could provide a highly efficient alternative route.²⁹⁶ Such active learning approaches provide both a quick estimate for the requested reaction rates based on the ab initio calculations already performed while also providing an estimate of how accurate this estimate is possibly resulting in the (automated) decision to invest in an additional ab initio calculation to improve the model.

4. Summary: perspectives and future challenges

Computational modeling provides a powerful approach to analyze the many processes involved in photocatalytic activity with nanocrystals, such as light absorption, electron transport, electron–hole recombination, and chemical reactivity, which cannot be isolated in an experimental setup. Therefore, multiscale modeling methods are critically needed to account for the finite size and shape of nanoparticles, which strongly affect catalytic activity.

Atomistic modeling primarily performed with DFT is important for atomically characterizing the reactivity. Additional methods, including TD-DFT, MBPT, GW, and BSE, are rarely used since they are computationally expensive for calculating the excited states of a surface for water splitting; thus, their large scale use is still unfeasible. To date, ground state DFT has provided important descriptors for studying the active site and identifying the mechanism and rate-limiting step. Particularly, intermediate adsorption is affected by peculiar electronic features at surface edges and by composition variations through the dopants/alloys/defects of nanoparticles or their substrates. The role of the photoexcited states needs to be emphasized; however, the dynamic aspects that can be approached by NAMD still represent a challenge.^297,298

Despite increased understanding of the role of electronic structure and band positions on reactivity, DFT is limited in accuracy by the choice of the exchange correlation functional and by the lack of dynamic information of atoms involved in water splitting, not to mention the complexity arising from the need to inspect the reactivity involving several potential energy surfaces. In contrast, information that can be obtained using MD includes the following: the diffusion coefficient, velocity in the vicinity of the active surface, radial distribution functions, relative alignment of the valence and conduction band edges with respect to the water redox potentials, understanding of solid–water interfaces, cell structures, bulk modulus and volume thermal expansivity, and catalytic mechanism. However, MD is limited to ground state chemistry, although NAMD approaches are being developed and applied.^299–302

Compared to DFT, there are far fewer studies for water splitting using MD simulations. There are a series of simulations for different applications, including photosynthesis, semiconducting materials in PECs, and dye-synthesized PECs. However, these simulations are limited to a small amount of materials (mostly Ti based) due to the large effort needed to parametrize the force fields for each and every material.

Notably, the MC method has also not been extensively used to simulate water splitting systems. However, three main areas of application of MC simulation to solve issues related to catalysis and photocatalysis can be identified: studies of charge transport and electron dynamics in nanostructured photoelectrodes, calculation of material properties using classical force fields, and simulation of reaction paths in photocatalytic processes.

MC approaches are applied through statistical sampling and random walk methods that are especially appealing for nanostructured water splitting systems due to the key role of the interplay between transport and recombination to achieve an efficient device. The nature of the reactivity, transport and recombination in nanostructured and disordered systems is quite stochastic, so the use of the MC method is particularly well suited to study the relevant mechanisms in nanocatalysts.

CM is most comparable to experiments in that it provides the same data under the same experimental conditions, such as current voltage-curves or impedance spectra. The different levels of CM include the following: (1) at the atomistic level, solvation models have been successful in predicting band edge positions but not for capturing external fields; (2) at the solvent/solid interface level, since experimental data are fitted to a physical circuit model that does not contain chemical information, microkinetic models have been developed to simulate current–voltage plots under experimental conditions and to calculate surface coverage that is difficult to measure, but these require system-specific developments; and (3) at the device level, multiphysics models are used for heat and mass transport to simulate the performance and quality control of the entire electrochemical device. Although the simulations are usually not computationally expensive and most of the time do not need supercomputers, CM relies on input data that usually depend on the output of other modeling approaches in a multiscale modeling chain and does not have atomic accuracy. Therefore, CM is thus far not a prominent path for modeling water splitting but is predicted to have a high impact by bridging models to experiments.

To meet the challenge of simulating catalysis for water splitting, we have to combine expertise at several scales to develop multiscale approaches in a coordinated research effort. Microkinetic modeling and flow equations are valuable for describing the dynamic concentration of different reactants and identifying ways to improve device efficiency, but we do not yet have a unified picture of a general catalyst under varying conditions. For example, microkinetic modeling often neglects the effect of the shape of the nanocatalyst on reactivity and selectivity. Most results to date concern the combination of two levels of theory, such as MD with kinetic modeling or DFT with kMC, and the combination of more than two methods and scales is still rare. Coupling DFT calculations for transition energies with a combined microkinetic-and-reactor model allows for a multiscale description that would be very useful for water splitting.

Multiscale modeling will provide a solution by combining the results at different scales (see Fig. 5): (1) DFT provides fundamental parameters such as geometries and reaction barriers or overpotentials; (2) molecular dynamics can describe the emerging chemical environment and reconstruction of nanocatalysts; (3) kMC provides the dynamics of reactions; (4) CM can provide the hydrodynamic flow of solvents, temperature distribution in a device, or electrochemical data, such as current–voltage curves or impedance spectra (using state-space models); and (5) process simulation models describe the operation of the reactor in an industrial setting.

The hierarchical multiscale approach outlined above needs to wisely spend computational resources at each level. Identifying those contributions by first treating the full problem by a low-accuracy method and then dispatching more accurate first-principles calculations will allow us to arrive at a tractable multiscale approach.

In summary, each method has made substantial contributions to understanding the catalytic behavior of materials. For example, DFT has been widely used for modeling heterogeneous catalysis and has revealed the correlation between reaction intermediate adsorption energies and overpotential. Larger scale approaches have been much less exploited. Future challenges in modeling complex nanocatalysts involve combining methods at different length scales, including excited state chemistry to describe photoexcited states, to account for the entire material system and representative effects. A true multiscale framework to describe heterogeneous photocatalysis for water splitting could interrelate phenomena at relevant time and length scales, bringing devices closer to the theoretical limit of photocatalytic efficiency.

Author contributions

Maytal Caspary Toroker: overall supervision, concept, writing and summary. Bipasa Samanta, Maytal Caspary Toroker: atomistic modeling. Ángel Morales-García, Francesc Illas: introduction, photocatalytic water splitting, modeling of photocatalysis. Nicolae Goga: molecular dynamics simulations. Juan Antonio Anta, Sofia Calero: mesoscale modeling. Anja Bieberle-Hütter: continuum modeling. Florian Libisch: multiscale approaches for the catalysis of water adsorption/oxygen desorption. Ana B. Muñoz-García, Michele Pavone: overall conceptualization. All authors: review and editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was supported in part by the Grand Technion Energy Program (GTEP). This article is based upon work from COST Action CA18234 (CompNanoEnergy) and is supported by COST (European Cooperation in Science and Technology) www.cost.eu. A.M.-G. and F. I. thanks the support of MCIN/AEI/10.13039/501100011033 through RTI2018-095460-B-I00, PID2020-115293RJ-I00, and María de Maeztu MDM-2017-0767 projects; the former also including fund from FEDER Una manera de hacer Europa.

References

1. International Energy Agency Web Page, http://www.iea.org.
2. The World Bank, http://data.worldbank.org/indicator/EG.USE.COMM.FO.ZS?end=2015&start=1960&view=chart (accessed May 2021).
3. N. Gupta, Renewable Sustainable Energy Rev., 2016, 71, 585–601.
4. B. Johnston, M. C. Mayo and A. Khare, Technovation, 2005, 25, 569–585.
5. S. Y. Tee, K. Y. Win, W. S. Teo, L. D. Koh, S. Liu, C. P. Teng and M. Y. Han, Adv. Sci., 2017, 4, 1600337.
6. C. Acar and I. Dincer, Int. J. Energy Res., 2015, 39, 1757–1768.
7. N. Z. Muradov and T. N. Veziroğlu, Int. J. Hydrogen Energy, 2008, 33, 6804–6839.
8. A. Fujishima and K. Honda, Nature, 1972, 238, 37–38.
9. A. Kudo and Y. Miseki, Chem. Soc. Rev., 2009, 38, 253–278.
10. F. E. Osterloh, ACS Energy Lett., 2017, 2, 445–453.
11. J. W. Ager, M. R. Shaner, K. A. Walczak, I. D. Sharp and S. Ardo, Energy Environ. Sci., 2015, 8, 2811–2824.
12. IARC, Radiation IARC Monographs on the Evaluation of Carcinogenic Risks to Humans Volume 100D, IARC, Lyon, FR, 2012.
13. K. Sivula and R. van de Krol, Nat. Rev. Mater., 2016, 1, 15010.
14. C. Xiang, S. K. Suram, J. A. Haber, D. W. Guevarra, E. Soedarmadji, J. Jin and J. M. Gregoire, ACS Comb. Sci., 2014, 16, 47–52.
15. K. Sliozberg, D. Schäfer, T. Erichsen, R. Meyer, C. Khare, A. Ludwig and W. Schuhmann, ChemSusChem, 2015, 8, 1270–1278.
16. R. Meyer, K. Sliozberg, C. Khare, W. Schuhmann and A. Ludwig, ChemSusChem, 2015, 8, 1279–1285.
17. I. E. Castelli, T. Olsen, S. Datta, D. D. Landis, S. Dahl, K. S. Thygesen and K. W. Jacobsen, Energy Environ. Sci., 2012, 5, 5814–5819.
18. M. Woodhouse, G. S. Herman and B. A. Parkinson, Chem. Mater., 2005, 17, 4318–4324.
19. M. Woodhouse and B. A. Parkinson, Chem. Mater., 2008, 20, 2495–2502.
20. M. Woodhouse and B. A. Parkinson, Chem. Soc. Rev., 2009, 38, 197–210.
21. T. Grewe, M. Meggouh and H. Tüysüz, Chem. – Asian J., 2016, 11, 22–42.
22. M. A. Fox and M. T. Dulay, Chem. Rev., 1993, 93, 341–357.
23. T. Mueller and E. Malic, NPJ 2D Mater. Appl., 2018, 2, 1–12.
24. S. Bai, C. Gao, J. Low and Y. Xiong, Nano Res., 2019, 12, 2031–2054.
25. K. Maeda and K. Domen, J. Phys. Chem. Lett., 2010, 1, 2655–2661.
26. G. Liu, H. G. Yang, J. Pan, Y. Q. Yang, G. Q. Lu and H. M. Cheng, Chem. Rev., 2014, 114, 9559–9612.
27. C. Di Valentin and G. Pacchioni, Acc. Chem. Res., 2014, 47, 3233–3241.
28. S. Tosoni, O. Lamiel-Garcia, D. F. Hevia, J. M. Doña and F. Illas, J. Phys. Chem. C, 2012, 116, 12738–12746.
29. F. De Angelis, C. Di Valentin, S. Fantacci, A. Vittadini and A. Selloni, Chem. Rev., 2014, 114, 9708–9753.
30. P. Erhart, K. Albe and A. Klein, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 205203.
31. H. V. Thang and G. Pacchioni, J. Phys. Chem. C, 2018, 122, 20880–20887.
32. D. Mora-Fonz, J. Buckeridge, A. J. Logsdail, D. O. Scanlon, A. A. Sokol, S. Woodley and C. R. A. Catlow, J. Phys. Chem. C, 2015, 119, 11598–11611.
33. F. Wang, C. Di Valentin and G. Pacchioni, J. Phys. Chem. C, 2011, 115, 8345–8353.
34. A. M. Márquez, J. J. Plata, Y. Ortega and J. F. Sanz, J. Phys. Chem. C, 2011, 115, 16970–16976.
35. H. Hamdi, E. K. H. Salje, P. Ghosez and E. Bousquet, Phys. Rev. B, 2016, 94, 245124.
36. X. Chen and S. S. Mao, Chem. Rev., 2007, 107, 2891–2959.
37. A. Kołodziejczak-Radzimska and T. Jesionowski, Materials, 2014, 7, 2833–2881.
38. C. M. Wu, S. Naseem, M. H. Chou, J. H. Wang and Y. Q. Jian, Front. Mater., 2019, 6, 49.
39. O. Lamiel-Garcia, K. C. Ko, J. Y. Lee, S. T. Bromley and F. Illas, J. Chem. Theory Comput., 2017, 13, 1785–1793.
40. O. Lamiel-Garcia, A. Cuko, M. Calatayud, F. Illas and S. T. Bromley, Nanoscale, 2017, 9, 1049–1058.
41. Á. Morales-García, A. Macià Escatllar, F. Illas and S. T. Bromley, Nanoscale, 2019, 11, 9032–9041.
42. F. Viñes, O. Lamiel-Garcia, F. Illas and S. T. Bromley, Nanoscale, 2017, 9, 10067–10074.
43. M. C. Per and D. M. Cleland, Nano Futures, 2020, 4, 032004.
44. L. González and R. Lindh, Quantum Chemistry and Dynamics of Excited States: Methods and Applications, Wiley, 2020.
45. B. M. Austin, D. Y. Zubarev and W. A. Lester Jr., Chem. Rev., 2012, 112, 263–288.
46. M. Ceriotti, C. Clementi and O. Anatole von Lilienfeld, Chem. Rev., 2021, 121, 9719–9721.
47. F. Spiegelman, N. Tarrat, J. Cuny, L. Dontot, E. Posenitskiy, C. Martí, A. Simon and M. Rapacioli, Adv. Phys. X, 2020, 5, 1710252.
48. K. Burke, J. Chem. Phys., 2012, 136, 150901.
49. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
50. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
51. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
52. M. Frisch, G. Trucks, H. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. J. Petersson and D. J. Fox, Gaussian 09, revision A.01, Gaussian, Inc., Wallingford, CT, 2009.
53. P. Blaha, K. Schwarz, F. Tran, R. Laskowski, G. K. Madsen and L. D. Marks, J. Chem. Phys., 2020, 152, 074101.
54. B. Delley, J. Chem. Phys., 1990, 92, 508–517.
55. B. Delley, Comput. Mater. Sci., 2000, 17, 122–126.
56. J. J. Mortensen, L. B. Hansen and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035109.
57. X. Gonze, B. Amadon, G. Antonius, F. Arnardi, L. Baguet, J. M. Beuken, J. Bieder, F. Bottin, J. Bouchet, E. Bousquet and N. Brouwer, Comput. Phys. Commun., 2020, 248, 107042.
58. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. Probert, K. Refson and M. C. Payne, Z. Kristallogr. Cryst. Mater., 2005, 220, 567–570.
59. T. D. Kuhne, et al. , J. Chem. Phys., 2020, 152, 194103.
60. F. Neese, The ORCA program system, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
61. F. Neese, Software update: the ORCA program system, version 4.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 8, e1327.
62. S. Smidstrup, et al. , J. Phys.: Condens. Matter, 2020, 32, 015901.
63. W. Moschkowitsch, K. Dhaka, S. Gonen, R. Attias, Y. Tsur, M. Caspary Toroker and L. Elbaz, ACS Catal., 2020, 10, 4879–4887.
64. E. Korkus Hamal and M. C. Toroker, Foundations of Molecular Modeling and Simulation: Select Papers from FOMMS 2018, 2021, pp. 1–23.
65. J. Xia, K. Dhaka, M. Volokh, G. Peng, Z. Wu, Y. Fu, M. C. Toroker, X. Wang and M. Shalom, Sustainable Energy Fuels, 2019, 3, 2006–2014.
66. M. B. Stevens, L. J. Enman, E. H. Korkus, J. Zaffran, C. D. Trang, J. Asbury, M. G. Kast, M. C. Toroker and S. W. Boettcher, Nano Res., 2019, 12, 2288–2295.
67. Z. L. Cai, M. J. Crossley, J. R. Reimers, R. Kobayashi and R. D. Amos, J. Phys. Chem., 2006, 110, 15624–15632.
68. Y. Ping, D. Rocca and G. Galli, Chem. Soc. Rev., 2013, 42, 2437–2469.
69. N. Yatom and M. C. Toroker, Catal. Lett., 2016, 146, 2009–2014.
70. N. Snir and M. C. Toroker, J. Chem. Theory Comput., 2020, 16, 4857–4864.
71. L. Hedin, J. Phys.: Condens. Matter, 1999, 11, R489.
72. A. Kazaryan, R. van Santen and E. J. Baerends, Phys. Chem. Chem. Phys., 2015, 17, 20308–20321.
73. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
74. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
75. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
76. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
77. R. Qin and N. Zheng, Chem, 2019, 5, 1935–1937.
78. X. Yan, L. Zhuang, Z. Zhu and X. Yao, Nanoscale, 2021, 13, 3327–3345.
79. G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360.
80. W. Yang and W. J. Mortier, J. Am. Chem. Soc., 1986, 108, 5708–5711.
81. P. Xiao, M. A. Sk, L. Thia, X. Ge, R. J. Lim, J. Y. Wang, K. H. Lim and X. Wang, Energy Environ. Sci., 2014, 7, 2624–2629.
82. Y. Gai, J. Li, S. S. Li, J. B. Xia and S. H. Wei, Phys. Rev. Lett., 2009, 102, 036402.
83. D. K. Kanan and E. A. Carter, J. Phys. Chem. C, 2012, 116, 9876–9887.
84. Y. Tan, P. Liu, L. Chen, W. Cong, Y. Ito, J. Han, X. Guo, Z. Tang, T. Fujita, A. Hirata and M. W. Chen, Adv. Mater., 2014, 26, 8023–8028.
85. X. Zou and Y. Zhang, Chem. Soc. Rev., 2015, 44, 5148–5180.
86. Z. W. Seh, J. Kibsgaard, C. F. Dickens, I. Chorkendorff, J. K. Nørskov and T. F. Jaramillo, Science, 2017, 355, eaad4998.
87. S. Anantharaj, S. R. Ede, K. Sakthikumar, K. Karthick, S. Mishra and S. Kundu, ACS Catal., 2016, 6, 8069–8097.
88. Y. J. Jang, T. A. Evans, B. Samanta, K. Zeng, M. C. Toroker and K. S. Choi, J. Mater. Chem. A, 2021, 9, 20453–20465.
89. J. L. C. Fajín, M. N. D. S. Cordeiro and J. R. B. Gomes, J. Phys. Chem. A, 2014, 118, 5832–5840.
90. J. L. Fajín, A. Bruix, M. N. Cordeiro, J. R. Gomes and F. Illas, J. Chem. Phys., 2012, 137, 034701.
91. A. A. Phatak, W. N. Delgass, F. H. Ribeiro and W. F. Schneider, J. Phys. Chem. C, 2009, 113, 7269–7276.
92. J. Kibsgaard, C. Tsai, K. Chan, J. D. Benck, J. K. Nørskov, F. Abild-Pedersen and T. F. Jaramillo, Energy Environ. Sci., 2015, 8, 3022–3029.
93. C. Tsai, K. Chan, J. K. Nørskov and F. Abild-Pedersen, Surf. Sci., 2015, 640, 133–140.
94. J. Rossmeisl, Z. W. Qu, H. Zhu, G. J. Kroes and J. K. Nørskov, J. Electroanal. Chem., 2007, 607, 83–89.
95. I. C. Man, H. Y. Su, F. Calle-Vallejo, H. A. Hansen, J. I. Martínez, N. G. Inoglu, J. Kitchin, T. F. Jaramillo, J. K. Nørskov and J. Rossmeisl, ChemCatChem, 2011, 3, 1159–1165.
96. D. Friebel, M. W. Louie, M. Bajdich, K. E. Sanwald, Y. Cai, A. M. Wise, M. J. Cheng, D. Sokaras, T. C. Weng, R. Alonso-Mori and R. C. Davis, J. Am. Chem. Soc., 2015, 137, 1305–1313.
97. M. Qiao, J. Liu, Y. Wang, Y. Li and Z. Chen, J. Am. Chem. Soc., 2018, 140, 12256–12262.
98. Y. Zhang, Y. Zhang, X. Li, J. Dai, F. Song, X. Cao, X. Lyu and J. C. Crittenden, ACS Omega, 2019, 4, 20142–20151.
99. Z. Luo, Z. Wang, J. Li, K. Yang and G. Zhou, Phys. Chem. Chem. Phys., 2020, 22, 11392–11399.
100. C. Wu, S. Xue, Z. Qin, M. Nazari, G. Yang, S. Yue, T. Tong, H. Ghasemi, F. C. R. Hernandez, S. Xue and D. Zhang, Appl. Catal., B, 2021, 282, 119557.
101. W. N. Zhao and Z. P. Liu, Chem. Sci., 2014, 5, 2256–2264.
102. S. Wei and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 8958–8981.
103. Y. Lee, H. Terashima, Y. Shimodaira, K. Teramura, M. Hara, H. Kobayashi, K. Domen and M. Yashima, J. Phys. Chem. C, 2007, 111, 1042–1048.
104. J. Deng, H. Li, S. Wang, D. Ding, M. Chen, C. Liu, Z. Tian, K. S. Novoselov, C. Ma, D. Deng and X. Bao, Nat. Commun., 2017, 8, 14430.
105. Y. Shimodaira, H. Kato, H. Kobayashi and A. Kudo, Bull. Chem. Soc. Jpn., 2007, 80, 885–893.
106. L. Wang, Q. Zhou, Z. Pu, Q. Zhang, X. Mu, H. Jing, S. Liu, C. Chen and S. Mu, Nano Energy, 2018, 53, 270–276.
107. F. Wang, C. Di Valentin and G. Pacchioni, J. Phys. Chem. C, 2012, 116, 8901–8909.
108. Y. Zheng, Y. Jiao, L. H. Li, T. Xing, Y. Chen, M. Jaroniec and S. Z. Qiao, ACS Nano, 2014, 8, 5290–5296.
109. Q. Liang, G. Brocks, X. Zhang and A. Bieberle-Hütter, J. Phys. Chem. C, 2019, 123, 26289–26298.
110. M. C. Toroker and E. A. Carter, J. Mater. Chem. A, 2013, 1, 2474–2484.
111. Y. Zheng, Y. Jiao, Y. Zhu, L. H. Li, Y. Han, Y. Chen, A. Du, M. Jaroniec and S. Z. Qiao, Nat. Commun., 2014, 5, 3783.
112. Y. Wang, T. Zhou, K. Jiang, P. Da, Z. Peng, J. Tang, B. Kong, W. B. Cai, Z. Yang and G. Zheng, Adv. Energy Mater., 2014, 4, 1400696.
113. R. Wu, J. Zhang, Y. Shi, D. Liu and B. Zhang, J. Am. Chem. Soc., 2015, 137, 6983–6986.
114. J. Du, T. Zhang, F. Cheng, W. Chu, Z. Wu and J. Chen, Inorg. Chem., 2014, 53, 9106–9114.
115. S. Peng, F. Gong, L. Li, D. Yu, D. Ji, T. Zhang, Z. Hu, Z. Zhang, S. Chou, Y. Du and S. Ramakrishna, J. Am. Chem. Soc., 2018, 140, 13644–13653.
116. J. T. Mefford, X. Rong, A. M. Abakumov, W. G. Hardin, S. Dai, A. M. Kolpak, K. P. Johnston and K. J. Stevenson, Nat. Commun., 2016, 7, 11053.
117. Y. Zhao, J. Zhang, W. Wu, X. Guo, P. Xiong, H. Liu and G. Wang, Nano Energy, 2018, 54, 129–137.
118. X. Zhang, P. Klaver, R. van Santen, M. C. M. van de Sanden and A. Bieberle-Hütter, J. Phys. Chem. C, 2016, 120, 18201–18208.
119. X. Zhang, C. Cao and A. Bieberle-Hütter, J. Phys. Chem. C, 2016, 120, 28694–28700.
120. X. Zhang, C. Cao and A. Bieberle-Hütter, Phys. Chem. Chem. Phys., 2017, 19, 31300–31305.
121. R. Kishore, X. Cao, X. Zhang and A. Bieberle-Hütter, Catal. Today, 2019, 321-322, 94–99.
122. K. George, X. Zhang and A. Bieberle-Hütter, J. Chem. Phys., 2019, 150, 041729.
123. J. Chen, Y. F. Li, P. Sit and A. Selloni, J. Am. Chem. Soc., 2013, 135, 18774–18777.
124. Á. Valdés, J. Brillet, M. Grätzel, H. Gudmundsdóttir, H. A. Hansen, H. Jónsson, P. Klüpfel, G. J. Kroes, F. Le Formal, I. C. Man, R. S. Martins, J. K. Nørskov, J. Rossmeisl, K. Sivula, A. Vojvodic and M. Zäch, Phys. Chem. Chem. Phys., 2012, 14, 49–70.
125. V. Viswanathan, K. L. Pickrahn, A. C. Luntz, S. F. Bent and J. K. Nørskov, Nano Lett., 2014, 14, 5853–5857.
126. P. Liao, M. C. Toroker and E. A. Carter, Nano Lett., 2011, 11, 1775–1781.
127. M. C. Toroker and E. A. Carter, J. Phys. Chem. C, 2012, 116, 17403–17413.
128. J. Xie, S. Li, X. Zhang, J. Zhang, R. Wang, H. Zhang, B. Pan and Y. Xie, Chem. Sci., 2014, 5, 4615–4620.
129. O. Neufeld and M. C. Toroker, J. Chem. Theory Comput., 2016, 12, 1572–1582.
130. R. Valero, Á. Morales-García and F. Illas, Phys. Chem. Chem. Phys., 2020, 22, 3017–3029.
131. M. Martynow, S. Kupfer, S. Rau and J. Guthmuller, Phys. Chem. Chem. Phys., 2019, 21, 9052–9060.
132. X. Liu, B. Jiang, Y. Liu, L. Liu, T. Xia, X. Zhang, C. Ye, Y. Yu and B. Wang, Coatings, 2020, 10, 1160.
133. Z. Ma, Z. Yi, J. Sun and K. Wu, J. Phys. Chem. C, 2012, 116, 25074–25080.
134. K. Chan and J. K. Nørskov, J. Phys. Chem. Lett., 2015, 6, 2663–2668.
135. H. Lin and D. G. Truhlar, Theor. Chem. Acc., 2007, 117, 185–199.
136. Y. Nam, L. Li, J. Y. Lee and O. V. Prezhdo, J. Phys. Chem. C, 2018, 122, 5201–5208.
137. D. Van Der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, GROMACS: Fast, flexible, and free, J. Comput. Chem., 2005, 26, 1701–1718.
138. K. Arifin, E. H. Majlan, W. R. Wan Daud and M. B. Kassim, Int. J. Hydrogen Energy, 2012, 37, 3066–3087.
139. L. Chong and M. Dutt, Appl. Surf. Sci., 2014, 323, 96–104.
140. S. Plimpton, J. Comput. Phys., 1995, 117, 1–19.
141. S. Riniker and W. F. van Gunsteren, J. Chem. Phys., 2011, 134, 084110.
142. V. Stevanović, S. Lany, D. S. Ginley, W. Tumas and A. Zunger, Phys. Chem. Chem. Phys., 2014, 16, 3706–3714.
143. Y. Wu, M. K. Y. Chan and G. Ceder, Phys. Rev. B, 2011, 83, 235301.
144. Y. Wu, P. Lazic, G. Hautier, K. Persson and G. Ceder, Energy Environ. Sci., 2013, 6, 157–168.
145. J. Cheng and M. Sprik, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 081406.
146. K. G. Reeves, D. Dambournet, C. Laberty-Robert, R. Vuilleumier and M. Salanne, RSC Adv., 2020, 10, 8982–8988.
147. R. Asahi, T. Morikawa, T. Ohwaki, K. Aoki and Y. Taga, Science, 2001, 293, 269–271.
148. Z. Zou, J. Ye, K. Sayama and H. Arakawa, Nature, 2001, 414, 625–627.
149. K. Koura and H. Matsumoto, Phys. Fluids A, 1991, 3, 2459–2465.
150. J. E. Jones, Proc. R. Soc. London, Ser. A, 1924, 106, 463–477.
151. S. Mushnoori, L. Chong and M. Dutt, Mater. Today: Proc., 2016, 3, 513–517.
152. A. V. Bandura and J. D. Kubicki, J. Phys. Chem. B, 2003, 107, 11072–11081.
153. W. N. Zhao and Z. P. Liu, Chem. Sci., 2014, 5, 2256–2264.
154. J. S. Murray and K. Sen, Molecular Electrostatic Potentials: Concepts and Applications, Elsevier, Amsterdam, NL, 1996.
155. J. Tersoff, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 6991–7000.
156. A. P. Sutton and J. Chen, Philos. Mag. Lett., 1990, 61, 139–146.
157. D. Biriukov, O. Kroutil and M. Předota, Phys. Chem. Chem. Phys., 2018, 20, 23954–23966.
158. O. Kroutil, Z. Chval, A. A. Skelton and M. Předota, J. Phys. Chem. C, 2015, 119, 9274–9286.
159. M. J. DelloStritto, J. D. Kubicki and J. O. Sofo, Langmuir, 2016, 32, 11353–11365.
160. K. J. Harmon, Y. Chen, E. J. Bylaska, J. G. Catalano, M. J. Bedzyk, J. H. Weare and P. Fenter, J. Phys. Chem. C, 2018, 122, 26934–26944.
161. J. N. Bracco, S. S. Lee, J. E. Stubbs, P. J. Eng, F. Heberling, P. Fenter and A. G. Stack, J. Phys. Chem. C, 2017, 121, 12236–12248.
162. A. YazdanYar, U. Aschauer and P. Bowen, Colloids Surf., B, 2018, 161, 563–577.
163. M. Matsui and M. Akaogi, Mol. Simul., 1991, 6, 239–244.
164. D. W. Kim, N. Enomoto, Z. E. Nakagawa and K. Kawamura, J. Am. Ceram. Soc., 1996, 79, 1095–1099.
165. D. R. Collins, W. Smith, N. M. Harrison and T. R. Forester, J. Mater. Chem. A, 1996, 6, 1385–1390.
166. P. Oliver, G. Watson, E. Kelsey and S. Parker, J. Mater. Chem., 1997, 7, 563–568.
167. D. G. Hetterscheid and J. N. Reek, Angew. Chem., Int. Ed., 2012, 51, 9740–9747.
168. J. J. Concepcion, J. W. Jurss, M. K. Brennaman, P. G. Hoertz, A. O. T. Patrocinio, N. Y. M. Iha, J. L. Templeton and T. J. Meyer, Acc. Chem. Res., 2009, 42, 1954–1965.
169. Y. Shao, J. M. de Ruiter, H. J. M. de Groot and F. Buda, J. Phys. Chem. C, 2019, 123, 21403–21414.
170. D. Frenkel and B. Smit, Understanding Molecular Simulation, Academic Press, San Diego, 2002.
171. J. A. Anta, Energy Environ. Sci., 2009, 2, 387–392.
172. J. Nelson and R. E. Chandler, Coord. Chem. Rev., 2004, 248, 1181–1194.
173. S. D. Baranovskii, Charge Transport in Disordered Solids with Applications in Electronics, Wiley, Weinheim, Germany, 2006.
174. J. Bisquert, Phys. Rev. Lett., 2003, 91, 010602.
175. S. D. Baranovskii, H. Cordes, F. Hensel and G. Leising, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 7934–7938.
176. M. Tachiya, J. Phys. Chem. A, 1993, 97, 5911–5916.
177. A. Cuetos and A. Patti, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 022302.
178. M. Ansari-Rad, J. A. Anta and J. Bisquert, J. Phys. Chem. C, 2013, 117, 16275–16289.
179. J. Nelson, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 15374–15380.
180. H. Scher and E. W. Montroll, Phys. Rev. B: Solid State, 1975, 12, 2455–2477.
181. J. Nelson, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 155209.
182. S. A. Haque, Y. Tachibana, R. L. Willis, J. E. Moser, M. Grätzel, D. R. Klug and J. R. Durrant, J. Phys. Chem. B, 2000, 104, 538–547.
183. A. V. Barzykin and M. Tachiya, J. Phys. Chem. B, 2002, 106, 4356–4363.
184. M. J. Cass, F. L. Qiu, A. B. Walker, A. C. Fisher and L. M. Peter, J. Phys. Chem. B, 2003, 107, 113–119.
185. J. A. Anta and V. Morales-Flórez, J. Phys. Chem. C, 2008, 112, 10287–10293.
186. J. P. Gonzalez-Vazquez, V. Morales-Flórez and J. A. Anta, J. Phys. Chem. Lett., 2012, 3, 386–393.
187. J. A. Anta, J. Nelson and N. Quirke, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 125324.
188. A. Petrozza, C. Groves and H. J. Snaith, J. Am. Chem. Soc., 2008, 130, 12912–12920.
189. J. A. Anta, I. Mora-Seró, T. Dittrich and J. Bisquert, Phys. Chem. Chem. Phys., 2008, 10, 4478–4485.
190. N. Kopidakis, E. A. Schiff, N. G. Park, J. van de Lagemaat and A. J. Frank, J. Phys. Chem. B, 2000, 104, 3930–3936.
191. J. van de Lagemaat and A. J. Frank, J. Phys. Chem. B, 2001, 105, 11194–11205.
192. J. A. Anta, I. Mora-Seró, T. Dittrich and J. Bisquert, J. Phys. Chem. C, 2007, 111, 13997–14000.
193. H. Ma, W. Ma, J. F. Chen, X. Y. Liu, Y. Y. Peng, Z. Y. Yang, H. Tian and Y. T. Long, J. Am. Chem. Soc., 2018, 140, 5272–5279.
194. M. Amft, L. E. Walle, D. Ragazzon, A. Borg, P. Uvdal, N. V. Skorodumova and A. Sandell, J. Phys. Chem. C, 2013, 117, 17078–17083.
195. S. Grieshammer, B. O. H. Grope, J. Koettgen and M. Martin, Phys. Chem. Chem. Phys., 2014, 16, 9974–9986.
196. J. Kullgren, M. J. Wolf, P. D. Mitev, K. Hermansson and W. J. Briels, J. Phys. Chem. C, 2017, 121, 15127–15134.
197. L. Li, J. T. Muckerman, M. S. Hybertsen and P. B. Allen, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 134202.
198. M. Moqadam, A. Lervik, E. Riccardi, V. Venkatraman, B. K. Alsberg and T. S. van Erp, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E4569–E4576.
199. E. Riccardi, O. Dahlen and T. S. van Erp, J. Phys. Chem. Lett., 2017, 8, 4456–4460.
200. C. Hareli and M. C. Toroker, J. Chem. Theory Comput., 2018, 14, 2380–2385.
201. S. Kerisit and K. M. Rosso, J. Chem. Phys., 2007, 127, 124706.
202. V. Sinha, D. Sun, E. J. Meijer, T. J. H. Vlugt and A. Bieberle-Hütter, Faraday Discuss., 2021, 229, 89–107.
203. E. V. Groesen and J. Molenaar, Continuum Modeling in the Physical Sciences, Society for Industrial and Applied Mathematics, Philadelphia, 2007.
204. W. Shyy, Computational Modeling for Fluid Flow and Interfacial Transport, Dover Publications, Mineola, NY, 1994.
205. S. P. Hoogendoorn and P. H. L. Bovy, Transp. Res. Part B: Methodol., 2000, 34, 123–146.
206. H. W. Ho and S. C. Wong, J. Transp. Syst. Eng. Inf. Technol., 2006, 6, 53–68.
207. A. Mitterdorfer and L. J. Gauckler, Solid State Ionics, 1999, 117, 203–217.
208. A. Mitterdorfer and L. J. Gauckler, Solid State Ionics, 1999, 117, 187–202.
209. A. Bieberle and L. J. Gauckler, Solid State Ionics, 2002, 146, 23–41.
210. K. George, M. van Berkel, X. Zhang, R. Sinha and A. Bieberle-Hütter, J. Phys. Chem. C, 2019, 123, 9981–9992.
211. K. George, T. Khachatrjan, M. van Berkel, V. Sinha and A. Bieberle-Hütter, ACS Catal., 2020, 10, 14649–14660.
212. Y. Ping, R. Sundararaman and W. A. Goddard III, Phys. Chem. Chem. Phys., 2015, 17, 30499–30509.
213. S. Haussener, C. Xiang, J. M. Spurgeon, S. Ardo, N. S. Lewis and A. Z. Weber, Energy Environ. Sci., 2012, 5, 9922–9935.
214. S. Haussener, Y. Gaudy and S. Tembhurne, in Advances in Photoelectrochemical Water Splitting: Theory, Experiment and Systems Analysis, ed. S. D. Tilley, S. Lany and R. van de Krol, The Royal Society of Chemistry, London, UK, 2018, pp. 239–263.
215. M. R. Singh, S. Haussener and A. Z. Weber, in Integrated Solar Fuel Generators, ed. I. D. Sharp, H. A. Atwater and H. J. Lewerenz, The Royal Society of Chemistry, London, UK, 2019, pp. 500–536.
216. X. Zhang and A. Bieberle-Hütter, ChemSusChem, 2016, 9, 1223–1242.
217. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
218. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
219. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502.
220. R. Sundararaman, K. A. Schwarz, K. Letchworth-Weaver and T. A. Arias, J. Chem. Phys., 2015, 142, 054102.
221. J. A. Gauthier, S. Ringe, C. F. Dickens, A. J. Garza, A. T. Bell, M. Head-Gordon, J. K. Nørskov and K. Chan, ACS Catal., 2019, 9, 920–931.
222. S. Ringe, H. Oberhofer, C. Hille, S. Matera and K. Reuter, J. Chem. Theory Comput., 2016, 12, 4052–4066.
223. K. Mathew and R. G. Hennig, 2016, arXiv:1601.03346.
224. Y. H. Fang, G. F. Wei and Z. P. Liu, Catal. Today, 2013, 202, 98–104.
225. R. Sundararaman and K. Schwarz, J. Chem. Phys., 2017, 146, 084111.
226. O. Andreussi, I. Dabo and N. Marzari, J. Chem. Phys., 2012, 136, 064102.
227. Y. Ping, R. J. Nielsen and W. A. Goddard, J. Am. Chem. Soc., 2017, 139, 149–155.
228. J. D. Goodpaster, A. T. Bell and M. Head-Gordon, J. Phys. Chem. Lett., 2016, 7, 1471–1477.
229. S. N. Steinmann, P. Sautet and C. Michel, Phys. Chem. Chem. Phys., 2016, 18, 31850–31861.
230. S. N. Steinmann, C. Michel, R. Schwiedernoch and P. Sautet, Phys. Chem. Chem. Phys., 2015, 17, 13949–13963.
231. C. A. Mesa, L. Francàs, K. R. Yang, P. Garrido-Barros, E. Pastor, Y. Ma, A. Kafizas, T. E. Rosser, M. T. Mayer, E. Reisner, M. Grätzel, V. S. Batista and J. R. Durrant, Nat. Chem., 2020, 12, 82–89.
232. A. Bieberle-Hütter, A. C. Bronneberg, K. George and M. C. M. van de Sanden, J. Phys. D: Appl. Phys., 2021, 54, 133001.
233. I. A. W. Filot, Introduction to Microkinetic Modeling, Technische Universiteit Eindhoven, Eindhoven, NL, 2018.
234. G. F. Franklin, J. D. Powell, A. Emami-Naeini and H. S. Sanjay, Feedback Control of Dynamic Systems, Pearson, London, 2015.
235. H. K. Khalil and J. W. Grizzle, Nonlinear Systems, Prentice hall, Upper Saddle River, NJ, 2002.
236. M. Vogler, A. Bieberle-Hütter, L. Gauckler, J. R. Warnatz and W. G. Bessler, J. Electrochem. Soc., 2009, 156, B663.
237. C. F. Dickens, C. Kirk and J. K. Nørskov, J. Phys. Chem. C, 2019, 123, 18960–18977.
238. O. Zandi and T. W. Hamann, Nat. Chem., 2016, 8, 778–783.
239. Y. Zhang, H. Zhang, A. Liu, C. Chen, W. Song and J. Zhao, J. Am. Chem. Soc., 2018, 140, 3264–3269.
240. R. Bove and S. Ubertini, J. Power Sources, 2006, 159, 543–559.
241. J. Yuan and B. Sundén, Int. J. Heat Mass Transfer, 2013, 58, 441–456.
242. J. Xu, Y. Ren and J. Li, J. Biomol. Struct. Dyn., 2013, 31, 779–787.
243. W. K. Tao and M. Moncrieff, Rev. Geophys., 2009, 47, 309–313.
244. C. Hellmich and D. Katti, MRS Bull., 2015, 40, 309–313.
245. M. F. Horstmeyer, Integrated Computational Materials Engineering (ICME) for Metals: Using Multiscale Modeling to Invigorate Engineering Design with Science, John Wiley & Sons, New Jersey, US, 2012.
246. M. Maestri, D. G. Vlachos, A. Beretta, G. Groppi and E. Tronconi, AIChE J., 2009, 55, 993–1008.
247. T. Bera, J. W. Thybaut and G. B. Marin, ACS Catal., 2012, 2, 1305–1318.
248. H. Stotz, L. Maier and O. Deutschmann, Top. Catal., 2017, 60, 83–109.
249. A. B. Mhadeshwar and D. G. Vlachos, J. Phys. Chem. B, 2005, 109, 16819–16835.
250. S. Liu, Z. J. Zhao, C. Yang, S. Zha, K. M. Neyman, F. Studt and J. Gong, ACS Catal., 2019, 9, 5011–5018.
251. H. Barron, G. Opletal, R. D. Tilley and A. S. Barnard, Catal. Sci. Technol., 2016, 6, 144–151.
252. J. Zhu, M. L. Yang, Y. Yu, Y. A. Zhu, Z. J. Sui, X. G. Zhou, A. Holmen and D. Chen, ACS Catal., 2015, 5, 6310–6319.
253. J. Yang, V. Frøseth, D. Chen and A. Holmen, Surf. Sci., 2016, 648, 67–73.
254. J. E. Mueller, D. Fantauzzi and T. Jacob, Multiscale Modeling of Electrochemical Systems, Wiley-VCH, Weinheim, 2013.
255. A. V. Akimov, A. J. Neukirch and O. V. Prezhdo, Chem. Rev., 2013, 113, 4496–4565.
256. A. C. T. van Duin, S. Dasgupta, F. Lorant and W. A. Goddard, J. Phys. Chem. A, 2001, 105, 9396–9409.
257. S. Y. Kim, N. Kumar, P. Persson, J. Sofo, A. C. T. van Duin and J. D. Kubicki, Langmuir, 2013, 29, 7838–7846.
258. M. Aryanpour, A. C. T. van Duin and J. D. Kubicki, J. Phys. Chem. A, 2010, 114, 6298–6307.
259. M. F. Russo, R. Li, M. Mench and A. C. T. van Duin, Int. J. Hydrogen Energy, 2011, 36, 5828–5835.
260. D. Raymand, A. C. T. van Duin, W. A. Goddard, K. Hermansson and D. Spångberg, J. Phys. Chem. C, 2011, 115, 8573–8579.
261. J. Yu, M. L. Sushko, S. Kerisit, K. M. Rosso and J. Liu, J. Phys. Chem. Lett., 2012, 3, 2076–2081.
262. V. Viswanathan, H. A. Hansen, J. Rossmeisl, T. F. Jaramillo, H. Pitsch and J. K. Nørskov, J. Phys. Chem. C, 2012, 116, 4698–4704.
263. S. Saerens, M. K. Sabbe, V. V. Galvita, E. A. Redekop, M. F. Reyniers and G. B. Marin, ACS Catal., 2017, 7, 7495–7508.
264. M. Huš, M. Grilc, A. Pavlišič, B. Likozar and A. Hellman, Catal. Today, 2019, 338, 128–140.
265. M. Maestri, Chem. Commun., 2017, 53, 10244–10254.
266. M. Karplus, M. Levitt and A. Warshel, Angew. Chem., Int. Ed., 2013, 52, 11972.
267. J. Klimeš, M. Kaltak and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 075125.
268. M. Kaltak, J. Klimeš and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 054115.
269. F. R. Manby, M. Stella, J. D. Goodpaster and T. F. Miller, J. Chem. Theory Comput., 2012, 8, 2564–2568.
270. F. Libisch, C. Huang and E. A. Carter, Acc. Chem. Res., 2014, 47, 2768–2775.
271. G. Knizia and G. K. Chan, Phys. Rev. Lett., 2012, 109, 186404.
272. T. A. Wesolowski, S. Shedge and X. Zhou, Chem. Rev., 2015, 115, 5891–5928.
273. C. Huang, M. Pavone and E. A. Carter, J. Chem. Phys., 2011, 134, 154110.
274. J. Cheng, F. Libisch, K. Yu, M. Chen, J. M. Dieterich and E. A. Carter, J. Chem. Theory Comput., 2017, 13, 1067–1080.
275. J. Cheng, K. Yu, F. Libisch, J. M. Dieterich and E. A. Carter, J. Chem. Theory Comput., 2017, 13, 1081–1093.
276. I. Bulik, G. Scuseria and J. Dukelsky, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 89, 035140.
277. F. Libisch, M. Marsman, J. Burgdörfer and G. Kresse, J. Chem. Phys., 2017, 147, 034110.
278. J. D. Goodpaster, T. A. Barnes, F. R. Manby and T. F. Miller, J. Chem. Phys., 2014, 140, 18A507.
279. K. Reuter, in Modeling Heterogeneous Catalytic Reactions: From the Molecular Process to the Technical System, ed. O. Deutschmann, Wiley-VCH, Weinheim, Germany, 2009.
280. B. Temel, H. Meskine, K. Reuter, M. Scheffler and H. Metiu, J. Chem. Phys., 2007, 126, 204711.
281. M. Stamatakis and D. G. Vlachos, ACS Catal., 2012, 2, 2648–2663.
282. M. Maestri, D. G. Vlachos, A. Beretta, G. Groppi and E. Tronconi, J. Catal., 2008, 259, 211–222.
283. M. M. Melander, M. J. Kuisma, T. E. K. Christensen and K. Honkala, J. Chem. Phys., 2018, 150, 041706.
284. R. Bird, W. Stewart and E. Lightfoot, Transport Phenomena, John Willey & Sons, Inc, New York/Chichester, 2002.
285. T. Maffei, G. Gentile, S. Rebughini, M. Bracconi, F. Manelli, S. Lipp, A. Cuoci and M. Maestri, Chem. Eng. J., 2016, 283, 1392–1404.
286. M. Jun, K. Smith and P. Graf, J. Power Sources, 2015, 273, 1226–1236.
287. F. Grasser and A. C. Rufer, Power Conversion Conference—Nagoya, IEEE, Nagoya, Japan, 2007, pp. 441–447.
288. S. V. Puranik, A. Keyhani and F. Khorrami, IEEE Trans. Energy Convers., 2010, 25, 804–813.
289. F. J. Keil, Comput. Math. Appl., 2013, 65, 1674–1697.
290. M. Maestri and A. Cuoci, Chem. Eng. Sci., 2013, 96, 106–117.
291. S. Matera and K. Reuter, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 085446.
292. S. Matera, M. Maestri, A. Cuoci and K. Reuter, ACS Catal., 2014, 4, 4081–4092.
293. M. Salciccioli, M. Stamatakis, S. Caratzoulas and D. G. Vlachos, Chem. Eng. Sci., 2011, 66, 4319–4355.
294. J. E. Sutton and D. G. Vlachos, Chem. Eng. Sci., 2015, 121, 190–199.
295. M. Maestri, D. Livio, A. Beretta and G. Groppi, Ind. Eng. Chem. Res., 2014, 53, 10914–10928.
296. M. Alber, A. Buganza Tepole, W. R. Cannon, S. De, S. Dura-Bernal, K. Garikipati, G. Karniadakis, W. W. Lytton, P. Perdikaris, L. Petzold and E. Kuhl, NPJ Dig. Med., 2019, 2, 115.
297. C. Draxl and M. Scheffler, MRS Bull., 2018, 43, 676–682.
298. C. Draxl and M. Scheffler, J. Phys.: Mater., 2019, 2, 036001.
299. A. V. Akimov and O. V. Prezhdo, J. Chem. Theory Comput., 2013, 9, 4959–4972.
300. S. Pal, D. J. Trivedi, A. V. Akimov, B. Aradi, T. Frauenheim and O. V. Prezhdo, J. Chem. Theory Comput., 2016, 12, 1436–1448.
301. Y. Wei, M. V. Tokina, A. V. Benderskii, Z. Zhou, R. Long and O. V. Prezhdo, J. Chem. Phys., 2020, 153, 044706.
302. Z. Zhou, J. Liu, R. Long, L. Li, L. Guo and O. V. Prezhdo, J. Am. Chem. Soc., 2017, 139, 6707–6717.

---